Trade-Off Analysis of Drive Dynamics Considering Speed and Current Loops
Abstract
1. Introduction
1.1. Motivation
1.2. Novelty and Contributions
- Establishing links between performance indicators of different kinds: electric, electronic, and mechanic.
- Tackling the concurrent tuning of the inner and outer loops of a variable speed drive.
- Providing evidence for the existence of complex relationships between mechanical and electrical indicators.
- Highlighting the importance of the mechanical operating point in the analysis.
2. Background on FSMPC Drive Control
2.1. Control Objectives
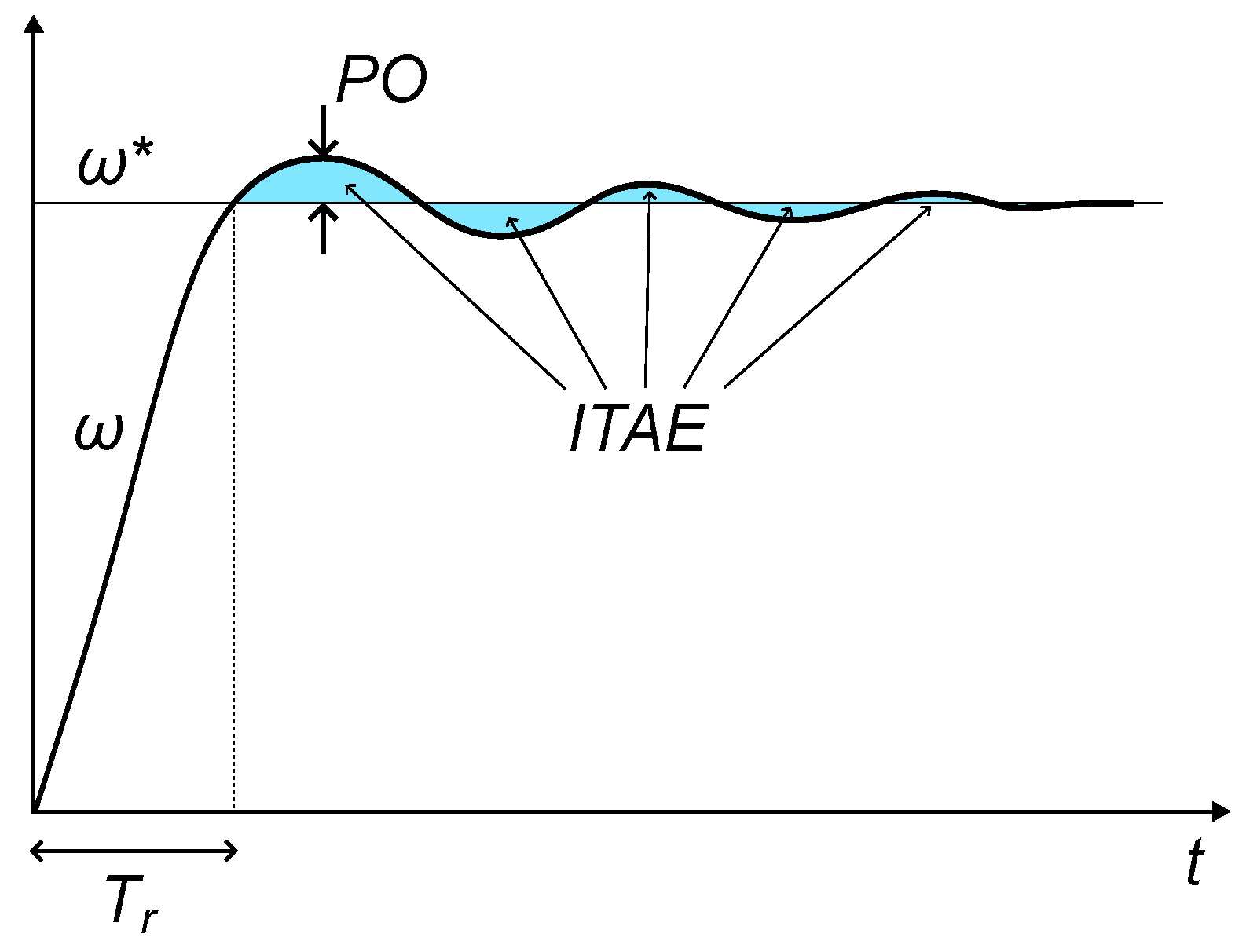
- Overshoot in mechanical speed (), Equation (8). Most applications tolerate a certain amount of overshoot, nevertheless a low value is sought after in most cases.
- Rise time of mechanical speed (), Equation (9). In over-damped systems, it is measured as the time needed to cover 90 % of the reference step. In under-damped systems, it is the time needed to reach the new reference. A low value is required in most applications.
- Integral Time Absolute Error () is a measure of tracking error that penalizes long-lasting errors more than initial transient ones as defined in Equation (10).
- Torque ripple (), Equation (11). This variable has an electro-magnetic origin as the produced torque and is directly defined by stator currents. At the same time, with torque as the driving force of the motor, torque ripple has an effect on speed. In fact, torque ripple can cause mechanical stress in the axis and so must be reduced.
- Harmonic content (), Equation (12) is an electrical variable that measures how much inefficiency is due to subspace content. The factor is used in the CF as a means to reduce currents.
- Average switching frequency (), Equation (13) is a measure of how often the VSI is changing the state of its switches. It must be kept within appropriate values depending on the VSI technology. The factor is introduced in the cost function precisely to reduce commutation frequency.
2.2. Cost Function Tuning
2.3. Experimental Setup
3. Trade-Off Analysis
3.1. Methodology
3.1.1. Research Design
3.1.2. Data Collection
- The performance indicators were then computed using (8)–(13) on the measured variables.
- The parameters of the PI and FSMPC were explored considering many different combinations of the WF of the CF and of the parameters of the PI.
- Performance maps were derived for the indicators as a function of the control parameters.
- The maps were then analyzed to draw conclusions that are valid for all possible tunings.
3.1.3. Analysis Method
3.2. Analysis
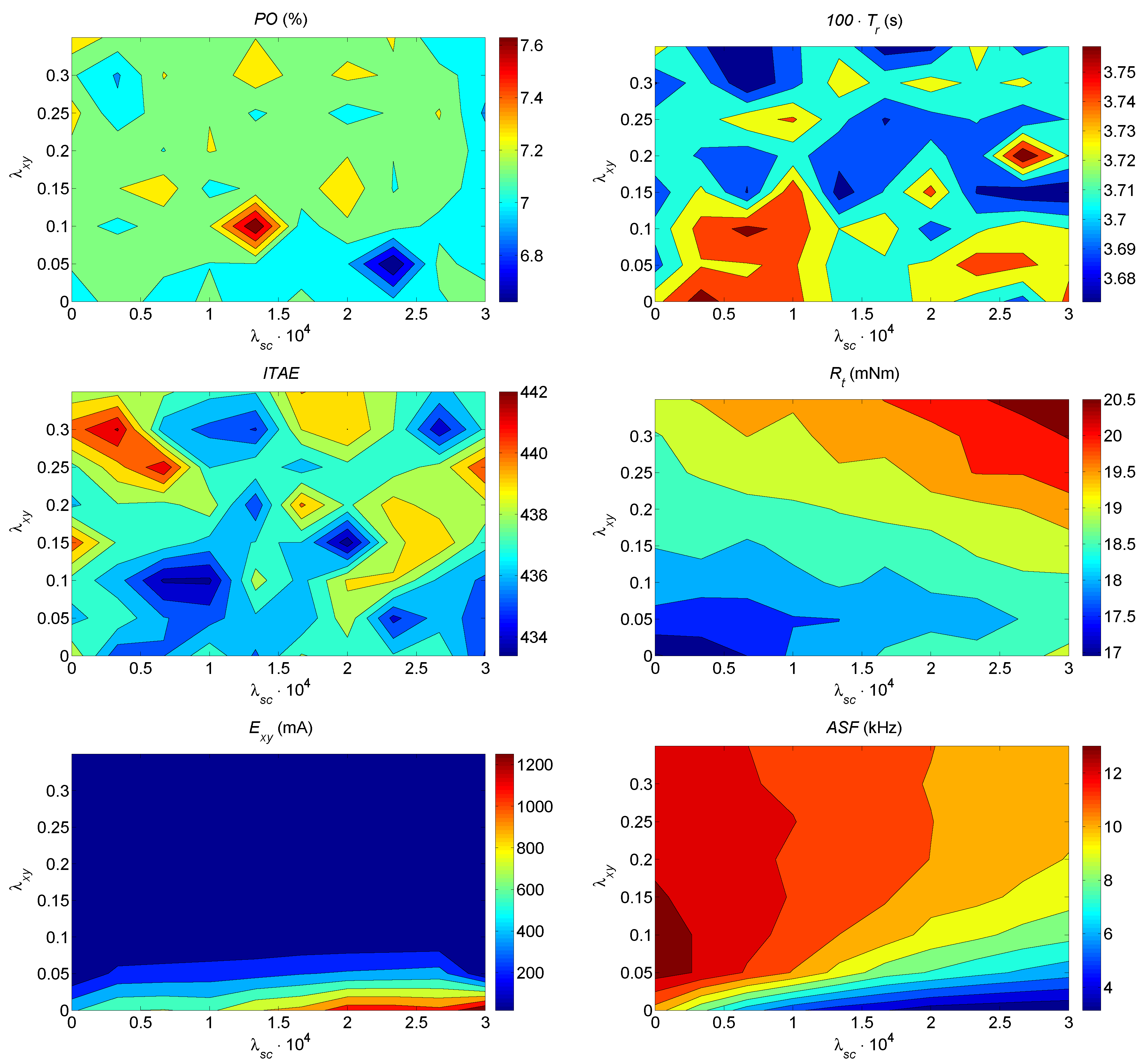
- The relationship between performance indices and controller parameters is non-linear. This is clearly seen for all performance indices as the contours are not straight lines.
- Minimizing all performance indices at once is not possible. This is clearly seen when comparing the values of and which have almost opposite behaviors. The , combinations that make low are around . However, for those parameters the value of is high. Similar trade-offs can be found for other combinations of performance indices for instance ASF and PO.
- Variables of different kinds are linked. This can be seen for instance considering values of and . The first variable is of the mechanical type, the second is of the electronic type affecting the power converter. The zone of low is the upper left corner, whereas the takes low values for the lower right corner. Similarly, connections between and and between and are clearly seen.
- From the map, it follows a clear dependence of on PI tuning. This means that hard constraints in cannot be satisfied independently of the outer PI configuration. This is an important fact that has not been previously reported. Recall that must be maintained below limits for risk of thermal damage to the power converter.
- The WF of the CF ( and ) cannot be set independently of each other. This is clearly seen in the maps of both and . For instance, a change in not only affects but also . The same happens with .
- The WF of the CF has a more noticeable effect on electrical/electronic variables ( and ) as expected; however, it also affects mechanical variables as can be clearly seen on the performance maps. This observation has not been reported before. The implications are of importance as this fact makes the tuning of the drive more challenging.
- It is interesting to see that the performance indicator acts as a link between purely mechanical variables (, , ) and electrical/electronic ones. This is also an interesting observation since most papers dealing with PI tuning in IFOC-like structures focus on mechanical variables alone. Conversely, papers dealing with converters do pay attention to but fail to connect it to mechanical variables.
3.3. Relevance for Tuning
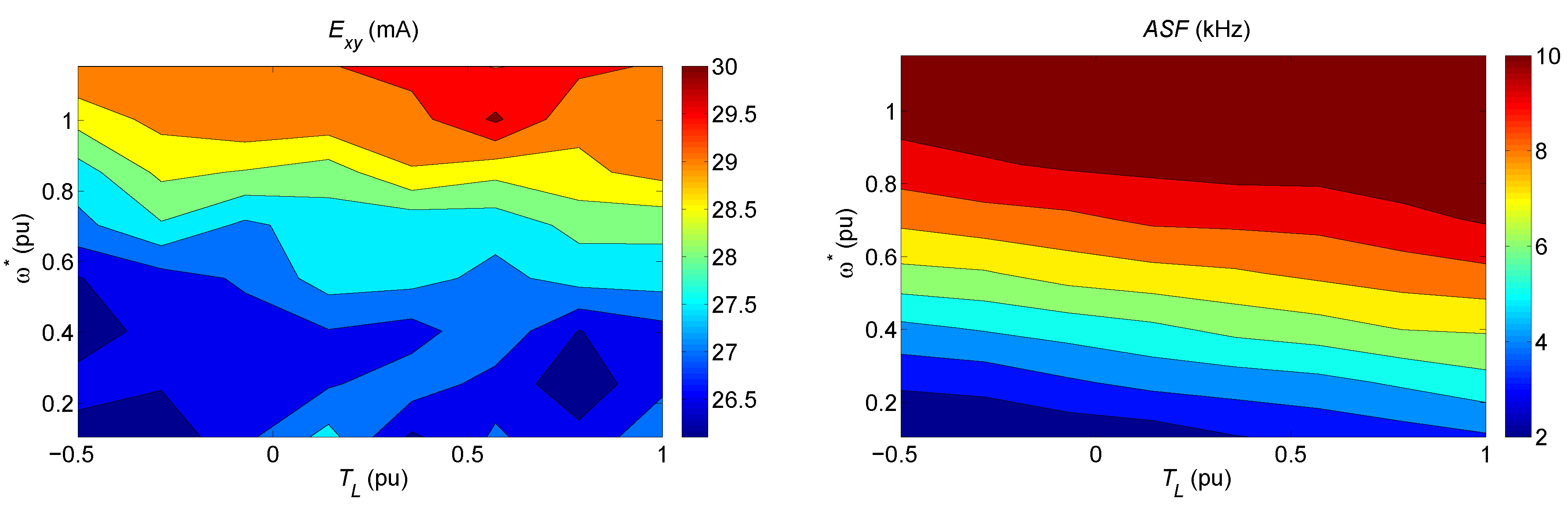
3.4. Dependence on the Operating Point
4. Discussion
- The links between variables of different kinds (mechanical, electrical, electronic) have been established thanks to the analysis of the performance maps. As a result, trade-offs appear involving different performance indicators of different types. The analysis has been made using maps for the indicators covering a wide range of tuning possibilities. The implication of this is that tuning alone cannot improve all performance indicators once the Pareto front has been reached. This should be taken into account when reporting improvements in the field.
- The concurrent tuning of inner (FSMPC) and outer (PI) loops in the drive is shown as an inevitable conclusion. Again, this has not yet appeared in the literature. In this regard, the present study presents a future research direction. In particular, the torque ripple appears as the main reason why both loops are linked. This can be seen in the performance maps. The implications of this are important as typical tuning does not consider both loops concurrently. This points in another direction for future research.
- The trade-off analysis shows that the usual practice of comparing one controller with another in a few scenarios is not thorough. The results shown here prompt a more complete assessment. Maps for different performance indicators should be provided. This observation should exist when reporting new controllers.
- The existence of complex relationships between mechanical and electrical indicators is a drawback for FSMPC because it makes tuning more complex than the case using PWM or any other modulation scheme where the switching frequency is constant. Whereas past works have deemed the tuning of FSMPC to be difficult, this analysis shows why.
- The operating point (in mechanical terms) has also been shown to influence electrical variables. Again, this fact is more often than not, not mentioned in the literature. Yet, it is of great importance for drives that must operate with different speeds and/or loads. The observation also points out a future line of research where the tuning is made dependent on the operating point.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASF | Average Switching Frequency |
| CF | Cost Function |
| DSP | Digital Signal Processor |
| FS | Finite State |
| IFOC | Indirect Field Oriented Control |
| IM | Induction Machine |
| ITAE | integral of time-weighted absolute error |
| MPC | Model Predictive Control |
| PI | Proportional Integral |
| PO | Percentage Overshoot |
| PID | Proportional Integral Derivative |
| PWM | Pulse Width Modulation |
| VSI | Voltage Source Inverter |
| WF | Weighting Factor |
References
- Lim, C.S.; Levi, E.; Jones, M.; Rahim, N.; Hew, W.P. A Comparative Study of Synchronous Current Control Schemes Based on FCS-MPC and PI-PWM for a Two-Motor Three-Phase Drive. Ind. Electron. Trans. 2014, 61, 3867–3878. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Zoric, I.; Duran, M.J.; Levi, E. Constrained model predictive control in nine-phase induction motor drives. IEEE Trans. Energy Convers. 2019, 34, 1881–1889. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Yang, G.; Li, S.; Deng, R. Harmonic currents injection strategy with optimal air gap flux distribution for multiphase induction machine. IEEE Trans. Power Electron. 2020, 36, 1054–1064. [Google Scholar] [CrossRef]
- García Entrambasaguas, P.; González-Prieto, I.; Durán, M.; Bermúdez, M.; Barrero, F. Fault Tolerance in Direct Torque Control with Virtual Voltage Vectors. Rev. Iberoam. Autom. Inform. Ind. 2019, 16, 56–65. [Google Scholar] [CrossRef]
- Arahal, M.R.; Barrero, F.; Satué, M.G.; Bermudez, M. Fast Finite-State Predictive Current Control of Electric Drives. IEEE Access 2023, 11, 12821–12828. [Google Scholar] [CrossRef]
- Peng, J.; Yao, M. Overview of predictive control technology for permanent magnet synchronous motor systems. Appl. Sci. 2023, 13, 6255. [Google Scholar] [CrossRef]
- Liu, C.; Luo, Y. Overview of advanced control strategies for electric machines. Chin. J. Electr. Eng. 2017, 3, 53–61. [Google Scholar]
- González, O.; Ayala, M.; Romero, C.; Rodas, J.; Gregor, R.; Delorme, L.; González-Prieto, I.; Durán, M.J.; Rivera, M. Comparative Assessment of Model Predictive Current Control Strategies applied to Six-Phase Induction Machines. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 1037–1043. [Google Scholar]
- Arahal, M.R.; Barrero, F.; Duran, M.J.; Ortega, M.G.; Martin, C. Trade-offs analysis in predictive current control of multi-phase induction machines. Control. Eng. Pract. 2018, 81, 105–113. [Google Scholar] [CrossRef]
- Fretes, H.; Rodas, J.; Doval-Gandoy, J.; Gomez, V.; Gomez, N.; Novak, M.; Rodriguez, J.; Dragičević, T. Pareto Optimal Weighting Factor Design of Predictive Current Controller of a Six-Phase Induction Machine based on Particle Swarm Optimization Algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 207–219. [Google Scholar] [CrossRef]
- Arahal, M.R.; Kowal, A.; Barrero, F.; Castilla, M. Cost function optimization for multi-phase induction machines predictive control. Rev. Iberoam. De Autom. E Inform. Ind. 2019, 16, 48–55. [Google Scholar] [CrossRef]
- Bakeer, A.; Alhasheem, M.; Peyghami, S. Efficient fixed-switching modulated finite control set-model predictive control based on artificial neural networks. Appl. Sci. 2022, 12, 3134. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, Y. A low-complexity double vector model predictive current control for permanent magnet synchronous motors. Energies 2023, 17, 147. [Google Scholar] [CrossRef]
- Yu, B.; Song, W.; Guo, Y.; Saeed, M.S. A finite control set model predictive control for five-phase PMSMs with improved DC-link utilization. IEEE Trans. Power Electron. 2021, 37, 3297–3307. [Google Scholar] [CrossRef]
- Makhamreh, H.; Trabelsi, M.; Kükrer, O.; Abu-Rub, H. A lyapunov-based model predictive control design with reduced sensors for a PUC7 rectifier. IEEE Trans. Ind. Electron. 2020, 68, 1139–1147. [Google Scholar] [CrossRef]
- Arshad, M.; Raja, M.M.; Zhao, Q. Neutral Point Voltage Balancing Using MOPSO based Weighting Factor Tuning for FCS-MPTC of Three Level T-Type VSI Fed IM Drive. IFAC-PapersOnLine 2023, 56, 435–440. [Google Scholar] [CrossRef]
- Penthala, T.; Kaliaperumal, S. Predictive control of induction motors using cascaded artificial neural network. Electr. Eng. 2024, 106, 2985–3000. [Google Scholar] [CrossRef]
- Dragičević, T.; Novak, M. Weighting factor design in model predictive control of power electronic converters: An artificial neural network approach. IEEE Trans. Ind. Electron. 2018, 66, 8870–8880. [Google Scholar] [CrossRef]
- Arahal, M.R.; Satué, M.G.; Barrero, F.; Ortega, M.G. Adaptive Cost Function FCSMPC for 6-Phase IMs. Energies 2021, 14, 5222. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, H.; Zhang, W.; Jiang, J. Ripple Attenuation for Induction Motor Finite Control Set Model Predictive Torque Control Using Novel Fuzzy Adaptive Techniques. Processes 2021, 9, 710. [Google Scholar] [CrossRef]
- Rodas, J.; Gonzalez-Prieto, I.; Kali, Y.; Saad, M.; Doval-Gandoy, J. Recent advances in model predictive and sliding mode current control techniques of multiphase induction machines. Front. Energy Res. 2021, 9, 729034. [Google Scholar] [CrossRef]
- Saghafinia, A.; Ping, H.W. High performance induction motor drive using fuzzy self-tuning hybrid fuzzy controller. In Proceedings of the 2010 IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia, 29 November–1 December 2010; pp. 468–473. [Google Scholar]
- Lotfi, C.; Youcef, Z.; Marwa, A.; Schulte, H.; Riad, B.; El-Arkam, M. Optimization of a Speed Controller of a DFIM with Metaheuristic Algorithms. Eng. Proc. 2023, 29, 13. [Google Scholar] [CrossRef]
- Martínez-Luzuriaga, P.N.; Reynoso-Meza, G. Influence of hyper-parameters in algorithms based on Differential Evolution for the adjustment of PID-type controllers in SISO processes through mono and multi-objective optimisation. Rev. Iberoam. De Autom. E Inform. Ind. 2023, 20, 44–55. [Google Scholar] [CrossRef]
- Muñoz Palomeque, E.; Sierra-García, J.E.; Santos, M. Intelligent control techniques for maximum power point tracking in wind turbines. Rev. Iberoam. De Autom. E Inform. Ind. 2024, 21, 193–204. [Google Scholar] [CrossRef]
- Yin, Z.; Zhao, H. Overshoot Reduction Inspired Recurrent RBF Neural Network Controller Design for PMSM. In Proceedings of the 2023 IEEE 32nd International Symposium on Industrial Electronics (ISIE), Helsinki, Finland, 19–21 June 2023; pp. 1–6. [Google Scholar]
- Abdel-Moneim, M.G.; Abdel-Azim, W.E.; Abdel-Khalik, A.S.; Hamed, M.S.; Ahmed, S. Model Predictive Current Control of Nine-Switch Inverter-Fed Six-Phase Induction Motor Drives Under Healthy and Fault Scenarios. IEEE Trans. Transp. Electrif. 2024. [Google Scholar] [CrossRef]
- Davari, S.A.; Nekoukar, V.; Azadi, S.; Flores-Bahamonde, F.; Garcia, C.; Rodriguez, J. Discrete Optimization of Weighting Factor in Model Predictive Control of Induction Motor. IEEE Open J. Ind. Electron. Soc. 2023, 4, 573–582. [Google Scholar] [CrossRef]
- Saberi, S.; Rezaie, B. Robust adaptive direct speed control of PMSG-based airborne wind energy system using FCS-MPC method. ISA Trans. 2022, 131, 43–60. [Google Scholar] [CrossRef]
- Colodro, F.; Mora, J.; Barrero, F.; Arahal, M.; Martinez-Heredia, J. Analysis and simulation of a novel speed estimation method based on oversampling and noise shaping techniques. Results Eng. 2024, 21, 101670. [Google Scholar] [CrossRef]
- Chen, L.; Chen, G.; Li, P.; Lopes, A.M.; Machado, J.T.; Xu, S. A variable-order fractional proportional-integral controller and its application to a permanent magnet synchronous motor. Alex. Eng. J. 2020, 59, 3247–3254. [Google Scholar] [CrossRef]
- Arahal, M.R.; Martín, C.; Kowal, A.; Castilla, M.; Barrero, F. Cost function optimization for predictive control of a five-phase IM drive. Optim. Control Appl. Methods 2020, 41, 84–93. [Google Scholar] [CrossRef]
- Zerdali, E.; Rivera, M.; Wheeler, P. A Review on Weighting Factor Design of Finite Control Set Model Predictive Control Strategies for AC Electric Drives. IEEE Trans. Power Electron. 2024, 39, 9967–9981. [Google Scholar] [CrossRef]




| Parameter | Value | Units |
|---|---|---|
| Stator resistance, | 12.85 | |
| Rotor resistance, | 4.80 | |
| Stator leakage inductance, | 79.93 | mH |
| Rotor leakage inductance, | 79.93 | mH |
| Mutual inductance, | 681.7 | mH |
| Rotational inertia, | 0.02 | kg m2 |
| Number of pairs of poles, P | 3 | - |
| Rated current, | 1.5 | A |
| Case | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (ms) | (mNm) | (mA) | (kHz) | ||||||
| (A) | 0.25 | 5 | 0.1 | 1.5 | 7.9 | 46.2 | 16.4 | 498 | 29.2 | 10.7 |
| (B) | 0.25 | 7 | 0.1 | 1.5 | 10.6 | 41.2 | 16.5 | 384 | 28.8 | 10.8 |
| (C) | 0.25 | 5 | 0.15 | 1.5 | 7.9 | 46.3 | 16.8 | 496 | 25.2 | 11.3 |
| (D) | 0.25 | 5 | 0.15 | 2.5 | 7.8 | 46.1 | 17.3 | 498 | 28.7 | 9.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arahal, M.R.; Satué, M.G.; Colodro, F.; Martínez-Heredia, J.M. Trade-Off Analysis of Drive Dynamics Considering Speed and Current Loops. Energies 2024, 17, 3649. https://doi.org/10.3390/en17153649
Arahal MR, Satué MG, Colodro F, Martínez-Heredia JM. Trade-Off Analysis of Drive Dynamics Considering Speed and Current Loops. Energies. 2024; 17(15):3649. https://doi.org/10.3390/en17153649
Chicago/Turabian StyleArahal, Manuel R., Manuel G. Satué, Francisco Colodro, and Juana M. Martínez-Heredia. 2024. "Trade-Off Analysis of Drive Dynamics Considering Speed and Current Loops" Energies 17, no. 15: 3649. https://doi.org/10.3390/en17153649
APA StyleArahal, M. R., Satué, M. G., Colodro, F., & Martínez-Heredia, J. M. (2024). Trade-Off Analysis of Drive Dynamics Considering Speed and Current Loops. Energies, 17(15), 3649. https://doi.org/10.3390/en17153649








