Convective Heat Transfer in PWR, BWR, CANDU, SMR, and MSR Nuclear Reactors—A Review
Abstract
1. Introduction
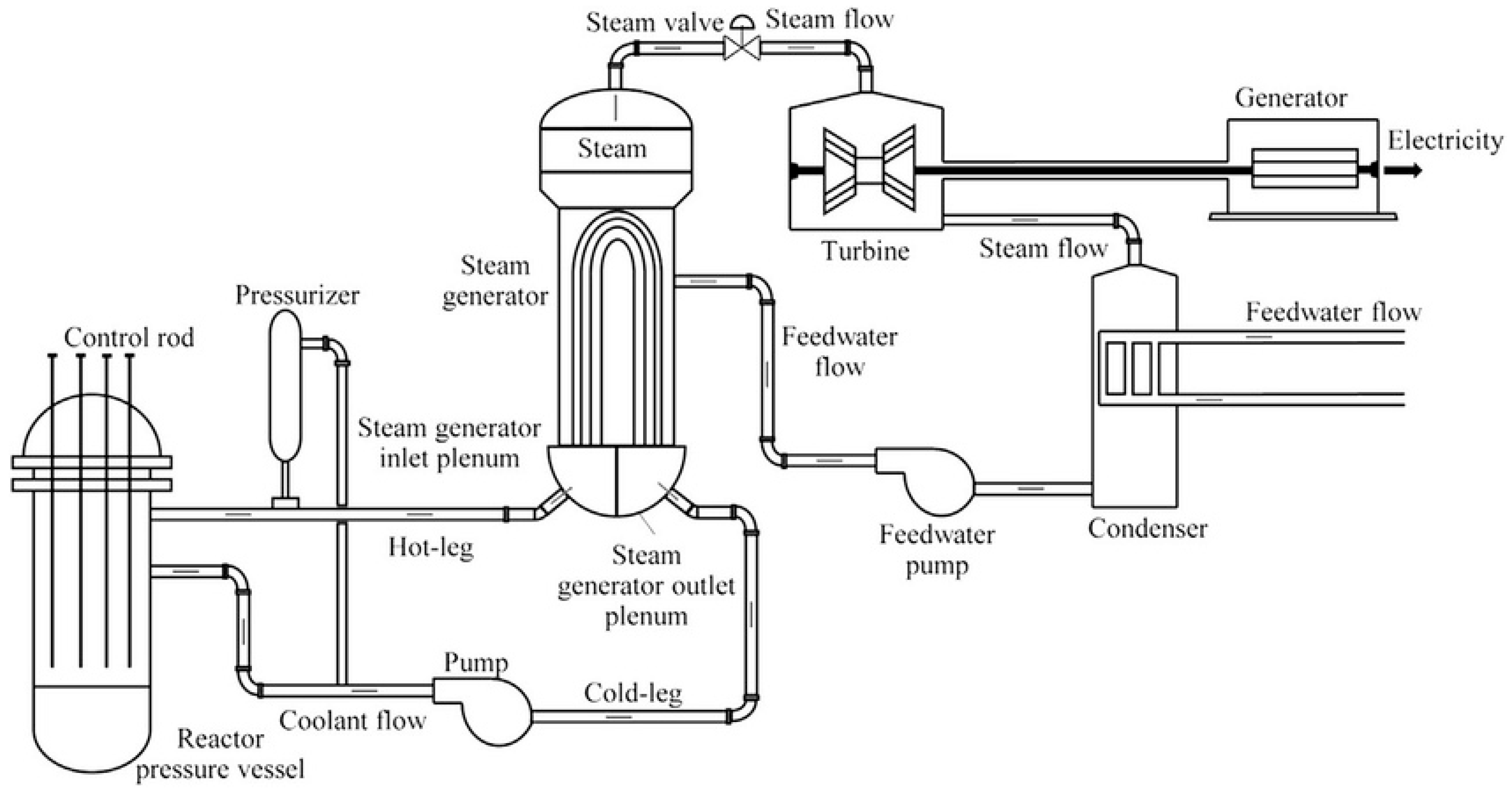
2. PWR Reactors
3. BWR Reactors
4. CANDU Reactors
5. Small Modular Reactors (SMRs)
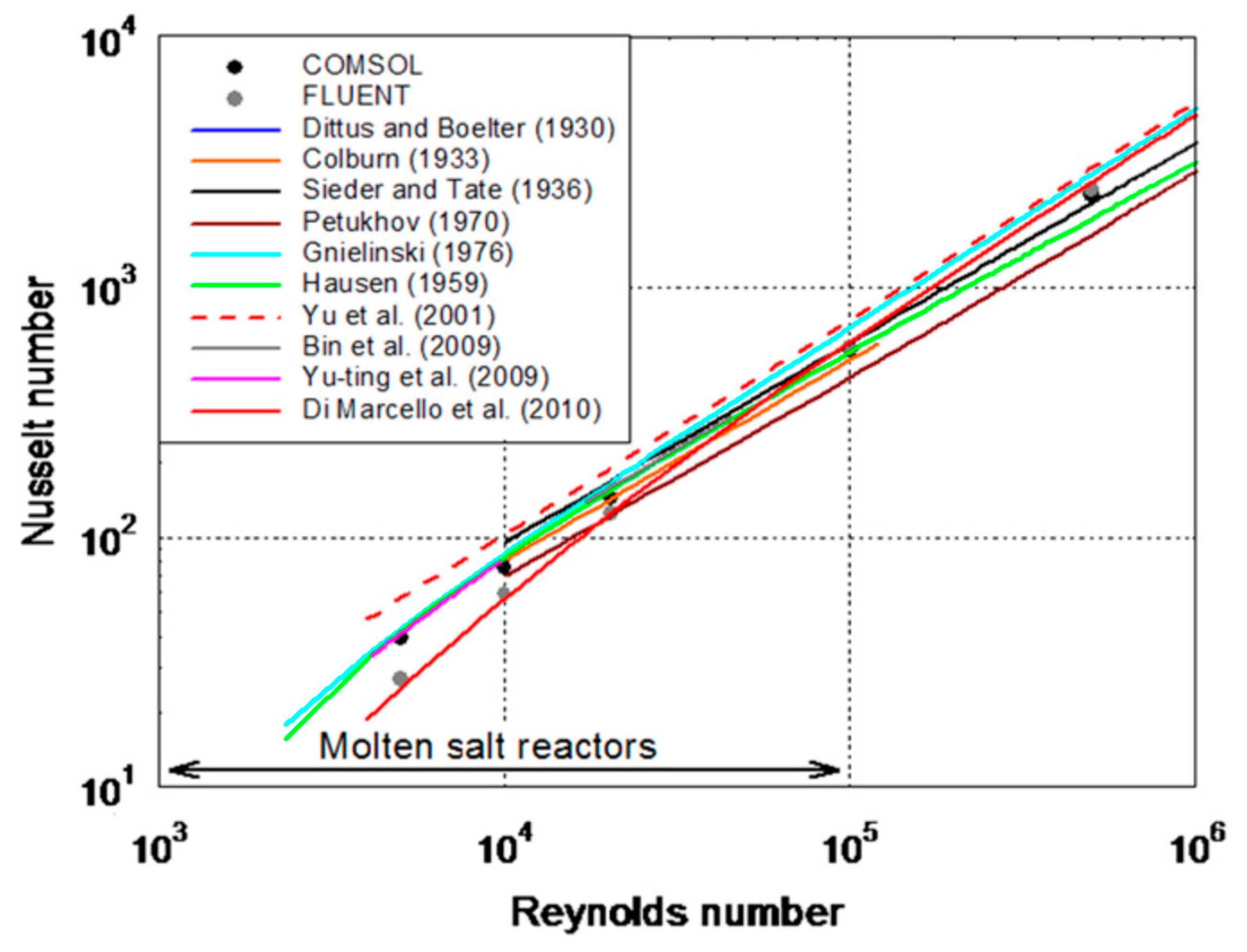
6. Molten Salt Reactors (MSR)
7. Summary and Conclusions
- Convective heat transfer is crucial physical process that occurs in nuclear reactors, maintaining their thermal stability and efficiency. Effective heat removal from the reactor core via convection is essential to prevent overheating, which could lead to core damage or meltdown. The review shows that convective heat transfer correlations which applied for simulation of emergency states of nuclear reactors are intensively studied in case of BWRs (see Table 2) due to the specific heat transfer conditions that occur in these reactors, such as working fluid evaporation inside the core. These correlations can be practically applied in simulation and design calculations.
- For each type of reviewed case, convective heat transfer can be characterized by specific correlations. The practical applicability of these correlations to other specific simulation or design cases can be assessed using similarity rules based on the heat transfer conditions and the limitations associated with each correlation (as detailed in Table 1, Table 2, Table 3, Table 4 and Table 5). The course of convective heat transfer in nuclear reactors is affected by various factors, such as thermo-physical properties of the coolant (i.e., viscosity, thermal conductivity, and specific heat), reactor geometry, surface characteristics of fuel rods, and the presence of turbulence. This finding is true for all types of studied reactors. Currently, there is a significant effort observed in research aimed at improving reactor design and applying innovative coolants (such as nanofluids) and simulating reactor failures (such as core meltdown). However, review results show that, especially in the case of PWRs, there is a large interest in the application of nanofluids to enhance heat transfer efficiency. The application of nanoparticles in coolant changes the thermophysical parameters of coolant; thus, a specific set of convective heat transfer correlations should be practically applied in simulation and design calculations (see Table 1).The review shows that in the case of CANDU-type nuclear reactors, the convective heat transfer correlations are similar to those practically applied for forced fluid flow inside the tubes (see Table 3).In the case of MSR reactors special set of correlations have to be applied in practical calculations and simulation due to the specific working fluid (see Table 4).
- The convective heat transfer mechanism in nuclear reactors can include both natural and forced convection. These processes are particularly important in case of SMRs, where the heat transfer process can vary depending on SMR type. Factors that affect this process include fuel composition, fuel enrichment, and the type of moderator and coolant (gas or liquid). As a result, different correlations are practically applied for reactor calculations and modeling, depending on these variables (see Table 4).
- Nowadays, advanced nuclear reactor models can be implemented and solved using computational fluid dynamics (CFD). CFD acts as a “virtual laboratory”, providing important insights into heat transfer and fluid flow processes.
- In case of PWRs, most of the reviewed research consists of computational studies. The modeling of convective heat transfer processes often relies on classical correlations such as those by Dittus–Boelter, Mayinger et al., or Kulacki and Emara. However, there are a limited amount of experimental data available for validating these correlations. Consequently, more experimental research is needed on PWRs to better understand the influence of different conditions on convective heat transfer.
- In case of BWRs, the two-phase flow during convective heat transfer adds significant complexity to the process. To perform simulations, researchers often need to make assumptions and simplifications, which can compromise the accuracy of the models. The limited number of experiments, particularly on full-scale BWR prototypes, further restricts the ability to validate and refine existing models. Additionally, further simulations of reactor behavior under abnormal and accident conditions remain crucial for comprehensive safety analysis.
- Development of the CANDU reactor technology remains a key focus for the future, as improving heat transfer is crucial for enhancing the efficiency of these units. The geometry of fuel channels in CANDU reactors is complex, leading to potential variations in temperature within the core. This can result in hot spots and temperature fluctuations. Most existing correlations are developed for one-dimensional, stationary and turbulent flow conditions. To address the complexity of CANDU reactor cores and better understand the heat transfer dynamics, it would be valuable to conduct numerical simulations for correlations described.
- SMR technology is among the most advanced in the nuclear power industry. As commercial SMRs and microreactors are some of the first of their kind, there are relatively little empirical data available to evaluate design concepts before implementation. Due to the wide variety of technologies used, detailed analyses must be conducted for each SMR design variation. Reactor heat transfer modeling is essential even before licensing. Design approval and licensing of reactor systems requires results that account for specific physical and test conditions. The biggest challenge for SMR technology is ensuring efficient heat transfer in the compact and densely packed reactor core to prevent hot spots and ensure uniform cooling. For instance, factors such as type of nuclear fuel and its enrichment, the shape and size of the reactor vessel, the type of coolant used, and the moderator can affect the maximum average fuel temperature, which is directly related to the heat transfer process in the SMR core. This makes experiments both complex and time-consuming. The unresolved issues in heat transfer and SMR technology include the ability to passively cool the reactor containment, increasing the life of nuclear fuel, improving safety and controlling the heat transfer process within the core.
- Despite the existence numerical models for MSR, further development is necessary to enhance their reliability for predicting heat transfer in these reactors. Specifically, improvements are needed in modeling thermal–hydraulic phenomena where recirculation occurs. In such cases, accurately addressing turbulence is crucial for obtaining reliable results. Current models are predominantly axially-symmetrical or two-dimensional. The development of more complex 3D models, which include the entire core of an MSR, is highly desirable. However, this advancement would require significant computational resources.
Author Contributions
Funding
Conflicts of Interest
References
- El-Sefy, M.; Ezzeldin, M.; El-Dakhakhni, W.; Wiebe, L.; Nagasaki, S. System dynamics simulation of the thermal dynamic processes in nuclear power plants. Nucl. Eng. Technol. 2019, 51, 1540–1553. [Google Scholar] [CrossRef]
- Shamim, J.A.; Bhowmik, P.K.; Chen, X.; Suh, K.Y. A new correlation for convective heat transfer coefficient of water–alumina nanofluid in a square array subchannel under PWR condition. Nucl. Eng. Des. 2016, 308, 194–204. [Google Scholar] [CrossRef]
- Hatami, M.; Ganji, M.; Sohrabiasl, I.; Jing, D. Optimization of the fuel rod’s arrangement cooled by turbulent nanofluids flow in pressurized water reactor (PWR). Chin. J. Chem. Eng. 2017, 25, 722–731. [Google Scholar] [CrossRef]
- Liu, C.; Ferng, Y.; Shih, C. CFD evaluation of turbulence models for flow simulation of the fuel rod bundle with a spacer assembly. Appl. Therm. Eng. 2012, 40, 389–396. [Google Scholar] [CrossRef]
- Ghazanfari, V.; Talebi, M.; Khorsandi, J.; Abdolahi, R. Thermal–hydraulic modeling of water/Al2O3 nanofluid as the coolant in annular fuels for a typical VVER-1000 core. Prog. Nucl. Energy 2016, 87, 67–73. [Google Scholar] [CrossRef]
- Vieira, C.B.; Romero, G.A.; Su, J. Computational Simulation of Natural Convection of a Molten Core in Lower Head of a PWR Pressure Vessel. In Proceedings of the 18th International Conference on Nuclear Engineering, Xi’an, China, 17–21 May 2010. [Google Scholar]
- Mayinger, F. Examination of Thermalhydraulic Processes and Heat Transfer in a Core Melt; Institut fur Verfahrenstechnik der T. U.: Halle, Germany, 1976. [Google Scholar]
- Kulacki, F.A.; Emara, A.A. High Rayleigh Numbers Convection in Enclosed Fluid Layers with Internal Heat Sources; US Nuclear Regulatory Commission, Division of Reactor Safety Research: Rockville, MD, USA, 1975.
- Zhang, X.; Chen, H.; Liu, F.; Zhan, D. Transient 3D simulation for heating and melting process of PWR core after SBO. Ann. Nucl. Energy 2018, 115, 256–267. [Google Scholar] [CrossRef]
- Holloway, M.V.; Beasley, D.E.; Conner, M.E. Single-phase convective heat transfer in rod bundles. Nucl. Eng. Des. 2008, 238, 848–858. [Google Scholar] [CrossRef]
- Liu, C.C.; Ferng, Y.M. Numerically simulating the thermal–hydraulic characteristics within the fuel rod bundle using CFD methodology. Nucl. Eng. Des. 2010, 240, 3078–3086. [Google Scholar] [CrossRef]
- Yao, S.C.; Hochreiter, L.E.; Leech, W.J. Heat-Transfer Augmentation in Rod Bundles Near Grid Spacers. J. Heat Transf. 1982, 104, 76–81. [Google Scholar] [CrossRef]
- Holloway, M.V.; McClusky, H.L.; Beasley, D.E.; Conner, M.E. The Effect of Support Grid Features on Local, Single-Phase Heat Transfer Measurements in Rod Bundles. J. Heat Transf. 2004, 126, 43–53. [Google Scholar] [CrossRef]
- Hadad, K.; Rahimian, A.; Nematollahi, M. Numerical study of single and two-phase models of water/Al2O3 nanofluid turbulent forced convection flow in VVER-1000 nuclear reactor. Ann. Nucl. Energy 2013, 60, 287–294. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and Heat Transfer Study of Dispersed Fluids with submicron Metallic Oxide Particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Maïga, S.E.B.; Nguyen, C.T.; Galanis, N.; Roy, G.; Maré, T.; Coqueux, M. Heat transfer enhancement in turbulent tube flow using Al2O3 nanoparticle suspension. Int. J. Numer. Methods Heat Fluid Flow 2006, 16, 275–292. [Google Scholar] [CrossRef]
- Fazio, S.; Recchioni, M.; Mathieux, F. (Eds.) Background Analysis of the Quality of the Energy Data to be Considered for the European Reference Life Cycle Database (ELCD); Publications Office of the European Union: Luxembourg, 2013. [Google Scholar]
- Sun, K.H.; Gonzalez-Santalo, J.M.; Tien, C.L. Calculations of Combined Radiation and Convection Heat Transfer in Rod Bundles under Emergency Cooling Conditions. J. Heat Transf. 1976, 98, 414–420. [Google Scholar] [CrossRef]
- Tran, C.T.; Kudinov, P.; Dinh, T.N. An approach to numerical simulation and analysis of molten corium coolability in a boiling water reactor lower head. Nucl. Eng. Des. 2010, 240, 2148–2159. [Google Scholar] [CrossRef]
- Tran, C.-T.; Dinh, T.-N. The effective convectivity model for simulation of melt pool heat transfer in a light water reactor pressure vessel lower head. Part I: Physical processes, modeling and model implementation. Prog. Nucl. Energy 2009, 51, 849–859. [Google Scholar] [CrossRef]
- Tran, C.-T.; Kudinov, P.; Toronto, H.; Tran, C.T. Local Heat Transfer from the Corium Melt Pool to the Boiling Water Reactor Pressure Vessel Wall. In Proceedings of the 14th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (Nureth-14) Nureth14-182, Toronto, ON, Canada, 25–30 September 2011. [Google Scholar] [CrossRef]
- Park, H.; Dhir, V.K.; Kastenberg, W.E. Effect of External Cooling on the Thermal Behavior of a Boiling Water Reactor Vessel Lower Head. Nucl. Technol. 1994, 108, 266–282. [Google Scholar] [CrossRef]
- Yoon, S.-J.; Agostinelli, G.; Baglietto, E. Assessment of Multiphase CFD with Zero Closure Model for Boiling Water Reactor Fuel Assemblies. United States, 2017. Available online: https://www.osti.gov/biblio/1409683 (accessed on 16 July 2024).
- Højerup, F.; Miettinen, J.; Puska, E.K.; Anttila, M.; Lindholm, I.; Nilsson, L.; Sjoevall, H. On Recriticality during Reflooding of a Degraded Boiling Water Reactor Core. Denmark, 1997. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/28/059/28059598.pdf (accessed on 16 July 2024).
- Michel, B. New set of convective heat transfer coefficients established for pools and validated against CLARA experiments for application to corium pools. Nucl. Eng. Des. 2015, 286, 278–285. [Google Scholar] [CrossRef]
- Espinosa-Paredes, G.; Verma, S.P.; Vázquez-Rodríguez, A.; Nuñez-Carrera, A. Mass flow rate sensitivity and uncertainty analysis in natural circulation boiling water reactor core from Monte Carlo simulations. Nucl. Eng. Des. 2010, 240, 1050–1062. [Google Scholar] [CrossRef]
- Chavez, V.J.; Imke, U.; Sanchez-Espinoza, V. TWOPORFLOW: A two-phase flow porous media code, main features and validation with BWR-relevant bundle experiments. Nucl. Eng. Des. 2018, 338, 181–188. [Google Scholar] [CrossRef]
- Chen, J.C. Correlation for Boiling Heat Transfer to Saturated Fluids in Convective Flow. Ind. Eng. Chem. Process. Des. Dev. 1966, 5, 322–329. [Google Scholar] [CrossRef]
- Sibamoto, Y.; Maruyama, Y.; Yonomoto, T.; Nakamura, H. Core Heat Transfer Coefficients Immediately Downstream of the Rewetting Front during Anticipated Operational Occurrences for BWRs. J. Nucl. Sci. Technol. 2011, 48, 440–453. [Google Scholar] [CrossRef]
- Yonomoto, T.; Koizumi, Y.; Tasaka, K. Core heat transfer analysis during a BWR LOCA simulation experiment at ROSA-III. Nucl. Eng. Des. 1987, 103, 239–250. [Google Scholar] [CrossRef]
- Griebe, R.W.; McConnell, J.W. Boiling Water Reactor-Full Length Emergency Core Cooling Heat Transfer (BWR-FLECHT) Tests Project; Final Report on Atmospheric Pressure Stainless Steel Experiments; Aerojet Nuclear Co.: Idaho Falls, ID, USA, 1973. [CrossRef]
- Duncan, J.; Leonard, J. Heat Transfer in a Simulated BWR Fuel Bundle Cooled by Spray under Loss-of-Coolant Conditions; U.S. Atomic Energy Commission: Washington, DC, USA, 1970. [CrossRef]
- Eklund, M.D.; Jevremovic, T. AGENT-TH scheme: New thermal hydraulics (TH) code coupled with the AGENT neutronics code for light water reactors modeling and analysis. Prog. Nucl. Energy 2016, 92, 175–196. [Google Scholar] [CrossRef]
- Cai, X.; Qiu, S.; Su, G.; Zhao, C. Steady-State Thermal-Hydraulic Analysis of a Particle-Bedded Boiling Water Reactor. In Proceedings of the 17th International Conference on Nuclear Engineering, Brussels, Belgium, 12–16 July 2009; pp. 275–281. [Google Scholar] [CrossRef]
- Sharma, A.K.; Pellegrini, M.; Okamoto, K.; Furuya, M.; Mizokami, S. Validation and application of numerical modeling for in-vessel melt retention in corium pools. Int. J. Heat Mass Transf. 2022, 196, 123313. [Google Scholar] [CrossRef]
- Martín-Fuertes, F.; Martín-Valdepeñas, J.M.; Mira, J.; Sánchez, M.J. A MELCOR Application to Two Light Water Reactor Nuclear Power Plant Core Melt Scenarios with Assumed Cavity Flooding Action. Nucl. Technol. 2003, 144, 34–48. [Google Scholar] [CrossRef]
- Valinčius, M.; Kaliatka, T.; Kaliatka, A.; Ušpuras, E. Modelling of Severe Accident and In-Vessel Melt Retention Possibilities in BWR Type Reactor. Sci. Technol. Nucl. Install. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Oettingen, M.; Skolik, K.; Malicki, M. Neutronic analysis of mixed thorium-uranium fuel bundle for CANDU reactors. IOP Conf. Ser. Earth Environ. Sci. 2019, 214, 012024. [Google Scholar] [CrossRef]
- Taler, D.; Taler, J. Simple heat transfer correlations for turbulent tube flow. E3S Web Conf. 2017, 13, 02008. [Google Scholar] [CrossRef]
- Yu, J.; Liu, H.; Jia, B. Sub-channel analysis of CANDU–SCWR and review of heat-transfer correlations. Prog. Nucl. Energy 2009, 51, 246–252. [Google Scholar] [CrossRef]
- Todreas, N.E.; Kazimi, M.S. Nuclear Systems Volume I, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Alameri, S.A.; Alkaabi, A.K. Fundamentals of nuclear reactors. In Nuclear Reactor Technology Development and Utilization; Elsevier: Amsterdam, The Netherlands, 2020; pp. 27–60. [Google Scholar] [CrossRef]
- Han, S.H.; Choi, Y.D.; Shin, J.K.; Kim, Y.C.; Kim, M.S. Turbulent heat transfer of supercritical carbon dioxide in square cross-sectional duct flow. J. Mech. Sci. Technol. 2008, 22, 2563–2577. [Google Scholar] [CrossRef]
- Pioro, I.L.; Duffey, R.B. Literature Survey of Heat Transfer and Hydraulic Resistance of Water, Carbon Dioxide, Helium and Other Fluids at Supercritical and Near-Critical Pressures. 2003. Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:35087435 (accessed on 18 December 2023).
- Pioro, I.L.; Khartabil, H.F.; Duffey, R.B. Heat transfer to supercritical fluids flowing in channels—Empirical correlations (survey). Nucl. Eng. Des. 2004, 230, 69–91. [Google Scholar] [CrossRef]
- Zahlan, H.; Leung, L.; Huang, Y.; Liu, G. General Assessment of Convection Heat Transfer Correlations for Multiple Geometries and Fluids at Supercritical Pressure. CNL Nucl. Rev. 2017, 7, 1–20. [Google Scholar] [CrossRef]
- Mokry, S.; Pioro, I.; Farah, A.; King, K.; Gupta, S.; Peiman, W.; Kirillov, P. Development of supercritical water heat-transfer correlation for vertical bare tubes. Nucl. Eng. Des. 2011, 241, 1126–1136. [Google Scholar] [CrossRef]
- Debrah, S.K.; Shitsi, E.; Chabi, S.; Sahebi, N. Assessment of heat transfer correlations in the sub-channels of proposed rod bundle geometry for supercritical water reactor. Heliyon 2019, 5, e02927. [Google Scholar] [CrossRef]
- Yamagata, K.; Nishikawa, K.; Hasegawa, S.; Fujii, T.; Yoshida, S. Forced convective heat transfer to supercritical water flowing in tubes. Int. J. Heat Mass Transf. 1972, 15, 2575–2593. [Google Scholar] [CrossRef]
- Griem, H. A new procedure for the prediction of forced convection heat transfer at near- and supercritical pressure. Heat Mass Transf. 1996, 31, 301–305. [Google Scholar] [CrossRef]
- Kitoh, K.; Koshizuka, S.; Oka, Y. Refinement of Transient Criteria and Safety Analysis for a High-Temperature Reactor Cooled by Supercritical Water. Nucl. Technol. 2001, 135, 252–264. [Google Scholar] [CrossRef]
- Chen, W.; Fang, X.; Xu, Y.; Su, X. An assessment of correlations of forced convection heat transfer to water at supercritical pressure. Ann. Nucl. Energy 2015, 76, 451–460. [Google Scholar] [CrossRef]
- Lokhov, A.; Cameron, R.; Sozoniuk, V. OECD/NEA Study on the Economics and Market of Small Reactors. Nucl. Eng. Technol. 2013, 45, 701–706. [Google Scholar] [CrossRef]
- Carelli, M.D.; Ingersoll, D.T. (Eds.) Handbook of Small Modular Nuclear Reactors; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Kim, M.S.; Jeong, Y.H. Conceptual design of small modular reactor driven by natural circulation and study of design characteristics using CFD & RELAP5 code. Nucl. Eng. Technol. 2020, 52, 2743–2759. [Google Scholar] [CrossRef]
- Lee, Y.-G.; Kim, J.-W.; Park, G.-C. Development of a thermal–hydraulic system code, TAPINS, for 10 MW regional energy reactor. Nucl. Eng. Des. 2012, 249, 364–378. [Google Scholar] [CrossRef]
- Sundén, B. Advanced Heat Transfer Topics in Complex Duct Flows. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2017; pp. 37–89. [Google Scholar] [CrossRef]
- Chai, X.; Li, W.; Chen, B.; Liu, X.; Xiong, J.; Cheng, X. Numerical simulation of turbulent natural convection in an enclosure with a curved surface heated from below. Prog. Nucl. Energy 2020, 126, 103392. [Google Scholar] [CrossRef]
- Ulucakli, M.E. Turbulent Natural Convection in an Enclosure with Localized Heating from Below. Exp. Heat Transf. 1996, 9, 305–321. [Google Scholar] [CrossRef]
- Venkateshwaran, A.; Kumar, M.; Kumar, S.; Sivakumar, R.; Joshi, A.; Pain, C. Numerical study of the effect of geometry on the behaviour of internally heated melt pools for in-vessel melt retention. Prog. Nucl. Energy 2023, 156, 104555. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Luo, S.; Tian, W.; Qiu, S.; Su, G. Results of simulant effect on large corium pool behavior based on COPRA facility. Prog. Nucl. Energy 2018, 108, 398–408. [Google Scholar] [CrossRef]
- Yang, S.; Bieder, U. LES of Natural Convection Along the Vertical Wall Applied for the Scale of Small Modular Reactor (Ra* ≈ 1019). In Proceedings of the Advances in Thermal Hydraulics (ATH 2022), Anaheim, CA, USA, 12–16 June 2022; pp. 311–314. [Google Scholar] [CrossRef]
- Vliet, G.C.; Liu, C.K. An Experimental Study of Turbulent Natural Convection Boundary Layers. J. Heat Transf. 1969, 91, 517–531. [Google Scholar] [CrossRef]
- Na, M.W.; Shin, D.; Park, J.H.; Lee, J.I.; Kim, S.J. Indefinite sustainability of passive residual heat removal system of small modular reactor using dry air cooling tower. Nucl. Eng. Technol. 2020, 52, 964–974. [Google Scholar] [CrossRef]
- Jiang, N.; Peng, M.; Cong, T. Thermal margin evaluation for the stratified molten pool in SMR-IP200. Nucl. Eng. Des. 2019, 355, 110354. [Google Scholar] [CrossRef]
- Globe, S.; Dropkin, D. Natural-Convection Heat Transfer in Liquids Confined by Two Horizontal Plates and Heated From Below. J. Heat Transf. 1959, 81, 24–28. [Google Scholar] [CrossRef]
- Theofanous, T.; Liu, C.; Additon, S.; Angelini, S.; Kymäläinen, O.; Salmassi, T. In-vessel coolability and retention of a core melt. Nucl. Eng. Des. 1997, 169, 1–48. [Google Scholar] [CrossRef]
- Bhowmik, P.K.; Shamim, J.A.; Chen, X.; Suh, K.Y. Rod bundle thermal-hydraulics experiment with water and water-nanofluid for small modular reactor. Ann. Nucl. Energy 2021, 150, 107870. [Google Scholar] [CrossRef]
- Weisman, J. Heat Transfer to Water Flowing Parallel to Tube Bundles. Nucl. Sci. Eng. 1959, 6, 78–79. [Google Scholar] [CrossRef]
- Liu, D.; Gu, H. Mixed convection heat transfer in a 5 × 5 rod bundles. Int. J. Heat Mass Transf. 2017, 113, 914–921. [Google Scholar] [CrossRef]
- Beliavskii, S.; Alhassan, S.; Danilenko, V.; Karvan, R.; Nesterov, V. Effect of changing the outer fuel element diameter on thermophysical parameters of KLT-40S reactor unit. Ann. Nucl. Energy 2023, 190, 109877. [Google Scholar] [CrossRef]
- Carlson, L.; Miller, J.; Wu, Z. Implications of HALEU fuel on the design of SMRs and micro-reactors. Nucl. Eng. Des. 2022, 389, 111648. [Google Scholar] [CrossRef]
- Farmer, M.T.; Hill, D.J.; Sienicki, J.J.; Spencer, B.W.; Wade, D.C. Thermal-Hydraulic Development a Small, Simplified, Proliferation-Resistant Reactor; No. ANL/RE/CP—98725; Argonne National Lab.: Lemont, IL, USA, 1999.
- El-Genk, M.S.; Schriener, T.M. Convection heat transfer of alkali liquid metals and LBE in hexagonal bundles of uniformly heated tubes with helical spacers. Therm. Sci. Eng. Prog. 2018, 5, 339–350. [Google Scholar] [CrossRef]
- Yu, H.; Peng, M.; Jiang, N.; Wang, H. Model development for the transient heat transfer in a corium pool. Nucl. Eng. Des. 2021, 371, 110946. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, Y.; Zhang, Y.; Tian, W.; Qiu, S.; Su, G. Natural convection heat transfer in corium pools: A review work of experimental studies. Prog. Nucl. Energy 2015, 79, 167–181. [Google Scholar] [CrossRef]
- Asfia, F.J.; Dhir, V.K. An experimental study of natural convection in a volumetrically heated spherical pool bounded on top with a rigid wall. Nucl. Eng. Des. 1996, 163, 333–348. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H. Correlating equations for laminar and turbulent free convection from a horizontal cylinder. Int. J. Heat Mass Transf. 1975, 18, 1049–1053. [Google Scholar] [CrossRef]
- Luzzi, L.; Cammi, A.; Di Marcello, V.; Fiorina, C. An approach for the modelling and the analysis of the MSR thermo-hydrodynamic behaviour. Chem. Eng. Sci. 2010, 65, 4873–4883. [Google Scholar] [CrossRef]
- Chiba, S.-Y.; Omae, M.; Yuki, K.; Hashizume, H.; Toda, S.; Sagara, A. Experimental Research on Heat Transfer Enhancement for High Prandtl-Number Fluid. Fusion Sci. Technol. 2005, 47, 569–573. [Google Scholar] [CrossRef]
- Liu, B.; Wu, Y.-T.; Ma, C.-F.; Ye, M.; Guo, H. Turbulent convective heat transfer with molten salt in a circular pipe. Int. Commun. Heat Mass Transf. 2009, 36, 912–916. [Google Scholar] [CrossRef]
- Wu, Y.-T.; Liu, B.; Ma, C.-F.; Guo, H. Convective heat transfer in the laminar–turbulent transition region with molten salt in a circular tube. Exp. Therm. Fluid Sci. 2009, 33, 1128–1132. [Google Scholar] [CrossRef]
- Di Marcello, V.; Cammi, A.; Luzzi, L. A generalized approach to heat transfer in pipe flow with internal heat generation. Chem. Eng. Sci. 2010, 65, 1301–1310. [Google Scholar] [CrossRef]
- Qian, L.; Qiu, S.; Zhang, D.; Su, G.; Tian, W. Numerical research on natural convection in molten salt reactor with non-uniformly distributed volumetric heat generation. Nucl. Eng. Des. 2010, 240, 796–806. [Google Scholar] [CrossRef]
- Boroushaki, M. Numerical solution of the neutron transport equation using cellular neural networks. Ann. Nucl. Energy 2009, 36, 15–27. [Google Scholar] [CrossRef]
- De, G.; Davis, V. Natural Convection of Air in A Square Cavity a Bench Mark Numerical Solution. Int. J. Numer. Methods Fluids 1983, 3, 249–264. [Google Scholar]
- Lee, J.-H.; Goldstein, R.J. An Experimental Study on Natural Convection Heat Transfer in an Inclined Square Enclosure Containing Internal Energy Sources. J. Heat Transf. 1988, 110, 345–349. [Google Scholar] [CrossRef]
- May, H.-O. A numerical study on natural convection in an inclined square enclosure containing internal heat sources. Int. J. Heat Mass Transf. 1991, 34, 919–928. [Google Scholar] [CrossRef]
- Kudariyawar, J.Y.; Aidya, A.M.V.; Maheshwari, N.K.; Satyamurthy, P.; Srivastava, A.K. Estimating Steady State and Transient Characteristics of Molten Salt Natural Circulation Loop Using CFD. Available online: www.hanser-elibrary.com (accessed on 16 July 2024).
- Shin, Y.; Bin Seo, S.; Kim, I.G.; Bang, I.C. Natural circulation with DOWTHERM RP and its MARS code implementation for molten salt-cooled reactors. Int. J. Energy Res. 2016, 40, 1122–1133. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, D.; Wang, C.; Qiu, S.; Su, G.; Tian, W. Experimental study on the heat transfer characteristics of fluoride salt in the new conceptual passive heat removal system of molten salt reactor. Int. J. Energy Res. 2018, 42, 1635–1648. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, D.; Wang, C.; Qiu, S.; Su, G.; Tian, W. Experimental study on heat transfer performance between fluoride salt and heat pipes in the new conceptual passive residual heat removal system of molten salt reactor. Nucl. Eng. Des. 2018, 339, 215–224. [Google Scholar] [CrossRef]
- Bin Seo, S.; Shin, Y.; Bang, I.C. Numerical analysis on spatial universality of similarity technique inside molten salt reactor system. Int. J. Heat Mass Transf. 2018, 116, 569–580. [Google Scholar] [CrossRef]
- Wang, C.-L.; Qin, H.; Zhang, D.-L.; Tian, W.-X.; Su, G.-H.; Qiu, S.-Z. Numerical investigation of natural convection characteristics of a heat pipe-cooled passive residual heat removal system for molten salt reactors. Nucl. Sci. Tech. 2020, 31, 1–9. [Google Scholar] [CrossRef]
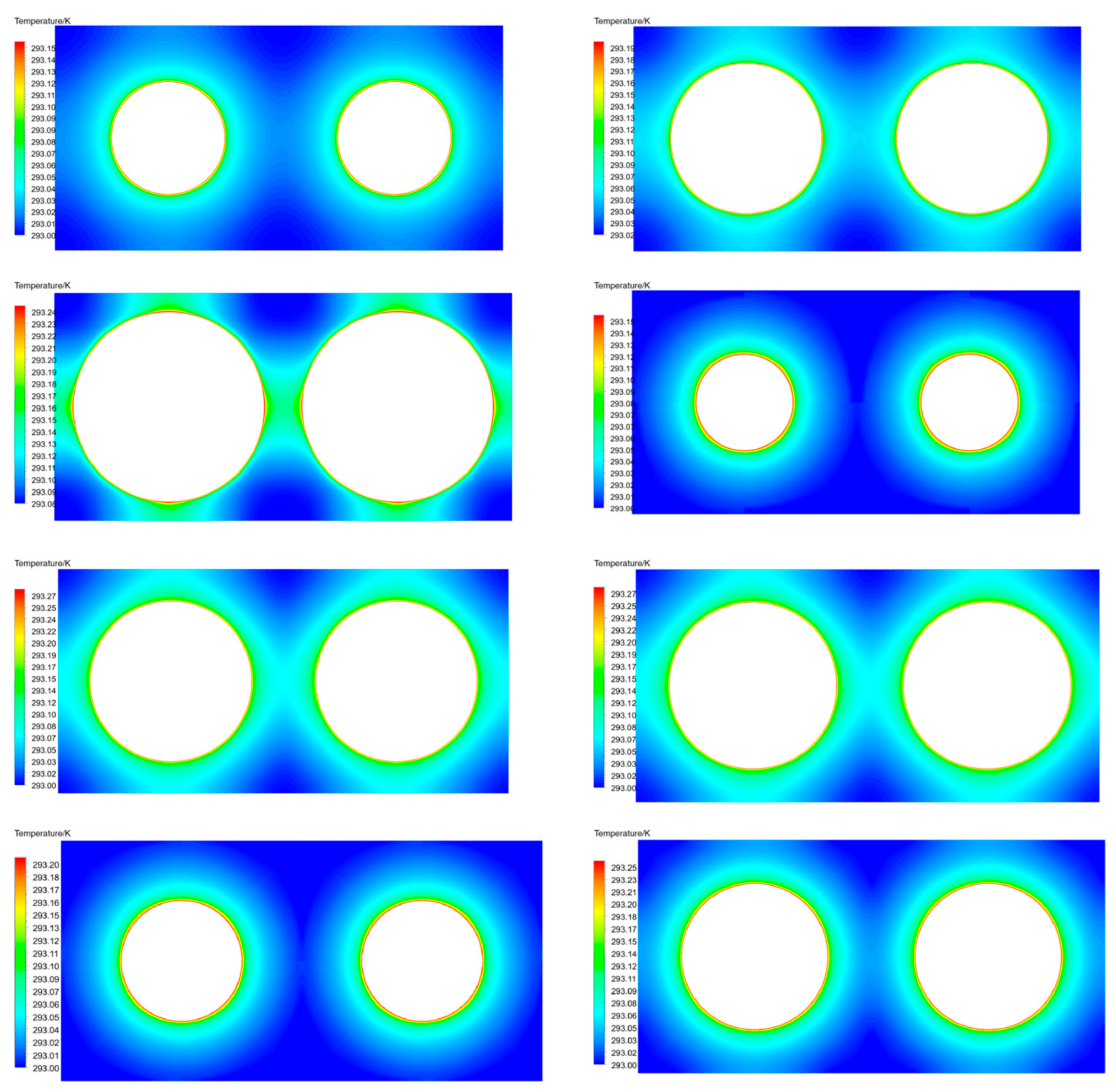


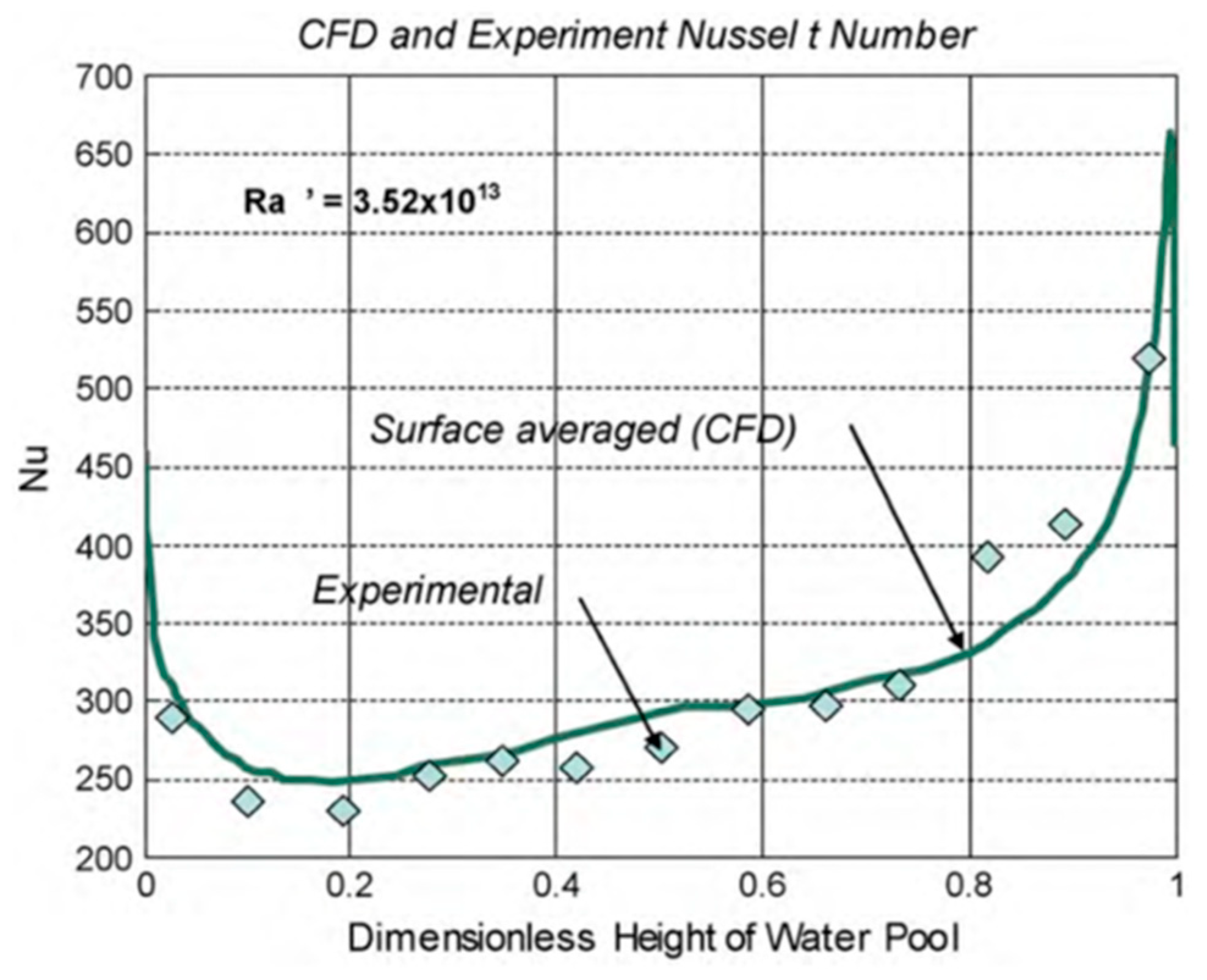

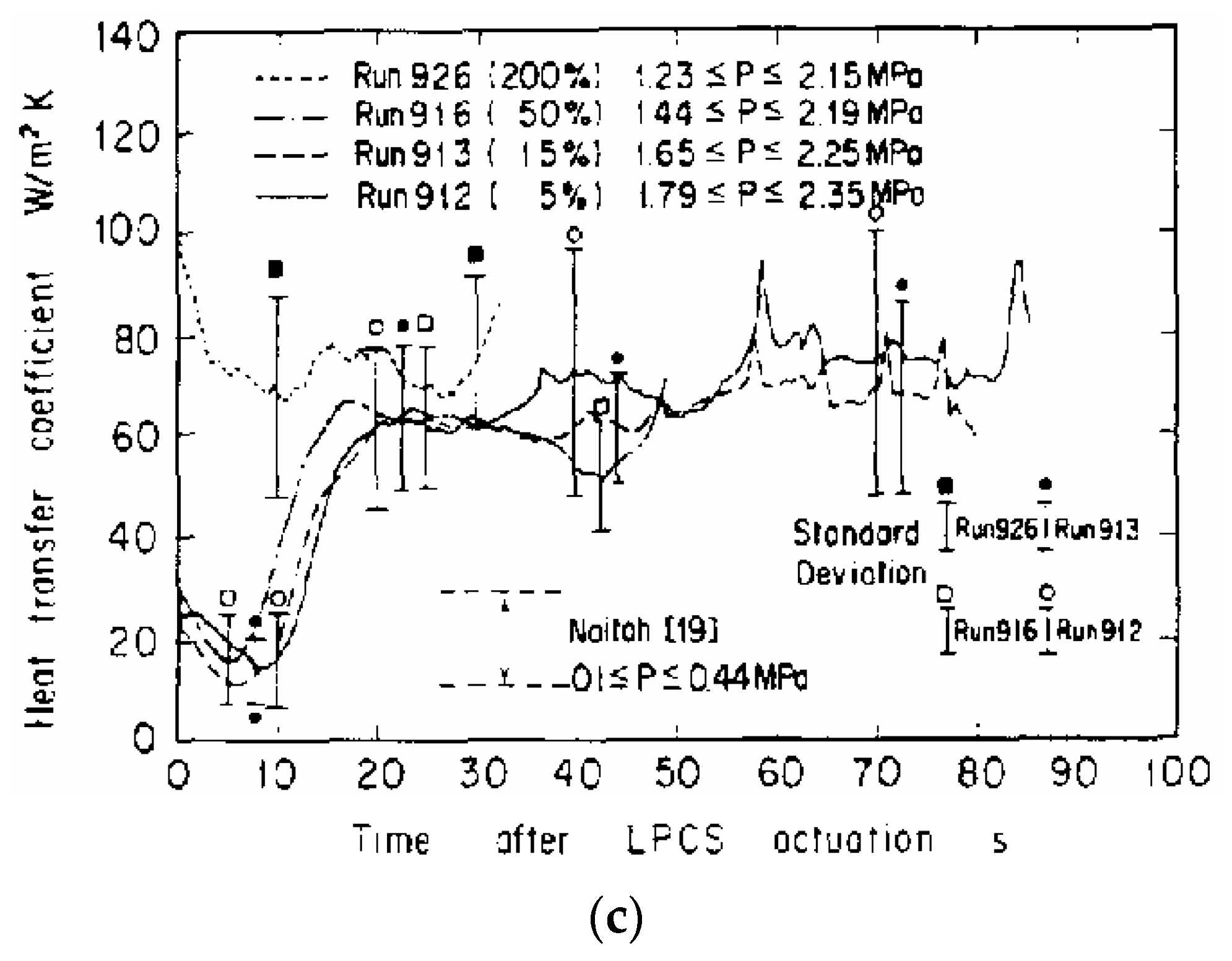
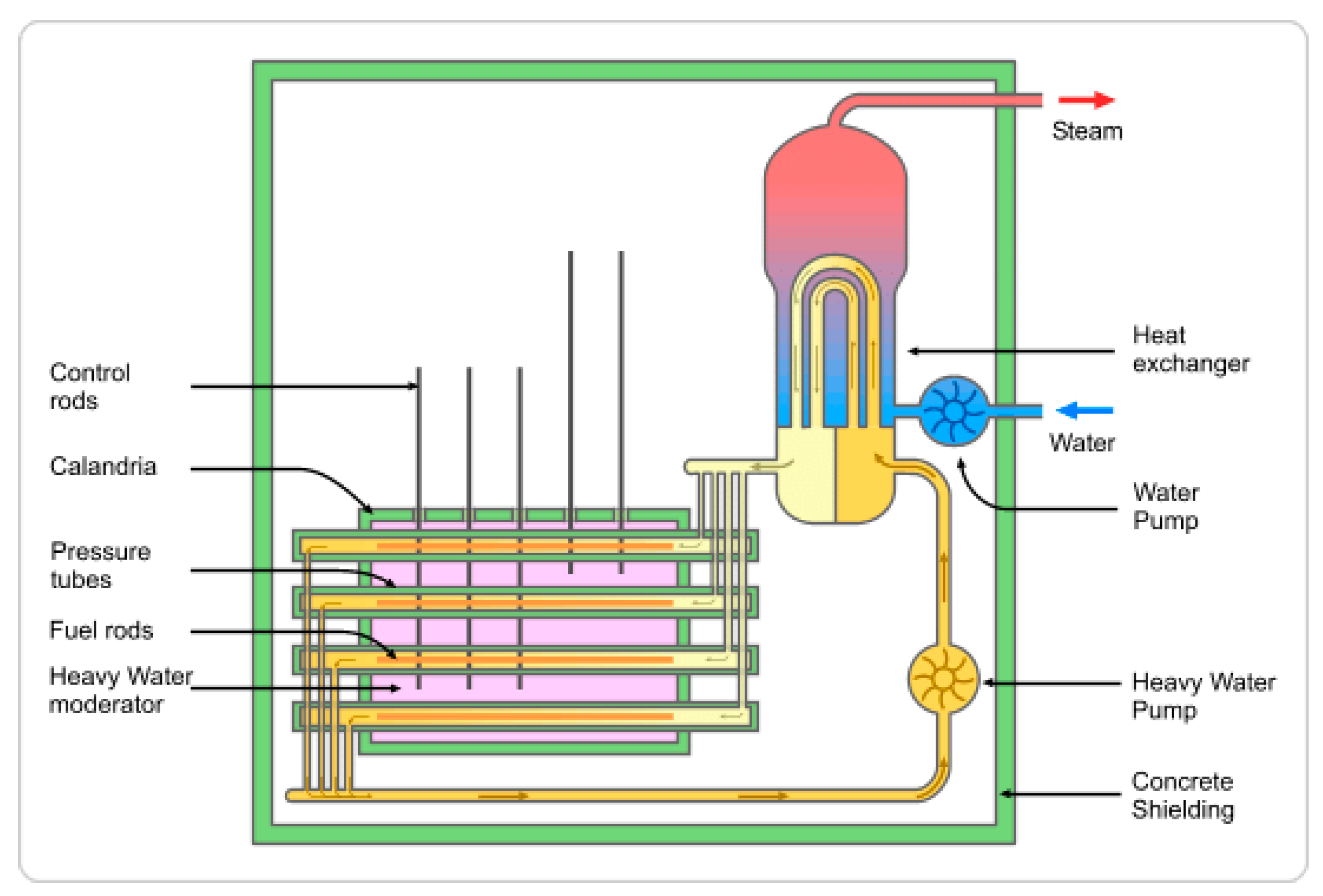
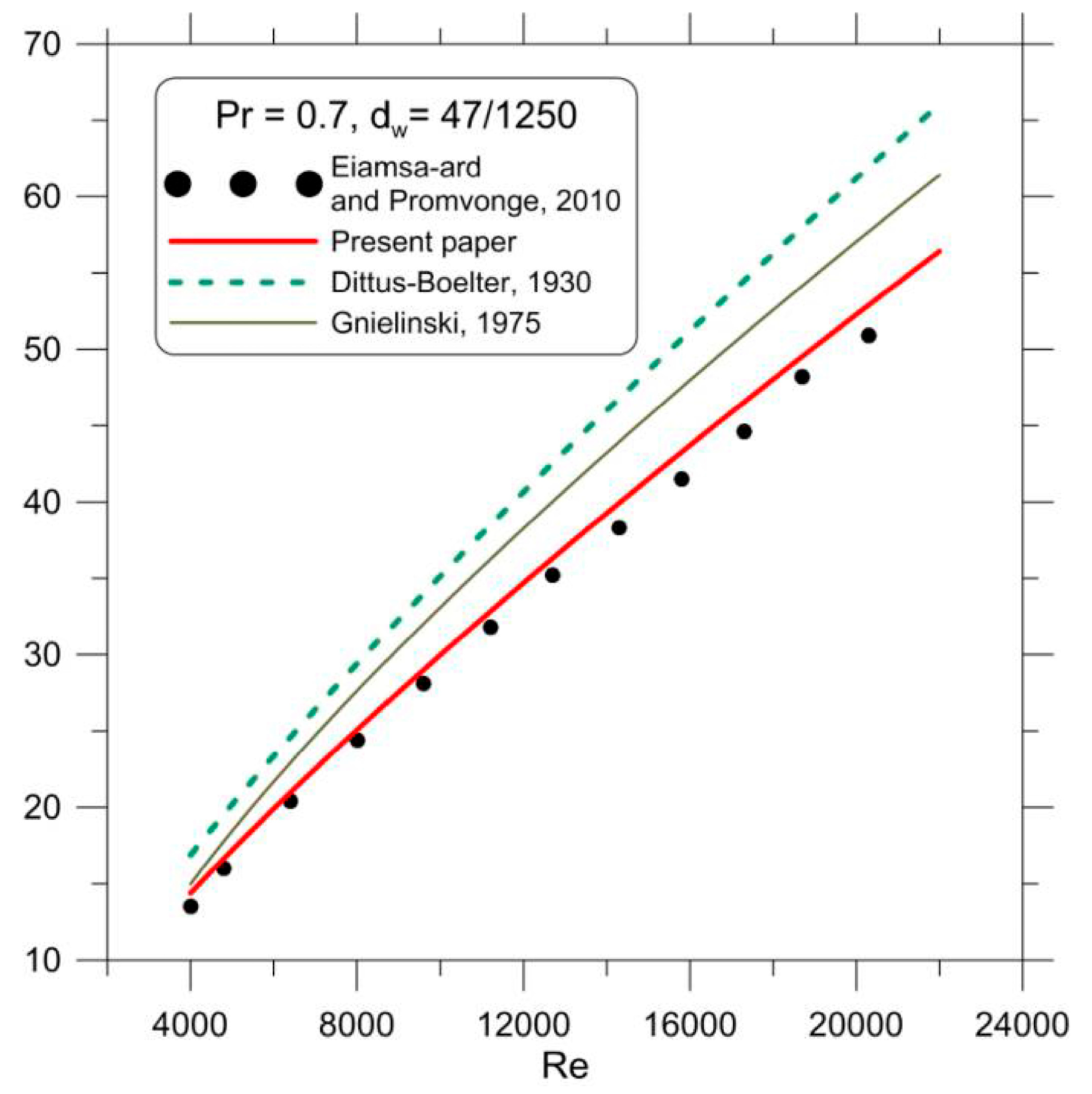

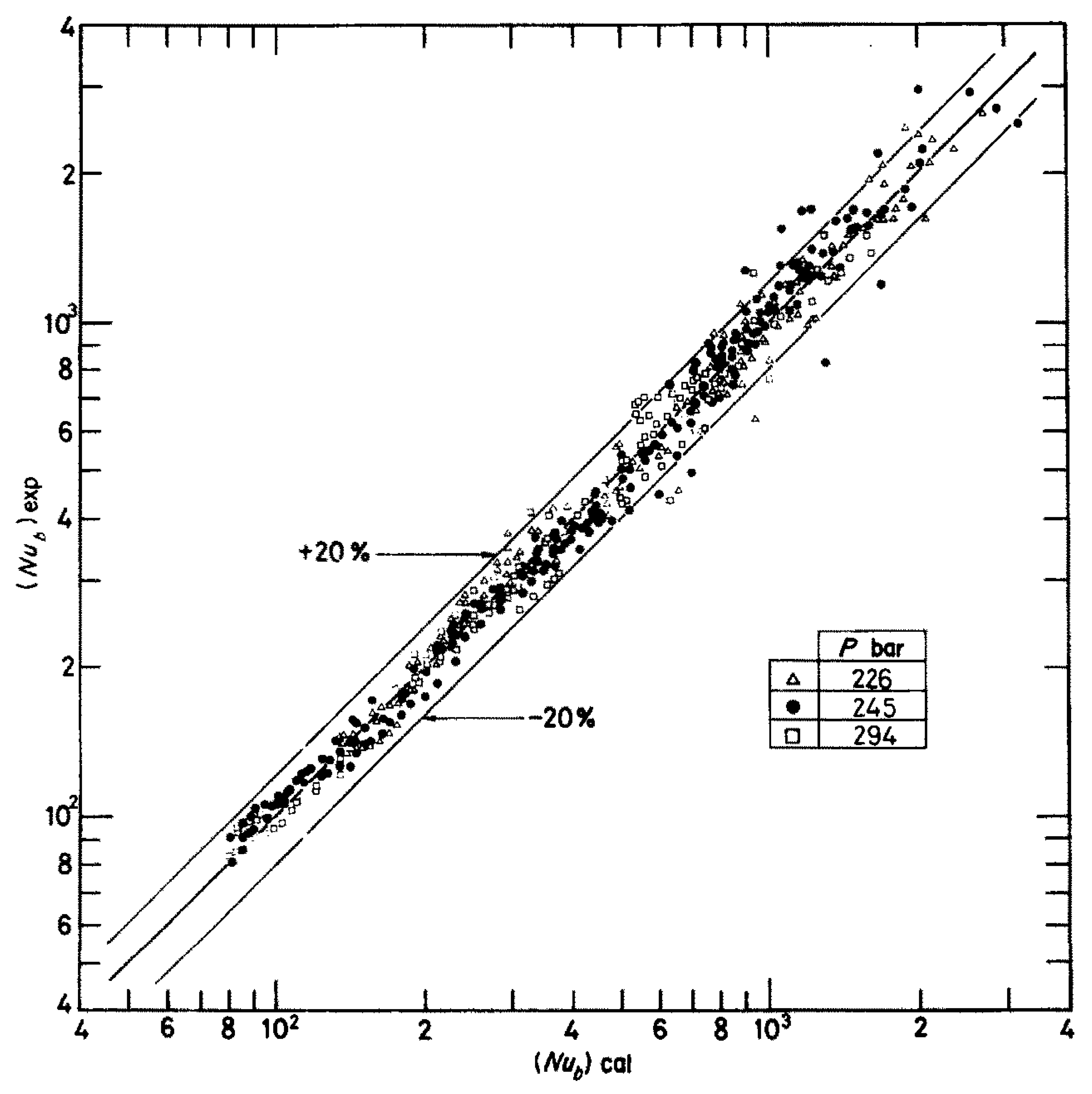
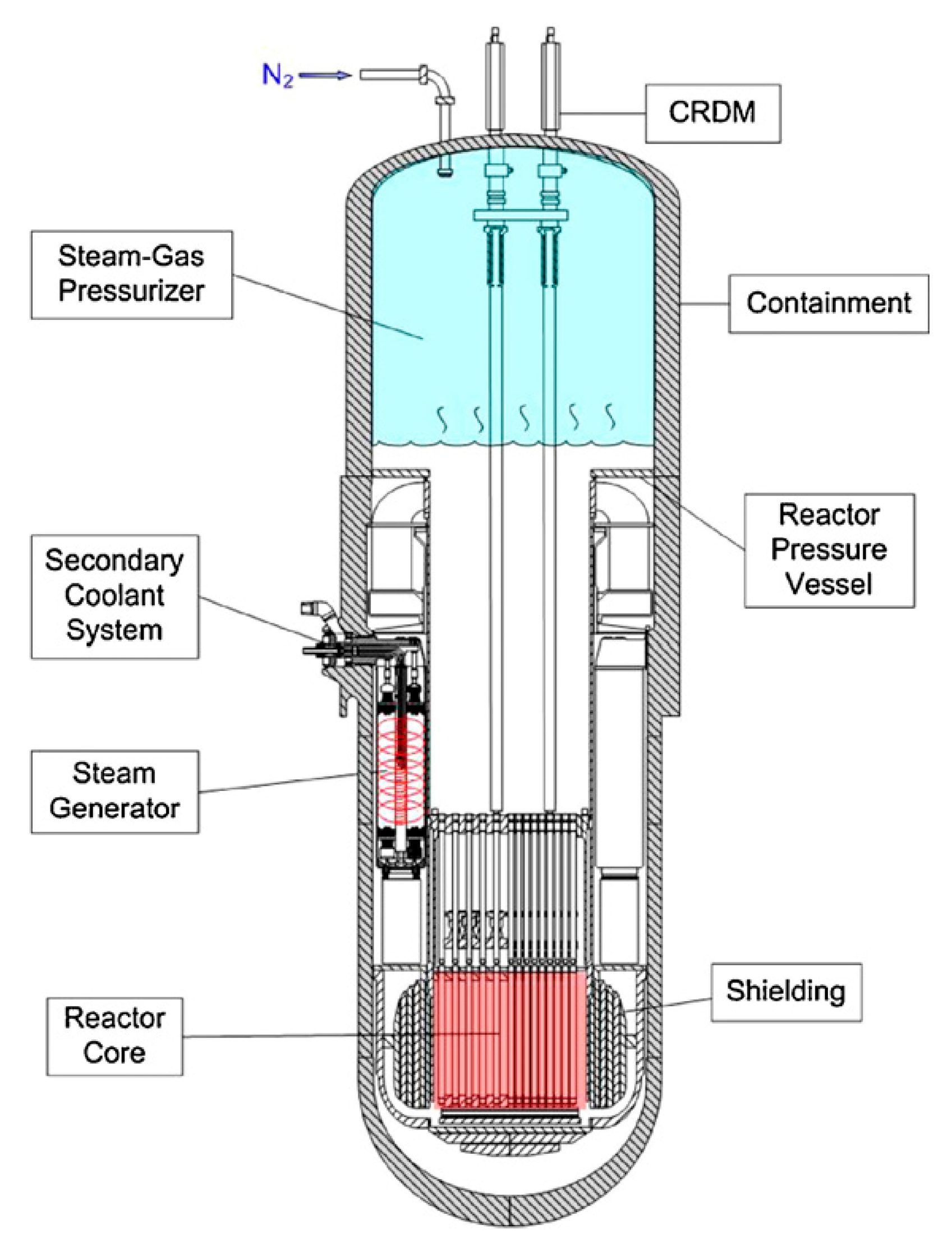
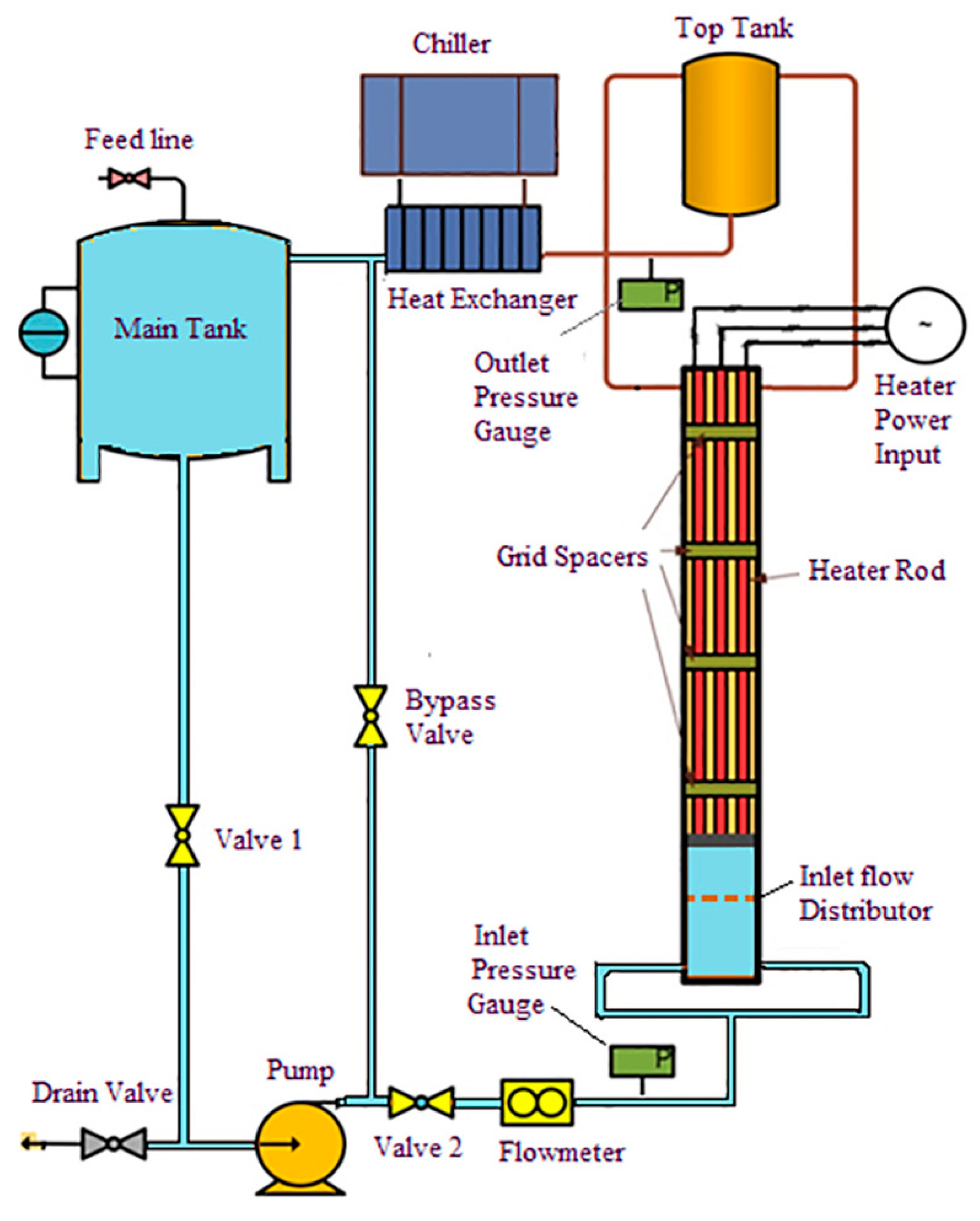
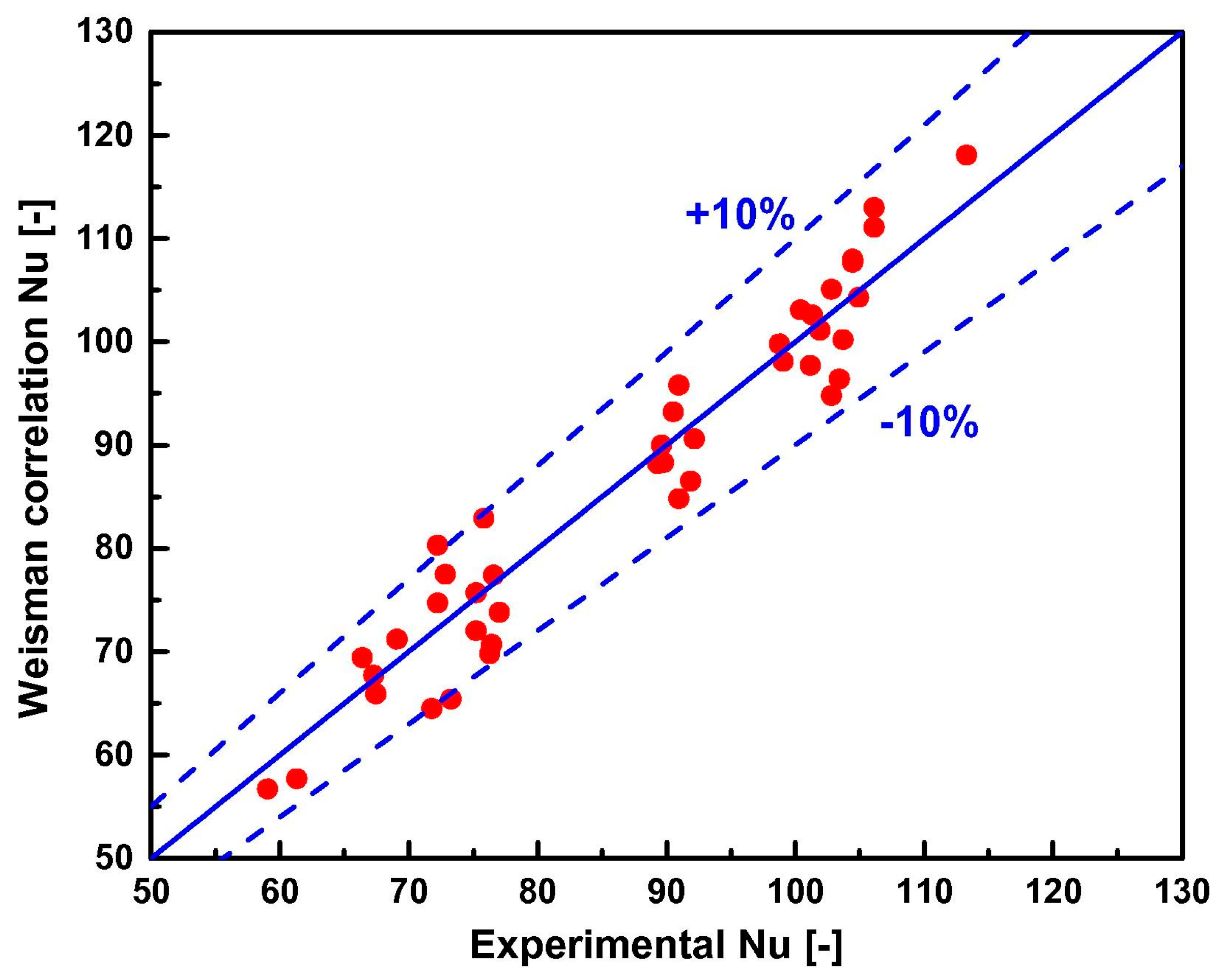

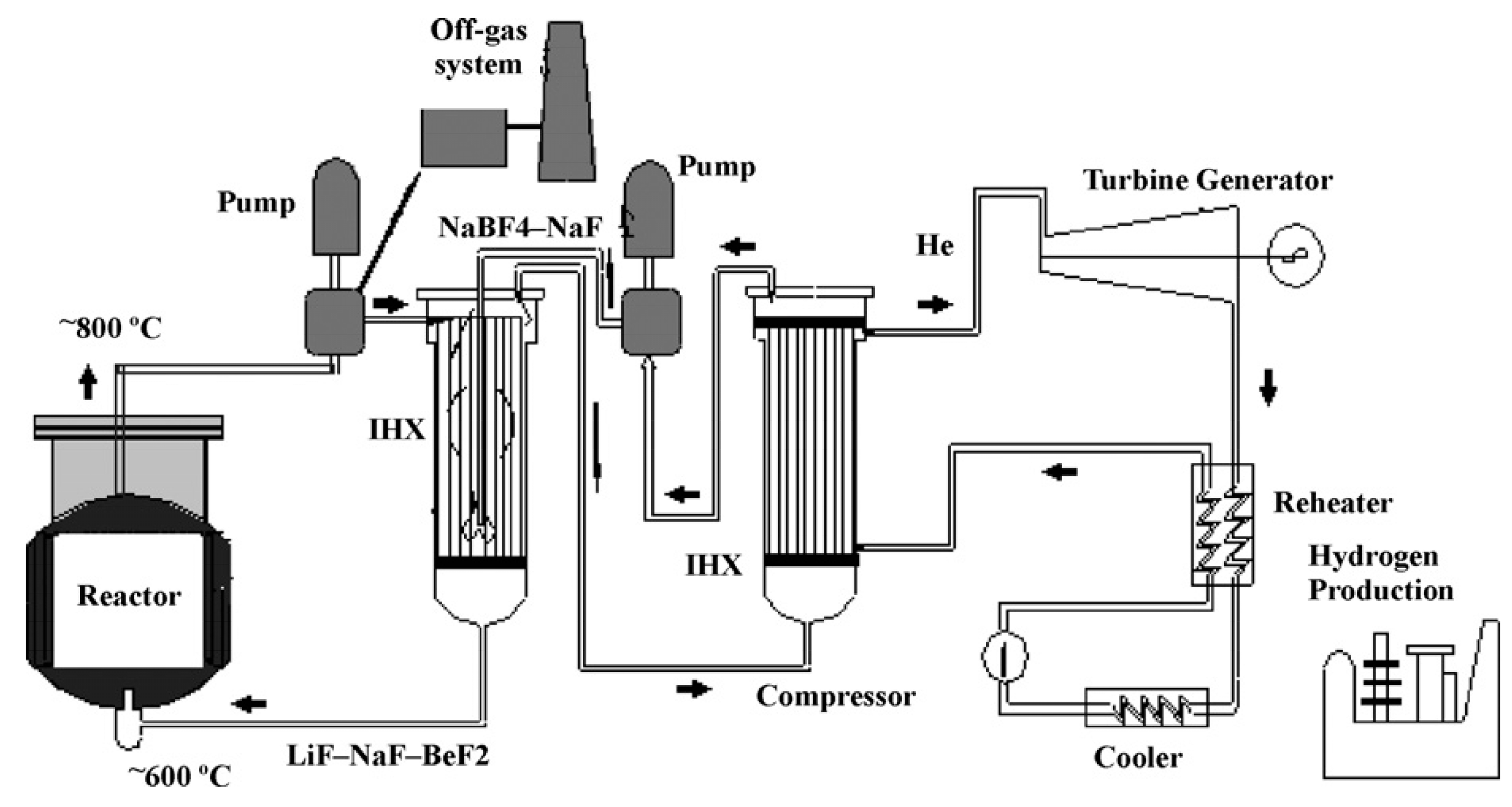
| Ref. | Field of the Research and Conditions | Correlation | Remarks/Applicability and Limitations | Equation No. |
|---|---|---|---|---|
| [2,3,15,16] | Hydro and thermo-dynamics 3D simulation of water–alumina nanofluid in a square array subchannel under typical PWR conditions (single-phase, turbulent flow, normal operation mode). The studies included both theoretical and numerical modeling. | φ is the volume concentration of nanoparticles, % 3·105 ≤ Re ≤ 6·106 0.847 ≤ Pr ≤ 1.011 1.25 ≤ P/D ≤ 1.35 0.5% ≤ φ ≤ 3.0% | (1) | |
| Re = 104–5·105 | (2) | |||
| [6,7,8] | Computational 2D simulation of turbulent natural convection of a molten core (emergency mode). | Pr = 7.0 107 ≤ Ra ≤ 5·1010 | (3) | |
| (4) | ||||
| 2.75 ≤ Pr ≤ 6.85 Ra ≤ 2·1012 | (5) | |||
| [9] | Numerical 3D simulation of transient heat transfer and melting process after a station blackout (emergency mode). | 0.1 < RaL1/4 d/L < 32 For water | (6) | |
| (7) | ||||
| 0.0006 < RaL1/4 d/L < 0.1 For steam | (8) | |||
| [10] | Experimental study of single-phase, turbulent convective heat transfer within the rod bundle area during normal operation. | (9) | ||
| Nuavg/Nufd—heat transfer enhancement; Kg—support grid pressure loss coefficient z—axial coordinate direction D∞—hydraulic diameter of typical subchannel | (10) | |||
| [11,12] | 3D computational simulation of thermal–hydraulic characteristics within the fuel rod bundle during normal operation mode (turbulent flow, single-phase). | Nu0—fully developed Nusselt number x—the axial distance from the downstream end of spacer D—hydraulic diameter of flow channel | (11) | |
| [13] | Experimental study on the impact of support grids on local, single-phase, turbulent heat transfer. | 2800 ≤ Ra ≤ 42,000 1.4 ≤ z/Dh ≤ 33.6 εs—blockage ratio of base grid strap with no flow-enhancing features z—axial coordinate direction Dh—hydraulic diameter of typical subchannel | (12) |
| Ref. | Field of the Research and Conditions | Correlation | Remarks/Applicability and Limitations | Equation No. |
|---|---|---|---|---|
| [18] | Combined radiation and convection heat transfer in rod bundles under emergency cooling conditions, (numerical, emergency conditions, two-phase, laminar, stationary, 3D). | 17 < Re < 70,000 | (13) | |
| [19] | Simulation and analysis of molten corium coolability in a boiling water reactor lower head (numerical, accidental conditions, two-phase, turbulent, non-stationary, 3D). | 108 < Ra < 1014 | (14) | |
| [20] | Simulation of melt pool heat transfer in a light water reactor pressure vessel lower head. Part I: Physical processes, modeling and model implementation (numerical, accidental conditions, two-phase, turbulent, non-stationary, 3D). | 5·1012 < Ra < 3·1013 Pr ≈ 7 | (15) | |
| (16) | ||||
| (17) | ||||
| [21] | Local heat transfer from the corium melt pool to the boiling water reactor pressure vessel wall (numerical, accidental conditions, two-phase, turbulent, non-stationary, 3D). | Ra = 5.86·1012 0.03 < Pr < 1.02 | (18) | |
| (19) | ||||
| NuSR—Steinberner–Reineke correlation Pr = 0.56 0 ≤ r ≤ 0.01 m | (20) | |||
| Pr = 0.56 0 ≤ r ≤ 0.01 m | (21) | |||
| Pr = 0.56 0.035 m < r | (22) | |||
| Pr = 0.03 0 ≤ r ≤ 0.02 m | (23) | |||
| Pr = 0.03 0.02 m ≤ r ≤ 0.07 m | (24) | |||
| Pr = 0.03 0.07 m < r | (25) | |||
| [22] | Effect of external cooling on the thermal behavior of a boiling water reactor vessel lower head (numerical, accidental conditions, laminar, single-phase, stationary, 2D). | Nu0 = 2 for spheres Nu0 = 0.36 for horizontal cylinders Nu0 = 0.68 for vertical plates Ra = 1.24·1017 | (26) | |
| Local Nusselt number for laminar film condensation on the vertical wall | (27) | |||
| Local Nusselt number for natural convection on vertical plate | (28) | |||
| [23] | Assessment of multiphase CDF with zero closure model for boiling water reactor fuel assemblies (numerical, normal operation, turbulent, two-phase, 3D). | Convective heat flux for liquid contact with the wall | (29) | |
| Convective heat flux for vapor contact with the wall | (30) | |||
| (31) | ||||
| [24] | Reflooding of a degraded boiling water reactor core (numerical, accident conditions. two-phase, turbulent, non-stationary, 3D). | Re > 2000; Nu = 4.36 for Re < 2000 | (32) | |
| [25] | New set of convective heat transfer coefficients established for pools and validated against CLARA experiments for application to corium pools (numerical, accidental conditions, two-phase, turbulent, 2D). | For pools of molten core, BWR and PWR v—vertical; h—horizontal; jg—superficial gas velocity | (33) | |
| (34) | ||||
| ReFrPr2.5 < 101.95 | (35) | |||
| ReFrPr2.5 ≥ 101.95 | (36) | |||
| ReFrPr2.5 < 103 | (37) | |||
| ReFrPr2.5 ≥ 103 | (38) | |||
| [26] | Mass flow rate sensitivity and uncertainty analysis in natural circulation boiling water reactor core from Monte Carlo simulations, (numerical, normal operation, single-phase, stationary, 1D). | (39) | ||
| (40) | ||||
| (41) | ||||
| (42) | ||||
| (43) | ||||
| [27] | TWOPORFLOW: A two-phase flow porous media code, main features and validation with BWR-relevant bundle experiments (numerical, accidental condition and normal operation, two-phase, stationary and transient, 3D). | Xtt is the Martinelli parameter | (44) | |
| [28] | Correlation for boiling heat transfer to saturated fluids in convective flow (numerical, normal operation, two-phase, turbulent, non-stationary, 3D). | (45) | ||
| (46) | ||||
| b—boiling | (47) | |||
| (48) | ||||
| (49) | ||||
| S approaches unity at a zero flow rate and zero at an infinite flow rate. | (50) | |||
| mac—macroconvective mic—microconvective | (51) | |||
| [29] | Core heat transfer coefficients immediately downstream of the rewetting front during anticipated operational occurrences for BWRs (experimental, abnormal conditions, turbulent, two-phase, non-stationary, 3D). | Fluid is assumed to have a fully developed turbulent velocity profile throughout the length of a pipe Pr = 0.7, 10, 100 50,000 < Re < 500,000 γ2n and An are dimensionless eigenvalues and constants, respectively | (52) | |
| [33] | AGENT-TH scheme: New thermal hydraulics (TH) code coupled with the AGENT neutronics code for light water reactors modeling and analysis (numerical, normal operation, two-phase, 1-, 2-, and 3D, non-stationary). | Le—entry length, distance of travel, before it fully develops (laminar flow) | (53) | |
| Before the flow reaches the entry length, L < Le 0.48 < Pr < 16 700 | (54) | |||
| For the fully developed region, L ≥ Le | (55) | |||
| For turbulent flow (Re > 10,000), 0.7 < Pr < 160 | (56) | |||
| [34] | Steady-state thermal–hydraulic analysis of a particle-bedded boiling water reactor (analytical, normal operation, turbulent, stationary, two-phase, 3D). | Single-phase flow | (57) | |
| Subcooled boiling | (58) | |||
| Single vapor flow | (59) | |||
| [35] | Validation and application of numerical modeling for in-vessel melt retention in corium pools, (numerical, accidental conditions, turbulent, single-phase, stationary, 3D). | 1015 < Raint < 1017 | (60) | |
| [36] | A MELCOR application to two light water reactor nuclear power plant core melt scenarios with assumed cavity flooding action (numerical, accidental conditions, turbulent, non-stationary, single-phase, 2D). | 1011 < Ra < 1014 | (61) | |
| (62) | ||||
| [37] | Modeling of severe accident and in-vessel melt retention possibilities in BWR type reactor (numerical, accidental conditions, single-phase, stationary, 2D). | First two are for the oxidic layer, third for the metallic | (63) |
| Ref. | Field of the Research and Conditions | Correlation | Remarks/Applicability and Limitations | Equation No. |
|---|---|---|---|---|
| [39,40] | Simple heat transfer correlations for turbulent tube flow (turbulent, 3D, single-phase, experimental, stationary). | L/D ≥ 60 0.7 < Pr < 10 0.6 < Pr < 160 Re > 10,000 n = 0.4 heated n = 0.3 cooled | (64) | |
| [41,42] | Heat transfer correlations for turbulent flow with high viscosity (turbulent, 1D, single-phase, experimental, stationary). | (65) | ||
| [39,42] | Gnielinski correlation (turbulent, 1D, single-phase, experimental, stationary). | (66) | ||
| [40] | Heat transfer in the critical region (transitional, 1D, single-phase, experimental, stationary). | Nux and Rex are evaluated at temperature tx: tx = tb for E < 0 tx = tpe for 0 ≤ E ≤ 1 tx = tw for E > 1 | (67) | |
| [7,9,10,11] | Heat transfer to water and steam at variable specific heat at near-critical region (turbulent, 1D, single-phase, experimental, stationary). | (68) | ||
| [44] | Heat transfer at supercritical region in flow of carbon dioxide and water in tubes, (turbulent, 1D, single-phase, experimental, stationary). | (69) | ||
| Consideration of the heat transfer properties of supercritical pressure water in connection with the cooling of advanced nuclear reactors, (turbulent, 1D, single-phase, experimental, stationary). | (70) | |||
| [43,44,45,46,47,48,49] | Heat transfer to supercritical fluids flowing in channels (1D, stationary and nonstationary). | Role of free convection in heat transfer | (71) | |
| Nu0 is the local value under turbulent flow in the circular tube [46] | (72) | |||
| [45] | Supercritical water flowing inside horizontal tubes. | tw ≥ 350 °C p = 233–263 MPa q = 0.58–4.65 MW/m2 | (73) | |
| 250 °C < tw < 350 °C | (74) | |||
| [47,50] | Forced convection heat transfer to water at near-critical temperature and supercritical pressures (turbulent, 1D, single-phase, experimental, stationary). | p = 22.7–27.6 MPa tb = 282–527 °C (bulk temperature) G = 651–3662 kg/m2s (mass flux) q = 0.31–3.46 MW/m2 | (75) | |
| [49] | Forced convective heat transfer to supercritical water flowing in tubes (turbulent, 1D, single-phase, experimental, stationary). | (76) | ||
| [50] | A new procedure for the prediction of forced convection heat transfer at near- and supercritical pressure (1D, laminar or turbulent, single-phase, experimental with some numerical modifications, stationary). | Modified Dittus–Boelter where constant is lowered to 70% | (77) | |
| [51] | Heat transfer to supercritical water in smooth-bore tubes (1D, turbulent, stationary, experimental based empirical equation, single-phase). | where, | p = 22.9–41.4 MPa tb = 75–576 °C (bulk temperature) tw = 93–649 °C (bulk temperature) G = 542–2150 kg/m2s (mass flux) | (78) |
| [51] | Refinement of transient criteria and safety analysis for a high temperature reactor cooled by supercritical water (1D, turbulent, stationary, experimental based empirical equation, single-phase). | Low enthalpy (0–1.5 MJ/kg) fc = 2.9·10−8 + 0.11/q″det Intermediate enthalpy (1.5–3.3 MJ/kg) fc = −8.7·10−8–0.65/q″det High enthalpy (3.3–4.0 MJ/kg) fc = −9.7·10−7 + 1.30/q″det | (79) | |
| [52] | Two-Phase Flow and Heat Transfer Study (turbulent, 1D, two-phase, experimental, stationary). | Hb > Hpc | (80) | |
| Hb < Hpc | (81) |
| Ref. | Field of the Research and Conditions | Correlation | Remarks/Applicability and Limitations | Equation No. |
|---|---|---|---|---|
| [56] | Development of a thermal–hydraulic system code, TAPINS, for a 10 MW regional energy reactor (numerical, turbulent, 1D, stationary, single-phase, stable). | Re < 10,000 | (82) | |
| [57] | Re > 10,000 | (83) | ||
| [58] | Numerical simulation of turbulent natural convection in an enclosure with a curved surface heated from below (numerical, turbulent, 2D, stable). | 109 ≤ Ra ≤ 5·1011 Ra = 5·1011 | (84) | |
| [59] | (85) | |||
| [60] | Numerical study of the effect of geometry on the behavior of internally heated melt pools for in-vessel melt retention (numerical, turbulent, 2D, non-stationary, emergency). | 1.270·1013 ≤ Ra ≤ 5.860·1015 | (86) | |
| [61] | LES of natural convection along the vertical wall applied for the scale of small modular reactor (numerical, turbulent, non-stationary problem, stable). | 2·106 < Ra < 1019 | (87) | |
| [64] | Indefinite sustainability of passive residual heat removal system of small modular reactor using dry air-cooling tower (numerical, 1D, stationary, two-phase, stable). | C = 0.023·(P/D) P/D is pitch-to-diameter ratio | (88) | |
| [66] | Experimental natural-convection heat transfer in liquids confined by two horizontal plates and heated from below. | 3·105 < Ra < 7·109 0.02 < Pr < 8750 | (89) | |
| [67] | Experience from the first two integrated approaches to in-vessel retention through external cooling (experimental, 3D, stationary, emergency). | 1012 < Ra < 7·1014 2.6 < Pr < 10.8 | (90) | |
| [67] | In-vessel coolability and retention of a core melt (experimental, emergency, 3D). | 1012 < Ra < 7·1014 2.6 < Pr < 10.8 | (91) | |
| [68] | Rod bundle thermal–hydraulics experiment with water and water–Al2O3 nanofluid for small modular reactor (experimental, turbulent, 3D, single- phase, stationary, stable). | ψ = 1.826·(P/D)−1.0430 1.1 ≤ P/D ≤ 1.3 for water | (92) | |
| [70] | Mixed convection heat transfer in a 5×5 rod bundles (experimental, turbulent, 3D, stationary, stable). | 1000 < Re < 30,000 0.9 < Pr < 1 1·10−6 < Bo < 5·10−12 | (93) | |
| (94) | ||||
| [71] | Effect of changing the outer fuel element diameter on thermophysical parameters of the KLT-40S reactor unit (turbulent, 3D, stationary, stable). | Re > 104 0.7 < Pr < 102 | (95) | |
| [72] | Implications of HALEU fuel on the design of SMRs and micro-reactors (numerical, 3D, non- stationary, stable). | 1.05 ≤ P/D ≤ 1.9 | (96) | |
| [73] | Thermal–hydraulic development a small, simplified, proliferation-resistant reactor (turbulent, 3D, stationary, stable). | 30 ≤ Re·Pr ≤ 2000 | (97) | |
| [74] | Convection heat transfer of alkali liquid metals and LBE in hexagonal bundles of uniformly heated tubes with helical spacers (experimental, turbulent, 3D, stationary, stable). | Bundles of 7–217 30 < Pe < 1070 1.194 < P/D < 1.31 | (98) | |
| [75] | Model development for the transient heat transfer in a corium pool (numerical, 3D stationary, emergency). | 2·1011 < Ra for water Ra < 1014 for ethanol H is characteristic length [m] | (99) |
| Ref. | Field of the Research and Conditions | Correlation | Remarks/Applicability and Limitations | Equation No. |
|---|---|---|---|---|
| [80] | Heat transfer enhancement in molten salt loop with a packed-bed tube (experimental, laminar and turbulent, single-phase). | Large Prandtl number Nusselt number and pressure drop increases for a packed-bed tubes | (100) | |
| [81] | Transition convective heat transfer with molten salt in a circular pipe (experimental, turbulent, single-phase). | No internal heat generation Re = 4100–9850 Pr = 13.7–18.4 | (101) | |
| No internal heat generation Re = 17,000–45,000 Pr = 12.7–14.7 | (102) | |||
| (103) | ||||
| [83] | Heat transfer in straight, smooth pipes with internal heat generation (steady state axial-symmetric numerical analysis, turbulent, single-phase). | Validated against experimental data 0.7 ≤ Pr ≤ 5 | (104) | |
| 5 ≤ Pr ≤ 100 | (105) | |||
| [84] | Natural convection with non-uniform heat generation in case of zero-power condition (steady state 2D numerical analysis, laminar, single-phase flow). | Pr = 11.6 | (106) | |
| [90] | Single-phase molten salt natural circulation loop (experimental and steady state numerical analysis, laminar, single-phase flow). | Pr = 41–98 Gr = 63·103–451·103 | (107) | |
| [91] | MSR equipped with heat pipes as heat removal system (experimental, laminar, single-phase). | Single heat pipe at the top | 4.86·106 ≤ Ra ≤ 1.16·107 | (108) |
| Single heat pipe in the middle | 3.97·106 ≤ Ra ≤ 1.14·107 | (109) | ||
| Single heat pipe at the bottom | 3.98·106 ≤ Ra ≤ 1.08·107 | (110) | ||
| [92] | MSR equipped with heat pipes as heat removal system (experimental, laminar, single-phase). | 5.7·106 ≤ Ra ≤ 1.31·107 | (111) | |
| [93] | Scaled MSR systems (transient numerical simulation using MARS-LMR code, turbulent, single-phase). | 0.6 ≤ Pr ≤ 160 ReD ≥ 10,000 L/D ≥ 10 | (112) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sikorska, D.; Brzozowska, J.; Pawełkiewicz, A.; Psykała, M.; Błasiak, P.; Kolasiński, P. Convective Heat Transfer in PWR, BWR, CANDU, SMR, and MSR Nuclear Reactors—A Review. Energies 2024, 17, 3652. https://doi.org/10.3390/en17153652
Sikorska D, Brzozowska J, Pawełkiewicz A, Psykała M, Błasiak P, Kolasiński P. Convective Heat Transfer in PWR, BWR, CANDU, SMR, and MSR Nuclear Reactors—A Review. Energies. 2024; 17(15):3652. https://doi.org/10.3390/en17153652
Chicago/Turabian StyleSikorska, Daria, Julia Brzozowska, Agata Pawełkiewicz, Mateusz Psykała, Przemysław Błasiak, and Piotr Kolasiński. 2024. "Convective Heat Transfer in PWR, BWR, CANDU, SMR, and MSR Nuclear Reactors—A Review" Energies 17, no. 15: 3652. https://doi.org/10.3390/en17153652
APA StyleSikorska, D., Brzozowska, J., Pawełkiewicz, A., Psykała, M., Błasiak, P., & Kolasiński, P. (2024). Convective Heat Transfer in PWR, BWR, CANDU, SMR, and MSR Nuclear Reactors—A Review. Energies, 17(15), 3652. https://doi.org/10.3390/en17153652







