Abstract
Climate change poses an unprecedented global challenge, which prompts nations to adopt new strategies to mitigate greenhouse gas emissions. The European Union emissions trading system (EU ETS) is a cornerstone of the EU’s efforts towards a cost-effective fight against climate change. This study examines the effectiveness of the EU ETS by analyzing monthly data from December 2008 to December 2021, with the focus on CO2 emission allowance futures prices, renewable energy indices, coal prices, oil prices, and fossil energy indices. The key findings are as follows: The CO2 emission allowance futures prices have averaged EUR 14.83 per ton, ranging from EUR 2.87 to EUR 76.81, which shows a significant upward trend. The renewable energy index also demonstrated strong growth, with a mean 1562.07 and maximum 4571.96. Coal prices have averaged EUR 65.32 per ton, while Brent oil prices averaged EUR 59.85 per barrel. A cointegration analysis revealed a long-run equilibrium relationship between these variables. The Vector Error Correction model (VECM) revealed significant negative responses to long-run equilibrium deviations of the renewable energy index (−0.0155) and oil prices (−0.0236), a significant negative short-run response of CO2 prices to their own lagged values (−0.223), and a significant positive short-run effect of oil prices on the fossil energy index (0.254). These results suggest the EU ETS has created significant linkages between carbon, energy, and financial markets. The study concludes that while the EU ETS has made progress in motivating emissions reductions and promoting renewable energy, the system’s efficacy still needs improvement.
1. Introduction
The European Commission (EC) has hailed its emissions trading system (EU ETS) as a crucial measure in the fight against climate change, so that the aim of achieving a carbon-neutral Europe by 2050 will be reached [1]. As a market-based instrument, the EU ETS aims to reduce carbon dioxide (CO2) emissions without the need for discretionary government intervention, like carbon taxes or regulation (see [2,3]). Upon its launch in 2005, the scheme covered 28 EU countries plus Norway, Iceland, and Liechtenstein, and was linked to the Swiss ETS. From the beginning of 2021, the UK ETS replaced British participation in the EU ETS.
The EU ETS aims to reduce greenhouse gas emissions by establishing a market price for CO2 emissions through tradable emission allowances. These financial assets get priced in allowance auctions (the primary market) and in market exchange (the secondary market). The secondary market is operated by the European Energy Exchange (EEX) in Germany and by Intercontinental Exchange Futures Europe (ICE-ECX) in the UK. One allowance entitles its holder company to emit one ton of CO2. The allowances must be used to compensate for emissions on a yearly basis. Otherwise, the companies face penalties, unless they have a surplus of allowances from previous years.
In Phase 1 (2005–2007) of the EU ETS, all allowances were allocated for free and the penalty for non-compliance was EUR 40 per ton of CO2. In Phase 2 (2008–2013), the system was revised to include market auctions and the penalty was increased to EUR 100 per ton. By the end of Phase 3 (2014–2020), the system covered about 40% of all greenhouse gas emissions in the EU, and 57% of the allowances were primarily auctioned. In Phase 4 (2021–2030), the sectors covered by the ETS, including industry, power generation and intra-European aviation, must reduce their emissions by 43% compared to the 2005 levels.
Economic measures like the EU ETS have gained strong scientific support. Brouwers et al. [4] showed that market instruments are effective in motivating emissions reductions, and Wang and Zhou [5] concluded that auctioning is the most efficient way to allocate the allowances. Nava et al. [6] used game theoretic models to show that the EU ETS reduces CO2 emissions in equilibrium, while Best et al. [7] provided empirical results showing that carbon emission pricing is effective in reducing CO2 emissions from fuel combustion. Furthermore, Vollebergh and Brink [8] highlighted the cost-efficacy of the EU ETS in reducing CO2 emission in Europe, and Gu et al. [9] confirmed that the same has been true in China, too.
As a market-oriented system, the EU ETS is expected to drive investments from fossil to clean energy. McCollum et al. [10] state that clean energy investments should outweigh global fossil energy investments by 2025 to fulfill the 2015 Paris Agreement [11]. These insights align with both emerging public opinion and the sentiment of responsible governments. For example, Germany is taking steps to reduce its coal use [12].
Proper functioning of the EU ETS hinges on three principles. The linking principle means that the market price of CO2 emission allowances should have explanatory power over the pricing of other energy assets. The leadership principle dictates that the CO2 allowance price should be the market leader, which the other energy asset prices would follow in the long run. Lastly, the direction principle states that an increase in the allowance price should lead to an increase in the price of clean energy assets and a decrease in the price of fossil energy assets. The intuition is that as the emission allowances make the production and use of fossil energy more expensive, the demand shifts from fossil to clean energy, thus affecting the asset prices in reverse order.
Since the asset price series tends to be nonstationary, these three principles must be scrutinized when analyzing the efficacy of the EU ETS. The relation between nonstationary assets can be assessed either by concentrating on returns (short-run effects), or by focusing on possible cointegration relations in prices (long-run effects). The latter requires identification of the relation over the whole observed period, whereas the relation in returns can last only one period.
The analysis of this paper proceeds in three steps. First, the earlier literature is reviewed to justify the use of monthly data in examining whether the five major European energy asset prices (including emission allowance prices) move together in the long run. That would reveal a linear cointegration among nonstationary energy assets, thereby supporting the linking principle. Second, possible leader–follower relationships are explored, to obtain support for the leadership principle. Third, the leaders and followers are identified, to gather evidence for the direction principle.
2. Literature Review
Creti et al. [13] conducted a study during Phase 2 of the EU ETS using daily data. They found cointegration between the allowance prices, Brent oil, coal, and the EuroStoxx50 index. Similarly, Charles et al. [14] found cointegration between the allowance prices and interest rates during Phase 2 with daily data. However, Koch et al. [15] found that cointegration disappeared when they used monthly data that covered the whole Phase 2.
It seems that the degree of correlation between energy assets depends both on the frequency of the data and on the number of lagged variables. Tian et al. [16] used daily data with one lag from 21st November 2005 to 5th December 2012 and found that changes in the EU ETS allowance prices were positively correlated with renewable energy stock returns and negatively correlated with fossil energy stock returns. Thus, their results indicated a short-run relationship. Da Silva et al. [17] used daily data from 1st January 2008 to 1st July 2014 and found cointegration between EU ETS prices and Spanish electricity industry prices, with a unidirectional Granger causality from allowance prices to electricity industry stock prices. The results held in Phase 2, but not at the beginning of Phase 3. Likewise, Jimenez-Rodriquez [18] failed to find cointegration between allowance prices and European stock indices when they used daily data over Phases 1, 2, and 3.
Ortas and Alvarez [19] had daily data consisting of stationary variables over Phase 2. They used the wavelet decomposition method and found that the EU ETS allowance returns and global energy commodity returns had time-varying lead–lag effects. The emission allowance returns were found to be the leaders and commodities returns were the followers in the long run. Soliman and Nasir [20] had daily data from 1st November 2007 to 31st October 2017 and found strong nonlinear co-movements between CO2 emission allowance returns, Brent oil returns, and natural gas returns, but they failed to detect cointegration. Garcia et al. [21] used daily panel data from six European countries and found cointegration between EU ETS allowance prices and European electricity asset prices. They detected a positive Granger causality from allowance prices to asset prices.
Jin et al. [22] used annual data of European green energy assets and fossil energy assets from 2000 to 2017 but were unable to find cointegration between the assets. He et al. [23] used weekly data from November 2003 to January 2020 and found nonlinear and positive cointegration between the European renewable energy stock index and oil prices. Hanif et al. [24] managed to find positive nonlinear and asymmetric long-run co-movements between European emission allowance returns and several renewable energy stock indices, using daily data from 18th May 2011 to 5th March 2020.
Chang et al. [25] detected unidirectional Granger causality from positive stock returns to reductions in CO2 emissions from coal combustion, using annual data from Austria, Belgium, Italy, and Norway over the preceding 50 years. Similarly, Kirikkaleli and Adebayo [26] found unidirectional causality from renewable energy consumption to CO2 emissions, using global annual data from 1985 to 2017.
In conclusion, the analysis of cointegration among European energy assets with daily, weekly, or annual data has mostly failed to reveal linear relationships. Therefore, we regard it advisable to choose monthly data in our cointegration analyses.
3. Data Description
Our data consist of EU ETS CO2 emission allowances, the European renewable energy stock index, European fossil energy stock index (containing 23 major European fossil fuel energy companies), coal ARA (delivered to Amsterdam, Rotterdam, or Antwerp), and Brent oil. The set of variables is reasonable because, in addition to renewable and fossil stock indices, they include the commodity assets coal ARA and Brent oil as representatives of major sources of CO2 emissions in Europe. Since the EU ETS operates in Euros, the coal ARA and Brent oil prices are converted to Euros.
The data are from Refinitiv Datastream, consisting of monthly prices over the period from December 2008 to December 2021, that is, over 157 months. The time span is due to the gradual maturation of the EU ETS from January 2005 to November 2008 (for discussion of data problems at the early stage of the EU ETS, see [27,28,29,30,31,32]). Table 1 describes the data.

Table 1.
Data Sources.
Table 2 presents the descriptive statistics of monthly prices and returns i.e., the changes in natural logarithmic price series. The prices are presented in Eurocurrency.

Table 2.
Descriptive Statistics.
Table 2 shows that the European emission allowances (CO2) have had the highest average monthly logarithmic returns of 1.025, indicating +12.3 logarithmic returns annually over the 157 months under study. At the other end, the European fossil energy stock index (Fo) has had the lowest average monthly logarithmic returns of 0.003, thereby resulting in +0.036 logarithmic returns annually. Note that the average returns are calculated before any dividends have been distributed to the stock indices.
Starting from Friedman [33] and Samuelson [34], the consensus is that competitive markets should create unique equilibria over time, producing stochastic trends and suggesting that all the series under analysis should be nonstationary. Substantial evidence in the economic literature supports the theory. Table 3 reports the Augmented Dickey–Fuller tests [35,36].

Table 3.
Unit root tests for monthly prices and returns (i.e., changes in natural logarithmic series).
The test results in Table 3 show that all the series are integrated of order one, I(1), because all changes of the natural logarithmic price series are stationary. Hence, all the series are nonstationary, and the first differences (i.e., returns) of the logarithmic series are stationary.
4. Method
4.1. Assessing the Direction Principle
The proper working of the EU ETS presumes that the emission allowance prices should have followed a significant upward trend during the study period, and the same should have happened with renewable energy assets. Meanwhile, fossil energy-related assets should have followed a significant downward trend due to changes in demand. Figure 1 shows the graphs of the monthly price series (solid line) and the adjusted nonlinear trend (dashed line) of European emission allowances (CO2), the European renewable stock index (Ae), coal ARA (Co), Brent oil (Oil), and European fossil energy stock index (Fo) between December 2008 and December 2021. The trend lines in all panels from 1a to 1e are fitted using a polynomial regression of order 2.
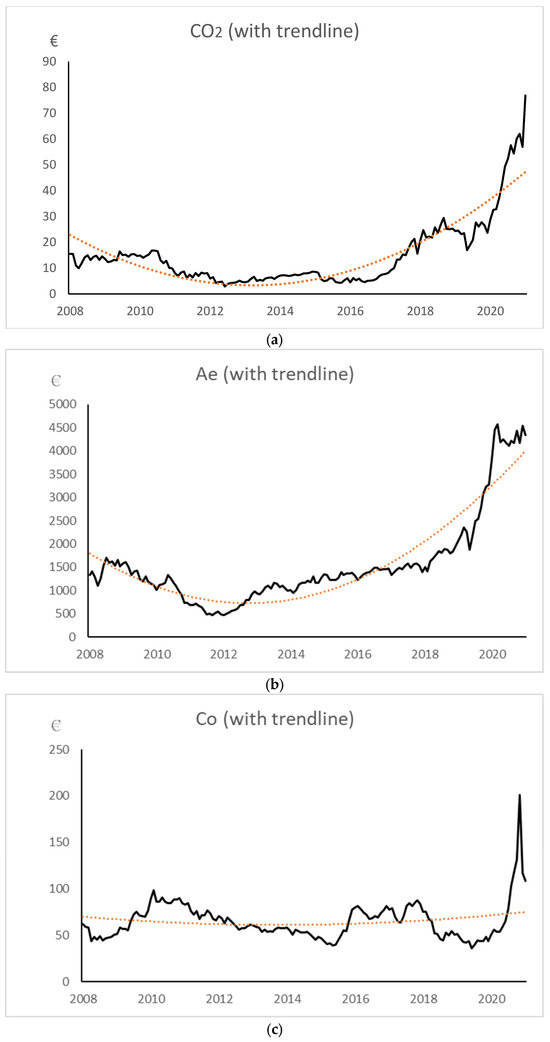
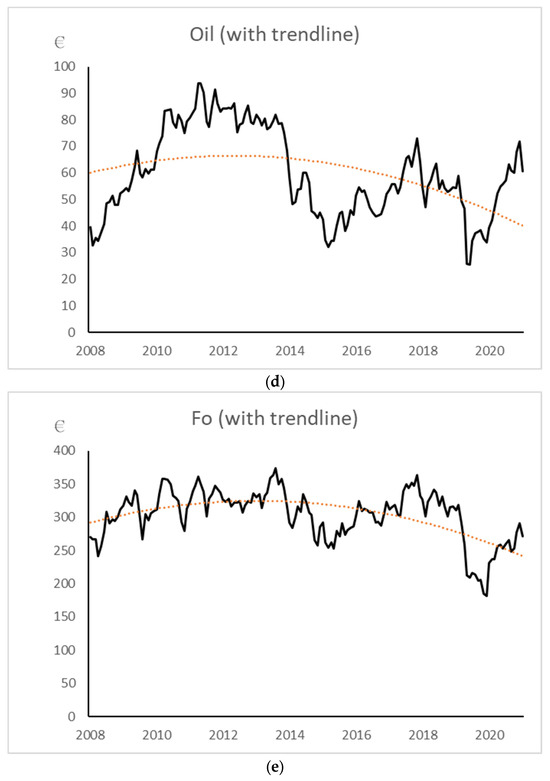
Figure 1.
Monthly prices with trendlines. (a) Panel CO2. (b) Panel Ae. (c) Panel Co. (d) Panel Oil. (e) Panel Fo.
In Figure 1, Panel CO2 presents the price fluctuation of the ICE-ECX one-month European carbon dioxide emission allowance futures, and the dashed line shows the significantly positive price trend during the study period. Panel Ae presents the prices of the Ardour Global Alternative Energy Index Europe and shows that the upward price trend is even steeper than that of CO2. Panel Co presents the prices for one ton of coal ARA (in one-month futures ICE-ECX in Euros), with a reasonably flat price trend during the period. Panel Oil shows the barrel prices of Brent crude oil (also in one-month futures ICE-ECX in Euros), with a significantly negative price trend. The last panel, Fo, presents the Euro values of the Stoxx600 Europe Oil & Gas price index, with a downward price trend. Hence, all but the coal ARA price trends are consistent with the direction principle as a prerequisite for the proper functionality of the EU ETS system.
As mentioned above, the trendlines in all panels of Figure 1, including Panels 1c and 1d, were fitted using a polynomial regression of order 2 (quadratic regression). This method was chosen because it allows for a more flexible fit than a simple linear trend, thus capturing potential nonlinear trends in the data, while still maintaining a relatively simple model. This approach provides a balance between capturing the overall trend and allowing for some curvature in long-term price movements, which makes it particularly useful for visualizing trends that may have changed direction or accelerated/decelerated over the 13-year period of our study.
4.2. Assessing the Linking and Leadership Principles
Several previous studies have documented higher-order interactions among energy assets (see, for example [37,38,39]). In this paper, we seek to provide evidence of long-run relationships between European energy-related assets by detecting linear cointegration with unidirectional Granger causality (note that Granger causality refers merely to a strong correlation, not to strict causality).
Figure 1 already confirmed that all prices except that of the coal ARA are consistent with the direction principle. However, as graphics may reveal spurious developments in the case that price series are nonstationary (see, for example [40]), further tests are needed. The existence of cointegration between the assets indicates real relationships between them, thus confirming the linking principle, while Granger causality [41,42] indicates lead–lag effects between the variables, thus confirming the leadership principle. Both properties must simultaneously prevail to warrant the proper functioning of the EU ETS in reducing CO2 emissions in a way that the allowance price acts as the market leader and the other energy-related asset prices are the followers in the long run.
For clarification, if CO2 and, e.g., Oil are cointegrated, they share a stationary linear combination of prices in the long run, which is a necessary condition for CO2 to affect Oil. In addition, if CO2 Granger-causes Oil, then Oil must react to changes in CO2 to be cointegrated, and CO2 leads Oil in the long run. Otherwise, CO2 and Oil would be equal variables in the equilibrium. A formal treatment of the procedure is presented in Appendix A.
Our empirical analysis contains the variables CO2, Ae, Fo, Co, and Oil, modeled according to Equation (A4) in Appendix A.
Table 4 reports the test results for the optimal lag structure of the variables.

Table 4.
VAR lag-order selection criteria.
By Table 4, both the final prediction error (FPE) and Akaike information criterion (AIC) say that lag two is optimal for the variables. Furthermore, Johansen [43] introduced a test for cointegration in the VAR space. Table 5 reports the findings.

Table 5.
Johansen cointegration test.
Table 5 suggests that, among the nonstationary variables CO2, Ae, Fo, Co, and Oil, there is one statistically significant cointegration relationship that can be estimated. The trace test implies one stationary relationship.
Granger causality [40,41] states that if a stochastic variable can significantly forecast another stochastic variable, then the former variable Granger-causes the latter. Table 6 presents the Likelihood Ratio (LR) tests in the cointegrated VAR space.

Table 6.
Likelihood Ratio Granger causality tests in VAR space.
By Table 6, the alphas of emission allowances, CO2, and coal prices, Co, can be restricted to zero. This implies that if the other variables react statistically significantly to the cointegration relationship (that is, there are statistically significant alphas in the stationary Vector Error Correction (VEC) model), then emission allowance and coal prices are the leaders, while the other variables are the followers in the long run. Taking CO2 and Co as leaders, the estimated cointegration relationship reads
Recall that while the variables CO2, Ae, Co, Oil, and Fo present nonstationary natural logarithmic prices, their linear combination is stationary (i.e., ECM). Note that the relationship must have a lag length of order one to estimate the parameters. Since Table 4 suggests two lags in the simultaneous estimations, the simultaneous VEC model is specified according to Equation (A5) in Appendix A.
In the ECM model, the dependent variables present the changes in the logarithms of the CO2 emission allowance price renewable energy stock index prices coal ARA prices Brent crude oil prices and European fossil energy stock index prices In addition, are the unknown parameters, and are the short-run reaction parameters to be estimated.
Moreover, according to the Likelihood Ratio (LR) Granger causality tests in Table 6, the short-run reaction of the changes in the logarithms of the CO2 allowance prices to the long-run equilibrium ECM, namely, , and the short-run reaction of the changes in the logarithms of coal prices to the long-run equilibrium ECM, namely, , are set to zero. Then, the primary interest is to examine the effect of the long-run relationship in Equation (A2), focusing on the parameters . In other words, the idea is to examine whether the statistically significant alphas and , and the statistically zero alphas and , can be found.
Table 7 reports the simultaneous equation VEC model and the Full Information Maximum Likelihood (FIML) estimation results. The Newey–West heteroskedasticity- and autocorrelation-consistent (HAC) standard errors show the short-run reactions that are subsumed in the long-run equilibrium of Equation (A5) in Appendix A.

Table 7.
VECM for reactions of long-run relationship and short-run reaction results of CO2 emission allowance and coal ARA.
Table 7 shows that the changes in the logarithmic European renewable stocks index (Ae), Brent oil prices (Oil), and European fossil energy stocks index (Fo) have statistically significant alphas at the 5% significance level in the VEC model. It also confirms that the emission allowance (CO2) and coal ARA (Co) prices do not react statistically significantly to the long-run equilibrium. This is to say that the EU carbon emission allowance price and coal ARA price have been the leaders, and the other variables have been the followers in the long run between December 2008 and December 2021.
Furthermore, Table 7 shows the estimation results of the short-run (one-month and two-month lags) reaction parameters according to the changes in logarithmic EU emission allowance and coal ARA prices. By the table, the changes in logarithmic coal ARA prices (ΔCot) react positively and statistically significantly to the previous month’s changes in the logarithmic emission allowance prices (ΔCOt−1) at a 5% significance level, and likewise to the lagged logarithmic Brent oil prices (ΔOilt−1) at a 1% level. On the other hand, the change in emission allowance price (ΔCO2t) reacts negatively and statistically significantly (at a 1% level) only to its own previous month’s change (ΔCO2t−1). The conclusion is that since the CO2 allowance price tends to make the coal ARA price rise after one month’s delay, the EU ETS emission allowance price is the leader and the coal ARA price is the follower in the short run.
5. Conclusions
This study examined the long-term relationships between key European energy-related assets over a 13-year period from December 2008 to December 2021, using monthly Eurocurrency data. The analysis revealed statistically significant evidence of cointegration between the market ratings of EU ETS allowances, Brent oil, coal ARA, the European renewable energy stock index, and European fossil energy stock index. These results support the linking principle between the selected variables. The direction principle was also found to hold, evidenced by the significantly positive price trends of CO2 emission allowance prices and the renewable energy stock index, and by the significantly negative price trends of Brent oil prices and the fossil energy stock index. Yet, coal Ara prices were observed to have a flat trend over the study period.
Cointegration helps to identify short-run responses to the long-run equilibrium. If a cointegrated variable does not react to the long-run equilibrium, it must be a leader among the cointegrated variables, while those that do react are the followers. Thus, detecting the leadership principle requires that the emission allowance price is the leader and other energy prices are the followers in the long-run equilibrium.
In this study, we found one cointegrating relationship among the variables such that it indicates a long-run equilibrium. Notably, both CO2 allowance prices and coal ARA prices emerged as leaders in the long run, while other variables including the renewable energy index, oil prices, and fossil energy index acted as followers. This finding contrasts with Koch et al. [15], who found no cointegration during Phase 2 of the EU ETS, but aligns more closely with Creti et al. [13] and Charles et al. [14], who managed to identify cointegration relationships using daily data. We used a broader timeframe with monthly data, which facilitated a more comprehensive view of the long-term market dynamics.
The main results showed that the EU ETS allowance price and coal price do not react statistically significantly to the long-run equilibrium. This means that they have been the leaders, while the other variables have been the followers in the long run between December 2008 and December 2021. However, the coal price has reacted positively to the previous month’s changes in allowance and oil prices, while the allowance price has reacted statistically significantly to its own previous month’s change. The positive reaction of the current coal price to the previous change in the allowance price tells that, in the short term, the EU ETS allowance has been the leader and the coal ARA price has been the follower.
We provided a unique contribution by showing a significant short-run influence from CO2 allowance prices to coal ARA prices with a one-month lag. This short-term relationship, combined with the identified long-term leadership roles, offers a nuanced perspective on the EU ETS’s effectiveness, which the previous studies have not captured.
The long-term leadership of coal ARA prices, contrary to the aims of the EU ETS, is indeed a somewhat counterintuitive finding of our study. There are both historical and economic factors behind this complexity. First, many European countries are significant exploiters of coal resources and increasingly concerned about their energy security. For example, Germany and Poland have historically trusted in coal in their baseload power generation, and Germany’s decision to phase out nuclear power has had its own effects. All this creates inertia in energy transition. Second, coal often remains a cost-competitive energy source, especially when considering the infrastructure already in place for its use. This economic advantage can persist, even in the face of any carbon pricing mechanisms. The shift from coal-based energy production is a gradual process, since the existing coal-fired power plants have long operational lifespans and replacing them takes time and huge investments.
In any case, the coal ARA price is still a key benchmark in the European energy market, thus affecting the market dynamics. The coal ARA price is also influenced by global coal markets, and the high demand of coal in the emerging economies may well contradict EU climate policy objectives. There are also some policy inconsistencies within the EU, like subsidies for regions dependent on coal production, which distort the efficacy of the EU ETS. Lastly, there are some defects in the EU ETS itself, like the over-allocation of emission allowances permits and price constraints.
The long-term leadership of coal ARA prices highlights a significant challenge to the EU’s efforts in transitioning from fossil fuels towards clean energy. It suggests that while the EU ETS has been effective in many ways, additional policy measures may be necessary to overcome the entrenched position of coal in the European energy mix. Our findings highlight the complex dynamics between carbon pricing, energy markets, and climate policy, suggesting that while the EU ETS has made progress, there is still room for improvement in its ability to drive substantial emissions reductions. Our comprehensive analysis of both short-term and long-term relationships provides valuable insights for policymakers and researchers who try to enhance the effectiveness of the market-based emissions trading system.
In summary, this study shows that the EU ETS has largely succeeded in steering European energy-related stock indices and Brent oil prices, thereby supporting the role of market-based approaches in tackling climate change. In the long run, a rise in the EU ETS allowance price can cause the European renewable energy stock index to rise, and the European fossil energy stock index and Brent oil prices to fall, and vice versa. From this viewpoint, the EU ETS seems to have worked appropriately in steering the EU towards carbon neutrality and more general environmental goals. Yet, the long-term leadership of coal somewhat mitigates the efficacy of the EU ETS in its battle against climate change.
This paper raises several interesting issues for future research. It is important to dig deeper into why coal ARA prices act as they have done, to what extent the phenomenon deteriorates the efficacy of the EU ETS, and what could be done from the policy perspective. An obvious line of research would also be to study how external events, like the crises after 2021, affect the direction-linking leadership pattern of the EU ETS and thus its efficacy. Furthermore, it would be interesting to compare the EU ETS with other large emissions-trading systems and their policy lessons.
Author Contributions
Conceptualization, C.-L.C., J.I. and H.L.; methodology, C.-L.C., J.I. and H.L.; software, C.-L.C. and J.I.; formal analysis, C.-L.C. and J.I.; resources, J.I. and H.L.; writing—original draft preparation, J.I. and H.L.; writing—review and editing, C.-L.C., J.I. and H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request from the authors.
Acknowledgments
The authors are deeply grateful to the late Michael McAleer (RIP) for his valuable insights on earlier drafts of this paper. The first author extends thanks to the National Science and Technology Council (NSTC), Taiwan, for their support. Special thanks are also extended to the Institute of Economic Research, Kyoto University (KIER), where this research was revised during the first author’s tenure as a visiting professor.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Following ref. [40], assume nonstationary variables and with variances and . As (in the long run), , . A stationary linear combination , suggests that and are cointegrated and is finite. If so, the nonstationary variables and are connected in the long run. Note that if , then as , so that cointegration is a necessary condition for a long-run connection between and .
The Granger representation theorem tells us that if cointegration exists between and , then an error correction mechanism (ECM) must also exist. Write
where and are unknown parameters, , and , are correlated white noise processes. Subtracting lagged values from both sides of the equations and defining produces the following autoregressive form:
where denotes changes in the variables, and and include a linear combination. Then, the error correction model reads
where is the error correction mechanism (ECM) that is a stationary linear combination of nonstationary variables, and is a reaction parameter for the changes in variables to the ECM. When , the model becomes
where . Even though and are cointegrated, only reacts to the long-run equilibrium indicating that is a leader and is a follower in the long run (with lagged).
Furthermore, ref. [44] introduced a simultaneous equation model, namely, the vector autoregressive (VAR) model, where the distinction between endogenous and exogenous variables does not have to be determined in advance. In our context,
where are unknown parameters to be estimated, and and are assumedly white noise processes (note that lagged changes and should be added into the model until and are white noise processes).
The VAR model assumes that the variables and are stationary, in Equation (A4). Yet, as suggested by ref. [40], linear combinations of nonstationary variables can also be stationary, if they are regarded to be in an equilibrious relationship that makes them move together in the long run. If so, the nonstationary series are cointegrated, which can be considered as a sign of long-run predictability, and the direction of Granger causality (namely, a strong correlation) can also be identified.
Including ECM into Equation (A4), cointegration can be modeled with the Vector Error Correction (VEC) model as
where is the lagged ECM and is a parameter that reveals how the dependent variable reacts to the long-run equilibrious relationship.
References
- European Commission. 2021. Available online: https://ec.europa.eu/clima/policies/ets_en (accessed on 20 December 2023).
- Eskander, S.; Fankhauser, S. Reduction in greenhouse gas emissions from national climate legislation. Nat. Clim. Chang. 2020, 10, 750–756. [Google Scholar] [CrossRef]
- Koch, N.; Naumann, L.; Pretis, F.; Ritter, N.; Schwarz, M. Attributing agnostically detected large reduction in road CO2 emissions to policy mixes. Nat. Energy 2022, 7, 844–856. [Google Scholar] [CrossRef]
- Brouwers, R.; Schoubben, F.; Van Hulle, C.; Van Uytbergen, S. The initial impact of EU ETS verification events on stock prices. Energy Policy 2016, 94, 138–149. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, P. Does emission permit allocation affect CO2 cost pass-through? A theoretical analysis. Energy Econ. 2017, 66, 140–146. [Google Scholar] [CrossRef]
- Nava, C.; Meleo, L.; Cassetta, E.; Morelli, G. The impact of the EU ETS on the aviation sector: Competitive effects of abatement efforts by airlines. Transp. Res. Part A Policy Pract. 2018, 113, 20–34. [Google Scholar] [CrossRef]
- Best, R.; Burke, P.; Jotzo, F. Carbon pricing efficacy: Cross-country Evidence. Environ. Resour. Econ. 2020, 77, 67–94. [Google Scholar] [CrossRef]
- Vollebergh, H.; Brink, C. What can we learn from EU ETS? ifo DICE Rep. 2020, 18, 23–29. [Google Scholar] [CrossRef]
- Gu, G.; Zheng, H.; Tong, L.; Dai, Y. Does carbon financial market as an environmental policy tool promote regional energy conversation and emission reduction? Evidence from China. Energy Policy 2022, 163, 112826. [Google Scholar] [CrossRef]
- McCollum, D.; Zhou, W.; Bertram, C.; de Boer, H.; Bosetti, V.; Busch, S.; Despres, J.; Drouet, L.; Emmerling, J.; Fay, M.; et al. Energy investment needs fulfilling the Paris Agreement and achieving the sustainable development goals. Nat. Energy 2018, 3, 589–599. [Google Scholar] [CrossRef]
- Paris Agreement. Decision1/CP.17; UNFCCC: New York, NY, USA, 2015. [Google Scholar]
- Rinscheid, A.; Wüstenhagen, R. Germany’s decision to phase out coal by 2038 lags behind citizen’ timing preferences. Nat. Energy 2019, 4, 856–863. [Google Scholar] [CrossRef]
- Creti, A.; Jouvet, P.-A.; Mignon, V. Carbon price drivers: Phase I versus Phase II equilibrium? Energy Econ. 2012, 43, 327–334. [Google Scholar] [CrossRef]
- Charles, A.; Darne, O.; Fouilloux, J. Market efficiency in the European carbon markets. Energy Policy 2013, 60, 785–792. [Google Scholar] [CrossRef]
- Koch, N.; Fuss, S.; Grosjean, G.; Edenhofer, O. Causes of the EU ETS price drop: Recession, CDM, renewable policies or bit of everything? New evidence. Energy Policy 2014, 73, 676–685. [Google Scholar] [CrossRef]
- Tian, Y.; Akimov, A.; Roca, E.; Wong, V. Does the carbon market help or hurt the stock price of electricity companies? Further evidence from the European context. J. Clean. Prod. 2016, 112, 1619–1626. [Google Scholar] [CrossRef]
- Da Silva, P.P.; Moreno, B.; Figueiredo, N.C. Firm specific impacts of CO2 prices on the stock market value of the Spanish power industry. Energy Policy 2016, 94, 492–501. [Google Scholar] [CrossRef]
- Jimenez-Rodriguez, R. What happens to the relationship between EU allowances prices and stock market indices in Europe? Energy Econ. 2019, 81, 13–24. [Google Scholar] [CrossRef]
- Ortas, E.; Alvarez, I. The efficacy of the European Union Emissions Trading Scheme: Depicting the co-movement of carbon assets and energy commodities through wavelet decomposition. J. Clean. Prod. 2016, 116, 40–49. [Google Scholar] [CrossRef]
- Soliman, A.; Nasir, M. Association between the energy and emission prices: An analysis of EU emission trading system. Resour. Policy 2019, 61, 369–374. [Google Scholar] [CrossRef]
- Garcia, A.; Garcia-Alvarez, M.; Moreno, B. The impact of EU allowance prices on the stock market indices of the European power industries: Evidence from the ongoing EU ETS Phase III. Organ. Environ. 2020, 34, 1–20. [Google Scholar] [CrossRef]
- Jin, W.; Shi, X.; Zhang, L. Energy transition without dirty capital stranding. Energy Econ. 2021, 102, 105508. [Google Scholar] [CrossRef]
- He, X.; Mishra, S.; Aman, A.; Shahbaz, M.; Razzaq, A.; Sharif, A. The linkage between clean energy stocks and the fluctuations in oil price and financial stress in the US and Europe? Evidence from QARDL approach. Resour. Policy 2021, 72, 102021. [Google Scholar] [CrossRef]
- Hanif, W.; Hernandez, J.; Mensi, W.; Kang, S.; Uddin, G.; Yoon, S.-M. Nonlinear dependence and connectedness between clean/renewable energy sector equity and European emission allowance prices. Energy Econ. 2021, 101, 105409. [Google Scholar] [CrossRef]
- Chang, C.-L.; Ilomäki, J.; Laurila, H.; McAleer, M. Causality between CO2 emissions and stock markets. Energies 2020, 13, 2893. [Google Scholar] [CrossRef]
- Kirikkaleli, D.; Adebayo, T. Do renewable energy consumption and financial development matter for environmental sustainability? New global evidence. Sustain. Dev. 2021, 29, 583–594. [Google Scholar] [CrossRef]
- Daskalakis, G.; Markellos, R. Are the European carbon markets efficient? Rev. Futures Mark. 2008, 17, 103–128. [Google Scholar]
- Montagnoli, A.; de Vries, F. Carbon trading thickness and market efficiency. Energy Econ. 2010, 32, 1331–1336. [Google Scholar] [CrossRef]
- Alexeeva-Talebi, V. Cost pass-through of the EU emissions allowances: Examining the European petroleum markets. Energy Econ. 2011, 33, S75–S83. [Google Scholar] [CrossRef]
- Medina, V.; Pardo, A.; Pascual, R. The timeline of trading frictions in the European carbon market. Energy Econ. 2014, 42, 378–394. [Google Scholar] [CrossRef]
- Oestreich, M.; Tsiakas, I. Carbon emissions and stocks returns: Evidence from the EU emissions trading scheme. J. Bank. Financ. 2015, 58, 294–308. [Google Scholar] [CrossRef]
- Chang, C.-L.; Ilomäki, J.; Laurila, H.; McAleer, M. Moving average market timing in European energy markets: Production versus emissions. Energies 2018, 11, 3281. [Google Scholar] [CrossRef]
- Friedman, M. Essays in Positive Economics; University of Chicago Press: Chicago, IL, USA, 1953. [Google Scholar]
- Samuelson, P. Proof that properly anticipated prices fluctuate randomly. Ind. Manag. Rev. 1965, 6, 4–12. [Google Scholar]
- Dickey, D.; Fuller, W. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Phillips, P.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Mai, T.-K.; Foley, M.; McAleer, M.; Chang, C.-L. Impact of COVID-19 on returns-volatility spillovers in national and regional carbon markets in China. Renew. Sustain. Energy Rev. 2022, 169, 112861. [Google Scholar] [CrossRef]
- Dai, X.; Xiao, L.; Wang, Q.; Dhesi, G. Multiscale interplay of higher-order moments between the carbon and energy markets during Phase III of the EU ETS. Energy Policy 2021, 156, 112428. [Google Scholar] [CrossRef]
- Chang, C.-L.; McAleer, M.; Wang, Y. Testing co-volatility spillovers for natural gas spot, futures and ETS spot using dynamic conditional covariances. Energy 2018, 151, 984–997. [Google Scholar] [CrossRef]
- Engle, R.; Granger, C. Co-integration and error correction: Representation, estimation, and testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Granger, C. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Granger, C. Testing for causality: A personal viewpoint. J. Econ. Dyn. Control 1980, 2, 329–352. [Google Scholar] [CrossRef]
- Johansen, S. Statistical analysis of cointegration vectors. J. Econ. Dyn. Control 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Sims, C. Macroeconomics and reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).