1. Introduction
A virtual power plant (VPP) is an energy management system realized through advanced information and communication technologies. Reference [
1] proposes integrating distributed generation, controllable loads, and storage devices for energy management and scheduling, thereby reducing the impact of the uncertainties associated with distributed generation on the stable operation of the power system. As the scale of distributed generation continues to expand, VPPs offer a broader space for improving energy utilization efficiency in the electricity market.
The control problem of peak shaving demand response (DR) participation in a virtual power plant involves the effective integration of the downward adjustment potential of a large number of distributed energy resources (DERs) to dynamically track predefined target load profiles. These target load profiles can be determined based on settlement results from electricity ancillary service markets [
2], customized operational strategies [
3], and discrepancies between DR baselines and actual response capacities [
4]. This control problem can be classified into two approaches: open-loop and closed-loop methods. Conventional open-loop control methods are suited for centrally dispatching energy storage systems, gas turbines, and other DERs with strong control capabilities within VPP operations [
5]. DERs with weaker control authority, such as air conditioning units, are more suitable for participating in peak shaving DR using adaptive closed-loop control methods that require rapid adaptation to changes. It should be noted that the effectiveness of closed-loop control methods may be adversely affected by uncertainties such as control delays and model-measurement errors [
6].
Reference [
7] proposes that many scholars both domestically and internationally have conducted extensive research on demand-side management inspired by game theory. For instance, reference [
8] considers the degree of demand response while setting electricity prices at the VPP control center, ultimately establishing a Stackelberg game optimization model for the internal units of the VPP. Reference [
9] proposes the concepts of “price-based quantity” and “quantity-based price” in the context of electric vehicle charging management, modeling the pursuit of maximum benefits by users and electricity retailers as a Stackelberg game. Reference [
10] presents a real-time optimal control model for demand-side response based on the Stackelberg game, with electricity retailers as leaders and various loads as followers, obtaining optimal strategies for all participants. Reference [
11] establishes a two-tier Stackelberg game model for market transactions involving electric vehicle operators and distributed generators. Reference [
12] constructs a two-stage Stackelberg model considering the operational hierarchy of the electricity market, involving the upper-level market, electricity retailers, and users. However, these studies mainly focus on demand-side management without game modeling for energy-side units, which is crucial for reducing power wastage on the energy side.
Deep reinforcement learning (DRL) provides powerful algorithms for solving problems in power system research. Reference [
13] proposes an optimization method for the operation of a photovoltaic-storage combined power plant’s energy storage system in the spot market environment based on DQN (Deep Q-network), considering deviation penalty costs, energy revenue, and frequency regulation ancillary service revenue, to maximize the economic benefits of the PV-storage combined power plant. Reference [
14] introduces the DDPG (Deep Deterministic Policy Gradient) algorithm, utilizing the experience replay mechanism and proportionally regulating perception learning to effectively enhance algorithm stability, successfully applied to the dynamic energy scheduling of power systems. References [
15,
16] propose the application of both the DDQN (Double Deep Q-network) algorithm and the Dueling-DQN (Dueling Deep Q-network) algorithm to the optimal scheduling of power systems. Additionally, reference [
17] uses the D3QN (Dueling Double Deep Q-network) algorithm for real-time energy management, but this algorithm may encounter strategy oscillation issues in continuous and complex decision-making environments, primarily because it relies on extensive exploration to maintain performance, potentially leading to instability in rapidly changing environments.
This paper designs a VPP containing energy storage, micro gas turbines, wind farms, photovoltaics, and temperature-controlled loads. Under the framework of setting electricity sales and purchase price strategies at the VPP control center with energy storage, considering the flexibility of micro gas turbines and the dispatchability of demand response resources, a VPP operation optimization model based on the Stackelberg game is established. An improved D3QN algorithm is proposed to adapt to the interactive supply and demand within the VPP, and the economic efficiency of the proposed model is verified through case studies.
The remaining sections of this work are organized as follows:
Section 2 presents the modeling of sources, loads, and storage within the virtual power plant.
Section 3 introduces the Stackelberg game model, focusing on the game-theoretic modeling between the virtual power plant and gas turbines.
Section 4 employs deep reinforcement learning to solve the game model, specifically attempting to integrate the D3QN algorithm with the electricity market to address strategic interactions in the virtual power plant context. In
Section 5, a case study is used to analyze and compare the algorithm, thereby validating its practical effectiveness. Finally,
Section 6 summarizes the main conclusions of this paper and outlines potential future research challenges.
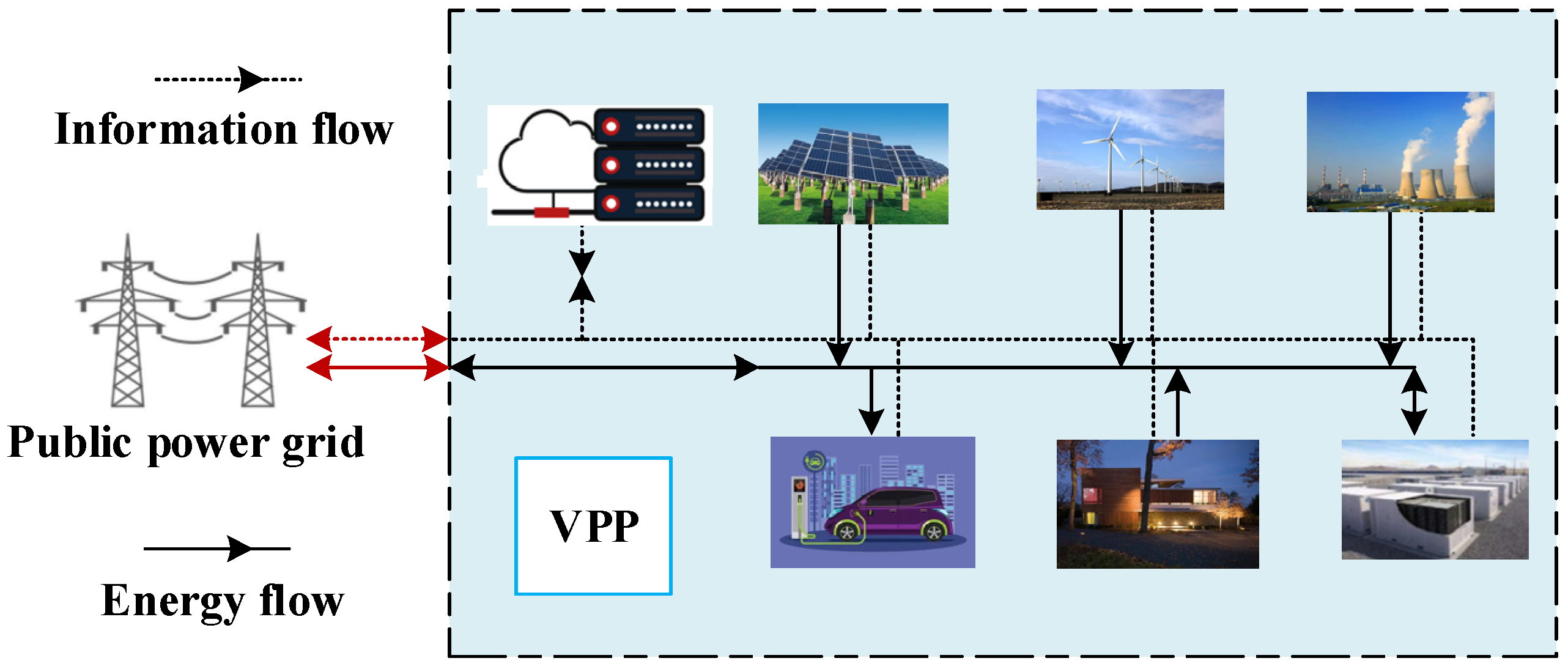
2. Framework of Virtual Power Plant with Energy Storage
The number of loads within a virtual power plant jurisdiction can be quite large, making it impractical for the dispatch center to manage each load individually. A more feasible approach to categorize the loads and model different types of loads separately is proposed in Reference [
18]. To streamline optimization, the load user groups within the VPP are equivalently considered as non-dispatchable loads and temperature-responsive loads, with the latter divided into air conditioning loads and water heater loads. In addition to distributed generation and loads, the VPP also includes energy storage and gas turbines, as shown in
Figure 1.
The operation of each entity within the VPP is as follows: The VPP control center predicts the output of distributed generation within the virtual power plant for the next day based on historical data and sets reasonable electricity purchase and sale prices in advance. It then selects the set temperatures for air conditioning and water heater loads based on weather information and real-time electricity prices. Finally, the micro gas turbine optimizes its output throughout the day based on the electricity prices provided by the VPP to maximize its own revenue.
This paper investigates the energy optimization and scheduling problem of a VPP. The VPP is connected to the main grid, allowing it to purchase electricity from the main grid in case of a power shortage and sell electricity to the main grid in case of a power surplus. This effectively addresses the supply–demand imbalance issues during the operation of the VPP system.
2.1. Distributed Generation Units
Distributed generation components are the core elements of a VPP. As the penetration rate of renewable energy generation within the VPP continues to increase, the uncertainty and variability of its power output present challenges for the economic operation of the VPP. The distributed generation data used in this paper are processed from real-time power generation data of typical photovoltaic and wind power plants in the East China region.
2.2. Micro Gas Turbine Power Generation
On the power supply side, there is a micro gas turbine primarily fueled by natural gas to provide electrical energy to the user side. The relationship between its fuel cost and the output electrical power of the unit in the
time period within a day can be expressed as
In the equations, represents the generation cost of the micro gas turbine during time period . represents the electricity generated by the micro gas turbine during time period . represents the unit price of natural gas. represents the lower heating value of natural gas. represents the efficiency of the gas turbine. represents the minimum active power of the generator. represents the minimum active power of the generator. and represent the power output of the gas turbine at the current moment and the previous moment, respectively. and represent the upper and lower limits of the ramping power of the gas turbine.
2.3. Constant-Temperature Control Load
2.3.1. Air Conditioning Load Model
The power variation of the air conditioning system is generally related to the temperature difference between indoors and outdoors. To model the air conditioning system, including the influence of outdoor temperature on its performance, a variation model dependent on outdoor temperature can be introduced. This type of model more accurately reflects the operational efficiency of the air conditioning system under different environmental temperatures. A common approach is to represent
as a function of outdoor temperature:
In these equations, represents the heat or cold load caused by the temperature difference between indoors and outdoors. The calculation method may vary depending on the cooling or heating requirements. is the heat transfer coefficient, representing the insulation performance of the building, with units of kW/°C. is the indoor temperature. represents the power consumption of the air conditioning load at time . is the performance coefficient of the air conditioning system, which varies with outdoor temperature . , , and are model parameters obtained through fitting with actual data. represents the outdoor temperature.
The air conditioning switch is set to
In this equation,
and
represent the states of the air conditioning system at the current moment and the previous moment, respectively.
represents the upper limit of the set temperature, while
represents the lower limit of the set temperature. The power of the air conditioning can be obtained as
An air conditioning energy consumption model has been obtained that takes into account the influence of outdoor temperature. This model can calculate the power consumption of the air conditioning system based on different outdoor temperatures, thereby assisting the virtual power plant in optimizing its dispatching strategy to adapt to various environmental conditions and operational efficiencies.
2.3.2. Water Heater Load Model
Electric water heaters are primarily used for bathing and kitchen water in daily life, and their internal load must accurately reflect the water usage habits at different times. Throughout the day, peak periods of hot water demand occur during morning and evening bathing peaks and meal preparation periods, during which the electricity consumption of the water heater noticeably increases.
Probability density functions for water heater usage are established for different time periods, and the overall probability density is calculated by integrating the probability density functions across different time periods. This probability density can describe the variation in the probability of water heater usage at different times throughout the day, as shown in Equation (9):
In these equations, represents the probability density of water usage during different time periods, including morning bathing, breakfast, lunch, dinner, and evening bathing.
Similar to air conditioning switch settings, electric water heater switches can be configured as follows:
In this equation, and represent the states of the water heater system at the current moment and the previous moment, respectively. represents the upper limit of the set temperature, while represents the lower limit of the set temperature.
2.4. Energy Storage Battery Model
The VPP control center directly controls the charging and discharging actions of the energy storage battery component. The charging and discharging constraints of the energy storage battery are as follows:
In these equations, represents the state of charge of the energy storage battery at time . and represent the charging and discharging amounts of the energy storage device at time . is a Boolean variable indicating the state of the energy storage device at time . and represent the charging power limits. and represent the efficiency of the energy storage charging and discharging equipment. represents the maximum capacity of the energy storage. represents the state of charge of the battery at the beginning of the day. represents the state of charge of the battery at the end of the day.
3. Real-Time Interactive Stackelberg Game Model
3.1. Stackelberg Game Framework
To study the game optimization operation of internal units within a VPP, this paper establishes a Stackelberg game model featuring the VPP control center and a micro gas turbine as the main entities, as shown in
Figure 2.
The upper-level leader is the VPP control center, while the lower-level follower is the micro gas turbine. Both the VPP control center and the micro gas turbine aim to maximize their respective profits. The decision variable for the VPP control center is the electricity purchase price from the micro gas turbine, and the decision variable for the micro gas turbine is its own power generation output.
The upper-level leader, the VPP control center, is constrained by the status of temperature-responsive loads, the operation status of energy storage, and the electricity purchase price from loads. The lower-level follower, the micro gas turbine, is constrained by its maximum and minimum operational power, as well as its maximum ramp rate.
3.2. Objective Function Design
Economic dispatch aims to maximize expected returns. To achieve the economic optimal operation control of the VPP control center, this paper takes the maximum operating profit of the VPP control center as the objective function for the economic optimization scheduling of the VPP. The operational costs for the VPP control center mainly include the cost of purchasing electricity from the micro gas turbine, the cost of distributed generation, and the cost of purchasing electricity from the main grid. The revenue of the VPP primarily comes from the profits gained from meeting various power load demands and selling electricity to the main grid. Therefore, the objective function of the VPP control center is set as follows:
In this equation, represents the profit of the VPP control center at time . is the electricity price for price-responsive loads. represents the output status of the daily load. is the electricity price for constant-temperature control loads. is the quantity of constant-temperature control loads. is the selling price of electricity to the main grid. is the purchasing price of electricity from the main grid. is the amount of electricity sold to the main grid. is the unit price for charging and discharging of the energy storage battery. is the amount of electricity purchased from the main grid. is the generation cost of distributed generation components. and are the charging and discharging amounts of the energy storage device at time . is the power generation of distributed generation components.
The objective function of the micro gas turbine is as follows:
In this equation, represents the profit of the micro gas turbine during time period . represents the generation cost of the micro gas turbine during time period . represents the electricity generation of the micro gas turbine during time period . represents the purchasing price offered by the virtual power plant to the micro gas turbine during time period .
5. Example Analysis
5.1. Scenario Description
This paper employs the Python language and utilizes the TensorFlow tool to design a virtual power plant as depicted in
Figure 1, to validate the feasibility and effectiveness of the proposed virtual power plant internal unit game method based on the improved D3QN algorithm.
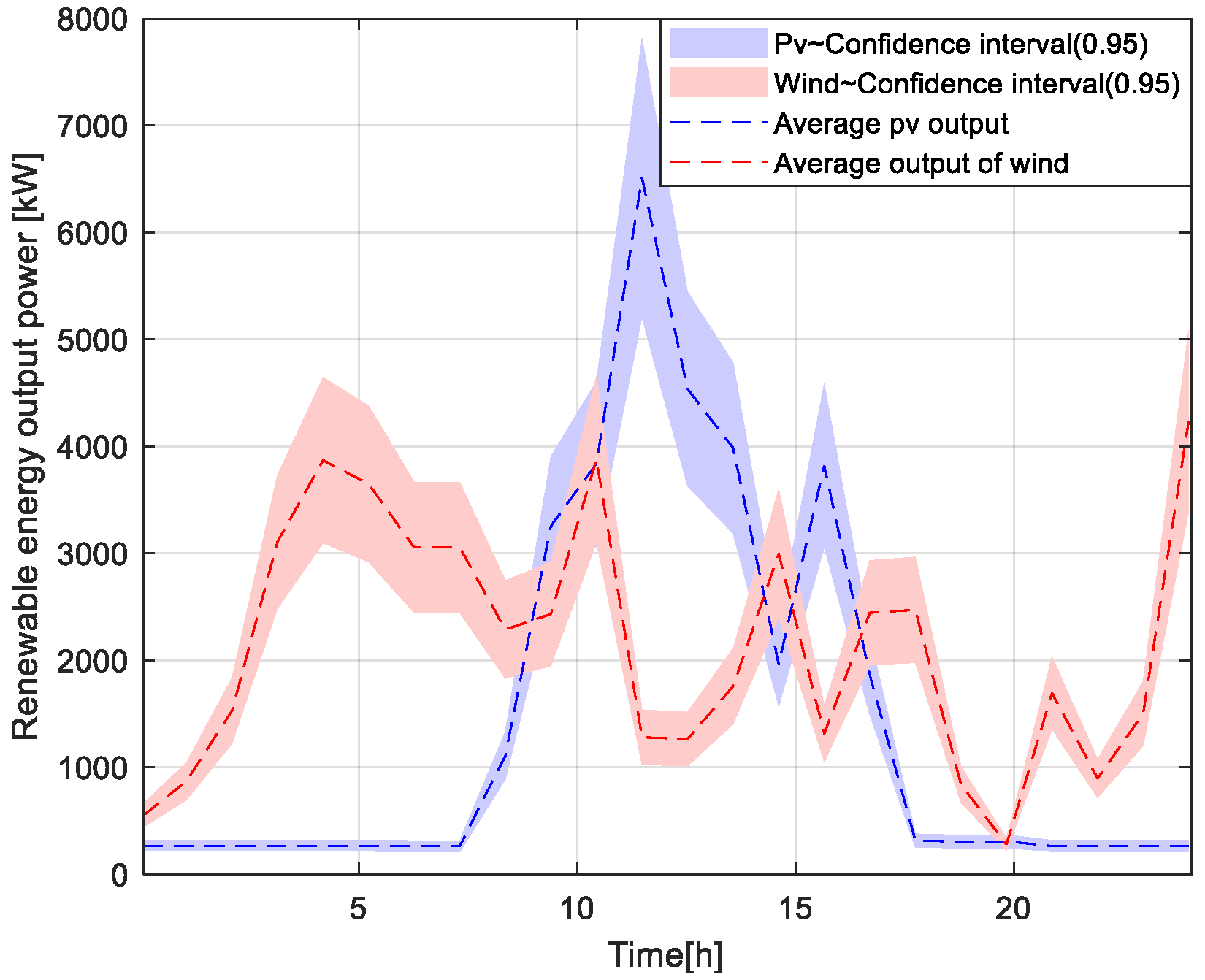
The distributed generation data and meteorological information required for the experiments were processed from real-time power generation data of typical photovoltaic and wind power plants in the East China region. The experimental sample data were collected once per hour, covering a year of characteristic information for the components within the virtual power plant. To maintain generality, the power generation data of distributed energy components were averaged over the year, as shown in
Figure 4.
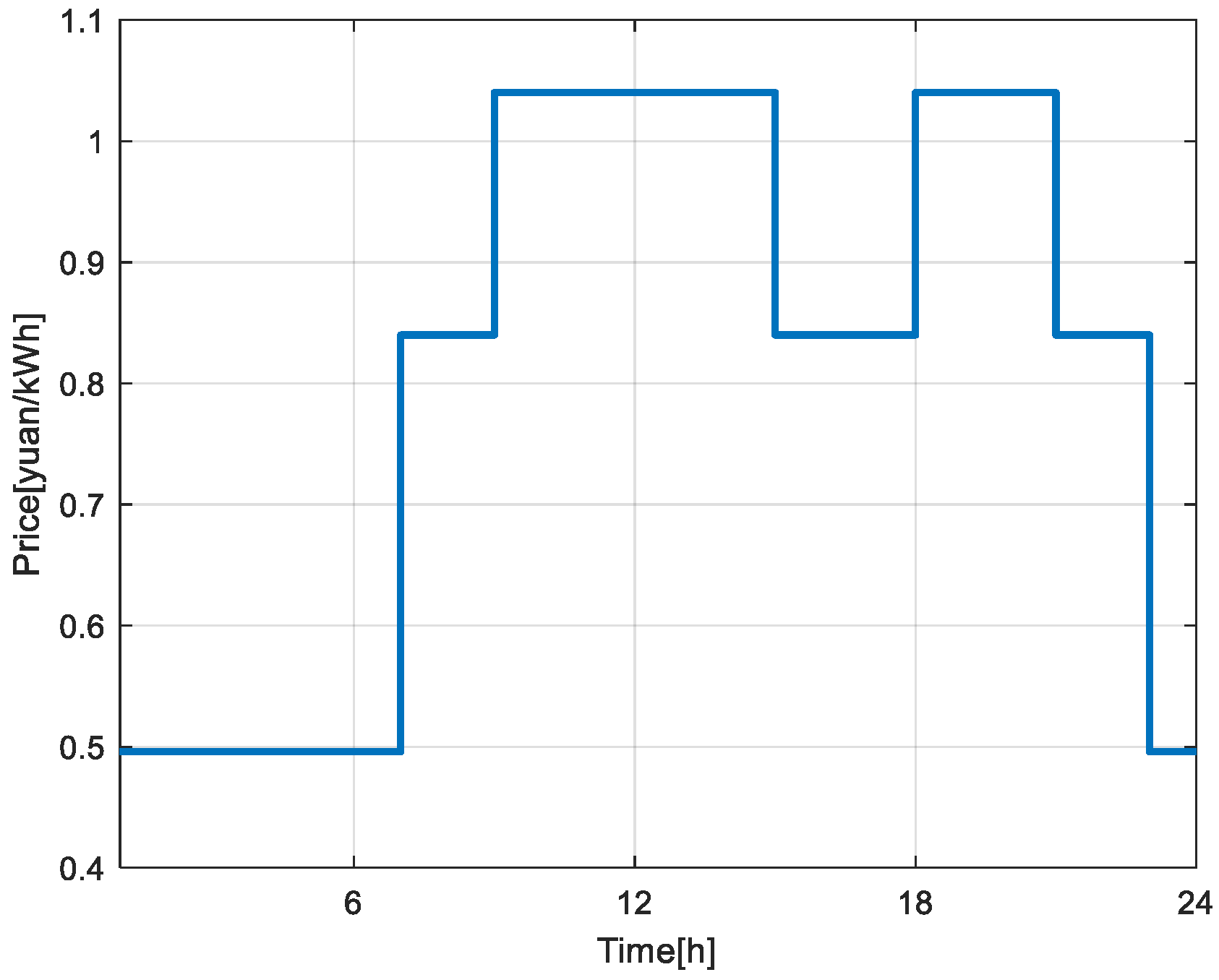
Figure 5 shows the price curve of the virtual power plant for selling electricity to residents.
The loads include non-adjustable loads and temperature-controlled loads, with the latter divided into air conditioning loads and water heater loads.
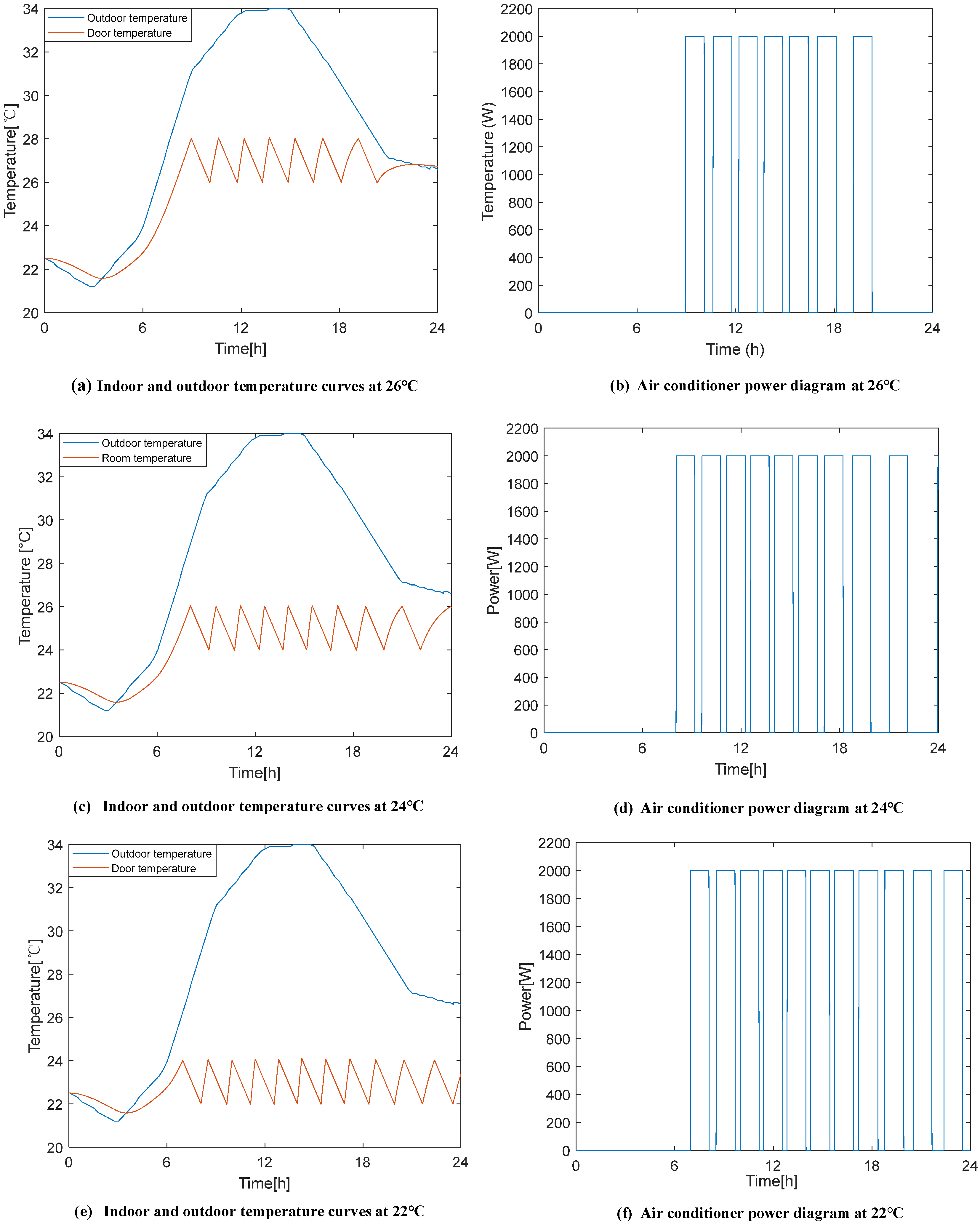
Figure 6 shows the power load of air conditioning for one day at different set temperatures. The outdoor temperature was processed using real-time summer temperatures from a specific location, with experimental sample data collected every 5 min.
Table 2 presents the probability density parameters for water heater usage.
Table 3 lists other parameters in the virtual power plant system environment.
5.2. Algorithm Performance Analysis
The algorithm was run on a computer with an Intel(R) Core(TM) i5-7300HQ CPU @ 2.50 GHz and 8 GB RAM. It was implemented using Python 3.10 and TensorFlow 2.11.0 as the deep learning framework.
In the algorithm, rewards were calculated every hour and accumulated to obtain the total daily reward. The training set for the VPP control center consisted of 2000 episodes, and 10 experiments were conducted under different algorithms to obtain the average reward value. The convergence of the VPP control center during iterations is shown in
Figure 7. The algorithm exhibited significant fluctuations in the first 30 episodes, primarily due to the randomness in strategy selection during this stage. Subsequently, while gradually optimizing its strategy, the VPP control center and the gas turbine engaged in a non-cooperative Stackelberg game, which dominated the reward fluctuations during this period.
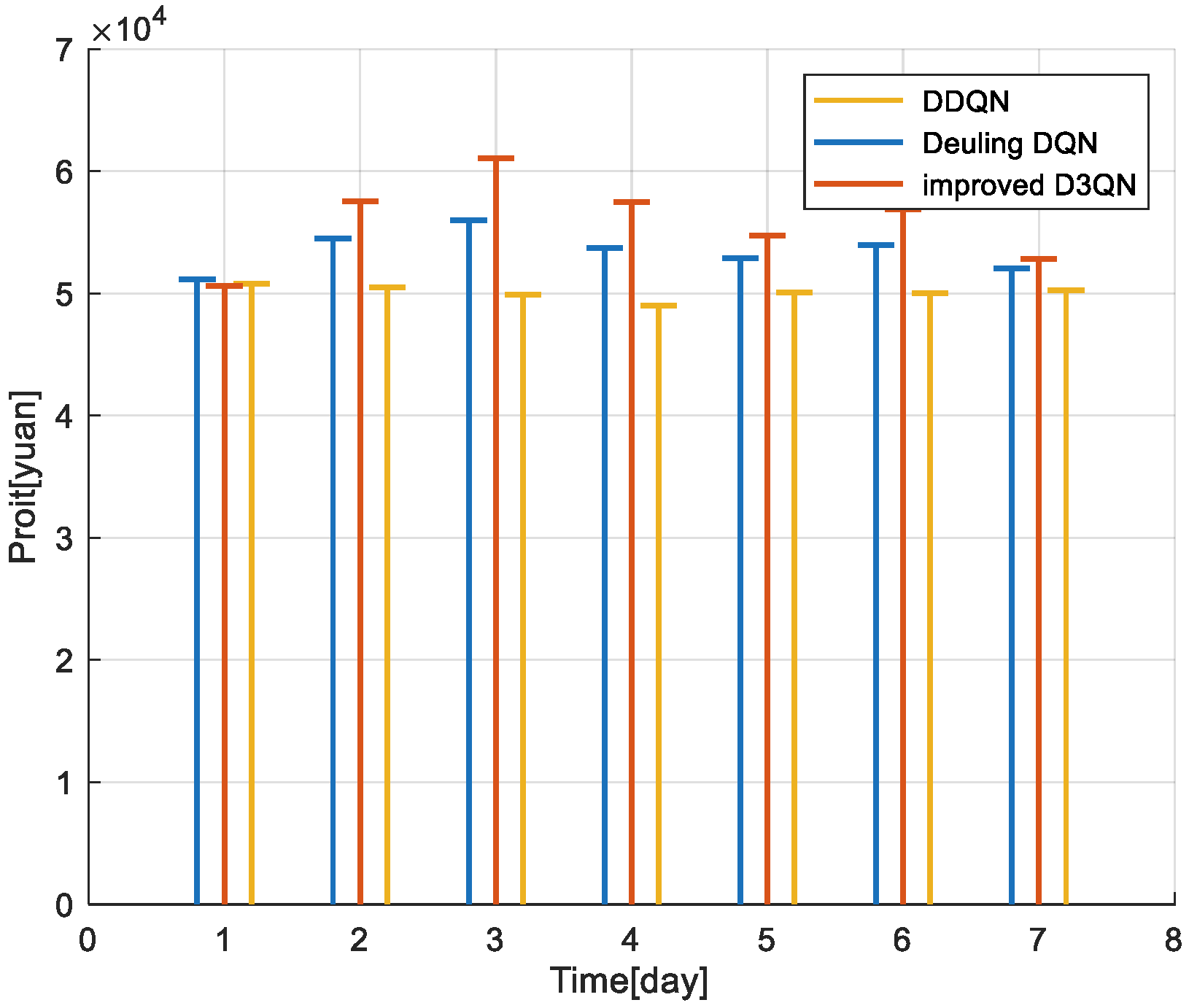
As observed from the figure, the convergence range of the Dueling DQN algorithm is between 510 and 530, the DDQN algorithm converges between 530 and 550, and the improved D3QN algorithm converges between 530 and 590. The convergence curves indicate that the improved D3QN algorithm exhibits better network optimization effects and has larger fluctuation amplitudes, making it less likely to fall into local optima.
To further verify the impact of real-time electricity price incentives on energy scheduling within a virtual power plant,
Figure 8 presents a comparison of the VPP control center’s profits over seven days under three different algorithms.
Under the DDQN algorithm, the total profit of the virtual power plant control over seven days is CNY 350,453.7. When using the Dueling DQN algorithm, the total profit is CNY 384,555.2. With the improved D3QN algorithm, the total profit over seven days for the VPP control center is CNY 391,069.6, representing an increase of 11.6% compared to the DDQN algorithm and 1.7% compared to the Dueling DQN algorithm.
5.3. Analyzing the Results of Reinforcement Learning Optimization Scheduling
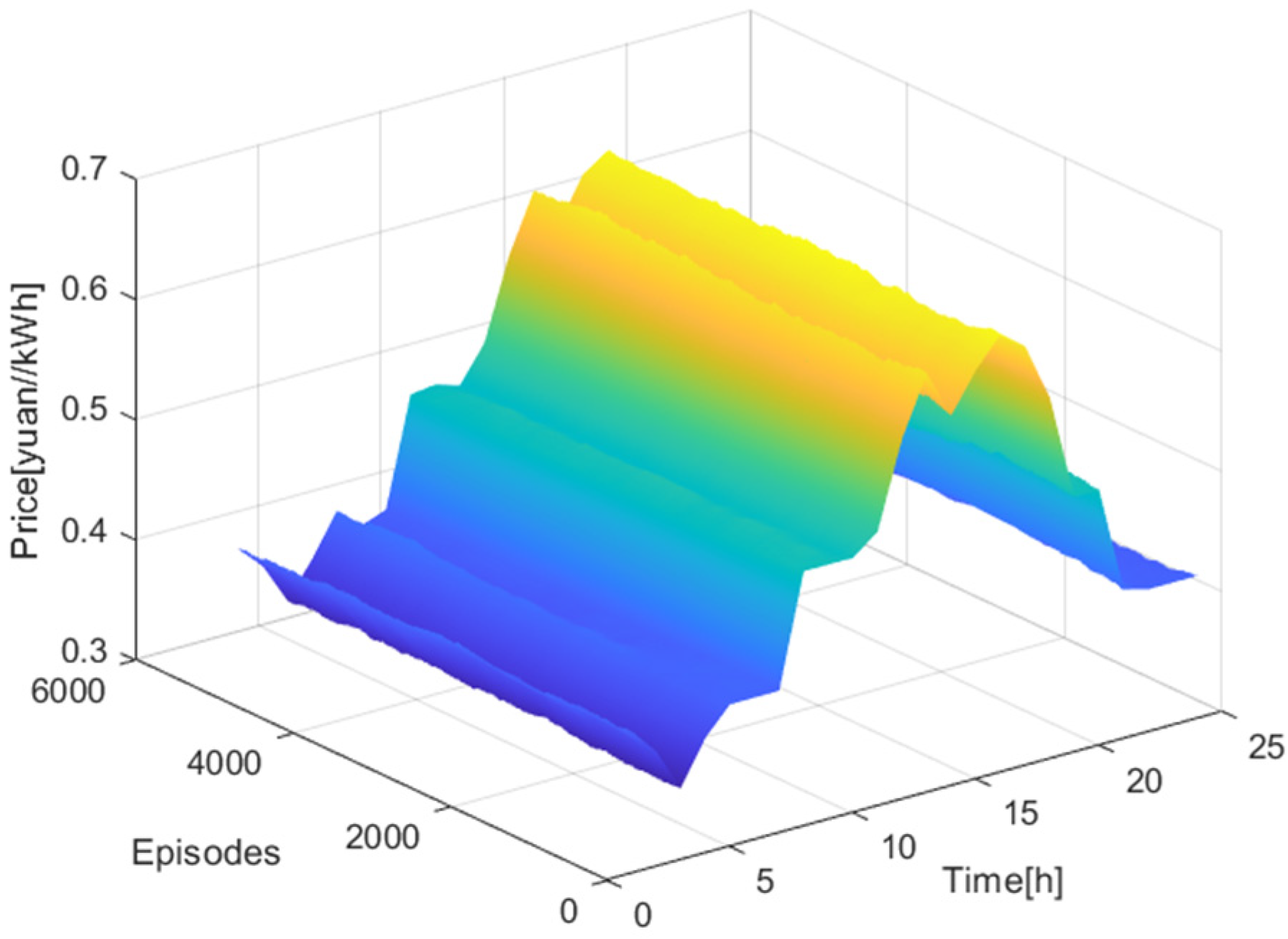
The improved D3QN algorithm was used for training the VPP control center and gas turbine agents. Using historical data, the agents were trained offline, with
Figure 9 showing the price changes over 5000 iterations. The colormap used ranges from blue to yellow, where blue represents lower price values and yellow represents higher price values. This visual aid allows for an easier comparison of how prices fluctuate over time and across different simulations.
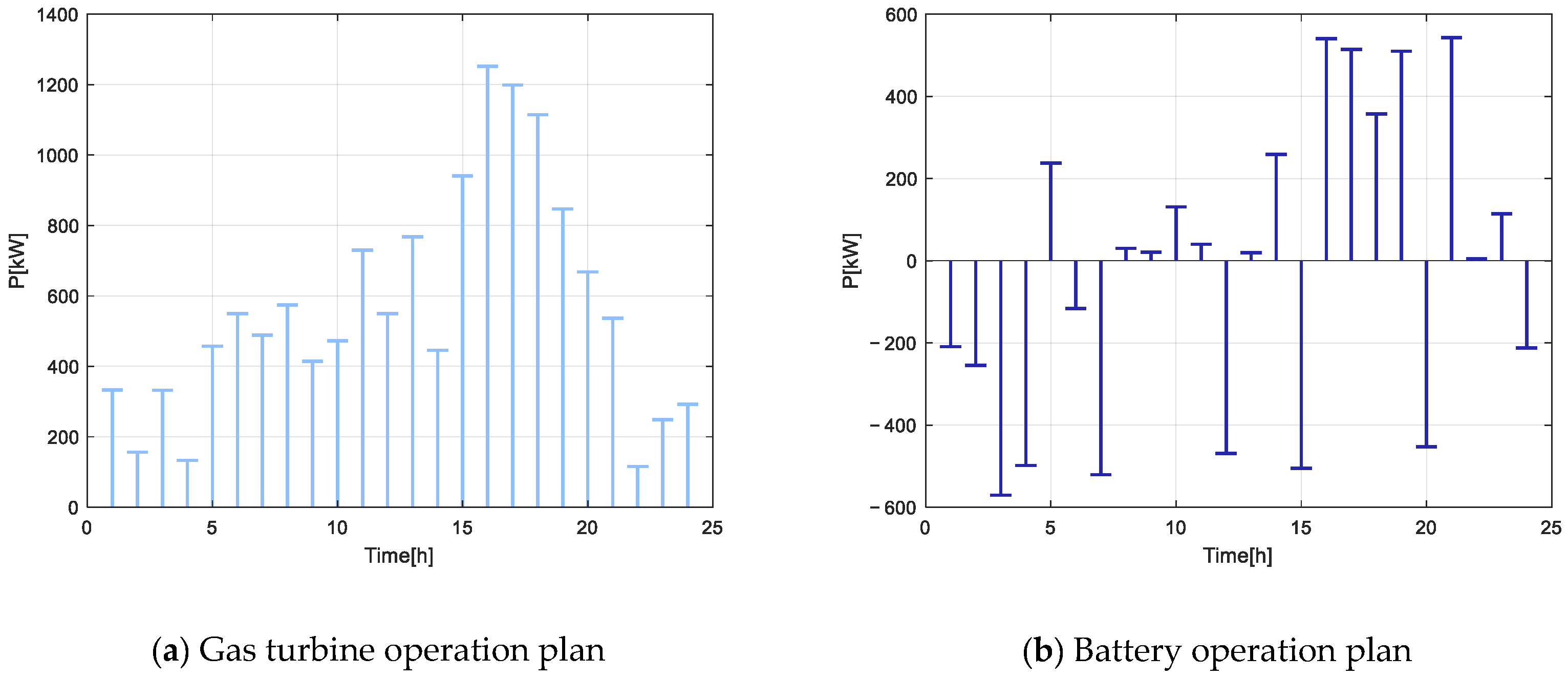
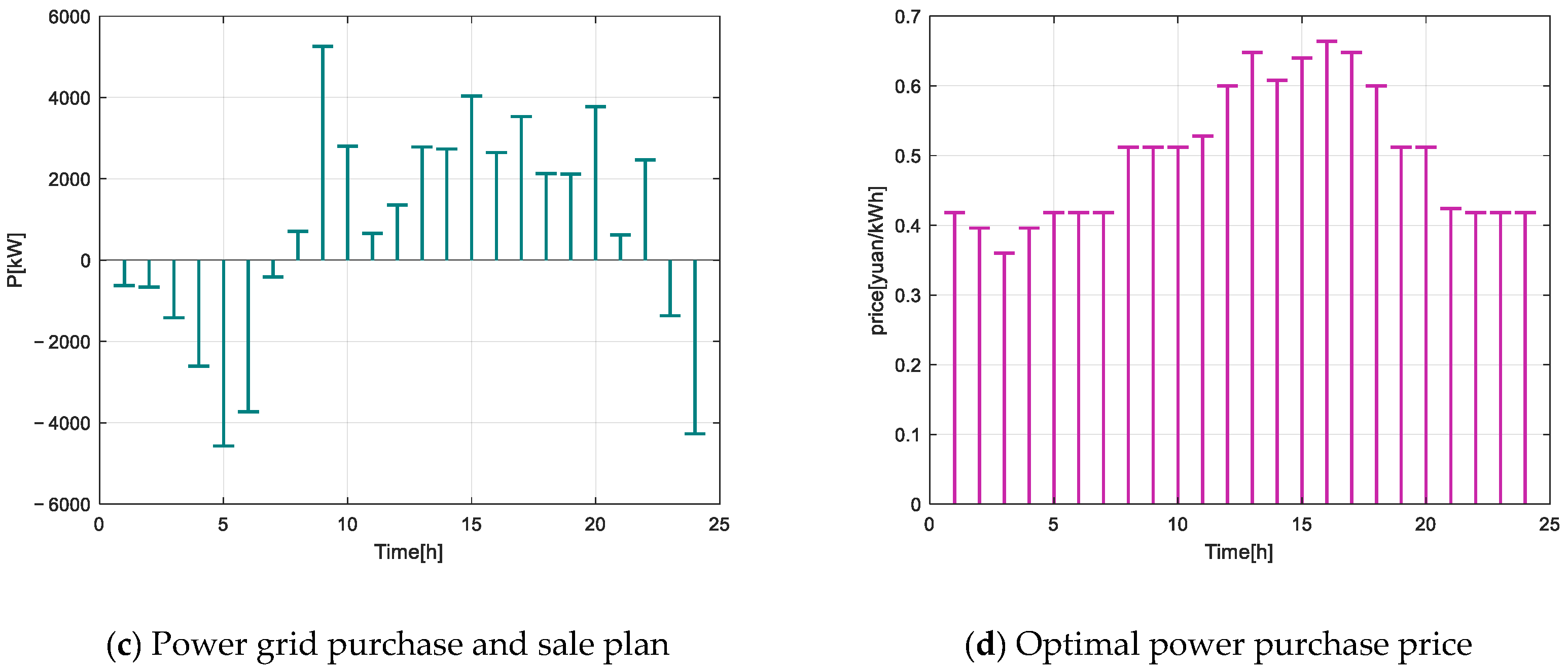
Figure 10 presents the scheduling results obtained after convergence.
From
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9 and
Figure 10, it can be seen that in the first half of the day, the wind farm generates a significant amount of electricity. During the 00:00–03:00 time period, when the electricity selling price to the main grid is low, the energy storage battery prioritizes charging. During the 12:00–18:00 period, when the electricity selling price is higher, the energy storage battery discharges in a timely manner. Additionally, the VPP purchases any shortfall from the main grid to meet the internal power load demands of the virtual power plant.
During periods when distributed generation in the virtual power plant management system is high, sufficient electricity is allocated to temperature-controlled loads to maintain a comfortable temperature for the rest of the day without needing additional power. Using the improved D3QN algorithm for virtual power plant energy scheduling can avoid purchasing large amounts of electricity during high-demand and low-generation periods. This approach achieves peak shaving and valley filling, enhancing the overall daytime revenue of the VPP control center. Consequently, it maximizes the economic dispatch benefits of the internal game units within the virtual power plant.
6. Conclusions
This paper successfully proposes an improved D3QN algorithm for optimizing the economic dispatch within a virtual power plant. First, a comprehensive VPP economic dispatch game model was established, encompassing various energy resources such as energy storage, micro gas turbines, wind power, and photovoltaics. By integrating a greedy selection mechanism and a noisy network into the D3QN algorithm, this study not only enhances the model’s capability to handle complex and dynamic market environments but also improves the real-time responsiveness and robustness of the decision-making process.
Simulation experiments based on real data demonstrated that the improved D3QN algorithm significantly outperforms traditional DDQN and Dueling DQN algorithms. It shows better adaptability in handling the challenges of continuous decision-making environments, effectively reducing operational costs while maximizing the satisfaction rate of power load demands and the profitability of power transactions with the main grid. Compared to the DDQN and Dueling DQN algorithms, the improved D3QN algorithm exhibited profit increases ranging from 11.6% to 1.7% across multiple cycles of experiments, thereby confirming its economic advantages.
Furthermore, the primary objective of this study is to investigate the optimal scheduling problem within a virtual power plant and to construct a model for the game between the virtual power plant and its internal units. Against this backdrop, the research contribution lies in the development of an internal game model for the virtual power plant and the application of an enhanced D3QN algorithm integrated with real-time electricity prices to solve the model. Ultimately, the case study demonstrates the economic feasibility of the model and the effectiveness of the algorithm.
The study also reveals the potential of demand-side management achieved through intelligent scheduling strategies, further validating the application value of deep reinforcement learning technologies in the field of energy system optimization. Future work will explore the integration of more real-time datasets and algorithm adjustments to further enhance the operational efficiency and responsiveness of the VPP.