Using Crested Porcupine Optimizer Algorithm and CNN-LSTM-Attention Model Combined with Deep Learning Methods to Enhance Short-Term Power Forecasting in PV Generation
Abstract
1. Introduction
- (1)
- The introduction of a deep learning model, CNN-LSTM, that incorporates an attention mechanism. By leveraging this model, we can fully extract the spatio-temporal changing features of parameters, enabling the CLA model to effectively focus on crucial historical data for future power prediction, thus enhancing the prediction performance.
- (2)
- To enhance the model’s predictive ability further, we integrated the CPO algorithm to more efficiently adjust LSTM network parameters, resulting in the formation of the CPO-CNN-LSTM-Attention model. Notably, this is the first instance where the CPO algorithm has been utilized for parameter optimization in the LSTM algorithm, to the best of our knowledge.
- (3)
- Experimental findings suggest that the proposed PV power prediction model surpasses other classical models in accuracy, demonstrating promising application prospects.
2. Model Construction
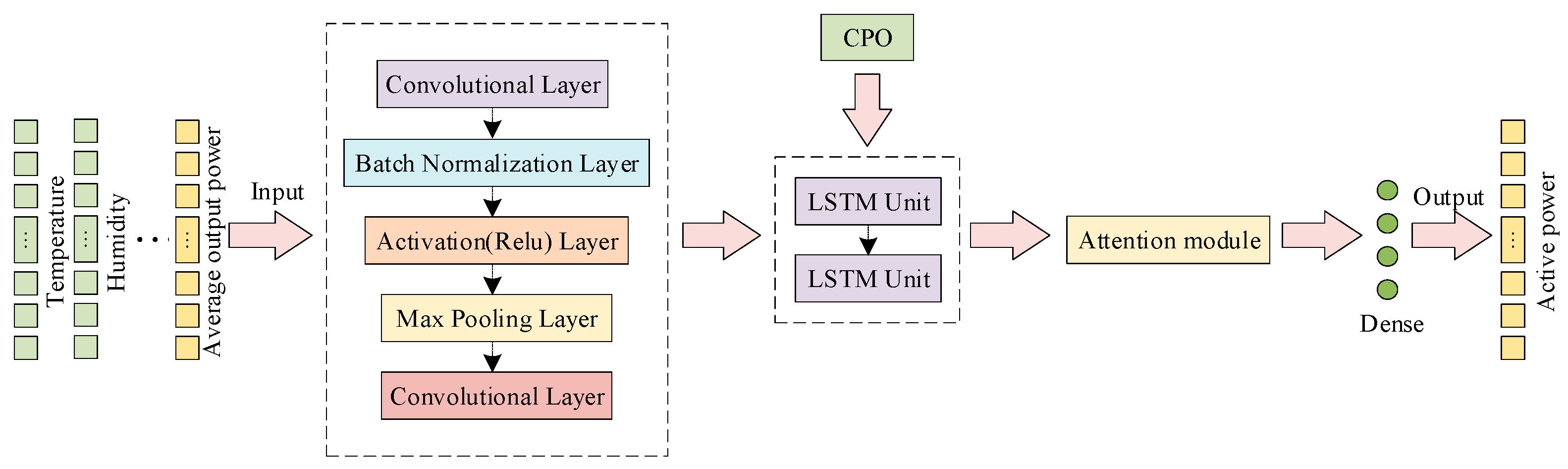
2.1. CNN-LSTM-Attention
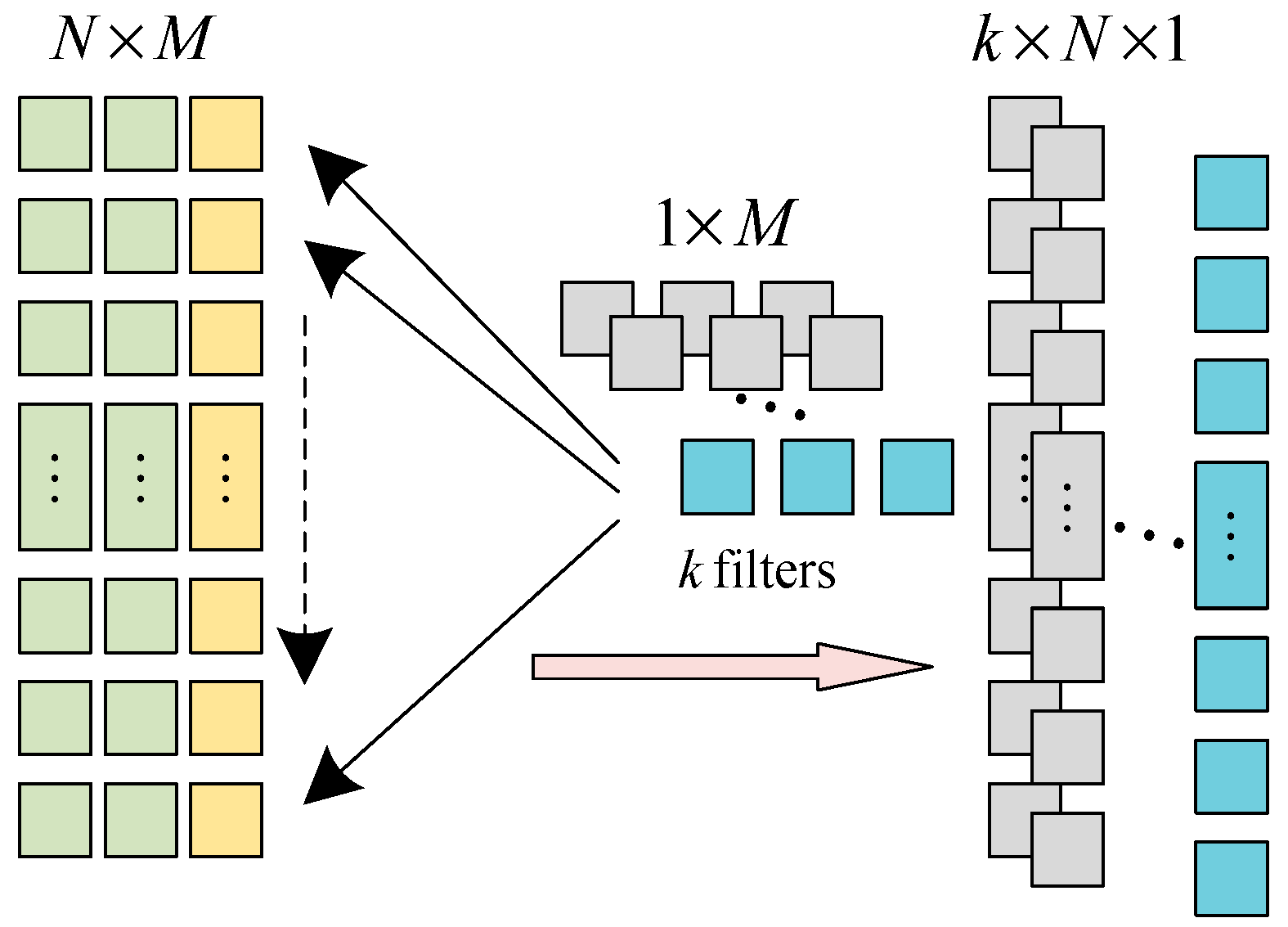
2.1.1. CNN
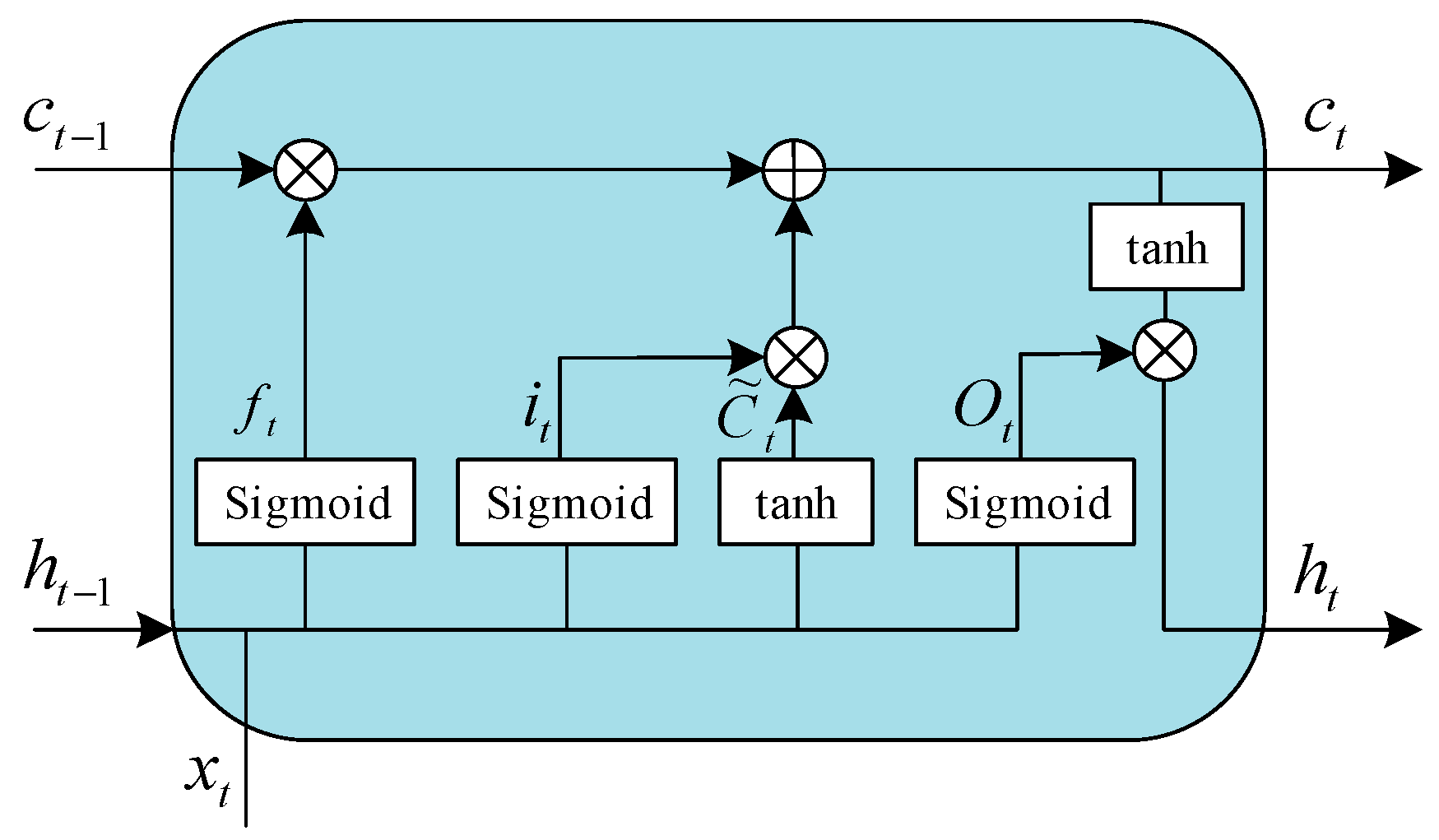
2.1.2. LSTM
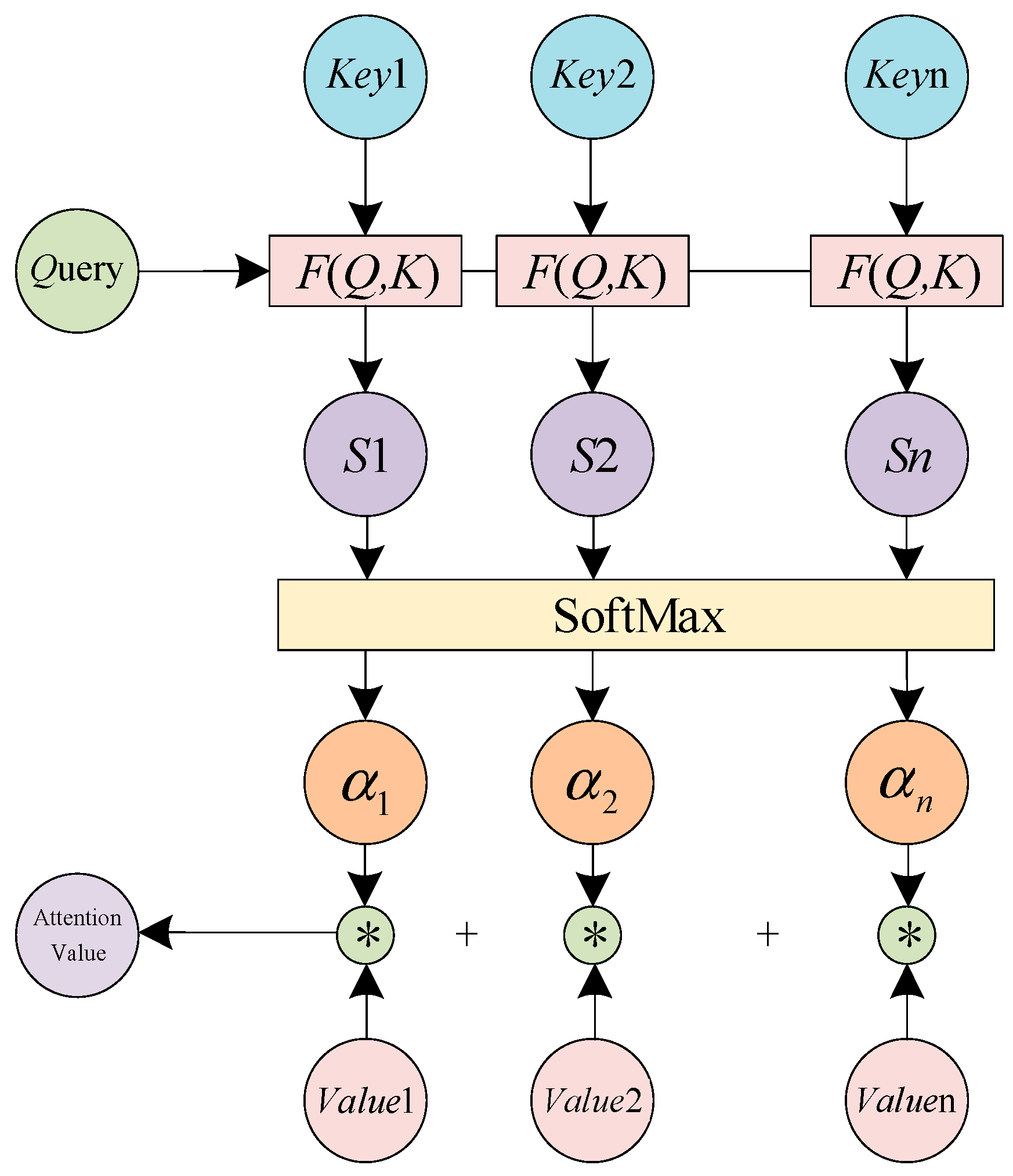
2.1.3. Attention
2.2. CPO
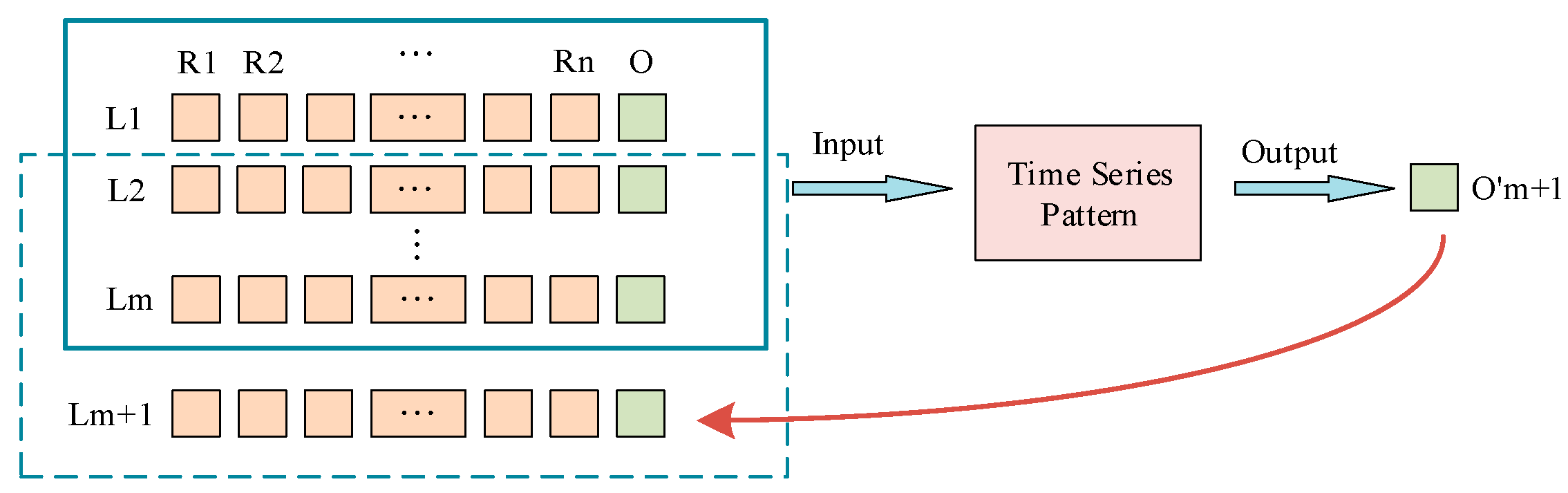
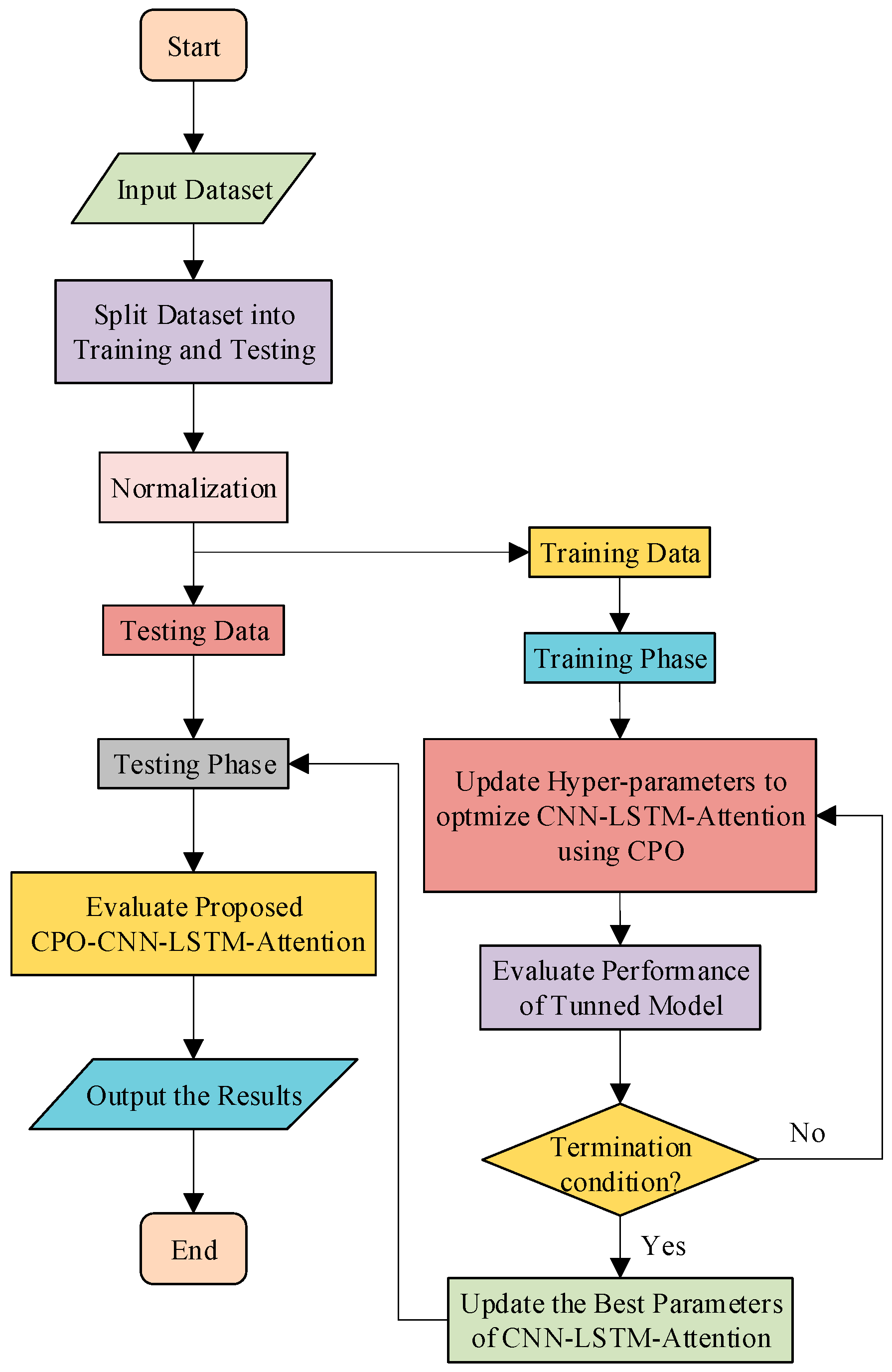
2.3. PV Power Forecasting Model
3. Results and Discussion
3.1. Data Collection and Processing
3.2. Objective Function and Evaluation Parameters
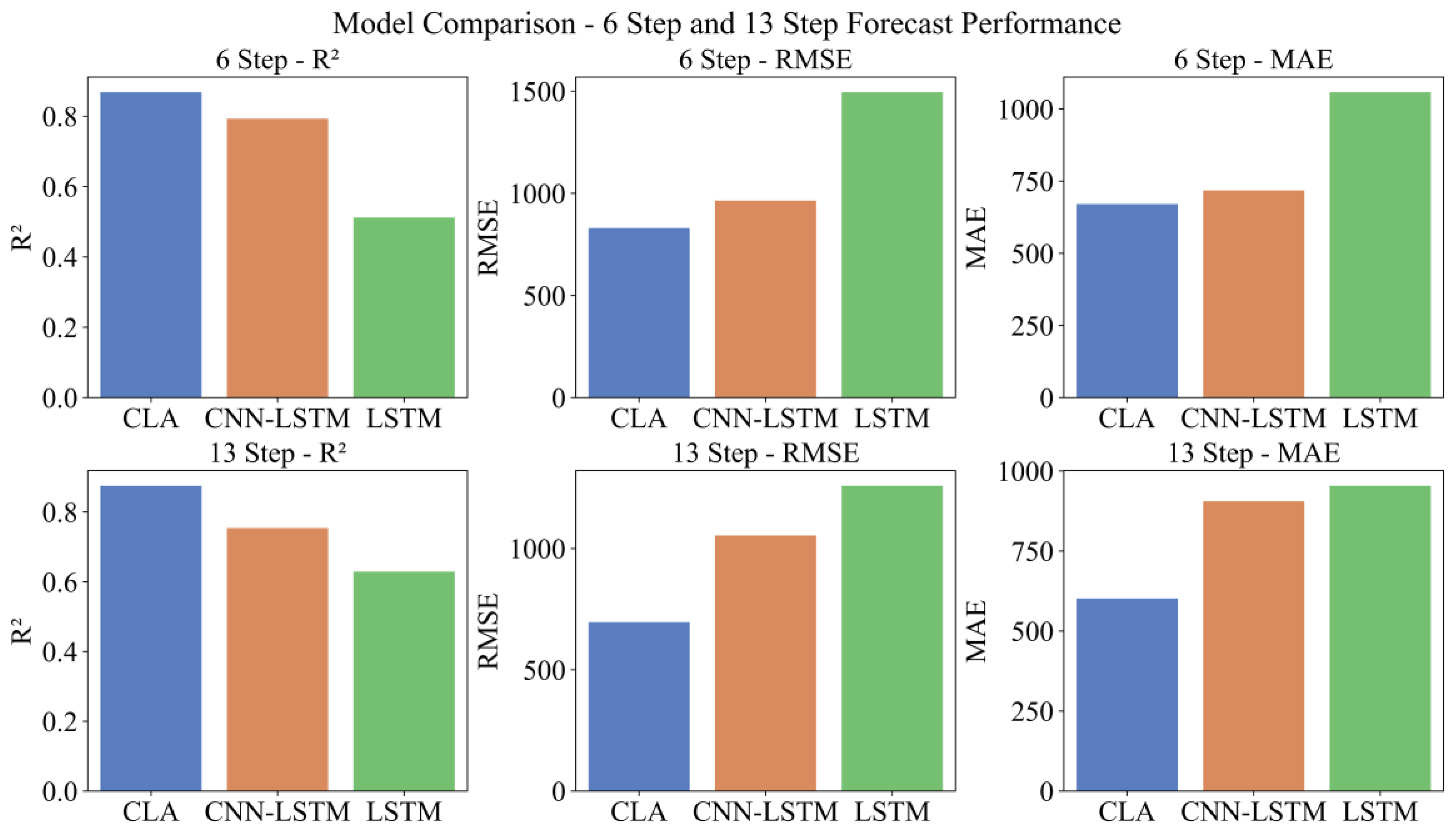
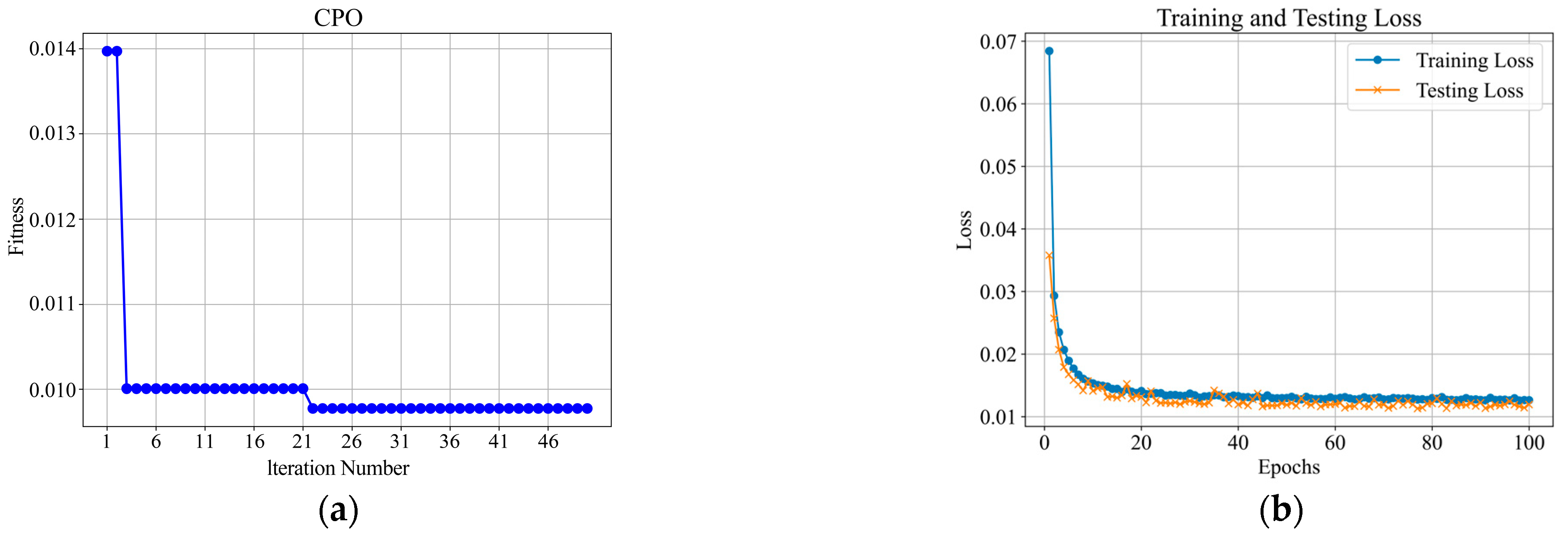
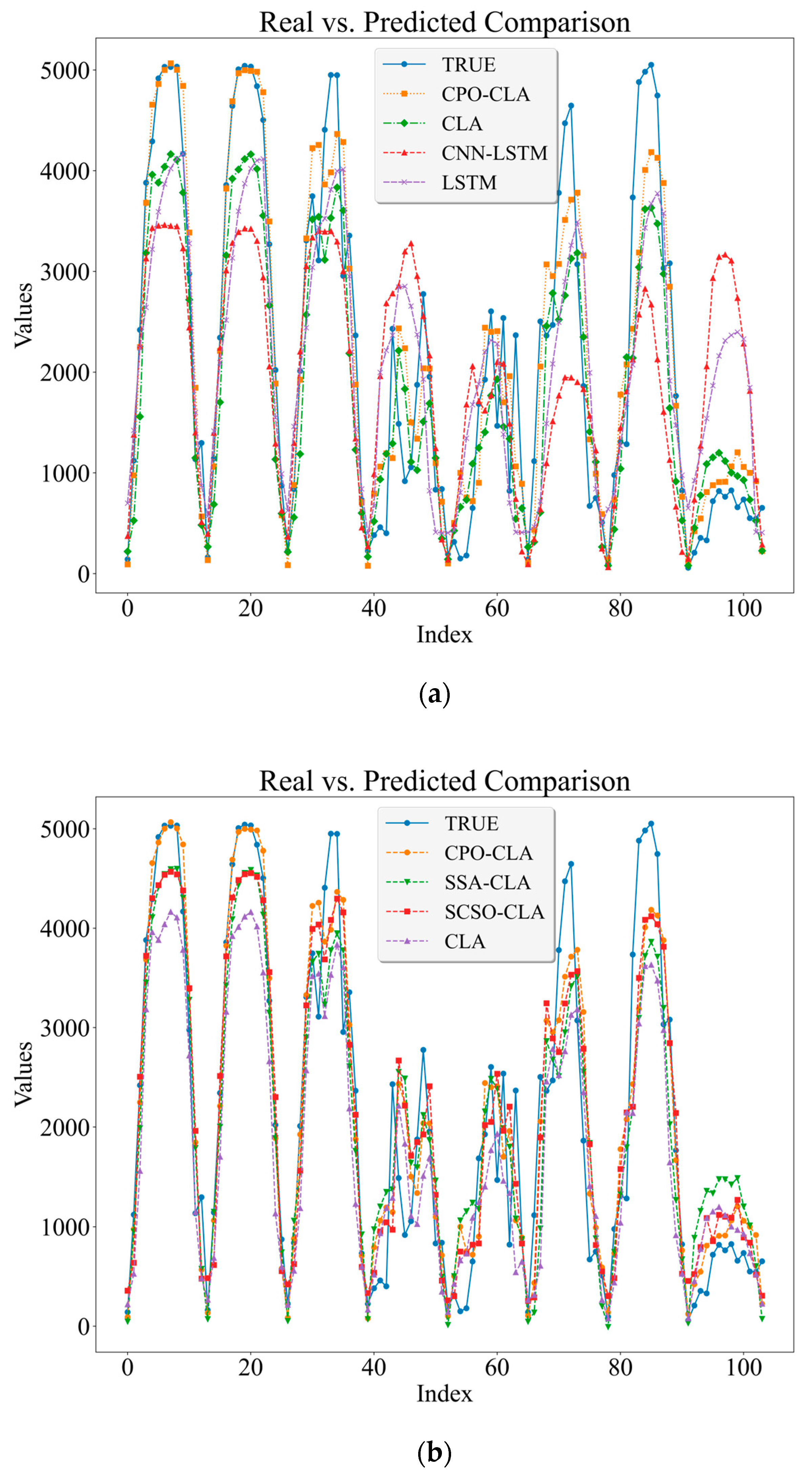
3.3. Prediction Model Result and Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gaviria, J.F.; Narváez, G.; Guillen, C.; Giraldo, L.F.; Bressan, M. Machine learning in photovoltaic systems: A review. Renew. Energy 2022, 196, 298–318. [Google Scholar] [CrossRef]
- Qi, L.; Song, J.; Wang, Y.; Yan, J. Deploying mobilized photovoltaic system between northern and southern hemisphere: Techno-economic assessment. Sol. Energy 2024, 269, 112365. [Google Scholar] [CrossRef]
- Hussain, A.; Khan, Z.A.; Hussain, T.; Ullah, F.U.M.; Rho, S.; Baik, S.W.; Wei, C. A Hybrid Deep Learning-Based Network for Photovoltaic Power Forecasting. Complexity 2022, 2022, 7040601. [Google Scholar] [CrossRef]
- Liu, W.; Ren, C.; Xu, Y. Missing-Data Tolerant Hybrid Learning Method for Solar Power Forecasting. IEEE Trans. Sustain. Energy 2022, 13, 1843–1852. [Google Scholar] [CrossRef]
- David, M.; Ramahatana, F.; Trombe, P.J.; Lauret, P. Probabilistic forecasting of the solar irradiance with recursive ARMA and GARCH models. Sol. Energy 2016, 133, 55–72. [Google Scholar] [CrossRef]
- Kushwaha, V.; Pindoriya, N.M. A SARIMA-RVFL hybrid model assisted by wavelet decomposition for very short-term solar PV power generation forecast. Renew. Energy 2019, 140, 124–139. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Wang, M.; Ma, X.; Wang, R.; Kari, T.; Tang, Z. Short-term photovoltaic power prediction model based on hierarchical clustering of K-means++ algorithm and deep learning hybrid model. J. Renew. Sustain. Energy 2024, 16, 026102. [Google Scholar] [CrossRef]
- Abubakar Mas’ud, A. Comparison of three machine learning models for the prediction of hourly PV output power in Saudi Arabia. Ain Shams Eng. J. 2022, 13, 101648. [Google Scholar] [CrossRef]
- Gulay, E.; Sen, M.; Akgun, O.B. Forecasting electricity production from various energy sources in Türkiye: A predictive analysis of time series, deep learning, and hybrid models. Energy 2024, 286, 129566. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; Houm, Y.E.; Ou Ali, I.H. CNN-LSTM: An efficient hybrid deep learning architecture for predicting short-term photovoltaic power production. Electr. Power Syst. Res. 2022, 208, 107908. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, Z.; Wang, H.; Wang, J.; Zhao, Z.; Wang, F. Achieving wind power and photovoltaic power prediction: An intelligent prediction system based on a deep learning approach. Energy 2023, 283, 129005. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, M. Wavelet-based neural network with genetic algorithm optimization for generation prediction of PV plants. Energy Rep. 2022, 8, 10976–10990. [Google Scholar] [CrossRef]
- Feng, H.; Yu, C. A novel hybrid model for short-term prediction of PV power based on KS-CEEMDAN-SE-LSTM. Renew. Energy Focus 2023, 47, 100497. [Google Scholar] [CrossRef]
- Nguyen Trong, T.; Vu Xuan Son, H.; Do Dinh, H.; Takano, H.; Nguyen Duc, T. Short-term PV power forecast using hybrid deep learning model and Variational Mode Decomposition. Energy Rep. 2023, 9, 712–717. [Google Scholar] [CrossRef]
- An, W.; Zheng, L.; Yu, J.; Wu, H. Ultra-short-term prediction method of PV power output based on the CNN–LSTM hybrid learning model driven by EWT. J. Renew. Sustain. Energy 2022, 14, 053501. [Google Scholar] [CrossRef]
- Feroz Mirza, A.; Mansoor, M.; Usman, M.; Ling, Q. Hybrid Inception-embedded deep neural network ResNet for short and medium-term PV-Wind forecasting. Energy Convers. Manag. 2023, 294, 117574. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Long short term memory–convolutional neural network based deep hybrid approach for solar irradiance forecasting. Appl. Energy 2021, 295, 117061. [Google Scholar] [CrossRef]
- Yan, Q.; Lu, Z.; Liu, H.; He, X.; Zhang, X.; Guo, J. Short-term prediction of integrated energy load aggregation using a bi-directional simple recurrent unit network with feature-temporal attention mechanism ensemble learning model. Appl. Energy 2024, 355, 122159. [Google Scholar] [CrossRef]
- Mirza, A.F.; Shu, Z.; Usman, M.; Mansoor, M.; Ling, Q. Quantile-transformed multi-attention residual framework (QT-MARF) for medium-term PV and wind power prediction. Renew. Energy 2024, 220, 119604. [Google Scholar] [CrossRef]
- Yin, L.; Zhao, M. Inception-embedded attention memory fully-connected network for short-term wind power prediction. Appl. Soft Comput. 2023, 141, 110279. [Google Scholar] [CrossRef]
- Wang, S.; Shi, J.; Yang, W.; Yin, Q. High and low frequency wind power prediction based on Transformer and BiGRU-Attention. Energy 2024, 288, 129753. [Google Scholar] [CrossRef]
- Abdulai, D.; Gyamfi, S.; Diawuo, F.A.; Acheampong, P. Data analytics for prediction of solar PV power generation and system performance: A real case of Bui Solar Generating Station, Ghana. Sci. Afr. 2023, 21, e01894. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y. Short-term self consumption PV plant power production forecasts based on hybrid CNN-LSTM, ConvLSTM models. Renew. Energy 2021, 177, 101–112. [Google Scholar] [CrossRef]
- Iweh, C.D.; Akupan, E.R. Control and optimization of a hybrid solar PV—Hydro power system for off-grid applications using particle swarm optimization (PSO) and differential evolution (DE). Energy Rep. 2023, 10, 4253–4270. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M. Crested Porcupine Optimizer: A new nature-inspired metaheuristic. Knowl. Based Syst. 2024, 284, 111257. [Google Scholar] [CrossRef]
- Al-Ja’afreh, M.A.A.; Mokryani, G.; Amjad, B. An enhanced CNN-LSTM based multi-stage framework for PV and load short-term forecasting: DSO scenarios. Energy Rep. 2023, 10, 1387–1408. [Google Scholar] [CrossRef]
- Ghimire, S.; Nguyen-Huy, T.; Deo, R.C.; Casillas-Pérez, D.; Salcedo-Sanz, S. Efficient daily solar radiation prediction with deep learning 4-phase convolutional neural network, dual stage stacked regression and support vector machine CNN-REGST hybrid model. Sustain. Mater. Technol. 2022, 32, e00429. [Google Scholar] [CrossRef]
- Wang, L.; Mao, M.; Xie, J.; Liao, Z.; Zhang, H.; Li, H. Accurate solar PV power prediction interval method based on frequency-domain decomposition and LSTM model. Energy 2023, 262, 125592. [Google Scholar] [CrossRef]
- Ehteram, M.; Afshari Nia, M.; Panahi, F.; Farrokhi, A. Read-First LSTM model: A new variant of long short term memory neural network for predicting solar radiation data. Energy Convers. Manag. 2024, 305, 118267. [Google Scholar] [CrossRef]
- Gao, B.; Huang, X.; Shi, J.; Tai, Y.; Zhang, J. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks. Renew. Energy 2020, 162, 1665–1683. [Google Scholar] [CrossRef]
- Tovar Rosas, M.A.; Pérez, M.R.; Martínez Pérez, E.R. Itineraries for charging and discharging a BESS using energy predictions based on a CNN-LSTM neural network model in BCS, Mexico. Renew. Energy 2022, 188, 1141–1165. [Google Scholar] [CrossRef]
- Hu, Z.; Gao, Y.; Ji, S.; Mae, M.; Imaizumi, T. Improved multistep ahead photovoltaic power prediction model based on LSTM and self-attention with weather forecast data. Appl. Energy 2024, 359, 122709. [Google Scholar] [CrossRef]
- Zuo, H.-M.; Qiu, J.; Jia, Y.-H.; Wang, Q.; Li, F.-F. Ten-minute prediction of solar irradiance based on cloud detection and a long short-term memory (LSTM) model. Energy Rep. 2022, 8, 5146–5157. [Google Scholar] [CrossRef]
- Elizabeth Michael, N.; Hasan, S.; Al-Durra, A.; Mishra, M. Short-term solar irradiance forecasting based on a novel Bayesian optimized deep Long Short-Term Memory neural network. Appl. Energy 2022, 324, 119727. [Google Scholar] [CrossRef]
- Qu, J.; Qian, Z.; Pei, Y. Day-ahead hourly photovoltaic power forecasting using attention-based CNN-LSTM neural network embedded with multiple relevant and target variables prediction pattern. Energy 2021, 232, 120996. [Google Scholar] [CrossRef]
- Liu, J.; Huang, X.; Li, Q.; Chen, Z.; Liu, G.; Tai, Y. Hourly stepwise forecasting for solar irradiance using integrated hybrid models CNN-LSTM-MLP combined with error correction and VMD. Energy Convers. Manag. 2023, 280, 116804. [Google Scholar] [CrossRef]
- Gao, C.; Zhang, N.; Li, Y.; Lin, Y.; Wan, H. Adversarial self-attentive time-variant neural networks for multi-step time series forecasting. Expert Syst. Appl. 2023, 231, 120722. [Google Scholar] [CrossRef]
- El Alani, O.; Abraim, M.; Ghennioui, H.; Ghennioui, A.; Ikenbi, I.; Dahr, F.-E. Short term solar irradiance forecasting using sky images based on a hybrid CNN–MLP model. Energy Rep. 2021, 7, 888–900. [Google Scholar] [CrossRef]
- Ni, Q.; Zhuang, S.; Sheng, H.; Kang, G.; Xiao, J. An ensemble prediction intervals approach for short-term PV power forecasting. Sol. Energy 2017, 155, 1072–1083. [Google Scholar] [CrossRef]
- Jalali, S.M.J.; Osorio, G.J.; Ahmadian, S.; Lotfi, M.; Campos, V.M.A.; Shafie-khah, M.; Khosravi, A.; Catalao, J.P.S. New Hybrid Deep Neural Architectural Search-Based Ensemble Reinforcement Learning Strategy for Wind Power Forecasting. IEEE Trans. Ind. Appl. 2022, 58, 15–27. [Google Scholar] [CrossRef]

| Feature | Value |
|---|---|
| Training data (80%) | 1 January 2020–6 May 2022 |
| Testing data (20%) | 6 May 2022–30 December 2022 |
| Vector length | 10 |
| Sampling rate | 1 h |
| Numerical environment | Python 3.11.0 |
| Libraries | Numpy, Scikit Learn, TensorFlow, Pandas, Scipy |
| Machine information | 12th Gen Intel(R) Core(TM) i7-12700H@2.30 GHz, 64-bit operating system, ×64-based processor |
| Parameters | Details |
|---|---|
| Epochs | 100 |
| Batch size | 256 |
| Optimizer | Adam |
| Learning rate | 0.001 |
| Parameters | Details | |
|---|---|---|
| Conv1D | Filter | 32 |
| Kernel size | 3 | |
| Activation | ReLu | |
| Kernel regularizer | L2 (strength 0.1) | |
| MaxPooling1D | pool size | 2 |
| Dropout | Dropout Rate | 0.3 |
| LSTM | units1 | 10 |
| units2 | 10 | |
| Attention | units | 20 |
| Dense1 | unites | 10 |
| Activation | ReLu | |
| Dense2 | unites | 1 |
| Model | 6 Step | 13 Step | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| CLA | 0.868 | 829.8 | 670.4 | 0.875 | 696.5 | 601.3 |
| CNN-LSTM | 0.793 | 964.8 | 718.1 | 0.754 | 1053.6 | 905.3 |
| LSTM | 0.512 | 1494.6 | 1057.6 | 0.629 | 1258.5 | 953.7 |
| Parameters | Details | |
|---|---|---|
| Pop | 3 | |
| MaxIter | 50 | |
| Dim | 4 | |
| Best parameters | LSTM units1 | [16, 128] |
| LSTM regularizer | [0.001, 0.01] | |
| LSTM units2 | [16, 64] | |
| Learning rate | [0.001, 0.01] | |
| Model | Train | Test | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | |
| CPO-CLA | 0.974 | 519.8 | 331.1 | 0.965 | 553.8 | 360.1 |
| SSA-CLA | 0.925 | 597.1 | 347.2 | 0.901 | 527.5 | 336.8 |
| SCSO-CLA | 0.956 | 531.9 | 313.3 | 0.919 | 550.1 | 313.9 |
| CLA | 0.874 | 792.5 | 598.0 | 0.857 | 846.3 | 641.3 |
| LSTM | 0.629 | 1258.5 | 852.6 | 0.616 | 1206.4 | 1008.5 |
| CNN-LSTM | 0.757 | 971.3 | 770.6 | 0.763 | 996.3 | 805.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Ma, Z.; Tang, W.; Liang, J.; Xu, P. Using Crested Porcupine Optimizer Algorithm and CNN-LSTM-Attention Model Combined with Deep Learning Methods to Enhance Short-Term Power Forecasting in PV Generation. Energies 2024, 17, 3435. https://doi.org/10.3390/en17143435
Fan Y, Ma Z, Tang W, Liang J, Xu P. Using Crested Porcupine Optimizer Algorithm and CNN-LSTM-Attention Model Combined with Deep Learning Methods to Enhance Short-Term Power Forecasting in PV Generation. Energies. 2024; 17(14):3435. https://doi.org/10.3390/en17143435
Chicago/Turabian StyleFan, Yiling, Zhuang Ma, Wanwei Tang, Jing Liang, and Pengfei Xu. 2024. "Using Crested Porcupine Optimizer Algorithm and CNN-LSTM-Attention Model Combined with Deep Learning Methods to Enhance Short-Term Power Forecasting in PV Generation" Energies 17, no. 14: 3435. https://doi.org/10.3390/en17143435
APA StyleFan, Y., Ma, Z., Tang, W., Liang, J., & Xu, P. (2024). Using Crested Porcupine Optimizer Algorithm and CNN-LSTM-Attention Model Combined with Deep Learning Methods to Enhance Short-Term Power Forecasting in PV Generation. Energies, 17(14), 3435. https://doi.org/10.3390/en17143435







