Performance Improvement of an MR-Damper-Based Vibration-Reduction System with Energy Harvesting at Sprung Mass Changes
Abstract
1. Introduction
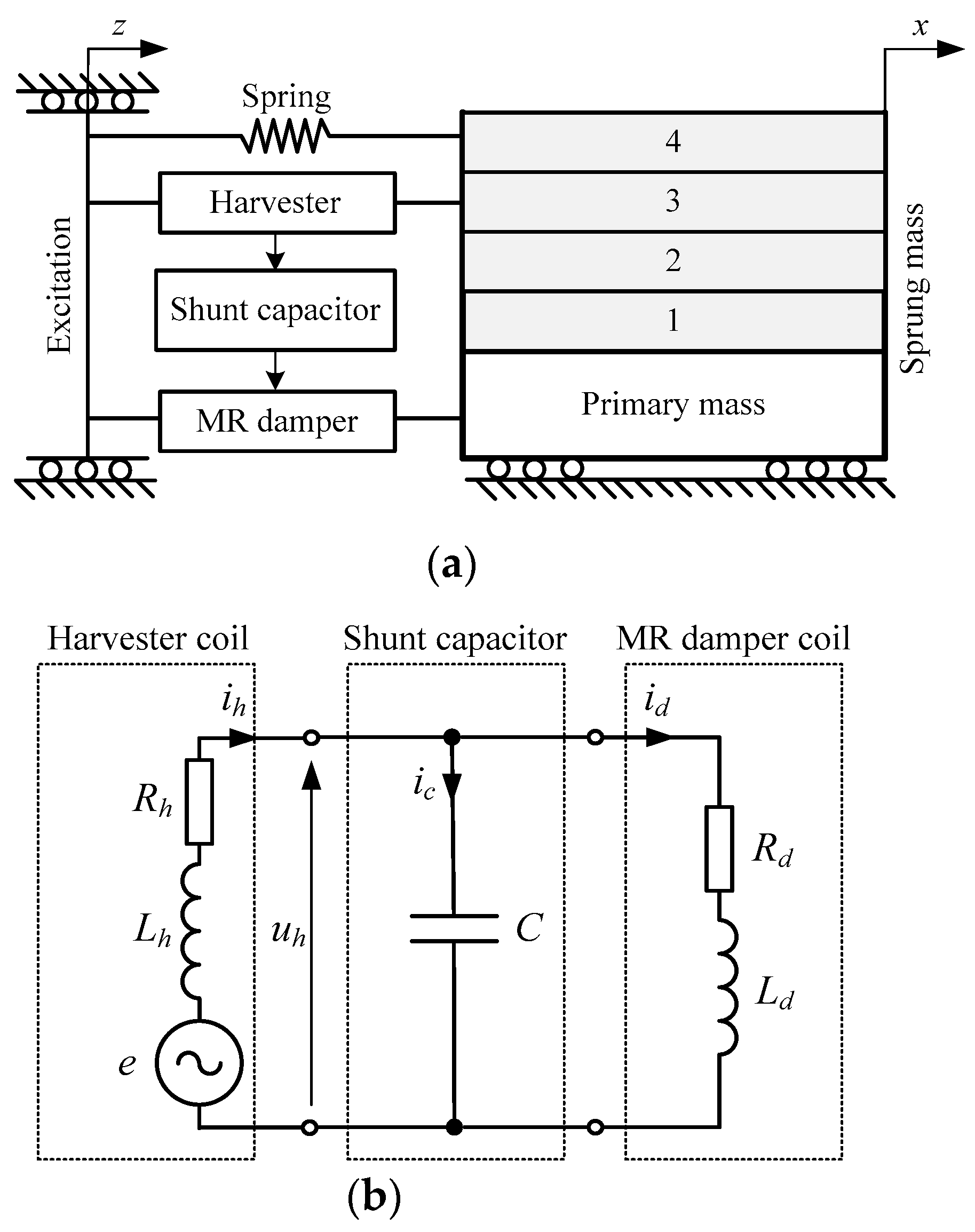
2. Structure of the System
3. Outline of the Approach
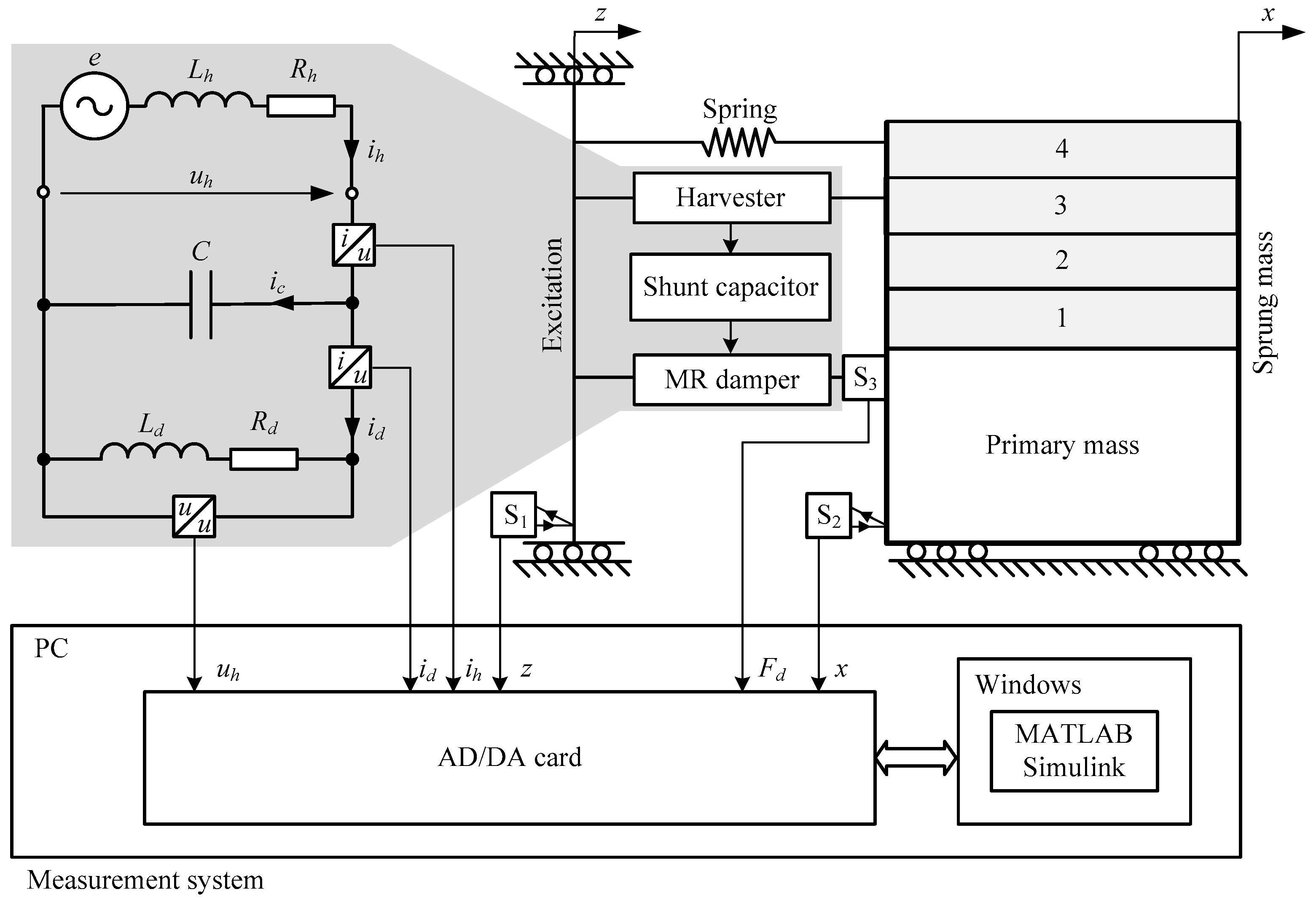
4. Testing Procedure and Performance Evaluation of the System
- The control coil was powered from an external power source by a constant current with various levels or alternating current from the harvester, assuming constant sprung mass;
- The control coil was not powered or powered by alternating current from the harvester, considering assumed sprung mass changes;
- The control coil was connected in parallel with shunt capacitors and powered by alternating current from the harvester and constant sprung mass.
4.1. Impact of Current in the Damper Control Coil
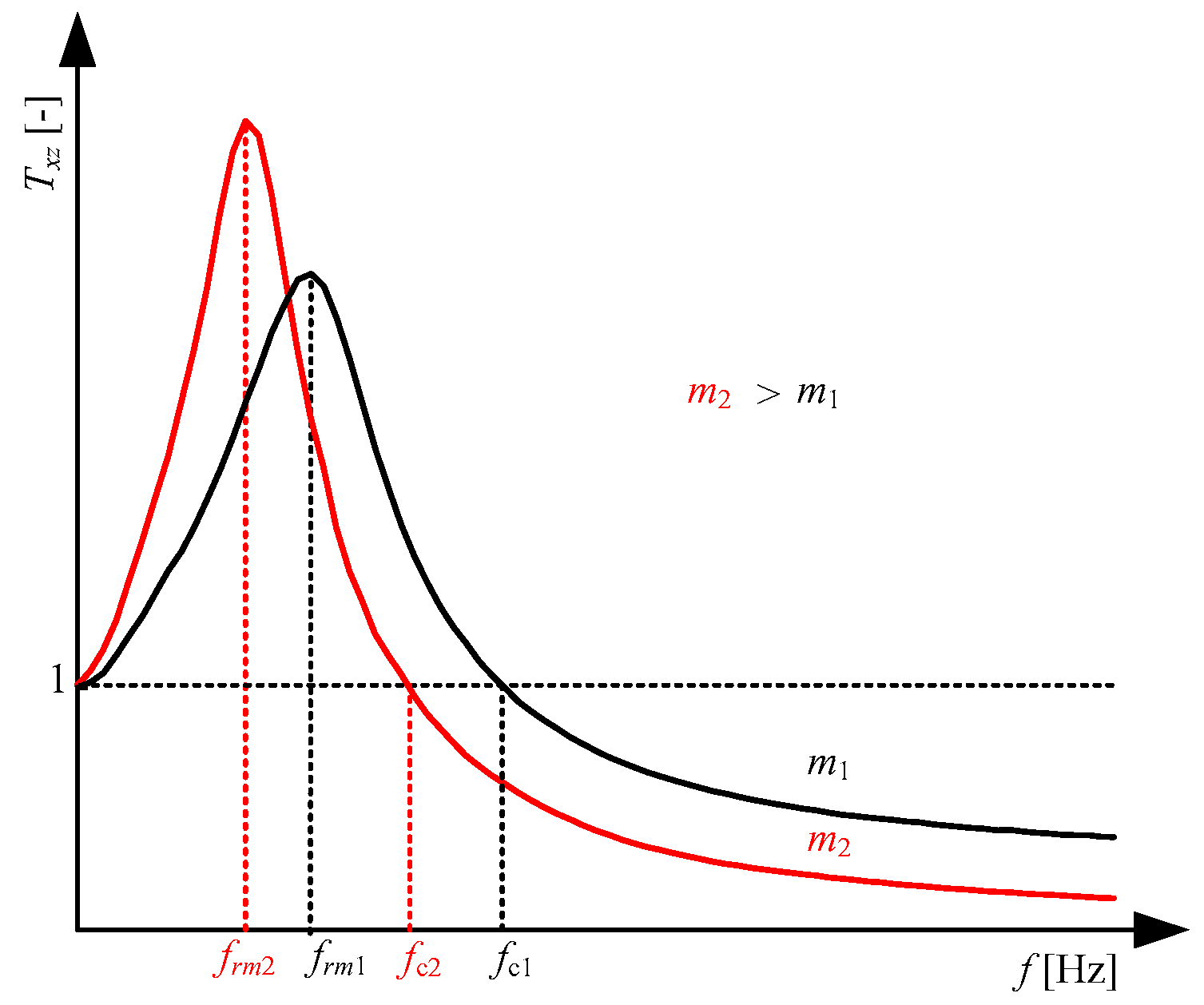
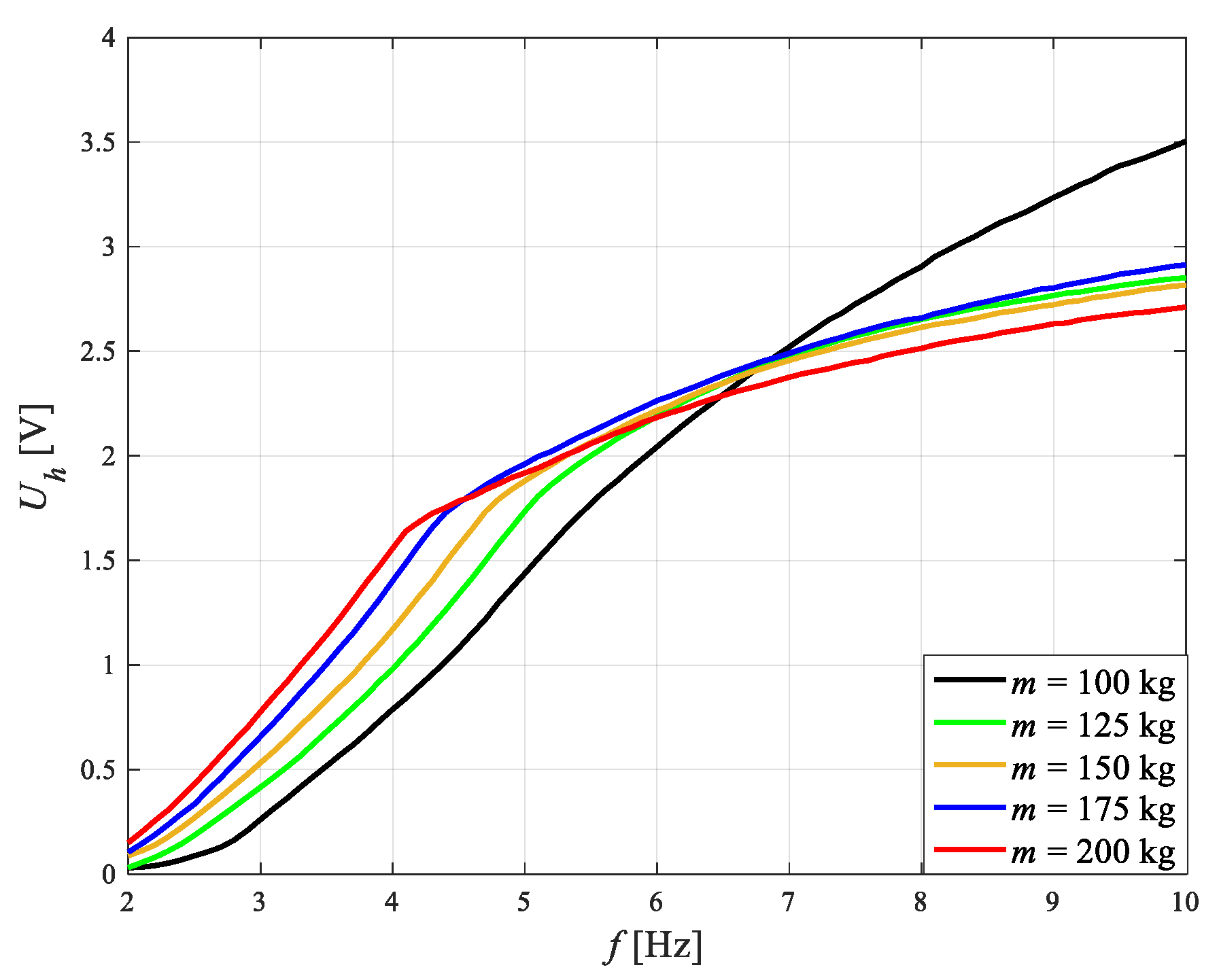
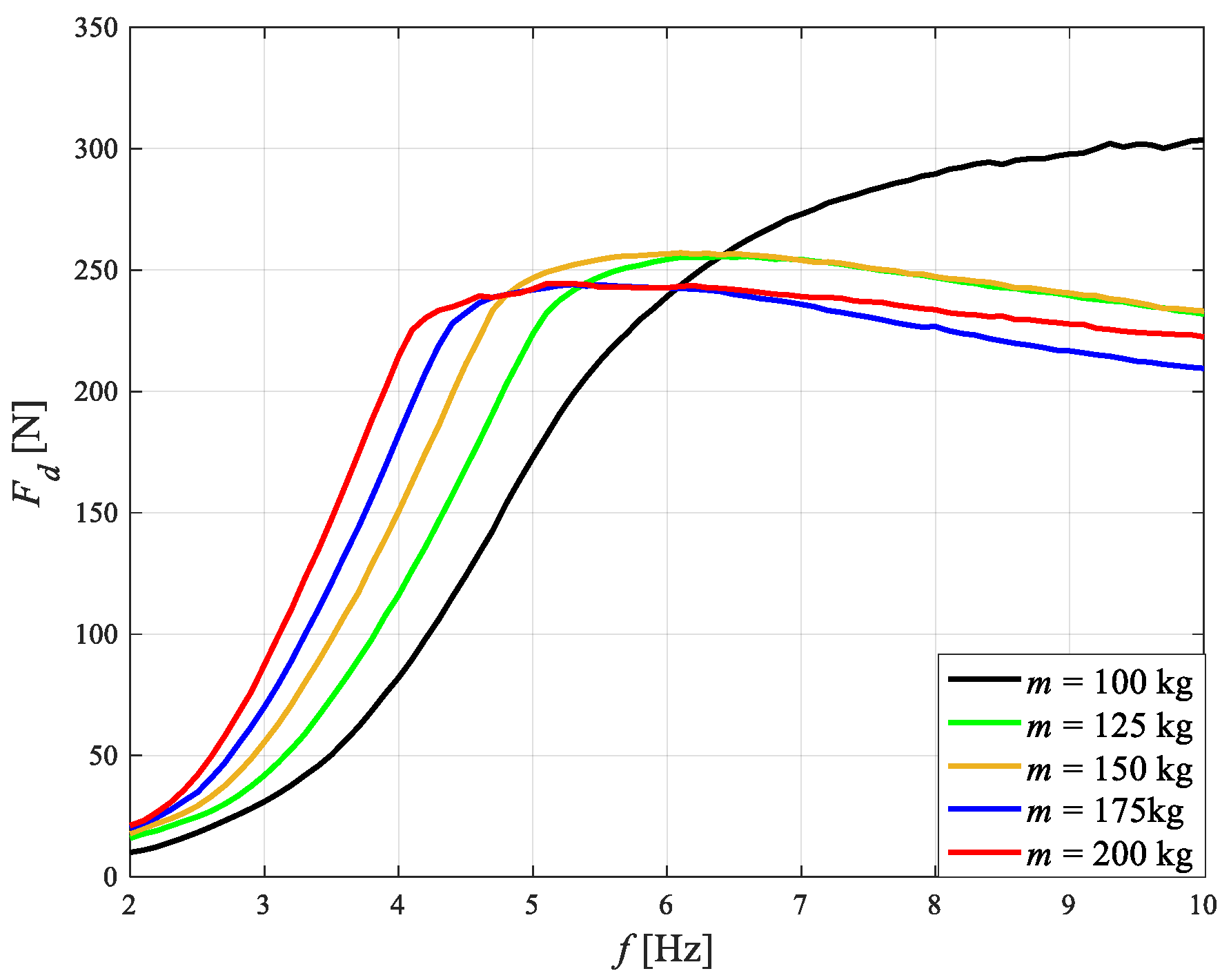
4.2. Impact of Sprung Mass
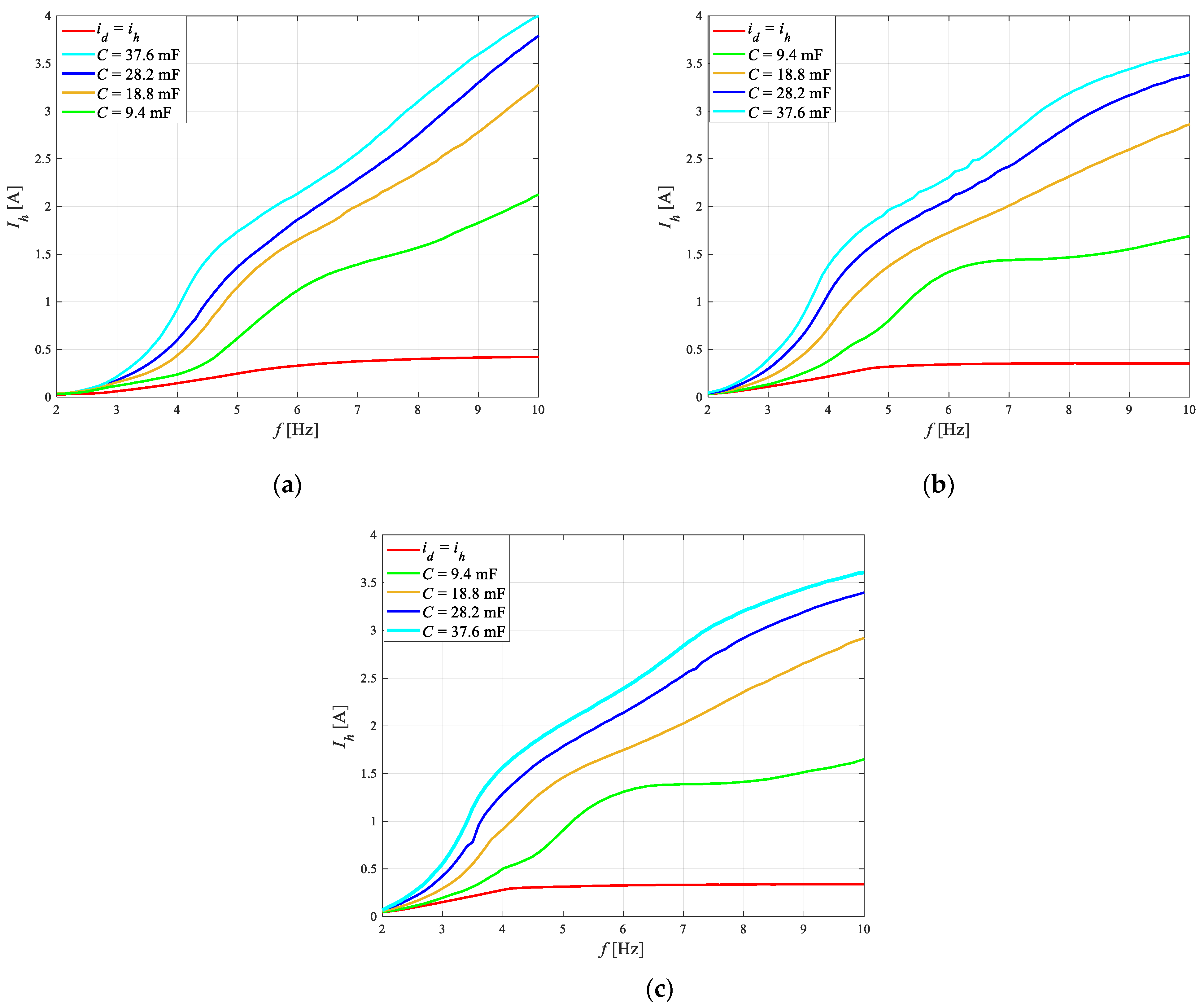
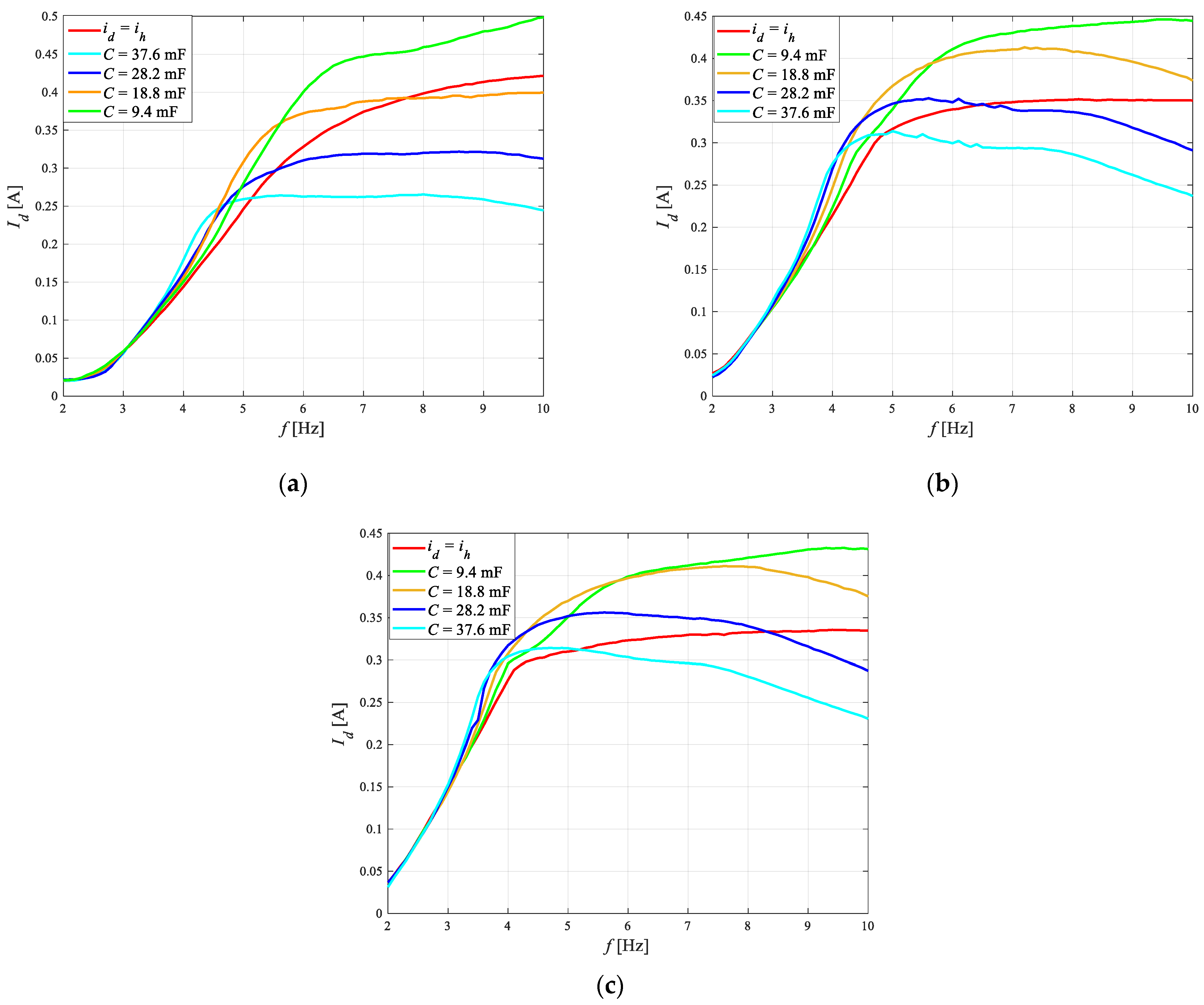
4.3. Impact of Shunt Capacitors Capacity
5. Summary and Conclusions
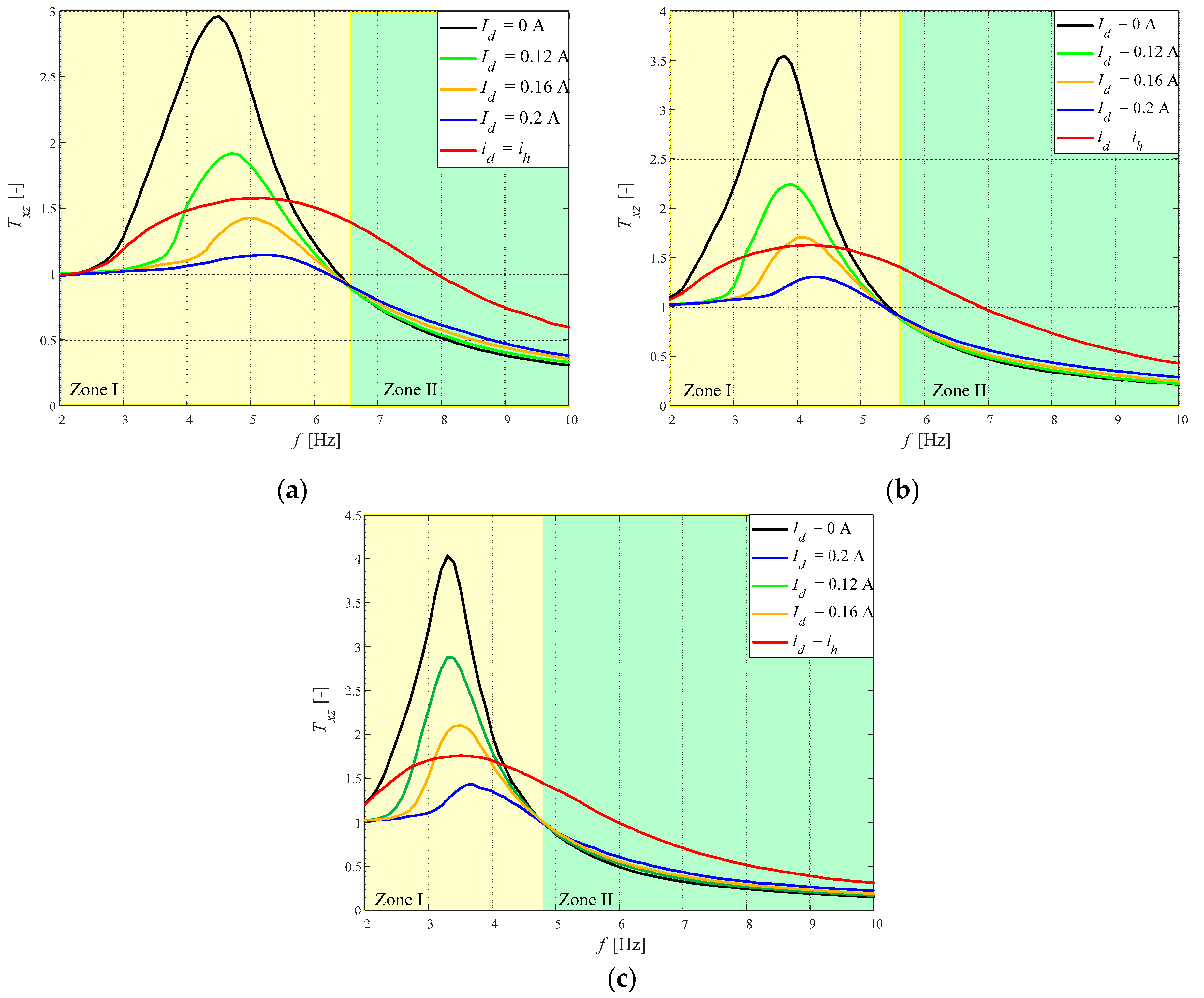
- An increase in current level Id results in a decrease in the sprung mass vibration amplitude in the range (2, fc) Hz (Zone I) and an increase in the range (fc, 10) Hz (Zone II).
- An increase in current level Id also results in a decrease in quality factor Q and the performance indexes J1 and J2; this is in contrast to the performance index J3, which takes higher values.
- Supplying the damper control coil by alternating voltage (produced by the harvester) uh, enables vibration amplitude of the sprung mass to be reduced in the near-resonance frequency range (the quality factor Q takes about two-fold lower values).
- In a whole frequency range of applied excitation, the value of the performance index J1 differs by only 4%, when comparing the damper control coil powered by alternating current id and Id = 0.
- In case of powering, the damper control coil is powered by alternating current id, the performance index J3 achieves its highest values at frequencies higher than frequency fc, and this disadvantage may be eliminated by connecting shunt capacitors in parallel with the electrical circuit.
- An increase in sprung mass m results in an increase in quality factor Q, a decrease both the frequency fr and fc, and relative damping ζ.
- Connecting shunt capacitors allows a significant decrease in the rms value of current Id at high frequencies and that results in a decrease in force Fd.
- The capacity of shunt capacitors 37.6 mF enables the reduction in the performance index to be significantly reduced, independent of the sprung mass.
- The maximal capacity of shunt capacitors is limited to the maximal rms value of the current harvester’s output, which should not exceed 4 A.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harb, A. Energy Harvesting: State-of-the-Art. Renew. Energy 2011, 36, 2641–2654. [Google Scholar] [CrossRef]
- Siang, J.; Lim, M.H.; Salman Leong, M. Review of Vibration-Based Energy Harvesting Technology: Mechanism and Architectural Approach. Int. J. Energy Res. 2018, 42, 1866–1893. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. A Comprehensive Review on Vibration Energy Harvesting: Modelling and Realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Sun, R.; Zhou, S.; Cheng, L. Ultra-Low Frequency Vibration Energy Harvesting: Mechanisms, Enhancement Techniques, and Scaling Laws. Energy Convers. Manag. 2023, 276, 116585. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Prentkovskis, O.; Deptuła, A.; Skačkauskas, P. Research of Vibrations Effect on Hydraulic Valves in Military Vehicles. Def. Technol. 2023, 30, 111–125. [Google Scholar] [CrossRef]
- Priya, S.; Inman, D.J. Energy Harvesting Technologies; Springer: Boston, MA, USA, 2009; ISBN 978-0-387-76463-4. [Google Scholar]
- Georgiadis, A.; Collado, A.; Tentzeris, M.M. Energy Harvesting: Technologies, Systems, and Challenges; Cambridge University Press: Cambridge, UK, 2021; ISBN 978-1-107-03937-7. [Google Scholar]
- Spreemann, D.; Manoli, Y. Electromagnetic Vibration Energy Harvesting Devices: Architectures, Design, Modeling and Optimization; Springer Series in Advanced Microelectronics; Springer: Dordrecht, The Netherlands, 2012; Volume 35, ISBN 978-94-007-2943-8. [Google Scholar]
- Wang, X.; Liang, X.; Wei, H. A Study of Electromagnetic Vibration Energy Harvesters with Different Interface Circuits. Mech. Syst. Signal Process. 2015, 58–59, 376–398. [Google Scholar] [CrossRef]
- Wang, X.; Liang, X.; Hao, Z.; Du, H.; Zhang, N.; Qian, M. Comparison of Electromagnetic and Piezoelectric Vibration Energy Harvesters with Different Interface Circuits. Mech. Syst. Signal Process. 2016, 72–73, 906–924. [Google Scholar] [CrossRef]
- Cai, Q.; Zhu, S. Enhancing the Performance of Electromagnetic Damper Cum Energy Harvester Using Microcontroller: Concept and Experiment Validation. Mech. Syst. Signal Process. 2019, 134, 106339. [Google Scholar] [CrossRef]
- Kozieł, A.; Jastrzębski, Ł.; Sapiński, B. Advanced Prototype of an Electrical Control Unit for an MR Damper Powered by Energy Harvested from Vibrations. Energies 2022, 15, 4537. [Google Scholar] [CrossRef]
- Cai, Q.; Zhu, S. The Nexus between Vibration-Based Energy Harvesting and Structural Vibration Control: A Comprehensive Review. Renew. Sustain. Energy Rev. 2022, 155, 111920. [Google Scholar] [CrossRef]
- Scruggs, J.; Lindner, D.K. Active Energy Control in Civil Structures. In Proceedings of the Smart Structures and Materials 1999: Smart Systems for Bridges, Structures, and Highways, Newport Beach, CA, USA, 1–2 March 1999; SPIE: Bellingham, WA, USA, 1999; Volume 3671, pp. 194–205. [Google Scholar]
- Cho, S.-W.; Jung, H.-J.; Lee, I.-W. Smart Passive System Based on Magnetorheological Damper. Smart Mater. Struct. 2005, 14, 707. [Google Scholar] [CrossRef]
- Hong, J.-H.; Choi, K.-M.; Lee, J.-H.; Oh, J.-W.; Lee, I. Experimental Study on Smart Passive System Based on MR Damper. In Proceedings of the 18th KKCNN Symposium on Civil Engineering, Taiwan, China, 18–20 December 2005. [Google Scholar]
- Choi, K.-M.; Jung, H.-J.; Lee, H.-J.; Cho, S.-W. Feasibility Study of an MR Damper-Based Smart Passive Control System Employing an Electromagnetic Induction Device. Smart Mater. Struct. 2007, 16, 2323. [Google Scholar] [CrossRef]
- Choi, K.-M.; Jung, H.-J.; Cho, S.-W.; Lee, I.-W. Application of Smart Passive Damping System Using MR Damper to Highway Bridge Structure. J. Mech. Sci. Technol. 2007, 21, 870–874. [Google Scholar] [CrossRef]
- Choi, Y.-T.; Wereley, N.M. Self-Powered Magnetorheological Dampers. J. Vib. Acoust. 2009, 131, 044501. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Z.; Spencer, B.F., Jr. Self-Powered and Sensing Control System Based on MR Damper: Presentation and Application. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2009, San Diego, CA, USA, 9–12 March 2009; SPIE: Bellingham, WA, USA; Volume 7292, pp. 1268–1277. [Google Scholar]
- Sapiński, B. Experimental Study of a Self-Powered and Sensing MR-Damper-Based Vibration Control System. Smart Mater. Struct. 2011, 20, 105007. [Google Scholar] [CrossRef]
- Sapiński, B.; Orkisz, P.; Jastrzębski, Ł. Experimental Analysis of Power Flows in the Regenerative Vibration Reduction System with a Magnetorheological Damper. Energies 2021, 14, 848. [Google Scholar] [CrossRef]
- Yamin, A.H.M.; Ab Talib, M.H.; Darus, I.Z.M.; Nor, N.S.M. Magneto-Rheological (MR) Damper–Parametric Modelling and Experimental Validation for LORD RD 8040-1. J. Teknol. 2022, 84, 27–34. [Google Scholar]
- Meirovitch, L. Elements of Vibration Analysis; McGraw-Hill: New York, NY, USA, 1986; ISBN 978-0-07-100271-4. [Google Scholar]
- Electrodynamic Shaker, LDS V780, Technical Documentation. Available online: https://www.bksv.com/en/instruments/vibration-testing-equipment/lds-shakers/low-force-shakers/lds-v780 (accessed on 13 May 2024).
- Power Amplifier, LDS HPA-K, Technical Documentation. Available online: https://www.bksv.com/en/instruments/vibration-testing-equipment/vibration-amplifiers/lds-shaker-amplifier/lds-hpa-k-amplifier (accessed on 13 May 2024).
- MR Damper, RD-8040-1, Technical Documentation. Available online: http://www.lordfulfillment.com/upload/DS7016.pdf (accessed on 13 May 2024).
- Sapiński, B. An Experimental Electromagnetic Induction Device for a Magnetorheological Damper. J. Theor. Appl. Mech. 2008, 46, 933–947. [Google Scholar]
- Sapiński, B. Vibration Power Generator for a Linear MR Damper. Smart Mater. Struct. 2010, 19, 105012. [Google Scholar] [CrossRef]
- Optical Sensor, FT 50RLA-70, Technical Documentation. Available online: http://sels.pl (accessed on 13 May 2024).
- Force Sensor, KMM30-5kN, Technical Documentation. Available online: https://wobit.com.pl (accessed on 13 May 2024).
- Measurement Card, RT-DAC4 PCI, Technical Documentation. Available online: http://www.inteco.com.pl/products/process-io-boards (accessed on 13 May 2024).

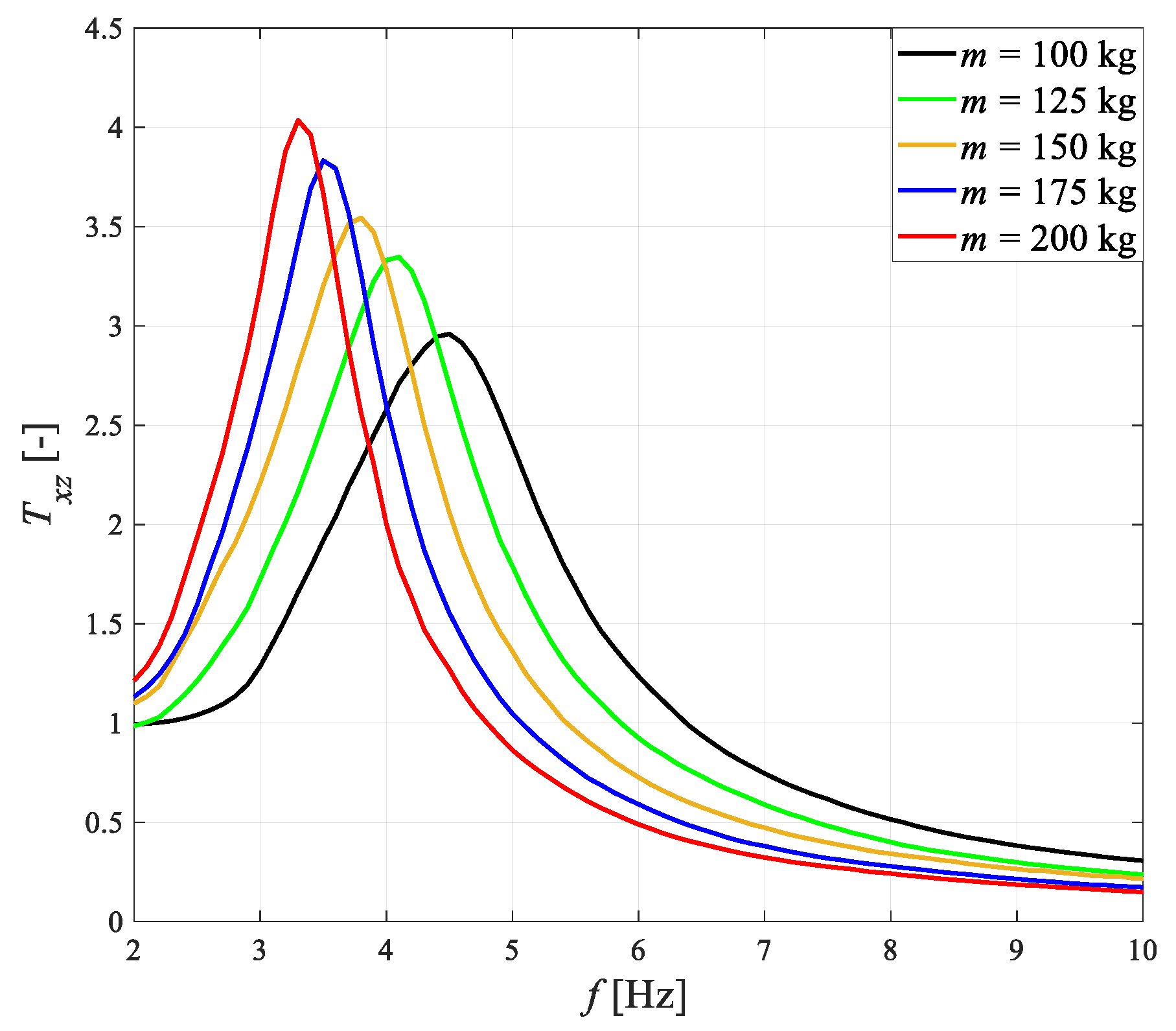
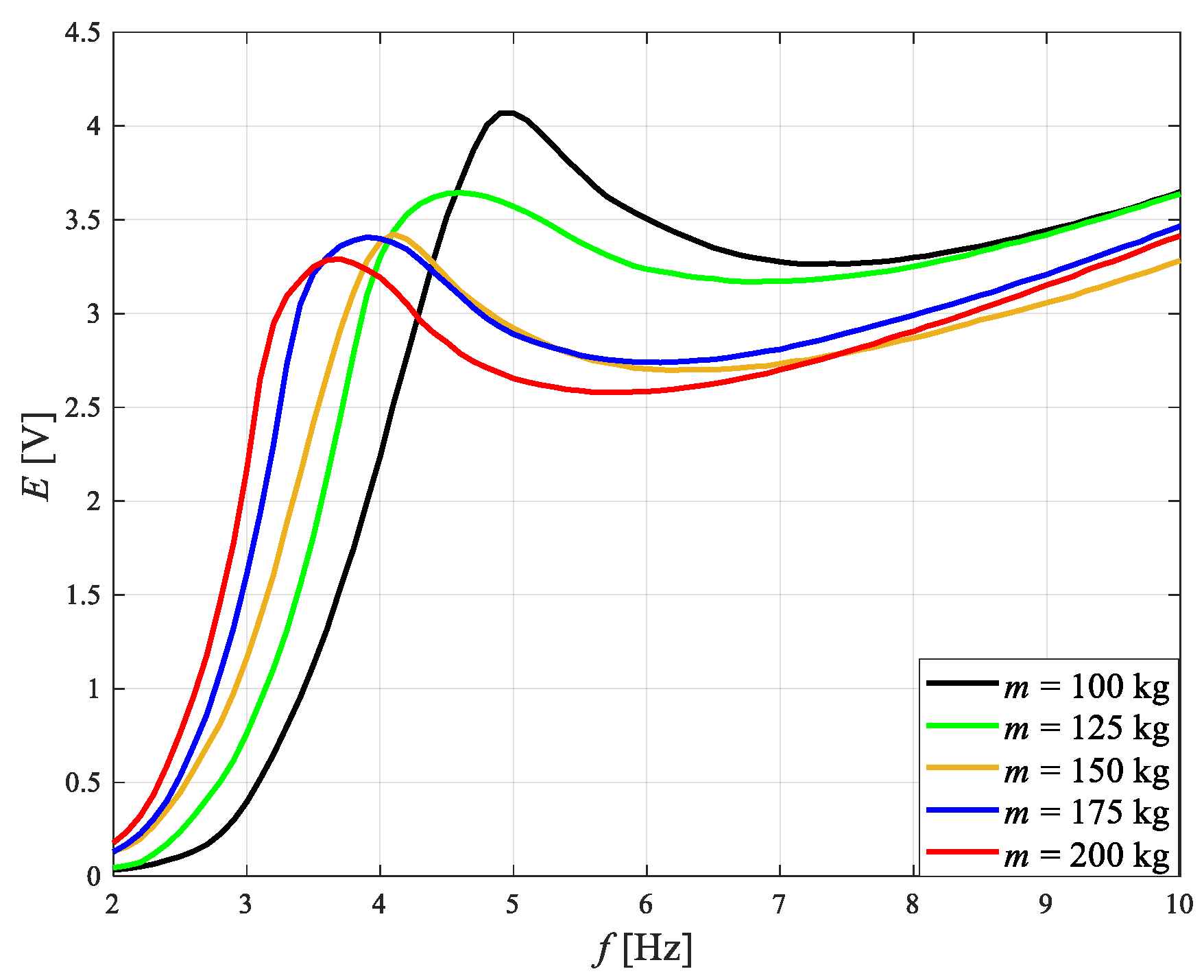
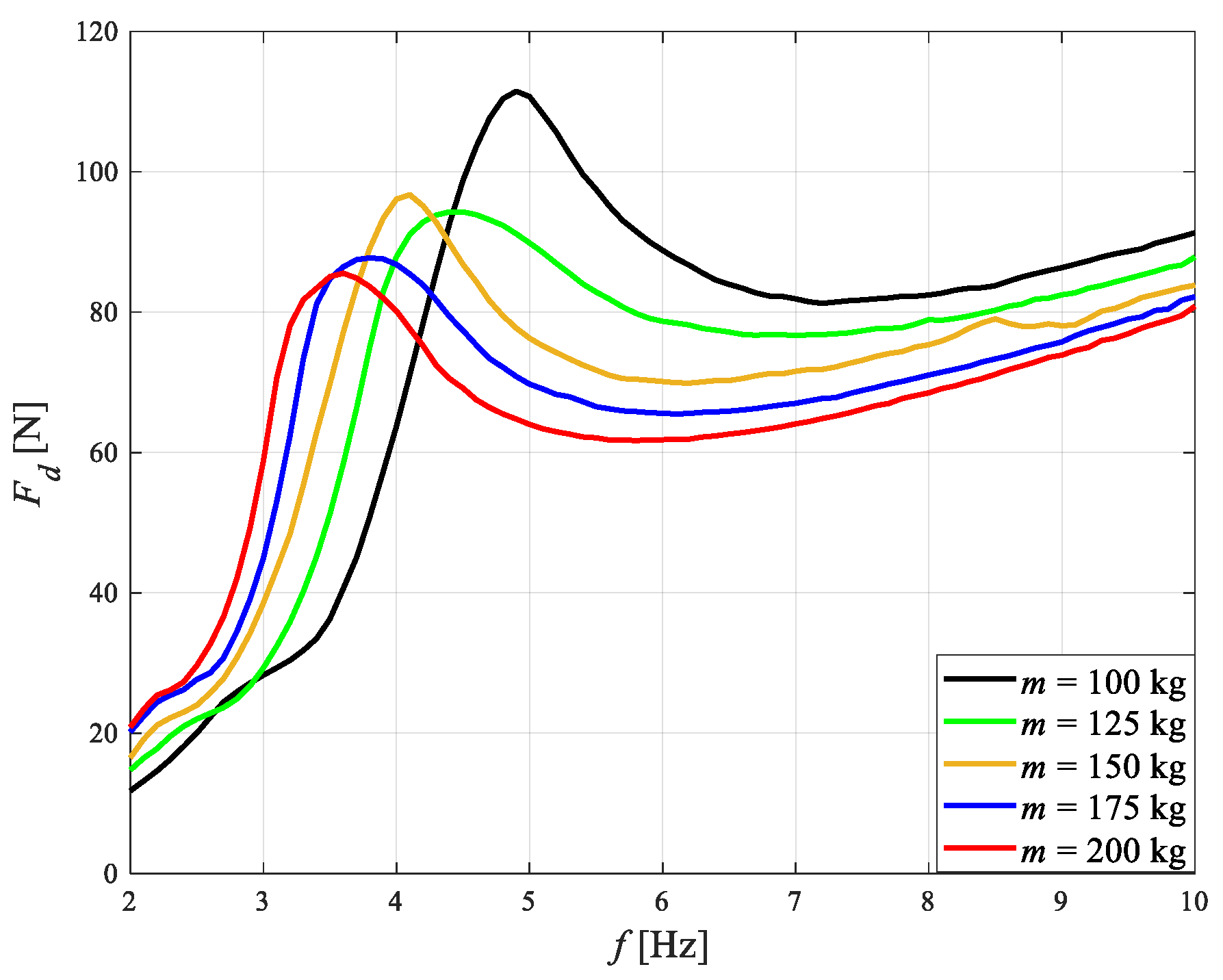
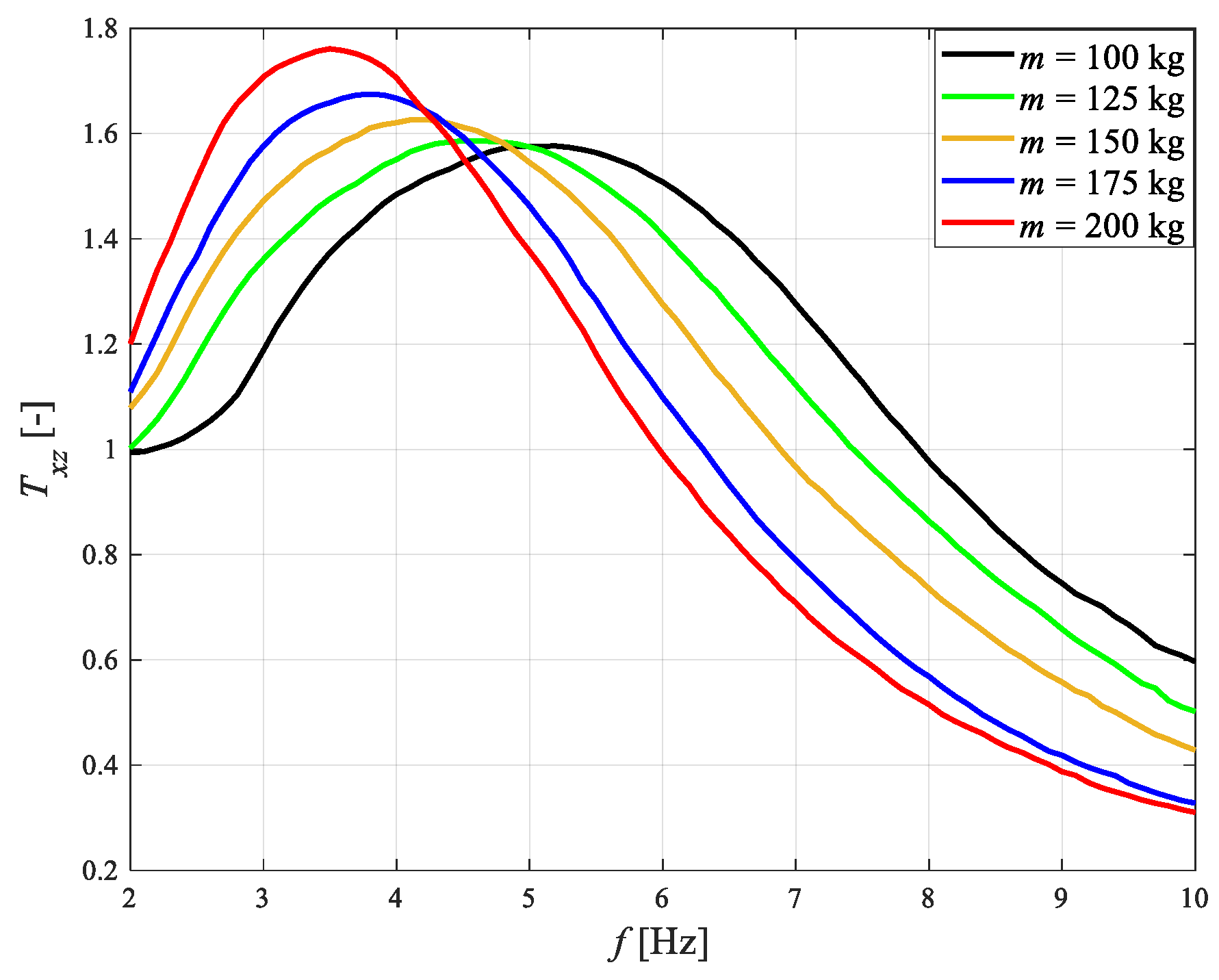



| Id [A] | fr [Hz] | Q [-] | J1 [-] | J2 [-] | J3 [-] | ζ [-] |
|---|---|---|---|---|---|---|
| 0 | 4.5 | 2.960 | 1.218 | 1.731 | 0.483 | 0.169 |
| 0.12 | 4.7 | 1.917 | 0.970 | 1.291 | 0.501 | 0.261 |
| 0.16 | 5.0 | 1.426 | 0.884 | 1.118 | 0.534 | 0.351 |
| 0.20 | 5.3 | 1.147 | 0.846 | 1.032 | 0.563 | 0.436 |
| id = ig | 5.2 | 1.576 | 1.180 | 1.358 | 0.895 | 0.317 |
| Id [A] | fr [Hz] | Q [-] | J1 [-] | J2 [-] | J3 [-] | ζ [-] |
|---|---|---|---|---|---|---|
| 0 | 3.8 | 3.545 | 1.148 | 2.013 | 0.401 | 0.141 |
| 0.12 | 3.9 | 2.245 | 0.891 | 1.437 | 0.412 | 0.223 |
| 0.16 | 4.1 | 1.708 | 0.812 | 1.231 | 0.440 | 0.293 |
| 0.20 | 4.3 | 1.305 | 0.772 | 1.095 | 0.481 | 0.383 |
| id = ig | 4.2 | 1.627 | 1.108 | 1.443 | 0.794 | 0.307 |
| Id [A] | fr [Hz] | Q [-] | J1 [-] | J2 [-] | J3 [-] | ζ [-] |
|---|---|---|---|---|---|---|
| 0 | 3.3 | 4.036 | 1.025 | 2.210 | 0.345 | 0.124 |
| 0.12 | 3.3 | 2.880 | 0.858 | 1.700 | 0.369 | 0.174 |
| 0.16 | 3.5 | 2.103 | 0.770 | 1.409 | 0.395 | 0.238 |
| 0.20 | 3.7 | 1.430 | 0.698 | 1.143 | 0.431 | 0.350 |
| id = ig | 3.5 | 1.761 | 1.013 | 1.553 | 0.684 | 0.284 |
| C [mF] | fr [Hz] | Q [-] | J1 [-] | J2 [-] | J3 [-] |
|---|---|---|---|---|---|
| Id = 0 A | 4.5 | 2.960 | 1.2178 | 1.7306 | 0.4831 |
| 9.4 | 5.7 | 1.798 | 1.1825 | 1.4764 | 0.7331 |
| 18.8 | 5.1 | 1.808 | 1.0468 | 1.4142 | 0.5103 |
| 28.2 | 4.6 | 1.625 | 0.9331 | 1.2521 | 0.4707 |
| 37.6 | 4.4 | 1.734 | 0.9151 | 1.2311 | 0.4596 |
| C [mF] | fr [Hz] | Q [-] | J1 [-] | J2 [-] | J3 [-] |
|---|---|---|---|---|---|
| Id = 0 A | 3.8 | 3.545 | 1.1477 | 2.0126 | 0.4005 |
| 9.4 | 5.1 | 1.739 | 1.1055 | 1.5226 | 0.7200 |
| 18.8 | 4.6 | 1.895 | 1.0223 | 1.5520 | 0.5468 |
| 28.2 | 4.3 | 1.922 | 0.9480 | 1.5112 | 0.4518 |
| 37.6 | 4.1 | 1.891 | 0.9021 | 1.4406 | 0.4314 |
| C [mF] | fr [Hz] | Q [-] | J1 [-] | J2 [-] | J3 [-] |
|---|---|---|---|---|---|
| Id = 0 A | 3.3 | 4.036 | 1.0250 | 2.2104 | 0.3454 |
| 9.4 | 3.6 | 1.773 | 0.9933 | 1.5675 | 0.6434 |
| 18.8 | 4.2 | 1.876 | 0.9423 | 1.6159 | 0.5369 |
| 28.2 | 3.9 | 1.962 | 0.8891 | 1.6301 | 0.4497 |
| 37.6 | 3.8 | 1.981 | 0.8406 | 1.5923 | 0.4002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapiński, B.; Jastrzębski, Ł. Performance Improvement of an MR-Damper-Based Vibration-Reduction System with Energy Harvesting at Sprung Mass Changes. Energies 2024, 17, 3436. https://doi.org/10.3390/en17143436
Sapiński B, Jastrzębski Ł. Performance Improvement of an MR-Damper-Based Vibration-Reduction System with Energy Harvesting at Sprung Mass Changes. Energies. 2024; 17(14):3436. https://doi.org/10.3390/en17143436
Chicago/Turabian StyleSapiński, Bogdan, and Łukasz Jastrzębski. 2024. "Performance Improvement of an MR-Damper-Based Vibration-Reduction System with Energy Harvesting at Sprung Mass Changes" Energies 17, no. 14: 3436. https://doi.org/10.3390/en17143436
APA StyleSapiński, B., & Jastrzębski, Ł. (2024). Performance Improvement of an MR-Damper-Based Vibration-Reduction System with Energy Harvesting at Sprung Mass Changes. Energies, 17(14), 3436. https://doi.org/10.3390/en17143436







