Interval Type-2 Fuzzy Logic Control of Linear Stages in Feedback-Error-Learning Structure Using Laser Interferometer
Abstract
1. Introduction
2. Methodology
2.1. Interval Type-2 Fuzzy Structures
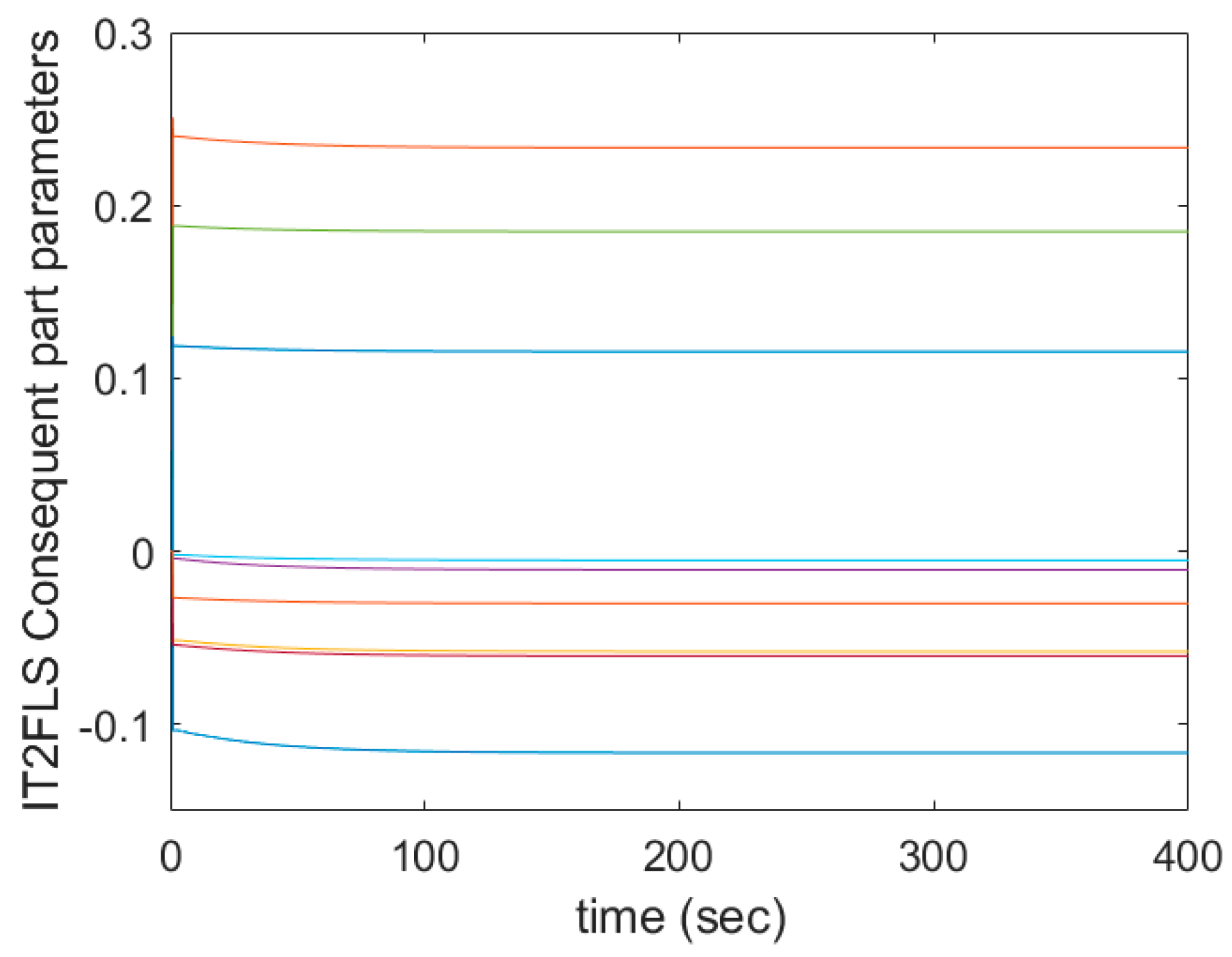
2.2. Gradient Descent Training Approach
| Calculating the Output of the IT2FLS | |
|---|---|
| Find the IT2MF’s values, as follows: | |
| (20) | |
| (21) | |
| as follows: | |
| (22) | |
| is as defined as in (2). | |
| as in (5) and (7). | |
| as in (9). | |
2.3. Kalman Filter Training Method
2.4. Feedback Error Learning
3. Experimental Setup
3.1. Laser Interferometer
3.2. Linear Stage
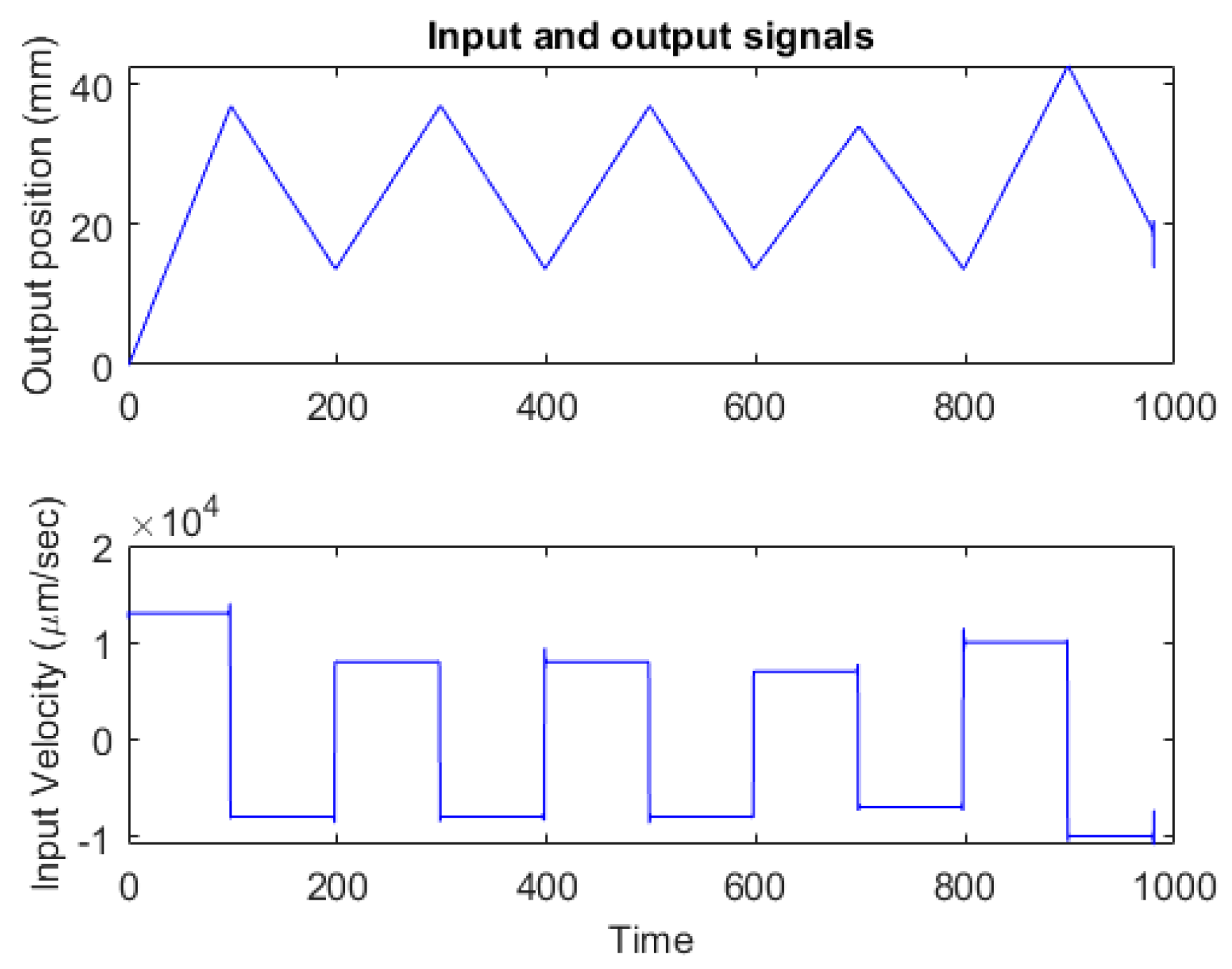
4. System Modelling Procedure
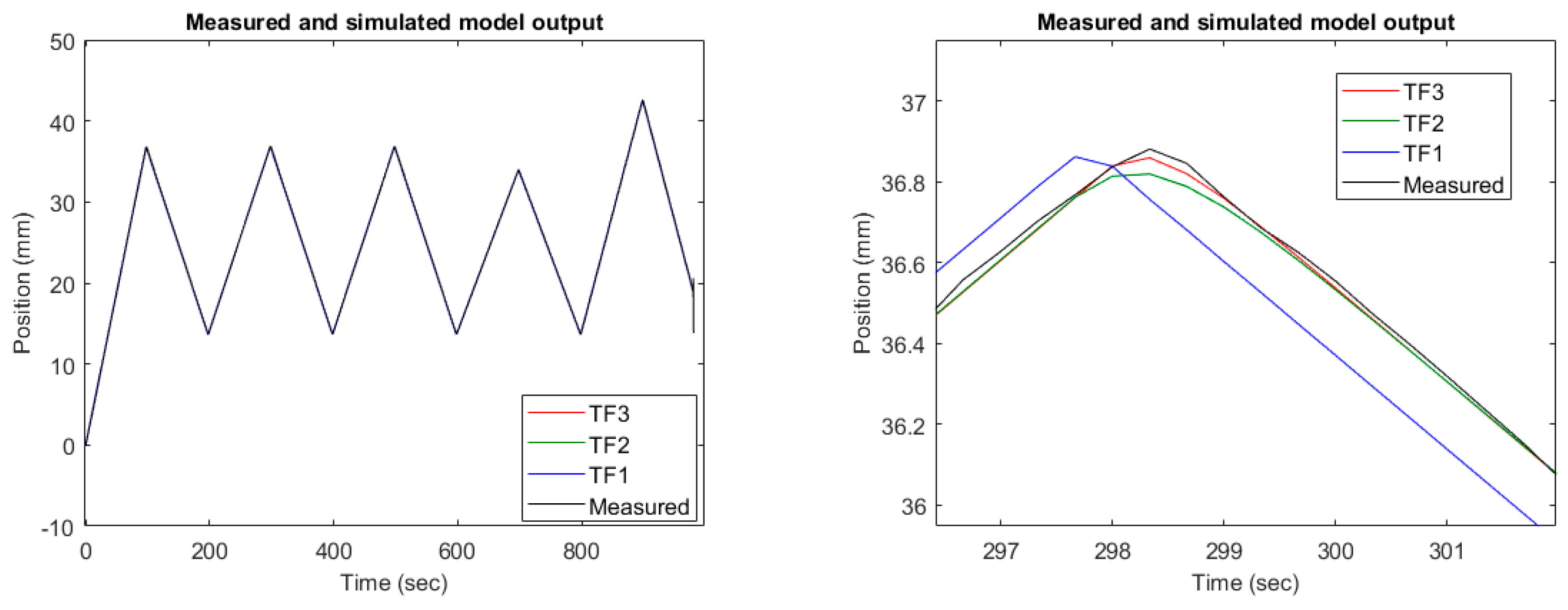
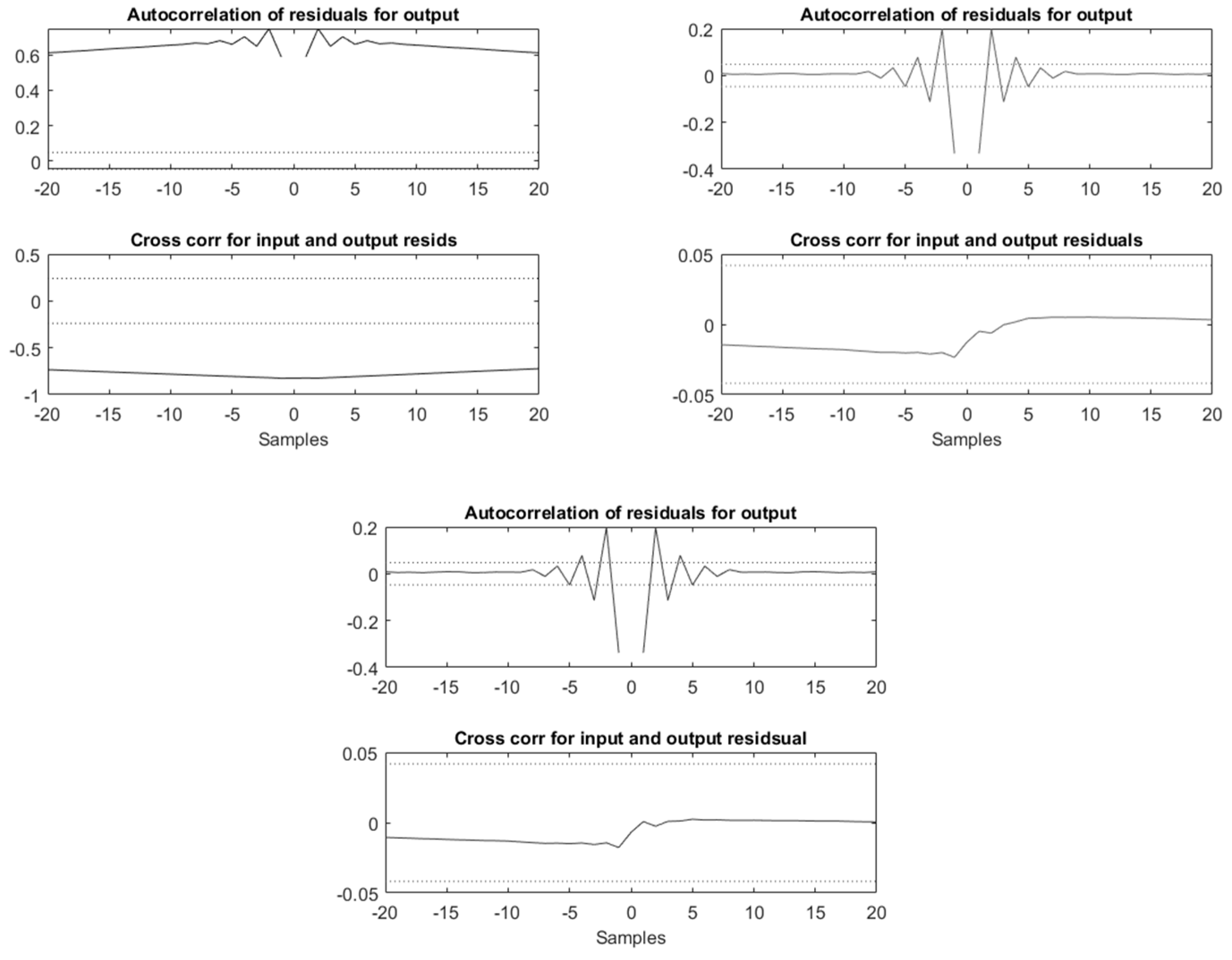
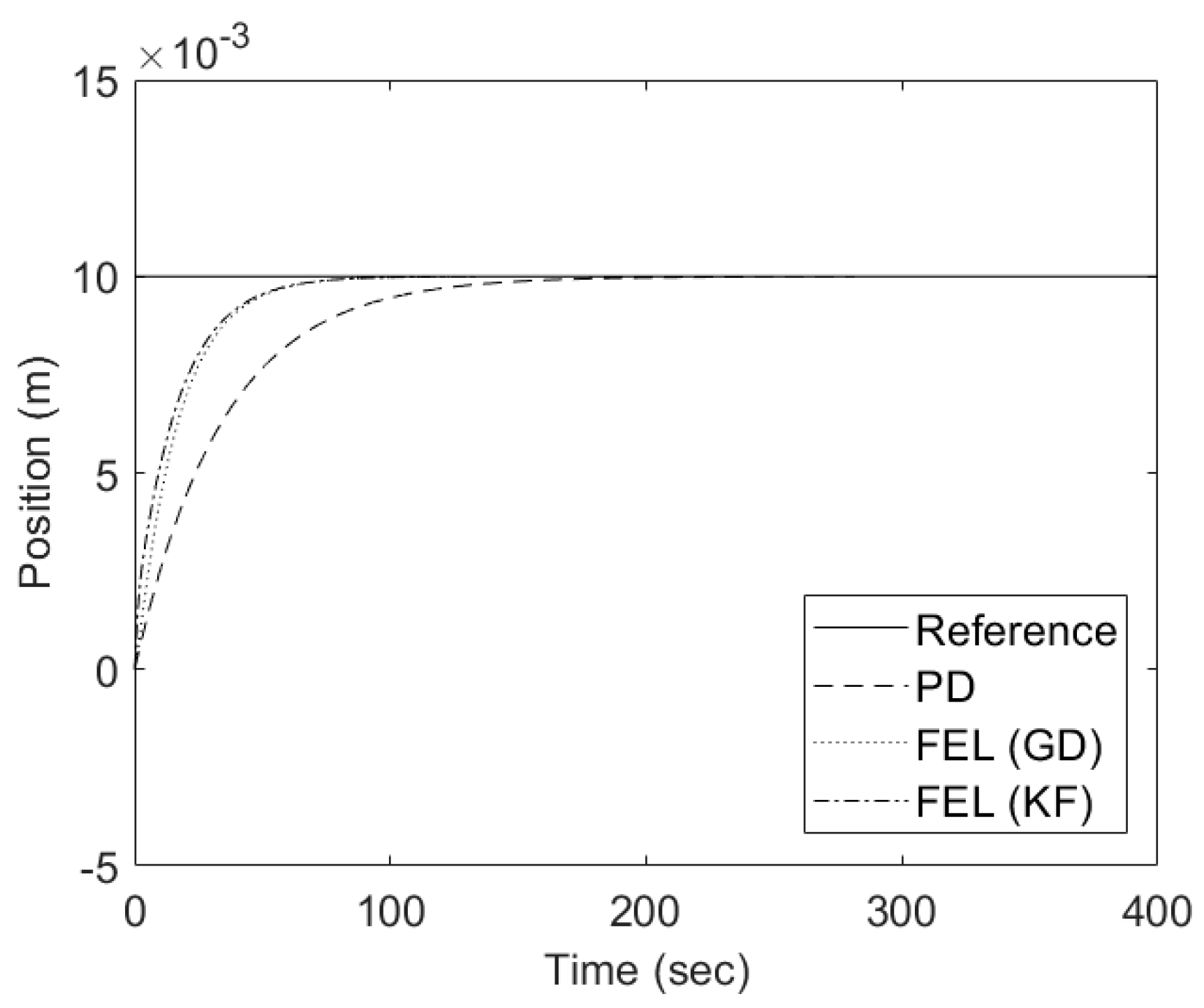
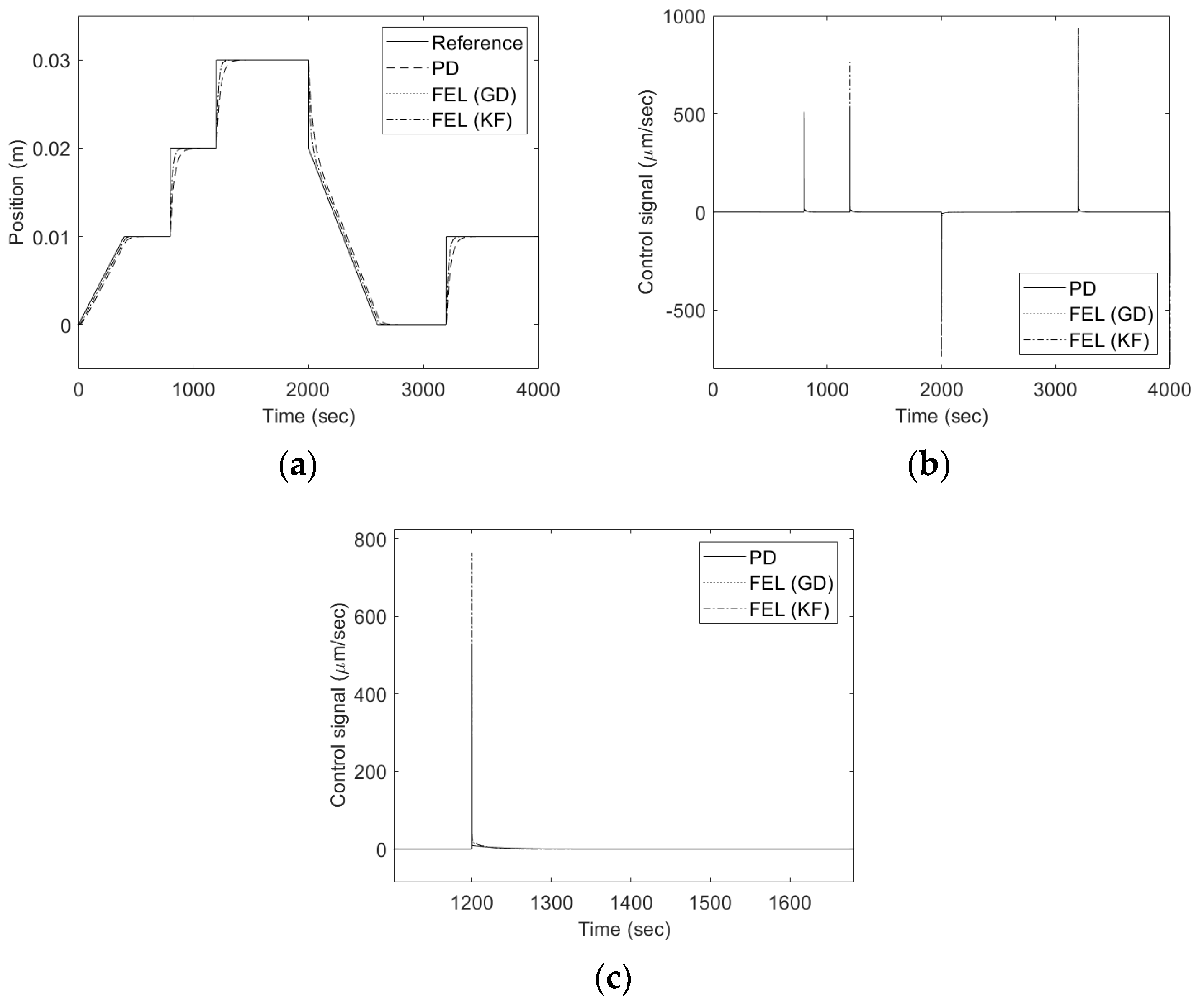
5. Simulation Results
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Acronyms
| Corr | Correlation |
| FEL | Feedback error learning |
| GD | Gradient descent |
| IT2FLS | interval type-2 fuzzy logic system |
| IT2MF | interval type-2 fuzzy membership function |
| KF | Kalman filter |
| PD | Proportional derivative |
| PPM | Part per million |
| SSE | Steady-state error |
| TR+D | Type-reduction + defuzzification |
References
- Hu, J.; Li, C.; Chen, Z.; Yao, B. Precision motion control of a 6-DoFs industrial robot with accurate payload estimation. IEEE/ASME Trans. Mechatron. 2020, 25, 1821–1829. [Google Scholar] [CrossRef]
- Nguyen, V.; Cvitanic, T.; Baxter, M.; Ahlin, K.; Johnson, J.; Freeman, P.; Balakirsky, S.; Brown, A.; Melkote, S. Precision robotic milling of fiberglass shims in aircraft wing assembly using laser tracker feedback. SAE Int. J. Aerosp. 2022, 15, 87–97. [Google Scholar] [CrossRef]
- Yuan, L.; Ding, D.; Pan, Z.; Yu, Z.; Wu, B.; van Duin, S.; Li, H.; Li, W. Application of multidirectional robotic wire arc additive manufacturing process for the fabrication of complex metallic parts. IEEE Trans. Ind. Inform. 2019, 16, 454–464. [Google Scholar] [CrossRef]
- Xiao, J.; Dou, S.; Zhao, W.; Liu, H. Sensorless human-robot collaborative assembly considering load and friction compensation. IEEE Robot. Autom. Lett. 2021, 6, 5945–5952. [Google Scholar] [CrossRef]
- Fan, Y.; Luo, J.; Tomizuka, M. A learning framework for high precision industrial assembly. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 811–817. [Google Scholar]
- Rout, A.; Deepak, B.; Biswal, B. Advances in weld seam tracking techniques for robotic welding: A review. Robot. Comput. Integr. Manuf. 2019, 56, 12–37. [Google Scholar] [CrossRef]
- Ghafarian, M.; Shirinzadeh, B.; Al-Jodah, A.; Das, T.K. Adaptive fuzzy sliding mode control for high-precision motion tracking of a multi-DOF micro/nano manipulator. IEEE Robot. Autom. Lett. 2020, 5, 4313–4320. [Google Scholar] [CrossRef]
- García-Chávez, R.E.; Silva-Ortigoza, R.; Hernández-guzmáN, V.M.; Marciano-Melchor, M.; Orta-Quintana, Á.A.; García-Sánchez, J.R.; Taud, H. A Robust Sliding Mode and PI-Based Tracking Control for the MIMO “DC/DC Buck Converter–Inverter–DC Motor” System. IEEE Access 2023, 11, 119396–119408. [Google Scholar] [CrossRef]
- de Jesús Rubio, J.; Orozco, E.; Cordova, D.A.; Hernandez, M.A.; Rosas, F.J.; Pacheco, J. Observer-based differential evolution constrained control for safe reference tracking in robots. Neural Netw. 2024, 175, 106273. [Google Scholar] [CrossRef]
- de Jesús Rubio, J.; Hernandez, M.A.; Rosas, F.J.; Orozco, E.; Balcazar, R.; Pacheco, J. Genetic high-gain controller to improve the position perturbation attenuation and compact high-gain controller to improve the velocity perturbation attenuation in inverted pendulums. Neural Netw. 2024, 170, 32–45. [Google Scholar] [CrossRef]
- de Jesús Rubio, J.; Hernandez, M.A.; Orozco, E.; Cordova, D.A.; Zacarias, A.; Pacheco, J. Observer-based model-free controller for the perturbations estimation and attenuation in robotic plants. Robot. Auton. Syst. 2024, 177, 104713. [Google Scholar] [CrossRef]
- Zhang, J.; Lou, Z.; Fan, K.-C. Accuracy improvement of a 3D passive laser tracker for the calibration of industrial robots. Robot. Comput. Integr. Manuf. 2023, 81, 102487. [Google Scholar] [CrossRef]
- Wan, Z.; Zhou, C.; Lin, Z.; Yan, H.; Tang, W.; Wang, Z.; Wu, J. An Improved Design of the MultiCal On-Site Calibration Device for Industrial Robots. Sensors 2023, 23, 5717. [Google Scholar] [CrossRef] [PubMed]
- Wan, Z.; Zhou, C.; Zhang, H.; Wu, J. Development of an onsite calibration device for robot manipulators. Front. Inf. Technol. Electron. Eng. 2023, 24, 217–230. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Sampled memory-event-triggered fuzzy load frequency control for wind power systems subject to outliers and transmission delays. IEEE Trans. Cybern. 2022, 53, 4043–4053. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Synchronization of delayed fuzzy neural networks with probabilistic communication delay and its application to image encryption. IEEE Trans. Fuzzy Syst. 2022, 31, 930–940. [Google Scholar] [CrossRef]
- Choi, J.; Baek, J.; Lee, W.; Lee, Y.S.; Han, S. Adaptive model-free control with nonsingular terminal sliding-mode for application to robot manipulators. IEEE Access 2020, 8, 169897–169907. [Google Scholar] [CrossRef]
- Alhama Blanco, P.J.; Abu-Dakka, F.J.; Abderrahim, M. Practical use of robot manipulators as intelligent manufacturing systems. Sensors 2018, 18, 2877. [Google Scholar] [CrossRef] [PubMed]
- Ning, Y.; Li, T.; Du, W.; Yao, C.; Zhang, Y.; Shao, J. Inverse kinematics and planning/control co-design method of redundant manipulator for precision operation: Design and experiments. Robot. Comput. Integr. Manuf. 2023, 80, 102457. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, Q.; Ye, Y.; Cheng, B.; Zhang, Z.; Cheng, R.; Zhang, L.; Li, H. Development of submicron precision three-dimensional low cross-interference air-floating motion stage. Rev. Sci. Instrum. 2023, 94, 065013. [Google Scholar] [CrossRef]
- Chang, Q.; Liu, Y.; Deng, J.; Zhang, S.; Chen, W. Design of a precise linear-rotary positioning stage for optical focusing based on the stick-slip mechanism. Mech. Syst. Signal Process. 2022, 165, 108398. [Google Scholar] [CrossRef]
- Al-Jodah, A.; Shirinzadeh, B.; Ghafarian, M.; Das, T.K.; Tian, Y.; Zhang, D. A fuzzy disturbance observer based control approach for a novel 1-DOF micropositioning mechanism. Mechatronics 2020, 65, 102317. [Google Scholar] [CrossRef]
- Go, G.; Kwak, D.; Piao, L.; Choi, H.; Jeong, S.; Lee, C.; Park, B.J.; Ko, S.Y.; Park, J.-o.; Park, S. Manipulation of micro-particles using a magnetically actuated microrobot. Mechatronics 2013, 23, 1037–1043. [Google Scholar] [CrossRef]
- Yang, P.; Takamura, T.; Takahashi, S.; Takamasu, K.; Sato, O.; Osawa, S.; Takatsuji, T. Development of high-precision micro-coordinate measuring machine: Multi-probe measurement system for measuring yaw and straightness motion error of XY linear stage. Precis. Eng. 2011, 35, 424–430. [Google Scholar] [CrossRef]
- Manske, E.; Fröhlich, T.; Füßl, R.; Ortlepp, I.; Mastylo, R.; Blumröder, U.; Dontsov, D.; Kühnel, M.; Köchert, P. Progress of nanopositioning and nanomeasuring machines for cross-scale measurement with sub-nanometre precision. Meas. Sci. Technol. 2020, 31, 085005. [Google Scholar] [CrossRef]
- Jeong, Y.; Dong, J.; Ferreira, P. Self-calibration of dual-actuated single-axis nanopositioners. Meas. Sci. Technol. 2008, 19, 045203. [Google Scholar] [CrossRef]
- Korpelainen, V.; Lassila, A. Calibration of a commercial AFM: Traceability for a coordinate system. Meas. Sci. Technol. 2007, 18, 395. [Google Scholar] [CrossRef]
- Xia, F.; Quigley, J.; Zhang, X.; Yang, C.; Wang, Y.; Youcef-Toumi, K. A modular low-cost atomic force microscope for precision mechatronics education. Mechatronics 2021, 76, 102550. [Google Scholar] [CrossRef]
- Dang, Q.; Yoo, S.; Kim, S.-W. Complete 3-D self-calibration of coordinate measuring machines. CIRP Ann. 2006, 55, 527–530. [Google Scholar] [CrossRef]
- Ochoa, P.; Castillo, O.; Melin, P.; Soria, J. Differential evolution with shadowed and general type-2 fuzzy systems for dynamic parameter adaptation in optimal design of fuzzy controllers. Axioms 2021, 10, 194. [Google Scholar] [CrossRef]
- Kavikumar, R.; Sakthivel, R.; Kwon, O.M.; Kaviarasan, B. Robust model reference tracking control for interval type-2 fuzzy stochastic systems. IET Control Theory Appl. 2020, 14, 1123–1134. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Yan, M.; Syam, W.P.; Piano, S.; Leach, R.K.; Branson, D.T. A Neural Network Separation Approach for the Inclusion of Static Friction in Nonlinear Static Models of Industrial Robots. IEEE/ASME Trans. Mechatron. 2023, 28, 3294–3304. [Google Scholar] [CrossRef]
- Xie, X.; Wei, C.; Gu, Z.; Shi, K. Relaxed resilient fuzzy stabilization of discrete-time Takagi–Sugeno systems via a higher order time-variant balanced matrix method. IEEE Trans. Fuzzy Syst. 2022, 30, 5044–5050. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, T.; Sun, K.; Rudas, I.J.; Gao, H. Disturbance observer-based adaptive fuzzy control for strict-feedback nonlinear systems with finite-time prescribed performance. IEEE Trans. Fuzzy Syst. 2021, 30, 1175–1184. [Google Scholar] [CrossRef]
- Chiu, C.-H.; Hung, Y.-T. One wheel vehicle real world control based on interval type 2 fuzzy controller. Mechatronics 2020, 70, 102387. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Kayacan, E.; Teshnehlab, M.; Kaynak, O. Levenberg marquardt algorithm for the training of type-2 fuzzy neuro systems with a novel type-2 fuzzy membership function. In Proceedings of the 2011 IEEE Symposium on Advances in Type-2 Fuzzy Logic Systems (T2FUZZ), Paris, France, 11–15 April 2011; pp. 88–93. [Google Scholar]
- Wu, D.; Mendel, J.M. Enhanced karnik--mendel algorithms. IEEE Trans. Fuzzy Syst. 2008, 17, 923–934. [Google Scholar]
- Hu, H.; Wang, Y.; Cai, Y. Advantages of the enhanced opposite direction searching algorithm for computing the centroid of an interval type-2 fuzzy set. Asian J. Control 2012, 14, 1422–1430. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Khakshour, A.J.; Kaynak, O.; Gao, H. Improving the speed of center of sets type reduction in interval type-2 fuzzy systems by eliminating the need for sorting. IEEE Trans. Fuzzy Syst. 2016, 25, 1193–1206. [Google Scholar] [CrossRef]
- Biglarbegian, M.; Melek, W.W.; Mendel, J.M. On the stability of interval type-2 TSK fuzzy logic control systems. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 40, 798–818. [Google Scholar] [CrossRef] [PubMed]
- Nie, M.; Tan, W.W. Towards an efficient type-reduction method for interval type-2 fuzzy logic systems. In Proceedings of the 2008 IEEE International Conference on Fuzzy Systems (IEEE World Congress on Computational Intelligence), Rio de Janeiro, Brazil, 1–6 June 2008; pp. 1425–1432. [Google Scholar]
- Khanesar, M.A.; Mendel, J.M. Maclaurin series expansion complexity-reduced center of sets type-reduction+ defuzzification for interval type-2 fuzzy systems. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2016; pp. 1224–1231. [Google Scholar]
- Sabahi, K.; Teshnehlab, M. Recurrent fuzzy neural network by using feedback error learning approaches for LFC in interconnected power system. Energy Convers. Manag. 2009, 50, 938–946. [Google Scholar] [CrossRef]
- Er, M.J.; Liew, K.C. Control of adept one SCARA robot using neural networks. IEEE Trans. Ind. Electron. 1997, 44, 762–768. [Google Scholar]
- Khanesar, M.A.; Kayacan, E.; Teshnehlab, M.; Kaynak, O. Extended Kalman filter based learning algorithm for type-2 fuzzy logic systems and its experimental evaluation. IEEE Trans. Ind. Electron. 2011, 59, 4443–4455. [Google Scholar] [CrossRef]
- Khanesar, M.; Branson, D.T. Prediction interval identification using interval type-2 fuzzy logic systems: Lake water level prediction using remote sensing data. IEEE Sens. J. 2021, 21, 13815–13827. [Google Scholar] [CrossRef]
- Kayacan, E.; Khanesar, M.A. Fuzzy Neural Networks for Real Time Control Applications: Concepts, Modeling and Algorithms for Fast Learning; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Eyoh, I.; John, R.; De Maere, G.; Kayacan, E. Hybrid learning for interval type-2 intuitionistic fuzzy logic systems as applied to identification and prediction problems. IEEE Trans. Fuzzy Syst. 2018, 26, 2672–2685. [Google Scholar] [CrossRef]
- Kawato, M.; Gomi, H. A computational model of four regions of the cerebellum based on feedback-error learning. Biol. Cybern. 1992, 68, 95–103. [Google Scholar] [CrossRef]
- Chapman, M. Environmental compensation of linear laser interferometer readings. In Renishaw Technical White Paper, TE329. 2013. Available online: https://www.renishaw.com/resourcecentre/en/details/White-paper-Environmental-compensation-of-linear-laser-interferometer-readings--94445?lang=en (accessed on 7 July 2024).
- Dusek, J.E.; Triantafyllou, M.S.; Lang, J.H. Piezoresistive foam sensor arrays for marine applications. Sens. Actuators A Phys. 2016, 248, 173–183. [Google Scholar] [CrossRef]
- Castellanos-Ramos, J.; Navas-González, R.; Fernández, I.; Vidal-Verdú, F. Insights into the mechanical behaviour of a layered flexible tactile sensor. Sensors 2015, 15, 25433–25462. [Google Scholar] [CrossRef]
- Arrington, C.B.; Rau, D.A.; Williams, C.B.; Long, T.E. UV-assisted direct ink write printing of fully aromatic Poly (amide imide) s: Elucidating the influence of an acrylic scaffold. Polymer 2021, 212, 123306. [Google Scholar] [CrossRef]




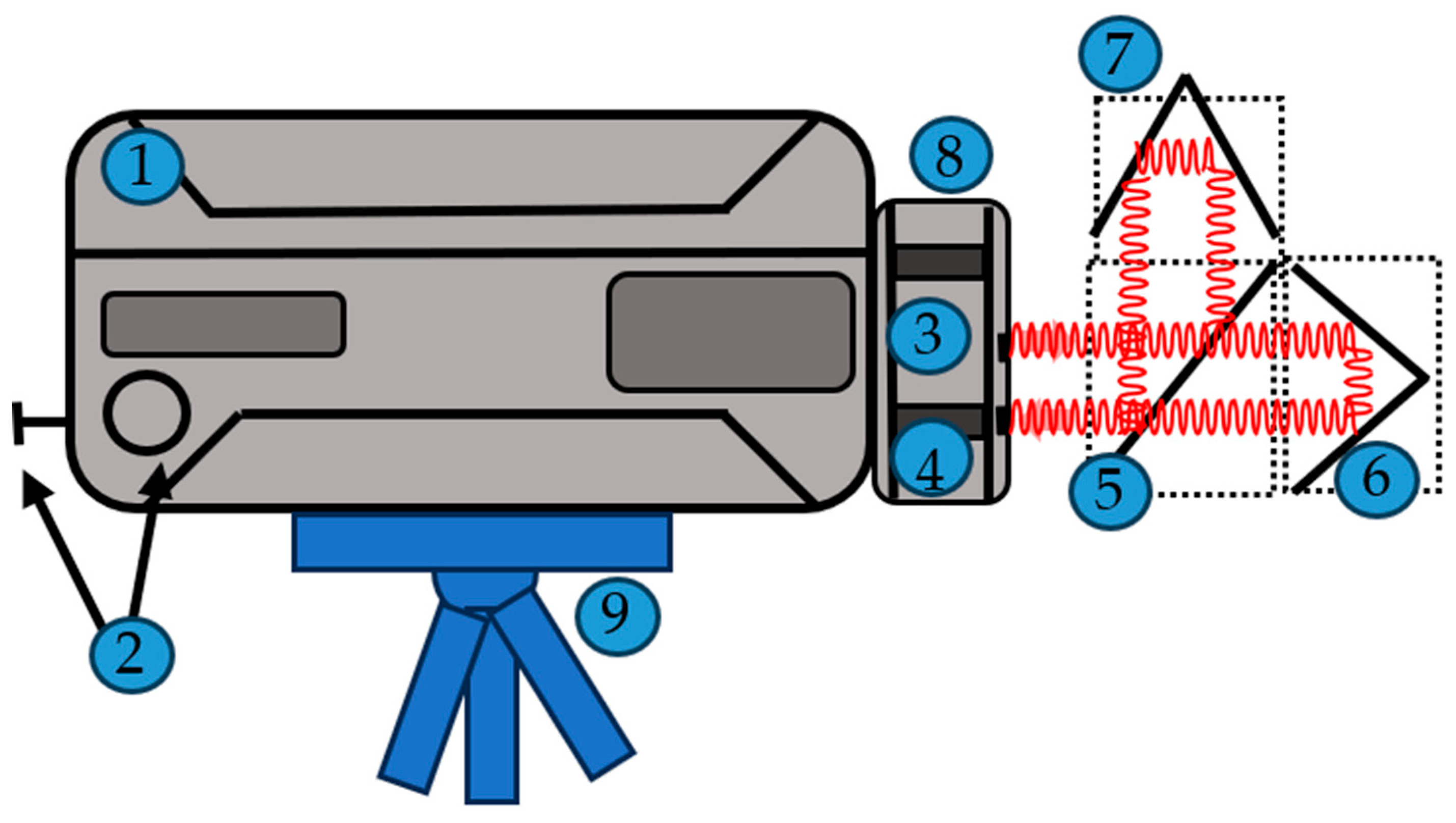





| 1 | Laser source and detector | 6 | Moving retroreflector |
| 2 | Adjustment screws for pitch and yaw of emitter/detector | 7 | Fixed retroreflector |
| 3 | Laser emitter | 8 | Rotating head |
| 4 | Laser detection | 9 | 6 DoF adjustable bases |
| 5 | Beam splitter |
| Controller | ) | ) | ) |
|---|---|---|---|
| PD working alone | |||
| FEL GD | |||
| FEL KF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khanesar, M.A.; Yan, M.; Karaca, A.; Isa, M.; Piano, S.; Branson, D. Interval Type-2 Fuzzy Logic Control of Linear Stages in Feedback-Error-Learning Structure Using Laser Interferometer. Energies 2024, 17, 3434. https://doi.org/10.3390/en17143434
Khanesar MA, Yan M, Karaca A, Isa M, Piano S, Branson D. Interval Type-2 Fuzzy Logic Control of Linear Stages in Feedback-Error-Learning Structure Using Laser Interferometer. Energies. 2024; 17(14):3434. https://doi.org/10.3390/en17143434
Chicago/Turabian StyleKhanesar, Mojtaba A., Minrui Yan, Aslihan Karaca, Mohammed Isa, Samanta Piano, and David Branson. 2024. "Interval Type-2 Fuzzy Logic Control of Linear Stages in Feedback-Error-Learning Structure Using Laser Interferometer" Energies 17, no. 14: 3434. https://doi.org/10.3390/en17143434
APA StyleKhanesar, M. A., Yan, M., Karaca, A., Isa, M., Piano, S., & Branson, D. (2024). Interval Type-2 Fuzzy Logic Control of Linear Stages in Feedback-Error-Learning Structure Using Laser Interferometer. Energies, 17(14), 3434. https://doi.org/10.3390/en17143434








