Enhancing Oil Recovery Predictions by Leveraging Polymer Flooding Simulations and Machine Learning Models on a Large-Scale Synthetic Dataset
Abstract
1. Introduction
2. Materials and Methods
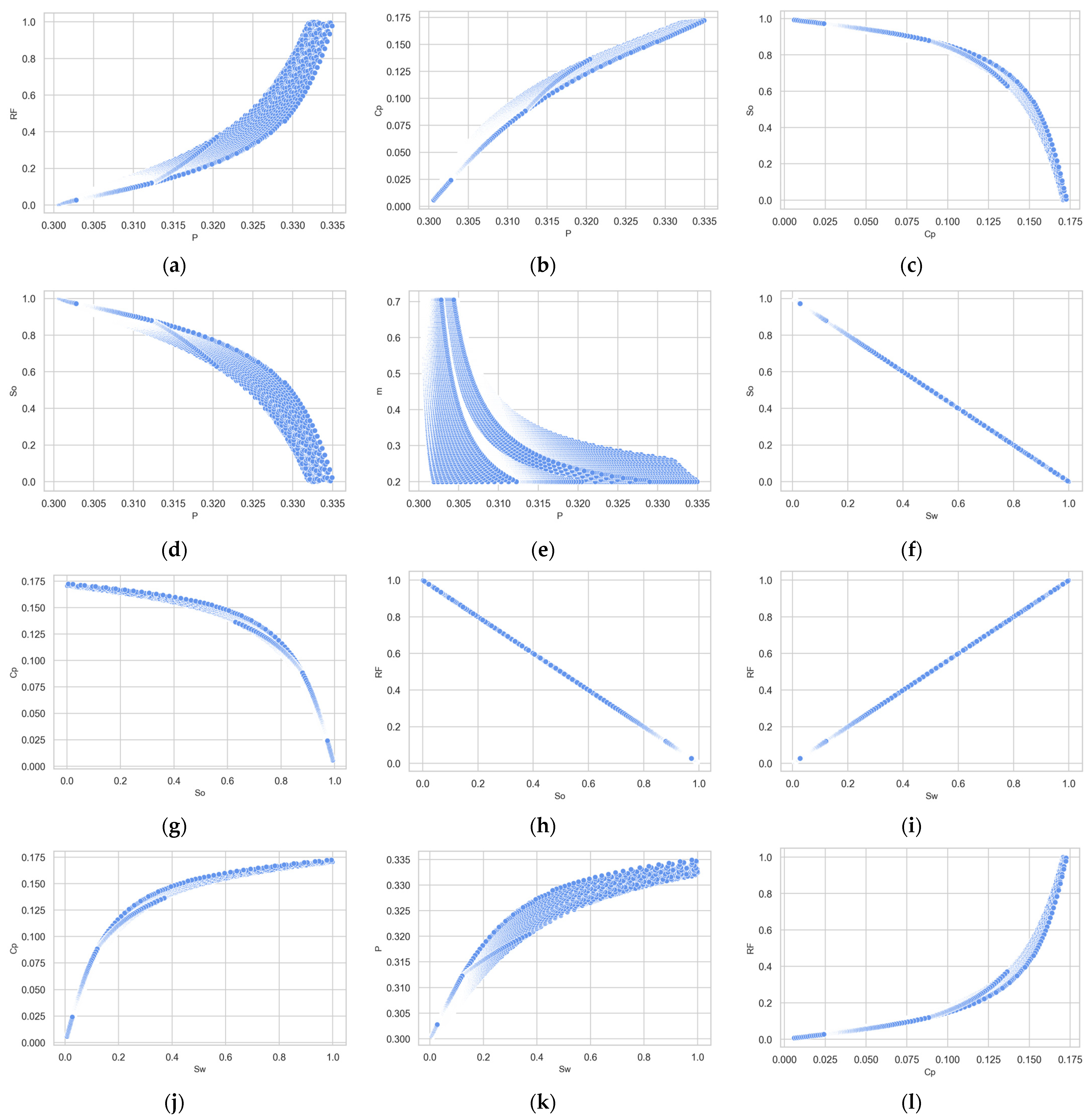
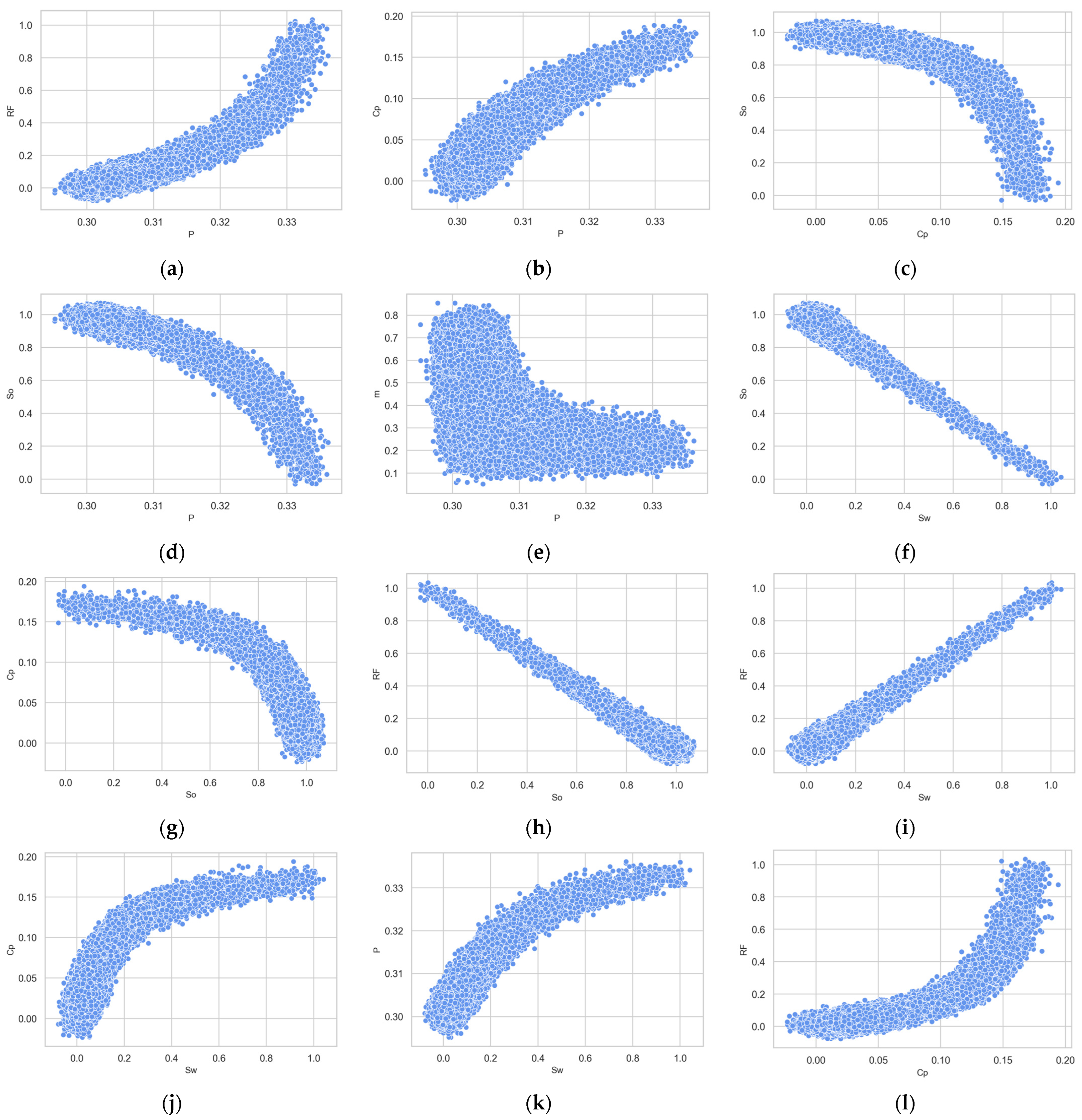
2.1. Dataset
2.2. Adding Artificial Noise
2.3. Machine Learning Algorithms
2.3.1. Linear Regression (LR)
2.3.2. Polynomial Regression (PR)
2.3.3. Decision Tree (DT)
2.3.4. Random Forest Regressor (RFR)
2.3.5. Gradient Boosting (GB)
2.3.6. Extreme Gradient Boosting (XGBoost)
2.3.7. Light Gradient Boosting (LightGBM)
2.3.8. Dense Neural Networks (DNNs)
2.3.9. Cascade-Forward Neural Networks (CFNN)
2.4. Metrics
2.4.1. Root Mean Squared Error (RMSE)
2.4.2. Mean Absolute Error (MAE)
2.4.3. Coefficient of Determination
2.4.4. Mean Absolute Percentage Error (MAPE)
3. Results and Discussion
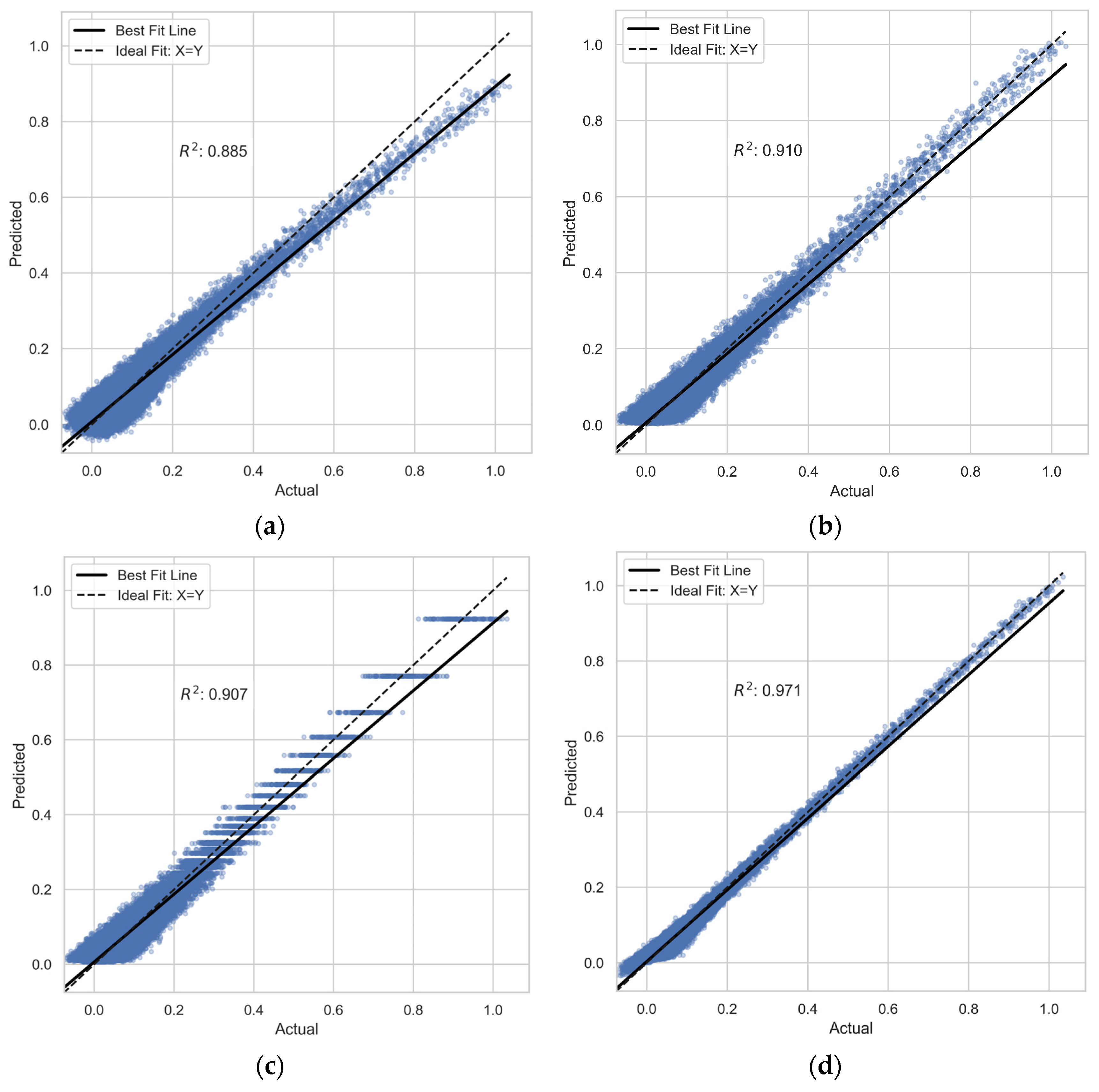
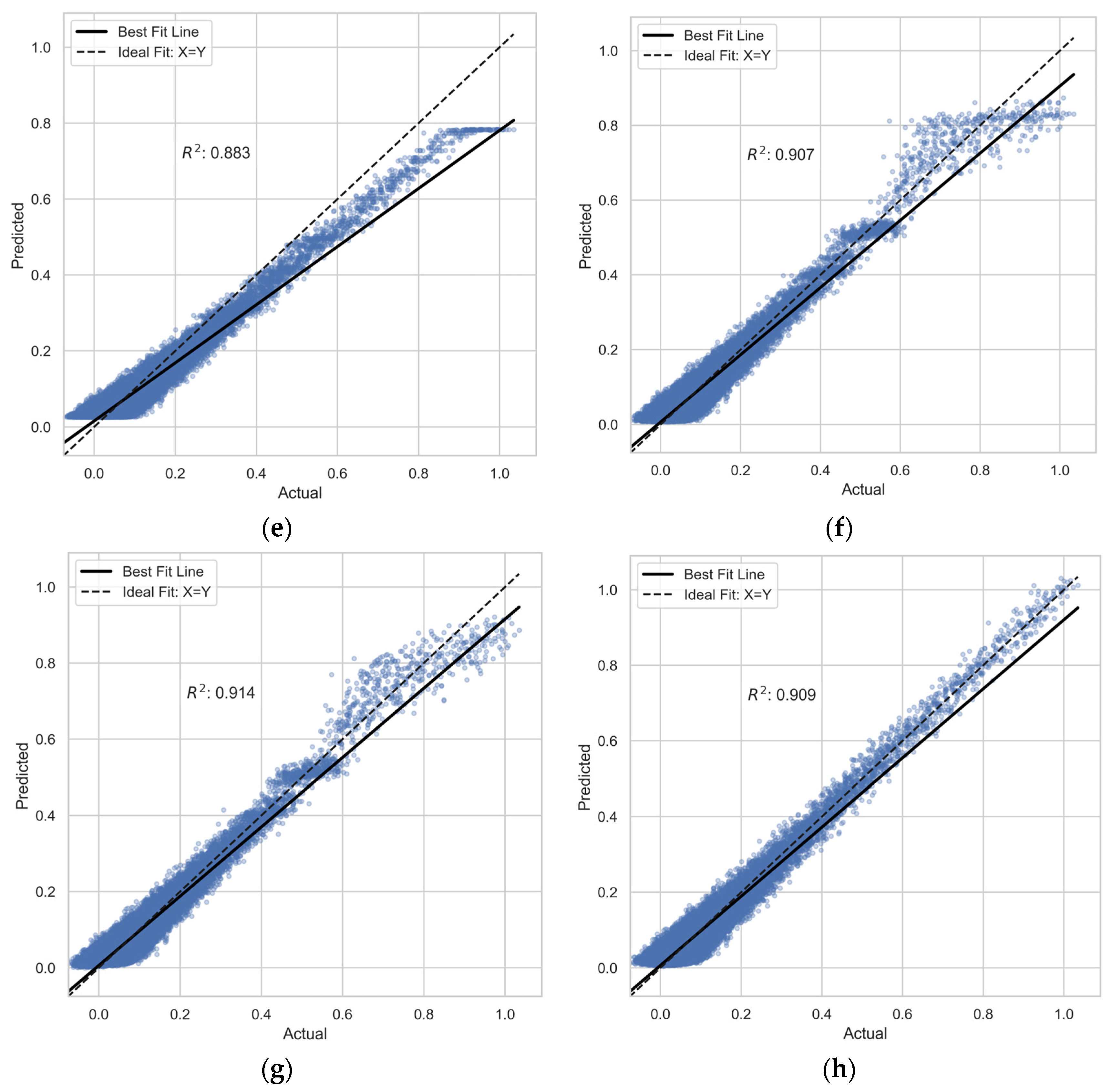
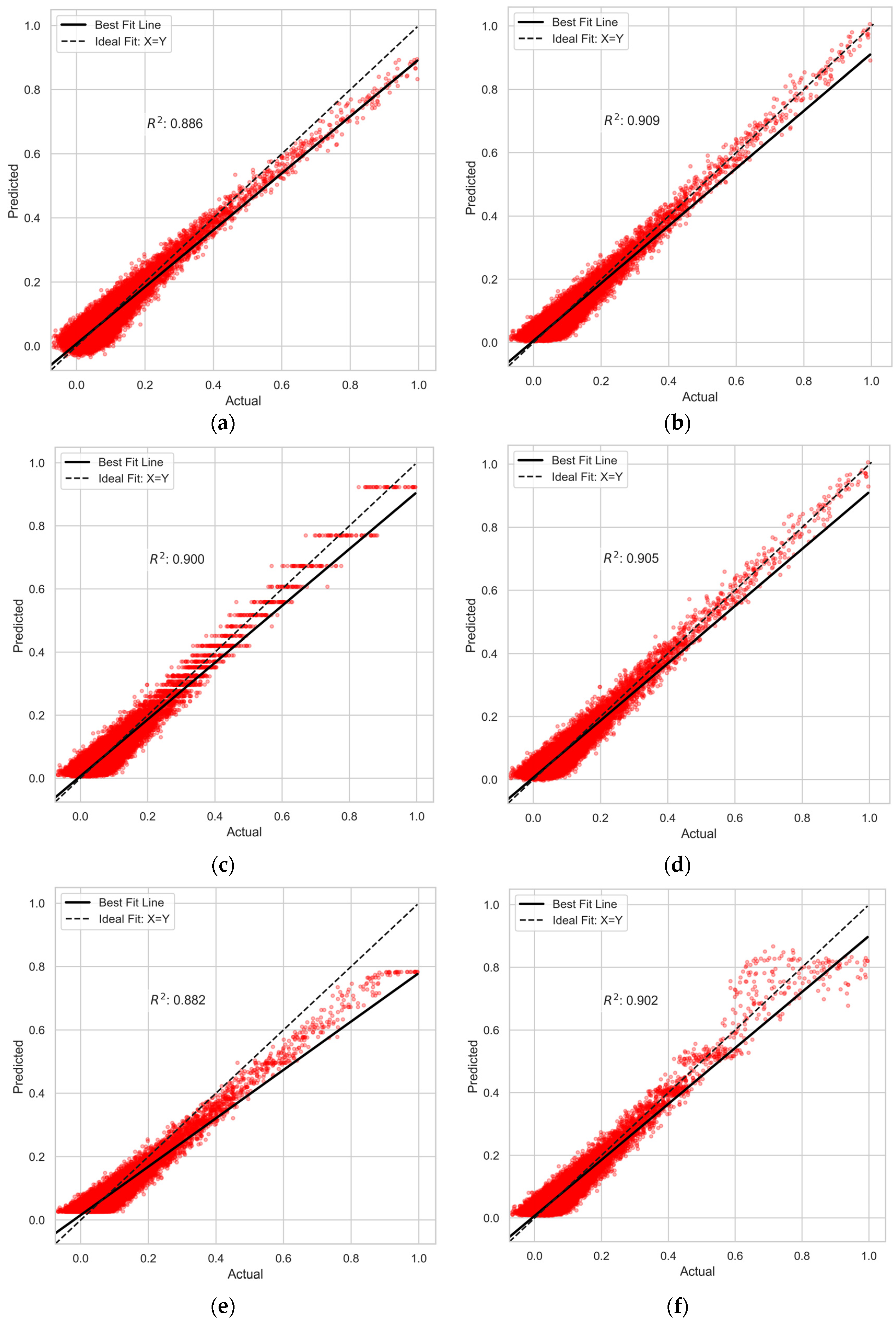
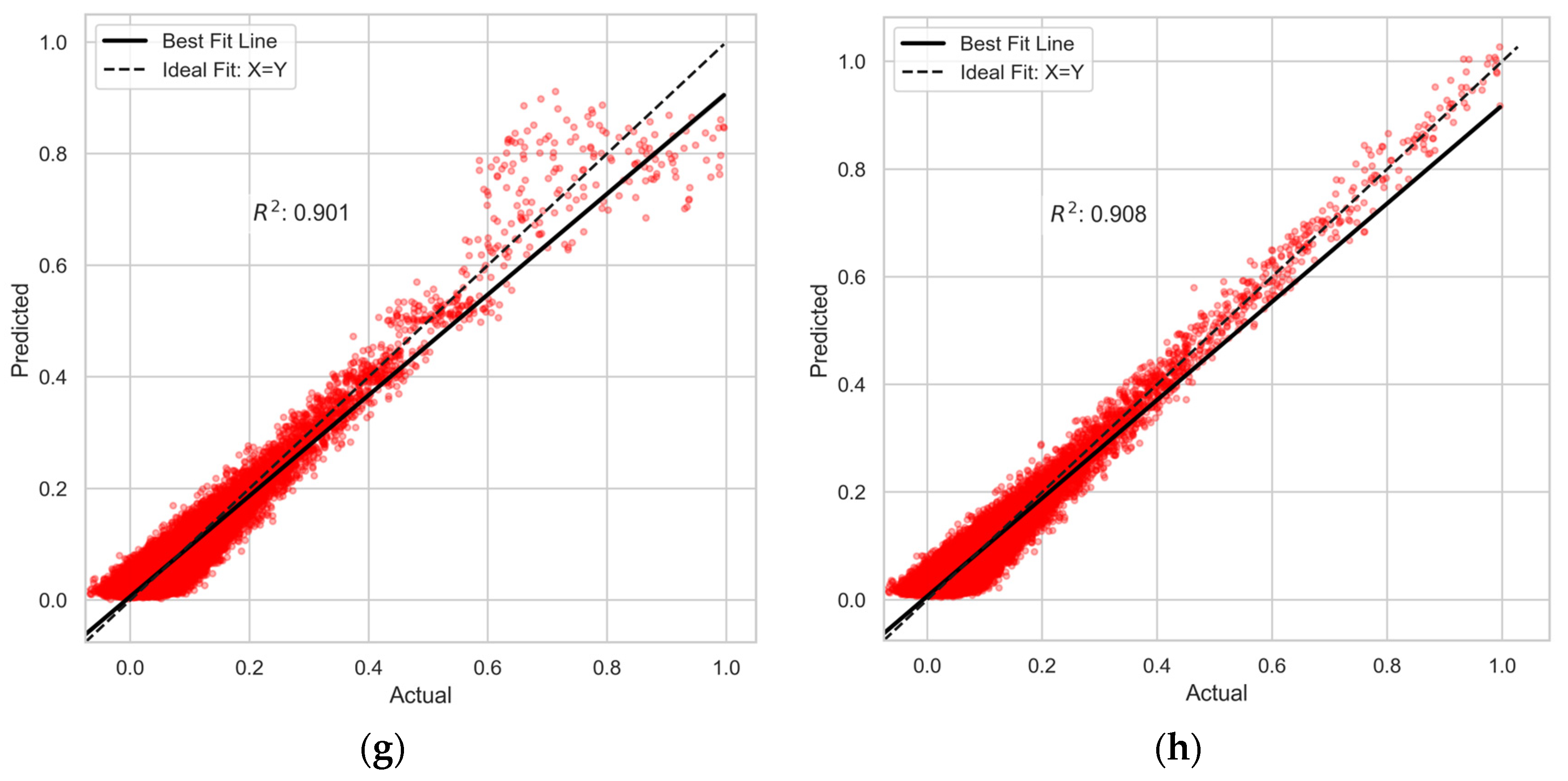
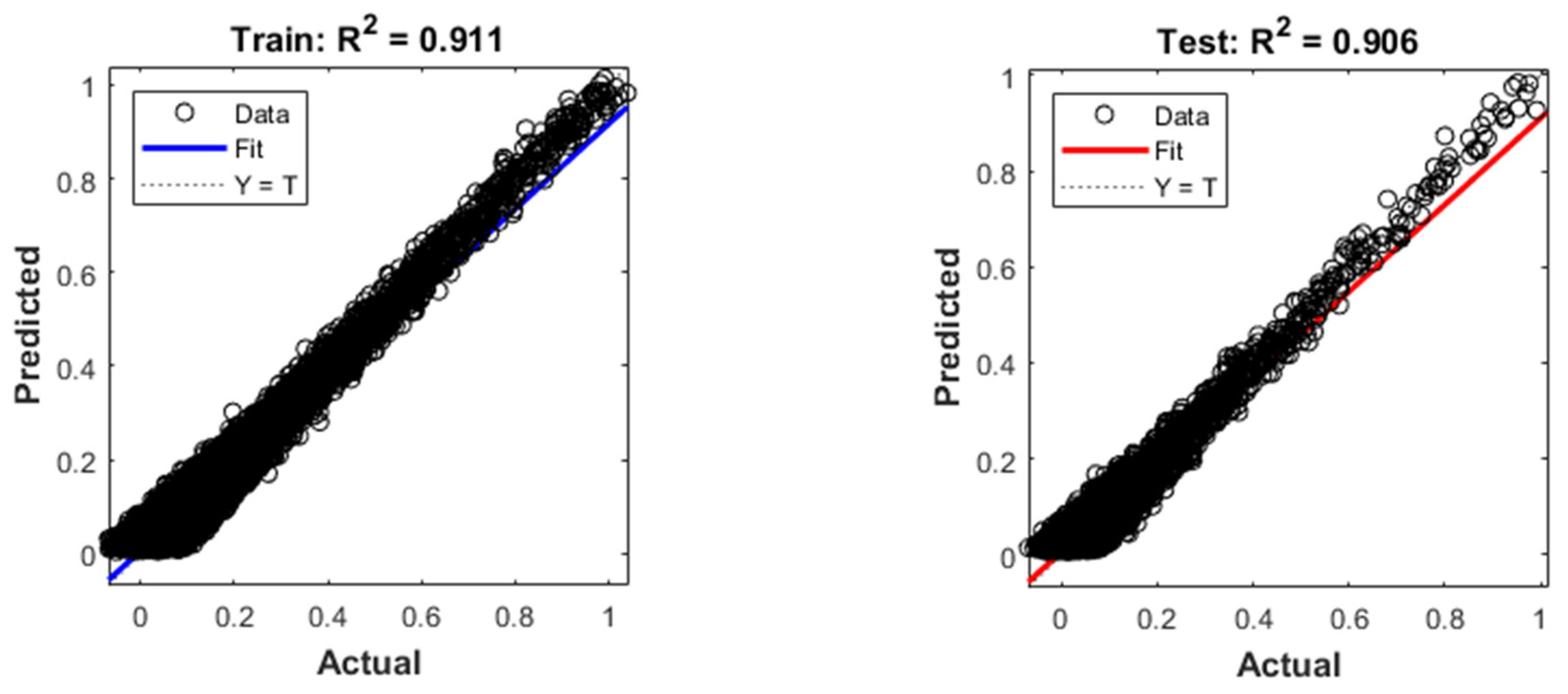
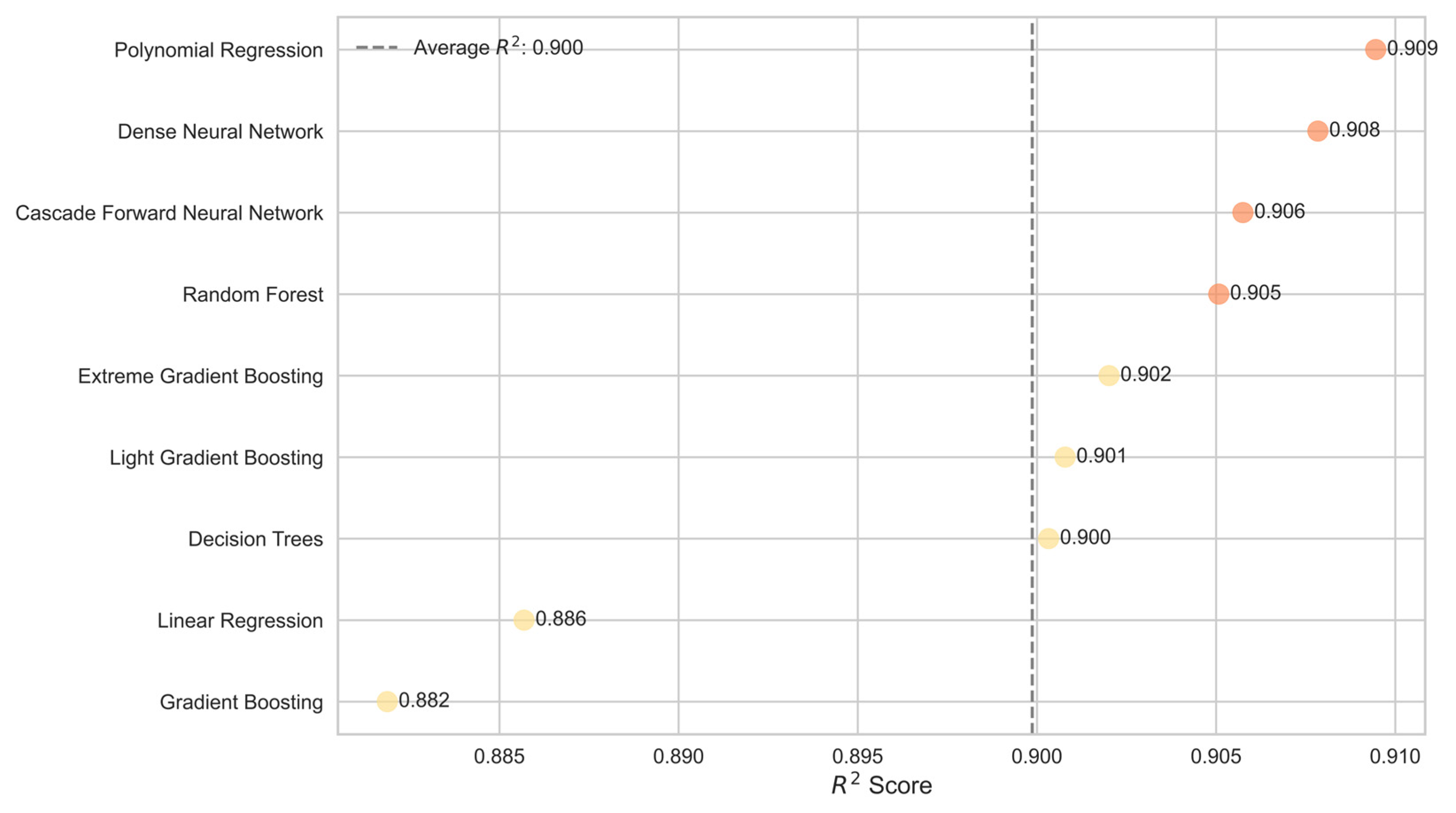
3.1. Model Evaluation Results
3.2. Permutation Feature Importance Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; Wang, B.; Cao, X.; Li, H. Application and Design of Alkaline-Surfactant-Polymer System to Close Well Spacing Pilot Gudong Oilfield. In Proceedings of the SPE Western Regional Meeting, Long Beach, CA, USA, 25 June 1997. [Google Scholar] [CrossRef]
- Sheng, J.J.; Leonhardt, B.; Azri, N. Status of Polymer-Flooding Technology. J. Can. Pet. Technol. 2015, 54, 116–126. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, M.; Bai, B.; Yang, H.; Kang, W. Survey and Data Analysis of the Pilot and Field Polymer Flooding Projects in China. In Proceedings of the All Days, Tulsa, OK, USA, 11 April 2016; p. SPE-179616-MS. [Google Scholar] [CrossRef]
- Kamari, A.; Gharagheizi, F.; Shokrollahi, A.; Arabloo, M.; Mohammadi, A.H. Integrating a Robust Model for Predicting Surfactant–Polymer Flooding Performance. J. Pet. Sci. Eng. 2016, 137, 87–96. [Google Scholar] [CrossRef]
- Sun, Q.; Ertekin, T. The Development of Artificial-Neural-Network-Based Universal Proxies to Study Steam Assisted Gravity Drainage (SAGD) and Cyclic Steam Stimulation (CSS) Processes. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 27–30 April 2015. [Google Scholar] [CrossRef]
- Amirian, E.; John Chen, Z. Cognitive Data-Driven Proxy Modeling for Performance Forecasting of Waterflooding Process. Glob. J. Technol. Optim. 2017, 8, 1–8. [Google Scholar] [CrossRef]
- Alade, O.; Al Shehri, D.; Mahmoud, M.; Sasaki, K. Viscosity–Temperature–Pressure Relationship of Extra-Heavy Oil (Bitumen): Empirical Modelling versus Artificial Neural Network (ANN). Energies 2019, 12, 2390. [Google Scholar] [CrossRef]
- Daribayev, B.; Mukhanbet, A.; Nurakhov, Y.; Imankulov, T. Implementation of The Solution to the Oil Displacement Problem Using Machine Learning Classifiers and Neural Networks. East.-Eur. J. Enterp. Technol. 2021, 5, 55–63. [Google Scholar] [CrossRef]
- Bansal, Y.; Ertekin, T.; Karpyn, Z.; Ayala, L.; Nejad, A.; Suleen, F.; Balogun, O.; Liebmann, D.; Sun, Q. Forecasting Well Performance in a Discontinuous Tight Oil Reservoir Using Artificial Neural Networks. In Proceedings of the SPE Unconventional Resources Conference/Gas Technology Symposium, The Woodlands, TX, USA, 10 April 2013. [Google Scholar] [CrossRef]
- Ertekin, T.; Sun, Q. Artificial Neural Network Applications in Reservoir Engineering. In Artificial Neural Networks in Chemical Engineering; NOVA: Hauppauge, NY, USA, 2017; pp. 123–204. [Google Scholar]
- Karambeigi, M.S.; Zabihi, R.; Hekmat, Z. Neuro-Simulation Modeling of Chemical Flooding. J. Pet. Sci. Eng. 2011, 78, 208–219. [Google Scholar] [CrossRef]
- Prasanphanich, J. Gas Reserves Estimation by Monte Carlo Simulation and Chemical Flooding Optimization Using Experimental Design and Response Surface Methodology. Ph.D. Thesis, The University of TEXAS at Austin, Austin, TX, USA, 2009. [Google Scholar] [CrossRef]
- Al-Dousari, M.M.; Garrouch, A.A. An Artificial Neural Network Model for Predicting the Recovery Performance of Surfactant Polymer Floods. J. Pet. Sci. Eng. 2013, 109, 51–62. [Google Scholar] [CrossRef]
- Alkhatib, A.; Babaei, M.; King, P.R.R. Decision Making Under Uncertainty: Applying the Least-Squares Monte Carlo Method in Surfactant-Flooding Implementation. SPE J. 2013, 18, 721–735. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Pournik, M. A Predictive Model of Chemical Flooding for Enhanced Oil Recovery Purposes: Application of Least Square Support Vector Machine. Petroleum 2016, 2, 177–182. [Google Scholar] [CrossRef]
- Jahani-Keleshteri, Z. A Robust Approach to Predict Distillate Rate through Steam Distillation Process for Oil Recovery. Pet. Sci. Technol. 2017, 35, 419–425. [Google Scholar] [CrossRef]
- Le Van, S.; Chon, B. Artificial Neural Network Model for Alkali-Surfactant-Polymer Flooding in Viscous Oil Reservoirs: Generation and Application. Energies 2016, 9, 1081. [Google Scholar] [CrossRef]
- Larestani, A.; Mousavi, S.P.; Hadavimoghaddam, F.; Ostadhassan, M.; Hemmati-Sarapardeh, A. Predicting the Surfactant-Polymer Flooding Performance in Chemical Enhanced Oil Recovery: Cascade Neural Network and Gradient Boosting Decision Tree. Alex. Eng. J. 2022, 61, 7715–7731. [Google Scholar] [CrossRef]
- Mohammadi, M.-R.; Hemmati-Sarapardeh, A.; Schaffie, M.; Husein, M.M.; Ranjbar, M. Application of Cascade Forward Neural Network and Group Method of Data Handling to Modeling Crude Oil Pyrolysis during Thermal Enhanced Oil Recovery. J. Pet. Sci. Eng. 2021, 205, 108836. [Google Scholar] [CrossRef]
- Ebaga-Ololo, J.; Chon, B. Prediction of Polymer Flooding Performance with an Artificial Neural Network: A Two-Polymer-Slug Case. Energies 2017, 10, 844. [Google Scholar] [CrossRef]
- Saboorian-Jooybari, H.; Dejam, M.; Chen, Z. Heavy Oil Polymer Flooding from Laboratory Core Floods to Pilot Tests and Field Applications: Half-Century Studies. J. Pet. Sci. Eng. 2016, 142, 85–100. [Google Scholar] [CrossRef]
- Alghazal, M. Development and Testing of Artificial Neural Network Based Models for Water Flooding and Polymer Gel Flooding in Naturally Fractured Reservoirs. Master’s Thesis, The Pennsylvania State University, Camp Hill, PA, USA, 2015. [Google Scholar]
- Norouzi, M.; Panjalizadeh, H.; Rashidi, F.; Mahdiani, M.R. DPR Polymer Gel Treatment in Oil Reservoirs: A Workflow for Treatment Optimization Using Static Proxy Models. J. Pet. Sci. Eng. 2017, 153, 97–110. [Google Scholar] [CrossRef]
- Amirian, E.; Dejam, M.; Chen, Z. Performance Forecasting for Polymer Flooding in Heavy Oil Reservoirs. Fuel 2018, 216, 83–100. [Google Scholar] [CrossRef]
- Sun, Q.; Ertekin, T. Screening and Optimization of Polymer Flooding Projects Using Artificial-Neural-Network (ANN) Based Proxies. J. Pet. Sci. Eng. 2020, 185, 106617. [Google Scholar] [CrossRef]
- Imankulov, T.; Kenzhebek, Y.; Makhmut, E.; Akhmed-Zaki, D. Using Machine Learning Algorithms to Solve Polymer Flooding Problem. In Proceedings of the ECMOR 2022, Hague, The Netherlands, 5–7 September 2022; Volume 2022, pp. 1–9. [Google Scholar] [CrossRef]
- Makhmut, E.; Imankulov, T.; Daribayev, B.; Akhmed-Zaki, D. Development of Hybrid Parallel Computing Models to Solve Polymer Flooding Problem. In Proceedings of the ECMOR 2022, Hague, The Netherlands, 5–7 September 2022; Volume 2022, pp. 1–14. [Google Scholar] [CrossRef]
- Saseendran, A.; Setia, L.; Chhabria, V.; Chakraborty, D.; Barman Roy, A. Impact of Noise in Dataset on Machine Learning Algorithms. Mach. Learn. Res. 2019. [Google Scholar] [CrossRef]
- Kalapanidas, E.; Avouris, N.; Craciun, M.; Neagu, D. Machine Learning Algorithms: A Study on Noise Sensitivity. 2003. Available online: http://delab.csd.auth.gr/bci1/Balkan/356kalapanidas.pdf (accessed on 28 March 2024).
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. Linear Regression. In An Introduction to Statistical Learning: With Applications in Python; James, G., Witten, D., Hastie, T., Tibshirani, R., Taylor, J., Eds.; Springer International Publishing: Cham, Swizterlands, 2023; pp. 69–134. [Google Scholar] [CrossRef]
- Lewis, R. An Introduction to Classification and Regression Tree (CART) Analysis. In Proceedings of the Annual Meeting of the Society for Academic Emergency Medicine, San Francisco, CA, USA, 22–25 May 2000. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, NY, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016; pp. 164–223. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Warsito, B.; Santoso, R.; Suparti; Yasin, H. Cascade Forward Neural Network for Time Series Prediction. J. Phys. Conf. Ser. 2018, 1025, 012097. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]






| Variables | Variable Type | Mean | Std | Min | Max |
|---|---|---|---|---|---|
| Absolute permeability (k) | Feature | 0.004 | 0.002 | 0.001 | 0.008 |
| Pressure (P) | Feature | 0.305 | 0.004 | 0.301 | 0.335 |
| Porosity (m) | Feature | 0.454 | 0.147 | 0.2 | 0.705 |
| Oil saturation (So) | Feature | 0.934 | 0.075 | 0.0003 | 0.993 |
| Water saturation (Sw) | Feature | 0.066 | 0.075 | 0.007 | 0.999 |
| Oil viscosity (μ) | Feature | 0.453 | 0.089 | 0.3 | 0.605 |
| Polymer concentration (Cp) | Feature | 0.045 | 0.029 | 0.006 | 0.172 |
| Oil recovery factor (RF) | Target | 0.066 | 0.075 | 0.007 | 0.999 |
| Metrics | LR | PR | DT | RFR | GB | XGBoost | LightGBM | |
|---|---|---|---|---|---|---|---|---|
| Train Set | RMSE | 0.027 | 0.024 | 0.024 | 0.013 | 0.027 | 0.024 | 0.023 |
| MAE | 0.021 | 0.019 | 0.019 | 0.011 | 0.021 | 0.019 | 0.018 | |
| 0.885 | 0.91 | 0.907 | 0.971 | 0.883 | 0.907 | 0.914 | ||
| MAPE | 2.948 | 3.075 | 3.014 | 1.943 | 3.872 | 3.082 | 2.98 | |
| Test set | RMSE | 0.026 | 0.024 | 0.025 | 0.024 | 0.027 | 0.024 | 0.025 |
| MAE | 0.021 | 0.019 | 0.02 | 0.019 | 0.021 | 0.019 | 0.019 | |
| 0.886 | 0.909 | 0.9 | 0.905 | 0.882 | 0.902 | 0.901 | ||
| MAPE | 2.614 | 2.508 | 2.639 | 2.511 | 3.331 | 2.565 | 2.494 |
| Metrics | DNN | CFNN | |
|---|---|---|---|
| Train Set | RMSE | 0.024 | 0.024 |
| MAE | 0.019 | 0.019 | |
| 0.909 | 0.911 | ||
| Test set | RMSE | 0.024 | 0.024 |
| MAE | 0.019 | 0.019 | |
| 0.908 | 0.906 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imankulov, T.; Kenzhebek, Y.; Bekele, S.D.; Makhmut, E. Enhancing Oil Recovery Predictions by Leveraging Polymer Flooding Simulations and Machine Learning Models on a Large-Scale Synthetic Dataset. Energies 2024, 17, 3397. https://doi.org/10.3390/en17143397
Imankulov T, Kenzhebek Y, Bekele SD, Makhmut E. Enhancing Oil Recovery Predictions by Leveraging Polymer Flooding Simulations and Machine Learning Models on a Large-Scale Synthetic Dataset. Energies. 2024; 17(14):3397. https://doi.org/10.3390/en17143397
Chicago/Turabian StyleImankulov, Timur, Yerzhan Kenzhebek, Samson Dawit Bekele, and Erlan Makhmut. 2024. "Enhancing Oil Recovery Predictions by Leveraging Polymer Flooding Simulations and Machine Learning Models on a Large-Scale Synthetic Dataset" Energies 17, no. 14: 3397. https://doi.org/10.3390/en17143397
APA StyleImankulov, T., Kenzhebek, Y., Bekele, S. D., & Makhmut, E. (2024). Enhancing Oil Recovery Predictions by Leveraging Polymer Flooding Simulations and Machine Learning Models on a Large-Scale Synthetic Dataset. Energies, 17(14), 3397. https://doi.org/10.3390/en17143397






