Numerical Simulation Method for the Aeroelasticity of Flexible Wind Turbine Blades under Standstill Conditions
Abstract
1. Introduction
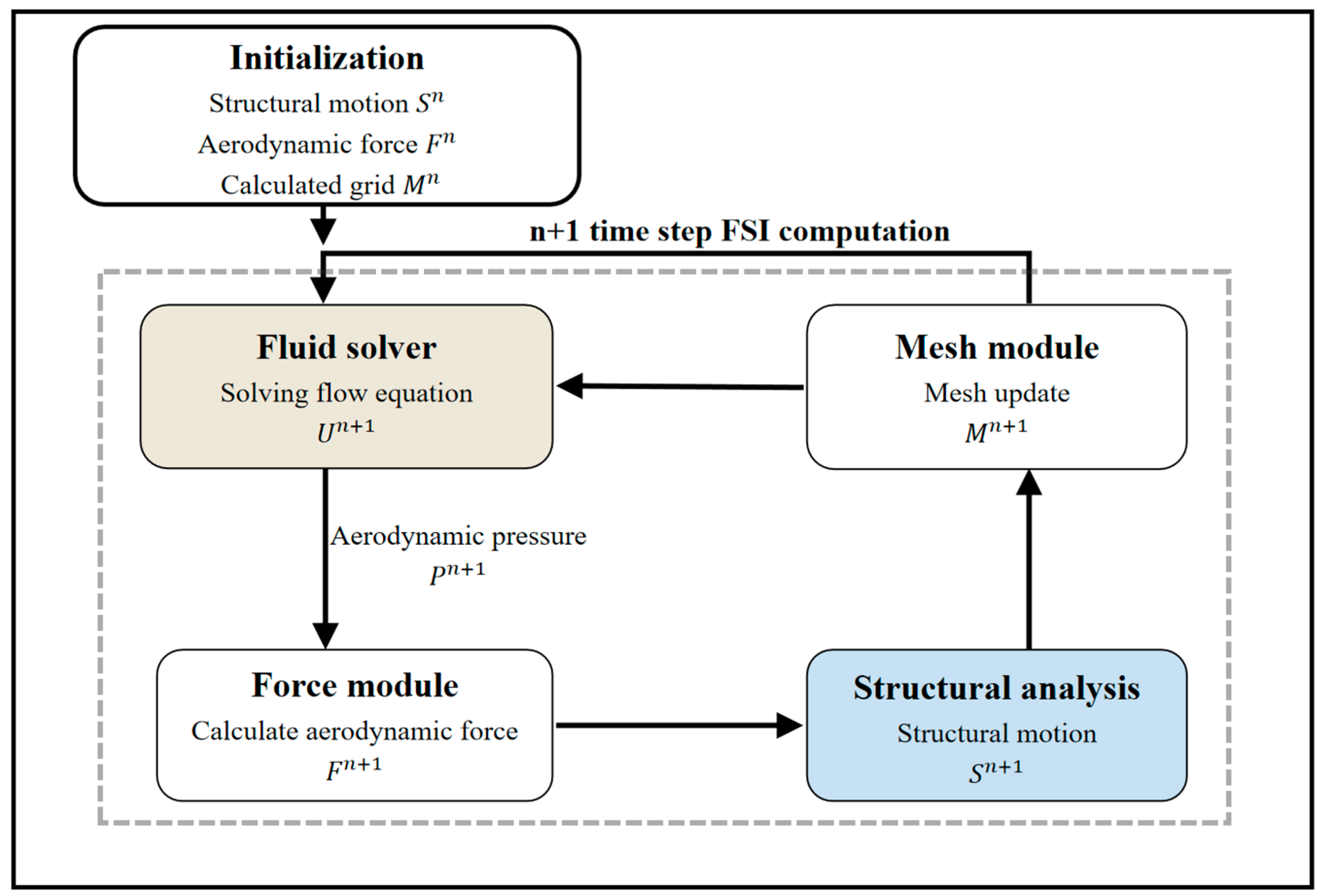
2. CFD-CSD Coupling Simulation Method
2.1. Flow Solver
2.1.1. Turbulence Model
2.1.2. Spatial Discretization Scheme
2.1.3. Temporal Discretization Scheme
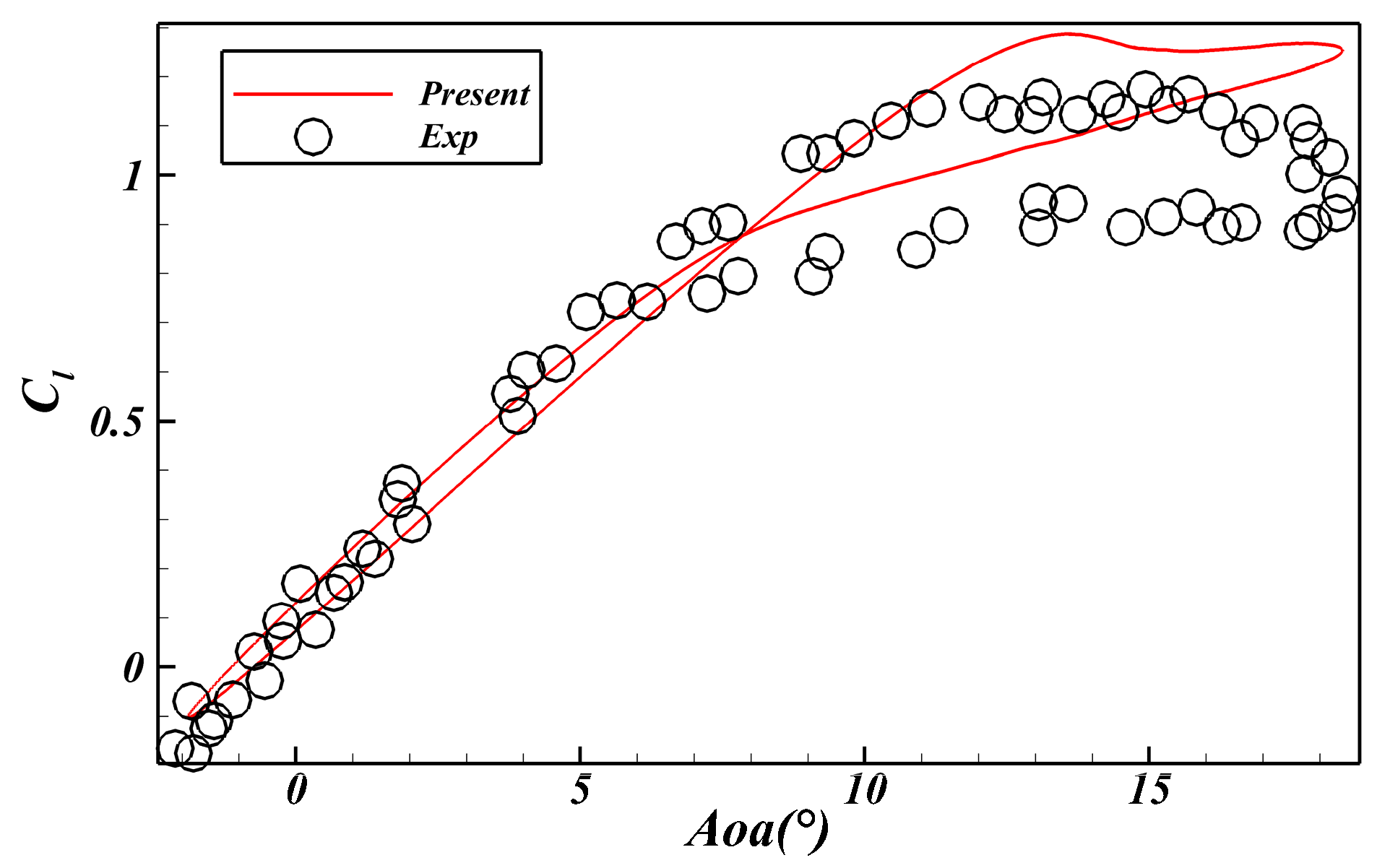
2.1.4. Verification of CFD Method
2.2. Structural Analysis
2.2.1. Geometrically Exact Beam Theory
2.2.2. Verification and Validation of the Structural Model
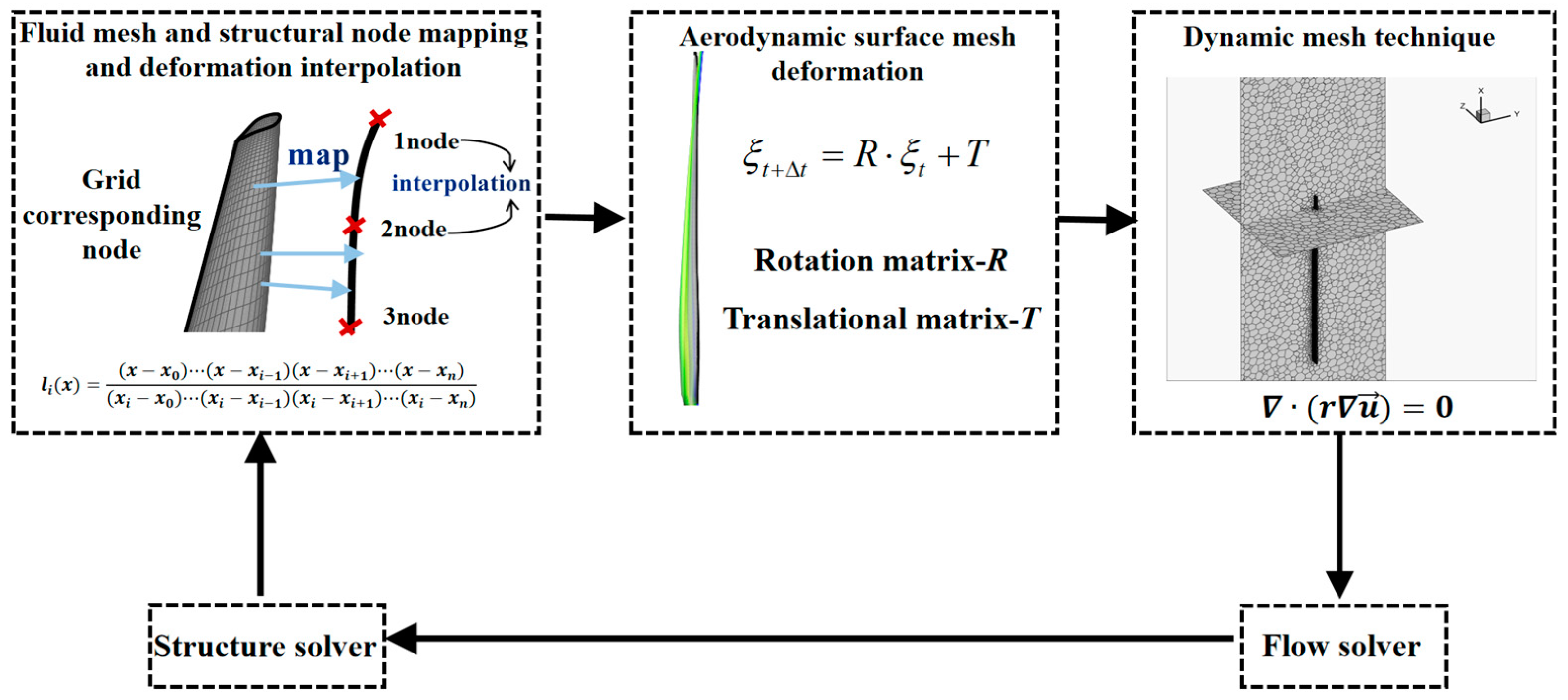
2.3. Grid Interpolation and Deformation Techniques
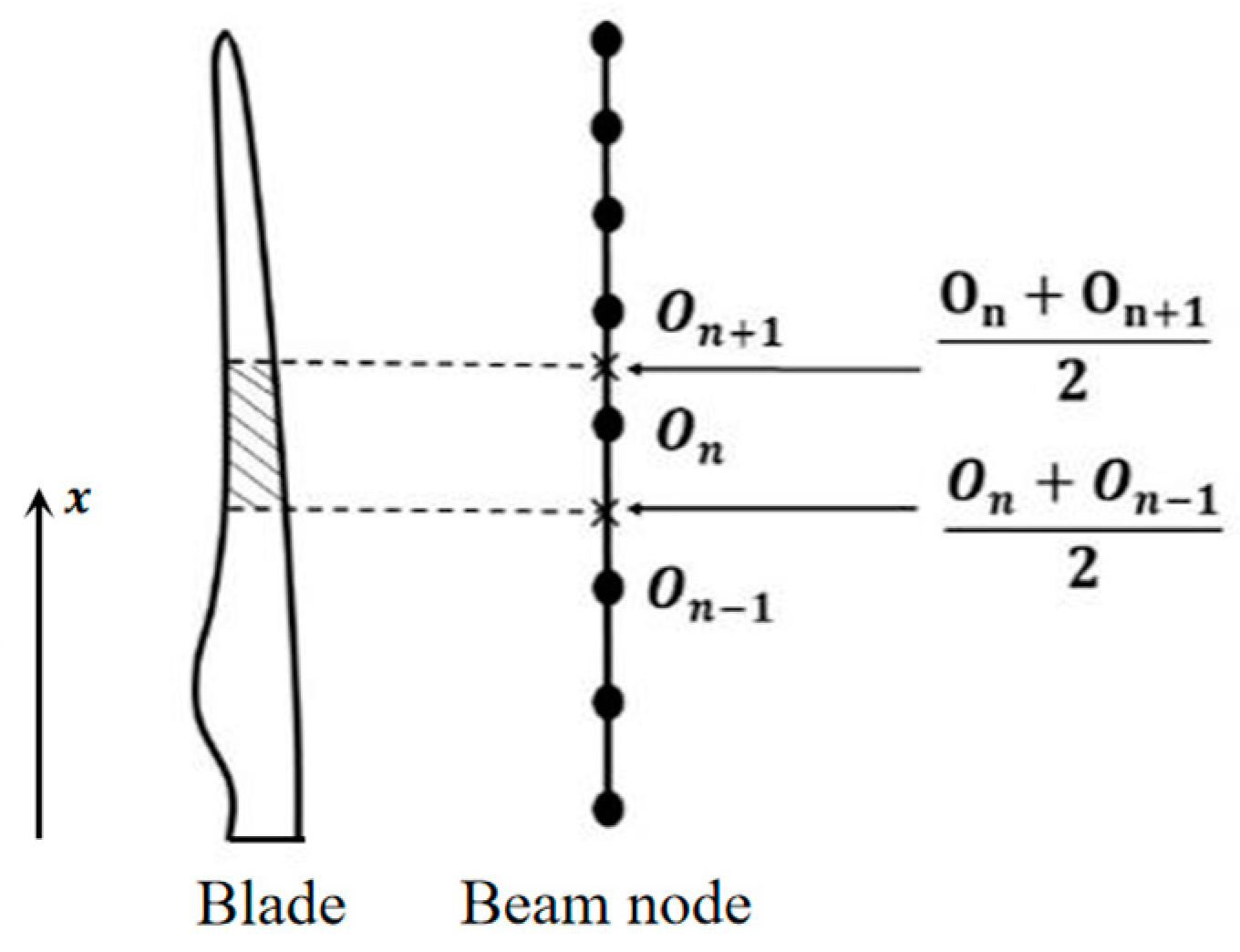
2.3.1. Beam Node Aerodynamic Force Integration
2.3.2. Mapping and Displacement Interpolation between Blade Element Centers and Beam Nodes
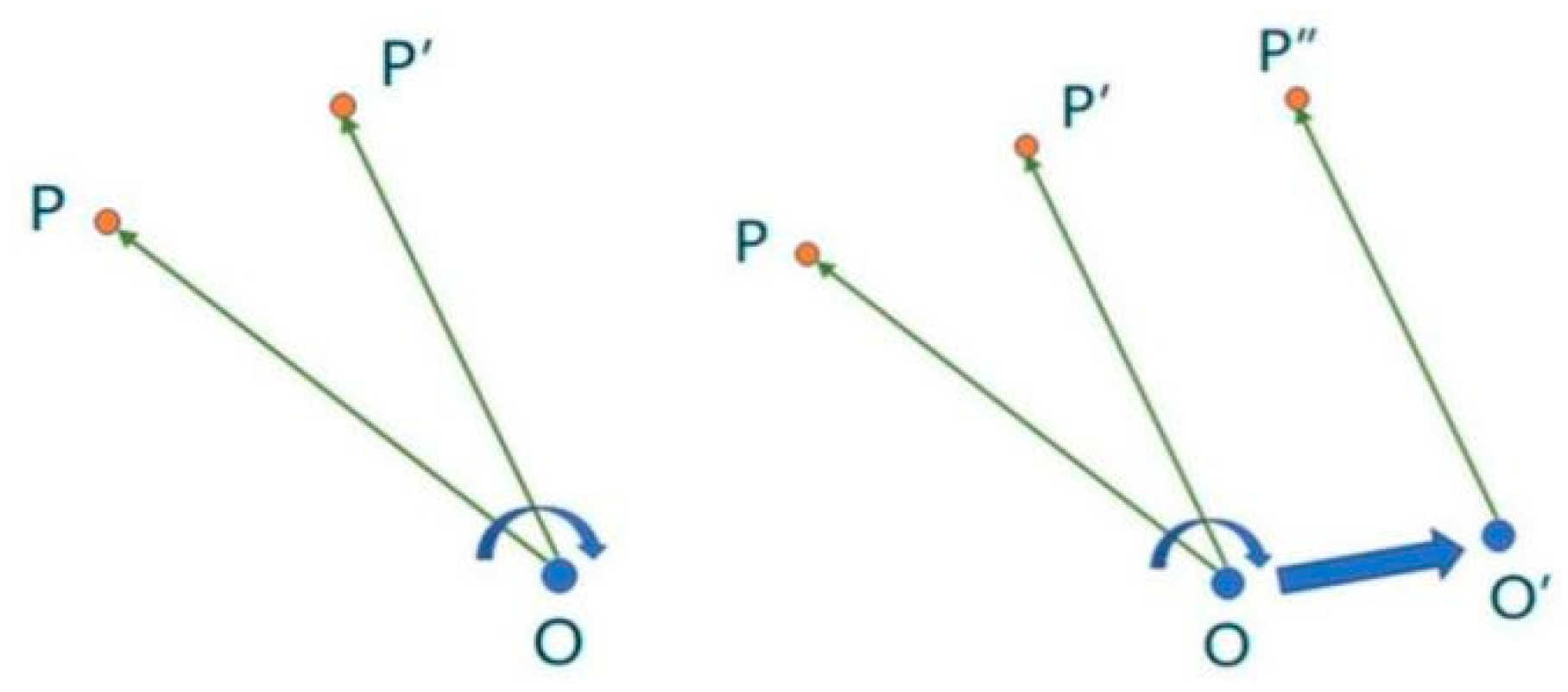
2.3.3. Aerodynamic Surface Mesh Deformation
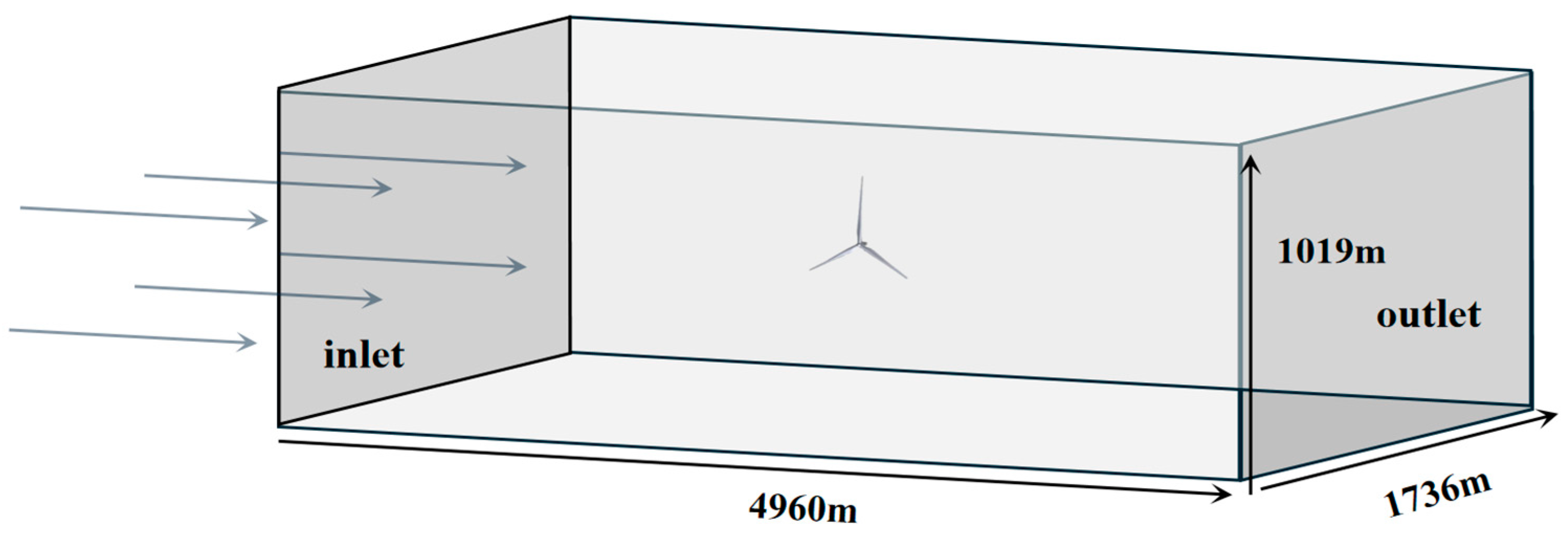
3. Simulation Setup
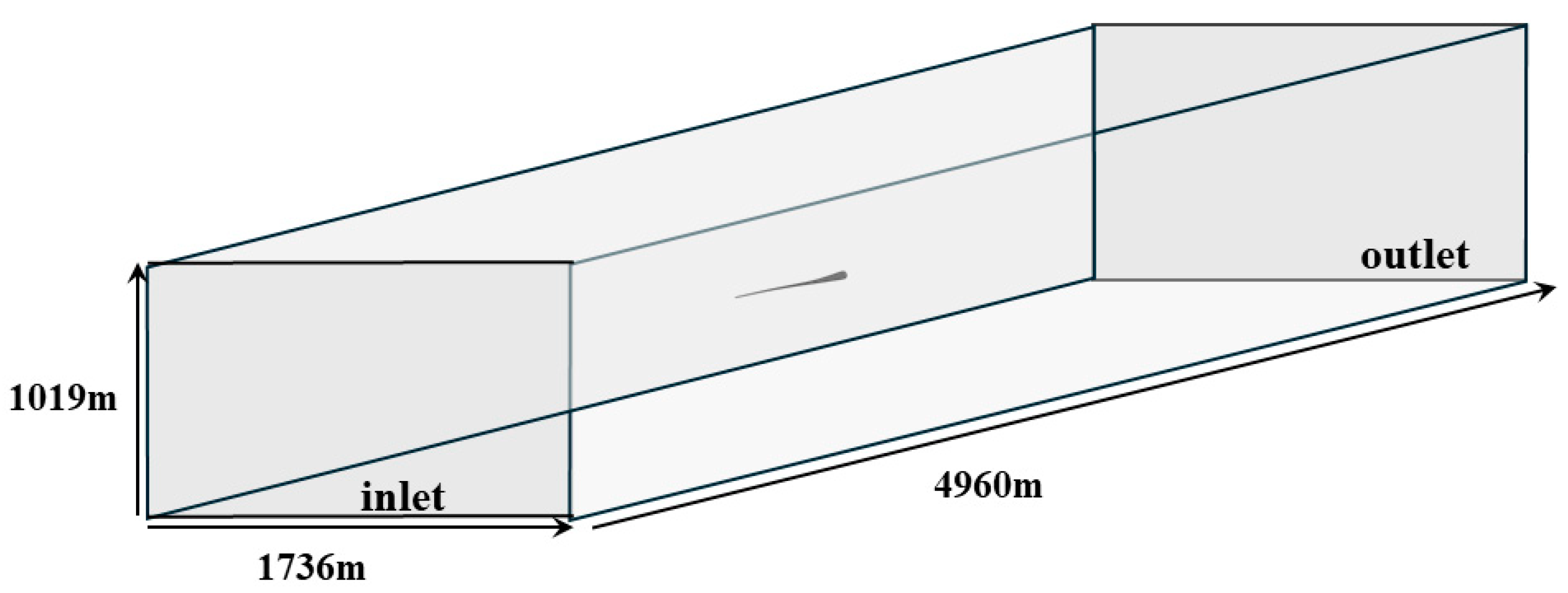
3.1. Introduction of Single-Blade Parameters and Calculation Conditions
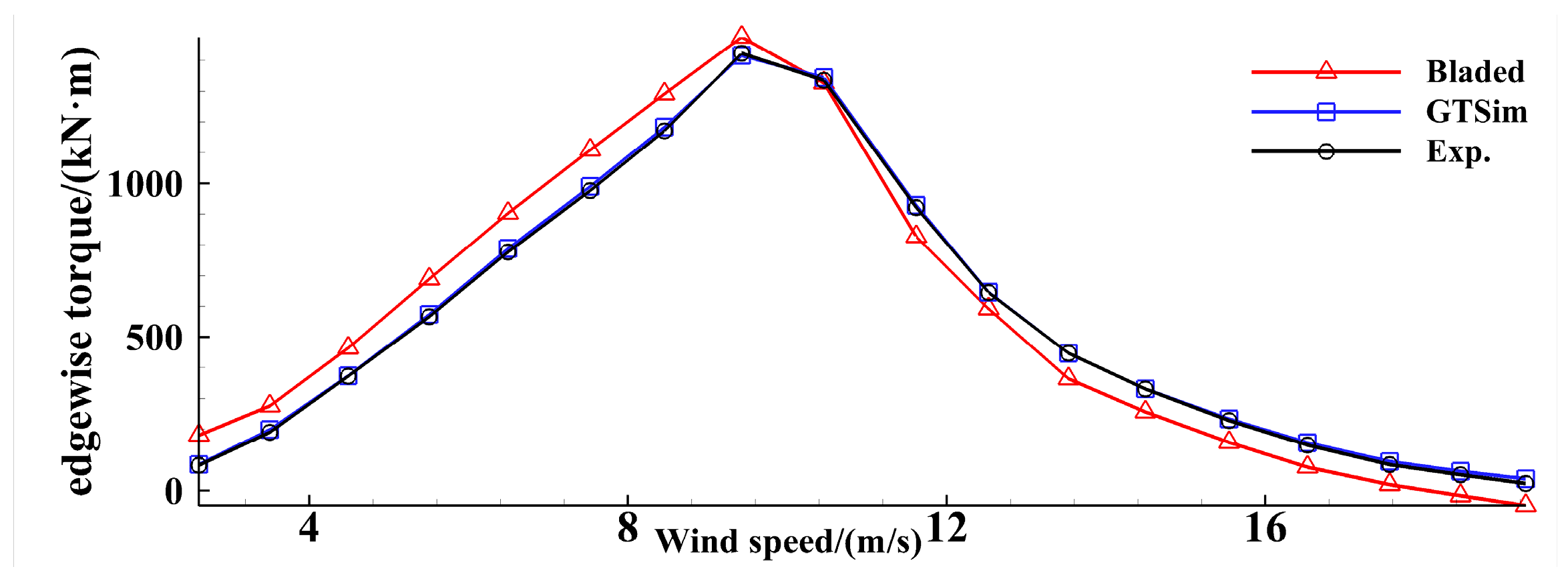
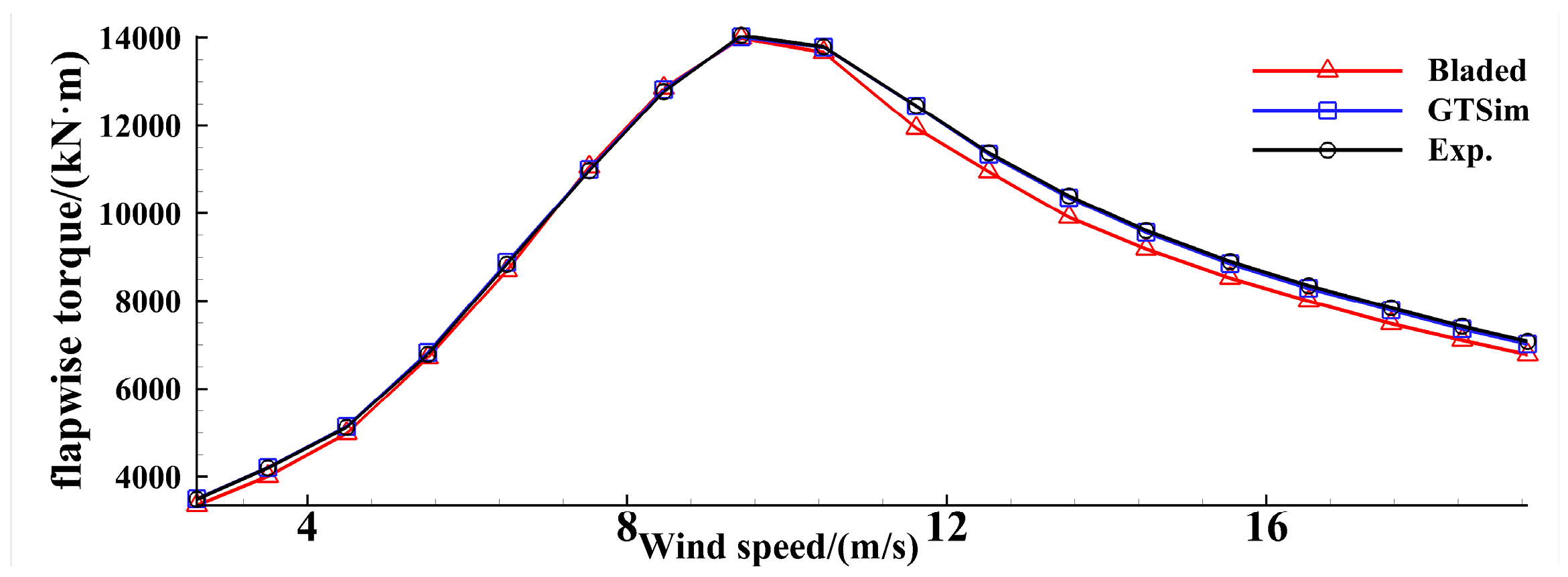
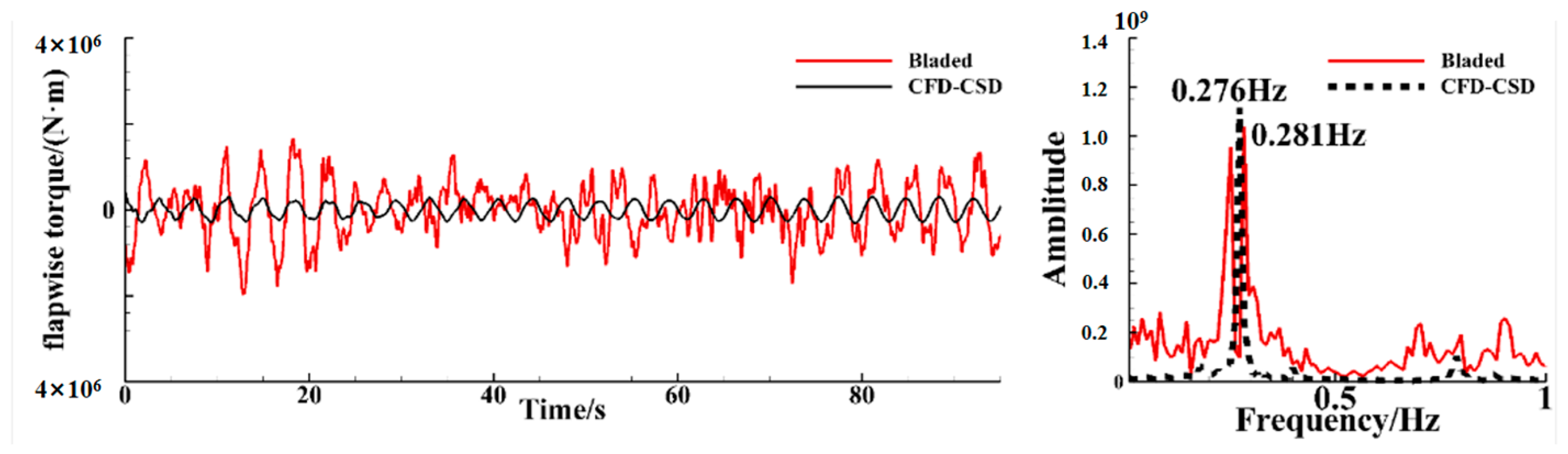
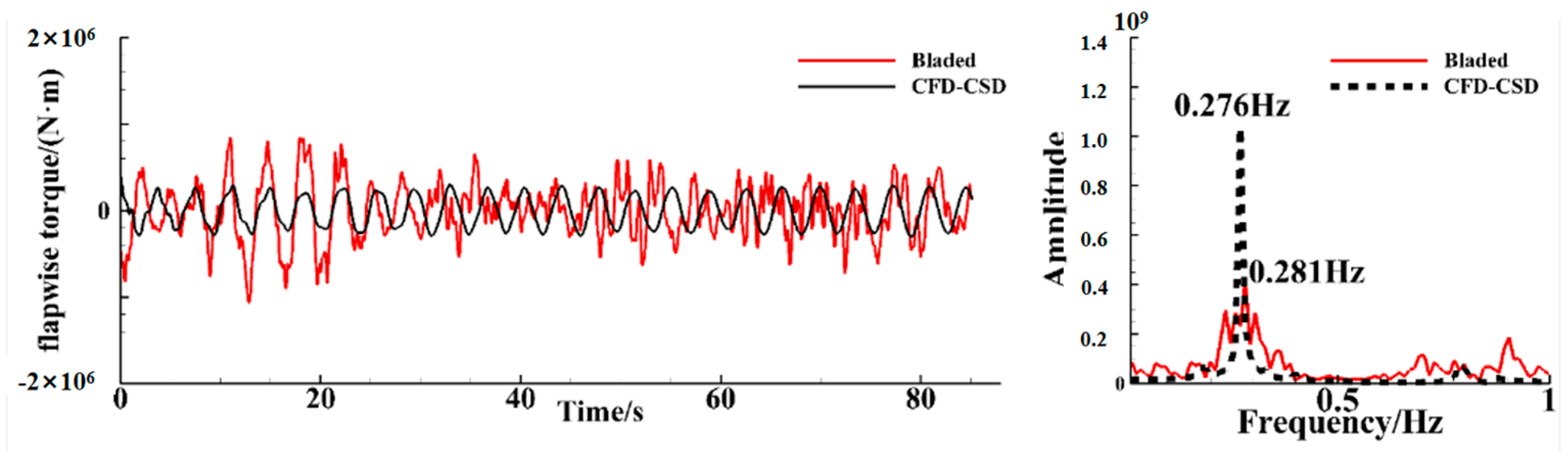
3.2. Method Verification
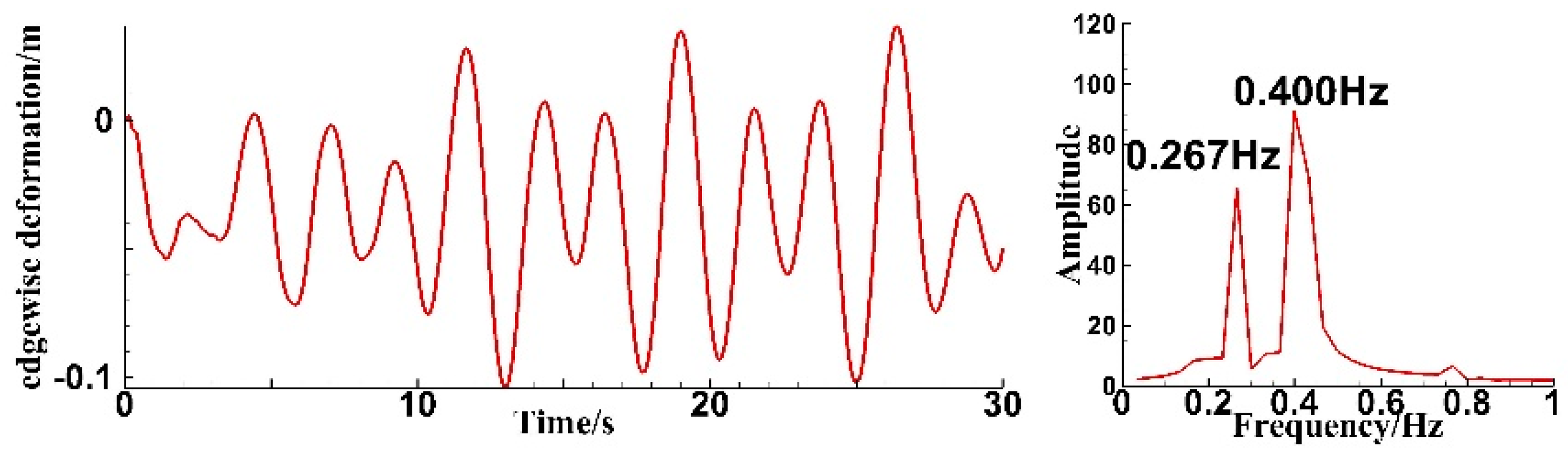
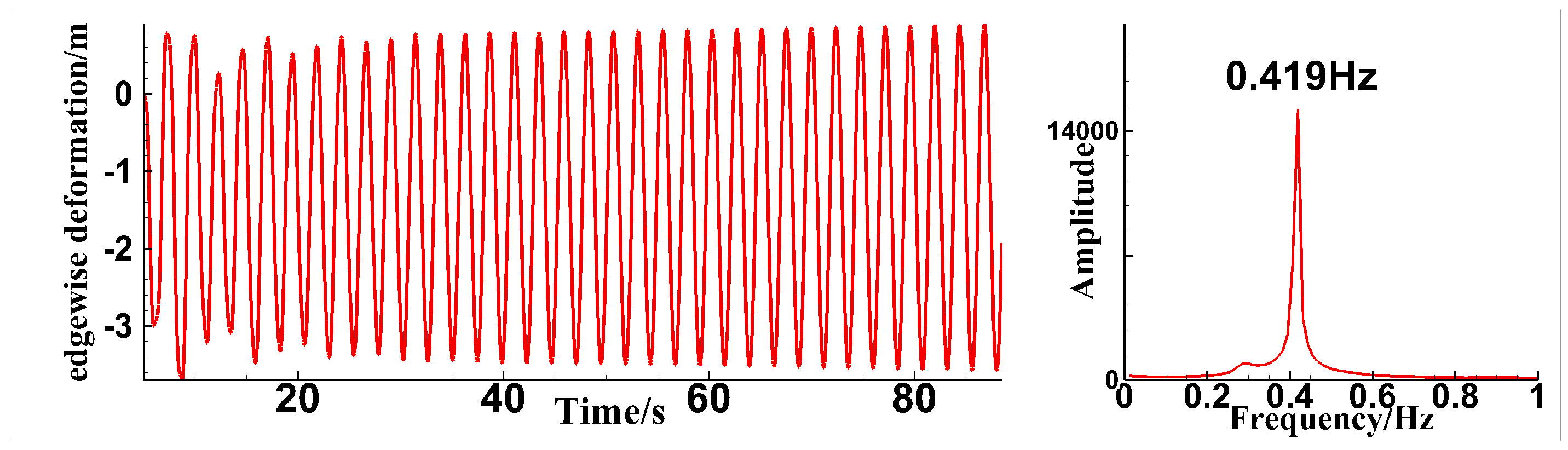
4. Results and Discussion
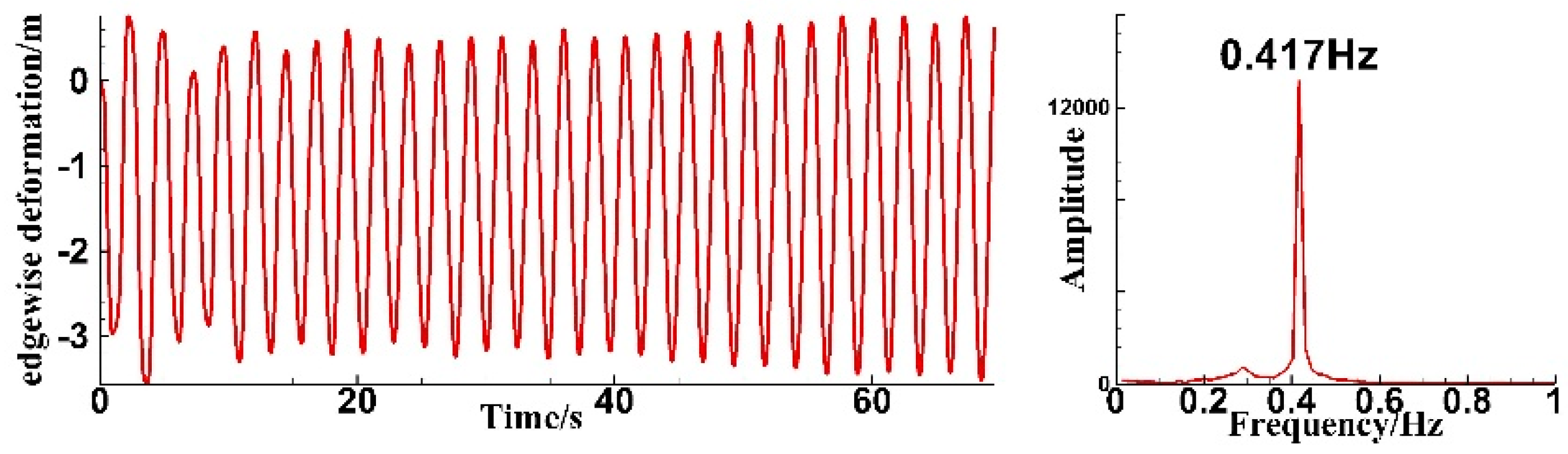
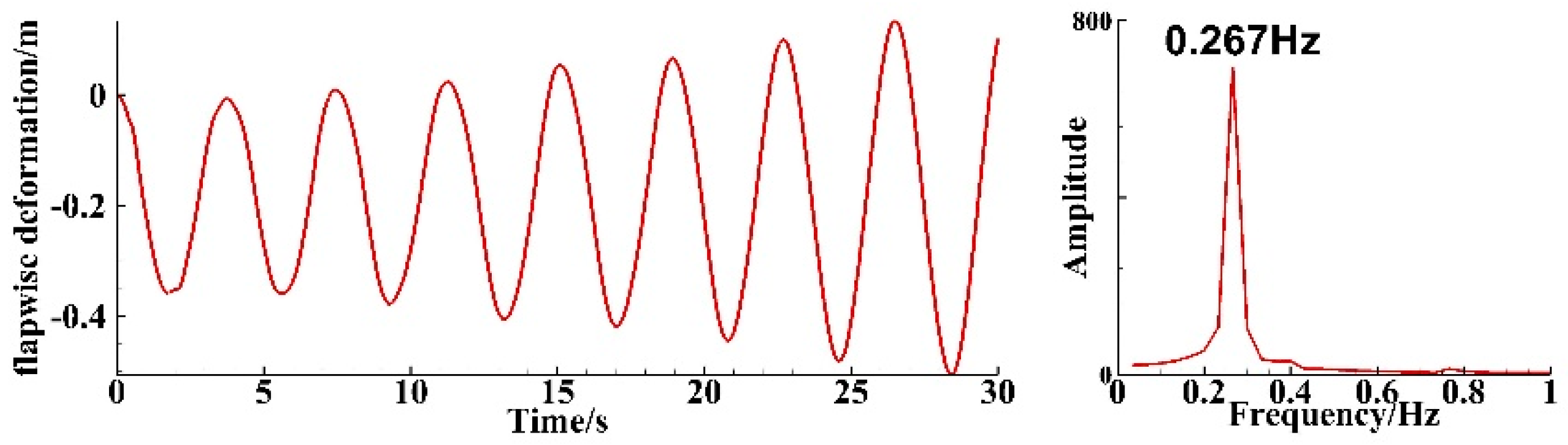
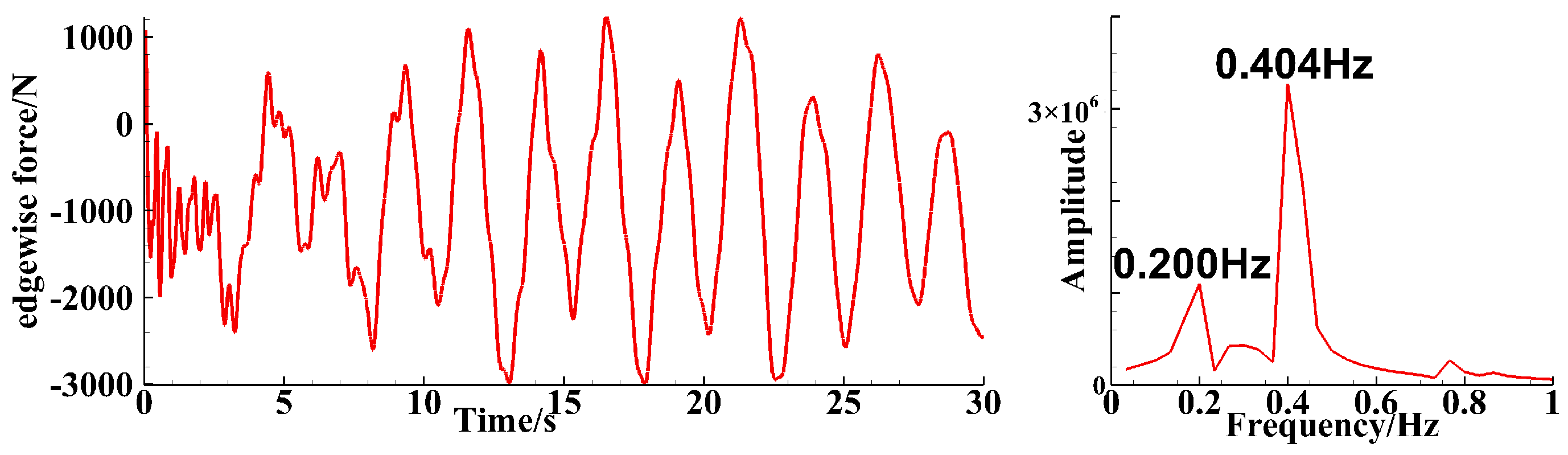
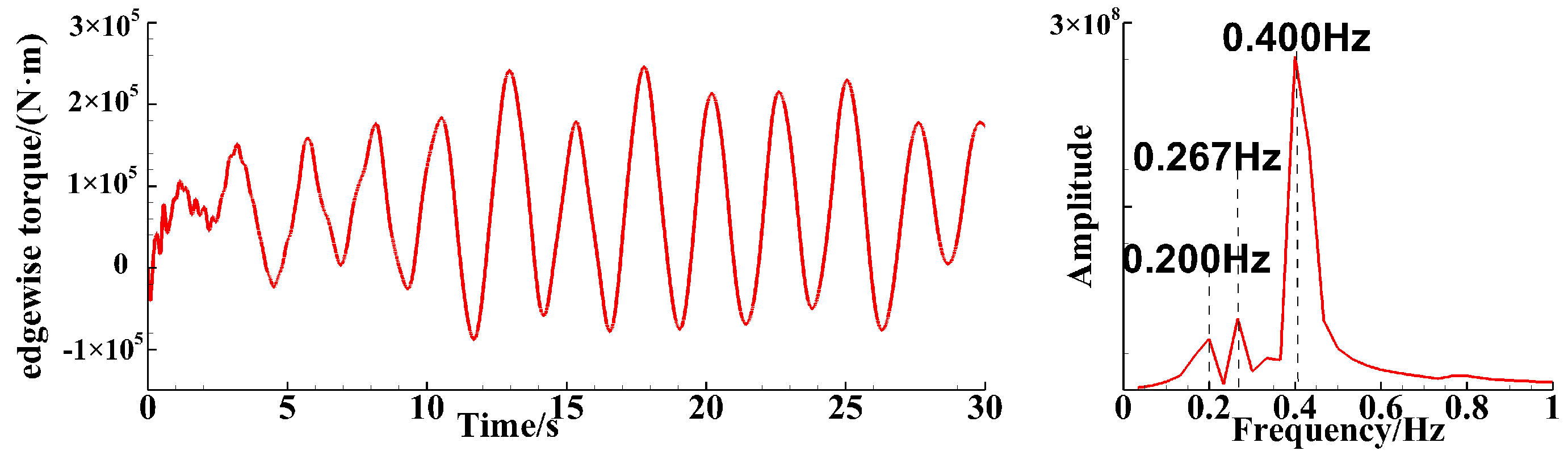
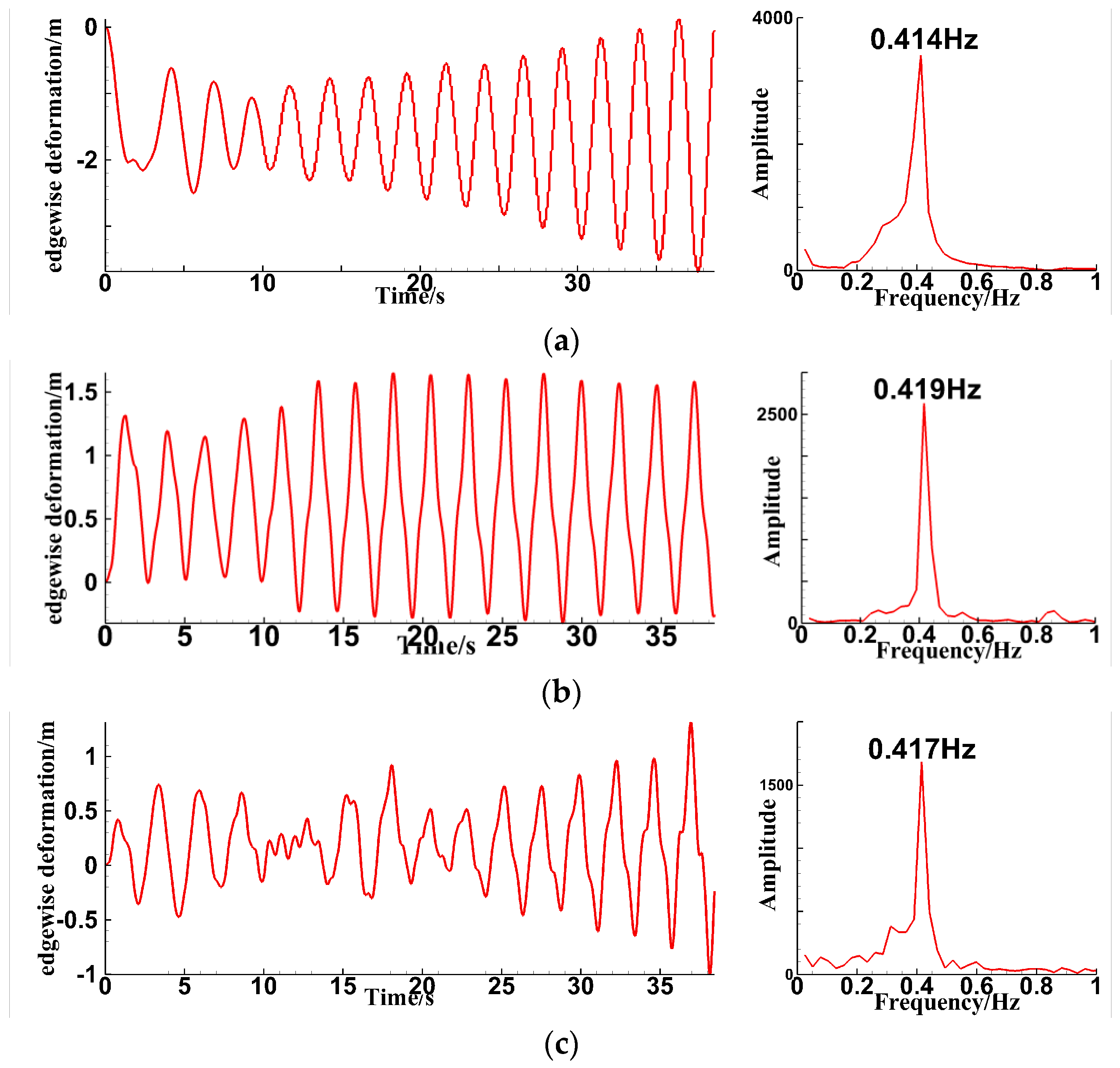
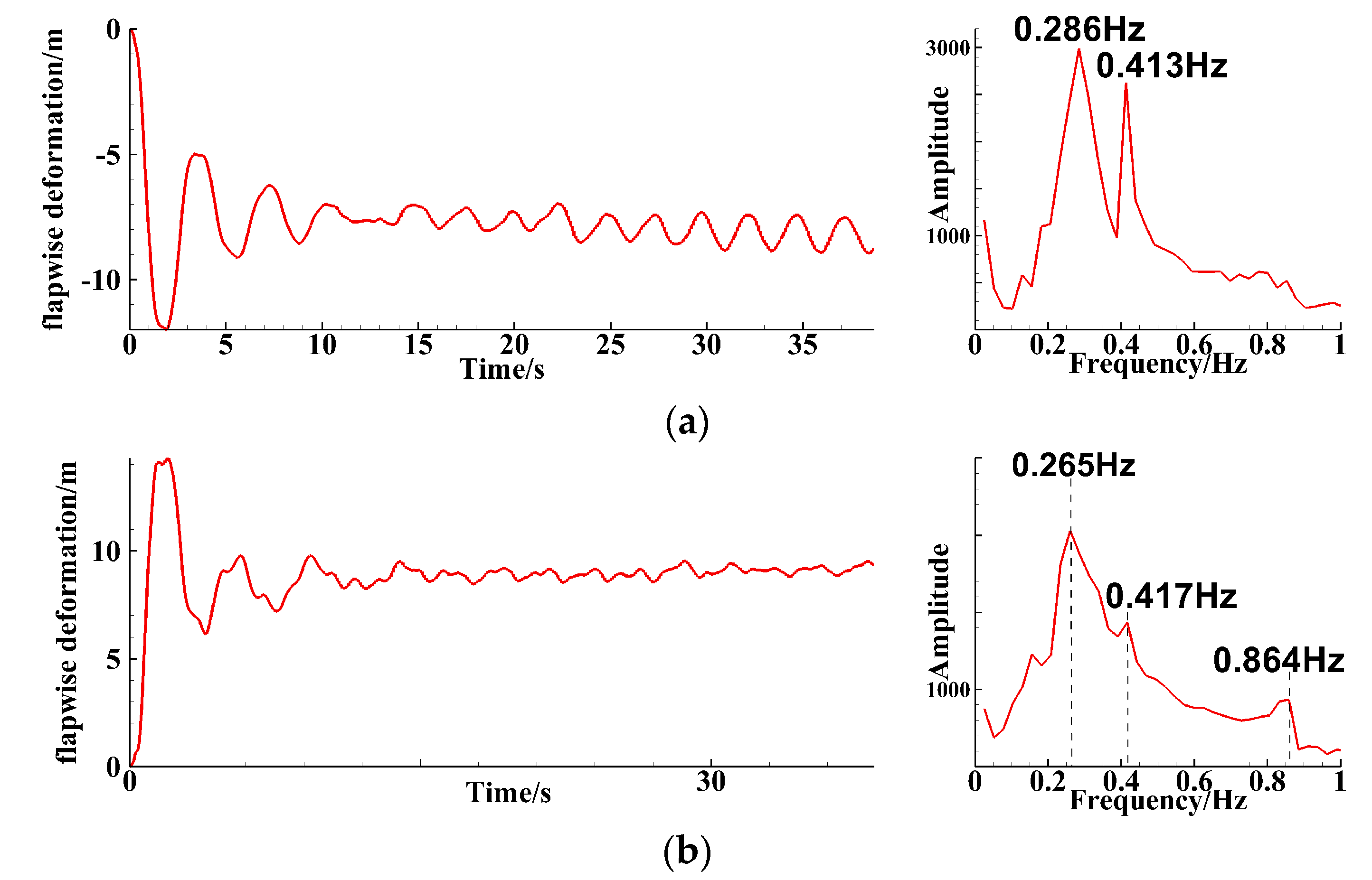
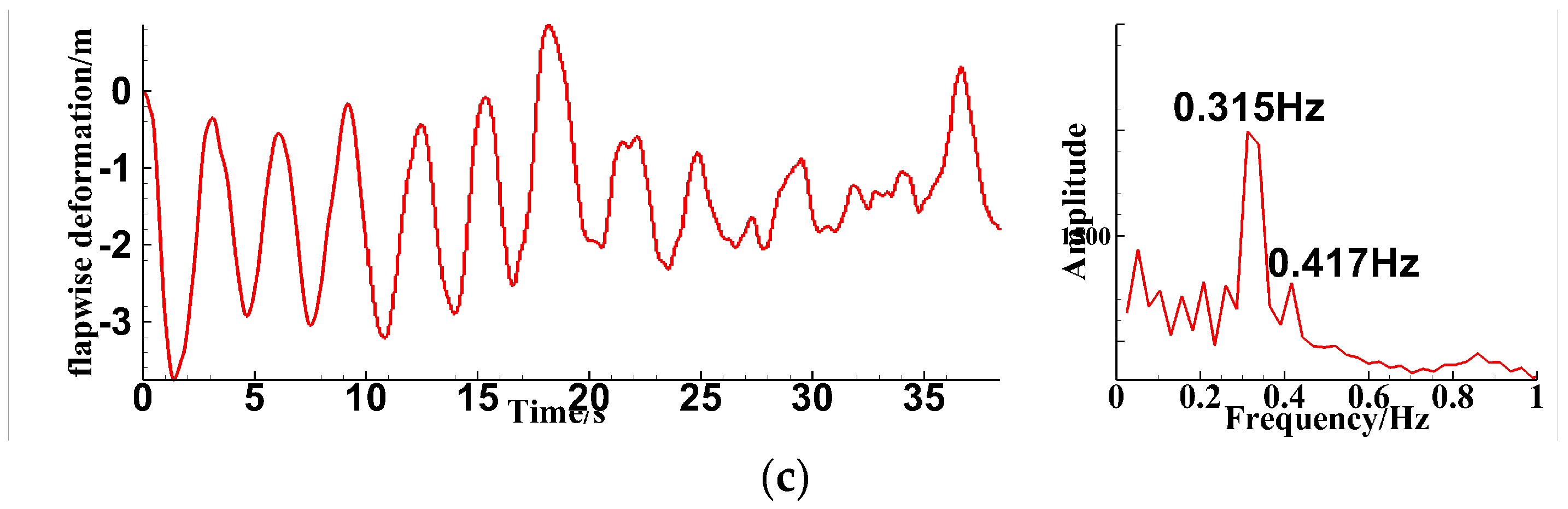
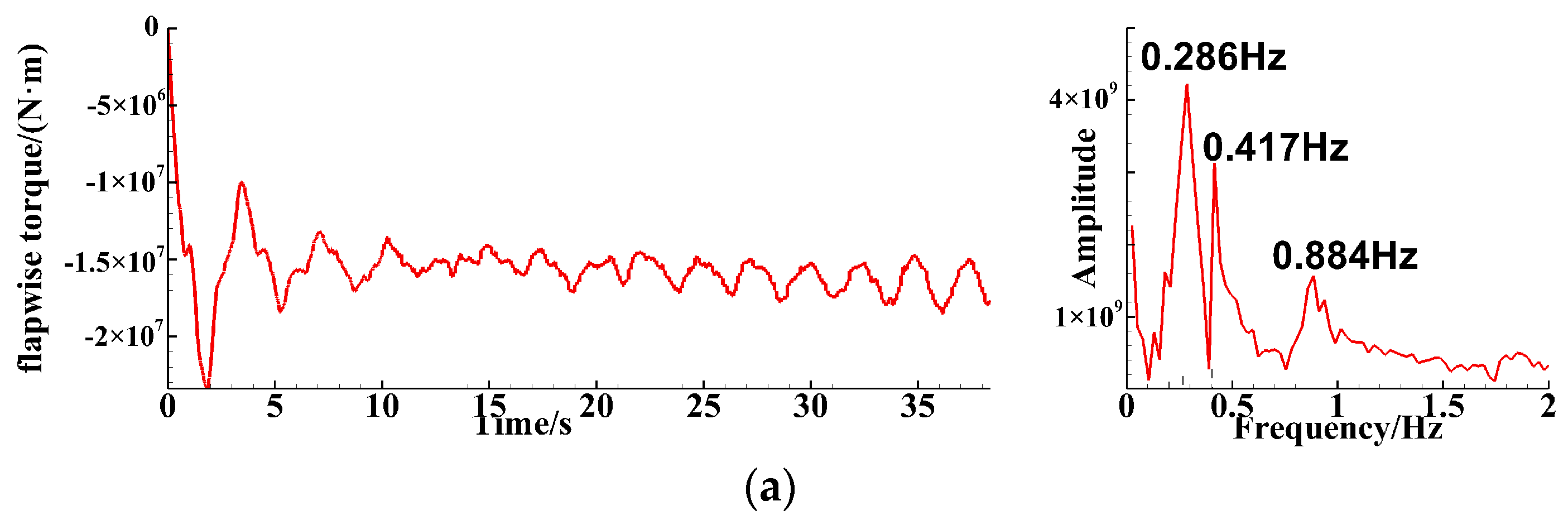
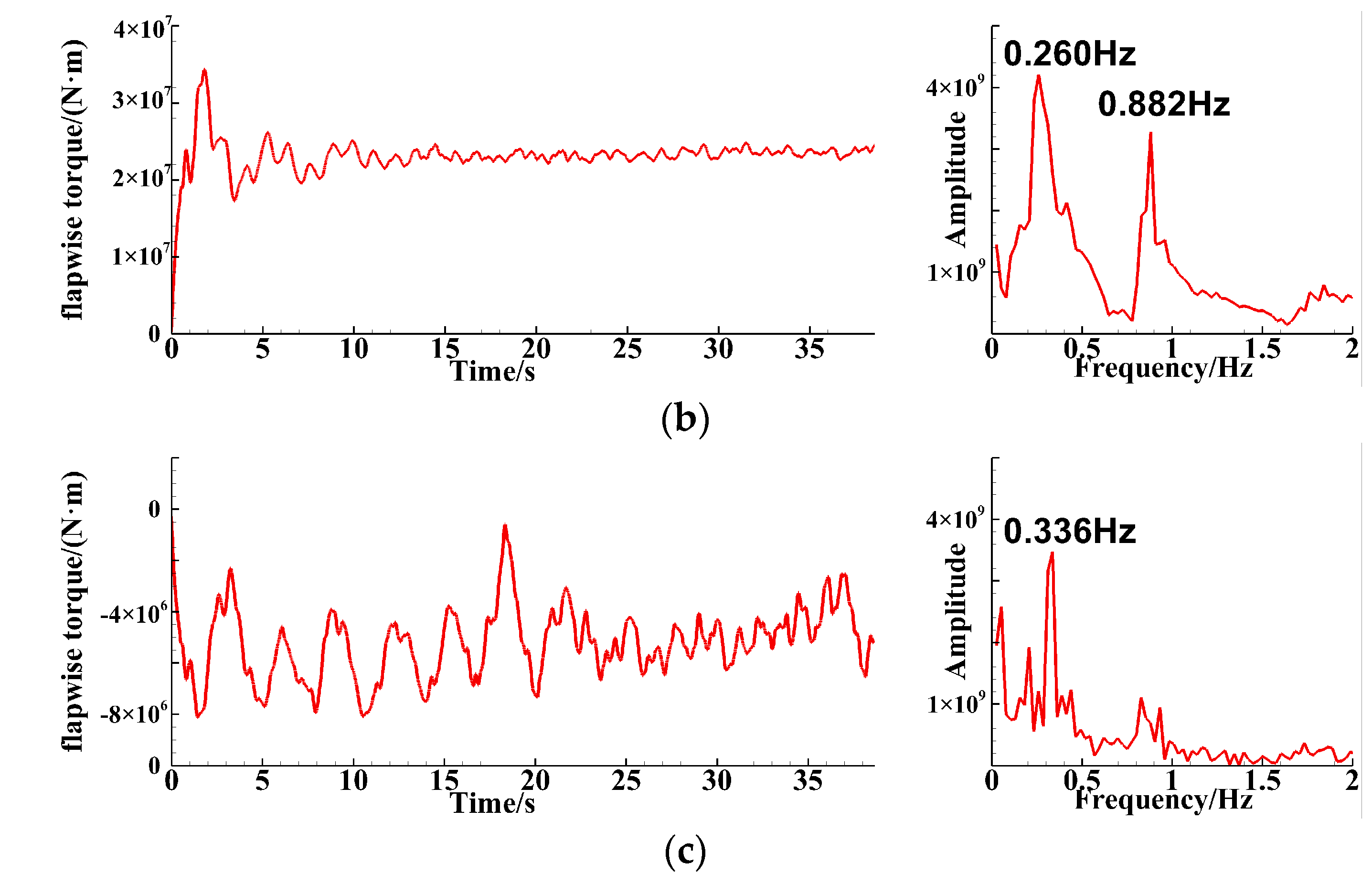
4.1. Analysis of Single-Blade Simulation Results
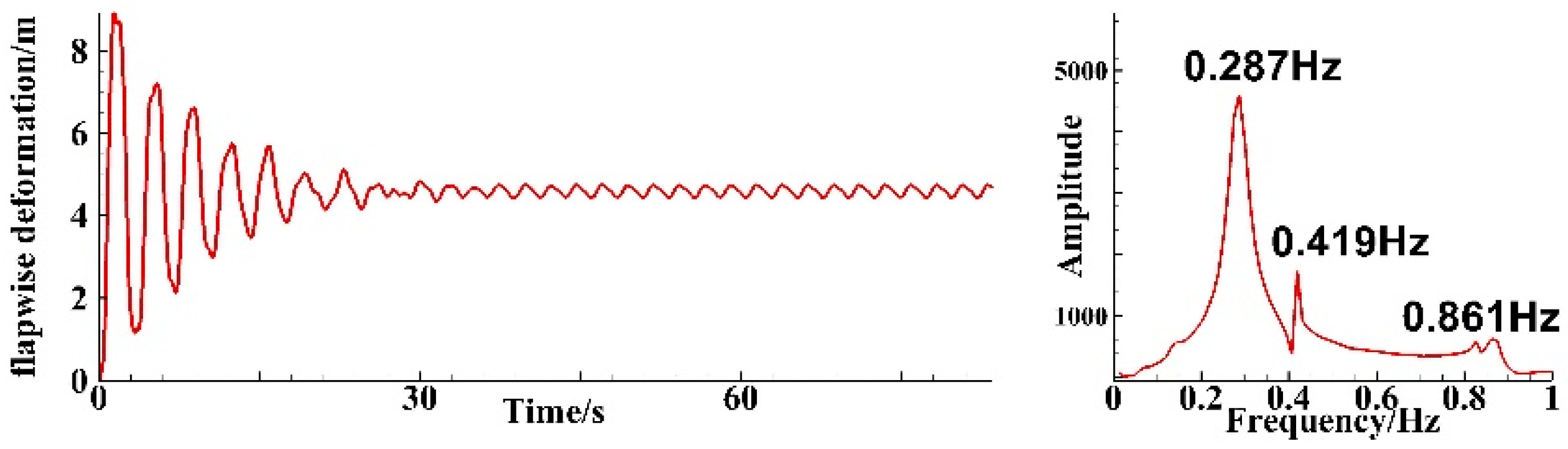
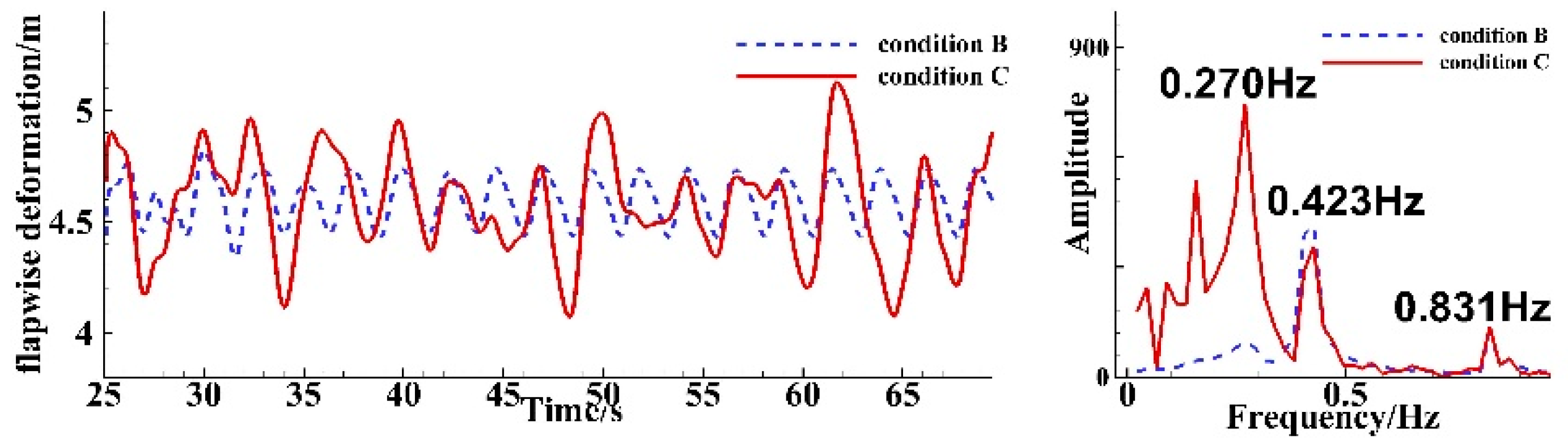
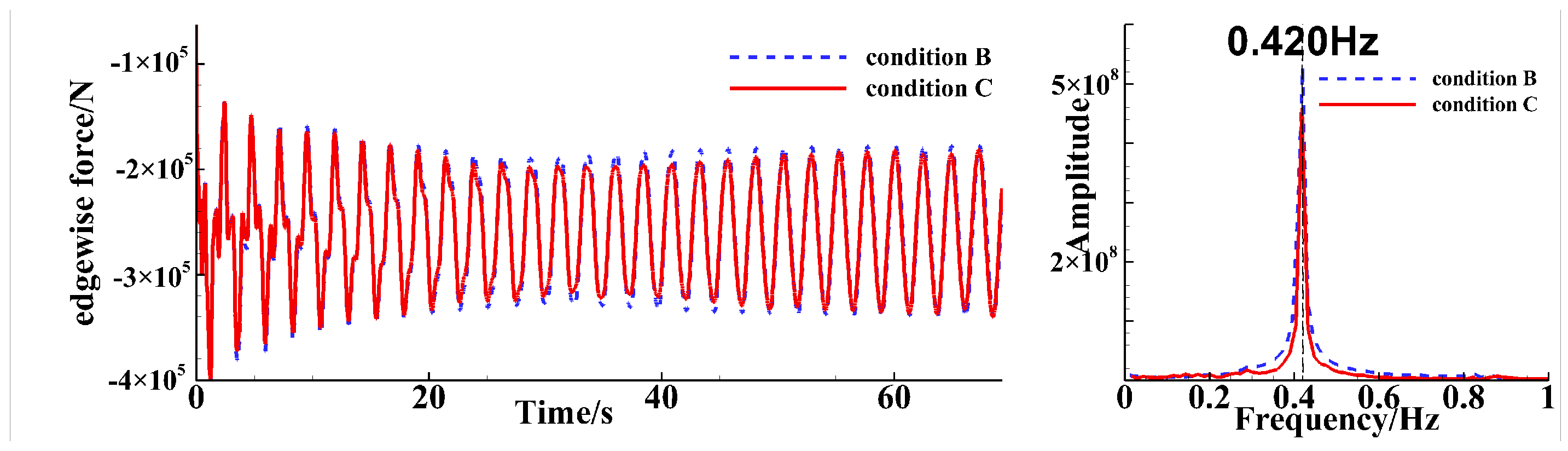
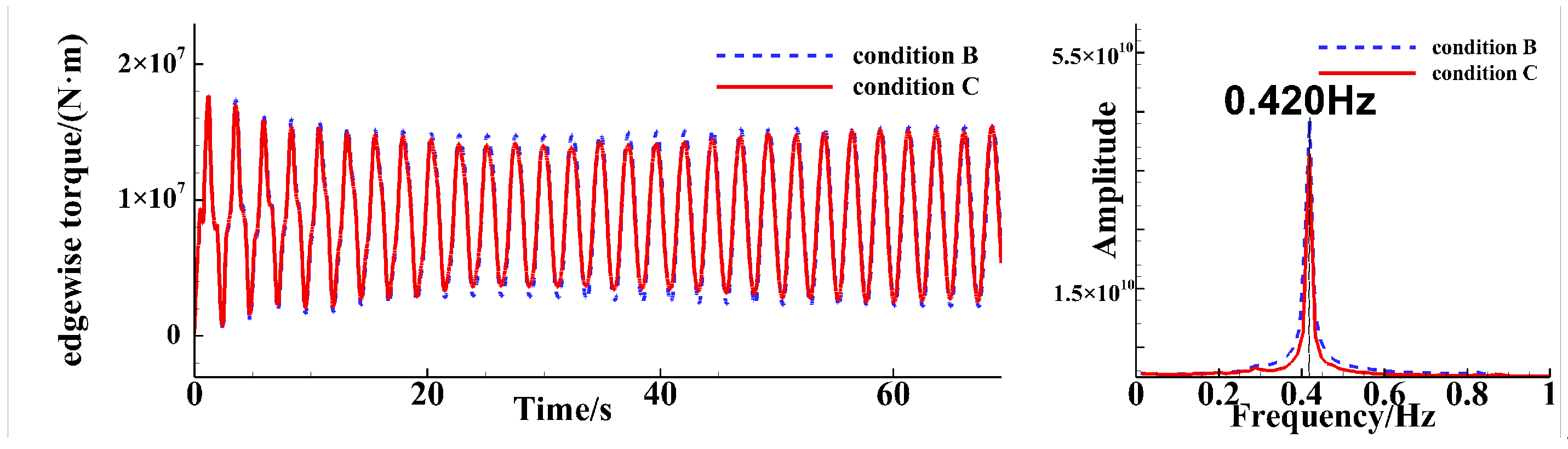
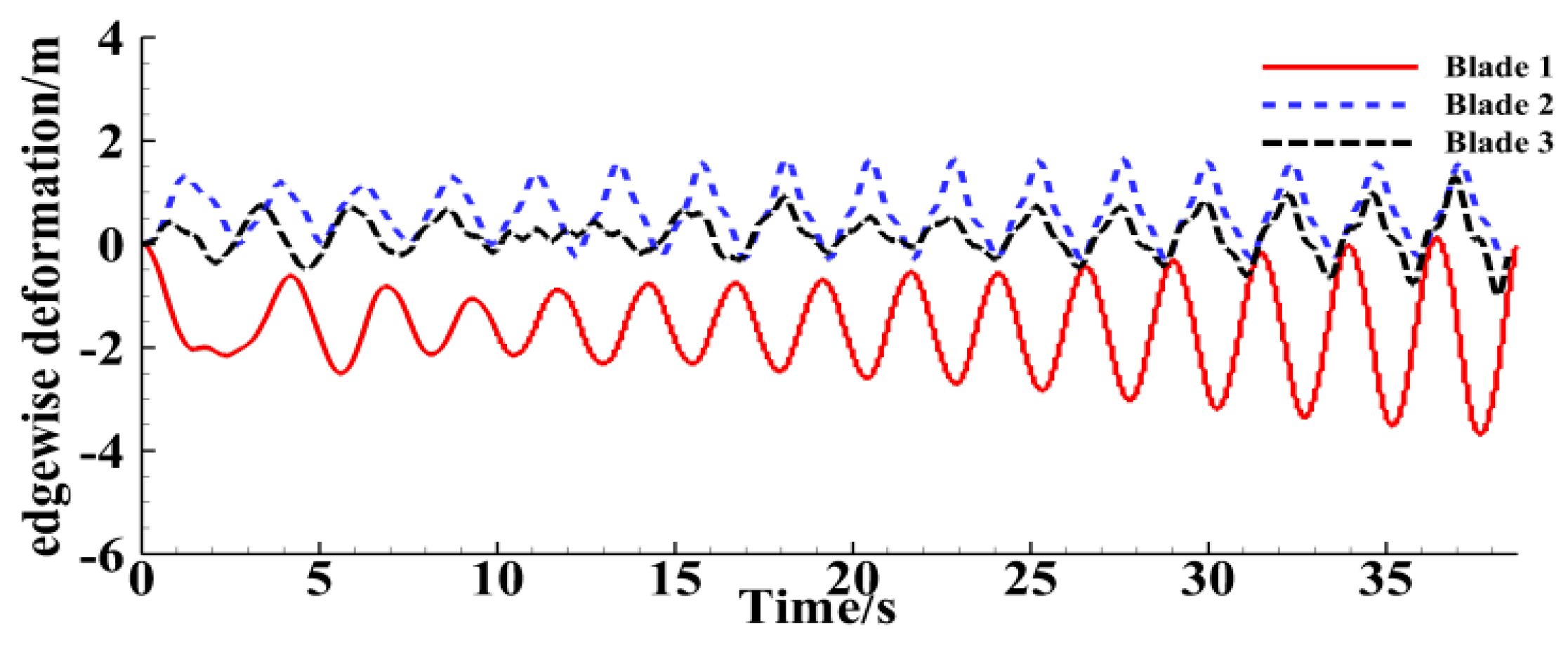
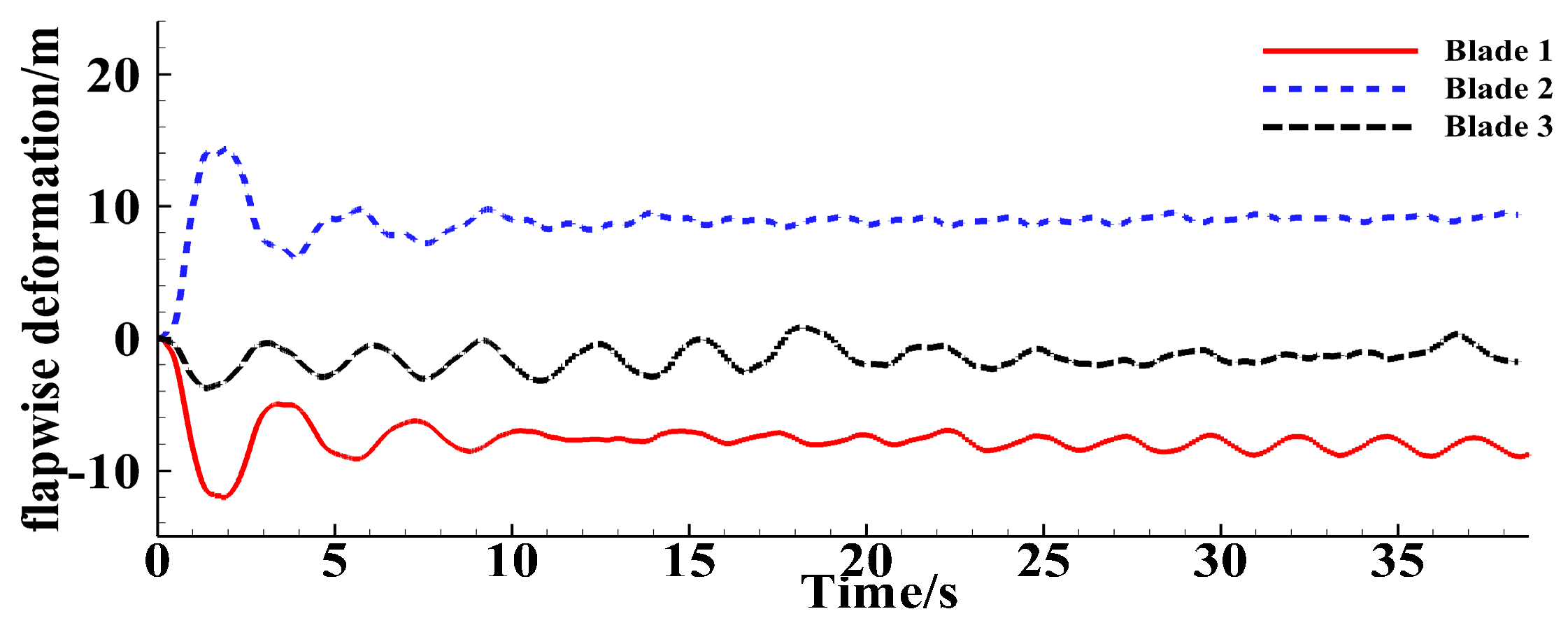
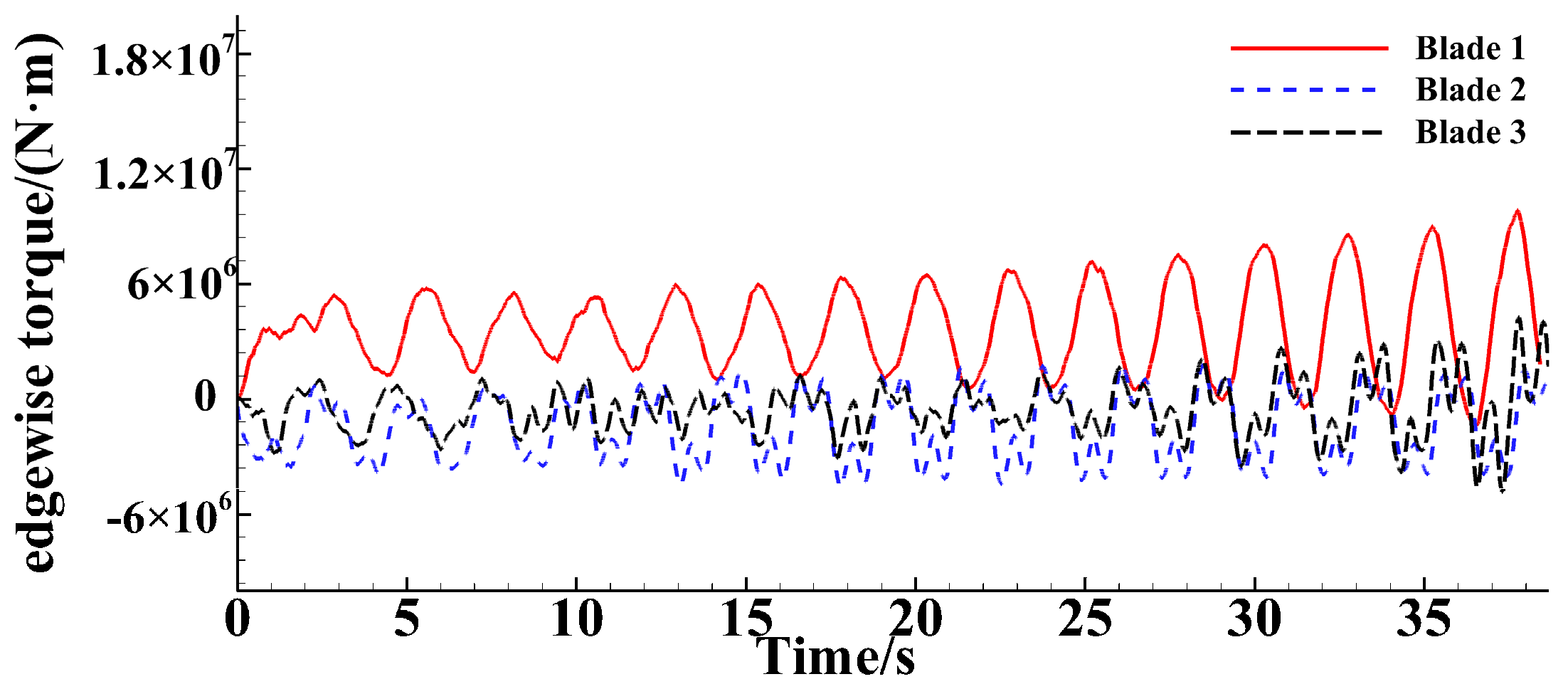
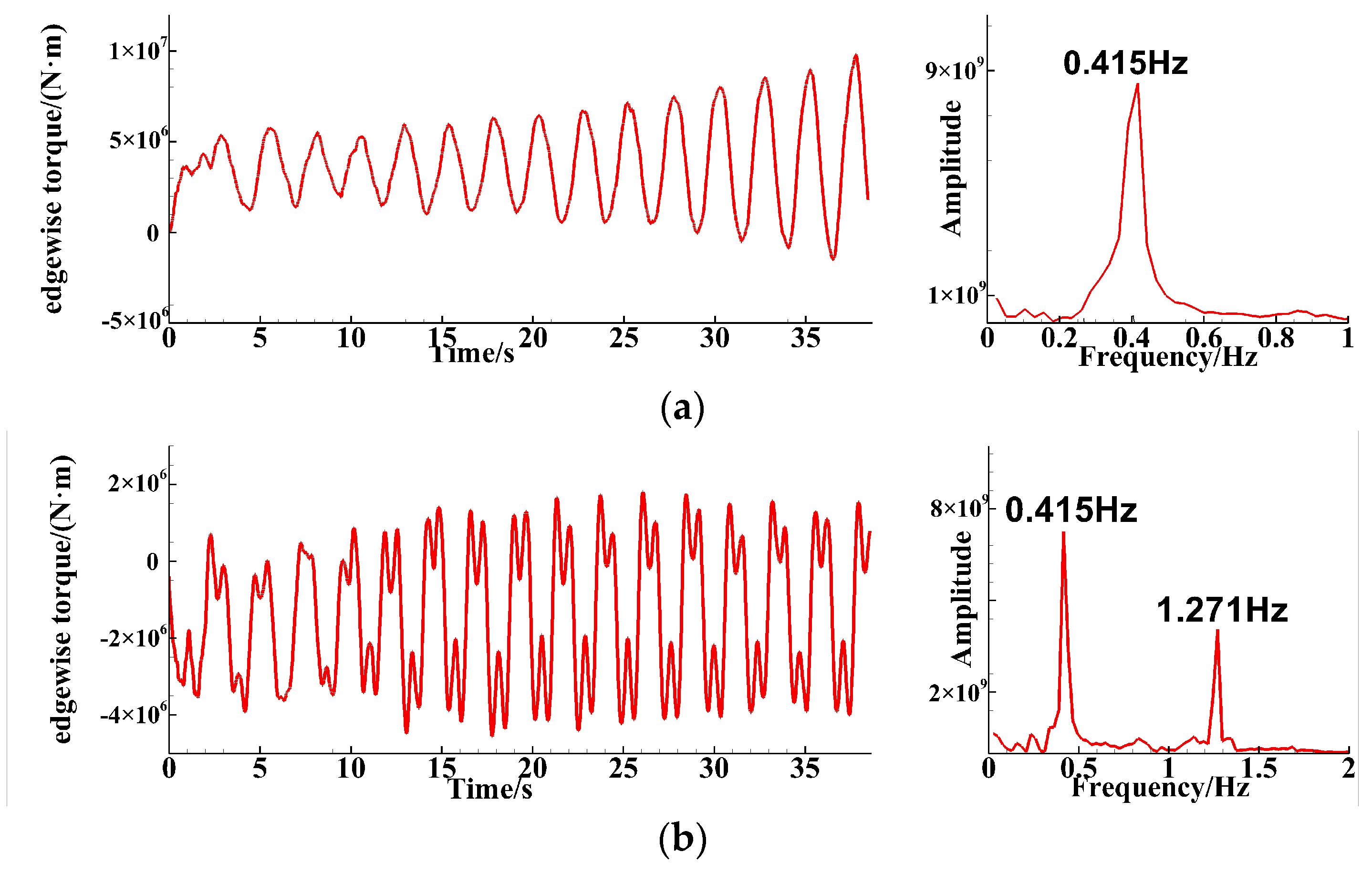
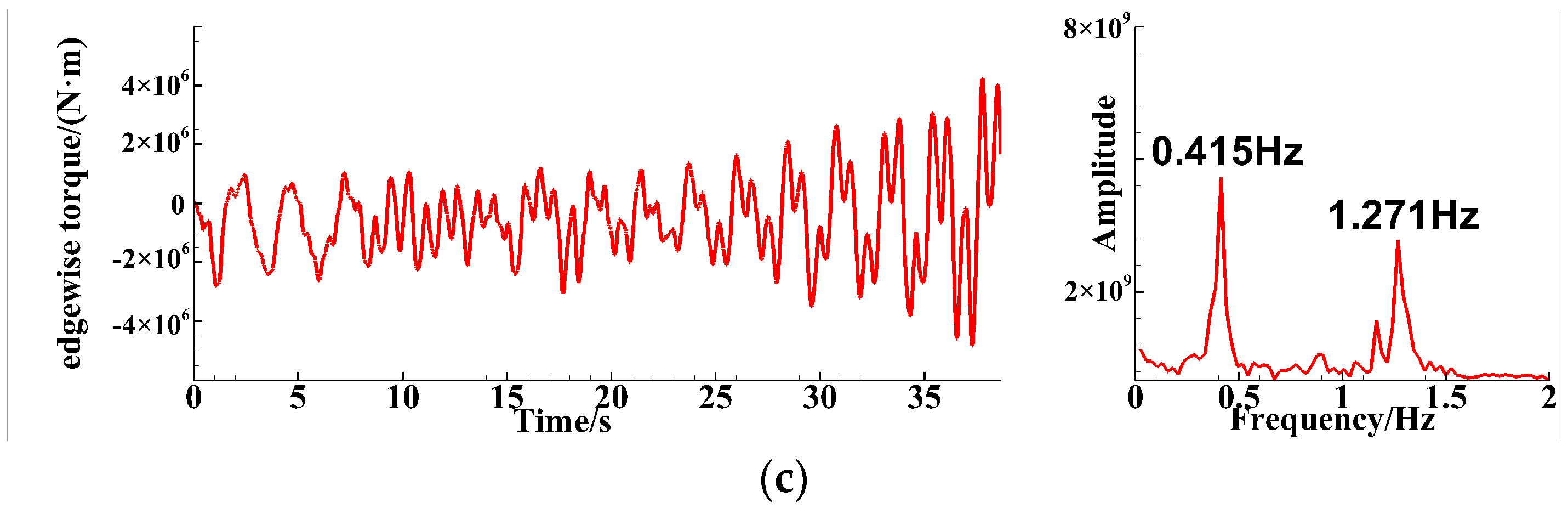
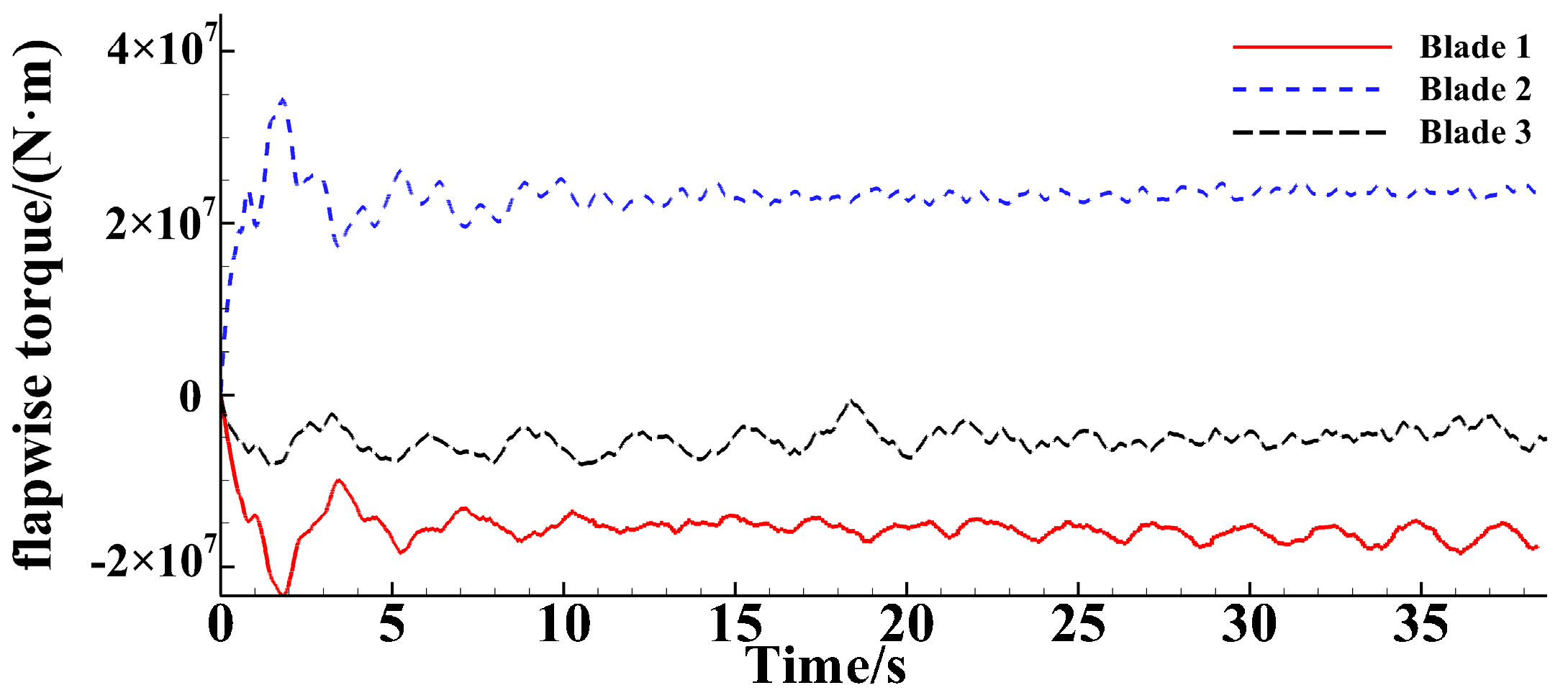
4.2. Analysis of Three-Blade Simulation Results
4.2.1. Blade Tip Deformation
4.2.2. Root Bending Moment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dose, B.; Rahimi, H.; Herráez, I.; Stoevesandt, B.; Peinke, J. Fluid-structure coupled computations of the NREL 5 MW wind turbine blade during standstill. J. Phys. Conf. Ser. 2016, 753, 022034. [Google Scholar] [CrossRef]
- Hansen, M.H. Aeroelastic instability problems for wind turbines. Wind Energy 2007, 10, 551–577. [Google Scholar] [CrossRef]
- Heinz, J.C.; Sørensen, N.N.; Zahle, F.; Skrzypiński, W. Vortex-induced vibrations on a modern wind turbine blade. Wind Energy 2016, 19, 2041–2051. [Google Scholar] [CrossRef]
- Hansen, M.H. Aeroelastic stability analysis of wind turbines using an eigenvalue approach. Wind Energy 2004, 7, 133–143. [Google Scholar] [CrossRef]
- Razak, N.A.; Andrianne, T.; Dimitriadis, G. Flutter and stall flutter of a rectangular wing in a wind tunnel. AIAA J. 2011, 49, 2258–2271. [Google Scholar] [CrossRef]
- Shitang, K.E.; Manman, L.U.; Hongxin, W.U.; Muen, G.A.; Wenxin, T.I.; Hao, W.A.; Shuo, W.A. Experimental study on the post-flutter morphological chracteristics and energy dissipation of a 15 MW wind turbine blade. Acta Aerodyn. Sin. 2022, 40, 169–180. [Google Scholar]
- Lu, M.M.; Ke, S.T.; Wu, H.X.; Gao, M.E.; Tian, W.X.; Wang, H. Blade root reaction method for predicting flutter critical wind speed of 15 MW ultra-long flexible blades based on aeroelastic tests. J. Vib. Eng. 2023, 36, 718–728. [Google Scholar]
- Liu, X.; Ma, X.-w.; Shen, S.; Chen, Y. Analysis of the influence of vibration and deformation of the blade on the aerodynamic damping. Acta Aerodyn. Sin. 2013, 31, 407–412. [Google Scholar]
- Yan, C.; Linwei, Z.; Xiong, L.; Qiong, L. Response analysis of aeroelasticity for hawt flexible blade. Acta Energiae Solaris Sin. 2014, 35, 74–82. [Google Scholar]
- Yang, B. Research on Fluid-Structure Coupling of Horizontal Axis Wind Turbine Blades Based on FAST. Master’s Thesis, North China Electric Power University, Baoding, China, 2020. [Google Scholar]
- Chen, A.-J.; Wang, C.; Jia, Y.-Y.; Liu, Q.-K. Computation and analysis of aerodynamic performance of wind turbine blade based on BEM. Eng. Mech. 2021, 38, 264–268. [Google Scholar]
- Skrzypiński, W.R.; Gaunaa, M.; Sørensen, N.; Zahle, F.; Heinz, J. Self-induced vibrations of a DU96-W-180 airfoil in stall. Wind Energy 2014, 17, 641–655. [Google Scholar] [CrossRef]
- Skrzypiński, W.; Gaunaa, M.; Sørensen, N.; Zahle, F.; Heinz, J. Vortex-induced vibrations of a DU96-W-180 airfoil at 90° angle of attack. Wind Energy 2014, 17, 1495–1514. [Google Scholar] [CrossRef]
- Heinz, J.C.; Sørensen, N.N.; Zahle, F. Fluid–structure interaction computations for geometrically resolved rotor simulations using CFD. Wind Energy 2016, 19, 2205–2221. [Google Scholar] [CrossRef]
- Dose, B.; Rahimi, H.; Herráez, I.; Stoevesandt, B.; Peinke, J. Fluid-structure coupled computations of the NREL 5 MW wind turbine by means of CFD. Renew. Energy 2018, 129, 591–605. [Google Scholar] [CrossRef]
- Lu, P. Research on Rotating Blade Solid Coupling of Large Horizontal Axis Wind Turbine. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2016. [Google Scholar]
- Leng, J.; Gao, Z.; Zheng, X.; Li, Y. Aeroelastic analysis of a 5 MW offshore wind turbine based on actuator line method. Acta Aerodyn. Sin. 2022, 40, 203–209. [Google Scholar]
- Savino, A.; Cocco, A.; Zanotti, A.; Tugnoli, M.; Masarati, P.; Muscarello, V. Coupling Mid-Fidelity Aerodynamics and Multibody Dynamics for the Aeroelastic Analysis of Rotary-Wing Vehicles. Energies 2021, 14, 6979. [Google Scholar] [CrossRef]
- Cocco, A.; Mazzetti, S.; Masarati, P.; van’t Hoff, S.; Timmerman, B. Numerical Whirl–Flutter analysis of a tiltrotor semi-span wind tunnel model. CEAS Aeronaut. J. 2022, 13, 923–938. [Google Scholar] [CrossRef]
- Leng, J.; Gao, Z.; Wu MC, H.; Guo, T.; Li, Y. A fluid–structure interaction model for large wind turbines based on flexible multibody dynamics and actuator line method. J. Fluids Struct. 2023, 118, 103857. [Google Scholar] [CrossRef]
- Reissner, E. On one-dimensional large-displacement finite-strain beam theory. Stud. Appl. Math. 1973, 52, 87–95. [Google Scholar] [CrossRef]
- Wang, Q.; Sprague, M.A.; Jonkman, J.; Johnson, N.; Jonkman, B. BeamDyn: A high-fidelity wind turbine blade solver in the FAST modular framework. Wind Energy 2017, 20, 1439–1462. [Google Scholar] [CrossRef]
- Hodges, D.H. Geometrically exact, intrinsic theory for dynamics of curved and twisted anisotropic beams. AIAA J. 2003, 41, 1131–1137. [Google Scholar] [CrossRef]
- Hsu, M.C.; Akkerman, I.; Bazilevs, Y. Finite element simulation of wind turbine aerodynamics: Validation study using NREL Phase VI experiment. Wind Energy 2014, 17, 461–481. [Google Scholar] [CrossRef]
- Jensen, F.M.; Arconada, J.O.; Werk, M.; Berggreen, C.; Sørensen, J.D.; Zhong, G.; Haans, W. Torsional Effects on Wind Turbine Blades and Impact on Field Damages. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1293, 012005. [Google Scholar] [CrossRef]
- Qiao, X.H.; Gao, Z.T.; Wang, T.G.; Wang, L.; Ke, S.T. Nonlinear aeroelastic response analysis of 100-meter-scale flexible wind turbine blades. Acta Aerodyn. Sin. 2022, 40, 220–230. [Google Scholar]
- Rmsay, R.F.; Hoffman, M.J.; Gregorek, G.M. Effects of Grit Roughness and Pitch Oscillations on the S810 Airfoil; National Renewable Energy Lab. (NREL): Golden, CO, USA, 1996. [Google Scholar]
- Janiszewska, J.M.; Ramsay, R.R.; Hoffmann, M.J.; Gregorek, G.M. Effects of Grit Roughness and Pitch Oscillations on the S814 Airfoil; National Renewable Energy Lab. (NREL): Golden, CO, USA, 1996. [Google Scholar]
- Couturier, P.J.; Skjoldan, P.F. Implementation of an advanced beam model in BHawC. J. Phys. Conf. Ser. 2018, 1037, 062015. [Google Scholar] [CrossRef]
- Hansen, M.H. Anisotropic damping of Timoshenko beam elements. (Denmark. Forskningscenter Risoe. Risoe-R; No. 1267). 2001. Available online: https://orbit.dtu.dk/en/publications/anisotropic-damping-of-timoshenko-beam-elements (accessed on 4 July 2024).
- Bazoune, Y.A.K. Shape functions of three-dimensional timoshenko beam element. J. Sound Vib. 2003, 259, 473–480. [Google Scholar] [CrossRef]
- Pradhan, S.; Modi, V.J.; Misra, A.K. Order N Formulation for Flexible Multibody Systems in Tree Topology: Lagrangian Approach. J. Guid. Control. Dyn. 1997, 20, 665672. [Google Scholar] [CrossRef]
- Torby, B.J.; Kimura, I. Dynamic Modeling of a Flexible Manipulator with Prismatic Links. J. Dyn. Syst. Meas. Control. 1999, 121, 691696. [Google Scholar] [CrossRef]
- Bir, G. Multi-blade coordinate transformation and its application to wind turbine analysis. In Proceedings of the 46th AIAA/ASME Wind Energy Symposium, Reno, NV, USA, 7–10 January 2008; pp. 82–86. [Google Scholar]
- Stewart, G.W. A Krylov–Schur Algorithm for Large Eigenproblems. SIAM J. Matrix Anal. Appl. 2001, 23, 601–614. [Google Scholar] [CrossRef]
- Wu, X.; Feng, K.; Li, Q. A Numerical Method for the Dynamics Analysis of Blade Fracture Faults in Wind Turbines Using Geometrically Exact Beam Theory and Its Validation. Energies 2024, 17, 824. [Google Scholar] [CrossRef]
- Guodong, R.; Wenlei, S.; Xiuling, R. Fatigue research on vane of wind power generator based on cosimulation. Mach. Tool Hydraul 2010, 38, 100–102. [Google Scholar]
- Lü, P.; Liao, M.; Xu, Y.; Yin, Y. Beam Finite Element for Wind Turbine Bladebased on Geometrically Exact Beam Theory. Acta Energiae Solaris Sin 2015, 36, 2422–2428. [Google Scholar]







| Modal Frequency | Bladed Hz | GTsim Hz | Deviation % |
|---|---|---|---|
| First flapwise mode | 0.2969 | 0.2984 | 0.51 |
| First edgewise mode | 0.4157 | 0.4165 | 0.21 |
| Second flapwise mode | 0.8779 | 0.8869 | 1.03 |
| Second edgewise mode | 1.2577 | 1.2629 | 0.42 |
| Calculate Working Conditions | Wind Speed | Turbulence % | Gravity |
|---|---|---|---|
| A | 35 | 0.01 | disregard |
| B | 35 | 0.01 | regard |
| C | 35 | 10 | regard |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Liu, R.; Li, Y.; Lv, P.; Gao, C.; Feng, K. Numerical Simulation Method for the Aeroelasticity of Flexible Wind Turbine Blades under Standstill Conditions. Energies 2024, 17, 3395. https://doi.org/10.3390/en17143395
Wu X, Liu R, Li Y, Lv P, Gao C, Feng K. Numerical Simulation Method for the Aeroelasticity of Flexible Wind Turbine Blades under Standstill Conditions. Energies. 2024; 17(14):3395. https://doi.org/10.3390/en17143395
Chicago/Turabian StyleWu, Xianyou, Rongxiang Liu, Yan Li, Pin Lv, Chuanqiang Gao, and Kai Feng. 2024. "Numerical Simulation Method for the Aeroelasticity of Flexible Wind Turbine Blades under Standstill Conditions" Energies 17, no. 14: 3395. https://doi.org/10.3390/en17143395
APA StyleWu, X., Liu, R., Li, Y., Lv, P., Gao, C., & Feng, K. (2024). Numerical Simulation Method for the Aeroelasticity of Flexible Wind Turbine Blades under Standstill Conditions. Energies, 17(14), 3395. https://doi.org/10.3390/en17143395






