Abstract
The manuscript analyzes the impact of the HVOF (high-velocity oxygen fuel) coating spraying technology on a substrate made of a light and high-specific-strength magnesium casting alloy from the AZ31 series. Among others, the following were examined: the influence of the spraying distance of coatings using commercial cermet powders (WC–Co, WC–Co–Cr, and WC–Cr3C2–Ni) on their resistance to erosive wear. It is worth emphasizing the energy savings resulting from the possibility of spraying on the surfaces of existing machine parts to protect or regenerate them. Energy savings result from the possibility of recycling the substrate material (AZ31), as well as from extending the functionality of an existing element without the need to dispose of it and the energy-intensive production of a new component. Tests have shown that the best resistance to the destructive effects of erodent in the form of hard corundum particles is characterized by a WC–Co–Cr coating sprayed at a distance of 320 mm.
1. Introduction
In the era of intensive industrial development (industry 4.0) [1,2], great emphasis is placed on sustainable development, with particular emphasis on care for the environment. Engineering solutions based on the optimization of quality, strength, and weight are constantly sought. In the design process, the method of disposal as well as possible recycling methods/elements should already be taken into account. The focus is on refurbishment—not throwing away—in order to save time, reduce production and operating costs, and, above all, save energy. It is an undeniable fact that the cost of regeneration of a device or structural element is lower than the cost of its production. Hence, numerous regeneration methods have been developed to not only restore functional functions but also to increase their durability several times. Scientific works show that an effective technique for increasing the durability of elements of various types of machines and devices used in environments exposed to erosive, corrosive, and abrasive wear is the use of various types of coatings on their surfaces [3,4]. It should be emphasized that modern technologies allow the use of various types of powders, including cermet. This protection of the working surface combines the beneficial properties of the core material with the hardness, wear resistance, and heat resistance of the coating [5]. Additionally, in this combination, the load transfer function is separate from the protection against the unfavorable influence of the working environment.
Magnesium alloys are a future-proof material increasingly used in the automotive, aviation, machine building, shipbuilding, chemical, energy, electronics, textile, and nuclear industries, as well as in the production of portable electronic devices. For this reason, alloys of non-ferrous metals, including magnesium, are the subject of research in numerous research and scientific centers and universities [6]. They owe their popularity to their extraordinary lightness (thanks to a density of 1.5–1.8 g/cm3), high specific strength, and the ability to work at temperatures up to 300 °C. Reducing the weight of the structure has a positive effect on energy savings. Good mechanical properties, vibration-damping ability, and the ability to recover and reuse industrial materials—recycling—support sustainable development [7,8]. They can be used as substitutes for both plastics and aluminum alloys. As mentioned earlier, they are gaining popularity in automotive applications because the introduction of parts made of magnesium alloys allows for a significant reduction in vehicle weight. Difficulties in processing can be considered a disadvantage—flammability, especially in the form of powder. However, their high application potential is limited by the chemical reactivity of magnesium and its susceptibility to corrosion, especially in the presence of chloride ions [9,10]. Therefore, the development of a protective coating applied in the least energy-intensive way will not only increase the scope of application of magnesium alloys but will also reduce the energy associated with the replacement or regeneration of an element operating in unfavorable conditions for a given material.
Erosive wear is a process initiated by the impact of solid, liquid, or gaseous particles on the working surface of the analyzed material. Erosive wear is often accompanied by cavitation (especially in truck pumps and on the turbine blades that power ships) [11,12]. It should be emphasized that the tribological system, which is a material exposed to the erosive impact of solid, liquid, or gaseous bodies, is an open system because the mentioned erodents are constantly replaced, which further intensifies the processes of destruction of the material surface [13]. Therefore, an extremely important scientific issue is the development of a surface–substrate connection produced in optimal conditions of sustainable production, saving energy and limiting the emission of harmful compounds into the atmosphere during the production process, and at the same time characterized by high resistance to erosive wear [14]. The experimental studies performed give insight into relationships between the composition of the coatings, the conditions of their preparation, and their wear resistance. The main aim of the research was the evaluation of the erosion wear energy of cermet coatings deposited by HVOF on magnesium alloy substrates.
2. Materials and Methods
The substrate material was an AZ31 magnesium alloy. The chemical composition and basic strength properties of the base material are presented in Table 1 and Table 2. The test samples had the shape of a disk with a diameter of 100 mm and a thickness of 5 mm. The coatings were sprayed with commercial cermet powders: WC–Co, WC–Co–Cr and WC–Cr3C2–Ni, sintered and agglomerated, and the particle size range of each of them was from −45 to +15 µm. HVOF (high-velocity oxygen fuel) coatings were sprayed with a JP 5000 TAFA gun (Indianapolis, USA) (outlet nozzle diameter φ = 11 mm; nozzle length 4 inches = 101.6 mm). The fuel used in the process was kerosene (kerosene K-1, physical and chemical properties in Table 3), the combustion gas was oxygen, and the carrier gas was nitrogen. The powder feeding speed was 70 g/min, the water flow was 23 slpm (standard liter per minute), the oxygen was 900 slpm, the kerosene was 26.1 L/h, and the nitrogen feed rate was 12 slpm. The coating spraying process was carried out manually using two distances: 320 mm and 400 mm (Figure 1).

Table 1.
Chemical composition of the AZ31 magnesium alloy.

Table 2.
Mechanical properties of bars made of magnesium alloy AZ31 were determined at room temperature.

Table 3.
Physicochemical properties of kerosene.
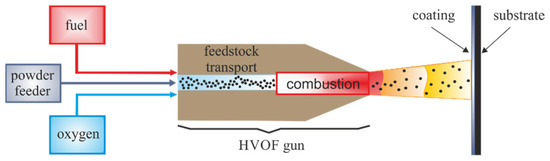
Figure 1.
Schematic representation of the HVOF method and its key process parameters inspired by high-velocity oxygen fuel spraying [15].
In the HVOF process, the material is applied to the substrate continuously. Combustible gas or liquid fuel is fed, together with oxygen, into the burner chamber, where it is burned. Flammable gases may be ethylene, propylene, propane, acetylene, and natural gas, while the liquid fuel is a mixture of aviation gasoline or aviation kerosene, which is a product of the distillation of crude oil at a temperature of 46.85–276.85 °C and is in a sprayed form during the process with oxygen or compressed air [16]. It should be emphasized that the presented research used kerosene with physicochemical properties tested in the laboratory before its use and presented in Table 3. It is a fuel that burns cleaner and can be used for indoor combustion (stoves, lamps). The gases produced as a result of combustion are directed to the nozzle, where their stream is formed. The powder material is fed on the burner axis or perpendicular to it using a stream of nitrogen or argon. The combustion chamber and nozzle are cooled during the process using water. The sprayed material is in a spherical form until the particle contacts the sprayed substrate. When it leaves the burner nozzle, a layer of oxides is formed on the surface of the heated particle, formed as a product of the oxidation reaction in contact with air. The impact of the particle on the substrate changes its shape, which causes the previously formed oxide layer to crack. It should be emphasized that disk-shaped particles in the coating structure only occur when the kinetic or thermal energy of the drop is small. Hence, the formation of irregularly shaped particles is more likely. As a result of the collision of two particles in a place exposed to the oxide layer, they are connected to each other by cohesive forces and adhesive forces on the surface of the substrate. For this reason, the substrate should be specially prepared before the spraying process [17]. Appropriate surface roughness causes the dynamically impacting particles to be embedded in the existing irregularities and fill them with the coating material. As a result, the resulting coating adapts to the surface and creates a more durable connection. As discussed in [18], the protective layer method is characterized by low porosity (<5%) as well as lower oxide content compared to plasma spraying methods. These differences are mainly due to the lower temperature of the sprayed particles, higher speeds, and thus higher kinetic energy. The parameter describing the interaction of the particle with the substrate is the Sommerfeld number, given by the formula:
where and are the Reynolds and Weber numbers, respectively.
The parameter S is closely related to the particle’s momentum. It has been shown that for S < 3, the particle reflects from the sprayed surface; at 3 < S < 58, the molecule forms a coating; and at S > 58, the energy is high enough to cause the particle to splash.
3. Energy Model of Erosion
The first attempts to describe the phenomenon of erosion were based on the concept of a constant value of energy needed to remove a unit volume of material. Experimental studies have shown that this value is practically independent of the speed of the abrasive particles, despite the fact that erosion at supersonic speeds causes local melting of the material and even its sublimation. The energy value depends on the material being eroded, and for steel, the value is about 6.4 times higher than for aluminum [18,19].
The concept of dynamic hardness (e) was introduced as the ratio of the kinetic energy of the eroding particle to the volume of the crater created in the material, and the concept of specific energy of crater formation (e0) was introduced as the ratio of the energy absorbed by the material during the impact of the particle to the volume of the crater measured after aligning the edges of the crater with the sample surface.
The tests showed that the e0 value is a material constant and does not depend on the speed and shape of the eroding particle [18,19]. The eroding particle may bounce off the surface, and then the empirical equation describing this phenomenon takes the form:
where
—restitution coefficient, ;
—particle incidence velocity, m/s
—speed of the reflected particle, m/s
A, B—material constants
It was assumed that the linear elasticity of the material and the occurrence of failure were along the line of maximum shear stress [18]. Beckmann and Gotzmann [20] considered the impact of a spherical particle in their wear model. They assumed that the volume of material removed during erosion was proportional to the work of shear forces performed in the surface layer. The theory is universal and can also be applied to frictional and abrasive wear. Then, the crater depth hp is described by the formula:
where
EI—reduced modulus of elasticity described by the relationship
E1 and E2—Young’s moduli of the disc material and abrasive particles, respectively,
ρ2—abrasive density,
μ1 and μ2—Poisson’s ratios of the disc material and the abrasive, respectively,
H1—hardness of the disc material,
v—particle speed, m/s
α—particle incidence angle.
Based on the original works of J.G. Bitter in the 1960s, two factors affecting the erosion of materials were considered: deformation wear and cutting wear. Deformation wear is caused by the cracking of the material as a result of the accumulation of energy provided by the falling particles. The disadvantage of the model is the need to experimentally determine the energy values needed to remove unit volumes of material by microcutting or deformational wear [21,22].
Neilson and Gilchrist [23] simplified the notation of the relationships resulting from Bitter’s model, assuming that Φ—energy needed to remove a unit mass of eroded material by cutting, ε—energy needed to remove a unit mass of material by deformation wear, then consumption value:
For α ≤ α0
And for α > α0
where
M—total mass of abrasive used in the tests, g
v—particle speed, m/s
vp—the horizontal component of the speed at which the abrasive particle leaves the material, m/s
vp = 0 dla α = α0,
K—the limiting velocity of the particle for which the collision can still be considered elastic, m/s
α—the angle of incidence of the particle; if α < α0, the particle leaves the material after impact.
Hutchings [24] assumed in his model that a material particle is removed after exceeding the critical strain value ef. The erosion intensity predicted by the model was proportional to V3/y3/2e2f, where v is the speed of the abrasive particle and y is the dynamic yield strength. The velocity exponent correlates quite well with the experimental data. The model explains the independence of erosion intensity from heat treatment or crushing. The increase in the dynamic yield strength achieved by these methods is usually combined with a decrease in ef.
Sundararajan and Shewmon [25], in their model, considered abrasive particles falling perpendicularly onto the surface. It was assumed that the material loss is related to exceeding the critical value of deformation ef when creating a metal flake. The deformations caused by subsequent falling particles add up. The model predicts WV erosion intensity:
where
Cp—specific heat, J/kg·K
TM—melting temperature, K
H—static hardness of the material, HV
v—particle velocity, m/s
The model explains the dependence of erosion intensity on the thermophysical properties of the material and its independence from heat treatment and crushing. The power–law exponent of the velocity is close to that observed experimentally.
Finnie [26] developed a model of erosive wear of plastic metals in which he assumed that the micromechanism of erosion is microcutting. The rotation of particles and their reflection from the surface were neglected. The model assumes that the ratio of the velocity components parallel to the surface and perpendicular to the surface of the material remains constant during the interaction of the abrasive particle with the surface. The value of the speed ratio was assumed to be 2, which resulted from the experiment carried out for abrasive wear. Then:
where
ρ—material density, g/cm3
Ψ—a parameter describing the geometry of the microchip
P—horizontal component of stress on the particle’s front surface
M—particle mass, g
V—particle speed, m/s
α—angle of incidence.
The types of ceramic cracking include transverse cracking, radial-central cracking, transgranular cracking, and intergranular cracking, depending on the properties of the disc and the parameters describing the erosion process. Experimental studies have shown that zirconium ceramics with increased fracture resistance absorb the energy of falling particles in plastic processes and show high resistance to erosion. Corundum ceramics with defects were subject to intense wear during erosion due to surface chipping caused by transverse cracks. Transverse cracks occur for hard-eroding particles, while for particles of lower hardness, the process of damage accumulation must occur for transverse cracks to appear [27]. For brittle materials such as glass and corundum, the erosion intensity is determined by the kinetic energy of the particles, the relative hardness, the size of the incident particles, and the fracture resistance of the disc and abrasive particles [27]. The intensity of the erosive wear of brittle materials is described by the formula [28]:
where
D—diameter of the abrasive particle, mm
H—hardness of the disc material, MPs
V—particle velocity, m/s
KIC—cracking resistance of the disc material, MPa·m1/2
Hardness determines the size of the elastic-plastic zone created during particle impact and thus influences the state of residual stresses caused by plastic deformation. KIC characterizes the cracking phenomenon caused by residual tensile stresses in the impact zone. The power law exponent of the velocity for brittle materials depends on the collision conditions for the quasi-static case n = 2.4 [29] and the dynamic case n = 3.2 [30]. The power–law exponent of the particle size is m = ⅔ in both models. The dynamic theory predicts a power–law relationship between erosion intensity and hardness with an exponent of −¼, while the quasi-static theory predicts −½. In the quasi-static model, low particle velocity and quasi-elastic properties of the target material are postulated. Material loss is caused by the intersection of transverse cracks created by adjacent impacts. In the dynamic model, higher particle velocities and elastic-plastic properties are considered [30]. In the work [27], a dependence of the power–law exponent of the speed on the hardness and fracture resistance of the eroding particles was found for glass, which was the lowest for diamond 2 and the highest for SiO2—2.7. The value of the particle size exponent was 4. For corundum, it was found that the velocity exponent was 5 for SiO2 and 2.3 for diamond. Deviations of the speed exponent from 2 were explained by the crumbling of the abrasive during impact and the penetration of fragments of abrasive grains into the disc.
The distribution of cracks and their symmetry depend on the shape of the contact zone between the incident particle and the target material [31]. Transverse cracks usually form on previously formed radial or conical cracks after the penetration phase. The radial crack size mainly depends on the fracture toughness of the disc and the velocity of the eroding particle, while the depth of transverse cracks mainly depends on the hardness of the disc and the particle speed, diameter, and density.
4. Results and Discussion
Table 4 shows the markings of the samples depending on the type of powder with which the coating was sprayed. The distances of the gun from the surface were determined during preliminary tests. The distance values have been optimally adjusted to the properties of the AZ31 material. The flame energy at a distance of 320 mm allows for low coating porosity without changing the base material. However, at distances greater than 400 mm, the coatings applied were characterized by lower adhesion to the surface and higher porosity due to the lower flame energy reaching the surface. At distances smaller than 320 mm, unfavorable phase transformations occurred in the structure of the base material. All coatings were sprayed to a thickness of approximately 250 µm (the number of passes was the same for each sample). Coatings with a porosity of approximately 2% were obtained. The surface of the obtained coatings is rather smooth; in some places, minor defects and irregularities could be observed. Sometimes, craters occur, which increase the surface roughness. However, in the case of all produced coatings, their topography is typical of coatings sprayed using the HVOF method [32].

Table 4.
The sample code.
The microhardness of the sprayed coatings was measured using a Vickers hardness tester according to the EN ISO 4516 standard [33] using an HV1000 hardness tester (Zhongyuan Innovation Metrology Technology Co., Ltd., Dongguan, China) under a load of 2.94 N (HV0.3). At least 10 indentations were left on the coating cross-section of each sample. Then, calculate the mean and standard deviation. Measurements of the roughness of sprayed coatings were carried out with a MarSurf PS 10 profilometer in accordance with the ISO 4288 standard [34], with Gaussian filters (ISO 16610-21 [35]). The results are presented in Table 5.

Table 5.
Microhardness and roughness of coatings.
Erosion resistance tests at room temperature were carried out on a test stand designed at the Department of Welding of the Silesian University of Technology in Gliwice in accordance with the ASTM G76-04 standard [36]. This study used Al2O3 abrasive with a particle size of 50 µm. The inclination angles of the nozzle relative to the sample were 30°, 60°, and 90°, respectively. The test duration was 10 min, and all tests were performed in the post-spray condition. To obtain reliable results, 10 tests were performed with the given parameters. According to the ASTM G76-04 standard, the erosion rate and erosion value were calculated. The erosion rate, mg/min, was calculated according to the formula (AER):
where
—mass loss, g
—test time, min.
The average erosion value, mm3/g, was determined using the formula (AEV):
where
—volume loss, mm3
—total mass of abrasive particle, g
The calculation results are presented in Table 6. Erosion rate for individual samples with cermet coatings and a reference sample made of the AZ31 substrate material (a) and the average erosion value of relevant samples (b).

Table 6.
Erosion rate for individual samples with cermet coatings and a reference sample made of the AZ31 substrate material (a) and the average erosion value of relevant samples (b).
In Figure 2, there are presented calculated energies for single particles (Figure 2a) and for whole coatings (Figure 2b).
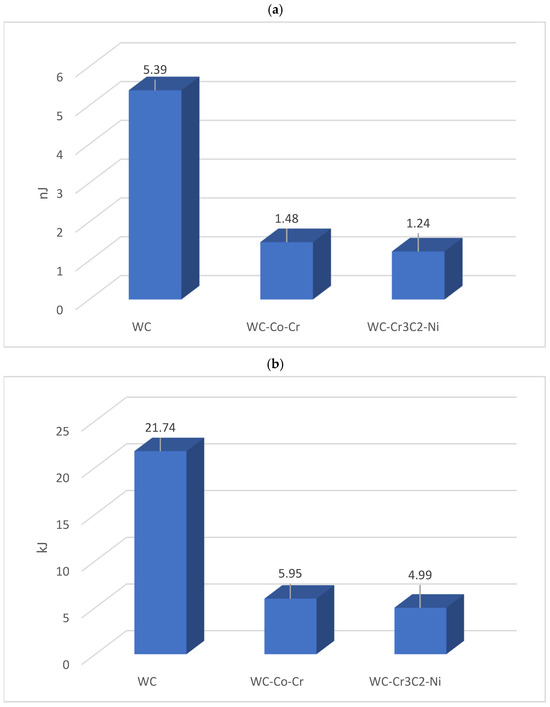
Figure 2.
Kinetic energy of (a) a single particle of commercial cermet powders and (b) the entire applied coating.
The mathematical model of coating formation using the HVOF method should include equations for heat transfer taking place inside the JP 5000 TAFA gun, taking into account detailed technical data related to both the geometry and the pressure in the combustion chamber, fuel, oxygen, nitrogen, and coolant flow rates. Moreover, the temperature of the particles is important, as it has a significant impact not only on their internal energy but also on the type and strength of their interaction with the surface on which they fall. Therefore, the article focuses on determining the kinetic energy of a single particle based on the material density of a single spherical grain of the deposited coatings. The calculation results are presented in the graph in Figure 2a.
Moreover, based on the measurements of the sample mass before and after applying the coating, the mass of individual coatings was calculated, which allowed for the calculation of the total kinetic energy of the particles forming the coating (Figure 2b). In the case of a sintered carbide coating, much higher kinetic energy is observed, both for a single particle and for the energy necessary to produce the entire coating.
Analyzing the images obtained using a scanning microscope (Figure 3), it is clearly visible that the higher kinetic energy of the WC–Co coating particles (C1-320) compared to C1-400 resulted in the deposition of a larger number of carbides in the matrix. At the same time, lower porosity is observed, which is confirmed by the results of the microhardness measurement (Table 4). It should be emphasized that a larger number of hard carbides in the matrix results in a higher roughness parameter of the analyzed coating (Table 4).

Figure 3.
The microstructure of the cross-section for selected deposited coatings, SEM.
The microstructure of the WC–Co–Cr (C2-320) coating shows WC particles embedded in the Co–Cr matrix, which constitutes the binder phase. Unmelted carbide particles embedded in the matrix are also visible, as are inclusions and cracks, which also negatively affect the microhardness of the coating (Table 4). In the case of this coating, the roughness parameter Ra is also higher in the case of a smaller distance of the burner from the sample surface, which confirms the fact that a larger number of hard carbide particles causes an increase in surface roughness (Table 4).
The kinetic energy of the erodent is 15 mJ acting on a unit of surface in one second, so during the test, the kinetic energy of corundum particles (9th degree of hardness on the Mohr scale—right after diamond) acts on the surface. Additionally, if the exposure to the erodent lasted for an hour, the kinetic energy of particles with a constant flow of only 2 g/min of corundum would already be 54 kJ (Figure 4).
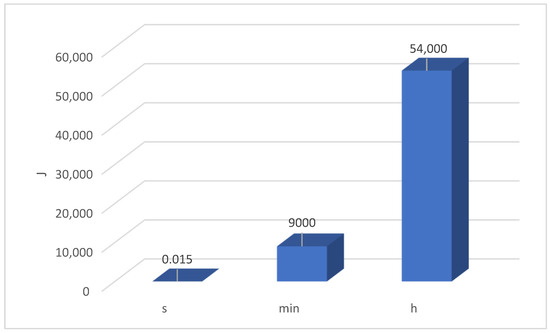
Figure 4.
The kinetic energy of corundum with a flow of 2 g/min in a second, minute, and hour.
5. Conclusions
Erosability results, as well as surface morphology and analysis, indicate a negligible impact of the surface roughness of sprayed coatings on the erosion rate. On the other hand, research confirms that the hardness and uniformity of coatings have a decisive impact on the erosion resistance of coatings. The shorter spray distance of 320 mm reduces porosity and increases the hardness of each coating. The combination of hardness and erosion results confirms that coatings sprayed at 320 mm are harder and show less material loss than those sprayed at 400 mm.
The brittleness results from the mixed nature of the cermet, consisting of a metallic binder and WC ceramics. In summary, the mechanism of particle erosion in cermet coatings is based on microcutting and grooving of the metal matrix, carbide separation, and brittle fracture. Compared to coatings sprayed from a spray distance of 320 mm, much more severe deterioration was observed for coatings sprayed from a longer distance (400 mm), which resulted in lower hardness and uniformity for cermet sprayed from a distance of 400 mm. A higher spray distance value results in a less compact structure and reduced coating consistency.
Tests have shown that the best resistance to the harmful effects of erodent in the form of very hard corundum particles is demonstrated by the WC–Co–Cr coating at an application distance of 320 mm. Consequently, the energy of the sprayed particles during HVOF treatment is not the decisive factor that would determine the erosion resistance of the formed coating.
Author Contributions
Conceptualization, O.O., E.J., E.K., L.Ł. and A.Ś.; methodology, O.O., E.J., E.K., L.Ł. and A.Ś.; software, O.O., E.J., E.K., L.Ł. and A.Ś.; validation, O.O., E.J., E.K., L.Ł. and A.Ś.; formal analysis, O.O., E.J., E.K., L.Ł. and A.Ś.; investigation, O.O., E.J., E.K., L.Ł. and A.Ś.; data curation, O.O., E.J., E.K., L.Ł. and A.Ś.; writing—original draft preparation, O.O., E.J., E.K., L.Ł. and A.Ś.; writing—review and editing, O.O., E.J., E.K., L.Ł. and A.Ś.; visualization, O.O., E.J., E.K., L.Ł. and A.Ś.; supervision, O.O., E.J., E.K., L.Ł. and A.Ś.; funding acquisition, O.O. and A.Ś. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed by the Bialystok University of Technology under the project WZ/WIZ-INZ/4/2022 (Olga Orynycz); research was conducted in part at the Lublin University of Technology in 2023 (Antoni Świć).
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Roy, S.; Rautela, R.; Kumar, S. Towards a Sustainable Future: Nexus between the Sustainable Development Goals and Waste Management in the Built Environment. J. Clean. Prod. 2023, 415, 137865. [Google Scholar] [CrossRef]
- Agarwal, A.; Ojha, R. Prioritizing Implications of Industry-4.0 on the Sustainable Development Goals: A Perspective from the Analytic Hierarchy Process in Manufacturing Operations. J. Clean. Prod. 2024, 444, 141189. [Google Scholar] [CrossRef]
- Matikainen, V.; Koivuluoto, H.; Vuoristo, P. A study of Cr3C2-based HVOF- and HVAF-sprayed coatings: Abrasion, dry particle erosion and cavitation erosion resistance. Wear 2020, 446–447, 203188. [Google Scholar] [CrossRef]
- Espallargas, N. Introduction to Thermal Spray Coatings. In Future Development of Thermal Spray Coatings; Elsevier: Amsterdam, The Netherlands, 2015; pp. 1–13. ISBN 978-0-85709-769-9. [Google Scholar]
- Pawlowski, L. The Science and Engineering of Thermal Spray Coatings; J. Wiley and Sons: Chichester, UK, 2008; ISBN 978-0-471-49049-4. [Google Scholar]
- Mordike, B.L.; Ebert, T. Magnesium Properties—Applications—Potential. Mater. Sci. Eng. A 2001, 302, 37–45. [Google Scholar] [CrossRef]
- Song, G.-L.; Xu, Z. The Surface, Microstructure and Corrosion of Magnesium Alloy AZ31 Sheet. Electrochim. Acta 2010, 55, 4148–4161. [Google Scholar] [CrossRef]
- Szymański, K.; Hernas, A.; Moskal, G.; Myalska, H. Thermally Sprayed Coatings Resistant to Erosion and Corrosion for Power Plant Boilers—A Review. Surf. Coat. Technol. 2015, 268, 153–164. [Google Scholar] [CrossRef]
- Lugscheider, E.; Parco, M.; Kainer, K.U.; Hort, N. Thermal Spraying of Magnesium Alloys for Corrosion and Wear Protection. In Magnesium; Kainer, K.U., Ed.; Wiley: Hoboken, NJ, USA, 2003; pp. 860–868. ISBN 978-3-527-30975-7. [Google Scholar]
- Yang, Z.; Li, J.; Zhang, J.; Lorimer, G.; Robson, J. Review on Research and Development of Magnesium Alloys. Acta Metall. Sin. (Engl. Lett.) 2008, 21, 313–328. [Google Scholar] [CrossRef]
- Matikainen, V.; Rubio Peregrina, S.; Ojala, N.; Koivuluoto, H.; Schubert, J.; Houdková, Š.; Vuoristo, P. Erosion wear performance of WC-10Co4Cr and Cr3C2-25NiCr coatings sprayed with high-velocity thermal spray processes. Surf. Coat. Technol. 2019, 370, 196–212. [Google Scholar] [CrossRef]
- Naik, G.M.; Sharma, P.; Anne, G.; Pittala, R.K.; Kumar, R.; Satapathi, G.S.; Kumar, C.S.; Fernandes, F. Improvement in Corrosion Performance of ECAPed AZ80/91 Mg Alloys Using SS316 HVOF Coating. Materials 2023, 16, 6651. [Google Scholar] [CrossRef] [PubMed]
- Lakkannavar, V.; Yogesha, K.B.; Prasad, C.D.; Mruthunjaya, M.; Suresh, R. A Review on Tribological and Corrosion Behaviour of Thermal Spray Coatings. J. Inst. Eng. India Ser. D 2024. [Google Scholar] [CrossRef]
- Yu, J.; Liu, X.; Yu, Y.; Li, H.; Liu, P.; Huang, K.; Sun, R. Research and Application of High-Velocity Oxygen Fuel Coatings. Coatings 2022, 12, 828. [Google Scholar] [CrossRef]
- Górnik, M.; Jonda, E.; Łatka, L.; Nowakowska, M.; Godzierz, M. Influence of Spray Distance on Mechanical and Tribological Properties of HVOF Sprayed WC-Co-Cr Coatings. Mater. Sci.-Pol. 2021, 39, 545–554. [Google Scholar] [CrossRef]
- Fauchais, P.L.; Heberlein, J.V.R.; Boulos, M.I. Thermal Spray; Springer: Boston, MA, USA, 2014; ISBN 978-0-387-28319-7. [Google Scholar]
- Oksa, M.; Turunen, E.; Suhonen, T.; Varis, T.; Hannula, S.-P. Optimization and Characterization of High Velocity Oxy-Fuel Sprayed Coatings: Techniques, Materials, and Applications. Coatings 2011, 1, 17–52. [Google Scholar] [CrossRef]
- Kleis, I.; Kulu, P. Solid Particle Erosion; Springer: London, UK, 2008; ISBN 978-1-84800-028-5. [Google Scholar]
- Ruff, A.W.; Ives, L.K. Measurement of Solid Particle Velocity in Erosive Wear. Wear 1975, 35, 195–199. [Google Scholar] [CrossRef]
- Beckmann, G.; Gotzmann, J. Analytical Model of the Blast Wear Intensity of Metals Based on a General Arrangement for Abrasive Wear. Wear 1981, 73, 325–353. [Google Scholar] [CrossRef]
- Oka, Y.I.; Okamura, K.; Yoshida, T. Practical Estimation of Erosion Damage Caused by Solid Particle Impact. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Parsi, M.; Najmi, K.; Najafifard, F.; Hassani, S.; McLaury, B.S.; Shirazi, S.A. A Comprehensive Review of Solid Particle Erosion Modeling for Oil and Gas Wells and Pipelines Applications. J. Nat. Gas Sci. Eng. 2014, 21, 850–873. [Google Scholar] [CrossRef]
- Arabnejad, H.; Mansouri, A.; Shirazi, S.A.; McLaury, B.S. Development of mechanistic erosion equation for solid particles. Wear 2015, 332–333, 1044–1050. [Google Scholar] [CrossRef]
- Hutchings, I.M. A Model for the Erosion of Metals by Spherical Particles at Normal Incidence. Wear 1981, 70, 269–281. [Google Scholar] [CrossRef]
- Sundararajan, G.; Shewmon, P.G. A New Model for the Erosion of Metals at Normal Incidence. Wear 1983, 84, 237–258. [Google Scholar] [CrossRef]
- Finnie, I.; Stevick, G.R.; Ridgely, J.R. The Influence of Impingement Angle on the Erosion of Ductile Metals by Angular Abrasive Particles. Wear 1992, 152, 91–98. [Google Scholar] [CrossRef]
- Feng, Z.; Ball, A. The Erosion of Four Materials Using Seven Erodents—Towards an Understanding. Wear 1999, 233–235, 674–684. [Google Scholar] [CrossRef]
- Srinivasan, S.; Scattergood, R.O. Erosion of Mg-PSZ by Solid Particle Impact. Adv. Ceram. Mater. 1988, 3, 345–352. [Google Scholar] [CrossRef]
- Evans, A.G.; Wilshaw, T.R. Quasi-Static Solid Particle Damage in Brittle Solids—I. Observations Analysis and Implications. Acta Metall. 1976, 24, 939–956. [Google Scholar] [CrossRef]
- Evans, A.G.; Gulden, M.E.; Rosenblatt, M. Impact Damage in Brittle Materials in the Elastic-Plastic Response Régime. Proc. R. Soc. Lond. A 1978, 361, 343–365. [Google Scholar] [CrossRef]
- Wiederhorn, S.M.; Lawn, B.R. Strength Degradation of Glass Impacted with Sharp Particles: I, Annealed Surfaces. J. Am. Ceram. Soc. 1979, 62, 66–70. [Google Scholar] [CrossRef]
- Jonda, E.; Łatka, L.; Tomiczek, A.; Godzierz, M.; Pakieła, W.; Nuckowski, P. Microstructure Investigation of WC-Based Coatings Prepared by HVOF onto AZ31 Substrate. Materials 2021, 15, 40. [Google Scholar] [CrossRef]
- ISO 4516:2002; Metallic and Other Inorganic Coatings, Vickers and Knoop Microhardness Tests. International Organization for Standardization: Geneva, Switzerland, 2002.
- ISO 4288:1996; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Rules and Procedures for the Assessment of Surface Texture. International Organization for Standardization: Geneva, Switzerland, 1996.
- ISO 16610-21:2011; Geometrical Product Specifications (GPS)—Filtration—Part 21: Linear Profile Filters: Gaussian Filters. International Organization for Standardization: Geneva, Switzerland, 2011.
- ASTM G76-04; Standard Test Method for Conducting Erosion Tests by Solid Particle Impingement Using Gas Jets. ASTM International: West Conshohocken, PA, USA, 2004.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).