Disturbance Observer-Based Feedback Linearized Controller for Grid-Forming Four-Leg VSI Supplying Unbalanced and Nonlinear Loads
Abstract
1. Introduction
- A novel control design for the grid-forming voltage control of four-leg VSIs is proposed. The design integrates a principal controller whose design is based on the feedback linearization (FL) method and a DO that is capable of compensating for multiple types of disturbances that include both non-oscillatory and oscillatory disturbances. This control is designed with the aim to equip the grid forming VSIs to reject the oscillating disturbances induced by imperfect loads and, thereby, achieves precise tracking performance by generating a balanced and smooth sinusoidal three-phase voltage, aligning with the standards set by IEEE [3,4];
- Secondly, it is worth noting that limited studies have explored the applicability of FL control for grid-forming applications that specifically address the challenges posed by unbalanced and nonlinear loads. Previous FL-based voltage controllers for VSIs, such as those presented in references [37,39], have not conducted detailed investigations into compensating for unbalanced loads. Furthermore, these controllers lack the capability to address disturbances originating from distorted loads and load disturbances. Therefore, the proposed controller integrates a DO into the principal FL controller that specifically targets the oscillatory disturbances;
- Thirdly, the existing FL-based grid-forming voltage controllers [38,39,40] employ the typical control scheme for voltage control which is the cascaded control structure with a nested current control loop. In contrast, the proposed FL controller deviates from the conventional cascaded approach by introducing a direct voltage control scheme. Furthermore, the proposed controller adopts the natural reference frame without employing any transformation frame.
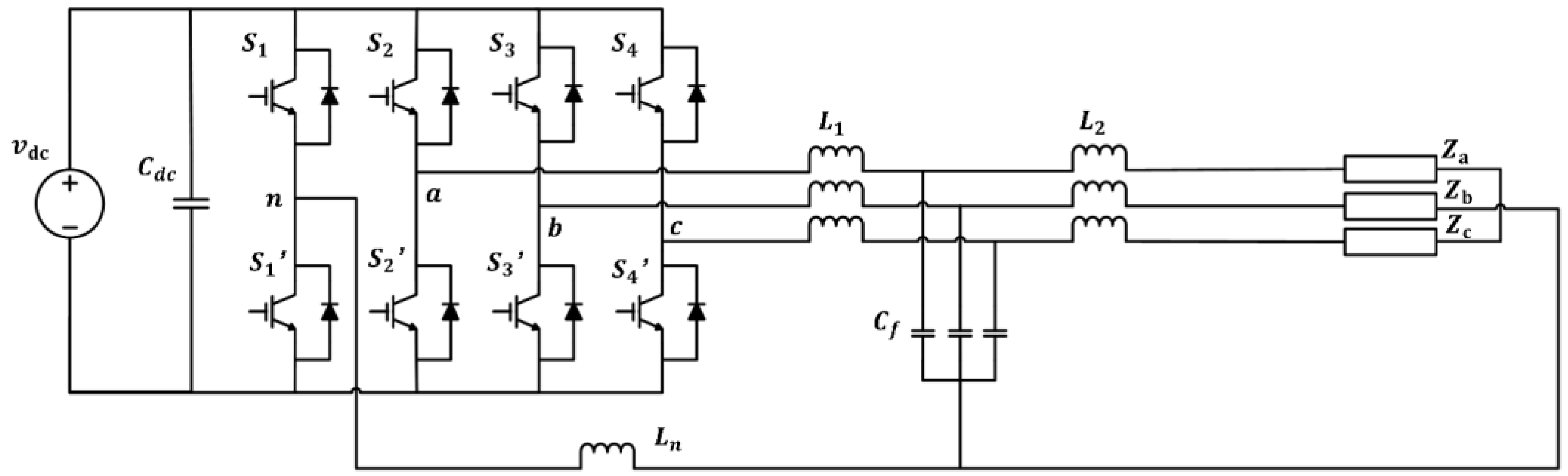
2. System Modelling
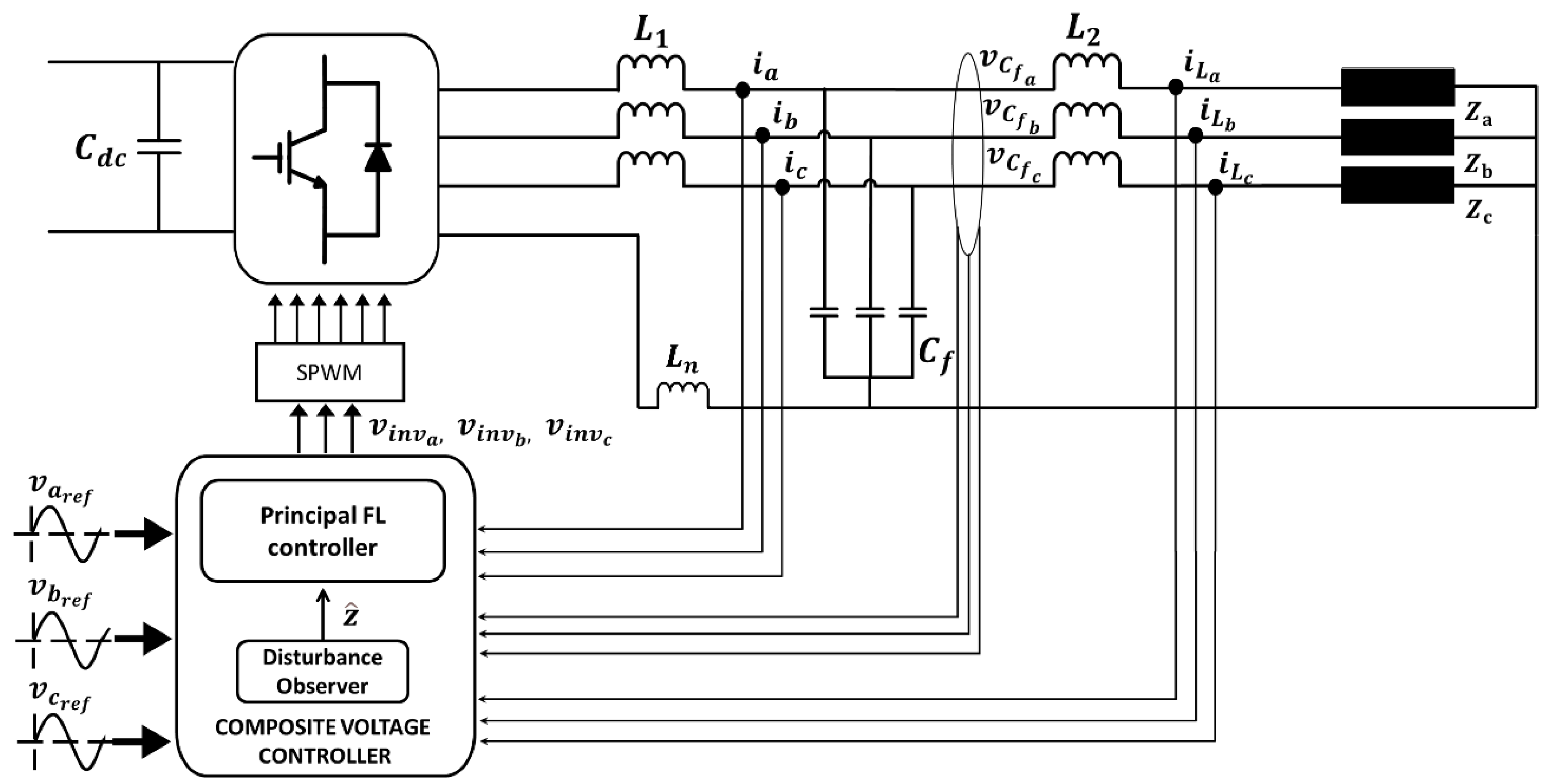
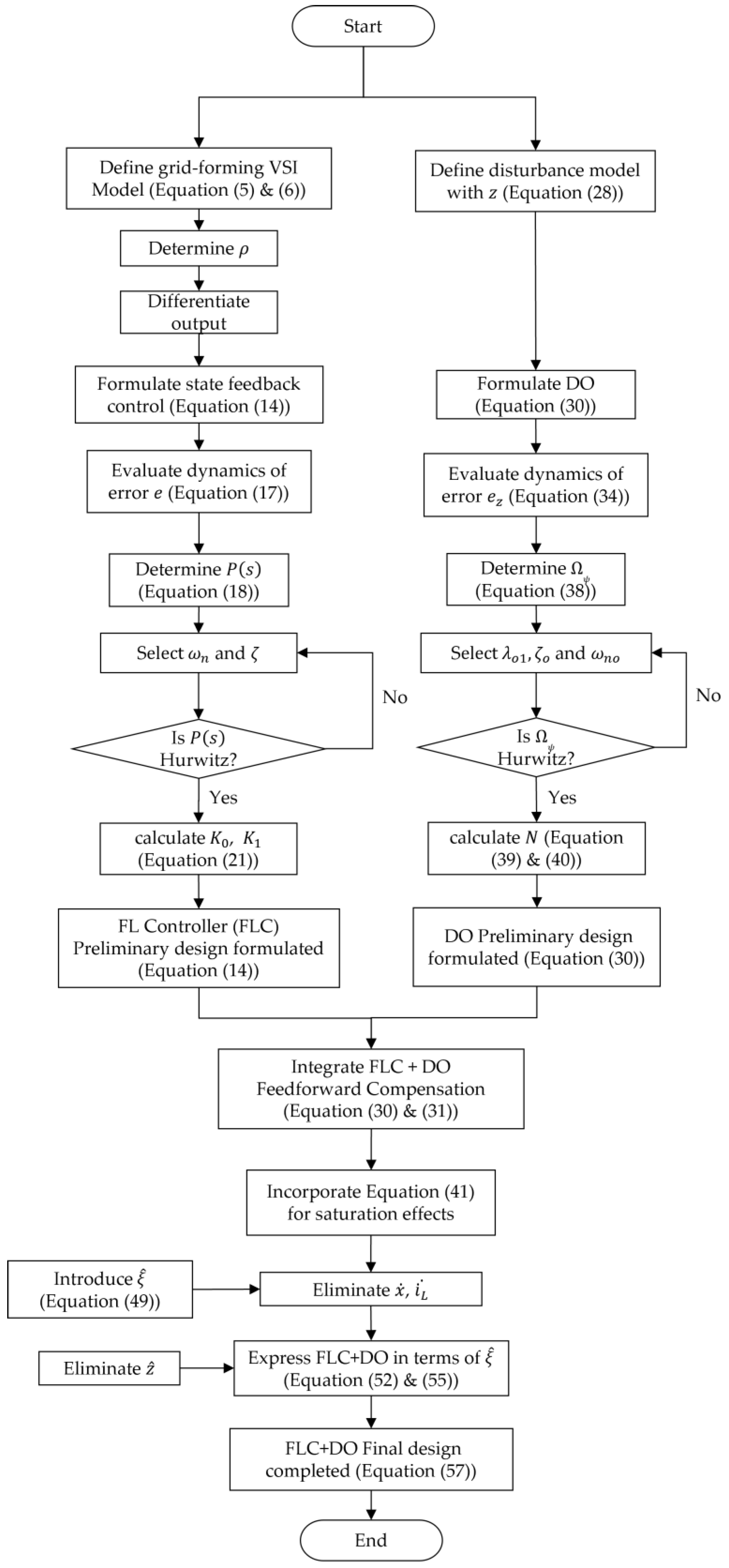
3. Control Design
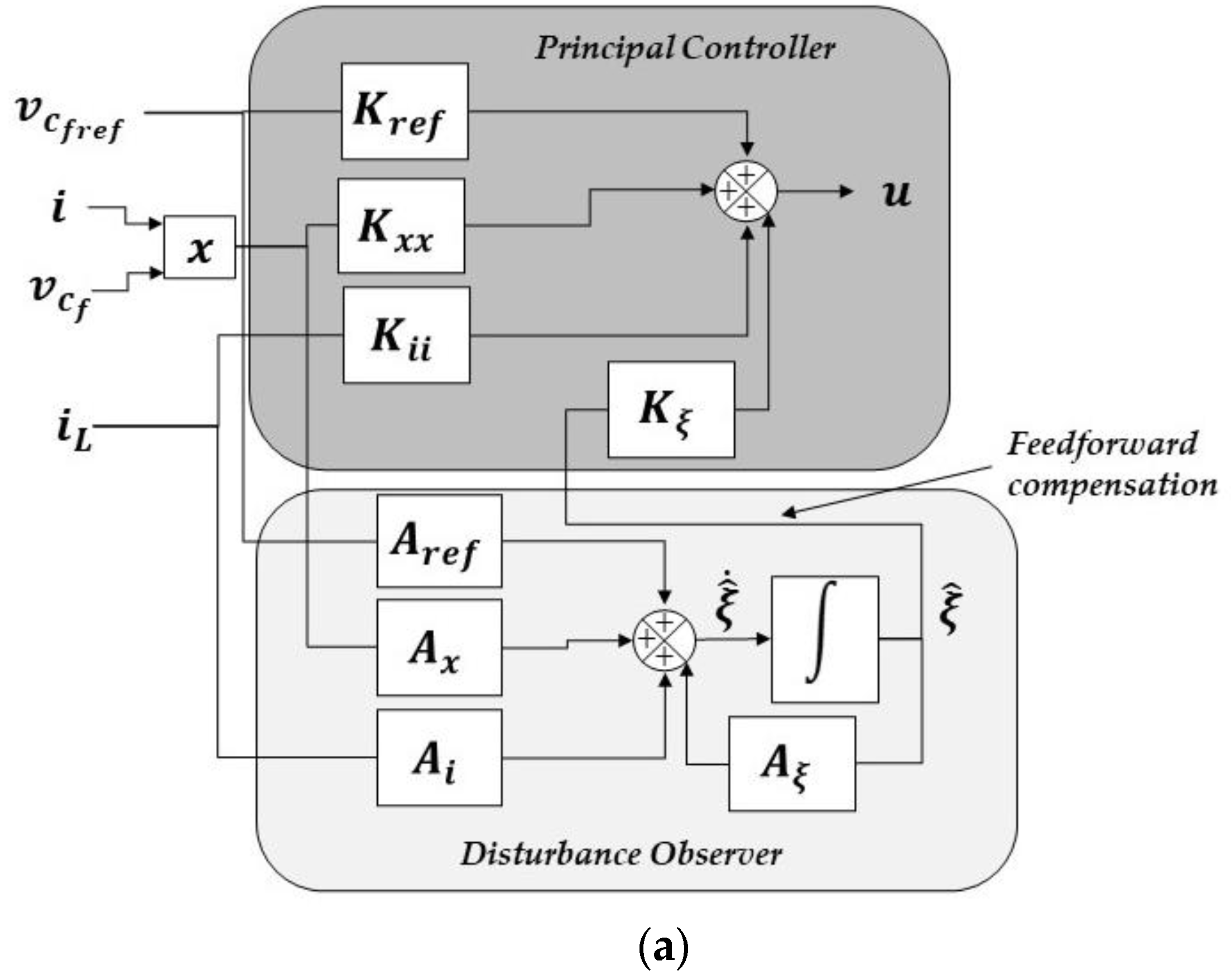
3.1. Design of Principal Controller
3.2. Stability Criterion for Principal Controller
3.3. Design of Disturbance Observer
3.4. Stability Criterion for Disturbance Observer
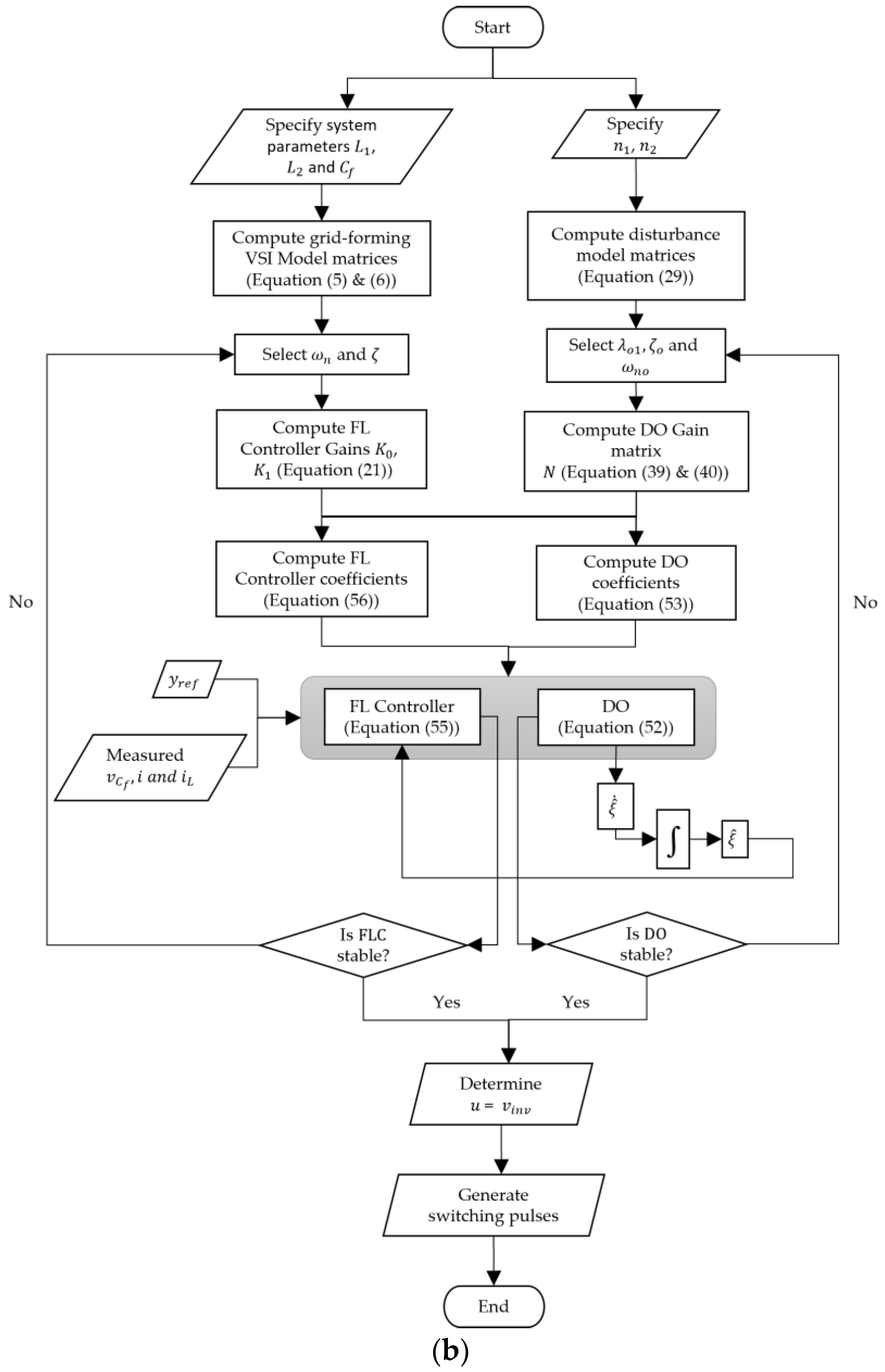
3.5. Disturbance Observer-Based Control for Real-Time Implementation
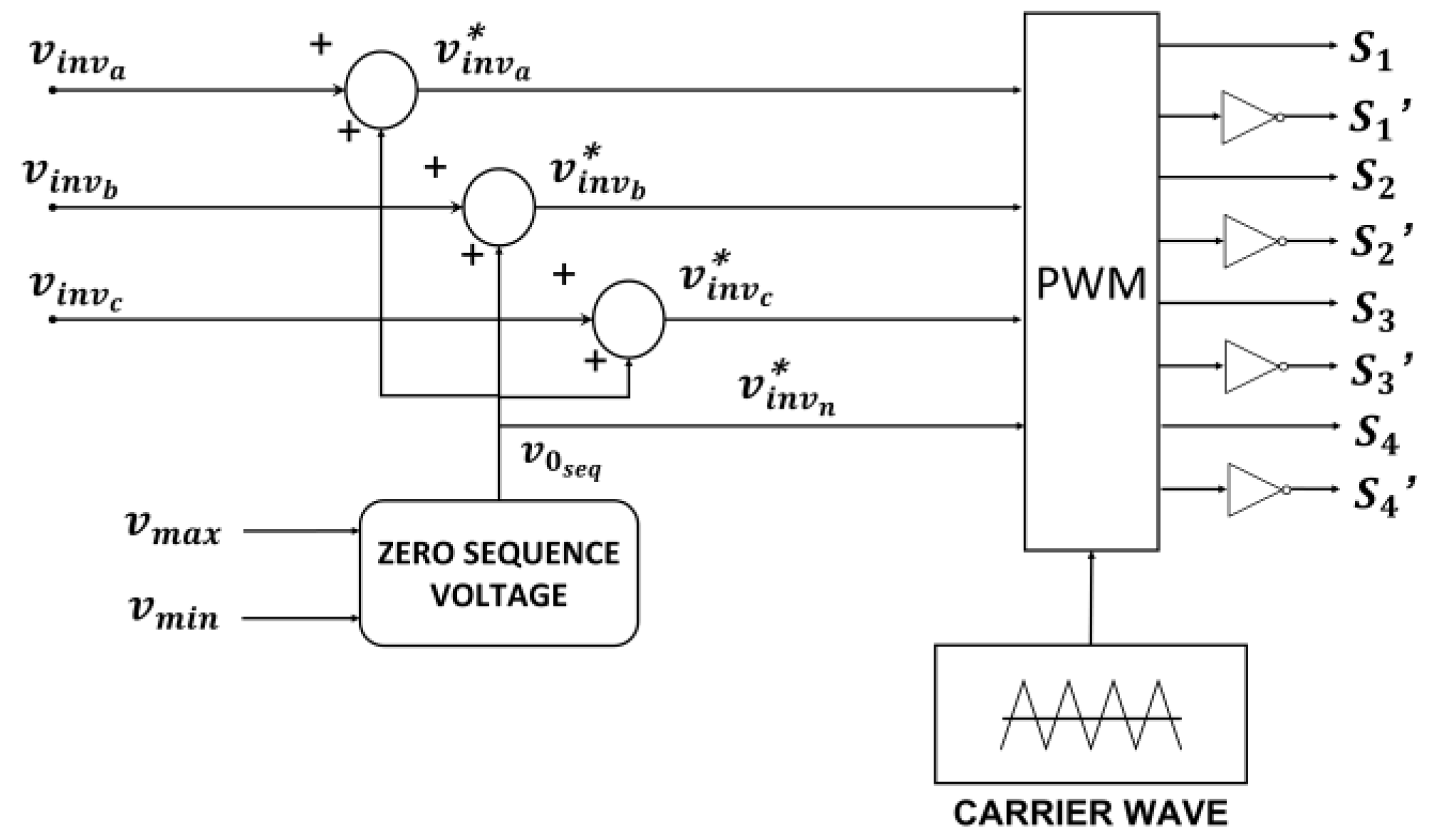
4. PWM Scheme
5. Performance Testing and Assessment
5.1. Simulation
5.2. Experimental Testing
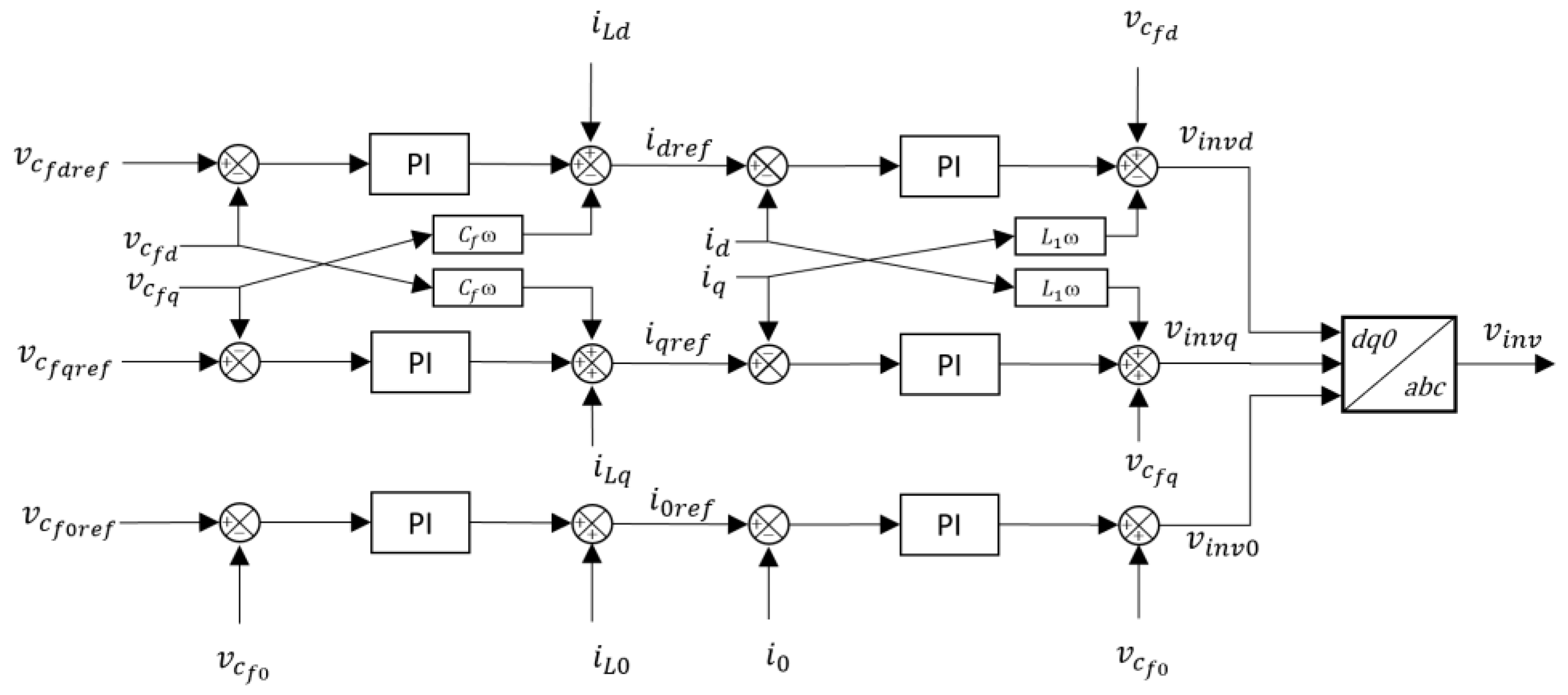
5.3. Performance Comparison
5.4. Performance Metrics
6. Results and Discussion
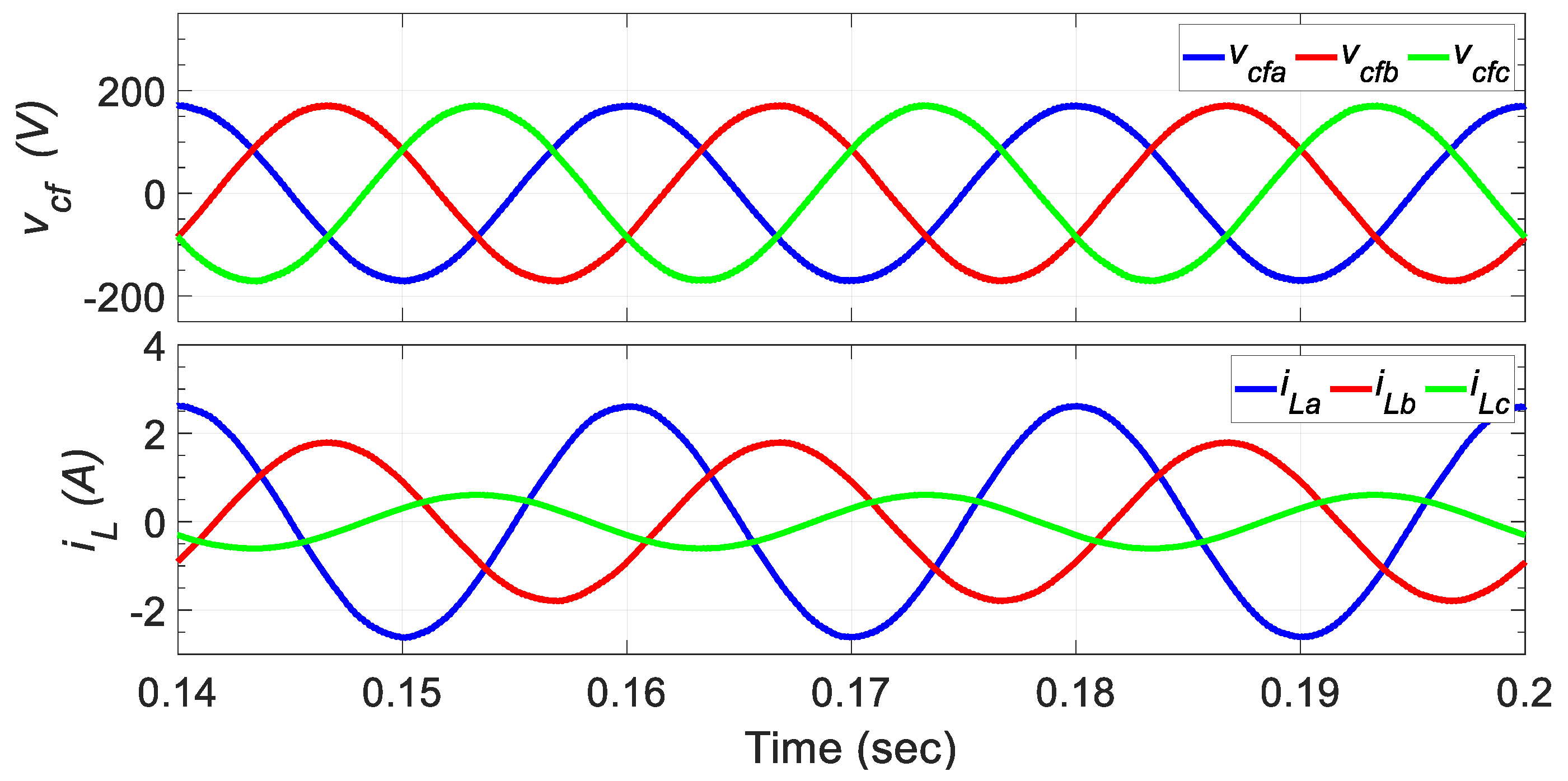
6.1. Simulation Results
6.1.1. Unbalanced Linear Loads
6.1.2. Nonlinear Loads
6.1.3. Transient Performance
6.2. Experimental Results
6.2.1. Unbalanced Linear Loads
6.2.2. Nonlinear Loads
6.2.3. Transient Performance
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Q.; Tao, Y.; Liu, X.; Deng, Y.; He, X. Voltage Unbalance and Harmonics Compensation for Islanded Microgrid Inverters. IET Power Electron. 2014, 7, 1055–1063. [Google Scholar] [CrossRef]
- Rafi, F.H.M.; Hossain, M.J.; Rahman, M.S.; Taghizadeh, S. An Overview of Unbalance Compensation Techniques Using Power Electronic Converters for Active Distribution Systems with Renewable Generation. Renew. Sustain. Energy Rev. 2020, 125, 109812. [Google Scholar] [CrossRef]
- IEEE Std 519-2022; IEEE Standard for Harmonic Control in Electric Power Systems. Revision of IEEE Std 519-2014; IEEE: Piscataway, NJ, USA, 2022; pp. 1–31.
- IEEE Std 1159-2019; IEEE Recommended Practice for Monitoring Electric Power Quality. Revision of IEEE Std 1159-2009; IEEE: Piscataway, NJ, USA, 2019; pp. 1–98.
- Rojas, F.; Cárdenas, R.; Burgos-Mellado, C.; Espina, E.; Pereda, J.; Pineda, C.; Arancibia, D.; Díaz, M. An Overview of Four-Leg Converters: Topologies, Modulations, Control and Applications. IEEE Access 2022, 10, 61277–61325. [Google Scholar] [CrossRef]
- Vechiu, I.; Camblong, H.; Tapia, G.; Dakyo, B.; Curea, O. Control of Four Leg Inverter for Hybrid Power System Applications with Unbalanced Load. Energy Convers. Manag. 2007, 48, 2119–2128. [Google Scholar] [CrossRef]
- Sinsukthavorn, W.; Ortjohann, E.; Mohd, A.; Hamsic, N.; Morton, D. Control Strategy for Three-/Four-Wire-Inverter-Based Distributed Generation. IEEE Trans. Ind. Electron. 2012, 59, 3890–3899. [Google Scholar] [CrossRef]
- Vechiu, I.; Curea, O.; Camblong, H. Transient Operation of a Four-Leg Inverter for Autonomous Applications with Unbalanced Load. IEEE Trans. Power Electron. 2010, 25, 399–407. [Google Scholar] [CrossRef]
- Hadidian Moghaddam, M.J.; Kalam, A.; Miveh, M.R.; Naderipour, A.; Gandoman, F.H.; Ghadimi, A.A.; Abdul-Malek, Z. Improved Voltage Unbalance and Harmonics Compensation Control Strategy for an Isolated Microgrid. Energies 2018, 11, 2688. [Google Scholar] [CrossRef]
- Pereira, L.F.A.; Flores, J.V.; Bonan, G.; Coutinho, D.F.; da Silva, J.M.G. Multiple Resonant Controllers for Uninterruptible Power Supplies—A Systematic Robust Control Design Approach. IEEE Trans. Ind. Electron. 2014, 61, 1528–1538. [Google Scholar] [CrossRef]
- Hasanzadeh, A.; Edrington, C.S.; Mokhtari, H.; Maghsoudlou, B.; Fleming, F. Multi-Loop Linear Resonant Voltage Source Inverter Controller Design for Distorted Loads Using the Linear Quadratic Regulator Method. IET Power Electron. 2012, 5, 841–851. [Google Scholar] [CrossRef]
- Loh, P.C.; Newman, M.J.; Zmood, D.N.; Holmes, D.G. A Comparative Analysis of Multiloop Voltage Regulation Strategies for Single and Three-Phase UPS Systems. IEEE Trans. Power Electron. 2003, 18, 1176–1185. [Google Scholar]
- Demirkutlu, E.; Hava, A.M. A Scalar Resonant-Filter-Bank-Based Output-Voltage Control Method and a Scalar Minimum-Switching-Loss Discontinuous PWM Method for the Four-Leg-Inverter-Based Three-Phase Four-Wire Power Supply. IEEE Trans. Ind. Appl. 2009, 45, 982–991. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zhao, Y. A Unified Control Strategy for Three-Phase Inverter in Distributed Generation. IEEE Trans Power Electron 2014, 29, 1176–1191. [Google Scholar] [CrossRef]
- Shahparasti, M.; Mohamadian, M.; Yazdian, A.; Ahmad, A.A.; Amini, M. Derivation of a Stationary-Frame Single-Loop Controller for Three-Phase Standalone Inverter Supplying Nonlinear Loads. IEEE Trans. Power Electron. 2014, 29, 5063–5071. [Google Scholar] [CrossRef]
- Cárdenas, R.; Juri, C.; Peña, R.; Wheeler, P.; Clare, J. The Application of Resonant Controllers to Four-Leg Matrix Converters Feeding Unbalanced or Nonlinear Loads. IEEE Trans. Power Electron. 2012, 27, 1120–1129. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, D.M.; Loh, P.C. Microgrid Power Quality Enhancement Using a Three-Phase Four-Wire Grid-Interfacing Compensator. IEEE Trans. Ind. Appl. 2005, 41, 1707–1719. [Google Scholar] [CrossRef]
- Etxeberria-Otadui, I.; Viscarret, U.; Caballero, M.; Rufer, A.; Bacha, S. New Optimized PWM VSC Control Structures and Strategies Under Unbalanced Voltage Transients. IEEE Trans. Ind. Electron. 2007, 54, 2902–2914. [Google Scholar] [CrossRef]
- Svensson, J.; Bongiorno, M.; Sannino, A. Practical Implementation of Delayed Signal Cancellation Method for Phase-Sequence Separation. IEEE Trans. Power Deliv. 2007, 22, 18–26. [Google Scholar] [CrossRef]
- Alepuz, S.; Busquets-Monge, S.; Bordonau, J.; Martinez-Velasco, J.A.; Silva, C.A.; Pontt, J.; Rodriguez, J. Control Strategies Based on Symmetrical Components for Grid-Connected Converters Under Voltage Dips. IEEE Trans. Ind. Electron. 2009, 56, 2162–2173. [Google Scholar] [CrossRef]
- Rao, U.K.; Mishra, M.K.; Ghosh, A. Control Strategies for Load Compensation Using Instantaneous Symmetrical Component Theory Under Different Supply Voltages. IEEE Trans. Power Deliv. 2008, 23, 2310–2317. [Google Scholar] [CrossRef]
- Cárdenas, R.; Peña, R.; Wheeler, P.; Clare, J.; Juri, C. Control of a Matrix Converter for the Operation of Autonomous Systems. Renew Energy 2012, 43, 343–353. [Google Scholar] [CrossRef]
- Fortescue, C.L. Method of Symmetrical Co-Ordinates Applied to the Solution of Polyphase Networks. In Proceedings of the Transactions of the American Institute of Electrical Engineers, Atlantic City, NJ, USA, 28 June 1918; Volume XXXVII, pp. 1027–1140. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Komurcugil, H. Rotating-Sliding-Line-Based Sliding-Mode Control for Single-Phase UPS Inverters. IEEE Trans. Ind. Electron. 2012, 59, 3719–3726. [Google Scholar] [CrossRef]
- Kukrer, O.; Komurcugil, H.; Doganalp, A. A Three-Level Hysteresis Function Approach to the Sliding-Mode Control of Single-Phase UPS Inverters. IEEE Trans. Ind. Electron. 2009, 56, 3477–3486. [Google Scholar] [CrossRef]
- Tai, T.-L.; Chen, J.-S. UPS Inverter Design Using Discrete-Time Sliding-Mode Control Scheme. IEEE Trans. Ind. Electron. 2002, 49, 67–75. [Google Scholar]
- Jung, S.-L.; Tzou, Y.-Y. Discrete Sliding-Mode Control of a PWM Inverter for Sinusoidal Output Waveform Synthesis with Optimal Sliding Curve. IEEE Trans. Power Electron. 1996, 11, 567–577. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Guzman, R.; de Vicuna, L.G.; Camacho, A.; Miret, J.; Rey, J.M. Receding-Horizon Model-Predictive Control for a Three-Phase VSI With an LCL Filter. IEEE Trans. Ind. Electron. 2019, 66, 6671–6680. [Google Scholar] [CrossRef]
- Nauman, M.; Hasan, A. Efficient Implicit Model-Predictive Control of a Three-Phase Inverter With an Output LC Filter. IEEE Trans. Power Electron. 2016, 31, 6075–6078. [Google Scholar] [CrossRef]
- Cortes, P.; Ortiz, G.; Yuz, J.I.; Rodriguez, J.; Vazquez, S.; Franquelo, L.G. Model Predictive Control of an Inverter with Output LC Filter for UPS Applications. IEEE Trans. Ind. Electron. 2009, 56, 1875–1883. [Google Scholar] [CrossRef]
- Lidozzi, A.; Ji, C.; Solero, L.; Zanchetta, P.; Crescimbini, F. Resonant–Repetitive Combined Control for Stand-Alone Power Supply Units. IEEE Trans. Ind. Appl. 2015, 51, 4653–4663. [Google Scholar] [CrossRef]
- Marati, N.; Prasad, D. A Modified Feedback Scheme Suitable for Repetitive Control of Inverter With Nonlinear Load. IEEE Trans. Power Electron. 2018, 33, 2588–2600. [Google Scholar] [CrossRef]
- Ramos, G.A.; Ruget, R.I.; Costa-Castello, R. Robust Repetitive Control of Power Inverters for Standalone Operation in DG Systems. IEEE Trans. Energy Convers. 2020, 35, 237–247. [Google Scholar] [CrossRef]
- Escobar, G.; Valdez, A.A.; Leyva-Ramos, J.; Mattavelli, P. Repetitive-Based Controller for a UPS Inverter to Compensate Unbalance and Harmonic Distortion. IEEE Trans. Ind. Electron. 2007, 54, 504–510. [Google Scholar] [CrossRef]
- Kim, D.E.; Lee, D.C. Feedback Linearization Control of Three-Phase UPS Inverter Systems. IEEE Trans. Ind. Electron. 2010, 57, 963–968. [Google Scholar]
- Nguyen, T.H.; Van, T.L.; Nawaz, A.; Natsheh, A. Feedback Linearization-Based Control Strategy for Interlinking Inverters of Hybrid Ac/Dc Microgrids with Seamless Operation Mode Transition. Energies 2021, 14, 5613. [Google Scholar] [CrossRef]
- Stephen, S.; Shareef, H.; Errouissi, R.; Viswambharan, A. Disturbance Observer-Based Feedback Linearization Control for Stand-Alone Inverters. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; Volume 2021. [Google Scholar]
- Valderrama, G.E.; Stankovic, A.M.; Mattavelli, P. Dissipativity-Based Adaptive and Robust Control of UPS in Unbalanced Operation. IEEE Trans. Power Electron. 2003, 18, 1056–1062. [Google Scholar] [CrossRef]
- Bernacki, R.; Davari, D. Passivity-Based Control Design Methodology for UPS Systems. Energies 2019, 12, 4301. [Google Scholar] [CrossRef]
- Arimoto, S.; Kawamura, S.; Miyazaki, F. Bettering Operation of Robots by Learning. J. Robot. Syst. 1984, 1, 123–140. [Google Scholar] [CrossRef]
- Francis, B.A.; Wonham, W.M. The Internal Model Principle of Control Theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]
- Xu, M.X.; Xu, D.; Lin, P.; Chen, M.; Ni, J.; Zhang, T. Understanding Repetitive Control and Resonant Control. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 621–627. [Google Scholar]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.-H.; Chen, X. Generalized Extended State Observer Based Control for Systems with Mismatched Uncertainties. IEEE Trans. Ind. Electron. 2012, 59, 4792–4802. [Google Scholar] [CrossRef]
- Guo, B.; Bacha, S.; Alamir, M.; Hably, A.; Boudinet, C. Generalized Integrator-Extended State Observer with Applications to Grid-Connected Converters in the Presence of Disturbances. IEEE Trans. Control. Syst. Technol. 2021, 29, 744–755. [Google Scholar] [CrossRef]
- Sira-Ramírez, H.; Linares-Flores, J.; García-Rodríguez, C.; Contreras-Ordaz, M.A. On the Control of the Permanent Magnet Synchronous Motor: An Active Disturbance Rejection Control Approach. IEEE Trans. Control. Syst. Technol. 2014, 22, 2056–2063. [Google Scholar] [CrossRef]
- Wang, J.; Wang, F.; Wang, G.; Li, S.; Yu, L. Generalized Proportional Integral Observer-Based Robust Finite Control Set Predictive Current Control for Induction Motor Systems with Time-Varying Disturbances. IEEE Trans. Ind. Inform. 2018, 14, 4159–4168. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, Y.; Yang, J.; Li, S.; Li, Q. Robust Voltage Regulation of a DC–AC Inverter with Load Variations via a HDOBC Approach. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1172–1176. [Google Scholar] [CrossRef]
- Errouissi, R.; Shareef, H.; Awwad, F. Disturbance Observer-Based Control for Three-Phase Grid-Tied Inverter with LCL Filter. IEEE Trans. Ind. Appl. 2021, 57, 5411–5424. [Google Scholar] [CrossRef]
- Sharma, R.K.; Mishra, S.; Mudaliyar, S.R. Nonlinear Disturbance Observer Based Control of Three Phase Grid Forming Inverter for Distributed Generation System. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Kim, J.-H.; Sul, S.-K. A Carrier-Based PWM Method for Three-Phase Four-Leg Voltage Source Converters. IEEE Trans. Power Electron. 2004, 19, 66–75. [Google Scholar]
- Jacobina, C.B.; Nogueira Lima, A.M.; da Silva, E.R.C.; Alves, R.N.C.; Seixas, P.F. Digital Scalar Pulse-Width Modulation: A Simple Approach to Introduce Nonsinusoidal Modulating Waveforms. IEEE Trans. Power Electron. 2001, 16, 351–359. [Google Scholar] [CrossRef]
- Zhang, R.; Prasad, V.H.; Boroyevich, D.; Lee, F.C. Three-Dimensional Space Vector Modulation for Four-Leg Voltage-Source Converters. IEEE Trans. Power Electron. 2002, 17, 314–326. [Google Scholar] [CrossRef]
- Fernandes, D.A.; Costa, F.F.; Vitorino, M.A.; Queiroz, K.I.P.M.; Salvadori, F. Carrier-Based PWM Scheme for Three-Phase Four-Leg Inverters. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 3353–3358. [Google Scholar]
- Miveh, M.R.; Rahmat, M.F.; Ghadimi, A.A.; Mustafa, M.W. Control Techniques for Three-Phase Four-Leg Voltage Source Inverters in Autonomous Microgrids: A Review. Renew. Sustain. Energy Rev. 2016, 54, 1592–1610. [Google Scholar] [CrossRef]


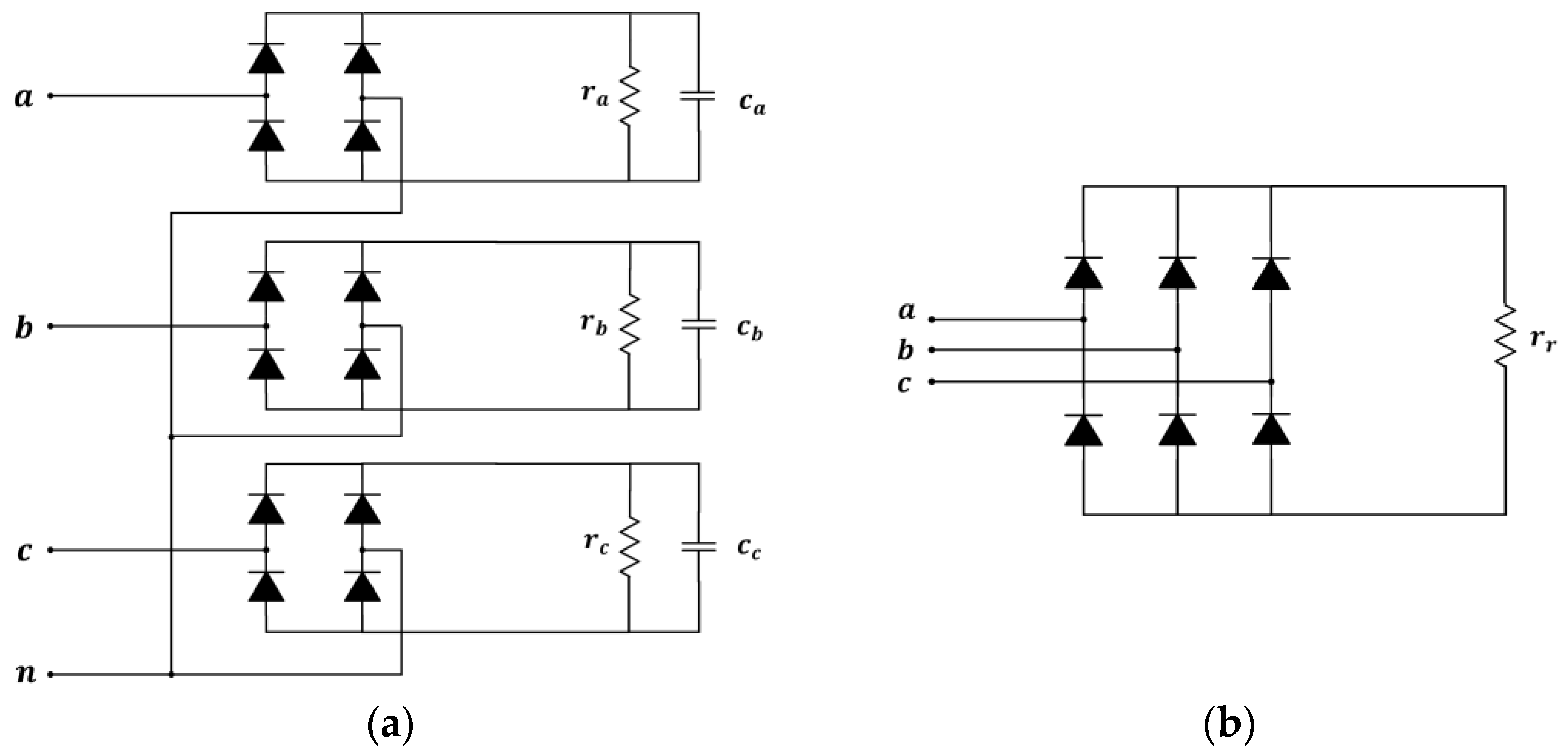
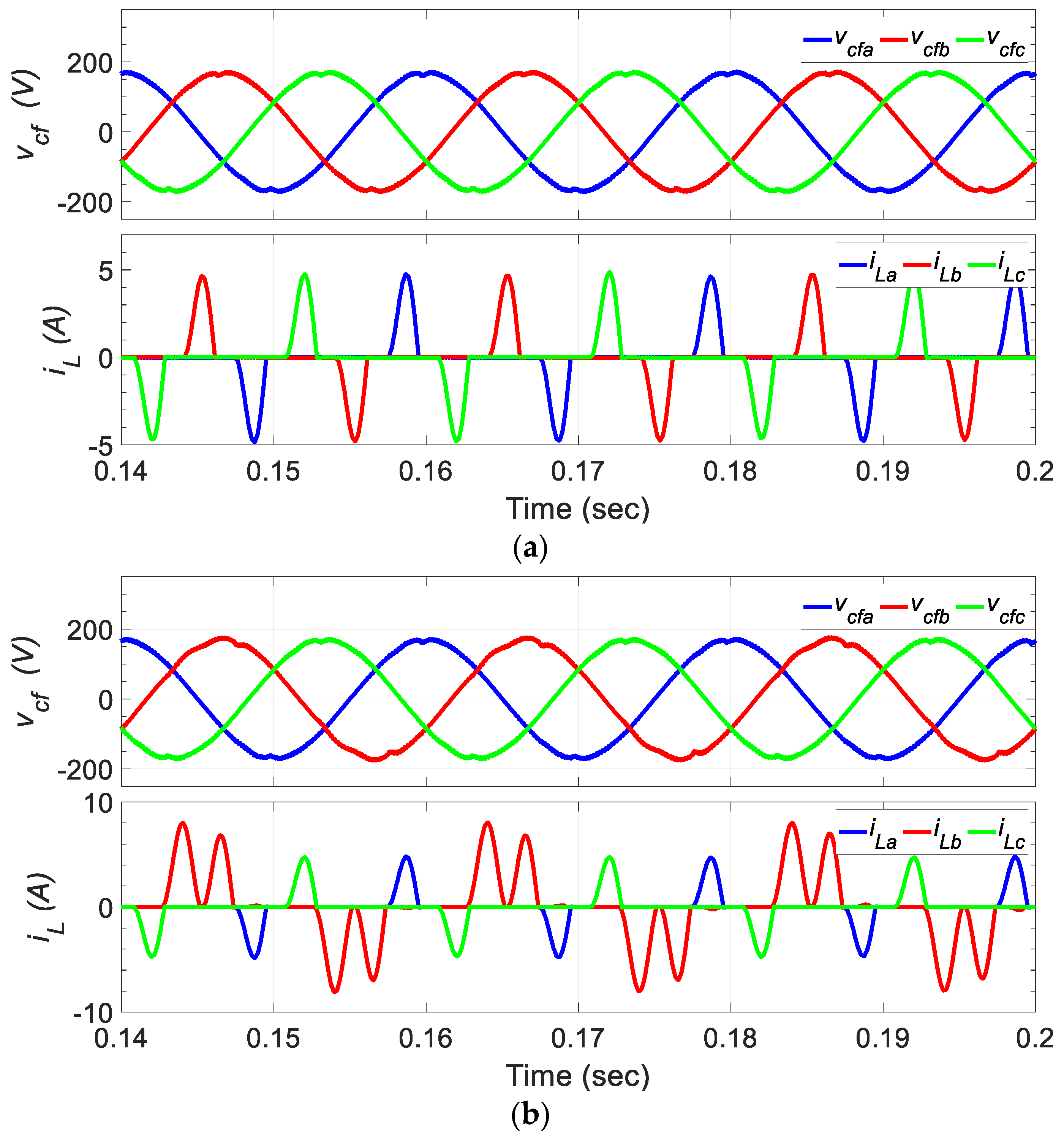
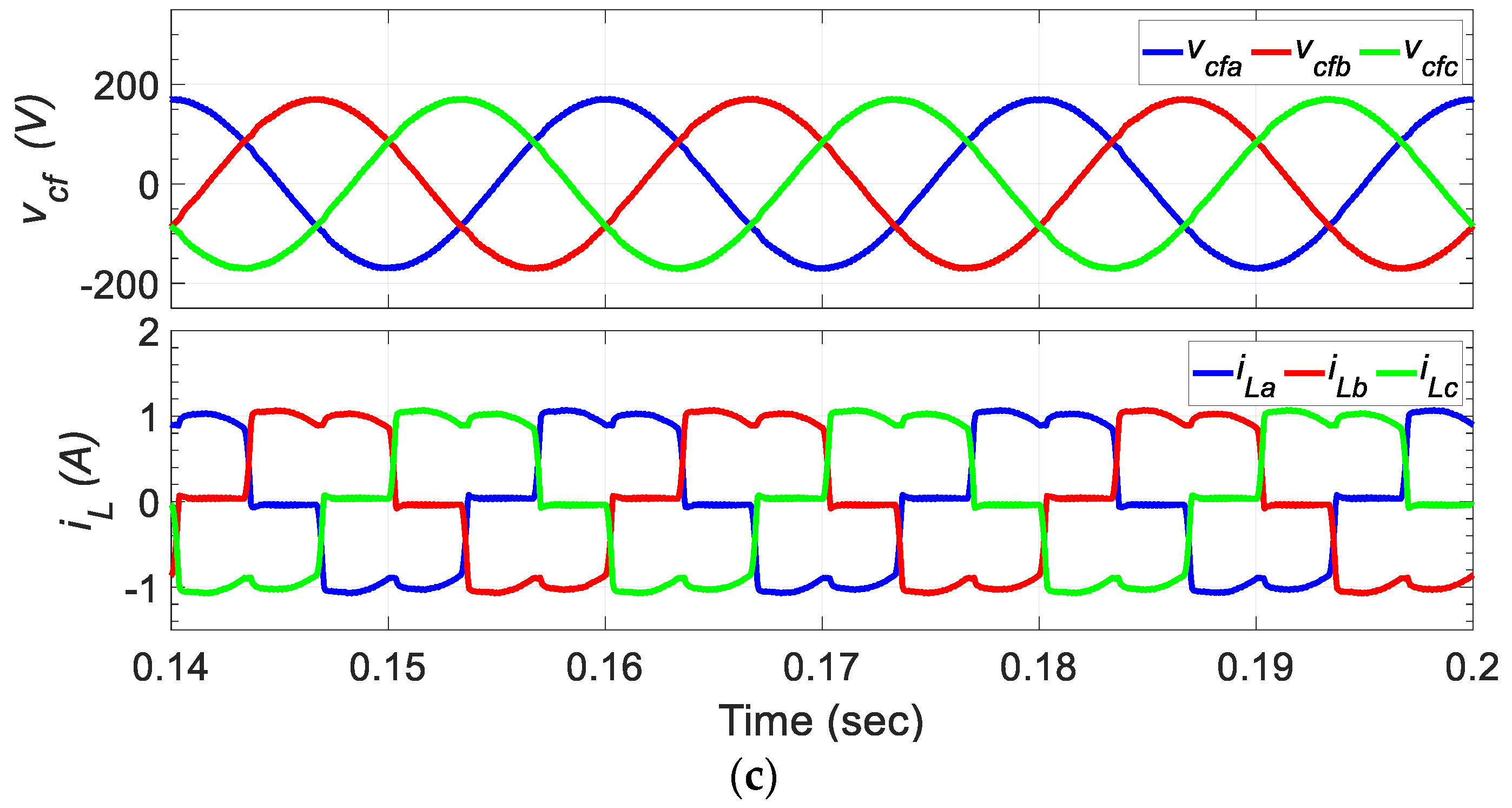


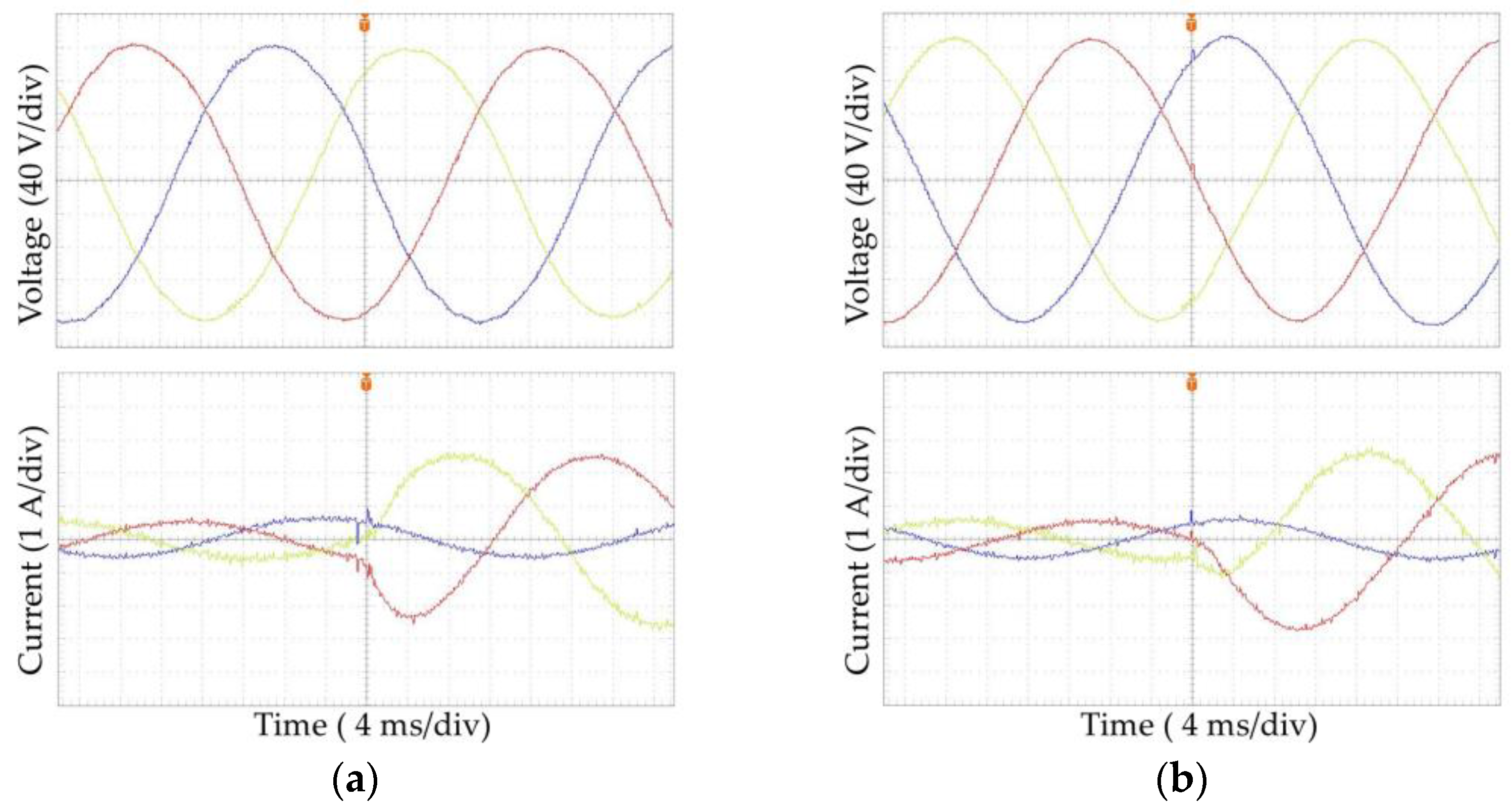
| Parameter | Value |
|---|---|
| DC input voltage of the inverter | vdc = 350 V |
| AC output voltage from the inverter | vac = 120 V rms |
| Sampling time | Ts = 1 µs |
| Switching frequency | fsw = 5000 Hz |
| DC-link capacitance | Cdc = 1.052 mF |
| LC filter | L1 = 4 mH, Cf = 15 µF, L2 = 2.5 mH |
| Neutral inductor | Ln = 2.5 mH |
| Internal resistances of filter components and DC link capacitor | rs = 1 µΩ−1 mΩ |
| Load Type | Parameter |
|---|---|
| Unbalanced linear load ZL | Ra = 65 Ω, Rb = 95 Ω, |
| Rc = 280 Ω | |
| Balanced nonlinear load ZNL1 | ra = 280 Ω, ca = 60 µF, |
| rb = 280 Ω, ca = 60 µF, | |
| rc = 280 Ω, cc = 60 µF | |
| Unbalanced nonlinear load ZNL2 | ra = 280 Ω, ca = 60 µF, |
| rb = 65 Ω, cb = 60 µF, | |
| rc = 280 Ω, cc = 60 µF | |
| Three-phase rectifier load ZNL3 | rr = 280 Ω |
| Controller | Parameters |
|---|---|
| Proposed | Controller parameters |
| Observer parameters | |
| dq0-PI (Dual loop) | Outer voltage loop |
| Inner current loop |
| Load | Controller | VUF (%) | THD (%) | ||
|---|---|---|---|---|---|
| va | vb | vc | |||
| ZL | Proposed | 0.05 | 0.89 | 0.87 | 0.81 |
| dq0-PI | 0.75 | 0.88 | 0.96 | 0.95 | |
| ZNL1 | Proposed | 0.007 | 1.83 | 1.81 | 1.73 |
| dq0-PI | 0.05 | 4.60 | 4.51 | 4.5 | |
| ZNL2 | Proposed | 0.07 | 1.82 | 2.54 | 1.76 |
| dq0-PI | 0.97 | 4.52 | 6.62 | 4.76 | |
| ZNL3 | Proposed | 0.05 | 0.97 | 0.98 | 1.01 |
| dq0-PI | 0.05 | 2.21 | 2.07 | 2.09 | |
| Controller | Parameters |
|---|---|
| Proposed | Controller parameters |
| Observer parameters | |
| dq0-PI (Dual loop) | Outer voltage loop |
| Inner current loop |
| Load | Controller | VUF (%) | THD (%) | ||
|---|---|---|---|---|---|
| va | vb | vc | |||
| ZL | Proposed | 0.2 | 2.0 | 1.9 | 1.3 |
| dq0-PI | 0.8 | 2.3 | 1.9 | 1.7 | |
| ZNL1 | Proposed | 0.2 | 3.9 | 3.7 | 3.6 |
| dq0-PI | 0.2 | 4.3 | 4.2 | 4.3 | |
| ZNL2 | Proposed | 0.6 | 4.9 | 4.7 | 4.7 |
| dq0-PI | 0.8 | 5.6 | 5.0 | 4.76 | |
| ZNL3 | Proposed | 0.18 | 2.3 | 2.4 | 2.2 |
| dq0-PI | 0.2 | 2.7 | 2.9 | 2.6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stephen, S.S.; Shareef, H.; Errouissi, R.; Eslami, M.; Hashfi, T.B. Disturbance Observer-Based Feedback Linearized Controller for Grid-Forming Four-Leg VSI Supplying Unbalanced and Nonlinear Loads. Energies 2024, 17, 3319. https://doi.org/10.3390/en17133319
Stephen SS, Shareef H, Errouissi R, Eslami M, Hashfi TB. Disturbance Observer-Based Feedback Linearized Controller for Grid-Forming Four-Leg VSI Supplying Unbalanced and Nonlinear Loads. Energies. 2024; 17(13):3319. https://doi.org/10.3390/en17133319
Chicago/Turabian StyleStephen, Samantha S., Hussain Shareef, Rachid Errouissi, Mahdiyeh Eslami, and Tuanku Badzlin Hashfi. 2024. "Disturbance Observer-Based Feedback Linearized Controller for Grid-Forming Four-Leg VSI Supplying Unbalanced and Nonlinear Loads" Energies 17, no. 13: 3319. https://doi.org/10.3390/en17133319
APA StyleStephen, S. S., Shareef, H., Errouissi, R., Eslami, M., & Hashfi, T. B. (2024). Disturbance Observer-Based Feedback Linearized Controller for Grid-Forming Four-Leg VSI Supplying Unbalanced and Nonlinear Loads. Energies, 17(13), 3319. https://doi.org/10.3390/en17133319







