New Opportunities in Real-Time Diagnostics of Induction Machines
Abstract
1. Introduction
- Develops methods to significantly improve the accuracy of dynamic models for the remote control of induction motors. These models are effective in both closed- and open-loop speed control systems and are crucial for real-time process monitoring.
- Introduces a technical solution for real-time monitoring involving the simultaneous measurement of input and output physical quantities. This approach overcomes the limitations of traditional diagnostic methods by addressing inaccuracies in collected data and analyzing dynamic, systematic errors due to the inertial properties of frequency converters.
- Incorporates advanced control methods, including a vector control method with a speed control scheme, alongside standard drive frequency control methods. This contribution addresses significant nonlinearities in torque formation and optimizes frequency converter settings, improving response characteristics and overall system performance.
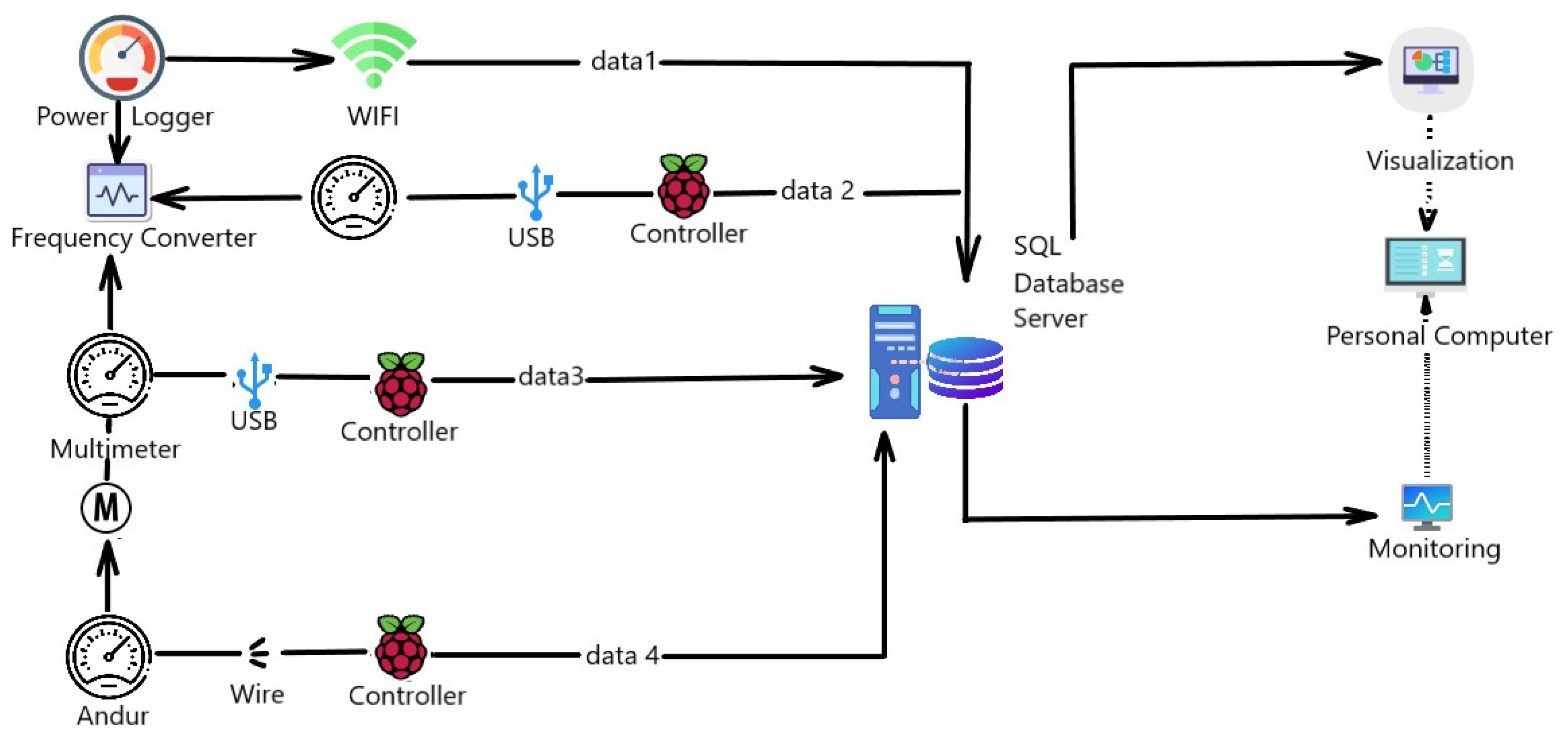
2. Experimental Setup
- Mobile-CASSY 2 Wi-Fi.
- VACON NX frequency converter with control panel for local/remote control applications.
- SG 56-4A 0.06 kW three-phase induction motors.
- Digital multimeters 34,470 A (71/2 digit).
- Fluke 1736 power logger.
- Test 4 signal simulator and multimeter handheld for analog signals.
- Software for obtaining information about the state of the drive in the general case of numerous time-varying and spatially distributed quantities characterizing this state.
- 17XX-Flex1500-12” current clamp (1500-1) A.
- A system for mounting a speed sensor on the motor shaft using Mounting Bell MG58A, Shaft Adapter WDGWA10M06, and Jointed Coupling ST27, which ensures the possibility of monitoring the misalignment of the sensor axis with the motor axis.
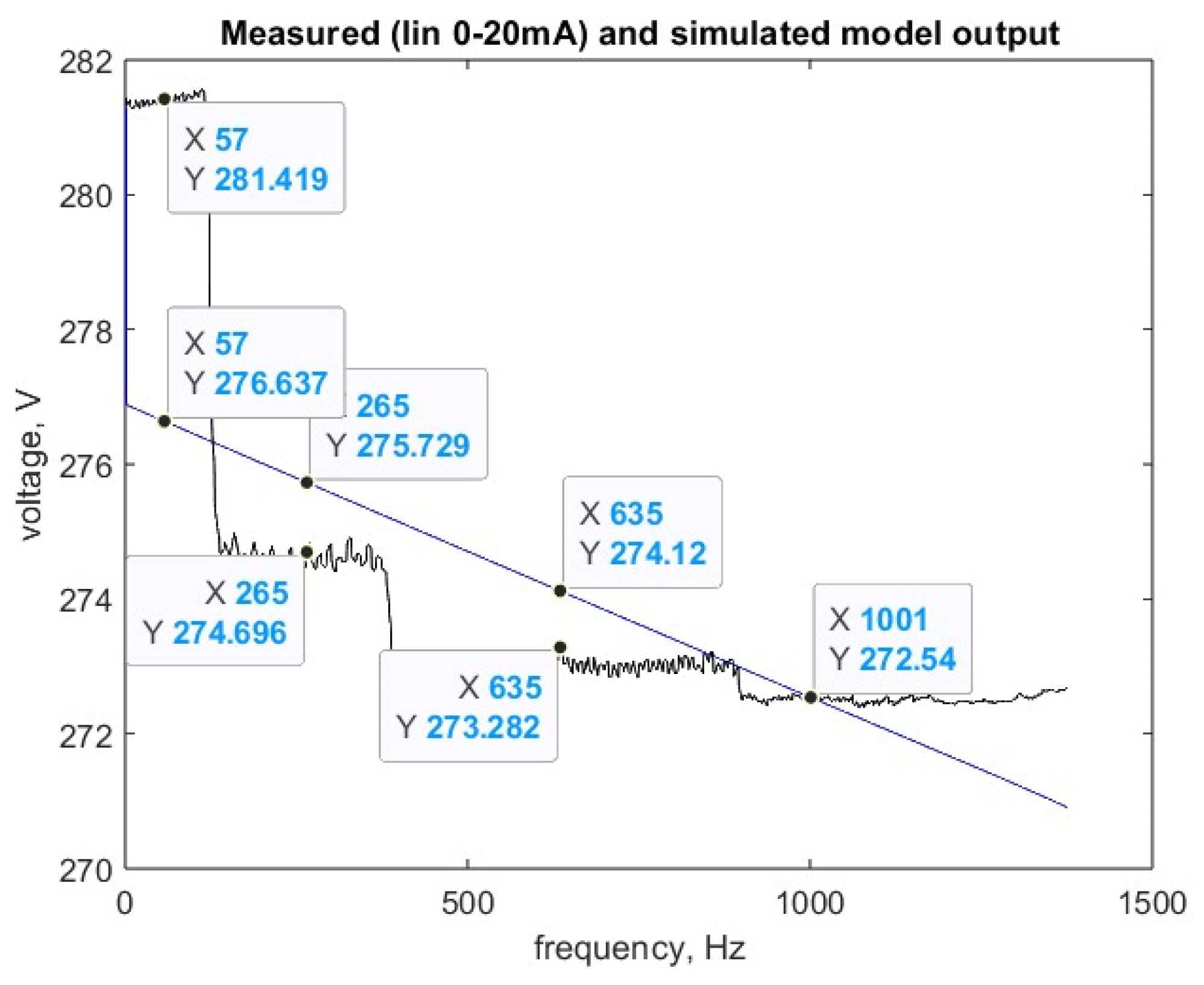
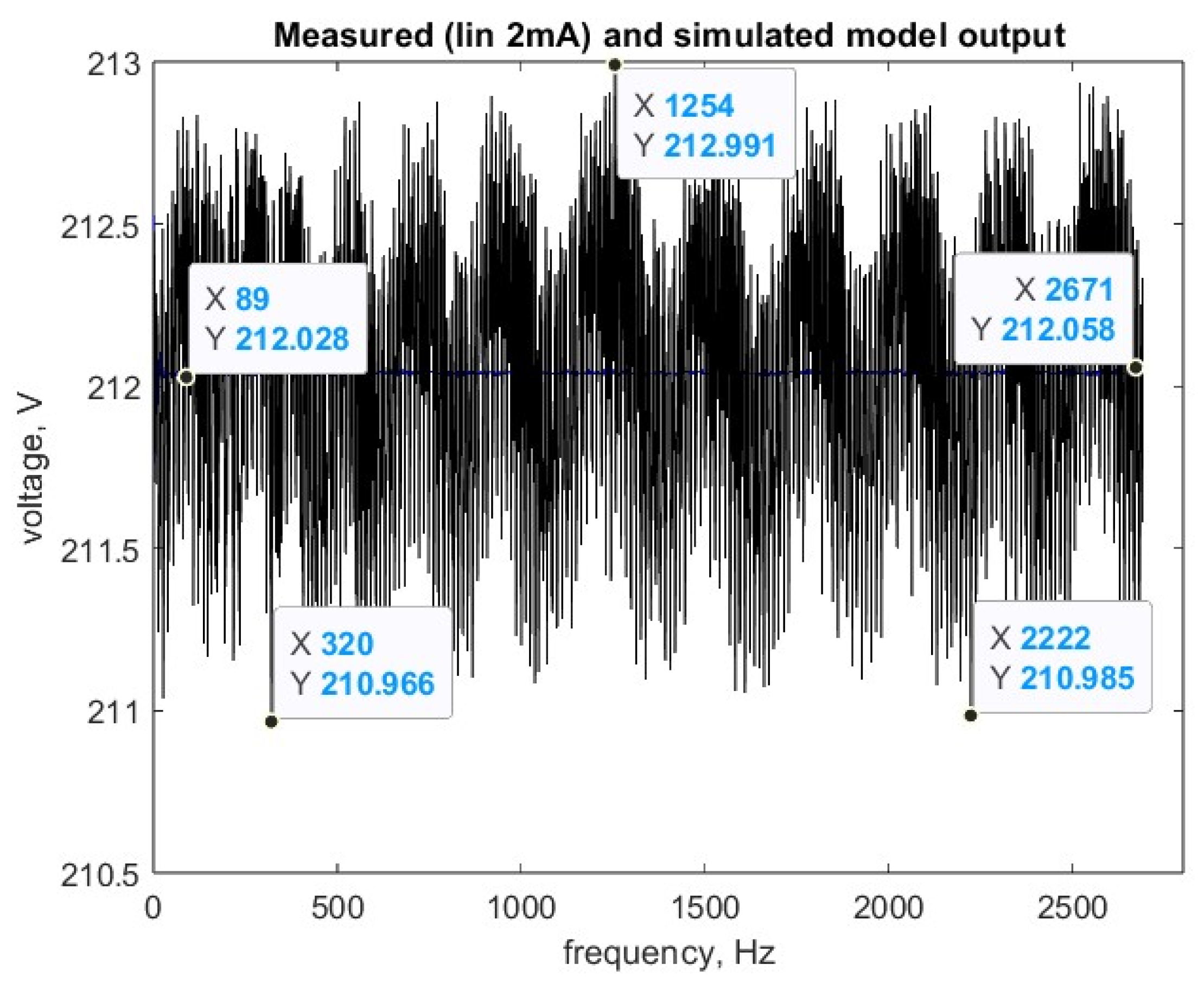
3. Experimental Verification of the Output EMC Filter
4. Mathematical Description of the Internal State of a Nonlinear System
- Power: 3~380/500 V–0.75…400 kW.
- Overload capacity: up to 150%.
- Output frequency: 0…320 Hz.
- Control method: Scalar (U/f), vector with open loop.
- Dynamic positive feedback.
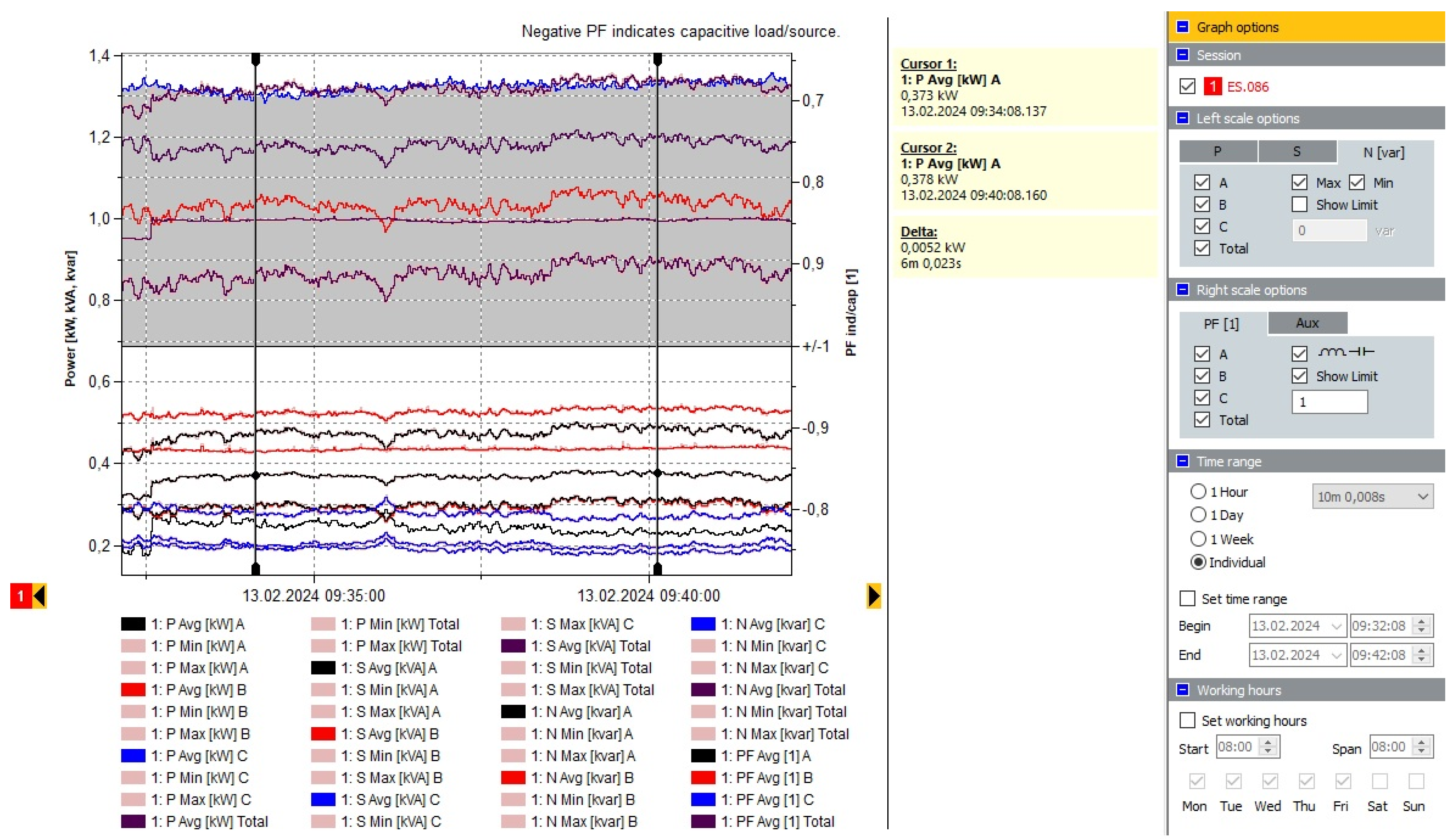
5. Experiment on Torque Control of an Induction Motor with a Squirrel-Cage Rotor (Predictive Torque Control Technique)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tetter, V.Y.; Sidorov, E.N.; Sidorova, E.A. Modeling of virtual standards of vibration of defective bearing units. Meas. Tech. 2013, 56, 278–282. [Google Scholar] [CrossRef]
- Komshin, A.S. Mathematical modeling of measurement computational monitoring of the electromechanical parameters of turbine units by a phase chronometric method. Meas. Tech. 2013, 56, 850–855. [Google Scholar] [CrossRef]
- Sengamalai, U.; Anbazhagan, G.; Thamizh Thentral, T.M.; Vishnuram, P.; Khurshaid, T.; Kamel, S. Three Phase Induction Motor Drive: A Systematic Review on Dynamic Modeling, Parameter Estimation, and Control Schemes. Energies 2022, 15, 8260. [Google Scholar] [CrossRef]
- Udomsuk, S.; Areerak, K.; Areerak, T.; Areerak, K. Online Estimation of Three-Phase Induction Motor Parameters Using an Extended Kalman Filter for Energy Saving. Energies 2024, 17, 2115. [Google Scholar] [CrossRef]
- Agamalov, Y.R. Aspects of measuring harmonic signal vectors in the presence of subharmonic noise and a method for suppressing it. Meas. Tech. 2013, 56, 837–841. [Google Scholar] [CrossRef]
- Liu, Y.T.; Chang, K.M.; Li, W.Z. Model reference adaptive control for a piezo-positioning system. Precis. Eng. J. Int. Soc. Precis. Eng. Nanotechnol. 2010, 34, 62–69. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Liu, T.; Yu, B.; Mou, X.; Dong, X.; Xing, Y. Dynamic Evaluation Technology of Measurement Performance Group of High Voltage Transformer Based on Virtual Standard Device. In Proceedings of the 3rd International Conference on Environmental Pollution and Governance (ICEPG 2023), Xiamen, China, 27–29 October 2023; Springer Nature: Cham, Switzerland, 2023; pp. 1205–1213. [Google Scholar]
- Tian, Y.; Yan, C.; Liu, Y.; Luo, W.; Kang, J.; Wang, Z.; Wu, L. Characteristics of vibration response of ball bearing with local defect considering skidding. J. Mech. Sci. Technol. 2023, 37, 156–169. [Google Scholar] [CrossRef]
- Valtchev, S.; Meshcheryakov, V.; Gracheva, E.; Sinyukov, A.; Sinyukova, T. Energy-Saving Control for Asynchronous Motor Motion System Based on Direct Torque Regulator. Energies 2023, 16, 3870. [Google Scholar] [CrossRef]
- Kodkin, V.L.; Baldenkov, A.A. Experimental Studies of the Processes of Stepped Torque Loads Parrying by Asynchronous Electric Drives and Interpretation of Experimental Results by Nonlinear Transfer Functions of Drives. Processes 2022, 10, 1204. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Xie, W.; Dou, M. Full-Speed Range Encoderless Control for Salient-Pole PMSM with a Novel Full-Order SMO. Energies 2018, 11, 2423. [Google Scholar] [CrossRef]
- Guidelines for the Measurement Method of Nonlinearity for Surface Acoustic Wave (SAW) and Bulk Acoustic Wave (BAW) Devices in Raadio Frequency (RF). Available online: https://standards.iteh.ai/catalog/standards/iec/c166a77a-9d03-4793-9a33-2f6e9359ca30/iec-62761-2014 (accessed on 19 February 2014).
- Ioannides, M.G.; Stamelos, A.P.; Papazis, S.A.; Stamataki, E.E.; Stamatakis, M.E. Internet of Things-Based Control of Induction Machines: Specifics of Electric Drives and Wind Energy Conversion Systems. Energies 2024, 17, 645. [Google Scholar] [CrossRef]
- Gnaciński, P.; Pepliński, M.; Muc, A.; Hallmann, D.; Jankowski, P. Effect of Ripple Control on Induction Motors. Energies 2023, 16, 7831. [Google Scholar] [CrossRef]
- Algburi, R.N.A.; Gao, H. Health Assessment and Fault Detection System for an Industrial Robot Using the Rotary Encoder Signal. Energies 2019, 12, 2816. [Google Scholar] [CrossRef]
- Zhao, X.; Qin, P.; Tang, Z. Equivalent Inertia Estimation of Asynchronous Motor and Its Effect on Power System Frequency Response. Energies 2022, 15, 8350. [Google Scholar] [CrossRef]
- Singh, R.R.; Chelliah, T.R. Enforcement of cost-effective energy conservation on single-fed asynchronous ma-chine using a novel switching strategy. Energy 2017, 126, 179–191. [Google Scholar] [CrossRef]
- Ioannides, M.G.; Koukoutsis, E.B.; Stamelos, A.P.; Papazis, S.A.; Stamataki, E.E.; Papoutsidakis, A.; Vikentios, V.; Apostolakis, N.; Stamatakis, M.E. Design and Operation of Internet of Things-Based Monitoring Control System for Induction Machines. Energies 2023, 16, 3049. [Google Scholar] [CrossRef]
- El-Kharashi, E.; Massoud, J.G.; Al-Ahmar, M.A. The impact of the unbalance in both the voltage and the frequency on the performance of single and cascaded induction motors. Energy 2019, 181, 561–575. [Google Scholar] [CrossRef]
- Cai, Z.; Liu, L.; de Paulis, F.; Qi, Y. Passive Intermodulation Measurement: Challenges and Solutions. Engineering 2022, 14, 181–191. [Google Scholar] [CrossRef]
- Lei, N.; An, D.; Guo, Y.; Su, K.; Liu, S.; Luo, Z.; Yau, S.T.; Gu, X. A Geometric Understanding of Deep Learning. Engineering 2020, 6, 361–374. [Google Scholar] [CrossRef]
- Yang, T.; Wang, T.; Miao, Y. Active decoupling control of the three-phase voltage source converter under nonlinear AC current. J. Power Electron. 2024, 24, 1–14. [Google Scholar] [CrossRef]
- Paramo, G.; Bretas, A.; Meyn, S. Research Trends and Applications of PMUs. Energies 2022, 15, 5329. [Google Scholar] [CrossRef]
- Bartels, J.-H.; Xu, R.; Kang, C.; Herrmann, R.; Marx, S. Experimental Investigation on the Transfer Behavior and Environmental Influences of Low-Noise Integrated Electronic Piezoelectric Acceleration Sensors. Metrology 2024, 4, 46–65. [Google Scholar] [CrossRef]
- Bedida, T.; Makhloufi, S.; Bekakra, Y.; Kermadi, M.; Bessous, N.; Kechida, R.; Taibi, D. Predictive torque control of induction motor for rotor bar faults diagnosis. Energy Rep. 2024, 11, 4940–4956. [Google Scholar] [CrossRef]
- Hassan, M.; Ge, X.; Woldegiorgis, A.T.; Mastoi, M.S.; Atif, R.; Shaikh, M.S.; Kumar, S. A look-up table-based model predictive torque control of IPMSM drives with duty cycle optimization. ISA Trans. 2023, 138, 670–686. [Google Scholar] [CrossRef] [PubMed]
- Aissa, O.; Reffas, A.; Krama, A.; Benkercha, R.; Talhaoui, H.; Abu-Rub, H. Advanced direct torque control based on neural tree controllers for induction motor drives. ISA Trans. 2024, 148, 92–104. [Google Scholar] [CrossRef]
- Sahu, A.; Mohanty, K.B.; Mishra, R.N. Development and experimental realization of an adaptive neural-based discrete model predictive direct torque and flux controller for induction motor drive. Appl. Soft Comput. 2021, 108, 107418. [Google Scholar] [CrossRef]
- Sivaraju, S.; Senthilkumar, T.; Sankar, R.; Anuradha, T.; Usha, S.; Bin Musirin, I. Improving the efficiency of induction motor drive by flux and torque control: A hybrid LSE-RERNN approach. ISA Trans. 2024, 147, 215–226. [Google Scholar] [CrossRef]
- Mahfoud, S.; El Ouanjli, N.; Derouich, A.; El Idrissi, A.; Hilali, A.; Chetouani, E. Higher performance enhancement of direct torque control by using artificial neural networks for doubly fed induction motor. E-Prime Adv. Electr. Eng. Electron. Energy 2024, 8, 100537. [Google Scholar] [CrossRef]
- Boyar, A.; Kabalci, E.; Kabalci, Y. Sensorless speed controller of an induction motor with MRAS-based model predictive control. Comput. Electr. Eng. 2024, 118, 109350. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, J.; Wang, H.; Zhang, Q.; Luo, X.; Xu, H.; Xiong, Y. Multi-objective optimum design of five-phase squirrel cage induction motor by differential evolution algorithm. Energy Rep. 2022, 8, 51–62. [Google Scholar] [CrossRef]
- Agapiou, J.S. Filling Friction Stir Welding In-Process Exit Holes in Copper Squirrel Cage Rotors for Electric Motors. Procedia Manuf. 2021, 53, 802–813. [Google Scholar] [CrossRef]
- Szántó, A.; Ádámkó, É.; Juhász, G.; Sziki, G. Simultaneous measurement of the moment of inertia and braking torque of electric motors applying additional inertia. Measurement 2022, 204, 112135. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.M.; Rodríguez, J.; Kennel, R. Model Reference Adaptive System with Finite-Set for Encoderless Control of PMSGs in Micro-Grid Systems. Energies 2020, 13, 4844. [Google Scholar] [CrossRef]
- Albrecht, C.; Klöck, J.; Martens, O.; Schumacher, W. Online Estimation and Correction of Systematic Encoder Line Errors. Machines 2017, 5, 1. [Google Scholar] [CrossRef]
- Gudiño-Ochoa, A.; Jalomo-Cuevas, J.; Molinar-Solís, J.E.; Ochoa-Ornelas, R. Analysis of Interharmonics Generation in Induction Motors Driven by Variable Frequency Drives and AC Choppers. Energies 2023, 16, 5538. [Google Scholar] [CrossRef]
- Nguyen-Vinh, Q.; Pham-Tran-Bich, T. Direct torque control of induction motor based on slidingmode. Electr. Eng. 2024, 106, 1–13. [Google Scholar] [CrossRef]
- Korayem, M.H.; Dehkordi, S.F.; Ghobadi, N. Wheel Slippage Compensation in Mobile Manipulators Through Combined Kinematic, Dynamic, and Sliding Mode Control. Arab. J. Sci. Eng. 2024, 49, 1–21. [Google Scholar] [CrossRef]
- Rodrigues, N.M.; Janeiro, F.M.; Ramos, P.M. Power Quality Transient Detection and Characterization Using Deep Learning Techniques. Energies 2023, 16, 1915. [Google Scholar] [CrossRef]
- Kumar, R.R.; Andriollo, M.; Cirrincione, G.; Cirrincione, M.; Tortella, A. A Comprehensive Review of Conventional and Intelligence-Based Approaches for the Fault Diagnosis and Condition Monitoring of Induction Motors. Energies 2022, 15, 8938. [Google Scholar] [CrossRef]
- Machado, J.P.Z.; Thaler, G.; Pacheco, A.L.S.; Flesch, R.C.C. Impact of Angular Speed Calculation Methods from Encoder Measurements on the Test Uncertainty of Electric Motor Efficiency. Metrology 2024, 4, 164–180. [Google Scholar] [CrossRef]
- Sun, G.; Ren, X.; Chen, Q.; Li, D. A modified dynamic surface approach for control of nonlinear systems with unknown input dead zone. Int. J. Robust Nonlinear Control. 2013, 23, 1145–1167. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Sun, M.; Sun, Q. A novel implementation of an uncertain dead-zone-input equipped extended state observer and sign estimator. Inf. Sci. 2023, 626, 75–93. [Google Scholar] [CrossRef]
- Kołodziejek, P.; Wachowiak, D. Fast Real-Time RDFT- and GDFT-Based Direct Fault Diagnosis of Induction Motor Drive. Energies 2022, 15, 1244. [Google Scholar] [CrossRef]


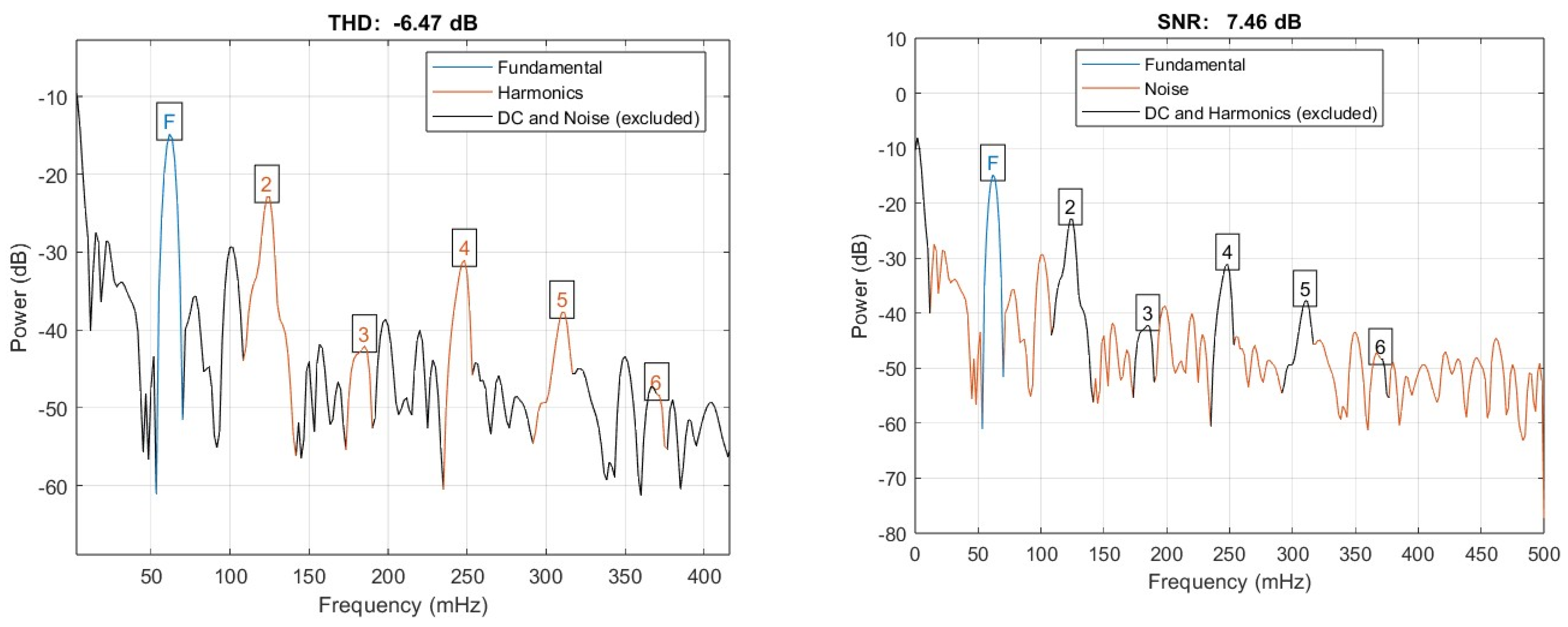
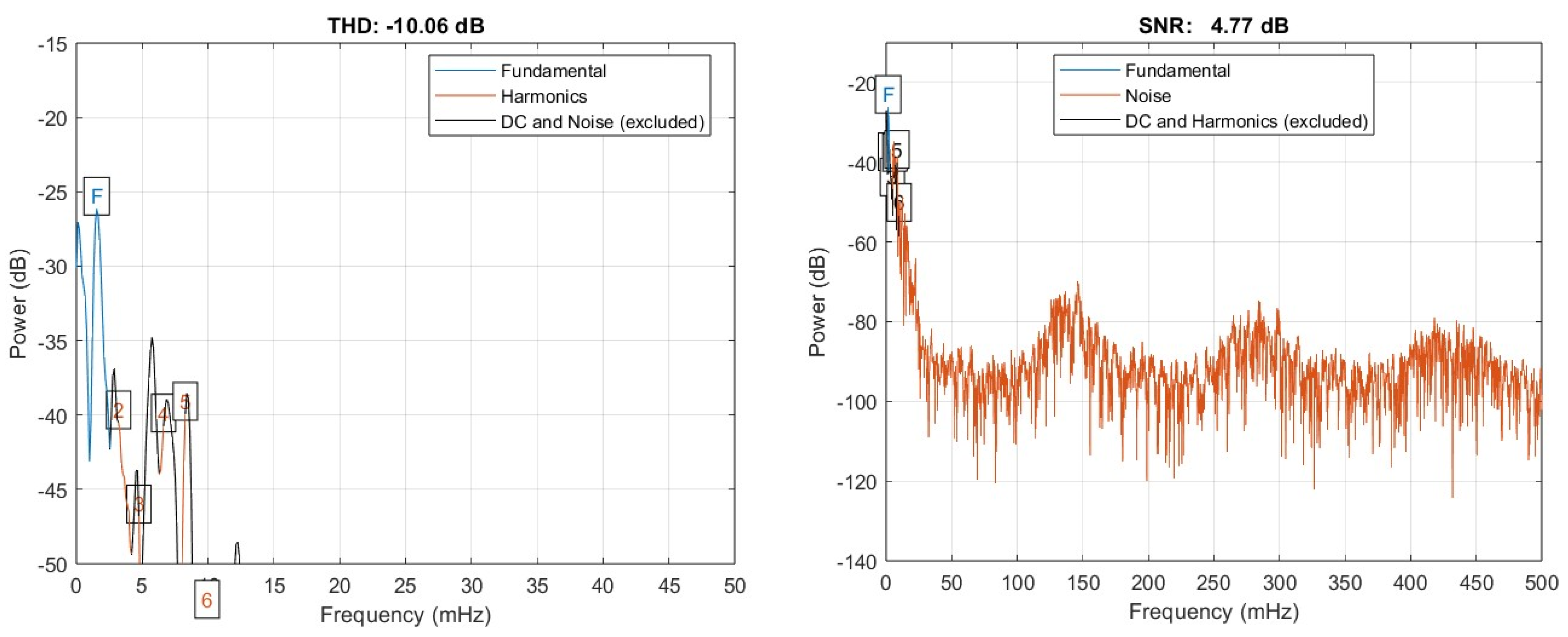
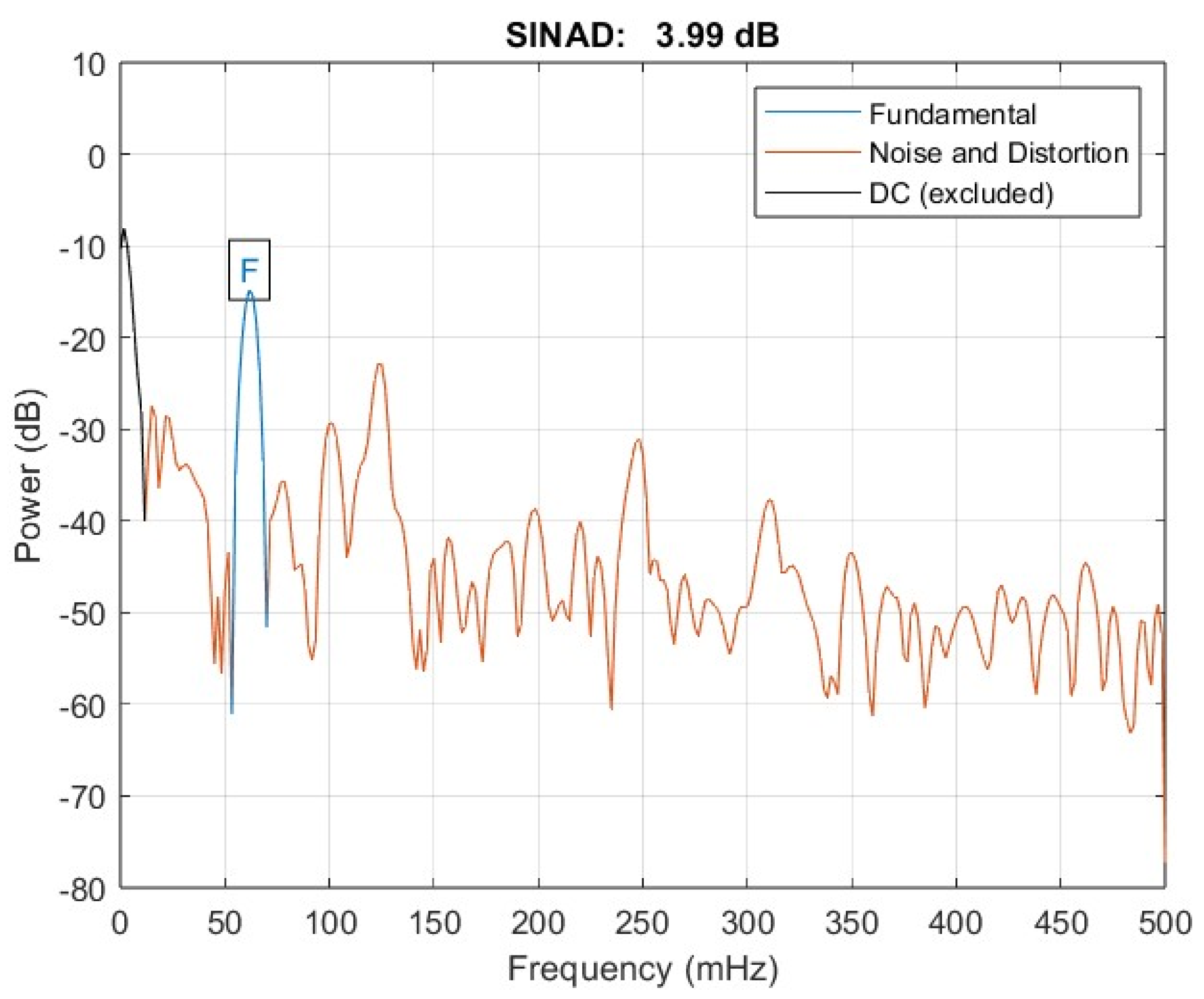
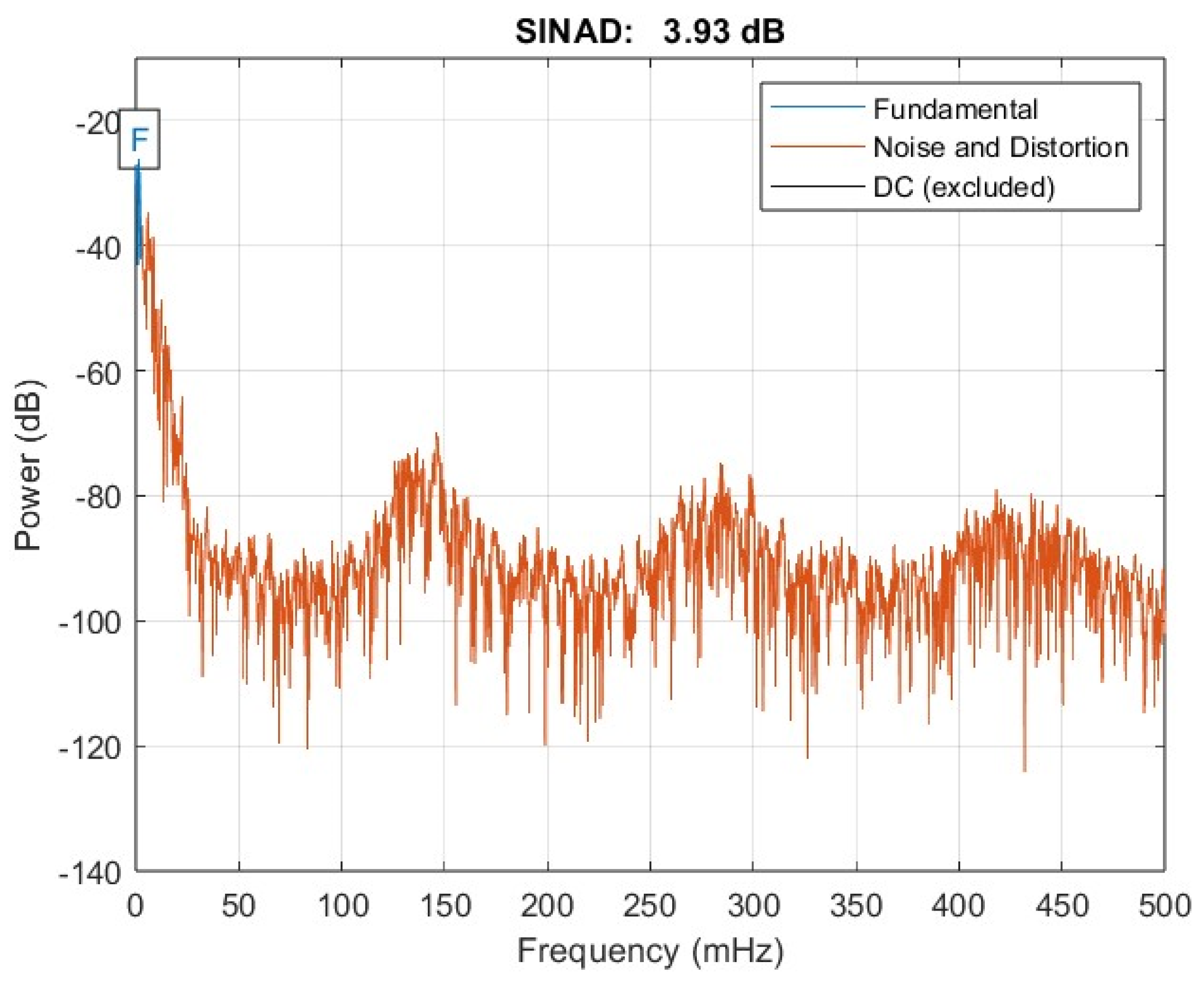
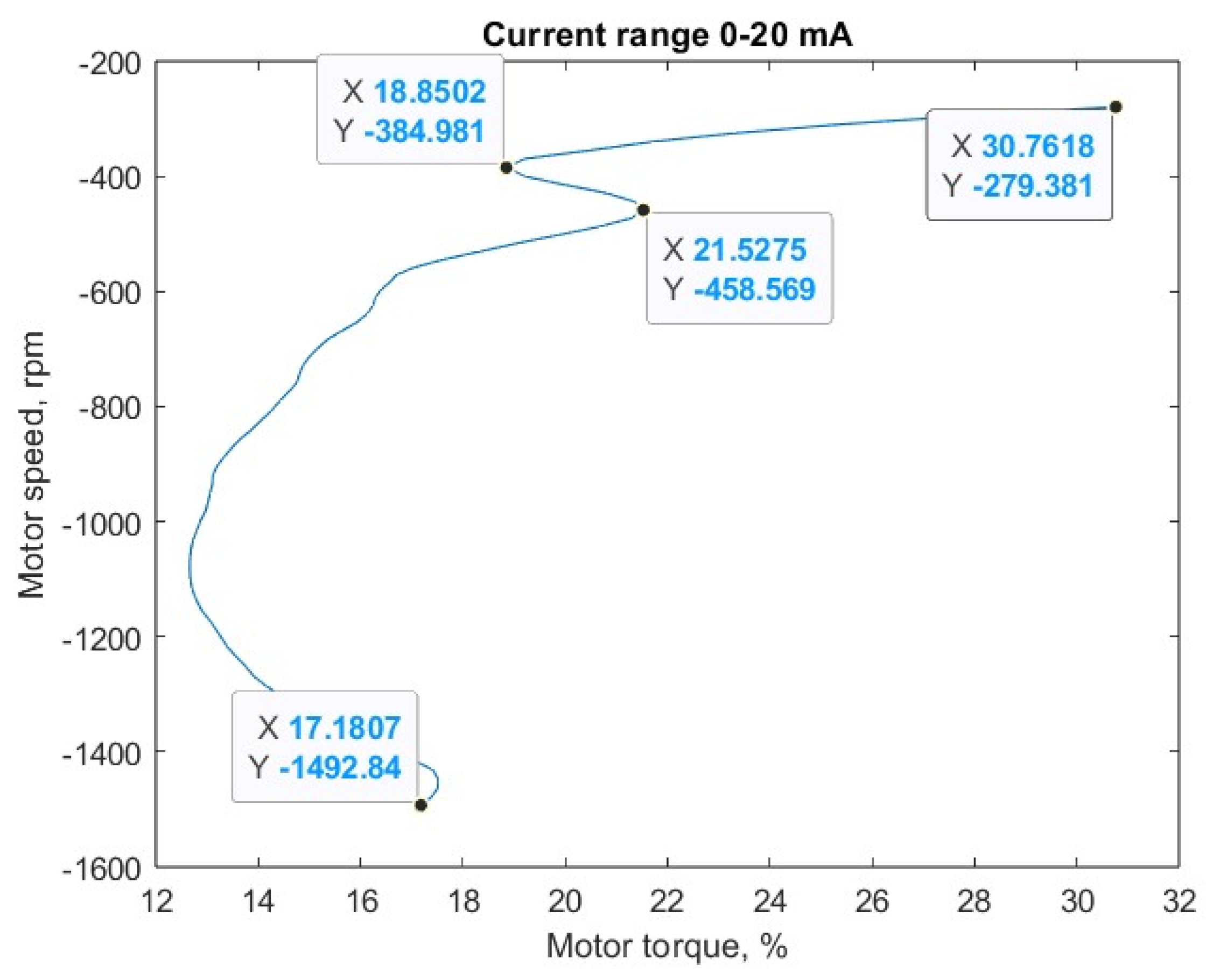
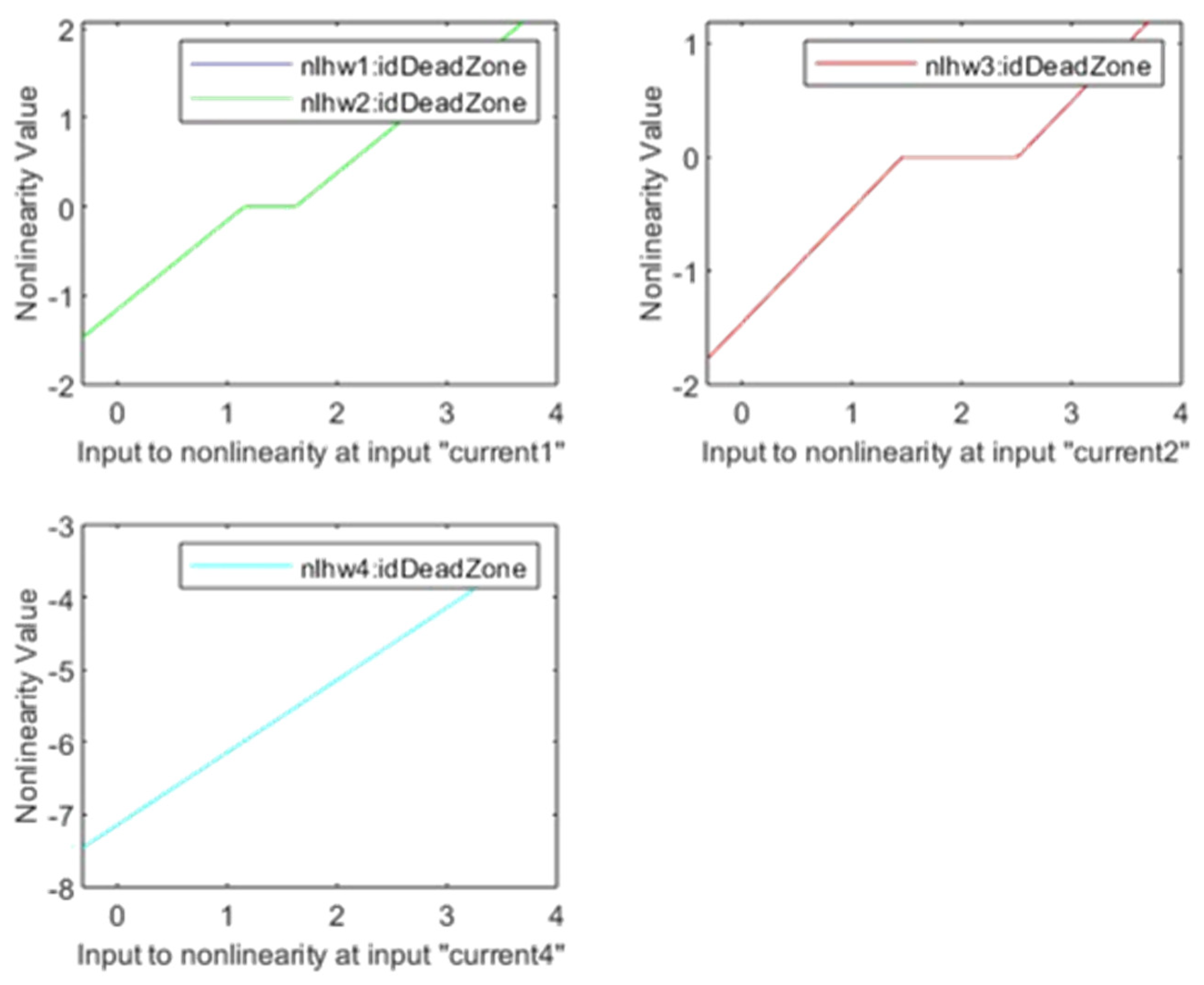

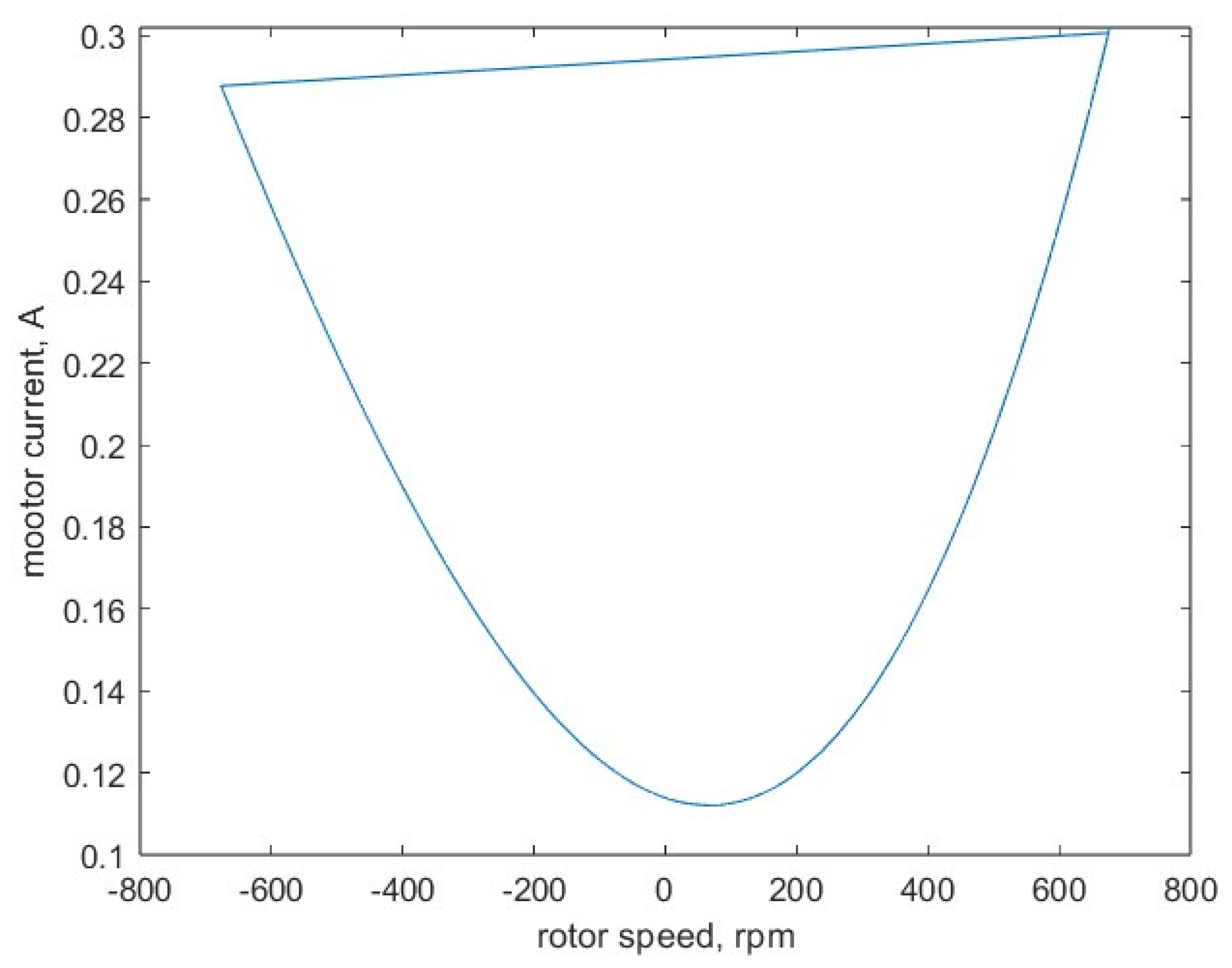
| Voltage Fluctuations | from the Filter Side | from the Network Side | on the Stator Winding |
|---|---|---|---|
| 0.0048 ± 0.0020 | 0.0044 ± 0.0033 | 0.0049 ± 0.0026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baraškova, T.; Kudelina, K.; Shirokova, V. New Opportunities in Real-Time Diagnostics of Induction Machines. Energies 2024, 17, 3265. https://doi.org/10.3390/en17133265
Baraškova T, Kudelina K, Shirokova V. New Opportunities in Real-Time Diagnostics of Induction Machines. Energies. 2024; 17(13):3265. https://doi.org/10.3390/en17133265
Chicago/Turabian StyleBaraškova, Tatjana, Karolina Kudelina, and Veroonika Shirokova. 2024. "New Opportunities in Real-Time Diagnostics of Induction Machines" Energies 17, no. 13: 3265. https://doi.org/10.3390/en17133265
APA StyleBaraškova, T., Kudelina, K., & Shirokova, V. (2024). New Opportunities in Real-Time Diagnostics of Induction Machines. Energies, 17(13), 3265. https://doi.org/10.3390/en17133265





