Abstract
This paper presents a review of the most common power converters and torque ripple minimisation approaches for switched reluctance motors (SRMs). Unlike conventional three-phase AC motors, namely squirrel cage induction motors and permanent magnet synchronous motors, which require a typical three-phase inverter for operation, the switched reluctance motor requires a different topology power converter for reliable and efficient operation. In addition, due to the non-linear, discrete nature of SRM torque production, torque ripple is severely pronounced, which is undesirable in servo applications like electric vehicles. Hence, deploying a proper torque control function for smooth and quiet motor operation is crucial. This paper sheds light over the most popular SRM power converters as well as torque ripple minimisation methods, and it suggests an optimal SRM drive topology for EV applications.
1. Introduction
The global climate change crisis forced researchers to seek alternative greener energy sources. Transportation is regarded as a major source of carbon emission; hence, transportation electrification is becoming increasingly vital. The deployment of electric vehicles (EVs) results in less emissions, hence a cleaner environment [1].
The heart of an EV is an electric machine; therefore, it should be selected wisely to meet the listed criteria:
- High power and torque density (/kg and /A);
- High torque to inertia ratio;
- High efficiency;
- Compact size and low weight;
- Low cost;
- Robust (electrically and mechanically) and fault tolerant;
- Wide constant torque/speed range;
- Wide temperature operating range;
- Low vibration and acoustic noise.
Various types of electric machines are utilised in electric vehicle (EV) applications, including switched reluctance machines (SRMs), squirrel cage induction machines (SCIMs), permanent magnet synchronous machines (PMSMs), brushless DC machines (BLDCs), and synchronous reluctance machines (SynRels) [2]. The PMSM is often favoured for its wide torque–speed range, high efficiency, and power density, making it a preferred choice for traction motors [3]. However, challenges such as supply constraints and rising costs of rare-earth materials used in PMSMs have prompted the exploration of alternative options. Ferrite permanent magnets (FPMs) are not a viable alternative due to their lower residual flux, susceptibility to demagnetisation, and reduced torque density compared to rare-earth PMSMs [4]. Consequently, research is shifting towards magnet-free machines.
While SCIMs are employed in some commercial EVs [5], their efficiency is lower than other traction motors. The rotor’s inherent heat generation complicates cooling, even with copper rotor bars, and the SCIM exhibits a poor power factor, particularly with light loads. SynRel motors are a potential option for main drivetrains as they typically do not incorporate permanent magnets [6]. However, they are characterised by a low power factor, high core loss, high torque ripple, low efficiency, and low torque density [7].
The SRM stands out as a contender in this field due to its stable, robust, and simple structure at a lower cost [8]. It boasts fault-tolerant capabilities, high torque, and a wide constant power range. Its design, without permanent magnets or rotor windings, simplifies the motor geometry and cooling process, as most heat is generated in the stator. This allows the SRM to operate in harsh environments and at high rotor temperatures [9]. Recent advancements in high-power SRM design for EVs show promising competitiveness with PMSMs in terms of power density, efficiency, and the torque–speed range [10,11].
Despite their advantages, SRMs face limitations that hinder their widespread adoption in the EV market, including lower power density compared to equivalent-sized PMSMs and highly non-linear characteristics (leading to high torque ripple and undesirable vibrations) [12]. Additionally, the power converters for SRMs differ from the conventional EV converters used for SCIMs or PMSMs. Table 1 gives a brief comparison between the SCIM, PMSM, and SRM.

Table 1.
Comparison between different propulsion motors for EV applications.
This paper reviews the most common power converters and torque ripple minimisation approaches for SRM drives. The paper is organised as follows: Section 2 presents and compares the most dominant power converters utilised to drive the SRM, highlighting the merits and disadvantages of each. Section 3 reviews the most common torque ripple minimisation techniques based on a machine design approach and a control approach. Section 4 provides a conclusion and suggests the optimal SRM drive topology for EV applications. Some future SRM drive research areas are highlighted.
2. SRM Power Converters
This section categorises and examines the typical power converters used to supplying the SRM. The distinction between hard- and soft-switching converters is illustrated, and key advantages and disadvantages of each topology are emphasised. Different power converters are compared to enable selection of the most suitable one for EV applications.
2.1. Introduction
The SRM cannot be directly connected to any AC or DC power source, but it requires a suitable power converter for its controlled operation. Its main function is to energise and de-energise each phase winding correctly to ensure continuous rotation. Numerous converter types have been proposed for SRM drives, and the chosen type significantly impacts on drive cost, size, and performance. The converter must meet several requirements to enhance SRM drive performance [13]:
- Fast magnetisation and demagnetisation of SRM phases: The converter should facilitate fast magnetisation to quickly reach the reference current in the phase winding, thereby increasing the SRM base speed. It should also minimise demagnetisation time by rapidly extinguishing phase current to eliminate the current tail, preventing the SRM from entering the negative torque production region. These conditions can be enhanced by boosting the DC supply voltage during magnetisation and demagnetisation periods.
- Phase overlap: The converter must be able to simultaneously energise the incoming phase and de-energise the outgoing phase.
- High efficiency: To improve SRM drive efficiency, the converter should efficiently return demagnetisation energy to the supply or store it for use in energising another phase rather than dissipating it as heat in winding resistance.
- Minimum cost: An economical converter provides excellent performance with a minimal number of switching devices. Fewer switches reduces switching losses, the number of gate drive circuits, and overall converter cost.
- Fault tolerance: For critical applications, a high-reliability converter is necessary to ensure continuous SRM rotation even after a phase failure.
- Low complexity: Simple design and control algorithms are preferred for the SRM converter.
2.2. Classification of SRM Power Converters
Generally, SRM converters are classified based on two criteria. The first criterion is the number of switching devices, while the second criterion depends on the commutation method [14]. However, classifying converters based solely on the number of switching devices does not fully capture the strengths and weaknesses of each converter type. Therefore, the second criterion, which categorises converters based on the commutation method, is adopted. Figure 1 illustrates this classification.
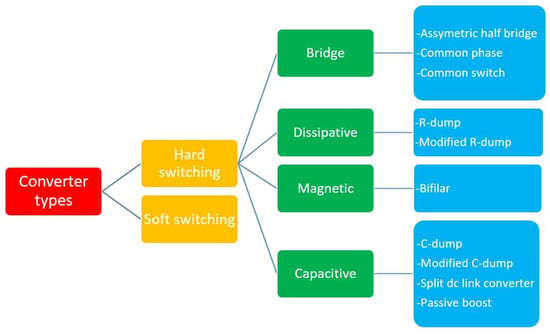
Figure 1.
Classification of SRM power converters.
2.3. Hard-Switching Converters
Most used converters are hard-switched, which typically requires simpler circuitry that is easier to implement compared to soft-switching converters. The hard-switching category includes four subgroups: bridge, dissipative, magnetic, and capacitive.
2.3.1. Bridge Converters
The bridge converter is the most common type of converter used in SRM drives. It includes variants like asymmetric half bridge (ASHB), common phase, and common switch converters, as follows.
Asymmetric Half Bridge
The ASHB is the most prevalent SRM converter [15] and its operation is detailed in this subsection. This converter utilises two switches and two diodes for each phase, as depicted in Figure 2 for a 4ϕ SRM.

Figure 2.
Asymmetric half bridge converter for a 4ϕ SRM.
The ASHB converter operates in three states: magnetisation, free-wheeling, and demagnetisation. These states are illustrated in Figure 3, and the following description is for a specific phase, .
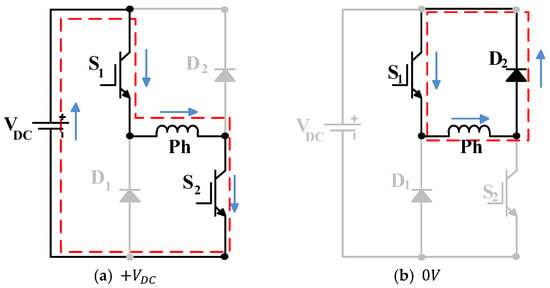
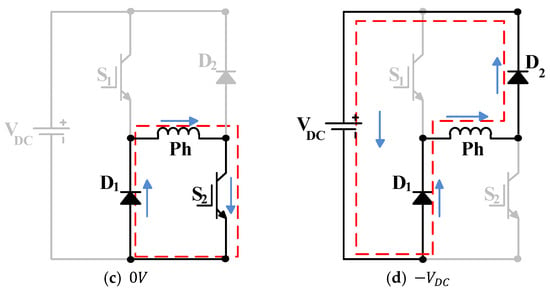
Figure 3.
ASHB converter states: (a) Magnetisation, (b,c) free-wheeling, and (d) demagnetisation.
Magnetisation (): In this state, switches and of the phase to be energised are turned on, as shown in Figure 3a. This action applies the full DC link voltage to the phase, forcing the current to build up.
Free-wheeling (0V): There are two possible switch patterns for this voltage level. The first pattern is with on and off, while the second pattern is with on and off. These patterns are illustrated in Figure 3 parts b and c, respectively, where zero voltage is applied across the phase winding. These two (0V) states can be alternated to balance bridge losses and heating.
Demagnetisation (): In this state, switches and are both off, as shown in Figure 3d. The demagnetisation current (energy) from the motor winding is then pumped back to the DC link, with the winding current reducing to zero before the phase enters the region of negative torque production.
Table 2 shows a summary of the three available converter voltage levels, while Figure 4 depicts typical voltage and current waveforms for the three states.

Table 2.
ASHB converter states.
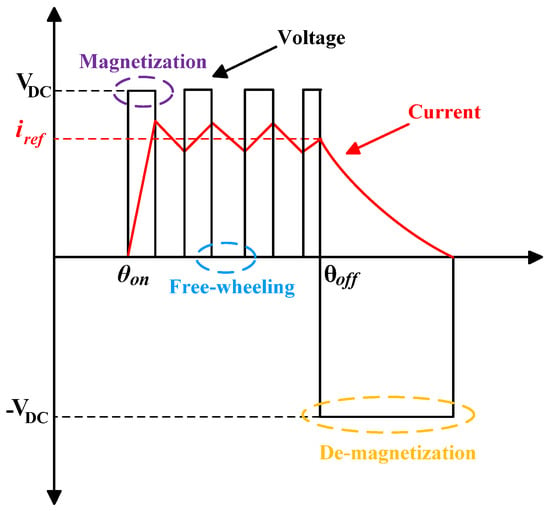
Figure 4.
Typical phase voltage and current waveforms with an ASHB.
Advantages:
- Independent control of each phase without overlap.
- Three available voltage levels, namely .
- Low complexity.
- High fault tolerance, with no link switch ‘shoot through’ path.
- High efficiency as stored magnetic energy in phase winding is fed back to the DClink during demagnetisation.
Drawbacks:
- Increase in semiconductor device number, as each phase requires two switches and two diodes.
- More conduction losses since two semiconductors are connected in series with the conducting phase winding.
- The relatively low magnetisation and demagnetisation voltage limits motor base speed.
Common-Phase Converter
The common-phase converter [16] represents an advancement over the ASHB converter, offering the same benefits but with fewer switches (1.5 switches per phase). Shown in Figure 5, this converter is applicable to the 4ϕ SRM and employs a two-bridge topology. Phases A and C (mechanically at quadrature) are placed in one bridge, sharing a common leg with switch , while phases B and D (mechanically quadrature phases) are in a second bridge with switch , common to both phases B and D. This arrangement utilises the fact that phases sharing a switch in the same bridge are 180° (electrical) out of phase, preventing phase current conduction overlap.
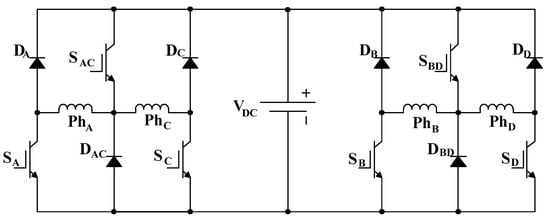
Figure 5.
Common-phase converter using two bridges.
This switch sharing topological approach is effective for SRMs with an even number of phases. Because of switch-sharing, its fault tolerance is reduced, since a fault in the common switch in either of the two bridges results in the loss of the phases incorporated in that bridge.
Common Switch Converter
To minimise the semiconductor device number in the ASHB converter, thus decreasing its cost and size, the common switch converter in Figure 6 was introduced [17].

Figure 6.
Common switch converter.
In this configuration, every phase is equipped with its own switch. A main switch, denoted as S, is common to all phases, effectively lowering the total switch count to n + 1 (where n is the number of phases). Despite its lower cost compared to the ASHB converter, this design sacrifices fault tolerance. It performs well at low speeds; at higher speeds, the off-going phase cannot be rapidly demagnetised (due to the common switch S being activated), leading to a prolonged current tail (only states +V and 0V exist). This, in turn, generates negative phase torque, ultimately reducing the overall developed torque.
2.3.2. Dissipative Converters
The dissipative converter is often seen as the most basic SRM converter, using the fewest number of switches, with just one switch per phase. In this setup, the energy stored in the phase winding is not returned to the power supply but is instead dissipated in a dump resistor. Consequently, this converter is not energy efficient, thus unsuitable for EV application. There are two versions: R-dump [18] and modified R-dump [19].
R-Dump Converter
Figure 7 depicts the R-dump converter, in which the energy stored that is released in the phase winding is dissipated in the dump resistor, . No 0V state (loop) exists. This configuration exhibits low efficiency and necessitates specific cooling for the dump resistor. Therefore, it is best suited for low-power, cost-sensitive applications.

Figure 7.
R-dump converter.
Modified R-Dump Converter
A variant of the R-dump converter is shown in Figure 8, featuring an additional switch, S, connected in parallel with the dump resistor. The time constant for current decay is given by (where, R and L are the phase winding resistance and inductance, respectively). By reducing the duty cycle, α, the effective dump resistance increases (as the 0V periods decease). Conversely, increasing the duty cycle reduces the effective dump resistance, enhancing efficiency during current chopping periods.

Figure 8.
Modified R-dump converter.
2.3.3. Magnetic Converters
The concept behind magnetic converters is to transfer the magnetic energy stored in the SRM phase to a coupled (bifilar) winding. This transferred energy can then be either returned to the power supply or used to energise the next incoming phase. Figure 9 depicts the configuration of a bifilar converter [20], which employs a single switch per phase, being the primary advantage. This configuration only supports two modes: magnetisation and demagnetisation. The free-wheeling mode is not feasible with this setup.

Figure 9.
Bifilar converter.
are the bifilar windings’ effective inductances.
This converter does not waste the demagnetisation energy; instead, it is recycled. The primary drawback of this topology is that each SRM phase needs to be connected to another winding, which adds complexity to the SRM manufacturing and decreases the available copper area for the stator winding. Inadequate coupling between the SRM’s bifilar windings (leakage inductance) leads to voltage spikes when a phase is turned off, necessitating the use of snubber circuits. With 1:1 coupled windings, the required semiconductor voltage ratings (diode and switch) are (at least) 2 VDC.
2.3.4. Capacitive Converters
The capacitive converter employs a dump capacitor to store the demagnetisation energy, which is then either returned to the power supply or utilised to energise the next incoming SRM phase winding. Variants of capacitive converters include C-dump, modified C-dump, split DC link, and passive boost, and these are discussed in the following subsections.
C-Dump Converter
Figure 10 illustrates a C-dump converter, which is classified as belonging to the n + 1 family (meaning that the number of semiconductor switches equals the number of SRM phases, plus one) [21].

Figure 10.
C-dump converter.
The energy stored in the SRM phase winding is transferred to a capacitor, . The voltage across the capacitor is maintained at twice the supply voltage, , to apply to the outgoing phase for quick current extinction. The transferred energy is then returned to the DC link using a buck circuit consisting of .
However, this topology has drawbacks. No 0V state exists. It requires a large capacitor and a buck converter (which includes a sizable inductor). The semiconductor devices need to be rated at double the DC link voltage. Additionally, to keep the voltage across the dump capacitor at , the switching frequency of needs to be high, leading to increased switching losses.
Modified C-Dump Converter
C-dump converter performance is enhanced in Figure 11 [22], where the inductor in the buck circuit is eliminated. The energy stored in the dump capacitor is utilised to directly power the next incoming phase instead of being fed back to the DC link.
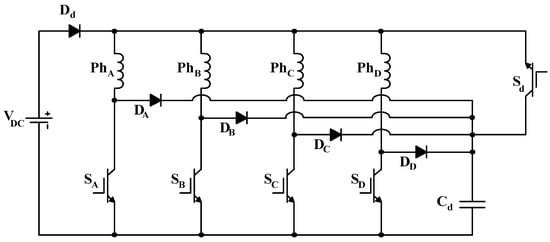
Figure 11.
Modified C-dump converter.
Despite the elimination of the inductor and the reduction in the switching frequency of , the switches are rated at , similar to the C-dump converter. The circuit control is complex, leading to suboptimal performance at high speeds.
Split DC Link Converter
The split DC link converter in Figure 12 [23] features a single switch per phase, thereby lowering the overall switch count. However, it necessitates an SRM with an even number of phases. It utilises only half of the DC link voltage for the magnetisation and demagnetisation of incoming and outgoing phases, respectively. This approach prevents rapid current buildup and decay, thereby limiting the SRM base speed. This converter cannot withstand any phase failure or phase imbalance.
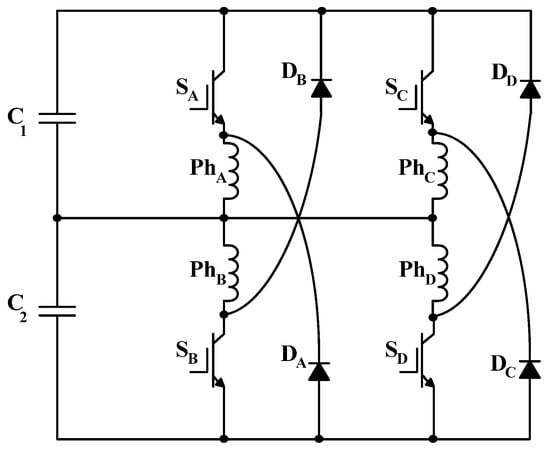
Figure 12.
Split DC link converter.
Passive Boost Converter
Improving SRM performance at high speeds is outlined in [24]. A boost capacitor with a blocking diode is introduced into the DC link. The demagnetisation energy from the outgoing phase is stored in the boost capacitor, reducing the current decay time and effectively extending the range of positive torque production before entering the negative torque region.
The stored energy, which raises the DC link voltage, is then transferred to the next incoming phase, enabling faster current buildup and increasing the motor base speed. Figure 13 illustrates a typical common-phase converter with boost capacitors.

Figure 13.
Common-phase converter with passive boost capacitors: (a) Without regenerative braking and (b) with regenerative braking circuitry.
The converter employs a double bridge topology, with phases A and C grouped in one bridge, sharing a common leg that includes switch . The remaining two phases, B and D, form an independent bridge with a common switch . By utilising the DC-link-blocking diodes and capacitors, the converter can boost the DC link voltage by directing the recovered current to charge the capacitors to levels exceeding the DC source voltage, .
This two-independent bridge configuration allows for more effective voltage boosting (as there is no phase overlap within each bridge) while using a minimal number of switches, as illustrated in Figure 13a. However, a drawback of this topology is that it requires semiconductor devices rated above the DC link voltage (with ratings dependent on the boost voltage). Additionally, due to the presence of DC-link-blocking diodes, circuit modifications are necessary for regenerative braking, if required.
Figure 13b shows the modified voltage-boosting common-phase converter with the regenerative braking circuitry [25]. During braking, the stored energy in the phase winding is not dissipated but returned back to the DC link. However, this energy cannot be pumped to the DC link capacitors, as the capacitors’ voltages will excessively increase. Therefore, the DC link switch and diodes Dx1 and Dy1 are needed to direct the phase winding energy to the DC link rather than to the capacitors.
2.4. Soft-Switching and Advanced Converters
Increasing converter switching frequency, hence decreasing current ripple, is a strategy to enhance SRM performance. However, this increase leads to higher switching losses and greater electromagnetic interference. To address these issues in high switching-frequency applications, soft-switching techniques employing resonant circuits have been suggested [26]; however, due to the resulting complexity and increased converter cost, this approach has been deemed impractical for EV applications.
In [27], a novel converter is introduced, offering performance comparable to the ASHB. This converter requires half the number of diodes but the same number of switches as the ASHB. Another approach, the ring converter proposed in [28], is limited to six-phase SRMs and exhibits significant distortion in phase currents, compromising its fault tolerance. In [29,30], two off-the-shelf inverters are utilised to improve fault tolerance in SRMs. However, this solution requires 12 switches, substantially increasing the converter’s cost, and is only suitable for three-phase SRMs. Reference [31] integrates standard six-pack plus dual modules for three-phase SRMs, offering a more economical solution compared to the ASHB. This converter uses only half the DC link voltage for magnetisation and demagnetisation to allow phase overlap between successive phases. In [32], a three-phase inverter is employed to power a six-phase SRM. Although the inverter is commercially available, the six-phase SRM requires a different winding configuration, limiting SRM drive fabrication. A new winding configuration in [33] allows higher voltages during demagnetisation. The required winding reconfiguration increases production costs. Also, a higher voltage is applied only during phase turn-off, without enhancing performance during phase turn-on.
Recent advancements in EVs include raising the DC link voltage from approximately 400 V to a range between 600 V and 950 V [34]. Consequently, the converter’s voltage rating must also increase. However, higher voltage-rated power semiconductor devices not only exhibit slower response times and lower overall efficiency but also result in higher costs and larger sizes. As a result, multilevel inverters have been proposed [35]. In [36], a comparison was made between a five-level Neutral-Point Diode-Clamped (NPC) converter and an Asymmetric Modular Multilevel Converter (MMC) for high-voltage, high-power applications. However, only the full DC link voltage is utilised, meaning SRM performance at different voltage levels is not fully leveraged. The fault-tolerant converter, based on the NPC topology in [37], has the drawback that half the switches must withstand the full DC link voltage.
In [38], the performance of a three-level NPC converter was compared with that of the conventional ASHB converter. Despite having the same overall rating, the NPC offers advantages such as lower losses, reduced current ripple, and less machine noise. However, motor performance (Nm/kg) is only enhanced at low speeds (below the base speed). Since SRMs can be utilised in high-speed applications (as in the EV), it is crucial to enhance its performance (W/kg) at higher speeds. Additionally, the NPC converter requires large DC link capacitances. In [39], an MMC SRM drive utilises multilevel voltages to decrease torque ripple. However, to accommodate various voltage levels, the number of submodules (SM) must increase, leading to higher converter costs. In [40], a five-voltage level converter was introduced to minimise current noise and torque ripple at low speeds, but its performance was not enhanced at speeds above base speed. An NPC converter with built-in DC link voltage-boosting capacitors was introduced for a four-phase SRM drive in [25]. The converter enhanced SRM drive performance at both low and high speeds. The boosted voltage raised the motor base speed, thereby improving output power and efficiency. The SRM power-to-weight ratio, with voltage boosting capability, was competitive with that of the PMSM, offering the added benefit of a higher torque-to-weight ratio. Regenerative braking could be employed for efficient and rapid braking. Additionally, the converter allowed for the series connection of fast, low-voltage, efficient switches. However, incorporating NPC intermediate dwell states resulted in topology penalties, such as a higher number of gate drives and increased control complexity.
An active boost power converter with self-balanced capacitor voltages is proposed in [41]. The converter has the merit of providing different voltage magnitudes, thus allowing precise current control. A similar adjustable voltage converter is presented in [42,43] for EV applications. A fast-demagnetising converter is proposed in [44] that requires only n+1 switches. Also, the demagnetisation voltage magnitude can be controlled. Finally, in [45], an eight-switch converter is proposed for a six-phase SRM. Although the number of switching devices is reduced, hence reducing the cost and complexity, the converter must operate at high switching frequencies.
Fast switching SiC technology is already used in EVs. Thus, with 1200 V and 1700 V technology readily available, and battery voltages of up to 950 VDC (Formula E Gen2, 756 VDC nominal), series device connected topologies are not necessary or viable. EVs tend to use distributed discrete devices (e.g., TO247) for better cooling. Given EV volume levels, a dedicated module specific for the SRM does not present a cost disadvantage over other machine drive types that use standard existing packages, like six-switch three-phase inverter bridges. If employed, module costs will be dictated by the number of contained devices, not production volume.
2.5. Comparing SRM Power Converters
Numerous converters applicable to SRM drives have been introduced. This section compares these various topologies to determine the most suitable converter for EV applications. Table 3 assesses some of the available converters based on cost, volume, complexity, efficiency, fault tolerance, performance, and, importantly, four quadrant operation (which therefore includes regenerative breaking capability).

Table 3.
Comparison between different power converters.
3. Torque Ripple Minimisation Approaches
This section provides an overview of various methods used to minimise SRM torque ripple (TR). It focuses on two main approaches: machine design and control. The text reviews torque sharing functions, current profiling with artificial neural networks, and direct instantaneous torque control.
3.1. Introduction to TR Approaches
The SRM offers advantages that include robustness, simple construction, and low cost. However, its use in servo applications is limited due to the acoustic noise caused by radial vibration [46,47], most dominate (Nm/A) around the pole alignment position. Additionally, the discrete nature of torque production, coupled with the SRM’s high non-linearity, can lead to significant torque ripple during commutation, where torque production transfers from one phase to the next. This high torque ripple can result in mechanical vibration stresses, potentially leading to mechanical resonance effects and speed oscillations, particularly at low speeds, which are undesirable in EV applications [48].
Since this paper aims to explore the use of SRMs in EV applications, this necessitates understanding the torque requirements specific to such applications, especially given the criticism regarding SRM torque ripple. To maintain a constant speed, the motor torque must counterbalance opposing vehicle forces like rolling resistance, drag, drive incline force, etc. Any torque produced by the motor beyond what is needed to overcome these resistive forces contributes to acceleration.
During acceleration, torque ripple is crucial across the entire torque range. As speed increases, drag force becomes dominant, as it is proportional to the square of the speed (power is proportional to the cube of speed). Conversely, during deceleration (without braking), the SRM-developed torque is less than the forces acting on the vehicle, causing the speed to decrease to balance the machine force with the physical forces acting on the vehicle. With regenerative braking, machine energy in excess of that need by the EV at that speed is recovered back to the DC link, causing a decrease in speed. Deceleration is required across the entire speed/torque range, during which torque ripple remains important.
To address the perceived limitation of SRM torque ripple in EV applications, it is essential to minimise torque ripple across the entire speed and torque ranges.
3.2. Classification of Torque Ripple Minimisation Approaches
Numerous solutions have been proposed to mitigate the undesirable SRM characteristics, such as noise, vibration, and torque ripple [49]. This paper concentrates on minimising torque ripple. Generally, two approaches are considered for reducing torque ripple: the motor design approach and the control approach [50], as illustrated in Figure 14. The following subsections discuss previous research related to these two approaches.

Figure 14.
Classification of torque ripple minimisation approaches.
3.2.1. Machine Design Approach
Increasing the number of stator and rotor poles in SRMs leads to the overlap of more than two phases during commutation (>8/6), which has the potential to reduce torque ripple. However, this approach also increases the switching frequency, resulting in higher converter and machine losses, especially at anticipated EV machine speeds rising towards 20,000 rpm. Also, a higher number of converter switches is needed if the number of phases increases, thereby increasing the overall converter cost and complexity [51].
A new SRM approach [52] explores a configuration with a higher number of rotor poles than stator poles (Ns < Nr). This novel motor concept offers lower mass and copper loss compared to conventional SRMs (Ns > Nr). The increased stator slot area allows for the use of windings with a higher turns number and/or increased Cu cross-sectional area [53]. Also, the higher rotor pole number helps reduce torque ripple [54]; however, the narrower interpolar rotor airgaps results in significantly higher unaligned inductance compared to conventional SRMs. This reduces the energy conversion area, leading to a decrease in developed torque [55]. Furthermore, the prolonged current rise time at phase turn-on due to the higher unaligned inductance necessitates the use of higher DC link voltages to increase the current rate of rise [56].
The introduction of a rotor pole notch, depicted in Figure 15a, was proposed [57] as a method for reducing torque ripple. This concept was further developed in [58] for a mutually coupled SRM. Another approach [59] involves the use of a rotor pole shoe, as shown in Figure 15b. A stator pole slant [60], illustrated in Figure 15c (and also as is shown in Figure 15d) [61], presents a non-uniform air gap for a two-phase SRM aimed at minimising torque ripple. Despite their effectiveness in reducing torque ripple, these rotor modifications tend to result in reduced machine torque density. Another approach [62] focuses on optimising the stator and rotor poles for a four-phase 8/6 SRM to increase average torque and reduce torque ripple. However, the method is limited to a narrow speed range and rated load conditions.

Figure 15.
SRM pole design: (a) Rotor pole notch, (b) rotor pole shoe, (c) stator pole slant, and (d) non-uniform air gap.
Importantly altering the basic rotor and stator design typically leads to decreased power output, which is an undesirable SRM limitation when compared to PMSMs in EVs.
3.2.2. Control Approach
In contrast to the machine design approach to reduce TR, the control approach is more cost-effective, efficient, and flexible, covering a broad speed/torque range [63]. Ripple-free torque can be achieved through current profiling [64], which generates optimal current contours for constant output torque based on static SRM data. The profiles are stored using lookup tables (LUTs), and current controllers track the profiles [65]. However, this method requires memory to store current profiles for different speeds, torque demands, and DC link voltages. Additionally, high-bandwidth current controllers are needed for accurate current tracking [66,67,68]. Using conventional pulse width modulation (PWM) leads to current tracking errors, particularly at high speeds [69,70,71,72]. Most current controllers are based on analytical SRM modelling, leading to inevitable inaccuracies [73]. In [74,75], current profiling and a new SRM design with a flat torque profile are combined to reduce torque ripple, but the design has a narrower speed range compared to conventional SRMs.
Optimal current profiles are typically generated as discrete points, and linear interpolation finds intermediate points. Increasing the number of points improves accuracy but requires more time and storage memory in the form of LUTs. In [76], harmonic coefficients are used to produce current profiles without interpolation, but this method relies on analytical model accuracy. Fuzzy logic and neural networks [77,78] can generate magnetisation data without huge memory but significantly increase computational complexity. In [79,80], a control scheme based on iterative learning control is developed, which does not rely on model accuracy or large memory for magnetisation data but has slow dynamics with poor transient response, which is unsuitable for EV applications.
Average torque control in [81,82] calculates torque using co-energy derived from terminal quantities (V, I) [83]. It is extended in [84] for four-quadrant operation at low speeds but requires precise voltage and current measurements. The effect of varying stator resistance (due to temperature change) is not considered, which affects co-energy estimation.
The principle of direct torque control [85,86] is similar to that used for induction motor control, controlling flux to control torque. Hysteresis controllers are used, leading to variable switching frequency, complicating digital implementation. To address this, a deadbeat torque controller [87] uses a fixed switching frequency but requires a complicated control algorithm. Improving the torque per ampere ratio and efficiency was considered in [88,89]. The model predictive controller in [90] selects a suitable voltage vector but relies on an SRM mathematical model that does not reflect machine non-linearity.
A torque sharing function (TSF) is a good method to minimise SRM torque ripple due to its discrete non-linear nature of torque production [91,92,93]. The total developed SRM torque at any instant is the sum of individual phase torques; thus, the TSF generates reference torque for each individual phase using the total reference torque. Each reference phase torque is transformed into a reference current using a LUT, depending on rotor position. The reference phase current is compared with the actual phase current, generating an error signal, where this error is minimised using a high bandwidth current controller. A similar concept is found in direct instantaneous torque control (DITC), where the total torque is controlled rather than individual phase torques.
Given that the most popular torque ripple minimisation approaches use current profiling, direct instantaneous torque control (DITC), and torque sharing functions (TSFs), these are discussed in the following three subsections.
Current Profiling
Ripple-free torque can be obtained by current profiling [94], where optimal current contours, producing constant output torque, are generated using static SRM data [95]. These current profiles are stored using lookup tables (LUTs), and current controllers are used to track the profiles [96]. Apart from using current profile LUTs, artificial neural networks (ANNs) could be used to replace the current profile LUTs. This subsection will discuss the general concept of current profiling, with a focus on using ANNs.
An ANN is a computational model that emulates the functioning of biological neural networks [97]. The fundamental unit within an ANN is the neuron, depicted in Figure 16, where ‘a’ represents the input, ‘s’ is the output, and ‘b’, ‘c’, ‘f’, and ‘r’ denote the bias, weight, transfer function, and net input, respectively.

Figure 16.
The basic structure of ANN (neuron).
The bias and the weight are scalar values that can be adjusted while the relation between the input and output of the neuron is given by (1).
The choice between linear or non-linear transfer functions depends on the specific requirements of the application. Figure 17 illustrates several commonly used transfer functions in ANNs, including linear, hard limit, and log sigmoid [98].
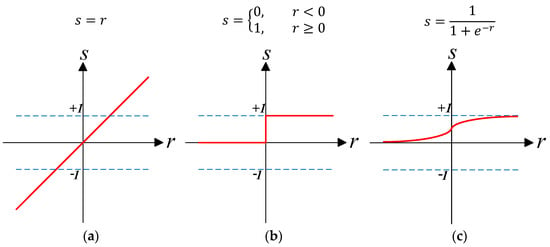
Figure 17.
Common transfer functions: (a) Linear, (b) hard limit, and (c) log sigmoid.
Describing the model with only a single neuron is inadequate. Consequently, multiple neurons are interconnected in parallel to constitute a layer. Multiple layers can be arranged in succession to construct the ANN.
Figure 18 shows a two-layer ANN comprising an input layer, one hidden layer, and an output layer. This model features two inputs, a hidden layer consisting of three neurons, and an output layer with a single neuron, reflecting the model’s single output.
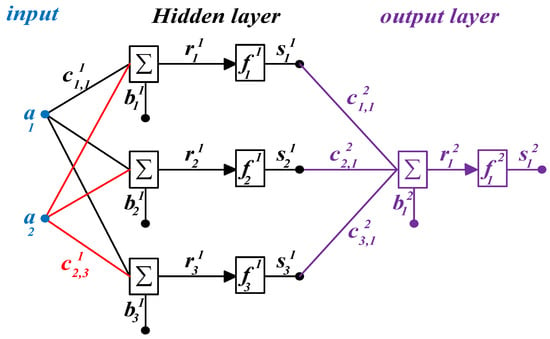
Figure 18.
Two-layer ANN.
Utilising an ANN can help generate the necessary current profile for each phase [99], thereby reducing the torque ripple. The inputs for the ANN consist of the rotor angle and the required torque . The ANN outputs the necessary current profiles [100]. Figure 19 illustrates the control system for minimising torque ripple in an SRM using an ANN. Current regulation is achieved using a hysteresis band current controller (HBCC).

Figure 19.
Illustration of current profiling using ANN.
Torque Sharing Function
A torque sharing function (TSF) is an effective method for reducing torque ripple in SRM drives, which is caused by the discrete, non-linear nature of torque production [101,102]. The most critical aspect of torque ripple reduction is minimising the ripple during commutation, that is the time when torque production is transferred from one active phase to the next. The total developed SRM torque at any instant is the sum of individual phase torques. Therefore, a TSF generates a reference torque for each phase based on the total reference torque. This reference phase torque is converted into a reference current using a lookup table (LUT) that depends on rotor position [103,104].
The reference phase current is then compared with the actual phase current to generate an error signal, which is minimised using a high-bandwidth current controller. The impact of phase turn-on and turn-off is discussed in [105]. Optimisation of the TSF concerning phase root-mean-square (rms) current and efficiency is examined in [106]. The non-linear TSF proposed in [107] accommodates SRM magnetic characteristics.
While it is possible to generate the reference current signal from the individual phase reference torque, inverting the LUT is challenging [108]. An alternative approach involves obtaining actual phase torques directly from actual phase currents using a LUT. The generated reference phase torques and the actual phase torques are then compared, and the command torque is adjusted by the controller [109]. Typically, a hysteresis band torque controller (HBTC) is employed to manage the error signal. Figure 20 illustrates the operation of the TSF method for a four-phase 8/6 SRM.
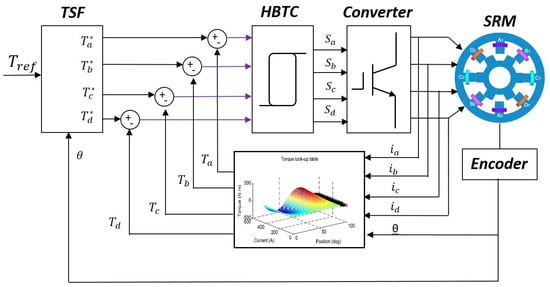
Figure 20.
Illustration of TSF control system.
Torque production in an SRM is categorised into two regions: single and double excitation regions, corresponding to one and two phases conducting, respectively [110]. In the single excitation region, only one phase generates the total required torque. In the double excitation region, the total torque developed is shared between two phases, the incoming and outgoing phases, while maintaining an overall torque equal to the reference torque value [111]. The method by which the two phases share the torque determines the type of torque sharing function (TSF) used. Primarily, two types of TSF are employed: linear and non-linear TSFs. Non-linear TSFs include cosine, cubic, and exponential functions, as illustrated in Figure 21. Non-linear TSF methods partly account for the non-linearity of SRMs, making them a more efficient approach [112].

Figure 21.
Types of TSF: (a) linear, (b) cos, (c) cubic, and (d) exponential.
Equation (2) defines the individual torque profile for an arbitrary phase k.
where is the turn-on angle, is the turn-off angle, is the overlap angle, and is the rotor pole pitch. is the demand torque.
The arbitrary phase k is energised depending on rotor position between the turn-on and turn-off angles; for the motoring mode, the turn-on and turn-of angles must satisfy (3).
where and are the unaligned and aligned rotor position, respectively.
The overlap angle represents the interval where the torque is shared between two phases, the incoming and outgoing phases. The maximum overlap angle is calculated using (4).
where is defined by:
where n is the number of phases and is the number of rotor poles.
During the interval of commutation, the function increases from 0 to 1 while the function decreases from 1 to 0. The function and subsequently depend on the type of TSF. The linear, cos, cubic and exponential TSFs are expressed in (6)–(9), respectively.
Direct Instantaneous Torque Control
Due to significant SRM non-linearity, the actual phase torque cannot perfectly track the reference torque near the unaligned and aligned positions, as with TSFs or current profiling. This leads to noticeable torque dips. To address this, an alternative method [113] treats the total torque as the control variable instead of the phase torque, as in TSFs [114,115,116,117]. Direct instantaneous torque control (DITC) can effectively regulate the instantaneous developed torque, thereby minimising torque ripple. A four-quadrant DITC was introduced in [118], but it relies on a hysteresis controller with variable switching frequency. To overcome this drawback, a predictive PWM method was presented in [119], which extends the approach for SRMs with more than four phases.
The approach involves measuring the actual phase currents and then converting them into phase torques based on rotor position using LUTs [120,121,122]. These individual phase-torques are summed to determine the total developed torque, which is then compared with the desired reference torque value [123,124]. A hysteresis band torque control (HBTC) is employed to generate the converter switching signals [125,126], as in Figure 22, for a four-phase SRM.
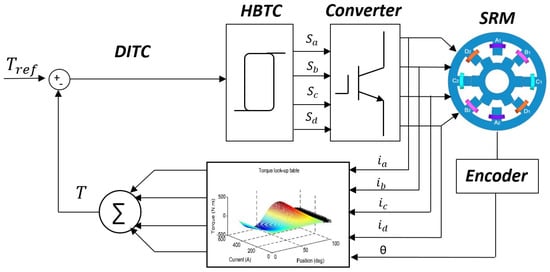
Figure 22.
Illustration of DITC control system.
3.3. Comparison of Torque Ripple Minimisation Approaches
This section provides a comparison between the three dominant torque ripple minimisation approaches in the literature, namely current profiling, TSF and DITC, as summarised in Table 4. The machine design approach requires modifications to the SRM construction during fabrication, which is not only an expensive but also a complex process. Hence, it is not a recommended approach and therefore is not included in the comparison.

Table 4.
Comparison between different torque ripple minimisation approaches.
Based on Table 4, the DITC approach proves to be the most efficient torque ripple minimisation approach. It offers flexibility over a wide torque/speed range and is simple to implement. RMS current minimisation, and subsequently loss reduction, could be achieved by adjusting the turn on/off angles. Finally, the merit of DITC is that it treats the total torque as the main control parameter, not the individual torques (as in a TSF) or the currents (as in current profiling).
4. Discussion and Conclusions
EVs are increasingly focused on reducing fossil fuel consumption and carbon dioxide emissions. SRMs are gaining interest for these vehicles due to their simple and robust structures, high reliability, and lack of rare-earth materials. However, the inherent SRM structure causes acoustic noise, limiting their development. In addition, an SRM requires a special power converter, not the standard three-phase inverter.
This paper comprehensively reviewed the most popular power converters used to drive SRMs. According to the analysis, the converter featuring shared phase and voltage boosting is the most promising power converter for SRM drives.
The paper also presents an overview of the most widely used SRM torque ripple minimisation approaches. The focus is on motor topology optimisation and control strategy improvement. From the review, it is evident that much effort has been devoted to optimising motor structure through new stator and rotor designs. However, this effort results in structural complexity and increased production costs. Improving control strategies is a more cost-effective and flexible approach to addressing the SRM torque ripple problem. The methods, advantages, and limitations of these approaches were summarised and compared. It was concluded that DITC is the most efficient and mature torque ripple minimisation approach.
Based on the research presented in this paper, the authors suggest a 4φ SRM driven by a passive boost and a shared phase converter, controlled using DITC. The proposed SRM drive, shown in Figure 23, suits EV applications. The 4φ SRM is selected for the following two reasons: Firstly, an even-phase SRM is required from the converter perspective. This excludes the three-phase and five-phase SRMs. Secondly, a compact converter with minimal switching losses is required, hence the six-phase SRM is excluded. Thus, the 4ϕ SRM represents the optimal choice with compromises between converter cost, complexity, and losses. Several torque ripple minimisation approaches can be deployed. However, as illustrated in Section 3, DITC is the most dominant and efficient control approach.
Figure 23.
Suggested SRM drive for EV applications.
The SRM drive senses the rotor position using a position sensor. An error signal, generated based on the required reference speed, is handled using a PID controller to generate the reference torque. The torque ripple minimisation block is illustrated in Figure 22, while the regenerative power converter is shown in Figure 13b.
Future research and forecasted research hotspots include:
- Investigating the performance of SRM power converters using SiC and GaN semiconductor devices.
- Investigating and developing torque ripple reduction techniques for converter fault conditions, including open and short circuit faults, using fewer additional power switches.
- Developing control schemes to reduce torque ripple over a wide speed range.
Author Contributions
Conceptualisation, A.A.-A. and M.E.; Analysis, A.A.-A.; Methodology, A.A.-A., M.E. and B.W.; Supervision, B.W.; Writing—Review and Editing, A.A.-A., M.E. and B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Habib, S.; Khan, M.M.; Abbas, F.; Sang, L.; Shahid, M.U.; Tang, H. A Comprehensive Study of Implemented International Standards, Technical Challenges, Impacts and Prospects for Electric Vehicles. IEEE Access 2018, 6, 13866–13890. [Google Scholar] [CrossRef]
- Bostanci, E.; Moallem, M.; Parsapour, A.; Fahimi, B. Opportunities and Challenges of Switched Reluctance Motor Drives for Electric Propulsion: A Comparative Study. IEEE Trans. Transp. Electrif. 2017, 3, 58–75. [Google Scholar] [CrossRef]
- Ramesh, P.; Lenin, N.C. High Power Density Electrical Machines for Electric Vehicles—Comprehensive Review Based on Material Technology. IEEE Trans. Magn. 2019, 55, 0900121. [Google Scholar] [CrossRef]
- Chiba, A.; Kiyota, K. Review of research and development of switched reluctance motor for hybrid electrical vehicle. In Proceedings of the 2015 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Turin, Italy, 26–27 March 2015; pp. 127–131. [Google Scholar] [CrossRef]
- Zeraoulia, M.; Benbouzid, M.E.H.; Diallo, D. Electric Motor Drive Selection Issues for HEV Propulsion Systems: A Comparative Study. IEEE Trans. Veh. Technol. 2006, 55, 1756–1764. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Carraro, E.; Castiello, M.; Fornasiero, E. Electric Vehicle Traction Based on Synchronous Reluctance Motors. IEEE Trans. Ind. Appl. 2016, 52, 4762–4769. [Google Scholar] [CrossRef]
- Kumar, G.; Chuang, C.; Lu, M.; Liaw, C. Development of an Electric Vehicle Synchronous Reluctance Motor Drive. IEEE Trans. Veh. Technol. 2020, 69, 5012–5024. [Google Scholar] [CrossRef]
- Rahman, K.; Fahimi, B.; Suresh, G.; Rajarathnam, A.; Ehsani, M. Advantages of switched reluctance motor applications to EV and HEV: Design and control issues. IEEE Trans. Ind. Appl. 2000, 36, 111–121. [Google Scholar] [CrossRef]
- Wang, S.; Zhan, Q.; Ma, Z.; Zhou, L. Implementation of a 50-kW four-phase switched reluctance motor drive system for hybrid electric vehicle. IEEE Trans. Magn. 2005, 41, 501–504. [Google Scholar] [CrossRef]
- Chiba, A.; Kiyota, K.; Hoshi, N.; Takemoto, M.; Ogasawara, S. Development of a Rare-Earth-Free SR Motor with High Torque Density for Hybrid Vehicles. IEEE Trans. Energy Convers. 2015, 30, 175–182. [Google Scholar] [CrossRef]
- Kiyota, K.; Kakishima, T.; Chiba, A. Comparison of Test Result and Design Stage Prediction of Switched Reluctance Motor Competitive with 60-kW Rare-Earth PM Motor. IEEE Trans. Ind. Electron. 2014, 61, 5712–5721. [Google Scholar] [CrossRef]
- Takeno, M.; Chiba, A.; Hoshi, N.; Ogasawara, S.; Takemoto, M.; Rahman, M.A. Test Results and Torque Improvement of the 50-kW Switched Reluctance Motor Designed for Hybrid Electric Vehicles. IEEE Trans. Ind. Appl. 2012, 48, 1327–1334. [Google Scholar] [CrossRef]
- Vukosavic, S.; Stefanovic, V. SRM inverter topologies: A comparative evaluation. IEEE Trans. Ind. Appl. 1991, 27, 1034–1047. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H. Switched reluctance motor converter topologies: A review. In Proceedings of the 2014 IEEE International Conference on Industrial Technology (ICIT), Busan, Republic of Korea, 26 February–1 March 2014; pp. 840–846. [Google Scholar]
- Hu, Y.; Wang, T.; Ding, W. Performance Evaluation on a Novel Power Converter with Minimum Number of Switches for a Six-Phase Switched Reluctance Motor. IEEE Trans. Ind. Electron. 2019, 66, 1693–1702. [Google Scholar] [CrossRef]
- Pollock, C.; Williams, B.W. Power converter circuits for switched reluctance motors with the minimum number of switches. IEE Proc. B Electr. Power Appl. 1990, 137, 373–384. [Google Scholar] [CrossRef]
- Jang, D.H.; Husain, I.; Ehsani, M. Modified (n+1) switch converter for switched reluctance motor drives. In Proceedings of the PESC ‘95—Power Electronics Specialist Conference, Atlanta, GA, USA, 18–22 June 1995; Volume 2, pp. 1121–1127. [Google Scholar]
- Krishnan, R.; Materu, P.N. Analysis and design of a low cost converter for switched reluctance motor drives. IEEE Trans. Ind. Appl. 1993, 29, 320–327. [Google Scholar] [CrossRef]
- Ehsani, M.; Husain, I.; Ramani, K.R.; Galloway, J.H. Dual-decay converter for switched reluctance motor drives in low-voltage applications. IEEE Trans. Power Electron. 1993, 8, 224–230. [Google Scholar] [CrossRef]
- Miller, T.J. Converter Volt-Ampere Requirements of the Switched Reluctance Motor Drive. IEEE Trans. Ind. Appl. 1985, IA-21, 1136–1144. [Google Scholar] [CrossRef]
- Mir, S.; Husain, I.; Elbuluk, M.E. Energy-efficient C-dump converters for switched reluctance motors. IEEE Trans. Power Electron. 1997, 12, 912–921. [Google Scholar] [CrossRef]
- Hava, A.M.; Blasko, V.; Lipo, T.A. A modified C-dump converter for variable-reluctance machines. IEEE Trans. Ind. Appl. 1992, 28, 1017–1022. [Google Scholar] [CrossRef]
- Ryoo, H.-J.; Kim, W.-H.; Rim, G.-H.; Kang, W.; Park, J.-H.; Won, C.-Y. A new split source type converter for SRM drives. In Proceedings of the PESC 98 Record. 29th Annual IEEE Power Electronics Specialists Conference (Cat. No.98CH36196), Fukuoka, Japan, 22 May 1998; Volume 2, pp. 1290–1294. [Google Scholar]
- Dessouky, Y.; Williams, B.; Fletcher, J. A novel power converter with voltage-boosting capacitors for a four-phase SRM drive. IEEE Trans. Ind. Electron. 1998, 45, 815–823. [Google Scholar] [CrossRef]
- Abdel-Aziz, A.A.; Ahmed, K.H.; Wang, S.; Massoud, A.M.; Williams, B.W. A Neutral-Point Diode-Clamped Converter with Inherent Voltage-Boosting for a Four-Phase SRM Drive. IEEE Trans. Ind. Electron. 2020, 67, 5313–5324. [Google Scholar] [CrossRef]
- Cabezuelo, D.; Andreu, J.; Kortabarria, I.; Ibarra, E.; Garate, I. SRM converter topologies for EV application: State of the technology. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 861–866. [Google Scholar]
- Xu, S.; Chen, H.; Yang, J.; Dong, F. Performance Evaluation and Reliability Enhancement of Switched Reluctance Drive System by a Novel Integrated Power Converter. IEEE Trans. Power Electron. 2019, 34, 11090–11102. [Google Scholar] [CrossRef]
- Deng, X.; Mecrow, B.C.; Wu, H.; Martin, R.; Gai, Y. Cost-Effective and High-Efficiency Variable-Speed Switched Reluctance Drives with Ring-Connected Winding Configuration. IEEE Trans. Energy Convers. 2019, 34, 120–129. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Gan, C.; Guo, J. Modular Full-Bridge Converter for Three-Phase Switched Reluctance Motors with Integrated Fault-Tolerance Capability. IEEE Trans. Power Electron. 2019, 34, 2622–2634. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, D.; Xu, L.; Wang, J.; Lin, Z.; Zhu, X. Fault-Tolerant Operation of a Novel Dual-Channel Switched Reluctance Motor Using Two 3-Phase Standard Inverters. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Song, S.; Xia, Z.; Zhang, Z.; Liu, W. Control Performance Analysis and Improvement of a Modular Power Converter for Three-Phase SRM with Y-Connected Windings and Neutral Line. IEEE Trans. Ind. Electron. 2016, 63, 6020–6030. [Google Scholar] [CrossRef]
- Martin, R.; Widmer, J.D.; Mecrow, B.C.; Kimiabeigi, M.; Mebarki, A.; Brown, N.L. Electromagnetic Considerations for a Six-Phase Switched Reluctance Motor Driven by a Three-Phase Inverter. IEEE Trans. Ind. Appl. 2016, 52, 3783–3791. [Google Scholar] [CrossRef]
- Elmutalab, M.A.; Elrayyah, A.; Husain, T.; Sozer, Y. Extending the Speed Range of a Switched Reluctance Motor Using a Fast-Demagnetizing Technique. IEEE Trans. Ind. Appl. 2018, 54, 3294–3304. [Google Scholar] [CrossRef]
- Jung, C. Power Up with 800-V Systems: The benefits of upgrading voltage power for battery-electric passenger vehicles. IEEE Electrif. Mag. 2017, 5, 53–58. [Google Scholar] [CrossRef]
- Gaafar, M.A.; Abdelmaksoud, A.; Orabi, M.; Chen, H.; Dardeer, M. Performance Investigation of Switched Reluctance Motor Driven by Quasi-Z-Source Integrated Multiport Converter with Different Switching Algorithms. Sustainability 2021, 13, 9517. [Google Scholar] [CrossRef]
- Pires, V.F.; Cordeiro, A.; Foito, D.; Pires, A.J. Fault-Tolerant Multilevel Converter to Feed a Switched Reluctance Machine. Machines 2022, 10, 35. [Google Scholar] [CrossRef]
- Borecki, J.; Orlik, B. Novel, multilevel converter topology for fault-tolerant operation of switched reluctance machines. In Proceedings of the 2017 11th IEEE International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Cadiz, Spain, 4–6 April 2017; pp. 375–380. [Google Scholar]
- Peng, F.; Ye, J.; Emadi, A. An asymmetric three-level neutral point diode clamped converter for switched reluctance motor drives. IEEE Trans. Power Electron. 2017, 32, 8618–8631. [Google Scholar] [CrossRef]
- Gan, C.; Sun, Q.; Wu, J.; Kong, W.; Shi, C.; Hu, Y. MMC-based SRM drives with decentralized battery energy storage system for hybrid electric vehicles. IEEE Trans. Power Electron. 2019, 34, 2608–2621. [Google Scholar] [CrossRef]
- Yuan, K.; Ma, M.; Wang, Z.; Wang, R.; Yang, S. A new five-level power converter for switched reluctance motor drive. In Proceedings of the Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar]
- Han, G.; Chen, H. Improved Power Converter of SRM Drive for Electric Vehicle with Self-Balanced Capacitor Voltages. IEEE Trans. Transp. Electrif. 2021, 7, 1339–1348. [Google Scholar] [CrossRef]
- Cai, J.; Zhao, X. An On-Board Charger Integrated Power Converter for EV Switched Reluctance Motor Drives. IEEE Trans. Ind. Electron. 2020, 68, 3683–3692. [Google Scholar] [CrossRef]
- Chithrabhanu, A.; Vasudevan, K. Analysis and Design Considerations of a Buck-Boost Energy Recovery-Based Power Converter for SRM Drive. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 886–900. [Google Scholar] [CrossRef]
- Rana, K.; Teja, A.V.R. Fast Discharging (N+1) Switch Converter with Regenerative Flyback Operation for N-Phase SRM Drives. IEEE Trans. Power Electron. 2022, 37, 8359–8368. [Google Scholar] [CrossRef]
- Guan, M.; Liu, C.; Han, S.; Sun, X. Analysis of Midpoint Current Characteristics for Novel Six-Phase N+2 Power Converter in Different Working Condition. IEEE Access 2020, 8, 105104–105117. [Google Scholar] [CrossRef]
- Dong, J.; Jiang, J.W.; Howey, B.; Li, H.; Bilgin, B.; Callegaro, A.D.; Emadi, A. Hybrid acoustic noise analysis approach of conventional and mutually coupled switched reluctance motors. IEEE Trans. Energy Convers. 2017, 32, 1042–1051. [Google Scholar] [CrossRef]
- Almirante, I.; Lorenzani, E. Simple Strategy for Torque Ripple Minimization in Switched Reluctance Motor Drives. Energies 2023, 16, 6885. [Google Scholar] [CrossRef]
- Rana, A.K.; Teja, A.V.R. A Mathematical Torque Ripple Minimization Technique Based on a Nonlinear Modulating Factor for Switched Reluctance Motor Drives. IEEE Trans. Ind. Electron. 2022, 69, 1356–1366. [Google Scholar] [CrossRef]
- Gan, C.; Wu, J.; Sun, Q.; Kong, W.; Li, H.; Hu, Y. A review on machine topologies and control techniques for low-noise switched reluctance motors in electric vehicle applications. IEEE Access 2018, 6, 31430–31443. [Google Scholar] [CrossRef]
- Hamouda, M.; Al-Amyal, F.; Odinaev, I.; Ibrahim, M.N.; Számel, L. A Novel Universal Torque Control of Switched Reluctance Motors for Electric Vehicles. Mathematics 2022, 10, 3833. [Google Scholar] [CrossRef]
- Deng, X.; Mecrow, B.; Wu, H.; Martin, R. Design and development of low torque ripple variable-speed drive system with six-phase switched reluctance motors. IEEE Trans. Energy Convers. 2017, 33, 420–429. [Google Scholar] [CrossRef]
- Jiang, J.; Bilgin, B.; Emadi, A. Three-phase 24/16 switched reluctance machine for a hybrid electric powertrain. IEEE Trans. Transp. Electrif. 2017, 3, 76–85. [Google Scholar] [CrossRef]
- Desai, P.C.; Krishnamurthy, M.; Schofield, N.; Emadi, A. Novel switched reluctance machine configuration with higher number of rotor poles than stator poles: Concept to implementation. IEEE Trans. Ind. Electron. 2010, 57, 649–659. [Google Scholar] [CrossRef]
- Bilgin, B.; Emadi, A.; Krishnamurthy, M. Design considerations for switched reluctance machines with a higher number of rotor poles. IEEE Trans. Ind. Electron. 2012, 59, 3745–3756. [Google Scholar] [CrossRef]
- Bilgin, B.; Emadi, A.; Krishnamurthy, M. Comprehensive evaluation of the dynamic performance of a 6/10 SRM for traction application in PHEVs. IEEE Trans. Ind. Electron. 2013, 60, 2564–2575. [Google Scholar] [CrossRef]
- Lin, J.; Schofield, N.; Emadi, A. External-rotor 6-10 switched reluctance motor for an electric bicycle. IEEE Trans. Transp. Electrif. 2015, 1, 348–356. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, H.S.; Kwon, B.I.; Kim, B.T. New rotor shape design for minimum torque ripple of SRM using FEM. IEEE Trans. Magn. 2004, 40, 754–757. [Google Scholar] [CrossRef]
- Li, G.; Ojeda, J.; Hlioui, S.; Hoang, E.; Lecrivain, M.; Gabsi, M. Modification in rotor pole geometry of mutually coupled switched reluctance machine for torque ripple mitigating. IEEE Trans. Magn. 2011, 48, 2025–2034. [Google Scholar] [CrossRef]
- Choi, Y.K.; Yoon, H.S.; Koh, C.S. Pole-shape optimization of a switched-reluctance motor for torque ripple reduction. IEEE Trans. Magn. 2007, 43, 1797–1800. [Google Scholar] [CrossRef]
- Sheth, N.; Rajagopal, K. Torque profiles of a switched reluctance motor having special pole face shapes and asymmetric stator poles. IEEE Trans. Magn. 2004, 40, 2035–2037. [Google Scholar] [CrossRef]
- Lee, D.H.; Pham, T.H.; Ahn, J.W. Design and operation characteristics of four-two pole high-speed SRM for torque ripple reduction. IEEE Trans. Ind. Electron. 2013, 60, 3637–3643. [Google Scholar] [CrossRef]
- Sheth, N.; Rajagopal, K. Optimum pole arcs for a switched reluctance motor for higher torque with reduced ripple. IEEE Trans. Magn. 2003, 39, 3214–3216. [Google Scholar] [CrossRef]
- Jing, B.; Dang, X.; Liu, Z.; Ji, J. Torque Ripple Suppression of Switched Reluctance Motor with Reference Torque Online Correction. Machines 2023, 11, 179. [Google Scholar] [CrossRef]
- He, X.; Yao, Y. An Improved Hybrid Control Scheme of a Switched Reluctance Motor for Torque Ripple Reduction. Appl. Sci. 2022, 12, 12283. [Google Scholar] [CrossRef]
- Dúbravka, P.; Rafajdus, P.; Makyš, P.; Szabó, L. Control of switched reluctance motor by current profiling under normal and open phase operating condition. IET Electr. Power Appl. 2017, 11, 548–556. [Google Scholar] [CrossRef]
- Schulz, S.; Rahman, K. High-performance digital PI current regulator for EV switched reluctance motor drives. IEEE Trans. Ind. Appl. 2003, 39, 1118–1126. [Google Scholar] [CrossRef]
- Gobbi, R.; Ramar, K. Optimization techniques for a hysteresis current controller to minimize torque ripple in switched reluctance motors. IET Electr. Power Appl. 2009, 3, 453–460. [Google Scholar] [CrossRef]
- Lin, Z.; Reay, D.; Williams, B.; He, X. High-performance current control for switched reluctance motors based on on-line estimated parameters. IET Electr. Power Appl. 2010, 4, 67–74. [Google Scholar] [CrossRef]
- Mikail, R.; Husain, I.; Sozer, Y.; Islam, M.S.; Sebastian, T. A fixed switching frequency predictive current control method for switched reluctance machines. IEEE Trans. Ind. Appl. 2014, 50, 3717–3726. [Google Scholar] [CrossRef]
- Ye, J.; Malysz, P.; Emadi, A. A fixed-switching-frequency integral sliding mode current controller for switched reluctance motor drives. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 381–394. [Google Scholar] [CrossRef]
- Li, X.; Shamsi, P. Model predictive current control of switched reluctance motors with inductance auto-calibration. IEEE Trans. Ind. Electron. 2016, 63, 3934–3941. [Google Scholar] [CrossRef]
- Peng, F.; Ye, J.; Emadi, A. A digital PWM current controller for switched reluctance motor drives. IEEE Trans. Power Electron. 2016, 31, 7087–7098. [Google Scholar]
- Zhang, X.; Yang, Q.; Ma, M.; Lin, Z.; Yang, S. A switched reluctance motor torque ripple reduction strategy with deadbeat current control and active thermal management. IEEE Trans. Veh. Technol. 2020, 69, 317–327. [Google Scholar] [CrossRef]
- Mikail, R.; Husain, I.; Sozer, Y.; Islam, M.; Sebastian, T. Torque-ripple minimization of switched reluctance machines using current profiling. IEEE Trans. Ind. Appl. 2013, 49, 1258–1267. [Google Scholar] [CrossRef]
- Mikail, R.; Husain, I.; Islam, M.; Sozer, Y.; Sebastian, T. Four quadrant torque ripple minimization of switched reluctance machine through current profiling with mitigation of rotor eccentricity problem and sensor errors. IEEE Trans. Ind. Appl. 2015, 51, 2079–2104. [Google Scholar] [CrossRef]
- Chapman, P.; Sudhoff, S. Design and precise realization of optimized current waveforms for an 8/6 switched reluctance drive. IEEE Trans. Power Electron. 2002, 17, 76–83. [Google Scholar] [CrossRef]
- Henriques, L.; Branco, P.C.; Rolim, L.; Suemitsu, W. Proposition of an offline learning current modulation for torque-ripple reduction in switched reluctance motors: Design and experimental evaluation. IEEE Trans. Ind. Electron. 2002, 49, 665–676. [Google Scholar] [CrossRef]
- Lin, Z.; Reay, D.; Williams, B.; He, X. Torque ripple reduction in switched reluctance motor drives using B-spline neural networks. IEEE Trans. Ind. Appl. 2006, 42, 1445–1453. [Google Scholar] [CrossRef]
- Sahoo, S.; Panda, S.; Xu, J. Iterative learning-based high-performance current controller for switched reluctance motors. IEEE Trans. Energy Convers. 2004, 19, 491–498. [Google Scholar] [CrossRef]
- Sahoo, S.; Panda, S.; Xu, J.-X. Indirect torque control of switched reluctance motors using iterative learning control. IEEE Trans. Power Electron. 2005, 20, 200–208. [Google Scholar] [CrossRef]
- Inderka, R.; De Doncker, R. High-dynamic direct average torque control for switched reluctance drives. IEEE Trans. Ind. Appl. 2003, 39, 1040–1045. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, H.; Yang, Z. Average torque control of switched reluctance machine drives for electric vehicles. IET Electr. Power Appl. 2015, 9, 459–468. [Google Scholar] [CrossRef]
- Wong, K.; Cheng, K.; Ho, S. On-line instantaneous torque control of a switched reluctance motor based on co-energy control. IET Electr. Power Appl. 2009, 3, 257–264. [Google Scholar] [CrossRef]
- Wong, K.; Cheng, K.; Ho, S. Four-quadrant instantaneous torque control of switched reluctance machine at low speed based on co-energy control. IET Electr. Power Appl. 2009, 3, 431–444. [Google Scholar] [CrossRef]
- Cheok, A.; Fukuda, Y. A new torque and flux control method for switched reluctance motor drives. IEEE Trans. Power Electron. 2002, 17, 543–557. [Google Scholar] [CrossRef]
- Ai-de, X.; Xianchao, Z.; Kunlun, H.; Yuzhao, C. Torque ripple reduction of SRM using optimized voltage vector in DTC. IET Electr. Syst. Transp. 2018, 8, 35–43. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, A.; Han, L.; Wang, S. Minimizing torque ripple of SRM by applying DB-DTFC. IET Electr. Power Appl. 2019, 13, 1883–1890. [Google Scholar] [CrossRef]
- Reddy, P.; Ronaki, D.; Perumal, P. Efficiency improvement and torque ripple minimization of four-phase switched reluctance motor drive using new direct torque control strategy. IET Electr. Power Appl. 2020, 14, 52–61. [Google Scholar] [CrossRef]
- Yan, N.; Cao, X.; Deng, Z. Direct torque control for switched reluctance motor to obtain high torque–ampere ratio. IEEE Trans. Ind. Electron. 2018, 66, 5144–5152. [Google Scholar] [CrossRef]
- Xu, A.; Shang, C.; Chen, J.; Zhu, J.; Han, L. A new control method based on DTC and MPC to reduce torque ripple in SRM. IEEE Access 2019, 7, 68584–68593. [Google Scholar] [CrossRef]
- Ye, J.; Bilgin, B.; Emadi, A. An Extended-Speed Low-Ripple Torque Control of Switched Reluctance Motor Drives. IEEE Trans. Power Electron. 2015, 30, 1457–1470. [Google Scholar] [CrossRef]
- Ye, J.; Bilgin, B.; Emadi, A. An Offline Torque Sharing Function for Torque Ripple Reduction in Switched Reluctance Motor Drives. IEEE Trans. Power Electron. 2015, 30, 726–735. [Google Scholar] [CrossRef]
- Li, H.; Bilgin, B.; Emadi, A. An Improved Torque Sharing Function for Torque Ripple Reduction in Switched Reluctance Machines. IEEE Trans. Power Electron. 2019, 34, 1635–1644. [Google Scholar] [CrossRef]
- Cai, H.; Wang, H.; Li, M.; Shen, S.; Feng, Y.; Zheng, J. Torque Ripple Reduction for Switched Reluctance Motor with Optimized PWM Control Strategy. Energies 2018, 11, 3215. [Google Scholar] [CrossRef]
- Huang, L.; Zhu, Z.Q.; Feng, J.; Guo, S.; Li, Y.; Shi, J.X. Novel Current Profile of Switched Reluctance Machines for Torque Density Enhancement in Low-Speed Applications. IEEE Trans. Ind. Electron. 2020, 67, 9623–9634. [Google Scholar] [CrossRef]
- Han, G.; Zhu, H.; Zhang, L.; Hong, J.; Zhu, B. Model-Free Current Predictive Control Method for Switched Reluctance Motors. IEEE Trans. Ind. Electron. 2024, 1–10. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M. Neural Networks Design; Oklahoma State University: Stillwater, OK, USA, 2014. [Google Scholar]
- Beale, H.M.; Demuth, H. Neural Networks Toolbox User’s Guide; Mathworks: Portola Valley, CA, USA, 1992. [Google Scholar]
- Reay, D.; Green, T.; Williams, B. Application of associative memory neural networks to the control of a switched reluctance motor. Proc. IECON 1993, 1, 200–206. [Google Scholar]
- Alharkan, H. Torque Ripple Minimization of Variable Reluctance Motor Using Reinforcement Dual NNs Learning Architecture. Energies 2023, 16, 4839. [Google Scholar] [CrossRef]
- Song, S.; Huang, S.; Zhao, Y.; Zhao, X.; Duan, X.; Ma, R.; Liu, W. Torque Ripple Reduction of Switched Reluctance Machine with Torque Distribution and Online Correction. IEEE Trans. Ind. Electron. 2023, 70, 8842–8852. [Google Scholar] [CrossRef]
- Ling, X.; Zhou, C.; Yang, L.; Zhang, J. Torque Ripple Suppression Method of Switched Reluctance Motor Based on an Improved Torque Distribution Function. Electronics 2022, 11, 1552. [Google Scholar] [CrossRef]
- Xia, Z.; Bilgin, B.; Nalakath, S.; Emadi, A. A New Torque Sharing Function Method for Switched Reluctance Machines with Lower Current Tracking Error. IEEE Trans. Ind. Electron. 2021, 68, 10612–10622. [Google Scholar] [CrossRef]
- Jing, B.; Dang, X.; Liu, Z.; Long, S. Torque Ripple Suppression of Switched Reluctance Motor Based on Fuzzy Indirect Instant Torque Control. IEEE Access 2022, 10, 75472–75481. [Google Scholar] [CrossRef]
- Xue, X.D.; Cheng, K.W.E.; Ho, S.L. Optimization and Evaluation of Torque-Sharing Functions for Torque Ripple Minimization in Switched Reluctance Motor Drives. IEEE Trans. Power Electron. 2009, 24, 2076–2090. [Google Scholar] [CrossRef]
- Vujičić, V.P. Minimization of Torque Ripple and Copper Losses in Switched Reluctance Drive. IEEE Trans. Power Electron. 2012, 27, 388–399. [Google Scholar] [CrossRef]
- Lee, D.-H.; Liang, J.; Lee, Z.-G.; Ahn, J.-W. A Simple Nonlinear Logical Torque Sharing Function for Low-Torque Ripple SR Drive. IEEE Trans. Ind. Electron. 2009, 56, 3021–3028. [Google Scholar] [CrossRef]
- Gan, C.; Wu, J.; Sun, Q.; Yang, S.; Hu, Y.; Jin, L. Low-cost direct instantaneous torque control for switched reluctance motors with bus current detection under soft-chopping mode. IET Power Electron. 2016, 9, 482–490. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Gan, C.; Hu, Y.; Si, J. OCTSF for torque ripple minimization in SRMs. IET Power Electron. 2016, 9, 2741–2750. [Google Scholar] [CrossRef]
- Al-Amyal, F.; Számel, L. Research on Novel Hybrid Torque Sharing Function for Switched Reluctance Motors. IEEE Access 2022, 10, 91306–91315. [Google Scholar] [CrossRef]
- Ge, L.; Fan, Z.; Huang, J.; Cheng, Q.; Zhao, D.; Song, S.; De Doncker, R.W. Model Predictive Control of Switched Reluctance Machines with Online Torque Sharing Function Based on Optimal Flux-linkage Curve. IEEE Trans. Transp. Electrif. 2023. [Google Scholar] [CrossRef]
- Feng, L.; Sun, X.; Yang, Z.; Diao, K. Optimal Torque Sharing Function Control for Switched Reluctance Motors Based on Active Disturbance Rejection Controller. IEEE/ASME Trans. Mechatron. 2023, 28, 2600–2608. [Google Scholar] [CrossRef]
- Inderka, R.; De Doncker, R. DITC-direct instantaneous torque control of switched reluctance drives. IEEE Trans. Ind. Appl. 2003, 39, 1046–1051. [Google Scholar] [CrossRef]
- Sun, X.; Wu, J.; Lei, G.; Guo, Y.; Zhu, J. Torque Ripple Reduction of SRM Drive Using Improved Direct Torque Control with Sliding Mode Controller and Observer. IEEE Trans. Ind. Electron. 2021, 68, 9334–9345. [Google Scholar] [CrossRef]
- Ronanki, D.; Pittam, K.R.; Dekka, A.; Perumal, P.; Beig, A.R. Phase Current Reconstruction Method with an Improved Direct Torque Control of SRM Drive for Electric Transportation Applications. IEEE Trans. Ind. Appl. 2022, 58, 7648–7657. [Google Scholar] [CrossRef]
- Hu, Y.; Gu, C.; Zhang, Z.; Kang, Z.; Li, Y. Torque Ripple Minimization of Six-Phase Switched Reluctance Motor Based on Enhanced Direct Instantaneous Torque Control. IEEE Trans. Transp. Electrif. 2023. [Google Scholar] [CrossRef]
- Mohanraj, D.; Gopalakrishnan, J.; Chokkalingam, B.; Ojo, J.O. An Enhanced Model Predictive Direct Torque Control of SRM Drive Based on a Novel Modified Switching Strategy for Low Torque Ripple. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 2203–2213. [Google Scholar] [CrossRef]
- Fuengwarodsakul, N.H.; Menne, M.; Inderka, R.B.; De Doncker, R.W. High-dynamic four-quadrant switched reluctance drive based on DITC. IEEE Trans. Ind. Appl. 2005, 41, 1232–1242. [Google Scholar] [CrossRef]
- Brauer, H.J.; Hennen, M.D.; De Doncker, R.W. Control for Polyphase Switched Reluctance Machines to Minimize Torque Ripple and Decrease Ohmic Machine Losses. IEEE Trans. Power Electron. 2012, 27, 370–378. [Google Scholar] [CrossRef]
- Liang, J.; Lee, D.H.; Ahn, J.W. Direct instantaneous torque control of switched reluctance machines using 4-level converters. IET Electr. Power Appl. 2009, 3, 313–323. [Google Scholar] [CrossRef]
- Zeng, H.; Chen, H.; Shi, J. Direct instantaneous torque control with wide operating range for switched reluctance motors. IET Electr. Power Appl. 2015, 9, 578–585. [Google Scholar] [CrossRef]
- Li, W.; Cui, Z.; Ding, S.; Chen, F.; Guo, Y. Model Predictive Direct Torque Control of Switched Reluctance Motors for Low-Speed Operation. IEEE Trans. Energy Convers. 2022, 37, 1406–1415. [Google Scholar] [CrossRef]
- Thirumalasetty, M.; Narayanan, G. PWM-Based Predictive Direct Torque Control of Switched Reluctance Machine for Accurate Torque Tracking with Minimization of Phase RMS Currents. IEEE Trans. Ind. Appl. 2024, 1–13. [Google Scholar] [CrossRef]
- Cai, Y.; Dong, Z.; Liu, H.; Liu, Y.; Wu, Y. Direct Instantaneous Torque Control of SRM Based on a Novel Multilevel Converter for Low Torque Ripple. World Electr. Veh. J. 2023, 14, 140. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, J.; Gan, C. Optimized Direct Instantaneous Torque Control for SRMs with Efficiency Improvement. IEEE Trans. Ind. Electron. 2021, 68, 2072–2082. [Google Scholar] [CrossRef]
- Sheng, L.; Wang, G.; Fan, Y.; Liu, J.; Liu, D.; Mu, D. An Improved Direct Predictive Torque Control for Torque Ripple and Copper Loss Reduction in SRM Drive. Appl. Sci. 2023, 13, 5319. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).