Abstract
The growing significance of mobile robots in a full spectrum of areas of life creates new challenges and opportunities in robotics. One critical aspect to consider is energy utilization, as accurate prediction plays a vital role in a robot’s reliability and safety. Furthermore, precise prediction offers economic advantages, particularly for robotic fleets, where energy management systems can optimize maintenance costs and operational efficiency. The following review describes the state of the art of energy usage prediction for different types of mobile robots, highlights current trends, and analyses algorithms’ complexity (in implementation and execution), accuracy, and universality.
1. Introduction
Optimizing energy consumption is becoming crucial for the industrial environment. The rising energy costs and the negative impact of low-efficiency machines on the natural environment push us to find improved technology. Unfortunately, the current geopolitical situation restrains investors from funding new projects, some research has been suspended, and employees have started to observe the job market closely. The necessity of budget reduction encourages factory owners to look for savings in current processes without investing money in newer technology. One way to achieve that goal is to reduce the power consumption of already deployed machines without degrading their performance.
The understanding of factors impacting power consumption should be the first step in planned changes. Such knowledge allows a model of energy utilization to be created that will be used for future optimization.
The main purpose of the following review is to present the state of the art of energy usage prediction for different types of robots. We consider not only robotic manipulators, which are still the most common type of industrial robots, but also various types of ground robots and even drones for outdoor assignments. Additionally, we show energetic models of uncommon robots, such as walking bipeds, with significantly different dynamics to wheeled ground robots, to complete the heterogenous collection.
An energy consumption prediction technique should be considered as an algorithm whose purpose is to answer the question of how much energy is necessary to complete a task assigned to a robot.
The rest of the review is divided into four sections in which we describe energy models for industrial manipulators, ground driving, and aerial robots, as well as an extra section for uncommon robot types. The sixth section includes a discussion of the state of the art and our proposal for future research.
2. Robotic Manipulators
The widely used industrial robotics arms represent the largest percentage of industrial robots. Luan et al. in [1] revised the power consumption of industrial robots in terms of environmental impact. Based on data from 74 countries and regions, the authors show that increased energy consumption by industrial robots leads to air deterioration. This indicates that energy prediction algorithms can support the creation of environmentally friendly robotic systems.
Diverse modeling approaches can be found in the literature. The authors of [2] propose to model the power consumption as a polynomial function with experimentally identified parameters. Three states, based on the movement type, have been distinguished:
- Upward movement;
- Downward movement;
- Horizontal movement.
A separate function represents each state. The model identification requires knowledge about the angle and angular velocity and acceleration, mass, and length of each link. The ANOVA method allowed the authors to identify models based around the Fluke 1732 robotic arm. The coefficient of determination value was above 0.95 for each type of movement.
Yao et al. in [3] divided the total power consumed by industrial manipulators into three systems:
- Drive system;
The power utilized from the main dynamic system, which is the hardest to model, was divided into mechanical, electromechanical loss, and electrical loss powers. The mechanical power can be modeled using joint variables such as torque, position, velocity, and acceleration. Additionally, information about the mass and center of gravity of the load is needed.
- Control system;
- Auxiliary system.
The power consumption of the above system has been considered to be constant. For modeling, the bidirectional recurrent neural network combined with the torque calculate network and the end-load Encoder Network was utilized. The authors showed a low prediction relative error (1%) for the KUKA KR210 and the UR5 industrial robotics arms.
Similar accuracy was achieved in the results of [4] utilizing a batch-normalized long short-term memory network to construct a robust energy-consumption prediction model. The authors used the values of velocity, acceleration, payload, control mode, joint torque, robot line current, and robot supply voltage. The data were collected using the six-degrees-of-freedom robotic manipulator Yaskawa GP7.
Even higher accuracy (99.5%) was achieved by the authors of [5] using an Artificial Neural Network (ANN) to model the energy consumption of the UR10 collaborative robotic arm. The network was trained using the 16 most relevant inputs read from the robot’s software, which include, among others, joint forces, transported payload, and type of movement.
Another deep learning-based model was introduced in [6]. The values of joint position, speed, motor current, torque, and the end pose TCP were used as inputs of the residual network (ResNet). The ResNet contains several convolutional layers and batch normalization. ReLu is used as an activation function. The authors conducted experiments using the UR3 and UR10 robotic arms and obtained a root mean squared error (RMSE) below 6 W when the average power consumption (based on plots) is about 60 W.
Jiang et al. [7] proposed a deep neural network based on long short-term memory that can predict energy consumption without identifying the parameters of the industrial robot. For training purposes, authors used reference joint position, velocity, and acceleration. As the trajectory can be scaled in time, to force the robot to finish the task faster or slower, the first- and second-order derivatives of the time scaling function were used as additional inputs. The algorithm was tested on the KUKA KR60-3 arm and obtained a mean absolute percentage error of less than 4.2%.
Industrial manipulators often work in specialized environments, which requires power consumption identification of the whole machine. Cao et al. [8] introduced a method for modeling a polishing robotic station. The machine power consumers can be divided into the following:
- Mechanical power of the robot;
- Workpiece mechanical power;
- Robotic polishing power;
- Electric loss power;
- Friction loss power.
Robotic polishing power can be divided further into the following:
- Mechanical power of abrasive belts;
- Mechanical power of belt wheels;
- Electric loss power of belt sanders’ motors;
- Friction loss power in the mechanical transmission of belt sanders.
Electric loss power impacts the following:
- Power consumed in motors;
- Inverters;
- DC bus;
- Rectifier;
- Cabinet PC;
- Control panel;
- Cooling system.
Due to the complexity of creating an analytical model, the authors decided to develop an energy characteristic model as a polynomial function based on experimental data. To achieve the best accuracy the following stages of the task execution have been distinguished:
- Idling;
- Loading;
- Handling;
- Polishing;
- Unloading.
The polynomial consists of five task energy coefficients and a scaling factor of execution time. The achieved accuracy of complex systems was above 93%.
Another example of a complex robotics workstation is presented by Zhou et al. [9] in which a model of a robotic laser processing system was verified with the KUKA KR60–3 manipulator. The authors used structural decomposition methodology to simplify the parametrized model tuned with experimental data. The total energy is the sum of energy consumed by a robot, laser device, and chiller. The further robot decomposition is presented below.
- Standby power;
- Power of brakes;
- Power of working servo system.
The complexity of the algorithm can be visualized by drawing a dependency diagram for the power of the working servo system, as shown in Figure 1.
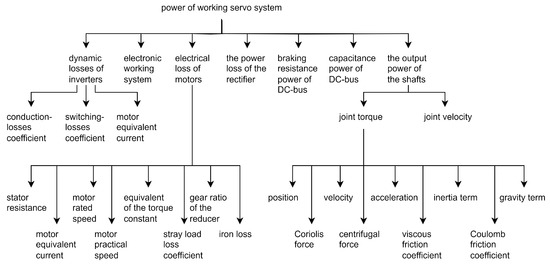
Figure 1.
Power of a working servo system decomposition.
The average error between measurements and interpolating calculation values was equal to 2.9%. It is worth noting that the researchers in [7,9] used the same KUKA KR60–3 manipulator. In the former, a much simpler approach allowed a model with 95.8% accuracy to be created, which is only 1 percentage point lower than the result achieved in the latter, which used a more complex approach (97.1% accuracy).
3. Ground Mobile Robots
A comprehensive review [10] of energy sources mentioned two formulas describing energy efficiency in mobile robotics. The first is named the Cost Of Transportation () and is described by Equation (1).
where P is the power of the movement, m is the mass of the robot, g is the gravitational acceleration, and v is the velocity of the robot.
The second is called Specific Resistance () and is described by Equation (2).
where E is the energy consumption, m is the mass of the robot, g is the gravitational acceleration, and d is the distance of the movement.
The latter concept was introduced in [11,12] and represents an equivalent solution to COT. The above coefficient is a variation of the Specific Resistance defined as long ago as 1950 [13] for any type of locomotive vehicle [13]. The authors use the ratio of the power divided by the product of the vehicle’s weight and velocity to compare transportation costs.
3.1. Differential Drive
Differential drive mobile robots have only two drive wheels and at least one passive wheel providing stability when the robot is not in motion. This type of robot has a simple kinematic structure described well in the literature.
The simplest energy models can be found in research from 1995. Barili et al. [14] assume that the robot is driving mainly in a forward direction so angular motion power can be neglected. The energy is proportional to kinetic energy and thus depends on the robot’s mass and linear velocity. The authors highlight that energy saving is a trade-off between travel distance and time.
Mei et al. [15,16] describe methods of energy conservation. The power model consists of the following three parts:
- Motion power;
- Sensing power;
- Computer power.
The first element can be represented as a function of the robot’s mass, linear velocity, and acceleration. The energy consumed by sensors is modeled as a linear function of their frequency. Computer power is assumed to be constant. The final model requires experimental data to identify the parameters of functions.
Unfortunately, authors often do not consider what impacts power consumption but use only the product of measured electrical voltage and current during tests to create an energy-saving algorithm [17,18]. Such an approach does not allow power consumption to be predicted but does allow its characteristic to be understood.
One application of autonomous ground mobile robots is exploration tasks. The authors of [19] created a parameterized simulation for reducing energy consumption in point-to-point travel. The authors introduced the term Energy Unit (EU), where one EU is equal to the cost of one traveling distance unit. An additional 0.5 EU is consumed when the robot stops and from 0.4 to 1 EU is needed for robot rotation from 45 to 180 degrees.
A more complex model is presented in [20]. The mathematical formula states that energy consumption depends on the following:
- Motion power;
- -
- Mass;
- -
- Linear velocity;
- -
- Linear acceleration;
- -
- Moment of inertia;
- -
- Angular velocity;
- -
- Angular acceleration;
- -
- Friction parameter;
- -
- Wheel radius;
- -
- The energy needed to overcome static friction;
- Computer and sensor power.
Model parameter identification requires performing experiments with a real robot. Unfortunately, the authors did not calculate accuracy metrics; however, based on a visual comparison of plots, the prediction seems to be sufficiently accurate.
Wang et al. [21] created a differential drive mobile robot energy model based on the DC motor equation. To create a valid model, knowledge of the following factors is required:
- Wheel radius;
- Rotation speed of the motor;
- Armature resistance;
- Back EMF constant;
- Torque constant;
- Inertia of the motor;
- Inertia of load;
- Load torque;
- Friction torque;
- Viscous damping.
To find all the needed information, the model should be calibrated using a real robot.
A different modeling approach is presented in [22]. A model of a vacuum cleaner robot was created using an Artificial Neural Network with Bayesian regularization. The authors assumed that power consumption is proportional to the number of steps needed to reach a target. The following inputs were used:
- Dimension of the working area;
- Number of obstacles;
- Target X coordinate;
- Target Y coordinate.
An experiment performed using the iRobot Create 2 showed that 96% of the time, the predicted energy was sufficient to finish the task. The prediction accuracy was not calculated but based on the “Predicted energy consumption versus Real energy consumption” plot, we can observe that there is a tendency to overestimate the energy needed for task completion. For example, the highest real energy consumption peak is equal to approximately 310 mAh while that of the prediction is about 850 mAh.
Some research considers the energy consumption of a group of collaborating robots. In [23], the authors proposed an energetic model of an Autonomous Mobile Robot (AMR) connected to a UR3 manipulator. The power usage was assessed using linear regression of battery state of charge versus time. Different linear coefficients were found for each of the following three test scenarios:
- Only the AMR traveling to the point of interest (POI) and being unloaded manually by a human;
- The AMR and UR3 traveling to POI but the manipulator is switched off;
- The AMR and UR3 traveling to POI and the manipulator performs an unloading process.
The test results showed an adjusted R-squared value above 99%.
3.2. Skid-Steer Drive
Lateral friction has a significant impact on the energy consumption of skid-steer mobile robots. Many assumptions used for modeling differential drive algorithms are not applicable here. In the case of creating a skid-steer energy consumption model, one of the most popular methods uses the concept of instantaneous centers of rotation (ICRs), which can be treated as points where equivalent wheels of a differential drive could be located.
Morales et al. [24] proposed an ICR-based method for tracked mobile robots. The model demands measurements of linear velocities of the left and right side of a robot, the ICR position, the distribution of normal forces acting on tracks, the friction coefficient, and the distance between track centerlines. The ICR position and other scaling parameters can be experimentally assessed by performing a special set of experiments. Although the whole process requires some time for calibration, the results are promising. In the research, for a robot that consumes 1 kW of power, the model’s Mean Absolute Error was approximately 80 W. A year later, the authors successfully adapted the model to a four-wheeled skid-steer mobile robot [25].
Pentzer at el. published three articles in 2014 [26], 2016 [27], and 2022 [28] utilizing the ICR-based method for modeling energy consumption for wheeled and tracked mobile robots in the outdoor environment. The authors expanded the model by adding coefficients of internal and rolling resistance, robot acceleration, and the terrain pitch. The robot drove on asphalt and grass and the energy estimation accuracy was between 95 and 99.5%.
We conducted experiments [29] comparing the accuracy of the above-mentioned model with a much simpler feed-forward Artificial Neural Network for three skid-steer mobile robots on different ground surfaces. The relative estimation error for the analytical model was slightly lower than for ANN.
Another method for modeling wheeled outdoor skid-steer robots is shown in [30]. The robot tests were performed on grass, asphalt, and rough field terrain. The authors checked the differences in power consumption when the robot is power supplied from lead-acid compared to Li-Po batteries. Tests were performed with and without an additional payload at different speed settings. The average power was calculated for each scenario. The results showed that Li-Po batteries provide lower power consumption due to their reduced weight and lower internal resistance. The power model was presented as a set of average power consumption parameters depending on operational condition.
3.3. Others
Omnidirectional Mobile Robots are a special type of ground mobile robot with the ability to perform holonomic motion. Mei et al. describe an energy model for such a three-wheeled type of robot [31]. In the design process, the authors considered a DC motor whose power was represented as a function of angular velocity that was approximated by a 6th order polynomial. The model was tested on a commercial Palm Pilot Robot Kit achieving a 96% prediction accuracy.
Mobile robots with Mecanum wheels have rollers attached to their circumference, each rotating about an axis at a 45-degree angle to the wheel plane, while they allow omnidirectional movement, they do not satisfy the strict holonomic constraints. Unlike true holonomic wheels, which can move instantaneously in any direction, Mecanum wheels exhibit some limitations due to their design.
A model of the four-wheeled Mecanum mobile robot is presented in [32]. The authors decomposed total consumed power into power utilized by the sensor, control, and motion systems. The consumption of the first element should depend on the robot’s velocity as a faster movement should cause an increasing frequency of sensor use. The middle element could be constant with consideration of the increased startup current consumption. The last system should be further divided into kinetic energy, friction dissipation, energy dissipation as heat, and mechanical dissipation (in terms of overcoming friction torque in actuators). These parameters are strictly connected with robot mass, movement speed, and the friction coefficient. The model accuracy in the real environment was 93%. Two years later, the authors increased the accuracy to 95% [33]. The decomposition of the new model is presented in Figure 2 below.
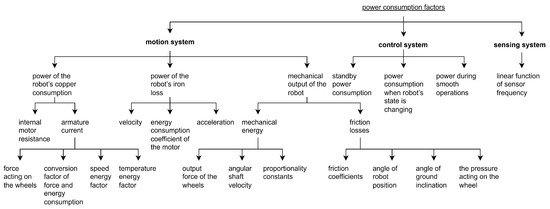
Figure 2.
The power factors of a Mecanum robot.
The last example shows the power consumption model for the Ackerman drive mobile robot introduced in [34]. This model, like most of the described research, is based on the brushed DC motor equations. The study shows that the following factors should be considered:
- Angular velocity of the motor;
- Back-EMF constant;
- Torque constant;
- Internal torque;
- Load friction torque;
- Internal damping force;
- Motor moment of inertia;
- Load moment of inertia;
- Wheel radius;
- Linear acceleration.
Unfortunately, the above model has not been tested in a real environment.
4. Unmanned Aerial Vehicles
Based on the quantity of recently published articles, we can claim that the most popular mobile robots are Unmanned Aerial Vehicles (UAVs).
A comprehensive overview of nonmilitary UAV use cases [35] considered the following applications:
- Drone-based construction inspection;
- Investigation and treatments in agriculture;
- Transport and delivery applications;
- Security supervision;
- Entertainment and filming;
- Others (communication links, serving cloud services to saving energy on mobile devices by taking computation tasks, monitoring disasters).
Energy consumption does not directly depend on mission type but the following factors should be considered during modeling:
- Type of drone (fixed wing vs. rotorcraft);
- Altitude (propellers have to rotate faster at higher altitudes because of lower air density);
- Type of flight (hovering vs. forward flight);
- Climbing speed;
- Payload;
- Weather conditions (such as wind, especially for small and micro drones).
Nevertheless, the energy consumption model can be simplified as shown in [36], in which the author calculates energy as a function of the transported payload in the optimal vehicle routing algorithm for a meal delivery task. A similar method of assuming that the energy consumed is only proportional to the payload of a drone was introduced in [37]. Furthermore, the authors of [38] use the energy consumption model as a function of payload assuming that the drone is traveling with constant speeds (10 m/s and 15 m/s) and the result is calculated in Joules per meter.
A different approach is to present UAV usage cost as a value proportional to traveled distance [39]. Total costs are calculated based on recharge stations, drone procurement, and usage costs.
Moore [40] validates intra-city package delivery methods to establish energy-efficient solutions. During the comparison, the author assumes a constant energy consumption rate for all transportation methods, for UAVs, it is equal to 100 Wh per mile.
The authors of [41] propose an optimal solution for delivery UAV path planning considering system constraints from the influence of battery weight on energy consumption. Their energy model assumes that the drone consumes the same power while hovering or flying at a constant speed. Consequently, they received a linear model. The impact of weather is ignored.
Chiang et al. [42] solve a package delivery problem by reducing carbon emissions and saving energy using UAVs. The authors assume that the UAV consumes a constant energy portion per mile. As carbon emissions are highly correlated with energy consumed, the proof of energy saving is sufficient to show CO2 emissions reduction. The authors did not confirm the energy model accuracy experimentally, they focused on the simulation of CO2 emissions reduction in the Matlab simulation environment.
The impact of drones’ CO2 emissions was compared to that of conventional transport vehicles in [43]. The author shows a model in which UAV energy consumption is proportional to aircraft mass and travel distance, not considering energy consumed by electronics, assuming that this energy consumption can be omitted when a drone travels long distances. The results indicate that UAVs are significantly more CO2-emission efficient than typical US diesel delivery trucks.
Ferrandez et al. [44] solve a traveling salesman problem for a truck–drone tandem using K-means clustering and the genetic algorithm. To estimate energy consumption, the authors assumed that the UAV consumes constant power per second and the truck consumes constant power per meter. The authors determined that drones are more energy efficient due to less weight, heat loss, and friction, so trucks could be used as recharging stations.
In the above-mentioned articles, there is an assumption that drones most of the time fly horizontally. However, the vertical movement can be crucial, as the authors of [45] show. The authors investigate the energy performance of a fleet of surveillance drones. To achieve energy consumption minimization, the authors control drone altitude. Drones flying higher can cover more area but also use more power. The estimation model depends on the potential energy of the drone. The authors prove that dynamic control of drone altitude can conserve as much as 150% of the energy consumed in scenarios in which UAVs are statically placed. A similar conclusion is drawn by the authors of [46]. They depict the trade-off in the application of UAVs to surveillance between energy consumption and flying altitude—drones at higher altitudes can observe larger areas at the cost of higher energy consumption.
In addition, the authors of [47] compare energy cost in a delivery task using a diesel vehicle, electric vehicle, and a UAV. The UAV power estimation model is approximated as the sum of the power required to overcome the air drag of the body and rotors, consumed during lifting and climbing and the power used by internal electronics. The algorithm depends on flight angle, speed, mass, and construction parameters (rotor disc area, solidity ratio, etc.). The flight angle was assumed to be equal to 45 degrees during ascent and descent and 0 degrees during level flight and hovering. The authors assume that head and tail winds create the need for higher and lower energy consumption during the flight, respectively. Additionally, they show that an optimal traveling speed exists and is determined by the shape of a convex function. UAV construction is a trade-off between travel and hover capabilities. For example, helicopters are designed to hover but airplanes are designed for travel. Due to UAVs being mostly designed for cruising, often hovering consumes higher energy compared to that consumed during level flight. According to the authors, UAVs consume more energy than road vehicles especially when small operational areas with high consumer density coverage are considered and significant wind is present. Nevertheless, a drone’s energy consumption is comparable to that of a road vehicle in large operational areas with small consumer density coverage (e.g., rural areas) when the wind is calm.
In [48], the authors examine the energy consumption of a delivery UAV. In the power estimation model, they use empirically found parameters, such as power efficiency, to lower the minimum power required to hover and to improve the effective drag coefficient. The authors show that power consumption depends on payload and traveling speed. Due to the convex shape of the power function, optimum velocities depend on the carried payload mass. The authors show that the relationship is nonlinear, similar to the exponential characteristics of power consumed as a function of total drone mass.
D’Andrea [49] investigates the feasibility of delivery drones by calculating total costs based on battery lifetime. To estimate power consumption, the author proposes a simple function of mass, cruising velocity, lift-to-drag ratio, power transfer efficiency, and power consumed by the electronics.
The authors of [50] calculate delivery UAV total costs as an estimation of power consumption by assuming that this is proportional to the sum of electronics power and the total mass multiplied by flying speed and divided by a factor including the lift-to-drag ratio and the power transfer efficiency.
The total power utilized by the UAV can be decomposed into three factors [51], namely, power consumed for hovering and by the avionics system and sensors. Only the first should be considered as the others are low enough to be omitted. The energy consumed by the hovering system can be calculated based on the force of gravity, air density, and total area of the rotor blades. The model was tested using an 8 kg drone and a 5% deviation was observed.
Li et al. [52] proposed a simulation model in which the energy consumed for hovering and flying can be presented by a curve of flying speed. Additionally, the authors claim that communication-related energy can be negligible when the distance is less than 50 m.
The authors of [53] show that a drone’s energy consumption depends on the altitude and the direction of acceleration. Considered parameters are the total mass, the flying speed, and air friction.
A more complex consideration is described in [54] in which the effects of UAV ground power consumption, communication, hovering, and vertical and horizontal motion on energy consumption were analyzed. The working states can be divided and parameterized as shown in Table 1.

Table 1.
UAV working modes and their dependencies.
Prasetia et al. [55] model the energy consumption as a black-box polynomial including upward vertical speed and distance, downward vertical speed and distance, horizontal speed and distance, and hover duration. The result of the model’s validation shows 97.5% prediction accuracy.
For the solar-powered UAV presented in [56], the horizontal (level flight energy consumption, hovering) and vertical (climbing, descending) components have been utilized for energy modeling. The authors assumed low, close to zero, acceleration and a constant cruising speed. To validate the model using a 1.28 kg DJI drone, they took into account robot mass, gravity acceleration, air density, rotor disk area, and vertical and horizontal speeds. The error was not presented but based on a diagram of consumption battery energy over time, we can see that the prediction error reaches as high as 35% for horizontal flight.
Another solar-powered UAV is introduced in [57], in which the authors extend the above-mentioned model by adding the blade drag profile, which is considered a nonlinear function. The function parameters are the profile drag coefficient (geometry of rotor blades), air density, total area of rotor disks, and linear, vertical velocities. Unfortunately, the model was not tested using a real drone.
The hexacopter energy model [58] depends on:
- Load torque of the propeller;
- Velocity constant of the rotor motor;
- Current needed to force the rotor to start spinning;
- Angular velocity of the motor;
- Resistance of the rotor motor winding.
In our previous research [59], we used machine-learning-based techniques to model hexacopter energy consumption. In our study, we considered altitude, linear velocities, roll, pitch, yaw angles, and total mass. As a result, our prediction error for the best methodology was below 2%.
The Gaussian Process Regression method was used in [60]. The authors compared our outcomes with models using different kernels (Mattern (3 variants), RBF, RQ). As a result, the relative error of the Gaussian Process was below 0.1%.
A comparison between the nonlinear energy model with a simpler linear approach is presented in [61]. The results show that the linear model can lead to routes being energy infeasible (energy consumption larger than battery capacity) in contrast to the nonlinear model. The model includes the influence of the total mass of the drone, air density, area of the spinning blade, and number of rotors. The authors claim the linear power function of mass overestimates real consumption for small masses and underestimates it for larger payloads. Moreover, the authors formulate the following conclusions:
- The linear model is more computationally efficient;
- The linear model can be infeasible for some routes calculated based on a nonlinear model;
- There is a 9-percentage-point gap in energy prediction between models.
The research does not consider take-off, landing states, and wind influence.
Zhang et al., in [62], formulate categories that have an impact on UAV energy consumption such as drone design (drone, battery, and payload weights), environment (air density, wind, weather conditions), drone dynamics (velocity, motion type, acceleration, angle of attack), and delivery operations (drone standing on driving robot, parachute, movement in fleet). The wind has a nonlinear impact on energy consumption, thus without wind, a drone consumes more power to stay at the goal height than with moderate wind, in which conditions, an ’air tunnel’ is created, which helps the drone to keep its position. Conversely, a high wind interrupts the drone’s operation as it struggles against the buffeting of the wind to keep its position. The authors depict that a low consideration of the wind impact is a bad approach in energy modeling because the drone can consume as much as 100% more energy in extreme wind conditions.
A theoretical investigation of Titan, one of the moons of Saturn, using a drone is described in [63]. The power of the rotor is assessed based on the vehicle mass, gravity acceleration, atmospheric density, rotor disc area, forces acting on the body, drone orientation, and other descriptive coefficients. The total aerodynamic power is introduced as a sum of the following four components:
- Parasitic power (dot product of body drag force and velocity);
- Induced power (caused by a lift of the rotors);
- Profile power (caused by a drag of the rotors);
- Power required to climb (dot product of velocity vector and the gravitational force).
Moreover, the authors show that the power in terms of air velocity is a convex function.
Yacef et al. [64] propose a polynomial interpolation to model the rotor efficiency function and integrate this interpolation to assess energy consumption.
The authors of [65] investigate battery-powered UAV performance in various scenarios. The authors show that drones are energy-efficient due to their light weight, however, it is still challenging to create long-runtime designs with limited battery capacity. The authors conducted empirical research using a 3DR Solo drone. They divided the consumed energy into major energy required to keep the UAV in the air and minor energy required for flying in some direction. The factors impacting energy consumption the greatest were hovering, horizontal and vertical movement, total mass, and flying against or with the wind. The results showed the following:
- Hovering cause a constant power consumption.
- Horizontal movement is characterized by very small power fluctuations. It is almost constant.
- Vertical movement is characterized by high power fluctuations.
- A payload change causes a proportional change in consumed power.
- Flying against the wind is characterized by a smaller consumption due to increased thrust translational lift, which makes hovering easier but it is limited by wind speed. A higher wind speed causes a power consumption increase.
The estimated energy error was 0.4%.
One of the most advanced power consumption models for UAVs is presented in [66]. The model decomposition and dependencies are presented in Figure 3.
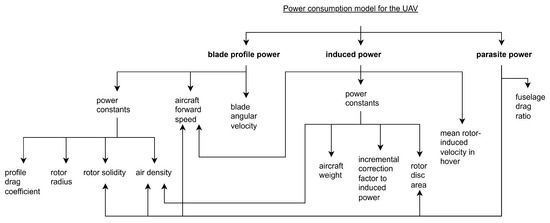
Figure 3.
Decomposition of the power of a working UAV.
The above model was further developed in [67] by adding an acceleration factor to the simulation.
5. Other Types of Robot
A theoretical consideration of the energy consumption of free-flying space robots has been described in [68]. The article aimed to minimize energy consumption by ellipse path planning. To achieve this goal, a kinematic-based model that included joint velocity, centrifugal forces, Coriolis forces, current, and the resistance of the motor armatures was built.
Humanoid robots are less popular than two-wheel robots but energy models can be found in the literature. Silva et al. [69] used a desired energy consumption calculation based on joint and angular velocity in a simulation environment. The same approach was utilized in [70] to control a biped robot with a different speed.
An energy consumption model for a one-legged electrically actuated mobile robot is presented in [71]. The authors showed that different amounts of power are needed in the stance and flight phases. Additionally, assessing Specific Resistance shows that the mean power requirement increases proportionally with speed.
A unique construction of a deformable capsule-like crawling robot based on scissor elements is presented in [72]. The power consumption was calculated as the average electrical power, which depends on the deformation frequency.
The authors of [73] evaluated the energy consumption of the AntBot hexapod robot. The energy model used gait type, duty factor, payload, and step characteristic (length, period, height) as inputs.
Animals often inspire researchers to build creative constructions. Yan et al. [74] proposed an energy model for the Cyber Dog quadruped robot. The mechanical energy consumption is considered as a product of each joint moment and its angular velocity.
The authors of [75] decided to create an empirical model of a 6-link snake robot. The exponential function of the desired joint angle was parameterized to estimate the needed pressure.
6. Discussion
To summarize, we compared different models proposed in the literature using the following three factors:
- Accuracy,
- Complexity,
which is our relative scoring factor. Models that require finding many coefficients and performing learning experiments are more complex than models using polynomial regression, which are, in turn, more complex than models assuming a linear relationship between measured values and the power. We score models on a scale from one to three, where one means a trivial model and three means a complex one.
- Universality,
which is another relative scoring factor. Models that have kinematic dependencies are less universal than models based on common values (e.g., mass, velocity). We score models on a scale from one to three, where one means a model strictly bound with a specific robot and three means a universal model that could be utilized to predict the power consumption of different robot types.
We used articles that contain calculated values of accuracy or estimation error, and the results are presented in Table 2.

Table 2.
Energy consumption model comparison.
The horizontal dividing lines group Table 2’s results based on robot type—from top to bottom: manipulators, ground robots, and aerial robots. We can see that creating accurate models for ground robots is complicated. The best algorithm cannot be determined, as all of the models are the result of trade-offs during the modeling process. The most suitable model depends on the designer’s requirements.
There is still a wide field to explore for research and development in robotics energy consumption modeling. All of the cited articles focus on a certain robot type. There are no trials of creating a unified energy consumption model that could be used for all types of robots. Most of the mentioned articles describe analytical methods that are strictly correlated with the robot’s kinematic structure. To increase accuracy, scientists extend models by adding more complex dependencies requiring special calibration techniques or identifying parameters of subsystems (e.g., motor parameters). Unfortunately, they do not consider how complexity impacts the costs of launching and maintaining the proposed solution. We believe the number of actions like calibration and manual parameter identification should be minimized to make the algorithms more attractive even when the accuracy slightly decreases. The technology is evolving and the perfect energy prediction algorithm should be self-adaptable. For that reason, we prefer black-box methods over analytical models. The polynomial extrapolation could be a good approach if combined with an automatic tuning mechanism. The universality could be provided by avoiding the use of robot-specific parameters such as distance between wheels or rotor angular speed. A better way is to base the approach on kinematic dependencies for a body moving in space such as linear velocity or robot mass. The other impacting factors could be modeled as uncertainty and tuned online.
The natural method for solving the above-mentioned challenge is using artificial intelligence’s generalizing abilities. Unfortunately, only a few articles use machine learning techniques to solve modeling assignments. The research shows positive outcomes and proves the potential of such solutions. A machine-learning-based model could be presented as a black-box, providing tuning and adaptive mechanisms allowing self-awareness of the robot. The model could start learning during the first robot movements and adjust its internal parameters when the robot changes its working environment (e.g., when it starts driving on a different ground surface or when the wind direction changes) and its structure (e.g., transporting additional payload, changing the type of suspension).
We strongly recommend future research to challenge our vision hoping it will satisfy the most demanding requirements.
7. Conclusions
The reviewed algorithms are a trade-off between accuracy, complexity, and universality. Improved approaches can be developed to provide better accuracy and universality. The usage of machine learning methods seems to be a prospective direction for future development.
In the next steps, we plan to investigate further the abilities of various machine learning techniques to satisfy those requirements.
Author Contributions
Conceptualization, K.G.; methodology, K.G.; formal analysis, K.G.; investigation, K.G.; resources, K.G.; writing—original draft preparation, K.G.; writing—review and editing, G.G.; supervision, G.G.; project administration, B.C.; funding acquisition, B.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Centre for Research and Development in Poland, (grant number LIDER/54/0286/L-12/20/NCBR/2021 and grant number LIDER/38/0210/L-10/18/NCBR/2019).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AMR | Autonomous Mobile Robot |
| ANN | Artificial Neural Network |
| COT | Cost Of Transportation |
| UAV | Unmanned Aerial Vehicle |
| UGV | Unmanned Ground Vehicle |
| ICR | Instantaneous Centers of Rotation |
References
- Luan, F.; Yang, X.; Chen, Y.; Regis, P.J. Industrial robots and air environment: A moderated mediation model of population density and energy consumption. Sustain. Prod. Consum. 2022, 30, 870–888. [Google Scholar] [CrossRef]
- Babski-Reeves, K.; Eksioglu, B.; Hampton, D. A 7-DOF Robotic Arm Energy Prediction Model for Smart Manufacturing. In Proceedings of the IIE Annual Conference, New Orleans, LA, USA, 21–23 May 2023; Institute of Industrial and Systems Engineers (IISE): Norcross, GA, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Yao, M.; Zhou, X.; Shao, Z.; Wang, L. A general energy modeling network for serial industrial robots integrating physical mechanism priors. Robot. Comput.-Integr. Manuf. 2024, 89, 102761. [Google Scholar] [CrossRef]
- Lin, H.I.; Mandal, R.; Wibowo, F.S. BN-LSTM-based energy consumption modeling approach for an industrial robot manipulator. Robot. Comput.-Integr. Manuf. 2024, 85, 102629. [Google Scholar] [CrossRef]
- Miranda, S.; Vázquez, C.R. Analysis and Prediction of Energy Consumption in a Collaborative Robot. IFAC-PapersOnLine 2023, 56, 3710–3715. [Google Scholar] [CrossRef]
- Yao, M.; Zhao, Q.; Shao, Z.; Zhao, Y. Research on power modeling of the industrial robot based on ResNet. In Proceedings of the 2022 7th International Conference on Automation, Control and Robotics Engineering (CACRE), Xi’an, China, 14–16 July 2022; pp. 87–92. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, Z.; Li, X.; Wang, X.V.; Yang, B.; Zheng, J. Energy consumption prediction and optimization of industrial robots based on LSTM. J. Manuf. Syst. 2023, 70, 137–148. [Google Scholar] [CrossRef]
- Cao, H.; Zhou, J.; Jiang, P.; Hon, K.K.B.; Yi, H.; Dong, C. An integrated processing energy modeling and optimization of automated robotic polishing system. Robot. Comput.-Integr. Manuf. 2020, 65, 101973. [Google Scholar] [CrossRef]
- Zhou, J.; Yi, H.; Cao, H.; Jiang, P.; Zhang, C.; Ge, W. Structural decomposition-based energy consumption modeling of robot laser processing systems and energy-efficient analysis. Robot. Comput.-Integr. Manuf. 2022, 76, 102327. [Google Scholar] [CrossRef]
- Mikołajczyk, T.; Mikołajewski, D.; Kłodowski, A.; Łukaszewicz, A.; Mikołajewska, E.; Paczkowski, T.; Macko, M.; Skornia, M. Energy Sources of Mobile Robot Power Systems: A Systematic Review and Comparison of Efficiency. Appl. Sci. 2023, 13, 7547. [Google Scholar] [CrossRef]
- Sakagami, Y.; Watanabe, R.; Aoyama, C.; Matsunaga, S.; Higaki, N.; Fujimura, K. The intelligent ASIMO: System overview and integration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 3, pp. 2478–2483. [Google Scholar] [CrossRef]
- Kajita, S.; Espiau, B. Springer Handbook of Robotics; Legged Robots: Berlin/Heidelberg, Germany, 2008; pp. 361–389. [Google Scholar] [CrossRef]
- Gabrielli, G.; von Karman, T. What Price Speed? Specific Power Required for Propulsion of Vehicles. Mech. Eng. 1950, 72, 775–781. [Google Scholar]
- Barili, A.; Ceresa, M.; Parisi, C. Energy-saving motion control for an autonomous mobile robot. In Proceedings of the 1995 IEEE International Symposium on Industrial Electronics, Athens, Greece, 10–14 July 1995; Volume 2, pp. 674–676. [Google Scholar] [CrossRef]
- Mei, Y.; Lu, Y.H.; Hu, Y.; Lee, C. A case study of mobile robot’s energy consumption and conservation techniques. In Proceedings of the 12th International Conference on Advanced Robotics ( ICAR ’05, Proceedings), Seattle, WA, USA, 18–20 July 2005; pp. 492–497. [Google Scholar] [CrossRef]
- Mei, Y.; Lu, Y.H.; Hu, Y.; Lee, C. Deployment of mobile robots with energy and timing constraints. IEEE Trans. Robot. 2006, 22, 507–522. [Google Scholar] [CrossRef]
- Rapalski, A.; Dudzik, S. Energy Consumption Analysis of the Selected Navigation Algorithms for Wheeled Mobile Robots. Energies 2023, 16, 1532. [Google Scholar] [CrossRef]
- Szeląg, P.; Dudzik, S.; Podsiedlik, A. Investigation on the Mobile Wheeled Robot in Terms of Energy Consumption, Travelling Time and Path Matching Accuracy. Energies 2023, 16, 1210. [Google Scholar] [CrossRef]
- Mei, Y.; Lu, Y.H.; Lee, C.; Hu, Y. Energy-efficient mobile robot exploration. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation (ICRA 2006), Orlando, FL, USA, 15–19 May 2006; pp. 505–511. [Google Scholar] [CrossRef]
- Liu, S.; Sun, D. Modeling and experimental study for minimization of energy consumption of a mobile robot. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kaohsiung, Taiwan, 11–14 July 2012; pp. 708–713. [Google Scholar] [CrossRef]
- Wang, G.; Irwin, M.J.; Berman, P.; Fu, H.; La Porta, T. Optimizing sensor movement planning for energy efficiency. In Proceedings of the 2005 International Symposium on Low Power Electronics and Design, New York, NY, USA, 8–10 August 2005; ISLPED ’05. pp. 215–220. [Google Scholar] [CrossRef]
- Caballero, L.; Perafan, Á.; Rinaldy, M.; Percybrooks, W. Predicting the Energy Consumption of a Robot in an Exploration Task Using Optimized Neural Networks. Electronics 2021, 10, 920. [Google Scholar] [CrossRef]
- Aliev, K.; Traini, E.; Asranov, M.; Awouda, A.; Chiabert, P. Prediction and estimation model of energy demand of the AMR with cobot for the designed path in automated logistics systems. Procedia CIRP 2021, 99, 116–121. [Google Scholar] [CrossRef]
- Morales, J.; Martinez, J.L.; Mandow, A.; Garcia-Cerezo, A.J.; Pedraza, S. Power Consumption Modeling of Skid-Steer Tracked Mobile Robots on Rigid Terrain. IEEE Trans. Robot. 2009, 25, 1098–1108. [Google Scholar] [CrossRef]
- Morales, J.; Martínez, J.L.; Mandow, A.; Pequeño-Boter, A.; García-Cerezo, A. Simplified power consumption modeling and identification for wheeled skid-steer robotic vehicles on hard horizontal ground. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4769–4774. [Google Scholar] [CrossRef]
- Pentzer, J.; Brennan, S.; Reichard, K. On-line estimation of vehicle motion and power model parameters for skid-steer robot energy use prediction. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 2786–2791. [Google Scholar] [CrossRef]
- Pentzer, J.; Reichard, K.; Brennan, S. Energy-based path planning for skid-steer vehicles operating in areas with mixed surface types. In Proceedings of the 2016 American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 2110–2115. [Google Scholar] [CrossRef]
- Pentzer, J.; Brennan, S.; Reichard, K. On-line estimation of power model parameters for skid-steer robots with applications in mission energy use prediction. J. Field Robot. 2022, 39, 763–782. [Google Scholar] [CrossRef]
- Góra, K.; Kujawinski, M.; Wroński, D.; Granosik, G. Comparison of Energy Prediction Algorithms for Differential and Skid-Steer Drive Mobile Robots on Different Ground Surfaces. Energies 2021, 14, 6722. [Google Scholar] [CrossRef]
- Loukatos, D.; Arapostathis, V.; Karavas, C.S.; Arvanitis, K.G.; Papadakis, G. Power Consumption Analysis of a Prototype Lightweight Autonomous Electric Cargo Robot in Agricultural Field Operation Scenarios. Energies 2024, 17, 1244. [Google Scholar] [CrossRef]
- Mei, Y.; Lu, Y.H.; Hu, Y.; Lee, C. Energy-efficient motion planning for mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation 2004 (Proceedings. ICRA ’04), New Orleans, LA, USA, 26 April–1 May 2004; Volume 5, pp. 4344–4349. [Google Scholar] [CrossRef]
- Hou, L.; Zhang, L.; Kim, J. Energy Modeling and Power Measurement for Mobile Robots. Energies 2019, 12, 27. [Google Scholar] [CrossRef]
- Hou, L.; Zhou, F.; Kim, K.; Zhang, L. Practical Model for Energy Consumption Analysis of Omnidirectional Mobile Robot. Sensors 2021, 21, 1800. [Google Scholar] [CrossRef]
- Tokekar, P.; Karnad, N.; Isler, V. Energy-optimal velocity profiles for car-like robots. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1457–1462. [Google Scholar] [CrossRef]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Liu, Y. An optimization-driven dynamic vehicle routing algorithm for on-demand meal delivery using drones. Comput. Oper. Res. 2019, 111, 1–20. [Google Scholar] [CrossRef]
- Chauhan, D.; Unnikrishnan, A.; Figliozzi, M. Maximum coverage capacitated facility location problem with range constrained drones. Transp. Res. Part C Emerg. Technol. 2019, 99, 1–18. [Google Scholar] [CrossRef]
- Poikonen, S.; Golden, B. Multi-visit drone routing problem. Comput. Oper. Res. 2020, 113, 104802. [Google Scholar] [CrossRef]
- Shavarani, S.M.; Nejad, M.G.; Rismanchian, F.; Izbirak, G. Application of hierarchical facility location problem for optimization of a drone delivery system: A case study of Amazon prime air in the city of San Francisco. Int. J. Adv. Manuf. Technol. 2018, 95, 3141–3153. [Google Scholar] [CrossRef]
- Moore, A.M. Innovative scenarios for modeling intra-city freight delivery. Transp. Res. Interdiscip. Perspect. 2019, 3, 100024. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 70–85. [Google Scholar] [CrossRef]
- Chiang, W.C.; Li, Y.; Shang, J.; Urban, T.L. Impact of drone delivery on sustainability and cost: Realizing the UAV potential through vehicle routing optimization. Appl. Energy 2019, 242, 1164–1175. [Google Scholar] [CrossRef]
- Figliozzi, M.A. Lifecycle modeling and assessment of unmanned aerial vehicles (Drones) CO2e emissions. Transp. Res. Part D Transp. Environ. 2017, 57, 251–261. [Google Scholar] [CrossRef]
- Ferrandez, S.; Harbison, T.; Weber, T.; Sturges, R.; Rich, R. Optimization of a truck-drone in tandem delivery network using k-means and genetic algorithm. J. Ind. Eng. Manag. 2016, 9, 374. [Google Scholar] [CrossRef]
- Zorbas, D.; Razafindralambo, T.; Luigi, D.P.P.; Guerriero, F. Energy Efficient Mobile Target Tracking Using Flying Drones. Procedia Comput. Sci. 2013, 19, 80–87. [Google Scholar] [CrossRef]
- Di Puglia Pugliese, L.; Guerriero, F.; Zorbas, D.; Razafindralambo, T. Modelling the mobile target covering problem using flying drones. Optim. Lett. 2016, 10, 1021–1052. [Google Scholar] [CrossRef]
- Kirschstein, T. Comparison of energy demands of drone-based and ground-based parcel delivery services. Transp. Res. Part D Transp. Environ. 2020, 78, 102209. [Google Scholar] [CrossRef]
- Stolaroff, J.K.; Samaras, C.; O’Neill, E.R.; Lubers, A.; Mitchell, A.S.; Ceperley, D. Energy use and life cycle greenhouse gas emissions of drones for commercial package delivery. Nat. Commun. 2018, 9, 409. [Google Scholar] [CrossRef]
- D’Andrea, R. Guest Editorial Can Drones Deliver? IEEE Trans. Autom. Sci. Eng. 2014, 11, 647–648. [Google Scholar] [CrossRef]
- Choi, Y.; Schonfeld, P. Optimization of Multi-package Drone Deliveries Considering Battery Capacity. In Proceedings of the 96th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 8–12 January 2017. [Google Scholar]
- Kingry, N.; Towers, L.; Liu, Y.C.; Zu, Y.; Wang, Y.; Staheli, B.; Katagiri, Y.; Cook, S.; Dai, R. Design, Modeling and Control of a Solar-Powered Quadcopter. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1251–1258. [Google Scholar] [CrossRef]
- Li, B.; Na, Z.; Lin, B. UAV Trajectory Planning from a Comprehensive Energy Efficiency Perspective in Harsh Environments. IEEE Netw. 2022, 36, 62–68. [Google Scholar] [CrossRef]
- Li, D.; Wang, X.; Sun, T. Energy-optimal coverage path planning on topographic map for environment survey with unmanned aerial vehicles. Electron. Lett. 2016, 52, 699–701. [Google Scholar] [CrossRef]
- Abeywickrama, H.V.; Jayawickrama, B.A.; He, Y.; Dutkiewicz, E. Comprehensive Energy Consumption Model for Unmanned Aerial Vehicles, Based on Empirical Studies of Battery Performance. IEEE Access 2018, 6, 58383–58394. [Google Scholar] [CrossRef]
- Prasetia, A.S.; Wai, R.J.; Wen, Y.L.; Wang, Y.K. Mission-Based Energy Consumption Prediction of Multirotor UAV. IEEE Access 2019, 7, 33055–33063. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; D’Andreagiovanni, F.; Liu, W.; Gutierrez, J.A.; Blefari-Melazzi, N.; Choo, K.K.R.; Alouini, M.S. Multi-Area Throughput and Energy Optimization of UAV-Aided Cellular Networks Powered by Solar Panels and Grid. IEEE Trans. Mob. Comput. 2021, 20, 2427–2444. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, D.; Ng, D.W.K.; Dai, L.; Schober, R. Optimal 3D-Trajectory Design and Resource Allocation for Solar-Powered UAV Communication Systems. IEEE Trans. Commun. 2019, 67, 4281–4298. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, X.; Jia, W.; Lei, J.; Wang, D.; Feng, T.; Zeng, Y.; Song, J. Multiobjective Energy Consumption Optimization of a Flying–Walking Power Transmission Line Inspection Robot during Flight Missions Using Improved NSGA-II. Appl. Sci. 2024, 14, 1637. [Google Scholar] [CrossRef]
- Góra, K.; Smyczyński, P.; Kujawiński, M.; Granosik, G. Machine Learning in Creating Energy Consumption Model for UAV. Energies 2022, 15, 6810. [Google Scholar] [CrossRef]
- Muñoz, J.; López, B.; Moreno, L. Gaussian Processes for Energy Consumption Estimation of Unmanned Aerial Vehicles. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Canary Islands, Spain, 19–21 July 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, C.; Adulyasak, Y.; Rousseau, L.M. Drone routing with energy function: Formulation and exact algorithm. Transp. Res. Part B Methodol. 2020, 139, 364–387. [Google Scholar] [CrossRef]
- Zhang, J.; Campbell, J.F.; II, D.C.S.; Hupman, A.C. Energy consumption models for delivery drones: A comparison and assessment. Transp. Res. Part D Transp. Environ. 2021, 90, 102668. [Google Scholar] [CrossRef]
- Langelaan, J.W.; Schmitz, S.; Palacios, J.; Lorenz, R.D. Energetics of rotary-wing exploration of Titan. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–11. [Google Scholar] [CrossRef]
- Yacef, F.; Rizoug, N.; Degaa, L.; Bouhali, O.; Hamerlain, M. Energy efficiency path planning for a quadrotor aerial vehicle. In Transactions of the Institute of Measurement and Control; SAGE Publications Ltd STM: New York, NY, USA, 2021; Volume 1, pp. 1133–1138. [Google Scholar] [CrossRef]
- Tseng, C.M.; Chau, C.K.; Elbassioni, K.; Khonji, M. Flight Tour Planning with Recharging Optimization for Battery-Operated Autonomous Drones. arXiv 2017, arXiv:abs/1703.10049. [Google Scholar]
- Zeng, Y.; Xu, J.; Zhang, R. Energy Minimization for Wireless Communication with Rotary-Wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Yan, H.; Chen, Y.; Yang, S.H. New Energy Consumption Model for Rotary-Wing UAV Propulsion. IEEE Wirel. Commun. Lett. 2021, 10, 2009–2012. [Google Scholar] [CrossRef]
- Katoh, R.; Ichiyama, O.; Yamamoto, T.; Ohkawa, F. A real-time path planning of space manipulator saving consumed energy. In Proceedings of the IECON’94—20th Annual Conference of IEEE Industrial Electronics, Bologna, Italy, 5–9 September 1994; Volume 2, pp. 1064–1067. [Google Scholar] [CrossRef]
- Silva, F.; Tenreiro Machado, J. Energy analysis during biped walking. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 1, pp. 59–64. [Google Scholar] [CrossRef]
- Yamasaki, F.; Hosoda, K.; Asada, M. An energy consumption based control for humanoid walking. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; Volume 3, pp. 2473–2477. [Google Scholar] [CrossRef]
- Gregorio, P.; Ahmadi, M.; Buehler, M. Design, control, and energetics of an electrically actuated legged robot. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1997, 27, 626–634. [Google Scholar] [CrossRef]
- Zhao, N.; Luo, Y.; Shen, Y. Design, modeling and validation of a deformable capsule-like crawling robot based on scissor elements. Mech. Mach. Theory 2023, 181, 105173. [Google Scholar] [CrossRef]
- Brodoline, I.; Sauvageot, E.; Viollet, S.; Serres, J.R. Shaping the energy curves of a servomotor-based hexapod robot. Sci. Rep. 2024, 14, 11675. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Ji, H.; Chang, Q. Energy Consumption Minimization of Quadruped Robot Based on Reinforcement Learning of DDPG Algorithm. Actuators 2024, 13, 18. [Google Scholar] [CrossRef]
- Lopez, M.; Haghshenas-Jaryani, M. A Study of Energy-Efficient and Optimal Locomotion in a Pneumatic Artificial Muscle-Driven Snake Robot. Robotics 2023, 12, 89. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).