Three-Level Secure Smart Protection for Ring Grid-Connected Distributed Generation

Abstract

The penetration increase in distributed generators (DGs) into smart grids (SGs) will lead to new challenges, especially in protection systems. In the case of ring grids, the behavior of the short-circuit current is affected by DGs, and the medium voltage (MV) transformer connections significantly influence the changes; therefore, the protection strategies must be adapted for these scenarios. This study provides a comprehensive protection system for the MV distribution system (DS), including reconfigurable smart ring grids. The proposed protection methods contain three protection algorithms. The first protection algorithm relies on communication among all protective devices (PDs) in the grid, whereas the second protection method uses communication among PDs along the same line. Then, a third algorithm built on the local data of each PD is suggested as a backup to prevent communication issues and offer more reliable protection. MATLABTM SIMULINK simulations and experimental results on a scalable hardware grid were also employed to validate the protection algorithms.

1. Introduction

Distributed generator (DG) penetration in distribution systems (DSs) is growing significantly. However, this increase causes several challenges due to various power-generating sites and changes in the current value of relay short-circuits, which impact the protective device (PD) settings. The DG penetrations into a DS may also impact the grid power flow [1].

Transformers are one of the essential components of electric power systems that significantly impact a distribution system. They can affect system loss, zero-sequence currents, the grounding method, and the protection strategy [2]. Transformers are connected in various distribution system configurations, affecting the system performance, including the phase shift’s impact on the relay protection and system operation. An example of this is the phase shift caused by the delta-grounded wye connection of distribution step-down transformers [3], which alters positive- and negative-sequence voltages. Consequently, the three phases’ magnitudes and phase-angle jumps will shift due to unbalanced voltage sag.

Another important factor that significantly impacts system performance and protective relaying is selecting the type of neutral grounding [4]. For example, in the case of a delta–wye transformer with grounded neutral, if there is a single line-to-ground fault on the wye side, due to the infinite zero-sequence impedance between the two windings, the ground relays on the delta side will not detect the fault. On the other hand, the phase relays will identify it as a phase-to-phase fault with a magnitude of 58% [5], less than the wye side. Therefore, a number of technical obstacles emerge in relation to this potentiality. The detection of faults by conventional protection systems is a challenging and complex matter, posing a significant challenge. This highlights the importance of employing intelligent protection strategies in order to enhance the efficiency of the network [6].

Different territories adopt several earthing systems according to the rated voltage level. For example,

Table 1. Grounding connection of the hv/mv power transformer.

Transformer Connection High Voltage/Medium Voltage (HV/MV)
YNd11
YNyn
YNyg grounded through a resistor
YNd11 grounded through zig-zag
YNd11 grounded through zig-zag and resistor

, obtained from the Spanish electrical company ENDESA, demonstrates different transformer connections depending on the utility [7,8]. Moreover, the same utility can adopt different earthing systems for each region, as shown in the second table of the Iberdrola company document regarding the particular customer facility regulations [8].

The protection of DSs has recently placed increasing emphasis on Artificial Intelligence (AI) approaches, mainly because of their ability to operate fast and deal with many inputs. Table 2 shows the advantages and disadvantages of the most common techniques. Furthermore, cyber security is one of the main challenges that has arisen with the increase in smart grids (SGs). Due to the increased reliance on communications for control and optimization in SGs, many issues have been raised, such as insecure communication protocols, insecure protocol translators similar to end-point device vulnerabilities, and poor communication network design [9]. Previous issues could lead to severe security problems as PD settings change or do not communicate promptly [10]. Moreover, communications and controls in the SG may differ due to the lack of standardization, leading to incompatibility issues [11].

It should also be considered that the SG may have different stability margins which improve the network operation but detrimentally impact system stability without proper understanding [12]. Also, in some cases, SGs suffer from a lack of firewalls and intrusion detection or have prevention systems that cannot block or detect malicious communications [13].

Table 2. A comparative analysis of ai methods [14].

	Artificial Neural Network (ANN)	Support Vector Machine (SVM)	Fuzzy Logic Control (FLC)	Genetic Algorithm (GA)	Matching Approach
Advantages	▪ Handle complex and high-dimensional data. ▪ Adapted to new information and uncovering hidden patterns.	▪ Rapidity, regardless the problem size, ▪ Small error margin. ▪ Interpretability	▪ Robustness. ▪ Interpretability.	▪ Optimal solutions for problems from various domains.	▪ Cost saving. ▪ Interest rate fluctuation risk.
Disadvantages	▪ Training quality affect the results. ▪ The need for large datasets. ▪ Significant computational resources.	▪ Strongly depends on parameters selection, and kernel function. ▪ Difficulties with noisy data.	▪ Computational complexity. ▪ Data acquisition, and scalability.	▪ Lack consistency over time. ▪ Low efficiency. ▪ Premature convergence	▪ Actual data matching depends on the simulated data. ▪ The process of creating a database is time-consuming.

Table 2. A comparative analysis of ai methods [14].

	Artificial Neural Network (ANN)	Support Vector Machine (SVM)	Fuzzy Logic Control (FLC)	Genetic Algorithm (GA)	Matching Approach
Advantages	▪ Handle complex and high-dimensional data. ▪ Adapted to new information and uncovering hidden patterns.	▪ Rapidity, regardless the problem size, ▪ Small error margin. ▪ Interpretability	▪ Robustness. ▪ Interpretability.	▪ Optimal solutions for problems from various domains.	▪ Cost saving. ▪ Interest rate fluctuation risk.
Disadvantages	▪ Training quality affect the results. ▪ The need for large datasets. ▪ Significant computational resources.	▪ Strongly depends on parameters selection, and kernel function. ▪ Difficulties with noisy data.	▪ Computational complexity. ▪ Data acquisition, and scalability.	▪ Lack consistency over time. ▪ Low efficiency. ▪ Premature convergence	▪ Actual data matching depends on the simulated data. ▪ The process of creating a database is time-consuming.

Various methods have been developed lately to locate and detect faults in DSs despite multiple fault sources. In [15], a protection scheme that uses a deep neural network (DNN) and sparse autoencoder (SAE) is proposed to discriminate between array and symmetrical line faults as well as guarantee secure fault detection. This scheme offers a rapid tripping action considering the communication rate under various DG penetration and fault resistance scenarios. However, it must be updated in case of grid reconfiguration and relies on communication channels. In [16], a fault detection method utilizing a communication-based directional relay system with an ANN is presented. However, the demerits of complex computations and long training are presented, and communication is employed. In [17], the authors proposed a two-step protection algorithm for detecting and isolating faults in DSs with DGs. The algorithm offers a fast and effective solution for the bi-directional power flow issue, especially in the cases of high fault resistances and high DG penetration. However, the algorithm regarding grid reconfiguration or communication dependability has not been tested.

In [18], a fault protection scheme has been proposed using negative- and positive-sequence components of the voltage signal. However, the scheme has not been tested in the case of an inverter-based DG. In [19], a protection algorithm has been proposed that relies on the harmonic analysis of each voltage phase. The algorithm utilizes the fast Fourier transform (FFT) to achieve lower harmonics and total harmonic distortion (THD). However, the FFT supposes a high computational burden for being implemented in a digital processor. The authors of [20] presented a communication-based algorithm that detects faults in various locations of a DS grid by utilizing a finite-state machine. The harmonics of the grid voltages are analyzed by the algorithm using a multiple second-order generalized integrator structure with a frequency-locked loop (MSOGI-FLL). This algorithm offers fast detection action with a low computational burden. However, security issues have not been avoided as the algorithm is based on communication channels.

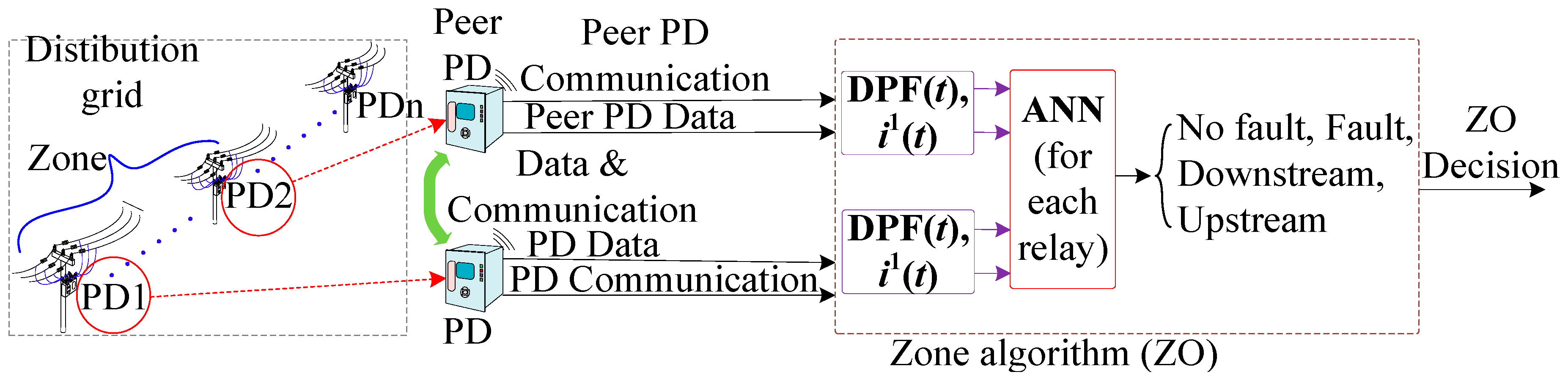
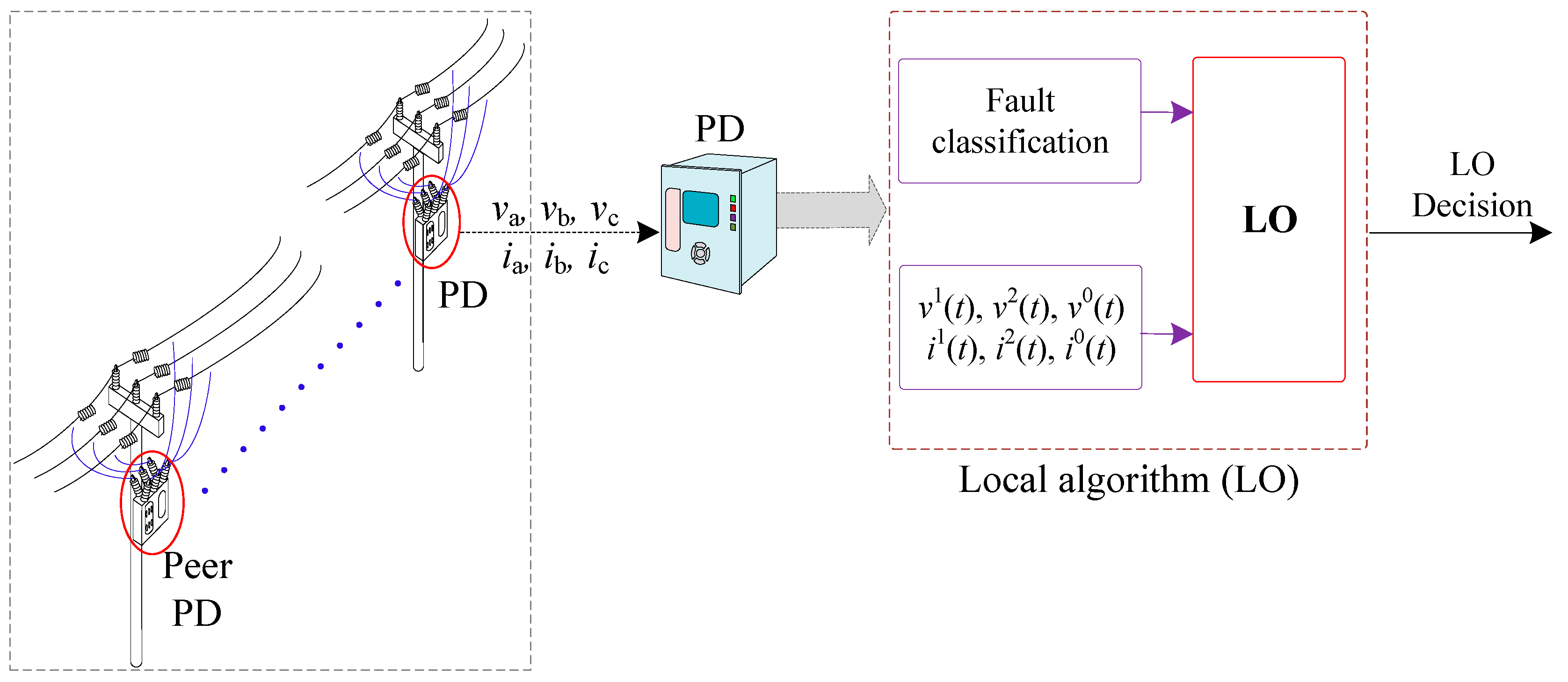
Previous research has mainly focused on communication, with no solutions for poor communication. As seen from the aforementioned studies, an integrated protection strategy that can operate for ring and radial DSs with high DG penetration in the case of reconfigurable grids is still needed. The authors’ prior study presents an AI protection approach based on three strategies [21,22]. The first strategy, the centralized algorithm (CE), uses grid-wide communication amongst all PDs. Furthermore, in the second strategy, known as the zone algorithm (ZO), the communication between the PDs in the same line is utilized, while the third protection strategy, called the local algorithm (LO), relies on each PD’s local measurements without relying on communication.

Without any inter-PD contact, the LO is based only on the local data of each PD. This fault isolation and localization method considers diverse fault types, variable load consumption, DG penetration, multiple fault locations, HV/MV transformer configuration, and low and high fault resistance, resulting in more redundant and secure protection. Since no communication is required and the LO is simple to adapt to various grids without the requirement for training, as with AI approaches, it can offer a more reliable, supporting approach that is also a more cost-effective protection strategy than other protection algorithms. In addition, the LO protects if the other two layers of protection are ineffective. It is crucial to emphasize that the factors influencing inverter-based generators, such as short transient durations, low short-circuit currents, and reversible power flow, have been considered. Another factor to consider is the ground connection of the HV/MV transformer, since this will impact the short-circuit current in the network, changing the protection system’s behavior.

This paper investigates various transformer connections obtained from different facilities. The most typical setups are the grounded or isolated transformers. In the case of a grounded transformer, the secondary of the HV/MV transformer is connected to the ground, i.e., YNyn grounded. Furthermore, in the case of an isolated transformer, a zig-zag transformer is used to provide an artificial neutral and isolate the transformer YNd11, which is grounded through zig-zag [8].

The main difference between the proposed algorithms in this context and the authors’ previous publications [22] can be concluded as follows:

• The protection algorithms have been adapted for ring rather than radial grids. In this case, the algorithms depend on the direction of power flow (DPF).
• The study of different HV/MV transformer connections in the case of ring grids.
• The effect of HV/MV transformer connections on the proposed protection algorithms has been studied.

The rest of the paper is organized as follows: The proposed LO protection algorithm is first introduced. Secondly, a discussion of the proposed protection algorithm’s validation analysis is presented. The experimental results are then explained. Finally, the paper’s conclusion is discussed.

2. Three-Level Protection Algorithms

As shown in Figure 1, a protection strategy employing three-level algorithms has been proposed. The initial algorithm is established through the transmission of data analyzed by every PD in the grid to a CE. The second algorithm, on the other hand, is founded upon a ZO that utilizes peer-to-peer communication. The proposed approach relies on a comparison of the decisions made by both algorithms in order to develop a redundant and more dependable system. Moreover, in the event of inadequate communication, a more robust protection system will be implemented through the utilization of the third algorithm, the LO. The grid fault will be isolated through the algorithm’s analysis of the local voltage and the current data of each PD. Each algorithm was evaluated for stiff and weak grids in a variety of scenarios involving fault types, fault locations, fault resistance, the quantity and location of DGs, their contribution, load consumption, and diverse neutral connections for the MV side of the HV/MV transformer.

2.1. Level 1: Centralize Algorithm (CE)

In this algorithm, every connection between the PDs and the CE is deemed to be accessible, as inputs to the CE, DPF data for the ring grid and positive-sequence current (i+) data for the radial grid are utilized in order to determine the correct course of action. This is feasible due to the short length of the lines and the insufficiency of the transversal capacitance to generate a significant current difference at both ends. The conceptual diagram of the CE controller is illustrated in Figure 2. Training for the ANN must incorporate variations in the short-circuit current and DPF of each PD. Using voltage and current, the DPF and i+ are computed locally at each PD; only the processed data are transmitted to the controller.

By obviating the necessity to convey voltages and currents to the CE, thereby streamlining the communication process, this measure will enhance the accessibility of the learning experience and reduce the percentage of errors. The authors have previously documented the training and testing of an ANN in their publications [21,23].

The main advantage of this system is that it performs state estimation and security evaluations while centralizing the whole system’s security into a single device [24]. On the other hand, problems with communications or the CE system caused by failure or safety concerns will result in a complete loss of protection until services are restored [25]. Additionally, communication delays must be considered. The overall communication delay comprises elements, as indicated in Figure 3, including transmission, queuing, propagation, and processing delays. The overall communication latency will be so minimal that the trip signals may be sent in less than one millisecond [26].

2.2. Level 2: Zone Algorithm (ZO)

This algorithm is found at each PD and relies on communicating between the two PDs in the same line to exchange DPF data to change each PD’s status under the defective area of the grid, as shown in Figure 4. The implementation of the ZO operates concurrently with the CE. Then, the decisions of both controllers are reviewed to increase the redundancy and security of the protection system. Encrypted communication and the ability to accommodate temporary grid reconfigurations are among its benefits. The trained fault ZO ANN controller parameters are detailed in the authors’ prior works [21,23].

2.3. Level 3: Local Algorithm (LO)

This approach does not require a complete connection between the PDs, so the protective mechanism can continue functioning even if communication is lost. As shown in Figure 5, using just the local knowledge of the PD, each PD should be able to determine if the fault is on the protected line or another line. The concept is based on utilizing each PD’s voltage and current sequence components during fault events. Figure 6 displays a ring DS’s single-line diagram with DG penetration and an LO algorithm. An algorithm for fault localization that is specific to each type of fault has been implemented. The sequence components will differ depending on whether the fault is symmetrical or asymmetrical, highlighting the importance of employing a fault classification method to determine the fault type prior to implementing the suggested LO algorithm. An ANN is selected as the instrument utilized by the LO to determine the fault type. The training and evaluation of ANNs are detailed in a prior publication by the authors [22].

In order to present the differences between the three protection strategies (CE, ZO, and LO), the main advantages and disadvantages of each algorithm are shown in

Table 3. Comparison between CE, ZO, and LO protection algorithms.

	Advantages	Disadvantages
CE	- Consolidates the security of the entire system into a single device, performing state estimation and security evaluations. - Fast tripping. - Ability to operate correctly under different circumstances.	- Fixed to the existing grid configuration. - Communications issues. - Necessitating additional training time and a more complex training procedure.
ZO	- The same ANN used for each PD can be utilized for the newly added line. - Less training time compared to CE. - Encrypted communication, and the ability to adapt to temporary grid reconfigurations. - Operate correctly under different circumstances.	- Communication problems. - Training data are required.
LO	- No communication is needed. - More secure. - Separate decision for each PD. - No training is needed.	- Need to be adapted for new grids. - Slow tripping compared to CE/ZO algorithms.

.

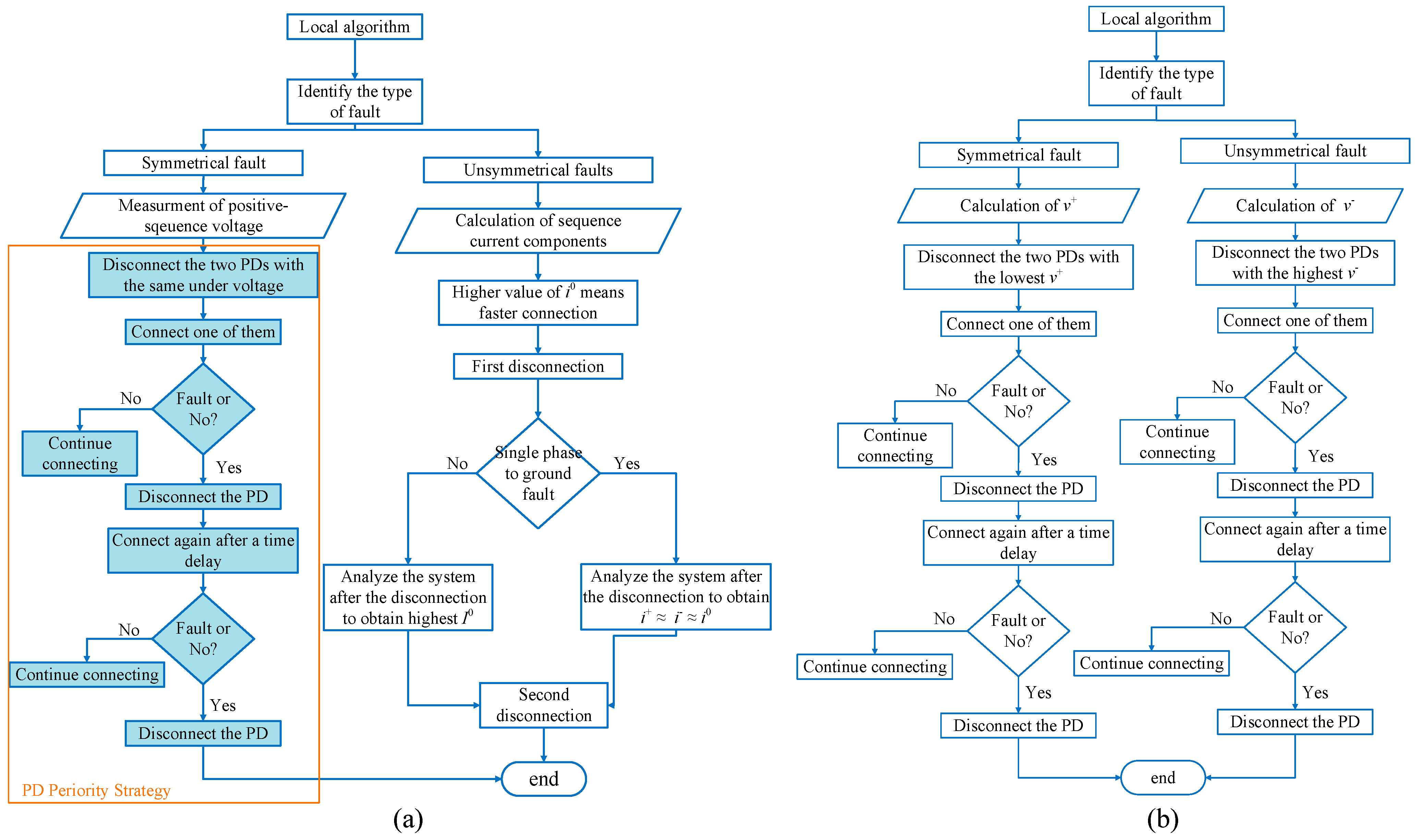
3. Proposed Protection Algorithms Modifications

This research has chosen the most common transformer connections: YNyn grounded, not isolated in normal operation, and YNd11 grounded through zig-zag, isolated in regular operation.

A comprehensive explanation of the LO protection algorithm will be provided in the subsequent subsections, encompassing two scenarios and every fault type. The MV side of the HV/MV transformer not being isolated will constitute the first scenario. The magnitude of the short-circuit current in the analyzed grid will be altered by this connection, which isolates the second scenario. In addition, the PD priority strategy will be discussed.

3.1. YNyn Grounded HV/MV Transformer

The faulty line can be identified by analyzing the zero-sequence current during the fault in the case of a single-phase fault with unisolated ground. During the fault, the zero-sequence current at the faulty line’s one end will be higher than any zero-sequence value on any other line. Consequently, a higher number indicates a quicker disengagement, as seen in Figure 6.

Examining the grid after disconnecting the PD with the highest zero-sequence current is the subsequent procedure. Upon disconnecting one end of the defective line, the three sequence currents at the other end will acquire an approximation of the identical value, as illustrated in Figure 6b. Thus, the faulty line in a single-phase fault can be isolated using these data.

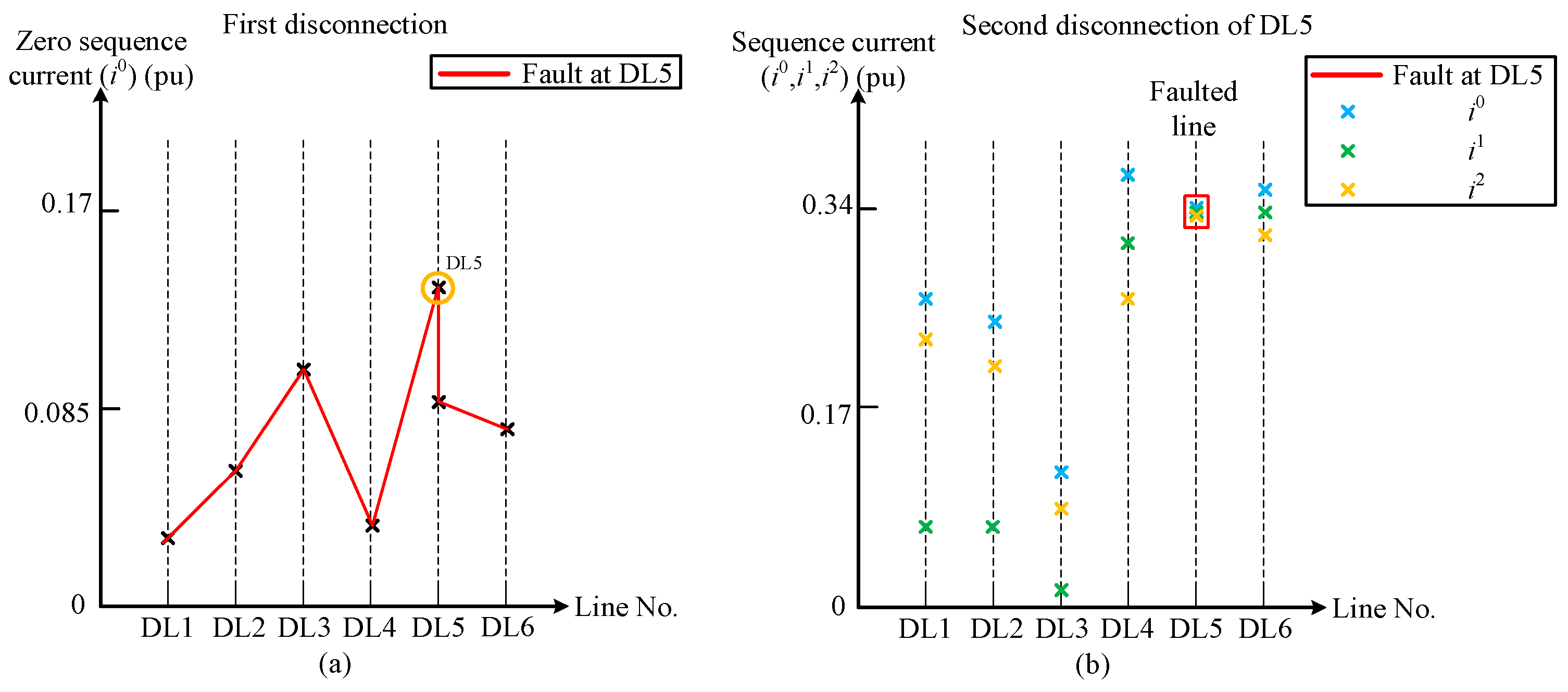
The zero-sequence current profile for a single-phase to ground fault at DL5 is illustrated in Figure 7. As shown in Figure 7, the trip is determined by the maximum zero-sequence current during the initial disconnection (a). As shown in Figure 7, the trip for the second disconnection is determined by three sequence currents at the opposite end of the faulted line that have values that are approximately equivalent (b).

When confronted with two-phase or two-phase to-ground faults, the initial disconnection can be executed using the identical methodology employed for single-phase faults. The zero-sequence current at one end of the faulted line during the fault can be utilized to locate the fault. Following the initial disconnection, a subsequent analysis of the grid is conducted. For the second disconnection, the maximum value of zero-sequence current at the opposite end of the faulty line will be acquired.

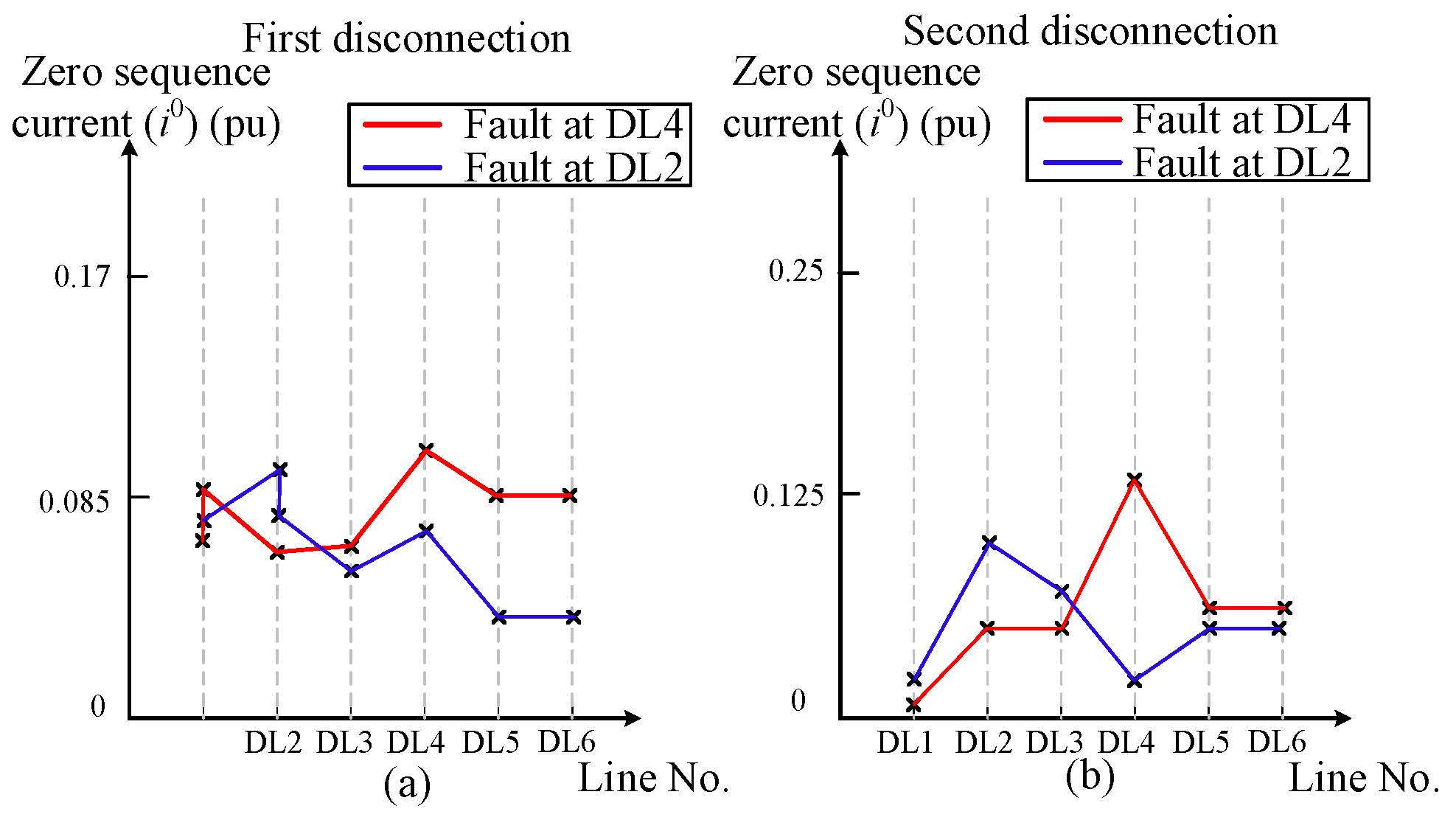
The current profile of the zero-sequence for the two-phase to-ground fault at DL2 and the two-phase fault at DL4 is illustrated in Figure 8. If the fault is located at DL4, this line has the greatest i0 (0.106 pu). When the highest i0 (0.145 pu) is observed at the opposite end of DL4 following the initial disconnection, both ends of the faulty line can be severed. Using the same principle, if the fault at DL2 causes the highest i0 value (0.101 pu) to be at one end of DL2, then i0 will be at its highest value (0.103 pu) at the other end of DL2 following the initial disconnection; therefore, the faulted line will be disconnected.

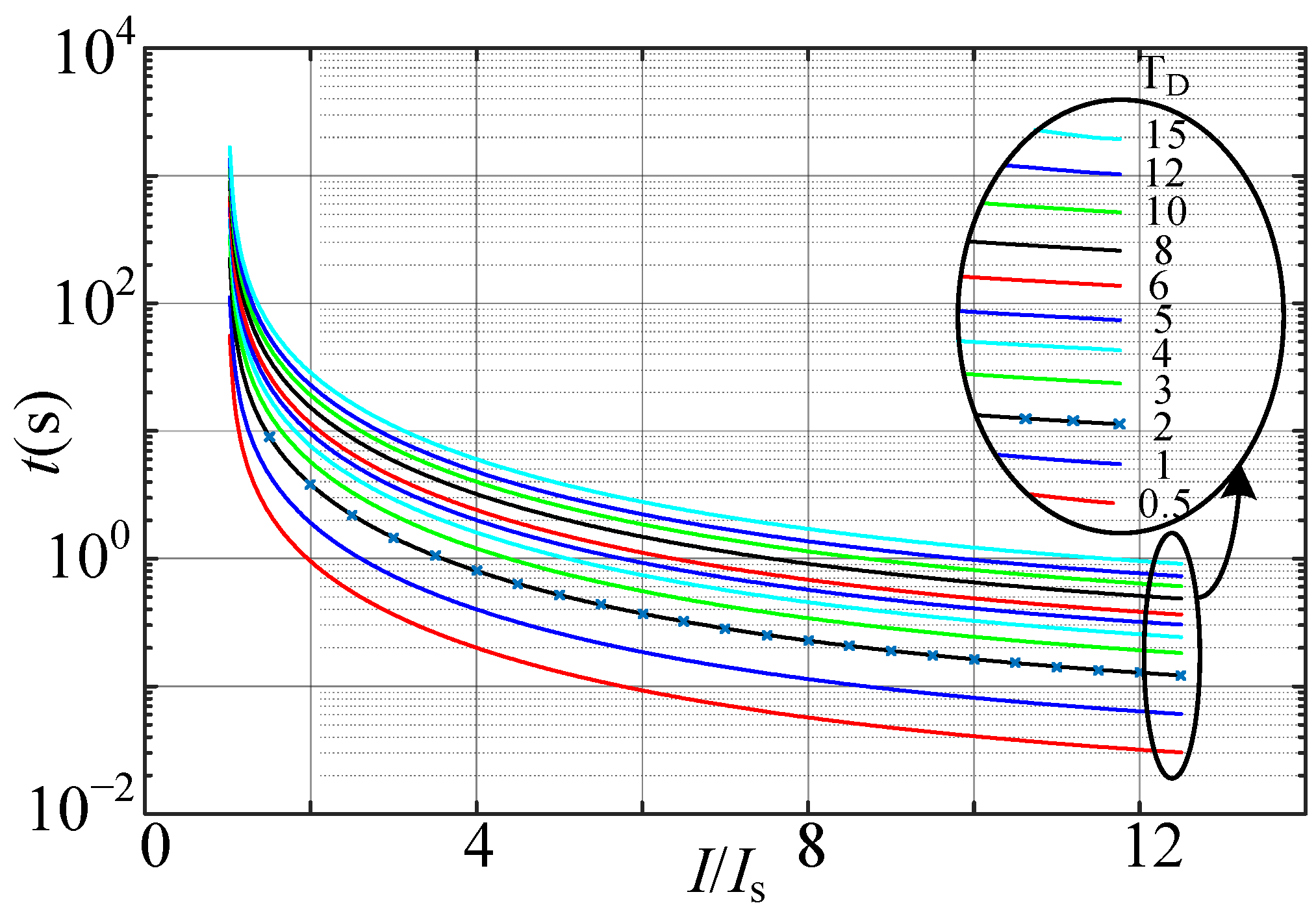
The designed curve for unsymmetrical faults utilizing a zero-sequence current is depicted in Figure 9. In order to design the curve, the zero-sequence current values for various grid configurations and scenarios were considered. This curve is adaptable to voltage levels and alternative grid configurations.

The under-voltage relay will be utilized to cut off one end of the faulty line in the case of a three-phase fault. After the initial disconnection, the opposite end of the faulty line will be disconnected using the same under-voltage criterion. Two ends of lines can achieve the same voltage by employing the under-voltage relay, which implies two PDs might disconnect simultaneously. So, a new method called the recloser algorithm will disconnect the PD at the faulty line.

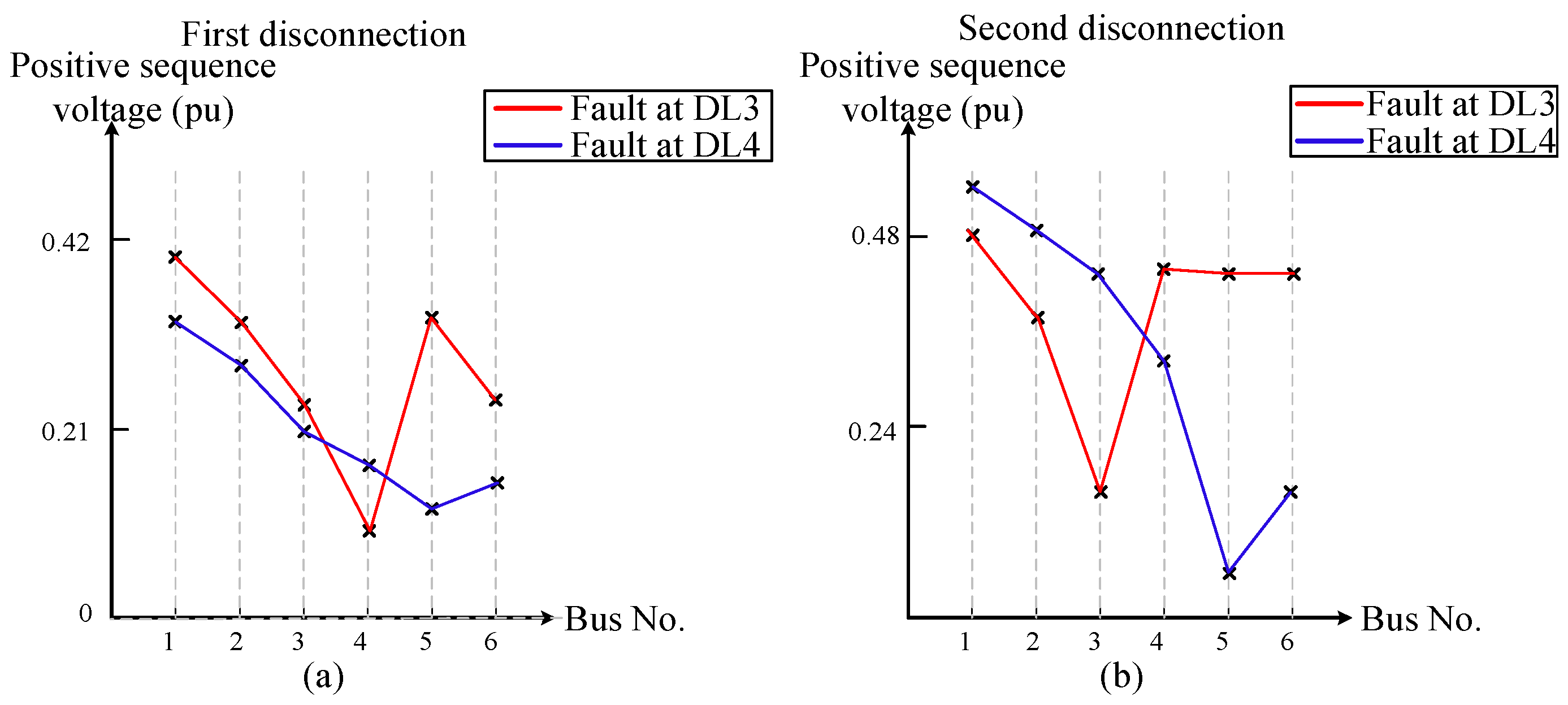
Explaining the LO algorithm for grounding the transformer with the zig-zag transformer connected to the MV side, the subsequent subsection will provide further clarification on the design of the definite time curve. The algorithm’s fundamental idea is to open and close using the recloser after a specific delay. The following subsection will cover the recloser algorithm’s precise concept. Figure 10 illustrates the voltage profile when a three-phase fault occurs. It has been demonstrated that, in the event of a three-phase fault at DL3, the minimum positive-sequence voltage (v+) is observed at one terminal of DL3, specifically bus 4. Subsequent to the disconnection of the faulty line at bus 3, identical behavior is observed. As seen in Figure 10, similar behavior is noticed when the fault is located at DL4.

3.1.1. Recloser Algorithm

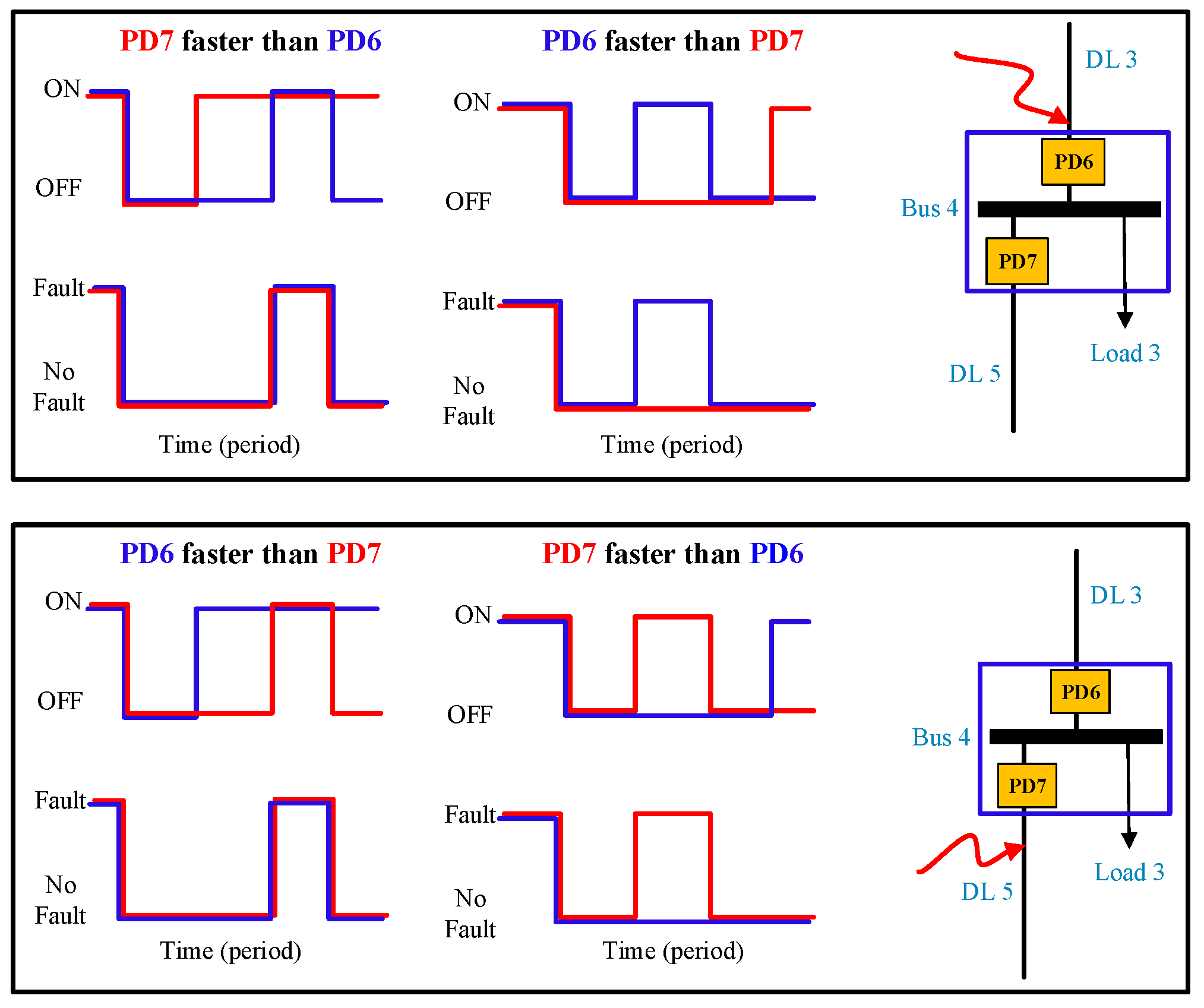
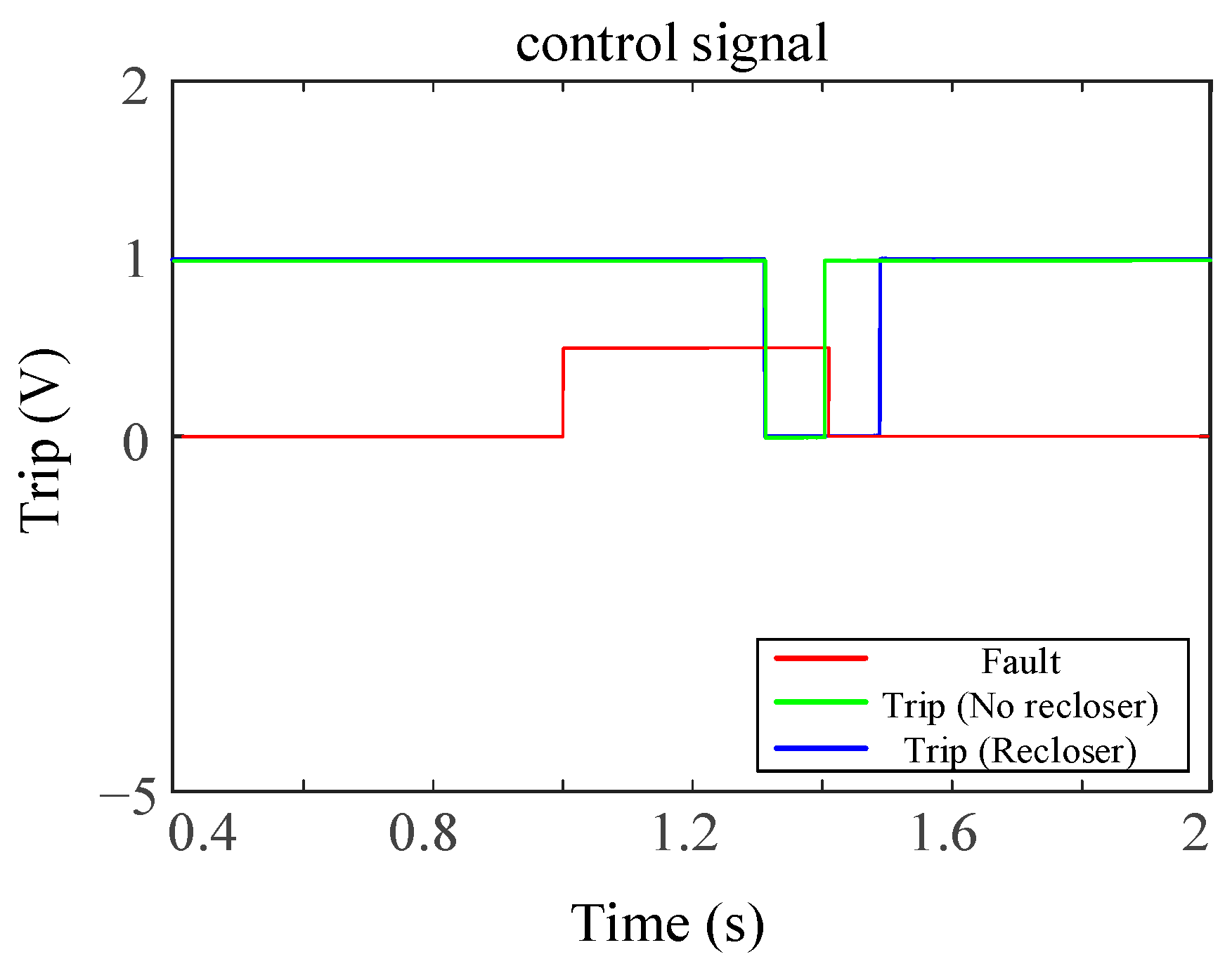
Two signals are utilized in Figure 11. The first is used to switch on and off the PD, while the second is used to indicate whether the PD has detected a fault. As shown in Figure 1, if there is a fault at the end of line 3 (DL3), PD6 and PD7 should disconnect simultaneously since they have the same under-voltage. If PD6 is a bit quicker than PD7, then they should both disconnect. Nevertheless, PD6 will reconnect after a predetermined interval. As shown in Figure 11, PD6 will permanently disconnect, and PD7 will connect after a longer specified time if there is a fault.

On the other hand, if PD7 is quicker than PD6, they both disconnect at first because of under-voltage. Since PD6 is still disconnected, PD7 will not detect errors and will connect first. As a result, PD7 will stay connected. After a delay, PD6 will reconnect and detect the fault, causing PD6 to disconnect again.

Four PDs connected to the two buses at either end of the faulty line will have the same under-voltage in the event of a line fault, and the recloser algorithm will be used for both ends of the line. Figure 12a shows the flowchart of the LO with the recloser algorithm. The highlighted blue part in the figure is related to the recloser algorithm.

3.1.2. Proposed LO Algorithm without Recloser

The recloser concept has the drawback of requiring additional time and steps to disconnect the fault. Consequently, an additional concept that has been put forth involves relocating the measurement signals. By positioning the measuring devices in front of the circuit breaker (Figure 13b) as opposed to behind it (Figure 13a), the concept is implemented. Instead of employing the time-consuming and multi-step recloser algorithm, which requires measured voltages to clear the fault, the presence of the fault can be determined directly.

As illustrated in Figure 13, measurement devices positioned between the bus and the circuit breaker will observe the same voltage and be disconnected from the fault when both beakers are disconnected subsequent to the disconnection of the bus. A recloser algorithm must subsequently be implemented to deactivate the circuit breaker in the faulty line.

However, if the measurement signals are positioned in front of the circuit breaker, one of them will be isolated from the fault while the other remains exposed to it following the disconnection of both breakers caused by under-voltage. Since this is the case, the recloser algorithm is unnecessary. Conversely, each breaker is capable of rendering an immediate and delay-free decision. Consequently, the duration required to detach the faulty component from the power grid is shortened.

The clearing time required to disconnect the faulted side of the line in the event of a three-phase fault with the LO is illustrated in

Table 4. Fault clearing time.

	Clearing Time (s)
With recloser algorithm	0.47
Without recloser algorithm	0.39
Time difference	0.06–0.08

and Figure 14. The delay time of the measuring instruments is deemed to be included in the total tripping time. That is to say, an additional delay time is acquired with each open or close, which indicates that the clearing time of the fault will be longer with the recloser algorithm than it would be without the algorithm.

It is essential to note that the algorithms for the other fault types will not be impacted by the implementation of this concept. The flowchart of the proposed LO algorithm without a recloser is illustrated in Figure 15.

3.2. YNd11 Isolated HV/MV Transformer

The principal advantage of this algorithm is that it operates independently from the grounding connection of the HV/MV transformer. It accomplishes this by relying on the sequence abc voltages at each bus and subsequently employing the recloser algorithm to isolate the defective component of the system.

One end of the faulty line can be identified by observing the negative-sequence voltage that occurs during a single-phase fault. When the negative-sequence voltage at one end of the faulty line between two PDs connected to the same bus (bus 3) is greater than any other negative-sequence voltage values observed on other lines during the fault, the recloser algorithm will be utilized to isolate the PD at the faulty line. The highest value, therefore, corresponds to a more rapid disconnection. Figure 12 illustrates the flowchart of the LO algorithm in the case where the grounded YNd11 side of the HV/MV transformer is connected via a zig-zag transformer (b).

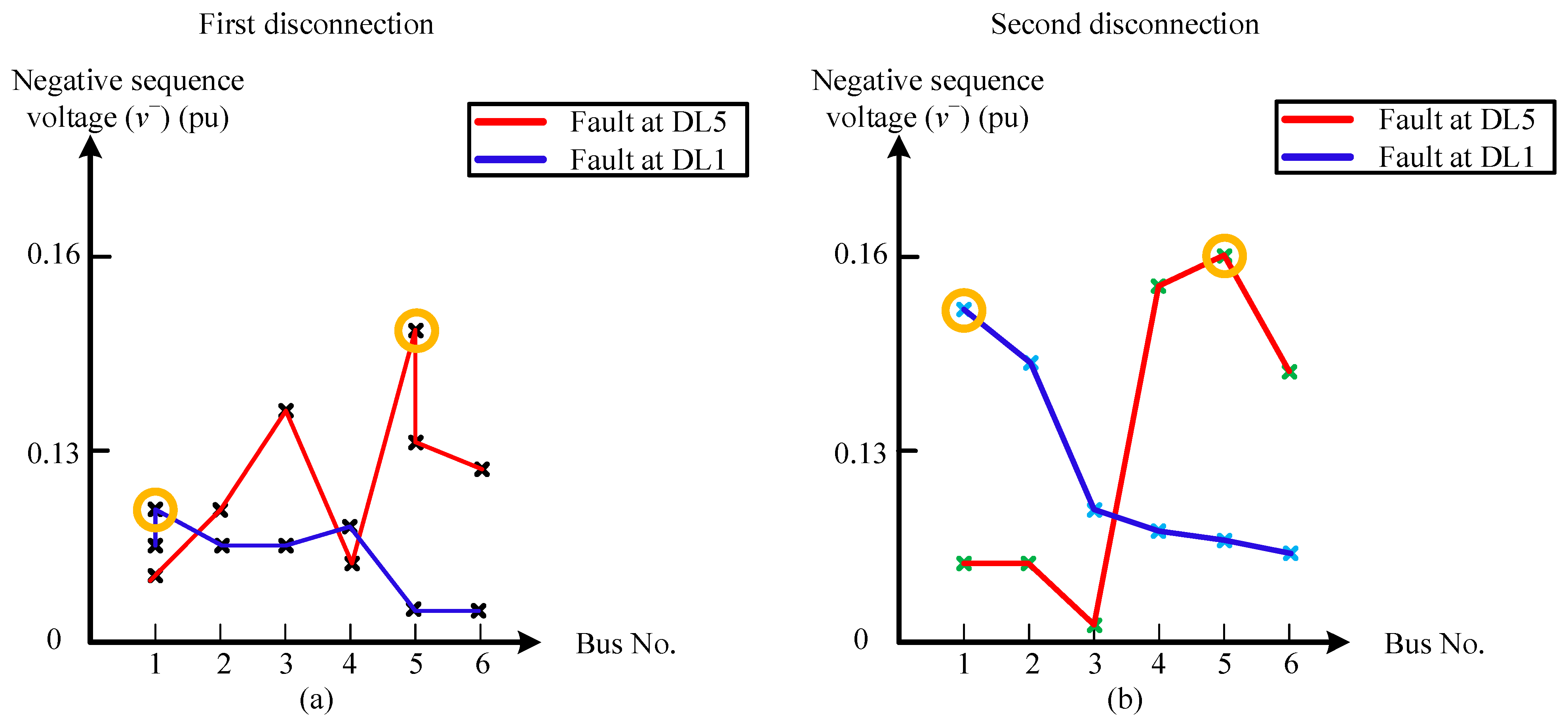
Following the disconnection of the PD with the highest voltage in the negative sequence, the grid is analyzed. In the event of a single-phase fault, the most significant value of the negative-sequence currents is obtained at the opposite end of the faulty line subsequent to disconnecting one end. This principle is employed to isolate the faulty line. Figure 16 illustrates the single-phase to ground fault zero-sequence current profile. The faulty line (DL5) has the greatest value for negative-sequence voltage (v⁻). Therefore, the first disconnection can be performed. The other end of the faulted line (DL5) can be disconnected using the same method. The behavior is similar when the fault is at DL1, as presented in Figure 16.

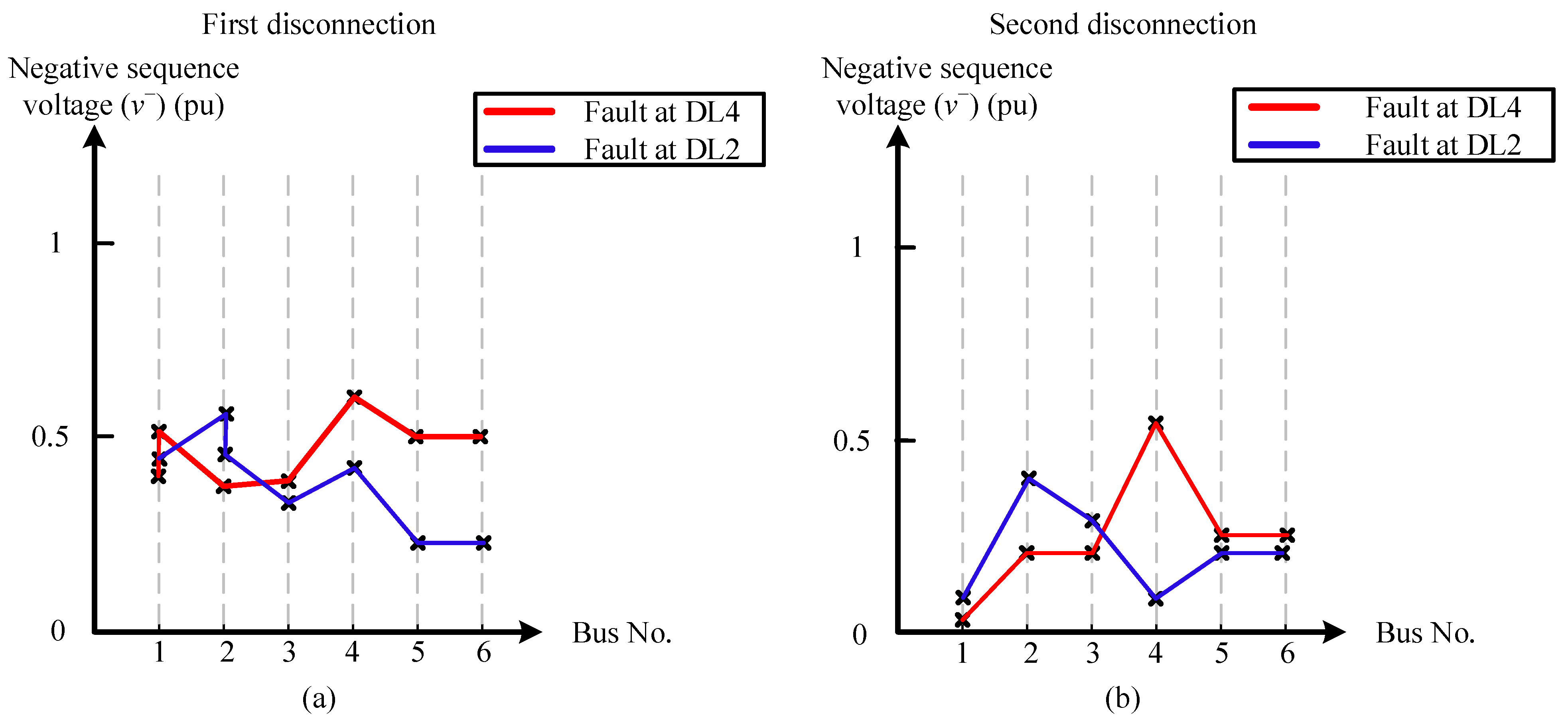
One end of the faulty line can be found in the case of a two-phase or two-phase to-ground fault using the same concept used in the case of a single-phase fault through the fault’s negative-sequence voltage. Figure 17 shows the case of two-phase faults. The negative-sequence voltage profile at the faulty line (DL4 or DL2) has the most significant value of v⁻ for implementing the first disconnection. The opposite end of the faulted line (DL4 or DL2) is disconnected using the same method.

Positive-sequence voltage is used in three-phase fault scenarios to identify the fault’s location and disconnect one end of the faulted line. First to trip is the PD, with the lowest positive-sequence voltage that recognizes the three-phase fault. After the initial disconnect, the opposite end of the faulty line is disconnected using the same principles.

The algorithm’s fundamental concept is to employ the recloser to reopen after a while, as explained in the preceding part. The IEEE Definite Time Standard [27,28] provides the basis for the equation used to describe the definite time–voltage characteristic curve. 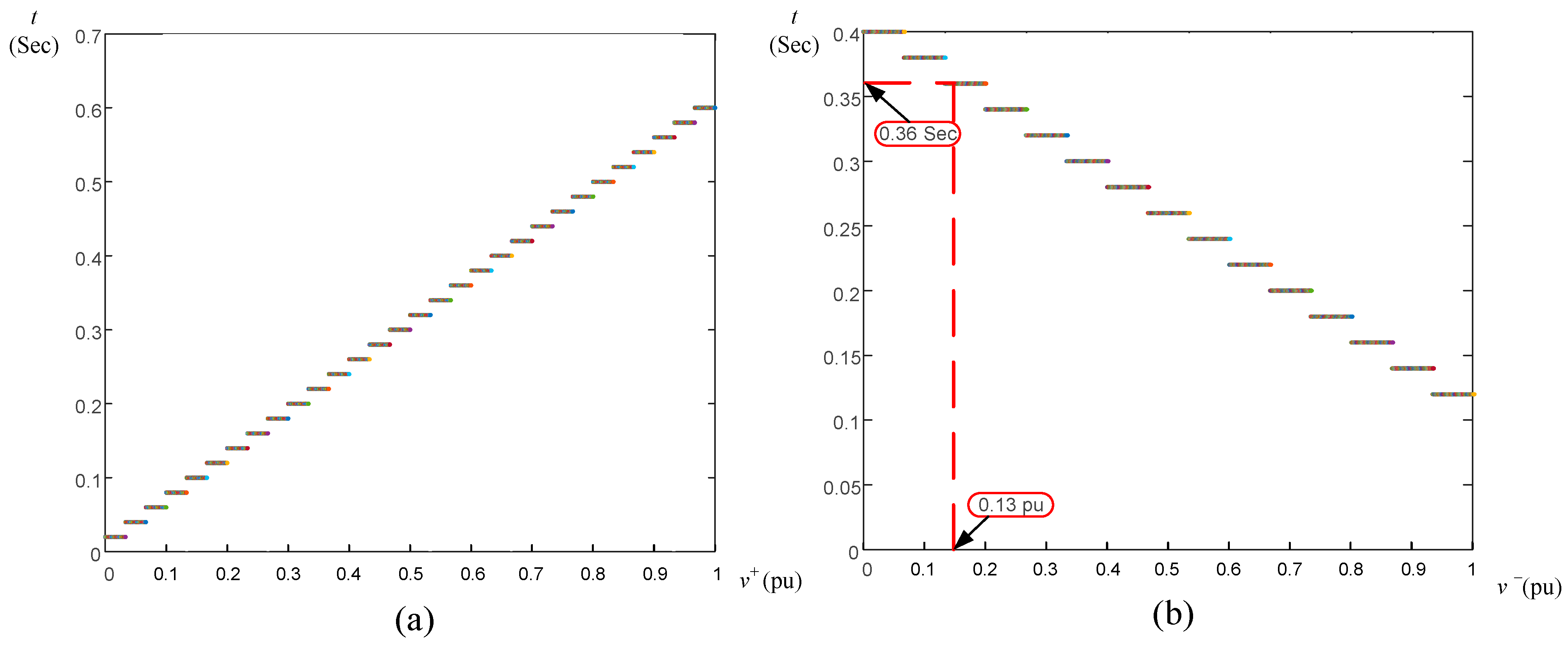According to the fault type, the first PD is disconnected based on the magnitude of the positive- or negative-sequence voltages’ definite time curves, as illustrated in Figure 18. Following that, the second PD is disconnected in accordance with the fault type algorithm. Positive- and negative-sequence voltages were considered for various grid configurations and circumstances when designing the curve. Depending on the analyzed grid, this curve may be adjusted to other grid configurations and voltage levels.

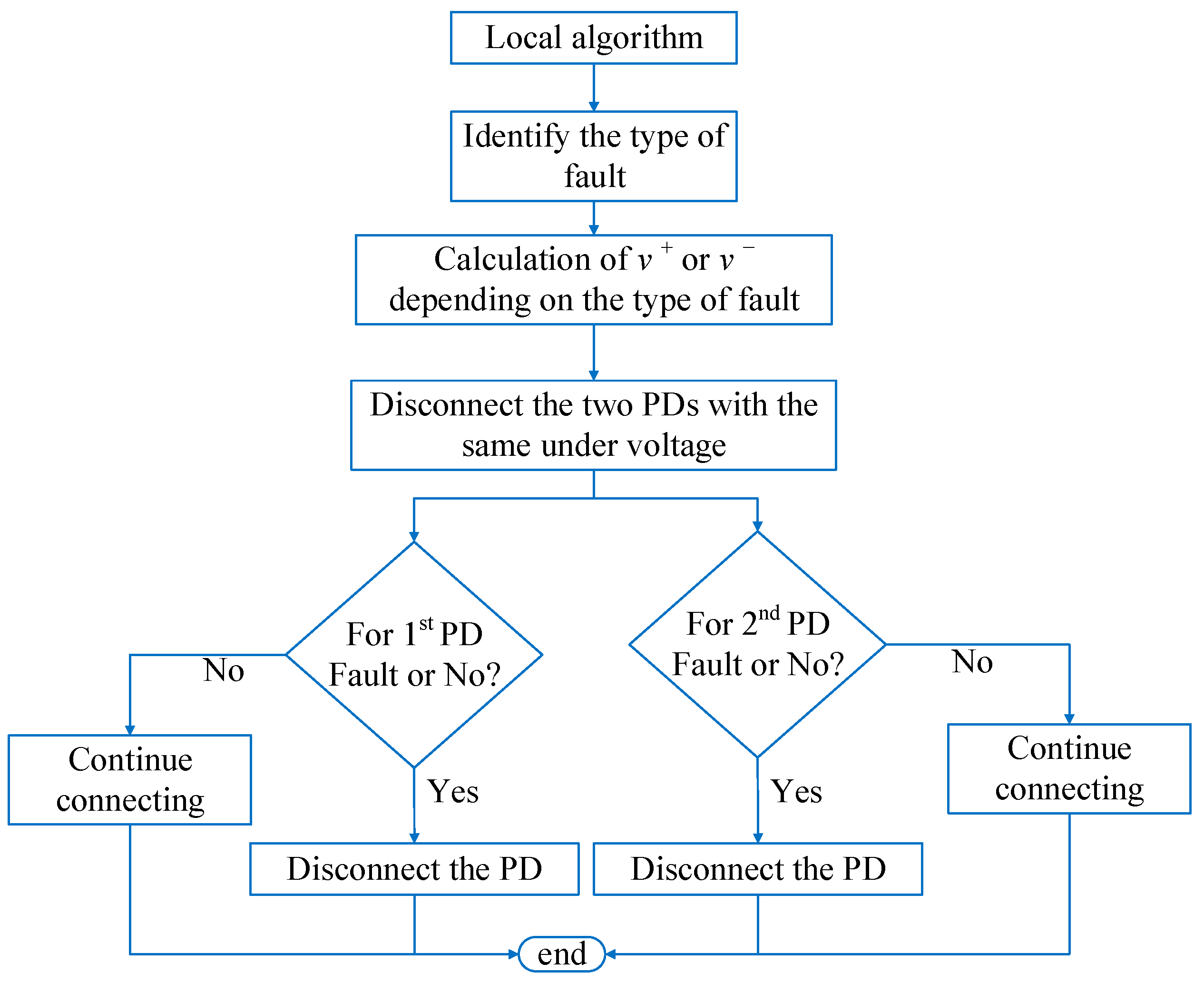
3.3. PD Priority Strategy

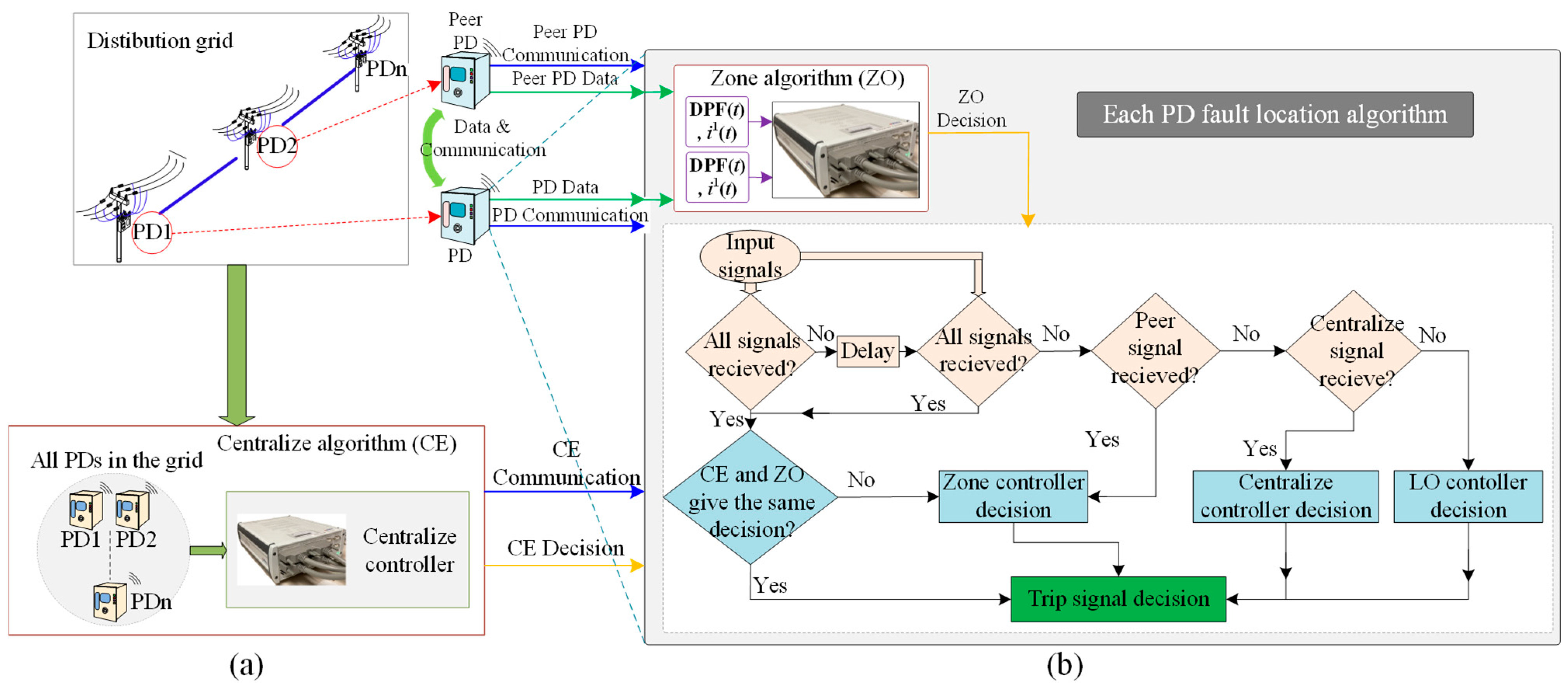
Each PD must render a local decision contingent on the results of the two algorithms, CE and ZO. This action will increase the redundancy of the system, thereby bolstering its security and dependability in the event of a failure. As illustrated in Figure 19, each algorithm is also required to transmit a communication check signal (represented by green arrows) to ensure that the decision is accessible (a).

Orange arrows indicate the evaluation of the CE and ZO controllers’ decisions (upon signal reception). If both controllers reach the same conclusion, the decision is executed; otherwise, the ZO’s decision is prioritized due to its possession of a greater number of encrypted communication signals. Only the peer signal would be assessed in the absence of received signals; the ZO determination would be reached in the event that the signals were received. In the absence of such signals, the CE will be examined; if none are detected, the LO algorithm will be implemented, and a trip signal will be transmitted to the PD. The flowchart of each PD fault location algorithm is illustrated in Figure 19b.

Due to the fact that the grounding connection of the HV/MV transformer modifies the configuration of all PDs in the grid and affects the values of the short-circuit current in the grid, this method has the benefit of grounding connection-independent algorithm operations. The new method would accelerate the protection system’s response to unanticipated grid disturbances while improving the system’s precision and efficiency. The benefits and drawbacks of three-level protection algorithms are detailed in

Table 5. Comparison between CE, ZO, and LO protection algorithms.

	Advantages	Disadvantages
CE	- Consolidates the security of the entire system into a single device, performing state estimation and security evaluations. - Fast tripping. - Ability to operate correctly under different circumstances.	- Fixed to the existing grid configuration. - Communications issues. - Necessitating additional training time and a more complex training procedure.
ZO	- The same ANN used for each PD can be utilized for the newly added line. - Less training time compared to CE. - Encrypted communication, and the ability to adapt to temporary grid reconfigurations. - Operate correctly under different circumstances.	- Communication problems. - Training data are required.
LO	- No communication is needed. - More secure. - Separate decision for each PD. - No training is needed.	- Need to be adapted for new grids. - Slow tripping compared to CE/ZO algorithms.

.

4. Interoperability of Proposed Protection Algorithms

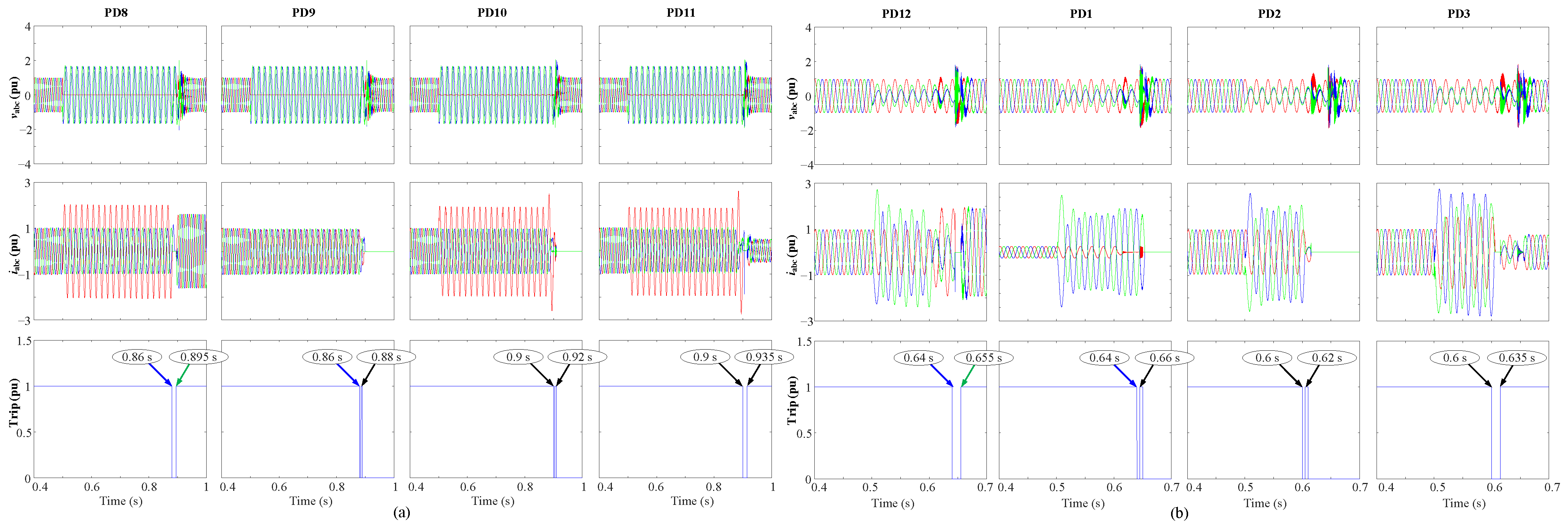
To validate the proposed protection algorithms, various fault types at various locations are examined. To examine the impact of DG penetration on the analyzed ring grid, Figure 20 illustrates asymmetrical faults located at DL1 and DL5. The analyzed ring grid with two DGs is shown in Figure 20a during a single-phase to-ground fault that occurred at DL5 at 0.5 s. Given that both PDs, PD8, and PD9, are both subject to the same negative-sequence voltage (0.13 pu), which corresponds to (0.36 s) in Figure 18, both PDs, PD8, and PD9, will trip at the same time of 0.86 s (blue arrows in Figure 20a). The recloser algorithm will then be used. As PD9 is exposed to the fault, it will close faster than PD8. When reconnected, it will still be exposed to the fault, which will cause PD9 to trip. At 0.895 s (green arrow in Figure 20a), PD8 will be connected again, and the fault will be cleared at that time, causing it to remain connected.

Since PD10 and PD11 are linked to the same bus and will measure the same negative-sequence voltage, the same concept is also repeated there. Then, PD10 will be connected first using the recloser procedure and will trip when it is exposed to the fault, as opposed to PD11, which will be appropriately connected following a delay of 0.015 s.

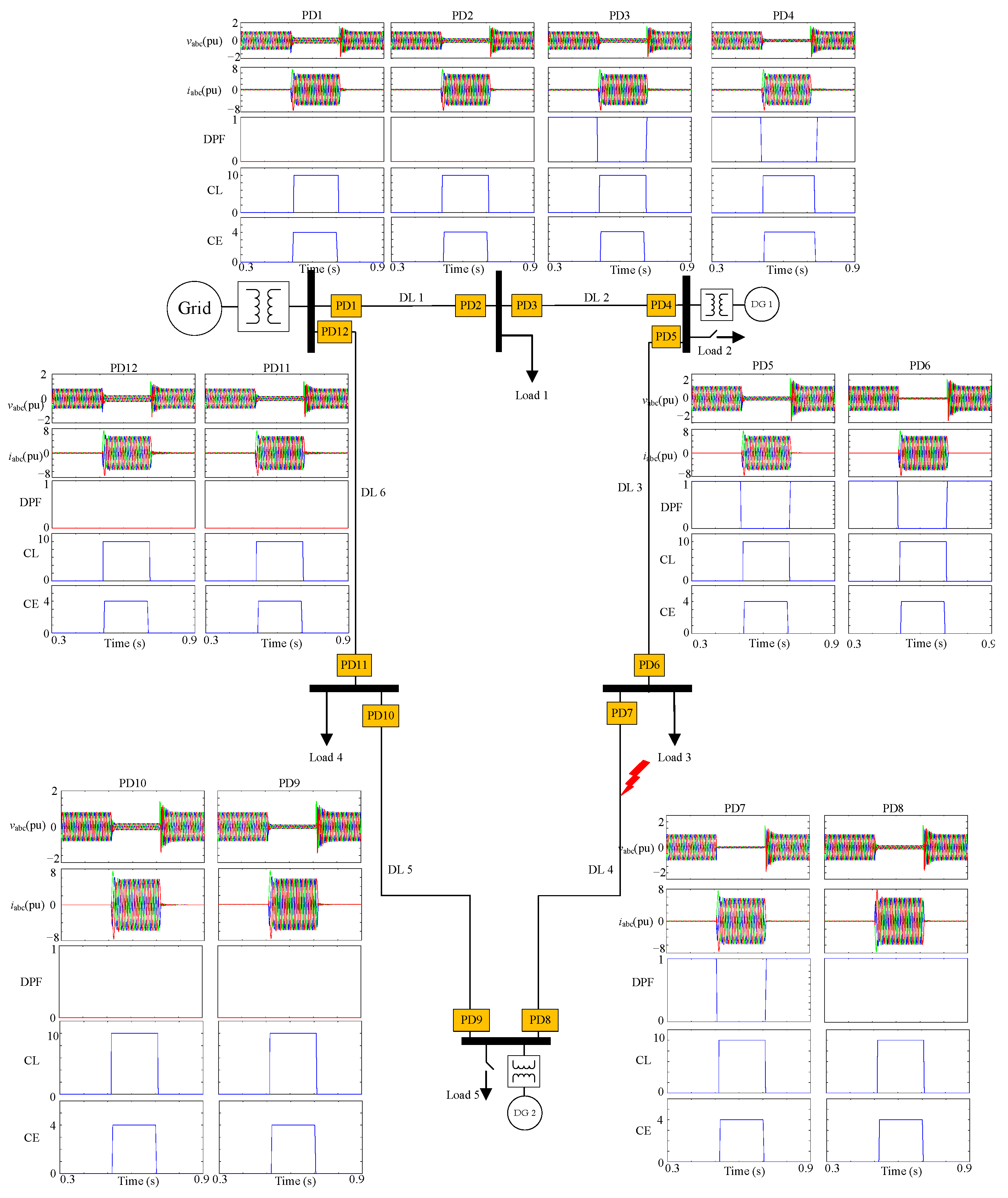
The behavior of the CE-ZO algorithm during symmetrical faults at DL4 is illustrated in Figure 21. The diagram illustrates the centralized ANN (CE), abc voltages, currents, DPF, and fault classification ANN (CL) of every relay in the grid. Using the fault classifier ANN, each relay is capable of accurately identifying the type of fault, as illustrated in the figure. If the fault is permanent, the fault location algorithm can identify the location of the fault and disconnect the affected portion of the network. As demonstrated, the DPF for the faulted line (DL4) breakers is altered from (1 → 0) at one end of the line, indicating that the fault is located at this line.

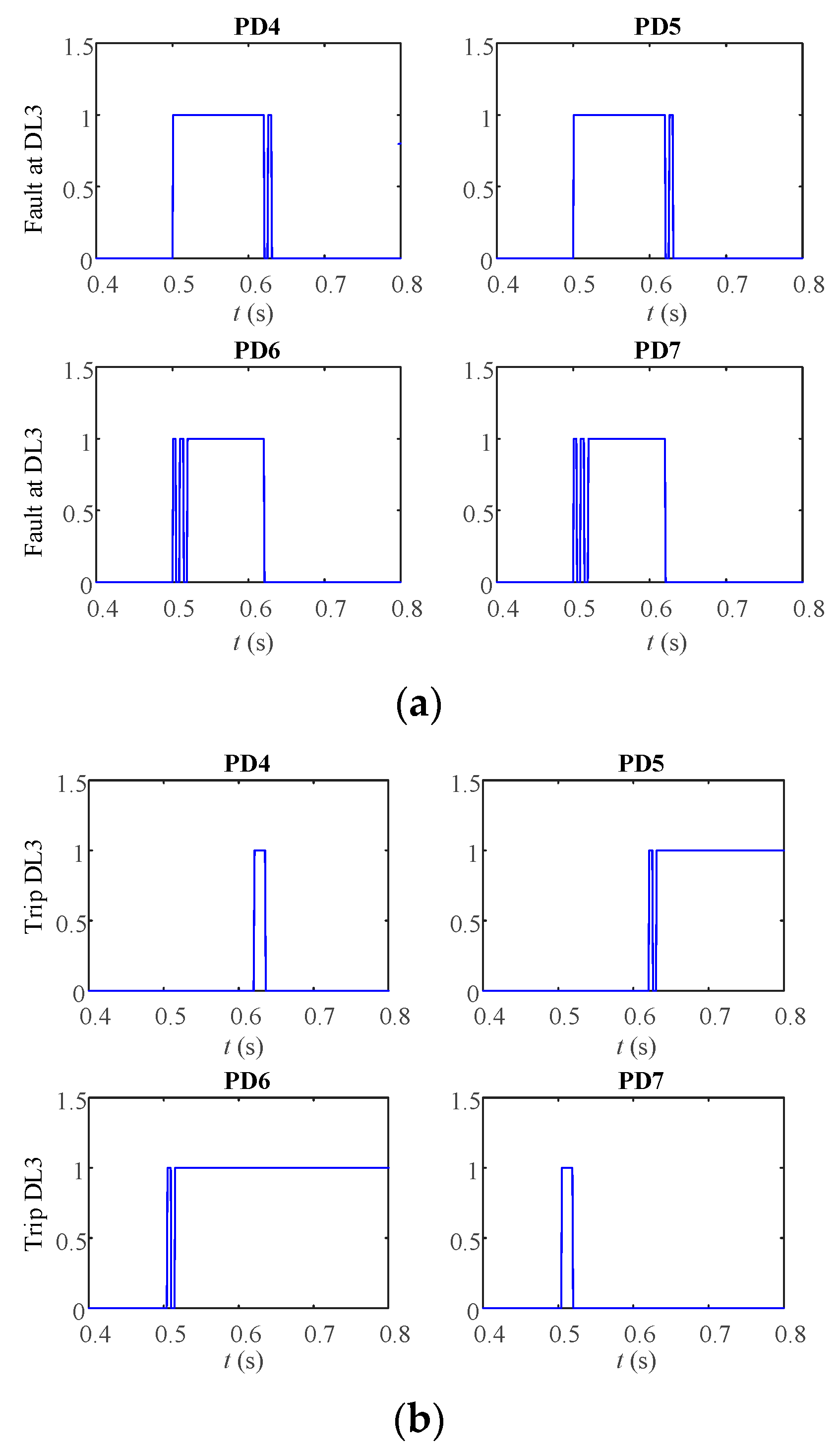
Figure 22 might provide a more accurate understanding of the LO with the recloser procedure when a symmetrical fault happens at DL3. These graphs display all the PDs linked to the buses at the end of the faulty line and trip signals. The protection method depends on the definite time curve corresponding to the positive-sequence voltage, as shown in Figure 22a. Due to their connection to the same bus, the fault signal at PD4 and PD5 is the same bus 3. The PD6 and PD7 linked to bus 4 experienced the same results. The trip signals of the corresponding PDs are shown in Figure 22b. PD6 and PD7 have the first disconnection because they have the same minimum positive-sequence value, and the two PDs are connected to the same bus trip simultaneously. PD4 and PD5 have the second disconnection in this case because their positive-sequence values are higher than the other PDs, PD6 and PD7. Then, after connecting PD6, which is exposed to the fault, the recloser procedure is used, causing it to trip another time. As soon as PD6 is disconnected and PD7 is attached, PD7 is not exposed to the fault and does not trip. The preceding conclusion applies to an unsymmetrical fault; the only difference is that the protection procedure in this situation depends on the negative-sequence voltage.

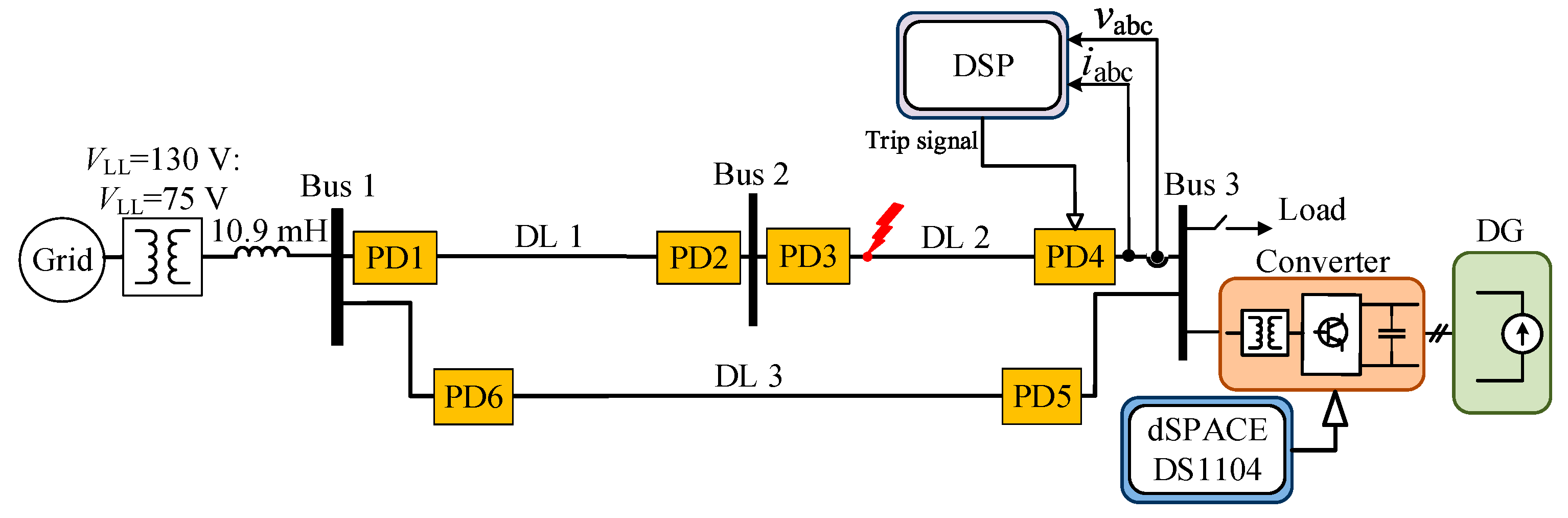
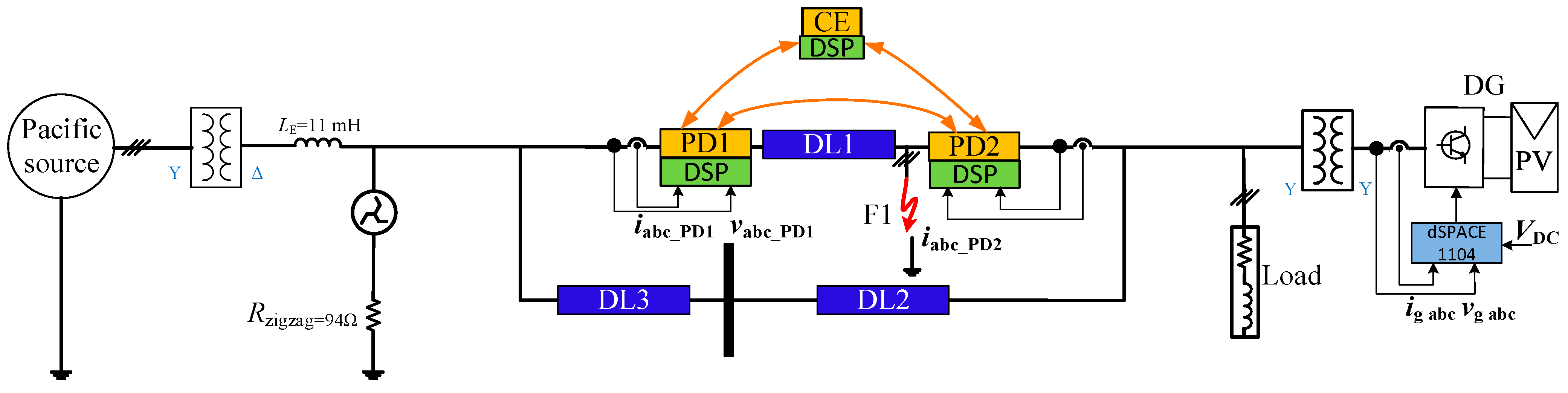
5. Experimental Validation

This section delineates the experimental validation of the proposed methodologies through the utilization of a physically scaled grid in an alternative grid configuration. In order to experimentally evaluate the proposed method, a model that replicates the response and dynamic behavior of the analyzed ring and radial grid was developed in the laboratory. An examination was conducted on two distinct network configurations, a ring grid and a radial grid, both with and without DGs. The suggested approach was executed utilizing a DSP-based numerical relay. Following the processing of sensor measurement data and execution of algorithms, the appropriate decision regarding trip signals was generated. In the analyzed radial grids, a solid-state relay (SSR) served as the PD; in the analyzed ring grids, a mechanical relay was utilized in place of the SSR. The ring grid implemented in the laboratory is illustrated in Figure 23. The parameters of the devices utilized to establish the grid are presented in

Table 6. List of components and their parameters for the grid.

Device	Parameters
Smart source	Rated power = 4.5 kVA
Three-phase power transformer	Rated power = 7.5 kVA, Rated L-L voltages: 380/220 V
Zig-zag transformer inductance	Lzig-zag = 6.9 mH
Inductor to emulate the grid	LE = 10.94 mH ≈ 11 mH
Fault resistance per phase	R = 2.3 Ω

. To streamline the experiment while ensuring that the overall analysis remained unaffected by the symmetry, aggregated lines were utilized to construct the grid in the laboratory. Nonetheless, analogous performance was attained. In addition, as illustrated in Figure 23, an inductor was positioned prior to bus 1 in order to replicate the grid impedance.

The goal is to perfectly correlate the constructed laboratory system and the real system regarding voltages, currents, and impedances. The actual DS grid has the following base values: VBase = 20 kV, SBase = 25 MVA, and IBase = 721.69 A. For both systems, the base values are presented in

Table 7. A comparison of the parameters of the actual grid and the laboratory grid.

	Analyzed Grid	Laboratory Grid
Base voltage	VBase = 20 kV	VBase = 75 V
Base apparent power	SBase = 25 MVA	SBase = 540 W
Base current	IBase rms = 721.69 A	IBase rms = 2.4 A
Base impedance	ZBase = 16 Ω	ZBase = 31.25 Ω
Line resistance	RLine_pu = 0.02 pu	RLine_pu = 0.02 pu
Line inductance	XL Line_pu = j0.0136 pu	XL Line_pu = j0.0138 pu
Fault resistance	Rfault_pu = 0.0746 pu	Rfault_pu = 0.0746 pu

. The objective is to calibrate the laboratory base values to operate at lower voltages and currents; however, the resulting values remain consistent with those acquired from the actual grid. The selection of these values ensures that the steady-state voltage and current in both grids are identical.

Table 8. System parameters.

	Parameter	Value
CINERGIATM Inverter	Rated power	10 kVA
	Rated voltage	400 V
Filter	Inductance (L)	10 mH
	Resistance (R)	0.2 Ω
DC bus	DC rated voltage	800 V
Three-phase Smart Power Source	345AMXT	4.5 kVA
SSR	Crydom H12WD4850	48–660 VAC
Distribution Lines (DL1, DL2, DL3)	Inductance (L1, L2, L3)	1.37, 2.74, 4.11 mH
	Resistance (R1, R2, R3)	625, 1250, 1875 mΩ
	Capacitance (C1, C2, C3)	0.316, 0.632, 10, 30 µF
Loads	Inductance (L1, L2)	10, 30 mH
	Resistance (R1, R2)	14.5, 42 Ω

presents the parameters of the laboratory grid, while Table 7 presents a comparison between these values and the observed real grids. In the laboratory, two grid configurations are implemented and evaluated to simulate the actual analyzed grid: (1) A three-line radial grid in its entirety, as illustrated in Figure 24. One DL is represented by DL1, two DLs by DL2, and three DLs by DL3. (2) The ring grid, as illustrated in Figure 25, is composed of three lines in order to simulate the actual analyzed grid. Multiple grid configurations that modify load consumption, DG penetration, fault locations, fault types, and the configuration of HV/MV transformers are utilized to assess the system.

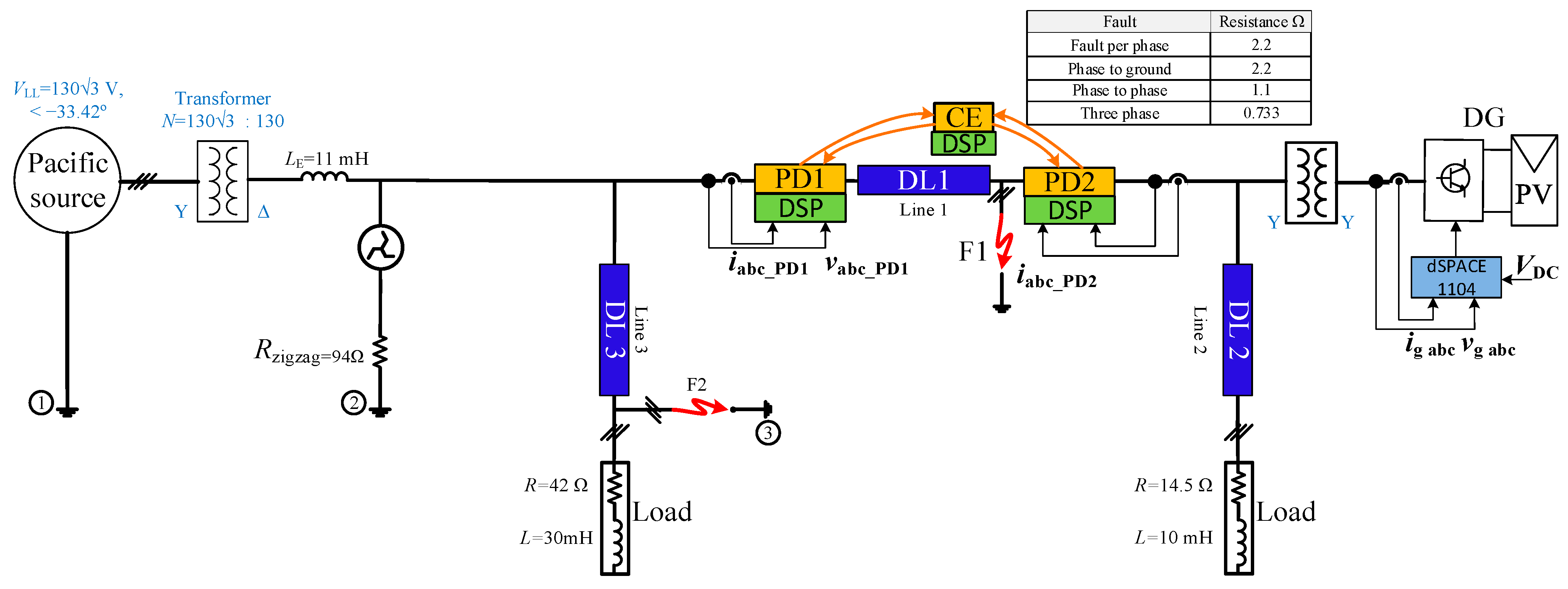
Figure 26 illustrates the experimental laboratory assembly of an equivalent system. The CE and ZO protection algorithms have been implemented using three DSPs of the TMS320F28335 type. ControlDesk and dSPACE^TM DS1104 were used to implement the inverter control. Utilizing the Matlab^TM software, all of the protection algorithms and inverter control have been developed. Due to the absence of DSPs in each line, the data corresponding to the remaining PDs are imposed in the DSP of the CE controller.

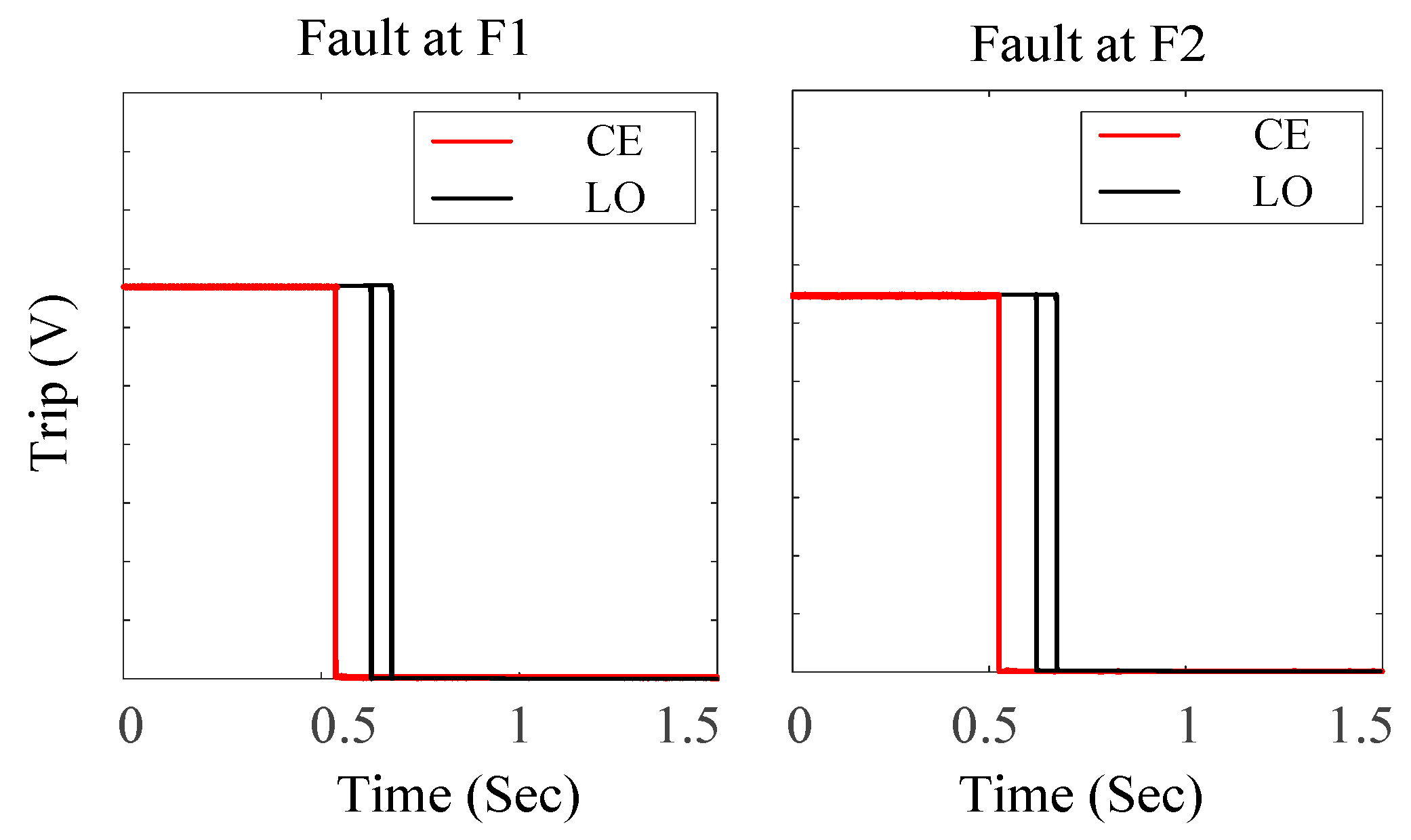
Figure 27 also provides the trip signals for the LO and CE-ZO protection strategies for symmetrical faults when the fault occurs at the F1 and F2. CE-ZO almost gives the same results in this case, while the LO is worse due to the trip curve.

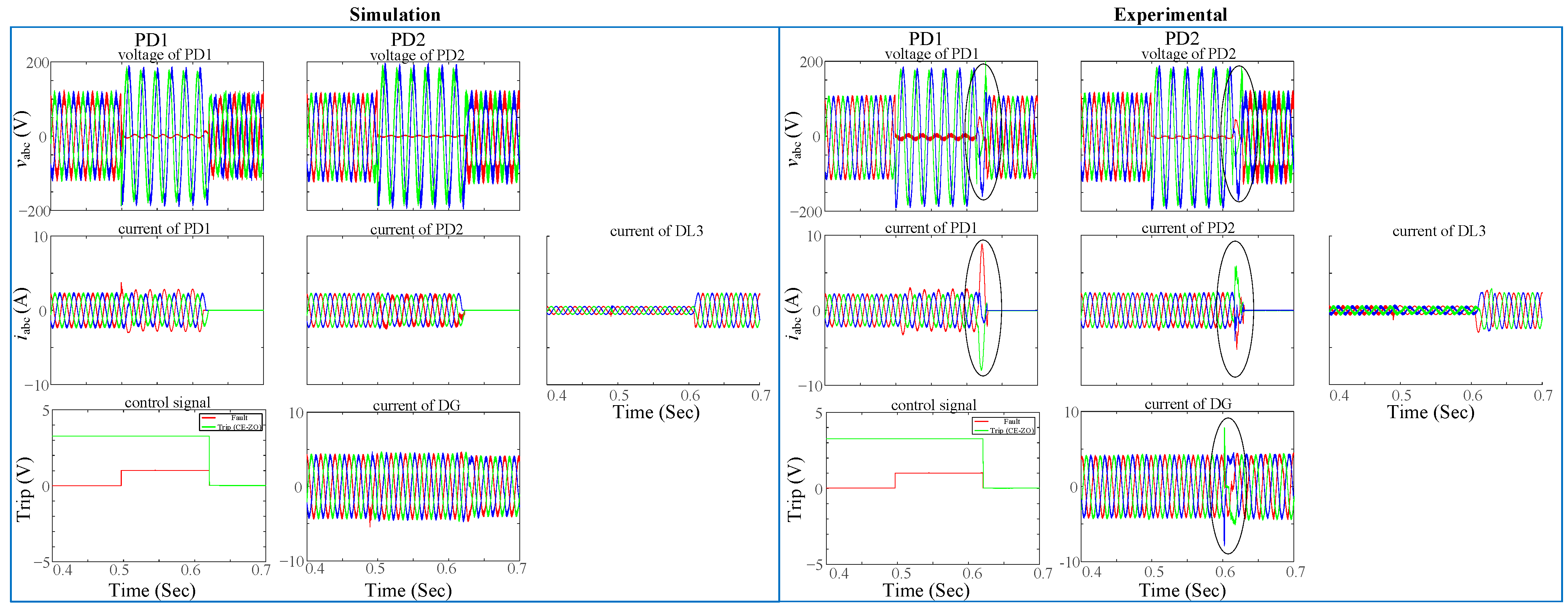
The performance of the CE-ZO algorithm has been evaluated for both types of faults, as illustrated in Figure 28 and Figure 29. The fault locations are indicated in Figure 25 at DL1 or DL2. The abc voltages and currents for both PDs at each end of the faulted line are depicted in the figures. Furthermore, the trip signal in opposition to the fault is displayed in the third row. The CE acquires the data of a single line as well as the data of the additional PDs imposed in the CE controller’s DSP.

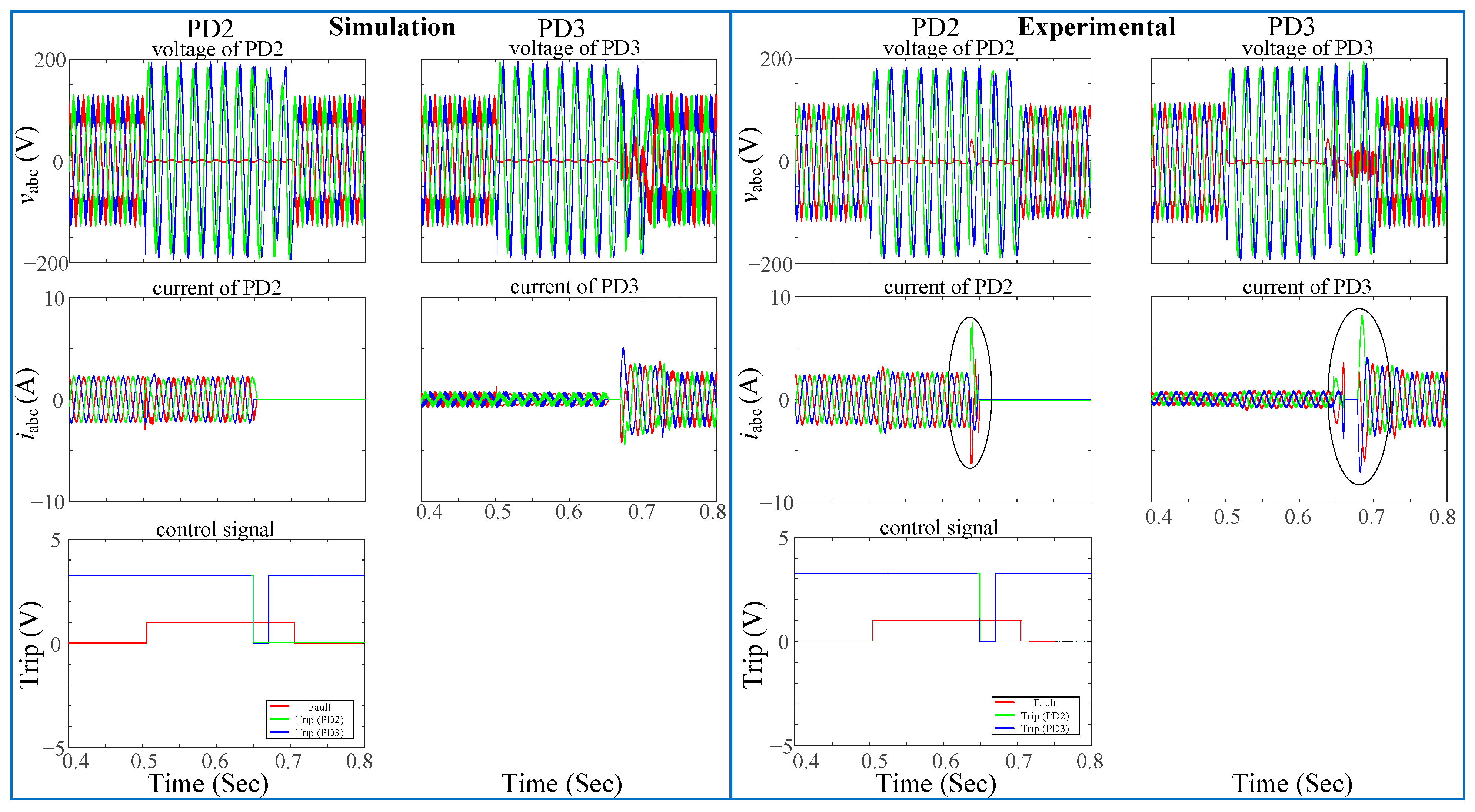
The experimental abc currents of PD1 and PD2 in the second row and third column of Figure 28 and Figure 30, respectively, differ from the simulated result in terms of overcurrent. The substitution of mechanical switches for SSRs in ring grids has caused this. In order to obtain a similar behavior to the experimental results, especially at the disconnection time, a mechanical switch model could be used in the simulation. However, the model of the mechanical switch is out of the scope of this research. The proposed protection algorithms, nevertheless, remain unaffected by this modification, as their operation is not contingent upon the type of switch.

There is a concurrence between the experimental and simulation outcomes depicted in Figure 28 and Figure 29. The injected current and voltage are disturbed due to the precise model and commutation frequency of the converter. Furthermore, the DLs are directly connected to the inverter of the DG. Connecting the two circuits via a Y-Y transformer to isolate them is an additional concept for future research.

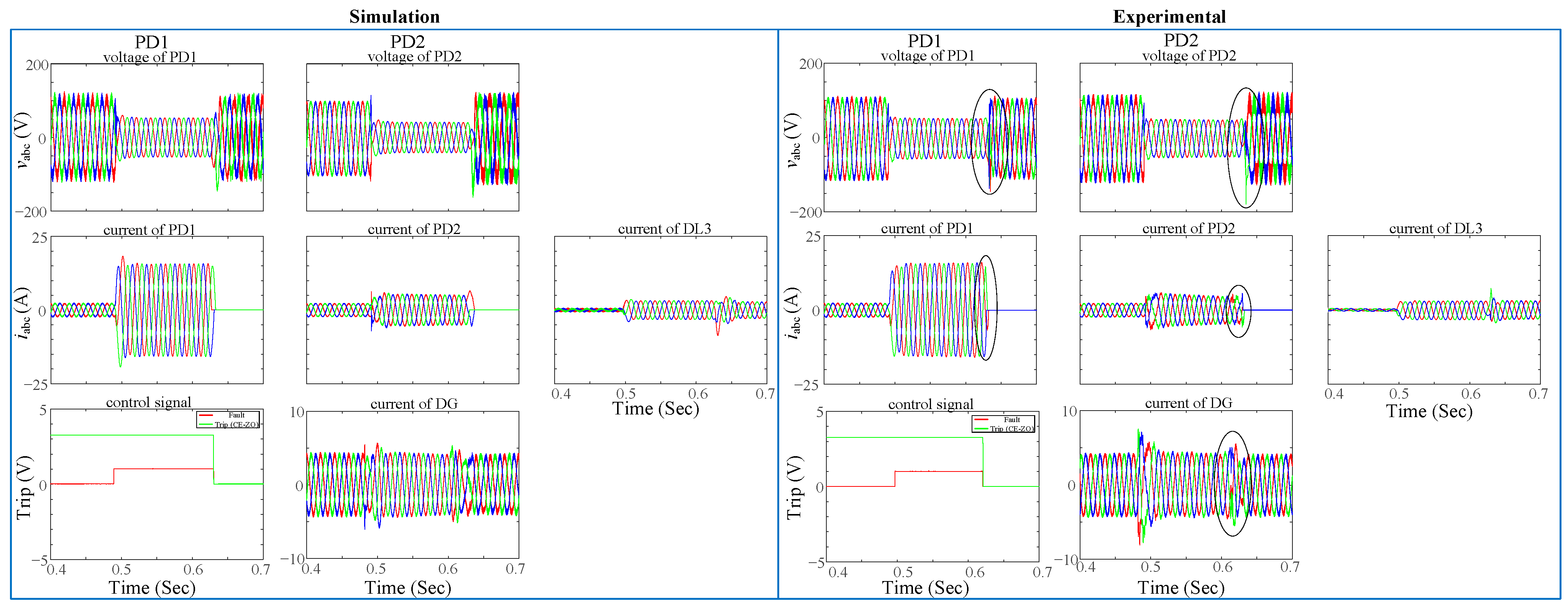
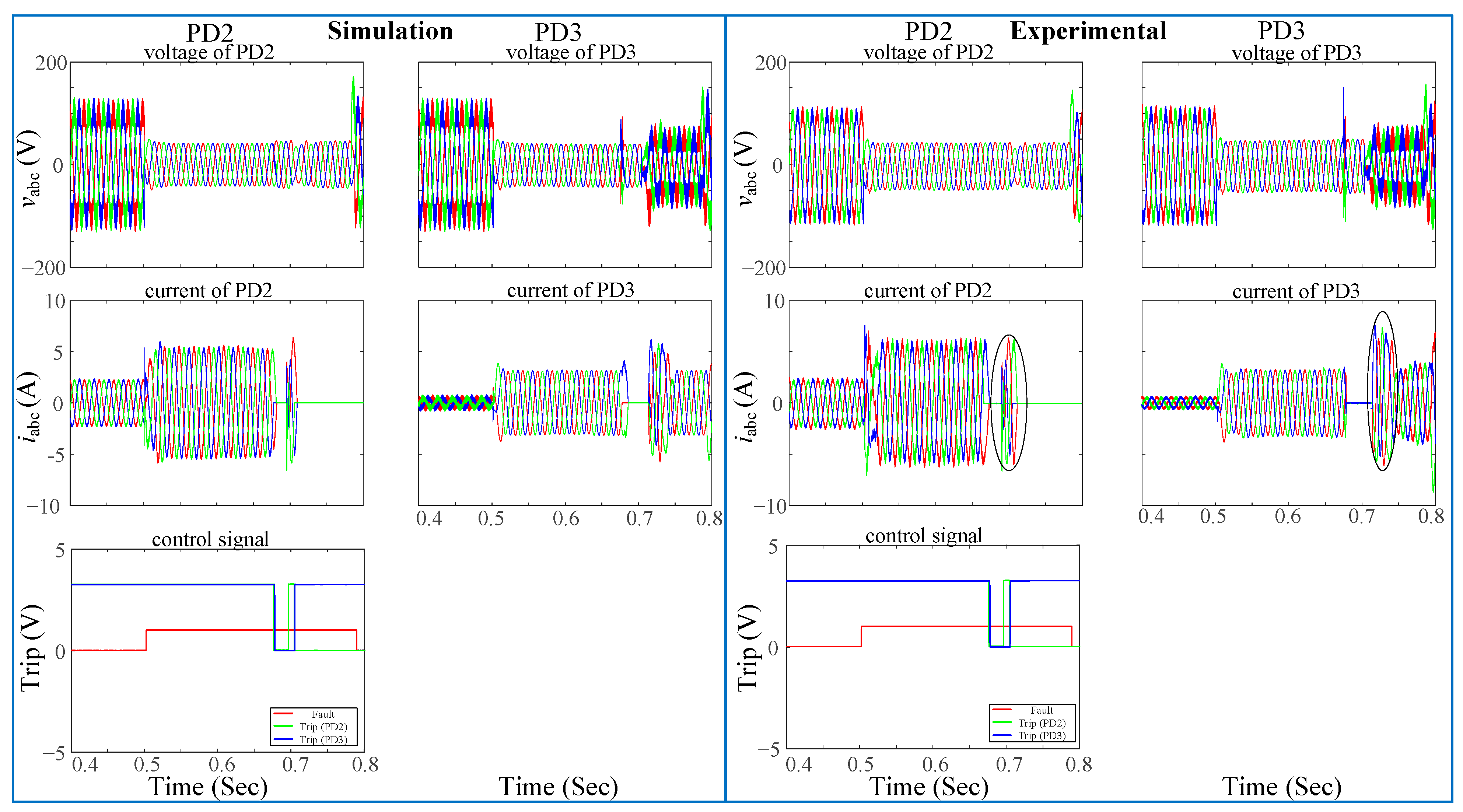
The fault location was at F1 or F2. The difference between simulation and experimental observations throughout steady-state, fault, and recovery periods is 5% for instantaneous abc voltages and 2% for instantaneous abc currents. The protection algorithm of the LO algorithm has been evaluated under both conditions—with and without a recloser. Without the recloser algorithm, the behavior of the LO algorithm for PD2 and PD3 is illustrated in Figure 30. The connections between a DG and the ring grid result in alterations to the values of the positive- and negative-sequence voltages. Figure 31 illustrates how the LO algorithm interacts with the recloser algorithm. Specifically, the recloser algorithm is utilized here.

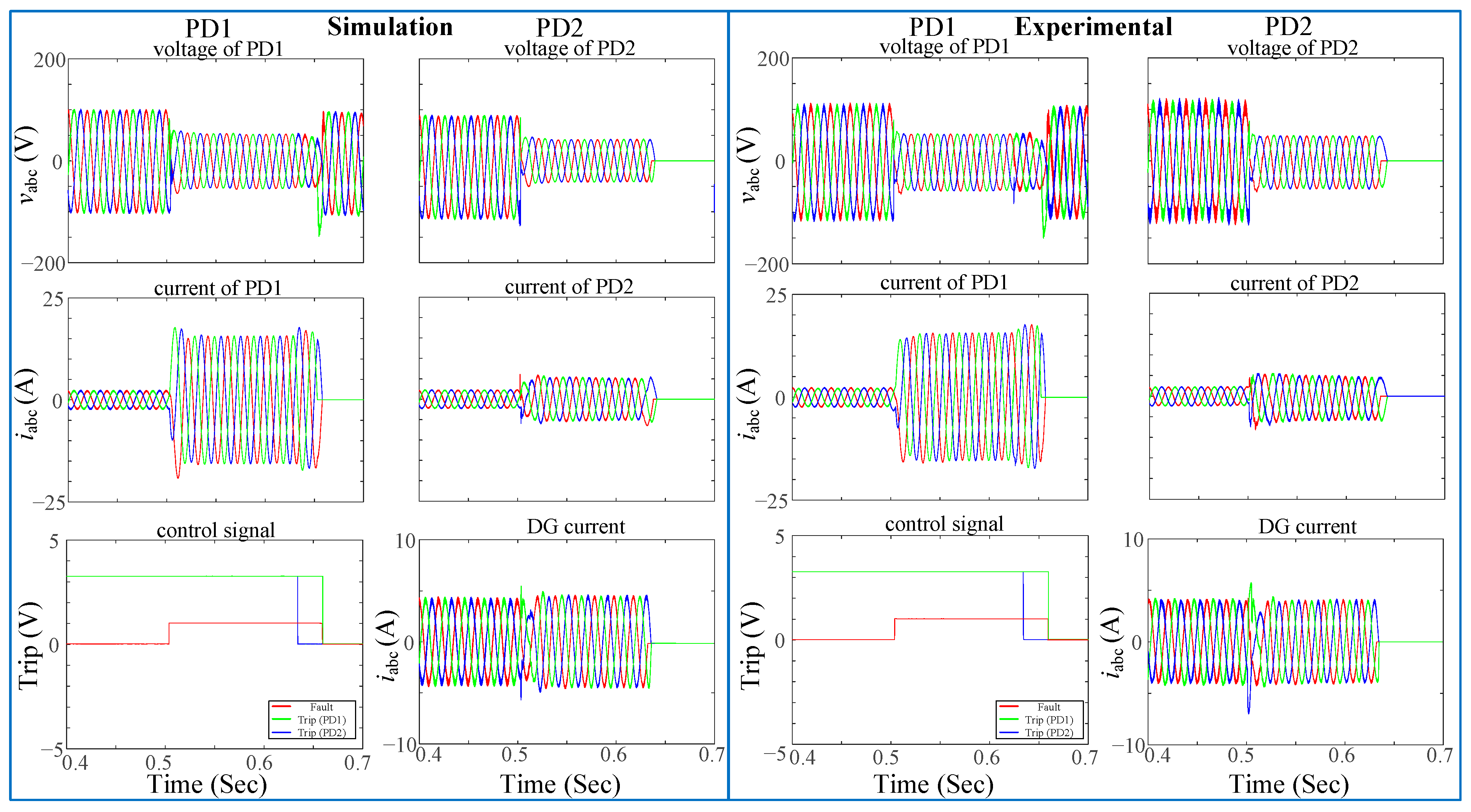
Figure 32 displays the trip signals, abc voltages, and currents at PD1 and PD2 at each end of DL1. The behavior of the LO algorithm for a three-phase faulty is demonstrated. The fault being close to the end of the line will cause PD2 to be disconnected first. In this scenario, the main grid and the DG would contribute to the value of the short-circuit current. An evaluation of the protection algorithms for symmetrical three-phase and unsymmetrical single-phase to-ground faults has been conducted.

Table 9. Comparison between different protection strategies.

Inverter-Based	Grid Reconfiguration	Experimental Verification	Trip Signal	Strategy	References
Yes	Yes	Yes	Very fast	Directional-based ANN	Proposed method
No	No	No	Moderate	OCR with DR	[29]
Yes	Yes	No	Fast	Linear programming	[30]
Yes	No	Yes	Very fast	Deep learning ANN (DNN)	[15]
Yes	No	No	Moderate	Directional relay	[31]
No	No	Yes	Not specified	Support vector machine (SVM) and ANN	[32]
Yes	No	No	Fast	Discrete wavelet transform (DWT)	[33]
No	No	No	Very fast	ANN	[34]
No	No	No	Moderate	Communication-based	[17]

illustrates different protection techniques from different aspects, including the DG connection, the grid configuration, and the speed of tripping decision.

6. Conclusions

Different algorithms for fault location in the MV DS ring grid with high DG penetration have been proposed in this study in order to prevent unintended tripping when inverter-based DGs are connected to the grid. Three protection algorithms comprise the proposed protection scheme: a CE, ZO, and LO. The three algorithms that are provided are capable of precisely identifying the location of a fault and isolating the defective component of the system.

All grid-wide PD data are collected and transmitted to a centralized controller via the CE. Its integration of the entire system’s security into a single device is its primary benefit. However, in the event that data are lost due to inadequate communication, the CE will be unable to pinpoint the precise location of the fault. The ZO, which integrates the data from the two PDs on the same line, is therefore proposed as an outcome of zone control via peer-to-peer communication. In contrast to the CE, which remains fixed to the given grid configuration, this methodology has the capability to accommodate any modifications in the grid. A third protection algorithm, the LO, is proposed that utilizes the local data acquired at each PD to pinpoint the precise location of a fault. Different methods are used based on the fault type, symmetrical or unsymmetrical, calculated using the sequence component. The LO has been suggested to operate independently from the communication between the PD; thus, the protection system can function efficiently in the event of communication loss. The primary benefit of this algorithm is that each PD makes an independent decision, thereby eliminating communication issues. Moreover, each algorithm functions as a redundancy for the others.

A variety of fault resistances, symmetrical and asymmetrical faults, fault locations, and stiff and weak grids were utilized to evaluate the algorithms. The protection strategies could adapt to different grid reconfigurations. Furthermore, comparing simulation results and experimental implementation demonstrated the high efficiency and dependability of the proposed algorithms in various grid circumstances for radial and ring structures with and without DG penetration.