Comparative Analysis of Machine Learning Techniques in Predicting Wind Power Generation: A Case Study of 2018–2021 Data from Guatemala
Abstract
1. Introduction
- To develop machine learning models for predicting wind power generation without relying on detailed meteorological data;
- To evaluate the performance of various machine learning techniques, including Simple, ensemble, and deep learning algorithms;
- To use time series cross-validation, Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), the Diebold–Mariano (DM) test, and Bayesian model comparison to assess and compare model performance;
- To provide insights for enhancing grid management and operational planning in the renewable energy sector by identifying the most accurate and robust models.
2. Methods
2.1. Proposed Framework
- Wind Power Grids: This module shows the spatial arrangement of three separate wind farms in Guatemala—SNT-E1, VBL-E1, and LCU-E1. Every farm is depicted on a simplified map, indicating the specific locations where data are collected. This visual representation highlights the distributed nature of data collecting across several wind power locations;
- Data Collection: Data from the three wind farms are systematically gathered and stored in various databases. These databases are represented by the cylinder icons in Figure 1, which symbolize the continuous and reliable process of data collection and maintenance;
- Data Preprocessing and Analytics: This crucial module involves handling missing values, applying filters, and combining data. The approach ensures the preservation of data quality and the standardization of datasets before their use in model training and validation, optimizing the accuracy of the forecasting models;
- ML—Time Series Cross Validation: This module describes the detailed methodology used to evaluate and compare different machine learning algorithms specifically designed for wind power forecasting. Additionally, it provides detailed explanations of various machine learning approaches, including baseline linear and ridge regressions, as well as more advanced models like neural networks and ensemble methods such as Random Forest and XGBoost. This study also investigates the effectiveness of advanced deep learning frameworks such as GRU, LSTM, and convolutional networks in analyzing time series data that represent wind direction. Furthermore, the models are trained and tested using data from the years 2018 to 2020 for training, and 2021 for testing. This stage also involves hyperparameter tuning to enhance the performance of each model, ensuring that the models are well-fitted to the historical data while also being capable of reliably predicting unseen data;
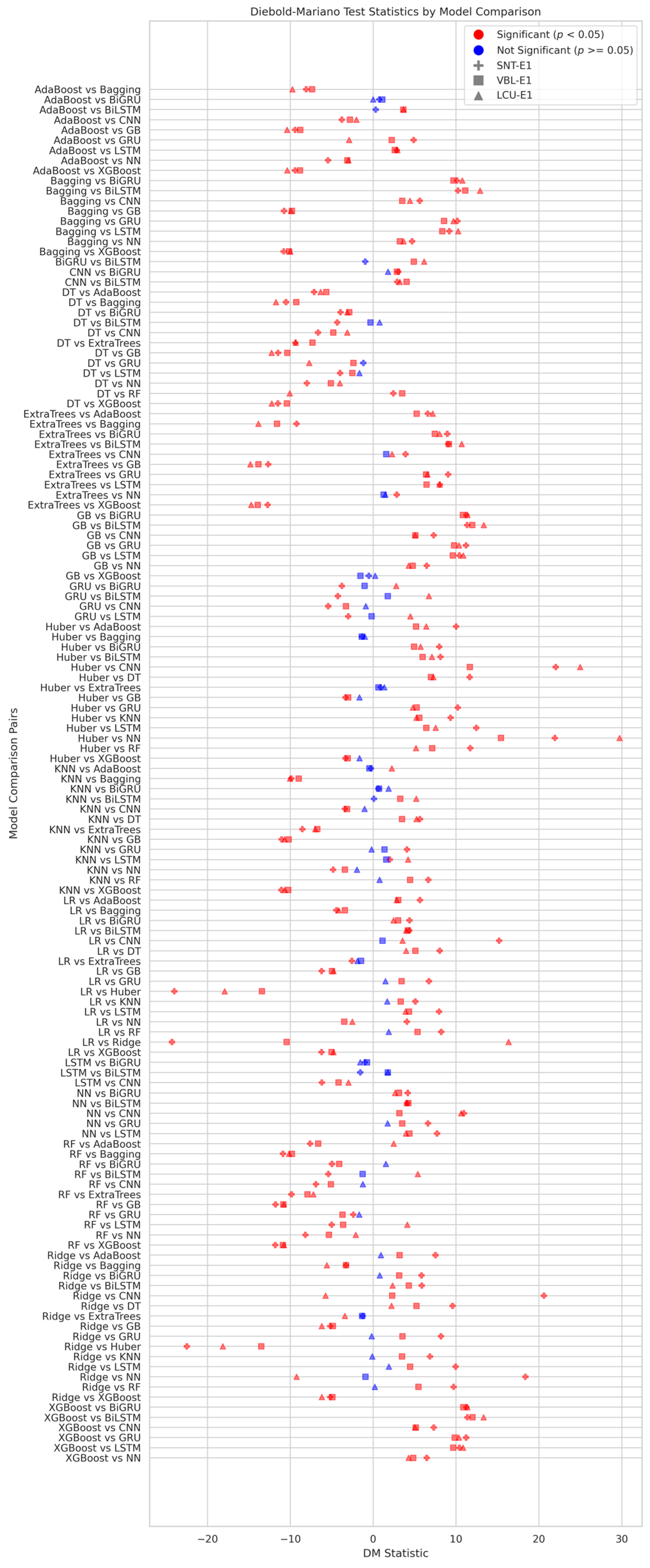
- The Diebold–Mariano Test: This test is utilized to statistically evaluate and compare the predictive accuracy of the models. The main objective is to analyze the variations in prediction errors using metrics like DM statistics (DM-stats) and p-values to determine if the disparities in model performance are statistically significant;
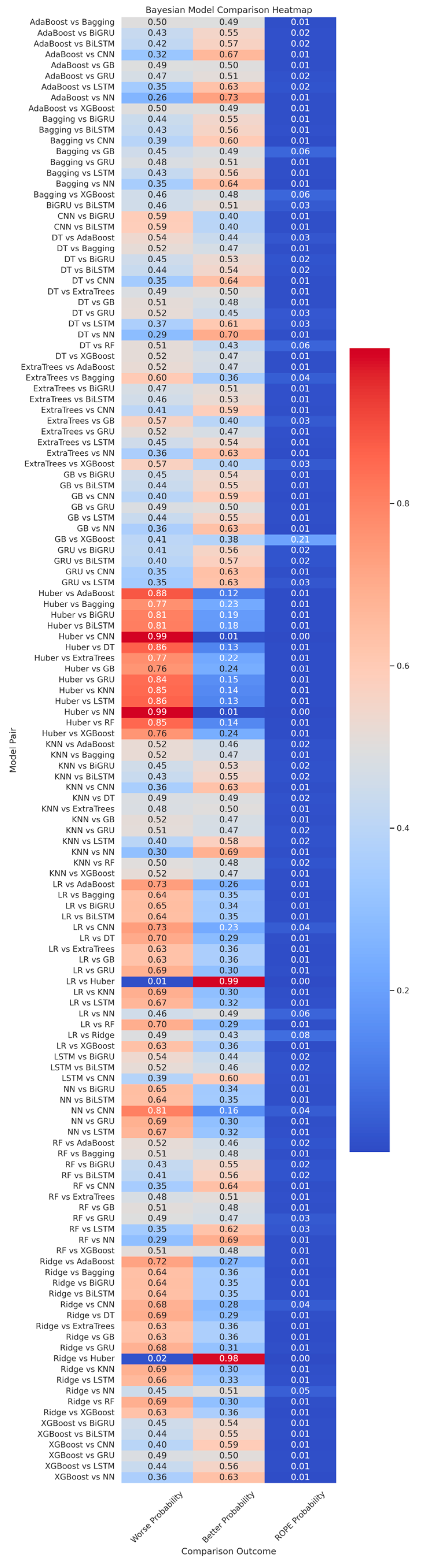
- Bayesian Comparison: This module uses Bayesian statistical methods to estimate the relative probabilities of several models being the best based on the available data through pairwise comparisons. This methodology offers a probabilistic perspective on the performance of a model, complementing the frequentist approach of the DM test;
- ML Comparison: The final module involves a thorough evaluation and comparison of the most effective models. The results of these comparisons determine the most efficient machine learning model or models for predicting wind power using the collected data and the analytical approaches employed.
2.2. Wind Power Grids
- San Antonio el Sitio: The wind farm consists of sixteen VESTAS V112/3300 wind turbines, each with a power rating of 3.3 MW, totaling 52.8 MW. It is located in the municipality of Villa Canales, in the department of Guatemala, Guatemala. The wind farm began commercial operations on 19 April 2015 [32];
- Viento Blanco, Sociedad Anónima: This wind farm has seven VESTAS V112/3300 wind turbines, each with a capacity of 3.3 MW, totaling 23.1 MW [33]. It is situated on the La Colina estate in the municipality of San Vicente Pacaya, Escuintla, Guatemala. It started commercial operations on 6 December 2015, and is shown in Figure 2;
- Las Cumbres de Agua Blanca: This wind farm, owned by the company Transmisora de Electricidad, Sociedad Anónima, contains fifteen GAMESA G114/2100 wind turbines, each with a capacity of 2.1 MW, totaling 31.5 MW [34]. It is located in the municipality of Agua Blanca, department of Jutiapa, Guatemala, in the community of Lagunilla, and began commercial operations on 25 March 2018.
2.3. Data Preprocessing and Analytics
2.4. Machine Learning Algorithms
2.4.1. Simple Learning Algorithms
- Linear Regression (LR): LR is a fundamental technique in predictive modeling used to determine the linear correlations between meteorological variables, such as wind speed and power production. Although LR is easy to understand and comprehend, its primary limitation is its inability to capture complex, non-linear relationships, which are often present in wind power data [35];
- Ridge Regression: The Ridge algorithm is an extension of Linear Regression that incorporates L2 regularization. This regularization technique penalizes large coefficients, hence mitigating the risk of overfitting. This feature makes it particularly well-suited for situations where there is multicollinearity among the input features [35]. As a result, it ensures stability and enhances the capacity to produce accurate forecasts in wind power scenarios;
- Huber Regression: Huber is a robust regression method that is effective in handling outliers. It combines the characteristics of both L2 and L1 regularization [35]. The strategy of the system is adapted based on the presence of outliers in the data, resulting in more dependable forecasts in the naturally turbulent environment of wind power data collection;
- K-Nearest Neighbors (KNN): KNN is a non-parametric algorithm that uses the nearest training examples in the feature space to predict outputs. KNN is proficient in dealing with non-linear data and can be highly efficient in wind power forecasting, particularly when patterns cannot be effectively approximated by parametric models [35];
- Decision Trees (DT): DT partitions the dataset into leaf nodes based on judgments made on feature values, resulting in a distinct and easily understandable structure of decisions. Although they are successful in handling both categorical and continuous inputs, they are prone to overfitting, particularly in datasets commonly encountered in wind energy forecasts [36].
2.4.2. Ensemble Learning Algorithms
- Random Forest (RF): RF enhances decision trees by constructing a collection of trees and combining their forecasts. By employing this method, the variability is much diminished without any accompanying increase in partiality, rendering RF an effective instrument for representing the stochastic and complex characteristics of wind speed and direction data. RF is outperformed by the ExtraTrees method in terms of speed and the reliability of its results, especially when it comes to mitigating overfitting and handling noisy data in wind power forecasting [35];
- ExtraTrees: ExtraTrees, also known as Extremely Randomized Trees, is a variant of the decision tree algorithm that introduces more extensive randomization in the tree splitting process;
- AdaBoost: AdaBoost is a boosting algorithm that belongs to the ensemble technique category. It works by adjusting the weights of examples that are mistakenly predicted, allowing succeeding models to focus more on these difficult examples [35]. In the context of wind power forecasting, “difficult examples” refer to instances where the prediction errors are higher, often due to irregularities or anomalies in the data. By prioritizing these more challenging examples, AdaBoost can improve the performance of decision tree models, thereby enhancing the overall accuracy of predictions;
- Bagging: Bagging, also known as Bootstrap Aggregating, mitigates overfitting by constructing numerous models (usually trees) from various subsets of the dataset and subsequently averaging their predictions. This approach is beneficial for generating more reliable forecasts in the unpredictable domain of wind power generation;
- Gradient Boosting (GB): GB is a machine learning technique that builds models in a sequential manner, where each new model is designed to rectify the errors created by the previously built models [35]. GB is highly efficient in non-linear situations, such as wind power forecasts, where each consecutive model is specifically designed to improve the accuracy of the residuals from the previous models;
- XGBoost: Extreme Gradient Boosting is renowned for its high efficiency and ability to process big and complex datasets that contain sparse features, which is common in wind data analysis. The inclusion of built-in regularization in this model aids in the prevention of overfitting [37], resulting in higher prediction accuracy for wind power forecasting.
2.4.3. Deep Learning Algorithms
- Neural Network (NN): A fully connected layer, commonly referred to as a dense layer or neural network, creates a multitude of connections with the previous layer. The architecture under consideration involves a dense layer where each neuron is connected to every neuron in the preceding layer. The widespread adoption of dense layers in artificial neural networks is attributed to their effectiveness in capturing complex patterns and relationships within data. Dense layers facilitate the acquisition of complex input data representations through extensive inter-neuron information exchange, making them a popular choice in diverse AI applications [35]. In general, NNs can represent complex and non-linear connections that simpler linear models may not be able to convey well. NNs are very valuable in forecasting wind power generation due to the interplay of several meteorological elements;
- Gated Recurrent Unit (GRU) and Long Short-Term Memory (LSTM): The GRU is a type of recurrent neural network (RNN) that was designed to address the issue of the vanishing gradient problem that is frequently encountered in conventional RNN structures. GRU networks offer a promising solution to the challenge of preserving and flowing information within sequential data, with design similarities to LSTM networks. LSTM networks are a distinct type of recurrent neural network that are designed to effectively capture and understand long-term dependencies, particularly in the context of sequence prediction tasks. LSTM networks are characterized by their exceptional capacity to preserve and efficiently exploit information across extended sequences [35]. The remarkable capacity of LSTM networks to retain memory makes them a potent instrument for examining time-dependent information and tackling complex sequential patterns [38]. GRU and LSTM are both very effective in modeling sequential data, such as time series of wind speeds. They possess a high level of skill in capturing long-term relationships in data, which is essential for making precise predictions about the generation of wind power over extended periods;
- Convolutional Neural Networks (CNN): CNNs are mostly utilized in image processing but they may also be modified to handle sequential data by considering it as a one-dimensional “image”. CNNs have the capability to capture local dependencies and quickly extract features, which is advantageous in dealing with complex wind energy or weather patterns that impact wind generation;
- BiGRU and BiLSTM: BiGRU and BiLSTM are bidirectional versions of GRU and LSTM, respectively. They are designed to process data in both forward and backward directions, enabling them to successfully capture both past and future context [35]. An in-depth comprehension of time is essential for effectively predicting wind power generation, allowing for the adaptation to the ever-changing climatic conditions.
2.5. Evaluation of ML Models
2.5.1. Performance Metrics
2.5.2. Time Series Cross-Validation
2.5.3. Diebold–Mariano Test
- Defining the forecast errors: first let us define the and to be the forecast errors of Model 1 and Model 2 at time t, which represent the errors observed in the test set;
- Calculate the loss differential based on the difference in the forecasted errors using a loss function L, which is selected as the squared error. The differential is shown in Equation (4):
- Compute the mean loss differential: the mean is calculated in Equation (5).
- The DM statistics (DM-stats) test is then typically computed in Equation (6).where represents the estimate of the variance , and T is the number of the forecasted periods.
- Hypothesis testing: Assuming the null hypothesis , which states that the forecasting accuracy of both models is identical. The test DM-stats follow a standard normal distribution asymptotically. A rejection of occurs when the absolute value of the DM statistic is significantly high, suggesting that the forecasting performance of the two models differs considerably.
2.5.4. Bayesian Model Comparison
- First, the marginal likelihood is computed given model M and given data D, shown in Equation (7).where P(D|θ,M) is the likelihood of the data given the parameters θ under model M. P(θ|M) is the prior distribution. In order to account for all possible parameter values, the integral effectively calculates the mean of the likelihood by summing over all possible values of θ;
- Second, the Bayes Factor (BF) is used to compare two models, and , and is defined as the ratio of the model’s marginal likelihood over each model, as shown in Equation (8).
- The BF provides a direct measure of the marginal likelihood in favor of one model over another. ≈ 1 indicates little to no difference between the models; indicates a strong marginal likelihood in favor of ; and indicates a strong marginal likelihood in favor of .
3. Results
3.1. Time Series Cross-Validation
3.2. Diebold–Mariano Test
3.3. Bayesian Model Comparison
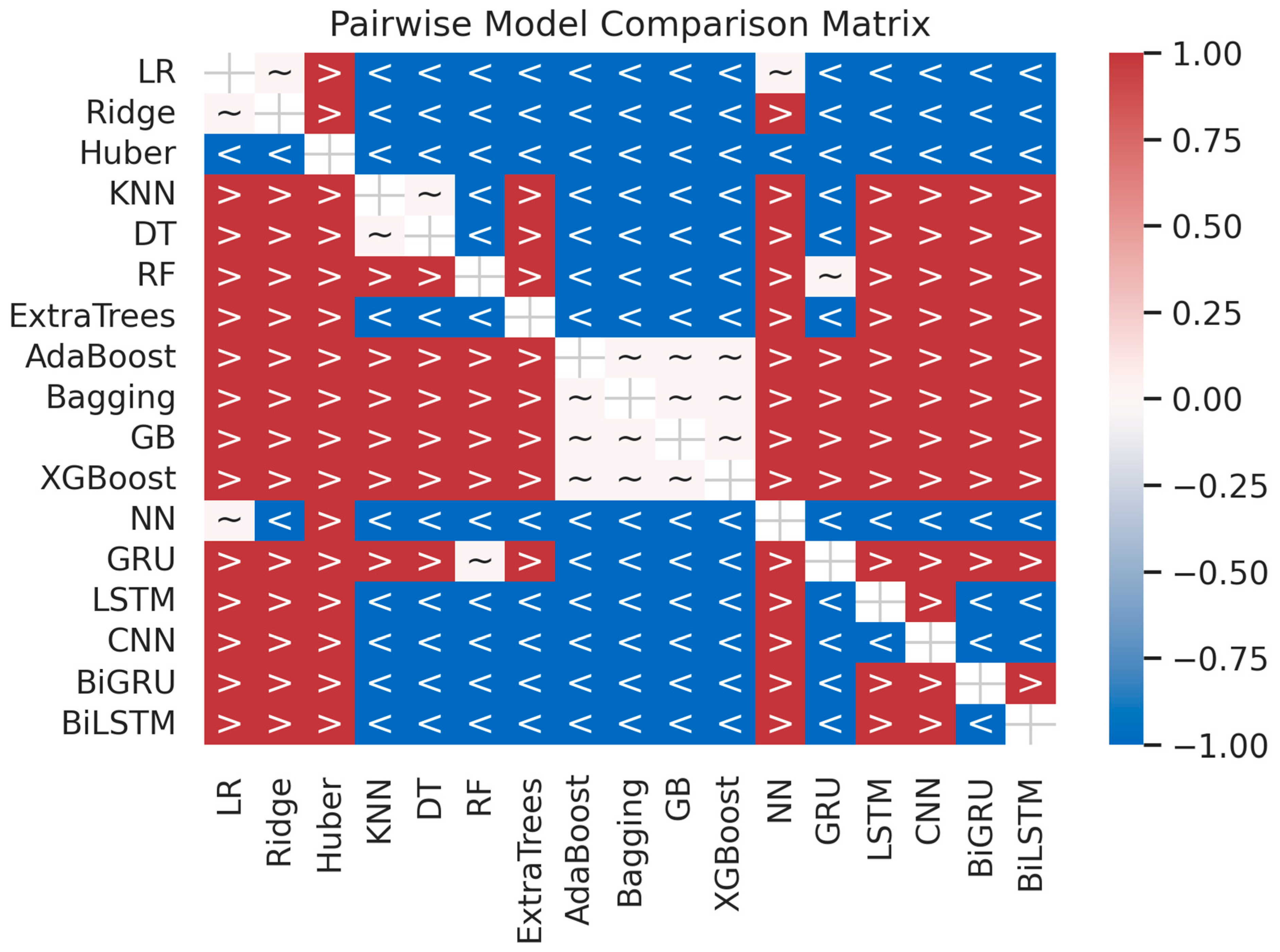
3.4. Comparison of Machine Learning Models
4. Conclusions
- One of the notable advantages of our models is their independence of the presence of meteorological data. This is particularly valuable in situations where weather data are not available, incomplete, or unreliable. Even with the sole use of historical power generation data, our models can produce accurate forecasts;
- Meteorological data may occasionally be susceptible to measurement inaccuracies, incomplete values, or delays in data collection. These issues are mitigated in our models through the utilization of operational data, which is typically more consistently recorded and maintained by wind farms. This enhances the robustness of the forecasting process;
- The complexity of data preprocessing and integration are reduced in our models by excluding weather data. This simplification can result in faster deployment and lower computational requirements, making the forecasting process more efficient.
- The models GRU, LSTM, and BiLSTM showed the lowest RMSE and MAE, proving their accuracy in predicting wind power generation;
- The performance of ensemble methods, specifically XGBoost and Bagging, was strong, consistently providing accurate predictions.
- The Diebold–Mariano (DM) Test confirmed the statistical significance of the performance disparities among models, underscoring the superior accuracy of GB, XGBoost, and Bagging;
- The Bayesian model comparison revealed that AdaBoost, Bagging, GB, and XGBoost presented robustness, as indicated by probabilistic evidence, surpassing other models.
- According to the findings, the implementation of advanced neural network architectures and ensemble methods can notably improve the reliability of wind power predictions. This improvement can lead to better grid stability and operational efficiency;
- Effective operational planning and resource allocation are facilitated by accurate wind power predictions, reducing reliance on fossil fuels and supporting renewable energy integration.
- Grid stability is improved through the use of accurate forecasting models, allowing for better management of supply and demand;
- Enhanced forecasting models enable more accurate operational planning, minimizing expenses linked to excess production and storage;
- Accurate wind power predictions facilitate the integration of renewable energy, decreasing greenhouse gas emissions and dependence on non-renewable sources.
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Model | Hyperparameters | Values or Distributions |
|---|---|---|
| LR | fit_intercept | [True, False] |
| Ridge | estimator__alpha | Uniform distribution (0.1, 10.0) |
| Huber | estimator__epsilon, estimator__alpha | Uniform distributions (1.35, 1.75), (0.01, 25.0) |
| KNN | estimator__n_neighbors, estimator__weights, estimator__algorithm | randint (2, 30), [‘uniform’, ‘distance’], [‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’] |
| DT | max_depth, min_samples_split, min_samples_leaf | randint (2, 30), randint (2, 10), randint (1, 4) |
| RF | n_estimators, max_depth, min_samples_split, min_samples_leaf | randint (5, 205), randint (2, 30), randint (2, 10), randint (1, 4) |
| ExtraTrees | n_estimators, max_depth | randint (5, 205), randint (2, 30) |
| AdaBoost | estimator__n_estimators, estimator__learning_rate, estimator__loss | randint (5, 205), Uniform (0.01, 0.99), [‘linear’, ‘square’, ‘exponential’] |
| Bagging | estimator__n_estimators | randint (5, 205) |
| GB | estimator__n_estimators, estimator__learning_rate, estimator__max_depth | randint (5, 205), Uniform (0.01, 1.0), randint (2, 30) |
| XGBoost | n_estimators, learning_rate, max_depth | randint (5, 205), Uniform (0.01, 1.0), randint (2, 30) |
| NN | regressor__estimator__hidden_layer_sizes, regressor__estimator__activation, regressor__estimator__solver, regressor__estimator__learning_rate | [(30, 30, 30, 3), (50, 50, 50, 3), (100, 60, 60, 60, 20, 10, 3)], [‘relu’, ‘tanh’, ‘logistic’], [‘adam’, ‘sgd’], [‘constant’, ‘adaptive’] |
| GRU | regressor__model__model_type, regressor__model__units, regressor__model__dropout_rate | [‘GRU’], randint (20, 100), Uniform (0.1, 0.3) |
| LSTM | regressor__model__model_type, regressor__model__units, regressor__model__dropout_rate | [‘LSTM’], randint (20, 100), Uniform (0.1, 0.3) |
| CNN | regressor__model__filters, regressor__model__kernel_size | randint (16, 64), [2, 3, 4] |
| BiGRU | regressor__model__model_type, regressor__model__units, regressor__model__dropout_rate, regressor__model__activation | [‘GRU’], randint (32, 128), Uniform (0.1, 0.3), [‘relu’, ‘tanh’] |
| BiLSTM | regressor__model__model_type, regressor__model__units, regressor__model__dropout_rate, regressor__model__activation | [‘LSTM’], randint (32, 128), Uniform (0.1, 0.3), [‘relu’, ‘tanh’] |
Appendix B
Appendix C
References
- Administration, U.S.E.I. Wind Explained—History of Wind Power. Available online: https://www.eia.gov/energyexplained/wind/history-of-wind-power.php (accessed on 1 June 2023).
- Lerner, J.; Grundmeyer, M.; Garvert, M. The importance of wind forecasting. Renew. Energy Focus 2009, 10, 64–66. [Google Scholar] [CrossRef]
- Jenkins, N.; Burton, T.L.; Bossanyi, E.; Sharpe, D.; Graham, M. Wind Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Ghofrani, M.; Alolayan, M. Time Series and Renewable Energy Forecasting; IntechOpen: London, UK, 2018; Volume 10. [Google Scholar]
- Carrera, B.; Sim, M.K.; Jung, J.-Y. PVHybNet: A Hybrid Framework for Predicting Photovoltaic Power Generation Using Both Weather Forecast and Observation Data. IET Renew. Power Gener. 2020, 14, 2192–2201. [Google Scholar] [CrossRef]
- Aslam, S.; Herodotou, H.; Mohsin, S.M.; Javaid, N.; Ashraf, N.; Aslam, S. A survey on deep learning methods for power load and renewable energy forecasting in smart microgrids. Renew. Sustain. Energy Rev. 2021, 144, 110992. [Google Scholar] [CrossRef]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A critical review of wind power forecasting methods—Past, present and future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Obregon, J.; Han, Y.-R.; Ho, C.W.; Mouraliraman, D.; Lee, C.W.; Jung, J.-Y. Convolutional autoencoder-based SOH estimation of lithium-ion batteries using electrochemical impedance spectroscopy. J. Energy Storage 2023, 60, 106680. [Google Scholar] [CrossRef]
- Kim, J.; Obregon, J.; Park, H.; Jung, J.-Y. Multi-step photovoltaic power forecasting using transformer and recurrent neural networks. Renew. Sustain. Energy Rev. 2024, 200, 114479. [Google Scholar] [CrossRef]
- Munoz, M.; Morales, J.M.; Pineda, S. Feature-driven improvement of renewable energy forecasting and trading. IEEE Trans. Power Syst. 2020, 35, 3753–3763. [Google Scholar] [CrossRef]
- Bellinguer, K.; Mahler, V.; Camal, S.; Kariniotakis, G. Probabilistic Forecasting of Regional Wind Power Generation for the eem20 Competition: A Physics-Oriented Machine Learning Approach. In Proceedings of the 2020 17th International Conference on the European Energy Market (EEM), Stockholm, Sweden, 16–18 September 2020; pp. 1–6. [Google Scholar]
- Li, L.-L.; Zhao, X.; Tseng, M.-L.; Tan, R.R. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J. Clean. Prod. 2020, 242, 118447. [Google Scholar] [CrossRef]
- da Silva, R.G.; Ribeiro, M.H.D.M.; Moreno, S.R.; Mariani, V.C.; dos Santos Coelho, L. A novel decomposition-ensemble learning framework for multi-step ahead wind energy forecasting. Energy 2021, 216, 119174. [Google Scholar] [CrossRef]
- Carrera, B.; Kim, K. Comparison analysis of machine learning techniques for photovoltaic prediction using weather sensor data. Sensors 2020, 20, 3129. [Google Scholar] [CrossRef]
- Lin, B.; Zhang, C. A novel hybrid machine learning model for short-term wind speed prediction in inner Mongolia, China. Renew. Energy 2021, 179, 1565–1577. [Google Scholar] [CrossRef]
- Stratigakos, A.; van Der Meer, D.; Camal, S.; Kariniotakis, G. End-to-End Learning for Hierarchical Forecasting of Renewable Energy Production with Missing Values. In Proceedings of the 2022 17th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Manchester, UK, 12–15 June 2022; pp. 1–6. [Google Scholar]
- Alkhayat, G.; Mehmood, R. A review and taxonomy of wind and solar energy forecasting methods based on deep learning. Energy AI 2021, 4, 100060. [Google Scholar] [CrossRef]
- Gu, C.; Li, H. Review on deep learning research and applications in wind and wave energy. Energies 2022, 15, 1510. [Google Scholar] [CrossRef]
- Baek, M.-W.; Sim, M.K.; Jung, J.-Y. Wind power generation prediction based on weather forecast data using deep neural networks. ICIC Express Lett. Part B Appl. 2020, 11, 863–868. [Google Scholar]
- Wu, Q.; Guan, F.; Lv, C.; Huang, Y. Ultra-short-term multi-step wind power forecasting based on CNN-LSTM. IET Renew. Power Gener. 2021, 15, 1019–1029. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 2021, 304, 117766. [Google Scholar] [CrossRef]
- Shahin, M.B.U.; Sarkar, A.; Sabrina, T.; Roy, S. Forecasting Solar Irradiance Using Machine Learning. In Proceedings of the 2020 2nd International Conference on Sustainable Technologies for Industry 4.0 (STI), Dhaka, Bangladesh, 19–20 December 2020; pp. 1–6. [Google Scholar]
- Kosovic, B.; Haupt, S.E.; Adriaansen, D.; Alessandrini, S.; Wiener, G.; Delle Monache, L.; Liu, Y.; Linden, S.; Jensen, T.; Cheng, W. A comprehensive wind power forecasting system integrating artificial intelligence and numerical weather prediction. Energies 2020, 13, 1372. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W.; Tian, X.; Fang, S.; Cheng, Y.; Chang, Y.; Liu, H. Short-term wind power forecasting using the hybrid model of improved variational mode decomposition and Correntropy Long Short-term memory neural network. Energy 2021, 214, 118980. [Google Scholar] [CrossRef]
- International Renewable Energy Agency (IRENA). Energy Profile Guatemala. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Statistics/Statistical_Profiles/Central%20America%20and%20the%20Caribbean/Guatemala_Central%20America%20and%20the%20Caribbean_RE_SP.pdf#:~:text=URL%3A%20https%3A%2F%2Fwww.irena.org%2F (accessed on 6 January 2024).
- Energypedia. Guatemala Energy Situation. Available online: https://energypedia.info/wiki/Guatemala_Energy_Situation (accessed on 6 January 2024).
- Evwind. Wind Energy in Guatemala. Available online: https://www.evwind.es/2020/06/25/wind-energy-in-guatemala/75323 (accessed on 6 January 2024).
- EnergiaGuatemala.com. Energy in Guatemala: Current Outlook for This Industry. Available online: https://energiaguatemala.com/en/energy-in-guatemala-current-outlook-for-this-industry/ (accessed on 6 January 2024).
- Fulbright, N.R. Renewable Energy in Latin America: Central America. Available online: https://www.nortonrosefulbright.com/en/knowledge/publications/1e7b0a75/renewable-energy-in-latin-america-central-america (accessed on 6 January 2024).
- Wiki, G.E.M. Energy Profile: Guatemala. Available online: https://www.gem.wiki/Energy_profile:_Guatemala (accessed on 6 January 2024).
- Gobierno de la Republica de Guatemala Ministerio de Energia y Minas. Nuevo Modulo de Estadisticas Energeticas en Guatemala. Available online: https://www.mem.gob.gt/wp-content/uploads/2017/11/MODULO.pdf (accessed on 6 January 2024).
- Renewables, C. San Antonio Wind Farm, First Guatemala Wind Farm. Available online: https://www.cjr-renewables.com/en/san-antonio-wind-farm/ (accessed on 6 January 2024).
- Viento Blanco. Available online: https://viento-blanco.com/wind-farm/?lang=en (accessed on 6 January 2024).
- Power, T.W. Available online: https://www.thewindpower.net/windfarm_es_27390_las-cumbres.php (accessed on 6 January 2024).
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 112. [Google Scholar]
- Robert, C. Machine Learning, a Probabilistic Perspective; The MIT Press: Cambridge, UK, 2014. [Google Scholar]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y. Xgboost: Extreme Gradient Boosting; R Package Version 0.4-2; CRAN.R-project.org; 2015; pp. 1–4. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1. [Google Scholar]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Mariano, R.S.; Preve, D. Statistical tests for multiple forecast comparison. J. Econom. 2012, 169, 123–130. [Google Scholar] [CrossRef]
- Diebold, F.X. Comparing predictive accuracy, twenty years later: A personal perspective on the use and abuse of Diebold–Mariano tests. J. Bus. Econ. Stat. 2015, 33, 1. [Google Scholar] [CrossRef]
- Mohammed, F.A.; Mousa, M.A. Applying Diebold–Mariano Test for Performance Evaluation between Individual and Hybrid Time-Series Models for Modeling Bivariate Time-Series Data and Forecasting the Unemployment Rate in the USA. In Proceedings of the Theory and Applications of Time Series Analysis: Selected Contributions from ITISE 2019, Granada, Spain, 25–27 September 2019; Springer: New York, NY, USA, 2020; pp. 443–458. [Google Scholar]
- Phillips, D.B.; Smith, A.F. Bayesian model comparison via. In Markov Chain Monte Carlo in Practice; Chapman & Hall: London, UK, 1995; pp. 215–240. [Google Scholar]
- Geweke, J. Bayesian model comparison and validation. Am. Econ. Rev. 2007, 97, 60–64. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, T.; Wang, Y.; Strbac, G.; Kang, C. Using Bayesian deep learning to capture uncertainty for residential net load forecasting. IEEE Trans. Power Syst. 2019, 35, 188–201. [Google Scholar] [CrossRef]





| ID | Name | Capacity [MW] | Starting Date | Region | Coordinates |
|---|---|---|---|---|---|
| SNT-E1 | San Antonio El Sitio | 52.80 | 19 April 2015 | Guatemala | 14.2124° N, 90.3315° W |
| VBL-E1 | Viento Blanco, S.A. | 23.10 | 6 December 2015 | Escuintla | 14.3912° N, 90.6638° W |
| LCU-E1 | Las Cumbres de Agua Blanca | 31.50 | 25 March 2018 | Jutiapa | 14.2620° N, 89.344° W |
| Wind Farm | Mean Generation [MW] | Standard Deviation [MW] | Minimum Generation [MW] | Maximum Generation [MW] |
|---|---|---|---|---|
| SNT-E1 | 19.90 | 27.55 | 0 | 340.55 |
| VBL-E1 | 10.45 | 13.90 | 0 | 151.48 |
| LCU-E1 | 17.37 | 21.39 | 0 | 214.06 |
| Category | Algorithms |
|---|---|
| Simple | Linear Regression (LR), Ridge, Huber, K-Nearest Neighbors (KNN), Decision Trees (DT) |
| Ensemble | Random Forest (RF), ExtraTrees, AdaBoost, Bagging, Gradient Boosting (GB), XGBoost |
| Deep Learning | Neural Network (NN), GRU, LSTM, CNN, BiGRU, BiLSTM |
| Model | Best Parameters |
|---|---|
| LR | fit_intercept = False |
| Ridge | alpha = 9.795213209218735 |
| Huber | alpha = 23.609862143899665, epsilon = 1.3795486160040937, max_iter = 10,000 |
| KNN | n_neighbors = 21, weights = ‘distance’ |
| DT | max_depth = 4, min_samples_leaf = 2, min_samples_split = 6 |
| RF | max_depth = 5, min_samples_split = 3, n_estimators = 82 |
| ExtraTrees | max_depth = 15, n_estimators = 86 |
| AdaBoost | learning_rate = 0.9472355241265569, n_estimators = 93 |
| Bagging | estimator = BaggingRegressor(n_estimators = 41) |
| GB | learning_rate = 0.22071792035854365, max_depth = 13, n_estimators = 69 |
| XGBoost | learning_rate = 0.5069668065851777, max_depth = 25, n_estimators = 190 |
| NN | activation = ‘logistic’, hidden_layer_sizes = (30, 30, 30, 3), learning_rate = ‘adaptive’, max_iter = 10,000, solver = ‘sgd’ |
| GRU | batch_size = 32, epochs = 50, dropout_rate = 0.11739125554241406, number of neurons = 65, verbose = 0 |
| LSTM | batch_size = 32, epochs = 50, dropout_rate = 0.1591187227490868, number of neurons = 93, verbose = 0 |
| CNN | batch_size = 32, epochs = 50, filters = 61, kernel_size = 4 |
| BiGRU | batch_size = 200, epochs = 128, activation = ‘tanh’, dropout_rate = 0.22956820690724705, number of neurons = 107 |
| BiLSTM | batch_size = 200, epochs = 128, model__activation = ‘tanh’, dropout_rate = 0.12150022102203821, number of neurons = 120 |
| Model | RMSE | MAE | ||
|---|---|---|---|---|
| Mean | STD | Mean | STD | |
| LR | 22.662 | 5.557 | 15.681 | 3.668 |
| Ridge | 23.499 | 4.519 | 16.859 | 2.944 |
| Huber | 22.536 | 6.034 | 14.543 | 3.791 |
| KNN | 18.842 | 4.949 | 11.988 | 3.077 |
| DT | 18.187 | 4.706 | 11.769 | 2.919 |
| RF | 18.067 | 4.759 | 11.594 | 2.835 |
| ExtraTrees | 21.230 | 5.329 | 12.845 | 2.950 |
| AdaBoost | 19.065 | 3.315 | 12.888 | 2.475 |
| Bagging | 21.387 | 5.068 | 12.731 | 2.823 |
| GB | 22.233 | 5.235 | 13.068 | 2.805 |
| XGBoost | 22.173 | 5.328 | 13.001 | 2.873 |
| NN | 20.312 | 5.198 | 13.399 | 2.564 |
| GRU | 17.860 | 4.449 | 11.585 | 2.921 |
| LSTM | 17.781 | 4.647 | 11.832 | 2.868 |
| CNN | 20.181 | 5.553 | 13.165 | 2.932 |
| BiGRU | 18.330 | 5.238 | 11.409 | 3.226 |
| BiLSTM | 17.870 | 4.681 | 11.392 | 3.123 |
| Model 1 | Model 2 | SNT-E1 | VBL-E1 | LCU-E1 | |||
|---|---|---|---|---|---|---|---|
| DM-Stats | p-Value | DM-Stats | p-Value | DM-Stats | p-Value | ||
| Bagging | BiLSTM | 10.2314 | 2.30 × 10−24 | 11.1001 | 2.41 × 10−28 | 12.9001 | 1.46 × 10−37 |
| Ridge | NN | 18.366 | 2.77 × 10−73 | −0.923 | 3.56 × 10−1 | −9.242 | 3.32 × 10−20 |
| Ridge | LSTM | 9.949 | 3.87 × 10−23 | 4.459 | 8.39 × 10−6 | 1.894 | 5.82 × 10−2 |
| Huber | NN | 21.923 | 1.95 × 10−102 | 15.406 | 1.59 × 10−52 | 29.742 | 4.29 × 10−181 |
| Huber | LSTM | 12.442 | 4.31 × 10−35 | 6.417 | 1.50 × 10−10 | 7.544 | 5.27 × 10−14 |
| ExtraTrees | BiLSTM | 9.063 | 1.70 × 10−19 | 9.140 | 8.48 × 10−20 | 10.685 | 2.11 × 10−26 |
| ExtraTrees | GB | −12.671 | 2.58 × 10−36 | −13.862 | 5.16 × 10−43 | −14.823 | 8.02E × 10−49 |
| ExtraTrees | XGBoost | −12.739 | 1.10 × 10−36 | −14.719 | 3.56 × 10−48 | −13.934 | 1.95E × 10−43 |
| GB | BiLSTM | 11.340 | 1.69 × 10−29 | 11.958 | 1.41 × 10−32 | 13.348 | 4.72E × 10−40 |
| XGBoost | BiLSTM | 11.366 | 1.27 × 10−29 | 11.994 | 9.24 × 10−33 | 13.329 | 5.99 × 10−40 |
| Model 1 | Model 2 | SNT-E1 | VBL-E1 | LCU-E1 | |||
|---|---|---|---|---|---|---|---|
| DM-Stats | p-Value | DM-Stats | p-Value | DM-Stats | p-Value | ||
| LR | LSTM | 7.951 | 2.20 × 10−15 | 4.314 | 1.63 × 10−5 | 3.907 | 9.46 × 10−5 |
| Ridge | BiGRU | 5.831 | 5.79 × 10−9 | 3.141 | 1.69 × 10−3 | 0.795 | 4.27 × 10−1 |
| Huber | LSTM | 12.442 | 4.31 × 10−35 | 6.417 | 1.50 × 10−10 | 7.544 | 5.27 × 10−14 |
| KNN | LSTM | 2.000 | 4.55 × 10−2 | 1.582 | 1.14 × 10−1 | 4.213 | 2.56 × 10−5 |
| RF | BiLSTM | −5.420 | 6.19 × 10−8 | −1.285 | 1.99 × 10−1 | 5.391 | 7.27 × 10−8 |
| Model 1 | Model 2 | SNT-E1 | VBL-E1 | LCU-E1 | |||
|---|---|---|---|---|---|---|---|
| DM-Stats | p-Value | DM-Stats | p-Value | DM-Stats | p-Value | ||
| LR | KNN | 5.088 | 3.73 × 10−7 | 3.326 | 8.88 × 10−4 | 1.698 | 8.96 × 10−2 |
| Ridge | ExtraTrees | −1.272 | 0.203 | −1.333 | 1.83 × 10−1 | −3.414 | 6.45 × 10−4 |
| Huber | ExtraTrees | 0.908 | 0.364 | 0.624 | 5.33 × 10−1 | 1.343 | 1.79 × 10−1 |
| DT | GRU | −1.187 | 0.235 | −2.386 | 1.71 × 10−2 | −7.715 | 1.41 × 10−14 |
| RF | BiGRU | −4.975 | 6.72 × 10−7 | −4.094 | 4.30 × 10−5 | 1.532 | 1.26 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrera, B.; Kim, K. Comparative Analysis of Machine Learning Techniques in Predicting Wind Power Generation: A Case Study of 2018–2021 Data from Guatemala. Energies 2024, 17, 3158. https://doi.org/10.3390/en17133158
Carrera B, Kim K. Comparative Analysis of Machine Learning Techniques in Predicting Wind Power Generation: A Case Study of 2018–2021 Data from Guatemala. Energies. 2024; 17(13):3158. https://doi.org/10.3390/en17133158
Chicago/Turabian StyleCarrera, Berny, and Kwanho Kim. 2024. "Comparative Analysis of Machine Learning Techniques in Predicting Wind Power Generation: A Case Study of 2018–2021 Data from Guatemala" Energies 17, no. 13: 3158. https://doi.org/10.3390/en17133158
APA StyleCarrera, B., & Kim, K. (2024). Comparative Analysis of Machine Learning Techniques in Predicting Wind Power Generation: A Case Study of 2018–2021 Data from Guatemala. Energies, 17(13), 3158. https://doi.org/10.3390/en17133158






