Abstract
In the face of the burgeoning electricity demands and the imperative for sustainable development amidst rapid industrialization, this study introduces a dynamic and adaptable framework suitable for policymakers and renewable energy experts working on integrating and optimizing renewable energy solutions. While using a case study representative model for Sub-Saharan Africa (SSA) to demonstrate the challenges and opportunities present in introducing optimization methods to bridge power supply deficits and the scalability of the model to other regions, this study presents an agile multi-criteria decision tool that pivots on four key development phases, advancing established methodologies and pioneering refined computational techniques, to select optimal configurations from a set of Policy Decision-Making Metrics (PDM-DPS). Central to this investigation lies a rigorous comparative analysis of variants of three advanced algorithmic approaches: Swarm-Based Multi-objective Particle Swarm Optimization (MOPSO), Decomposition-Based Multi-objective Evolutionary Algorithm (MOEA/D), and Evolutionary-Based Strength Pareto Evolutionary Algorithm (SPEA2). These are applied to a grid-connected hybrid system, evaluated through a comprehensive 8760-hour simulation over a 20-year planning horizon. The evaluation is further enhanced by a set of refined Algorithm Performance Evaluation Metrics (AL-PEM) tailored to the specific constraints. The findings not only underscore the robustness and consistency of the SPEA2 variant over 15 runs of 200 generations each, which ranks first on the AL-PEM scale, but the findings also validate the strategic merit of combining multiple technologies and empowering policymakers with a versatile toolkit for informed decision-making.
1. Introduction
1.1. Background
The pandemic’s combined effects and the ensuing energy shortages brought on by the crisis in Eastern Europe have reversed the progress made in expanding access to electricity over the past decade. In 2022, the global population lacking access to electricity increased for the first time in many years, reaching an estimated 760 million people. This increase was caused by about 6 million people. The bulk of the world’s unelectrified population is in SSA, where this regression has mostly been seen [1], with about 600 million people without access to electricity. As energy remains a pivotal element in societal development, a notion underscored by the United Nations Sustainable Development Goal 7 (UNSDG7), which strives for global access to sustainable energy by 2030 [2], the need to resume the upward trajectory seen before the pandemic is imminent. Sierra Leone, a small nation in the SSA, bounded by the Atlantic, however, has seen notable progress in their journey toward sustainable energy, yet challenges remain. The nation’s electrification rate has risen to 26% from about 15% in 2019 but still with a marked disparity as rural access hovers at 6% [3]. High unemployment at 3.63% [4] and exorbitant electricity tariffs compound the issue, undermining the UNSDG7 objectives. Currently, Sierra Leone’s attempts to meet a national demand of around 700 MW, which includes the mining sector, lean on unsustainable practices like diesel generation, despite environmental concerns. The Sustainable Energy for All (SE4ALL) initiative has set an ambitious target for Sierra Leone to boost access to electricity to 92% by 2030, necessitating a significant shift towards renewable energy to alleviate government subsidies on electricity, priced at 0.150 USD/kWh for residential use and 0.170 USD/kWh for industrial use [5]. Although Sierra Leone has considerable potential in solar, hydro, and biomass energy, its total government-owned generation capacity is limited to 155 MW with an additional 50 MW sourced from diesel power rentals and 27 MW sourced from the West African Power Pool (WAPP) project, leading to high operational costs and a heavy reliance on government subsidies. This research is undertaken in the context of these challenges. The opportunities herein aim to offer policymakers solutions through the use of advanced computational techniques and underscore the advantages of combining multiple technologies with the highest premium laid on renewable energy integration in an effort to contribute to the sustainable energy transition in Sierra Leone, the sub-region, and elsewhere with similar challenges.
1.2. Previous Research
The literature on Hybrid Energy Systems (HES) has grown significantly over the past decade, encompassing residential, institutional, industrial, off-grid, and grid applications. These studies have demonstrated the critical role of Renewable Distributed Generations (RDGs) in power systems, as they enhance energy security, reduce power losses, and improve overall efficiency while promoting environmental protection [6]. Many of these contributions have also revealed the challenges in the adoption of RDGs and how the adaptation of an HES can overcome these challenges. In the literature review in our previous work [7], a comprehensive analysis was performed on a wide range of applications, revealing the use of HES in overcoming the stochastic nature of Renewable Energy Sources (RES) and reduce overall energy consumption and CO2 emissions [8,9]. The summary also highlighted contributions that utilized modern approaches for optimal electric power system planning, including the Analytic Hierarchy Process [10], multi-criteria decision-making methods [11,12], scenario-based comparative analysis, and techno-economic analysis of grid-connected hybrid systems [13,14,15,16,17]. Numerous researchers have employed various tools for integrating renewable energy sources, such as the Holistic Grid Resource Integration and Development (HiGRID) tool [18] and the HOMER simulator [19]. The study cited in [20] explores dynamic operational and control techniques for microgrid hybrid energy systems, implementing the Particle Swarm Optimization (PSO) algorithm to evaluate the performance of PV power systems. In multi-objective optimization, especially when dealing with large-scale problems, the major challenge is the selection and development of high-performance optimization strategies that balance exploration and exploitation within a robust and adaptable framework while also maintaining the consistency and accuracy of the optimal results. These challenges have been met with hybrid optimization methods employed for HRES in recent developments [21,22,23]. The research in [6] applied a hybrid methodology combining PSO with the Gravitational Search Algorithm (PSOGSA) to identify the optimal placement of PV and wind systems, aiming to minimize system power losses and operational expenses while enhancing voltage profiles and stability. Comprehensive reviews on the optimization of Hybrid Renewable Energy Systems (HRES) [22,23,24,25] presented the advantages and disadvantages of the various algorithms over the past decade, highlighting their robustness over a wide spectrum of performance metrics. Despite these advancements, there still remains a gap in the literature for a comprehensive approach that not only integrates advanced computational techniques but presents a clear strategy for policymakers and energy specialists to adopt when considering renewable energy expansion. Three standard multi-objective optimization algorithms (MOPSO, MOEA/D, SPEA2) from three different domains (swarm-based, decomposition-based, and evolutionary-based approaches), as shown in Figure 1, have been modified and examined in this research in a bid to construct the most suitable method for the adoption of HRES.
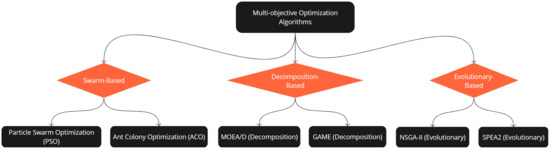
Figure 1.
Algorithm competitive landscape.
1.3. Problem Formulation and Main Contributions
Designing and implementing hybrid renewable energy systems (HRES) in Sub-Saharan Africa presents a distinct set of challenges and opportunities. To maximize the benefits of HRES, a robust decision-making framework that effectively addresses technical, economic, environmental, and social factors must be applied. This document outlines the challenges and opportunities in integrating and optimizing renewable energy solutions within the context of Sub-Saharan Africa (SSA), drawing from a representative case study model. The primary problem this research addresses is the deficit in power supply against the backdrop of an escalating population and economic growth, particularly in SSA where an estimated 600 million individuals lack access to electricity. The specific challenges identified include the following:
- The intermittency and variability of renewable energy sources (RES), necessitating the need for innovative hybrid energy systems (HES) that guarantee energy security while mitigating environmental impacts.
- The integration of multiple technologies within grid-connected systems, which complicates the optimization process due to the stochastic nature of RES.
- The requirement for advanced computational tools that balance exploration and exploitation within multi-objective optimization frameworks to ensure robust and consistent optimal results.
- The need for a scalable and adaptable framework that can be applied to other regions with similar energy challenges and constraints.
Existing approaches in the literature, some of which are shown in Table 1, often utilize limited statistical metrics to evaluate optimization algorithms, potentially leading to sub-optimal system configurations. Most of them use a multi-objective algorithm or soft computing tool that is evaluated through basic statistical parameters such as minimum and maximum values, standard deviation, and mean. Very few studies on grid-connected hybrid systems compared two or more optimization techniques and employed other performance metrics like convergence, generational distance, and other advanced metrics to compare the optimization algorithms in a competitive landscape.

Table 1.
Brief summary of recent works on computational techniques for sustainable energy solutions.
Therefore, the central problem addressed in this research lies in the following:
- Limited Evaluation of Optimization Algorithms: HRES design involves complex multi-objective decision-making processes. Current evaluation methods for optimization algorithms often rely on basic metrics, providing an incomplete assessment of their suitability for identifying the truly optimal HRES configuration within the feasible solution space.
- Lack of Comprehensive Decision Framework: A holistic framework to guide policymakers and energy specialists in selecting and integrating renewable energy solutions is needed, particularly for regions like Sub-Saharan Africa where energy access and sustainability are critical concerns.
In a bid to address these challenges the following contributions have been made:
- A Comprehensive Algorithm Selection: Utilization of variants of algorithms from three different domains (swarm, decomposition, and evolutionary), slightly modified for robustness and consistency within the specified constraints of the case study.
- A Comprehensive Algorithm Evaluation: A clear presentation of the chosen algorithms’ variants scrutinized through seven performance metrics, the authors described as the AL-PEM approach, and directly applied to a real-world grid-connected scenario that utilizes five technologies and five objective functions to determine the efficacy of the algorithms over a 20-year planning horizon. The AL-PEM approach incorporates the average spacing, rate of convergence, generational distance, computational time, maximum spread, the optimal Euclidean distance of the solutions to the origin, and the amount of storage used up by each algorithm. Table 1 presents a summary of the most recent works on HRES that use at least two soft computing tools and highlights from the performance metrics and statistical methods used; this table has been created for comparison to the methods adopted in this paper.
- A Clear Presentation of the Agile Multi-Criteria Decision Tool: This tool highlights four key developmental phases from resource assessment to the construction and O&M phase that forms a practical framework that can be adapted for policymaking and optimization of renewable energy systems.
2. Methodology
In our previous work, a comprehensive evaluation necessary for determining the feasibility of renewable energy projects—underpinned by the ‘Pentagonal Decision Criteria’ for renewable energy integration, as illustrated in Figure 1 of [7]—was conducted. The summary laid out a holistic and structured approach for evaluating renewable energy projects, ensuring they meet the following five benchmarks that are strictly interdependent on each other: political [32,33], resource [34,35], social and environmental [36], technological [37,38], and economic [39] benchmarks. These benchmarks are necessary for successful integration into SSA and beyond.
In this work, we have laid out a methodology that focuses on the technological and economic benchmarks with the following specific objectives:
- System Optimization: Use the MOPSO technique to determine the optimal configuration of PV panels, OWTs, biomass combustion plants, BESS, and DG systems that aligns power generation with demand and minimizes life cycle costs over a 20-year project horizon.
- Comparative Analysis: Conduct a comparative analysis of the MOPSO technique against modified MOEA/D and SPEA 2 algorithms, using the highlighted AL-PEM approach to establish the most effective optimization method specific to the chosen HRES.
- Sustainability Evaluation: Evaluate the environmental impact by aiming to minimize CO2 emissions and the Diesel Energy Fraction (DEF) in the energy mix, thereby contributing to sustainable energy development goals.
- Policy Framework Development:Provide policymakers with a decision-making framework based on the study’s findings that integrates economic viability, environmental sustainability, and social equity considerations.
- Scalability Assessment: Investigate the scalability of the proposed optimization framework in a real-life case study-based approach.
2.1. Study Area and Resource Assessment
The scope of this study covers the same domain and areas of operations covered by our previous work, as detailed in the methodology section and the study area sub-section of [7] with very few improvements made in the generation capacity as listed in Table 2. Despite the addition of new generating facilities, there are still many that are not fully operational due to aging and persistent operational issues, limiting the overall reliability of the system. Figure 2 of [7] illustrates the estimated grid capacity and demand of the entire nation. The introduction of new generating facilities, such as the 6 MW solar farm in Table 2, does not significantly impact the overall grid capacity due to the presence of non-operational generating units. Additionally, there are no off-grid wind turbine installations.

Table 2.
Existing generation facilities.
In our previous study, we used the Weibull distribution and other statistical methods to approximate the potential and characteristics of solar, wind, and biomass energy. The scope of these assessment methods and the results obtained are maintained in this journal for consistency.
2.2. Configuration and Scheme
Similar to the selection process performed in our previous work, 5 combinations of hybrid systems have been selected according to the selection scheme shown in Figure 2. When the selected technologies go through a thorough assessment, they are considered to determine feasible pairings. The letters A, B, C, D, and E are used to designate the PV plant, wind turbines, biomass plant, battery bank, and diesel generator set, respectively, for ease of referencing the components of the blocks (Blocks 1–5) considered. The specifications of each component of the hybrid system for the respective blocks are fed into the optimization and parameter tuning phase as shown in the proposed decision criteria in Figure 3. This method is explained in the next subsection (Decision Criteria and Performance Metrics). The hybrid system’s configuration in Figure 4 represents Block 1.
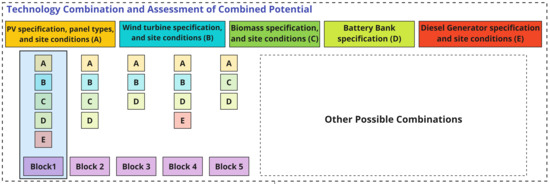
Figure 2.
Hybrid system selection scheme. Other possible combinations: Figure 11 [7].
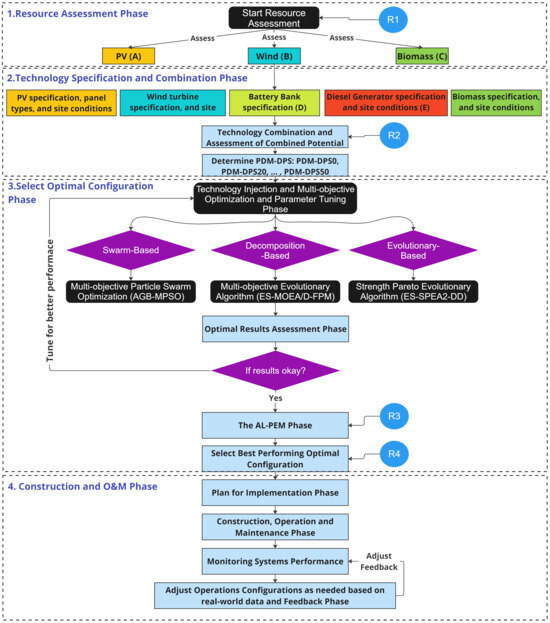
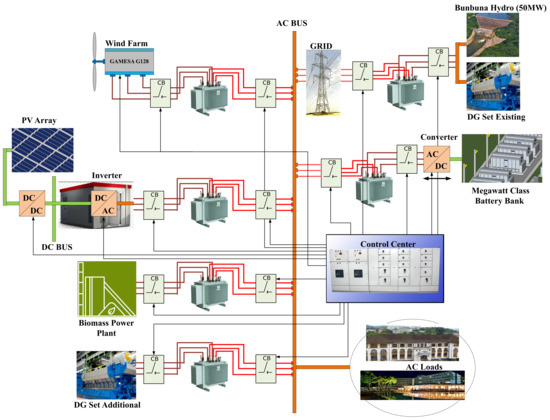
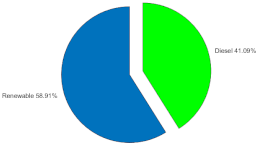
Figure 4.
Hybrid system configuration [7].
2.3. Decision Criteria and Performance Metrics
The decision criteria can be summarized in a series of phases, as represented in the flow chart, which are outlined as follows:
- Resource Assessment Phase: This initial phase involves the assessment of natural resources and the evaluation of wind, PV (photovoltaic), and biomass potential.
- Technology Specification Phase: Subsequent to the resource evaluation, this phase specifies the technical details and capacities of the technologies under consideration.
- Combination Consideration: Here, various combinations of the assessed technologies are considered to determine feasible pairings.
- Technology Injection Condition Phase: This phase takes into account the different conditions under which power supply might be deficient and considers the budget constraints set by policymakers.
- Multi-Objective Optimization: The considered technology combinations and injection conditions are input into three multi-objective optimization algorithms. These algorithms aid in selecting the optimal configuration that aligns with the project’s budget.
- Plan for Implementation Phase: A detailed plan for the implementation of the selected technology configuration is developed.
- Construction Phase: This phase covers the actual construction and installation of energy technologies.
- Operation and Maintenance Phase: This phase involves the daily operation and upkeep of the implemented technologies.
- Monitoring Systems Performance Phase: Continuous monitoring of the system’s performance is conducted to ensure efficiency and reliability.
- Adjusting Configurations and Feedback Phase: The final phase allows for adjustments to the configurations based on feedback and operational data to optimize performance.
2.4. Optimization Methods
2.4.1. M-O Particle Swarm Optimization (MOPSO)
Multi-objective Particle Swarm Optimization (MOPSO) is an adaptation of standard Particle Swarm Optimization (PSO) designed for multi-objective problems. It utilizes the concept of Pareto dominance to direct the swarm towards the Pareto-optimal front. Each particle in the swarm represents a potential solution, and the swarm explores the search space to optimize multiple objectives simultaneously. The position and velocity of each particle in the swarm are updated according to the following equations [40]:
where
- w is the inertia weight.
- and are the cognitive and social acceleration coefficients, respectively.
- and are random numbers uniformly distributed in [0, 1].
- is the personal best position of particle i.
- is the global best position found by the entire swarm.
The pseudocode for MOPSO is presented in Algorithm 1.
| Algorithm 1 Multi-objective Particle Swarm Optimization (MOPSO) |
|
The Modified Multi-objective Particle Swarm Optimization, Dynamic Adaptive Mutation-Based MOPSO (DAM-MOPSO) algorithm introduces a series of enhancements to the original framework aimed at refining optimization efficacy and solution diversity. It incorporates adaptive mutation and a focuses on diversity. Its key distinctions are as follows:
- Leader Selection Mechanism: A stochastic leader selection approach such as the Roulette Wheel approach is implemented to guide particles diversely through the search space.
- Adaptive Mutation: The algorithm adopts an adaptive mutation step, adjusting the mutation probability with the iteration number, promoting exploration initially and exploitation subsequently.
- Repository Update: The repository’s maintenance is explicitly detailed, ensuring the preservation and continual update of a diverse solution set.
- Grid Update and Dominance: An explicit step is included for revising the grid structure based on the repository, which is crucial for sustaining diversity. Moreover, the process for culling dominated and surplus particles is specifically mentioned.
- Normalization of the Pareto Front: Prior to the final iteration, the Pareto front is normalized, which aids in delineating the true Pareto optimal solutions.
- Resulting Set: The algorithm yields a repository-derived set of non-dominated solutions as its final output, indicating a refined solution set.
These modifications target potential shortcomings in the original MOPSO, such as premature convergence and population diversity, and enhance the search space’s exploration and exploitation capabilities. The modified methodology suggests a dynamic and adaptive optimization process, likely to yield superior performance in discerning a high-quality set of Pareto-optimal solutions for complex multi-objective problems. The pseudocode for the DAM-MOPSO algorithm is presented in Algorithm 2.
| Algorithm 2 Algorithm Framework of DAM-MOPSO |
|
2.4.2. M-O Evolutionary Algorithm Based on Decomposition (MOEA/D-M2)
Decomposition-based algorithms, such as MOEA/D-M2, address complex multi-objective optimization by decomposing the problem into a number of scalar optimization subproblems. Each subproblem optimizes a weighted aggregation of the objectives, and the solutions to these subproblems contribute to the construction of the Pareto front.
Mathematical Description
MOEA/D-M2 decomposes a multi-objective optimization problem into a number of scalar optimization problems using a set of weight vectors. The algorithm then uses evolutionary operations to optimize these subproblems simultaneously.
Given a multi-objective problem with objectives , the scalarized objective function for a weight vector and a solution x is given by:
where is the ideal point for the i-th objective, and is the i-th element of the weight vector .
The pseudocode for MOEA/D-M2, show in Algorithm 3, is a simplified representation and does not cover all aspects of the MOEA/D-M2 algorithm, such as constraint handling and parameter tuning.
| Algorithm 3 General framework of MOEA/D-M2 |
|
In order to modify the general MOEA/D framework, the authors adopted an Enhanced Strategy (ES) for Multi-Objective Evolutionary Algorithm based on Decomposition, not too far from the general framework but with Focused Perturbation Mechanism (ES-MOEA/D-FPM). This evolutionary strategy, shown in Algorithm 4 augments the standard MOEA/D. The integrated focused perturbation mechanism is aimed at reinforcing the exploration and exploitation phases of the optimization process. The methodology is outlined as follows:
- Population Initialization: The population and weight vectors are initialized along with the neighbourhood structure.
- Reference Point Initialization: A reference point is established to assist in scalarizing function computations.
- Evolutionary Loop: The loop continues until a termination criterion is met, iterating over the following steps:
- Neighbouring individuals are selected for mating using a crossover operator, followed by a polynomial mutation to generate offspring.
- Any constraint violation by the offspring invokes a repair mechanism.
- The offspring’s objective function is evaluated and compared against the current solutions using a weighted sum scalarizing function.
- The reference point is updated if the new solution provides a better scalarized value.
- Individual Update: Each individual in the population is compared against the new offspring, and updates are made if the offspring’s scalarized value is superior.
- External Population Maintenance: The external population is pruned of dominated solutions, and non-dominated offspring are included.
- Result Compilation: The algorithm concludes by returning the external population as the result, which comprises the non-dominated solutions.
The ES-MOEA/D-FPM algorithm’s focused perturbation mechanism is expected to yield a robust set of Pareto-optimal solutions, enhancing the multi-objective optimization process’s efficiency and effectiveness.
| Algorithm 4 Algorithm framework of ES-MOEA/D-FPM |
|
2.4.3. Strength Pareto Evolutionary Algorithm (SPEA2)
The Strength Pareto Evolutionary Algorithm (SPEA2) is an evolutionary algorithm designed for solving multi-objective optimization problems. It incorporates the concept of Pareto dominance into its selection mechanism and introduces a fitness assignment strategy that accounts for both the dominance and density of solutions.
Mathematical Description
SPEA2 uses a fitness function that combines both dominance strength and density estimation. It improves upon its predecessor, SPEA, by introducing fine-grained fitness assignment, a nearest-neighbour density estimation technique, and an enhanced archive truncation method. The strength of a solution is defined by the number of solutions it dominates, while the density estimation is inversely related to the distance to the k-th nearest neighbour in the objective space.
The fitness of an individual x is given by:
where is the strength value, and is the density value.
The pseudo-code for the general framework for SPEA2 algorithm is outlined in Algorithm 5.
| Algorithm 5 Strength Pareto Evolutionary Algorithm (SPEA2) |
|
A slight modification of the general framework was performed as outlined in Algorithm 5 to obtain an Enhanced Strength Pareto Evolutionary Algorithm to preserve diversity and control population density (ES-SPEA2-DD). The pseudo-code outlined in Algorithm 6 encapsulates the diversity–density methodology of ES-SPEA2-DD. ES-SPEA2-DD emphasizes the importance of diversity and density within the evolutionary process, seeking to improve upon the convergence and distribution of solutions along the Pareto front. This approach is particularly good at tackling challenges in multi-objective optimization where maintaining a varied and evenly spread set of solutions is crucial. In a bid to determine the robustness of ES-MOEA/D-FPM and ES-SPEA2-DD, they were compared against other modified algorithms found in previous works.
| Algorithm 6 Algorithm framework of ES-SPEA2-DD |
|
ES-MOEA/D-FPM was evaluated against a stable-state multi-objective evolutionary algorithm based on decomposition (MOEA/D-SS) and the original MOEA/D. The objective of this strategy is to dynamically adjust the neighbourhood size based on factors such as the convergence level within the neighbourhood, the state of the population, and historical neighbourhood information. This ensures it meets the requirements at any stage of population iteration and evolution [41]. The ES-SPEA2-DD was evaluated against the Grid Density Search and Elite Guidance Strength Pareto Evolutionary Algorithm (GDSEG-SPEA2) [42]. It employs a sophisticated methodology that combines grid density search with elite guidance strategies to enhance solution diversity and convergence towards the Pareto front. The next section details a robustness comparison table that highlights the strength of the algorithms against features common to them.
2.4.4. Performance Metrics and Their Relation to HRES Optimization
To effectively evaluate the optimization algorithms for HRES, several performance metrics are considered. Each metric provides insight into different aspects of the algorithm’s capabilities and their impact on the optimization process.
- Computational Time: The duration that the algorithm requires to converge to a solution or complete a defined set of iterations. For HRES, minimizing computational time is crucial for enabling rapid analysis and adaptive decision-making in response to fluctuating energy supplies and demands.
- Storage Used: This represents the algorithm’s memory requirement. A consistent memory usage, regardless of the operational conditions, suggests the stability and scalability of the algorithm when applied to HRES.
- Spacing: A measure of the diversity and distribution of the solutions along the Pareto front. In HRES optimization, a lower spacing value is preferred as it indicates a more evenly distributed set of solutions which can lead to more balanced decision-making.
- Average Rate of Convergence: This metric indicates the swiftness with which an algorithm approaches an optimal solution. A faster rate of convergence is beneficial for HRES optimization, as it contributes to quicker system adaptability and efficiency.
- Maximum Spread: This metric assesses the extent of the distribution of solutions across the Pareto front, with a larger spread denoting a broader range of potential system configurations. This diversity is advantageous for policymakers in choosing HRES designs that can meet a wide array of performance objectives.
- Generational Distance: Gauges the closeness of the algorithm-generated solutions to the true Pareto front. A smaller generational distance is indicative of the algorithm’s accuracy in identifying optimal HRES configurations, which is pivotal for the system’s performance and sustainability.
These metrics collectively provide a comprehensive evaluation of the optimization algorithms. An ideal HRES optimization algorithm would demonstrate low computational time, moderate storage use, minimal spacing, rapid average rate of convergence, maximum spread, and minimal generational distance, ensuring a quick, efficient, diverse, and accurate solution to the HRES design problem.
2.4.5. Robustness Comparison
In the pursuit of optimal solutions for multi-objective problems, the robustness of an algorithm is pivotal. This section provides a comprehensive comparison of the robustness of DAM-MOPSO, ES-MOEA/D-FPM and ES-SPEA2-DD along with their respective variants found in previous works. In this context, robustness refers to the algorithms’ adaptability, diversity maintenance, convergence rate, and overall stability in the face of varying problem landscapes and constraints.
Table 3 presents a side-by-side evaluation of the original MOPSO against DAM-MOPSO and Table 4 presents an evaluation of the original MOEA/D and SPEA2 algorithms, alongside their enhanced variants, such as ES-MOEA/D-FPM (Evolutionary Strategy MOEA/D with Focused Perturbation Mechanism), MOEA/D-SS (MOEA/D with Stable-State mechanism), ES-SPEA2-DD (ES-SPEA2 with Dynamic Diversity), and GDSEG-SPEA2 (Grid Density Search and Elite Guidance SPEA2). The comparison focuses on key algorithmic features that contribute to robustness, including adaptability to complex problem geometries, ability to preserve solution diversity, effectiveness in converging to the Pareto front, and strategies for mutation, crossover, and constraint handling. By examining the mechanisms and strategies employed by each variant, we aim to provide a nuanced understanding of how different approaches impact the robustness and effectiveness of MOEA/D and SPEA2 algorithms in solving complex multi-objective optimization problems.

Table 3.
Robustness comparison table for original MOPSO and DAM-MOPSO.

Table 4.
Robustness Comparison Table for MOEA/D and SPEA2 Variants.
2.5. Summary of Objectives
In concluding the methodology section of our study, we affirm that the physical, economic, and environmental systems criteria have been maintained as established in our prior work [7]. This consistency ensures that the comparative analysis of the algorithmic performance is grounded on a stable and reliable basis, facilitating a direct and transparent evaluation of enhancements and efficiencies brought by the algorithmic advancements.
The crux of our methodological exploration lies in the rigorous performance assessment of the considered algorithms. The focus has been judiciously placed on their capability to navigate the multi-dimensional search spaces effectively, their efficiency in converging towards optimal solutions, and their resilience in maintaining diversity across the solution spectra. The systematic evaluation, hence, does not reinvent the systems criteria; instead, it reiterates their validity while shifting the analytical lens towards the robustness, adaptability, and operational merit of the algorithmic frameworks under scrutiny. However, for ease of reference, we have highlighted below the mathematical representation of the objective functions as presented in [7].
This approach not only underlines the significance of algorithmic evolution in multi-objective optimization but also ensures that our findings are anchored in a well-established evaluative context, providing a clear trajectory for the subsequent results and discussions.
The objective functions considered are thus summarized below:
where , , , and are the economic objective or LCC, DEF, DPSP, and environmental objective or CO2 emissions, respectively.
3. Results and Discussions
This study has yielded insightful revelations about the operational capabilities of the advanced algorithmic variants modified DAM-MOPSO, ES-MOEA/D-FPM, and ES-SPEA2-DD, particularly in the application to grid-connected hybrid systems.
3.1. Performance Metrics Insights
The obtained results, encapsulated in Table 5 and Table 6, suggest that the ES-SPEA2-DD algorithm demonstrates superior robustness and consistency across multiple performance metrics. The Pareto plots (Figure 5a,b), performance metrics plots (Figure 5c,d), and parallel coordinates plots (Figure 6a–c) all provide a visual confirmation of these findings, illustrating ES-SPEA2-DD’s balanced trade-offs and its capacity for a well-tuned balance between exploration and exploitation. This balance is crucial in navigating the complex multi-objective optimization landscape, as it indicates a harmonized consideration of multiple objectives without excessive compromise on any single metric.

Table 5.
Performance evaluation metrics for the MOPSO, MOEA/D and SPEA2 variants.

Table 6.
Statistical analysis.
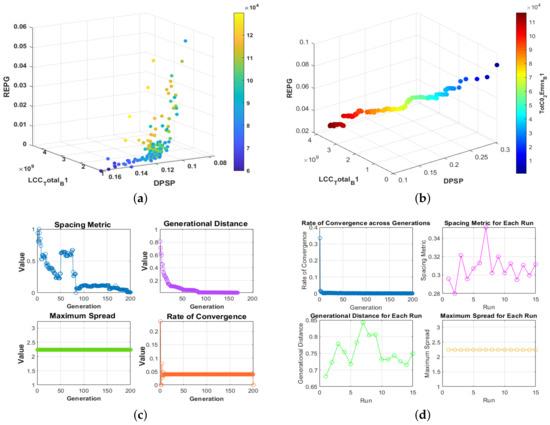
Figure 5.
Pareto front plots for DAM-MOPSO (a) and ES-SPEA2-DD (b). Spacing, maximum spread, rate of convergence and generational distance plots for DAM-MOPSO (c) and ES-SPEA2-DD (d).
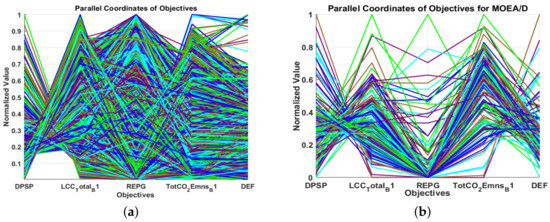
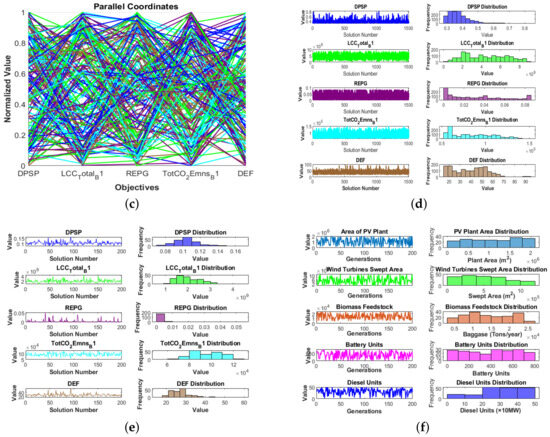
Figure 6.
Parallel coordinates plots for DAM-MOPSO (a), ES-MOEA/D-FPM (b), and ES-SPEA2-DD (c). Distribution plots for DAM-MOPSO (d), ES-MOEA/D-FPM (e), and ES-SPEA2-DD (f).
DAM-MOPSO, while exhibiting significant computational time, has shown a wide range of solutions in both the parallel coordinates plot (Figure 6a) and its distribution plot (Figure 6d). This behaviour raises questions about its scalability and practical application but also highlights its ability to explore a vast solution space, potentially uncovering novel solutions that are unattainable by more focused algorithms.
The distribution plots for each algorithm variant (Figure 6d–f) further enrich this analysis. ES-MOEA/D-FPM’s distribution plots (Figure 6e) indicate a concentrated approach towards the objectives, reflective of its targeted search strategy which may limit diversity but improves performance on specific objectives. In contrast, ES-SPEA2-DD’s distributions (Figure 6f) show not only efficiency in storage usage and convergence rate but also suggest a balance in the spread of solutions across objectives, underlining its versatility and robustness in achieving high-quality solutions.
Collectively, these visual insights corroborate the quantitative findings, painting a comprehensive picture of each algorithm’s strengths and weaknesses. While ES-SPEA2-DD stands out for its overall performance, DAM-MOPSO’s diverse exploration enriches the comparative benchmark, and ES-MOEA/D-FPM’s focused approach offers valuable insights into algorithmic efficiency and targeted optimization.
3.2. Policy Decision-Making Implications
In the realm of policymaking, particularly in energy-deficient regions such as Sub-Saharan Africa, the selection of optimization algorithms goes beyond mere technical performance; it has real-world implications for energy stability and supply quality. Our findings, based on the Policy Decision Metric based on Deficiency of Power Supply (PDM-DPS0) as consolidated in the overall rank Table 7, point towards ES-SPEA2-DD’s superior ability to align with policy objectives, demonstrated by its positive impact across all objective functions. It also emphasizes the practical significance of the algorithms’ outcomes in terms of tangible effects on energy supply stability and quality. Conversely, ES-MOEA/D-FPM, while theoretically promising with its scalarization approach, falls short in the overall practical considerations as evidenced by its overall rank.

Table 7.
Overall Rank.
3.3. Algorithmic Adaptability, Sustainability
Sustainability and adaptability are the foundation of energy system optimization in volatile environments. The ES-SPEA2-DD algorithm’s dominance across various performance metrics, including CO2 emissions and diesel energy fraction (DEF), underscores its potential for creating scalable and environmentally conscious energy solutions, a crucial advantage for sustainable development initiatives.
The comprehensive set of Algorithm Performance Evaluation Metrics (AL-PEM) employed in this study provides a nuanced perspective on the strengths and operational efficiency of the considered algorithms. The ES-SPEA2-DD’s performance, marked by favourable outcomes in terms of spacing, convergence, and computational time, clearly positions it as the frontrunner, while DAM-MOPSO, despite its second-place rank, shows commendable performance that may be suitable in scenarios where computational speed is less critical.
4. Conclusions
4.1. Synthesis with Previous Studies
The methodology of this research, which employs a comprehensive set of Algorithm Performance Evaluation Metrics (AL-PEM), advances the evaluative techniques used in previous studies. By incorporating a nuanced array of metrics—including average spacing, generational distance, and optimal Euclidean distance—the study provides a multifaceted understanding of algorithmic efficiency that transcends traditional evaluation methods. Comprehensive data collection was done to ensure the validity of the results across fuel consumption of diesel generator units, additional physical, environmental, and economic parameters defined for this study. Appendix A, Table A1 shows fuel consumption values for the existing DG units considered in this study [7] and Table A2 lists all parameters used in this study.
4.2. Comprehensive Algorithm Assessment
The rigorous evaluation conducted highlights ES-SPEA2-DD as the premier algorithm for optimizing hybrid renewable energy systems within the explored case study. This algorithm demonstrates exemplary performance across various decision metrics critical to policymaking, such as life cycle costs, diesel energy fraction, and CO2 emissions. The deployment of ES-SPEA2-DD, detailed in the Final AL-PEM for ES-SPEA2-DD Based on Policy Decision Metrics (Table 8), affords experts and policymakers a robust framework, furnishing them with a versatile toolkit for informed decision-making in the integration and optimization of renewable energy systems. The capabilities of ES-SPEA2-DD to address the deficiency of power supply under varying conditions can be observed. The comprehensive data and strategy presented reaffirm not only the robustness and consistency of the ES-SPEA2-DD algorithm in managing diverse scenarios effectively but also the capabilities of DAM-MOPSO, which is second-place ranked, in scenarios where computational speed is less critical. This approach offers a promising solution for sustainable and efficient energy system development.

Table 8.
Final AL-PEM for ES-SPEA2-DD based on Policy Decision Metrics.
Author Contributions
The main idea, methodology, development of algorithms, and data acquisition of this paper were proposed and obtained by D.A.K. All authors contributed to the data analysis, development of algorithms, and writing of the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy and legal reasons. The data will be used for future research work.
Acknowledgments
The authors acknowledge the unwavering support of staff from the Electricity Generation and Transmission Company and the Distribution Supply Authority of Sierra Leone for helping in providing relevant data on the daily operations of the power plants across the country.
Conflicts of Interest
The authors declare no conflicts of interests.
Abbreviations
The following abbreviations are used in this manuscript:
| AL-PEM | Algorithm Performance Evaluation Metrics |
| BM | Biomass |
| DG | Diesel Generator |
| ES-SPEA2-DD | Enhanced Strength Pareto Evolutionary Algorithm 2 with Dynamic Diversity |
| HES | Hybrid Energy Systems |
| MOPSO | Multi-objective Particle Swarm Optimization |
| MOEA/D | Multi-objective Evolutionary Algorithm based on Decomposition |
| NPV | Net Present Value |
| OM | Operation and Maintenance |
| PDM-DPS | Policy Decision Metric Based on Deficiency of Power Supply |
| RES | Renewable Energy Sources |
| SPEA2 | Strength Pareto Evolutionary Algorithm 2 |
| SSA | Sub-Saharan Africa |
| NPV of the total operation and maintenance cost of the biomass plant | |
| Annual growth rate of the BM cost | |
| Annual operation and maintenance cost of BM | |
| NPV of the resale price of the biomass plant | |
| Total cost recovered from resale | |
| Initial cost of the biomass plant | |
| Life cycle cost of the biomass power plant | |
| NPV of the replacement cost of the biomass plant | |
| Capital cost of the DG power plant | |
| Initial cost of DG | |
| NPV of the total operation and maintenance cost of DG | |
| Operation and maintenance cost of DG | |
| Annual growth rate of the DG cost | |
| NPV of the resale price of DG | |
| Total resale price of DG at the end of the project life | |
| Initial cost of DG plant |
Appendix A

Table A1.
Fuel Consumption of DG units across the country [7].
Table A1.
Fuel Consumption of DG units across the country [7].
| Fuel Consumption for Existing DG Units Considered | |||
|---|---|---|---|
| DG Unit | Fuel Operation | Number of Units | Consumption (L/h) |
| A | Diesel Oil | 20 | 240 |
| B1 | Diesel Oil | 3 | 350 |
| B2 | Diesel Oil | 5 | 240 |
| K | Heavy Fuel oil | 2 | 700 |
| Diesel Oil | 620 | ||
| L | Heavy Fuel oil | 3 | 470 |
| Diesel Oil | 430 | ||
| N1 and N2 | Heavy Fuel oil | 2 | 1024 |
| Diesel Oil | 981 | ||
| W1 and W2 | Heavy Fuel oil | 2 | 1300 |
| Diesel Oil | 1230 | ||
| M | Diesel Oil | 2 | 300 |
| LO | Diesel Oil | 1 | 300 |
| MA | Diesel Oil | 1 | 240 |

Table A2.
Physical, Environmental, and Economic Parameters [7].
Table A2.
Physical, Environmental, and Economic Parameters [7].
| Physical and Environmental Parameters | |||
|---|---|---|---|
| Technology Type | Variable | Notation | Value |
| Wind Turbine GAMESA G128-5.0 MW/ G132-5.0 MW | Rated Power | (kW) | 5000 |
| Cut-in speed | (m/s) | 1.5 | |
| Rated Speed | (m/s) | 13 | |
| Cut-off speed | 27 | ||
| H (m) | 100 | ||
| Wind Turbine lifetime | 20 | ||
| PV Panel Sun Power X Series | Maximum Power | (W) | 360 |
| Efficiency of Panel | 22.2 | ||
| Area of PV panel | (m2) | 1.63 | |
| PV lifetime | 20 | ||
| Biomass CFB Combustion Plant | Net calorific value of Baggase | (MJ/Kg) | 16 |
| Baggase Emissions Factor | (mmBtu/kg) | 0.0161 | |
| Efficiency of Plant | 0.42 | ||
| Lifetime of Biomass plant | 20 | ||
| Diesel Generator (DG) Nigatta Dual Fuel Diesel Plant | Unit Plant Capacity | 10,000 | |
| Lifetime of DG plant | 20 | ||
| Net calorific value of Heavy Fuel Oil (HFO) | (mmBtu/gal) | 0.15 | |
| Net calorific value of Diesel Oil (DO) | (mmBtu/gal) | 0.148 | |
| HFO Emissions Factor | (kgCO2/mmBtu) | 75.1 | |
| DO Emissions Factor | (kgCO2/mmBtu) | 74.92 | |
| Battery Bank Lithium Ion | Hourly Self Discharge | 0 | |
| Battery charging efficiency | 0.9 | ||
| Battery Discharging efficiency | 0.9 | ||
| Nominal Capacity of Battery (kWh) | 1200 | ||
| Lifetime of Battery Bank | 10 | ||
| Economic Parameters | |||
| Project lifetime | N | 20 | |
| Interest rate | i (%) | 10 | |
| Inflation rate | (%) | 4 | |
| Escalation rate | (%) | 5 | |
| Inverter efficiency | (%) | 90 | |
| Wind Turbine | Capital cost of Wind Turbine | ($/m2) | 544 |
| Yearly Operations and Maintenance Cost | 1.5 | ||
| Reselling Price | 30 | ||
| PV Panel | Capital cost of PV Panel | ($/kW) | 519.7 |
| Yearly Operations and Maintenance Cost | 1 | ||
| Reselling Price | 25 | ||
| Biomass Plant | Capital cost of Biomass Plant | ($/kW) | 1440 |
| Cost of Bagasse | ($/ton) | 25 | |
| Cost of Storage | ($/ton) | 12 | |
| Cost of loading | ($/ton) | 5 | |
| Cost of Transportation | ($/ton/km) | 0.057 | |
| Yearly Operations and Maintenance Cost | 0.017 | ||
| Reselling Price | 30 | ||
| Diesel Generator | Capital cost of DG plant | ($/kW) | 1000 |
| Cost of HFO | ($/L) | 0.45 | |
| Cost of DO | ($/L) | 0.607 | |
| HFO Consumption | (L/h) | 1024 | |
| DO Consumption | (L/h) | 981 | |
| Yearly Operations and Maintenance Cost | ($/kWh) | 0.032 | |
| Reselling Price | 30 | ||
| Battery Bank | Capital Cost of Battery | ($/kW) | 283 |
| Replacement Cost | - | ||
References
- Special Report: Energy Access Outlook. International Energy Agency, France. 2017. Available online: http://www.iea.org (accessed on 10 August 2018).
- Lee, J.T.; Callaway, D.S. The cost of reliability in decentralized solar power systems in sub-Saharan Africa. Nat. Energy 2018, 3, 960–968. [Google Scholar] [CrossRef]
- Sierra Leone Sustainable Energy For All (SE4ALL) Country Action Agenda: Sustainable Energy for All. 30 July 2015. Available online: https://www.se4all-africa.org (accessed on 30 August 2018).
- Sierra Leone Unemployment Rate. The Statistics Portal. Available online: https://www.statista.com (accessed on 30 August 2018).
- Sierra Leone Electricity Prices. GlobalPetrolPrices.com. Available online: https://www.globalpetrolprices.com/ (accessed on 24 December 2023).
- Tolba, M.; Rezk, H.; Tulsky, V.; Diab, A.; Abdelaziz, A.; Vanin, A. Impact of Optimum Allocation of Renewable Distributed Generations on Distribution Networks Based on Different Optimization Algorithms. Energies 2018, 11, 245. [Google Scholar] [CrossRef]
- Abdul, K.D.; Rashid, H.H.O.; Ryuto, S.; Tomonobu, S.; Shantanu, C.; Narayanan, K. A Multi-Criteria Decision Maker for Grid-Connected Hybrid Renewable Energy Systems Selection Using Multi-Objective Particle Swarm Optimization. Sustainability 2019, 11, 1188. [Google Scholar] [CrossRef]
- González, A.; Riba, J.R.; Rius, A. Optimal Sizing of a Hybrid Grid-Connected. Photovoltaic-Wind-Biomass Power System. Sustainability 2015, 7, 12787–12806. [Google Scholar] [CrossRef]
- Nižetić, S.; Papadopoulos, A.; Tina, G.; Rosa-Clot, M. Hybrid energy scenarios for residential applications based on the heat pump split air-conditioning units for operation in the Mediterranean climate conditions. Energy Build. 2017, 140, 110–120. [Google Scholar] [CrossRef]
- Vishnupriyan, J.; Manoharan, P. Multi-criteria decision analysis for renewable energy integration: A southern India focus. Renew. Energy 2018, 121, 474–488. [Google Scholar] [CrossRef]
- Theodorou, S.; Florides, G.; Tassou, S. The use of multiple criteria decision making methodologies for the promotion of RES through funding schemes in Cyprus, A review. Energy Policy 2010, 38, 7783–7792. [Google Scholar] [CrossRef]
- Wang, J.J.; Jing, Y.Y.; Zhang, C.F.; Zhao, J.H. Review on multi-criteria decision analysis aid in sustainable energy decision-making. Renew. Sustain. Energy Rev. 2009, 13, 2263–2278. [Google Scholar] [CrossRef]
- Usman, M.; Khan, M.T.; Rana, A.S.; Ali, S. Techno-economic analysis of hybrid solar-diesel-grid connected power generation system. J. Electr. Syst. Inf. Technol. 2018, 5, 653–662. [Google Scholar] [CrossRef]
- Saiprasad, N.; Kalam, A.; Zayegh, A. Techno-economic and environmental analysis of hybrid energy systems for a university in Australia. Aust. J. Electr. Electron. Eng. 2018, 15, 168–174. [Google Scholar] [CrossRef]
- Alharthi, Y.Z.; Siddiki, M.K.; Chaudhry, G.M. Resource Assessment and echno-Economic Analysis of a Grid-Connected Solar PV-Wind Hybrid System for Different Locations in Saudi Arabia. Sustainability 2018, 10, 3690. [Google Scholar] [CrossRef]
- Adewuyi, O.B.; Shigenobu, R.; Senjyu, T.; Lotfy, M.E.; Howlader, A.M. Multiobjective mix generation planning considering utility-scale. solar PV system and voltage stability: Nigerian case study. Electr. Power Syst. Res. 2019, 168, 269–282. [Google Scholar] [CrossRef]
- Konneh, D.A.; Lotfy, M.E.; Shigenobu, R.; Senjyu, T. Optimal Sizing of Grid-connected Renewable Energy System in Freetown Sierra Leone. IFAC-PapersOnLine 2018, 51, 191–196. [Google Scholar] [CrossRef]
- Eichman, J.; Mueller, F.; Tarroja, B.; Smith Schell, L.; Samuelsen, S. Exploration of the integration of renewable resources into California’s electric system using the Holistic Grid Resource Integration and Deployment (HiGRID) tool. Energy 2013, 50, 353–363. [Google Scholar] [CrossRef]
- Yimen, N.; Hamandjoda, O.; Meva’a, L.; Ndzana, B.; Nganhou, J. Analyzing of a Photovoltaic/Wind/Biogas/Pumped-Hydro Off-Grid Hybrid System for Rural Electrification in Sub-Saharan Africa—Case Study of Djoundé in Northern Cameroon. Energies 2018, 11, 2644. [Google Scholar] [CrossRef]
- Ou, T.C.; Hong, C.M. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Divya, S.; Paramathma, M.K.; Sheela, A.; Kumar, S. Dilip. Hybrid renewable energy source optimization using black widow optimization techniques with uncertainty constraints. Meas. Sensors 2024, 31, 100968. [Google Scholar] [CrossRef]
- Hamed, Y.; Mehdi, B.; Mahmood, Y. Techno-economic and environmental design of hybrid energy systems using multi-objective optimization and multi-criteria decision making methods. Energy Convers. Manag. 2023, 282, 116873. [Google Scholar] [CrossRef]
- Batista, N.E.; Carvalho, P.C.M.; Fernández-Ramírez, L.M.; Braga, A.P.S. Optimizing methodologies of hybrid renewable energy systems powered reverse osmosis plants. Renew. Sustain. Energy Rev. 2023, 182, 113377. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y.; Lala, H. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew. Sustain. Energy Rev. 2023, 176, 113192. [Google Scholar] [CrossRef]
- Sarad, B.; Karine, D.; Luis, L.M.; Cécile, P.M. A review on recent standalone and grid integrated hybrid renewable energy systems: System optimization and energy management strategies. Renew. Energy Focus 2023, 46, 103–125. [Google Scholar] [CrossRef]
- Adetoro, S.A.; Olatomiwa, L.; Tsado, J.; Dauda, S.M. Techno-economic and environmental impact assessment of a hybrid renewable energy system employing an enhanced combined dispatch strategy. Green Energy Resour. 2023, 1, 100044. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Lala, H.; Sawle, Y. Techno-economic-environmental analysis of off-grid hybrid energy systems using honey badger optimizer. Renew. Energy 2023, 218, 119247. [Google Scholar] [CrossRef]
- Movahediyan, Z.; Askarzadeh, A. Multi-objective optimization framework of a photovoltaic-diesel generator hybrid energy system considering operating reserve. Sustain. Cities Soc. 2018, 41, 1–12. [Google Scholar] [CrossRef]
- Das, G.; De, M.; Mandal, K.K. Multi-objective optimization of hybrid renewable energy system by using novel autonomic soft computing techniques. Comput. Electr. Eng. 2021, 94, 107350. [Google Scholar] [CrossRef]
- Barakat, S.; Ibrahim, H.; Elbaset, A.A. Multi-objective optimization of grid-connected PV-wind hybrid system considering reliability, cost, and environmental aspects. Sustain. Cities Soc. 2020, 60, 102178. [Google Scholar] [CrossRef]
- Sadeghi, D.; Hesami Naghshbandy, A.; Bahramara, S. Optimal sizing of hybrid renewable energy systems in presence of electric vehicles using multi-objective particle swarm optimization. Energy 2020, 209, 118471. [Google Scholar] [CrossRef]
- Remco, F.; Jenny Lopez, S.S. Barriers and Drivers to Renewable Energy Investment in Sub-Saharan Africa. J. Environ. Investig. 2011, 2, 54–80. [Google Scholar]
- A Framework for Transforming Africa towards a Renewable Energy Powered Future with Access for All. Africa Renewable Energy Initiative (AREI). 2015. Available online: https://www.arei.org (accessed on 10 October 2018).
- Arslan, T.; Bulut, Y.M.; Altın Yavuz, A. Comparative study of numerical methods for determining Weibull parameters for wind energy potential. Renew. Sustain. Energy Rev. 2014, 40, 820–825. [Google Scholar] [CrossRef]
- Lee, N.; Roberts, B. Technical Potential Assessment for the Renewable Energy Zone (REZ) Process: A GIS-Based Approach; National Renewable Energy Laboratory, United State Department of Energy: Golden, CO, USA, 2018. Available online: https://www.nrel.gov/docs/fy18osti/71004.pdf (accessed on 15 October 2018).
- Dorji, G. Environmental Aspect of Electric Energy Generation; Seminar Report; Department of Electrical Engineering, College of Science and Technology: Phuentsholing, Bhutan, 2015. [Google Scholar] [CrossRef]
- Glenting, C.; Jakobsen, N. Converting Biomass to Energy: A Guide for Developers and Investors (English); World Bank Group: Washington, DC, USA, 2017; Available online: http://documents.worldbank.org (accessed on 20 October 2018).
- Adam, B.; Simone, L.E.M.; Sung, J. The Clean Energy Technology Assessment Methodology: International Energy Agency Laboratory; OECD/IEA: Paris, France, 2016; Available online: https://www.iea.org (accessed on 25 October 2018).
- Economic and Financial Analysis Tools: National Renewable Energy Laboratory. Available online: https://www.nrel.gov/analysis/economic-financial-tools.html (accessed on 25 October 2018).
- James, K.; Russell, E. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Y.; Huang, P.; Peng, H.; Wu, Z. A stable-state multi-objective evolutionary algorithm based on decomposition. Expert Syst. Appl. 2024, 239, 122452. [Google Scholar] [CrossRef]
- Zhou, P.; Li, H.; Chai, T. Improved Strength Pareto Evolutionary Algorithm 2 based on grid density search and elite guidance for multi-objective operation optimization of WWTP. Appl. Soft Comput. 2023, 144, 110529. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).