Performance Evaluation and Working Fluid Screening of Direct Vapor Generation for Solar ORC Using Low-Global Warming Potential (GWP) Working Fluids

Abstract

Traditional working fluids used in direct vapor generation for solar organic Rankine cycle (DVG-ORC) systems have a high global warming potential (GWP), making it imperative to find environmentally friendly alternative working fluids for these systems. This paper evaluates the performance of the DVG-ORC system under different operating conditions. By comparing the results of traditional working fluids with those of low-GWP fluids, the feasibility of using low-GWP fluids as alternative working fluids is explored. Additionally, to screen the working fluids suitable for this system further, the system is optimized with net output power as the objective function. The results show that evaporation temperature has different impacts on system performance. R245ca and R1336mzz(Z) exhibit higher net output power at different evaporation temperatures, with R1336mzz(Z) only reducing it by 3.73–5.26% compared to R245ca. However, an increase in condensation temperature negatively affects system performance, leading to a decrease in net output power and various efficiencies. Net output power increases with an increase in mass flow rate, indicating that higher mass flow rates can enhance system performance. The optimization results show that the net output power of low-GWP working fluid R1336mzz(Z) decreases by only 3.44% compared to R245ca, which achieves the maximum net output power. Moreover, among low-GWP working fluids, R1336mzz(Z) demonstrates the highest ORC efficiency and system efficiency, making it the most suitable working fluid for the DVG-ORC system due to its environmental friendliness and safety.

1. Introduction

The increasing demand for energy exacerbates the issues of energy scarcity and environmental pollution [1]. To address this issue, there are two primary approaches. One is to make rational use of existing energy sources and improve their energy utilization efficiency. The other is to develop renewable energy sources and gradually phase out traditional ones [2]. Solar energy, as a renewable energy source, has attracted widespread attention due to its abundant reserves, ease of extraction, and lack of environmental pollution [3]. Solar-powered electricity generation technologies mainly include PV/T generation, traditional ORC generation, direct steam generation, and direct vapor ORC generation.

The efficiency of photovoltaic cells depends on their operating temperature, and an increase in operating temperature will lead to a decrease in their electricity generation [4]. PV/T (photovoltaic–thermal) power generation technology uses collectors to remove some of the heat, which can control the operating temperature of photovoltaic cells to a certain extent [5]. By coupling collectors with other systems, it can improve both the electricity generation efficiency and the overall utilization efficiency of solar energy. However, this technology has the drawbacks of a complex structure, high initial investment, and difficult maintenance [6].

Unlike the Rankine cycle, ORC utilizes organic working fluids with low boiling points, making it suitable for a wide range of medium to low-temperature thermal energy applications [7,8,9]. The use of solar collectors can meet the temperatures required for ORC operation [10,11]. In traditional ORC power generation technology, the heat transfer fluid conveys the heat collected by the solar collector to the ORC working fluid through heat exchange equipment, causing the working fluid to absorb heat and evaporate, thereby performing work [12,13,14,15]. Although ORC power generation technology has the advantages of simple structure, low maintenance requirements, and good thermodynamic performance [16,17], its significant thermal losses during the heat exchange process increase the irreversibility of the system. Additionally, at low mass flow rates, the efficiency of the collector decreases due to the increase in the inlet and outlet temperatures of the heat transfer fluid [18].

Direct steam power generation (DSG) does not utilize heat transfer fluids. Instead, it uses the collector as the evaporator, where the pressurized working fluid from the pump directly enters the collector to absorb heat. After reaching saturated vapor, the fluid enters the expander to produce electricity. This technology eliminates the need for additional heat transfer fluids and heat exchange equipment for heat transfer between the heat transfer fluid and the working fluid, thereby reducing equipment costs [18]. Although this technology was proposed as early as the 1990s and has matured in its applications, in most direct steam power generation systems, water is predominantly used as the working fluid. Within the collector, a certain amount of heat is required to superheat the water to avoid damage to the expander, thereby increasing equipment costs. Additionally, due to the high operating pressure required within the collector (approximately 10 MPa) [19], there are elevated equipment technology requirements.

The structure of a DVG-ORC power generation system is similar to that of DSG. However, unlike the latter, this system can overcome the drawback of high operating pressure in the collector using low-boiling-point organic fluids. Additionally, by selecting appropriate organic dry working fluids, the problem of damage to the expander caused by gas–liquid entrainment within the expander can be avoided. Despite the aforementioned advantages of DVG-ORC power generation, research on it is still relatively limited at present; only a few reports have been published on experimental studies of DVG systems using organic fluid as the working fluid [20,21,22,23]. V.M. Maytorena et al. [24] simulated the heat transfer characteristics of benzene as the working fluid in a DVG-ORC system using PTC. K.E. Dami et al. [25] simulated the performance of a DVG-ORC system with an evacuated tube collector using acetone as the working fluid under different heat flux densities, and the results showed that the system could generate 218 kWh of electricity per year. J. Li et al. [18] proposed a DVG-ORC system with energy storage and investigated the influence of different working fluids on the system efficiency. The results indicated that under the same operating conditions, the system performance was related to the critical temperature of the working fluid. A higher critical temperature of the working fluid resulted in higher thermal efficiency and lower collector efficiency but led to higher overall system efficiency. Among them, R123 exhibited the best overall performance and was deemed the most suitable working fluid for the system. G. Xu et al. [26] evaluated a supercritical DVG-ORC system using a linear Fresnel collector and found that increasing the saturation temperature could improve system efficiency. Cyclohexane demonstrated the highest system efficiency, reaching 19.65%, and also had the highest net power output at higher temperatures, making it considered the most suitable working fluid for the system. M. Marion et al. [27] conducted experimental and simulation studies on a DVG-ORC system using R365mfc as the working fluid. The results showed that solar irradiance, wind speed, and atmospheric temperature significantly impact the optimal output power. J. Z. Alvi et al. [1] analyzed a DVG-ORC system with phase change energy storage and used the finite difference method to perform a 1D simulation of the storage tank to evaluate system performance. The results indicated that among the selected 12 dry or isentropic working fluids, although higher critical temperatures generally resulted in higher system efficiency for most fluids, R245ca and RE245fa2 achieved high system efficiency despite having lower critical temperatures. P. Li et al. [28] proposed a DVG system combining a steam Rankine cycle and an ORC. Four organic fluids were selected as the working fluids for the bottom ORC cycle, and the thermodynamic performance and economic evaluation of the system were conducted. The results showed that when benzene was used as the ORC working fluid, the system achieved the highest efficiency. The proposed system has a shorter equivalent payback period compared to other conventional solar generation systems.

In summary, despite the attractive advantages of DVG-ORC, there is still insufficient research due to limited relevant literature, especially regarding the influence of different operating conditions on system performance. Moreover, most studies have been based on high-GWP working fluids, whose use is restricted by the Kigali Amendment [29]. Given the high heat collection efficiency of PTC and its suitability for DSG [30,31], this paper explores the impact of new low-GWP working fluids on system performance under various operating conditions (including evaporation temperature, condenser temperature, and mass flow rate) using PTC as the solar collector in the DVG-ORC system. Furthermore, it compares them with traditional high-GWP working fluids used in DVG systems to explore their feasibility as alternative working fluids. Subsequently, the optimal working fluid for the system is selected based on the optimization goal of net power output.

2. Methodology

2.1. System Description

Figure 1 shows a schematic diagram of the DVG-ORC system. The system is mainly composed of four components: the parabolic trough collector (PTC), the expander, the condenser, and the working fluid pump. The ORC working fluid is first pressurized by the pump before entering the PTC. The PTC collects solar irradiance heat to provide to the working fluid, heating the pressurized subcooled liquid phase working fluid to a saturated vapor phase within the PTC. The high-pressure vapor phase working fluid at the PTC outlet enters the expander to perform work. After performing the work, the low-pressure saturated vapor phase working fluid enters the condenser and is condensed to a saturated liquid phase by cooling water. It then enters the working fluid pump, thus completing a cycle. To simplify calculations, the following assumptions are made during system operation: pressure losses of the working fluid in the pipeline flow are neglected, the working fluid pressure is assumed to remain constant during the heat exchange process (in the PTC and the condenser), and all system components are assumed to operate under steady-state conditions.

2.2. Working Fluid Selection

Dry working fluids offer superior efficiency compared to wet working fluids and mitigate the risk of expander damage caused by gas–liquid entrainment. Given the high temperatures reached by the PTC, the chosen working fluid must possess a high critical temperature. Additionally, it should be non-flammable or possess low flammability, be non-toxic, and exhibit low ozone depletion potential (ODP) and global warming potential (GWP) to minimize environmental impact. Hence, for this study, the selected working fluids are R1233zd(E), R1336mzz(Z), R1234ze(Z), and R1224yd(Z). Furthermore, to assess the viability of these low-GWP alternatives, traditional high GWP working fluids previously utilized in DVG-ORC systems are also considered for comparative analysis, including R245fa, R113, R245ca, and R123.

Table 1. Properties of the selected working fluids.

Working Fluid	Critical Temperature [°C]	ODP	GWP	Toxicity	Flammability
R1233zd(E)	161.45	0.00034	1	None	None
R1336mzz(Z)	166.35	0	7	-	None
R1234ze(Z)	145.12	0	<1	None	Low
R1224yd(Z)	150.54	0.00023	0.88	None	None
R245fa	148.86	0	1030	None	None
R113	209.06	1.0	6130	Low	None
R245ca	169.42	0	693	-	-
R123	178.681	0.02	77	High	None

shows the selected working fluids and their respective physical properties in this paper.

2.3. Thermodynamic Modeling

To evaluate the system performance of different working fluids, this paper discusses the evaluation criteria of net power output (W_net), ORC efficiency (η_ORC), PTC efficiency (η_PTC), and system efficiency (η_sys). The W_net of the system is calculated by the following [32,33]:

$$W_{net}=W_e-W_p,$$

(1)

$$W_{\mathrm{e}}=m(h_{\mathrm{e},i}-h_{e,o}),$$

(2)

$$W_p=m(h_{p,o}-h_{p,i}),$$

(3)

where W_e and W_p represent the power generated by expander and the power consumed by the pump, m is the mass flow rate of the working fluid, h is the specific enthalpy of the working fluid, and subscripts e and p denote the expander and the pump, while subscripts i and o denote the inlet and outlet points.

The ORC efficiency is calculated by the following:

$${\eta }_{ORC}=\frac{W_{net}}{Q},$$

(4)

$$Q=m(h_{e,i}-h_{p,o}),$$

(5)

where Q represents the heat absorbed by the working fluid in the PTC.

The PTC efficiency is calculated by the following:

$${\eta }_{PTC}=\frac{Q}{G(S_{lp}+S_{tp})},$$

(6)

where G represents solar irradiance, S_lp denotes the area required for the liquid phase region of the working fluid in the PTC, where it absorbs heat from the subcooled liquid phase to the saturated liquid phase, and S_tp represents the area required for the two-phase region of the working fluid in the PTC, where it absorbs heat from saturated liquid phase to saturated vapor phase.

Since the temperature remains constant during the process of the working fluid absorbing heat from the saturated liquid phase to the saturated vapor phase, S_tp can be calculated using the following equation [26]:

$$S_{tp}=\frac{Q_{tp}}{G{\eta }_{PTC,tp}},$$

(7)

$${\eta }_{PTC,tp}={\eta }_{PTC,0}-\frac{A}{G}(T_{eva}-T_0)-\frac{B}{G}{(T_{eva}-T_0)}^2,$$

(8)

where Q_tp represents the heat absorbed by the working fluid in the two-phase region, η_PTC,tp denotes the efficiency of the two-phase region of the PTC, and η_PTC,0 represents the optical efficiency of the PTC, which is taken as 0.661. A and B are the first and second heat loss coefficients, taken as 0.82 W/m²/K and 0.0064 W/m²/K², respectively. T_eva stands for the evaporation temperature of the working fluid, and T₀ is the ambient temperature.

For the liquid phase region of the working fluid, the specific heat capacity of the working fluid can be calculated by linear interpolation due to the small temperature difference between adjacent collectors.

$$C_p(T)=C_{p,eva}+\alpha (T-T_{eva}).$$

(9)

Let c₁ = A/G and c₂ = B/G. The required heating area for the liquid phase region of the working fluid is calculated by the following [18]:

$$S_{lp}=\frac{m}{c_{2}G({\theta }_2-{\theta }_1)}\left[(C_{p,0}+\alpha {\theta }_1)\ln \frac{T_{eva}-T_0-{\theta }_1}{T_{p,o}-T_0-{\theta }_1}+(C_{p,0}+\alpha {\theta }_2)\ln \frac{{\theta }_2-T_{p,o}+T_0}{{\theta }_2-T_{eva}+T_0}\right],$$

(10)

$${\eta }_{PTC,0}-c_1\theta -c_2{\theta }^2=0,$$

(11)

where θ₁ and θ₂ are the arithmetic square roots of Equation (11),respectively, where θ₁ < 0 and θ₂ > 0.

The system efficiency is calculated by the following:

$${\eta }_{sys}={\eta }_{ORC}\cdot {\eta }_{PTC}$$

(12)

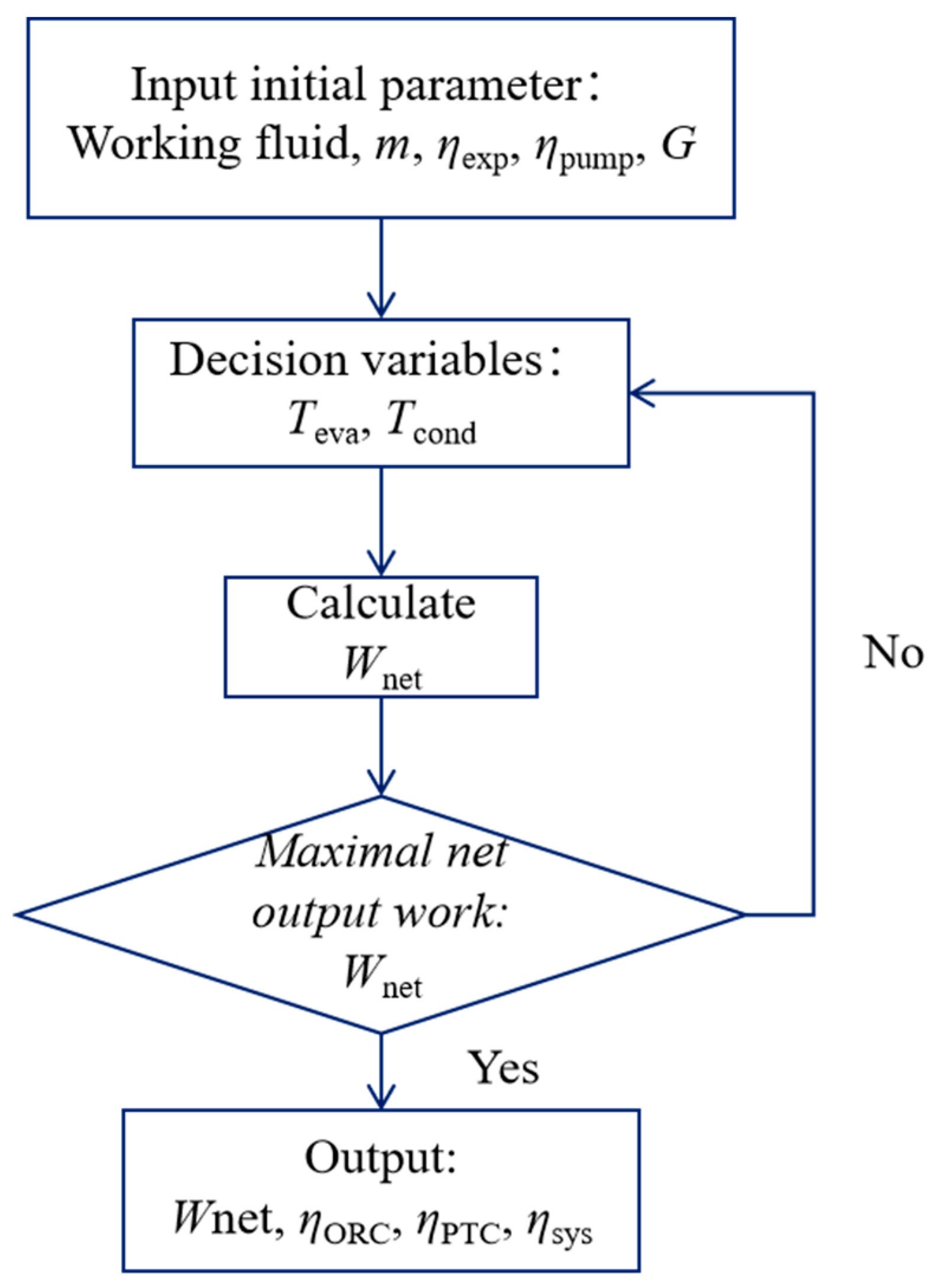
2.4. System Optimization

Figure 2 shows the system optimization flowchart. This optimization targets the W_net of the system, with the evaporation temperature and condensation temperature as decision variables. By inputting initial parameters and calculating the objective function values under different variables, when the objective function value reaches its maximum, the output results (including W_net, η_ORC, η_PTC, and η_sys) are obtained. The fixed parameter values for the optimization process are shown in

Table 2. The fixed parameter values for the optimization process.

Parameter	Value
G	500 W/m2
m	1 kg/s
ηexp	0.75
ηpump	0.65

.

3. Results and Discussion

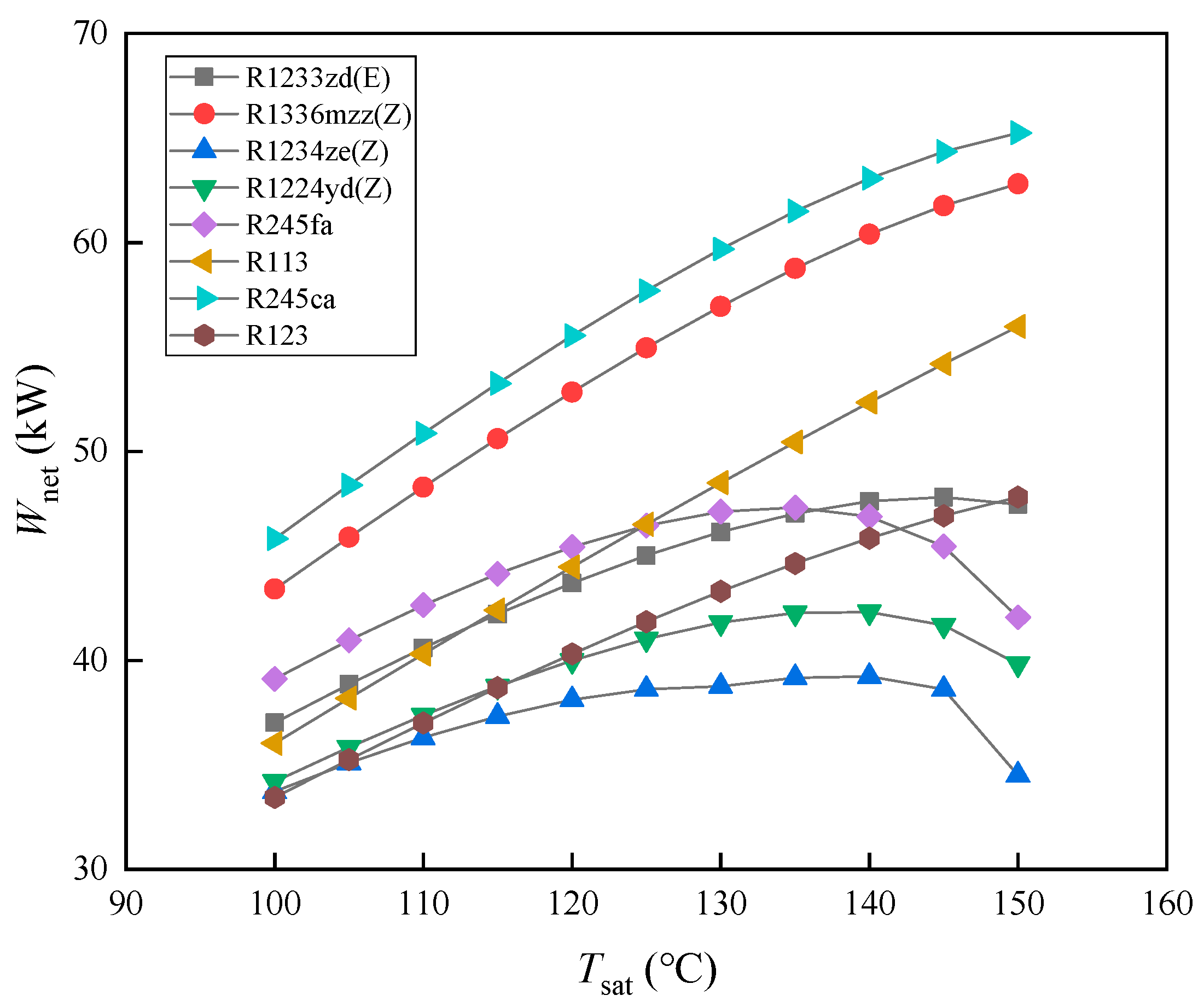
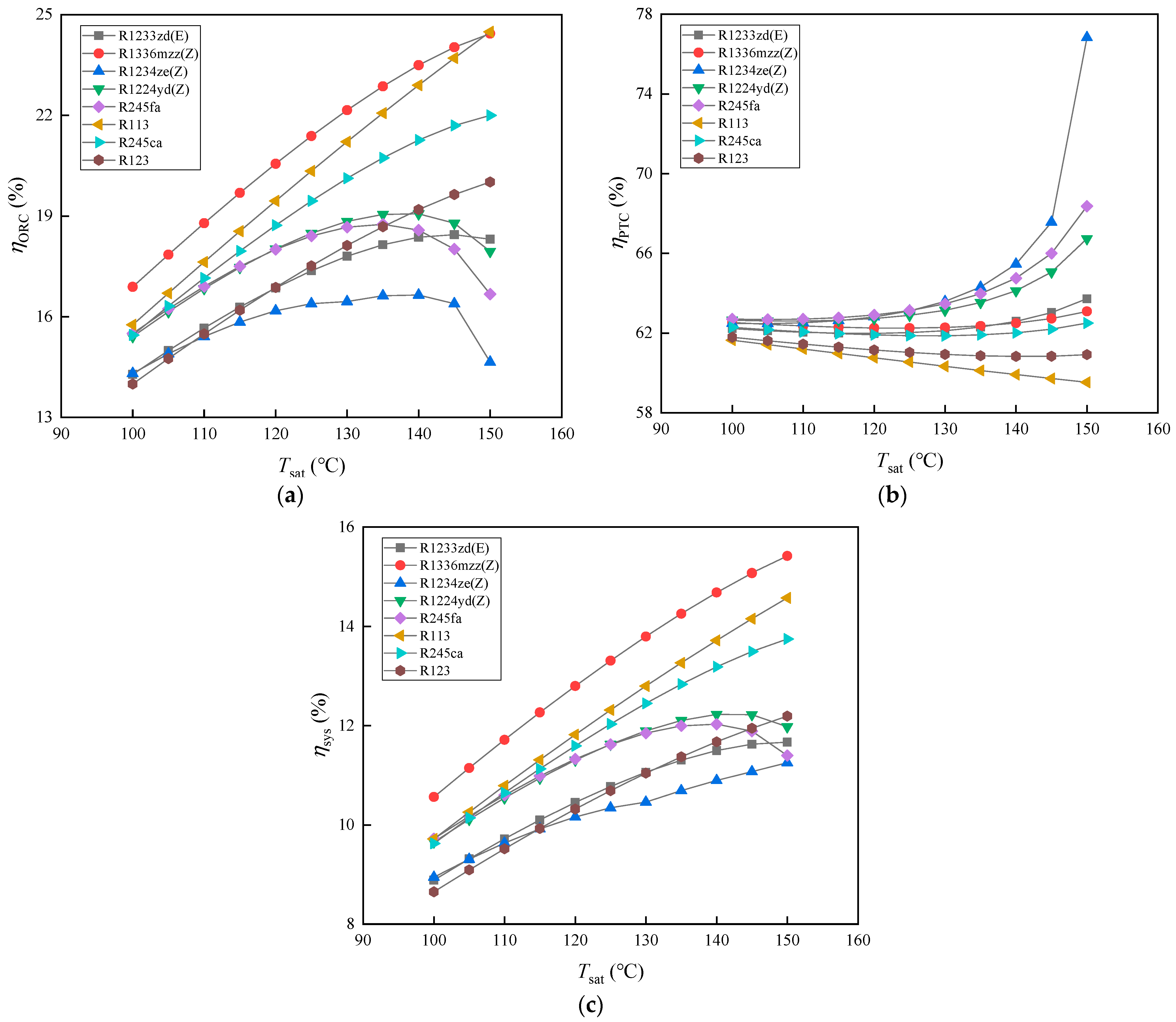
3.1. The Impact of Saturation Temperature on System Performance

Figure 3 illustrates the effect of evaporation temperature on net power output. The results show that the evaporation temperature has different impacts on the net output power of each working fluid, which may be related to the physical properties of the fluids. An increase in evaporation temperature results in more work being carried out by the expander and higher power consumption by the working fluid pump. When the increase in work conducted by the expander is less than the increase in power consumption by the working fluid pump, the net output power decreases. For high GWP working fluids, the net power output of R245fa initially increases with evaporation temperature and then decreases at higher evaporation temperatures, while the net power output of other working fluids increases with the evaporation temperature. Among them, R245ca exhibits the highest net power output at different evaporation temperatures. At lower evaporation temperatures, the net power output of R245fa is only slightly lower than that of R245ca. However, as the evaporation temperature increases, the net power output of R245fa gradually becomes lower than that of R113 and R123.

For low-GWP working fluids, the net power output of R1336mzz(Z) increases with the evaporation temperature, whereas the net power output of other working fluids initially rises with the evaporation temperature but subsequently declines at higher evaporation temperatures. At each evaporation temperature, R1336mzz(Z) demonstrates the highest net power output, trailing only 3.73–5.26% behind R245ca. While R1224yd(Z) and R1234ze(Z) exhibit comparable net power outputs to R123 at lower evaporation temperatures, the disparity between them and R123 widens as the evaporation temperature increases, with R1234ze(Z) registering the lowest net power output at each evaporation temperature.

Figure 4 illustrates the effect of evaporation temperature on the efficiencies of the system. The impact of evaporation temperature on the ORC efficiency of each working fluid shows a trend similar to that of net output power. For working fluids where net output power first increases and then decreases with rising evaporation temperature, ORC efficiency also first increases and then decreases. However, for PTC efficiency, changes in evaporation temperature significantly affect the heat absorption of the working fluid. As the evaporation temperature increases, the heat absorption in the two-phase region decreases. In the single-phase region, due to differences in physical properties, the heat absorption of the working fluid varies, resulting in different impacts of evaporation temperature on PTC efficiency.

The ORC efficiency of R1336mzz(Z) demonstrates a notable increase as the evaporation temperature rises, albeit this upward trajectory gradually plateaus at higher temperatures. Conversely, R113 exhibits the most substantial efficiency boost with increasing evaporation temperature among all considered working fluids. While its efficiency trails that of R1336mzz(Z) at lower temperatures, at 150 °C, R113 outperforms R1336mzz(Z) by 0.22%. Despite yielding a higher net power output, the ORC efficiency of R245ca falls below that of the aforementioned two fluids. Initially comparable to R245ca at lower temperatures, R1224yd(Z) and R245fa witness their ORC efficiencies peaking and then declining as the evaporation temperature rises, eventually trailing behind R245ca, with R245fa slightly lagging R1224yd(Z). Although R123 starts with the lowest ORC efficiency at lower temperatures, its efficiency gradually surpasses that of R1234ze(Z) and R1233zd(E) as the evaporation temperature escalates, with R1234ze(Z) exhibiting the lowest efficiency at higher temperatures.

In terms of PTC efficiency, R113 and R123 exhibit a consistent decrease with increasing evaporation temperature, with R113 recording the lowest efficiency and R123 slightly ahead. Conversely, the PTC efficiencies of other fluids demonstrate a declining trend followed by an increase as the evaporation temperature rises. Notably, R1234ze(Z), R245fa, and R1224yd(Z) show significant increases, with their PTC efficiencies climbing by 22.94%, 9.02%, and 6.54%, respectively, as the evaporation temperature rises.

In terms of system efficiency, R1336mzz(Z) stands out with the highest performance, owing to its superior ORC and PTC efficiencies. Although R113 achieves peak ORC efficiency at 150 °C, its lower PTC efficiency translates to inferior system efficiency compared to R1336mzz(Z). The efficiency trends of most working fluids mirror their ORC efficiency shifts with evaporation temperature, displaying either a steady increase or an initial rise followed by a decline. However, R1234ze(Z) diverges in system efficiency from its ORC efficiency trend; instead of decreasing at higher temperatures, it steadily ascends with rising evaporation temperature, attributed to its heightened PTC efficiency in those conditions. Nonetheless, its lower ORC efficiency keeps the system efficiency of R1234ze(Z) comparatively modest.

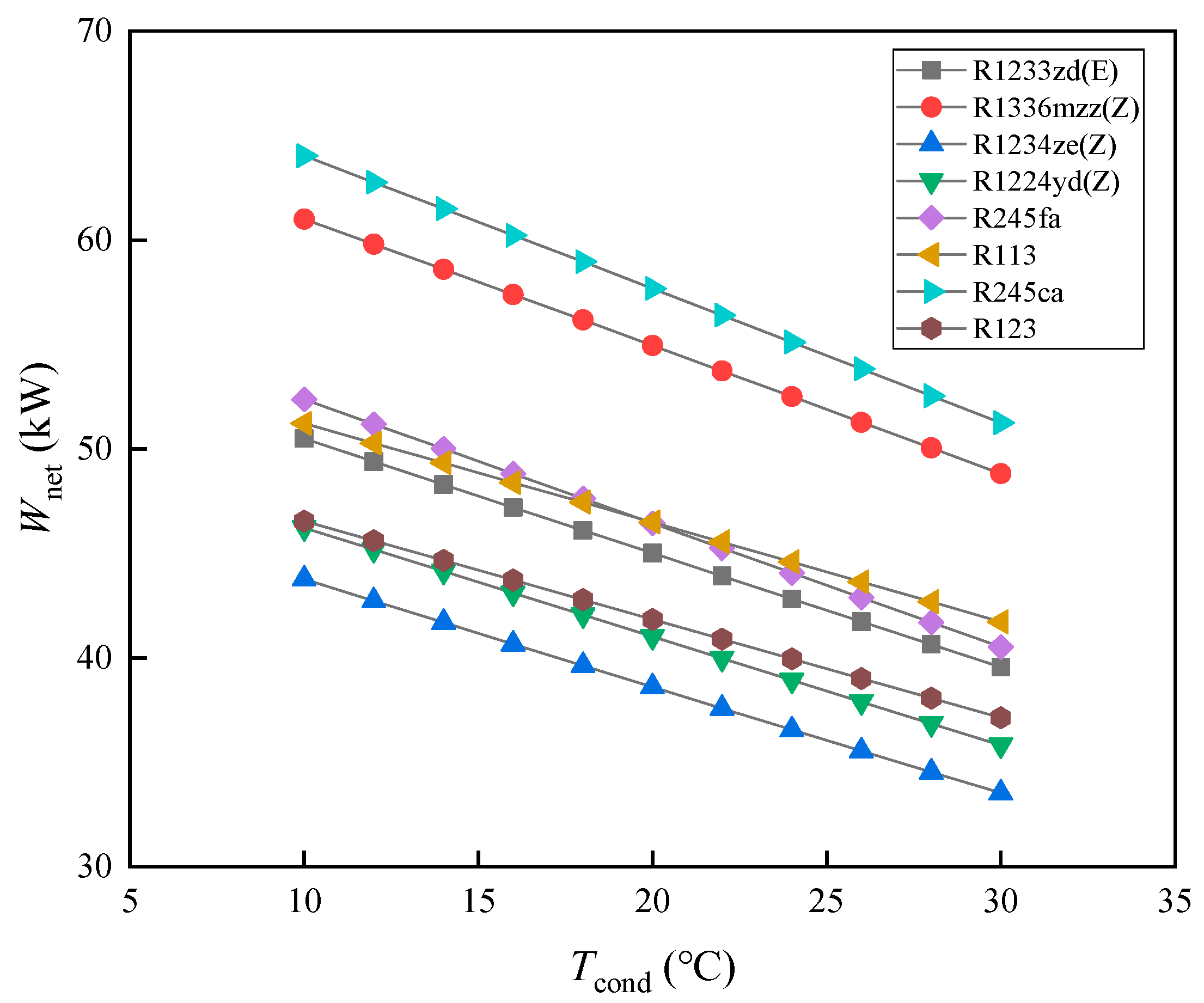
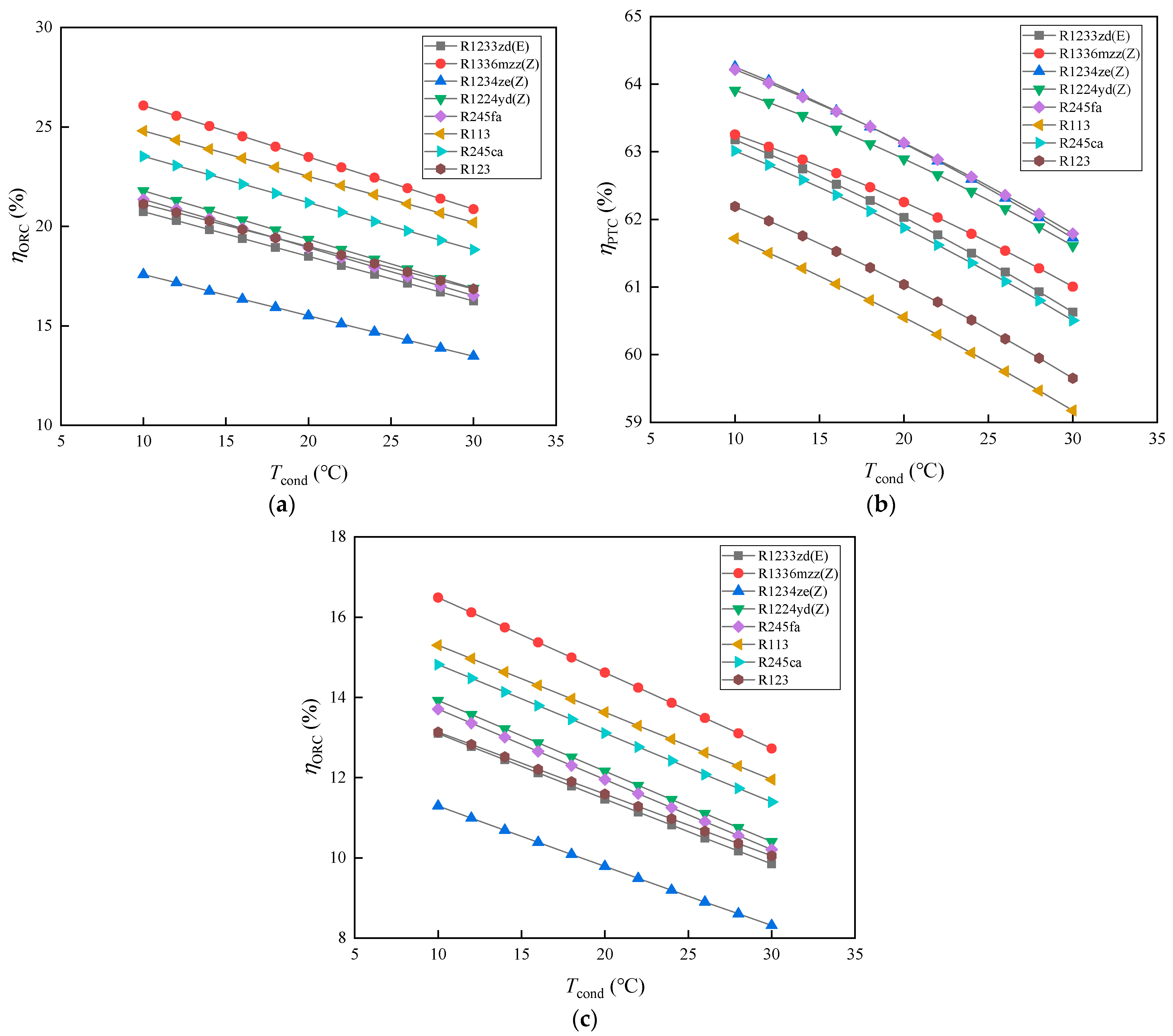
3.2. The Impact of Condensation Temperature on System Performance

Figure 5 illustrates the effect of condensation temperature on net output power. The net output power of each working fluid decreases as the condensation temperature rises. This is because an increase in condensation temperature leads to higher temperatures at the inlet of the working fluid pump and the outlet of the expander. According to Equations (1)–(3), this phenomenon results in an increase in power consumption of the working fluid pump and a decrease in work carried out by the expander, thereby reducing the net output power. Therefore, an increase in condensation temperature has a negative effect on net output power. Among them, R245ca, as a high GWP working fluid, exhibits the highest net output power. For R1336mzz(Z), a low-GWP working fluid, the net output power is slightly lower than that of R245ca, with a reduction of only 4.73% to 4.75% compared to R245ca. R1234ze(Z) has the lowest net output power. R245fa shows higher net output power than R113 at lower condensation temperatures; however, due to the significant impact of condensation temperature, its net output power is lower than that of R113 at higher condensation temperatures.

Figure 6 illustrates the effect of condensation temperature on the various efficiencies of the system. All efficiencies decrease as the condensation temperature rises, indicating a negative impact of increasing condensation temperature on system performance. This is because an increase in condensation temperature leads to higher temperatures at the inlet of the working fluid pump and the outlet of the expander. According to Equations (1)–(3), this phenomenon results in an increase in power consumption of the working fluid pump and a decrease in work carried out by the expander, thereby reducing the net output power. Therefore, an increase in condensation temperature has a negative effect on net output power. It is worth noting that although working fluids with higher ORC efficiency may have lower PTC efficiency, the order of system efficiency values for each working fluid aligns with the order of ORC efficiency values. The sequence is as follows: R1336mzz(Z) > R113 > R245ca > R1224yd(Z) > R123 > R245fa > R1233zd(E) > R1234ze(Z). Considering that, ORC efficiency may have a significant impact on system efficiency at different condensation temperatures.

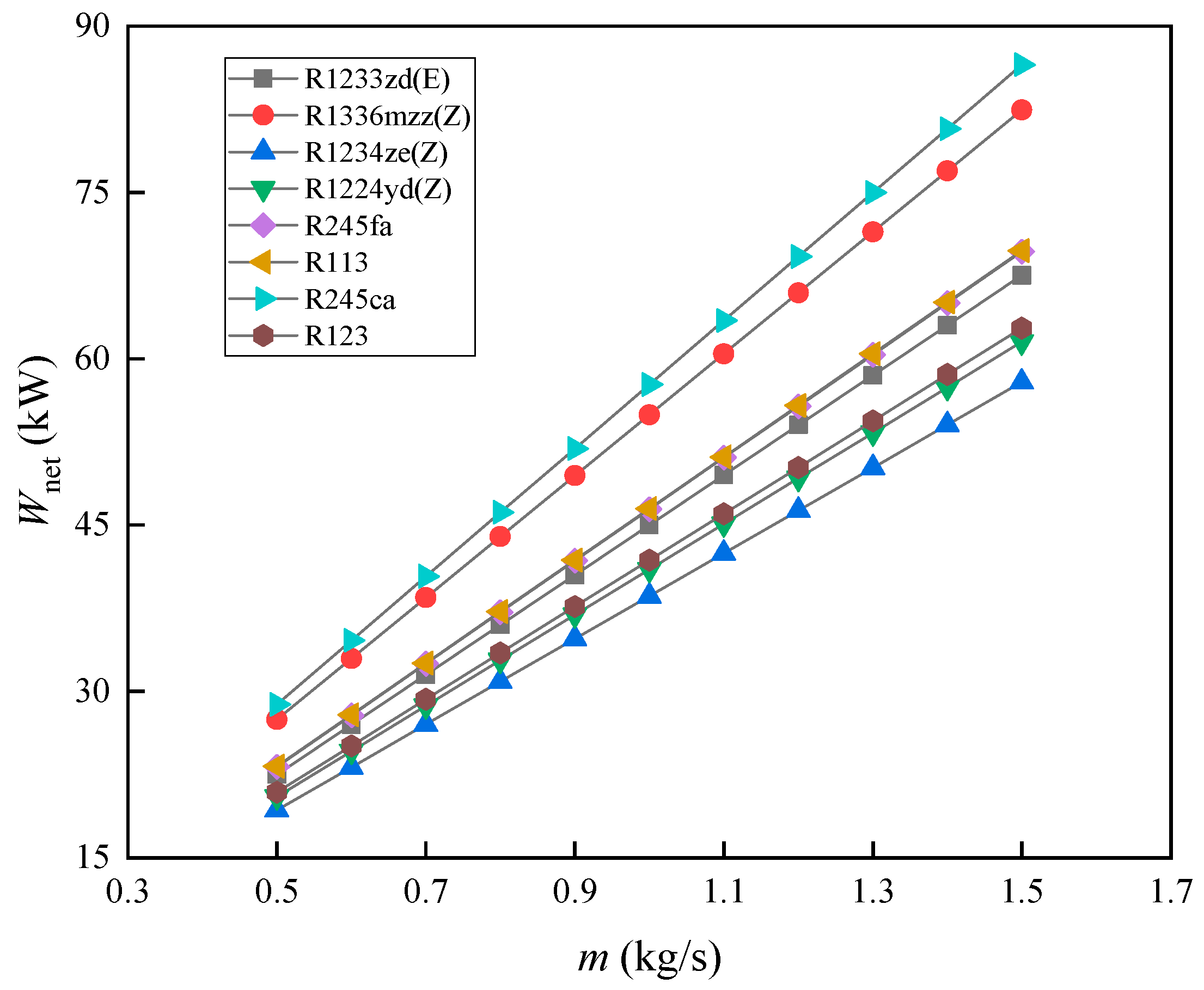
3.3. The Impact of Mass Velocity on System Performance

The thermodynamic performance calculation model presented in Section 2 reveals that variations in mass flow rate have no impact on ORC efficiency and PTC efficiency. Therefore, only changes in the mass flow rate’s influence on net output power are considered, as depicted in Figure 7. The findings indicate that increasing the mass flow rate correlates with a rise in net output power. Among the studied fluids, R245ca boasts the highest net output power, closely followed by R1336mzz(Z). R245fa and R113 exhibit comparable net output power, while R123 and R1234ze(Z) register the lowest net output power among both high and low-GWP working fluids, respectively.

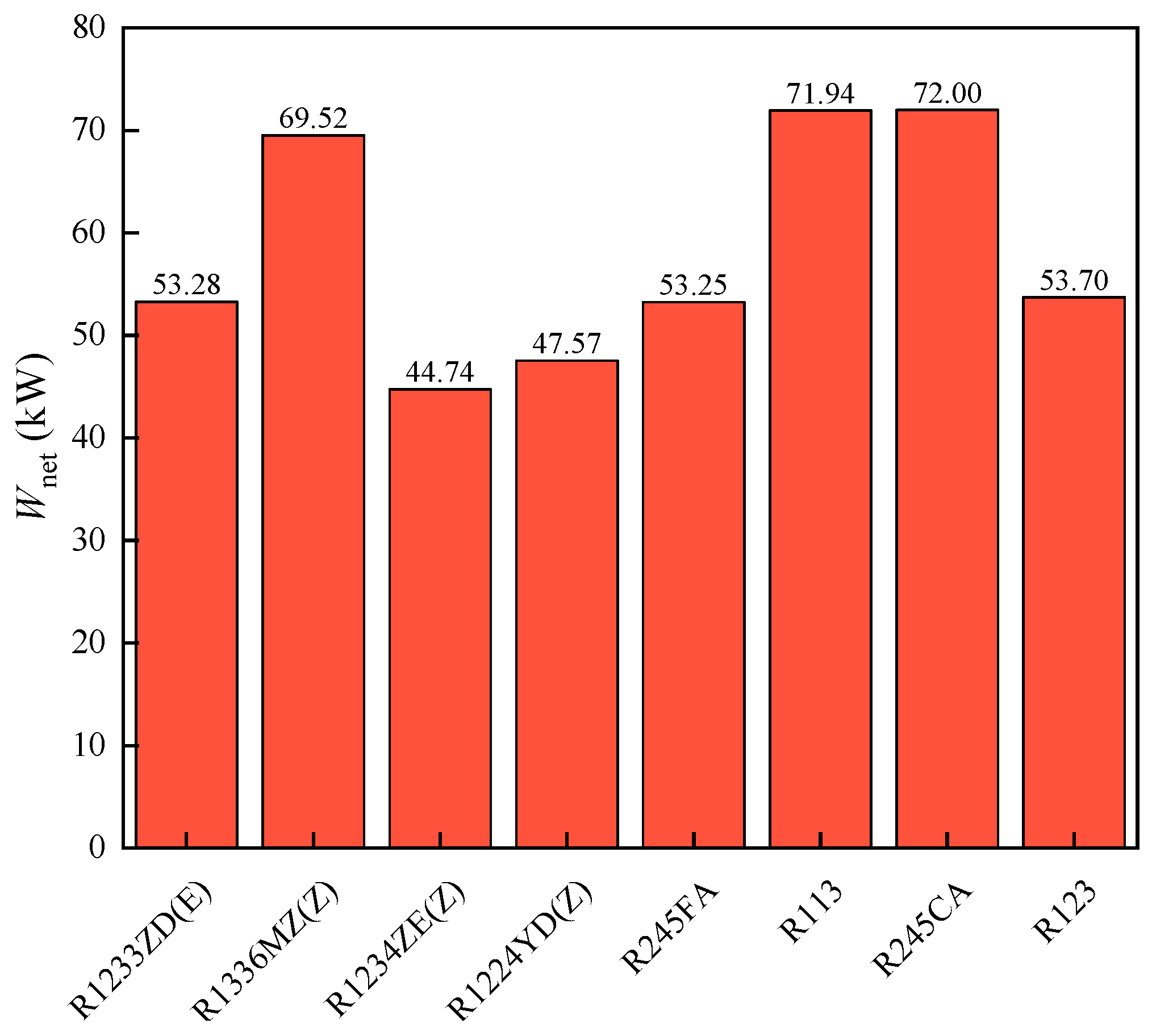
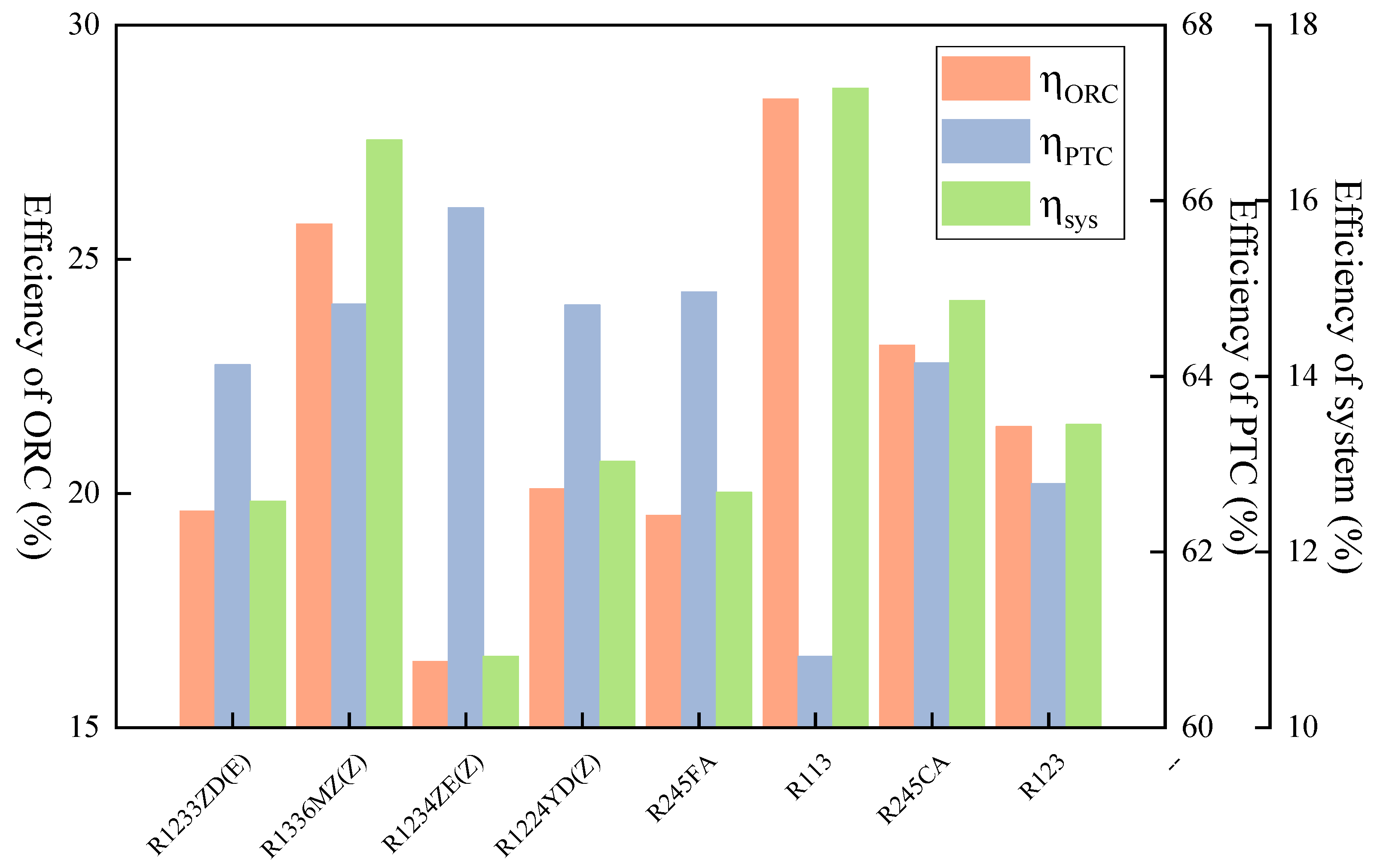
3.4. Results of Optimization

To further screen for the optimal working fluid for the system, the system was optimized with net output power as the objective. Taking into account the influence of the aforementioned different operating parameters on system performance, this optimization process selects the evaporation and condensation temperatures as optimization variables, with the output result being the optimal net output power. Simultaneously, the optimization results consider W_net as the objective, and the environmental performance of the working fluid serves as the screening criteria for the selection of the working fluid. The optimization results are shown in Figure 8. Among them, R113 and R245ca exhibit higher net output power. However, due to their high GWP, they have a negative environmental impact. Among the low-GWP working fluids, R1336mzz(Z) demonstrates the optimal net output power, being only 3.44% lower than the highest net output power obtained by R245ca. To observe the other system performance under the operating conditions corresponding to the optimization results for each working fluid, Figure 9 illustrates the system efficiencies based on the optimization results. Despite R245ca having the highest net output power, its system efficiency is relatively low. Among low-GWP working fluids, R1336mzz(Z) not only has higher net output power but also exhibits the highest ORC efficiency. Although its PTC efficiency is slightly lower than that of R1234ze(Z), it achieves the highest system efficiency. Additionally, due to its good environmental and safety characteristics (as shown in Table 1), it can be considered the most suitable working fluid for the DVG-ORC system.

4. Conclusions

This study, based on the DVG-ORC system using PTC, investigated the impact of low-GWP working fluids on system performance under different evaporating temperatures, condensing temperatures, and mass flow rates, with net output power, ORC efficiency, PTC efficiency, and system efficiency as evaluation metrics. A comparison was made with traditional high GWP working fluids used in DVG systems to explore their feasibility as alternative working fluids. Subsequently, optimal working fluids suitable for the system were selected with net output power as the optimization objective. The conclusions are as follows:

• R245ca and R1336mzz(Z), as high- and low-GWP working fluids, respectively, exhibit high net output power at different evaporating temperatures. R1336mzz(Z) reduces net output power by only 3.73–5.26% compared to R245ca. At lower evaporating temperatures, R1336mzz(Z) has the highest ORC efficiency, but at 150 °C, R113’s ORC efficiency is 0.22% higher than that of R1336mzz(Z). However, R1336mzz(Z) achieves the highest system efficiency due to its higher PTC efficiency.
• The performance of each working fluid decreases with increasing condensing temperature, indicating the negative impact of higher condensing temperatures on system performance. R1336mzz(Z) has a net output power slightly lower than R245ca, decreasing only by 4.73–4.75%. Although working fluids with higher ORC efficiency may have lower PTC efficiency, the ranking of system efficiency values for each working fluid is the same as that of ORC efficiency values. Considering that, ORC efficiency may have a significant impact on system efficiency at different condensing temperatures.
• Changes in mass flow rate do not affect the efficiency of the system. The net output power of each working fluid increases with increasing mass flow rate. R1336mzz(Z) has a net output power slightly lower than R245ca. Moreover, R1234ze(Z) has the lowest net output power.
• Optimization results based on net output power as the objective show that the net output power of low-GWP working fluid R1336mzz(Z) is only 3.44% lower than that of R245ca, which yields the maximum net output power. Additionally, among low-GWP working fluids, R1336mzz(Z) has the highest ORC efficiency and system efficiency. Due to its good environmental and safety characteristics, it can be considered the most suitable working fluid for the DVG-ORC system.