A Wind Power Fluctuation Smoothing Control Strategy for Energy Storage Systems Considering the State of Charge
Abstract
1. Introduction
- (1)
- We have constructed a system model for smoothing wind power fluctuations using a BESS based on MPC. We propose an objective function aimed at minimizing the deviation of grid-connected power from the target power and the deviation of the residual capacity of the BESS from the ideal value in the wind storage cogeneration system. This objective function comprehensively considers the smoothing effect of the BESS while preventing SOC from overrunning the limit and entering the dead zone.
- (2)
- We propose a method for adjusting the BESS’s charging and discharging power using two-layer fuzzy control rules. By integrating the smoothing effect and SOC interval division, we employ the first layer of fuzzy control rules to dynamically adjust the weight coefficients of the objective function in real time. This enhancement improves the BESS’s ability to smooth wind power fluctuations while preventing SOC from exceeding the limit and entering the dead zone. Additionally, the second layer of fuzzy control rules is utilized to proactively adjust the BESS’s charging and discharging power, thereby enhancing its ability to smooth future wind power fluctuations.
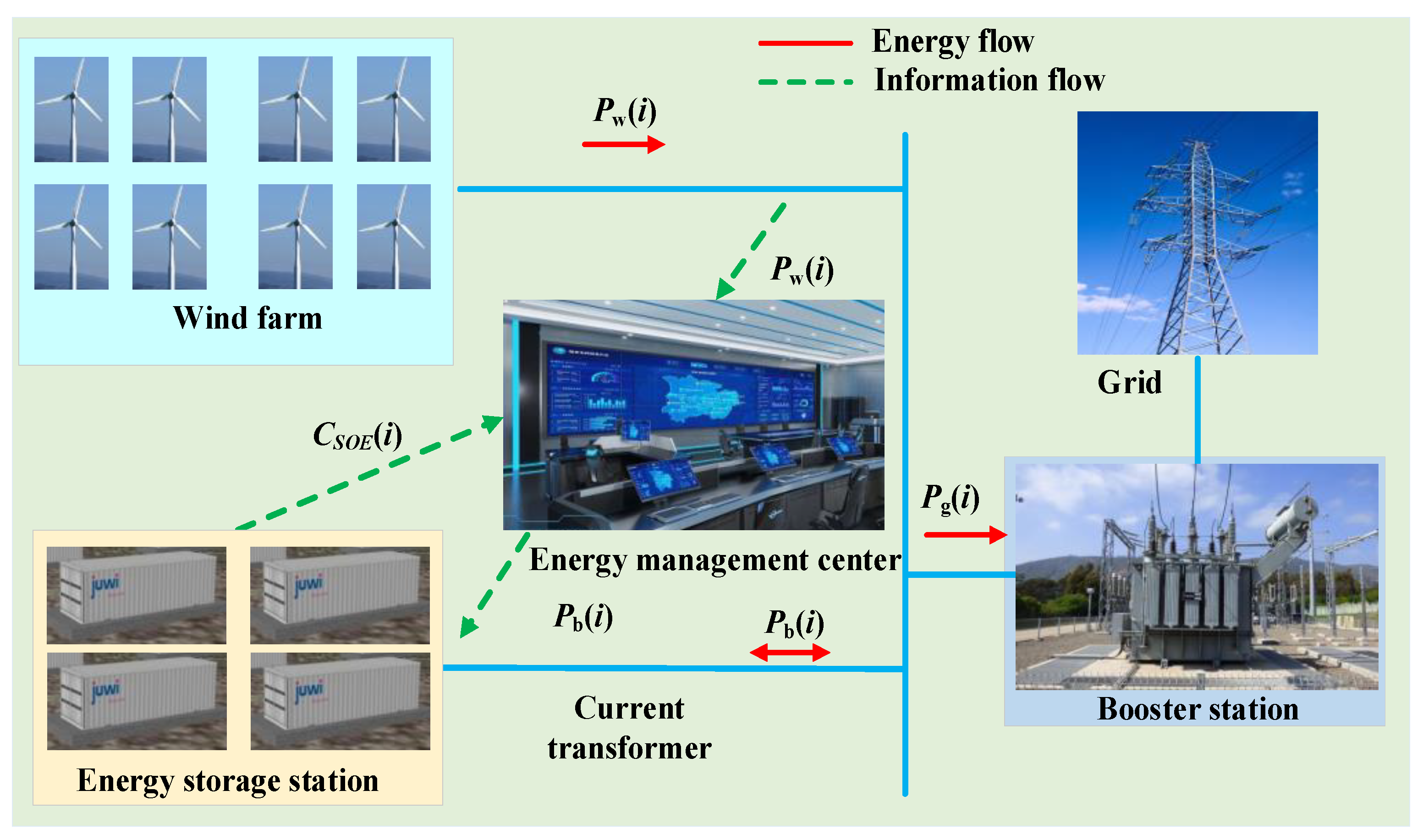
2. Wind Storage Cogeneration System and Power Relation
2.1. Wind Storage Cogeneration Systems and Grid-Connected Power Fluctuation Requirements
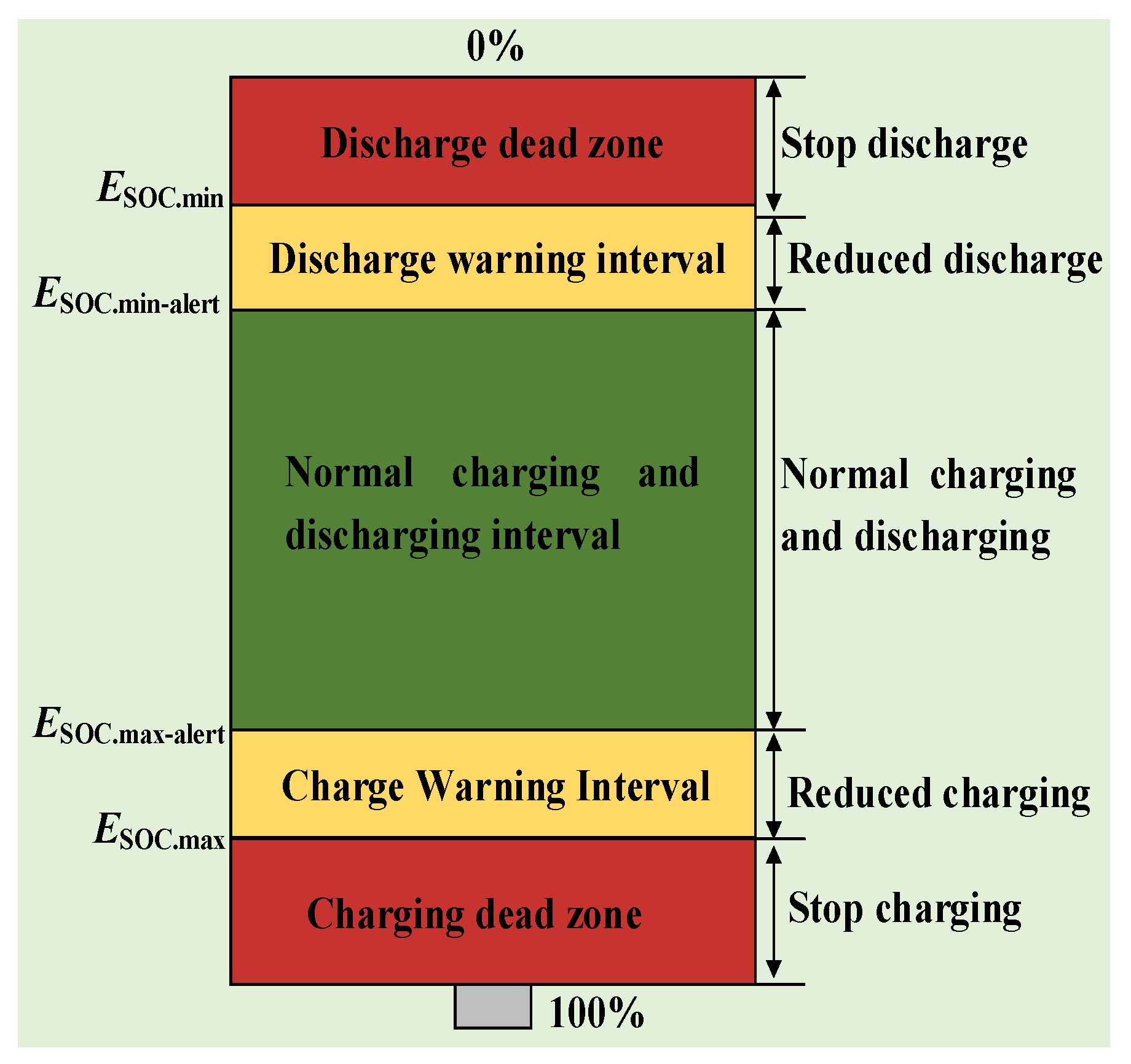
2.2. SOC Partitioning for BESS
- (1)
- Discharge dead zone [0%, ESOC.min]: This interval indicates that the SOC of the BESS is critically low, nearing complete depletion. In this interval, the BESS cannot discharge further and should not be permitted. Immediate charging is necessary to prevent prolonged depletion, which could compromise the battery’s lifespan.
- (2)
- Discharge warning interval [ESOC.min, ESOC.min-alert]: This interval indicates that the SOC of the BESS is low and has surpassed the overdischarge warning threshold. During this phase, discharge operations must be conducted cautiously to prevent the SOC from entering the discharge dead zone.
- (3)
- Normal charging and discharging interval [ESOC.min-alert, ESOC.max-alert]: This interval indicates a favorable SOC range for the BESS. In this interval, the SOC of the BESS is considered healthy, allowing for a margin of capacity for charging and discharging operations.
- (4)
- Charge warning interval [ESOC.min-alert, ESOC.max]: This interval indicates that the SOC of the BESS is high and has surpassed the overcharging warning threshold. During this phase, charging operations must be performed cautiously to prevent the SOC from entering the charging dead zone.
- (5)
- Charging dead zone [ESOC.max, 100%]: This interval indicates that the SOC of the BESS is excessively high, nearing theoretical full charge. In this interval, the BESS loses its charging capability and must not undergo further charging. Immediate discharge is necessary to prevent prolonged full charge, which could significantly impact the service life of the energy storage battery.
3. BESS Smoothing Wind Power Fluctuation Model Based on MPC
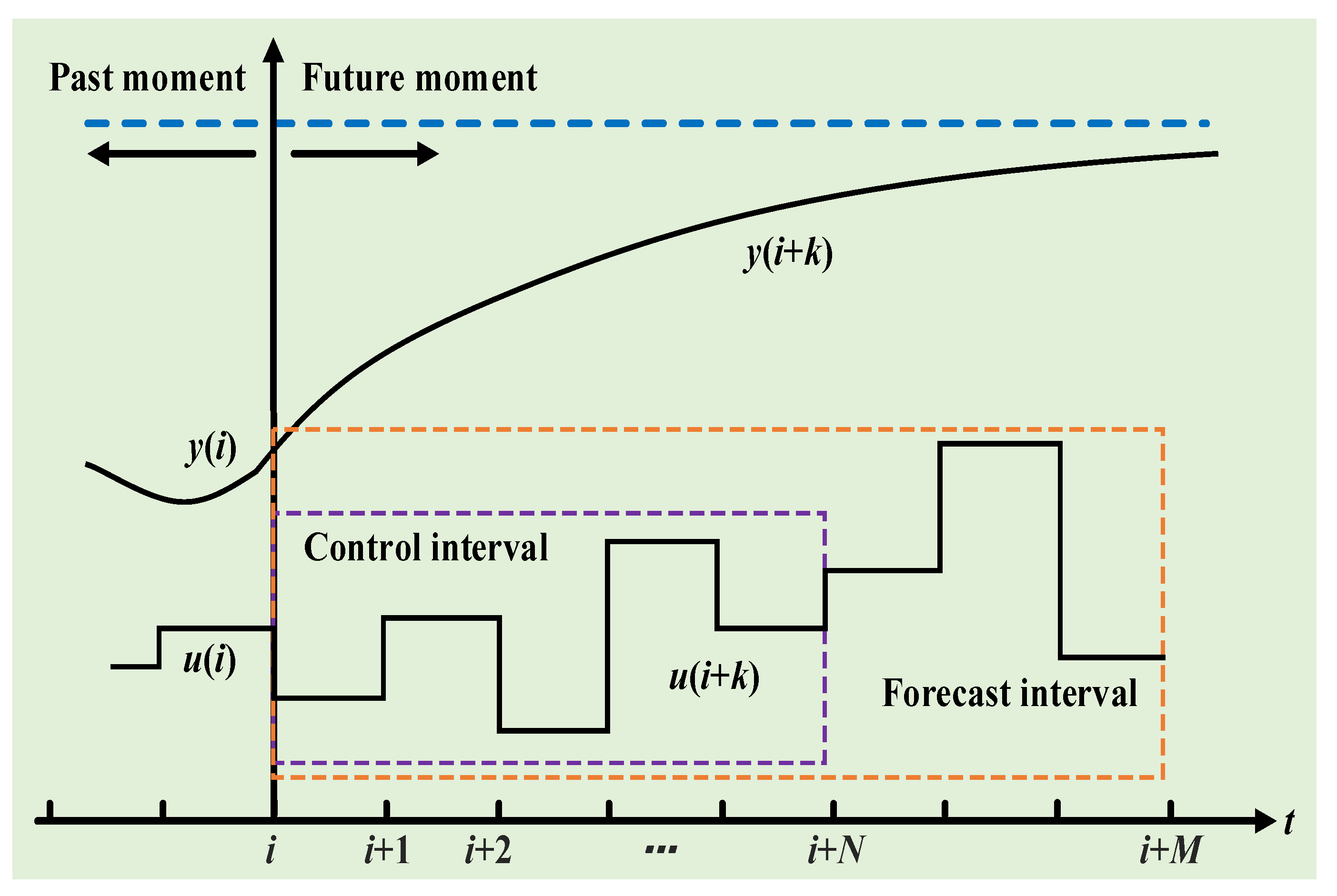
3.1. Fundamentals of the MPC Algorithm
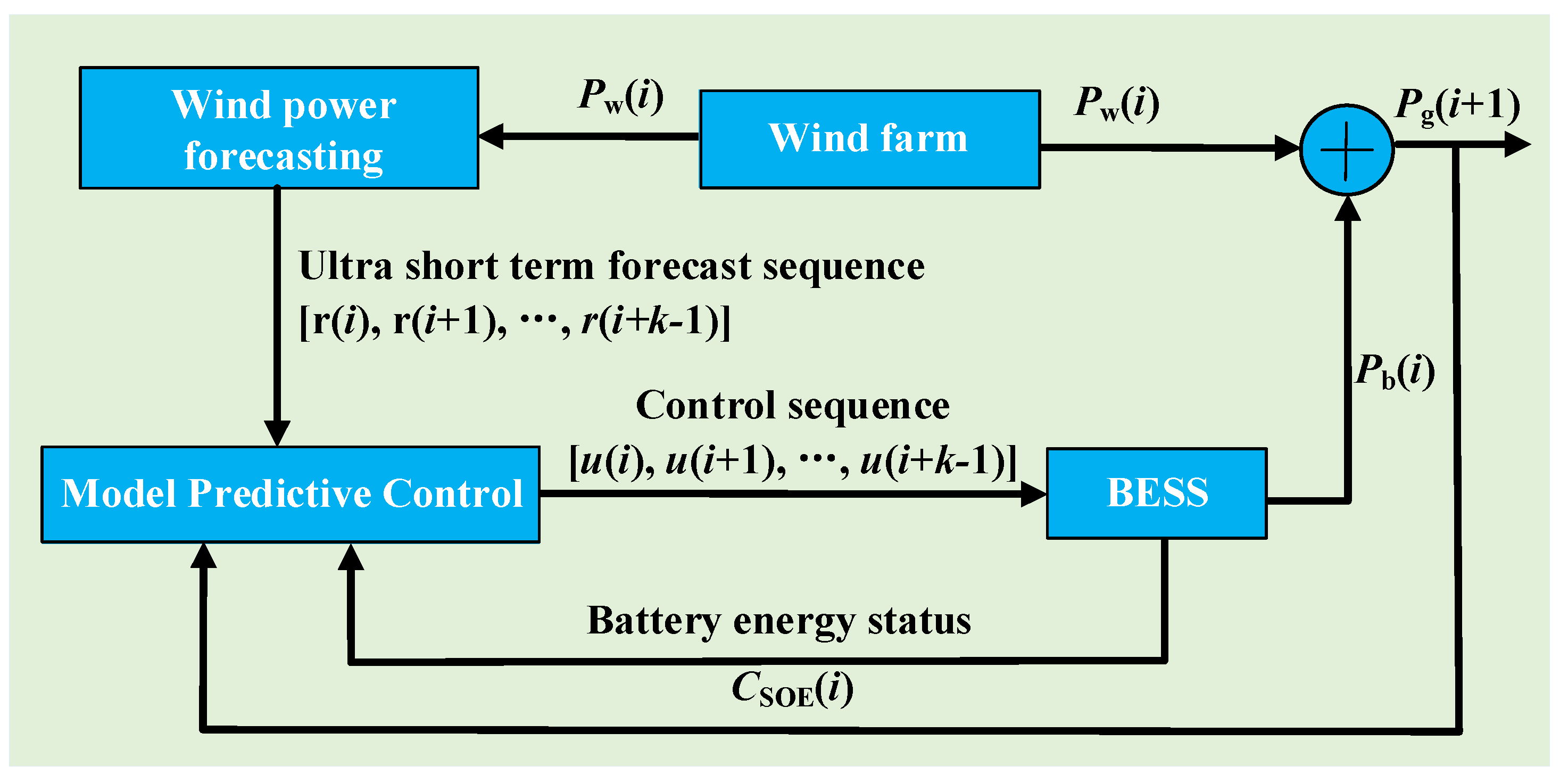
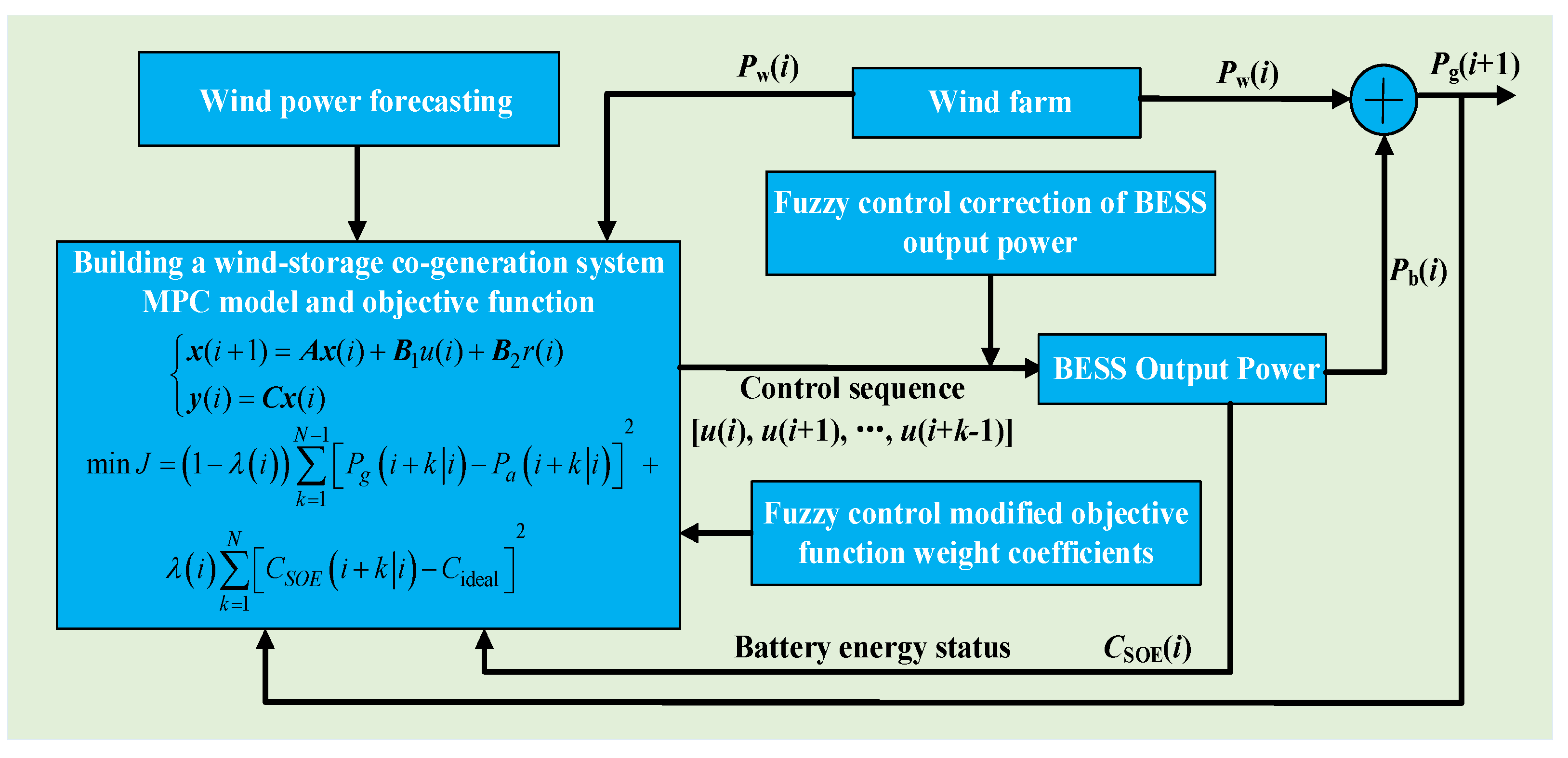
3.2. MPC-Based Wind Storage Cogeneration System
3.3. Objective Function and Constraints
- (1)
- BESS power constraints
- (2)
- BESS capacity constraints
4. Charging and Discharging Power Correction for BESS Based on Two-Layer Fuzzy Control
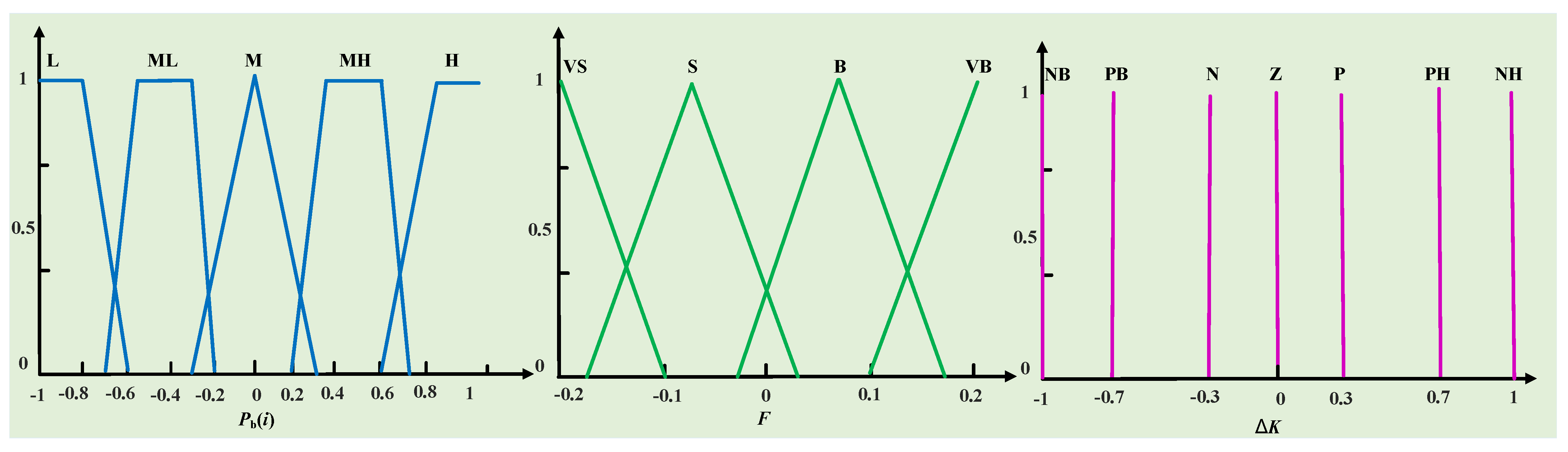
4.1. Single-Layer Fuzzy Control Strategy
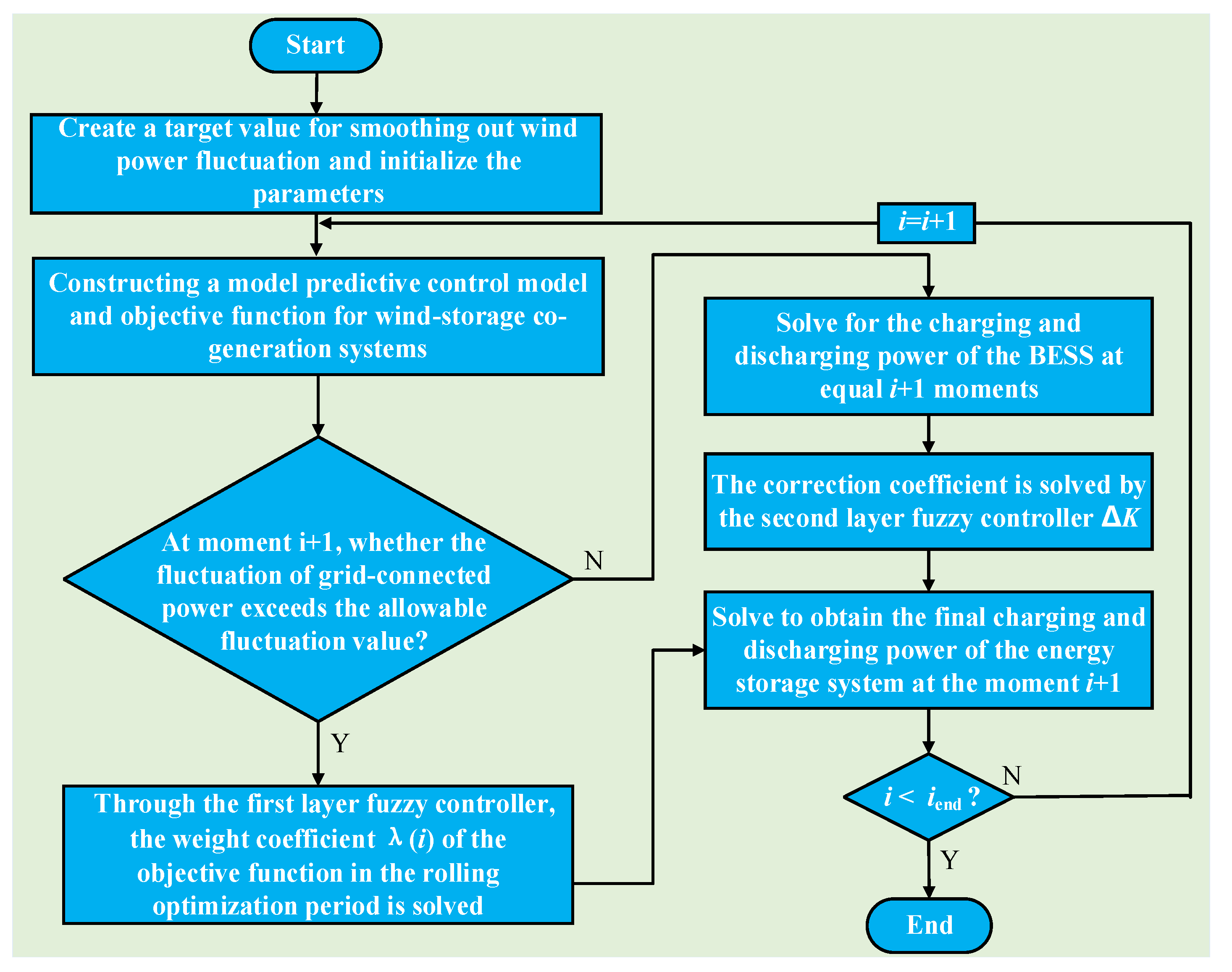
4.2. Two-Layer Fuzzy Control Strategy
- Step 1:
- Establish a target value for smoothing wind power fluctuations and initialize the parameters.
- Step 2:
- The MPC model for the wind storage cogeneration system is established with the short-term predicted wind power as the input variable, the future finite time domain’s incremental storage active power as the control variable, the current output power of the storage system as the initial value, and the grid-connected power and remaining capacity of the storage system as the output variables.
- Step 3:
- Define the objective function incorporating the deviation of the energy storage system’s remaining capacity from the ideal value and minimizing the difference between the grid-connected power and the target power. Establish the necessary constraints.
- Step 4:
- Check if the grid-connected power at time i + 1 surpasses the permissible fluctuation value. If it does not, proceed directly to step 6; otherwise, move to step 5.
- Step 5:
- The objective function’s weight coefficient λ(i) is adjusted using the first layer fuzzy controller.
- Step 6:
- The second layer of the fuzzy controller is employed to rectify the BESS output power.
- Step 7:
- Optimize the sequence of control variables within the constraint of N future periods using the CPLEX solver.
- Step 8:
- Extract the first control variable and compute the BESS power at time i + 1, along with the corresponding output in the model.
- Step 9:
- Compute the BESS power for i + 1 moments.
- Step 10:
- Utilize the actual output of the BESS at time i + 1 as the initial value for the optimization model. Then, return to step 2 and iterate through the rolling optimization process until completion.
5. Algorithm Analysis
5.1. Evaluation Index
- (1)
- Average absolute value of power fluctuation ∆Pg.mean.
- (2)
- BESS enters dead time Td.
- (3)
- BESS output capacity evaluation coefficient Cb.
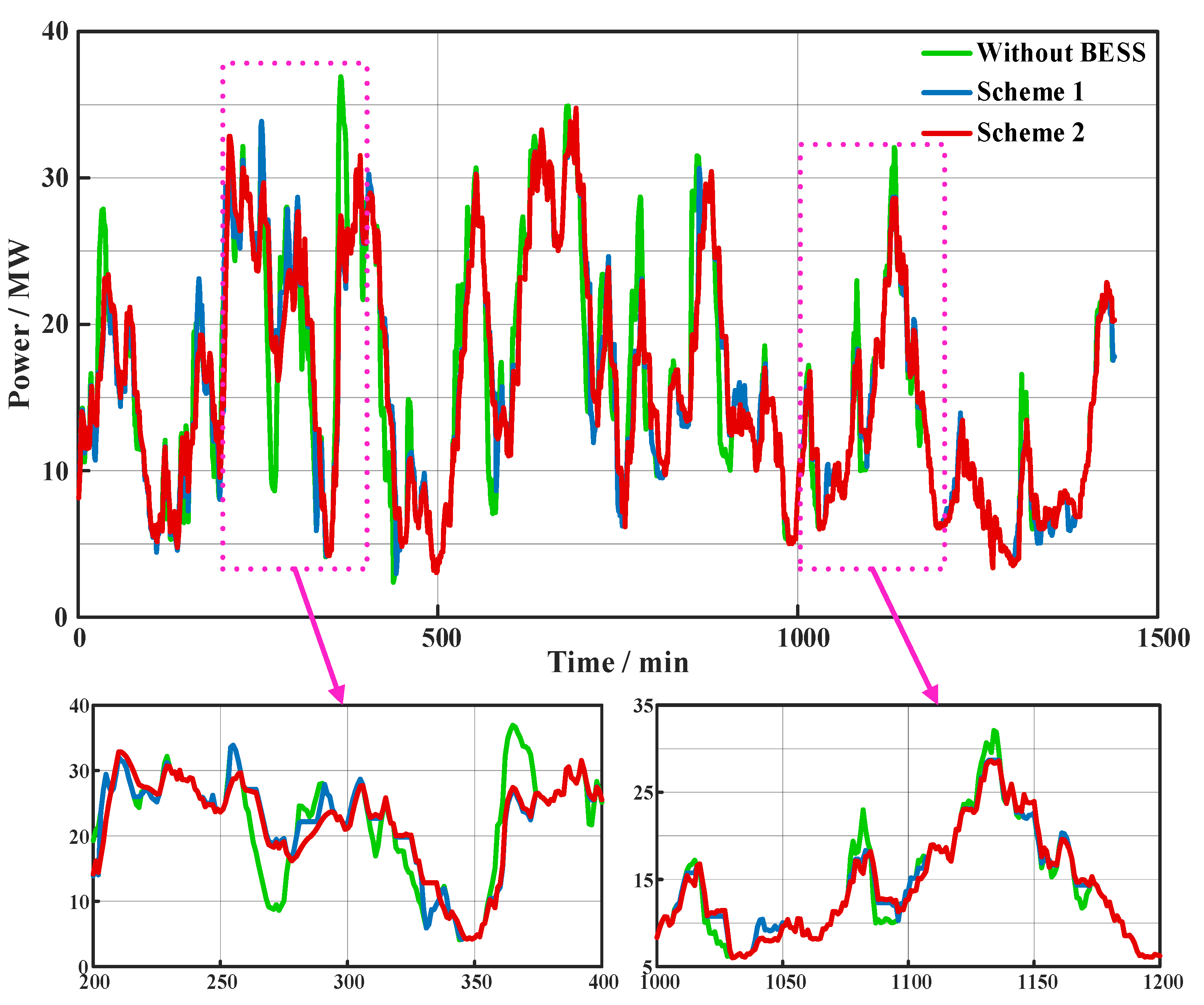
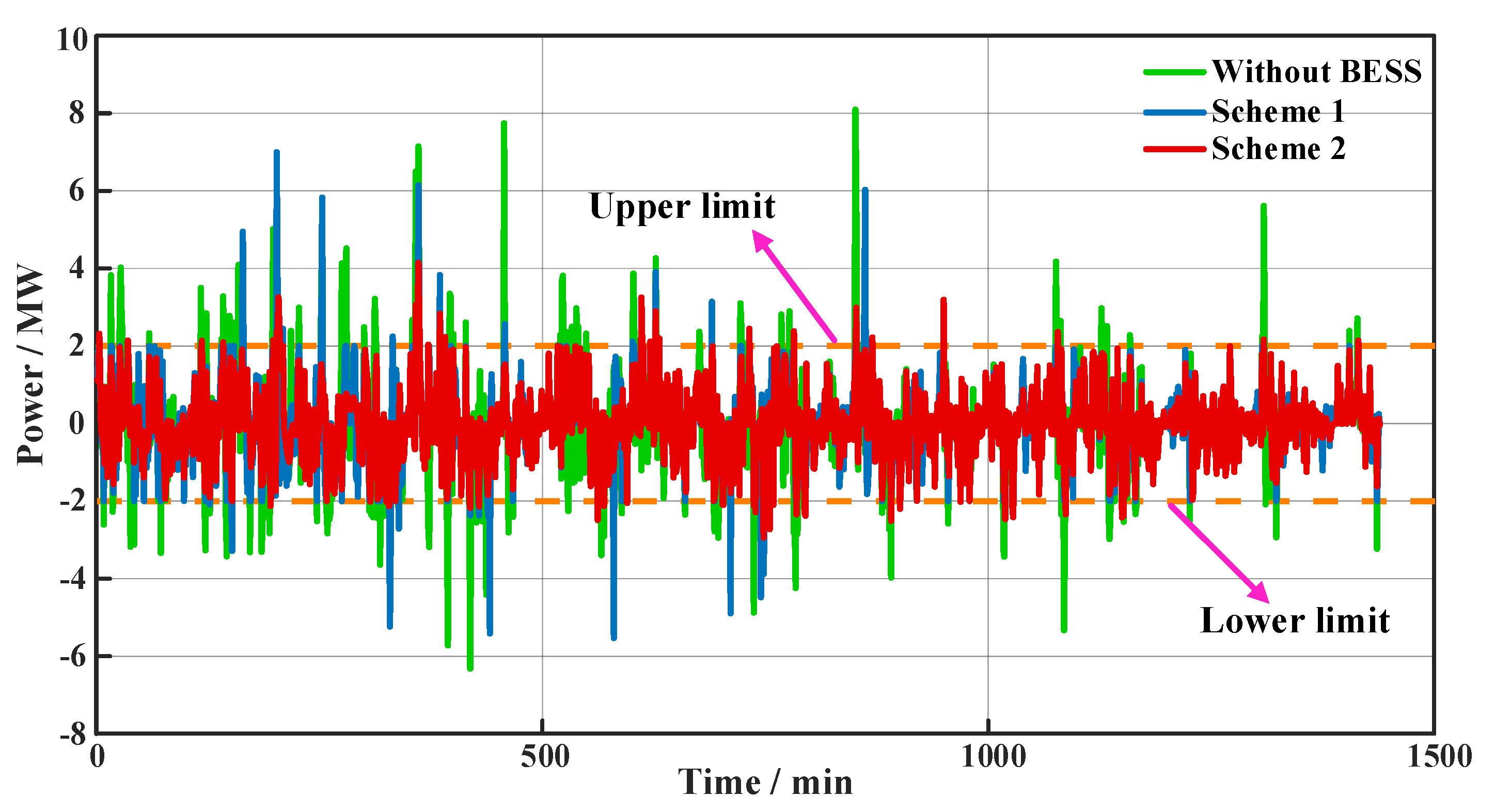
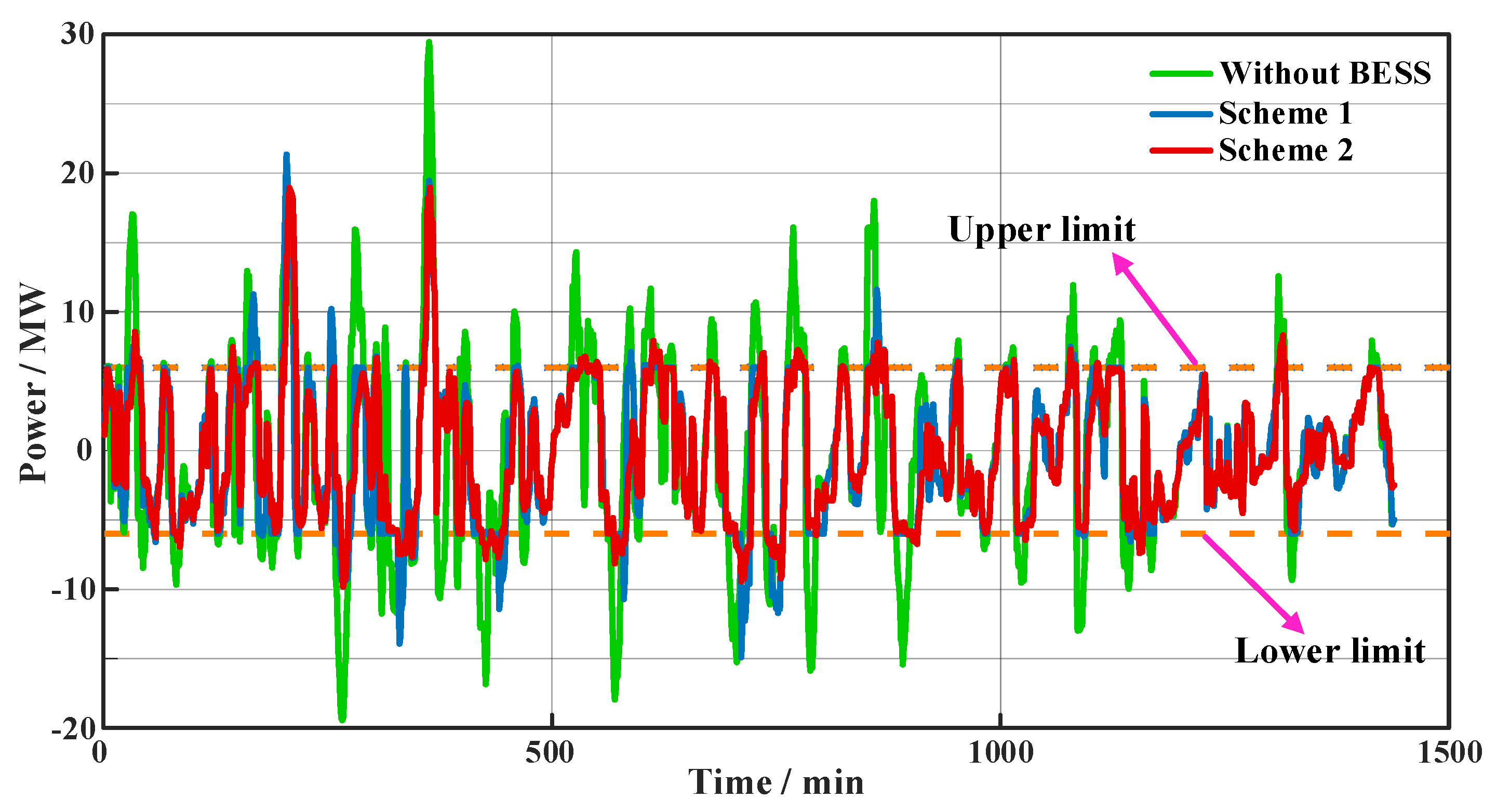
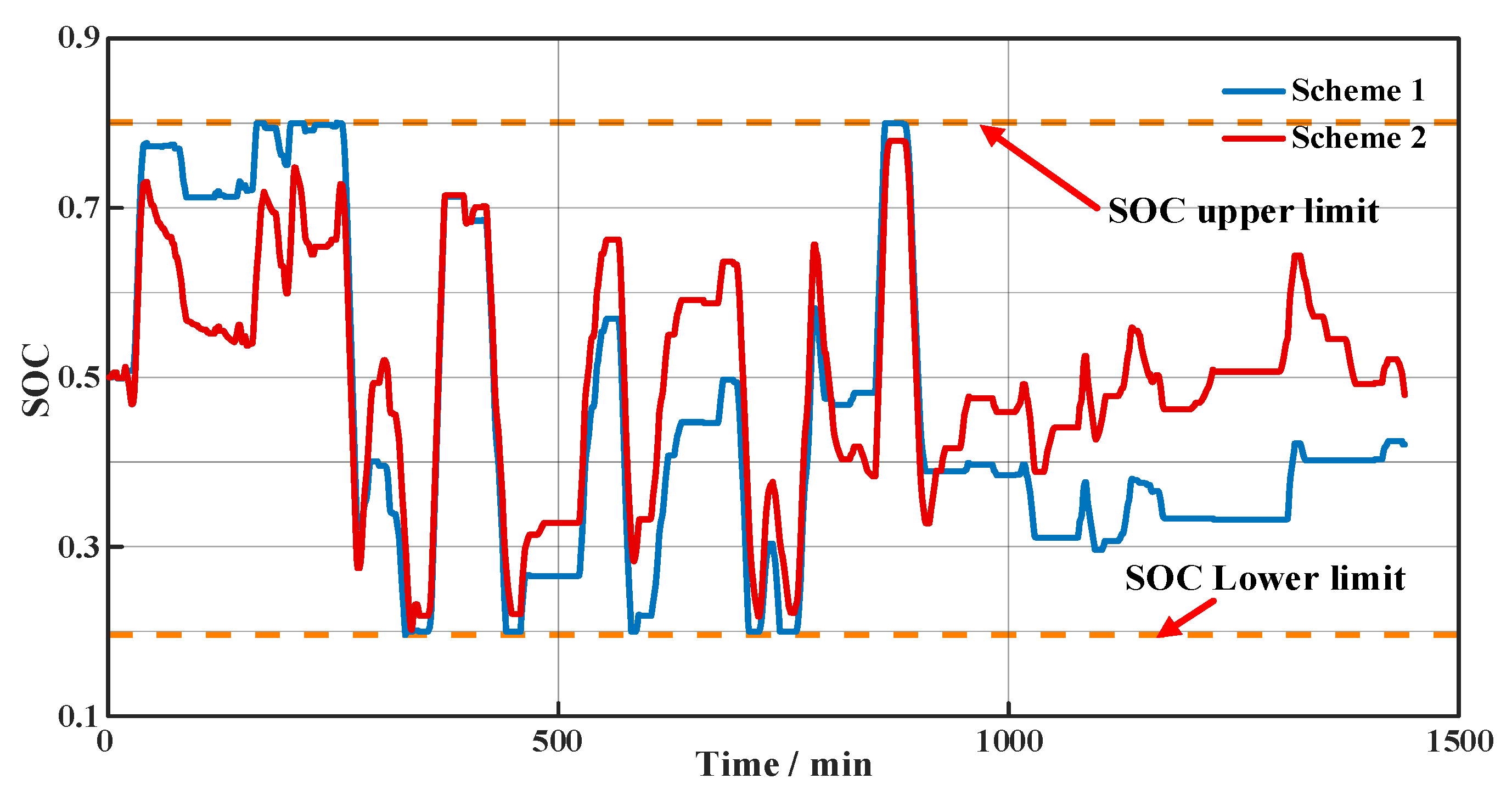
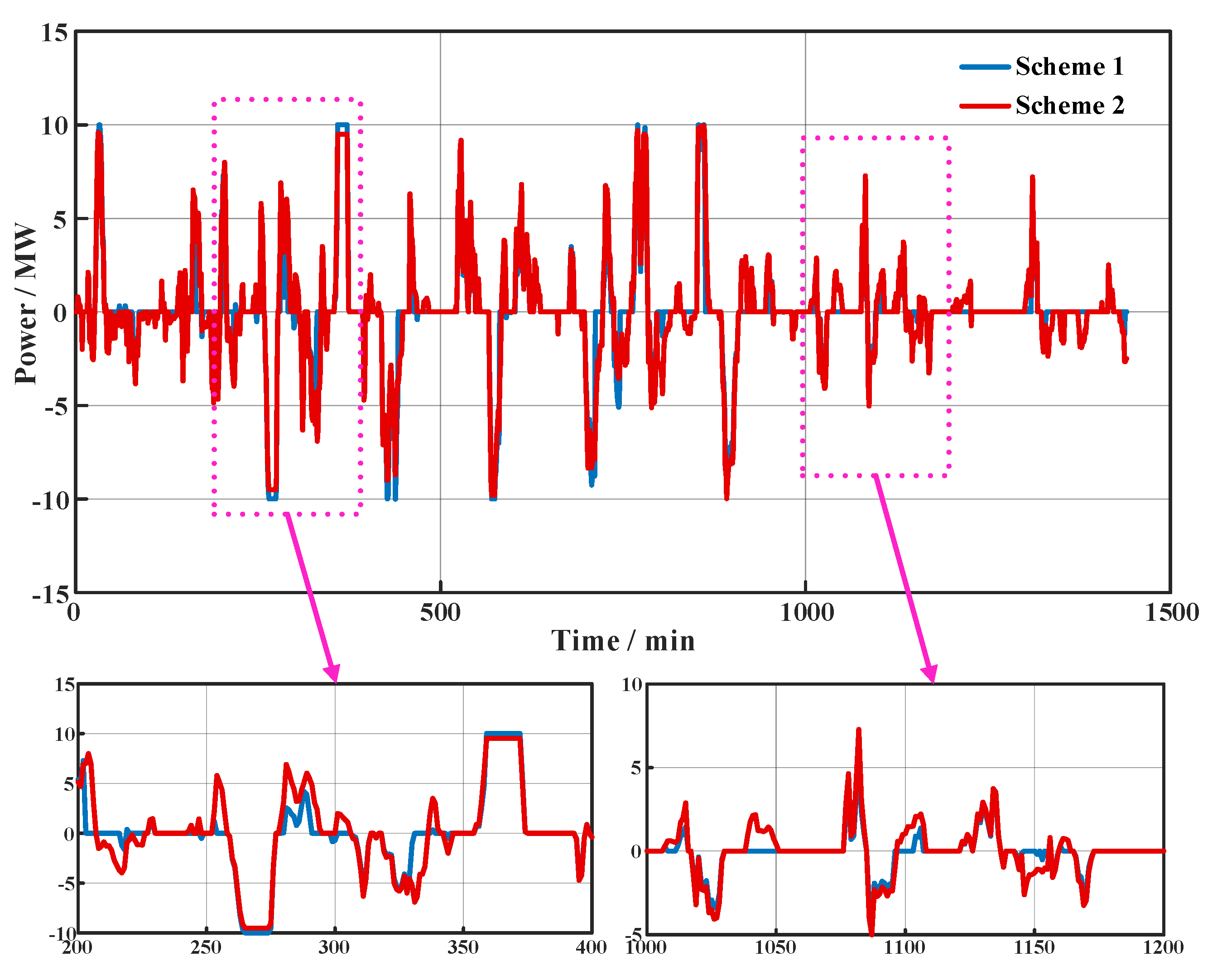
5.2. Analysis of Simulation Results
6. Conclusions
- (1)
- The method employs a first layer of fuzzy control to adjust the weight coefficients of the objective function, thereby enhancing the ESS’s ability to smooth wind power fluctuations while reducing the instances of the BESS entering dead and warning zones. Compared to control Scheme 1, control Scheme 2 exhibits a 17.7% decrease in the absolute mean value of wind grid-connected power fluctuations. Additionally, the time for SOC to enter the dead and warning intervals is reduced by 123 and 278 min, respectively. Consequently, control Scheme 2 effectively maintains SOC within a reasonable range and significantly improves the smoothing performance of the BESS for wind power.
- (2)
- A method is introduced to adjust the charging and discharging power of the BESS using the second layer of fuzzy control, thereby enhancing the BESS’s capacity to mitigate future wind power fluctuations. Compared to control Scheme 1, control Scheme 2 demonstrates a decrease of 31.6% in the BESS output coefficient. Consequently, control Scheme 2 effectively allocates sufficient chargeable capacity to smooth future wind power fluctuations by implementing advanced charging and discharging strategies.
- (3)
- Compared to control Scheme 1, the control method presented in this paper, utilizing fuzzy control rules to adjust charge and discharge power, leads to a certain increase in BESS charge and discharge cycles. Additionally, the effectiveness of the proposed control method is influenced by the accuracy of wind power predictions. Further research will explore the impact of wind power prediction errors on control effects and potential solutions. Additionally, battery charging and discharging strategies that consider the service life of BESS and the effective smoothing of wind power fluctuations will be investigated. These efforts aim to advance the efficient integration of energy storage systems with new energy sources.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Z.; Chen, H.; Wu, Q.; Li, W.; Li, M.; Ji, T. Mean-tracking model based stochastic economic dispatch for power systems with high penetration of wind power. Energy 2020, 193, 116826. [Google Scholar] [CrossRef]
- Su, Y.; Teh, J. Two-stage Optimal Dispatching of AC/DC Hybrid Active Distribution Systems Considering Network Flexibility. J. Mod. Power Syst. Clean Energy 2023, 33, 52–65. [Google Scholar] [CrossRef]
- Yang, J.; Yang, T.; Luo, L.; Peng, L. Tracking-dispatch of a combined wind-storage system based on model predictive control and two-layer fuzzy control strategy. Prot. Control. Mod. PowerSyst. 2023, 8, 974–989. [Google Scholar] [CrossRef]
- Li, X.; Ma, R.; Gan, W.; Yan, S. Optimal Dispatch for Battery Energy Storage Station in Distribution Network Considering Voltage Distribution Improvement and Peak Load Shifting. J. Mod. Power Syst. Clean Energy 2022, 10, 131–139. [Google Scholar] [CrossRef]
- Mazzoni, S.; Sze, J.Y.; Nastasi, B.; Ooi, S.; Desideri, U.; Romagnoli, A. A techno-economic assessment on the adoption of latent heat thermal energy storage systems for district cooling optimal dispatch & operations. Appl. Energy 2021, 289, 116646. [Google Scholar]
- Siqueira, D.; Maria Silva, L.; Wei, P. Control strategy to smooth wind power output using battery energy storage system: A review. J. Energy Storage 2021, 35, 102252–102264. [Google Scholar] [CrossRef]
- Zheng, P.; Young, D.; Yang, T.; Xiao, Y.; Li, Z. Powering battery sustainability: A review of the recent progress and evolving challenges in recycling lithium-ion batteries. Front. Sustain. Resour. Manag. 2023, 2, 1127001. [Google Scholar] [CrossRef]
- Jin, L.; Kazemi, M.; Comodi, G.; Papadimitriou, C. Assessing battery degradation as a key performance indicator for multi-objective optimization of multi-carrier energy systems. Appl. Energy 2024, 361, 122925. [Google Scholar] [CrossRef]
- Choopani, K.; Effatnejad, R.; Hedayati, M. Coordination of energy storage and wind power plant considering energy and reserve market for a resilience smart grid. J. Energy Storage 2020, 30, 101542. [Google Scholar] [CrossRef]
- Teixeira, T.P.; Borges, C.L.T. Operation strategies for coordinating battery energy storage with wind power generation and their effects on system reliability. J. Mod. Power Syst. Clean Energy 2021, 9, 190–198. [Google Scholar] [CrossRef]
- Zhai, Y.; Zhang, J.; Tan, Z.; Liu, X.; Shen, B.; Coombs, T.; Liu, P.; Huang, S. Research on the application of superconducting magnetic energy storage in the wind power generation system for smoothing wind power fluctuations. IEEE Trans. Appl. Supercond. 2021, 31, 5700205. [Google Scholar] [CrossRef]
- de Carvalho, W.C.; Bataglioli, R.P.; Fernandes, R.A.; Coury, D.V. Fuzzy-based approach for power smoothing of a full-converter wind turbine generator using a supercapacitor energy storage. Electr. Power Syst. Res. 2020, 184, 106287. [Google Scholar] [CrossRef]
- Zhang, F.; Meng, K.; Xu, Z.; Dong, Z.; Zhang, L.; Wan, C.; Liang, J. Battery ESS planning for wind smoothing via variable-interval reference modulation and self-adaptive SOC control strategy. IEEE Trans. Sustain. Energy 2017, 8, 695–707. [Google Scholar] [CrossRef]
- Cao, M.; Xu, Q.; Qin, X.; Cai, J. Battery energy storage sizing based on a modelpredictive control strategy with operational constraints to smooth the wind power. Int. J. Electr. Power Energy Syst. 2020, 115, 105471. [Google Scholar] [CrossRef]
- Teleke, S.; Baran, M.E.; Huang, A.Q.; Bhattacharya, S.; Anderson, L. Control strategies for battery energy storage for wind farm dispatching. IEEE Trans. Energy Convers. 2009, 24, 725–732. [Google Scholar] [CrossRef]
- Teleke, S.; Baran, M.E.; Bhattacharya, S.; Huang, A.Q. Optimal control of battery energy storage for wind farm dispatching. IEEE Trans. Energy Convers. 2010, 25, 787–794. [Google Scholar] [CrossRef]
- Jiang, Q.Y.; Wang, H.J. Two-time-scale coordination control for a battery energy storage system to mitigate wind power fluctuations. IEEE Trans. Energy Convers. 2013, 28, 52–61. [Google Scholar] [CrossRef]
- Addisu, A.; George, L.; Courbin, P.; Sciandra, V. Smoothing of renewable energy generation using gaussian-based method with power constraints. Energy Procedia 2017, 134, 171–180. [Google Scholar] [CrossRef]
- Guo, T.; Liu, Y.; Zhao, J.; Zhu, Y.; Liu, J. A dynamic waveletbased robust wind power smoothing approach using hybrid energy storage system. Electr. Power Energy Syst. 2020, 116, 105579. [Google Scholar] [CrossRef]
- Yang, X.; Yue, H.; Ren, J. Fuzzy empirical mode decomposition for smoothing wind power with battery energy storage system. IFAC Pap. OnLine 2017, 50, 8769–8774. [Google Scholar] [CrossRef]
- Kani, S.A.P.; Wild, P.; Saha, T.K. Improving Predictability of Renewable Generation Through Optimal Battery Sizing. IEEE Trans. Sustain. Energy 2020, 11, 37–47. [Google Scholar] [CrossRef]
- Trung, T.T.; Ahn, S.J.; Choi, J.H.; Go, S.I.; Nam, S.R. Real-time wavelet-based coordinated control of hybrid energy storage systems for denoising and flattening wind power output. Energies 2014, 7, 6620–6644. [Google Scholar] [CrossRef]
- Jiang, Q.; Hong, H. Wavelet-based capacity configuration and coordinated control of hybrid energy storage system for smoothing out wind power fluctuations. IEEE Trans. Power Syst. 2013, 28, 1363–1372. [Google Scholar] [CrossRef]
- Li, Y.N.; Wang, Q.; Song, W.F.; Wang, X.Y. Variational mode decomposition and fuzzy control strategy for smooth wind power output. Dianli Xitong Baohu Yu Kongzhi 2019, 47, 58–65. [Google Scholar]
- Yang, X.; Jia, C.; Zhang, P.; Yi, F.; Sun, Z.; Zhang, J. Fuzzy control strategy of energy storage for wind-storage system. In Proceedings of the 2015 18th International Conference on Electrical Machines and Systems (ICEMS), Pattaya, Thailand, 25–28 October 2015; pp. 1080–1085. [Google Scholar]
- Jiao, D.D.; Chen, J.; Fang, Y.; Fu, J.X.; Deng, H.; Zhang, B.M. Control strategy for wind power output fluctuation using hybrid energy storage based on variational mode decomposition. Electr. Meas. Instrum. 2021, 5, 14–19. [Google Scholar]
- Wu, J.; Ding, M. Wind power fluctuation smoothing strategy of hybrid energy storage system using self: Adaptive wavelet packet decomposition. Autom. Electr. Power Syst. 2017, 41, 7–12. [Google Scholar]
- Ma, L.; Xie, L.R.; Ye, L. A wind power smoothing strategy based on two-layer model algorithm control. J. Energy Storage 2023, 60, 106617. [Google Scholar] [CrossRef]
- Moghaddam, I.N.; Chowdhury, B.H.; Mohajeryami, S. Predictive operation and optimal sizing of battery energy storage with high wind energy penetration. IEEE Trans. Ind. Electron. 2018, 65, 6686–6695. [Google Scholar] [CrossRef]
- Chabok, H.; Aghaei, J.; Sheikh, M.; Roustaei, M.; Zare, M.; Niknam, T.; Lehtonen, M.; Shafi-khah, M.; Catalão, J.P. Transmission-constrained optimal allocation of price-maker wind-storage units in electricity markets. Appl. Energy 2020, 310, 118542. [Google Scholar] [CrossRef]
- Heredia, F.J.; Cuadrado, M.D.; Corchero, C. On optimal participation in the electricity markets of wind power plants with battery energy storage systems. Comput. Oper. Res. 2018, 96, 316–329. [Google Scholar] [CrossRef]
- Yang, X.Y.; Cao, C.; Li, X.J.; Yang, T. Control strategy of smoothing wind power output using battery energy storage system based on fuzzy empirical mode decomposition. Electr. Power Constr. 2016, 37, 134–140. [Google Scholar]
- Jannati, M.; Hosseinian, S.H.; Vahidi, B.; Li, G.J. ADALINE (ADAptive Linear NEuron)-based coordinated control for wind power fluctuations smoothing with reduced ESS (battery energy storage system) capacity. Energy 2016, 101, 1–8. [Google Scholar] [CrossRef]
- Khalid, M.; Savkin, A.V. A model predictive control approach to the problem of wind power smoothing with controlled battery storage. Renew. Energy 2010, 35, 1520–1526. [Google Scholar] [CrossRef]
- Esmaeili, S.; Amini, M.; Khorsandi, A.; Fathi, S.H.; Hosseinian, S.H.; Millimonfared, J. Market-oriented Optimal Control Strategy for an Integrated Energy Storage System and Wind Farm. In Proceedings of the 2021 29th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 18–20 May 2021; pp. 407–411. [Google Scholar]
- Guo, T.; Zhu, Y.; Liu, Y.; Gu, C.; Liu, J. Two-stage optimal MPC for hybrid energy storage operation to enable smooth wind power integration. IET Renew. Power Gener. 2020, 14, 2477–2486. [Google Scholar] [CrossRef]
- Sun, Y.; Tang, X.; Sun, X.; Jia, D.; Cao, Z.; Pan, J.; Xu, B. Model predictive control and improved low-pass filtering strategies based on wind power fluctuation mitigation. J. Mod. Power Syst. Clean Energy 2019, 7, 512–524. [Google Scholar] [CrossRef]
- Yang, J.; Peng, L.; Luo, L.; Yang, T. Control Strategy for Energy-Storage Systems to Smooth Wind Power Fluctuation Based on Interval and Fuzzy Control. IEEE Access 2023, 11, 20979–20993. [Google Scholar] [CrossRef]
- Yun, P.P.; Chen, Q.T.; Mi, Y.; Ren, B.; Miao, Y.; Ren, Y. Improved Wavelet Packet of Hybrid Energy Storage to Smooth Wind Power Fluctuation. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 November 2021; pp. 1160–1165. [Google Scholar]
- Long, B.; Liao, Y.; Chong, K.T.; Rodríguez, J.; Guerrero, J.M. Enhancement of frequency regulation in AC microgrid: A fuzzy-MPC controlled virtual synchronous generator. IEEE Trans. Smart Grid 2021, 12, 3138–3149. [Google Scholar] [CrossRef]


| Wind Farm Installation Capacity/MW | 10 min Active Power Change Maximum Limit/MW | 1 min Active Power Change Maximum Limit/MW |
|---|---|---|
| <30 | 10 | 3 |
| 30–150 | Installed capacity/3 | Installed capacity/10 |
| >150 | 50 | 15 |
| ESOC(i) | Pb(i) | ||||
|---|---|---|---|---|---|
| PB | PS | Z | NS | NB | |
| VS | VB | VB | B | M | M |
| S | B | B | M | M | S |
| M | S | VS | VS | VS | S |
| B | S | M | M | B | B |
| VB | M | M | B | VB | VB |
| F | Pb(i) | ||||
|---|---|---|---|---|---|
| L | LM | M | MH | H | |
| VS | NB | PB | P | NH | P |
| S | PB | N | Z | PH | Z |
| B | P | PH | Z | N | PB |
| VB | PH | NH | PB | PB | NB |
| Parameters | Symbol | Value and Units |
|---|---|---|
| Installed capacity of wind farms | Cinstall | 50 MW |
| Cycle of control | Tc | 1 min |
| Rated capacity of BESS | Crated | 5 MW·h |
| Rated capacity of BESS | Prated | 10 MW |
| Cycle of control | Ts | 1 min |
| Optimize interval length | N | 15 |
| Charge dead zone boundary | ESOC.max | 0.8 |
| Discharge dead zone boundary | ESOC.min | 0.2 |
| Charge warning interval boundary | ESOC.max-alert | 0.7 |
| Discharge warning interval boundary | ESOC.min-alert | 0.3 |
| Control Scheme | ∆Pg.mean/MW | Td/min | Cb |
|---|---|---|---|
| Without BESS | 0.92 | — | — |
| Scheme 1 | 0.74 | 123 | 0.19 |
| Scheme 2 | 0.61 | 0 | 0.13 |
| Control Scheme | Discharge Dead Zone/min | Discharge Warning Interval/min | Normal Charging and Discharging Interval/min | Charge Warning Interval/min | Charging Dead Zone/min |
|---|---|---|---|---|---|
| Scheme 1 | 73 | 155 | 929 | 233 | 50 |
| Scheme 2 | 0 | 103 | 1230 | 107 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, L.; Luo, L.; Yang, J.; Li, W. A Wind Power Fluctuation Smoothing Control Strategy for Energy Storage Systems Considering the State of Charge. Energies 2024, 17, 3132. https://doi.org/10.3390/en17133132
Peng L, Luo L, Yang J, Li W. A Wind Power Fluctuation Smoothing Control Strategy for Energy Storage Systems Considering the State of Charge. Energies. 2024; 17(13):3132. https://doi.org/10.3390/en17133132
Chicago/Turabian StylePeng, Li, Longfu Luo, Jingyu Yang, and Wanting Li. 2024. "A Wind Power Fluctuation Smoothing Control Strategy for Energy Storage Systems Considering the State of Charge" Energies 17, no. 13: 3132. https://doi.org/10.3390/en17133132
APA StylePeng, L., Luo, L., Yang, J., & Li, W. (2024). A Wind Power Fluctuation Smoothing Control Strategy for Energy Storage Systems Considering the State of Charge. Energies, 17(13), 3132. https://doi.org/10.3390/en17133132






