Abstract
Striving to increase the speed of rail vehicles and thus improve the comfort of traveling passengers at the same time, undertakes activities in the sphere of ensuring an appropriate level of safety of rail, passenger, and freight transport. One of the elements of activities in this area is the training of train drivers. Until recently, this training consisted of a theoretical and practical part on the vehicle, alongside an experienced train driver. Considering the increasing level of automation of railway traffic control systems and locomotive equipment, as well as training costs and requirements related to the introduction of TSI, it is becoming an increasingly common requirement to conduct practical training on railway vehicle traffic simulators, while the conditions in the simulator cabin and the trainee’s feelings should correspond to the actual driving conditions. A locomotive driving simulator is a system consisting of a cabin of a suitable type of locomotive or EMU, mapped in 1:1 scale, coupled with a motion excitation system and computer programs connected together forming the software of the cab visualization and dynamics system. The basic program simulating the dynamics and kinematics of the cabin’s motion is a program containing a motion dynamics model that generates signals forcing the movement of the exciters on which the cabin’s platform is mounted. The correct operation of the simulation model depends on the created mathematical model, which can be built in several ways. This article presents the issue of building a mathematical model describing the dynamics of the rail vehicle motion, which can then be used in the simulation model of the simulator cabin motion. Two ways of proceeding in the process of approaching the construction of a mathematical model of rail vehicle motion dynamics will be presented, with the possibility of later use in creating a simulation model of the motion of the locomotive simulator cabin. One of the possible routes was used in the past in the construction of the EP09 locomotive simulator.
1. Introduction
The universal pursuit of comprehensive development of transport has both positive and negative effects. One of the positive elements of this trend, in the case of rail transport, is increasing speed and improving travel comfort in rail passenger transport [1,2,3,4]. However, negative phenomena include railway accidents and disasters; the greater the speed of moving vehicles, the more tragic the consequences [5,6]. As research shows, the driver of a road vehicle or a railway vehicle and their skills are the link in the transport process that significantly determines the safety of participants in this process [7]. Therefore, activities aimed at improving the skills of train drivers have been an important element of railway safety activities for over a dozen years. These activities can be carried out in many ways. The two basic methods are providing railway vehicle drivers with theoretical knowledge about the behavior of rail vehicles in various operating conditions and acquiring increasingly greater practical skills in driving trains, which can reach speeds of up to 350 km/h in normal operation and, in the case of experimental runs, even up to 600 km/h. Gaining experience in driving rail vehicles takes place, as in the case of any means of transport, by driving in real conditions as a training employee or as a co-pilot in aviation, and it is a long and arduous road—it certainly cannot be neglected. This method is also expensive and carries the risk of accidents, because the training takes place in real conditions using a real means of transport. Therefore, for over a dozen years, research and implementation work were carried out to develop new education methods that allow for the acquisition of skills in driving rail vehicles, cars, aircraft, and ships in a safe and effective manner.
These methods are training using simulation technologies, including simulators, i.e., devices using computer simulation methods to visualize objects and simulate the conditions and sensations experienced by the driver of a means of transport while driving a vehicle in real operation [8].
The development of simulation technologies plays a key role in shaping the future of rail transport, ensuring safety, efficiency, and sustainability. In the light of the latest research and innovation, the four most important directions that dominate global trends in the field of railway simulators are [9,10,11,12,13,14]:
- Integration with digital technologies,
- Increasing the realism of the simulation,
- Development of training methods,
- Focus on ecological aspects.
In the era of digitalization, integration with digital technologies is becoming inevitable. Technologies such as virtual and augmented reality (VR/AR), artificial intelligence and neural networks (AI), and machine learning (ML) are becoming integral elements of railway simulators. The integration of these technologies allows for the creation of advanced, interactive simulation environments that not only offer a higher degree of immersion, but also enable the personalization of training experiences. Thanks to AI and ML, simulators can adapt scenarios in real time, adapting the level of difficulty and the presented challenges to the individual skills and needs of the user, which increases the effectiveness of the teaching process [14,15,16,17].
In the case of striving for the most faithful reproduction of reality, it is necessary to increase the realism of the simulation, which is a kind of direction in the development of technology related to the construction of railway simulators. This includes not only visual aspects, but also accurate simulation of the physics of railway vehicles, driving dynamics, as well as the interaction between the vehicle and the track infrastructure. The development of advanced mathematical and physical models allows for the simulation of a wide range of operational conditions, including various types of failures, weather conditions and specific characteristics of railway tracks. This realism is crucial not only for effective train drivers, but also for research on new technologies and solutions in rail transport.
The basis for the development of simulators is the work on methods and tools in the area of computer simulations carried out since the mid-20th century [18,19,20]. A simulation can concern virtually all phenomena occurring in the world around us, in particular processes occurring in the social, economic, or climatic sphere, or existing, designed, or abstract devices or objects. In the case of railways, computer simulation methods and tools have been developed for over 50 years [21,22,23,24,25,26] and, along with the development of information technologies, are the basis for the development of new solutions in the field of rolling stock, traffic control, and organization of the transport process, in particular high-speed railways. Each simulator is a combination of mechanical and hardware systems with broadly understood software, but the basis is always a numerical program containing a mathematical model describing the phenomenon we are interested in. In the case of motion simulators, these are programs that simulate the movement of a vehicle and its kinematic and dynamic characteristics at selected points. The processed results of these simulations are used to visualize phenomena accompanying a moving vehicle and are signals generating cabin excitations of the vehicle simulator, in the case of full-range cabin simulators, the so-called “world class” [7,27]. The subject of this article will be considerations regarding the modeling of rail vehicles, but with a view to using their models in the process of creating a mathematical simulation model later used in the construction of a rail vehicle simulator.
2. Reference Books Analysis
The current analysis of the literature indicates several directions of development in building railway simulators. The guidelines for their construction focus on several key aspects to ensure the highest possible training effectiveness, realism of experiences, and integration with the latest technologies. In a given scope, several necessary key issues can be distinguished, such as [1,2,18,19,21,25]:
- Use of virtual and augmented reality technology (VR/AR). VR-enabled simulators provide an immersive training environment where operators can experience realistic operational and emergency scenarios without safety risks. VR allows you to model complex environments such as stations, intersections and various weather conditions. AR (augmented reality): AR technology is used to overlay virtual elements on a real image of the cabin, which can be used for training on real equipment with additional visualizations, e.g., displaying telemetry data directly on the windshield.
- Advanced physical and mathematical modeling. These simulators use advanced physical and mathematical models to most accurately reproduce the behavior of railway vehicles, driving dynamics, the impact of weather conditions, and interactions between the wheel and the track. This modeling also includes the simulation of failures and unforeseen events.
- Modular design and configurability. Many modern simulators are designed with modularity in mind, which allows for easy configuration and adaptation to different types of railway vehicles and training scenarios. This allows training on various types of locomotives and wagons without having to change the entire equipment.
- Interactive control panels and user interfaces. The simulators are equipped with interactive, often touch-sensitive control panels that precisely reproduce the layout and functionality of real railway vehicle control panels. User interfaces are designed to be intuitive and reflect real working conditions.
- Integration with railway traffic management systems. Modern simulators are often integrated with railway traffic management systems (e.g., ETCS), which allows train drivers to be trained on simulators in the use of these systems in real operational conditions.
- Data analysis and results-based training. The design solutions also include systems for collecting training data and analyzing results, which allows for adapting training programs to the individual needs of participants, monitoring progress and identifying areas requiring additional practice.
- Ecological and energy-saving solutions. In response to growing ecological awareness, simulator manufacturers are also implementing solutions aimed at reducing energy consumption and environmental impact, e.g., by optimizing software and hardware.
The development of railway simulators is a continuous process in which engineers and scientists strive for greater accuracy, realism, and training effectiveness, while taking care of ecological and economic aspects.
Of the listed components related to simulator technology, the authors of this article focused on issues related to advanced physical and mathematical modeling in terms of generating inputs from the operator’s cabin of the glue vehicle. It should be noted that the modular design and configurability of simulator technologies is directly related to the possibility of reconfiguring a railway vehicle from a locomotive to an electric multiple unit or another, e.g., light metro railway vehicle.
The use of technologies related to artificial intelligence was presented in article [18]. The presented research concerned the detection of faults in first-stage suspension shock absorbers in railway vehicles using artificial neural networks (ANNs), focusing on the dynamic responses caused by such faults. The initial analysis included a passenger car model that was tested in the MSC. Adams environment with the VI-Rail package. The acceleration signals from the simulation were used as input for the ANN, which attempted to identify faults based on the spectrum of signals. Despite different ANN configurations, the fault detection accuracy remained below 63%. The results suggest that although ANNs can identify some suspension faults, this type of approach can be used to create scenarios of vehicle behavior while moving.
Modular design and configurability in vehicle simulators are key aspects that enable flexible adaptation of simulation systems to a variety of training and research requirements. Modularity allows for easy replacement or updating of individual simulator components, such as visual systems, simulation software, user interfaces, or vehicle dynamics models. Thanks to this, simulators can be quickly adapted to new types of vehicles, training scenarios, or changing technological standards [25,27]. Configurability, in turn, provides users with the ability to adjust simulation parameters such as weather conditions, vehicle settings, and emergency scenarios, which increases the educational value and realism of training. These aspects support the development driver and operator competencies, enabling them to become hands-on with a variety of operational situations in a controlled virtual environment.
Interactive control panels and user interfaces in modern engineering systems play a key role in ensuring intuitive and effective communication between the user and the machine. They enable operators to quickly adjust operating parameters, monitor system status in real time, and effectively diagnose possible problems [3]. When designing interactive panels, engineers emphasize ergonomics, personalization of user experiences, and the use of advanced technologies such as touch screens, gesture recognition, or virtual and augmented reality. These innovative interfaces increase operational security, improve work efficiency, and enrich the training process by providing users with tools for deeper understanding and better control of complex systems.
One of the possibilities of mapping the motion of a railway vehicle is to place the vehicle’s cabin on the Stewart–Gough platform (Figure 1), which was presented in [28,29]. The Stewart–Gough platform is an advanced mechanism for simulating and testing movement in six degrees of freedom. It is characterized by a structure based on six independently controlled telescopic actuators, allowing precise manipulation of the position and orientation of the work platform. Thanks to its ability to accurately reproduce movements, this platform is used in vehicle simulators, research on vehicle dynamics, and in advanced automation and production systems. The development of control technology and mathematical modeling has enabled the creation of effective algorithms for precise platform control, which opens up new possibilities in the design of advanced mechanical and testing systems.

Figure 1.
Stewart–Gough platform equipped with electric actuators [28].
The capabilities of the Hexapod simulation platform [Figure 2 and Figure 3], which is a kind of modification of the Stewart platform, is an advanced device used to simulate movement in six degrees of freedom: forward/backward, left/right, up/down, tilt, rotation and pitch [9,30,31]. It uses six independently controlled actuators to precisely move the platform on which an object or simulator can be placed. Thanks to its ability to accurately reproduce movements, the Hexapod platform is used in many areas, such as aviation, automotive, industrial production, scientific research, and entertainment. It enables the study of the impact of movements and vibrations on objects, components, and people, which is crucial for design and testing in environments requiring high precision and realistic simulation conditions.

Figure 2.
Vehicle motion simulator placed on the Hexapod platform [29].

Figure 3.
VTI simulator on the Hexapod platform [29].
Works [32,33,34,35,36,37,38,39] focused on the validation process of railway vehicle dynamics models used in training simulators. The validation process, called the Dynamic Modeling Validation Process (DyMVaP), is crucial to ensuring the credibility of the simulators, which play an important role in driver training. This process includes five stages:
- Preparation of validation scenarios,
- Arrangement of sensors,
- Collecting real data, preparing data
- Comparison of simulated and measured data.
The authors describe each stage in detail, emphasizing the importance of collecting synchronous data from various sensors and then comparing them with simulation data.
Articles [10,20,31] present the issues of implementing simulators in the process of training railway drivers, proposing the adoption of solutions similar to those used in air transport. In [10], the author argues for introducing changes to Polish legal regulations to create a coherent education system using simulators. He emphasizes that the current use of simulators in the education of railway drivers is inadequate compared to solutions in aviation, where simulators are an integral part of training. The author points out the need to define clear requirements for simulators, their certification, and adaptation to various types of traction vehicles, which would increase the effectiveness of training and safety in rail transport.
Data analysis and performance-based training in vehicle simulators is a key element in improving the skills of operators and drivers. The use of advanced data analysis techniques allows for detailed tracking of user behavior during simulation, indicating areas requiring improvement and enabling personalization of training content [8,40,41]. Data collected during simulation sessions, such as reaction time, accuracy of performed maneuvers, and compliance with safety procedures, are analyzed to identify behavioral patterns that may affect work safety and efficiency. Technologies such as machine learning and artificial intelligence are used to process this data, enabling the creation of personalized training programs that dynamically adapt to the learner’s progress. Focusing on results not only enables a better understanding of individual training needs, but also ensures that training progress and effectiveness can be continuously monitored, resulting in significant improvements in operational safety and driver competence.
3. Analytical Mathematical Model of a Rail Vehicle Simulator
According to various sources, including publications affiliated with the Stanford Research Institute (Menlo Park, CA, USA), the use of simulation methods is considered a key technology that will continue to play a leading role in basic and utilitarian research in this century. The spectrum of use of simulation methods is very wide and it is currently difficult to find an area of life where they are not used. Generally, simulation methods are used to reproduce real processes and obtain information about their course, but in the case of the topic we are interested in, we will be more interested in obtaining quantitative rather than qualitative information. The basis for simulation methods is a mathematical model, which has many definitions, terms and classifications in the literature [2,5,42]. The model is not a clear concept, although its common understanding does not pose any problems.
Following Gutenbaum [32], it can be said that a model is a representation of the examined object or phenomenon in a form different from that in which it occurs in reality. The form of the model depends on the modeling methods used. We can therefore talk about analytical models, written in the form of equations; geometric models, described using geometric figures connected by lines indicating the flow of information; or verbal models described with logical text. In the case of simulators, the model, which contains formulas describing the properties of a real object, is to process the stored formulas, e.g., by solving equations, and as a result, obtaining expressions describing the behavior of selected points of the real object. However, the task of the simulation model is to generate signals imitating the behavior of the object in real conditions and to provide information about the environment in which the object is currently located. In this case, the input data to the model should also be information about the characteristics of the object that change during the operation of the object in real conditions. Figure 4 shows the interconnections of the real object, model, simulation model, and simulator.
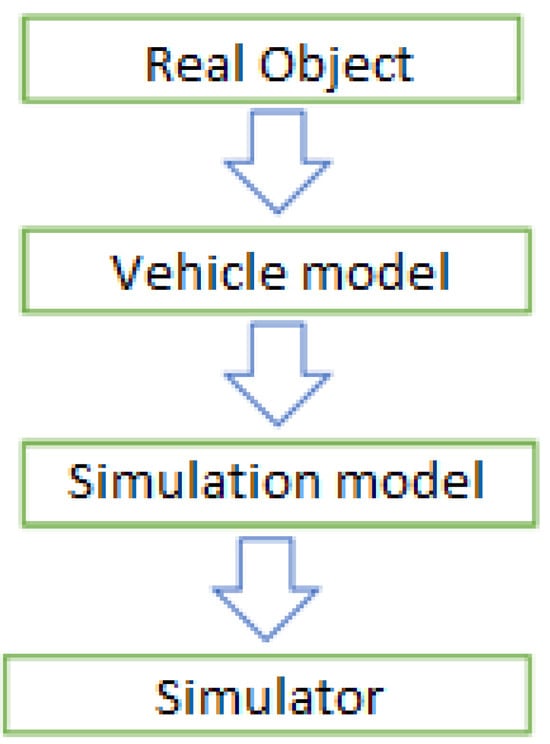
Figure 4.
Interaction between the real object, model, simulation model, and simulator in terms of information flow.
The previously mentioned analytical mathematical model should be, in accordance with the adopted assumptions, a faithful reflection of the physical model, written in the form of dynamic equations of motion describing the behavior of the vehicle, or may contain equations describing the form of functions characterizing the time courses of displacements or accelerations of selected points of a real object, obtained from the conducted experimental research. Therefore, there are two ways to simulate motion in simulators. The use of dynamic equations of motion in the case of motor vehicle simulators has been presented in works such as [7,14,29,43]. In the case of rail vehicles, there are also many reports in the literature [24,25,35,44,45,46].
Below, we will present the process of modeling the dynamics of a rail vehicle with the possibility of using it in simulators of these vehicles.
The physical model of a rail vehicle, shown in Figure 5, can be presented in the form of a structure composed of 7 solids connected with each other by constraints representing flexible systems of the first and second degree of suspension [46].
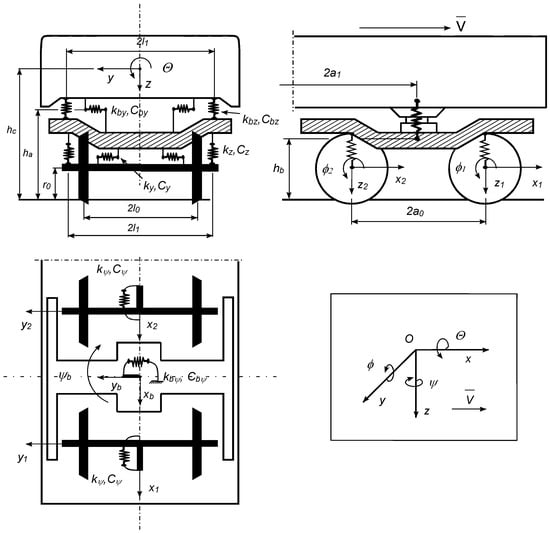
Figure 5.
Physical model of a rail vehicle [46].
The basic assumptions about the vehicle model are as follows:
- The mathematical model has 27 degrees of freedom and consists of rigid bodies such as:
- Wagon body,
- Two trolley frames,
- Four wheel sets connected with spring-damping elements.
- The motion of each set is described by equations using 3 degrees of freedom:
- Lateral displacement (y),
- Approach angle (Ψ),
- Winding angle (χ).
- The constraints regarding the motion of each wheel set result from its cooperation with the rigid track. As a result, the vertical displacement (z) and the angle of rotation around the longitudinal axis of the track (φ) depend on the lateral displacement of the set (y) and on its approach angle (Ψ); the coordinate describing the position of the center of the set along the track axis (x) depends on the angle of rotation around the symmetry axis of this set (χ). The form of the constraints is non-linear (can be determined numerically) and depends on the geometric parameters of the wheel set and track, including on the track width, transverse rail inclination, wheel and rail profiles, and set wheel center spacing.
- Wheel profiles were adopted in accordance with the measurements of the nominal or worn S1002 wheel. It should be noted, however, that any wheel and rail profile defined in accordance with formal requirements can be adopted in the discussed simulation model. It was assumed that all wheels of the vehicle model have the same profiles.
- The bogie frame, like the wagon body, has 5 degrees of freedom: lateral (y) and vertical (z) displacement, and rotation angles Ψ, χ and φ.
- The elastic and damping characteristics of the suspension are linear functions of the relative displacements and velocities.
- Spring and damping elements are massless.
- The movement is described relative to the lifting system associated with the vehicle moving in a steady manner (v = const.).
- Inertial forces are determined numerically and tangential wheel–rail forces, as mentioned earlier, using the FASTSIM program.
4. Mathematical Model Reflecting the Structure of the Vehicle
The mathematical model of the system presented in Figure 5 can be written in general form as follows [46]:
where
M, C, and K represent the square matrices of inertia, damping, gyroscopic, and stiffness respectively.
The columnar matrix q contains independent coordinates describing the motion of the rigid bodies of the system. The column matrix p represents the forces. It can be interpreted as the sum of two matrices:
where
is a vector containing forces arising from track unevenness and external influences, e.g., wind, and ) is a vector of nonlinear forces containing contact forces between the wheel and the rail.
Assuming that the set does not lose contact with the track and that we are dealing with a single-point contact, the reaction equations derived from the track can be written as follows [16]:
where
—vertical displacement, rotation of the wheel set around the longitudinal axis (values, among others, resulting from the constraints in the system) and local track superelevation,
m, Jx—mass of the wheelset, and moment of inertia about the longitudinal axis,
—vertical and lateral forces acting on the wheelset,
—force action arms for the left and right sides of the rail track and rolling radii of the wheels,
G—static load on the track by the wheelset,
Fz, Mx—vertical force and torque acting on the set and resulting from the movement of the bogie frame and wagon body.
The normal forces are determined according to the equations:
where
—contact angles for left and right wheels,
—transverse tangential forces
By solving the system of Equations (1)–(6), we obtain functions qi (t) describing the course of generalized coordinates, including the displacements of the centers of mass and angles of rotation, wheel sets of the bogie frame, and the body, which are the result of excitations coming from the geometric irregularities of the track. These results allow for obtaining the waveforms of kinematic quantities and forces at any point in the model, and thus in the real object. These functions constitute input data to the simulation model (Figure 4) that generates the form of kinematic excitations of the simulator–vehicle body in the case of simulators called full-range or “world class” in the literature.
Figure 6 shows exemplary courses of vertical and lateral forces occurring in the turning pin of a freight wagon, obtained from a simulation model for geometric track irregularities shown in Figure 7.
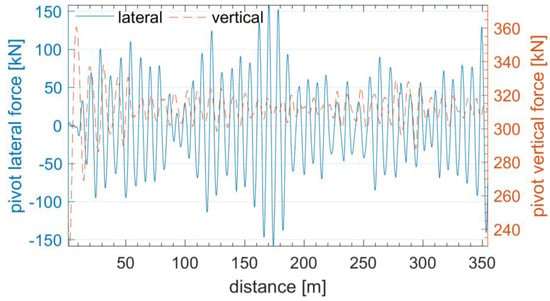
Figure 6.
Examples of results of the course of lateral and vertical forces in the turning pin of the bogie of the Y25 freight wagon, obtained from the simulation model for a speed of 100 km/h and geometric track irregularities obtained from measurements of the actual track.
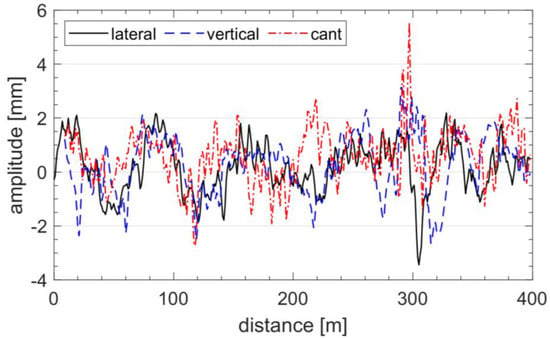
Figure 7.
Geometric irregularities of the track obtained from measurements (according to the UIC 518 card [3] and the EN1436 standard [19], irregularities and such courses characterize a track in a very good condition).
5. Mathematical Model Using the Results of Experimental Research
The disadvantage of using the method presented above is the need to solve the system of Equations (1)–(6) at each time step, taking into account the actual profiles of wheels and rails, the form of geometric irregularities of the track, and the contact conditions of the wheel with the rail in order to obtain the courses of the physical quantities of interest at selected points in the model. This requires access to a computer with significant computing capabilities to obtain results in real time, without significant delays.
The assumption was made that the accelerations of the base of the driver’s (operator’s) seat in the cab of the electric locomotive and the simulator should show compliance of their spectra in the frequency range relevant for the simulated system with the assumed accuracy. For the purposes of building a model in this concept, an experiment was performed, described later in the work.
The functions generating vibrations of the appropriate actuators of the simulator cabin platform have the form of polyharmonic functions [25,44]. Using the theory of operator calculus and methods of analyzing and measuring random signals, we can represent each function f(t) that meets the appropriate conditions as a Fourier series [44,45]:
where
A0—constant component,
Ak—amplitude of the k-th harmonic,
ω—fundamental frequency,
φk—phase of the k-th harmonic,
t—time.
Assuming that the function x(t) describes the course of accelerations of a selected point of the real object. By introducing time quantization ti in the form ti = iδt and limiting to m harmonics and substituting fn = nω, we will obtain:
where
t = {ti, ti = iδt, i = 1, …, k}.
Function x(t) represents a signal with stationary and ergodic properties, xn is the n-th amplitude of the acceleration signal spectrum, and fn is the corresponding frequency in the spectrum.
The above function should be modified so that the driving speed ν and track class j ∈ {0, 1, 2, 3, 4, 5} can be formally included.
Expression (9) constitutes the basic formula for generating control functions for actuators, forcing vibrations of the simulator. The next step in model construction is the introduction of the ability to consider the choice of appropriate sections of the travel route (straight track, curves, turnouts) and appropriate disturbances of the signal spectrum amplitude caused by these sections.
The quantities e1 and e2 appearing in (10) are Boolean functions, taking values from the set {0,1} indicating the vehicle’s presence on a given track section:
e1—corresponds to travel on a straight track,
e2—corresponds to travel on a curve,
δxn—is the increase in amplitude of the n-th harmonic xn caused by passing through the remaining transitional sections of the track.
The quantities fn, xn appearing in Equations (8)–(10) can be obtained from the analysis of signals obtained as a result of conducted experiments, under real conditions using a rail vehicle. The experiment consisted of recording the courses of kinematic quantities at selected points of the vehicle according to a previously developed scenario, which assumed the registration of these signals for speeds from v1 to v2, at a certain step of speed changes of the vehicle δv. Since the process of controlling the movement of the vehicle’s cabin simulator should be a continuous process, reflecting the smooth ride of the real vehicle, it was assumed that the values of parameters appearing in the expression (10) defining the form of the function will be calculated using linear interpolation. For speed v ∈(v1, v2), the adopted formulas are as follows:
The values of the functions x_(0,), obtained from the analysis of measurement signals, allowing for the realization of control by forcing the simulator platform, are stored in a multidimensional array called by the control program at every time step for given route parameters, driving speeds, or other quantities characteristic of the set simulation conditions of driving. It remains to determine the phase of the n-th harmonic φn. Calculating this value based on the experiment is a difficult and time-consuming task, and the obtained results can be significantly erroneous. Therefore, the phase values for the subsequent spectral bands were adopted using a random number generator with a uniform distribution from the range (0, 1):
The number of harmonics m is chosen so that the energy of the generator signal is similar to the energy of the measurement signal. Equations (8)–(13) were applied to all acceleration signals recorded during measurements. Taking into account the track class, characteristic sections of the route, and driving speeds, result files were created containing spectra of linear accelerations in the longitudinal, vertical, and lateral directions of selected points of the cabin platform. The aforementioned experiment was conducted on the CMK railway line, on the Szeligi-Strzałki section, under the following assumptions:
- A single EP09 type locomotive was selected, which, in terms of dynamic behavior on different track sections, represents characteristics similar to most specimens of this type,
- Measurement drives were conducted in agreement with PKP on five track sections of different classes, i.e., with different permissible speeds,
- The registration of acceleration signals was carried out at the minimum number of points to unequivocally describe the cabin’s vibrations,
- The frequency range for signal analysis was 0.2–20 [Hz]. Measurements were made during experimental train runs at constant speeds, as well as in the state of acceleration to the speed anticipated for the given track class and braking. The recorded signals were then subjected to frequency analysis to obtain data for the acceleration generator forcing cabin vibrations. Example courses of lateral and vertical accelerations, at the mounting point of the driver’s seat, for a case of driving at a speed of 80 km/h on a track consisting of a straight section, a curve, and a straight section, are presented in Figure 8.
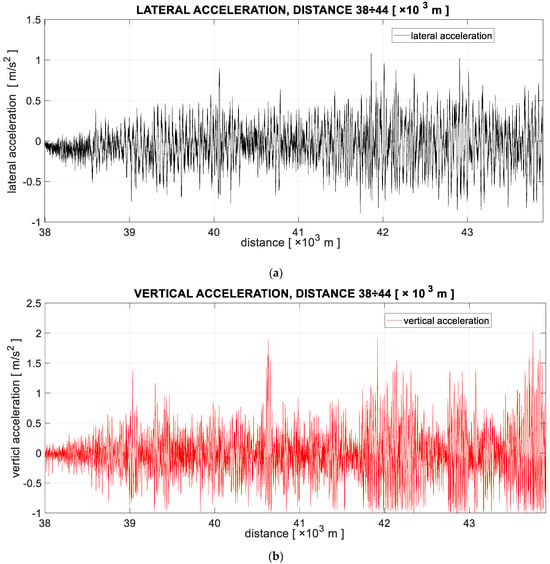 Figure 8. Example courses of lateral (a) and vertical (b) accelerations recorded on the floor of the driver’s cabin, at the location of the driver’s seat mounting.
Figure 8. Example courses of lateral (a) and vertical (b) accelerations recorded on the floor of the driver’s cabin, at the location of the driver’s seat mounting.
6. Example of Using the Model to Control the Simulator Platform Movement
As mentioned earlier, signals recorded during experimental research and subjected to analysis were used to control the movement of the simulator cabin shown in Figure 9.
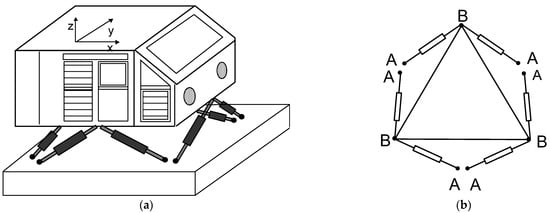
Figure 9.
Graphical interpretation of the simulator system: (a) general view of the locomotive cabin simulator, (b) connection of the actuator system between the simulator cabin and the ground (A: connection points between the actuators and the ground on which the cabin simulator is placed, B: connection points between the actuators and the floor of the simulator) [25].
The structure of the control program for the simulator platform movement, forced by six actuators, was shown in block form in Figure 10. Using the created files, the computer program generates functions described by Equations (11)–(13).
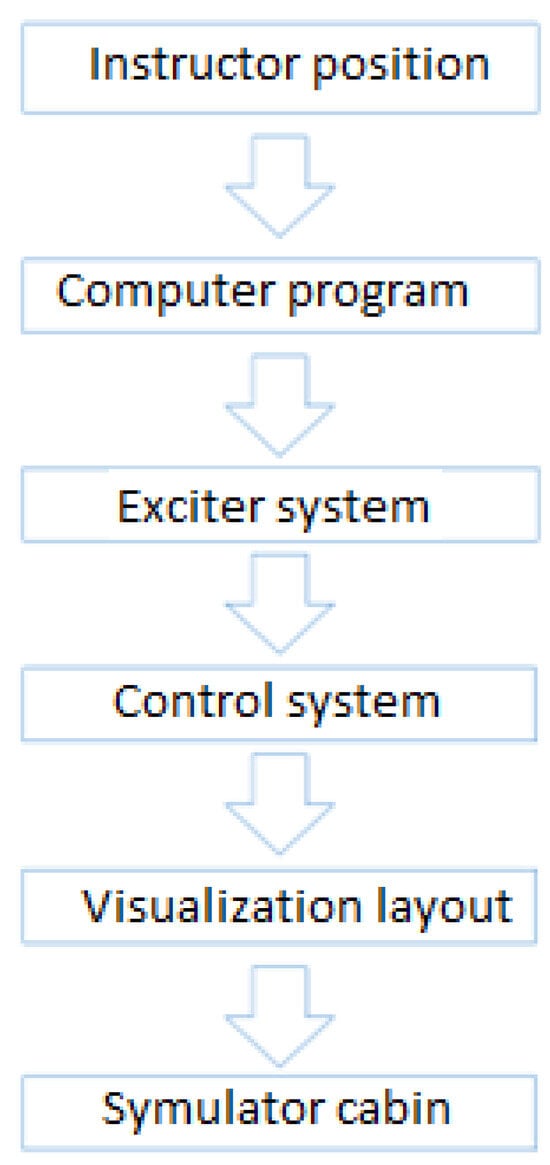
Figure 10.
Structure of the simulator platform control program.
The formulas introduced in the previous section were applied to all acceleration signals recorded during measurements. Taking into account the track class, characteristic sections of the route, and driving speeds, result files were created containing spectra of linear accelerations in the longitudinal, vertical, and lateral directions of selected points of the cabin platform. The control program for the simulator platform movement, forced by six actuators (Figure 9), using the created files generates functions described by Equations (11) and (12). Figure 11a shows the course of lateral accelerations obtained from the experiment and from the generator (Figure 11b) for one point of the platform, at a driving speed of 80 km/h during a curve.
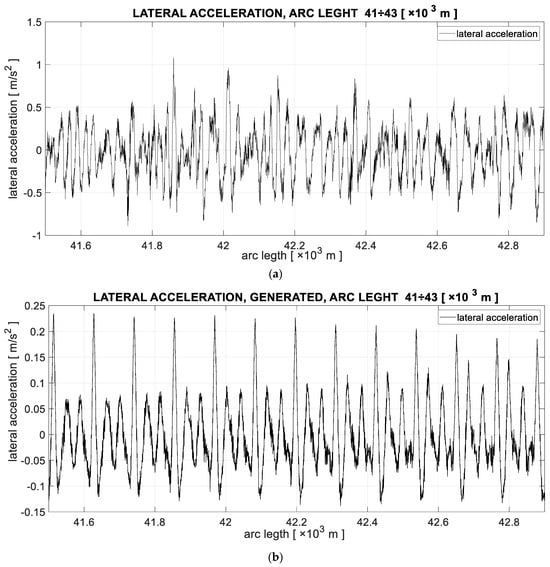
Figure 11.
Example courses of lateral (a) accelerations recorded on the floor of the driver’s cabin and lateral (b) accelerations generated on the simulation process of the driver’s cabin floor, at the location of the driver’s seat mounting.
However, Figure 12 shows the corresponding frequency characteristics in the form of spectral power densities.
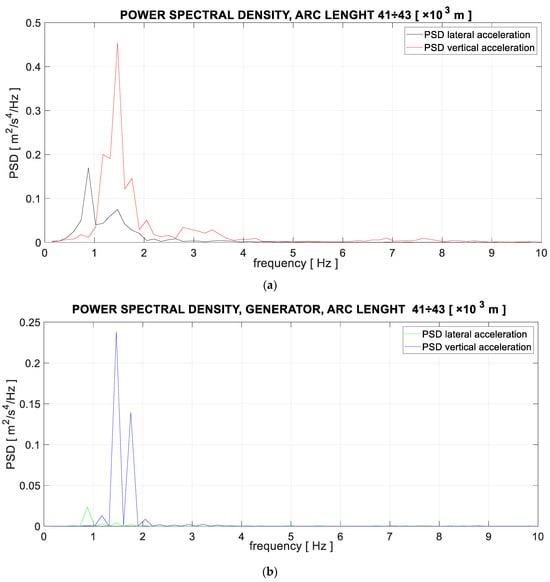
Figure 12.
Power spectral density plots of signals: (a) signal recorded during the experiment, (b) signal generated.
Comparing the realizations of acceleration signals, Figure 11a,b, it is difficult to assess the conformity both qualitatively and quantitatively. However, in the case of their frequency characteristics in the form of spectral power densities, it can be considered that satisfactory qualitative conformity was achieved in this and other cases, considering the frequency range up to 10 Hz. This result is significant considering the behavior of the simulated cabin, because as shown in works [21,24], frequencies from this range have a significant impact on the dynamic behavior of the rail vehicle, including the locomotive cabin.
In the study, scenarios were presented in which the movement forces of the vehicle simulator are associated with forces stemming from the subgrade. When considering the rail track, it is necessary to include the individual components that make up the passage route, that is, straight track, transition curves, arcs, turnouts, and welded rail joints. It should be noted that forces can also come from the vehicle’s suspension elements, or rather from the detuning of the nominal suspension parameters of the vehicle, which has been presented in works [20,22]. Besides the aspects related to the movement of the vehicle in the interoperable railway system, it is necessary to consider the possibility of vehicles moving on dedicated infrastructure in terms of meeting safety requirements, as presented in works [23,24]. Significant factors during the modeling of the locomotive cabin forces are issues related to the vehicle’s aerodynamics and the forces that are generated while the vehicle is moving in difficult weather conditions, which among others was presented in work [25].
The described model generating platform forces of the simulator was applied in the built simulator of the EP09 locomotive [25].
7. Summary
Railway simulators play a key role in staff education and training. Modern training methods using simulators focus on increasing interactivity, engaging participants, and the possibility of practical application of acquired knowledge in a safe, controlled environment. The development of gamification techniques that introduce game elements into the training process is a promising direction aimed at increasing the motivation and involvement of participants. In addition, simulators offer the opportunity to repeatedly practice complex procedures and emergency situations, which is impossible to achieve in traditional forms of training.
In the context of global efforts towards sustainable development, railway simulators are becoming a tool supporting ecological aspects of transport. By simulating various operational scenarios and their impact on the environment, it is possible to optimize work procedures and strategies to minimize emissions of harmful substances and energy consumption. Moreover, simulators enable the exploration and testing of innovative technological solutions, such as new types of drives or energy regeneration systems, before they are implemented in a real operational environment.
Current development directions and research in the field of railway simulators indicate the growing role of digital technologies, emphasis on realism, and training effectiveness, as well as the increasing consideration of ecological aspects in rail. The development of railway simulators not only contributes to the safety and efficiency of rail transport, but also opens new opportunities for research, innovation and sustainable development in this field. Further technological and scientific advances will be crucial in shaping the future of simulation in rail transport, with benefits for both industry and society.
This study addressed the issue of using mathematical models to generate signals that force the motion of the platform of a rail vehicle’s cabin simulator. Two types of models were presented. The classical mathematical model in the form of dynamic equations of motion, whose solution in the form of time histories of coordinates describing the behavior of characteristic points of the real object, can be used to generate signals that force the movement of the simulator cabin platform.
The described model was used in the construction of the simulator cabin of an EU09 type locomotive. The built simulator allows driving on straight tracks, turnouts, and on tracks with curves, allowed depending on the speed of travel, in the conditions of Polish railways, in accordance with the conditions set out in the regulations of the EU and the Polish PKP operator. It is also possible to simulate different seasons and weather conditions. The built simulator allows driving on straight tracks, turnouts and on tracks with curves, allowed depending on the speed of travel, in the conditions of Polish railways, in accordance with the conditions set out in the regulations of the EU and the Polish PKP operator. It is also possible to simulate different seasons and weather conditions. The built and launched simulator can be considered an implementation of the method described in the article and is a continuation of the work described in the work.
The second model described is based on the use of time histories recorded at appropriately selected points of the object during experiments conducted according to designed scenarios on the real object under real operating conditions. Functions were defined to allow the use of recorded formulas in the simulation model and control program. The described method of generating control signals for actuators that force the movement of the simulator cabin platform does not require solving nonlinear dynamic equations of motion at every time step, which, in the case of including a nonlinear contact model and nonlinear functions describing rail track irregularities, requires access to a fast computer with significant computing power. The second model described was used in the construction of the simulator cabin of an EU09 type locomotive.
Author Contributions
Conceptualization—A.C., I.G., J.G., S.K., A.K. and A.S.; methodology—A.C., I.G. and J.G.; software—S.K. and A.S.; validation—I.G., S.K. and A.K.; formal analysis—A.C., I.G.; investigation—A.C., I.G., J.G., S.K., A.K. and A.S.; resources—I.G., A.K. and S.K.; data curation—S.K.; writing—A.C., I.G., J.G., S.K., A.K. and A.S.; visualization—S.K. and A.S.; supervision—A.C. and J.G.; project administration—A.S. Funding acquisition—A.S. All authors have read and agreed to the published version of the manuscript.
Funding
Administrative support provided by the administrative services of the Faculty of Transport of the Warsaw University of Technology.
Data Availability Statement
The datasets presented in this article are not readily available because are part of the technical tests performed by the rolling stock testing laboratory of the Railway Institute in Warsaw, in which the authors of the article participated. The results of these studies are not publicly available.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Maryniak, J. Dynamiczna Teoria Obiektów Ruchomych; Politechnika Warszawska, Prace Naukowe, Mechanika Nr 32, Oficyna Wydawnicza Politechniki Warszawskiej: Warszawa, Poland, 1976. [Google Scholar]
- Chudzikiewicz, A.; Drożdziel, J.; Kisilowski, J.; Żochowski, A. Modelowanie I Analiza Dynamiki Układu Mechanicznego Tor-Pojazd; PWN: Warszawa, Poland, 1982. [Google Scholar]
- Uic Leaflet. Uic 518, Testing and Approval of Railway Vehicles from the Point of View of their Dynamic Behaviour–Safety–Track Fatigue–Ride Quality; International Union of Railways (Uic) Leaflet: Paris, France, 2009. [Google Scholar]
- En 14363; Railway Applications—Testing for the Acceptance of Running Characteristics of Railway Vehicles—Testing of Running Behaviour and Stationary Tests. European Committee for Standardization: Bruxelles, Belgium, 2016.
- Sowiński, B.; Stelmach, A.; Chudzikiewicz, A. Simulation Analysis of the Influence of Changes in track Parameters on Running Saffor of a Rail Vehicle. Energies 2021, 14, 5882. [Google Scholar] [CrossRef]
- Railway Passenger Transport Statistics—Quarterly and Annual Data. Eurostat. 2023. Available online: https://ec.europa.eu/eusurvey/runner/EStatUSS2024 (accessed on 17 February 2024).
- Jankowski, J. Research and Training Car Driving Simulator with Weight Up to 3.5 Tons Dedicated to Physical Disabled Drivers. Mechanik 2019, 8–9, 571–573. [Google Scholar] [CrossRef]
- Gudzbeler, G. Symulatory Pojazdów W Procesie Szkolenia Podmiotów Odpowiedzialnych Za Bezpieczeństwo Wewnętrzne; Difin: Warszawa, Poland, 2018; 208p. [Google Scholar]
- Öztürk, V.; Arar, Ö.F.; Rende, F.; Öztemel, E.; Sezer, S. Validation of Railway Vehicle Dynamic Models in Training Simulators. Veh. Syst. Dynamics 2017, 55, 41–71. [Google Scholar] [CrossRef]
- Drewnowski, A. The Use of Simulators of Traction Vehicles in Train Drivers’ Training in Rail Transport in Poland; Zeszyty Naukowe Uniwersytetu Szczecińskiego Problemy Transportu i Logistyki: Szczecin, Poland, 2018; Volume 43, pp. 33–41. [Google Scholar]
- Drewnowski, A. Problems Related to the Implementation of a Complex Training System and Professional Development of Train Drivers Using Traction Vehicle Simulators in the Polish Railway Transport. Procedia Comput. Sci. 2021, 192, 4486–4492. [Google Scholar] [CrossRef]
- Tucki, K.; Wasiak, A.; Orynycz, O.; Mruk, R. Computer Simulation as a Tool for Managing the Technical Development of Methods for Diagnosing the Technical Condition of a Vehicle. Energies 2020, 13, 2869. [Google Scholar] [CrossRef]
- Melnik, R.; Koziak, S. Rail Vehicle Suspension Condition Monitoring—Approach and Implementation. J. Vibroeng. 2017, 19, 1. [Google Scholar] [CrossRef]
- Vignati, M.; Debattisti, N.; Bacci, M.L.; Tarsitano, D. A Software-in-the-Loop Simulation of Vehicle Control Unit Algorithms for a Driverless Railway Vehicle. Appl. Sci. 2021, 11, 6730. [Google Scholar] [CrossRef]
- Melnik, R.L.; Koziak, S.L.; Dižo, J.; Kuźmierowski, T.; Piotrowska, E. Feasibility Study of a Rail Vehicle Damper Fault Detection by Artificial Neural Indexed by: Networks. Eksploat Niezawodn.-Maint. Reliab. 2023, 25, 5. [Google Scholar] [CrossRef]
- Ke, Q.; Zhang, Y. Research on Automatic Operation Control Algorithm of High Speed Train Based on Artificial Neural Network. IOP Conf. Series Mater. Sci. Eng. 2019, 677, 042046. [Google Scholar] [CrossRef]
- Koper, E.; Kochan, A. Testing the Smooth Driving of a Train Using a Neural Network. Sustainability 2020, 12, 4622. [Google Scholar] [CrossRef]
- Nordmark, S. Vti Driving Simulator. Mathematical Model of a Four-Wheeled Vehicle for Simulation in Real Time; Vti Repart Nr 0267A; Swedish Road & Traffic Research Institute: Linkoping, Sweden, 1984. [Google Scholar]
- Kortum, W.; Schiehlen, W. General Purpose Vehicle System Dynamics Software Based on Multibody Formalisms. Veh. Syst. Dynamics 1985, 14, 229–263. [Google Scholar] [CrossRef]
- Jamson, S.L.; Jamson, A.H. The validity of a low-cost simulator for the assessment of the effects of in-vehicle information systems. Saf. Sci. 2010, 48, 1477–1483. [Google Scholar] [CrossRef]
- Wickens, A.H. Paper 1: The Dynamics of Railway Vehicles on Straight Track: Fundamental Considerations of Lateral Stability. Proc. Inst. Mech. Eng. Conf. Proc. 1965, 180 Pt 3, 29–44. [Google Scholar] [CrossRef]
- Wickens, A. Fundamentals of Rail Vehicle Dynamics: Guidance and Stability; Swets & Zettlinger: Lisse, The Netherlands; CRC Press: London, UK, 2003. [Google Scholar]
- Kalker, J.J. Three-Dimensional Elastic Bodies in Rolling Contact; Kluwer Acadamic Publishers: Alphen aan den Rijn, The Netherlands, 1990. [Google Scholar]
- Kisilowski, J.; Knothe, K. Advanced Railway Vehicle System Dynamics; Kisilowski, J., Knothe, K., Eds.; WNT: Warszawa, Poland, 1991. [Google Scholar]
- Chudzikiewicz, A.; Droździel, J.; Szulczyk, A. A Model of a Cabin simulator for Assessing Vibrations in an Electric Locomotive. In Proceedings of the Fifth International Conference “Comprail’96”, Berlin, Germany, 21–23 August 1996; Computers in Railways, V.; Computational Mechanics Publications. WIT Press: Southampton, UK, 1996; Volume 2. [Google Scholar]
- Wittenbeck, L.; Milecki, S.; Barna, G. Platforma Stewarta-Gougha jako układ ruchu symulatora jazdy pojazdu szynowego. Pojazdy Szyn. 2012, 2012, 64–70. [Google Scholar] [CrossRef]
- Dąbrowski, A.; Koszela, J.; Król, D.; Szafrański, Z.; Wantoch-Rekowski, R. Projekt Nowoczesnego Demonstratora Symulatora Dla Operatorów Pojazdów Szynowych; TTS—Technika Transportu Szynowego: Radom, Poland, 2015. [Google Scholar]
- Lozia, Z. Application of Modelling and Simulation in Durability Tests of Vehicles and Their Components. Energies 2022, 15, 9398. [Google Scholar] [CrossRef]
- Blissing, B. Driving in Virtual Reality: Requirements for Automotive Research and Development. In Linköping Studies in Science and Technology; Linköping Studies in Science and Technology; Dissertations; T. 2085; Linköping University Electronic Press: Linköping, Sweeden, 2020. [Google Scholar]
- Rill, G.; Castro, A.A. Road Vehicle Dynamics. Fundamentals and Modeling with Matlab®, 2nd ed.; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2020; ISBN 9780367199739. [Google Scholar]
- Xu, X.; Yang, L.; Gao, Z.; Long, J. Simulations for Train Track Flow on Single-Track Railways with Speed Limits and Slopes. J. Simul. 2017, 11, 346–356. [Google Scholar] [CrossRef]
- Findeisen, W.; Gutenbaum, J. Modele W Analizie Systemowej. Analiza Systemowa—Podstawy I Metodologia; PWN: Warszawa, Poland, 1985. [Google Scholar]
- Jia, C.; Xu, H.; Wang, L. Nonlinear Hybrid Multipoint Model of High-Speed Train with Traction/Braking Dynamic and Speed Estimation Law. Math. Probl. Eng. 2019, 2019, 1364657. [Google Scholar] [CrossRef]
- Chudzikiewicz, A.; Sowińska, M. Modelling the Dynamics of an Unconventional Rail Vehicle Bogie with Independently Rotating Wheels with the Use of Boltzmann-Hamel Equations. Veh. Syst. Dynamics 2022, 60, 865–883. [Google Scholar] [CrossRef]
- Myśliński, A.; Chudzikiewicz, A. Power Dissipation and Wear Modeling in Wheel-Rail Contact. Appl. Sci. 2023, 14, 165. [Google Scholar] [CrossRef]
- Kocsis, L.; Iclodean, C.D.; Gaspar, F.; Burnete, N.V. Comparison of International Vehicle Testing Cycles Using Simulation. Rom. J. Tech. Sci. 2018, 1, 25–35. [Google Scholar]
- Hu, L.; Fang, S.; Yang, J. Study of the Vehicle Controllability and Stability Based on Multi-Body System Dynamics. Open Mech. Eng. J. 2014, 8, 865–871. [Google Scholar] [CrossRef]
- Negrut, D.; Serban, R.; Mazhar, H.; Heyn, T. Parallel Computing in Multibody System Dynamics: Why, When and How. J. Comput. Nonlinear Dyn. 2014, 9, 041007. [Google Scholar] [CrossRef]
- Mei, T.X.; Zhou, Y.J. Systems-On-Chip Approach for Real-Time Simulation of Wheel–Rail Contact Laws. Veh. Syst. Dynamics 2013, 51, 542–553. [Google Scholar] [CrossRef]
- Wu, Q.; Spiryagin, M.; Persson, I.; Bosomworth, C.; Cole, C. Parallel Computing of Wheel-Rail Contact. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 1109–1116. [Google Scholar] [CrossRef]
- Shrestha, S.; Spiryagin, M.; Wu, Q. Real-Time Multibody Modeling and Simulation of a Scaled Bogie Test Rig. Railw. Eng. Sci. 2020, 28, 146–159. [Google Scholar] [CrossRef]
- Gąsowski, W. Aerodynamika Pociągu; Wydawnictwo I Zakład Poligrafii Instytutu Technologii I Eksploatacji: Warszawa, Poland, 1998; ISBN 83-7204-041-9. [Google Scholar]
- Tomczuk, P.; Koniak, M.; Jaskowski, P.; Mytrovtsiy, S.; Kowalski, R. Budowa Symulatora Jazdy Samochodem Przeznaczonego Do Badania Procesów Ruchu Drogowego. Pr. Nauk. Politech. Warsz. Transp. 2017, Z.118, 313–324. [Google Scholar]
- Bendat, J.S.; Piersol, A.G. Metody Analizy I Pomiaru Sygnałów Losowych; PWN: Warszawa, Poland, 1976. [Google Scholar]
- Osiowski, J. Zarys Rachunku Operatorowego; WNT: Warszawa, Poland, 1965. [Google Scholar]
- Chudzikiewicz, A. Red.: Monitorowanie Stanu Układu Dynamicznego Pojazd Szynowy—Tor; Warsaw University of Technology Publishing: Warsaw, Poland, 2012; ISBN 978-83-7814-050-4. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).