Power and Energy Losses in Medium-Voltage Power Grids as a Function of Current Asymmetry—An Example from Poland
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rafał, K.; Biskupski, J.; Bykuć, S.; Chaja, P. Dynamic Voltage Regulation and Unbalance Compensation in a Low-Voltage Distribution Network Using Energy Storage System. Appl. Sci. 2022, 12, 11678. [Google Scholar] [CrossRef]
- Pourasl, H.H.; Barenji, R.V.; Khojastehnezhad, V.M. Solar energy status in the world: A comprehensive review. Energy Rep. 2023, 10, 3474–3493. [Google Scholar] [CrossRef]
- Larina, Y.; Galchynska, J.; Kucheruk, P.; Zghurska, O.; Ortina, G.; Al-Nadzhar, F.; Marusei, T.; Kubon, M.; Dzieniszewski, G. Estimation of the Domestic Agricultural Sector Potential for the Growth of Energy Cultures for Bioenergy Fuel Production. Agric. Eng. 2021, 25, 73–82. [Google Scholar] [CrossRef]
- Ismael, S.M.; Abdel Aleem, S.H.E.; Abdelaziz, A.Y.; Zobaa, A.F. State-of-the-art of hosting capacity in modern power systems with distributed generation. Renew. Energy 2019, 130, 1002–1020. [Google Scholar] [CrossRef]
- Babu, V.V.; Roselyn, J.P.; Sundaravadivel, P. Coordination of SRF-PLL and Grid Forming Inverter Control in Microgrid with Solar PV and Energy Storage. J. Low Power Electron. Appl. 2024, 14, 29. [Google Scholar] [CrossRef]
- Al Kez, D.; Foley, A.M.; McIlwaine, N.; Morrow, D.J.; Hayes, B.P.; Zehir, M.A.; Mehigan, L.; Papari, B.; Edrington, C.S.; Baran, M. A critical evaluation of grid stability and codes, energy storage and smart loads in power systems with wind generation. Energy 2020, 205, 117671. [Google Scholar] [CrossRef]
- Hołdyński, G.; Skibko, Z.; Borusiewicz, A. Analysis of the Influence of Load on the Value of Zero-Voltage Asymmetry in Medium-Voltage Networks Operating with Renewable Energy Sources. Energies 2023, 16, 580. [Google Scholar] [CrossRef]
- Hołdyński, G.; Skibko, Z.; Firlit, A.; Walendziuk, W. Analysis of the Impact of a Photovoltaic Farm on Selected Parameters of Power Quality in a Medium-Voltage Power Grid. Energies 2024, 17, 623. [Google Scholar] [CrossRef]
- Ferreira, P.D.F.; Carvalho, P.M.S.; Ferreira, L.A.F.M.; Ilic, M.D. Distributed energy resources integration challenges in low-voltage networks: Voltage control limitations and risk of cascading. IEEE Trans. Sustain. Energy 2013, 4, 82–88. [Google Scholar] [CrossRef]
- Ghosh, S.; Rahman, S.; Pipattanasomporn, M. Distribution Voltage Regulation Through Active Power Curtailment with PV Inverters and Solar Generation Forecasts. IEEE Trans. Sustain. Energy 2017, 8, 13–22. [Google Scholar] [CrossRef]
- Demirok, E.; González, P.C.; Frederiksen, K.H.B.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local Reactive Power Control Methods for Overvoltage Prevention of Distributed Solar Inverters in Low-Voltage Grids. IEEE J. Photovolt. 2011, 2, 174–182. [Google Scholar] [CrossRef]
- Nejabatkhah, F.; Li, Y.W. Flexible Unbalanced Compensation of Three-Phase Distribution System Using Single-Phase Distributed Generation Inverters. IEEE Trans. Smart Grid 2017, 10, 1845–1857. [Google Scholar] [CrossRef]
- Kabir, M.N.; Mishra, Y.; Ledwich, G.; Dong, Z.Y.; Wong, K.P. Coordinated Control of Grid-Connected Photovoltaic Reactive Power and Battery Energy Storage Systems to Improve the Voltage Profile of a Residential Distribution Feeder. IEEE Trans. Ind. Inform. 2014, 10, 967–977. [Google Scholar] [CrossRef]
- Kuboń, M.; Skibko, Z.; Tabor, S.; Malaga-Toboła, U.; Borusiewicz, A.; Romaniuk, W.; Zarajczyk, J.; Neuberger, P. Analysis of Voltage Distortions in the Power Grid Arising from Agricultural Biogas Plant Operation. Energies 2023, 16, 6189. [Google Scholar] [CrossRef]
- Pamuk, N.; Uzun, U.E. Optimal Allocation of Distributed Generations and Capacitor Banks in Distribution Systems Using Arithmetic Optimization Algorithm. Appl. Sci. 2024, 14, 831. [Google Scholar] [CrossRef]
- Watson, J.D.; Watson, N.R.; Lestas, I. Optimized dispatch of energy storage systems in unbalanced distribution networks. IEEE Trans. Sustain. Energy 2017, 9, 639–650. [Google Scholar] [CrossRef]
- Hock, R.T.; de Novaes, Y.R.; Batschauer, A.L. A Voltage Regulator for Power Quality Improvement in Low-Voltage Distribution Grids. IEEE Trans. Power Electron. 2018, 33, 2050–2060. [Google Scholar] [CrossRef]
- El-Naggar, A.; Erlich, I. Control approach of three-phase grid connected PV inverters for voltage unbalance mitigation in low-voltage distribution grids. IET Renew. Power Gener. 2016, 10, 1577–1586. [Google Scholar] [CrossRef]
- Prístavka, M.; Findura, P.; Beloev, I.; Kuboń, M.; Hrdá, V.; Kovalyshyn, S.; Shchur, T. Verification of the Measurement System in a Production Organization. Agric. Eng. 2022, 26, 81–90. Available online: https://sciendo.com/article/10.2478/agriceng-2022-0007 (accessed on 24 June 2024). [CrossRef]
- Shahnia, F.; Majumder, R.; Ghosh, A.; Ledwich, G.; Zare, F. Voltage imbalance analysis in residential low voltage distribution networks with rooftop PVs. Electr. Power Syst. Res. 2011, 81, 1805–1814. [Google Scholar] [CrossRef]
- Ciontea, C.I.; Iov, F. A Study of Load Imbalance Influence on Power Quality Assessment for Distribution Networks. Electricity 2021, 2, 77–90. [Google Scholar] [CrossRef]
- Hussan, M.R.; Sarwar, M.I.; Sarwar, A.; Tariq, M.; Ahmad, S.; Shah Noor Mohamed, A.; Khan, I.A.; Ali Khan, M.M. Aquila Optimization Based Harmonic Elimination in a Modified H-Bridge Inverter. Sustainability 2022, 14, 929. [Google Scholar] [CrossRef]
- Bajo, C.G.; Hashemi, S.; Kjær, S.B.; Yang, G.; Østergaard, J. Voltage unbalance mitigation in LV networks using three-phase PV systems. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015. [Google Scholar] [CrossRef]
- Caldon, R.; Coppo, M.; Turri, R. Distributed voltage control strategy for LV networks with inverter-interfaced generators. Electr. Power Syst. Res. 2014, 107, 85–92. [Google Scholar] [CrossRef]
- Tamoor, M.; Habib, S.; Bhatti, A.R.; Butt, A.D.; Awan, A.B.; Ahmed, E.M. Designing and Energy Estimation of Photovoltaic Energy Generation System and Prediction of Plant Performance with the Variation of Tilt Angle and Interrow Spacing. Sustainability 2022, 14, 627. [Google Scholar] [CrossRef]
- Chang, C.-K.; Cheng, S.-T.; Boyanapalli, B.-K. Three-Phase Unbalance Improvement for Distribution Systems Based on the Particle Swarm Current Injection Algorithm. Energies 2022, 15, 3460. [Google Scholar] [CrossRef]
- Weckx, S.; Driesen, J. Load balancing with EV chargers and PV inverters in unbalanced distribution grids. IEEE Trans. Sustain. Energy 2015, 6, 635–643. [Google Scholar] [CrossRef]
- Freire, R.; Delgado, J.; Santos, J.M.; De Almeida, A.T. Integration of renewable energy generation with EV charging strategies to optimize grid load balancing. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 392–396. [Google Scholar] [CrossRef]
- Ma, K.; Fang, L.; Kong, W. Review of distribution network phase imbalance: Scale, causes, consequences, solutions, and future research directions. CSEE J. Power Energy Syst. 2020, 6, 479–488. [Google Scholar] [CrossRef]
- Ciontea, C.I. The use of symmetrical components in electrical protection. In Proceedings of the 72nd Conference for Protective Relay Engineers (CPRE), College Station, TX, USA, 25–28 March 2019. [Google Scholar] [CrossRef]
- Martins, A.P.; Rodrigues, P.; Hassan, M.; Morais, V.A. Voltage Unbalance, Power Factor and Losses Optimization in Electrified Railways Using an Electronic Balancer. Electricity 2021, 2, 554–572. [Google Scholar] [CrossRef]
- Skobiej, K. Energy efficiency in rail vehicles: Analysis of contemporary technologies in reducing energy consumption. Rail Veh. 2023, 3–4, 64–70. [Google Scholar] [CrossRef]
- Gruber, R.; O’Brien, D. Use of Modular Multilevel Converter (MMC) Technology in Rail Electrification. In Proceedings of the AusRAIL 2014, Making Making Innovation Work, Perth, Australia, 11–12 November 2014; Available online: https://trid.trb.org/view/1341047 (accessed on 24 June 2024).
- Leemput, N.; Geth, F.; Van Roy, J.; Delnooz, A.; Buscher, J.; Driesen, J. Impact of Electric Vehicle On-Board Single-Phase Charging Strategies on a Flemish residential Grid. IEEE Trans. Smart Grid 2014, 5, 1815–1822. [Google Scholar] [CrossRef]
- Huang, S.; Pillai, J.R.; Bak-Jensen, B.; Thøgersen, P. Voltage support from electric vehicles in distribution grid. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Nájera, J.; Mendonça, H.; de Castro, R.M.; Arribas, J.R. Strategies Comparison for Voltage Unbalance Mitigation in LV Distribution Networks Using EV Chargers. Electronics 2019, 8, 289. [Google Scholar] [CrossRef]
- Singh, D.; Misra, R.K.; Mishra, S. Distribution system feeder re-phasing considering voltage-dependency of loads. Int. J. Electr. Power Energy Syst. 2016, 76, 107–119. [Google Scholar] [CrossRef]
- Abril, I.P. NSGA-II phase balancing of primary distribution circuits by the reconnection of their circuit laterals and distribution transformers. Electr. Power Syst. Res. 2014, 109, 1–7. [Google Scholar] [CrossRef]
- Wang, W.; Wang, W.; Song, S.; Hu, W.; Guo, Q. Study on Daily Line Loss Calculation Based on Operation Data and Resistance Characteristics of Low Voltage Distribution Transformer Area. In Proceedings of the 2021 International Conference on Power System Technology (POWERCON), Haikou, China, 8–9 December 2021; pp. 2093–2096. [Google Scholar] [CrossRef]
- Dai, Z.; Shi, K.; Zhu, Y.; Zhang, X.; Luo, Y. Intelligent Prediction of Transformer Loss for Low Voltage Recovery in Distribution Network with Unbalanced Load. Energies 2023, 16, 4432. [Google Scholar] [CrossRef]
- Nithya, S.; Jeyanthi, K.M. Genetic algorithm based bacterial foraging optimization with three-pass protocol concept for heterogeneous network security enhancement. J. Comput. Sci. 2017, 21, 275–282. [Google Scholar] [CrossRef]
- Naveen, S.; Kumar, K.S.; Rajalakshmi, K. Distribution system reconfiguration for loss minimization using modified bacterial foraging optimization algorithm. Int. J. Electr. Power Energy Syst. 2015, 69, 90–97. [Google Scholar] [CrossRef]
- Saad, N.H.; El-Sattar, A.A.; Marei, M.E. Improved bacterial foraging optimization for grid connected wind energy conversion system based PMSG with matrix converter. Ain Shams Eng. J. 2018, 9, 2183–2193. [Google Scholar] [CrossRef]
- Zhou, L.; Han, W.; Qi, J.; Zhou, Z. Adaptive PI + VPI Harmonic Current Compensation Strategy under Weak Grid Conditions. Appl. Sci. 2023, 13, 5983. [Google Scholar] [CrossRef]
- Fan, Y.; Jun, L.; Bingbing, L. Design and application of integrated distribution network line loss analysis system. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, B.; Xiang, K.; Yang, L.; Su, Q.; Huang, D.; Huang, T. Theoretical Line Loss Calculation of Distribution Network Based on the Integrated Electricity and Line Loss Management System. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 2531–2535. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Song, S.; Hu, W.; Guo, Q. Distribution Network Monthly Line Loss Calculate and Improvement with Convolutional Neural Network. In Proceedings of the 2021 China International Conference on Electricity Distribution (CICED), Shanghai, China, 7–9 April 2021; pp. 1035–1039. [Google Scholar] [CrossRef]
- Sołjan, Z.; Hołdyński, G.; Zajkowski, M. CPC-Based Minimizing of Balancing Compensators in Four-Wire Nonsinusoidal Asymmetrical Systems. Energies 2021, 14, 1815. [Google Scholar] [CrossRef]
- Oliveira, M.E.; Ochoa, L.F.; Padilha-Feltrin, A.; Mantovani, J.R.S. Network reconfiguration and loss allocation in a deregulated environment of distribution systems. In Proceedings of the 18th International Conference on Electricity Distribution, Turin, Italy, 6–9 June 2005. [Google Scholar] [CrossRef]
- Savier, J.S.; Das, D. Impact of network reconfiguration on loss allocation of radial distribution systems. IEEE Trans. Power Deliv. 2007, 22, 2473–2480. [Google Scholar] [CrossRef]
- Chandramohan, S.; Atturulu, N.; Devi, R.P.K.; Venkatesh, B. Operating cost minimization of a radial distribution system in a deregulated electricity market through reconfiguration using NSGA method. Int. J. Electr. Power Energy Syst. 2010, 32, 126–132. [Google Scholar] [CrossRef]
- Atanasovski, M.; Taleski, R. Power summation method for loss allocation in radial distribution networks with DG. IEEE Trans. Power Syst. 2011, 26, 2491–2499. [Google Scholar] [CrossRef]
- Chen, B.; Ye, L.; Cui, T.; Bi, W. Power loss analysis for low-voltage distribution networks with single-phase connected photovoltaic generation. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; pp. 1929–1934. [Google Scholar] [CrossRef]
- Gerkusov; Gracheva, E.; Shumikhina, O.; Valtchev, S. Effect of Unbalanced Load on Electrical Energy Losses in Distribution Grids with a Voltage of 0.4–20 Kv. In Proceedings of the 2022 4th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA), Lipetsk, Russian Federation, 9–11 November 2022; pp. 842–848. [Google Scholar] [CrossRef]
- Porumb, R.; Toader, C.; Golovanov, N.; Leonida, T.; Seritan, G. Energy efficiency rating of transformers under unbalanced linear regime. In Proceedings of the 2015 Intl Aegean Conference on Electrical Machines & Power Electronics (ACEMP), 2015 Intl Conference on Optimization of Electrical & Electronic Equipment (OPTIM) & 2015 Intl Symposium on Advanced Electromechanical Motion Systems (ELECTROMOTION), Side, Turkey, 2–4 September 2015; pp. 538–544. [Google Scholar] [CrossRef]
- Costea, M.; Leonida, T. An Analyze of Power Losses in Distribution Transformers in Unbalanced and Distorted Loadings Conditions. In Proceedings of the 2023 11th International Conference on ENERGY and ENVIRONMENT (CIEM), Bucharest, Romania, 26–27 October 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Niebrzydowski, J. Mathematical Methods for Estimating Selected Operating States of Rural Power Grids; Bialystok University of Technology Publications: Bialystok, Poland, 2001. (In Polish) [Google Scholar]
- Gawlak, A. Calculation of losses in a set of elements consisting of overhead low-voltage rural lines. Arch. Electr. Eng. 1997, XLVI, 367–378. [Google Scholar]
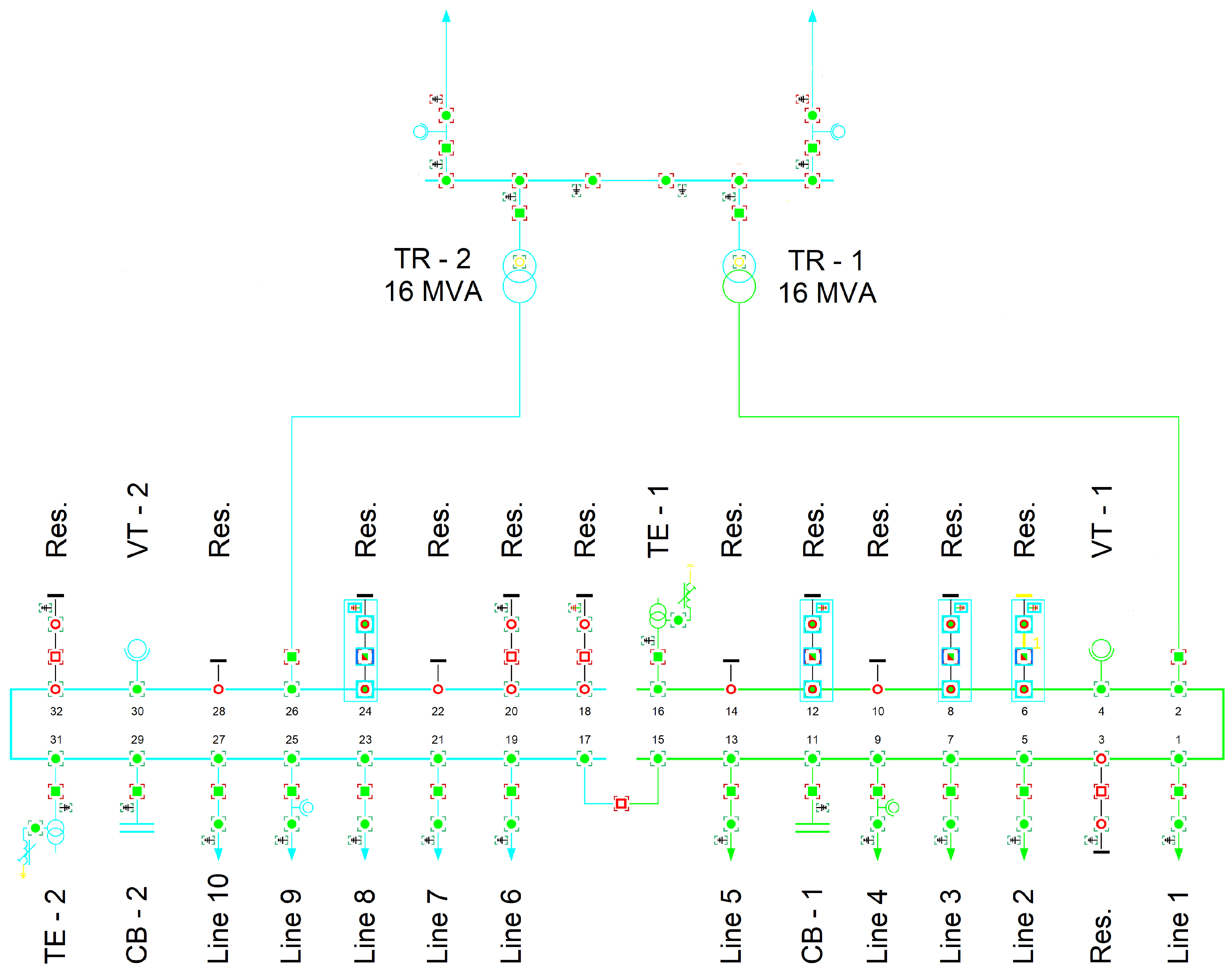
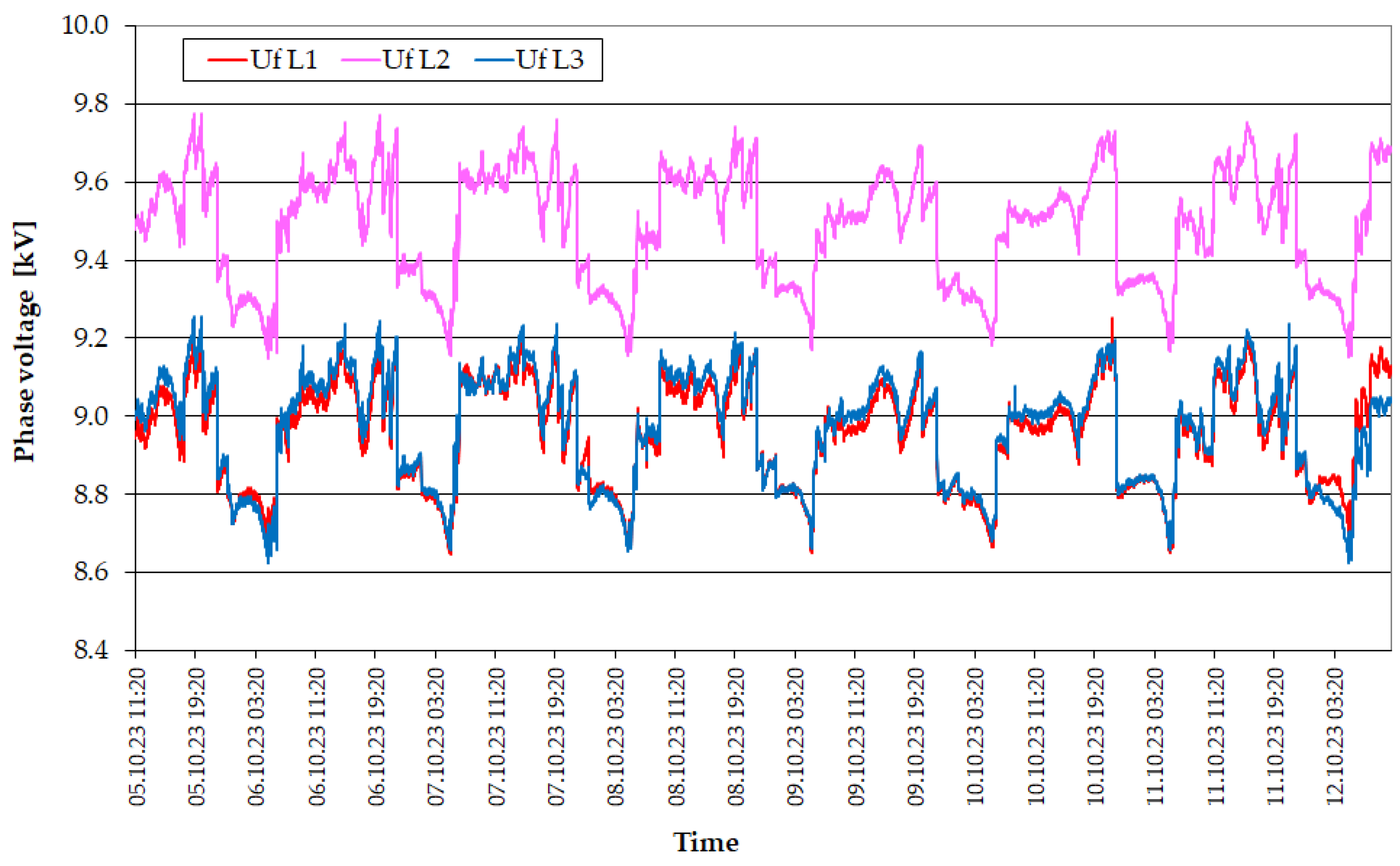

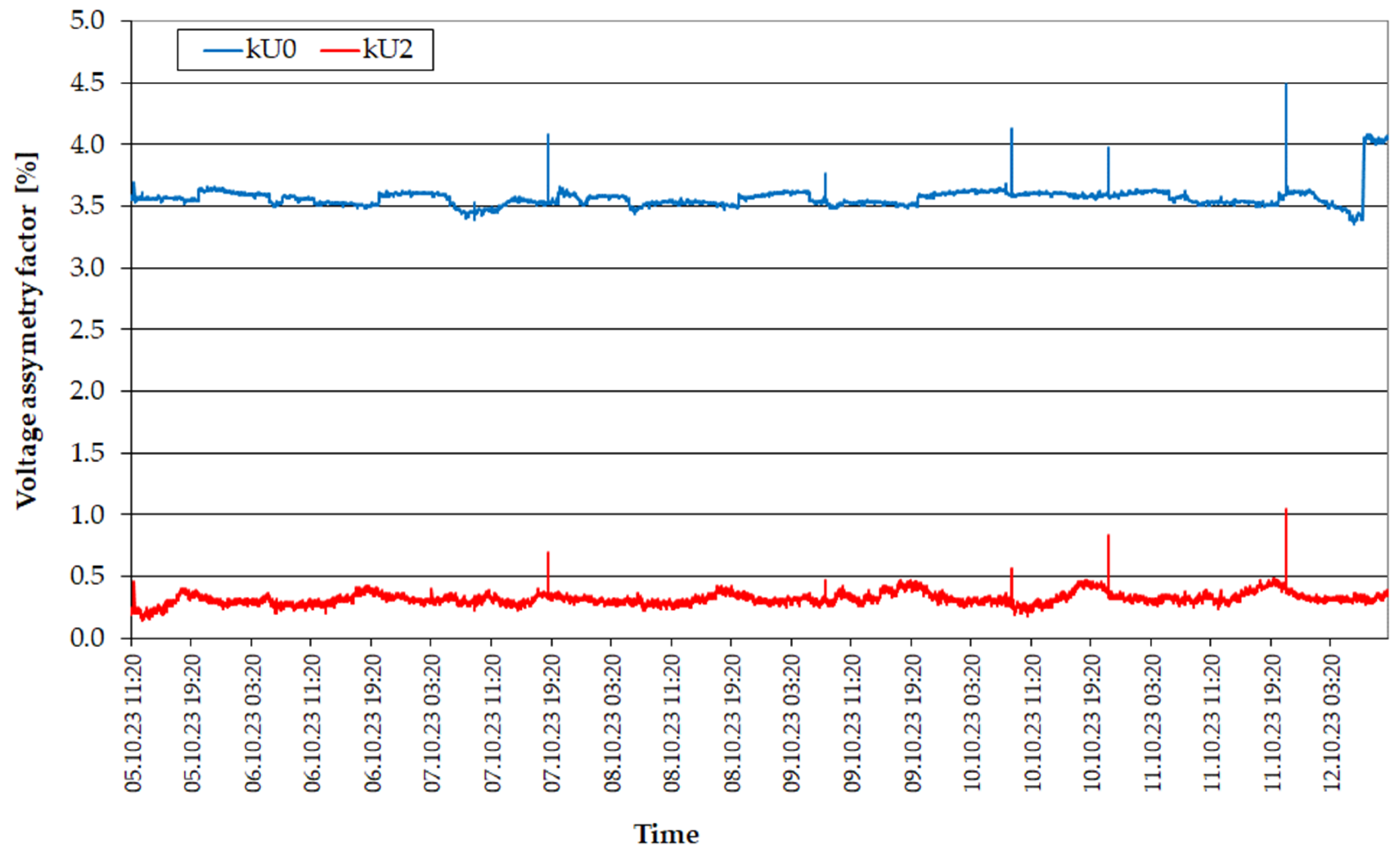
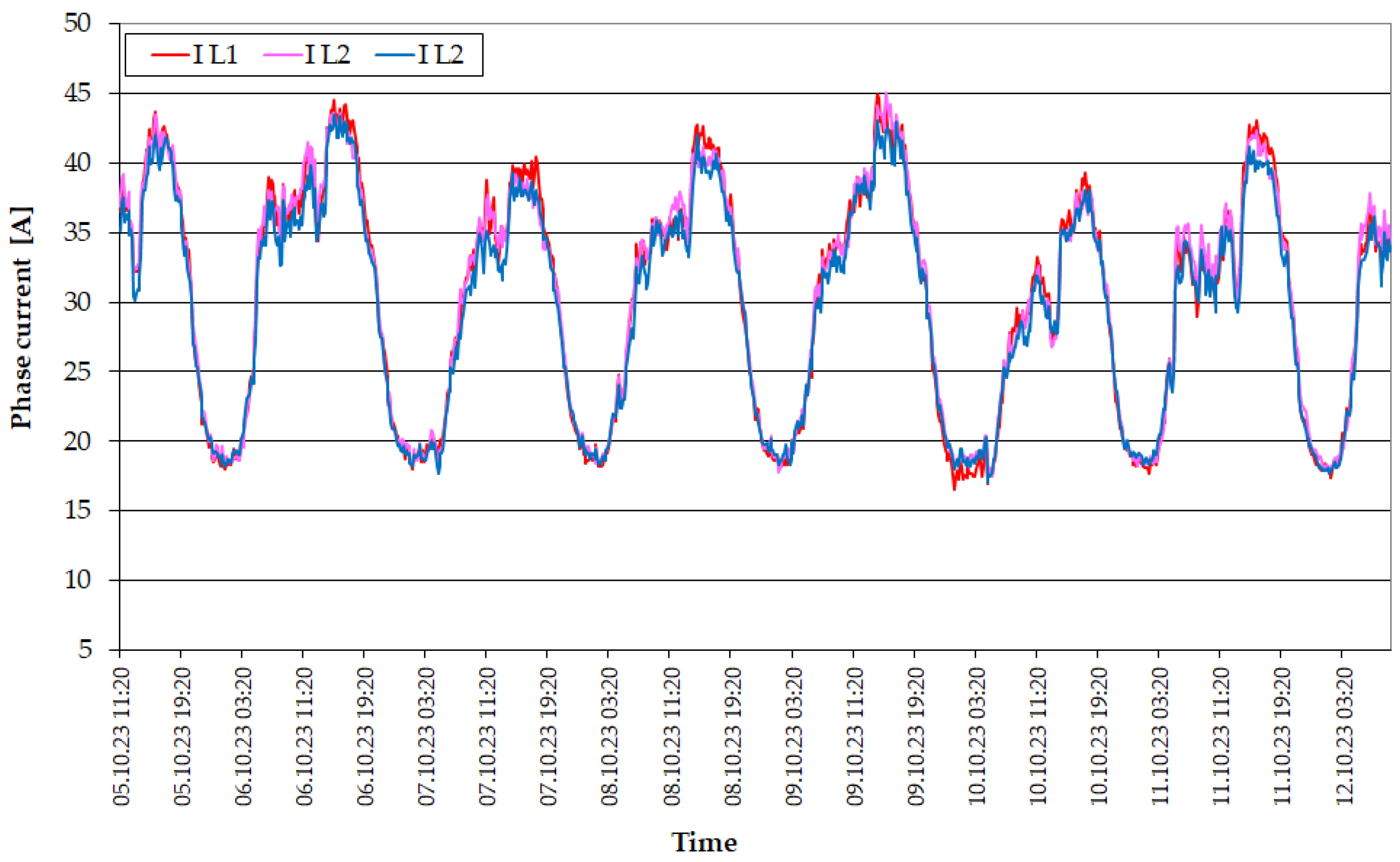



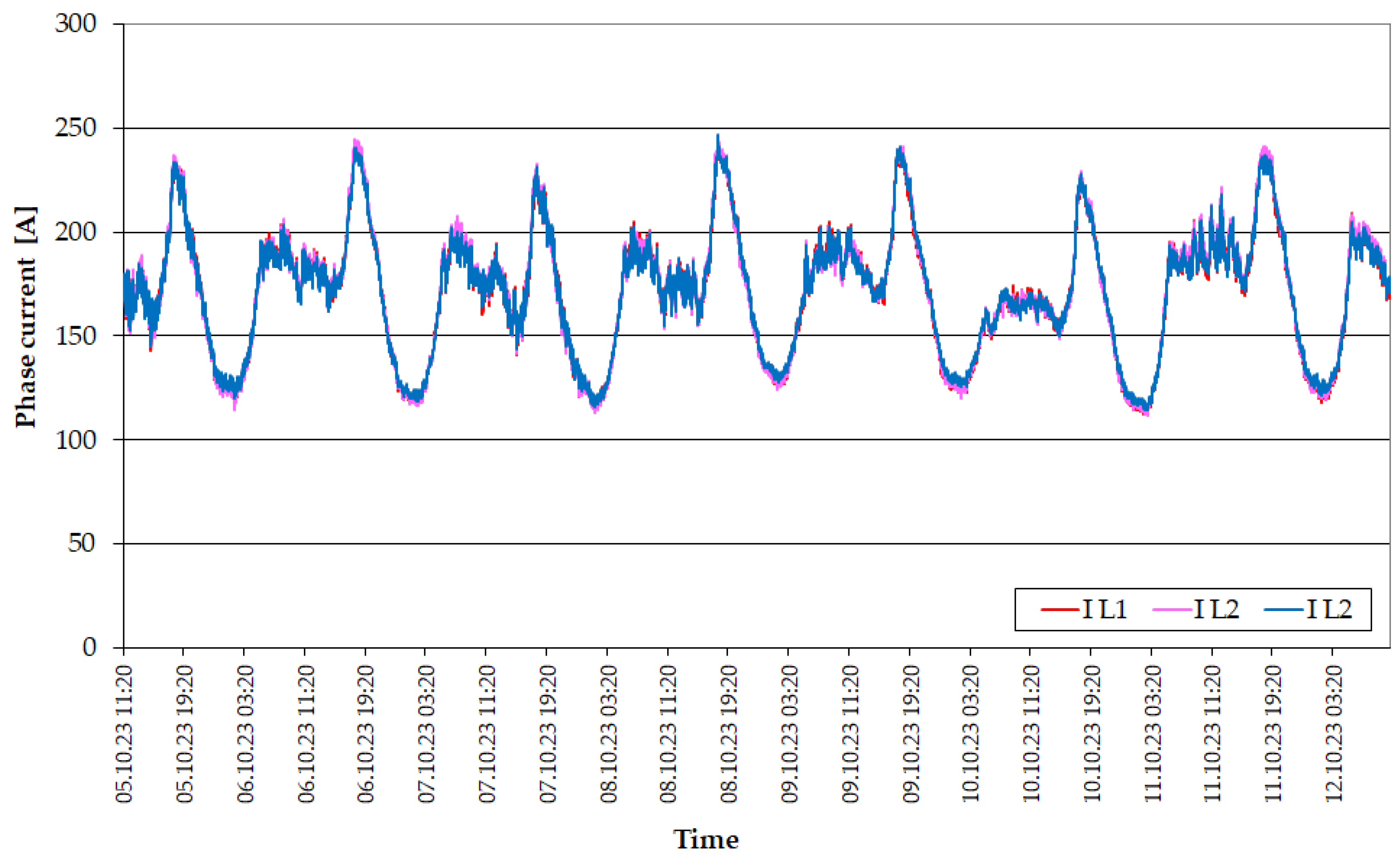
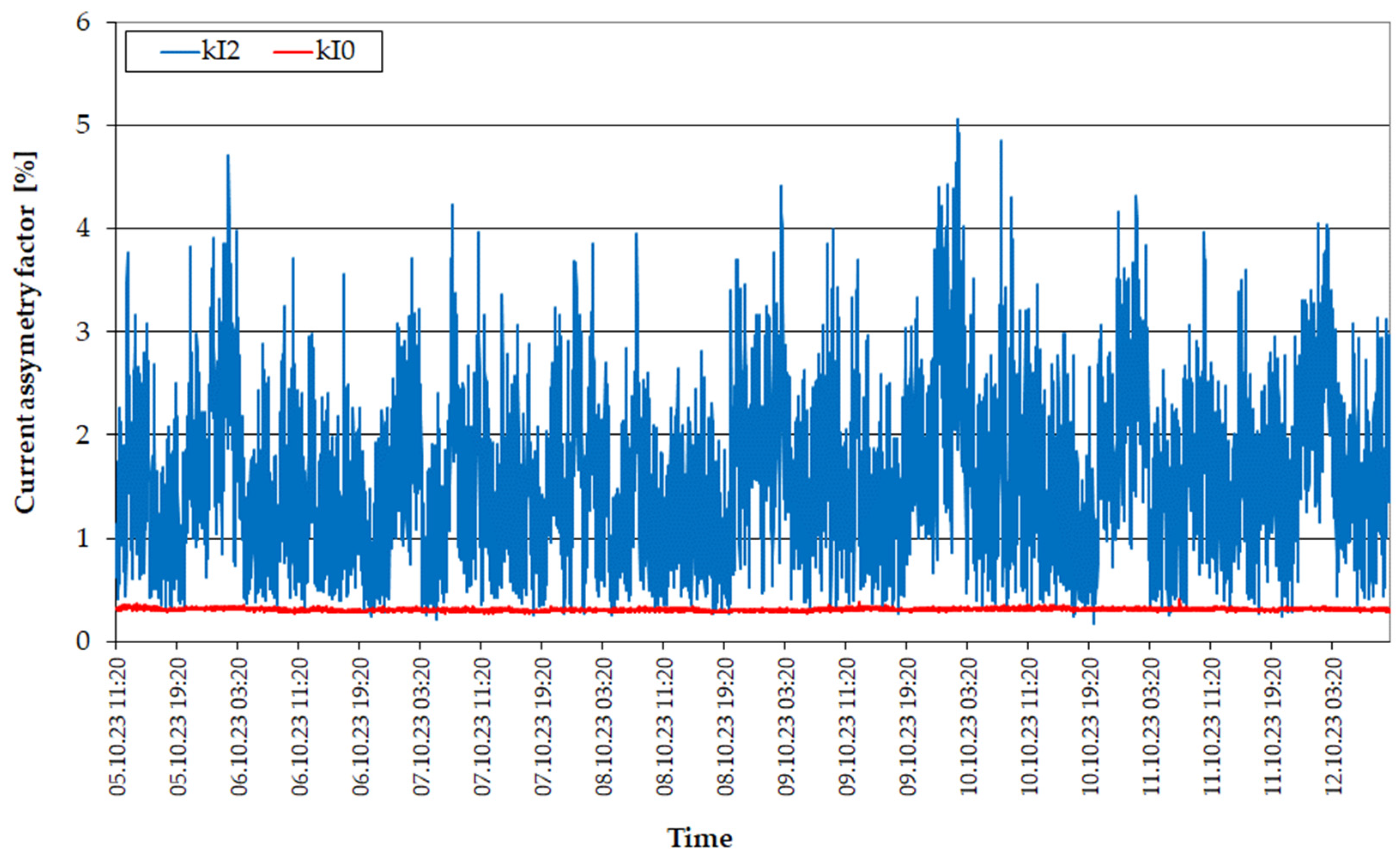
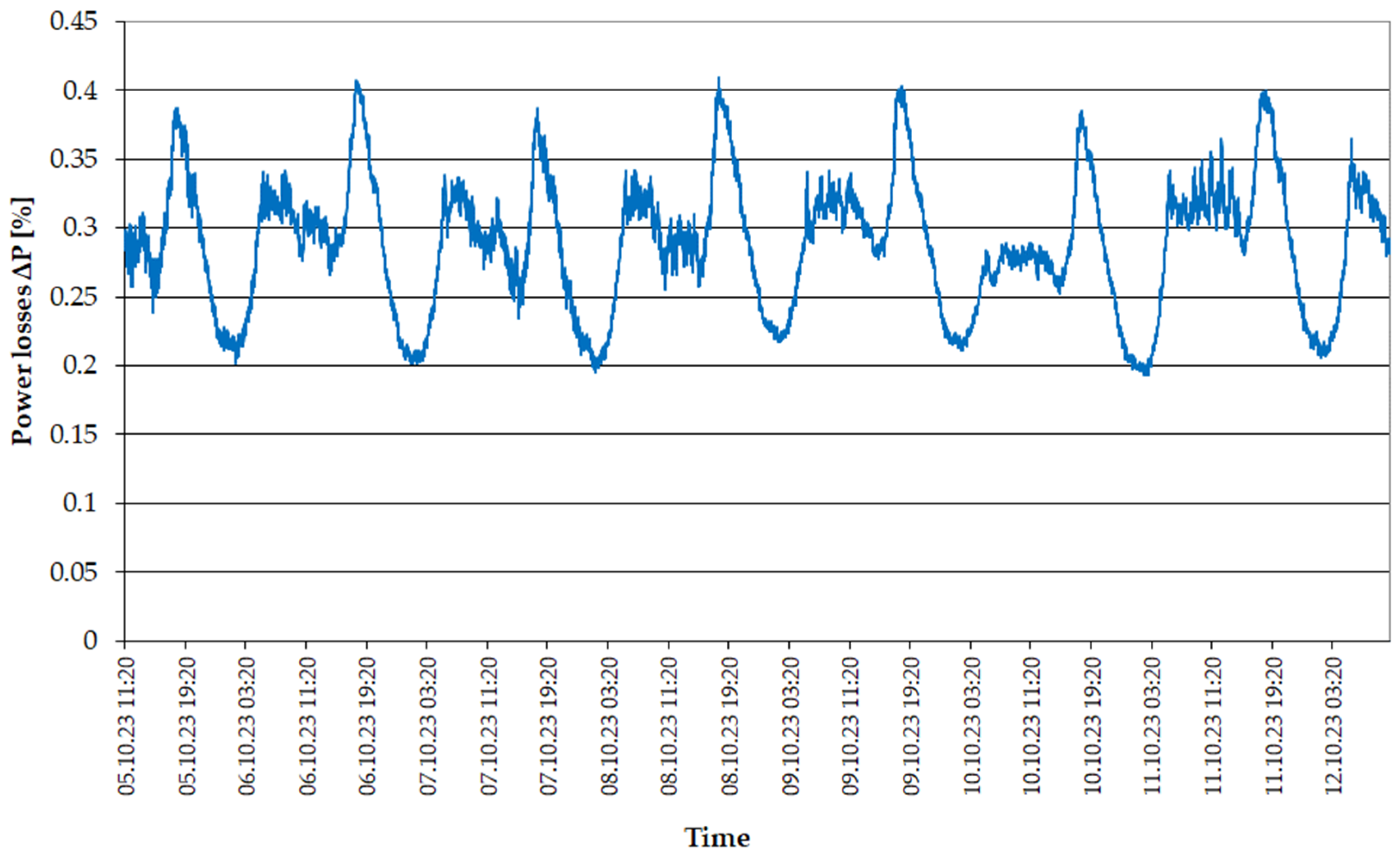
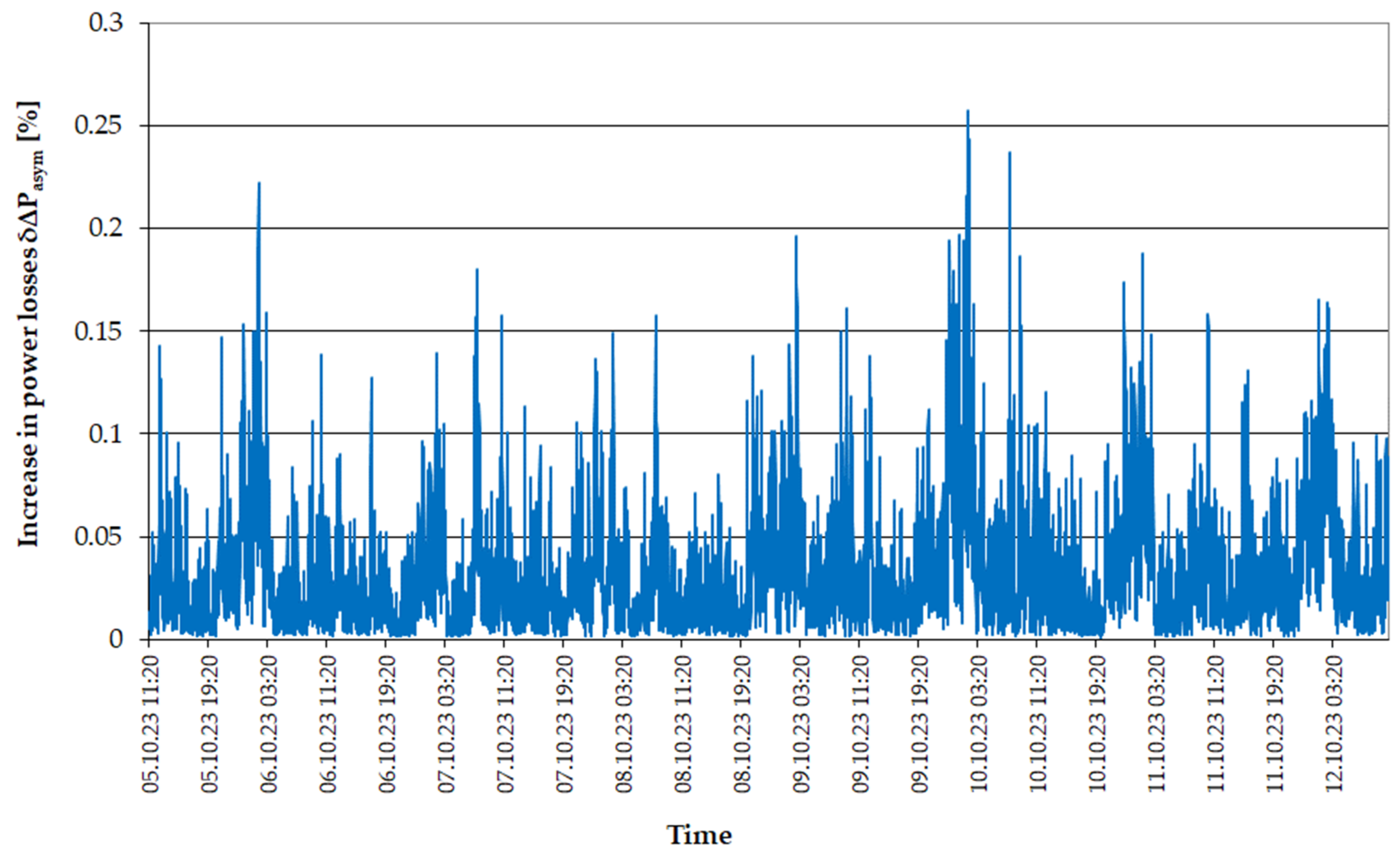


| Transformer Name | Rated Power [MVA] | Rated Voltage [kV] | Vector Group [-] | Impedance Voltage [%] | Load Losses [kW] | No-Load Losses [kW] |
|---|---|---|---|---|---|---|
| TR-1 | 16 | 115/16.5 | Ynd11 | 11.89 | 87.07 | 13.82 |
| TR-2 | 16 | 115/16.5 | Ynd11 | 10.93 | 90.99 | 15.11 |
| Switch-Bay Number | Line Name | Cable Type | Line Length [km] | Number of MV/LV Substations [pcs.] | Total Power of MV/LV Substations [MVA] |
|---|---|---|---|---|---|
| 1 | Line 1 | ACSR 50 | 89 | 56 | 4.6 |
| 5 | Line 2 | ACSR 70 | 21.34 | 30 | 2.52 |
| ACSR 35 | 28.46 | ||||
| 7 | Line 3 | ACSR 50 | 72.3 | 57 | 3.3 |
| 9 | Line 4 | ACSR 70 | 22.86 | 56 | 3.52 |
| ACSR 35 | 53.94 | ||||
| 13 | Line 5 | ACSR 70 | 39.67 | 63 | 4.57 |
| ACSR 35 | 46.98 | ||||
| 19 | Line 6 | ACSR 70 | 20.31 | 40 | 2.67 |
| ACSR 35 | 31.39 | ||||
| 21 | Line 7 | ACSR 70 | 24.9 | 58 | 5.54 |
| ACSR 35 | 30.35 | ||||
| 23 | Line 8 | ACSR 70 | 30.5 | 69 | 4.3 |
| ACSR 50 | 34.2 | ||||
| 25 | Line 9 | ACSR 70 | 23.95 | 62 | 5.83 |
| ACSR 35 | 72.93 | ||||
| 27 | Line 10 | ACSR 50 | 59.6 | 51 | 2.9 |
| Element Name | Average Three-Phase Load PIII [kW] | Average Three-Phase Power Losses ΔPIII [kW] | Average Percentage Power Loss ΔPIII% [%] | Average Power Loss Due to Asymmetry ΔPasym [kW] | Average Percentage Power Loss Due to Asymmetry ΔPasym% [%] |
|---|---|---|---|---|---|
| Line 1 | 1072.70 | 104.44 | 8.810 | 0.2904 | 0.3650 |
| Line 2 | 599.88 | 18.30 | 2.738 | 0.0276 | 0.2118 |
| Line 3 | 807.29 | 42.48 | 4.920 | 0.1117 | 0.2696 |
| Line 4 | 921.29 | 65.73 | 6.479 | 1.5468 | 2.1898 |
| Line 5 | 1206.64 | 118.13 | 9.378 | 0.5042 | 0.4364 |
| Line 6 | 675.10 | 24.16 | 3.365 | 0.2648 | 1.3874 |
| Line 7 | 1566.07 | 125.60 | 7.704 | 4.9347 | 4.7807 |
| Line 8 | 1252.35 | 137.10 | 11.700 | 0.2475 | 0.2389 |
| Line 9 | 1631.72 | 299.02 | 17.446 | 0.5502 | 0.1896 |
| Line 10 | 692.15 | 26.31 | 3.634 | 0.1290 | 0.5413 |
| TR-1 | 4683.306 | 13.91 | 0.288 | 0.0040 | 0.0319 |
| TR-2 | 5906.148 | 22.38 | 0.368 | 0.0594 | 0.2865 |
| Total | 21,014.64 | 997.56 | 4.75 | 8.6703 | 0.8691 |
| Element Name | Measured Average Three-Phase Power Losses ΔPIII [kW] | Average Three-Phase Power Losses Calculated by the Section Summation Method ΔPIII [kW] | Average Three-Phase Power Losses Calculated by the Equivalent Resistance Method ΔPIII [kW] | Accuracy of the Section Summation Method δΔPIII [%] | Accuracy of the Equivalent Resistance Method δΔPIII [%] |
|---|---|---|---|---|---|
| Line 3 | 44.21 | 41.76 | 42.48 | −5.54 | −3.91 |
| Line 7 | 128.33 | 122.72 | 125.60 | −4.37 | −2.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hołdyński, G.; Skibko, Z.; Walendziuk, W. Power and Energy Losses in Medium-Voltage Power Grids as a Function of Current Asymmetry—An Example from Poland. Energies 2024, 17, 3706. https://doi.org/10.3390/en17153706
Hołdyński G, Skibko Z, Walendziuk W. Power and Energy Losses in Medium-Voltage Power Grids as a Function of Current Asymmetry—An Example from Poland. Energies. 2024; 17(15):3706. https://doi.org/10.3390/en17153706
Chicago/Turabian StyleHołdyński, Grzegorz, Zbigniew Skibko, and Wojciech Walendziuk. 2024. "Power and Energy Losses in Medium-Voltage Power Grids as a Function of Current Asymmetry—An Example from Poland" Energies 17, no. 15: 3706. https://doi.org/10.3390/en17153706
APA StyleHołdyński, G., Skibko, Z., & Walendziuk, W. (2024). Power and Energy Losses in Medium-Voltage Power Grids as a Function of Current Asymmetry—An Example from Poland. Energies, 17(15), 3706. https://doi.org/10.3390/en17153706







