Abstract
Photovoltaic (PV) power generation has attracted widespread interest as a clean and sustainable energy source, with increasing global attention given to renewable energy. However, the operation and monitoring of PV power generation systems often result in large amounts of data containing missing values, outliers, and noise, posing challenges for data analysis and application. Therefore, PV data cleaning plays a crucial role in ensuring data quality, enhancing data availability and reliability. This study proposes a PV data cleaning method based on Rasterized Data Image Processing (RDIP) technology, which integrates rasterization and image processing techniques to select optimal contours and extract essential data. To validate the effectiveness of our method, we conducted comparative experiments using three data cleaning methods, including our RDIP algorithm, the Pearson correlation coefficient interpolation method, and cubic spline interpolation method. Subsequently, the cleaned datasets from these methods were utilized for power prediction using two linear regression models and two neural network models. The experimental results demonstrated that data cleaned using the RDIP algorithm improved the short-term forecast accuracy by approximately 1.0% and 3.7%, respectively, compared to the other two methods, indicating the feasibility and effectiveness of the RDIP approach. However, it is worth noting that the RDIP technique has limitations due to its reliance on integer parameters for grid division, potentially leading to coarse grid divisions. Future research efforts could focus on optimizing the selection of binarization thresholds to achieve better cleaning results and exploring other potential applications of RDIP in PV data analysis.
1. Introduction
With increasing global attention on renewable energy, photovoltaic (PV) power generation has garnered widespread attention and application as a pivotal solution to address the global energy demand, owing to its clean and sustainable nature. However, the operation and monitoring of PV power generation systems often generate a large amount of data, which may contain missing values, outliers, and noise, posing significant challenges for data analysis and application [1,2,3,4,5]. Therefore, PV data cleaning plays a crucial role in ensuring data quality, improving data availability and reliability [6,7].
In recent years, there have been significant advancements in the field of data cleaning, encompassing aspects, such as missing value handling, outlier detection and treatment, and noise reduction. Several studies have proposed targeted methods and techniques for cleaning PV data. For instance, Wang and Deng (2023) introduced a PV data cleaning method based on interpolation and outlier detection [8], effectively handling missing values and outliers. Additionally, Ilyas and Rekatsinas (2022) explored machine learning algorithms for time-series data cleaning [9], which are of significant importance for preprocessing PV generation data. Furthermore, Ray P K et al., (2019) proposed an anomaly detection method for PV power generation data using principal component analysis (PCA) and a support vector machine [10]. Ibrahim M et al., (2022) proposed an anomaly detection method for PV power generation data based on learning techniques [11]. Zhang et al., (2019) developed a hybrid forecasting model for PV power generation data using PCA and an Elman neural network [12].
By comprehensively applying these data cleaning techniques, the quality and reliability of PV power generation data can be effectively enhanced, providing a reliable foundation for subsequent data analysis and applications. For new energy plants, power prediction is a critical task, where the actual total radiation and power serve as key data for model training. To ensure the accuracy of predictions, data cleaning is essential. The aforementioned methods mostly employ statistical and regression-based approaches for data processing.
This study attempts to clean data from the perspective of image processing. After simple cleaning, irradiance power scatter data are rasterized, generating rasterized images with different resolutions based on grid step size. The rasterized images undergo image processing techniques, such as morphological operations, contour extraction, and filtering. Contours satisfying criterion (minimizing dispersion and maximizing area S) are selected as our optimal contours. Scatter data within the contours are retained as the required data. Finally, the effectiveness of data cleaning is validated by comparing the accuracy of different power prediction algorithms.
2. Related Work
Various methods and techniques have been proposed for photovoltaic (PV) data cleaning [13,14]. Sun and Zhang (2018), Wang et al., (2023), and Li et al., (2021) introduced a PV data cleaning method based on interpolation and outlier detection algorithms [1,4,6], which effectively handles missing values and outliers. Despite their advantages, these methods have lower efficiency in handling high-dimensional data and large data volumes, and they may perform poorly on nonlinear and non-stationary time-series data. Additionally, Micheli et al., (2021), as well as Ranjan and Prusty (2019), discussed techniques for time-series data cleaning [15,16], including sliding window smoothing and exponential weighted moving average methods, aimed at reducing noise and fluctuations in data to enhance stability and reliability. However, these methods may lead to data lagging and blurring, thereby affecting the accuracy of subsequent data analysis. Furthermore, Hopwood et al., (2020) employed principal component analysis (PCA) to improve data quality and interpretability by dimensionality reduction and redundant information removal [17]. While these methods have achieved certain effectiveness in data cleaning, they may lose important information, especially when the main variation patterns of data do not conform to linear assumptions. Moreover, Balachandran and Devisridhivyadharshini et al., (2024) combined multiple data cleaning techniques into a comprehensive data cleaning process to achieve thorough cleaning and preprocessing of PV data [18]. Although this method has certain advantages, it requires a reasonable design of the cleaning process to avoid information loss or excessive processing time.
In addition to traditional data cleaning methods, in recent years, image processing techniques have also attracted extensive attention in the field of data cleaning [19,20,21,22,23,24]. Contour extraction in image processing and boundary extraction in data extraction share similarities, involving target detection and extraction, shape and structural information, processing steps, and application domains. The feasibility of using image processing methods [25] to achieve data cleaning is demonstrated by the flexibility, generality, and efficiency of image processing methods, which can be applied to various types of data processing tasks. The application of image processing methods in data cleaning mainly lies in the similarity of data representation, the flexibility of image processing methods, and the efficiency of image processing algorithms. In summary, applying image processing methods to achieve data cleaning will provide new insights and methods for data cleaning.
3. Materials and Methods
3.1. Photovoltaic Anomalous Data Analysis
There exists a close relationship between photovoltaic (PV) power and irradiance data (including global radiation, direct radiation, diffuse radiation, etc.) [26], as the working principle of PV systems involves converting solar energy into electrical energy. Direct radiation refers to solar radiation directly from the sun, whose intensity is influenced by factors such as solar angle and atmospheric transparency. Under ideal conditions, higher direct radiation results in more light energy absorbed by PV cell components, thereby increasing PV power generation. Diffuse radiation refers to solar radiation scattered in the atmosphere before reaching the ground, and its intensity is affected by atmospheric particulates and cloud cover, among other factors. Although diffuse radiation is not as intense as direct radiation, it still provides some light energy to PV cell components, thereby affecting PV power generation.
where G is global radiation; D is direct radiation; is diffuse radiation.
Equation (1) illustrates that global radiation (G) is the sum of direct radiation (D) and diffuse radiation (). Global radiation serves as a crucial indicator for measuring total solar radiation, directly impacting the efficiency of PV cell components in generating electricity [27]. Therefore, there exists a close relationship between global radiation and power output. Higher global radiation results in increased PV power generation.
Figure 1 depicts the relationship between global radiation and power generation at a specific PV station located in Guizhou Province, China. It can be observed that the relationship between PV power generation and total radiation is not simply linear but exhibits certain fluctuating characteristics. Additionally, the data collection process often contains numerous anomalous data points, whose direct utilization in training power prediction models may lead to significant prediction errors.
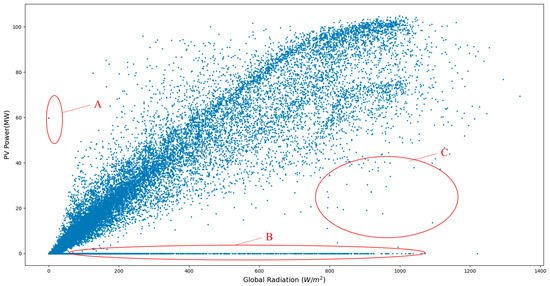
Figure 1.
Relationship between global radiation and PV power.
It is evident from the figure that the relationship between PV power generation and total radiation is not purely linear but demonstrates certain fluctuating characteristics. Furthermore, it is noted that during the data collection process, there are numerous anomalous data points. Utilizing these data directly for training power prediction models undoubtedly leads to considerable prediction errors. Various factors contribute to the generation of anomalous data [28,29,30], including equipment malfunctions, issues with data collection devices, and data quality concerns. Equipment malfunctions represent a significant source of anomalous data generation. Equipment within PV stations, including PV cell components and inverters, may experience performance degradation or failure due to factors such as natural environmental conditions and operational loads, thereby resulting in anomalous data (see red circle B). Additionally, issues with data collection devices commonly contribute to anomalous data. Problems, such as sensor malfunctions, data transmission interruptions, and data recording errors, may lead to inaccurate or anomalous data collection (see red circle A). Moreover, deliberate power limitations or environmental factors often contribute to a significant portion of anomalous data (see red circle C).
3.2. Design and Implementation of RDIP Technology
In order to identify and process anomalous data, we employed the RDIP (Rasterized Data Image Processing) technology method. The specific process for anomalous data analysis is illustrated in Figure 2. To retain the most reasonable data, we devised five sets of cleansing schemes with different resolutions, selecting the most appropriate cleansing scheme based on the maximum contour principle. Initially, the data underwent a simple cleansing process, where records with either total radiation or power generation data being zero were deleted, as these are obvious outlier values.
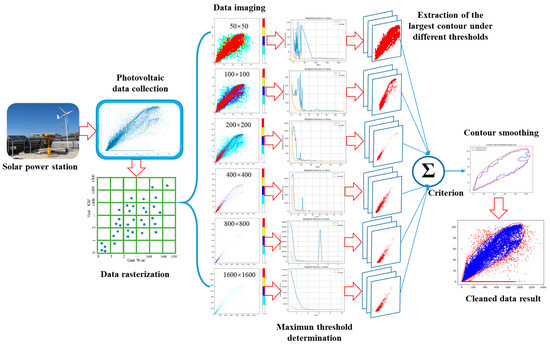
Figure 2.
Processing flow of RDIP technology.
- a.
- Data Rasterization and Visualization
The data cleansing process essentially involves retaining frequently occurring data points while eliminating those that occur infrequently. In the Central China region, total radiation values range from 0 to 1500 W/m2. For a PV station with an installed capacity of 150 MW, if the data are rasterized using a ratio of 1 W/m2 to 1 kW, a maximum of 1500 × 1500 grid blocks will be generated. The PV data mapped to grid blocks were then tabulated to generate a rasterized data table containing data quantities, as depicted in Figure 3.
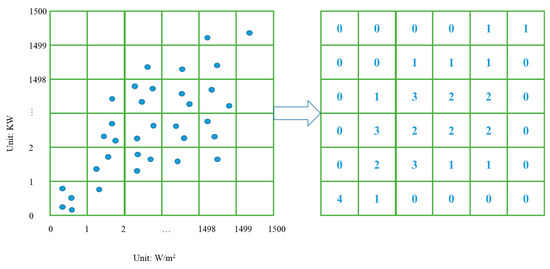
Figure 3.
Schematic of data rasterization.
However, the rasterized data cannot be directly converted into image data as the data quantity for grid block (0, 0) needs correction. Since nighttime data predominantly fall within this grid block, accounting for half of the total data quantity, directly converting the raster table into images would result in distortion. The correction involves substituting the maximum value from other grid blocks. The visualization process essentially involves mapping the raster data to different colors through numerical mapping, akin to converting matrix data into a heatmap. Figure 4 shows the rasterized data transformed into images of different resolutions.
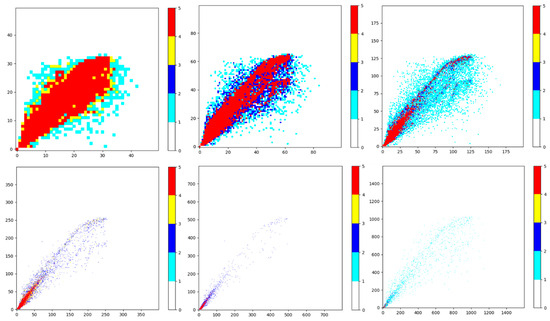
Figure 4.
Rasterized data visualization under different resolutions.
- b.
- Image Morphological Operations and Contour Extraction
The objective of cleansing is to extract the maximum contours to encompass as much valid data as possible. An essential step in contour extraction is binarizing the grayscale image, with the threshold value being critical. Setting the threshold value too low would include all data points, defeating the purpose of cleansing, while setting it too high would cause excessive pixel separation, hindering contour extraction. Figure 5 illustrates the images decomposed from a 50 × 50 resolution with different heat values.
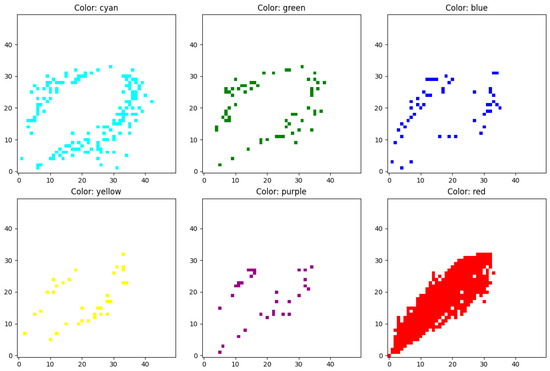
Figure 5.
Extraction of images with different heat values.
The red areas represent the contours to be extracted. To ensure the extraction of maximum contours, a common practice in image processing is to perform morphological opening operations on the image before binarization. This involves erosion (Formula (1)) followed by dilation (Formula (2)), aimed at eliminating small pixels, separating contours in narrow areas, and smoothing large contour boundaries.
Furthermore, downsampling the image is another method for contour extraction (refer to Figure 6). It is important to note that the extracted image after downsampling needs to be restored to the original image resolution. Hence, we designed six identical processing workflows, differing only in image resolution. Since the resolution of adjacent images differs by a factor of 4, the threshold selection for morphological opening and binarization should also differ by a factor of 4 for adjacent images.
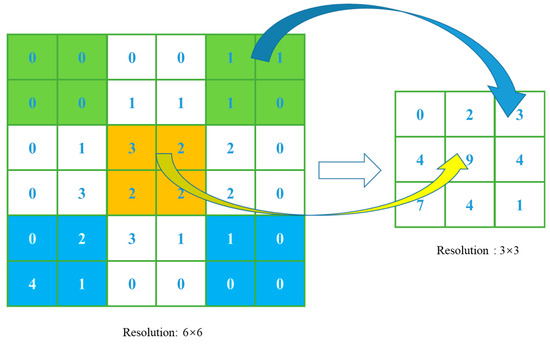
Figure 6.
Schematic of resolution reduction operation.
- c.
- Maximum Contour Extraction and Resolution Selection
After morphological opening, contour extraction, and contour smoothing, the maximum contour area can be computed. Since the threshold selection between adjacent images is aligned by a factor of 4, the area statistics should be aligned accordingly, meaning that the contour area of lower-resolution images should be expanded by a factor of 4. It can be observed that the selection of threshold H is inversely proportional to the contour area S, and under the same threshold conditions, the image resolution is directly proportional to the contour area. We aim to select the smallest possible threshold to obtain the largest possible contour area; thus, a balance needs to be found between the threshold and the image resolution.
where N is the total number of data points, k is the number of samples, ni is the number of data points in the i-th sample, and Si is the dispersion matrix of the i-th sample.
The data cleansing process is essentially a clustering process, and the intra-class dispersion Sw (Equation (4)) can also be used to assess the effectiveness of data cleansing. Minimizing intra-class dispersion is the goal of cleansing, while simultaneously ensuring data quantity as much as possible. Therefore, we use the weighted dispersion matrix Sk (Equation (5)) instead.
where is the weighted dispersion, n is the number of samples, represents the coordinates of the i-th sample, represents the coordinates of the sample mean, and represents the weight of the i-th sample. denotes the Euclidean distance between the i-th sample and the sample mean.
The weights are determined through the following steps:
- For each numerical value, extract all its coordinates in the matrix to form a coordinate set.
- Then, for all coordinates of that numerical value, consider them as a sample set. When computing the weighted dispersion, use the number of samples as weights. In other words, the weight of each sample equals the number of times that numerical value appears in the matrix.
- Finally, according to the formula for calculating weighted dispersion, use these weights to compute the dispersion, ensuring that the number of samples is correctly applied as weights.
The purpose of this approach is to ensure that different occurrences of each numerical value have corresponding effects when computing the weighted dispersion. Finally, a cleansing criterion function () is designed:
Since S and are both integers, when S takes the maximum value and takes the minimum value, can achieve the maximum value.
3.3. Experimental Design and Evaluation Metrics
An essential aspect of photovoltaic (PV) data cleansing is its impact on power prediction for PV stations, where prediction accuracy serves as the primary metric for evaluating prediction performance. The formula for short-term prediction accuracy (PA) is provided below (Equation (8)). This calculation formula is derived from the “Implementation Rules for Auxiliary Services Management of Grid-connected Power Plants in the Southern Region” and the “Implementation Rules for Grid-connected Operation Management of Power Plants in the Southern Region” (collectively referred to as the “Two Regulations”).
We will employ representative statistical regression prediction models, namely Random Forest [31] and Lasso [32], as well as deep learning prediction models, specifically CNN + LSTM [33] and DWT + EN + GRU [34], to conduct a comparative analysis in the domain of power prediction.
where represents the predicted PV power, represents the actual PV power, represents the installed capacity, and PA represents the prediction accuracy.
4. Experimental Results and Analysis
4.1. Data Acquisition and Processing
This study utilized data from a photovoltaic (PV) station with an installed capacity of 150MW located in Guizhou Province, China (Shown in Figure 7). Solar power prediction in Guizhou Province encounters unique challenges distinct from other regions, primarily due to two factors:

Figure 7.
PV station with an installed capacity of 150 MW.
- The region’s intricate and varied terrain, encompassing mountainous, hilly, and plain areas, which heightens uncertainty in solar radiation owing to terrain-induced effects;
- The humid climate, susceptible to weather elements like clouds and rainfall, necessitating prediction models to incorporate additional meteorological variables such as precipitation.
A total of 73,824 data points were extracted from this station between 1 February 2021 and 1 October 2023, including time, total radiation, direct radiation, diffuse radiation, and actual power, spanning five dimensions. As total radiation is a key factor influencing actual power, these two types of data must be processed first, as shown in Figure 1.
For the dataset, A and B class abnormal data points are obvious, thus requiring initial cleaning. The cleaned data are illustrated in Figure 8.
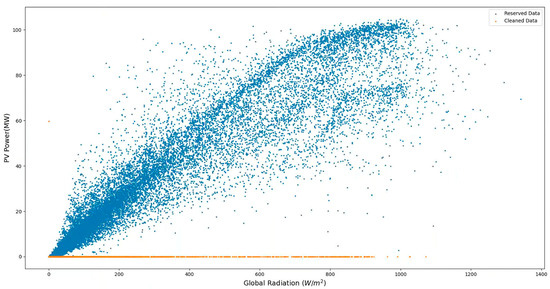
Figure 8.
Effect of simple cleaning on radiation power data.
To reduce errors during image processing caused by rasterizing the data, it is common practice to maintain the image size as a power of 2. Therefore, this study sets the maximum resolution of the images to 1600 × 1600. Additionally, resolutions of 800 × 800, 400 × 400, 200 × 200, 100 × 100, and 50 × 50 are designed. According to the processing method described, it is known that smaller thresholds in contour extraction can yield larger contour areas. Hence, in this study, only the values 1–6 are analyzed for the threshold. The most reasonable parameters satisfying cleaning criterion Jw are selected. The six different-resolution images corresponding to thresholds 1–6 are shown in Figure 9.
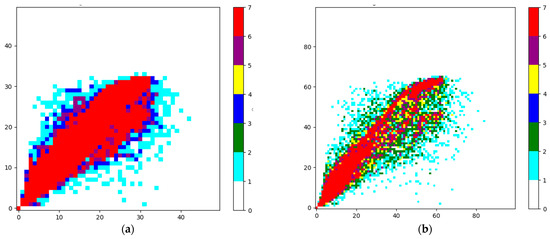
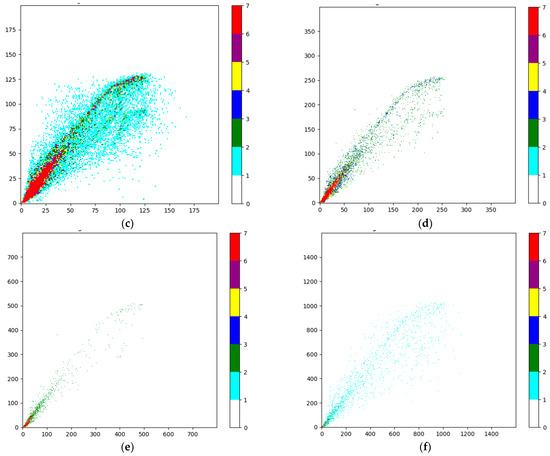
Figure 9.
Rasterized images at different resolutions. (a) Rasterized image with resolution of 50 × 50, (b) Rasterized image with resolution of 100 × 100, (c) Rasterized image with resolution of 200 × 200, (d) Rasterized image with resolution of 400 × 400, (e) Rasterized image with resolution of 800 × 800, (f) Rasterized image with resolution of 1600 × 1600.
4.2. Experimental Results Analysis
By selecting different thresholds and resolutions, maximum contour extraction is performed after binarizing the images. Calculating the area of the largest contour allows us to obtain parameters, such as area S (scaled with respect to the resolution of 1600 × 1600), sample size N, intra-sample dispersion Sk, and cleaning criterion . Refer to Table 1 for details.

Table 1.
Comparison of accuracy with different cleaning methods and different forecast models.
By applying threshold selection, the binarization of images with different resolutions can be performed, and the corresponding largest contours can be extracted. We consider the power irradiance scatter data contained within the largest contour as valid data and calculate the weighted dispersion Sk of these data. As shown in Figure 10a, the higher the resolution of the image, the greater the weighted dispersion. Except for the rasterized image with a resolution of 1600 × 1600, the weighted dispersion of valid data contained within the largest contours at other resolutions achieves its minimum value when the threshold is 4 or 5. Subsequently, as the threshold increases, the weighted dispersion also increases. This is understandable, since higher thresholds result in fewer valid data points being included (see Figure 10b). Since we aim for the smallest possible weighted dispersion, the threshold selection only needs to consider values less than 6. Additionally, we observe that as the resolution decreases, the number of valid data points increases. When the resolution is reduced to 100 × 100, the number of valid data points tends to stabilize. Our goal is to include as many valid data points as possible; thus, analyzing resolutions of 50 × 50 and above is sufficient.
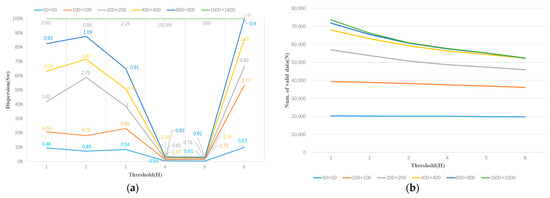
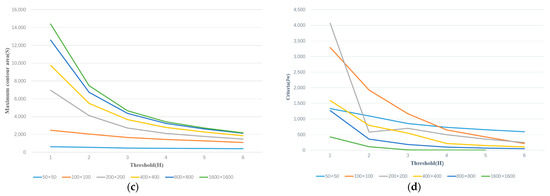
Figure 10.
Threshold vs. different parameters (different resolutions). (a) Threshold vs. Dispersion, (b) Threshold vs. Num. of valid data, (c) Threshold vs. Maximum contour area, (d) Threshold vs. Cleaning Criterion.
It can be observed that there is a monotonically decreasing relationship between the threshold and the largest extracted contour (see Figure 10c). By calculating the maximum cleaning criterion coefficient for rasterized images of different resolutions according to Equation (6), it can be found that when the threshold is 1 and the resolution is 200 × 200, the maximum cleaning criterion coefficient is obtained in the rasterized image (see Figure 10d).
The largest contour extracted after binarization of the image with a resolution of 200 × 200 is illustrated in Figure 11.
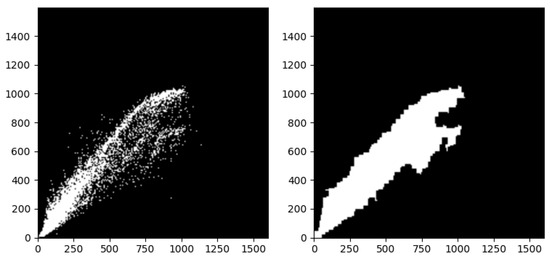
Figure 11.
Binarization and maximum contour extraction of the rasterized image with a resolution of 200 × 200.
The opening operation is performed on the maximum contour using a 5 × 5 template to eliminate small objects, separate objects in narrow areas, and smooth large object boundaries. The results are shown in Figure 12.
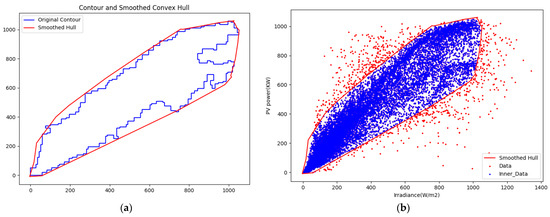
Figure 12.
Final cleaning results. (a) Contour and smoothed convex hull, (b) Cleaning result with hull.
4.3. Discussion of Results
To validate the effectiveness of our algorithm, we selected a fusion of the Pearson correlation coefficient interpolation method [8] and cubic spline interpolation method [35] for comparison. Additionally, we chose two linear regression models and two neural network prediction models to compare accuracy and mean squared error. As shown in Table 2, applying the data cleaned by our RDIP algorithm to model training resulted in approximate 1.0% and 3.7% improvements in short-term forecast accuracy, indicating the feasibility of this approach.

Table 2.
Comparison of prediction accuracy: cleaned vs. uncleaned data.
To further verify whether our proposed cleaning algorithm improves the subsequent performance prediction, we conducted short-term forecast validation for the months of March, June, September, and December 2023 for the station. These four months were selected to represent the four seasons: spring, summer, autumn, and winter. It is known that the accuracy of photovoltaic power prediction follows a pattern of “high in spring, low in summer, high in autumn, and low in winter”. This is due to stable weather conditions in spring and autumn, which result in higher prediction accuracy, while extreme weather and unstable climate factors in summer and winter lead to lower accuracy.
As shown in Table 2, after data cleaning, the accuracy of all four prediction methods improved by an average of 2.28%. Additionally, we observed that the forecast accuracy in June and December narrowed by nearly 1% compared to April and September. This indicates that the cleaned data better reflect the intrinsic patterns of the photovoltaic power station.
To test the applicability of our cleaning algorithm, we additionally selected two other photovoltaic power stations in Guizhou Province (Yongxin Station and Gangpingzhan) for validation. From the historical data (see Figure 13), we can see that the data quality of these two stations is significantly inferior to that of Zhenliang Station. In fact, these two stations often undergo assessments due to their forecast accuracy not meeting the standards. According to feedback from meteorological departments, these two stations are located in valleys, and the influence of local microclimates causes the coarse-gridded numerical forecast data used to fail to reflect the intrinsic local conditions.
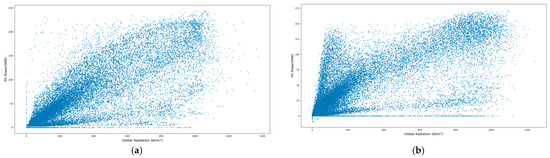
Figure 13.
Relationship between global radiation and PV power: (a) Station of Yongxin; (b) Station of Gangping.
Using our proposed RDIP algorithm for data cleaning, Yongxin Station achieved the best cleaning coefficient, with a threshold of 2 and a resolution of 100 × 160, while Gangping Station achieved the maximum cleaning coefficient, with a threshold of 3 and a resolution of 100 × 160. The cleaning results are shown in Figure 14. Applying the aforementioned four models to calculate the accuracy for these two stations, we found that the accuracy after cleaning increased by nearly 3.7% compared to the accuracy before cleaning. This demonstrates a significant improvement.
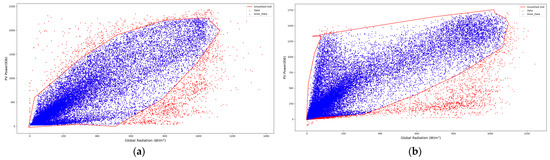
Figure 14.
Final cleaning results: (a) Station of Yongxin; (b) Station of Gangping.
5. Conclusions and Future Work
The PV data cleaning method based on RDIP technology proposed in this study approaches data cleaning from a perspective considering both the density and frequency of data distribution. The cleaned data after processing can more effectively ensure that training data reflect the intrinsic patterns of PV data. The accuracy results also validate the effectiveness of data cleaning, laying a foundation for the further development of PV power prediction models and contributing to the safe and stable operation of the power grid. However, the current data gridization process only considers integer parameters, resulting in somewhat coarse grid division. Future work could focus on refining the selection of binarization thresholds to achieve better cleaning results and exploring other potential applications of RDIP in PV data analysis.
Author Contributions
Conceptualization, N.Z.; data curation, Y.T. and C.Y.; formal analysis, R.L. and N.Z.; funding acquisition, N.Z.; investigation, B.J. and N.Z.; methodology, R.L., C.Y. and N.Z.; project administration, N.Z.; software, Y.T. and B.J.; supervision, C.Y., Z.Y. and N.Z.; writing—original draft, N.Z.; writing—review and editing, R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Huadian Group’s 2023 Science and Technology Project (CHDKJ23-02-40): Research and Application of Meteorology-Enabled Photovoltaic Plant Safety and Efficient Early Warning Prediction Technology, and the Qianqi Science and Technology Cooperation Project (TD[2024]04): Research on Wind and Solar Power Prediction Technology.
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
Authors Ning Zang, Zuoteng Yuan and Bailin Jing were employed by the company New Energy Branch of Guizhou Qianyuan Electric Power Co., Ltd.; Authors Yong Tao and Chen Yuan were employed by the company Guizhou New Meteorological Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sun, L.; Zhou, K.; Zhang, X.; Yang, S. Outlier data treatment methods toward smart grid applications. IEEE Access 2018, 6, 39849–39859. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C. Data processing strategies in wind energy forecasting models and applications: A comprehensive review. Appl. Energy 2019, 249, 392–408. [Google Scholar] [CrossRef]
- Eroshenko, S.A.; Khalyasmaa, A.I.; Snegirev, D.A.; Dubailova, V.V.; Romanov, A.M.; Butusov, D.N. The impact of data filtration on the accuracy of multiple time-domain forecasting for photovoltaic power plants generation. Appl. Sci. 2020, 10, 8265. [Google Scholar] [CrossRef]
- Li, B.; Delpha, C.; Migan-Dubois, A.; Diallo, D. Fault diagnosis of photovoltaic panels using full I–V characteristics and machine learning techniques. Energy Convers. Manag. 2021, 248, 114785. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, M.; Chen, Z.; Wang, B.; Cheng, C.; Liu, R. A deep learning framework for day ahead wind power short-term prediction. Appl. Sci. 2023, 13, 4042. [Google Scholar] [CrossRef]
- Celikel, R.; Yilmaz, M.; Gundogdu, A. A voltage scanning-based MPPT method for PV power systems under complex partial shading conditions. Renew. Energy 2022, 184, 361–373. [Google Scholar] [CrossRef]
- Akinci, T.C.; Akgun, O.; Yilmaz, M.; Martinez-Morales, A.A. High order spectral analysis of ferroresonance phenomena in electric power systems. IEEE Access 2023, 11, 61289–61297. [Google Scholar] [CrossRef]
- Wang, B.; Deng, X.; Chen, T.; Li, Y. Photovoltaic data cleaning method based on DBSCAN clustering, quartile algorithm and Pearson correlation coefficient interpolation method. In Proceedings of the 2023 6th International Conference on Energy, Electrical and Power Engineering (CEEPE), Guangzhou, China, 12–14 May 2023; IEEE: Piscataway, NJ, USA; pp. 1539–1544. [Google Scholar]
- Ilyas, I.F.; Rekatsinas, T. Machine learning and data cleaning: Which serves the other? ACM J. Data Inf. Qual. (JDIQ) 2022, 14, 1–11. [Google Scholar] [CrossRef]
- Ray, P.K.; Mohanty, A.; Panigrahi, T. Power quality analysis in solar PV integrated microgrid using independent component analysis and support vector machine. Optik 2019, 180, 691–698. [Google Scholar] [CrossRef]
- Ibrahim, M.; Alsheikh, A.; Awaysheh, F.M.; Alshehri, M.D. Machine learning schemes for anomaly detection in solar power plants. Energies 2022, 15, 1082. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Pan, G.; Zhao, Y. A novel hybrid model based on VMD-WT and PCA-BP-RBF neural network for short-term wind speed forecasting. Energy Convers. Manag. 2019, 195, 180–197. [Google Scholar] [CrossRef]
- de Oliveira AK, V.; Aghaei, M.; Rüther, R. Automatic inspection of photovoltaic power plants using aerial infrared thermography: A review. Energies 2022, 15, 2055. [Google Scholar] [CrossRef]
- Bassous, G.F.; Calili, R.F.; Barbosa, C.H. Development of a low-cost data acquisition system for very short-term photovoltaic power forecasting. Energies 2021, 14, 6075. [Google Scholar] [CrossRef]
- Micheli, L.; Fernández, E.F.; Almonacid, F. Photovoltaic cleaning optimization through the analysis of historical time series of environmental parameters. Sol. Energy 2021, 227, 645–654. [Google Scholar] [CrossRef]
- Ranjan, K.G.; Prusty, B.R.; Jena, D. Comparison of two data cleaning methods as applied to volatile time-series. In Proceedings of the 2019 International Conference on Power Electronics Applications and Technology in Present Energy Scenario (PETPES), Mangalore, India, 29–31 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Hopwood, M.; Gunda, T.; Seigneur, H.; Walters, J. An assessment of the value of principal component analysis for photovoltaic IV trace classification of physically-induced failures. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, AB, Canada, 15 June–21 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 798–802. [Google Scholar]
- Balachandran, G.B.; Devisridhivyadharshini, M.; Ramachandran, M.E.; Santhiya, R. Comparative investigation of imaging techniques, pre-processing and visual fault diagnosis using artificial intelligence models for solar photovoltaic system–A comprehensive review. Measurement 2024, 232, 114683. [Google Scholar] [CrossRef]
- Saquib, D.; Nasser, M.N.; Ramaswamy, S. Image Processing Based Dust Detection and prediction of Power using ANN in PV systems. In Proceedings of the 2020 Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1286–1292. [Google Scholar]
- Yap, W.K.; Galet, R.; Yeo, K.C. Quantitative analysis of dust and soiling on solar pv panels in the tropics utilizing image-processing methods. In Proceedings of the Asia-Pacific Solar Research Conference 2015, Canberra, Australia, 29 November–1 December 2016. [Google Scholar]
- Natarajan, K.; Bala, P.K.; Sampath, V. Fault detection of solar PV system using SVM and thermal image processing. Int. J. Renew. Energy Res. 2020, 10, 967–977. [Google Scholar]
- Dantas, G.M.; Mendes, O.L.; Maia, S.M.; de Alexandria, A.R. Dust detection in solar panel using image processing techniques: A review. Res. Soc. Dev. 2020, 9, e321985107. [Google Scholar] [CrossRef]
- Gönenç, A.; Acar, E.; Demir, İ.; Yılmaz, M. Artificial Intelligence Based Regression Models for Prediction of Smart Grid Stability. In Proceedings of the 2022 Global Energy Conference (GEC), Batman, Turkey, 26–29 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 374–378. [Google Scholar]
- Tang, L.; Deng, Y.; Ma, Y.; Huang, J.; Ma, J. SuperFusion: A versatile image registration and fusion network with semantic awareness. IEEE/CAA J. Autom. Sin. 2022, 9, 2121–2137. [Google Scholar] [CrossRef]
- Rezvani, A.; Bigverdi, M.; Rohban, M.H. Image-based cell profiling enhancement via data cleaning methods. PLoS ONE 2022, 17, e0267280. [Google Scholar] [CrossRef]
- Lanini, F. Division of Global Radiation into Direct Radiation and Diffuse Radiation. Master’s Thesis, University of Bern, Bern, Switzerland, 2010. [Google Scholar]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Review and statistical analysis of different global solar radiation sunshine models. Renew. Sustain. Energy Rev. 2015, 52, 1869–1880. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, Q.; Li, D.; Kang, D.; Lv, Q.; Shang, L. Hierarchical anomaly detection and multimodal classification in large-scale photovoltaic systems. IEEE Trans. Sustain. Energy 2018, 10, 1351–1361. [Google Scholar] [CrossRef]
- Yao, S.; Kang, Q.; Zhou, M.; Abusorrah, A.; Al-Turki, Y. Intelligent and data-driven fault detection of photovoltaic plants. Processes 2021, 9, 1711. [Google Scholar] [CrossRef]
- Hussin, M.Z.; Sin, N.D.; Zainuddin, H.; Omar, A.M.; Shaari, S. Anomaly Detection of Grid Connected Photovoltaic System Based on Degradation Rate: A Case Study in Malaysia. Pertanika J. Trop. Agric. Sci. 2021, 29, 3143–3159. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Hossain, M.J.; Duck, B.C. An optimized offline random forests-based model for ultra-short-term prediction of PV characteristics. IEEE Trans. Ind. Inform. 2019, 16, 202–214. [Google Scholar] [CrossRef]
- Cruz, J.; Mamani, W.; Romero, C.; Pineda, F. Selection of Characteristics by Hybrid Method: RFE, Ridge, Lasso, and Bayesian for the Power Forecast for a Photovoltaic System. SN Comput. Sci. 2021, 2, 202. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y.; Ali, I.H. CNN-LSTM: An efficient hybrid deep learning architecture for predicting short-term photovoltaic power production. Electr. Power Syst. Res. 2022, 208, 107908. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, X.; Ma, T.; Liu, D.; Wang, H.; Hu, W. A Multi-step ahead photovoltaic power forecasting model based on TimeGAN, Soft DTW-based K-medoids clustering, and a CNN-GRU hybrid neural network. Energy Rep. 2022, 8, 10346–10362. [Google Scholar] [CrossRef]
- Lindig, S.; Louwen, A.; Moser, D.; Topic, M. Outdoor PV system monitoring—Input data quality, data imputation and filtering approaches. Energies 2020, 13, 5099. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).