Power System State Estimation Based on Fusion of PMU and SCADA Data
Abstract
1. Introduction
2. The Model of the Power System
2.1. Power System Dynamical Equations
2.2. Measurement Equation
2.2.1. PMU Measurements
2.2.2. SCADA Measurements
3. Dynamic State Estimation Model
3.1. PMU-Only State Estimation
3.2. SCADA-Only State Estimation
3.3. The SCADA State Estimation at Scale
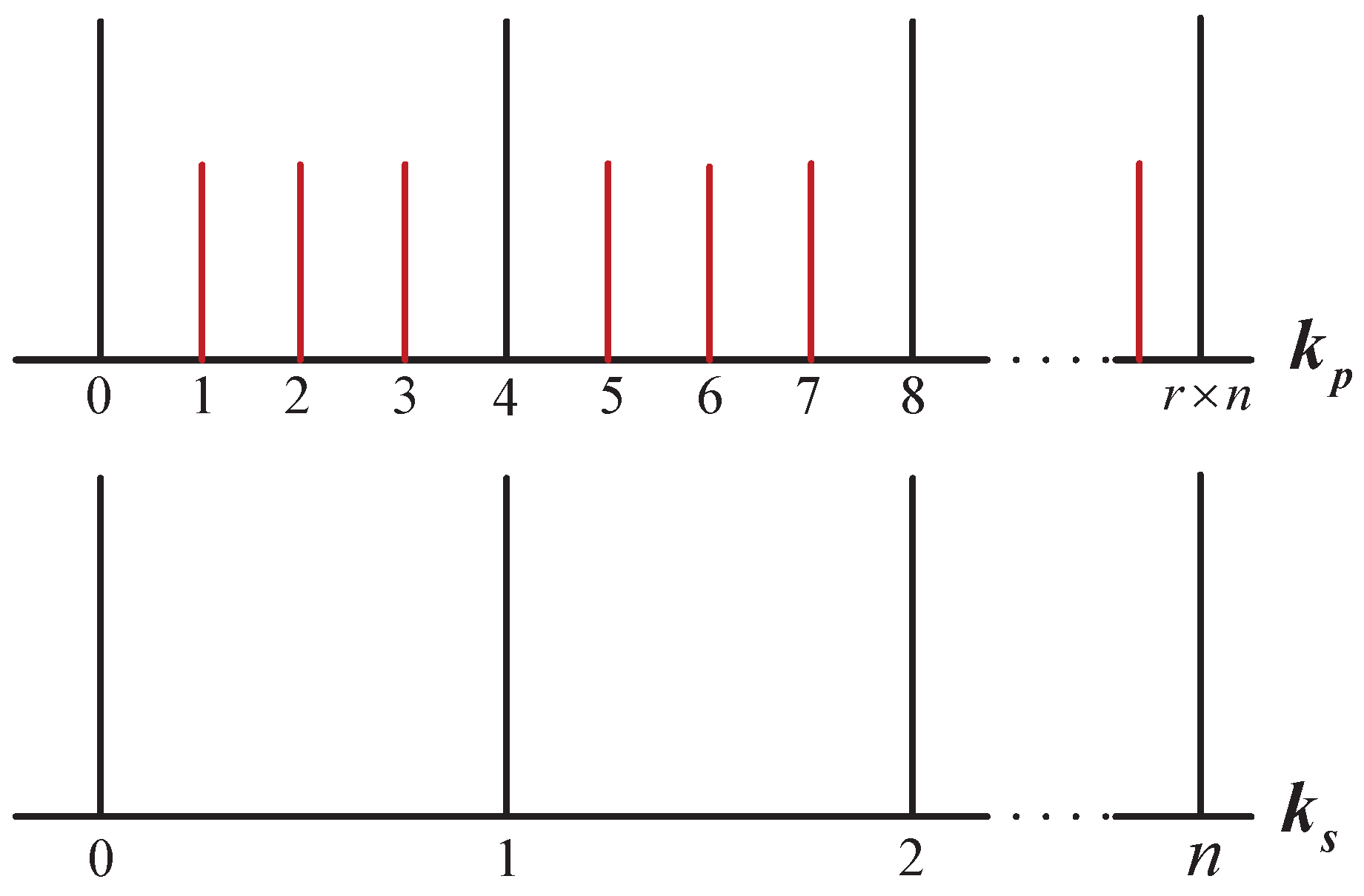
4. Data Fusion
4.1. Filter Step
4.2. PMU Observability Issues
4.3. Bar-Shalom–Campo Data Fusion
| Algorithm 1 Multi-sensor multi-rate fusion method |
| Input: Sampling period , ; measurement value , ; initial state and state error covariance ; noise covariance matrix , ; smoothing factor ,. |
Output: integrated estimation result ;
|
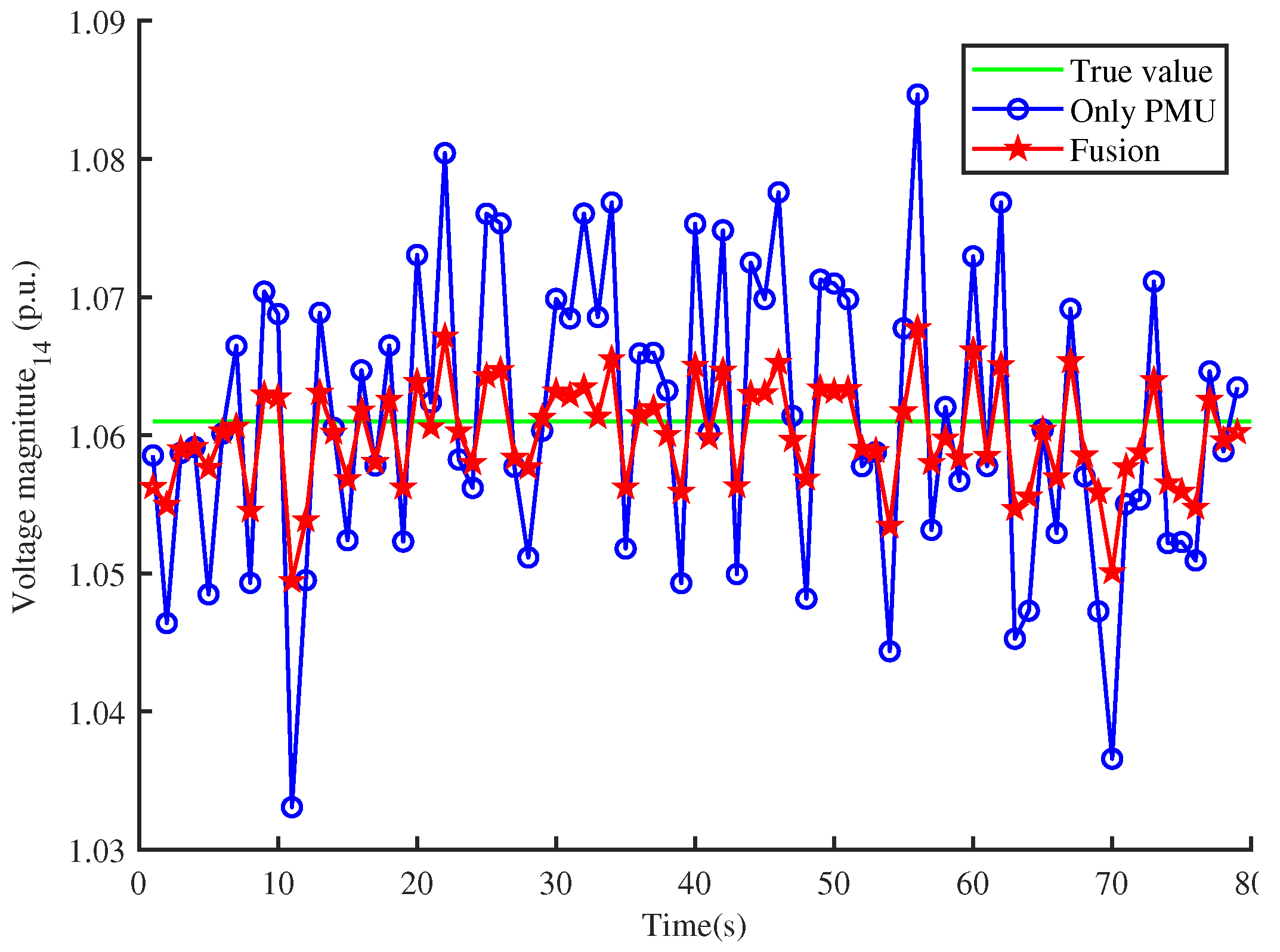
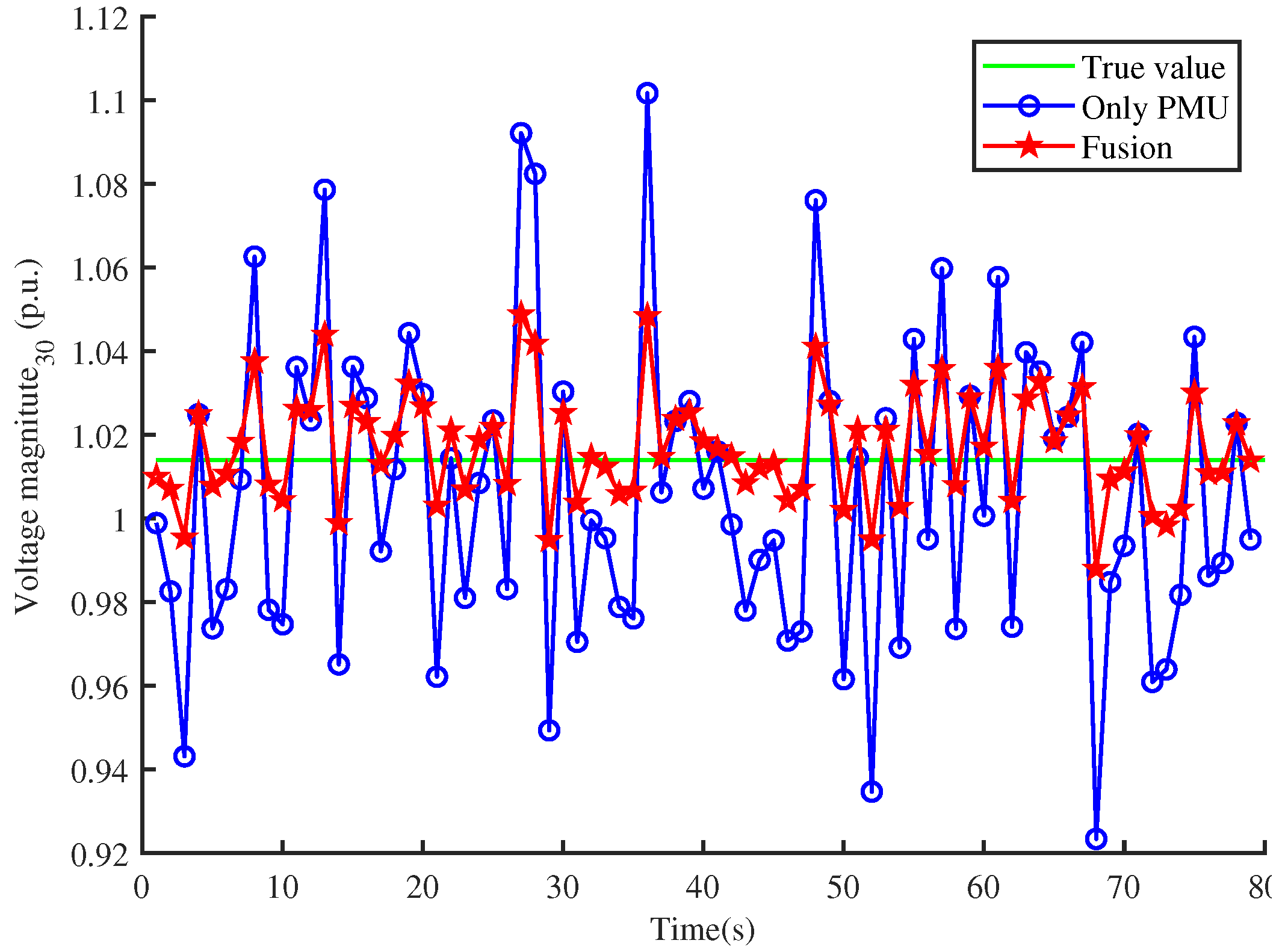
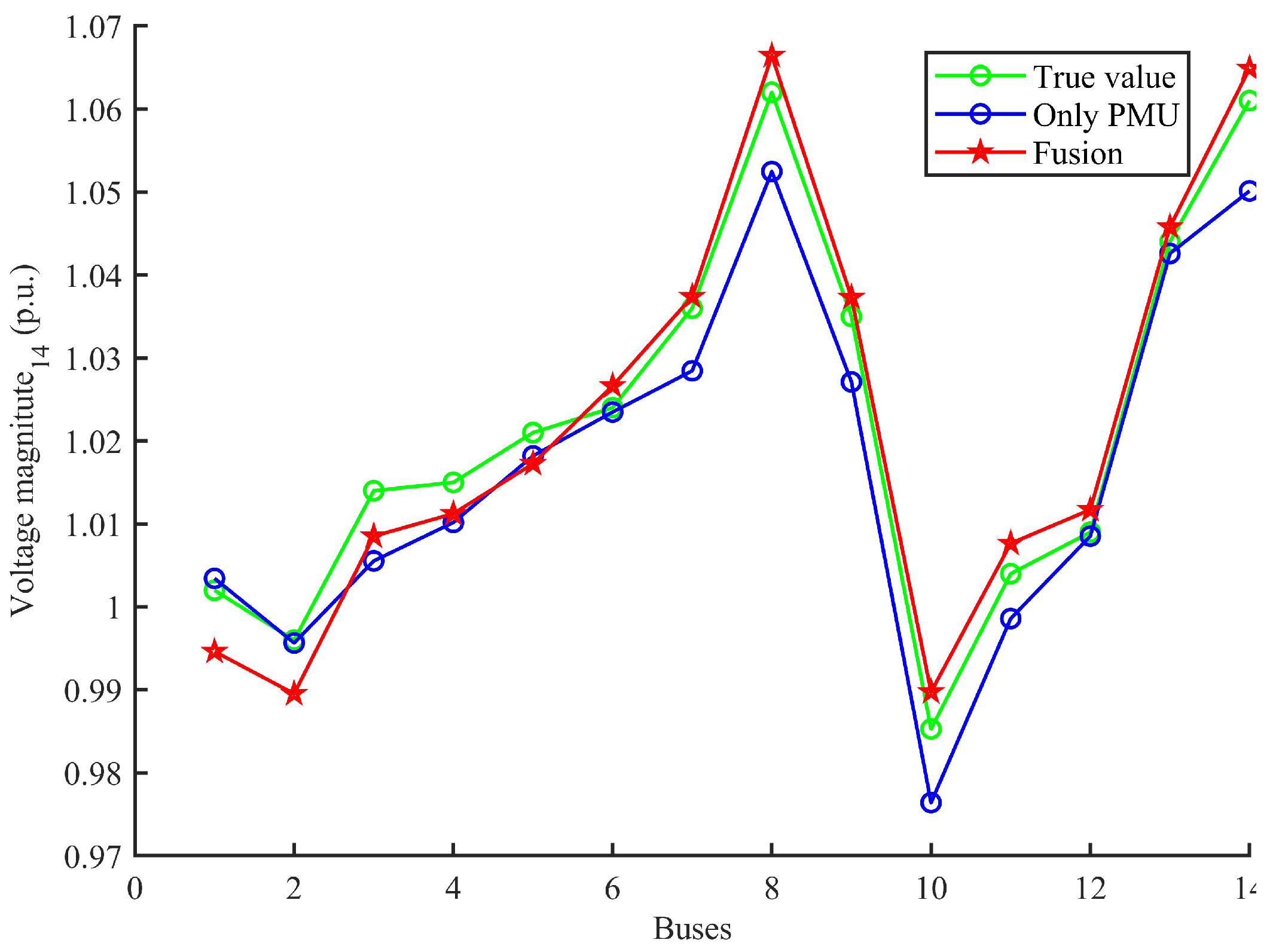
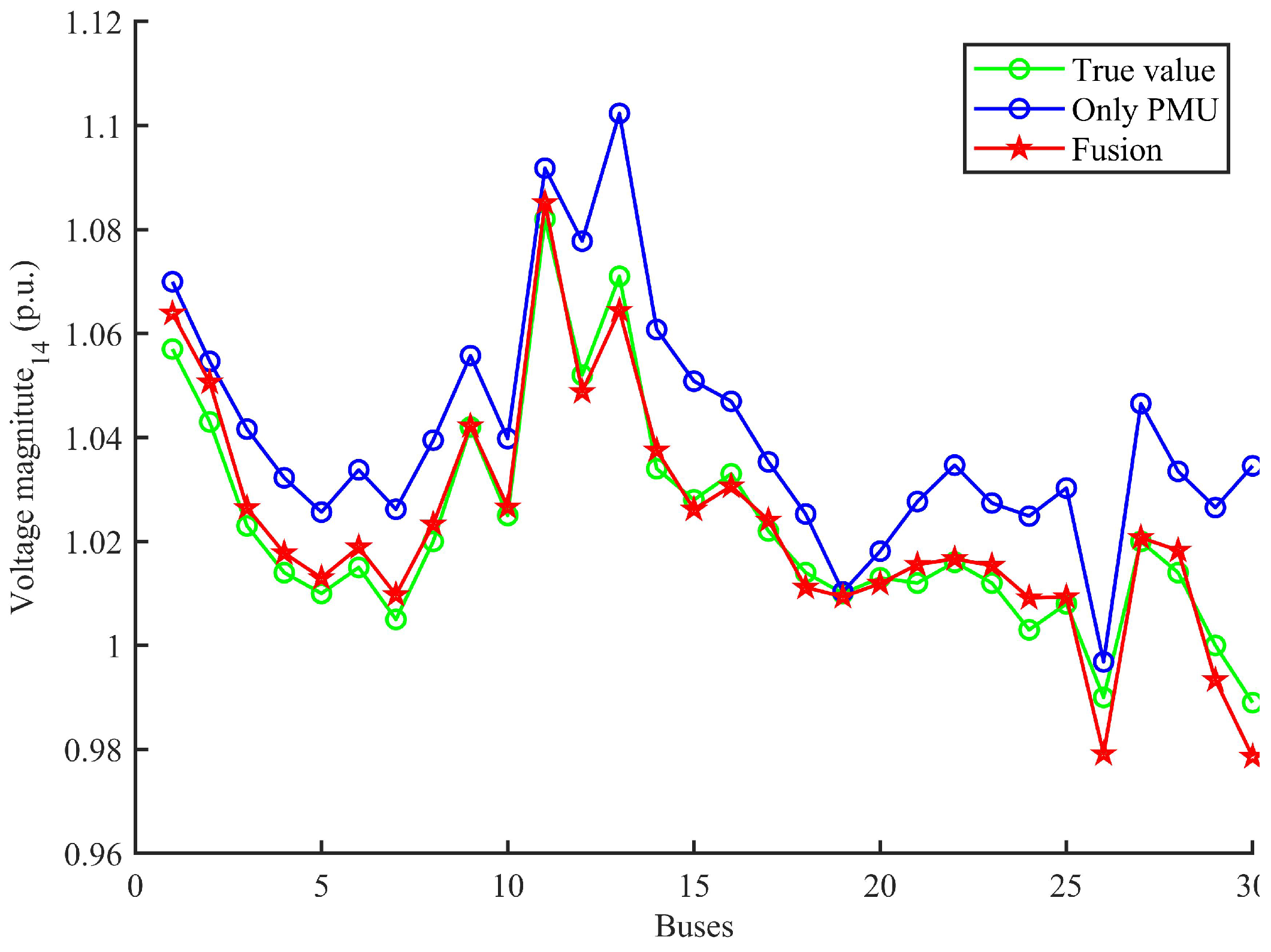
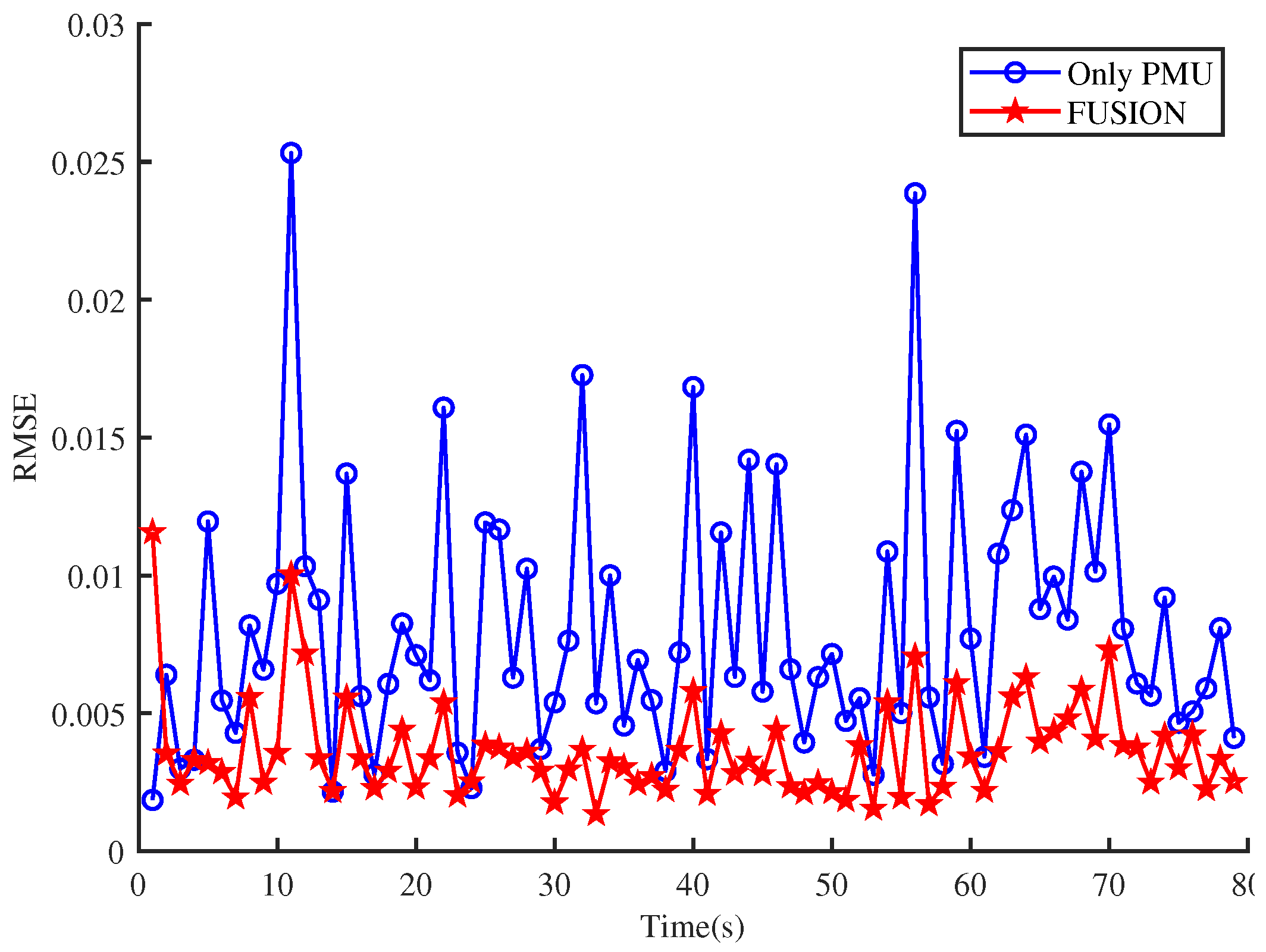
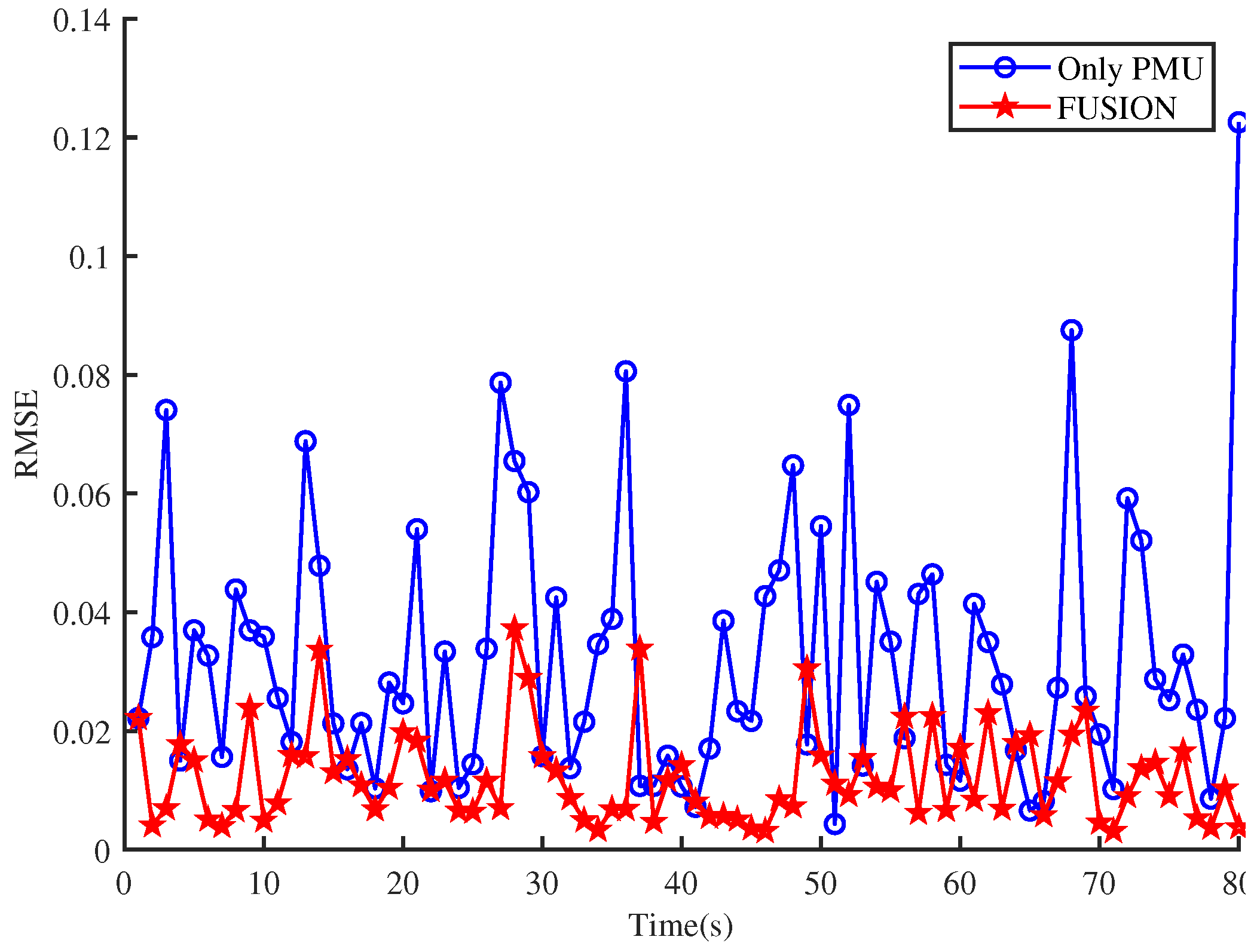
5. Simulation Result
5.1. Comparison of State Values between Single Estimator and Fusion Estimator
5.2. Analysis of Differentiation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jesus, P.M.D.O.; Rodriguez, N.A.; Celeita, D.F.; Ramos, G.A. PMU-Based System State Estimation for Multigrounded Distribution Systems. IEEE Trans. Power Syst. 2021, 36, 1071–1081. [Google Scholar] [CrossRef]
- Zhao, J.; Netto, M.; Huang, Z.; Yu, S.S.; Gómez-Expósito, A.; Wang, S.; Kamwa, I.; Akhlaghi, S.; Mili, L.; Terzija, V.; et al. Roles of Dynamic State Estimation in Power System Modeling, Monitoring and Operation. IEEE Trans. Power Syst. 2021, 36, 2462–2472. [Google Scholar] [CrossRef]
- Abooshahab, M.A.; Hovd, M.; Brekke, E.; Song, X. A Covariance Consistent Data Fusion method for Power Networks with Multirate Sensors. In Proceedings of the 2020 IEEE Conference on Control Technology and Applications (CCTA), Montreal, QC, Canada, 24–26 August 2020; pp. 807–814. [Google Scholar]
- Dobakhshari, A.S.; Azizi, S.; Paolone, M.; Terzija, V. Ultra Fast Linear State Estimation Utilizing SCADA Measurements. IEEE Trans. Power Syst. 2019, 34, 2622–2631. [Google Scholar] [CrossRef]
- Bose, A. Smart Transmission Grid Applications and Their Supporting Infrastructure. IEEE Trans. Smart Grid. 2010, 1, 11–19. [Google Scholar] [CrossRef]
- Dong, Q.; Sun, J.; Wu, Q.; Liu, Y. A Method for Filtering Low Frequency Disturbance in PMU Data Before Coordinated Usage in SCADA. IEEE Trans. Power Syst. 2017, 32, 2810–2816. [Google Scholar] [CrossRef]
- Cheng, G.; Lin, Y.; Zhao, J.; Yan, J. A Two-Stage State Estimator for Dynamic Monitoring of Power Systems. IEEE Trans. J. 2017, 11, 1767–1776. [Google Scholar]
- Zhou, N.; Meng, D.; Huang, Z.; Welch, G. Dynamic state estimation of a synchronous machine using PMU data: A comparative study. IEEE Trans. Smart Grid. 2015, 6, 450–460. [Google Scholar] [CrossRef]
- Sun, K.; Huang, M.; Wei, Z.; Zhao, J.; Sun, G. A Real-Time Recursion Correction Hybrid Linear State Estimator Using Stream Processing. IEEE Trans. Ind. Inf. 2023, 19, 2317–2329. [Google Scholar] [CrossRef]
- Sun, K.; Huang, M.; Wei, Z.; Sun, G. High-Refresh-Rate Robust State Estimation Based on Recursive Correction for Large-Scale Power Systems. IEEE Trans. Instrum. Meas. 2023, 72, 9002413. [Google Scholar] [CrossRef]
- Jorjani, M.; Seifi, H.; Varjani, A.Y. SCADA and PMU Measurements for Improving Power System State Estimation. IEEE Lat. Am. Trans. 2015, 13, 2245–2251. [Google Scholar]
- Kabiri, M.; Amjady, N. A New Hybrid State Estimation Considering Different Accuracy Levels of PMU and SCADA Measurements. IEEE Trans. Instrum. Meas. 2019, 68, 3078–3089. [Google Scholar] [CrossRef]
- Du, J.; Ma, S.; Wu, Y.-C.; Poor, H.V. Distributed Hybrid Power State Estimation Under PMU Sampling Phase Errors. IEEE Trans. Signal Process. 2014, 62, 4052–4063. [Google Scholar] [CrossRef]
- Rabha, P.; Shyam, C.C.; Sinha, A.K. Hybrid state estimation of power system using conventional and phasor measurements. In Proceedings of the 2015 International Conference on Energy, Power and Environment: Towards Sustainable Growth (ICEPE), Shillong, India, 12–13 June 2015; pp. 1–6. [Google Scholar]
- Albuquerque, A.; Bez, D.; Simões, A. Multistage strategies to incorporate phasor measurements into power system state estimation. In Proceedings of the 2013 IREP Symposium Bulk Power System Dynamics and Control—IX Optimization, Security and Control of the Emerging Power Grid, Rethymno, Greece, 25–30 August 2013; pp. 1–11. [Google Scholar]
- Netto, M.; Zhao, J.; Mili, L. A robust extended Kalman filter for power system dynamic state estimation using PMU measurements. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Aminifar, F.; Shahidehpour, M.; Fotuhi-Firuzabad, M.; Kamalinia, S. Power System Dynamic State Estimation With Synchronized Phasor Measurements. IEEE Trans. Instrum. Meas. 2014, 63, 352–363. [Google Scholar] [CrossRef]
- Bi, T.S.; Qin, X.H.; Yang, Q.X. A novel hybrid state estimator for including synchronized phasor measurements. Electr. Power Syst. Res. 2018, 78, 1343–1352. [Google Scholar] [CrossRef]
- Ghosal, M.; Rao, V. Fusion of Multirate Measurements for Nonlinear Dynamic State Estimation of the Power Systemss. IEEE Trans. Smart Grid. 2019, 10, 216–226. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Liu, B.; Yu, S.S.; Shi, P. A Stochastic Event-Triggered Robust Cubature Kalman Filtering Approach to Power System Dynamic State Estimation with Non–Gaussian Measurement Noises. IEEE Trans. Contr. Syst. Technol. 2023, 31, 889–896. [Google Scholar] [CrossRef]
- Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Sakis Power System Dynamic State Estimation: Motivations, Definitions, Methodologies, and Future Work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, X.; Zhang, X.; Wang, C.; Chiang, H.-D.; Li, P. Adaptive Dynamic State Estimation of Distribution Network Based on Interacting Multiple Model. IEEE Trans. Sustain. Energy 2022, 13, 643–652. [Google Scholar] [CrossRef]
- Abur, A.; Expoisito, A.G. Power System State Estimation: Theory and Implementation, 1st ed.; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Liu, H.; Liang, F.; Hu, T.; Hong, J.; Ma, H. Multi-Scale Fusion Model Based on Gated Recurrent Unit for Enhancing Prediction Accuracy of State-of-Charge in Battery Energy Storage Systems. J. Mod. Power Syst. Clean Energy 2024, 12, 405–414. [Google Scholar] [CrossRef]
- Cristi, R.; Tummala, M. Multirate, multiresolution, recursive Kalman filter. Signal Process. 2000, 80, 1945–1958. [Google Scholar] [CrossRef]
- Chen, J.; Yue, D.; Hu, S.; Ge, H.; Zhang, H. Power System Fusion State Estimation Based on a Switched System Model: Comparison Between EKF and UKF. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 7280–7284. [Google Scholar]
- Kiio, M.N.; Wekesa, C.W.; Kamau, S.I. Evaluating Performance of a Linear Hybrid State Estimator Utilizing Measurements from RTUs and Optimally Placed PMUs. IEEE Access 2022, 10, 63113–63131. [Google Scholar] [CrossRef]
- He, Y.; Mendis, G.J.; Wei, J. Observability Analysis and Measurement Placement for Systems with PMUs. In Proceedings of the 2014 International Conference on Computing, Networking and Communications (ICNC), New York, NY, USA, 10–13 October 2004; pp. 943–946. [Google Scholar]
- Göl, M.; Abur, A. A Hybrid State Estimator For Systems With Limited Number of PMUs. IEEE Trans. Power Syst. 2015, 30, 1511–1517. [Google Scholar] [CrossRef]
- Wakti, M.H.; Putranto, L.M.; Hadi, S.P.; Yasirroni, M.; Marsiano, A.F.D. PMU Location Determination in a Hybrid PMU-SCADA System. In Proceedings of the 2020 12th International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 6–8 July 2020; pp. 245–250. [Google Scholar]
- Simões Costa, A.; Albuquerque, A.; Bez, D. An estimation fusion method for including phasor measurements into power system real-time modeling. IEEE Trans. Power Syst. 2013, 28, 1910–1920. [Google Scholar] [CrossRef]
- Moslemi, R.; Mesbahi, A.; Velni, J.M. The Effect of the Common Process Noise on the Two-Sensor Fused-Track Covariance. IEEE Trans. Aerosp. Electron. Syst. 1986, 22, 803–805. [Google Scholar]
- Chen, Y.; Huang, S.; Liu, F.; Wang, Z.; Sun, X. Enhancement of hybrid state estimation using pseudo flow measurements. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]

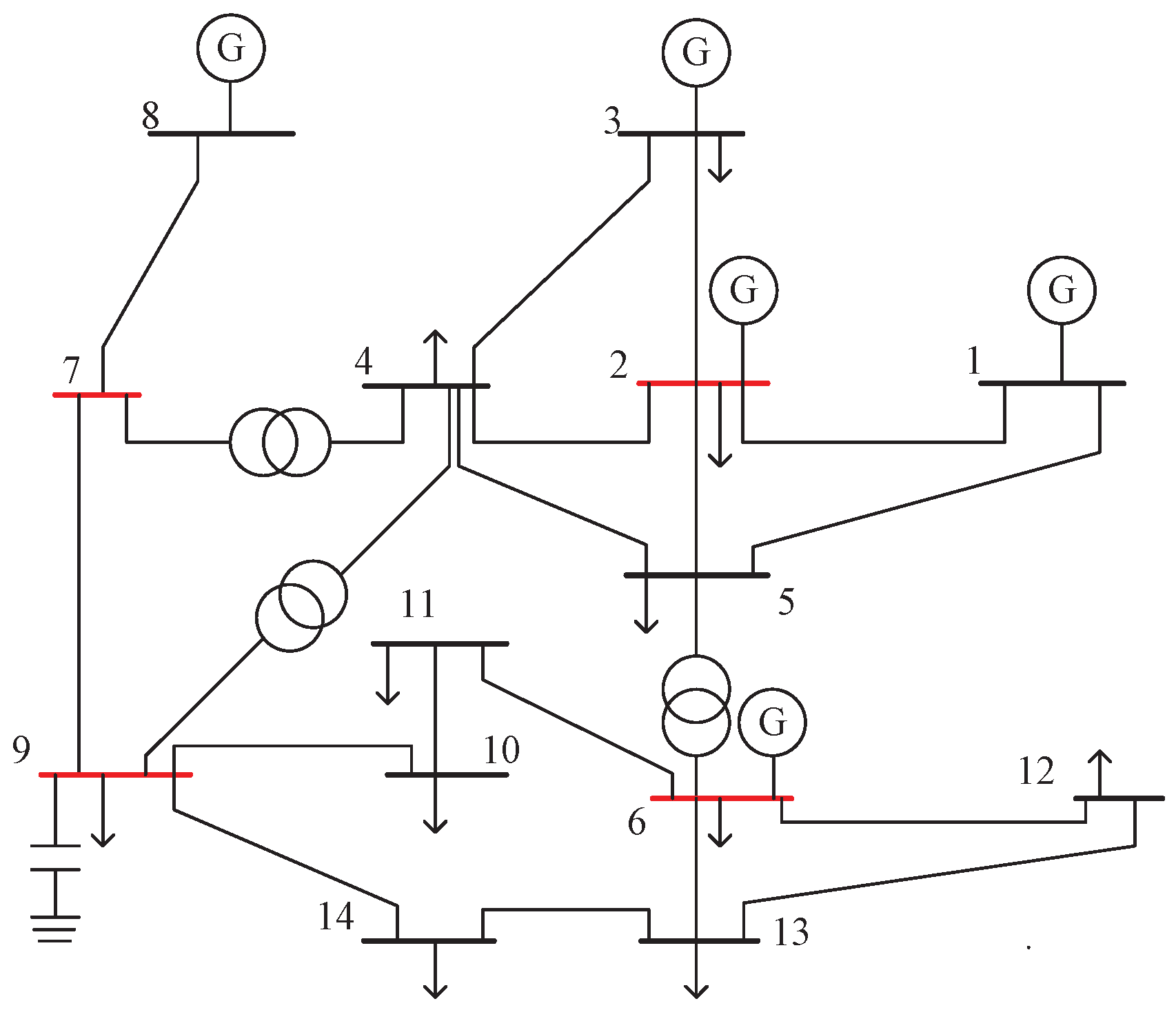
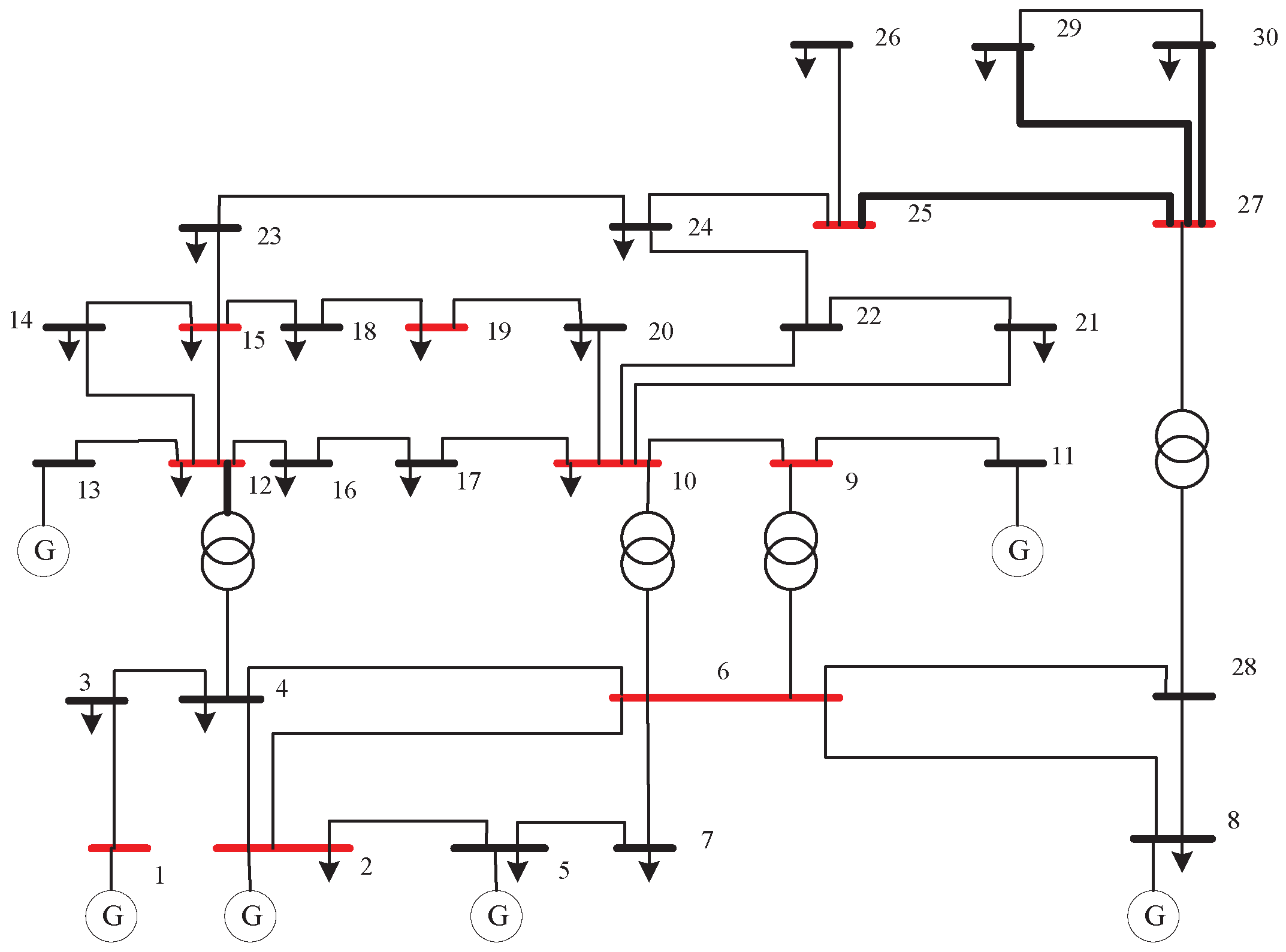
| Type | Magn | Angle | From Bus | To Bus |
|---|---|---|---|---|
| Voltage Phasor | 2 | 0 | ||
| 6 | 0 | |||
| 7 | 0 | |||
| 9 | 0 | |||
| Current Phasor | 2 | 1 | ||
| 2 | 3 | |||
| 2 | 4 | |||
| 2 | 5 | |||
| 6 | 11 | |||
| 6 | 12 | |||
| 6 | 13 | |||
| 7 | 8 | |||
| 7 | 9 | |||
| 9 | 10 | |||
| 9 | 14 |
| Buses | SCADA (p.u.) | PMU (p.u.) |
|---|---|---|
| IEEE-14 | ||
| IEEE-30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Gao, W.; Li, Y.; Guo, X.; Zhang, G.; Sun, W. Power System State Estimation Based on Fusion of PMU and SCADA Data. Energies 2024, 17, 2609. https://doi.org/10.3390/en17112609
Zhu J, Gao W, Li Y, Guo X, Zhang G, Sun W. Power System State Estimation Based on Fusion of PMU and SCADA Data. Energies. 2024; 17(11):2609. https://doi.org/10.3390/en17112609
Chicago/Turabian StyleZhu, Jiaming, Wengen Gao, Yunfei Li, Xinxin Guo, Guoqing Zhang, and Wanjun Sun. 2024. "Power System State Estimation Based on Fusion of PMU and SCADA Data" Energies 17, no. 11: 2609. https://doi.org/10.3390/en17112609
APA StyleZhu, J., Gao, W., Li, Y., Guo, X., Zhang, G., & Sun, W. (2024). Power System State Estimation Based on Fusion of PMU and SCADA Data. Energies, 17(11), 2609. https://doi.org/10.3390/en17112609






