Single-Stage MV-Connected Charger Using an Ac/Ac Modular Multilevel Converter
Abstract
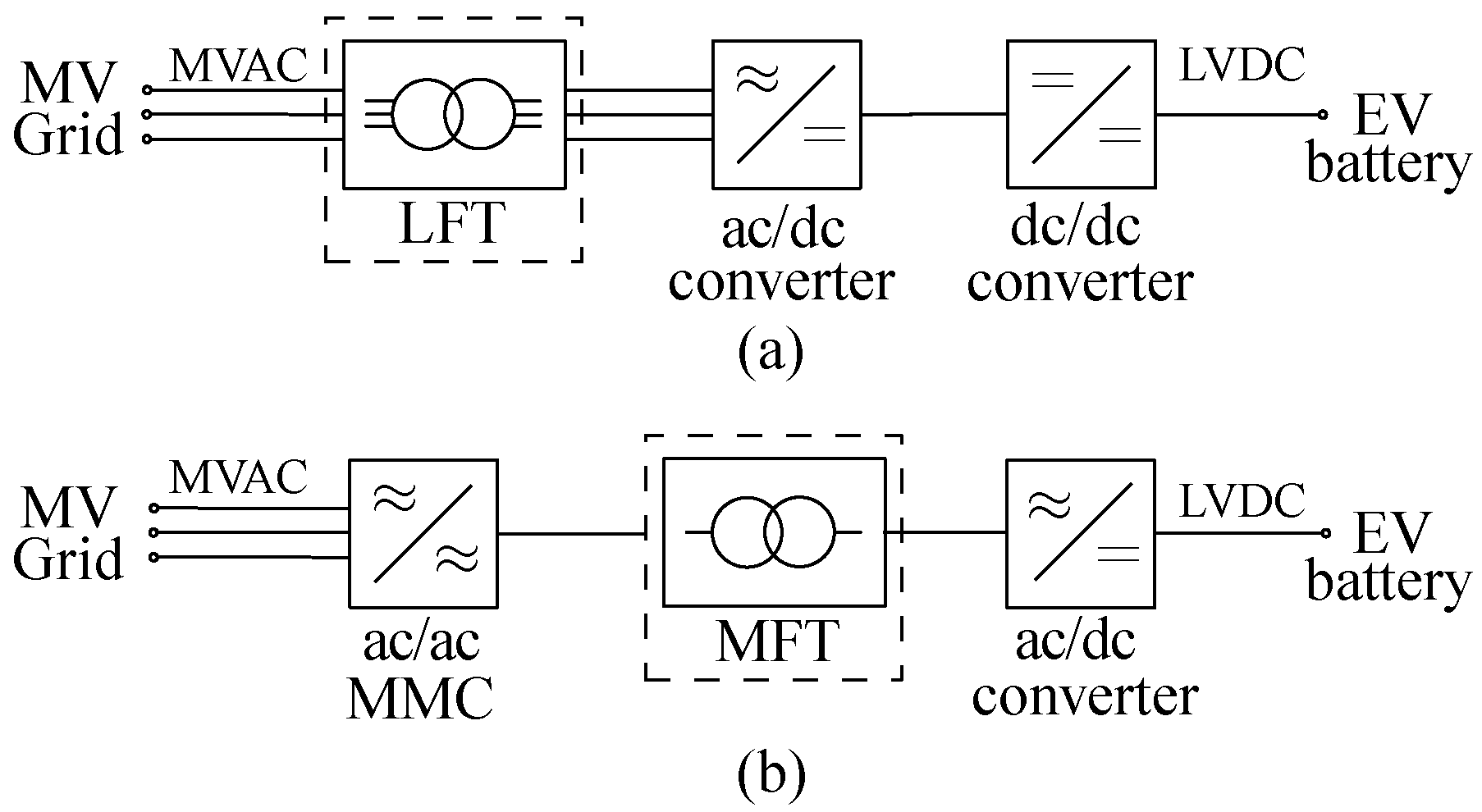
1. Introduction
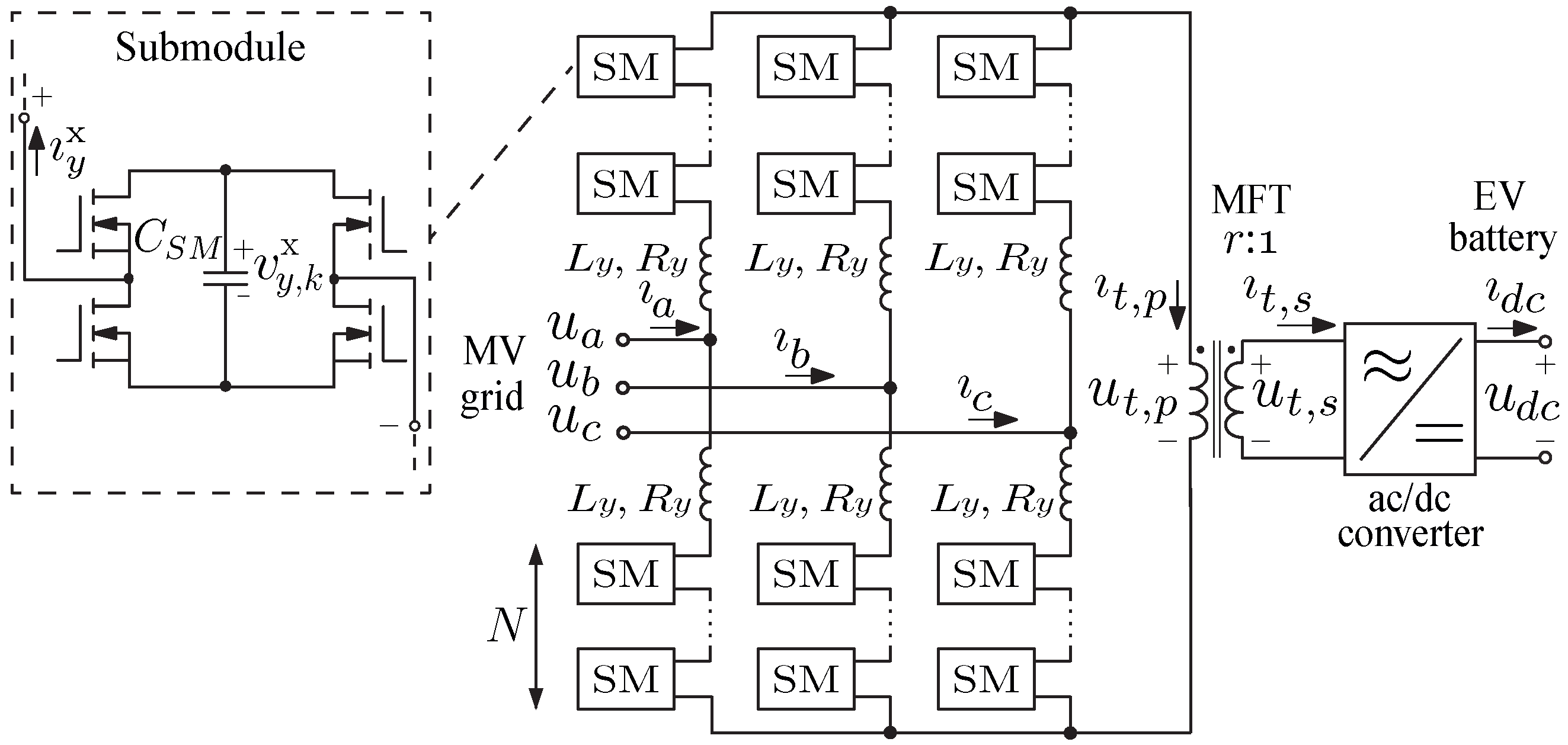
2. Modular Multilevel Converter
2.1. Fundamentals
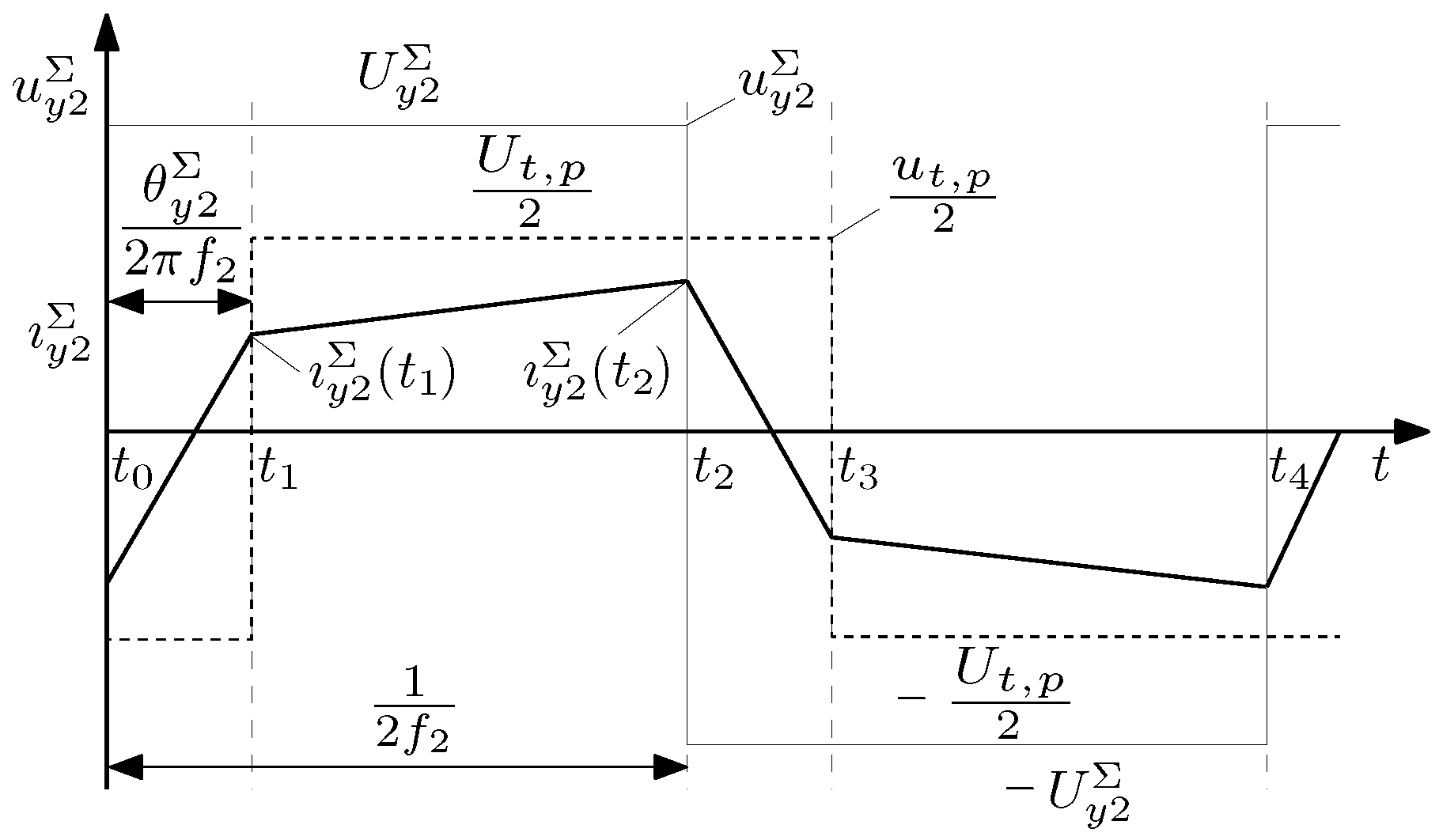
2.2. Decomposition of Circuit States
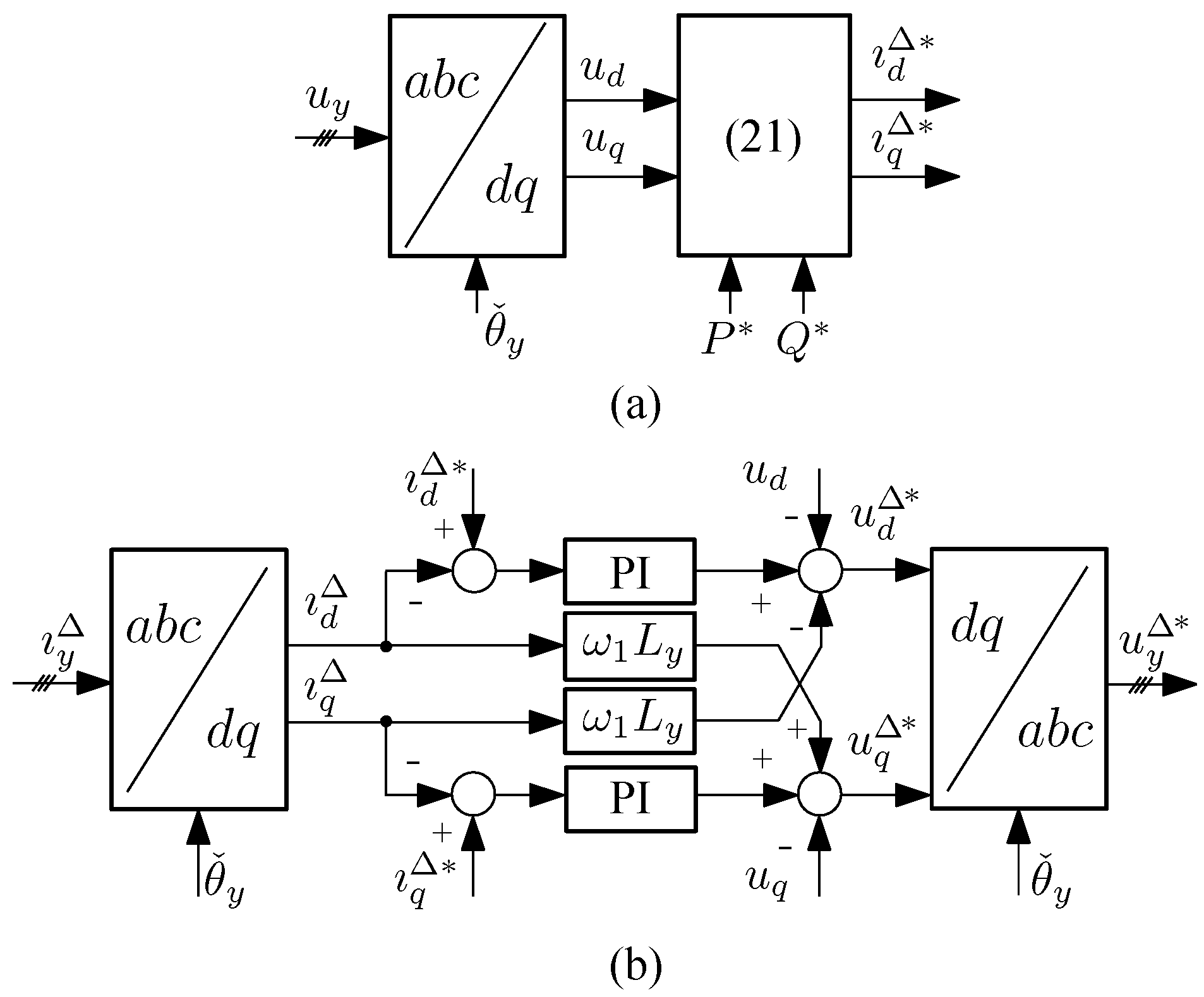
3. MMC Control
3.1. Three-Phase ac Grid Current Control
3.2. Cell Balancing and Common-Mode Current Control
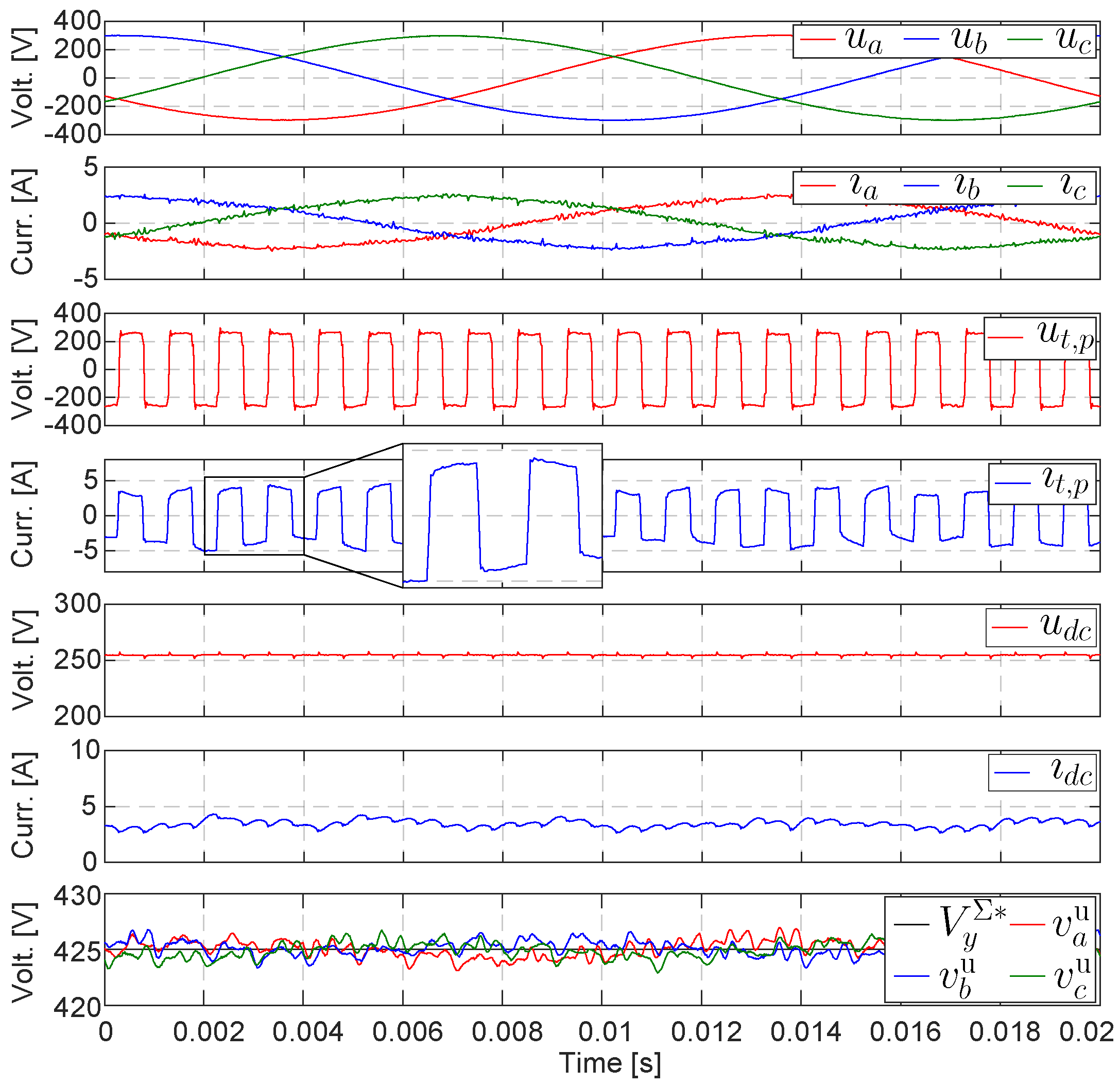
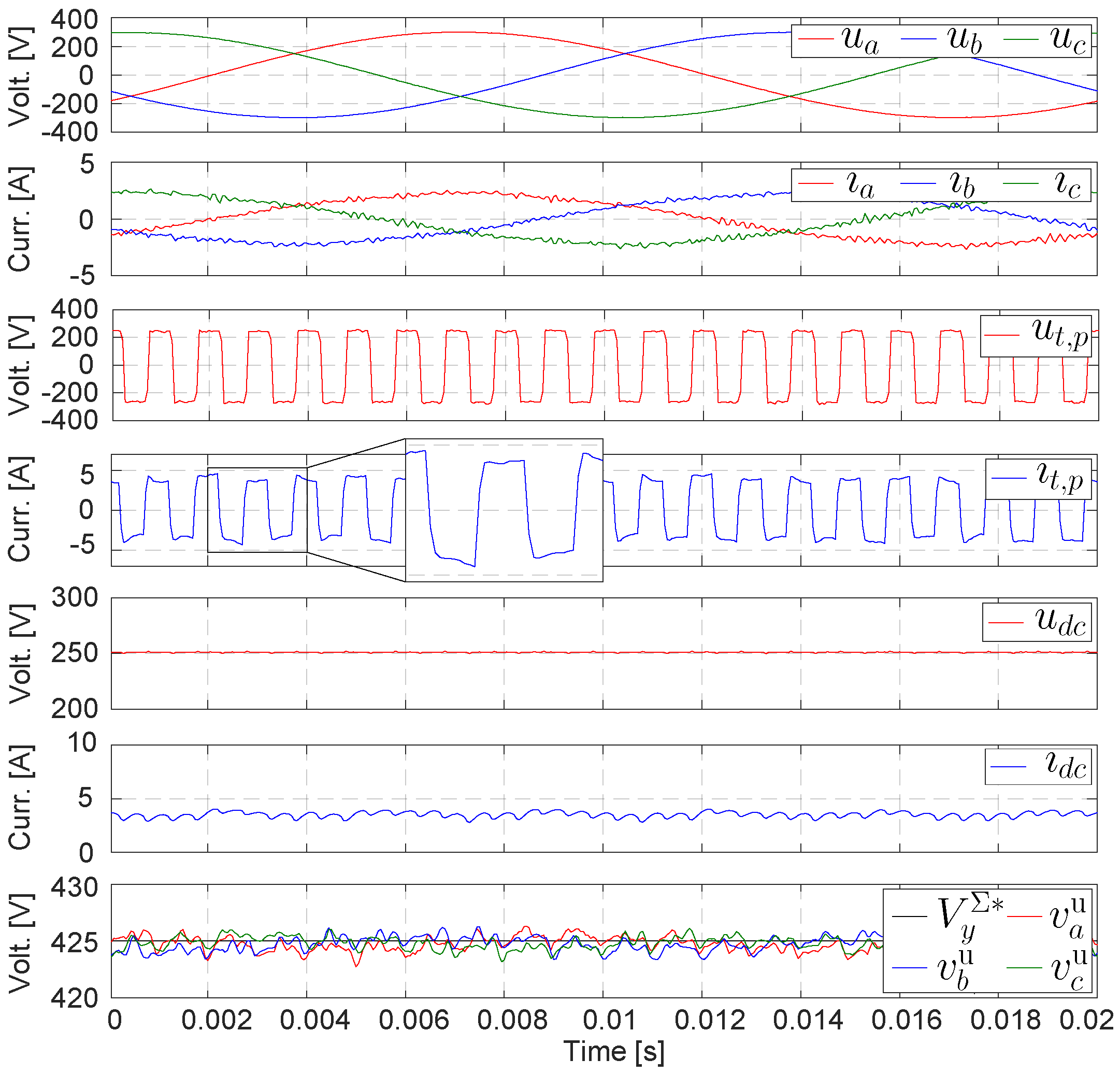
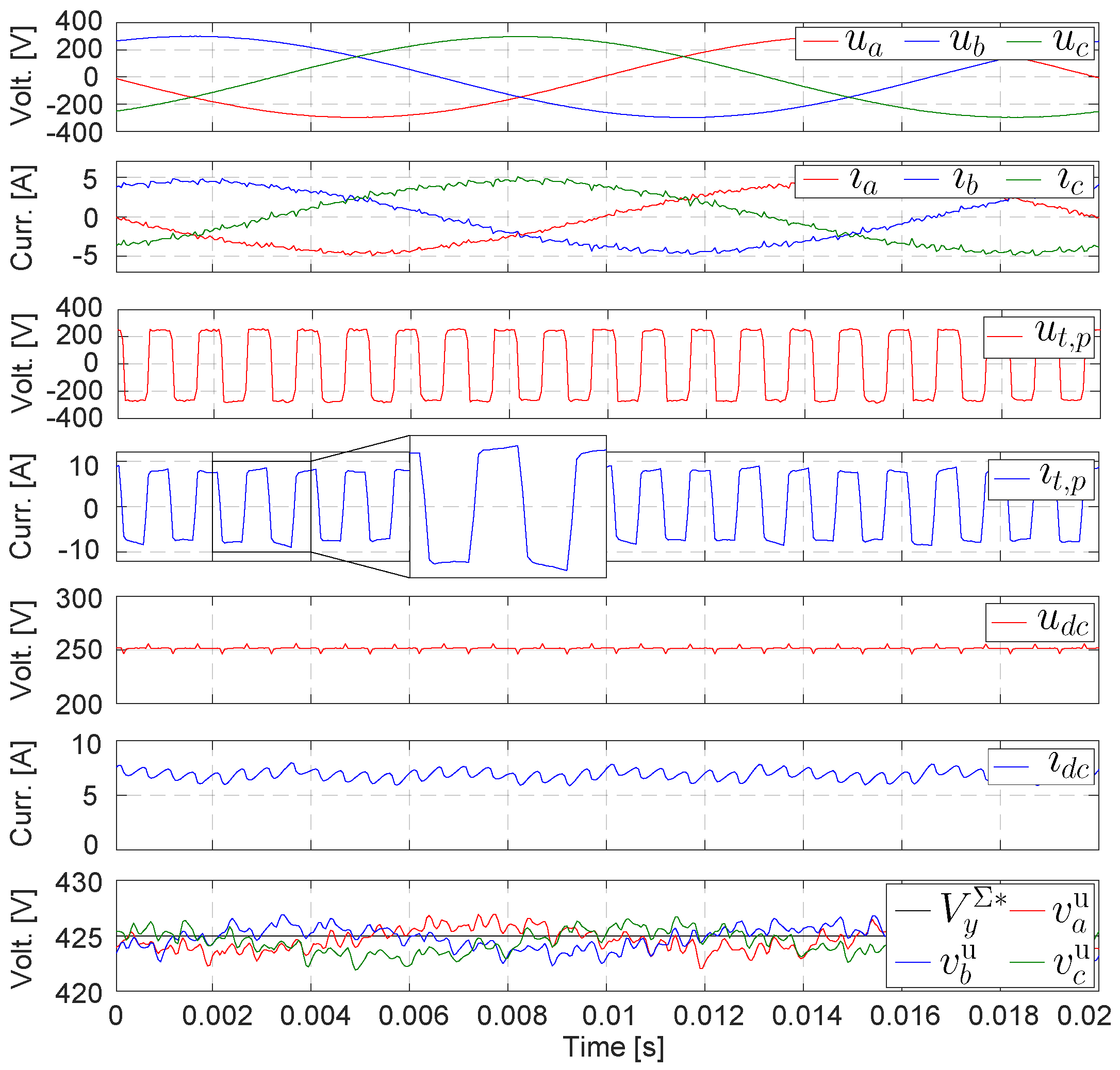
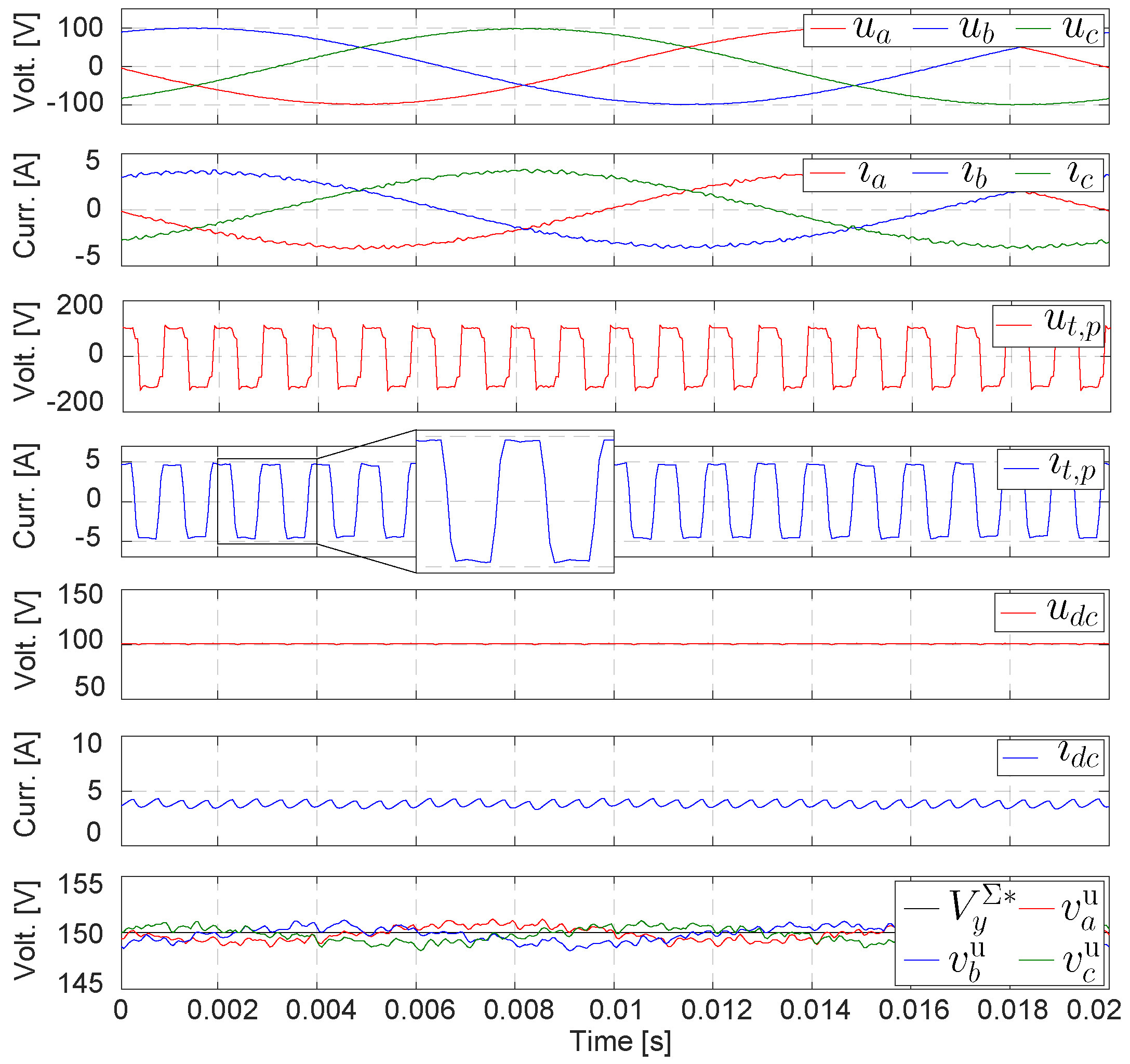
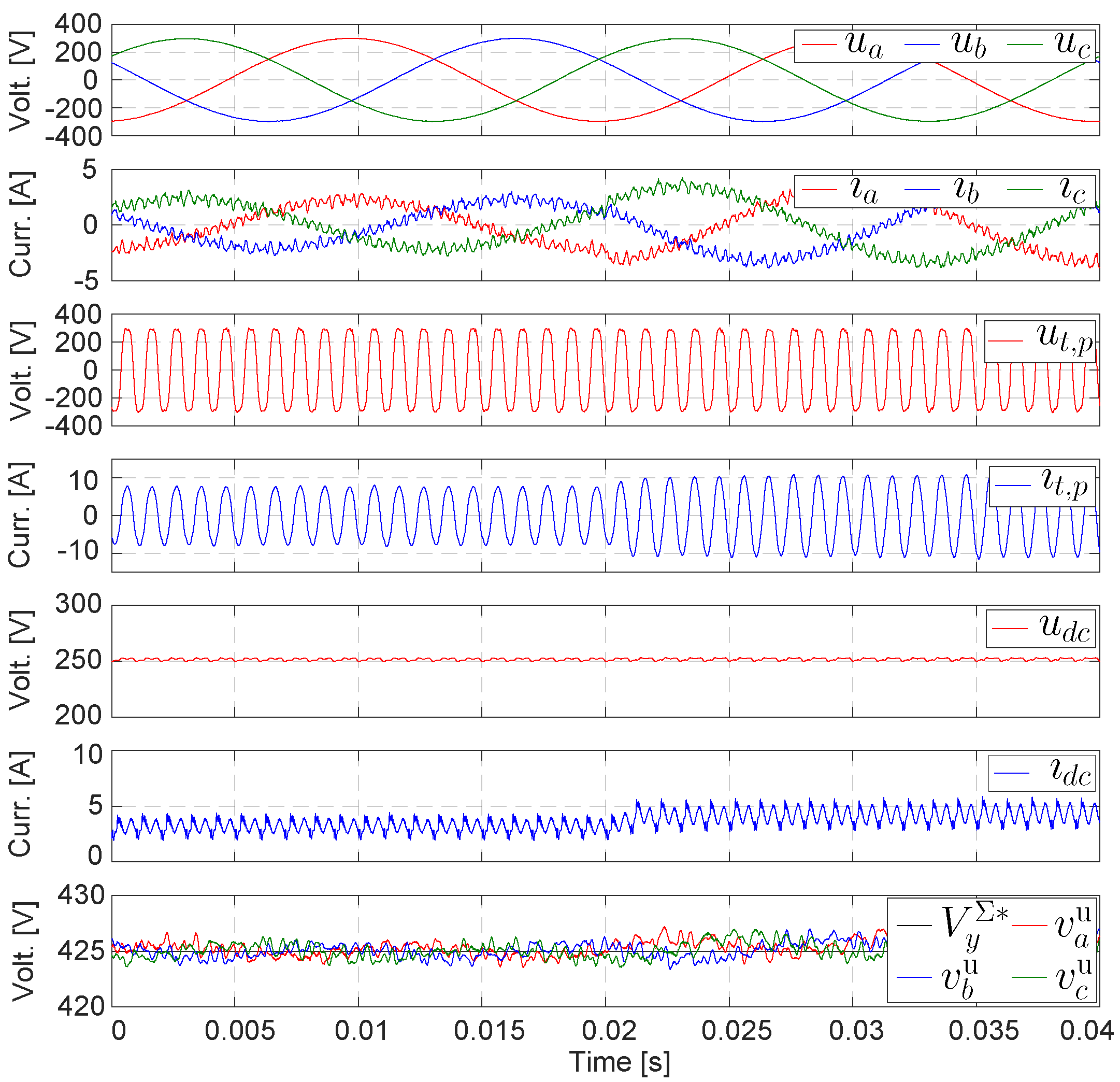
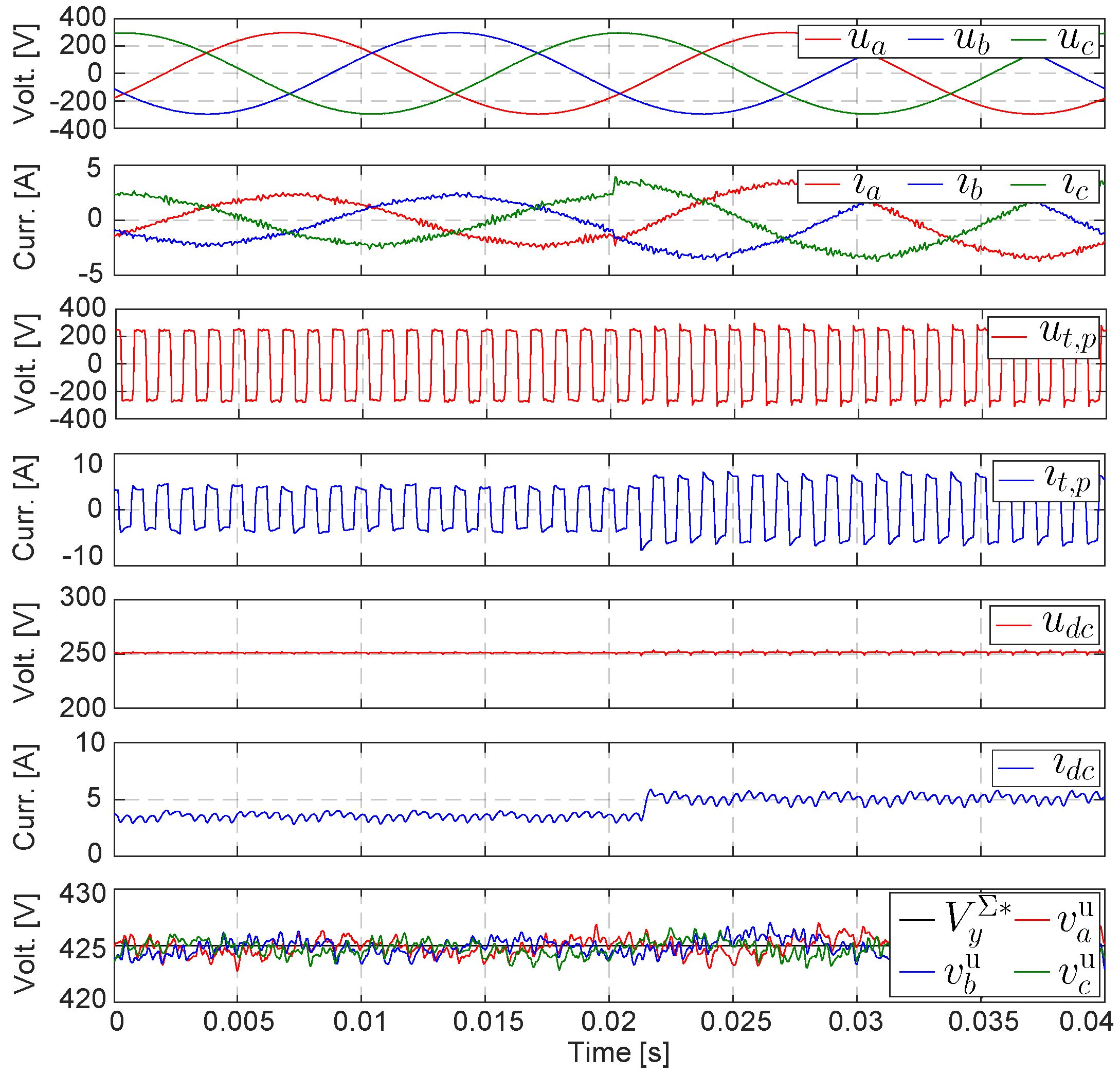
4. Simulation Results
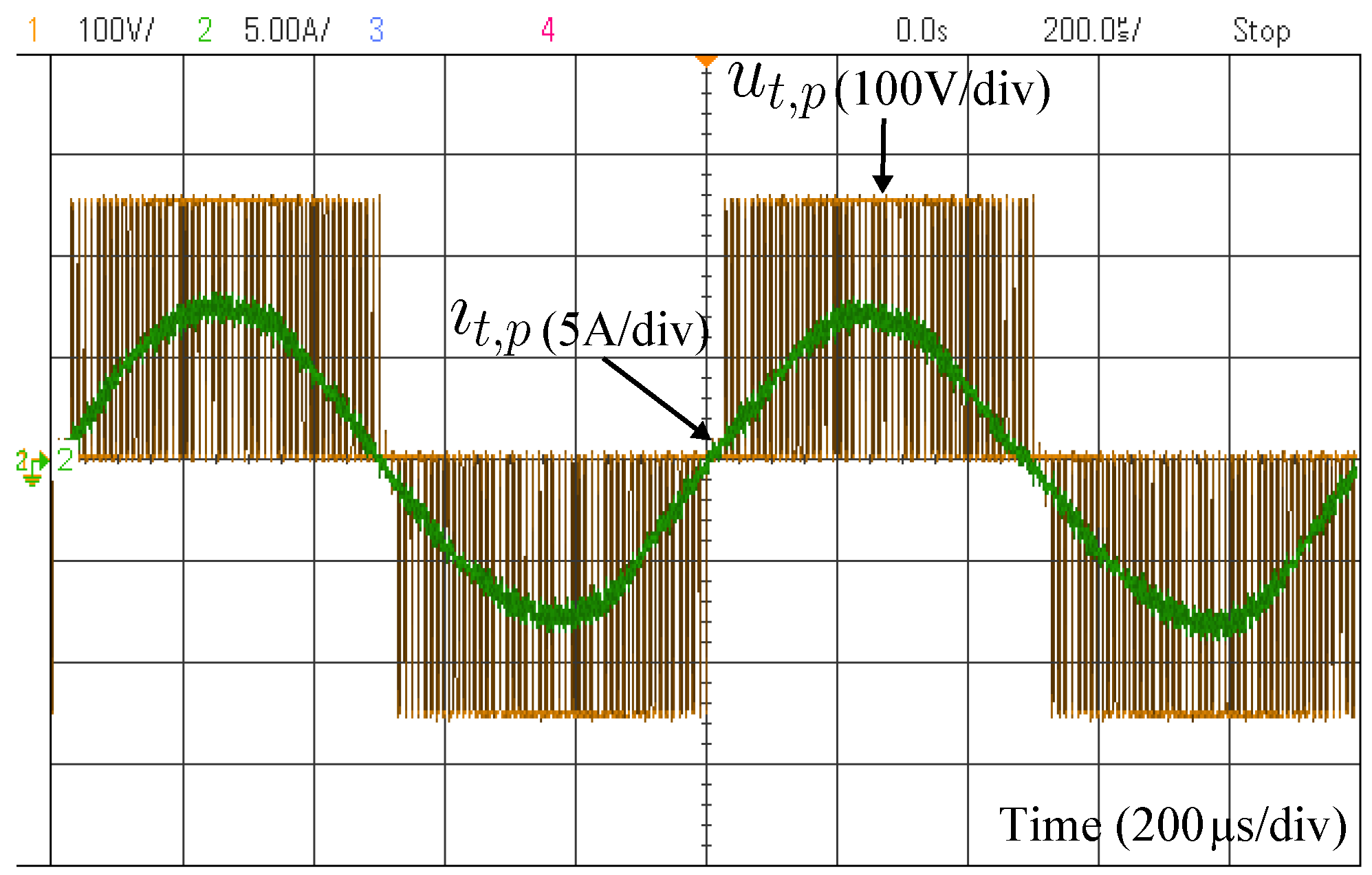
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmad, A.; Qin, Z.; Wijekoon, T.; Bauer, P. An Overview on Medium Voltage Grid Integration of Ultra-Fast Charging Stations: Current Status and Future Trends. IEEE Open J. Ind. Electron. Soc. 2022, 3, 420–447. [Google Scholar] [CrossRef]
- Ronanki, D.; Kelkar, A.; Williamson, S.S. Extreme Fast Charging Technology—Prospects to Enhance Sustainable Electric Transportation. Energies 2019, 12, 3721. [Google Scholar] [CrossRef]
- Srdic, S.; Lukic, S. Toward Extreme Fast Charging: Challenges and Opportunities in Directly Connecting to Medium-Voltage Line. IEEE Electrif. Mag. 2019, 7, 22–31. [Google Scholar] [CrossRef]
- Lüth, T.; Merlin, M.M.C.; Green, T.C.; Hassan, F.; Barker, C.D. High-Frequency Operation of a DC/AC/DC System for HVDC Applications. IEEE Trans. Power Electron. 2014, 29, 4107–4115. [Google Scholar] [CrossRef]
- Kenzelmann, S.; Rufer, A.; Dujic, D.; Canales, F.; de Novaes, Y.R. Isolated DC/DC Structure Based on Modular Multilevel Converter. IEEE Trans. Power Electron. 2015, 30, 89–98. [Google Scholar] [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme Fast Charging of Electric Vehicles: A Technology Overview. IEEE Trans. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Vasiladiotis, M.; Rufer, A.; Béguin, A. Modular converter architecture for medium voltage ultra fast EV charging stations: Global system considerations. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Marca, Y.P.; Roes, M.G.L.; Duarte, J.L.; Wijnands, K.G.E. Isolated MMC-based ac/ac stage for ultrafast chargers. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Rojas, F.; Díaz, M.; Espinoza, M.; Cárdenas, R. A solid state transformer based on a three-phase to single-phase Modular Multilevel Converter for power distribution networks. In Proceedings of the 2017 IEEE Southern Power Electronics Conference (SPEC), Puerto Varas, Chile, 4–7 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Marca, Y.P.; Roes, M.G.L.; Duarte, J.L.; Wijnands, K. Square wave operation to reduce pulsating power in isolated MMC-based ultrafast chargers. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hanover, Germany, 5–9 September 2022; pp. 1–7. [Google Scholar]
- Marca, Y.P.; Roes, M.G.L.; Wijnands, K.G.E. Capacitor voltage ripple and capacitance evaluation in a direct three-phase to single-phase ac/ac MMC. In Proceedings of the 2023 11th International Conference on Power Electronics and ECCE Asia (ICPE 2023—ECCE Asia), Jeju Island, Republic of Korea, 22–25 May 2023; pp. 2278–2283. [Google Scholar] [CrossRef]
- Mondal, G.; Nielebock, S. Control of M2C direct converter for AC to AC conversion with wide frequency range. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, Y.; Kang, Y. Modeling and control of the modular multilevel converter (MMC) based solid state transformer (SST) with magnetic integration. CES Trans. Electr. Mach. Syst. 2020, 4, 309–318. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, Y.; Kang, Y. A Modular Multilevel Converter (MMC) Based Solid-State Transformer (SST) Topology with Simplified Energy Conversion Process and Magnetic Integration. IEEE Trans. Ind. Electron. 2021, 68, 7725–7735. [Google Scholar] [CrossRef]
- Purkayastha, B.; Bhattacharya, T. Submodule Capacitor Voltage Regulation of Modular Multilevel Converter Based Traction Propulsion System with Medium Frequency Isolation. IEEE Trans. Ind. Appl. 2021, 57, 904–914. [Google Scholar] [CrossRef]
- Bessegato, L.; Ilves, K.; Harnefors, L.; Norrga, S.; Östlund, S. Control and Admittance Modeling of an AC/AC Modular Multilevel Converter for Railway Supplies. IEEE Trans. Power Electron. 2020, 35, 2411–2423. [Google Scholar] [CrossRef]
- Vasiladiotis, M.; Cherix, N.; Rufer, A. Operation and control of single-to-three-phase direct AC/AC Modular Multilevel Converters under asymmetric grid conditions. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Republic of Korea, 1–5 June 2015; pp. 1061–1066. [Google Scholar] [CrossRef]
- Glinka, M. Prototype of multiphase modular-multilevel-converter with 2 MW power rating and 17-level-output-voltage. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 4, pp. 2572–2576. [Google Scholar] [CrossRef]
- Glinka, M.; Marquardt, R. A new AC/AC-multilevel converter family applied to a single-phase converter. In Proceedings of the The Fifth International Conference on Power Electronics and Drive Systems, PEDS 2003, Singapore, 17–20 November 2003; Volume 1, pp. 16–23. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, K.; Chen, X.; Xiong, J. Simplified model and submodule capacitor voltage balancing of single-phase AC/AC modular multilevel converter for railway traction purpose. IET Power Electron. 2016, 9, 951–959. [Google Scholar] [CrossRef]
- Hamasaki, S.i.; Takahashi, K.; Fujita, Y.; Daido, T. New Circuit Structure Applying MMC and Its Control for Quick Charger System. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022- ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 2364–2369. [Google Scholar] [CrossRef]
- Budo, K.; Takeshita, T. An Isolated Medium-Voltage AC-DC Converter Using Level-Shifted PWM Control of a Modular Matrix Converter. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Schnarrenberger, M.; Kammerer, F.; Gommeringer, M.; Kolb, J.; Braun, M. Current control and energy balancing of a square-wave powered 1AC-3AC modular multilevel converter. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3607–3614. [Google Scholar] [CrossRef]
- Pouresmaeil, K.; Roes, M.G.L.; Baars, N.H.; Wijnands, C.G.E. Switching Loss Reduction for an MMC-Fed AC/DC Converter. IEEE Open J. Power Electron. 2024, 5, 70–78. [Google Scholar] [CrossRef]
- Brando, G.; Bova, B.; Cervone, A.; Dannier, A.; Del Pizzo, A. A Distribution Power Electronic Transformer with MMC. Appl. Sci. 2018, 8, 120. [Google Scholar] [CrossRef]
- Liao, Z.; Jiao, Y.; Suo, Z.; Li, B.; Zhao, X.; Han, L.; Xu, D. A Three-Port Power Electronic Transformer Based on Magnetic Integration. Appl. Sci. 2022, 12, 11607. [Google Scholar] [CrossRef]
- Ma, D.; Chen, W.; Shu, L.; Qu, X.; Hou, K. A MMC-Based Multiport Power Electronic Transformer With Shared Medium-Frequency Transformer. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 727–731. [Google Scholar] [CrossRef]
- Teng, J.; Sun, X.; Pan, Y.; Liu, X.; Zhang, Y.; Zhao, W.; Li, X. An Inductive-Filtering Strategy of Submodule Ripple-Power in Triple-Port MMC-Based SST Applied to Hybrid Medium and Low Voltage AC/DC Interface. IEEE Trans. Power Electron. 2022, 37, 8015–8032. [Google Scholar] [CrossRef]
- Pei, Z.; Kong, D.; Liu, C.; Liu, C.; Guo, D.; Zhu, D.; Sun, Y.; Heldwein, M.L. Hybrid Isolated Modular Multilevel Converter Based Solid-State Transformer Topology with Simplified Power Conversion Process and Uneven Voltage Ratio. IEEE Trans. Power Electron. 2023, 38, 12757–12773. [Google Scholar] [CrossRef]
- Bu, Z.; Teng, J.; Sun, X.; Pan, Y.; Pan, Y. Low-Frequency Voltage Ripples Decoupling with Switched-Capacitor Conversion for an MMC-Based SST. IEEE Trans. Ind. Electron. 2022, 69, 11293–11303. [Google Scholar] [CrossRef]
- Bu, Z.; Zhao, W.; Zhang, M.; Teng, J.; Li, X.; Sun, X. Dynamic Performance Evaluation and Optimization of Common HFAC Bus Lightweight MMC-SST. IEEE Trans. Power Electron. 2024, 39, 2035–2050. [Google Scholar] [CrossRef]
- Sharifabadi, K.; Harnefors, L.; Nee, H.P.; Norrga, S.; Teodorescu, R. Design, Control, and Application of Modular Multilevel Converters for HVDC Transmission Systems, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Antonopoulos, A.; Angquist, L.; Nee, H.P. On dynamics and voltage control of the Modular Multilevel Converter. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Ludois, D.C.; Venkataramanan, G. Simplified Terminal Behavioral Model for a Modular Multilevel Converter. IEEE Trans. Power Electron. 2014, 29, 1622–1631. [Google Scholar] [CrossRef]
- Pouresmaeil, K.; Duarte, J.; Wijnands, K.; Roes, M.; Baars, N. Single-Phase Bidirectional ZVZCS AC-DC Converter for MVConnected Ultra-fast Chargers. In Proceedings of the PCIM Europe 2022; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 10–12 May 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Mo, R.; Li, H.; Shi, Y. A Phase-Shifted Square Wave Modulation (PS-SWM) for Modular Multilevel Converter (MMC) and DC Transformer for Medium Voltage Applications. IEEE Trans. Power Electron. 2019, 34, 6004–6008. [Google Scholar] [CrossRef]
- Hirofumi, A.; Edson, H.W.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gui, Y.; Wang, X.; Blaabjerg, F. Vector Current Control Derived from Direct Power Control for Grid-Connected Inverters. IEEE Trans. Power Electron. 2019, 34, 9224–9235. [Google Scholar] [CrossRef]
- Rodríguez, A.; Vázquez, A.; Lamar, D.G.; Hernando, M.M.; Sebastián, J. Different Purpose Design Strategies and Techniques to Improve the Performance of a Dual Active Bridge With Phase-Shift Control. IEEE Trans. Power Electron. 2015, 30, 790–804. [Google Scholar] [CrossRef]
- Krismer, F. Modeling and Optimization of Bidirectional Dual Active Bridge DC-DC Converter Topologies. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2010. [Google Scholar]
- De Doncker, R.W.A.A.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high-power-density DC/DC converter for high-power applications. IEEE Trans. Ind. Appl. 1991, 27, 63–73. [Google Scholar] [CrossRef]
- Du, Y.; Huang, A.Q. A high resolution digital phase-shift modulation scheme for ultra-high frequency dual active bridge converters. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1684–1691. [Google Scholar] [CrossRef]
- Shao, S.; Chen, L.; Shan, Z.; Gao, F.; Chen, H.; Sha, D.; Dragičević, T. Modeling and Advanced Control of Dual-Active-Bridge DC–DC Converters: A Review. IEEE Trans. Power Electron. 2022, 37, 1524–1547. [Google Scholar] [CrossRef]
- Chen, B.; Chen, Y.; Tian, C.; Yuan, J.; Yao, X. Analysis and Suppression of Circulating Harmonic Currents in a Modular Multilevel Converter Considering the Impact of Dead Time. IEEE Trans. Power Electron. 2015, 30, 3542–3552. [Google Scholar] [CrossRef]
- Deng, F.; Yu, Q.; Wang, Q.; Zhu, R.; Cai, X.; Chen, Z. Suppression of DC-Link Current Ripple for Modular Multilevel Converters Under Phase-Disposition PWM. IEEE Trans. Power Electron. 2020, 35, 3310–3324. [Google Scholar] [CrossRef]
- Yu, Q.; Deng, F.; Liu, C.; Zhao, J.; Blaabjerg, F.; Abulanwar, S. DC-Link High-Frequency Current Ripple Elimination Strategy for MMCs Using Phase-Shifted Double-Group Multicarrier-Based Phase-Disposition PWM. IEEE Trans. Power Electron. 2021, 36, 8872–8886. [Google Scholar] [CrossRef]
- Mohamed Ismail, H.; Kaliyaperumal, S. Enhanced Voltage Sorting Algorithm for Balancing the Capacitor Voltage in Modular Multilevel Converter. IEEE Access 2021, 9, 167489–167502. [Google Scholar] [CrossRef]
- Peng, H.; Maksimovic, D.; Prodic, A.; Alarcon, E. Modeling of quantization effects in digitally controlled DC-DC converters. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4312–4318. [Google Scholar] [CrossRef]
- Peterchev, A.V.; Sanders, S.R. Quantization resolution and limit cycling in digitally controlled PWM converters. IEEE Trans. Power Electron. 2003, 18, 301–308. [Google Scholar] [CrossRef]




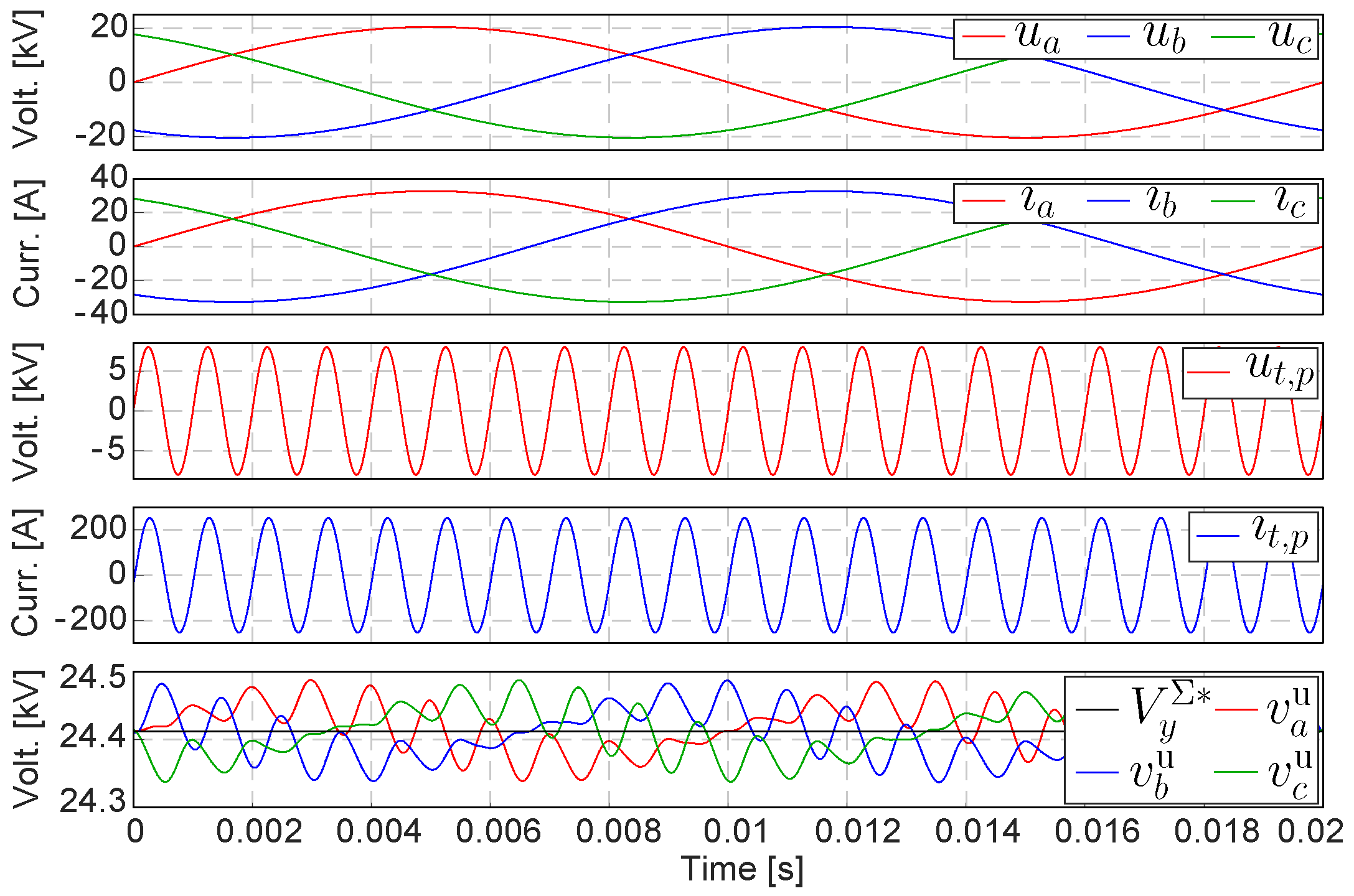

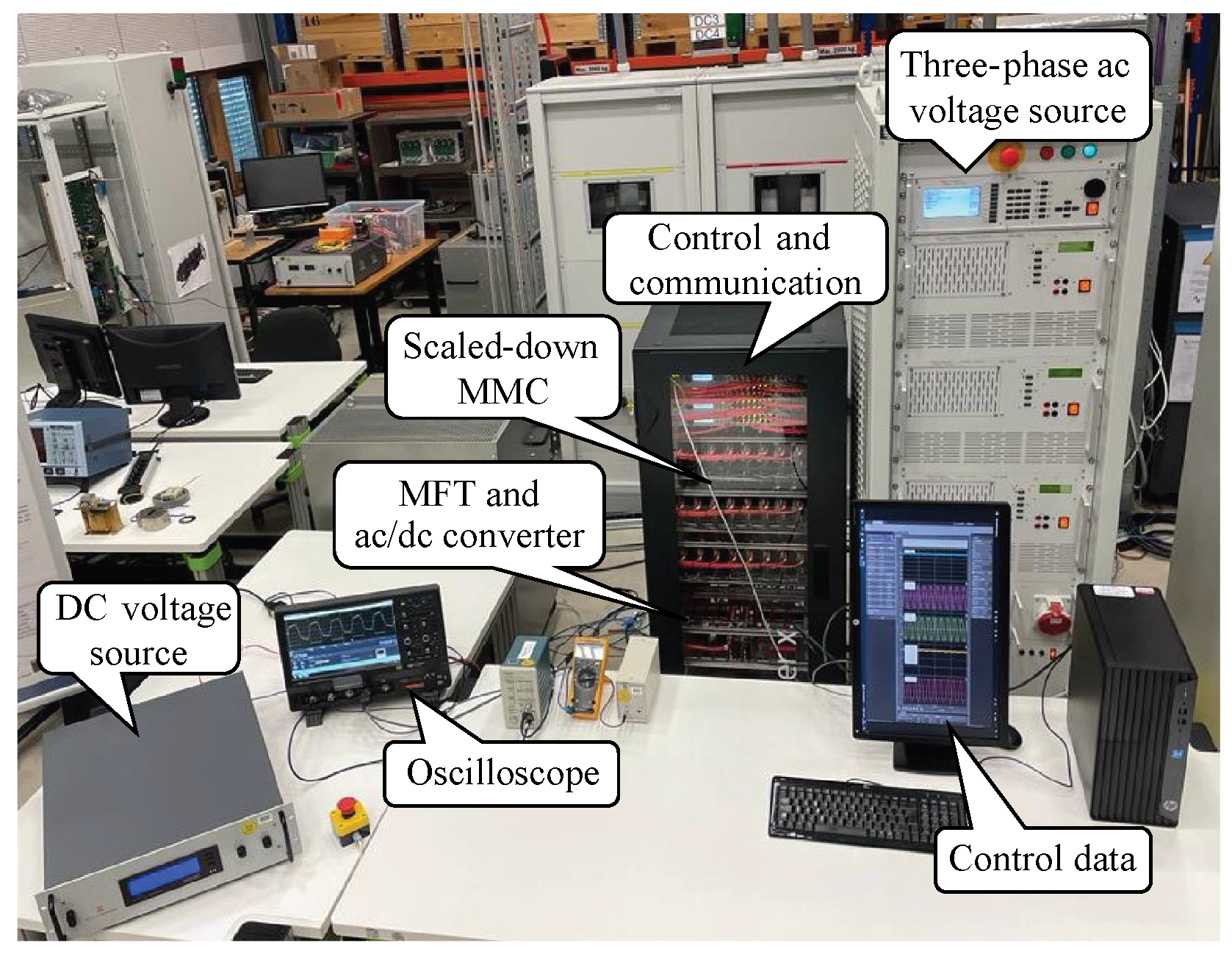
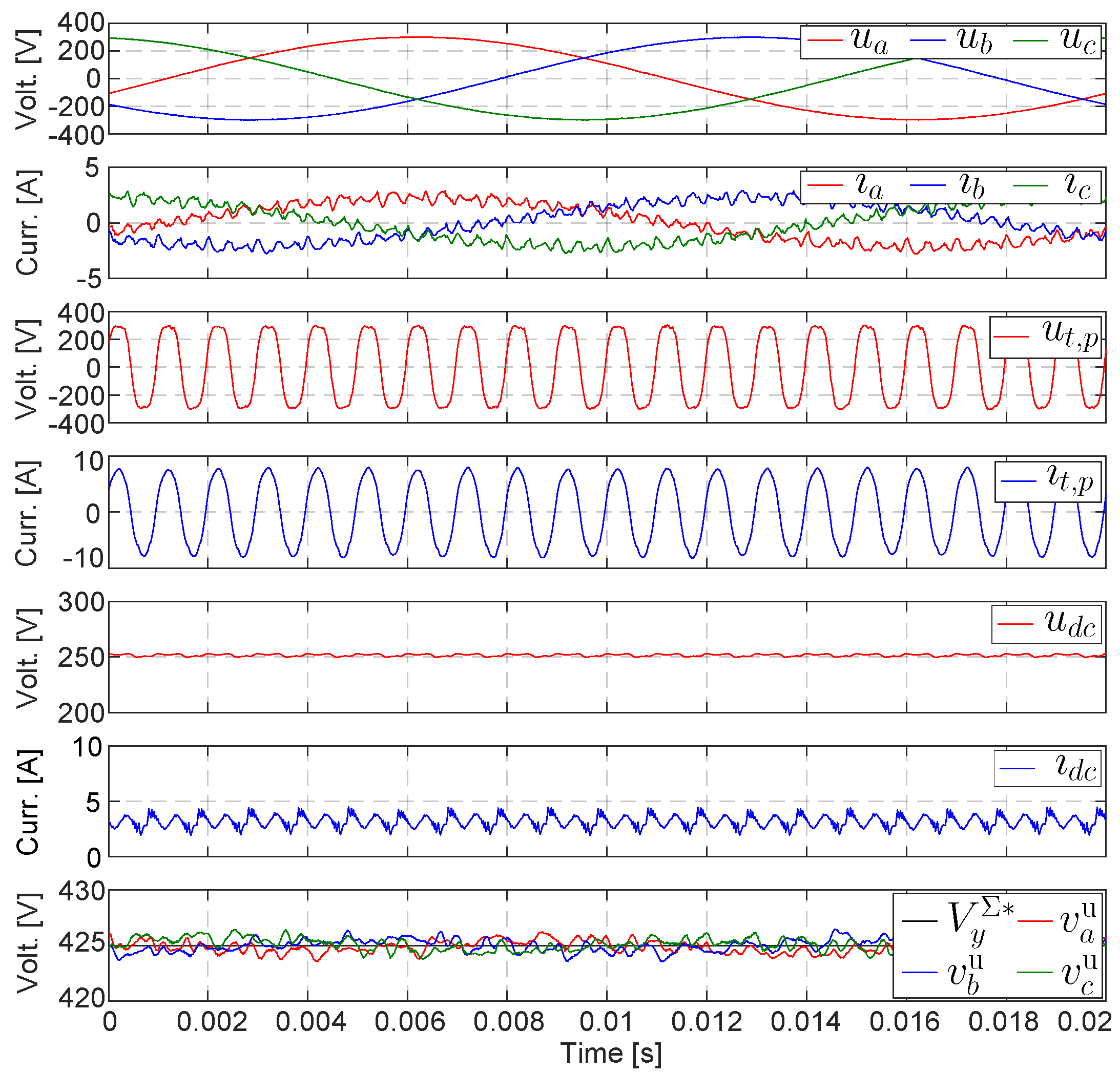
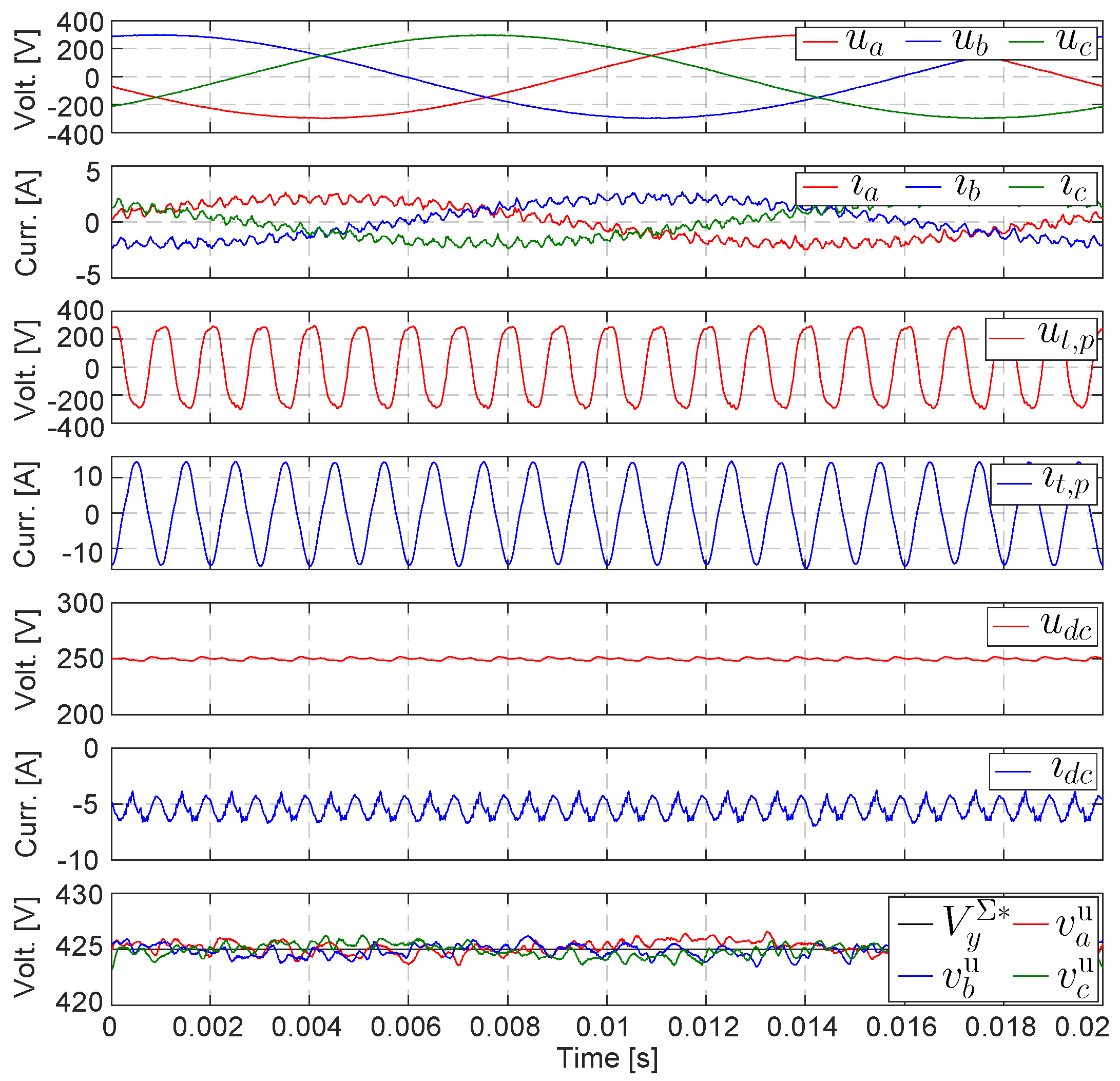



| Quantity | Parameter | Value | Unit |
|---|---|---|---|
| Active power reference | 1 | MW | |
| Reactive power reference | 0 | VAr | |
| Grid phase-to-neutral peak voltage | kV | ||
| Single-phase peak voltage | 8000 | V | |
| DC voltage | 800 | V | |
| Summed cap. voltage reference | kV | ||
| Grid frequency | 50 | Hz | |
| MFT frequency | 1 | kHz | |
| MFT turns ratio | r:1 | 10:1 | − |
| Arm capacitance | mF | ||
| Arm inductance | 1 | mH |
| Quantity | Parameter | Value | Unit |
|---|---|---|---|
| Active power reference | 1 | kW | |
| Reactive power reference | 0 | VAr | |
| Grid phase-to-neutral peak voltage | 300 | V | |
| Single-phase peak voltage | 250 | V | |
| DC voltage | 250 | V | |
| Summed cap. voltage reference | 425 | V | |
| Grid frequency | 50 | Hz | |
| MFT frequency | 1 | kHz | |
| Switching frequency | 50 | kHz | |
| MFT turn ratio | r:1 | 1:1 | − |
| Arm capacitance | mF | ||
| Arm inductance | mH | ||
| Number of SMs per arm | N | 4 | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marca, Y.P.; Roes, M.G.L.; Wijnands, C.G.E.; Duarte, J.L.; Huisman, H. Single-Stage MV-Connected Charger Using an Ac/Ac Modular Multilevel Converter. Energies 2024, 17, 2998. https://doi.org/10.3390/en17122998
Marca YP, Roes MGL, Wijnands CGE, Duarte JL, Huisman H. Single-Stage MV-Connected Charger Using an Ac/Ac Modular Multilevel Converter. Energies. 2024; 17(12):2998. https://doi.org/10.3390/en17122998
Chicago/Turabian StyleMarca, Ygor Pereira, Maurice G. L. Roes, Cornelis G. E. Wijnands, Jorge L. Duarte, and Henk Huisman. 2024. "Single-Stage MV-Connected Charger Using an Ac/Ac Modular Multilevel Converter" Energies 17, no. 12: 2998. https://doi.org/10.3390/en17122998
APA StyleMarca, Y. P., Roes, M. G. L., Wijnands, C. G. E., Duarte, J. L., & Huisman, H. (2024). Single-Stage MV-Connected Charger Using an Ac/Ac Modular Multilevel Converter. Energies, 17(12), 2998. https://doi.org/10.3390/en17122998








