Decision Tree Variations and Online Tuning for Real-Time Control of a Building in a Two-Stage Management Strategy
Abstract
1. Introduction
- The replacement of a real-time MPC stage with an interpretable, lightweight, real-time controller based on Decision Trees.
- The investigation of different Decision Trees’ implementations depending on architectures and input training data.
- The online tuning of a Decision Tree following an offline training based on a model of the controlled system.
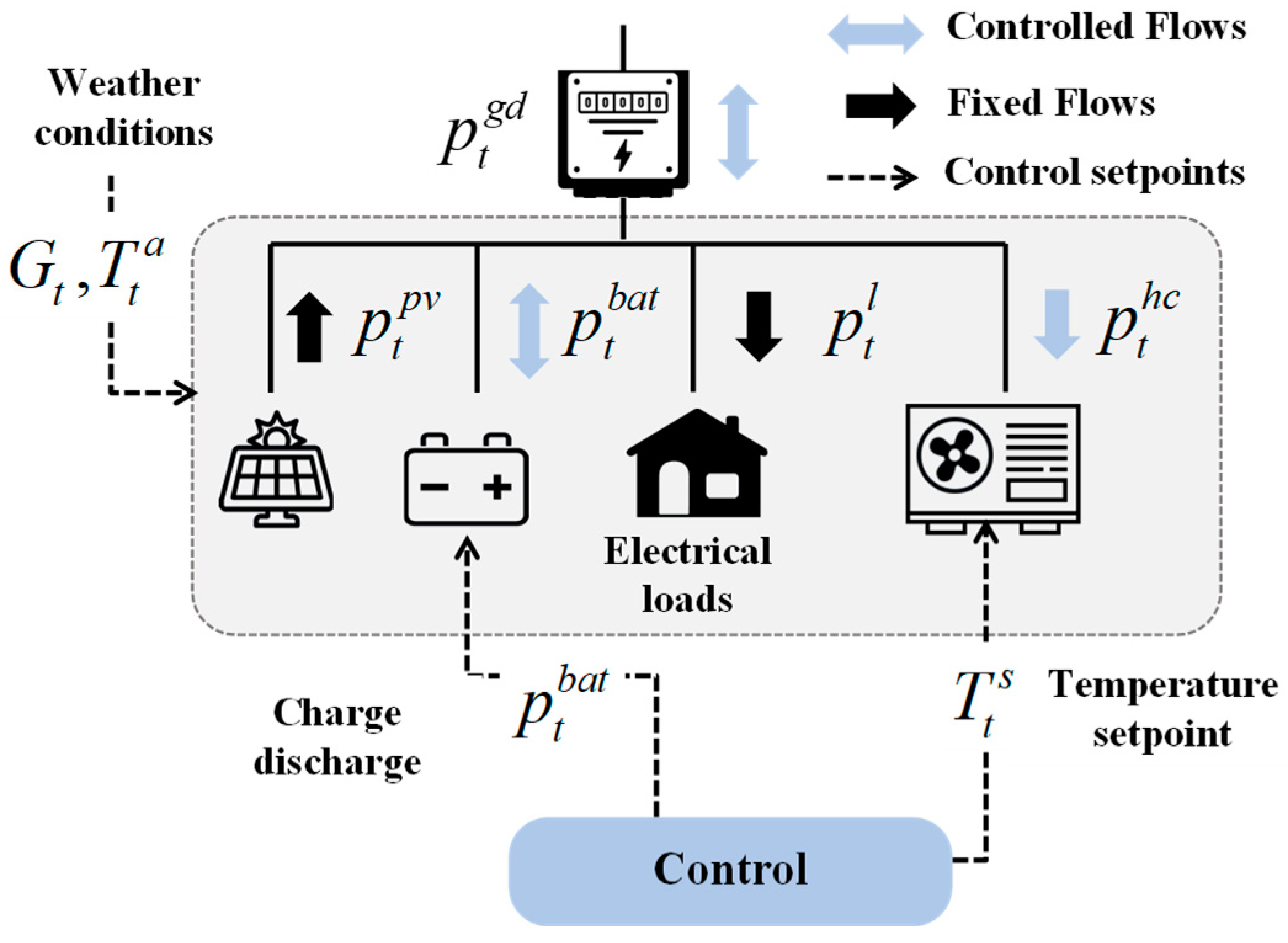
2. Case Study
2.1. Day-Ahead Optimal Scheduling
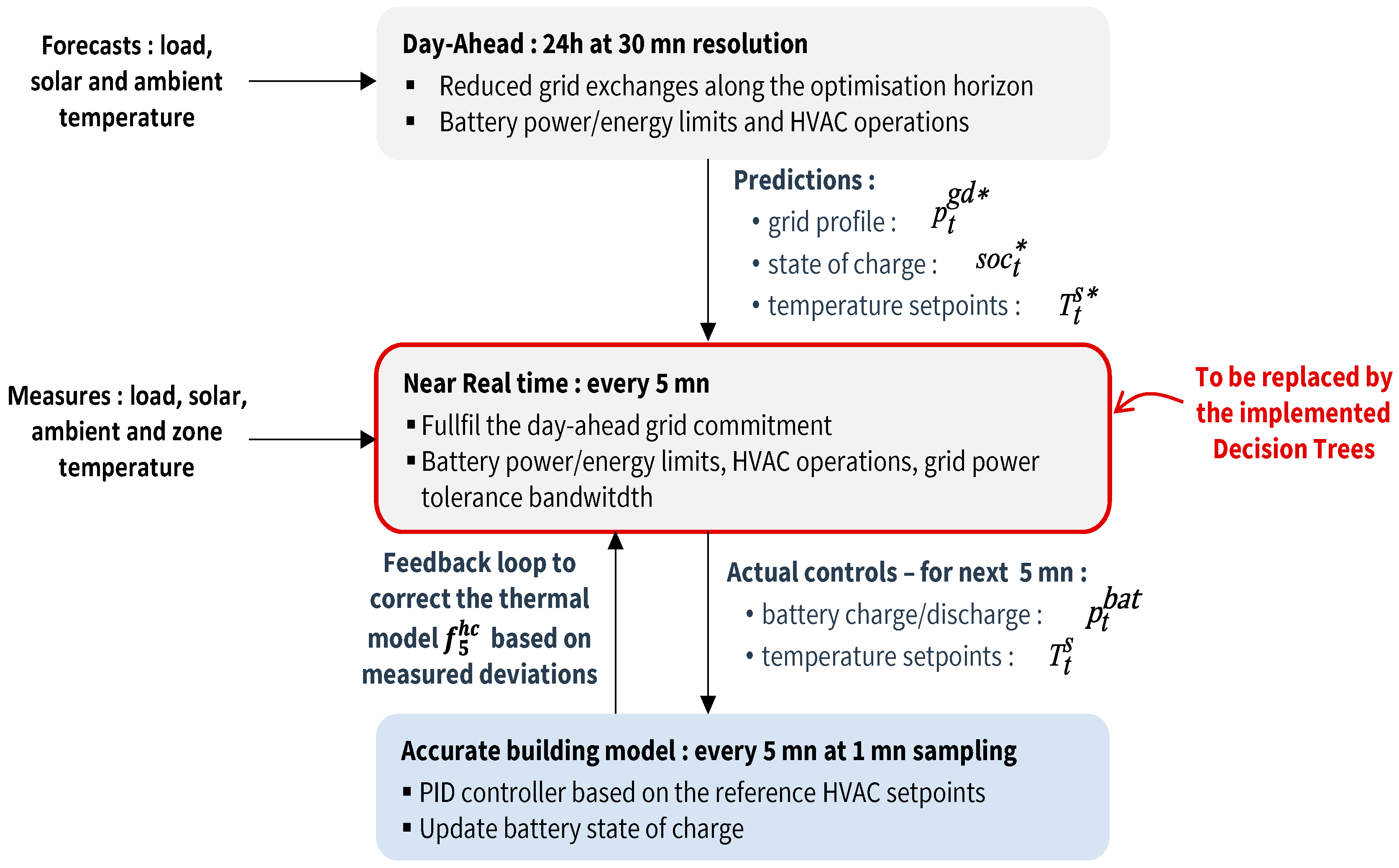
2.2. Near Real-Time Control
3. Motivation for a Lightweight Real-Time Controller
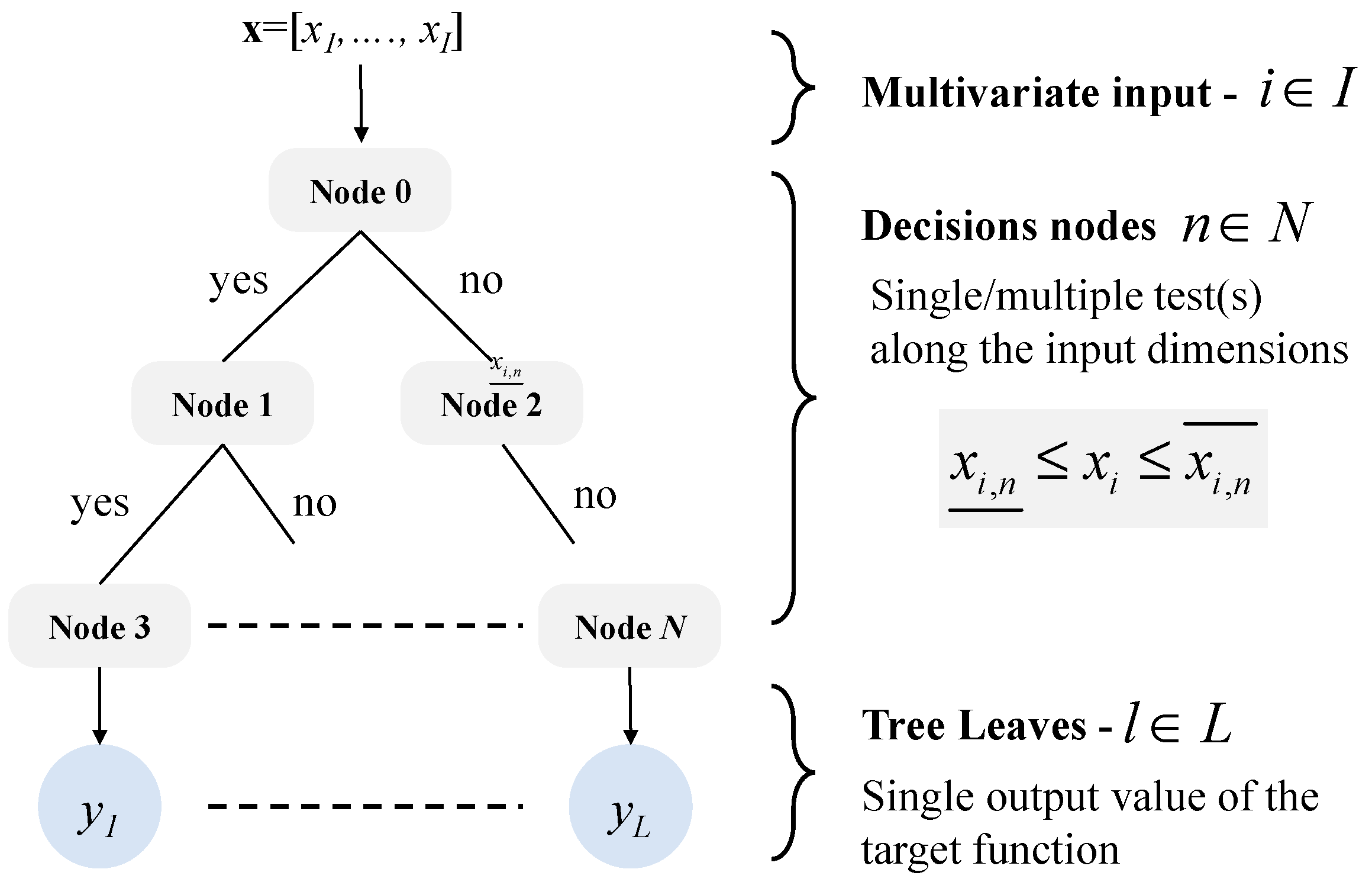
4. Decision Trees’ Implementations, Training, and Tuning
4.1. Investigated Decision Trees (DTs)
4.1.1. Regular DTs
4.1.2. Regressor DTs
4.1.3. Linear Functional DTs
4.2. Investigated Implementations
4.2.1. Inputs/Outputs
4.2.2. Training Based on MPC Historical Results
- ▪ Training Set A: 1 month (Jan)
- ▪ Training Set B: 5 months (Jan–May)
- ▪ Testing Set: 7 months (Jun–Dec)
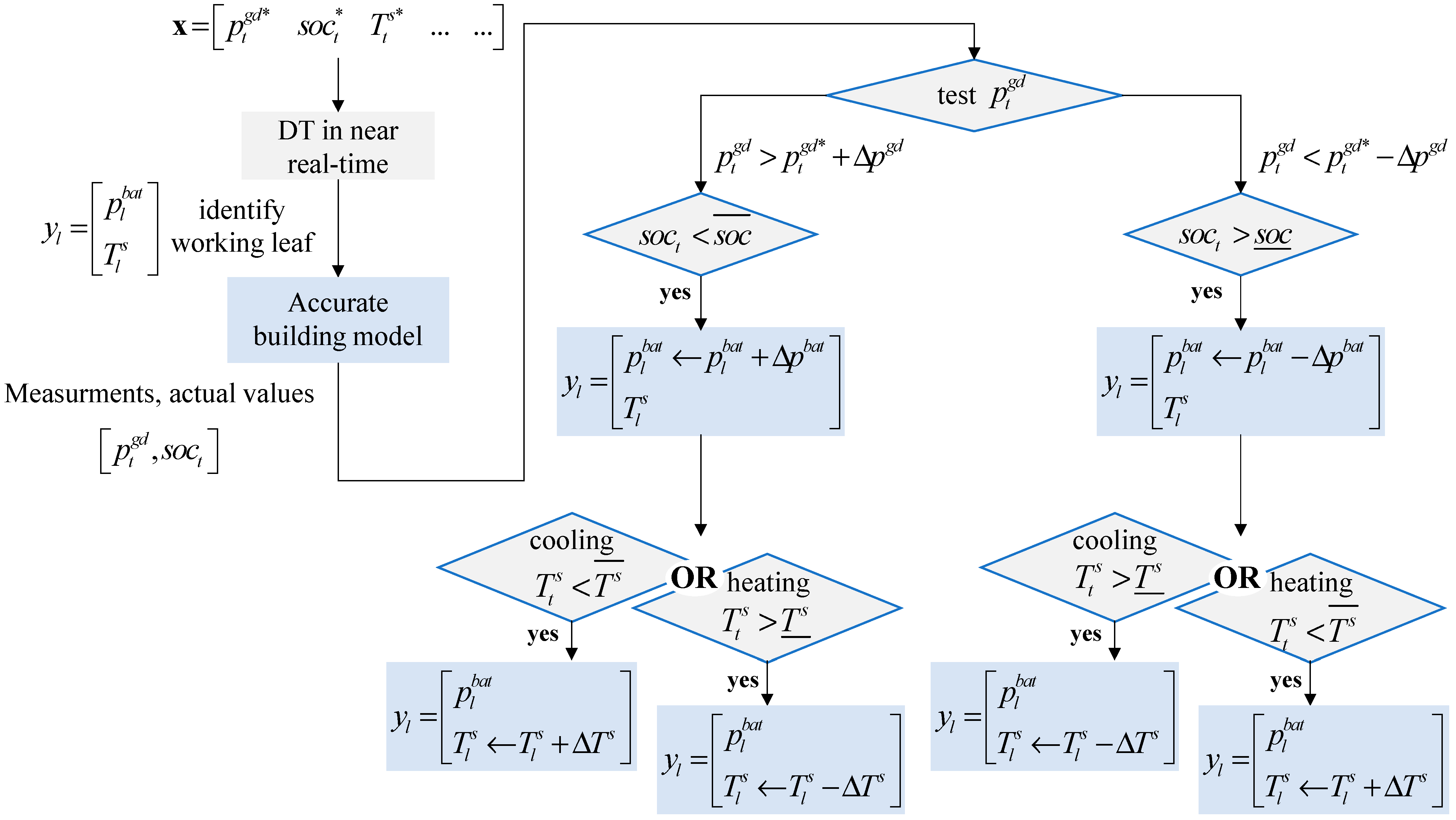
4.2.3. Training Based on Model and Online Tuning
5. Results and Discussions
5.1. Input Data and Performance Metrics
5.2. Training on Historical MPC
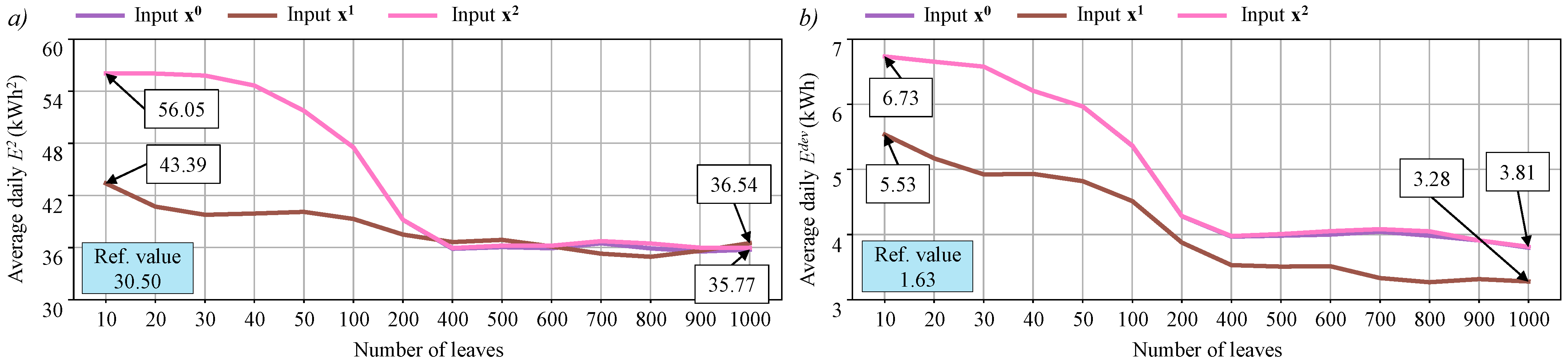
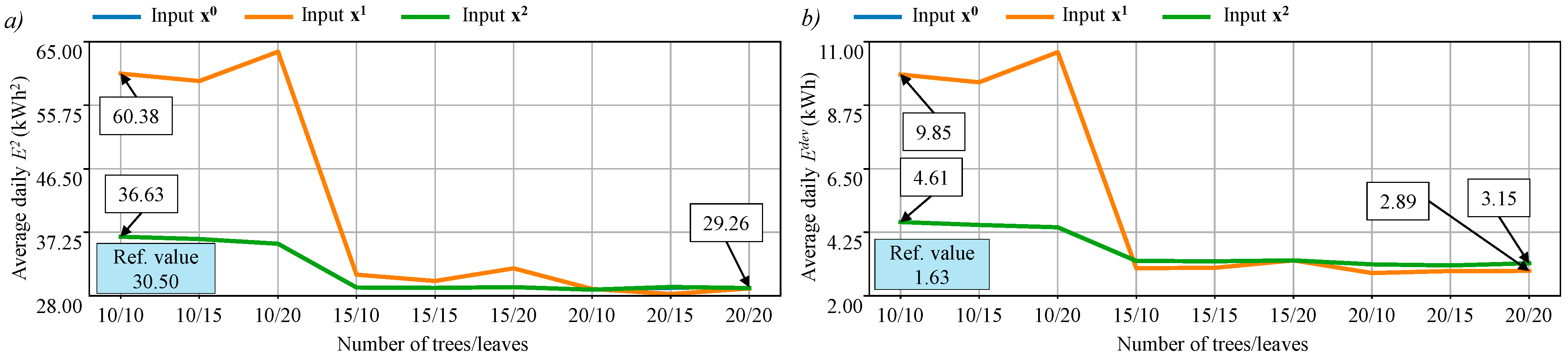
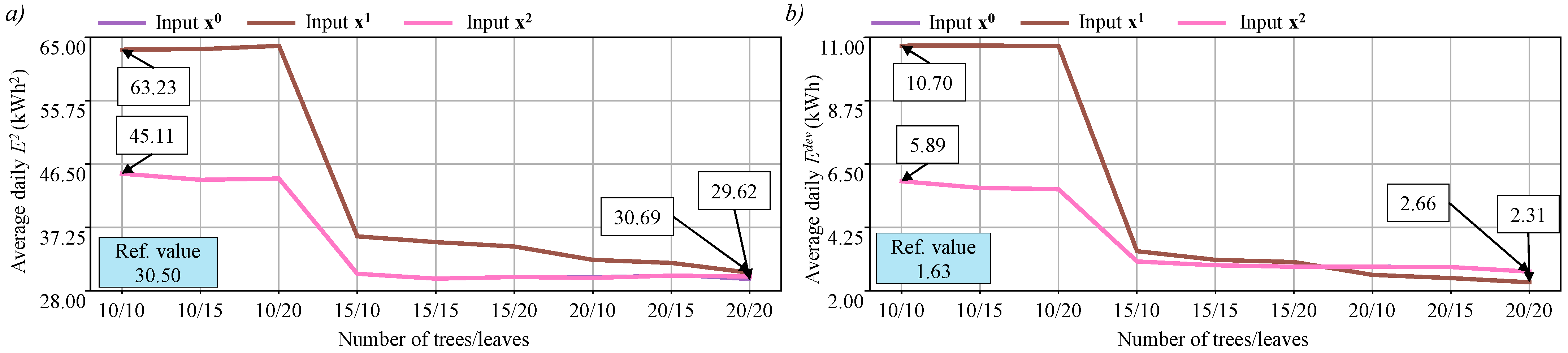
5.2.1. Regular DTs
5.2.2. Regressor DTs
5.2.3. Linear DTs
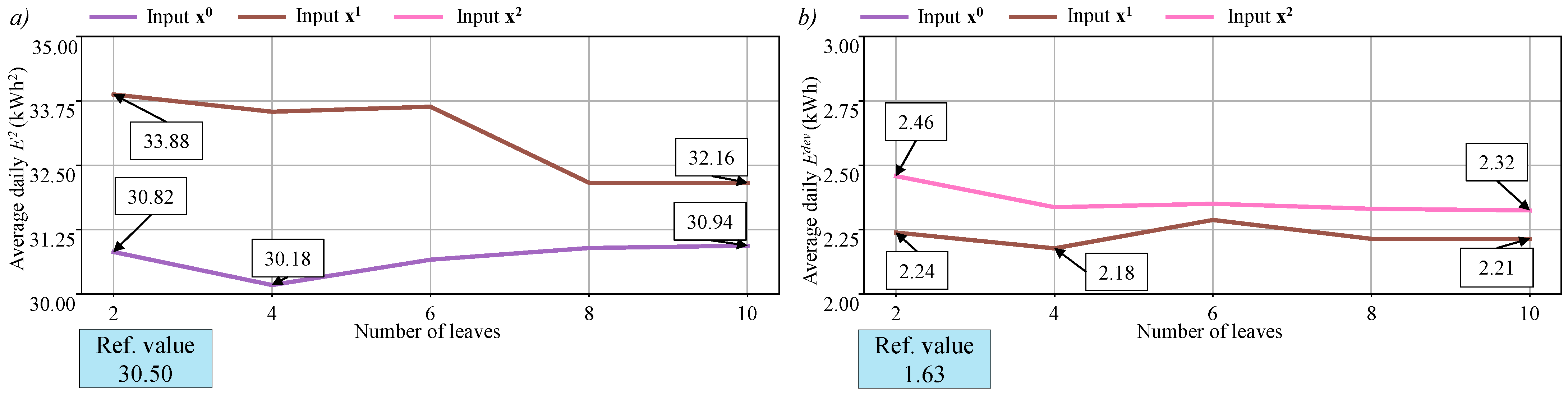
5.3. Training on Model MPC and Online Tuning
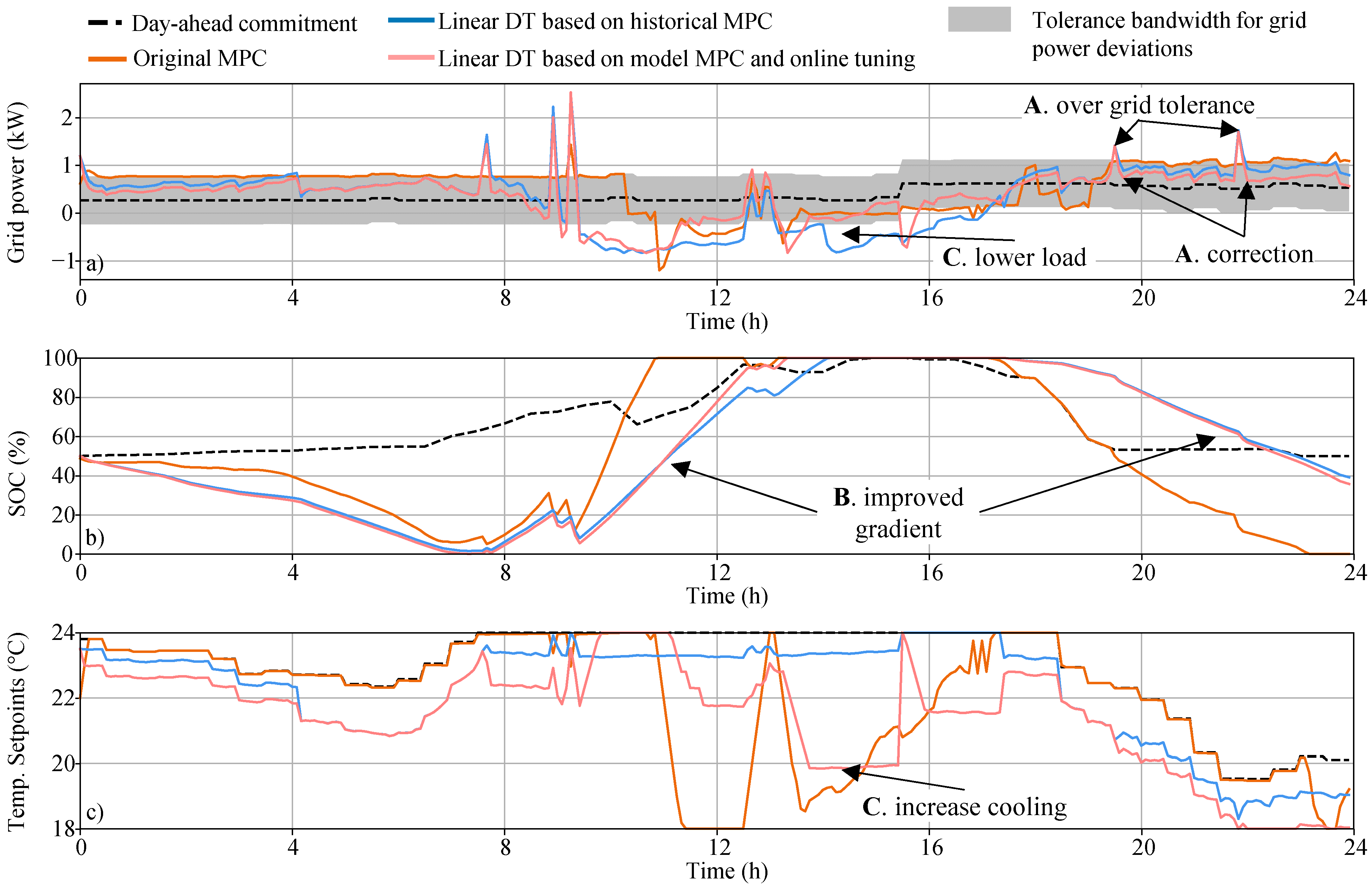
5.3.1. Controller Performances
5.3.2. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ‘Renewables 2023—Analysis’, IEA. Available online: https://www.iea.org/reports/renewables-2023 (accessed on 5 March 2024).
- Vasiliev, M.; Nur-E-Alam, M.; Alameh, K. Recent Developments in Solar Energy-Harvesting Technologies for Building Integration and Distributed Energy Generation. Energies 2019, 12, 1080. [Google Scholar] [CrossRef]
- Klingler, A.-L. Self-consumption with PV + Battery systems: A market diffusion model considering individual consumer behaviour and preferences. Appl. Energy 2017, 205, 1560–1570. [Google Scholar] [CrossRef]
- Huy, T.H.B.; Dinh, H.T.; Kim, D. Multi-objective framework for a home energy management system with the integration of solar energy and an electric vehicle using an augmented ε-constraint method and lexicographic optimization. Sustain. Cities Soc. 2023, 88, 104289. [Google Scholar] [CrossRef]
- Mir, U.; Abbasi, U.; Mir, T.; Kanwal, S.; Alamri, S. Energy Management in Smart Buildings and Homes: Current Approaches, a Hypothetical Solution, and Open Issues and Challenges. IEEE Access 2021, 9, 94132–94148. [Google Scholar] [CrossRef]
- Dadashi-Rad, M.H.; Ghasemi-Marzbali, A.; Ahangar, R.A. Modeling and planning of smart buildings energy in power system considering demand response. Energy 2020, 213, 118770. [Google Scholar] [CrossRef]
- Ghayour, S.S.; Barforoushi, T. Optimal scheduling of electrical and thermal resources and appliances in a smart home under uncertainty. Energy 2022, 261, 125292. [Google Scholar] [CrossRef]
- Gholamzadehmir, M.; Del Pero, C.; Buffa, S.; Fedrizzi, R.; Aste, N. Adaptive-predictive control strategy for HVAC systems in smart buildings—A review. Sustain. Cities Soc. 2020, 63, 102480. [Google Scholar] [CrossRef]
- Di Piazza, M.; La Tona, G.; Luna, M.; Di Piazza, A. A two-stage Energy Management System for smart buildings reducing the impact of demand uncertainty. Energy Build. 2017, 139, 1–9. [Google Scholar] [CrossRef]
- Blad, C.; Bøgh, S.; Kallesøe, C.S. Data-driven Offline Reinforcement Learning for HVAC-systems. Energy 2022, 261, 125290. [Google Scholar] [CrossRef]
- Pinto, G.; Deltetto, D.; Capozzoli, A. Data-driven district energy management with surrogate models and deep reinforcement learning. Appl. Energy 2021, 304, 117642. [Google Scholar] [CrossRef]
- Lork, C.; Li, W.-T.; Qin, Y.; Zhou, Y.; Yuen, C.; Tushar, W.; Saha, T.K. An uncertainty-aware deep reinforcement learning framework for residential air conditioning energy management. Appl. Energy 2020, 276, 115426. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Sun, M.; Sun, C. Hybrid Policy-Based Reinforcement Learning of Adaptive Energy Management for the Energy Transmission-Constrained Island Group. IEEE Trans. Ind. Inform. 2023, 19, 10751–10762. [Google Scholar] [CrossRef]
- Arroyo, J.; Manna, C.; Spiessens, F.; Helsen, L. Reinforced model predictive control (RL-MPC) for building energy management. Appl. Energy 2022, 309, 118346. [Google Scholar] [CrossRef]
- Kumar, S.R.; Easwaran, A.; Delinchant, B.; Rigo-Mariani, R. Behavioural cloning based RL agents for district energy management. In Proceedings of the 9th ACM International Conference on Systems for Energy-Efficient Buildings, Cities, and Transportation, in BuildSys ’22, Boston, MA, USA, 9–10 November 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 466–470. [Google Scholar] [CrossRef]
- Chen, B.; Cai, Z.; Berges, M. Gnu-RL: A Practical and Scalable Reinforcement Learning Solution for Building HVAC Control Using a Differentiable MPC Policy. Front. Built Environ. 2020, 6, 562239. [Google Scholar] [CrossRef]
- Ngarambe, J.; Yun, G.Y.; Santamouris, M. The use of artificial intelligence (AI) methods in the prediction of thermal comfort in buildings: Energy implications of AI-based thermal comfort controls. Energy Build. 2020, 211, 109807. [Google Scholar] [CrossRef]
- Zhang, Z.; Chong, A.; Pan, Y.; Zhang, C.; Lam, K.P. Whole building energy model for HVAC optimal control: A practical framework based on deep reinforcement learning. Energy Build. 2019, 199, 472–490. [Google Scholar] [CrossRef]
- Panda, S.P.; Genest, B.; Easwaran, A.; Rigo-Mariani, R.; Lin, P. Methods for mitigating uncertainty in real-time operations of a connected microgrid. Sustain. Energy Grids Netw. 2024, 38, 101334. [Google Scholar] [CrossRef]
- El Maghraoui, A.; Ledmaoui, Y.; Laayati, O.; El Hadraoui, H.; Chebak, A. Smart Energy Management: A Comparative Study of Energy Consumption Forecasting Algorithms for an Experimental Open-Pit Mine. Energies 2022, 15, 4569. [Google Scholar] [CrossRef]
- Kontogiannis, D.; Bargiotas, D.; Daskalopulu, A. Fuzzy Control System for Smart Energy Management in Residential Buildings Based on Environmental Data. Energies 2021, 14, 752. [Google Scholar] [CrossRef]
- Rigo-Mariani, R.; Ahmed, A. Smart home energy management with mitigation of power profile uncertainties and model errors. Energy Build. 2023, 294, 113223. [Google Scholar] [CrossRef]
- Troitzsch, S. kaiATtum, tomschelo, and arifa7med, mesmo-dev/mesmo: Zenodo. 2021. Available online: https://zenodo.org/record/5674243 (accessed on 11 April 2023).
- Kirschen, D.; Strbac, G. Fundamentals of Power System Economics—Daniel S. Kirschen, Goran Strbac—Google Books, 2nd ed. Wiley. 2018. Available online: https://books.google.fr/books/about/Fundamentals_of_Power_System_Economics.html?id=rm61AAAAIAAJ&source=kp_book_description&redir_esc=y (accessed on 2 March 2022).
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Jahan, I.S.; Snasel, V.; Misak, S. Intelligent Systems for Power Load Forecasting: A Study Review. Energies 2020, 13, 6105. [Google Scholar] [CrossRef]
- Meenal, R.; Binu, D.; Ramya, K.C.; Michael, P.A.; Kumar, K.V.; Rajasekaran, E.; Sangeetha, B. Weather Forecasting for Renewable Energy System: A Review. Arch. Comput. Methods Eng. 2022, 29, 2875–2891. [Google Scholar] [CrossRef]
- Moutis, P.; Skarvelis-Kazakos, S.; Brucoli, M. Decision tree aided planning and energy balancing of planned community microgrids. Appl. Energy 2016, 161, 197–205. [Google Scholar] [CrossRef]
- Luo, X.; Xia, J.; Liu, Y. Extraction of dynamic operation strategy for standalone solar-based multi-energy systems: A method based on decision tree algorithm. Sustain. Cities Soc. 2021, 70, 102917. [Google Scholar] [CrossRef]
- XGBoost|Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Available online: https://dl.acm.org/doi/10.1145/2939672.2939785 (accessed on 25 March 2024).
- Gama, J. Functional Trees. Mach. Learn. 2004, 55, 219–250. [Google Scholar] [CrossRef]
- Murray, D.; Stankovic, L.; Stankovic, V. An electrical load measurements dataset of United Kingdom households from a two-year longitudinal study. Sci. Data 2017, 4, 160122. [Google Scholar] [CrossRef]
- Diamond, H.J.; Karl, T.R.; Palecki, M.A.; Baker, C.B.; Bell, J.E.; Leeper, R.D.; Easterling, D.R.; Lawrimore, J.H.; Meyers, T.P.; Helfert, M.R.; et al. U.S. Climate Reference Network after One Decade of Operations: Status and Assessment. Bull. Am. Meteorol. Soc. 2013, 94, 485–498. Available online: https://journals-ametsoc-org.sid2nomade-1.grenet.fr/view/journals/bams/94/4/bams-d-12-00170.1.xml (accessed on 11 April 2023). [CrossRef]





| E2 (kWh2) | Edev (kWh) | |
|---|---|---|
| Reference MPC and online tuning | 30.50 | 1.63 |
| Linear DT based on historical MPC data | 30.18 | 2.34 |
| Linear DT based on model MPC data | 36.65 | 2.94 |
| Linear DT based on model MPC and online tuning | 33.82 | 2.19 |
| Historical Training | Model Training | MPC | ||||
|---|---|---|---|---|---|---|
| Regular DTs | Regular DTs | Linear DTs | Linear DTs | Linear DTs + Tuning | ||
| Performances Metric E2 | + | + | + + | − | + | + + |
| Performances Metric Edev | + | + | + + | − | + | + + |
| Implementation | − | − | − | + + | + | + |
| Running Time | + + | ++ | + + | + + | + + | − |
| Explainability | − | − | + + | + + | + + | + + |
| Training Time | + + | ++ | + + | + + | + + | N.A. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigo-Mariani, R.; Yakub, A. Decision Tree Variations and Online Tuning for Real-Time Control of a Building in a Two-Stage Management Strategy. Energies 2024, 17, 2730. https://doi.org/10.3390/en17112730
Rigo-Mariani R, Yakub A. Decision Tree Variations and Online Tuning for Real-Time Control of a Building in a Two-Stage Management Strategy. Energies. 2024; 17(11):2730. https://doi.org/10.3390/en17112730
Chicago/Turabian StyleRigo-Mariani, Rémy, and Alim Yakub. 2024. "Decision Tree Variations and Online Tuning for Real-Time Control of a Building in a Two-Stage Management Strategy" Energies 17, no. 11: 2730. https://doi.org/10.3390/en17112730
APA StyleRigo-Mariani, R., & Yakub, A. (2024). Decision Tree Variations and Online Tuning for Real-Time Control of a Building in a Two-Stage Management Strategy. Energies, 17(11), 2730. https://doi.org/10.3390/en17112730








