A Strategy for Enhanced Carbon Storage: A Hybrid CO₂ and Aqueous Formate Solution Injection to Control Buoyancy and Reduce Risk

Abstract

Conventional Carbon Capture and Storage (CCS) operations use the direct injection of CO₂ in a gaseous phase from the surface as a carbon carrier. Due to CO₂ properties under reservoir conditions with lower density and viscosity than in situ brine, CO₂ flux is mainly gravity-dominated. CO₂ moves toward the top and accumulates below the top seal, thus reinforcing the risk of possible leakage to the surface through unexpected hydraulic paths (e.g., reactivated faults, fractures, and abandoned wells) or in sites without an effective sealing caprock. Considering the risks, the potential benefits of the interplay between CO₂ and an aqueous solution of formate ions (HCOO¯) were evaluated when combined to control CO₂ gravity segregation in porous media. Three combined strategies were evaluated and compared with those where either pure CO₂ or a formate solution was injected. The first strategy consisted of a pre-flush of formate solution followed by continuous CO₂ injection, and it was not effective in controlling the vertical propagation of the CO₂ plume. However, the injection of a formate solution slug in a continuous or alternated way, simultaneously with the CO₂ continuous injection, was effective in slowing down the vertical migration of the CO₂ plume and keeping it permanently stationary deeper than the surface depth.

1. Introduction

The scenarios analyzed by international entities, such as the International Energy Agency (IEA), underscore the intricate nature of the actions required to achieve the established goals for reducing Greenhouse Gas emissions in the forthcoming decades while simultaneously transforming energy generation sources. The “World Energy Outlook 2022” report [1] emphasizes that a synergistic deployment of multiple technologies and energy sources will play a pivotal role in providing sustainable energy resources for the planet. Among the various options for curtailing CO₂ emissions, Carbon Capture and Storage (CCS) arises as a technology with substantial potential to mitigate CO₂ emissions in a probable scenario characterized by ongoing fossil fuel utilization in the future.

A CCS project encompasses the capture of CO₂ from industries with high emission rates and its subsequent injection into geological formations, such as aquifers and depleted hydrocarbon reservoirs. One of the primary challenges associated with long-term and large-scale CO₂ storage in geological formations pertains to ensuring the safety and reliability of storage. To address this challenge, diverse trapping mechanisms within porous media can be studied [2,3,4,5]. For instance, during the initial phase of a CO₂ injection, the migration of free CO₂ is controlled by structural and stratigraphic trapping facilitated by the caprock, which is known as the primary trapping mechanism. Over the medium and long term, a portion of the mobile CO₂ will undergo dissolution in water through a process known as solubility trapping. This phenomenon is particularly pronounced in low-salinity brine under conditions of high pressure and low temperature [6,7]. The dissolution of CO₂ into brine is facilitated by molecular diffusion and brine solubility. As CO₂ dissolves into saline water, the resulting CO_2(aq)-dissolved brine becomes denser. This density contrast between the CO_2(aq)-dissolved brine and the pure brine causes the denser CO_2(aq) to sink while the pure brine rises [8,9]. The resulting density-driven convection accelerates the rate of CO₂ mass transfer, promotes further dissolution, and enhances the stability and safety of geological storage [10,11,12].

In addition to solubility trapping, changes in saturation induced by the upward movement of the CO₂ plume can result in additional trapping as a residual phase, attributable to relative permeability and capillary hysteresis [13]. Additionally, in specific cases, certain CO₂ molecules can be trapped in the form of minerals, influenced by the pH of the brine and the mineralogy of the rock [14]. These secondary trapping mechanisms bolster storage security by immobilizing buoyant CO₂ within the pore space or converting it into a non-free phase.

According to Bachu [13], the contribution of secondary trapping mechanisms is almost negligible during the injection phase. Consequently, during this stage, the caprock assumes a critical role in ensuring the security of the CCS operation, as the buoyancy of CO₂ has the potential to induce its migration toward the surface or seafloor in the case of offshore storage sites. In the Frio CO₂ field demonstration project conducted in the U.S. [15], CO₂ was injected in a deeper zone below several well-known shale seals. However, certain authors [16] are currently reevaluating the necessity of a caprock to control the upward movement of the CO₂ plume, given the absence of prescriptive regulations pertaining to geologic seals. Furthermore, there is ongoing consideration of a composite confining system comprising discontinuous barriers that create prolonged and convoluted pathways to attenuate the saturation of mobile CO₂.

Where the caprock cannot be effective, additional control over the CO₂ buoyancy is desired to support the discontinuous geologic barriers. Some authors have worked with aqueous solutions based on formic acid [17] to enhance the CO₂ solubility in brine or on formate ions [18,19] to enhance the pore-space utilization in carbon storage while avoiding various issues with CO₂ storage. Additional benefits of the formate solution have been found for carbonate rocks concerning the wettability alteration to enhance oil recovery [18,20,21,22].

A formate ion (HCOO¯) is the simplest carboxylate and the conjugate base of formic acid (HCOOH). Both compounds can be used as precursors for additional chemicals in energy-related applications, such as hydrogen storage and carbon carrier materials. The estimated global market for formic acid is 1,300,000 tons by 2035 [23] as a result of its growing utilization in these areas.

Currently, formate ion production is based on thermochemical processes in which syngas and steam generation are needed, resulting in energy-intensive reactions with carbon dioxide emissions [24]. Alternatively, the electrochemical reduction in CO₂ (ECR-CO₂) is a technology with the potential to produce formate species (including formic acid) under ambient conditions utilizing renewable energy and contributing to atmospheric carbon removal [24,25].

Different reported techno-economic analyses (TEA) have stated the feasibility of formic acid production by electrochemical reduction in CO₂, providing a reaction energy consumption between 4.5 and 4.7 kWh/kg HCOOH [26,27] for the best scenario using 0.95 kg CO₂/kg HCOOH and 0.60 kg H₂O/kg HCOOH consumption rates [26]. Under these conditions, the overall production cost is estimated to be US $0.46–0.75/kg HCOOH [26,27], which is quite competitive since the current market price is US $0.68–1/kg HCOOH [25,26].

Although no commercial CO₂ electrolyzer is available, great progress has been made to successfully develop industrial-scale technologies, achieving a current TRL of 6. Experimental work has demonstrated a reaction energy consumption of around 5.5 kWh/kg HCOOH [28] and stable long-term performance for 1000 h, which is a promising scenario for large-scale formic acid production by electrochemical reduction in CO₂.

In this study, the aqueous solution of formate ions, referred to as a formate solution, combined with CO₂ (injected as a gas from the surface) was evaluated to support the gravity control of the plume in porous media, unlike Oyenowo et al.’s work [29], who evaluated only a formate injection as a carbon carrier. The following three combined strategies were tested: (1) a pre-flush of the formate solution slug preceding the continuous CO₂ injection; (2) injecting the formate solution slug in a continuous or alternated way with CO₂; and (3) injecting formate solution simultaneously with CO₂ using a dual completion well similar to that in simultaneous water alternating gas injection projects [30]. All our simulations considered the mentioned secondary trapping mechanisms in two geological models, a synthetic one and an actual aquifer in Brazil, with little evidence of effective caprock. The main assumptions in this paper include the following:

• No geomechanical or caprock modeling;
• A pure CO₂ stream is injected at a typical commercial rate;
• No consideration of surface facility modeling. Focus on the subsurface flow and the impact of formate on CO₂ fate and transport in a saline aquifer.

2. Modeling Geochemical Reactions

In the simulation of CO₂ injection for CCS, both in the synthetic model and in the real cases to be discussed in the subsequent section, the numerical simulation was performed using CMG-GEM [31]. This simulator was used considering the following features:

• The diffusion coefficient (D) for super-critical CO₂ in brine equals 3.65 × 10⁻⁵ cm²/s, according to Ahmadi et al. [32]. This coefficient is applied to compute the effective CO₂ diffusion (D_eff) considering a porous medium with a tortuosity τ.

$$D_{eff}=\frac{D}{\tau }$$

(1)

• The solubility of CO₂ in brine can be estimated using the method proposed by Li and Nghiem [33], which is based on Henry’s law. This model calculates Henry’s constant based on Equation (2), which is a function of pressure and temperature. However, the influence of salt on the solubility of CO₂ in the aqueous phase is taken into account through the use of a salting-out coefficient [34].
  $$ln\left(H_i\right)=ln\left(H_i^{*}\right)+\frac{\overline{v_i}}{RT}\left(p-p^{*}\right)$$

  (2)

  where
  $H_i$: Henry’s constant at current pressure (p) and temperature (T);
  $H_i^{*}$: Henry’s constant at reference pressure (p^*) and temperature (T);
  $\overline{v_i}$: partial molar volume at infinite dilution;
  R: universal gas constant;
  i: species dissolved in water (CO₂ in this work).

• Water acid reactions for bicarbonate and carbonate ion generation using kinetic parameters from the PHREEQC database [35,36]:

OH⁻ + H⁺ = H₂O

(3)

CO₂ + H₂O = H⁺ + HCO₃⁻

(4)

CO₃²⁻ + H⁺ = HCO₃⁻

(5)

• Reactions between a formate ion and other species in brine using kinetic parameters from the MINTEQ database [37]:

H⁺ + HCOO⁻ = HCO₂H

(6)

Ca²⁺ + HCOO⁻ = Ca(HCO₂)₂

(7)

Mg²⁺ + HCOO⁻ = Mg(HCO₂)₂

(8)

• Reactions with primary minerals using kinetic parameters from PHREEQC for the Transition-State-Theory (TST)-derived rate laws:

  -

  In the synthetic aquifer model:

  Calcite [CaCO₃] + H⁺ = Ca²⁺ + HCO₃⁻

  (9)

  -

  In the real aquifer model:

Quartz [SiO₂] = SiO_{2 (aq)}

(10)

K-feldspar [KAlSi₃O₈] + 4 H⁺ = 3 SiO_{2 (aq)} + Al³⁺ + K⁺ + 2 H₂O

(11)

Albite [NaAlSi₃O₈] + 4 H⁺ = 3 SiO_{2 (aq)} + Al³⁺ + Na⁺ + 2 H₂O

(12)

• Permeability alteration due to mineral precipitation or dissolution was computed by applying the Kozeny–Carman equation with an exponent value of 3, as Zeidouni et al. [38] recommended as follows:
  $$k_k=k_n/rf,$$

  (13)

  and
  $$rf={rf}_n{\left(\frac{{\phi }_n}{{\phi }_k}\right)}^3{\left(\frac{{1-\phi }_k}{{1-\phi }_n}\right),}^2$$

  (14)

  where the resistance factor rf is modeled by the Kozeny–Carman equation or the power law relationship; k_n and k_k refer to permeability at previous (n) and current (k) timesteps, respectively. The porosity, φ, in (14) is calculated as follows:
  $$\phi =\left[1+c_f\left(p-p^{*}\right)\right]\left[{\phi }^{*}-{\sum }_{j=1}^n\left(\frac{N_j}{{\rho }_{m,j}}-\frac{N_j^0}{{\rho }_{m,j}}\right)\right],$$

  (15)

  where:
  φ* is the reference porosity without mineral precipitation/dissolution;
  N_j is the total moles of mineral j per bulk volume at the current time;
  $N_j^0$ is the total moles of mineral j per bulk volume at the initial time;
  ρ_m,j is the mineral molar density;
  c_f is the rock compressibility;
  p* is the reference pressure.

• The aqueous formate solution used in this study considered the formulation of Wang et al. [21], with a formate concentration of 30 wt% in brine, with a total salinity of 468,333 ppm (Na⁺: 159,236 ppm; Cl⁻: 9097 ppm; HCOO⁻: 300,000 ppm) and pH adjusted to 7. The resulting density of this formate solution is around 2300 kg/m³ with a viscosity of about 3 cP at the real average reservoir pressure and temperature conditions, as will be detailed in the following sections.

3. Case Study 1: Synthetic Model

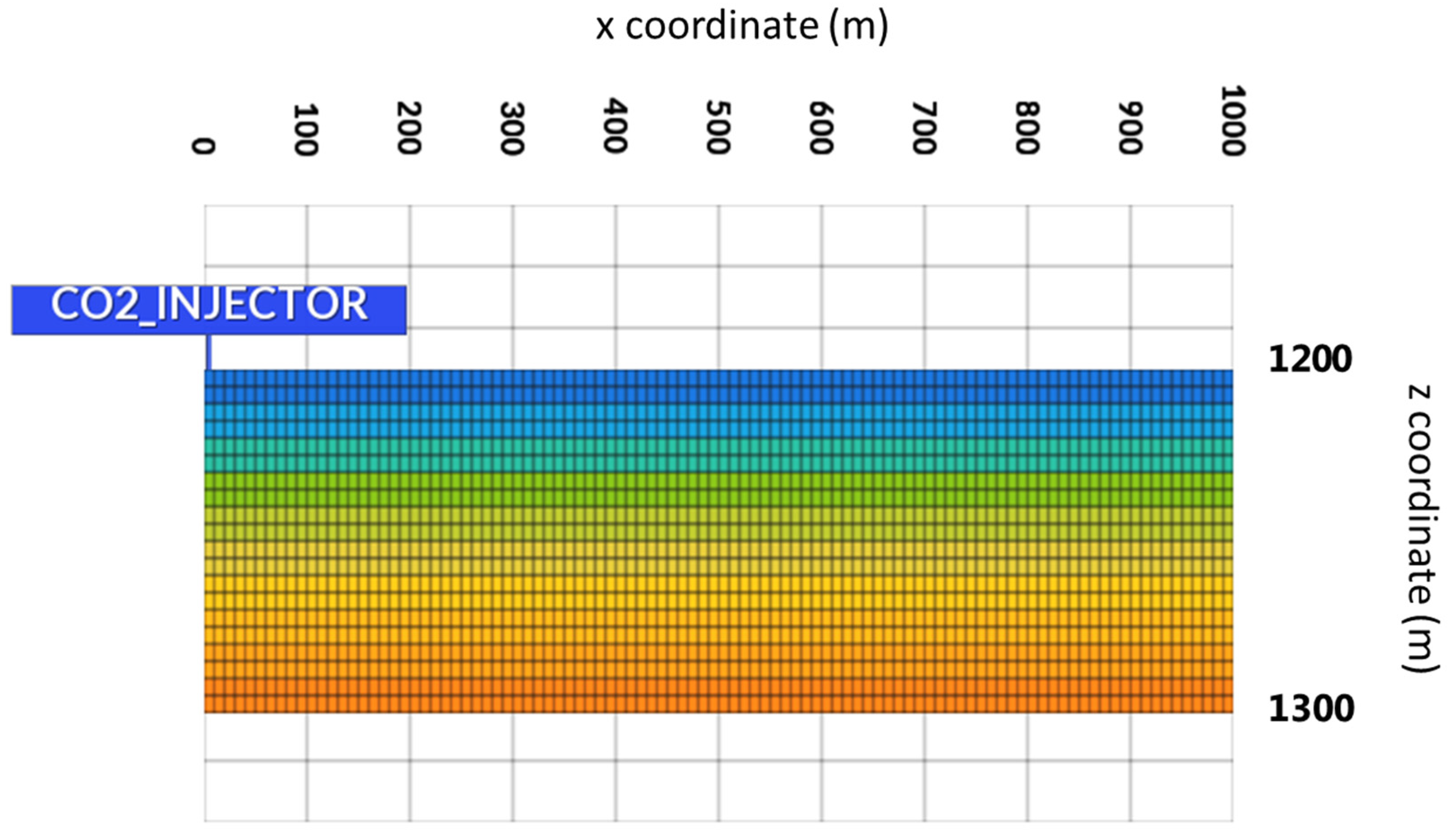
3.1. Geological Model

To gain a deeper understanding of the impact of a formate solution in conjunction with a CO₂ injection, a 2D synthetic model of a saline aquifer was built. The model was designed to have homogeneous petrophysical properties. A vertical injection well was placed at the edge of the model, with perforations in the three bottom layers. Figure 1 illustrates the dimensions of the model, which was discretized into a grid consisting of 100 × 100 × 20 gridblocks, each with a volume of 10 × 10 × 5 m³. This model discretization was validated and has been utilized for various applications related to reactive flow transport, as documented in the available literature [39,40,41].

Other properties of the synthetic model are summarized in

Table 1. Summary of the main petrophysical and fluid properties—synthetic model.

Total model pore volume	180,000 m3
Average horizontal permeability	100 mD
Ratio of vertical/horizontal permeabilities	0.10
Average porosity	0.18
Initial pressure @ datum	8.963 MPa
Temperature Initial pH	41 °C 7.3
CO2 injection rate Aqueous formate solution injection rate	1.0 metric tons/d 0.65 m3/d
Relative permeability curves Capillary pressure curves	Figure 2 Figure 2

, obtained from Oyenowo et al. [29].

The assumed synthetic relative permeability and capillary pressure curves [39] are represented in Figure 2. The maximum trapped gas saturation (S_gt) is assumed to be 0.4 in the Carlson hysteresis model [42], corresponding to the Land’s constant (C) [43] of 2, according to Equation (16):

$$S_{gt}=\frac{S_{g max}}{1+C{S}_{g max}}$$

(16)

where S_{g max} is the maximum gas saturation.

The synthetic water composition assigned for this case is represented in

Table 2. Ionic composition of formation water.

Ions	Concentration (ppm)
H+	1.4872 × 10−5
Ca2+	11,307
Na+	17,763
Cl− HCO3−	39,604 425

[39].

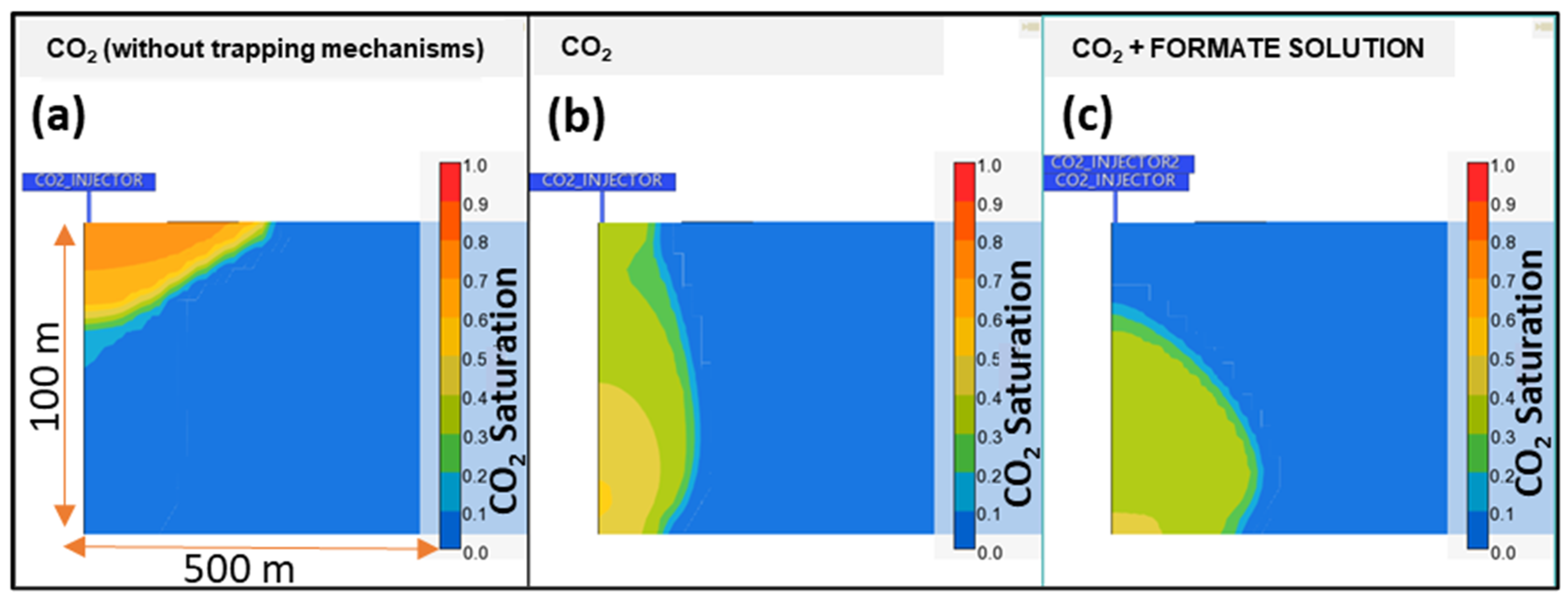
3.2. Results

Oyenowo et al. [29] performed numerical simulations injecting an aqueous formate solution into an aquifer and an oil reservoir. They showed no upward buoyancy-driven flux when they used the formate solution as a single carbon carrier. This result inspired us to evaluate the combination of formate and CO₂ injections to enhance the amount of carbon stored and to control the stability of the displacement process and buoyant forces due to the higher density and viscosity of the formate solution. Firstly, this approach was tested in the synthetic model and also coupled with the abovementioned geochemical reactions to capture trapping mechanisms such as solubility, including ionic trapping (bicarbonate and carbonate ion generation), residual, and mineral trapping.

Figure 3a shows the CO₂ injection without consideration of all the aforementioned trapping mechanisms, highlighting the CO₂ rising as a mobile super-critical CO₂ phase trapped by the caprock. In Figure 3b, the trapping mechanisms were included, and the CO₂ plume was simulated to spread along the aquifer thickness, less dependent on the structural trapping. However, when formate solution was injected (30 wt%) simultaneously with the CO₂ in an equal volume in the aquifer conditions, the CO₂ plume did not reach the caprock, reducing the importance of structural trapping in the storage projects (Figure 3c). This observation reinforced our motivation to test the co-injection of CO₂ and formate to minimize the risk associated with the caprock’s effectiveness as a barrier to the CO₂ plume.

A secondary effect observed by this simulation is the buffer solution with a basic pH mainly around the well when the formate solution is injected in a calcite-rich matrix, as shown in Figure 4A. Regarding this effect, Wang et al. [21] showed that either brine with calcite or a 20 wt% formate solution with calcite reached the same equilibrium pH between 8.5 and 9 from their static bottle tests and corefloods with Texas Cream limestone cores. Without calcite, the formate solution in brine showed no reactivity and no change from the initial pH, which was 7.0. Figure 4A (left) shows a zone with a pH greater than 9, but such large pH values were not observed experimentally in [18,21].

Generally, calcite precipitation tends to be induced in a basic pH environment if carbonate ions are in contact with calcium ions in the resident brine or generated from the dissolution of carbonate minerals. To emulate this, a carbonate matrix with 63% of the volume of calcite [44] was assumed to see the impact of the pH changes on the reaction (Equation (9)). Other minerals present in the rock matrix are mainly quartz, kaolinite, and oligoclase. Our simulation study could reproduce the following mechanism:

Increased pH when a formate solution is injected into a carbonate rock (orange curve in Figure 5), as experimentally observed by [18,21]. This is the sodium formate solution injection with no CO₂ injection. The small precipitation of calcite comes from formate-induced calcite dissolution and then re-precipitation because bicarbonate ions from the resident brine (Table 2) cause calcite to precipitate in Figure 4A (right) upon the pH increase in Figure 4A (left). Note that the large pH values in Figure 4A are numerically simulated under the simulation conditions; therefore, the simulation results in Figure 4 must be interpreted qualitatively;

Nearly constant pH when a formate solution is injected into a rock without calcite (green curve in Figure 5), as reported by Wang [21];

Acidification occurs when CO₂ is injected into a carbonate matrix (red curve in Figure 5), as expected by the generation of carbonic acid;

Less intense acidification occurs when a formate solution is injected simultaneously with the CO₂ (blue curve in Figure 5). In this case, part of the CO₂ injected is converted to bicarbonate induced by the buffer solution with an alkaline pH created by the formate injection, concentrated on the bottom of Figure 4B (left). Meanwhile, some of the CO₂ rises (Figure 3c) and creates a lower pH zone (blue zone in Figure 4B on the left), inducing more significant calcite dissolution (red area in Figure 4B on the right) than when only formate is injected. In the same Figure, calcite re-precipitation is observed on the bottom induced by the buffer solution.

In summary, if only CO₂ is injected, an acidic pH is expected to promote the calcite to dissolve (red curves in Figure 6) and increase the initial calcium concentration in brine. As shown in Figure 6 (orange curve on the top), the pH tends to increase if an aqueous solution of sodium formate is injected without adjusting the pH, for example, by formic acid [19,29]. If properly designed for a given formation and its operating conditions, an injection of aqueous formate solution can be used to control the CO₂ mineralization trapping mechanism (the orange curve on the bottom) besides controlling the CO₂ plume rise.

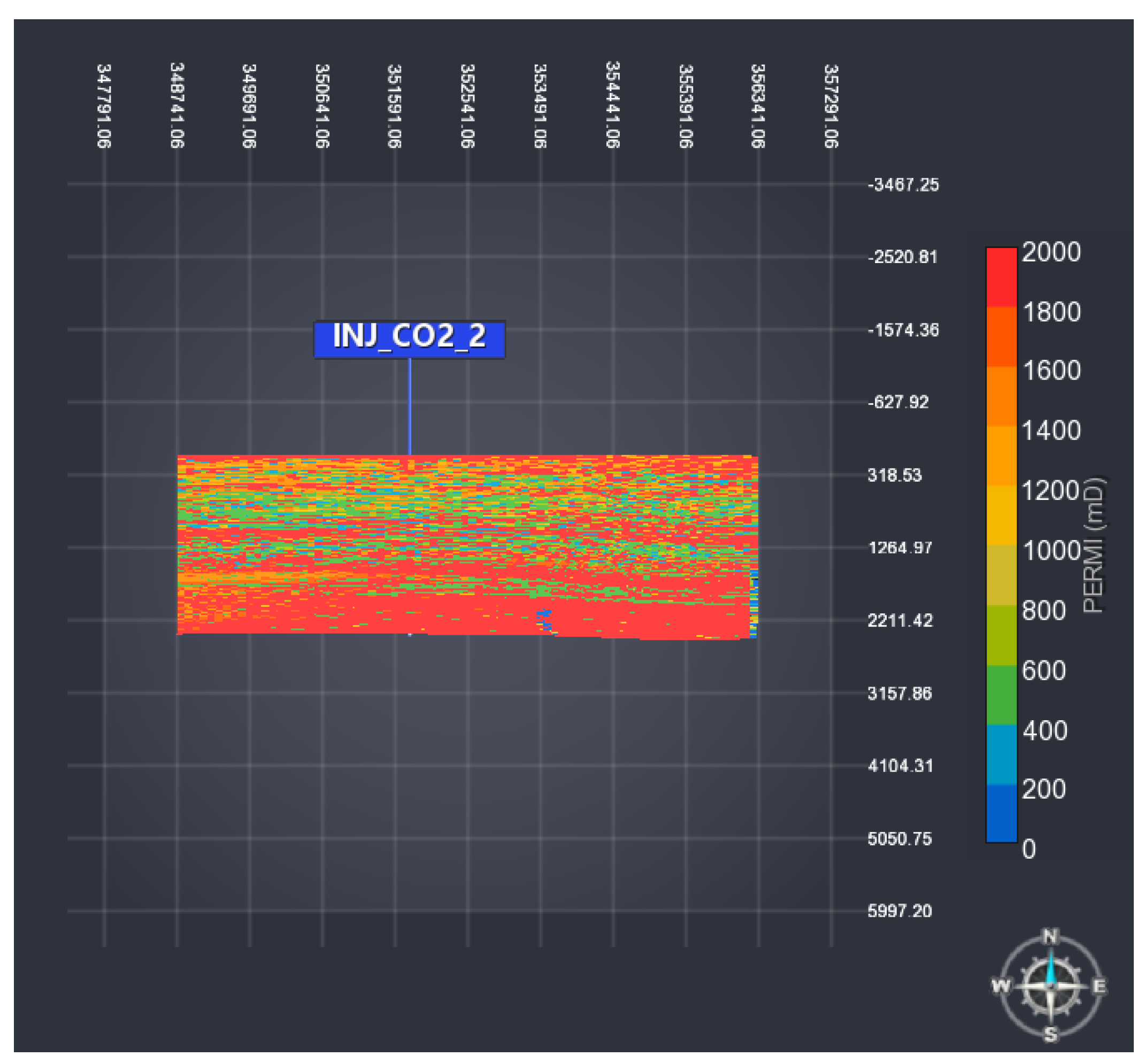
4. Case Study 2: Real Aquifer

4.1. Geological Model

The final evaluation was conducted in a model of an actual sandstone aquifer built with seismic and well data from three wells drilled in that area. The aquifer covers an onshore and offshore area in the Campos basin, Rio de Janeiro state, Brazil (red square in Figure 7). The sand grains are composed of quartz and feldspars, with a significant presence of granitic lithoclasts (a mechanically formed and deposited fragment of rock derived from an older one). The total porosity is 25%, and its origin is mainly secondary, generated by matrix contraction, grain dissolution, or grain fracturing, resulting in an average permeability of 1.5 D. Its rock mineralogy [45], in volumetric fraction, is composed of the following main minerals: quartz (29.5%), K-feldspar (8%), and plagioclase (5%), assumed here as albite.

The full reservoir model encompasses a pore volume of over 150 billion m³, but a sector model with a pore volume of about 30 billion m³ was considered in this work (Figure 8). The gridblock size is 100 × 100 m² horizontally and 5 m thick. A grid refinement was performed around the injector to reduce the gridblock size from 100 m to 25 m using the workflow proposed by Machado et al. [39].

The CO₂ injection was evaluated over twenty years (2025–2045) with a constant rate of 1.5 million metric tons/yr through a centrally located vertical injector in the bottom layers. In this selected area, there is no evidence of an existing caprock, only a set of discontinuous shale lenses fitting the composite confining system classification, according to the concept introduced by Bump et al. [16]. Therefore, they can work as barriers to the CO₂ plume. However, due to the geologic uncertainty of the occurrence and distribution of the dispersed barriers, it would be desirable to count on an additional control to prevent CO₂ buoyancy on the surface or seafloor. In this context, the formate solution is anticipated to have a significant impact, which justifies the selection of this particular geological model for conducting the investigation. This model was chosen due to its suitability for examining and understanding the specific effects and implications associated with using a formate solution within the given scenario.

Other properties of the real case model are summarized in

Table 3. Ionic composition of formation water [46].

Ions	Concentration (ppm)
H+	1.4767 × 10−4
Ca2+	998
Mg2+	627
Na+	27,094
Cl− HCO3−	42,685 1337

.

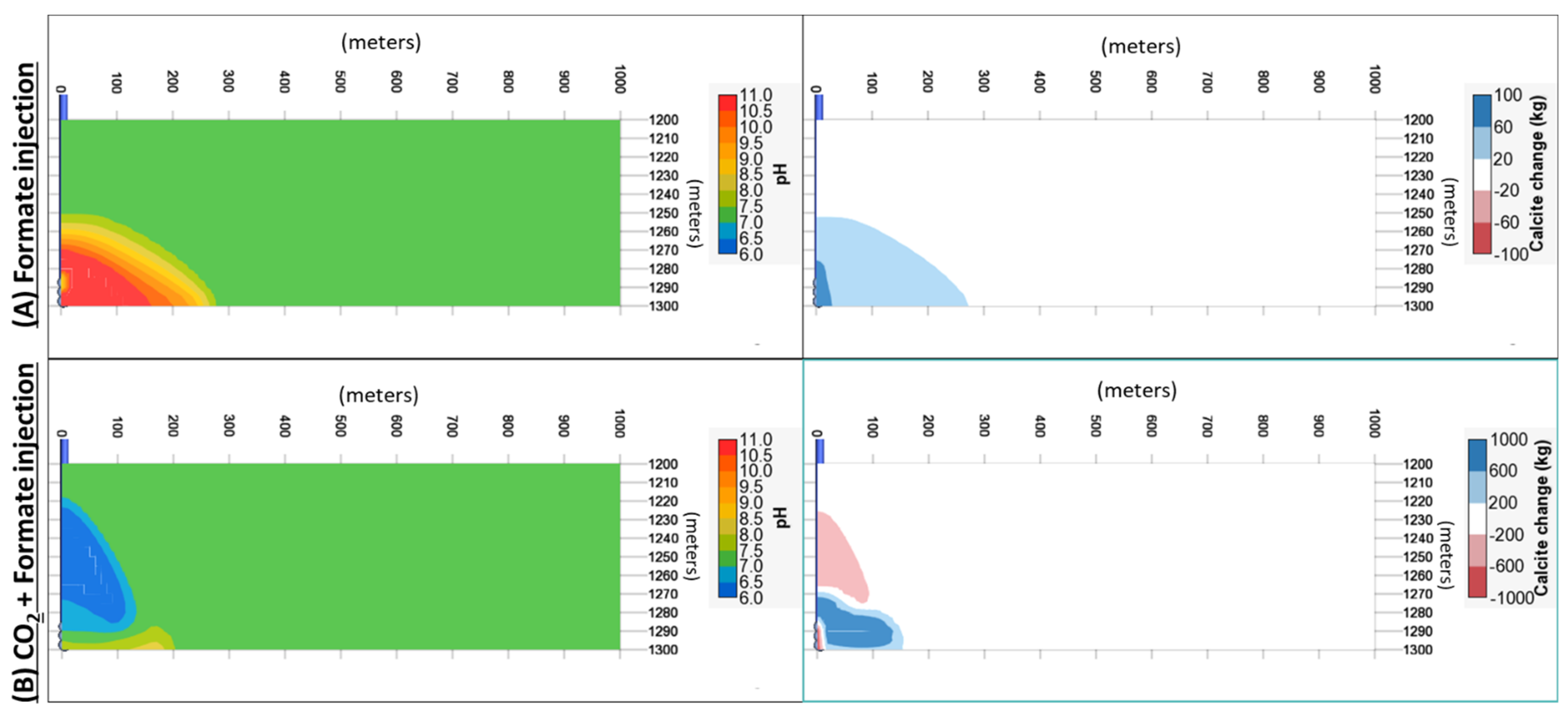
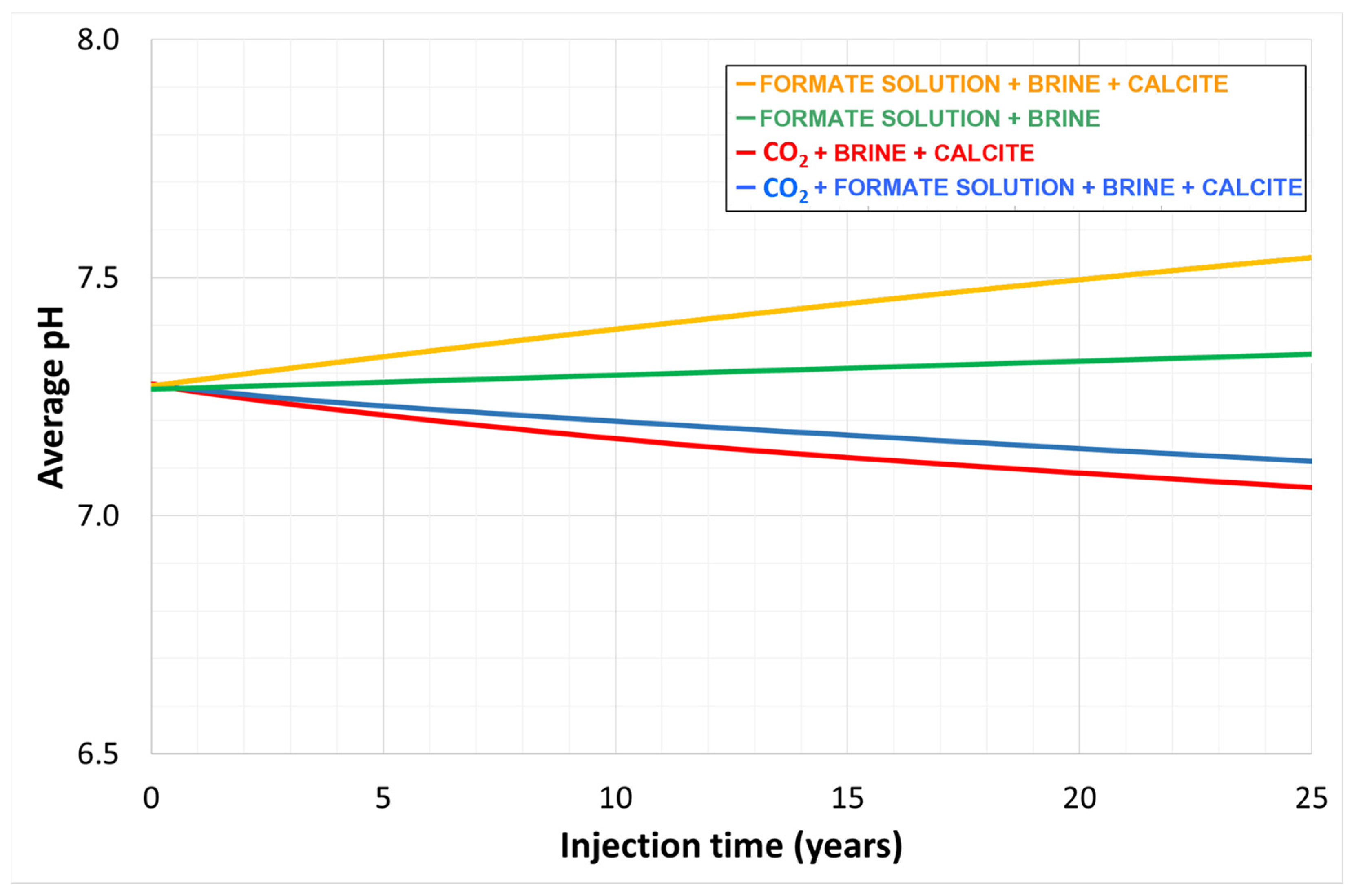
4.2. Results

Based on the potential benefits of the co-injection of a formate solution with CO₂ using the synthetic model, application in an actual aquifer model is discussed in this section. Due to the larger amounts of CO₂ to be injected, we need to optimize how and the quantity of the formate solution will be injected. Therefore, the following steps were proposed:

• Start injecting the same volume of CO₂ and formate solution. In this case, 1.5 million metric tons/yr of CO₂ was assumed based on the field project design;
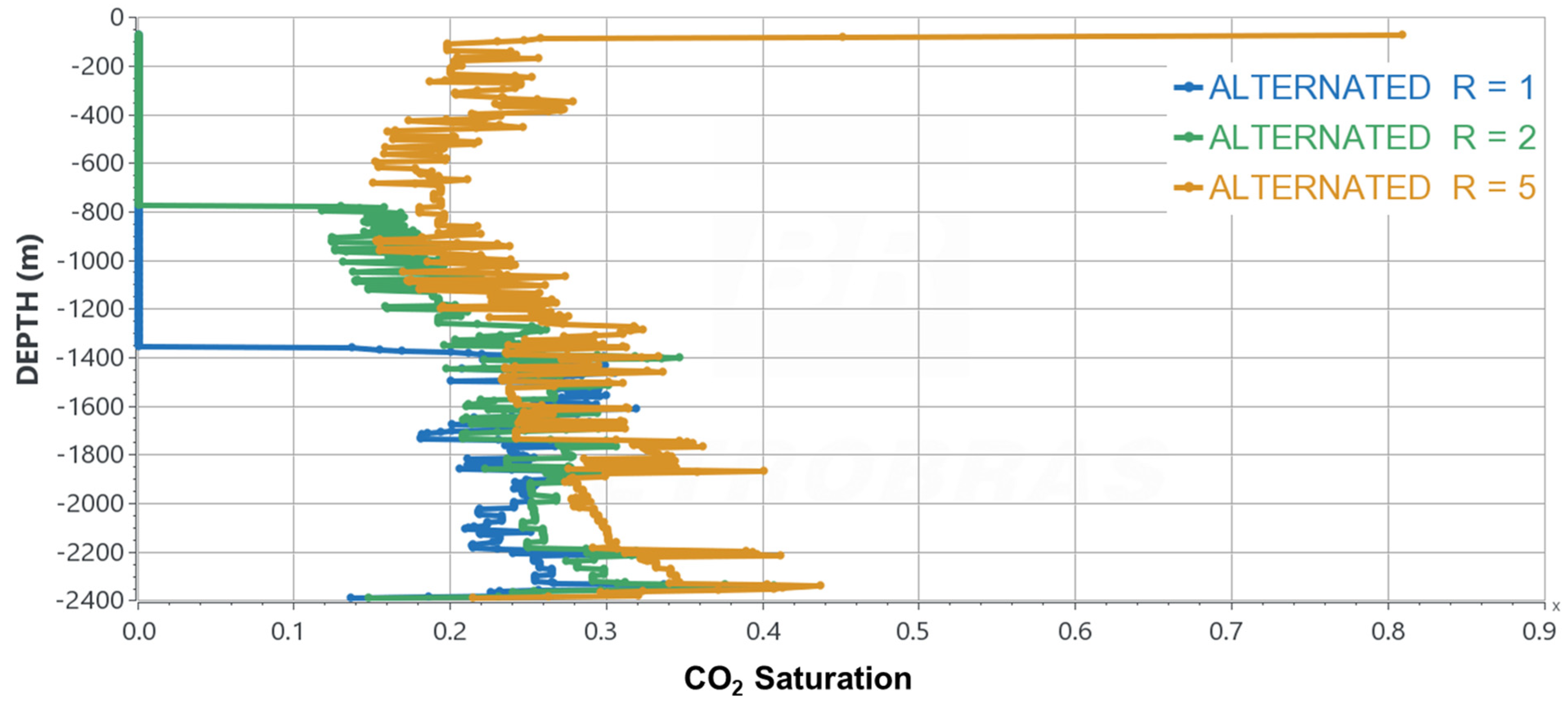
• Evaluate different CO₂/formate volumetric ratios (R);
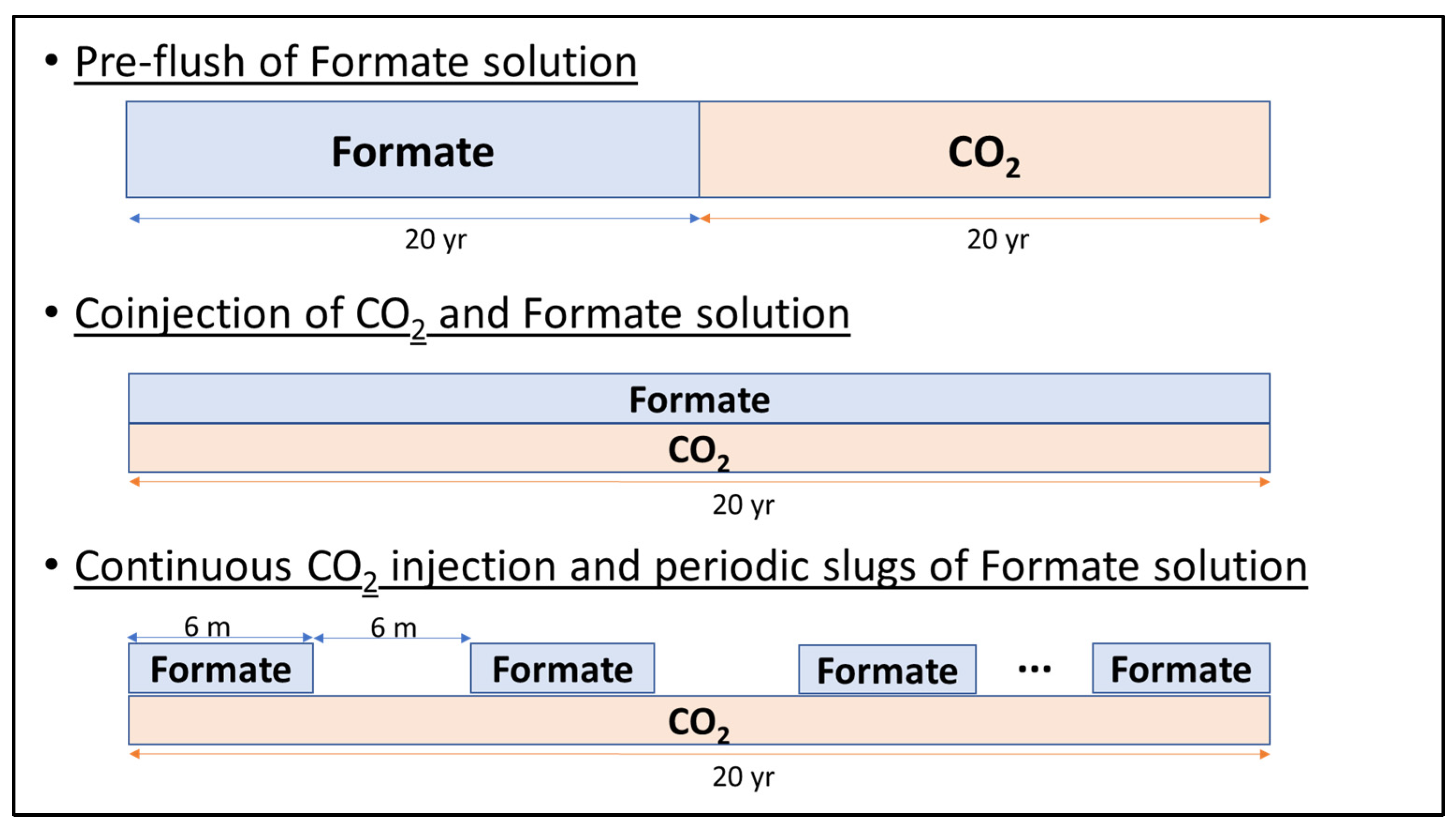
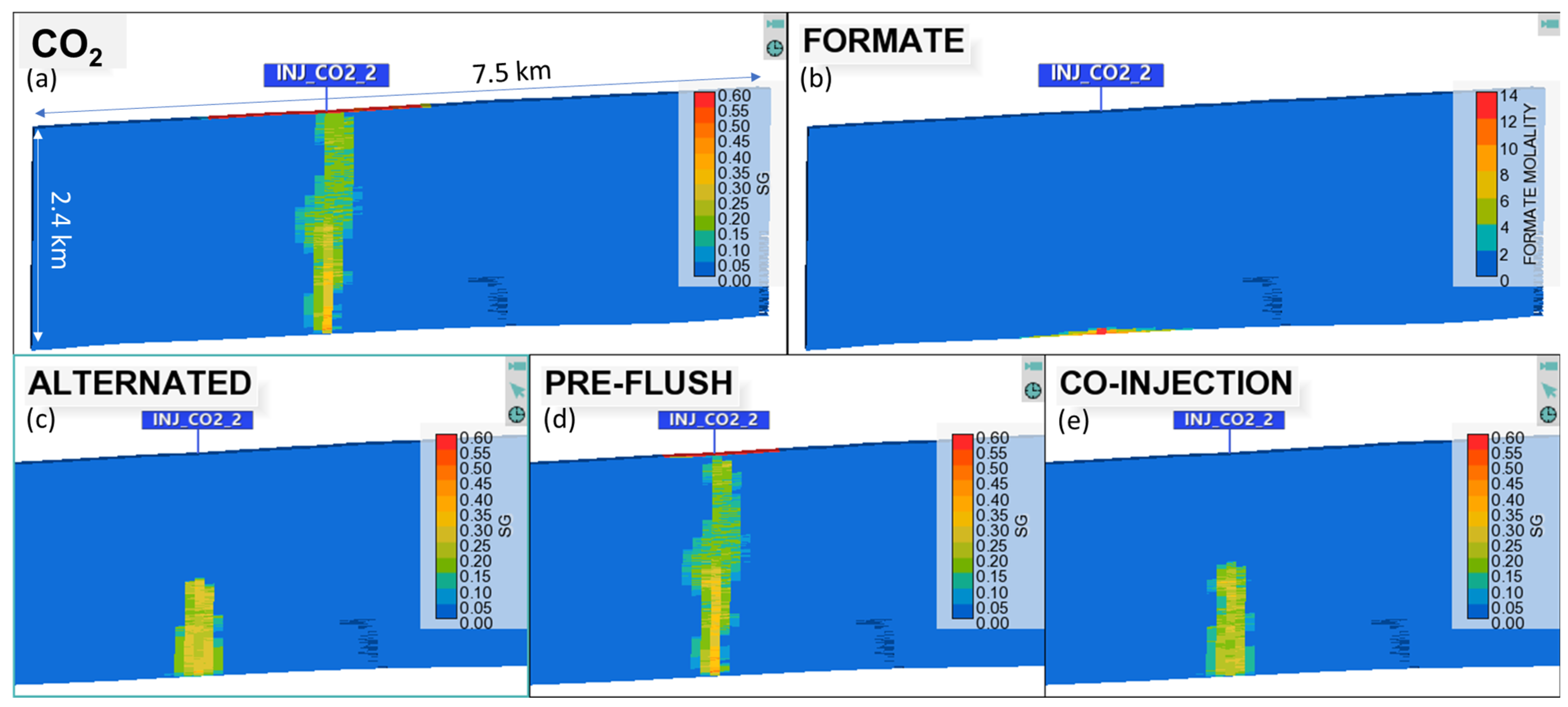
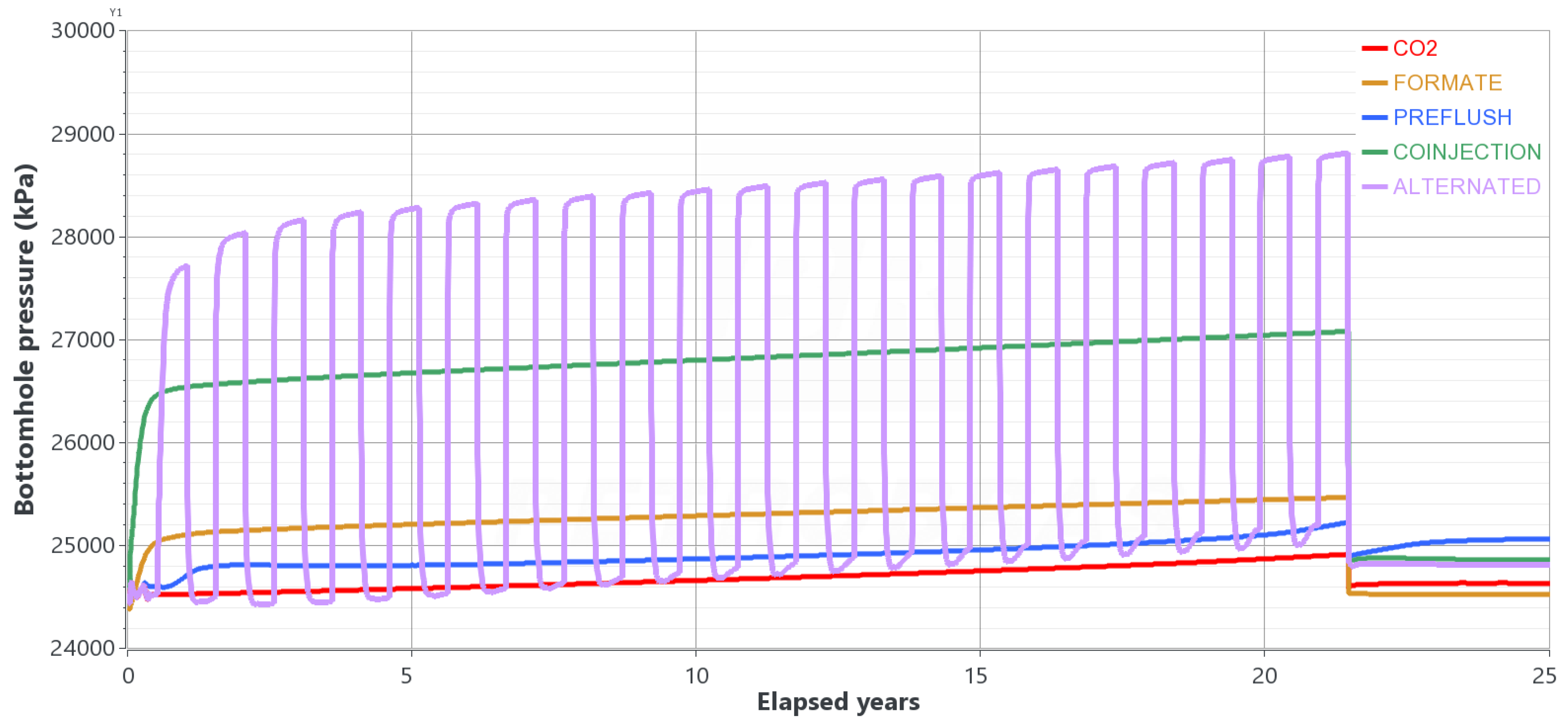
• With the best R-value, test different hybrid strategies: (i) pre-flush of formate preceding the CO₂ injection, called “pre-flush”; (ii) simultaneous and continuous injections of both fluids, called “co-injection”; (iii) continuous CO₂ injection and alternating and simultaneous formate injection with 6-month slugs, called “alternated.” Figure 9 illustrates the different injection strategies.

To make a fair comparison, the volume of the formate solution used in the simulations is the same in all cases over 20 years of injections (2025–2045), and it corresponds to approximately 3.6 million tons (i.e., 1.08 million tons of formate ions, not formate salts), which is a considerable amount and could raise some concerns about the economic viability of this process. However, as mentioned in the Introduction section, formate species can also be generated by the electrochemical reduction in CO₂ [47], contributing to carbon emission reduction goals. Therefore, the combination of CO₂ and formate solution injections brings synergistic benefits: it makes the storage safer by providing buoyancy control and, at the same time, enhances the amount of carbon stored since the gravity-controlling agent (formate solution) can be generated from CO₂ electrochemical reduction on the surface.

In this work, R values of more than 1 were considered due to economic viability concerns. This is because producing a larger volume of formate solution would be required compared to the CO₂ volume. Additionally, the formate solution exhibits higher viscosity than CO₂, with an average viscosity of 3 cP compared to 0.05 cP for CO₂ at downhole conditions. Consequently, the injection rate of formate would need to be limited after the second year of injections when testing an R = 0.5, as illustrated in Figure 10. This limitation is necessary to ensure that the pressure during operation remains below the fracture gradient, which establishes a maximum bottomhole pressure of 30,000 kPa for this specific aquifer. Hence, operating with an R-value less than 1 could pose operational challenges, particularly for cases with low- and mid-permeability, where issues related to injectivity are more likely to arise.

After following the optimization steps (a) and (b), the best R-value (CO₂/formate ratio) to control the plume rise was when the volumetric amounts of CO₂ and the formate solution were the same, e.g., R = 1.0. Figure 11 compares three R values considering the alternated CO₂/formate injection strategy. The results indicate that the case with R = 1 poses a lower risk compared to the other case. When R = 5, representing a CO₂ injected volume five times that of the formate volume, the CO₂ plume reaches the surface after 20 years of injections (2045).

Figure 12 presents a comparison of different injection strategies with R = 1. The first row of the figure displays the cases of only a CO₂ injection or only a formate solution injection, while the second row showcases the hybrid techniques. It is important to note that the injection point for all strategies remains consistent and is placed at the bottom of the aquifer. The regime is less gravity-dominant when only a formate solution is injected, in agreement with the results obtained by Oyenowo et al. [29]. However, the primary goal of this study is to evaluate hybrid strategies. Therefore, the best hybrid plans were the co-injection and alternate ones. The pre-flush case could not prevent CO₂ upward buoyancy flux to the surface/seafloor depth.

Even in the combined strategies, where the total injection rate was higher, it was possible to inject below the maximum bottomhole pressure (BHP) of 30,000 kPa (Figure 13) for this saline aquifer to avoid fracturing the rock, highlighting that it is operationally possible to inject both CO₂ and the formate solution [46]. The curves show a consistent behavior when only CO₂ is injected (lower viscosity phase), developing lower pressures (red curve). The co-injection presented an average curve for BHP (green curve) when compared with that of the alternated case (light-purple curve), since the injected masses (CO₂ and formate) were the same.

After 100 years of redistribution (Year 2145), the CO₂ plume in the best strategies (co-injection and alternate injection) remained stationary/immobile below the surface depth, as shown in Figure 14, highlighting the effectiveness of the buoyancy control exerted by the formate solution over the CO₂ plume in those combined strategies.

Regarding the aquifer average pressure, its build-up was less intense than it was observed in the wellbore, mitigating geomechanical risks associated with the high pressure, such as fracture initialization or fault activation. Figure 15 compares the average pressures of the cases where only CO₂ is injected with the two best options when the CO₂ injection is combined with the formate solution in co-injection and alternated ways. The wavy behavior in the curve of the alternated case (light purple) is due to the injection of the formate solution in periodic slugs.

Regarding the possible CO₂ mineralization induced by the higher pH generated by the formate injection around the injector well, mineral precipitation was not observed since this case is a sandstone matrix without reactive carbonate minerals, and the formation brine presents a low concentration of Ca²⁺ ions.

4.3. Sensitivity to the Formate Volume

Figure 11 shows the relationship between the volumes of CO₂ and the formate solution injected. For more significant amounts of CO₂ compared to the formate solution, this combination was not effective in controlling the CO₂ plume rise. For this study, the optimal ratio R should be lower or equal to 1. However, as commented before, R < 1 would require a larger mass of formate per well, which can be costly. Although economic evaluation is outside the scope of this work, some simulations for CCUS projects can be found in [29]. Economic evaluation depends on each country’s carbon credit and tax relief policies, which vary over time, besides the subsurface pressure, depth, and CO₂ injection rate.

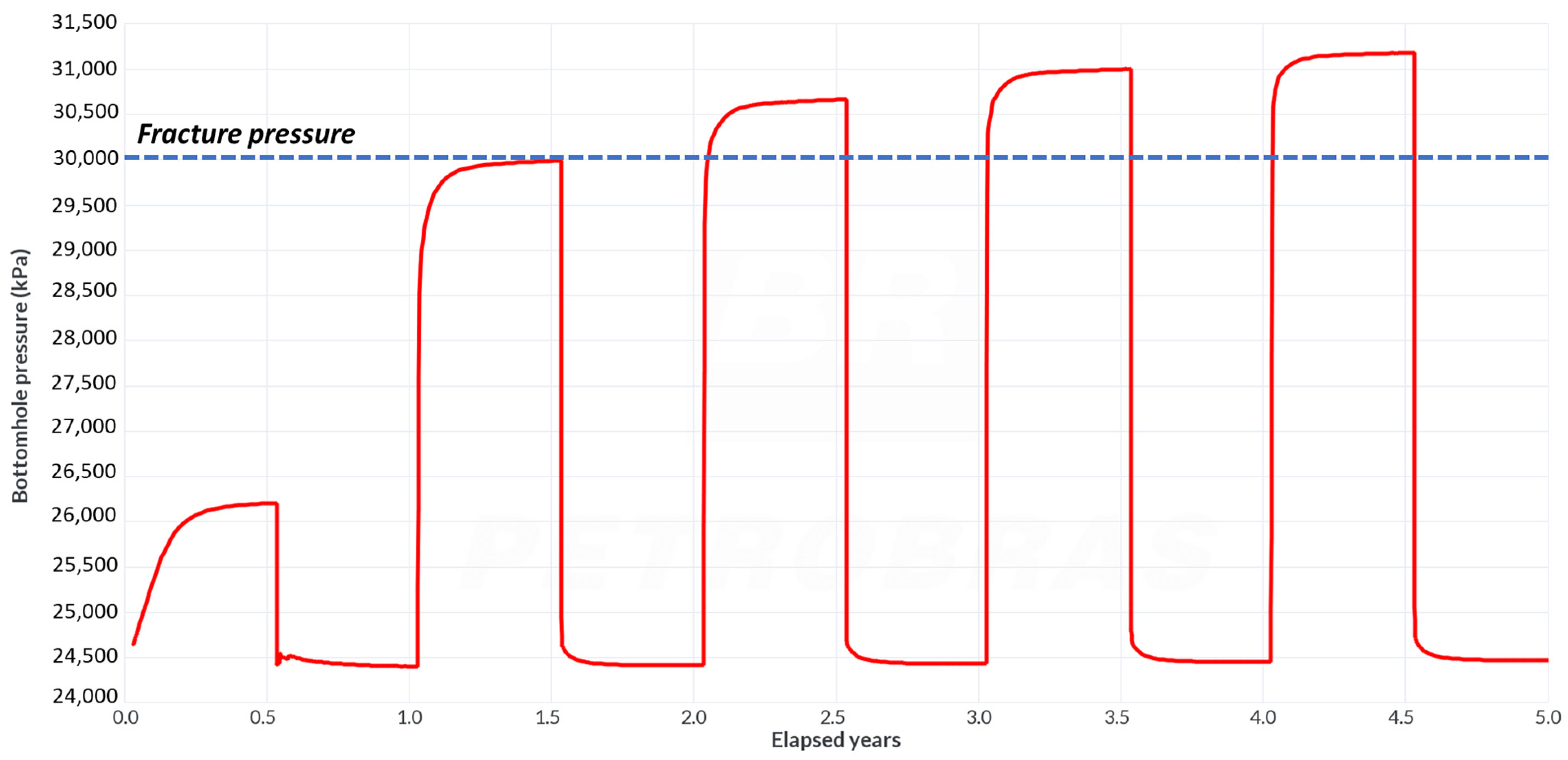
4.4. Sensitivity to Rock Permeability

Injectivity can be a concern because of the higher viscosity of the formate solution (3 cP in this study) than CO₂ (0.05 cP). However, this technique is still possible for lower injection rates in mid-permeability cases (average of 150 mD), despite the lower injectivity than CO₂. Supposing the permeability of the model is reduced by a factor of 10, the co-injection and alternated cases can still operate with typical CO₂ injection capacities, respecting the maximum BHP of 30,000 kPa, as shown in

Table 4. CO₂ injected over 20 years, considering a reduction of 10 times in the horizontal permeability of the model.

Case	Cumulative CO2 Injected
	Original Permeability (Mean: 1500 mD)	Reduced Permeability (Mean: 150 mD)
Alternated	30 million metric tons	3.10 million metric tons
Co-injection	30 million metric tons	1.85 million metric tons

. According to data from different storage sites [48,49], those rates are practical for a CCS project, ranging from 0.1 million metric tons/yr. In the co-injection strategy, the total mobility of the fluids injected (CO₂ + formate) is higher, so the injectivity is more affected than in the alternated case.

5. Conclusions

This paper discussed the risk of CO₂ leakage in CCS projects where the caprock is not an effective barrier and investigated the possibility of controlling the buoyancy-driven upward flux of CO₂ by injecting an aqueous solution of formate species. The main conclusions are summarized below:

• The co-injection of an aqueous formate solution could make the gravity-dominant regime less intense during CO₂ injection for carbon storage purposes, especially when the CO₂ and formate solution volumes are approximately the same;
• Three injection strategies were evaluated against the single fluid injection (only CO₂ or formate). The best strategies combine the simultaneous injection of the two fluids, either continuous or alternated slugs of formate solution. Both cases prevent a CO₂ plume from rising to the surface and keep the plume stationary over hundreds of years of redistribution;
• A secondary benefit of the formate solution is the pH buffering, which results in a suppressed change in pH when CO₂ is injected. This mechanism induced calcite precipitation from brines in the studied case. Thus, it could be an additional and permanent CO₂ trapping mechanism in this buffer zone in carbonate rocks.