Experimental Investigation on Heat Transfer Enhancement of Phase Change Materials by Fractal Fins
Abstract
1. Introduction
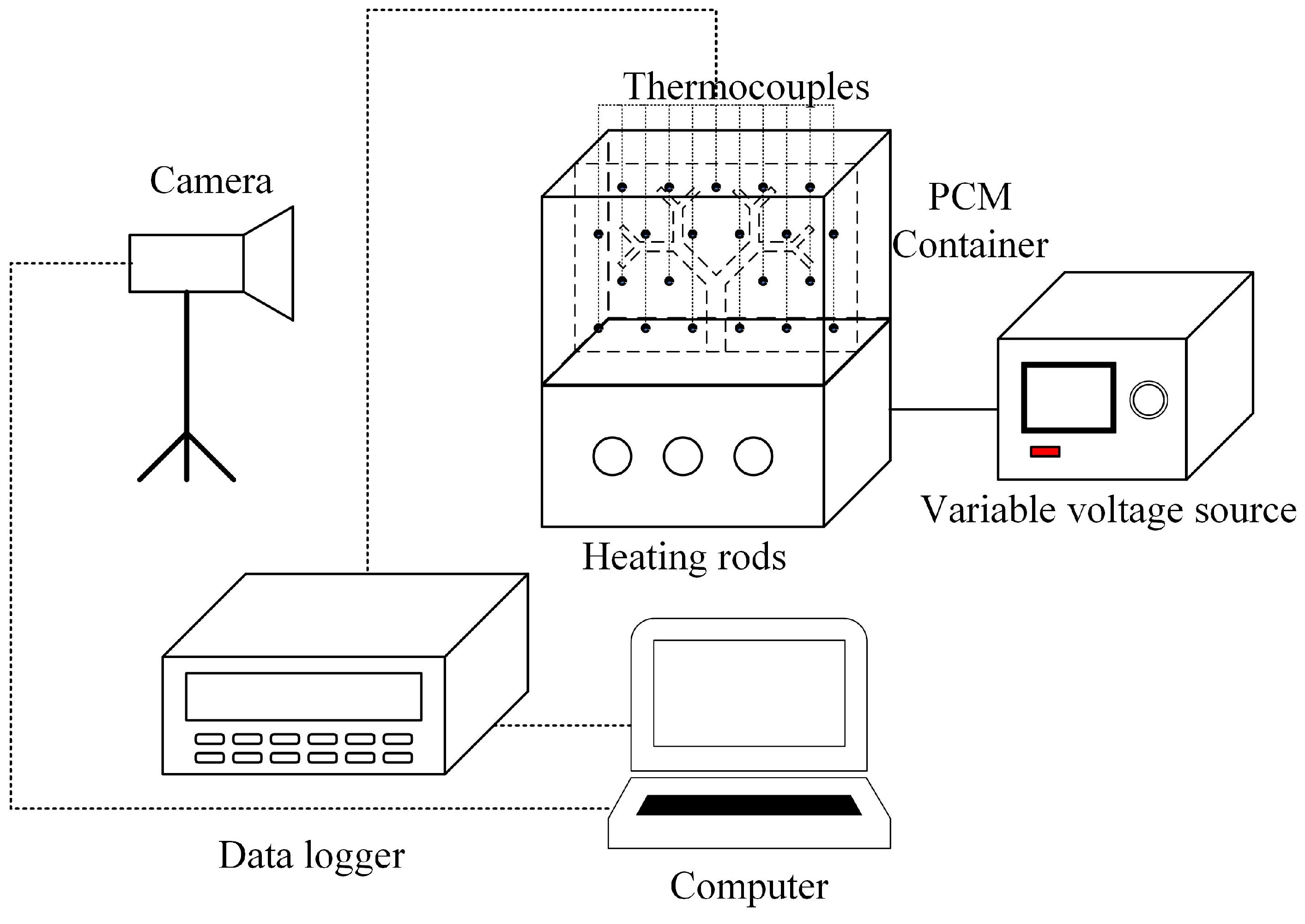
2. Experimental Apparatus and Procedure
3. Results and Discussion
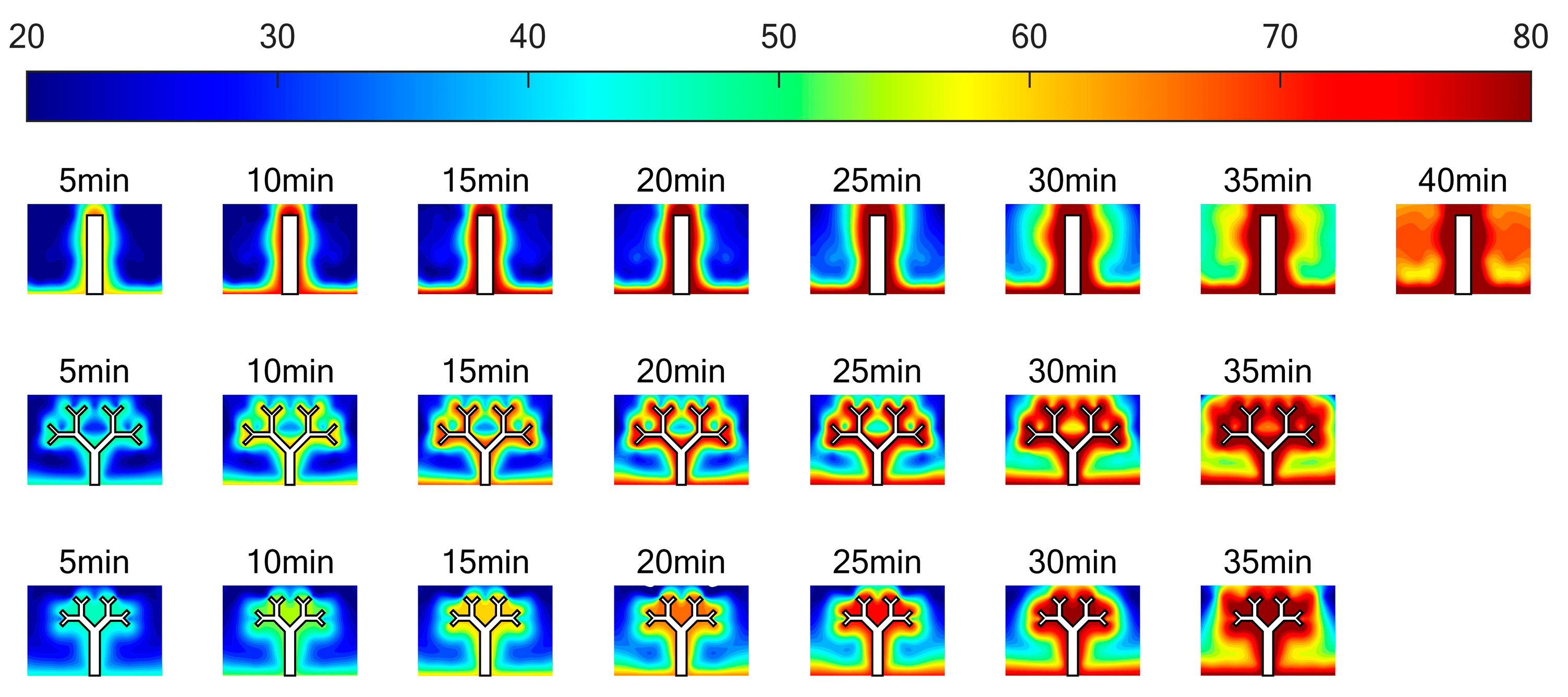
3.1. Solid–Liquid Interface
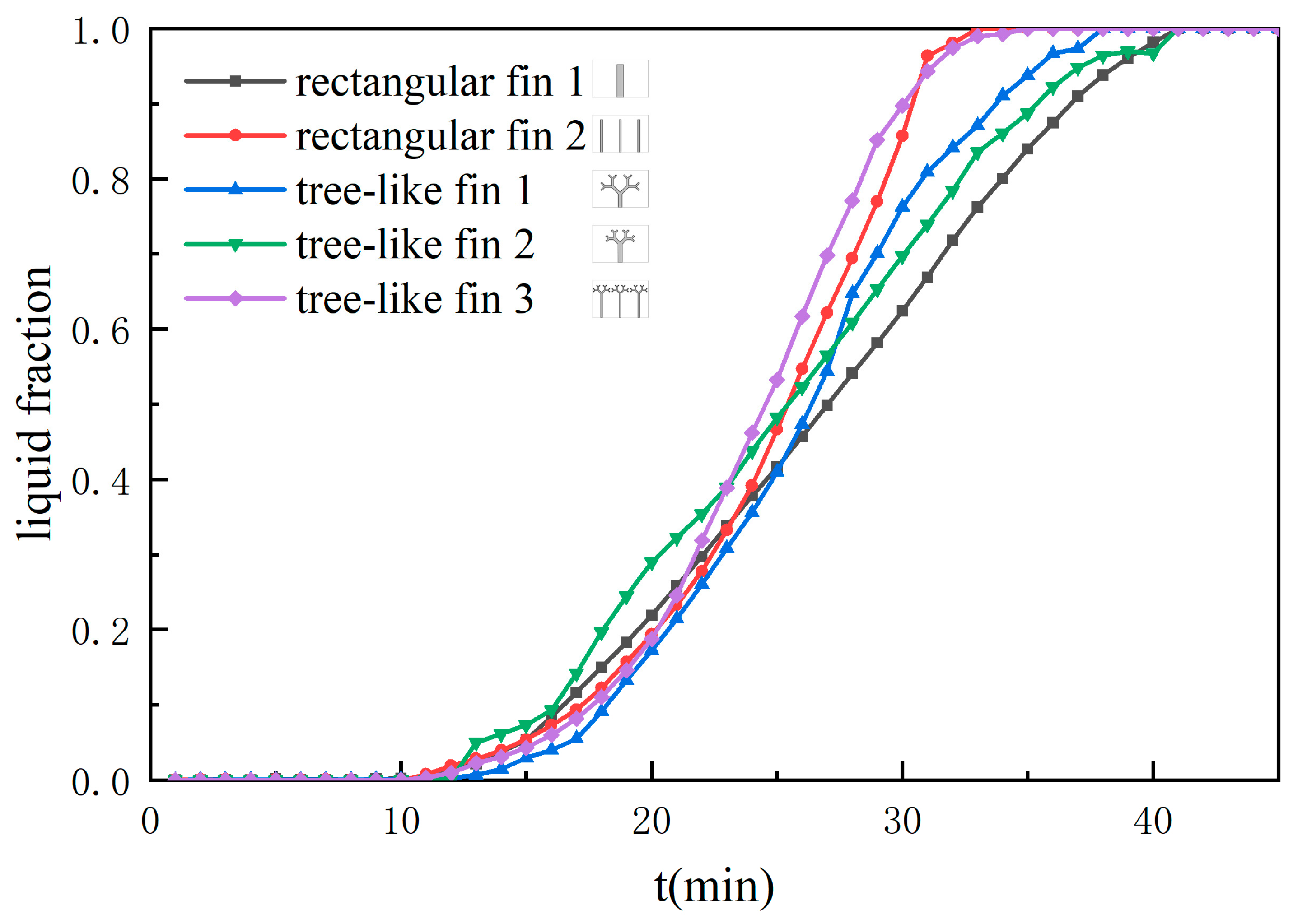
3.2. Liquid Fraction
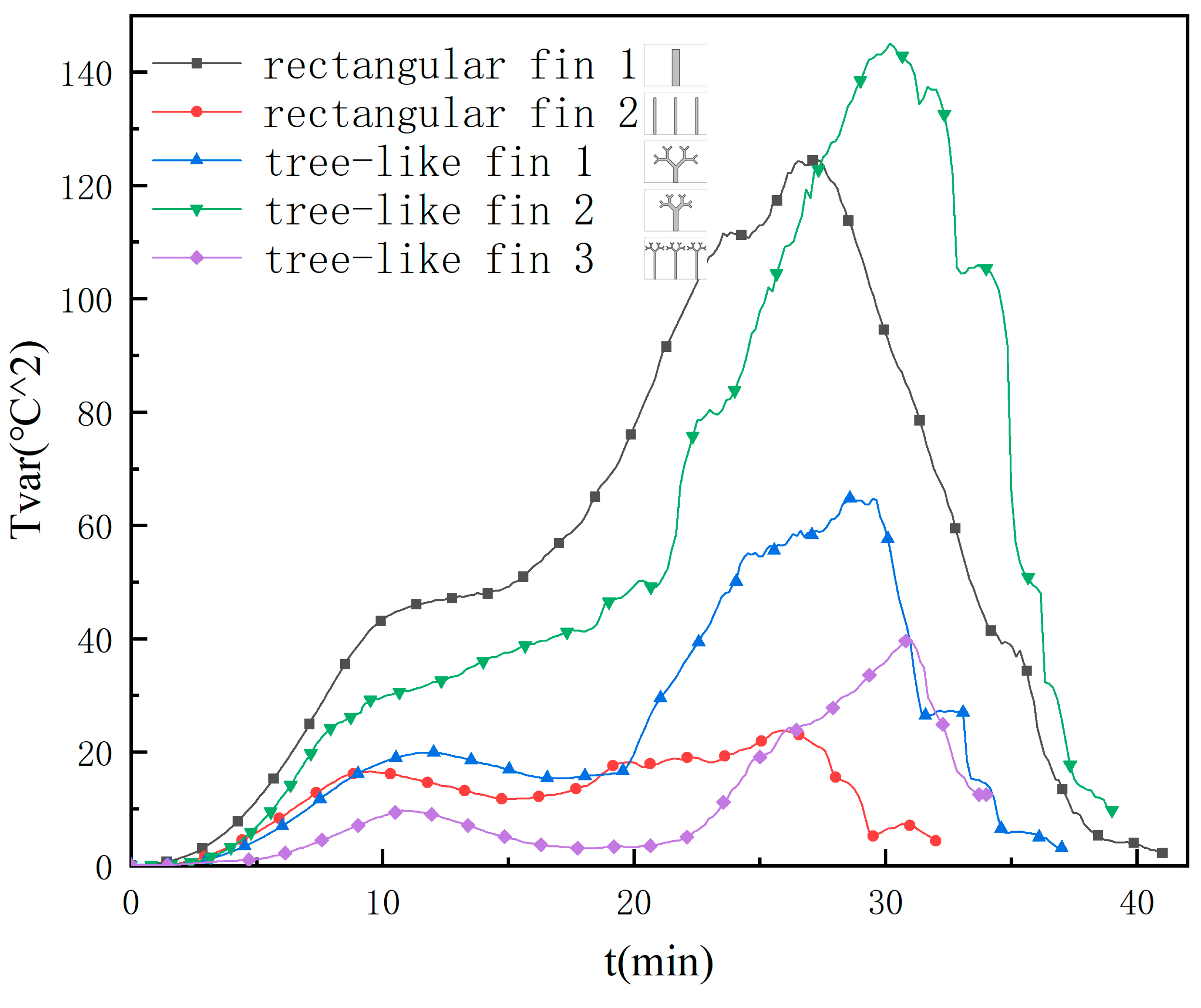
3.3. Temperature Distribution
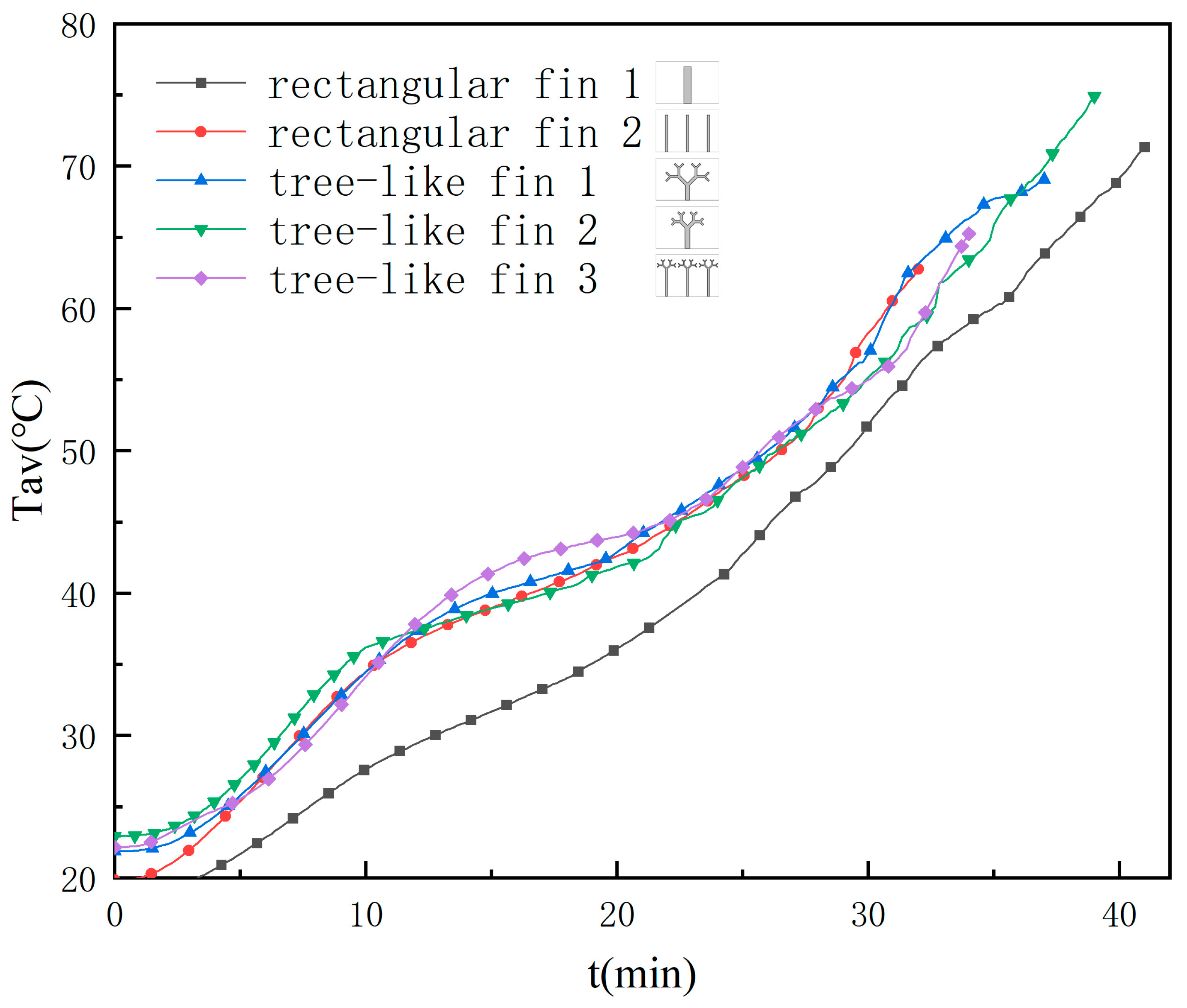
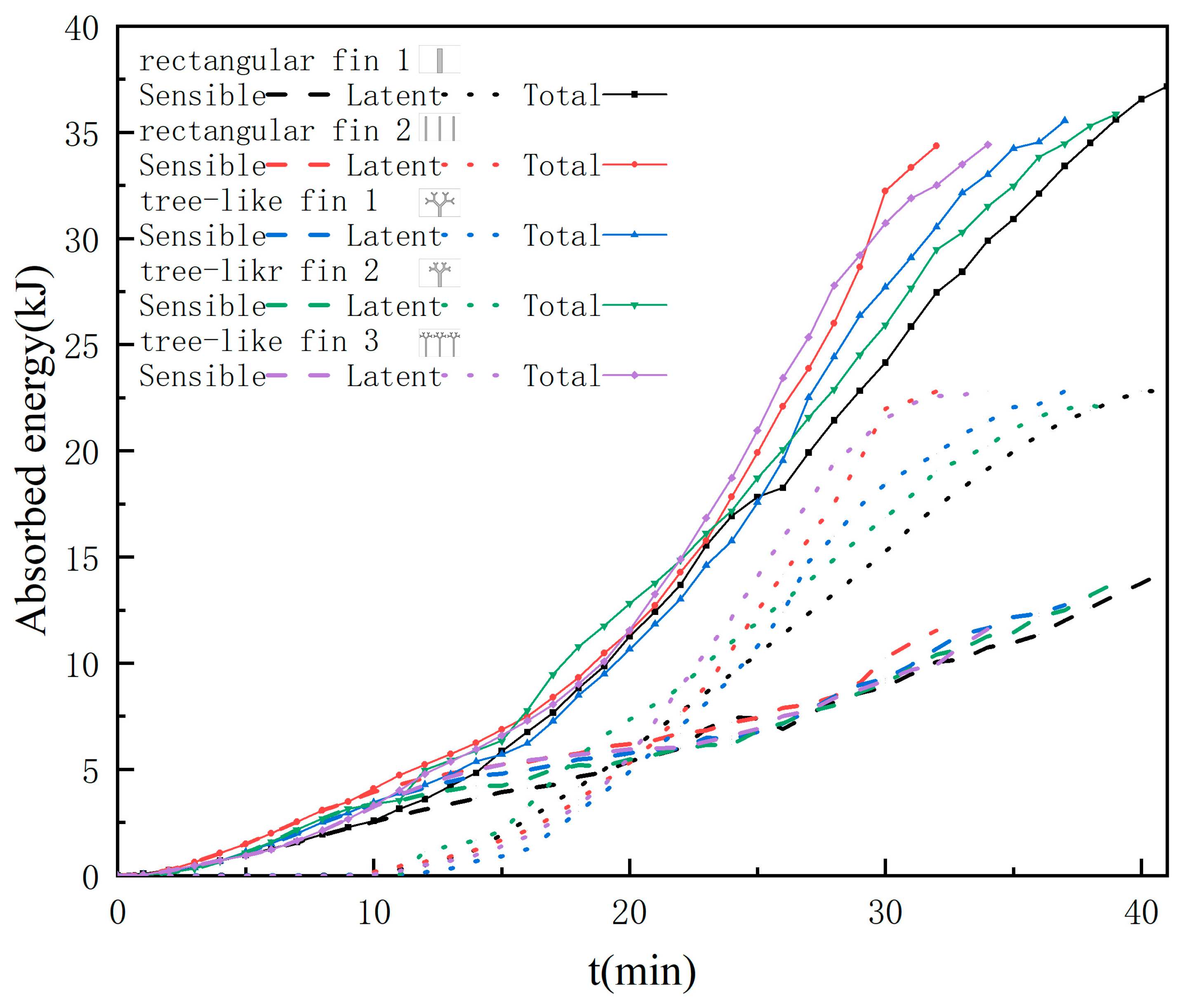
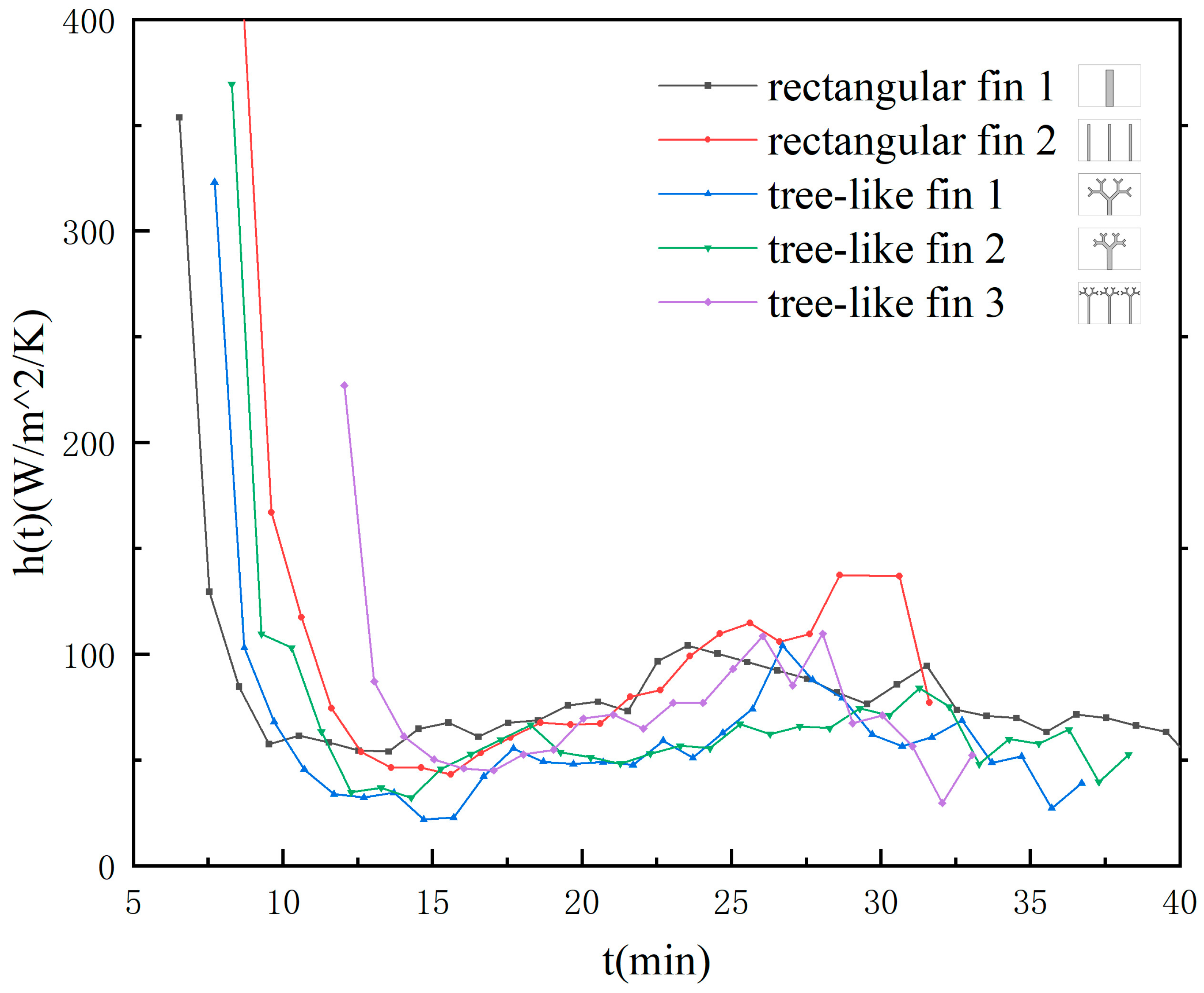
3.4. Heat Transfer Characteristics
4. Summary
- The tree-like fins significantly improve the heating performance of LHTES. Among the one-fin units, compared with the rectangular fin, the full melting time of the unit with tree-like fin 1 is reduced by 9.76% because the improvement of the heat conduction of the tree-like fins is greater than the inhibition of natural convection.
- The tree-like fins are beneficial to controlling the heating surface temperature. At the end of the melting process, the bottom surface temperatures of the two units with tree-like fins were 14.42% and 13.19% lower than that of the unit with rectangular fin 1. The branched structure facilitates the conduction of heat from point to surface, making the temperature distribution more uniform during the melting process.
- The structure and number of fins are two key factors that affect the heat transfer performance of the LHTES unit. Increasing the number of fins can enhance heat transfer within the phase change unit. Compared with the unit with one rectangular fin, the full melting time of the unit with three rectangular fins and the unit with three tree-like fins are reduced by 21.95% and 17.07%, respectively, and the temperature distribution within the unit is more uniform. However, as the number of fins increases, the suppression of natural convection by the tree-like fin may exceed the enhancement of heat conduction, which results in a lower heat transfer performance of the unit with tree-like fin 3 compared to the unit with rectangular fin 2.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cabeza, L.F.; Sole, C.; Castell, A.; Oro, E.; Gil, A. Review of Solar Thermal Storage Techniques and Associated Heat Transfer Technologies. Proc. IEEE 2012, 100, 525–538. [Google Scholar] [CrossRef]
- Li, D.; Wang, J.; Ding, Y.; Yao, H.; Huang, Y. Dynamic thermal management for industrial waste heat recovery based on phase change material thermal storage. Appl. Energy 2019, 236, 1168–1182. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Lin, K.P.; Yang, R.; Di, H.F.; Jiang, Y. Preparation, thermal performance and application of shape-stabilized PCM in energy efficient buildings. Energy Build. 2006, 38, 1262–1269. [Google Scholar] [CrossRef]
- Tao, Y.B.; He, Y.-L. A review of phase change material and performance enhancement method for latent heat storage system. Renew. Sustain. Energy Rev. 2018, 93, 245–259. [Google Scholar] [CrossRef]
- Wang, C.; Lin, T.; Li, N.; Zheng, H. Heat transfer enhancement of phase change composite material: Copper foam/paraffin. Renew. Energy 2016, 96, 960–965. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, P.; Li, M. Effective thermal conductivity of open-cell metal foams impregnated with pure paraffin for latent heat storage. Int. J. Therm. Sci. 2014, 81, 94–105. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, Y.; Wu, H. Numerical modeling for solid–liquid phase change phenomena in porous media: Shell-and-tube type latent heat thermal energy storage. Appl. Energy 2013, 112, 1222–1232. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Zhang, C.; Huang, Y.; Chen, Y. Melting behaviors of PCM in porous metal foam characterized by fractal geometry. Int. J. Heat Mass Transf. 2017, 113, 1031–1042. [Google Scholar] [CrossRef]
- Nemati, H.; Souriaee, V.; Habibi, M.; Vafai, K. Design and Taguchi-based optimization of the latent heat thermal storage in the form of structured porous-coated pipe. Energy 2023, 263, 125947. [Google Scholar] [CrossRef]
- Wang, J.; Xie, H.; Xin, Z.; Li, Y.; Chen, L. Enhancing thermal conductivity of palmitic acid based phase change materials with carbon nanotubes as fillers. Sol. Energy 2010, 84, 339–344. [Google Scholar] [CrossRef]
- Lohrasbi, S.; Sheikholeslami, M.; Ganji, D.D. Discharging process expedition of NEPCM in fin-assisted Latent Heat Thermal Energy Storage System. J. Mol. Liq. 2016, 221, 833–841. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhao, W.; Sabol, J.C.; Tuzla, K.; Neti, S.; Oztekin, A.; Chen, J.C. Encapsulated phase change materials for energy storage—Characterization by calorimetry. Sol. Energy 2013, 87, 117–126. [Google Scholar] [CrossRef]
- Felix Regin, A.; Solanki, S.C.; Saini, J.S. An analysis of a packed bed latent heat thermal energy storage system using PCM capsules: Numerical investigation. Renew. Energy 2009, 34, 1765–1773. [Google Scholar] [CrossRef]
- Sarı, A.; Alkan, C.; Bilgin, C. Micro/nano encapsulation of some paraffin eutectic mixtures with poly(methyl methacrylate) shell: Preparation, characterization and latent heat thermal energy storage properties. Appl. Energy 2014, 136, 217–227. [Google Scholar] [CrossRef]
- Yuan, Y.; Cao, X.; Xiang, B.; Du, Y. Effect of installation angle of fins on melting characteristics of annular unit for latent heat thermal energy storage. Sol. Energy 2016, 136, 365–378. [Google Scholar] [CrossRef]
- Baby, R.; Balaji, C. Thermal optimization of PCM based pin fin heat sinks: An experimental study. Appl. Therm. Eng. 2013, 54, 65–77. [Google Scholar] [CrossRef]
- Shahsavar, A.; Goodarzi, A.; Mohammed, H.I.; Shirneshan, A.; Talebizadehsardari, P. Thermal performance evaluation of non-uniform fin array in a finned double-pipe latent heat storage system. Energy 2020, 193, 116800. [Google Scholar] [CrossRef]
- Baghaei Oskouei, S.; Bayer, Ö. Experimental and numerical investigation of melting and solidification enhancement using Fibonacci-inspired fins in a latent thermal energy storage unit. Int. J. Heat Mass Transf. 2023, 210, 124180. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, B.; Wang, Z.; Zhu, J.; Zhang, J.; Wang, C. Experimental investigation on the charging and discharging performance enhancement of a vertical latent heat thermal energy storage unit via snowflake fin design. Int. J. Heat Mass Transf. 2022, 199, 123455. [Google Scholar] [CrossRef]
- Triki, R.; Chtourou, S.; Baccar, M. Heat transfer enhancement of phase change materials PCMs using innovative fractal H-shaped fin configurations. J. Energy Storage 2023, 73, 109020. [Google Scholar] [CrossRef]
- Du, J.; Bai, D.; Meng, X.; Jiao, F.; Hong, Y. Effect of Cantor fractal fin arrangements on the thermal performance of a photovoltaic-phase change material system: An experimental study. Int. J. Heat Mass Transf. 2024, 219, 124853. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, X.; Liu, X. Numerical analysis and improvement of the thermal performance in a latent heat thermal energy storage device with spiderweb-like fins. J. Energy Storage 2020, 32, 101768. [Google Scholar] [CrossRef]
- Bejan, A. Constructal tree-shaped paths for conduction and convection. Int. J. Energy Res. 2003, 27, 283–299. [Google Scholar] [CrossRef]
- Huang, G.; Zhu, Y.; Liao, Z.; Xu, R.; Jiang, P.-X. Biomimetic self-pumping transpiration cooling for additive manufactured porous module with tree-like micro-channel. Int. J. Heat Mass Transf. 2019, 131, 403–410. [Google Scholar] [CrossRef]
- Xu, S.; Guo, Z.; Qin, J.; Cai, Q.; Hu, G.; Wang, W. Three Dimensional Numerical Simulation of Fluid Flow and Heat Transfer in Tree-shaped Microchannels. China Mech. Eng. 2014, 25, 1185–1188. [Google Scholar]
- Xue, Z.; Yan, Y.; He, Z.; Shen, K.; Zhang, C. Exergy analysis and energy output improvement of the micro-thermophotovoltaic system via investigating the fractal angles of secondary Y-shaped fins in the micro combustor. Fuel 2023, 334, 126504. [Google Scholar] [CrossRef]
- Calamas, D.; Baker, J. Tree-like branching fins: Performance and natural convective heat transfer behavior. Int. J. Heat Mass Transf. 2013, 62, 350–361. [Google Scholar] [CrossRef]
- Li, F.; Sheikholeslami, M.; Dara, R.N.; Jafaryar, M.; Shafee, A.; Nguyen-Thoi, T.; Li, Z. Numerical study for nanofluid behavior inside a storage finned enclosure involving melting process. J. Mol. Liq. 2020, 297, 111939. [Google Scholar] [CrossRef]
- Yıldız, Ç.; Arıcı, M.; Nižetić, S.; Shahsavar, A. Numerical investigation of natural convection behavior of molten PCM in an enclosure having rectangular and tree-like branching fins. Energy 2020, 207, 118223. [Google Scholar] [CrossRef]
- Vogel, J.; Johnson, M. Natural convection during melting in vertical finned tube latent thermal energy storage systems. Appl. Energy 2019, 246, 38–52. [Google Scholar] [CrossRef]
- Li, Q.; Jiang, J.; Hong, Y.; Du, J. Numerical investigation of thermal management performances in a solar photovoltaic system by using the phase change material coupled with bifurcated fractal fins. J. Energy Storage 2022, 56, 106156. [Google Scholar] [CrossRef]
- Luo, X.M.; Gu, J.A.; Ma, H.Q.; Xie, Y.; Li, A.Y.; Wang, J.Y.; Ding, R.X. Numerical study on enhanced melting heat transfer of PCM by the combined fractal fins. J. Energy Storage 2022, 45, 103780. [Google Scholar] [CrossRef]
- Peng, H.; Yan, W.; Wang, Y.; Feng, S. Discharging process and thermal evaluation in the thermal energy storage system with fractal tree-like fins. Int. J. Heat Mass Transf. 2022, 183, 122073. [Google Scholar] [CrossRef]
- Shi, S.; Niu, J.; Wu, Z.; Luo, S.; Gao, X.; Fang, Y.; Zhang, Z. Experimental and numerical investigation on heat transfer enhancement of vertical triplex tube heat exchanger with fractal fins for latent thermal energy storage. Int. J. Heat Mass Transf. 2022, 198, 123386. [Google Scholar] [CrossRef]
- Jiang, J.; Hong, Y.; Li, Q.; Du, J. Numerical analysis on heat transfer and melting characteristics of a solid-liquid phase change process in a rectangular cavity inserted with bifurcated fractal fins. Int. Commun. Heat Mass Transf. 2023, 142, 106616. [Google Scholar] [CrossRef]
- Li, W.; Wang, J.; Zhang, Y.; Zhang, X.; Wei, F.; Zhao, J. Numerical study and parametric analysis on performance enhancement of a latent heat storage unit with fractal fins. J. Energy Storage 2022, 55, 105814. [Google Scholar] [CrossRef]
- Yu, D.; Qiu, Y.; Zhang, X.; Liu, F. Research on the energy discharging performance of Y-shaped fin. J. Energy Storage 2022, 50, 104704. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Gagliardi, F.; Verda, V. Maximization of performance of a PCM latent heat storage system with innovative fins. Appl. Energy 2015, 137, 707–715. [Google Scholar] [CrossRef]
- Deng, Z.L.; Wu, S.C.; Xu, H.; Chen, Y.P. Melting heat transfer enhancement of a horizontal latent heat storage unit by fern-fractal fins. Chin. J. Chem. Eng. 2020, 28, 2857–2871. [Google Scholar] [CrossRef]
- Luo, X.M.; Liao, S.M. Numerical Study on Melting Heat Transfer in Dendritic Heat Exchangers. Energies 2018, 11, 2504. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, X. Charging and discharging enhancement of a vertical latent heat storage unit by fractal tree-shaped fins. Renew. Energy 2021, 174, 199–217. [Google Scholar] [CrossRef]
- Liu, X.; Huang, Y.; Zhang, X.; Zhang, C.; Zhou, B. Investigation on charging enhancement of a latent thermal energy storage device with uneven tree-like fins. Appl. Therm. Eng. 2020, 179, 115749. [Google Scholar] [CrossRef]
- Huang, Y.; Cao, D.; Sun, D.; Liu, X. Experimental and numerical studies on the heat transfer improvement of a latent heat storage unit using gradient tree-shaped fins. Int. J. Heat Mass Transf. 2022, 182, 121920. [Google Scholar] [CrossRef]
- Lijun, L.; Yaqian, N.; Xiaoqing, L.; Xiaoyan, L. Numerical simulation of the improvement of latent heat storage unit performance in solidification process by eccentric fractal finned tube. J. Energy Storage 2023, 57, 106044. [Google Scholar] [CrossRef]
- Yang, B. Study on Microstructural Evolution and Heat & Mass Transport Mechanisms in Mushy Zone during Solid-Liquid Phase Transitions. Ph.D. Thesis, University of Chinese Academy of Sciences (Institute of Electrical Engineering Chinese Academy of Sciences), Beijing, China, 2020. [Google Scholar]
- Shokouhmand, H.; Kamkari, B. Experimental investigation on melting heat transfer characteristics of lauric acid in a rectangular thermal storage unit. Exp. Therm. Fluid Sci. 2013, 50, 201–212. [Google Scholar] [CrossRef]









| Unit | Lauric Acid | Plexiglass | Aluminum Alloy | EPDM | |
|---|---|---|---|---|---|
| Density ρ | kg/m3 | Solid: 940 | 1180 | 2700 | 210.7 |
| Liquid: 885 | |||||
| Thermal conductivity k | W/m/K | Solid: 0.16 | 0.19 | 130 | 0.027 |
| Liquid: 0.14 | |||||
| Specific heat capacity cp | J/kg/K | Solid: 2180 | 1464 | 900 | 2300 |
| Liquid: 2390 | |||||
| Melting range Ts–Tl | °C | 43.5–48.2 | - | - | - |
| Latent heat of fusion L | J/kg | 187,210 | - | - | - |
| Rectangular Fin 1 | Rectangular Fin 2 | Tree-like Fin 1 | Tree-like Fin 2 | Tree-like Fin 3 | |
|---|---|---|---|---|---|
| L0 | 35 mm | 35 mm | 14.22 mm | 9.56 mm | 6.08 mm |
| L0′ | - | - | - | 10 mm | 20 mm |
| L1 | - | - | 10.05 mm | 6.76 mm | 4.30 mm |
| L2 | - | - | 7.11 mm | 4.78 mm | 3.04 mm |
| L3 | - | - | 5.03 mm | 3.38 mm | 2.15 mm |
| w0 | 7 mm | 2.28 mm | 4 mm | 4.64 mm | 1.75 mm |
| w1 | - | - | 2.84 mm | 3.28 mm | 1.24 mm |
| w2 | - | - | 2 mm | 2.32 mm | 0.88 mm |
| w3 | - | - | 1.42 mm | 1.64 mm | 0.62 mm |
| Maximum height of a fin Lmax | 35 mm | 35 mm | 35 mm | 35 mm | 35 mm |
| Maximum width of a fin wmax | 7 mm | 2.28 mm | 41.56 mm | 30.87 mm | 17.84 mm |
| Fin surface area Afin | 4620 mm2 | 13,010.4 mm2 | 13,041.6 mm2 | 10,776 mm2 | 23,947.2 mm2 |
| Total area Aw | 7800 mm2 | 16,200 mm2 | 16,401.6 mm2 | 14,097.6 mm2 | 27,237.6 mm2 |
| Rectangular Fin 1 | Rectangular Fin 2 | Tree-like Fin 1 | Tree-like Fin 2 | Tree-like Fin 3 | |
|---|---|---|---|---|---|
| full melting time tall (min) | 41 | 32 | 37 | 39 | 34 |
| melting time ratio rt | 1 | 0.78 | 0.90 | 0.95 | 0.83 |
| full melting time reduction percentage | - | 21.95% | 9.76% | 4.88% | 17.07% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Xu, L.; Sun, F.; Sun, S. Experimental Investigation on Heat Transfer Enhancement of Phase Change Materials by Fractal Fins. Energies 2024, 17, 2657. https://doi.org/10.3390/en17112657
Guo Z, Xu L, Sun F, Sun S. Experimental Investigation on Heat Transfer Enhancement of Phase Change Materials by Fractal Fins. Energies. 2024; 17(11):2657. https://doi.org/10.3390/en17112657
Chicago/Turabian StyleGuo, Zishuo, Li Xu, Feihu Sun, and Si Sun. 2024. "Experimental Investigation on Heat Transfer Enhancement of Phase Change Materials by Fractal Fins" Energies 17, no. 11: 2657. https://doi.org/10.3390/en17112657
APA StyleGuo, Z., Xu, L., Sun, F., & Sun, S. (2024). Experimental Investigation on Heat Transfer Enhancement of Phase Change Materials by Fractal Fins. Energies, 17(11), 2657. https://doi.org/10.3390/en17112657





