Improved Model-Free Deadbeat Predictive Current Controller for PMSMs Based on Ultralocal Model and H∞ Norm
Abstract
1. Introduction
1.1. Motivation
1.2. Related Research
1.3. Contributions and Organizations
2. PMSM Model and Traditional DPCC
2.1. Model of the PMSM
2.2. Traditional DPCC
3. Introduction of the MFCC
3.1. Traditional ESO-DPCC
3.2. Model-Free DPCC
4. H∞-Based Coefficient Design
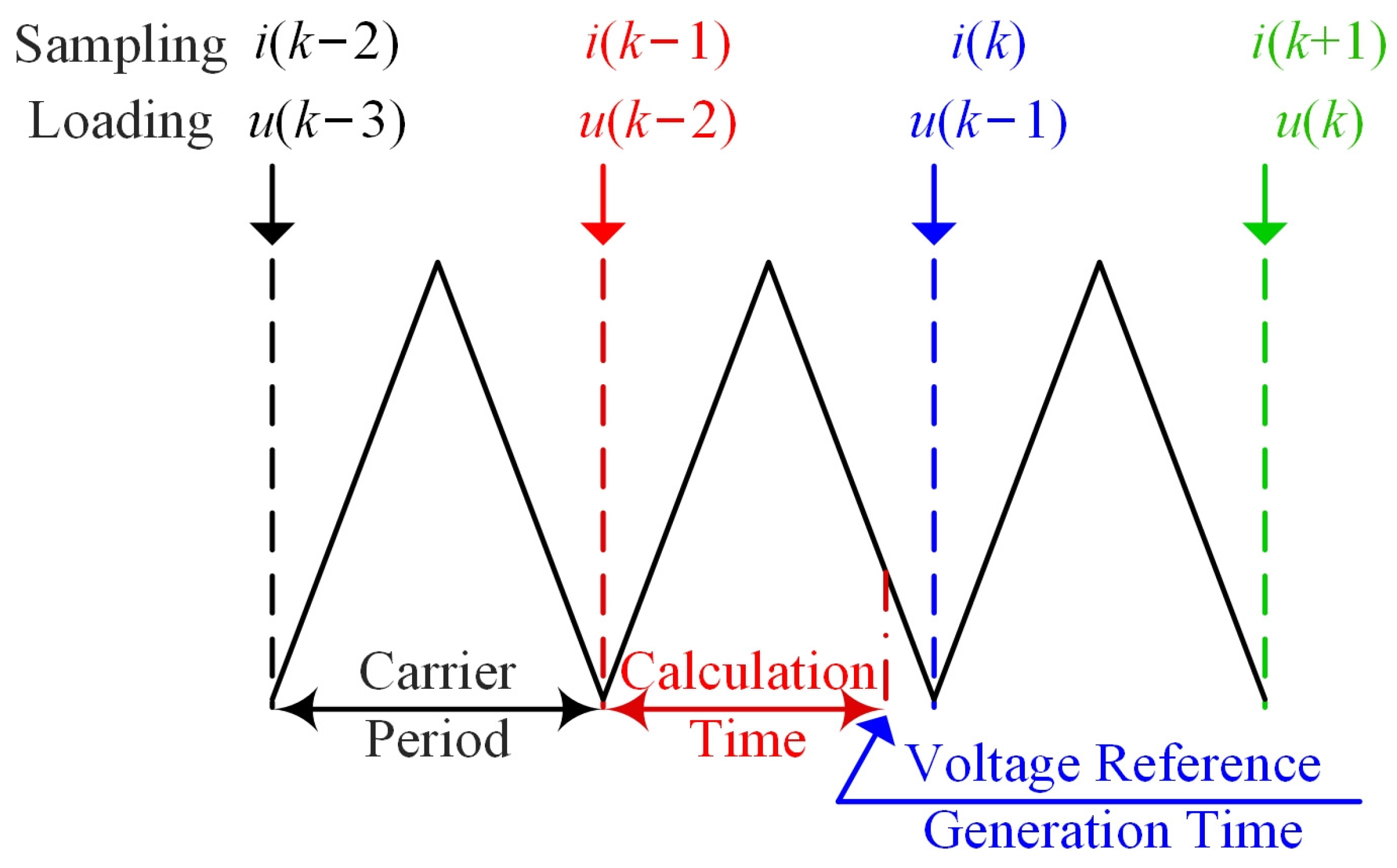
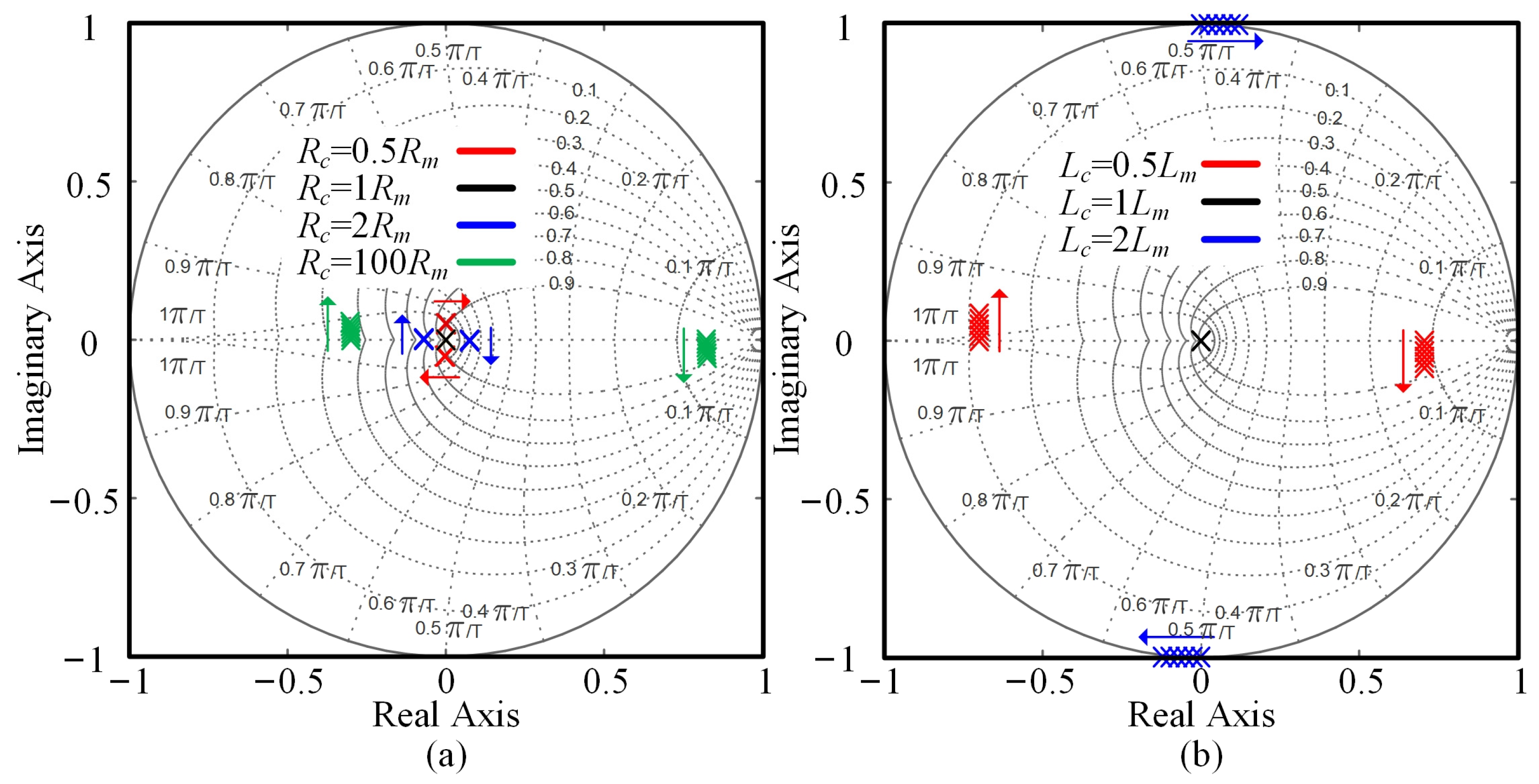
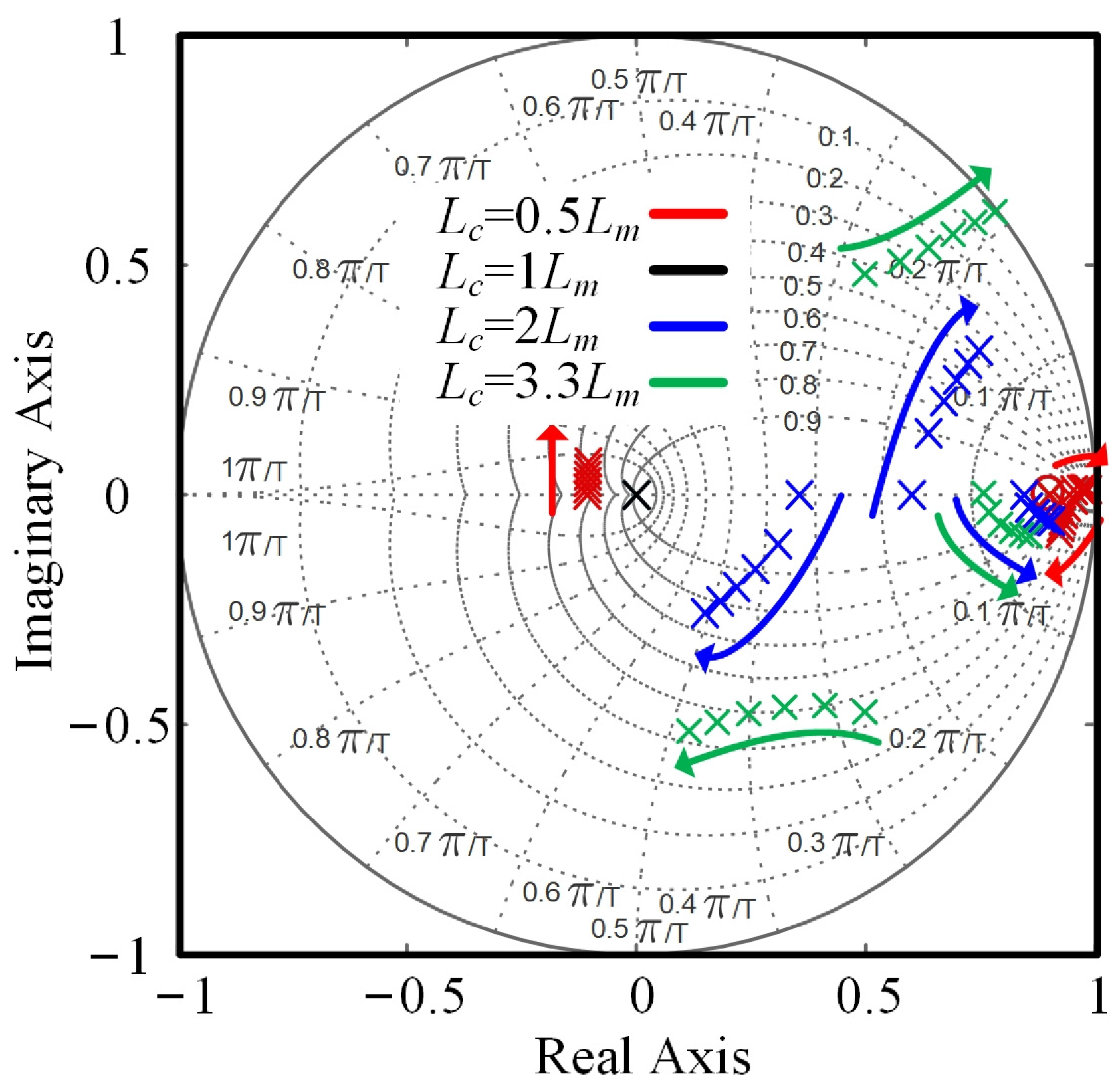
4.1. Influence Analysis of Coefficient on Robustness
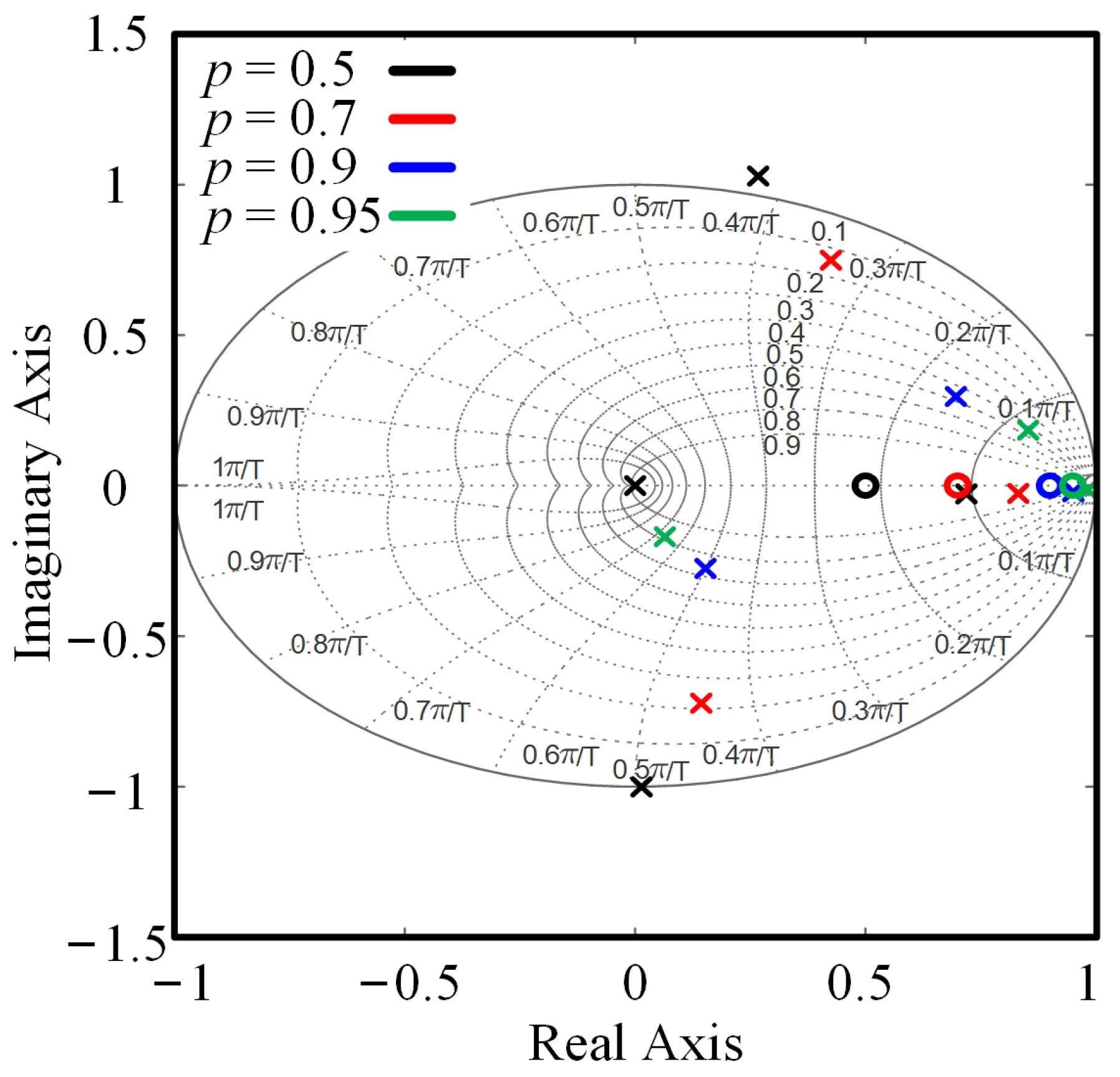
4.2. Coefficient Design
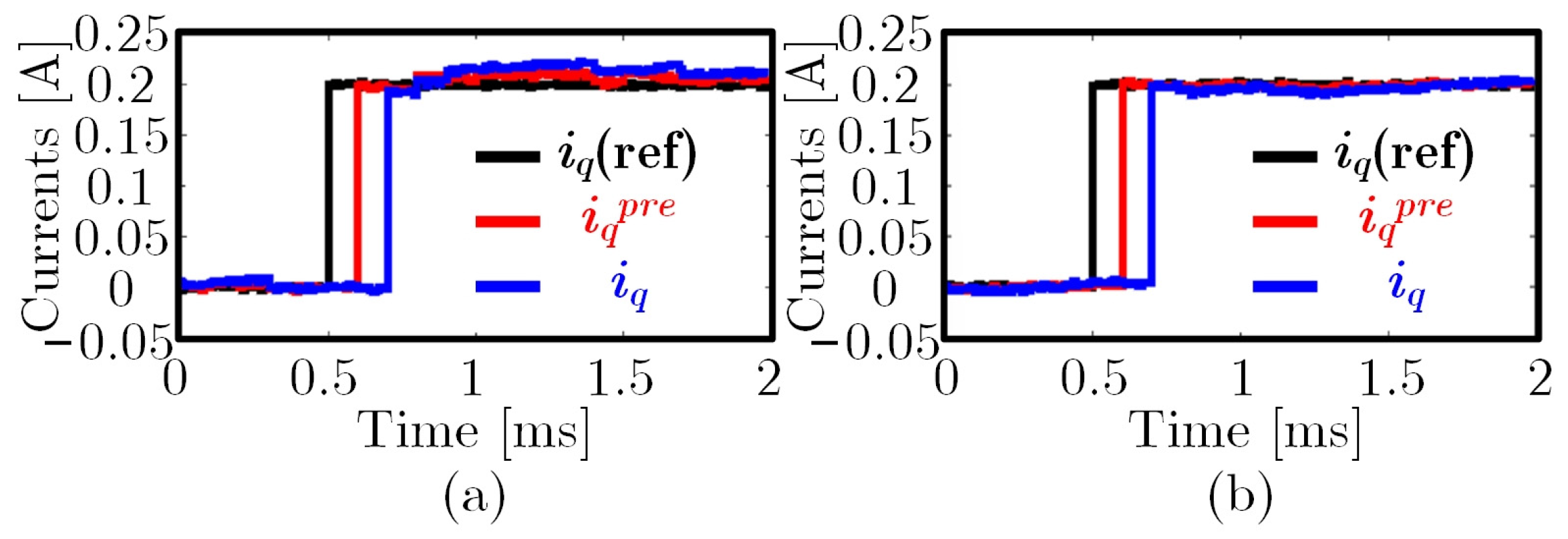
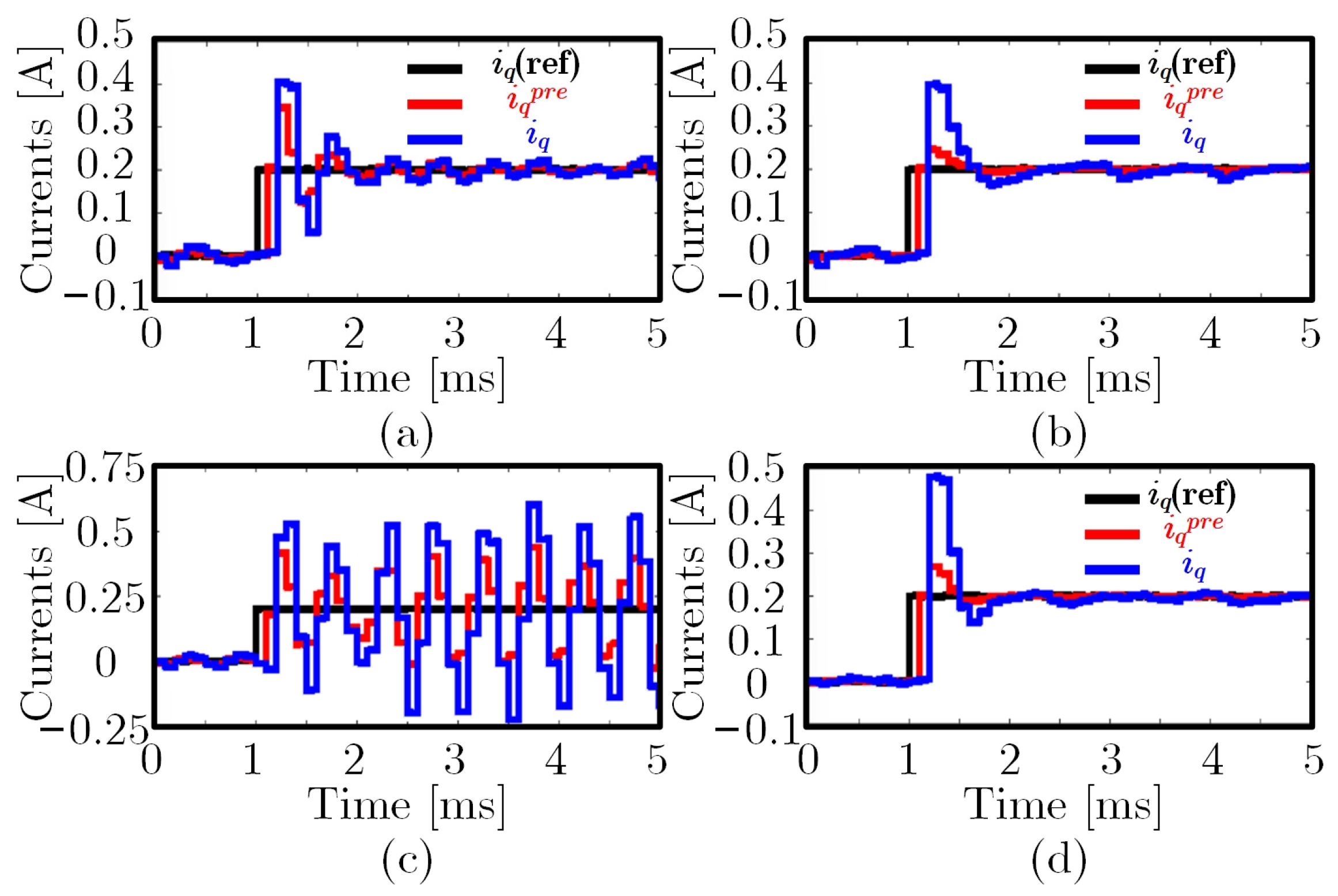
5. Experimental Verification
5.1. Test Bench Setup
5.2. Comparative Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Wei, Z.; Zhao, Y.; Wang, X.; Hua, W. Design and Analysis of Surface-Mounted Permanent-Magnet Field-Modulation Machine for Achieving High Power Factor. IEEE Trans. Ind. Electron. 2024, 71, 4375–4386. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Dong, Y.; Lu, K.; Feng, X. Design and Analysis of Electric-Excitation Claw-Pole Field-Modulated Machine Considering Effective Harmonics. IEEE Trans. Ind. Appl. 2024, 60, 3893–3902. [Google Scholar] [CrossRef]
- Jia, S.; Chen, P.; Yang, D.; Feng, S.; Liang, D. Field Orientation Control for a Dual Winding Dual Magnet Flux Modulated Machine With Torque Distribution Capability. IEEE Trans. Ind. Appl. 2024, 60, 343–352. [Google Scholar] [CrossRef]
- Chen, J.; Fan, Y.; Cheng, M.; Zhang, Q.; Chen, Q. Parameter-Free Ultralocal Model-Based Deadbeat Predictive Current Control for PMVMs Using Finite-Time Gradient Method. IEEE Trans. Ind. Electron. 2024, 70, 5549–5559. [Google Scholar] [CrossRef]
- Hussain, H.A. Tuning and Performance Evaluation of 2DOF PI Current Controllers for PMSM Drives. IEEE Trans. Transp. Electr. 2021, 7, 1401–1414. [Google Scholar] [CrossRef]
- Lu, K.; Li, X.; Zhao, Y.; Yi, P.; Yan, B.; Hua, W. A Novel Three-Vector-Based Model Predictive Flux Control with Low Computation Complexity for SPMSM. IEEE Trans. Transp. Electr. 2024. [Google Scholar] [CrossRef]
- Gao, J.; Gong, C.; Li, W.; Liu, J. Novel Compensation Strategy for Calculation Delay of Finite Control Set Model Predictive Current Control in PMSM. IEEE Trans. Ind. Electron. 2020, 67, 5816–5819. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Two-Vector-Based Model Predictive Torque Control Without Weighting Factors for Induction Motor Drives. IEEE Trans. Power Electr. 2016, 31, 1381–1390. [Google Scholar] [CrossRef]
- Monfared, K.K.; Iman-Eini, H.; Neyshabouri, Y.; Liserre, M. Model Predictive Control With Reduced Common-Mode Voltage Based on Optimal Switching Sequences for Nested Neutral Point Clamped Inverter. IEEE Trans. Ind. Electron. 2024, 71, 27–38. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Rodríguez, J. Torque Ripple Reduction of Predictive Torque Control for PMSM Drives With Parameter Mismatch. IEEE Trans. Power Electr. 2017, 32, 7160–7168. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Bai, H. Sliding-Mode-Based Deadbeat Predictive Current Control for PMSM Drives. IEEE J. Emerg. Select Top. Power Electron. 2023, 11, 962–969. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, W.; Huang, S.; Zhang, J.; Yang, M.; Li, C.; Huang, S. A Robust DPCC for IPMSM Based on a Full Parameter Identification Method. IEEE Trans. Ind. Electron. 2023, 70, 7695–7705. [Google Scholar] [CrossRef]
- Xia, C.; Wang, M.; Song, Z.; Liu, T. Robust Model Predictive Current Control of Three-Phase Voltage Source PWM Rectifier with Online Disturbance Observation. IEEE Trans. Ind. Inform. 2012, 8, 459–471. [Google Scholar] [CrossRef]
- Sun, X.; Lin, X.; Guo, D.; Lei, G.; Yao, M. Improved Deadbeat Predictive Current Control With Extended State Observer for Dual Three-Phase PMSMs. IEEE Trans. Power Electr. 2024, 39, 6769–6782. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, Y.; Mao, C. A Gain Design Method for a Linear Extended State Observers to Improve Robustness of Deadbeat Control. IEEE Trans. Energy Convers. 2020, 35, 2231–2239. [Google Scholar] [CrossRef]
- Chen, W.; Liu, J.; Fang, Y.; Zhao, J. Timber Knot Detector with Low False-Positive Results by Integrating an Overlapping Bounding Box Filter with Faster R-CNN Algorithm. Bioresources 2023, 18, 4964–4976. [Google Scholar] [CrossRef]
- Fang, Y.; Guo, X.; Chen, K.; Zhou, Z.; Ye, Q. Accurate and Automated Detection of Surface Knots on Sawn Timbers Using YOLO-V5 Model. Bioresources 2021, 16, 5390–5406. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Model-Free Control. Int. J. Control. 2013, 86, 2228–2252. [Google Scholar] [CrossRef]
- Zhao, K.; Liu, W.; Zhou, R.; Dai, W.; Wu, S.; Qiu, P.; Yin, Y.; Jia, N.; Yi, J.; Huang, G. Model-Free Fast Integral Terminal Sliding-Mode Control Method based on Improved Fast Terminal Sliding-Mode Observer for PMSM with Unknown Disturbances. ISA Trans. 2023, 143, 572–581. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Deng, Y.; Wang, J.; Li, H.; Cao, H. Improved Cascaded Model-Free Predictive Speed Control for PMSM Speed Ripple Minimization based on Ultra-local Model. ISA Trans. 2023, 143, 666–677. [Google Scholar] [CrossRef]
- Mousavi, M.S.; Davari, S.A.; Nekoukar, V.; Garcia, C.; Rodriguez, J. A Robust Torque and Flux Prediction Model by a Modified Disturbance Rejection Method for Finite-Set Model-Predictive Control of Induction Motor. IEEE Trans. Power Electr. 2021, 36, 9322–9333. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-Free Predictive Current Control of PMSM Drives Based on Extended State Observer Using Ultralocal Model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar] [CrossRef]







| PI Controller | Model Predictive Controller | Deadbeat Predictive Current Controller | |
|---|---|---|---|
| Fast Dynamic Performance | ★ | ★★ | ★★★ |
| Strong Robustness | ★★ | ★ | ★ |
| Easy Implementation | ★★ | ★ | ★★★ |
| β1 | β2 | H∞ | Max(|pole(fclo)|) | |
|---|---|---|---|---|
| P1 | 0.85 − 0.15 j | 0.9 + 0.7 j | 2.2257 | 0.9235 |
| P2 | 0.85 − 0.15 j | 0.15 + 0.2 j | 2.1986 | 0.9913 |
| P3 | 0.85 | 0.50625 | 3.518 | 0.9712 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Chen, J. Improved Model-Free Deadbeat Predictive Current Controller for PMSMs Based on Ultralocal Model and H∞ Norm. Energies 2024, 17, 2649. https://doi.org/10.3390/en17112649
Fang Y, Chen J. Improved Model-Free Deadbeat Predictive Current Controller for PMSMs Based on Ultralocal Model and H∞ Norm. Energies. 2024; 17(11):2649. https://doi.org/10.3390/en17112649
Chicago/Turabian StyleFang, Yiming, and Junlei Chen. 2024. "Improved Model-Free Deadbeat Predictive Current Controller for PMSMs Based on Ultralocal Model and H∞ Norm" Energies 17, no. 11: 2649. https://doi.org/10.3390/en17112649
APA StyleFang, Y., & Chen, J. (2024). Improved Model-Free Deadbeat Predictive Current Controller for PMSMs Based on Ultralocal Model and H∞ Norm. Energies, 17(11), 2649. https://doi.org/10.3390/en17112649







