An Innovative Approach to Radiality Representation in Electrical Distribution System Reconfiguration: Enhanced Efficiency and Computational Performance
Abstract
1. Introduction
2. Literature Review
| Ref. | Year | Model Description | Radiality Conditions | Apparent Power |
|---|---|---|---|---|
| [5] | 1975 | Quadratic Programming Model—Linearization of the Objective Function | The solution is updated iteratively by opening branches until the number of active branches equals the number of nodes minus one. | Network is assumed to be purely resistive. |
| [16] | 1990 | Quadratic loss function. DC power flow. | The radial topology of the circuit is described using circuit component trace. | Distribution system power factor near to 1. DC power flow model. |
| [12] | 1991 | Algorithm based on the linear transportation problem. Efficient for small networks. | It solves the linear uncapacitated transshipment problem to ensure radial topology. | Power losses are estimated using a radial power flow method (i.e., a backward and forward trace procedure). |
| [13] | 2010 | Mixed-integer quadratic programming model. Voltage drops approximated through Blondel equation. | Every node of the final network must have at most one active path. They expressed radiality conditions as ; in this study, a path is defined as a set of branches connecting bus bar I to the substation. | It is expressed as the inequality: |
| [7] | 2012 | Mixed-integer conic linear programming model—Mixed-integer linear programming model (polyhedral representation of conic constraints). | Spanning tree constraints of the form: | The authors proposed a convex relaxation for the equation: In the form of |
| [14] | 2012 | Nonlinear programming model with generalized radiality conditions. | Generalization of radiality conditions to equation It also introduces single commodity flow constraints to guarantee the network is connected. | Active and reactive power flows are expressed in terms of voltages and phase angles between bus bars, leading to a high nonlinear model. |
| [4] | 2014 | Method based on MILP, involving the linearization of the equation relating currents, voltages, and active and reactive powers. | The radiality is guaranteed with the following set of equations: | Linearization of y through piecewise linear approximations, and by linearizing |
| [2] | 2022 | Method based on mixed-integer linear programming with distributed generation in the network. | The radiality is guaranteed with the following set of equations: , | The authors used the same approach described in [4]. |
- Introducing and evaluating the impact of alternative radiality conditions, by expressing the spanning tree constraints in a more compact way.
- Proposing a simplified linearization approach for calculating currents, based on the power flow model originally proposed by [1].
- Assessing the methodology of linearization along with its advantages and limitations.
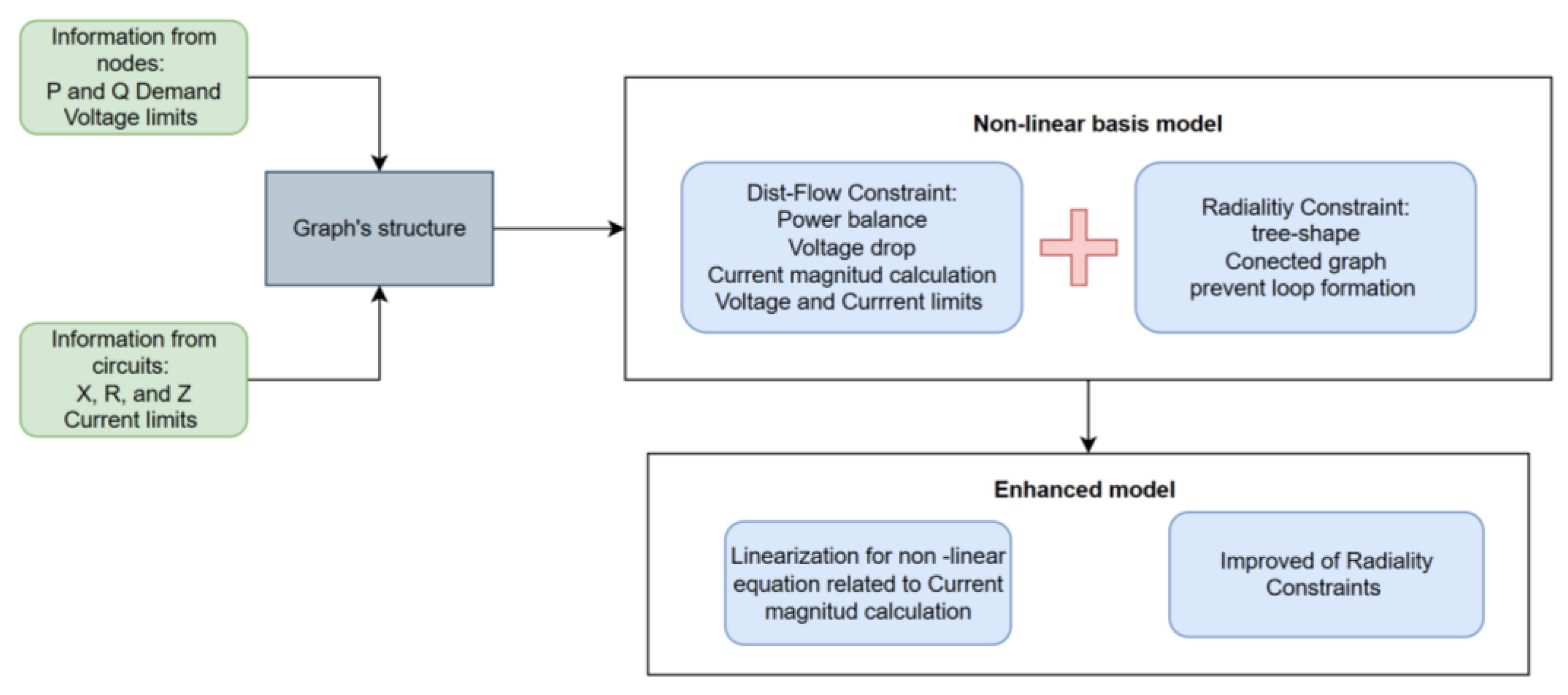
3. Proposed Methodology
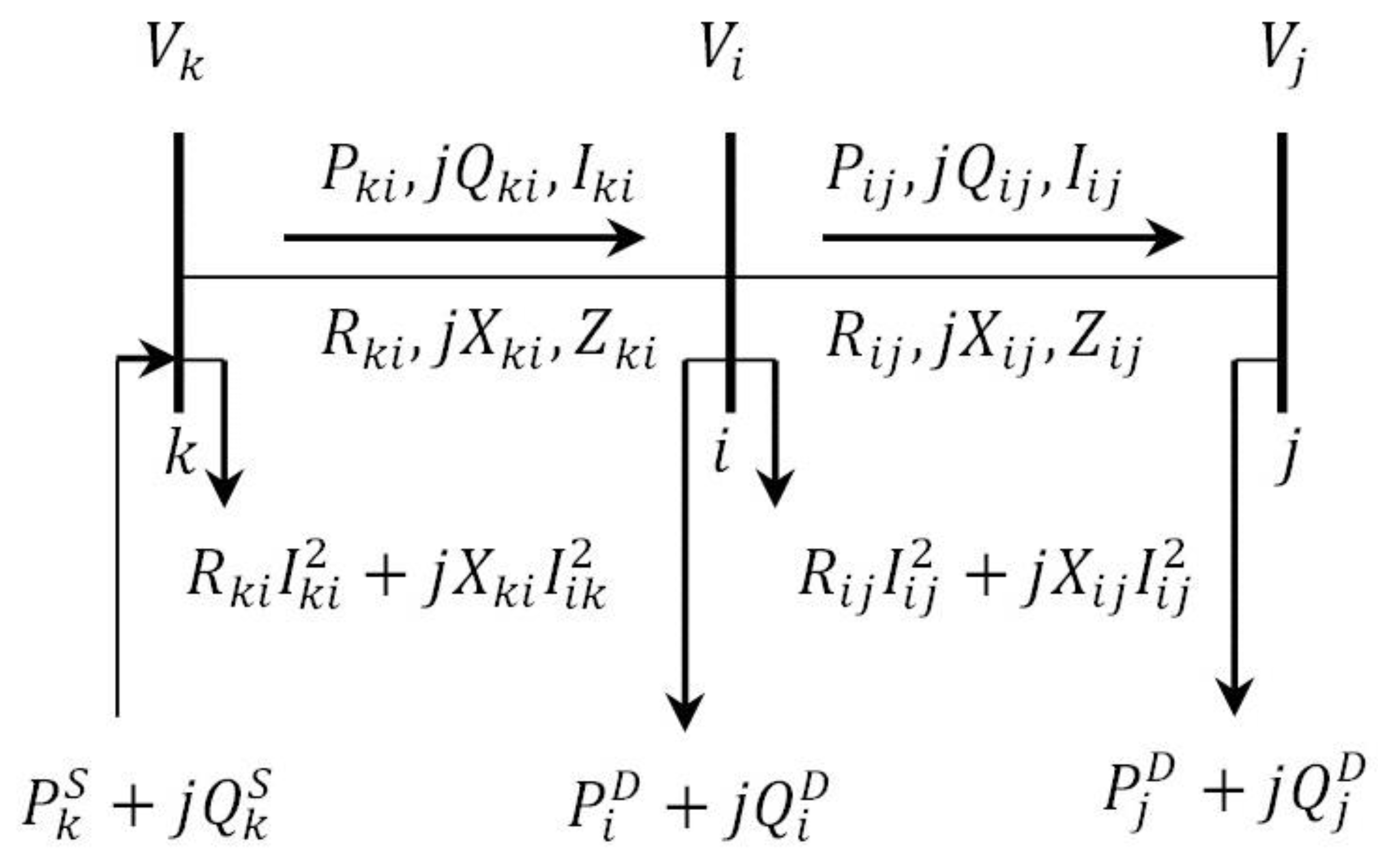
3.1. Nonlinear Non-Convex Integer Basis Model
3.2. Enhanced Model
4. Numerical Results
- Nonlinear non–convex integer basis model [4]: the base model consists of Constraints (2)–(9)
- Model with modified Radiality Constraints: the base model can be modified by including the modified Radiality Constraints; in this case, the incumbent constraints are (2)–(8), (14) and (15)
- Model with a simplification of the term : in this case, Constraint (11) is included instead of Constraint (6); the model then consists of Constraints (2)–(5), (7), (8) and (11)–(13)
- Model with a double power triangle constraint: in this case, the set of Constraints (10) and (11) is included instead of Constraint (6); the model then consists of Constraints (2)–(5), (7), (8) and (10)–(13)
- It would be useful to note that, except for the base model, all other models are modifications proposed within this research, as outlined in Section 2. These modifications represent novel contributions aimed at enhancing computational efficiency in the context of the DPSR.
4.1. Instances’ Description
- Active power losses: These refer to the power losses due to Joule effect and are estimated using the objective function (1).
- Computation time: This corresponds to the time taken by the code to load the data, build the model in the Gurobi off-the-shelf optimizer, and solve the system. The total time refers to the sum of these three times.
4.2. Discussion of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variables | |
| Electrical current flowing through branch (i,j). | |
| Active power flowing through branch i,j. | |
| Active power demand at node i. | |
| Active power generation at node i. | |
| Reactive power flowing through branch (i,j). | |
| Reactive power demand at node i. | |
| Reactive power demand at node i. | |
| Voltage of bus bar i. | |
| Boolean state of branch i,j switch | |
| Voltage slack through branch (k,i) | |
| Parameters | |
| Current upper limit through branch i,j. | |
| Current upper limit through branch i,j. | |
| Electrical resistance of branch i,j. | |
| Inductive reactance of branch i,j. | |
| Voltage upper limit of bus bar i | |
| Voltage lower limit of bus bar i | |
| Sets | |
| Bus bar set for the considered electrical network. | |
| Set of substations | |
| Branches set in the electrical network. |
Appendix A. Instances’ Solutions
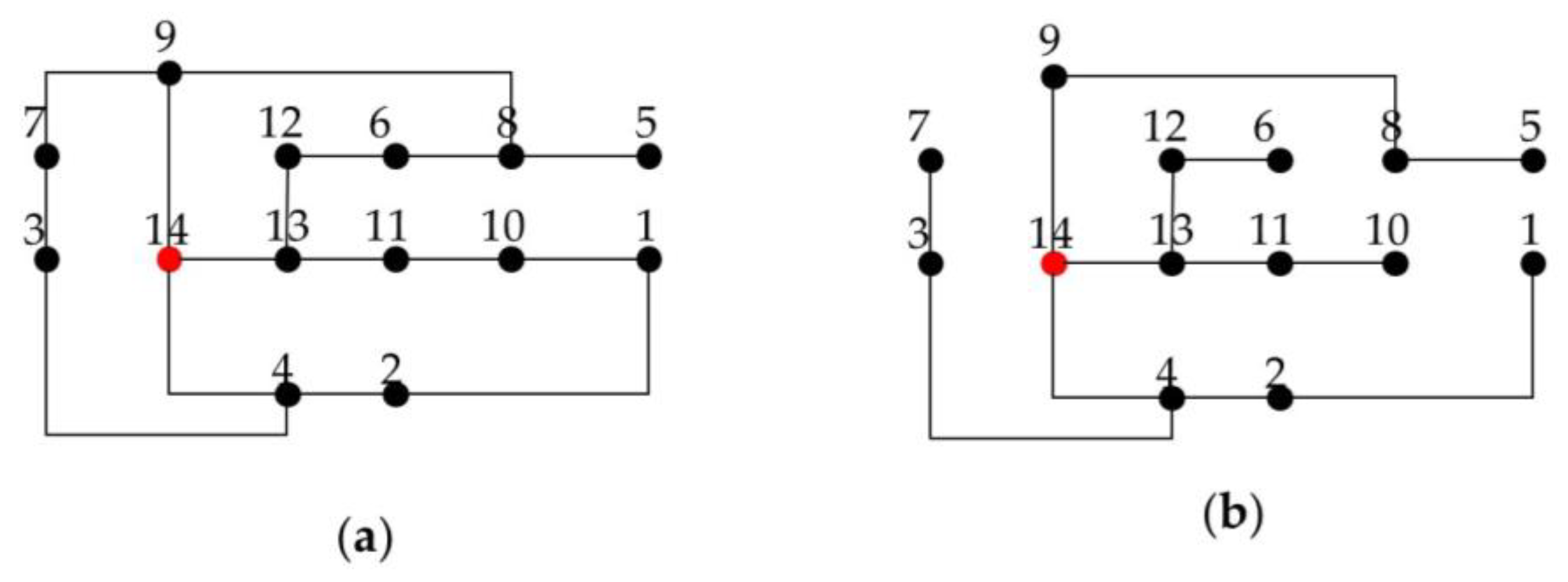
Appendix A.1. 14 Buses Instance
| Model | Optimal Tree |
|---|---|
| Base model | (14-13), (14-9), (14-4), (13-12), (13-11), (12-6), (11-10), (9-8), (8-5), (4-3), (4-2), (3-7), (2-1) |
| Model with radiality reformulated | (14-13), (14-9), (14-4), (13-12), (13-11), (12-6), (11-10), (9-8), (8-5), (4-3), (4-2), (3-7), (2-1) |
| Linearization of term | (14-13), (14-9), (14-4), (13-12), (13-11), (12-6), (11-10), (9-8), (8-5), (4-3), (4-2), (3-7), (2-1) |
| Double constraint for power triangle | (14-13), (14-9), (14-4), (13-12), (13-11), (12-6), (11-10), (9-8), (8-5), (4-3), (4-2), (3-7), (2-1) |
Appendix A.2. 33 Buses Instance
| Model | Optimal Tree |
|---|---|
| Base model | (1-2), (2-3), (2-19), (3-4), (3-23), (4-5), (5-6), (6-7), (6-26), (8-9), (9-15), (11-10), (12-11), (12-13), (13-14), (15-16), (16-17), (17-18), (18-33), (19-20), (20-21), (21-22), (21-8), (22-12), (23-24), (24-25), (26-27), (27-28), (28-29), (29-30), (30-31), (31-32) |
| Model with radiality reformulated | (1-2), (2-3), (2-19), (3-4), (3-23), (4-5), (5-6), (6-7), (6-26), (8-9), (9-15), (11-10), (12-11), (12-13), (13-14), (15-16), (16-17), (17-18), (18-33), (19-20), (20-21), (21-22), (21-8), (22-12), (23-24), (24-25), (26-27), (27-28), (28-29), (29-30), (30-31), (31-32) |
| Linearization of term | (1-2), (2-3), (2-19), (3-4), (3-23), (4-5), (5-6), (6-7), (6-26), (8-9), (9-15), (11-10), (12-11), (12-13), (13-14), (15-16), (16-17), (17-18), (18-33), (19-20), (20-21), (21-22), (21-8), (22-12), (23-24), (24-25), (26-27), (27-28), (28-29), (29-30), (30-31), (31-32) |
| Double constraint for power triangle | (1-2), (2-3), (2-19), (3-4), (3-23), (4-5), (5-6), (6-7), (6-26), (8-9), (9-15), (11-10), (12-11), (12-13), (13-14), (15-16), (16-17), (17-18), (18-33), (19-20), (20-21), (21-22), (21-8), (22-12), (23-24), (24-25), (26-27), (27-28), (28-29), (29-30), (30-31), (31-32) |
Appendix A.3. 84 Nodes Instance
| Model | Optimal Tree |
|---|---|
| Base model | (1-2), (84-1), (84-11), (84-15), (84-25), (84-30), (84-43), (84-47), (84-56), (84-65), (84-73), (84-77), (2-3), (3-4), (4-5), (5-6), (5-55), (7-8), (7-9), (7-10), (11-12), (12-14), (12-72), (15-16), (16-17), (17-18), (18-19), (19-20), (20-21), (20-83), (21-22), (21-23), (23-24), (25-26), (26-27), (27-28), (28-29), (29-39), (30-31), (31-32), (32-33), (34-35), (35-36), (36-37), (37-38), (38-41), (39-40), (40-42), (43-44), (44-45), (45-46), (46-34), (47-48), (48-49), (49-50), (50-51), (51-52), (52-53), (53-54), (53-64), (56-57), (57-58), (58-59), (59-60), (60-61), (60-7), (63-62), (64-63), (65-66), (66-67), (67-68), (68-69), (69-70), (70-71), (73-74), (74-75), (75-76), (76-13), (77-78), (78-79), (79-80), (80-81), (81-82) |
| Model with radiality reformulated | (1-2), (84-1), (84-11), (84-15), (84-25), (84-30), (84-43), (84-47), (84-56), (84-65), (84-73), (84-77), (2-3), (3-4), (4-5), (5-6), (5-55), (7-8), (7-9), (7-10), (11-12), (12-14), (12-72), (15-16), (16-17), (17-18), (18-19), (19-20), (20-21), (20-83), (21-22), (21-23), (23-24), (25-26), (26-27), (27-28), (28-29), (29-39), (30-31), (31-32), (32-33), (34-35), (35-36), (36-37), (37-38), (38-41), (39-40), (40-42), (43-44), (44-45), (45-46), (46-34), (47-48), (48-49), (49-50), (50-51), (51-52), (52-53), (53-54), (53-64), (56-57), (57-58), (58-59), (59-60), (60-61), (60-7), (63-62), (64-63), (65-66), (66-67), (67-68), (68-69), (69-70), (70-71), (73-74), (74-75), (75-76), (76-13), (77-78), (78-79), (79-80), (80-81), (81-82) |
| Linearization of term | (1-2), (84-1), (84-11), (84-15), (84-25), (84-30), (84-43), (84-47), (84-56), (84-65), (84-73), (84-77), (2-3), (3-4), (4-5), (5-6), (5-55), (7-8), (7-9), (7-10), (11-12), (12-14), (12-72), (15-16), (16-17), (17-18), (18-19), (19-20), (20-21), (20-83), (21-22), (21-23), (23-24), (25-26), (26-27), (27-28), (28-29), (29-39), (30-31), (31-32), (32-33), (34-35), (35-36), (36-37), (37-38), (38-41), (39-40), (40-42), (43-44), (44-45), (45-46), (46-34), (47-48), (48-49), (49-50), (50-51), (51-52), (52-53), (53-54), (53-64), (56-57), (57-58), (58-59), (59-60), (60-61), (60-7), (63-62), (64-63), (65-66), (66-67), (67-68), (68-69), (69-70), (70-71), (73-74), (74-75), (75-76), (76-13), (77-78), (78-79), (79-80), (80-81), (81-82) |
| Double constraint for power triangle | (1-2), (84-1), (84-11), (84-15), (84-25), (84-30), (84-43), (84-47), (84-56), (84-65), (84-73), (84-77), (2-3), (3-4), (4-5), (5-6), (5-55), (7-8), (7-9), (7-10), (11-12), (12-14), (12-72), (15-16), (16-17), (17-18), (18-19), (19-20), (20-21), (20-83), (21-22), (21-23), (23-24), (25-26), (26-27), (27-28), (28-29), (29-39), (30-31), (31-32), (32-33), (34-35), (35-36), (36-37), (37-38), (38-41), (39-40), (40-42), (43-44), (44-45), (45-46), (46-34), (47-48), (48-49), (49-50), (50-51), (51-52), (52-53), (53-54), (53-64), (56-57), (57-58), (58-59), (59-60), (60-61), (60-7), (63-62), (64-63), (65-66), (66-67), (67-68), (68-69), (69-70), (70-71), (73-74), (74-75), (75-76), (76-13), (77-78), (78-79), (79-80), (80-81), (81-82) |
Appendix A.4. 133 Nodes Instance
| Model | Optimal Tree |
|---|---|
| Base model | No feasible solution found |
| Model with radiality reformulated | (136-1), (136-17), (136-39), (136-63), (136-75), (136-85), (136-99), (136-121), (1-2), (2-3), (3-4), (4-5), (5-6), (6-8), (8-9), (8-10), (10-11), (10-12), (10-13), (13-14), (13-15), (15-16), (17-18), (18-19), (19-20), (20-21), (20-22), (22-23), (22-24), (24-25), (25-26), (25-51), (26-27), (27-28), (28-29), (28-31), (29-30), (31-32), (32-33), (33-34), (35-36), (36-37), (38-35), (39-40), (40-41), (40-42), (42-43), (43-44), (43-45), (45-46), (46-47), (47-48), (47-62), (47-110), (48-49), (49-50), (51-52), (52-53), (52-56), (53-54), (56-57), (57-58), (58-59), (59-60), (60-61), (62-120), (63-64), (64-65), (65-66), (66-67), (67-68), (68-69), (68-70), (70-71), (70-73), (71-72), (73-74), (73-7), (75-76), (76-77), (76-126), (77-78), (78-79), (79-80), (80-81), (81-82), (81-83), (83-84), (85-86), (86-87), (86-88), (88-89), (90-91), (91-92), (92-93), (93-94), (93-97), (94-95), (97-98), (98-55), (98-135), (99-100), (100-101), (101-102), (101-103), (103-104), (103-90), (104-105), (107-106), (107-108), (108-109), (108-114), (109-116), (110-107), (110-111), (111-112), (112-113), (114-115), (116-117), (119-118), (120-119), (120-96), (121-122), (122-123), (123-124), (123-125), (125-127), (127-128), (127-129), (129-130), (130-131), (131-132), (132-133), (133-134), (135-38) |
| Linearization of term | (136-1), (136-17), (136-39), (136-63), (136-75), (136-85), (136-99), (136-121), (1-2), (2-3), (3-4), (4-5), (5-6), (6-8), (8-10), (10-11), (10-12), (10-13), (13-14), (13-15), (15-16), (17-18), (18-19), (19-20), (20-21), (20-22), (22-23), (22-24), (24-25), (24-9), (25-26), (25-51), (26-27), (27-28), (28-29), (28-31), (29-30), (31-32), (31-35), (32-33), (33-34), (35-36), (36-37), (39-40), (40-41), (40-42), (42-43), (43-44), (43-45), (45-46), (46-47), (47-48), (47-62), (47-110), (48-49), (49-50), (50-96), (51-52), (52-56), (54-53), (55-54), (56-57), (57-58), (58-59), (59-60), (60-61), (62-120), (63-64), (64-65), (65-66), (66-67), (67-68), (68-69), (68-70), (70-71), (70-73), (71-72), (73-74), (73-7), (75-76), (76-77), (77-78), (78-79), (79-80), (80-81), (81-82), (81-83), (85-86), (86-87), (86-88), (88-89), (90-91), (91-92), (92-93), (93-94), (93-97), (96-95), (97-98), (98-55), (99-100), (100-101), (101-102), (101-103), (103-104), (103-90), (104-105), (104-118), (105-106), (107-108), (108-109), (108-114), (109-116), (110-107), (110-111), (111-112), (112-113), (114-115), (116-117), (120-119), (121-122), (122-123), (123-124), (123-125), (125-126), (125-127), (127-128), (127-129), (129-130), (130-131), (131-132), (132-133), (133-134), (134-135), (135-38), (135-84) |
| Double constraint for power triangle | (136-1), (136-17), (136-39), (136-63), (136-75), (136-85), (136-99), (136-121), (1-2), (2-3), (3-4), (4-5), (5-6), (6-8), (8-9), (8-10), (10-11), (10-12), (10-13), (13-14), (13-15), (15-16), (17-18), (18-19), (19-20), (20-21), (20-22), (22-23), (22-24), (24-25), (25-26), (25-51), (26-27), (27-28), (28-29), (28-31), (29-30), (31-32), (32-33), (33-34), (35-36), (36-37), (38-35), (39-40), (40-41), (40-42), (42-43), (43-44), (43-45), (45-46), (46-47), (47-48), (47-62), (47-110), (48-49), (49-50), (51-52), (52-53), (52-56), (53-54), (56-57), (57-58), (58-59), (59-60), (60-61), (62-120), (63-64), (64-65), (65-66), (66-67), (67-68), (68-69), (68-70), (70-71), (70-73), (71-72), (73-74), (73-7), (75-76), (76-77), (76-126), (77-78), (78-79), (79-80), (80-81), (81-82), (81-83), (83-84), (85-86), (86-87), (86-88), (88-89), (90-91), (91-92), (92-93), (93-94), (93-97), (94-95), (97-98), (98-55), (98-135), (99-100), (100-101), (101-102), (101-103), (103-104), (103-90), (104-105), (107-106), (107-108), (108-109), (108-114), (109-116), (110-107), (110-111), (111-112), (112-113), (114-115), (116-117), (119-118), (120-119), (120-96), (121-122), (122-123), (123-124), (123-125), (125-127), (127-128), (127-129), (129-130), (130-131), (131-132), (132-133), (133-134), (135-38) |
Appendix A.5. 417 Buses Instance
| Model | Optimal Tree |
|---|---|
| Base Model | No Feasible Solution Found |
| Model with radiality reformulated | (68-93), (68-67), (89-88), (67-89), (67-64), (225-224), (224-222), (21-47), (21-50), (21-49), (21-57), (72-21), (72-74), (66-252), (3-20), (3-9), (20-44), (20-33), (222-221), (74-75), (382-70), (382-66), (51-52), (221-344), (52-56), (220-223), (75-81), (81-76), (59-77), (56-27), (1-273), (1-274), (1-123), (1-92), (1-351), (1-350), (1-211), (1-215), (1-190), (1-373), (1-362), (1-364), (85-68), (27-31), (274-275), (31-40), (275-276), (73-72), (73-80), (60-61), (58-60), (209-208), (209-210), (80-82), (65-69), (71-65), (47-34), (276-264), (77-73), (69-59), (54-51), (264-263), (24-54), (263-262), (79-78), (83-79), (63-71), (61-63), (29-24), (262-261), (34-29), (261-259), (259-257), (90-83), (62-58), (257-254), (257-258), (64-62), (44-32), (372-239), (239-240), (239-243), (123-120), (265-339), (265-367), (120-94), (94-113), (94-111), (94-119), (94-98), (35-25), (369-347), (369-370), (38-35), (370-348), (370-383), (370-90), (92-2), (92-87), (41-38), (112-115), (2-17), (2-14), (2-13), (43-41), (383-382), (113-114), (48-43), (17-18), (50-48), (50-46), (208-277), (208-236), (277-278), (277-279), (106-95), (95-112), (6-7), (7-3), (33-55), (33-22), (84-104), (84-109), (84-107), (279-280), (111-106), (18-5), (5-6), (28-36), (36-45), (280-281), (119-121), (119-122), (119-200), (49-39), (235-234), (14-16), (55-23), (23-28), (282-283), (234-282), (234-233), (122-118), (236-235), (16-19), (19-8), (104-105), (232-293), (207-349), (13-4), (42-37), (380-229), (229-228), (109-108), (4-12), (12-15), (46-42), (228-371), (15-11), (231-232), (11-86), (11-10), (103-110), (107-103), (86-91), (53-26), (22-53), (304-378), (304-303), (304-311), (306-304), (97-117), (116-97), (26-30), (378-377), (99-84), (101-100), (96-101), (309-314), (307-309), (307-312), (100-102), (314-317), (314-318), (317-313), (102-99), (187-167) (167-175), (318-319), (138-194), (138-149), (117-96), (175-181), (301-305), (301-302), (305-310), (305-308), (155-138), (151-155), (151-152), (181-160), (181-178), (310-315), (310-306), (310-320), (124-126), (124-158), (98-116), (160-180), (180-177), (180-174), (351-379), (129-141), (129-154), (129-151), (346-129), (350-203), (162-169), (203-204), (203-206), (153-132), (141-153), (141-130), (183-162), (379-380), (142-147), (182-183), (182-186), (204-205), (136-142), (243-384), (243-355), (243-356), (243-246), (243-249), (132-136), (244-85), (206-207), (163-171), (352-414), (352-212), (352-353), (414-385), (414-401), (184-163), (184-187), (125-128), (401-386), (401-402), (375-202), (127-124), (128-127), (128-125), (131-157), (157-133), (402-387), (402-403), (130-131), (211-209), (200-201), (403-388), (403-404), (133-140), (202-375), (404-400), (404-405), (404-407), (368-345), (368-343), (345-346), (345-369), (373-352), (199-192), (199-197), (154-156), (154-134), (197-191), (137-144), (144-148), (353-213), (353-214), (159-199), (159-161), (159-182), (159-184), (148-150), (156-137), (405-389), (405-406), (190-159), (190-189), (215-216), (161-172), (161-185), (150-143), (406-390), (406-391), (216-217), (216-218), (172-188), (188-168), (134-139), (218-219), (168-176), (407-392), (407-408), (219-220), (176-179), (408-409), (408-410), (223-237), (185-164), (409-393), (409-394), (237-238), (237-372), (164-165), (145-146), (165-173), (152-135), (135-145), (135-195), (410-415), (410-411), (411-395), (411-412), (355-354), (354-242), (354-241), (186-166), (412-399), (412-398), (412-413), (166-170), (189-198), (189-193), (198-196), (356-357), (413-397), (413-396), (357-244), (357-245), (290-292), (290-291), (289-290), (246-247), (247-248), (266-265), (266-324), (288-289), (267-266), (300-288), (300-286), (300-301), (300-307), (249-358), (268-267), (268-327), (268-297), (358-359), (269-268), (359-250), (365-269), (365-366), (285-300), (366-270), (366-271), (360-251), (363-365), (363-381), (253-360), (362-363), (362-272), (254-253), (254-361), (254-255), (361-256), (296-260), (296-299), (296-298), (260-287), (312-316), (364-284), (364-285), (324-326), (324-325), (334-336), (334-335), (336-323), (327-328), (338-337), (322-329), (233-376), (297-296), (339-338), (321-322), (376-230), (299-321), (230-231), (367-340), (340-341), (329-330), (329-333), (371-374), (294-295), (341-342), (341-368), (330-331), (374-227), (374-226), (292-294), (331-332), (226-225), (333-334) |
| Linearization of term | (384-68), (68-93), (68-67), (89-88), (67-89), (67-64), (225-224), (224-222), (21-47), (21-50), (72-21), (72-74), (72-76), (3-20), (20-51), (20-44), (222-221), (74-75), (70-59), (382-70), (51-52), (51-54), (221-344), (76-81), (52-56), (220-223), (59-69), (56-27), (1-273), (1-274), (1-123), (1-92), (1-351), (1-350), (1-375), (1-211), (1-215), (1-190), (1-373), (1-362), (1-364), (274-275), (275-276), (73-72), (73-80), (60-58), (40-31), (209-208), (209-210), (80-82), (65-71), (71-63), (47-40), (276-264), (77-73), (69-65), (54-24), (264-263), (264-265), (78-77), (24-29), (263-262), (79-78), (83-79), (63-61), (61-60), (29-34), (262-261), (261-259), (90-83), (257-254), (257-258), (64-62), (44-25), (44-32), (372-239), (239-240), (239-243), (123-120), (25-35), (265-339), (265-367), (120-94), (94-113), (94-111), (94-119), (94-98), (35-38), (369-347), (369-370), (38-41), (370-348), (370-90), (114-115), (115-112), (92-2), (92-87), (2-17), (2-14), (2-13), (383-382), (251-383), (251-359), (251-252), (113-114), (48-43), (17-18), (50-48), (50-46), (208-277), (208-236), (277-278), (277-279), (106-95), (6-7), (33-55), (33-22), (84-33), (84-104), (84-109), (84-110), (84-107), (279-280), (111-106), (18-5), (5-6), (28-36), (36-45), (280-281), (45-49), (119-121), (119-122), (119-200), (49-39), (235-234), (14-16), (55-23), (23-28), (282-283), (118-84), (8-9), (9-3), (234-282), (122-118), (236-235), (16-19), (19-8), (104-105), (32-37), (232-231), (232-293), (349-232), (37-42), (207-349), (13-4), (380-229), (229-228), (109-108), (4-12), (12-15), (228-371), (15-11), (231-230), (110-103), (11-86), (86-91), (53-26), (22-53), (304-378), (97-117), (116-97), (26-30), (378-377), (101-100), (96-101), (88-10), (309-314), (309-313), (307-309), (307-312), (100-102), (57-147), (57-149), (57-148), (314-318), (314-310), (317-319), (102-99), (187-167), (167-175), (318-315), (138-194), (117-96), (175-181), (301-305), (301-302), (305-304), (151-155), (151-152), (181-178), (310-306), (310-320), (315-311), (124-126), (124-127), (98-116), (160-129), (180-160), (180-177), (351-379), (129-141), (129-154), (129-151), (350-203), (147-140), (162-169), (203-204), (203-206), (153-132), (141-153), (141-130), (183-162), (379-380), (182-183), (182-186), (252-66), (204-205), (136-142), (243-384), (243-355), (243-356), (243-246), (243-249), (132-136), (244-85), (206-207), (163-171), (352-414), (352-212), (352-353), (414-385), (414-401), (149-146), (149-138), (184-163), (184-187), (125-57), (401-386), (401-402), (375-202), (127-128), (128-125), (131-157), (157-133), (402-387), (402-403), (130-131), (211-209), (200-201), (200-158), (403-388), (403-404), (158-124), (404-400), (404-405), (404-407), (368-345), (368-343), (345-346), (345-369), (373-352), (199-192), (199-197), (154-156), (154-134), (197-191), (137-144), (353-213), (353-214), (159-199), (159-161), (159-182), (159-184), (148-150), (156-137), (405-389), (405-406), (190-159), (190-189), (215-216), (161-172), (161-185), (150-143), (406-390), (406-391), (216-217), (216-218), (172-188), (188-168), (134-139), (218-219), (168-176), (407-392), (407-408), (219-220), (176-179), (179-173), (408-409), (408-410), (223-237), (185-164), (409-393), (409-394), (237-238), (237-372), (164-165), (152-135), (135-145), (135-195), (410-415), (410-411), (411-395), (411-412), (355-354), (354-242), (354-241), (186-166), (412-399), (412-398), (412-413), (166-170), (189-198), (189-193), (170-174), (198-196), (356-357), (174-180), (413-397), (413-396), (357-244), (357-245), (290-291), (289-290), (246-247), (247-248), (266-324), (288-289), (267-266), (300-288), (300-286), (300-301), (300-307), (268-267), (268-327), (268-297), (268-292), (269-268), (359-358), (359-250), (365-269), (365-366), (285-300), (313-317), (366-270), (366-271), (302-303), (360-251), (363-365), (363-381), (253-360), (362-363), (362-272), (254-253), (254-361), (254-255), (361-256), (316-308), (296-260), (296-299), (296-298), (260-287), (312-316), (364-284), (364-285), (324-326), (324-325), (324-323), (334-335), (283-257), (323-336), (327-328), (338-337), (322-329), (297-296), (339-338), (321-322), (376-233), (299-321), (230-376), (367-340), (340-341), (329-330), (329-333), (371-374), (294-295), (341-342), (341-368), (330-331), (374-227), (374-226), (292-294), (331-332), (226-225), (333-334) |
| Double constraint for power triangle | (384-68), (384-66), (68-93), (68-67), (89-88), (67-89), (67-64), (225-224), (224-222), (21-47), (21-50), (72-21), (72-74), (72-76), (3-20), (20-51), (20-44), (222-221), (74-75), (70-59), (382-70), (51-52), (51-54), (221-344), (76-81), (52-56), (220-223), (59-69), (56-27), (1-273), (1-274), (1-123), (1-92), (1-351), (1-350), (1-375), (1-211), (1-215), (1-190), (1-373), (1-362), (1-364), (274-275), (275-276), (73-72), (73-80), (60-58), (40-31), (209-208), (209-210), (80-82), (65-71), (71-63), (47-40), (276-264), (77-73), (69-65), (54-24), (264-263), (264-265), (78-77), (24-29), (263-262), (79-78), (83-79), (63-61), (61-60), (29-34), (262-261), (90-83), (257-259), (257-254), (257-258), (64-62), (44-25), (44-32), (372-239), (239-240), (239-243), (123-120), (25-35), (265-339), (265-367), (120-94), (94-113), (94-111), (94-119), (94-98), (35-38), (369-347), (369-370), (38-41), (370-348), (370-90), (114-115), (115-112), (92-2), (92-87), (2-17), (2-14), (2-13), (383-382), (251-383), (251-359), (251-252), (113-114), (48-43), (17-18), (50-48), (50-46), (208-277), (208-236), (277-278), (277-279), (106-95), (6-7), (33-55), (33-22), (84-33), (84-104), (84-109), (84-110), (84-107), (279-280), (111-106), (18-5), (5-6), (28-36), (36-45), (280-281), (45-49), (119-121), (119-122), (119-200), (235-234), (14-16), (55-23), (23-28), (282-283), (118-84), (8-9), (9-3), (234-282), (122-118), (236-235), (16-19), (19-8), (104-105), (32-37), (232-231), (232-293), (349-232), (37-42), (207-349), (13-4), (380-229), (229-228), (109-108), (4-12), (12-15), (228-371), (15-11), (231-230), (110-103), (11-86), (30-39), (86-91), (53-26), (22-53), (304-378), (97-117), (116-97), (26-30), (378-377), (101-100), (96-101), (88-10), (309-314), (309-313), (307-309), (307-312), (100-102), (57-149), (57-148), (314-318), (314-310), (317-319), (102-99), (187-167), (167-175), (318-315), (138-194), (117-96), (175-181), (301-305), (301-302), (305-304), (305-308), (151-155), (151-152), (181-178), (310-306), (310-320), (315-311), (124-126), (124-127), (98-116), (160-129), (160-179), (180-160), (180-177), (351-379), (129-141), (129-154), (129-151), (350-203), (162-169), (203-204), (203-206), (153-132), (141-153), (141-130), (183-162), (379-380), (142-147), (182-183), (182-186), (204-205), (136-142), (243-384), (243-355), (243-356), (243-246), (243-249), (132-136), (244-85), (206-207), (163-171), (352-414), (352-212), (352-353), (414-385), (414-401), (149-146), (149-138), (184-163), (184-187), (125-57), (401-386), (401-402), (375-202), (127-128), (128-125), (131-157), (157-133), (402-387), (402-403), (130-131), (211-209), (200-201), (200-158), (403-388), (403-404), (133-140), (158-124), (404-400), (404-405), (404-407), (368-345), (368-343), (345-346), (345-369), (373-352), (199-192), (199-197), (154-156), (154-134), (197-191), (137-144), (353-213), (353-214), (159-199), (159-161), (159-182), (159-184), (148-150), (156-137), (405-389), (405-406), (190-159), (190-189), (215-216), (161-172), (161-185), (150-143), (406-390), (406-391), (216-217), (216-218), (172-188), (188-168), (134-139), (218-219), (168-176), (407-392), (407-408), (219-220), (408-409), (408-410), (223-237), (185-164), (409-393), (409-394), (237-238), (237-372), (164-165), (165-173), (152-135), (135-145), (135-195), (410-415), (410-411), (411-395), (411-412), (355-354), (354-242), (354-241), (186-166), (412-399), (412-398), (412-413), (166-170), (189-198), (189-193), (170-174), (198-196), (356-357), (174-180), (413-397), (413-396), (357-244), (357-245), (290-291), (289-290), (246-247), (247-248), (266-324), (288-289), (267-266), (300-288), (300-286), (300-301), (300-307), (268-267), (268-327), (268-297), (268-292), (269-268), (359-358), (359-250), (365-269), (365-366), (285-300), (313-317), (366-270), (366-271), (302-303), (360-251), (363-365), (363-381), (253-360), (362-363), (362-272), (254-253), (254-361), (254-255), (308-316), (361-256), (296-260), (296-299), (296-298), (260-287), (364-284), (364-285), (324-326), (324-325), (324-323), (334-335), (283-257), (323-336), (327-328), (338-337), (322-329), (297-296), (339-338), (321-322), (376-233), (299-321), (230-376), (367-340), (340-341), (329-330), (329-333), (371-374), (294-295), (341-342), (341-368), (330-331), (374-227), (374-226), (292-294), (331-332), (226-225), (333-334) |
| Optimal tree | (384-68), (68-93), (68-67), (89-88), (67-89), (67-64), (225-224), (224-222), (21-47), (21-50), (72-21), (72-74), (72-76), (3-20), (20-51), (20-44), (222-221), (74-75), (70-59), (382-70), (51-52), (51-54), (221-344), (76-81), (52-56), (220-223), (59-69), (56-27), (1-273), (1-274), (1-123), (1-92), (1-351), (1-350), (1-375), (1-211), (1-215), (1-190), (1-373), (1-362), (1-364), (274-275), (275-276), (73-72), (73-80), (60-58), (40-31), (209-208), (209-210), (80-82), (65-71), (71-63), (47-40), (276-264), (77-73), (69-65), (54-24), (264-263), (264-265), (78-77), (24-29), (263-262), (79-78), (83-79), (63-61), (61-60), (29-34), (262-261), (90-83), (257-259), (257-254), (257-258), (64-62), (44-25), (44-32), (372-239), (239-240), (239-243), (123-120), (25-35), (265-339), (265-367), (120-94), (94-113), (94-111), (94-119), (94-98), (35-38), (369-347), (369-370), (38-41), (370-348), (370-90), (114-115), (115-112), (92-2), (92-87), (41-43), (2-17), (2-14), (2-13), (383-382), (251-383), (251-359), (251-252), (113-114), (17-18), (50-48), (50-46), (208-277), (208-236), (277-278), (277-279), (106-95), (6-7), (33-55), (33-22), (84-33), (84-104), (84-109), (84-110), (84-107), (279-280), (111-106), (18-5), (5-6), (28-36), (36-45), (280-281), (45-49), (119-121), (119-122), (119-200), (235-234), (14-16), (55-23), (23-28), (282-283), (118-84), (8-9), (9-3), (234-282), (122-118), (236-235), (16-19), (19-8), (104-105), (32-37), (232-231), (232-293), (349-232), (37-42), (207-349), (13-4), (380-229), (229-228), (109-108), (4-12), (12-15), (228-371), (231-230), (110-103), (11-86), (30-39), (86-91), (53-26), (22-53), (304-306), (304-378), (97-117), (116-97), (10-11), (26-30), (378-377), (101-100), (96-101), (88-10), (309-314), (309-313), (307-309), (307-312), (100-102), (57-147), (57-149), (57-148), (314-318), (314-310), (317-319), (102-99), (187-167), (167-175), (318-315), (138-194), (117-96), (175-181), (301-305), (301-302), (305-304), (155-138), (151-155), (151-152), (181-178), (310-320), (315-311), (124-126), (124-127), (98-116), (160-129), (180-160), (180-177), (351-379), (129-141), (129-154), (129-151), (350-203), (147-140), (162-169), (203-204), (203-206), (153-132), (141-153), (141-130), (183-162), (379-380), (182-183), (182-186), (252-66), (204-205), (136-142), (243-384), (243-355), (243-356), (243-246), (132-136), (244-85), (206-207), (163-171), (352-414), (352-212), (352-353), (414-385), (414-401), (149-146), (184-163), (184-187), (125-57), (401-386), (401-402), (375-202), (127-128), (128-125), (131-157), (157-133), (402-387), (402-403), (130-131), (211-209), (200-201), (200-158), (403-388), (403-404), (158-124), (404-400), (404-405), (404-407), (368-345), (368-343), (345-346), (345-369), (373-352), (199-192), (199-197), (154-156), (154-134), (197-191), (137-144), (353-213), (353-214), (159-199), (159-161), (159-182), (159-184), (148-150), (156-137), (405-389), (405-406), (190-159), (190-189), (215-216), (161-172), (161-185), (150-143), (406-390), (406-391), (216-217), (216-218), (172-188), (188-168), (134-139), (218-219), (168-176), (407-392), (407-408), (219-220), (176-179), (179-173), (408-409), (408-410), (223-237), (185-164), (409-393), (409-394), (237-238), (237-372), (164-165), (146-145), (152-135), (135-195), (410-415), (410-411), (411-395), (411-412), (355-354), (354-242), (354-241), (186-166), (412-399), (412-398), (412-413), (166-170), (189-198), (189-193), (170-174), (198-196), (356-357), (174-180), (413-397), (413-396), (357-244), (357-245), (290-291), (289-290), (246-247), (247-248), (266-324), (288-289), (267-266), (300-288), (300-286), (300-301), (300-307), (268-267), (268-327), (268-297), (268-292), (358-249), (269-268), (359-358), (359-250), (365-269), (365-366), (285-300), (313-317), (366-270), (366-271), (302-303), (360-251), (363-365), (363-381), (253-360), (362-363), (362-272), (254-253), (254-361), (254-255), (361-256), (316-308), (296-260), (296-299), (296-298), (260-287), (312-316), (364-284), (364-285), (324-326), (324-325), (324-323), (334-335), (283-257), (323-336), (327-328), (338-337), (322-329), (297-296), (339-338), (321-322), (376-233), (299-321), (230-376), (367-340), (340-341), (329-330), (329-333), (371-374), (294-295), (341-342), (341-368), (330-331), (374-227), (374-226), (292-294), (331-332), (226-225), (333-334) |
References
- Baran, E.; Wu, F.F. Network Reconfiguration in Distribution Systems for Loss Reduction and Load Balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Pareja, L.A.G.; López-Lezama, J.M.; Carmona, O.G. A Mixed-Integer Linear Programming Model for the Simultaneous Optimal Distribution Network Reconfiguration and Optimal Placement of Distributed Generation. Energies 2022, 15, 3063. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, F.; Zhou, X.; Gao, Z. Overview on algorithms of distribution network reconfiguration. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 10657–10661. [Google Scholar] [CrossRef]
- Borges, M.C.O.; Franco, J.F.; Rider, M.J. Optimal reconfiguration of electrical distribution systems using mathematical programming. J. Control Autom. Electr. Syst. 2014, 25, 103–111. [Google Scholar] [CrossRef]
- Merlin, A.; Back, H. Search for a minimal-loss operating spanning tree configuration in an urban power distribution system. In Proceedings of the Fifth Power Systems Computation Conference, Cambridge, UK, 1–5 September 1975. [Google Scholar]
- Sarfi, R.J.; Salama, M.M.A.; Chikhani, A.Y. A survey of the state of the art in distribution system reconfiguration for system loss reduction. Electr. Power Syst. Res. 1994, 31, 61–70. [Google Scholar] [CrossRef]
- Jabr, R.A.; Singh, R.; Pal, B.C. Minimum loss network reconfiguration using mixed-integer convex programming. IEEE Trans. Power Syst. 2012, 27, 1106–1115. [Google Scholar] [CrossRef]
- Mahdavi, M.; Alhelou, H.H.; Hatziargyriou, N.D.; Jurado, F. Reconfiguration of Electric Power Distribution Systems: Comprehensive Review and Classification. IEEE Access 2021, 9, 118502–118527. [Google Scholar] [CrossRef]
- Möller, M.; Vuik, C. On the impact of quantum computing technology on future developments in high-performance scientific computing. Ethic-Inf. Technol. 2017, 19, 253–269. [Google Scholar] [CrossRef]
- Mahdavi, M.; Alhelou, H.H.; Bagheri, A.; Djokic, S.Z.; Ramos, R.A.V. A Comprehensive Review of Metaheuristic Methods for the Reconfiguration of Electric Power Distribution Systems and Comparison with a Novel Approach Based on Efficient Genetic Algorithm. IEEE Access 2021, 9, 122872–122906. [Google Scholar] [CrossRef]
- Behbahani, M.R.; Jalilian, A.; Bahmanyar, A.; Ernst, D. Comprehensive Review on Static and Dynamic Distribution Network Reconfiguration Methodologies. IEEE Access 2024, 12, 9510–9525. [Google Scholar] [CrossRef]
- Liu, C.-C.; Lee, S.J.; Vu, K. Loss Minimization of Distribution Feeders: Optimality and Algorithms. IEEE Trans. Power Deliv. 1989, 4, 1281–1289. [Google Scholar] [CrossRef]
- Ramos, E.R.; Expósito, A.G.; Santos, J.R.; Iborra, F.L. Path-based distribution network modeling: Application to reconfiguration for loss reduction. IEEE Trans. Power Syst. 2005, 20, 556–564. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing radiality constraints in distribution system optimization problems. IEEE Trans. Power Syst. 2012, 27, 172–180. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Morales-Duran, J.C.; Velez-Garcia, S.; Montoya, O.D.; Gil-González, W. Power flow methods used in AC distribution networks: An analysis of convergence and processing times in radial and meshed grid configurations. Results Eng. 2023, 17, 100915. [Google Scholar] [CrossRef]
- Huddleston, C.T.; Broadwatert, R.P.; Chandrasekaran, A. Reconfiguration Algorithm for Minimizing Losses in Radial Electric Distribution Systems. Electr. Power Syst. Res. 1990, 18, 57–66. [Google Scholar] [CrossRef]
- Departamento de Engenharia Elétrica. [Online]. Available online: https://www.feis.unesp.br/#!/departamentos/engenharia-eletrica/pesquisas-e-projetos/lapsee/downloads/materiais-de-cursos1193/ (accessed on 12 November 2023).
- Jacob, R.A.; Paul, S.; Li, W.; Chowdhury, S.; Gel, Y.R.; Zhang, J. Reconfiguring Unbalanced Distribution Networks using Reinforcement Learning over Graphs. In Proceedings of the 2022 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 28 February–1 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Khamees, A.K.; Abdelaziz, A.Y.; Eskaros, M.R.; Attia, M.A.; Badr, A.O. The Mixture of Probability Distribution Functions for Wind and Photovoltaic Power Systems Using a Metaheuristic Method. Processes 2022, 10, 2446. [Google Scholar] [CrossRef]
| # of Bus Bars | # of Switches | Ref. Node | Base Voltage (kV) | Base Apparent Power (MVA) |
|---|---|---|---|---|
| 14 | 16 | 14 | 23 | 100 |
| 33 | 74 | 1 | 12.66 | 10 |
| 84 | 192 | 84 | 11.4 | 10 |
| 136 | 312 | 1 | 13.8 | 100 |
| 417 | 473 | 1 | 10 | 100 |
| Ins | Base Model | Model with Radiality Modified | Model with a Simplification of the Term | Double Power Triangle Constraint | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TT | PPA | GO | TT | PPA | GO | TT | PPA | GO | OF | %ER | TT | PPA | GO | |
| 14 | 0.509 | 605.9 | 0 | 0.8642 | 605.9 | 0 | 0.4471 | 605.7 | 0 | 577.7 | 4.62 | 0.4991 | 605.9 | 0 |
| 33 | 1.735 | 139.4 | 0 | 1.1662 | 139.4 | 0 | 1.0551 | 139.2 | 0 | 131.8 | 5.31 | 1.0024 | 139.4 | 0 |
| 84 | 8.0939 | 469.3 | 0 | 3.0809 | 469.3 | 0 | 2.7497 | 468.6 | 0 | 447.4 | 4.52 | 3.7231 | 469.3 | 0 |
| 133 | 3601.85 ** | NSF | NSF | 82.785 | 279.6 | 0 | 8.0224 | 287.9 | 0 | 265.8 | 6.7 | 32.702 | 279.6 | 0 |
| 417 | 3606.13 ** | NSF | NSF | 3606.6 ** | 1653 *** | 68.5 | 3606.3 ** | 581.5 *** | 2.55 | 565.0 | 2.8 | 3606.8 | 582.5 | 3.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cortés Sanabria, P.J.; Tabares Pozos, A.; Álvarez-Martínez, D.; Noriega Barbosa, D.A. An Innovative Approach to Radiality Representation in Electrical Distribution System Reconfiguration: Enhanced Efficiency and Computational Performance. Energies 2024, 17, 2633. https://doi.org/10.3390/en17112633
Cortés Sanabria PJ, Tabares Pozos A, Álvarez-Martínez D, Noriega Barbosa DA. An Innovative Approach to Radiality Representation in Electrical Distribution System Reconfiguration: Enhanced Efficiency and Computational Performance. Energies. 2024; 17(11):2633. https://doi.org/10.3390/en17112633
Chicago/Turabian StyleCortés Sanabria, Pablo José, Alejandra Tabares Pozos, David Álvarez-Martínez, and Diego Alejandro Noriega Barbosa. 2024. "An Innovative Approach to Radiality Representation in Electrical Distribution System Reconfiguration: Enhanced Efficiency and Computational Performance" Energies 17, no. 11: 2633. https://doi.org/10.3390/en17112633
APA StyleCortés Sanabria, P. J., Tabares Pozos, A., Álvarez-Martínez, D., & Noriega Barbosa, D. A. (2024). An Innovative Approach to Radiality Representation in Electrical Distribution System Reconfiguration: Enhanced Efficiency and Computational Performance. Energies, 17(11), 2633. https://doi.org/10.3390/en17112633






