Modeling Wind-Speed Statistics beyond the Weibull Distribution
Abstract
1. Introduction: What Is the Model Underlying Wind-Speed Distributions?
2. Models, Methods, and Data
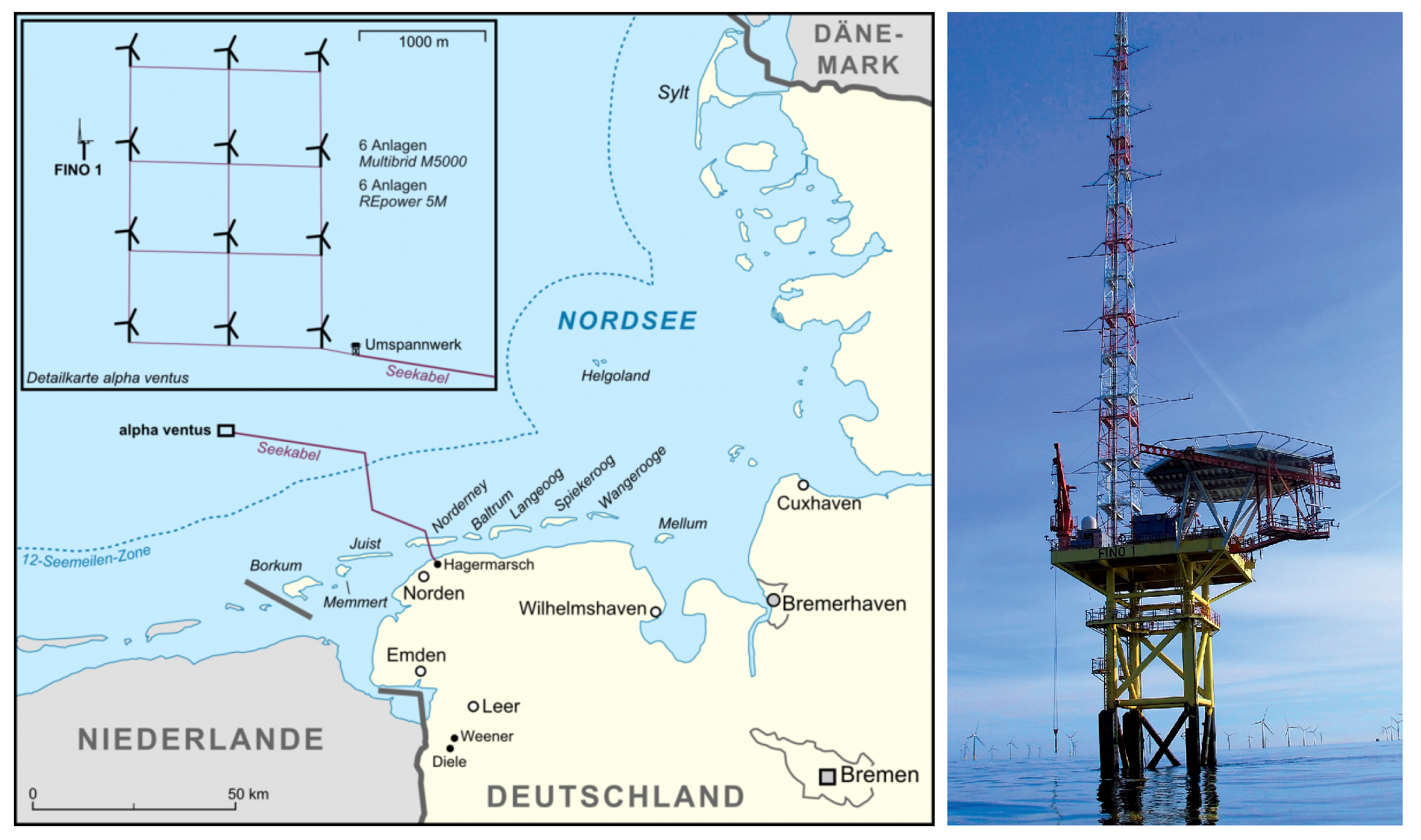
2.1. Wind Data Measured at FINO-1 Tower at the North Sea
2.2. The Weibull Distribution as a Model for Wind-Speed Measurements and Some of Its “Cousins”
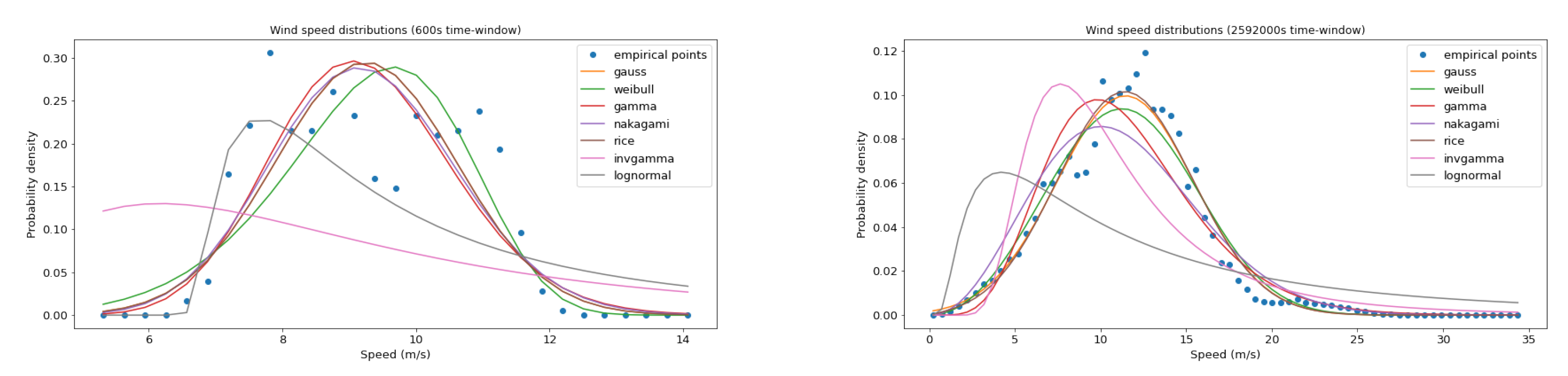
2.3. Performance Measures: Evaluating the Fitness of Each Model
- (I)
- How well does each model enable one to predict the next value of the wind speed?
- (II)
- How well does each distribution model fit the empirical histogram of measurements?
- (III)
- How well does each model enable one to predict the energy associated with the wind speed, i.e., the square of the wind speed?
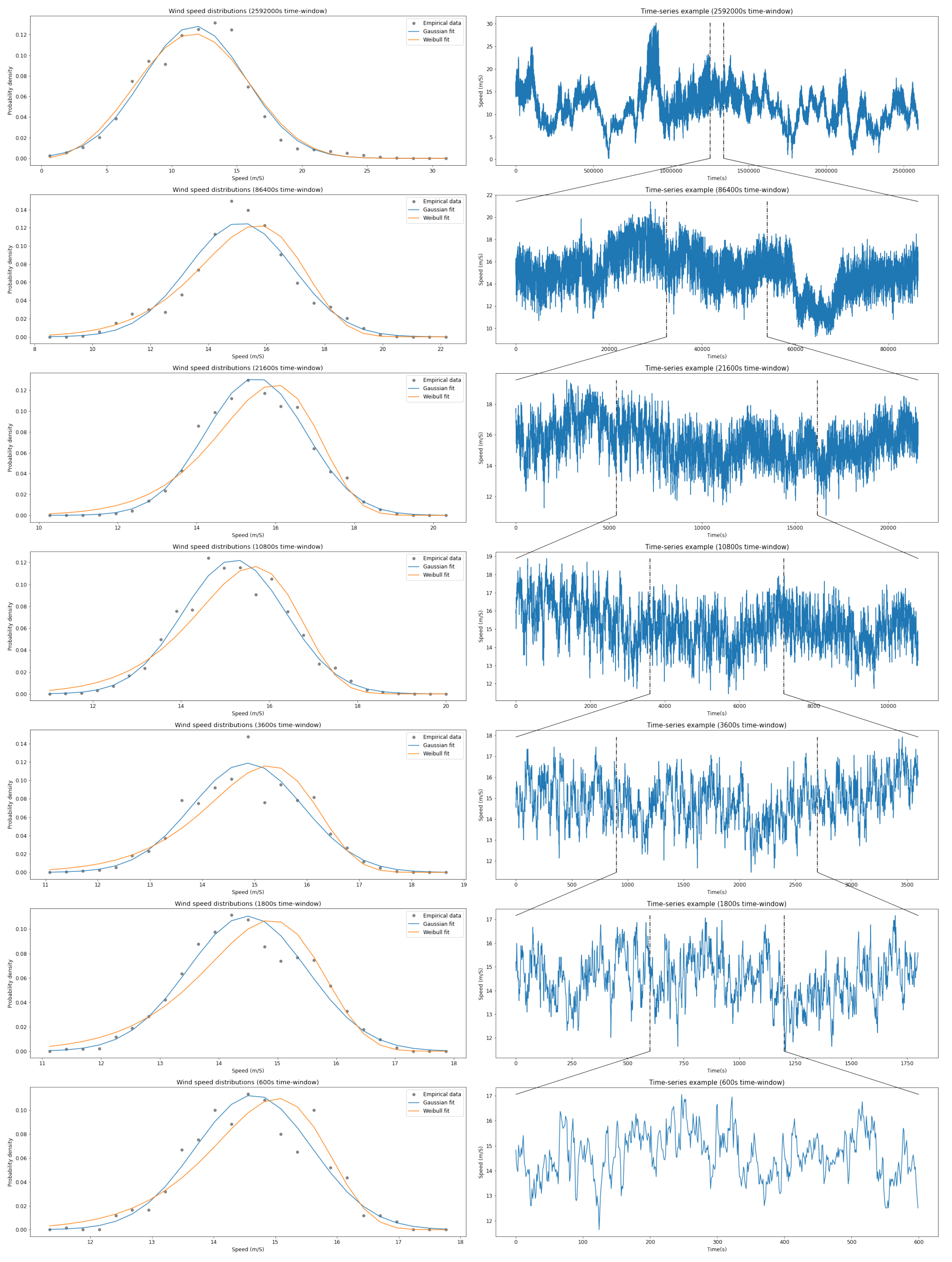
3. Results: Turbulence Features, Wind-Speed Statistics, and Prediction of Speed and Energy
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tuller, S.E.; Brett, A.C. The characteristics of wind velocity that favor the fitting of a Weibull distribution in wind speed analysis. J. Appl. Meteorol. Climatol. 1984, 23, 124–134. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Global comparison of the goodness-of-fit of wind speed distributions. Energy Convers. Manag. 2017, 133, 216–234. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Wind speed distribution selection—A review of recent development and progress. Renew. Sustain. Energy Rev. 2019, 114, 109290. [Google Scholar] [CrossRef]
- Akgül, F.G.; Şenoğlu, B.; Arslan, T. An alternative distribution to Weibull for modeling the wind speed data: Inverse Weibull distribution. Energy Convers. Manag. 2016, 114, 234–240. [Google Scholar] [CrossRef]
- Ouahabi, M.H.; Benabdelouahab, F.; Khamlichi, A. Analyzing wind speed data and wind power density of Tetouan city in Morocco by adjustment to Weibull and Rayleigh distribution functions. Wind Eng. 2017, 41, 174–184. [Google Scholar] [CrossRef]
- Serban, A.; Paraschiv, L.S.; Paraschiv, S. Assessment of wind energy potential based on Weibull and Rayleigh distribution models. Energy Rep. 2020, 6, 250–267. [Google Scholar] [CrossRef]
- Rocha, P.; Raischel, F.; Boto, J.; Lind, P. Uncovering the evolution of non-stationary stochastic variables: The example of asset volume-price fluctuations. Phys. Rev. E 2016, 93, 052122. [Google Scholar] [CrossRef] [PubMed]
- Inglesi-Lotz, R.; Dogan, E. The role of renewable versus non-renewable energy to the level of CO2 emissions a panel analysis of sub-Saharan Africa’s Big 10 electricity generators. Renew. Energy 2018, 123, 36–43. [Google Scholar] [CrossRef]
- Furlan, C.; Mortarino, C. Forecasting the impact of renewable energies in competition with non-renewable sources. Renew. Sustain. Energy Rev. 2018, 81, 1879–1886. [Google Scholar] [CrossRef]
- Milan, P.; Wächter, M.; Peinke, J. Stochastic modeling and performance monitoring of wind farm power production. J. Renew. Sustain. Energy 2014, 6, 033119. [Google Scholar] [CrossRef]
- Milan, P.; Wächter, M.; Peinke, J. Turbulent Character of Wind Energy. Phys. Rev. Lett. 2013, 110, 138701. [Google Scholar] [CrossRef] [PubMed]
- Raischel, F.; Scholz, T.; Lopes, V.; Lind, P. Uncovering wind turbine properties through two-dimensional stochastic modeling of wind dynamics. Phys. Rev. E 2013, 88, 042146. [Google Scholar] [CrossRef]
- Hansen, K.; Mathiesen, B.V.; Skov, I.R. Full energy system transition towards 100% renewable energy in Germany in 2050. Renew. Sustain. Energy Rev. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Akermi, R.; Triki, A. The green energy transition and civil society in Tunisia: Actions, motivations and barriers. Energy Procedia 2017, 136, 79–84. [Google Scholar] [CrossRef]
- Zafar, U.; Rashid, T.U.; Khosa, A.A.; Khalil, M.S.; Rashid, M. An overview of implemented renewable energy policy of Pakistan. Renew. Sustain. Energy Rev. 2018, 82, 654–665. [Google Scholar] [CrossRef]
- Cadoret, I.; Padovano, F. The political drivers of renewable energies policies. Energy Econ. 2016, 56, 261–269. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Technology-specific Cost and Performance Parameters. In Climate Change 2014: Mitigation of Climate Change: Working Group III Contribution to the IPCC Fifth Assessment Report; Cambridge University Press: Cambridge, UK, 2015; pp. 1329–1356. [Google Scholar] [CrossRef]
- Kampers, G.; Wächter, M.; Hölling, M.; Lind, P.G.; Queirós, S.M.; Peinke, J. Disentangling stochastic signals superposed on short localized oscillations. Phys. Lett. A 2020, 384, 126307. [Google Scholar] [CrossRef]
- Srinivasan, S.; Kumarasamy, S.; Andreadakis, Z.E.; Lind, P.G. Artificial Intelligence and Mathematical Models of Power Grids Driven by Renewable Energy Sources: A Survey. Energies 2023, 16, 5383. [Google Scholar] [CrossRef]
- Sim, S.K.; Maass, P.; Lind, P.G. Wind Speed Modeling by Nested ARIMA Processes. Energies 2019, 12, 69. [Google Scholar] [CrossRef]
- Friedrich, R.; Peinke, J. Description of a turbulent cascade by a Fokker-Planck equation. Phys. Rev. Lett. 1997, 78, 863–866. [Google Scholar] [CrossRef]
- Siegert, S.; Friedrich, R.; Peinke, J. Analysis of data sets of stochastic systems. Phys. Lett. A 1998, 243, 275–280. [Google Scholar] [CrossRef]
- Friedrich, R.; Peinke, J.; Sahimi, M.; Tabar, M. Approaching complexity by stochastic methods: From biological systems to turbulence. Phys. Rep. 2011, 506, 87–162. [Google Scholar] [CrossRef]
- Wächter, M.; Milan, P.; Mücke, T.; Peinke, J. Power performance of wind energy converters characterized as stochastic process: Applications of the Langevin power curve. Wind Energy 2011, 14, 711–717. [Google Scholar] [CrossRef]
- Anvari, M.; Lohmann, G.; Wächter, M.; Milan, P.; Lorenz, E.; Heinemann, D.; Kleinhans, D.; Rahimi Tabar, M.R. Short-term fluctuations of wind and solar power systems. New J. Phys. 2016, 18, 063027. [Google Scholar] [CrossRef]
- Lind, P.G.; Vera-Tudela, L.; Wächter, M.; Kühn, M.; Peinke, J. Normal Behaviour Models for Wind Turbine Vibrations: Comparison of Neural Networks and a Stochastic Approach. Energies 2017, 10, 1944. [Google Scholar] [CrossRef]
- Lind, P.G.; Wächter, M.; Peinke, J. Reconstructing the intermittent dynamics of the torque in wind turbines. J. Phys. Conf. Ser. 2014, 524, 012179. [Google Scholar] [CrossRef]
- Lind, P.G.; Herráez, I.; Wächter, M.; Peinke, J. Fatigue Loads Estimation Through a Simple Stochastic Model. Energies 2014, 7, 8279–8293. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. ASME J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Abernethy, R. The New Weibull Handbook Fifth Edition, Reliability and Statistical Analysis for Predicting Life, Safety, Supportability, Risk, Cost and Warranty Claims, 5th ed.; Dr. Robert. Abernethy: Boston, MA, USA, 2006. [Google Scholar]
- Harris, R.; Cook, N. The parent wind speed distribution: Why Weibull? J. Wind Eng. Ind. Aerodyn. 2014, 131, 72–87. [Google Scholar] [CrossRef]
- Carrillo, C.; Cidrás, J.; Díaz-Dorado, E.; Obando-Montaño, A.F. An Approach to Determine the Weibull Parameters for Wind Energy Analysis: The Case of Galicia (Spain). Energies 2014, 7, 2676–2700. [Google Scholar] [CrossRef]
- Yu, J.; Fu, Y.; Yu, Y.; Wu, S.; Wu, Y.; You, M.; Guo, S.; Li, M. Assessment of Offshore Wind Characteristics and Wind Energy Potential in Bohai Bay, China. Energies 2019, 12, 2879. [Google Scholar] [CrossRef]
- Rice, S.O. Mathematical analysis of random noise. Bell Syst. Tech. J. 1944, 23, 282–332. [Google Scholar] [CrossRef]
- Nakagami, M. The m-distribution—A general formula of intensity distribution of rapid fading. In Statistical Methods in Radio Wave Propagation; Elsevier: Amsterdam, The Netherlands, 1960; pp. 3–36. [Google Scholar]
- Hershey, J.R.; Olsen, P.A. Approximating the Kullback Leibler Divergence between Gaussian Mixture Models. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing—ICASSP ’07, Honolulu, HI, USA, 15–20 April 2007; Volume 4, pp. IV–317–IV–320. [Google Scholar]

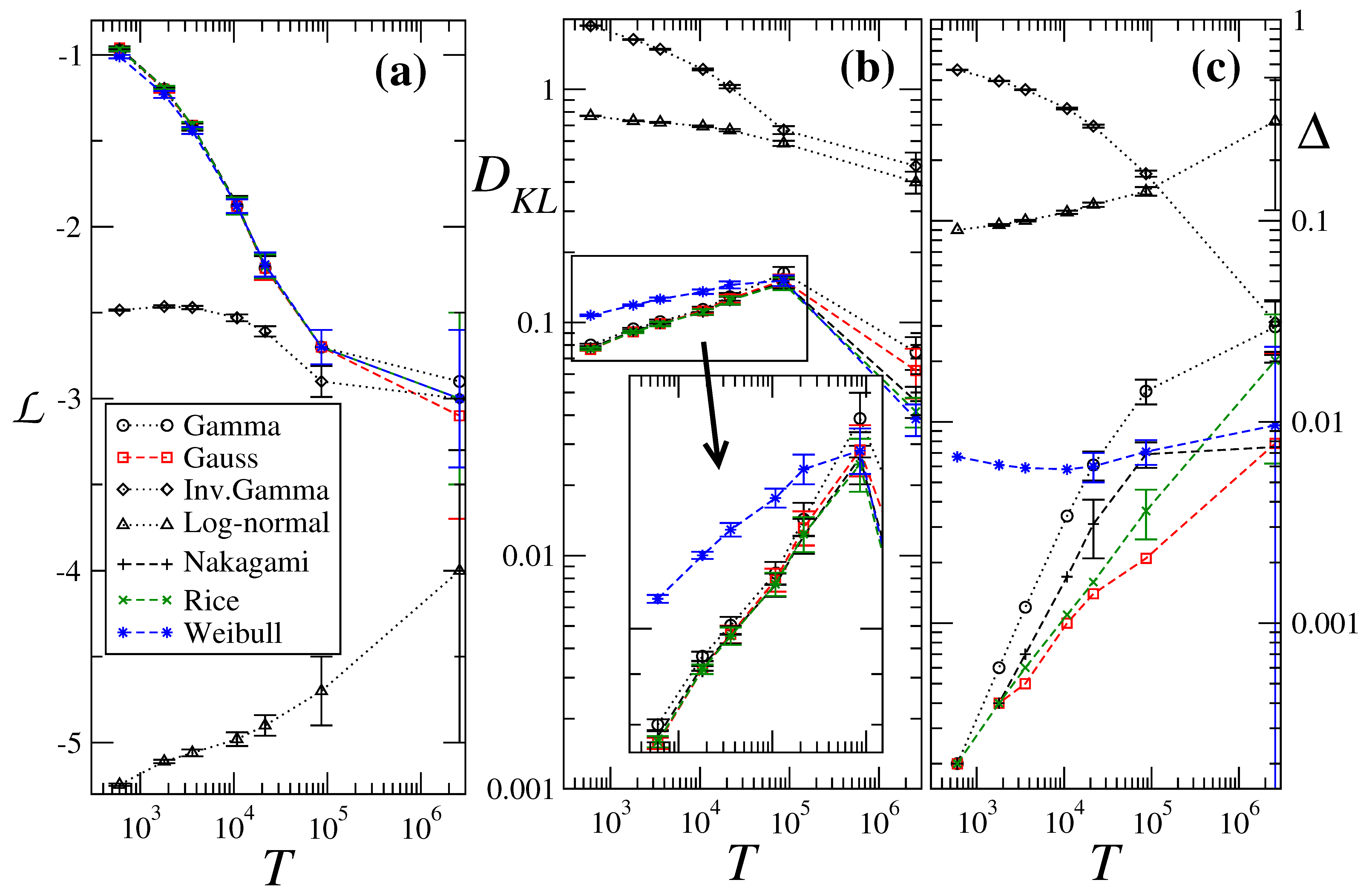
| Time(s) | Gauss | Weibull | Gamma | InvGam | Nakagami | Rice | LogN | |
|---|---|---|---|---|---|---|---|---|
| 600 | 0.077 | 0.107 | 0.080 | 1.875 | 0.078 | 0.077 | 0.769 | |
| (±0.001) | (±0.001) | (±0.001) | (±0.004) | (±0.001) | (±0.001) | (±0.002) | ||
| 1800 | 0.0910 | 0.119 | 0.094 | 1.636 | 0.092 | 0.091 | 0.733 | |
| (±0.001) | (±0.001) | (±0.001) | (±0.006) | (±0.001) | (±0.001) | (±0.003) | ||
| 3600 | 0.099 | 0.126 | 0.101 | 1.487 | 0.099 | 0.098 | 0.721 | |
| (±0.002) | (±0.002) | (±0.002) | (±0.008) | (±0.002) | (±0.002) | (±0.004) | ||
| 10,800 | 0.112 | 0.135 | 0.114 | 1.22 | 0.111 | 0.111 | 0.694 | |
| (±0.003) | (±0.003) | (±0.003) | (±0.01) | (±0.003) | (±0.003) | (±0.006) | ||
| 21,600 | 0.126 | 0.145 | 0.129 | 1.03 | 0.124 | 0.124 | 0.668 | |
| (±0.005) | (±0.005) | (±0.005) | (±0.02) | (±0.005) | (±0.005) | (±0.008) | ||
| 86,400 | 0.151 | 0.151 | 0.16 | 0.67 | 0.149 | 0.146 | 0.59 | |
| (±0.009) | (±0.008) | (±0.01) | (±0.03) | (±0.009) | (±0.009) | (±0.02) | ||
| 2,592,000 | 0.06 | 0.039 | 0.07 | 0.47 | 0.046 | 0.041 | 0.40 | |
| (±0.015) | (±0.006) | (±0.01) | (±0.07) | (±0.007) | (±0.006) | (±0.04) | ||
| 600 | −0.96 | −1.01 | −0.97 | −2.485 | −0.96 | −0.97 | −5.245 | |
| (±0.01) | (±0.01) | (±0.01) | (±0.004) | (±0.01) | (±0.01) | (±0.007) | ||
| 1800 | −1.20 | −1.23 | −1.20 | −2.464 | −1.19 | −1.19 | −5.11 | |
| (±0.02) | (±0.02) | (±0.01) | (±0.007) | (± 0.01) | (±0.01) | (±0.01) | ||
| 3600 | −1.41 | −1.44 | −1.42 | −2.47 | −1.41 | −1.41 | −5.06 | |
| (±0.02) | (±0.02) | (±0.02) | (±0.01) | (±0.02) | (±0.02) | (±0.02) | ||
| 10,800 | −1.88 | −1.88 | −1.88 | −2.53 | −1.87 | −1.88 | −4.98 | |
| (±0.04) | (±0.04) | (±0.05) | (±0.02) | (±0.05) | (±0.05) | (±0.04) | ||
| 21,600 | −2.24 | −2.22 | −2.24 | −2.61 | −2.23 | −2.23 | −4.90 | |
| (±0.07) | (±0.07) | (±0.07) | (±0.03) | (±0.06) | (±0.07) | (±0.06) | ||
| 86,400 | −2.7 | −2.7 | −2.7 | −2.90 | −2.7 | −2.7 | −4.7 | |
| (±0.1) | (±0.1) | (±0.1) | (±0.09) | (±0.1) | (±0.1) | (±0.2) | ||
| 2,592,000 | −3.1 | −3.0 | −2.9 | −3.0 | −3.0 | −3.0 | −4 | |
| (±0.6) | (±0.4) | (±0.4) | (±0.4) | (±0.5) | (±0.5) | (±1) | ||
| 600 | 0.0002 | 0.0067 | 0.0002 | 0.563 | 0.0002 | 0.0002 | 0.0901 | |
| (±0.0001) | (±0.0001) | (±0.0001) | (±0.001) | (±0.0001) | (±0.0001) | (±0.0001) | ||
| 1800 | 0.0004 | 0.0061 | 0.0006 | 0.496 | 0.0004 | 0.0004 | 0.095 | |
| (±0.0001) | (±0.0001) | (±0.0001) | (±0.001) | (±0.0001) | (±0.0001) | (±0.001) | ||
| 3600 | 0.0005 | 0.0059 | 0.0012 | 0.449 | 0.0007 | 0.0006 | 0.100 | |
| (±0.0001) | (±0.0001) | (±0.0001) | (±0.002) | (±0.0001) | (±0.0001) | (±0.001) | ||
| 10,800 | 0.0010 | 0.0058 | 0.0034 | 0.361 | 0.0017 | 0.0011 | 0.110 | |
| (±0.0001) | (±0.0001) | (±0.0001) | (±0.004) | (±0.0001) | (±0.0001) | (±0.002) | ||
| 21,600 | 0.0014 | 0.006 | 0.006 | 0.296 | 0.003 | 0.0016 | 0.120 | |
| (±0.0001) | (±0.001) | (±0.001) | (±0.005) | (±0.001) | (±0.0001) | (±0.003) | ||
| 86,400 | 0.0021 | 0.007 | 0.014 | 0.172 | 0.007 | 0.004 | 0.140 | |
| (±0.0001) | (±0.001) | (±0.002) | (±0.006) | (±0.001) | (±0.001) | (±0.007) | ||
| 2,592,000 | 0.01 | 0.01 | 0.03 | 0.031 | 0.01 | 0.02 | 0.3 | |
| (±0.01) | (±0.01) | (±0.01) | (±0.009) | (±0.01) | (±0.01) | (±0.2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lencastre, P.; Yazidi, A.; Lind, P.G. Modeling Wind-Speed Statistics beyond the Weibull Distribution. Energies 2024, 17, 2621. https://doi.org/10.3390/en17112621
Lencastre P, Yazidi A, Lind PG. Modeling Wind-Speed Statistics beyond the Weibull Distribution. Energies. 2024; 17(11):2621. https://doi.org/10.3390/en17112621
Chicago/Turabian StyleLencastre, Pedro, Anis Yazidi, and Pedro G. Lind. 2024. "Modeling Wind-Speed Statistics beyond the Weibull Distribution" Energies 17, no. 11: 2621. https://doi.org/10.3390/en17112621
APA StyleLencastre, P., Yazidi, A., & Lind, P. G. (2024). Modeling Wind-Speed Statistics beyond the Weibull Distribution. Energies, 17(11), 2621. https://doi.org/10.3390/en17112621






