Performance Analysis and Optimization of Compressed Air Energy Storage Integrated with Latent Thermal Energy Storage
Abstract
1. Introduction
2. System Description and Simulation Model
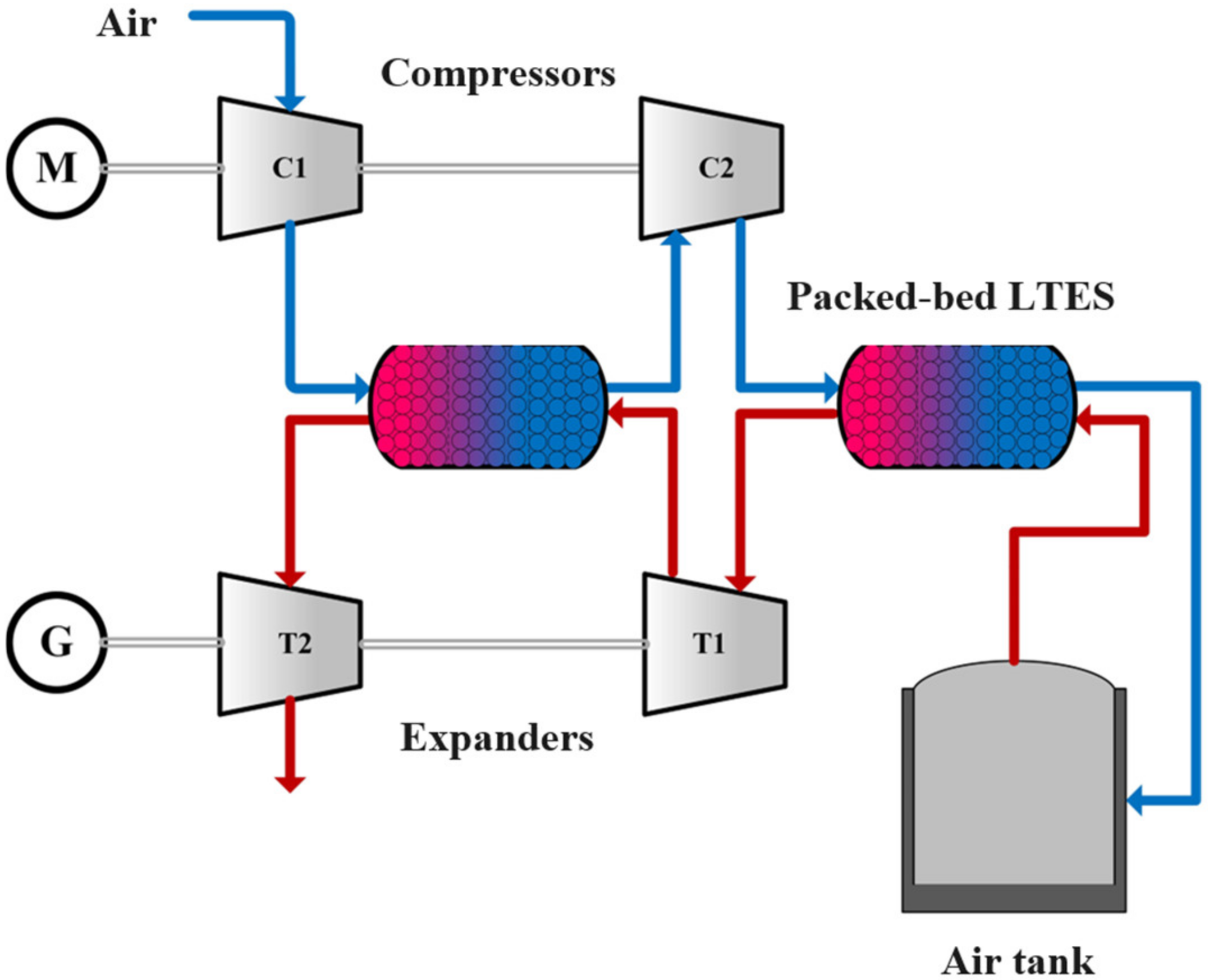
2.1. System Description
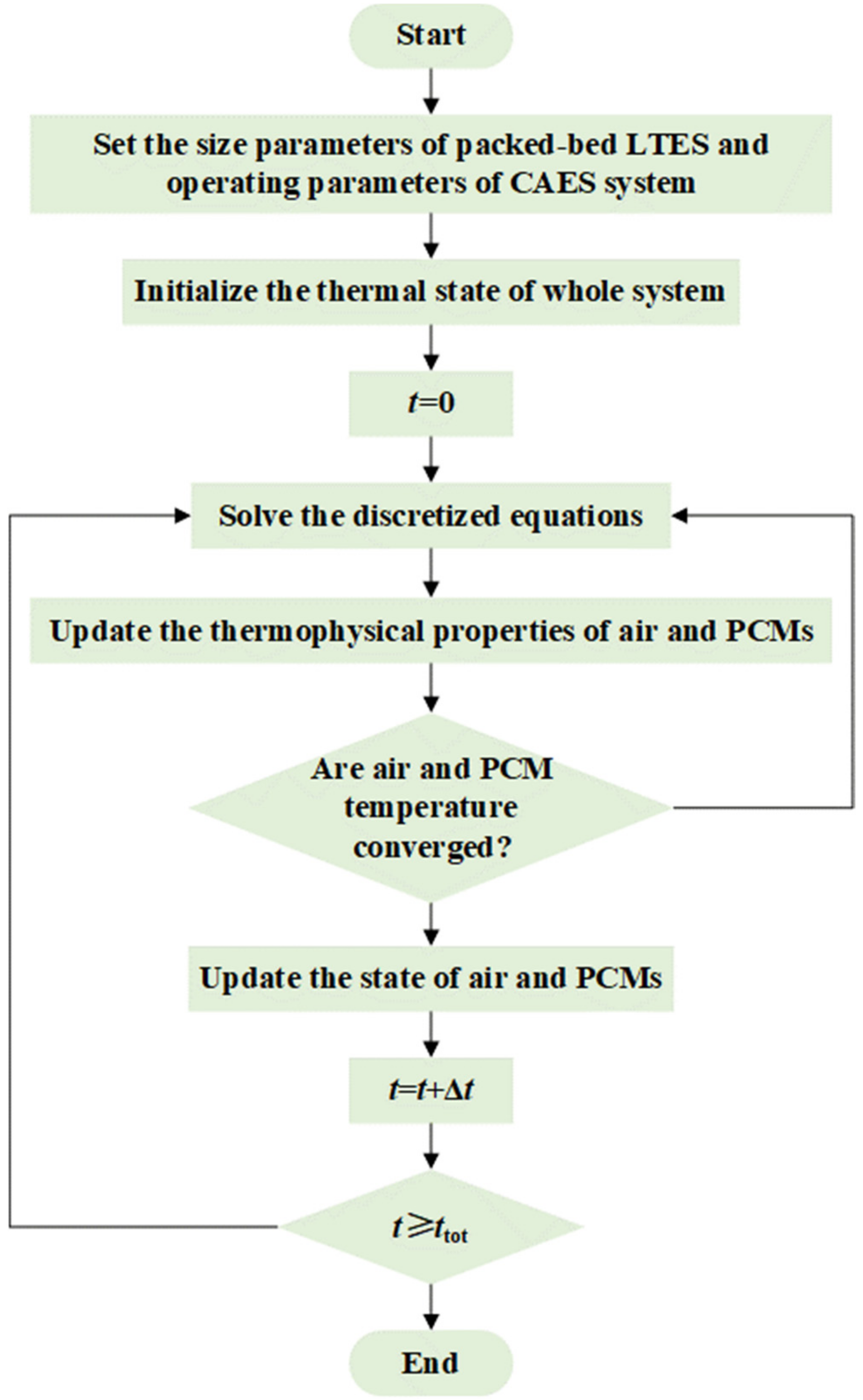
2.2. Models
2.2.1. Model for Compressors
2.2.2. Model for Expanders
2.2.3. Model for Air Tank
2.2.4. Model for Packed-Bed LTES
- (1)
- Heat loss at the inlet and outlet of packed-bed LTES is neglected.
- (2)
- The encapsulated PCM balls have the same size and are distributed uniformly inside, and the porosity is the same between any adjacent PCM balls.
- (3)
- Thermal radiation between the air and PCM balls is ignored.
- (4)
- Temperature gradients of PCM balls at each layer along the radial direction are not considered, and this is the same for the air at each layer.
- (5)
- The natural convection inside PCM balls is ignored due to their small size.
- (6)
- The isentropic efficiencies of compressors, turbines, pumps, and ammonia turbine are fixed.
- (7)
- The energy loss due to the pressure drop in the heat exchangers is neglected.
2.2.5. Initial and Boundary Conditions
2.3. Performance Evaluation Indicators
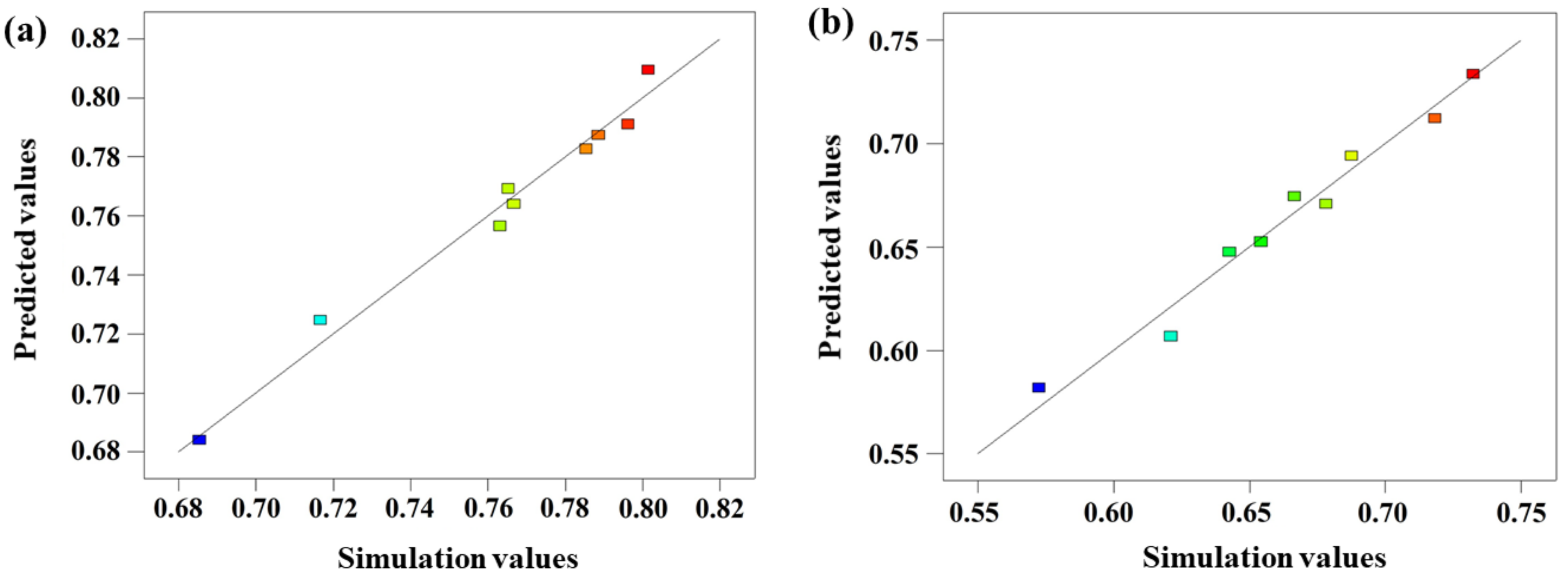
2.4. Model Validation
3. Results and Discussion
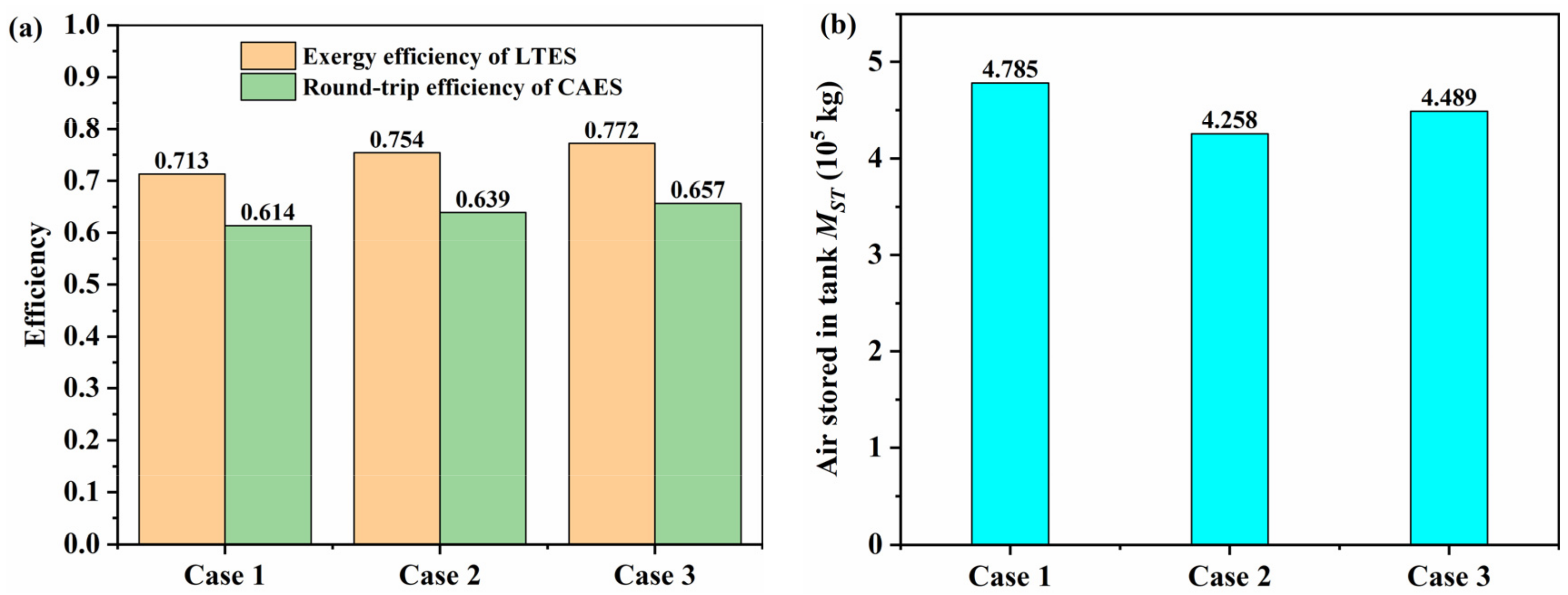
3.1. Comparion of Various PCM Layouts in Packed-Bed LTES
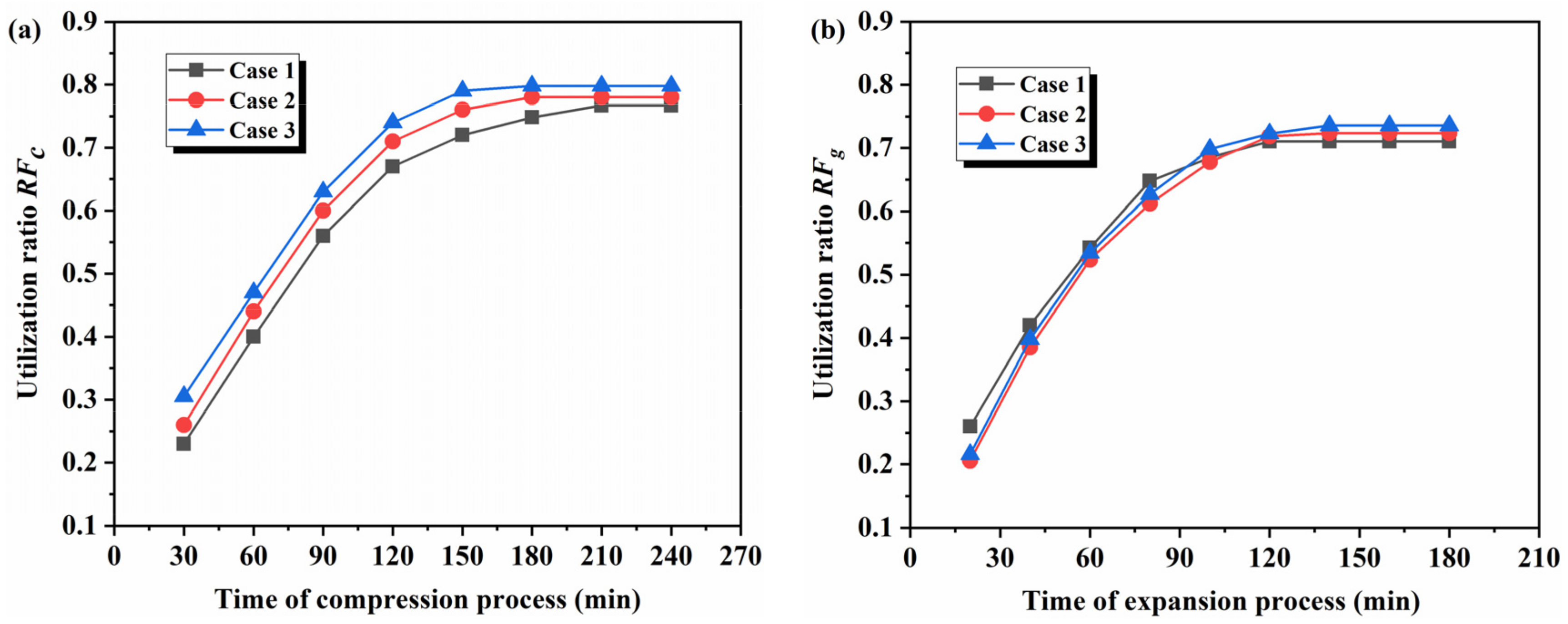
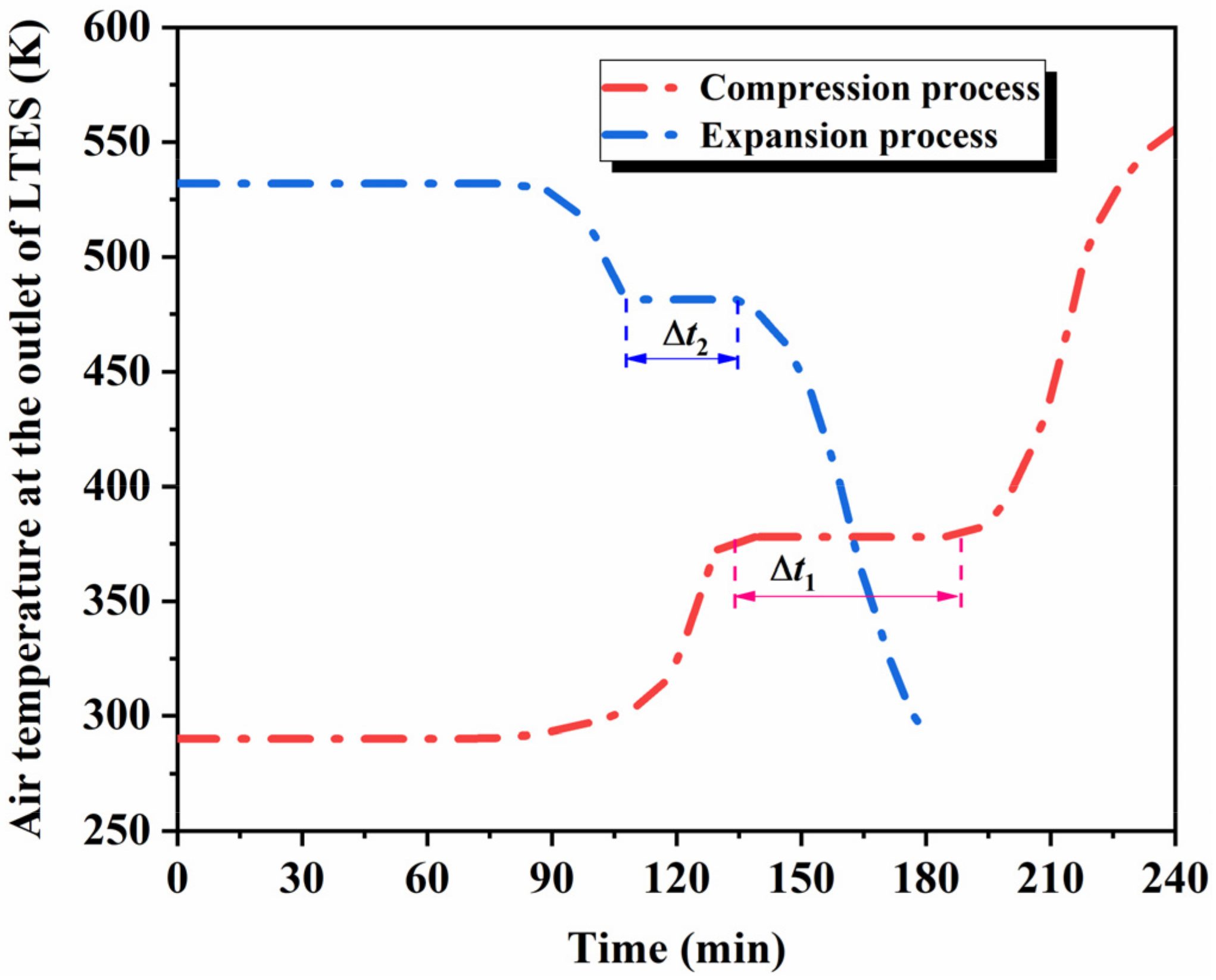
3.2. Charging–Discharging Performance of Packed-Bed LTES
3.3. Proportion Optimization of PCMs in Packed-Bed LTES
3.3.1. Response Surface Model
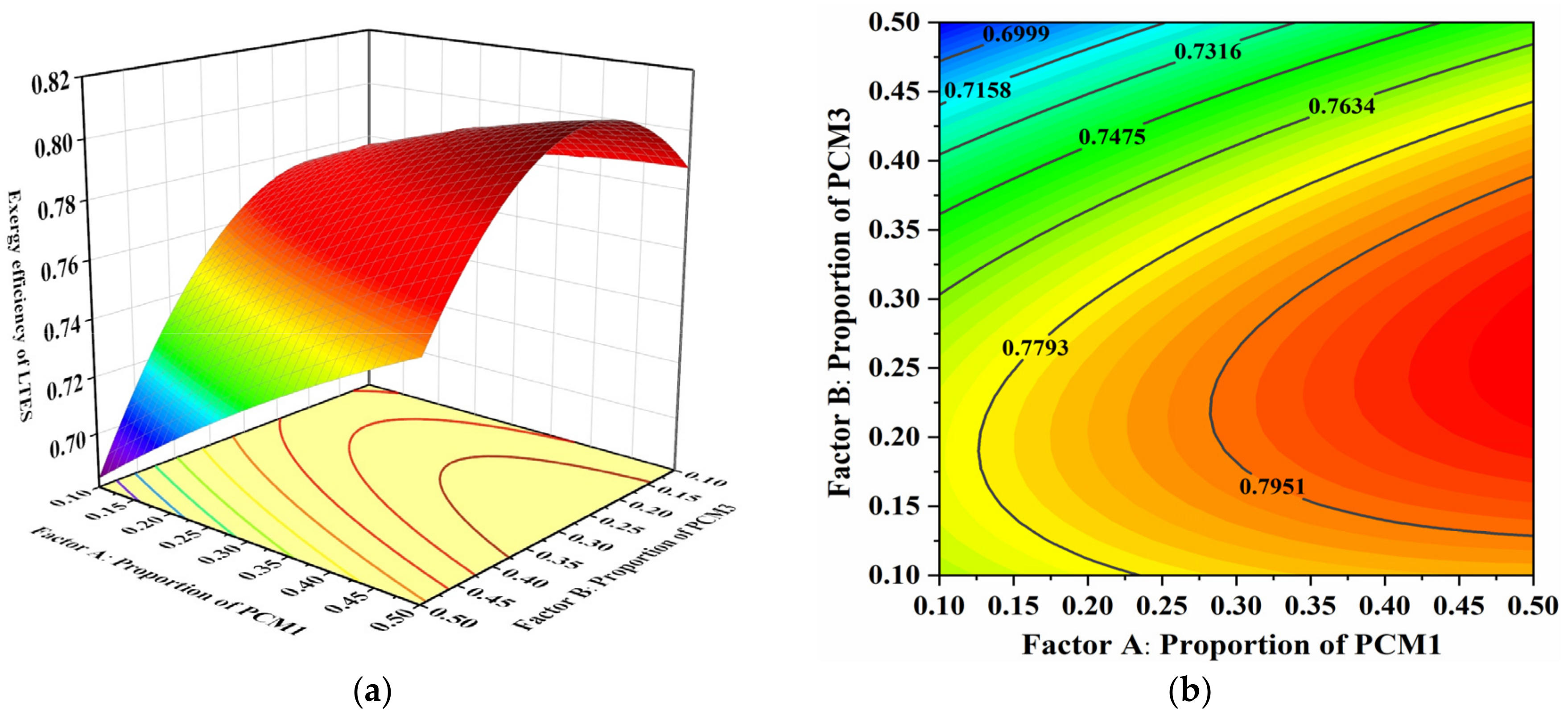
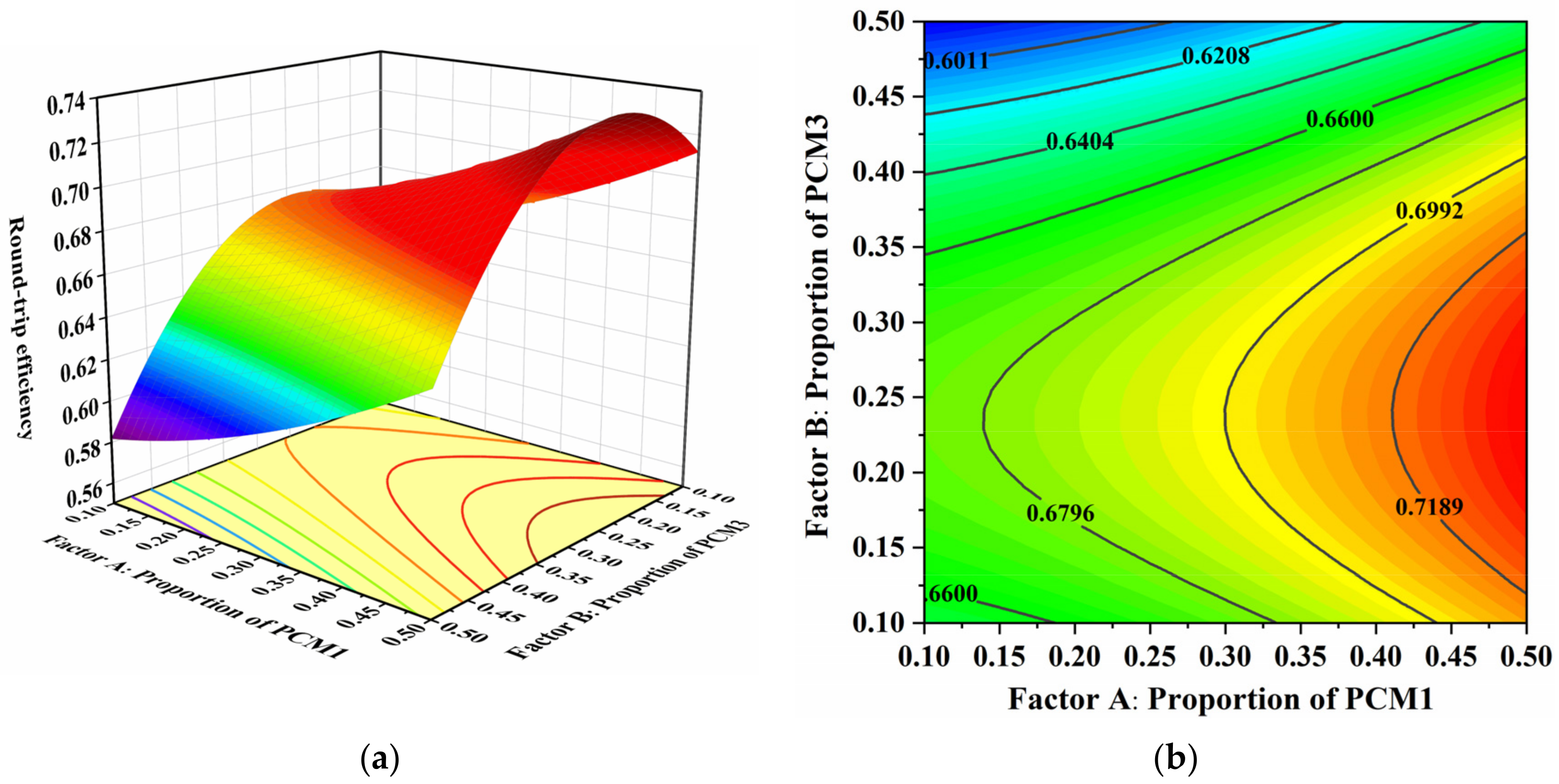
3.3.2. Optimization Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Lu, Y.; Huang, R.; Chang, J.; Yu, X.; Jiang, R.; Yu, X.; Roskilly, A.P. Applications and technological challenges for heat recovery, storage and utilisation with latent thermal energy storage. Appl. Energy 2021, 283, 116277. [Google Scholar] [CrossRef]
- He, F.; Liu, Y.; Pan, J.; Ye, X.; Jiao, P. Advanced ocean wave energy harvesting: Current progress and future trends. J. Zhejiang Univ.-Sci. A 2023, 24, 91–108. [Google Scholar] [CrossRef]
- Suliman, F.E.M. Solar- and Wind-Energy Utilization in the Kingdom of Saudi Arabia: A Comprehensive Review. Energies 2024, 17, 1894. [Google Scholar] [CrossRef]
- Fang, J.; Yang, M.; Dong, X.; Luo, T.; Pan, C.; Liu, Z.; Zhang, C.; Wang, H. Electrochemical-thermochemical complementary hydrogen production system for efficient full-spectrum solar energy storage. Therm. Sci. Eng. Prog. 2024, 49, 102501. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, H.; Yang, Y.; Zhang, J.; Yang, F.; Yan, D.; Yang, H.; Wang, Y. Optimization of energy management strategy for extended range electric vehicles using multi-island genetic algorithm. J. Energy Storage 2023, 61, 106802. [Google Scholar] [CrossRef]
- Chatzistylianos, E.S.; Psarros, G.N.; Papathanassiou, S.A. Insights from a Comprehensive Capacity Expansion Planning Modeling on the Operation and Value of Hydropower Plants under High Renewable Penetrations. Energies 2024, 17, 1723. [Google Scholar] [CrossRef]
- Wang, H.; Wang, F.; Wang, B.; Wu, J.; Lu, H.; Wang, C. Partial flow separation in guide-vane region of large-capacity/low-head pumped hydro energy storage system with horizontal shaft. J. Energy Storage 2023, 71, 108173. [Google Scholar] [CrossRef]
- Selvakumar, R.D.; Wu, J.; Alkaabi, A.K. Electrohydrodynamic acceleration of charging process in a latent heat thermal energy storage module. Appl. Therm. Eng. 2024, 242, 122475. [Google Scholar] [CrossRef]
- Mitali, J.; Dhinakaran, S.; Mohamad, A.A. Energy storage systems: A review. Energy Storage Sav. 2022, 1, 166–216. [Google Scholar] [CrossRef]
- Cacciali, L.; Battisti, L.; Benini, E. Maximizing Efficiency in Compressed Air Energy Storage: Insights from Thermal Energy Integration and Optimization. Energies 2024, 17, 1552. [Google Scholar] [CrossRef]
- Ghorbani, B.; Mehrpooya, M.; Ardehali, A. Energy and exergy analysis of wind farm integrated with compressed air energy storage using multi-stage phase change material. J. Clean. Prod. 2020, 259, 120906. [Google Scholar] [CrossRef]
- Liu, C.; Su, X.; Yin, Z.; Sheng, Y.; Zhou, X.; Xu, Y.; Wang, X.; Chen, H. Experimental study on the feasibility of isobaric compressed air energy storage as wind power side energy storage. Appl. Energy 2024, 364, 123129. [Google Scholar] [CrossRef]
- Niu, J.; Zhang, C.; Li, Y.; Wu, Y.; Sun, H. Design and investigation of cold storage material for large-scale application in supercritical compressed air energy storage system. J. Energy Storage 2024, 75, 109680. [Google Scholar] [CrossRef]
- Meng, J.W.T.; Li, J.; Liu, W. Energy storage salt cavern construction and evaluation technology. Adv. Geo-Energy Res. 2023, 9, 5. [Google Scholar]
- Wan, M.; Ji, W.; Wan, J.; He, Y.; Li, J.; Liu, W.; Jurado, M.J. Compressed air energy storage in salt caverns in China: Development and outlook. Adv. Geo-Energy Res. 2023, 9, 14. [Google Scholar] [CrossRef]
- Wan, J.; Sun, Y.; He, Y.; Ji, W.; Li, J.; Jiang, L.; Jurado, M.J. Development and technology status of energy storage in depleted gas reservoirs. Int. J. Coal Sci. Technol. 2024, 11, 29. [Google Scholar] [CrossRef]
- Raju, M.; Kumar Khaitan, S. Modeling and simulation of compressed air storage in caverns: A case study of the Huntorf plant. Appl. Energy 2012, 89, 474–481. [Google Scholar] [CrossRef]
- Li, L.; Liang, W.; Lian, H.; Yang, J.; Dusseault, M. Compressed air energy storage: Characteristics, basic principles, and geological considerations. Adv. Geo-Energy Res. 2018, 2, 135–147. [Google Scholar] [CrossRef]
- Matos, C.R.; Silva, P.P.; Carneiro, J.F. Overview of compressed air energy storage projects and regulatory framework for energy storage. J. Energy Storage 2022, 55, 105862. [Google Scholar] [CrossRef]
- Opitz, F.; Treffinger, P. Packed bed thermal energy storage model—Generalized approach and experimental validation. Appl. Therm. Eng. 2014, 73, 245–252. [Google Scholar] [CrossRef]
- Ortega-Fernández, I.; Zavattoni, S.A.; Rodríguez-Aseguinolaza, J.; D’Aguanno, B.; Barbato, M.C. Analysis of an integrated packed bed thermal energy storage system for heat recovery in compressed air energy storage technology. Appl. Energy 2017, 205, 280–293. [Google Scholar] [CrossRef]
- Barbour, E.; Mignard, D.; Ding, Y.; Li, Y. Adiabatic Compressed Air Energy Storage with packed bed thermal energy storage. Appl. Energy 2015, 155, 804–815. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, P.; Xu, W.; Lai, Y.; Wang, J.; Dai, Y. Off-design performance analysis of a-caes system with two-stage packed bed heat storage unit. Acta Energiae Solaris Sin. 2022, 43, 294–299. [Google Scholar]
- Zhou, Q.; Du, D.; Lu, C.; He, Q.; Liu, W. A review of thermal energy storage in compressed air energy storage system. Energy 2019, 188, 115993. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, R.; Li, Z.; Qian, G.; Wang, B.; Wang, L.; Huang, R. Synergistic improvement of melting rate and heat storage capacity by a rotation-based method for shell-and-tube latent thermal energy storage. Appl. Therm. Eng. 2023, 219, 119480. [Google Scholar] [CrossRef]
- Javaheri, M.; Shafiei Ghazani, A. Energy and exergy analysis of a novel advanced adiabatic compressed air energy storage hybridized with reverse osmosis system. J. Energy Storage 2023, 73, 109250. [Google Scholar] [CrossRef]
- Bashiri Mousavi, S.; Adib, M.; Soltani, M.; Razmi, A.R.; Nathwani, J. Transient thermodynamic modeling and economic analysis of an adiabatic compressed air energy storage (A-CAES) based on cascade packed bed thermal energy storage with encapsulated phase change materials. Energy Convers. Manag. 2021, 243, 114379. [Google Scholar] [CrossRef]
- Li, R.; Zhang, Y.; Chen, H.; Zhang, H.; Yang, Z.; Yao, E.; Wang, H. Exploring thermodynamic potential of multiple phase change thermal energy storage for adiabatic compressed air energy storage system. J. Energy Storage 2021, 33, 102054. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, Z.; Qian, G.; Jiang, R.; Wang, L.; Huang, R.; Li, Z. Evaluation of PCM thermophysical properties on a compressed air energy storage system integrated with packed-bed latent thermal energy storage. J. Energy Storage 2024, 81, 110519. [Google Scholar] [CrossRef]
- Gong, Z.-X.; Mujumdar, A.S. Exergetic Analysis of Energy Storage using Multiple Phase-Change Materials. J. Energy Resour. Technol. 1996, 118, 242–248. [Google Scholar] [CrossRef]
- Ismail, K.A.R.; Henríquez, J.R. Numerical and experimental study of spherical capsules packed bed latent heat storage system. Appl. Therm. Eng. 2002, 22, 1705–1716. [Google Scholar] [CrossRef]
- Guo, W.; He, Z.; Zhang, Y.; Zhang, P. Thermal performance of the packed bed thermal energy storage system with encapsulated phase change material. Renew. Energy 2022, 196, 1345–1356. [Google Scholar] [CrossRef]
- Peng, H.; Li, R.; Ling, X.; Dong, H. Modeling on heat storage performance of compressed air in a packed bed system. Appl. Energy 2015, 160, 1–9. [Google Scholar] [CrossRef]
- Gonzo, E.E. Estimating correlations for the effective thermal conductivity of granular materials. Chem. Eng. J. 2002, 90, 299–302. [Google Scholar] [CrossRef]
- Beek, J. Design of Packed Catalytic Reactors. In Advances in Chemical Engineering; Drew, T.B., Hoopes, J.W., Vermeulen, T., Eds.; Academic Press: Cambridge, MA, USA, 1962; Volume 3, pp. 203–271. [Google Scholar]
- Du Plessis, J.P.; Woudberg, S. Pore-scale derivation of the Ergun equation to enhance its adaptability and generalization. Chem. Eng. Sci. 2008, 63, 2576–2586. [Google Scholar] [CrossRef]
- Bellan, S.; Alam, T.E.; González-Aguilar, J.; Romero, M.; Rahman, M.M.; Goswami, D.Y.; Stefanakos, E.K. Numerical and experimental studies on heat transfer characteristics of thermal energy storage system packed with molten salt PCM capsules. Appl. Therm. Eng. 2015, 90, 970–979. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, Y.; Zhao, X.; Zhang, Y. Application of response surface method based on new strategy in structural reliability analysis. Structures 2023, 57, 105202. [Google Scholar] [CrossRef]





| Parameters | Values | Units |
|---|---|---|
| Height | 6 | m |
| Diameter | 2 | m |
| Porosity | 0.4 | - |
| Diameter of PCM balls | 0.02 | m |
| Insulator thickness | 0.2 | m |
| No. | Selected PCMs | Tm (K) | ρ (kg/m3) | L (kJ/kg) | cp J/(kg·K) | λ W/(m·K) |
|---|---|---|---|---|---|---|
| P1 | 481 | 2350 | 369 | 1560 | 0.63 | |
| P2 | 429 | 2296 | 233 | 1910 | 0.66 | |
| P3 | Oxalic acid dihydrate | 378 | 1653 | 264 | 2890 | 0.70 |
| Factors | Levels | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| A (Proportion of PCM1) | 0.1 | 0.3 | 0.5 |
| B (Proportion of PCM3) | 0.1 | 0.3 | 0.5 |
| Trial No. | Factor A | Factor B | Exergy Efficiency (%) | Round-Trip Efficiency (%) |
|---|---|---|---|---|
| 1 | 0.1 | 0.3 | 76.67 | 67.81 |
| 2 | 0.1 | 0.5 | 68.54 | 57.25 |
| 3 | 0.5 | 0.3 | 80.15 | 73.23 |
| 4 | 0.3 | 0.3 | 79.62 | 68.75 |
| 5 | 0.3 | 0.5 | 71.67 | 62.10 |
| 6 | 0.5 | 0.5 | 76.31 | 64.26 |
| 7 | 0.3 | 0.1 | 78.54 | 66.65 |
| 8 | 0.1 | 0.1 | 76.52 | 65.42 |
| 9 | 0.5 | 0.1 | 78.86 | 71.82 |
| Terms | Factor A | Factor B | Exergy Efficiency (%) | Round-Trip Efficiency (%) |
|---|---|---|---|---|
| Ranges | 0.1~0.5 | 0.1~0.5 | 0~100 | 0~100 |
| Optimal values | 0.48 | 0.22 | 80.9 | 73.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Dou, W.; Zhang, Z.; Hong, Y.; Qian, G.; Li, Z. Performance Analysis and Optimization of Compressed Air Energy Storage Integrated with Latent Thermal Energy Storage. Energies 2024, 17, 2608. https://doi.org/10.3390/en17112608
Yu X, Dou W, Zhang Z, Hong Y, Qian G, Li Z. Performance Analysis and Optimization of Compressed Air Energy Storage Integrated with Latent Thermal Energy Storage. Energies. 2024; 17(11):2608. https://doi.org/10.3390/en17112608
Chicago/Turabian StyleYu, Xiaoli, Wenbo Dou, Zhiping Zhang, Yan Hong, Gao Qian, and Zhi Li. 2024. "Performance Analysis and Optimization of Compressed Air Energy Storage Integrated with Latent Thermal Energy Storage" Energies 17, no. 11: 2608. https://doi.org/10.3390/en17112608
APA StyleYu, X., Dou, W., Zhang, Z., Hong, Y., Qian, G., & Li, Z. (2024). Performance Analysis and Optimization of Compressed Air Energy Storage Integrated with Latent Thermal Energy Storage. Energies, 17(11), 2608. https://doi.org/10.3390/en17112608










