Numerical Study on Heat Generation Characteristics of Charge and Discharge Cycle of the Lithium-Ion Battery
Abstract
:1. Introduction
2. Electrochemical–Thermal Coupling Model Development
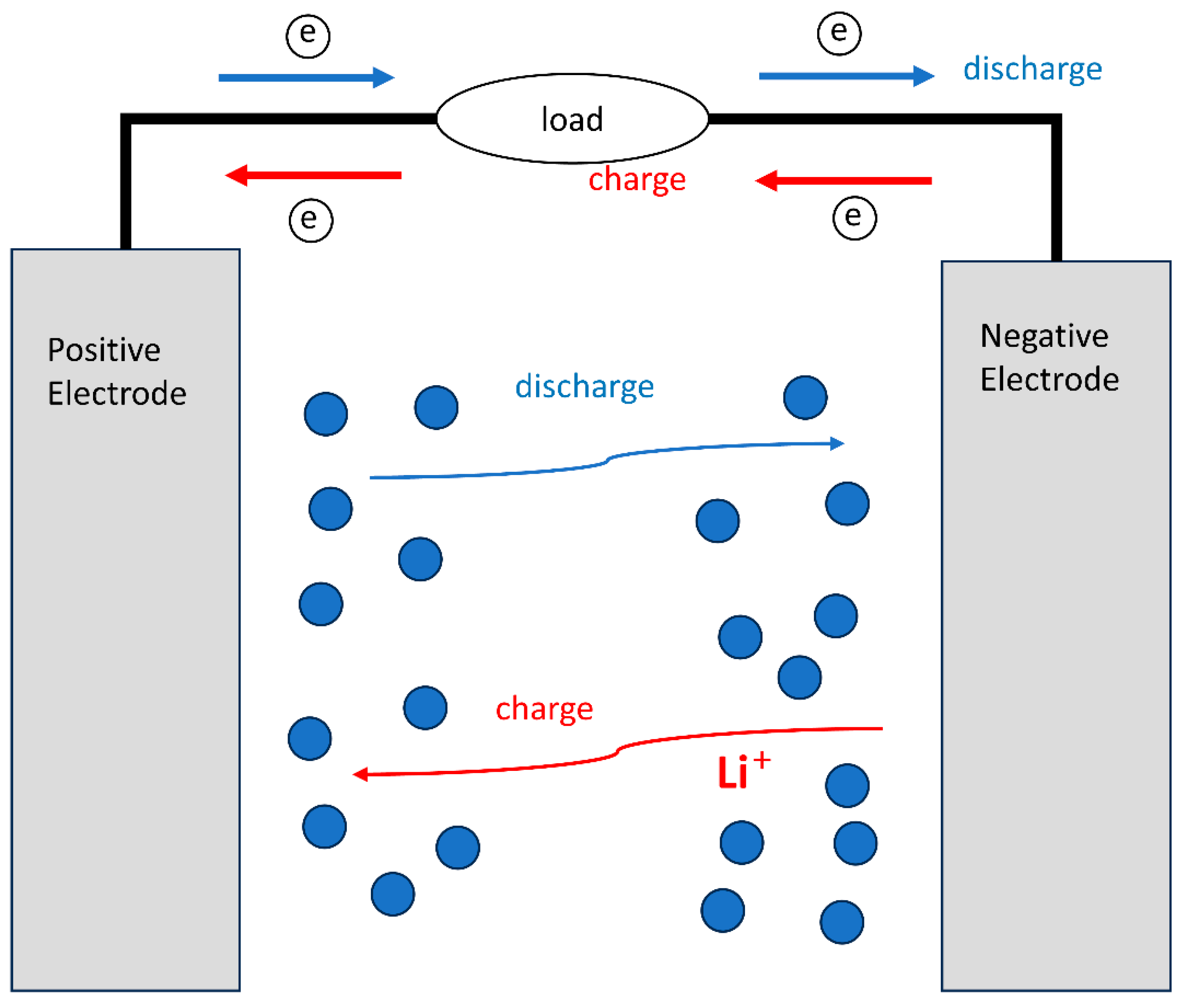
2.1. Physical Model and Mesh Division
2.2. Control Equations and Boundary Conditions
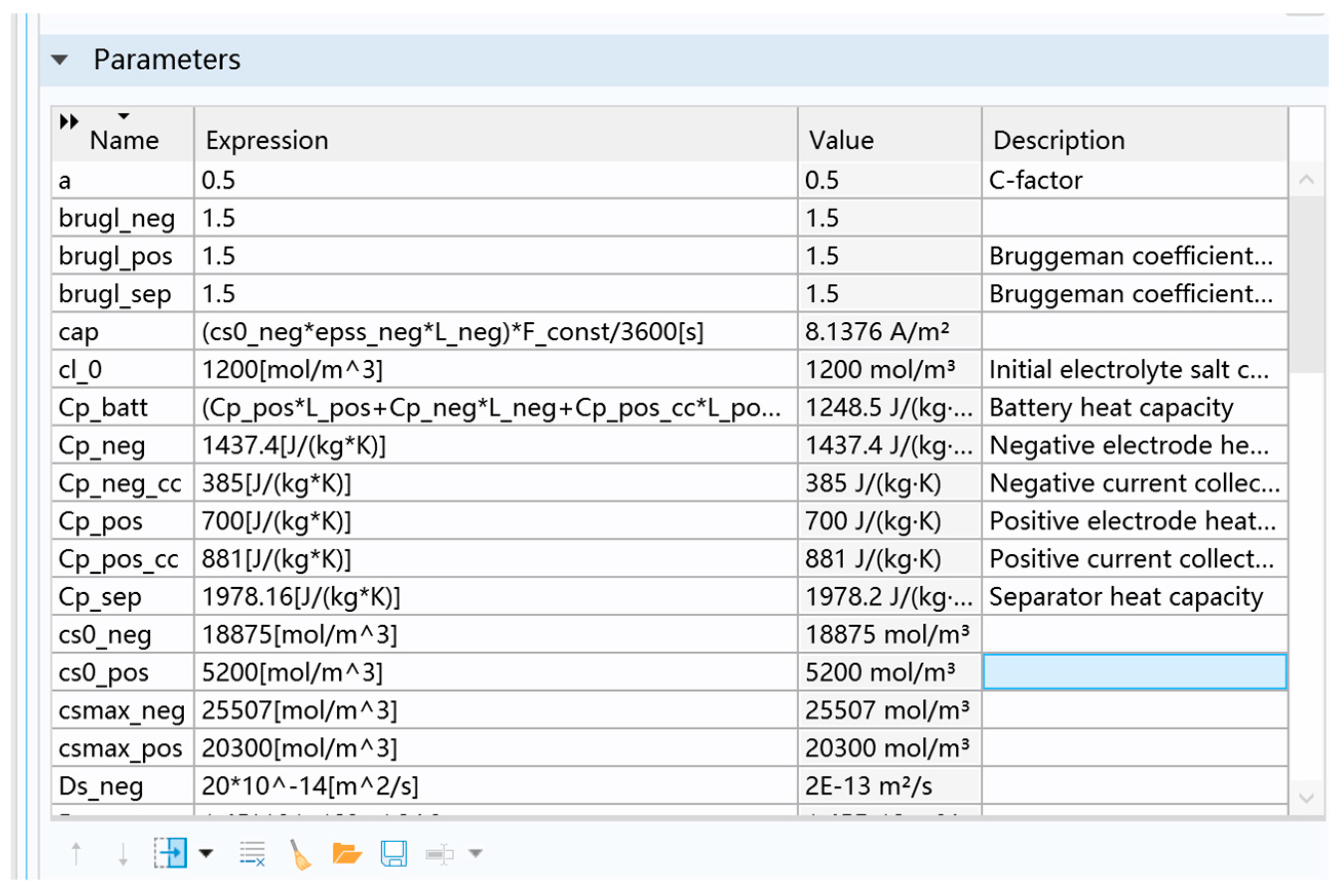
2.3. Model Parameters
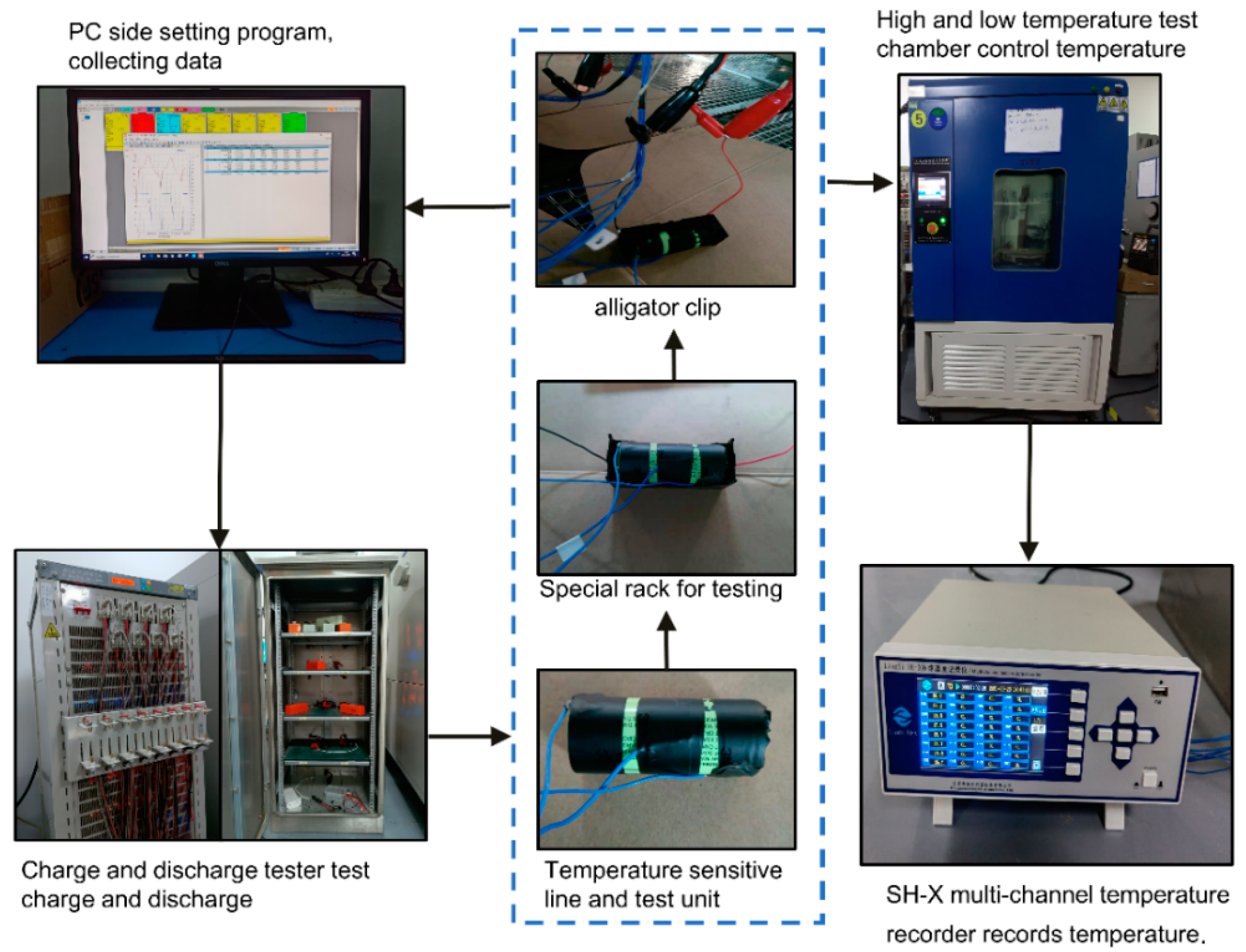
2.4. Experimental Setup
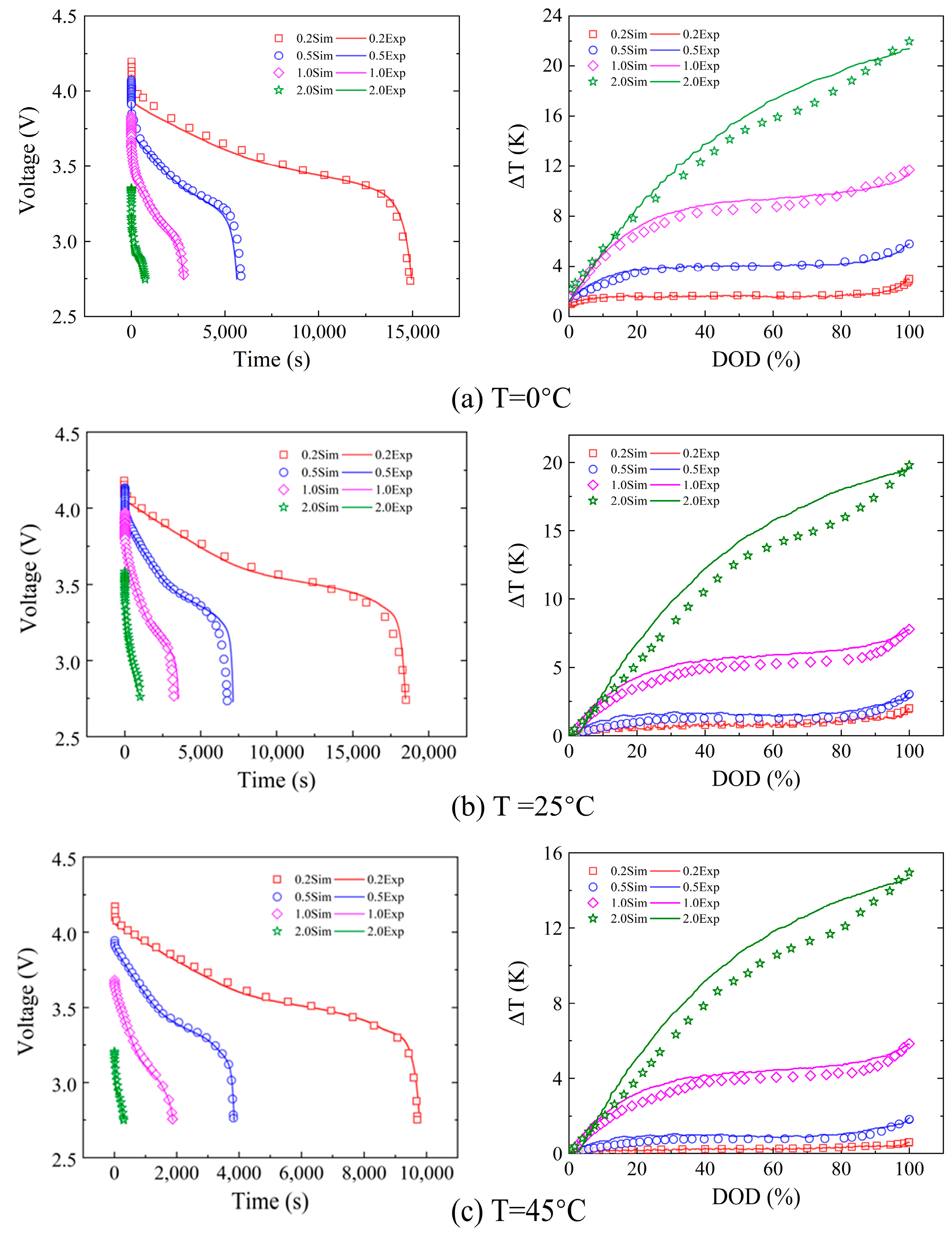
2.5. Model Validation
3. Results and Discussion
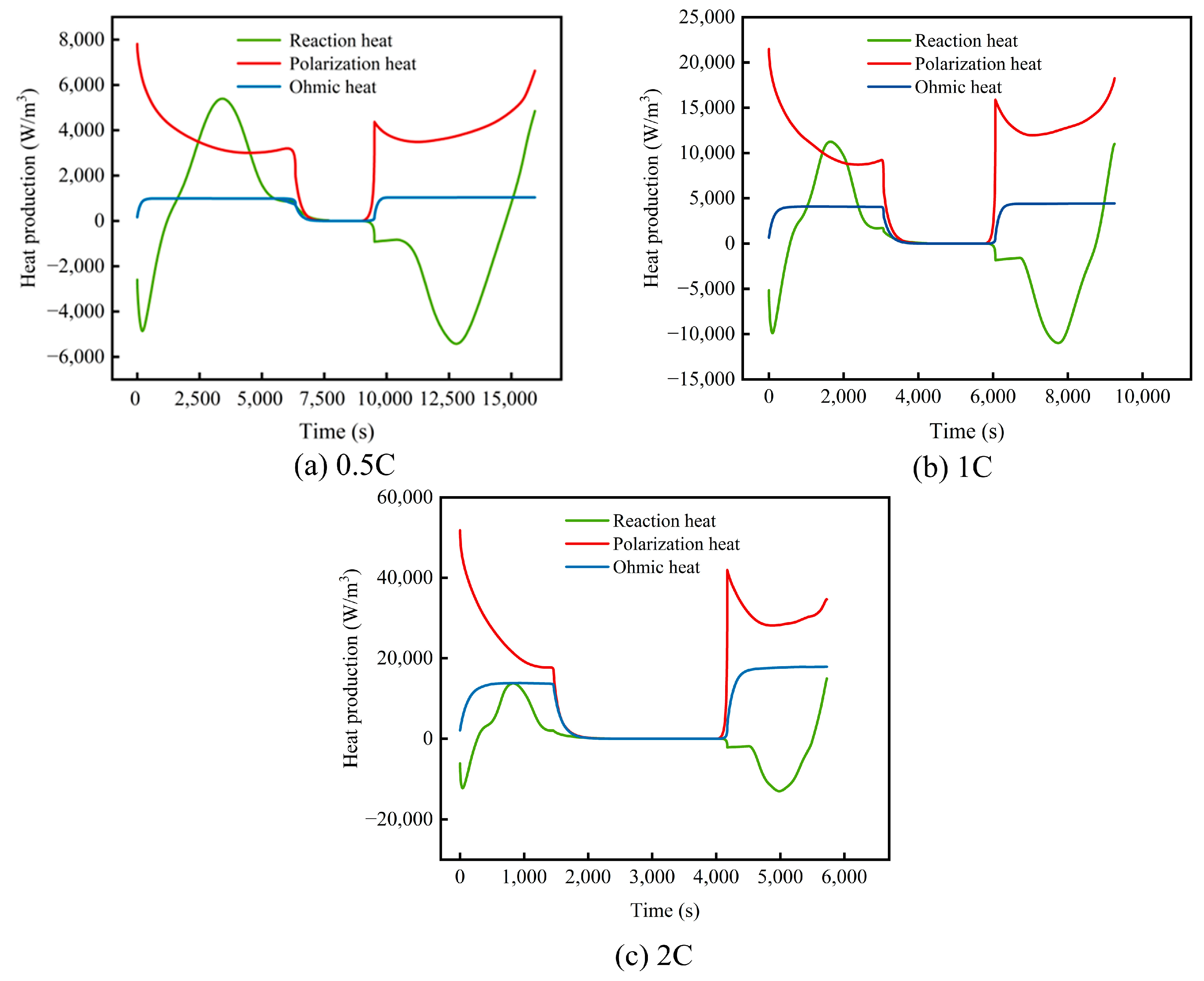
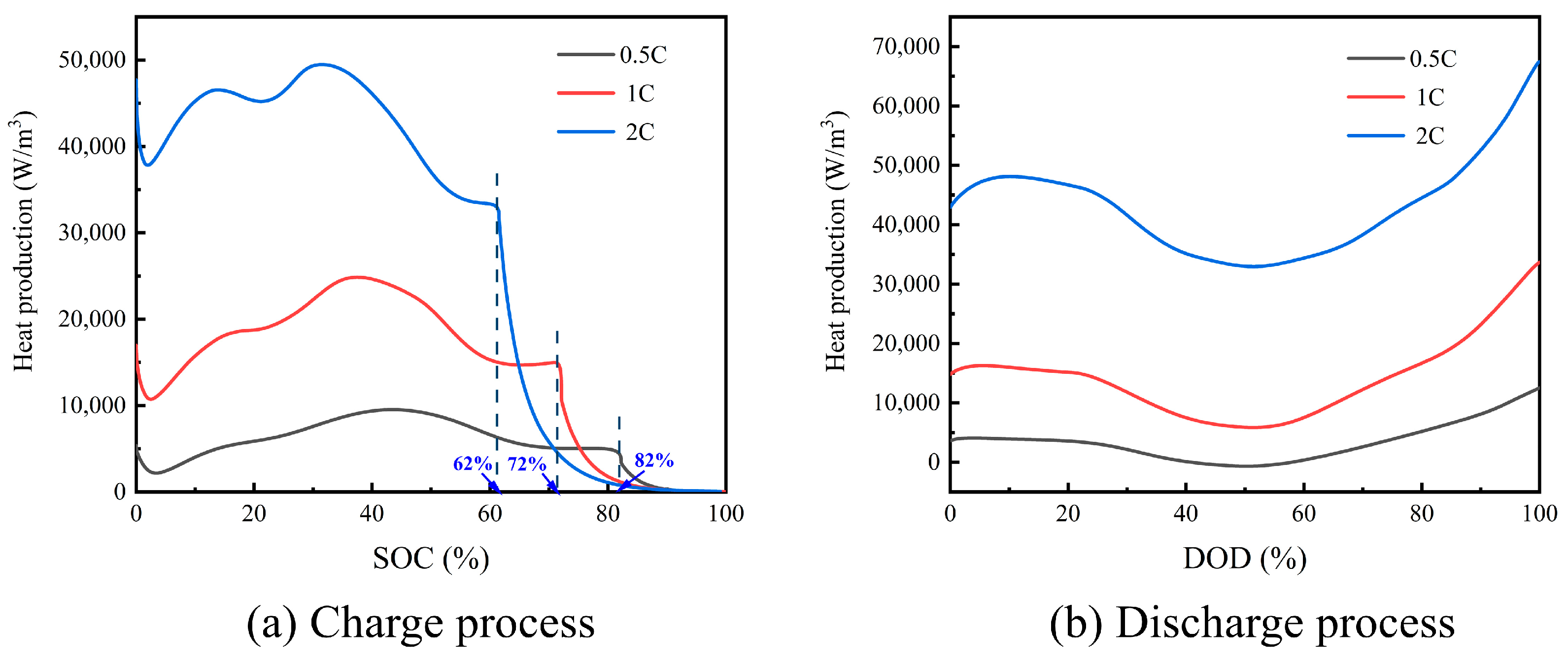
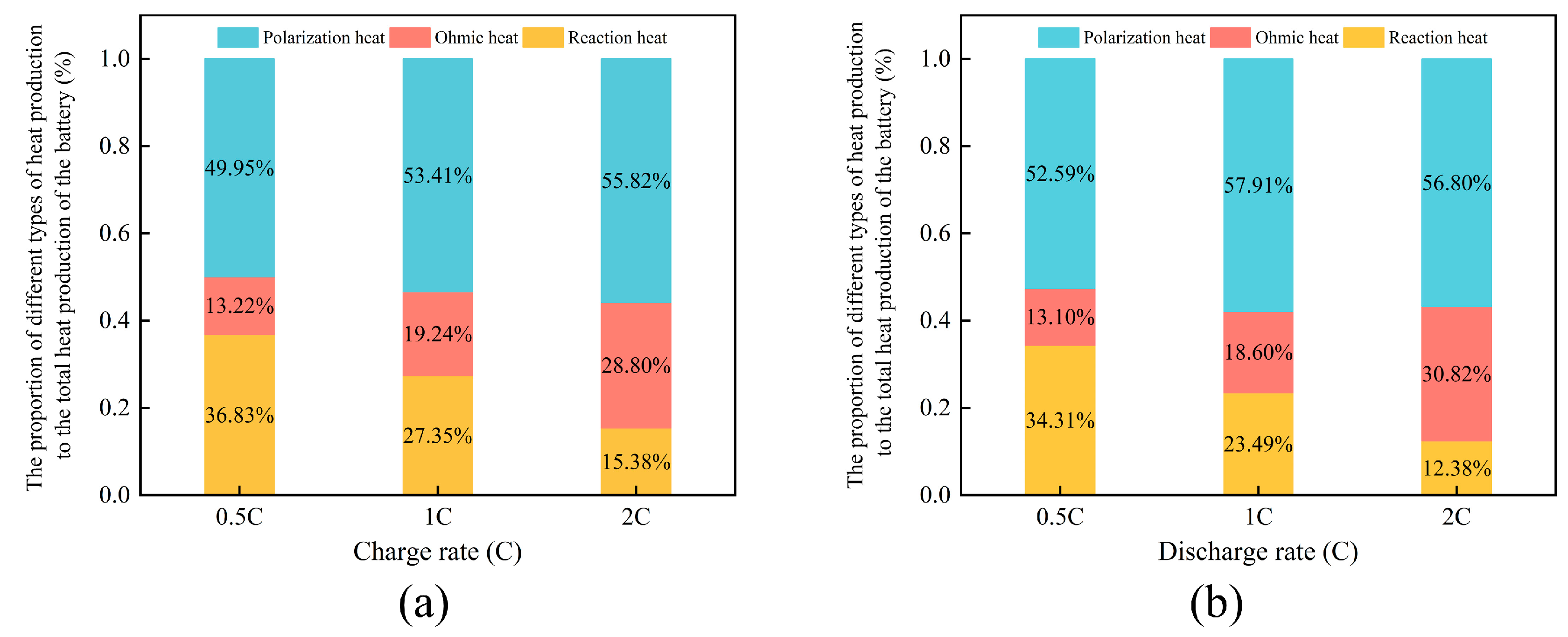
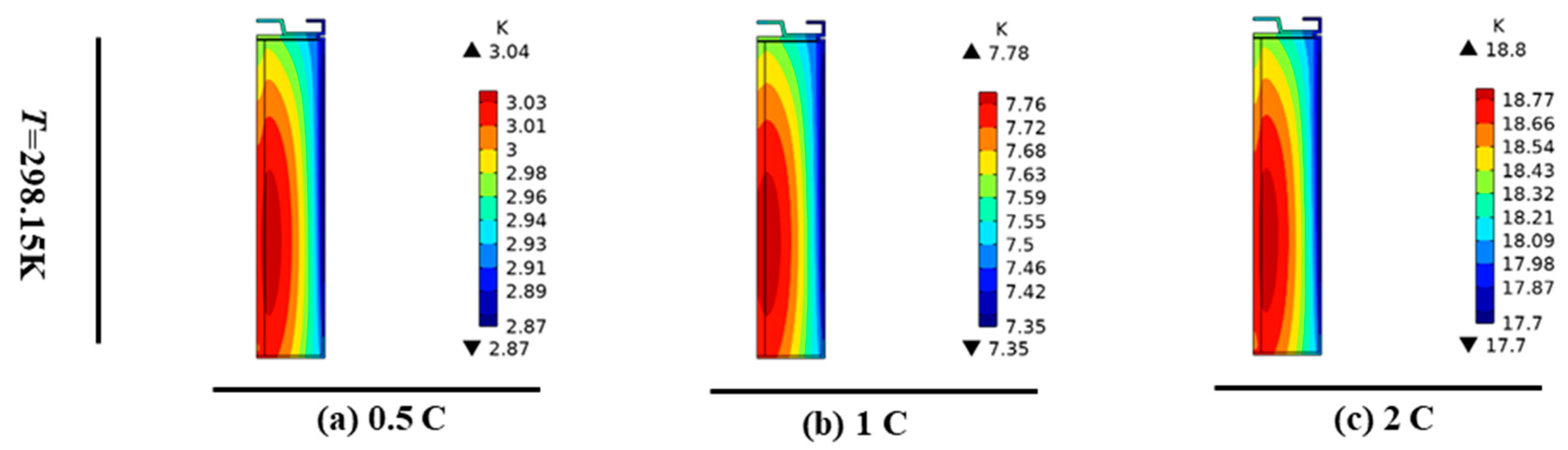
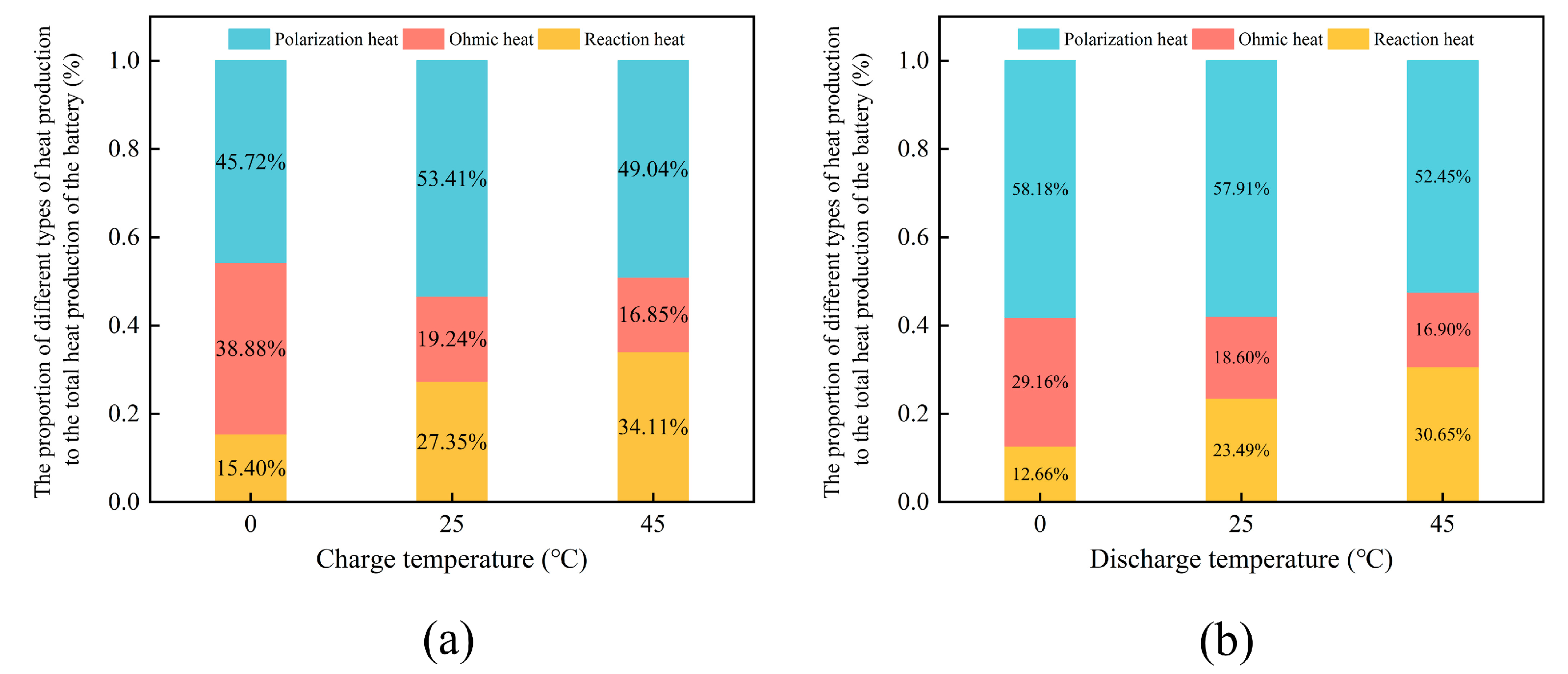
3.1. Heat Generation Mechanism of a Single Cell at Different Rates
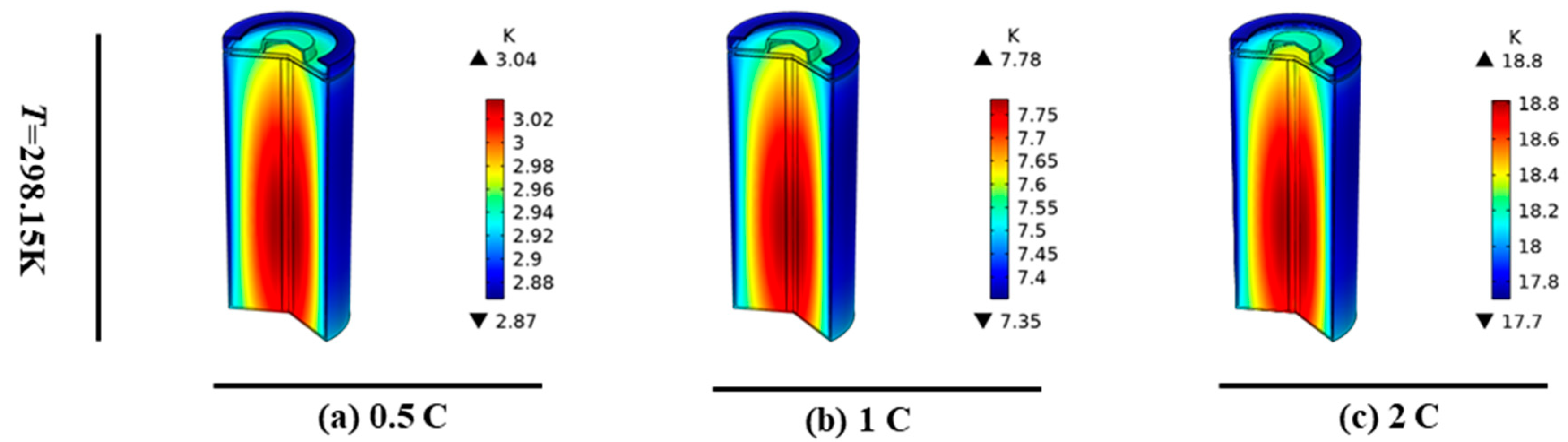
3.2. Single-Cell Discharge Temperature Distribution at Different Rates
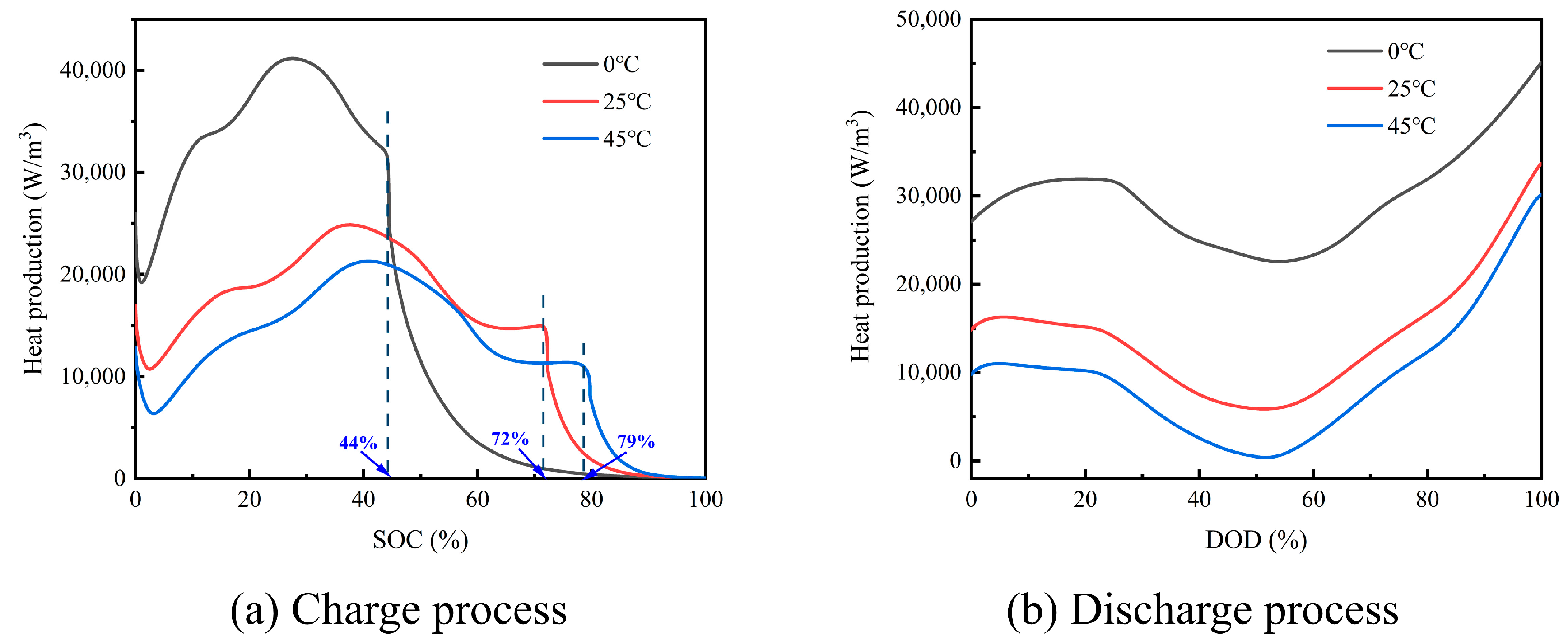
3.3. Heat Generation Mechanism of a Single Cell at Different Ambient Temperatures
3.4. Discharge Temperature Distribution of Single Cell at Different Ambient Temperatures
4. Conclusions
- Further investigation into the transitional phases of individual battery cells from controllable temperature rise to thermal runaway temperature rise. By exploring the dynamic changes in battery thermal behavior under extreme conditions, a more comprehensive understanding of the stability of batteries in various working environments can be obtained.
- Our next studies tend to consider extending the individual battery cell heat generation model to the battery pack level to address thermal management issues in grouped batteries. The thermal behavior of battery packs involves the mutual influence of multiple individual battery cells, which is crucial to practical applications such as electric vehicles and energy storage systems. Future research can optimize thermal management strategies to enhance the performance, lifespan, and safety of battery packs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| The concentration of the electrolyte, mol/m3 | |
| Specific heat capacity, J/(kg·K) | |
| Active particle radius, | |
| Lithium-ion diffusion coefficient of the negative electrode | |
| Diffusion coefficient | |
| Faraday’s constant, (C/mol) | |
| electrical conductivity, S/m | |
| Total battery heat production, W/m3 | |
| heat of reaction, W/m3 | |
| Temperature, °C | |
| SOC | State of Charge |
| Overpotential | |
| Boltzmann’s constant | |
| Heat transfer coefficient, W/(m2·K) | |
| Electrolyte activity correlation | |
| Charge–discharge rate | |
| Lithium-ion diffusion coefficient of the positive electrode | |
| Equilibrium potential | |
| Current density, A/m3 | |
| Thermal conductivity, W/(m·K) | |
| Ohmic heating, W/m3 | |
| Polarization heat, W/m3 | |
| DOD | Depth of discharge |
| Radiance, J/K | |
| Density; kg/m3 | |
| Heat transfer coefficient, W/(m2·K) | |
| Electrolyte activity correlation | |
| Charge–discharge rate | |
| Lithium-ion diffusion coefficient of the positive electrode | |
| Equilibrium potential |
References
- Song, D.; Meng, W.; Dong, M.; Yang, J.; Wang, J.; Chen, X.; Huang, L. A critical survey of integrated energy system: Summaries, methodologies and analysis. Energy Convers. Manag. 2022, 266, 115863. [Google Scholar] [CrossRef]
- Auto Review. Monthly Data Tracking of New Energy Vehicles. Available online: https://autoreview.com.cn/m/show_article-12776.html (accessed on 11 November 2023).
- Rao, Z.; Wang, S. A review of power battery thermal energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Zybert, M.; Ronduda, H.; Raróg-Pilecka, W.; Wieczorek, W. Application of rare earth elements as modifiers for Ni-rich cathode materials for Li-ion batteries: A mini review. Front. Energy Res. 2023, 11, 1248641. [Google Scholar] [CrossRef]
- Zybert, M.; Ronduda, H.; Dąbrowska, K.; Ostrowski, A.; Sobczak, K.; Moszyński, D.; Hamankiewicz, B.; Rogulski, Z.; Rarog-Pilecka, W.; Wieczorek, W. Suppressing Ni/Li disordering in LiNi0.6Mn0.2Co0.2O2 cathode material for Li-ion batteries by rare earth element doping. Energy Rep. 2022, 8, 3995–4005. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Luo, L.; Fan, Y.; Du, Z. A review on thermal management of lithium-ion batteries for electric vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, W.; Li, H.; Wan, W.; Zhang, W.; Zhuo, W.; Liu, Q. Heat transfer characteristics and low-temperature performance of a lithium-ion battery with an inner cooling/heating structure. Appl. Therm. Eng. 2023, 219, 119352. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5. [Google Scholar] [CrossRef]
- Xie, Y.; Shi, S.; Tang, J.; Wu, H.; Yu, J. Experimental and analytical study on heat generation characteristics of a lithium-ion power battery. Int. J. Heat Mass Transf. 2018, 122, 884–894. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. The use of mathematical modeling in the design of lithium/polymer battery systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Srinivasan, V.; Wang, C.-Y. Analysis of electrochemical and thermal behavior of Li-ion cells. J. Electrochem. Soc. 2002, 150, A98. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. Two-dimensional electrochemical–thermal coupled modeling of cylindrical LiFePO4 batteries. J. Power Sources 2014, 256, 233–243. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, J.; Liu, J. An investigation on the significance of reversible heat to the thermal behavior of lithium ion battery through simulations. J. Power Sources 2014, 266, 422–432. [Google Scholar] [CrossRef]
- Lai, Y.; Du, S.; Ai, L.; Ai, L.; Cheng, Y.; Tang, Y.; Jia, M. Insight into heat generation of lithium ion batteries based on the electrochemical-thermal model at high discharge rates. Int. J. Hydrog. Energy 2015, 40, 13039–13049. [Google Scholar] [CrossRef]
- Du, S.; Lai, Y.; Ai, L.; Ai, L.; Cheng, Y.; Tang, Y.; Jia, M. An investigation of irreversible heat generation in lithium ion batteries based on a thermo-electrochemical coupling method. Appl. Therm. Eng. 2017, 121, 501–510. [Google Scholar] [CrossRef]
- Chiew, J.; Chin, C.; Toh, W.; Gao, Z.; Jia, J.; Zhang, C. A pseudo three-dimensional electrochemical-thermal model of a cylindrical LiFePO4/graphite battery. Appl. Therm. Eng. 2019, 147, 450–463. [Google Scholar] [CrossRef]
- Han, X.; Huang, Y.; Lai, H. Electrochemical-thermal coupled investigation of lithium iron phosphate cell performances under air-cooled conditions. Appl. Therm. Eng. 2019, 147, 908–916. [Google Scholar] [CrossRef]
- Xu, W. Simulation Research on Thermal Behavior and Liquid Cooling Strategy for Lithium-Ion Battery during Charge–Discharge Cycle. Master’s Thesis, University of Science and Technology of China, Hefei, China, 2020. [Google Scholar]
- Li, H.; Saini, A.; Liu, C.; Yang, J.; Wang, Y.; Yang, T.; Pan, C.; Chen, L.; Jiang, H. Electrochemical and thermal characteristics of prismatic lithium-ion battery based on a three-dimensional electrochemical-thermal coupled model. J. Energy Storage 2021, 42, 102976. [Google Scholar] [CrossRef]
- Rao, L.; Newman, J. Heat-generation rate and general energy balance for insertion battery systems. J. Electrochem. Soc. 1997, 144, 2697. [Google Scholar] [CrossRef]
- Li, G.; Li, S. Physics-based CFD simulation of lithium-ion battery under the FUDS driving cycle. ECS Trans. 2015, 64, 1. [Google Scholar] [CrossRef]
- Mei, W.; Chen, H.; Sun, J.; Wang, Q. Numerical study on tab dimension optimization of lithium-ion battery from the thermal safety perspective. Appl. Therm. Eng. 2018, 142, 148–165. [Google Scholar] [CrossRef]
- Mei, W.; Chen, H.; Sun, J.; Wang, Q. The effect of electrode design parameters on battery performance and optimization of electrode thickness based on the electrochemical–thermal coupling model. Sustain. Energy Fuels 2019, 3, 148–165. [Google Scholar] [CrossRef]
- COMSOL Multiphysics; C.M. Library: Charlotte, NC, USA, 2016.
- Dong, T.; Peng, P.; Jiang, F. Numerical modeling and analysis of the thermal behavior of NCM lithium-ion batteries subjected to very high C-rate discharge/charge operations. Int. J. Heat Mass Transf. 2018, 117, 261–272. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Y.; Jia, M.; Tang, Y.; Lin, Y.; Zhang, Z.; Liu, Y. An electrochemical–thermal model based on dynamic responses for lithium iron phosphate battery. J. Power Sources 2014, 255, 130–143. [Google Scholar] [CrossRef]
- Xu, W.; Hu, P. Numerical study on thermal behavior and a liquid cooling strategy for lithium-ion battery. Int. J. Energy Res. 2020, 44, 7645–7659. [Google Scholar] [CrossRef]




| Parameter | Domestic Battery |
|---|---|
| Model | 26,650 NMC lithium polymer battery |
| product accumulation size (mm) | 26 × 65 |
| nominal voltage (V) | 4.2 |
| practical capacity (Ah) | 5.2 |
| nominal capacity (Ah) | 5.0 |
| charge–discharge cut-off voltage (V) | 4.2/2.75 |
| charge–discharge rate (C) | 0.5, 1, 2 |
| ambient temperature (°C) | 0, 25, 45 |
| internal resistance (mΩ) | 18~22 |
| Parameter | Cathode | Diaphragm | Anode |
|---|---|---|---|
| ) | 8.0 | - | 1.0 |
| 0.444 | 0.37 | 0.35 | |
| 0.384 | - | 0.391 | |
| Reference reaction rate constant, m | - | ||
| 1200 | 1200 | 1200 | |
| 18,875 | - | 5200 | |
| 25,507 | - | 20,300 | |
| 0.5 0.5 | - | 0.5 0.5 | |
| 100 | - | 100 | |
| , ( | - | ||
| Bruggeman | 1.5 | 1.5 | 1.5 |
| Transfer coefficient of lithium-ion | 0.363 | 0.363 | 0.363 |
| reference temperature, (K) | 293.15 | - | - |
| Thickness (μm) | 42 | 25 | 30 |
| The surface emissivity of the thermoplastic layer | 0.65 | - | - |
| Battery spindle radius (mm) | 1.5 | - | - |
| ) | 5 | - | - |
| Parameter | Density ρ, kg/m3 | Ratio Thermal Cp, J/(kg·K) | Conductivity kT, W/(m·K) |
|---|---|---|---|
| Negative electrode material | 1347.33 | 1437.4 | 1.04 |
| Negative current collector | 8933 | 385 | 398 |
| Positive electrode materials | 1500 | 700 | 1 |
| Positive current collector | 2702 | 903 | 238 |
| Diaphragm | 1008.98 | 1978.16 | 0.344 |
| Electrolyte | 1210 | 1578.16 | 1.48 |
| Measuring Equipment | Manufacturer and Equipment Model | Technical Parameters | Uncertainty |
|---|---|---|---|
| Charging and discharging machine | Xinwei (CT4008-40V30A-NA) | 1. Battery pulse charge and discharge detection 2. Maximum number of cycles detection | Measurement accuracy is ±0.05% |
| high and low temperature alternating damp heat experimental box | MGDW-408-40 | The measurement temperature range is −40~150 °C | The temperature deviation is within ±2.0 °C, and the display accuracy is 0.01 C |
| SH-X multi-channel thermometer | The working temperature is in the range of −20~70 °C | The temperature deviation is within ±0.5 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Y.; Li, Y.; Gu, Y.; Liu, W.; Fang, J.; Pan, C. Numerical Study on Heat Generation Characteristics of Charge and Discharge Cycle of the Lithium-Ion Battery. Energies 2024, 17, 178. https://doi.org/10.3390/en17010178
Tan Y, Li Y, Gu Y, Liu W, Fang J, Pan C. Numerical Study on Heat Generation Characteristics of Charge and Discharge Cycle of the Lithium-Ion Battery. Energies. 2024; 17(1):178. https://doi.org/10.3390/en17010178
Chicago/Turabian StyleTan, Yuxuan, Yue Li, Yueqing Gu, Wenjie Liu, Juan Fang, and Chongchao Pan. 2024. "Numerical Study on Heat Generation Characteristics of Charge and Discharge Cycle of the Lithium-Ion Battery" Energies 17, no. 1: 178. https://doi.org/10.3390/en17010178
APA StyleTan, Y., Li, Y., Gu, Y., Liu, W., Fang, J., & Pan, C. (2024). Numerical Study on Heat Generation Characteristics of Charge and Discharge Cycle of the Lithium-Ion Battery. Energies, 17(1), 178. https://doi.org/10.3390/en17010178







