Abstract
With the rapid development of the new energy industry, supercapacitors have become key devices in the field of energy storage. To forecast the remaining useful life (RUL) of supercapacitors, we introduce a new technology that integrates variational mode decomposition (VMD) with a bidirectional long short-term memory (BiLSTM) neural network. Firstly, the aging experiments of supercapacitors under various temperatures and voltages were carried out to obtain aging data. Then, VMD was implemented to decompose the aging data, which helped to eliminate disturbances, including capacity recovery and test errors. Then, the hyperparameters of BiLSTM were adjusted, employing the sparrow search algorithm (SSA) to improve the consistency between the input data and the network structure. After obtaining the optimal hyperparameters of BiLSTM, the decomposed aging data were input into BiLSTM for prediction. The experimental results showed that the VMD-SSA-BiLSTM model proposed in this paper has high prediction accuracy and high robustness under different temperatures and voltages, with an average RMSE of 0.112519, a decrease of 44.3% compared to BiLSTM, and a minimum of 0.031426.
1. Introduction
Supercapacitors constitute an emerging class of energy storage device, characterized by their high energy density and power density, as well as high charging and discharging efficiency, wide operating temperature range, and long useful life [1,2,3]. Therefore, they are widely used in various applications. For example, in the field of transportation, supercapacitors can improve the acceleration performance of electric vehicles that frequently start and stop due to their high instantaneous power [4]. In wind power generation, the unstable current generated by wind turbines can extremely easily damage batteries, but supercapacitors have good power characteristics and weak current collection capabilities, which can be used to handle the impulse current generated by wind turbines [5,6]. In distributed generation, supercapacitors can be used to maintain the stability of busbar voltage and reduce the impact of distributed generation on the power grid during grid connection [7,8]. Although the initial investment of supercapacitors may be higher than that of traditional batteries, their overall cost of ownership is more advantageous in many applications due to their long lifespan and low maintenance costs [9,10,11]. Especially in situations where frequent starting, stopping, or rapid responses are required, predicting the RUL of supercapacitors reduces the frequency of maintenance and replacement with high reliability, thereby saving long-term operating costs [12]. As the core component of energy storage systems, the health status of supercapacitors plays a significant role in the safe operation of the entire energy storage system. Therefore the accurate prediction of the lifespan of supercapacitors has become a top priority [13,14,15].
Methods for predicting supercapacitor life can generally be divided into two categories: model-based methods and data-driven methods [16,17]. Model-based methods need to create an equivalent circuit model that mirrors the aging process of the supercapacitor, which can be used to predict the lifespan through parameter identification [18]. Based on data-driven methods, researchers have used various techniques, including traditional statistical methods, machine learning, and deep-learning techniques [19,20,21]. Statistical methods are one of the earliest methods used for estimating the lifespan of supercapacitors [22]. These methods include linear regression, support vector machine (SVM), principal component analysis (PCA), etc. [23,24,25]. Statistical methods typically rely on linear relationships of data and have limited modeling capabilities for complex relationships. Nevertheless, they are still effective when dealing with small datasets and simple models. Machine learning methods, such as decision trees and random forests, provide more powerful nonlinear modeling capabilities than statistical methods [26,27,28]. The application of machine learning methods in estimating the lifespan of supercapacitors is gradually increasing, but their performance may be affected due to the lack of sufficient annotated data [29,30]. Deep-learning methods, such as convolutional neural networks (CNNs), recurrent neural networks (RNNs), long short-term memory networks (LSTMs), etc., can automatically learn the hierarchical structure of data through multi-layer neural networks, thereby capturing complex nonlinear relationships [31,32,33]. The data-driven methods, on the other hand, continuously learn from a large amount of aging data and predict the lifespan accordingly [34]. In contrast to model-based techniques, data-driven methods eliminate the need for complex mathematical frameworks to emulate the internal aging processes of supercapacitors and mainly rely on a large amount of data [35,36]. Zhou et al. proposed a life prediction method based on the LSTM neural network [37]. The data of the supercapacitor were segmented into a training dataset and a predictive dataset to serve as the input for the neural network [38]. The overall results showed that the method exhibited great performance in the prediction of the RUL of the supercapacitor. Li et al. introduced an optimized forecasting model, which was a combination of the extreme learning machine (ELM) and the heuristic Kalman filter (HKF) algorithm, designed for predicting the capacity of supercapacitors [39]. Furthermore, a mode of the RNN using a stacked BiLSTM was proposed by Liu et al. [40].
The LSTM effectively solves the problem of gradient explosion and vanishing in RNNs [41,42]. Although the LSTM can obtain long-distance feature information, the information obtained is all from before the output time and does not utilize reverse information [43,44]. The BiLSTM network has the capability to explore deeper into the connections among the current data points and their corresponding past and future time data, thus enhancing the predictive accuracy of the model and making more comprehensive and detailed decisions using past and future information [45,46,47].
The SSA represents a new approach to swarm-based optimization, drawing inspiration from sparrows’ foraging and anti-predator strategies [48,49]. It is superior to other algorithms, like grey wolf optimization (GWO) and particle swarm optimization (PSO) in terms of the local search strength and speed of convergence [50,51].
Because the actual capacity of a fully charged supercapacitor can directly reflect the attenuation of the supercapacitor RUL, it can serve as a crucial indicator of supercapacitor health in predicting the remaining lifespan [52]. However, there are noise and capacity recovery phenomena in the degradation curve of supercapacitors, which makes it difficult to accurately track the degradation trend of supercapacitors using capacity prediction directly [53].
Following the aforementioned analysis, this article proposes the VMD-SSA-BiLSTM model. VMD has been proven to have good performance in handling nonstationary signals, as well as having good decomposition ability and resistance to noise interference [54,55]. Therefore, in this article, VMD was used to process the aging data of supercapacitors, obtaining a sequence of intrinsic mode functions (IMFs) characterizing local features in order to remove noise interference and better extract the capacity degradation features. Then, a multi-layer BiLSTM model was used to predict multiple IMF components separately. To solve the issue of the model’s unstable prediction, the SSA was used to improve the count of concealed units in BiLSTM, as well as to adjust the number of epochs and the starting learning rate. Eventually, the forecasts from each component were merged to achieve the ultimate prediction outcome. To ensure the generalization ability of the model, the RULs of the supercapacitors under various temperatures and voltages were predicted. The results of this experiment indicate that the model exhibits strong generalization ability under various working conditions.
The rest of the paper is organized as follows: In Section 2, the VMD-SSA-BiLSTM method is presented. In Section 3, the aging state is introduced. In Section 4, the introduced model is used to forecast the RULs of supercapacitors under various temperature and voltage conditions. The conclusion is presented in Section 5.
The main research content of the article is shown in Figure 1. Firstly, obtain aging data under different voltage, current, and temperature conditions. The aging data obtained from the battery experiments were decomposed to five IMF components using the VMD method, and then the RULs of supercapacitors under different operating conditions were predicted using the SSA-BiLSTM method.
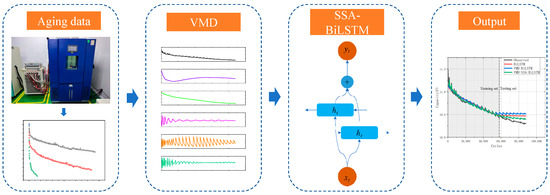
Figure 1.
The main research content.
2. VMD-SSA-BiLSTM Method
2.1. VMD
VMD was introduced by Dragomiretskiy et al. in 2014 [54]. Constructing a constrained variational model is the essence of the VMD algorithm, and the adaptive decomposition signal is achieved through the quest for the best solution within this model [56,57].
Firstly, original signal of the supercapacitor is decomposed into K components , with the following expression:
When solving this model, it is necessary to introduce and to transform a constrained variational issue into an unconstrained variational issue. The expression is as follows:
Initialize , , and , and use the alternating direction algorithm to adjust the values of , , and to search for the saddle point of the Lagrangian expression (2), which corresponds to the optimal solution of the problem. The updated expressions are as follows:
where , , and are the corresponding Fourier transforms of , , and , respectively, and is the number of iterations.
Expression (6) tests whether each component of the IMF can reach the required error accuracy and stop updating after meeting the requirements, which is as follows:
2.2. BiLSTM
In the BiLSTM architecture, at each layer is composed of a combination of three components: , , and . The combination process of each hidden layer state is represented by Equation (7).
In the equation, LSTM stands for the computation procedures of the traditional LSTM network.
From Figure 2, it can be observed that BiLSTM incorporates a data stream moving from the future toward the past, which is in addition to the unidirectional flow from the past to the future in standard LSTM models. The hidden layers from previous and subsequent time steps are not connected, which allows BiLSTM to better explore the temporal features of the data. However, the number of units in the hidden layer, the epochs required for the iterative optimization of the loss function, and the starting learning rate can all affect the accuracy of the predicted output data. The manual tuning of these parameters can be time-consuming and may not result in optimal parameters. Therefore, a sparrow swarm particle dimension was constructed based on the number of hyperparameters requiring optimization, using the SSA to adjust those parameters.
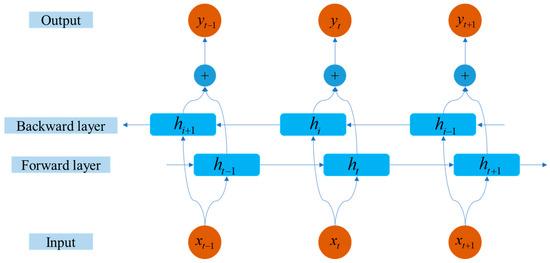
Figure 2.
The framework of the BiLSTM neural network.
2.3. SSA
The SSA is inspired by the foraging and anti-predator strategies of sparrows [50]. The location of the sparrows is represented as follows:
The fitness values of all the sparrows can be represented as the following vector:
The values in each row of represent individual fitness values.
In the SSA, it is the responsibility of the producers to forage for sustenance and direct the travel path of the group. The positional information of the producers is as follows:
In the formula, (0,1], [0,1], [0.5,1], and is a 1 d matrix with all elements equal to 1.
Scroungers persistently keep an eye on the producers. Once the producers stumble upon better food, the scroungers promptly leave their existing position to contend for the food, thus updating their location as follows:
where is the best position in generation t + 1. A is a 1 d matrix, where each element is randomly assigned either 1 or −1, and .
The algorithm presupposes that between 10% and 20% of individuals within the population will become aware of the threat. The starting location for these individuals is randomly generated within the population as follows:
where [−1,1] and are a constant.
The flowchart of the supercapacitor RUL prediction method based on VMD-SSA-BiLSTM is shown in Figure 3. VMD decomposition can effectively reduce the noise interference in the data through modular processing, such as capacity recovery and testing errors; the BiLSTM network can capture complex features in time series data; the SSA, with its powerful optimization ability and fast convergence speed, is used to optimize the number of hidden layer units, epochs, and initial learning rate of BiLSTM networks, thereby improving the matching degree between the data and network structure.
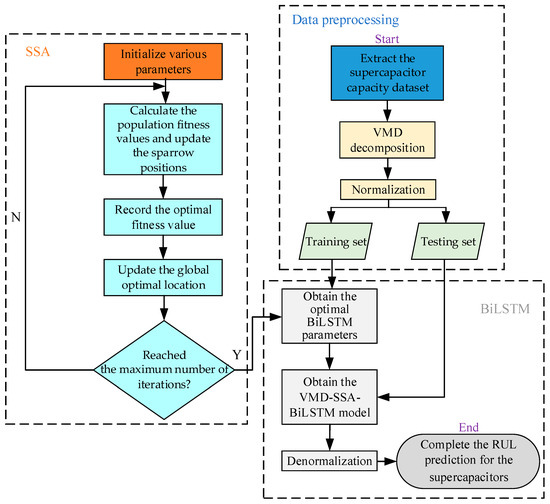
Figure 3.
Flowchart of the RUL prediction method for supercapacitors based on VMD-SSA-BiLSTM.
3. Supercapacitor Aging State Test
3.1. Test Platform and Aging Data
The aging status testing platform for the supercapacitors is mainly divided into three parts: the tester, the temperature chamber, and the computer. The model of the tester was NEWARE CT-4008-5V100A. The temperature chamber was employed to furnish a particular temperature environment to test the aging status of the supercapacitors, and the model was MENTEK MHP-150-AA. Figure 4 displays the aging supercapacitor test platform.

Figure 4.
Supercapacitor aging test platform.
In this study, we used the Maxwell BCAP0010 P270 T01 capacitor. This supercapacitor comes with the following characteristics: a rated capacity of 10 F, a minimum capacity of 8 F, a maximum equivalent series resistance (ESR) of 75 mΩ, a rated voltage of 2.7 V, a maximum voltage not exceeding 2.85 V, a maximum current not exceeding 7.2 A, a leakage current of 0.030 mA, an operating temperature range of −40 °C to 85 °C, and an energy storage temperature range of −40 °C to 70 °C. This model of supercapacitor has been widely used in consumer electronics, UPS uninterruptible power supplies, intelligent instruments, car recorders, toys, program-controlled switches, etc.
The aging of the supercapacitors shows that the aging factors are mainly the voltage, temperature, and discharge/charge current [58,59]. In order to confirm the adaptability of the proposed model, aging experiments on the supercapacitors under various temperatures and voltages were carried out, and the aging data were measured and predicted. Table 1 provides detailed information. SC1 represents the first supercapacitor, and so on.

Table 1.
Data for the supercapacitors.
3.2. Simulation Platform
The methodology introduced in this article was implemented using MATLAB 2021b, running on a Windows 10 operating system, and executed on a hardware platform consisting of an Intel Core i5-7300 CPU and NVIDIA GTX 1050 GPU.
4. Predictions and Result Analysis
4.1. Decomposition of Supercapacitor Capacity Sequences Using VMD
In the degradation curves of the supercapacitors, noise and capacity recovery phenomena exist [60,61]. VMD was applied to decompose the supercapacitor capacity sequences into K IMF components, and the predictive results of each component were superimposed as the final output. Gradually increasing K during the training process, this work selected K = 5, corresponding to the optimal tradeoff between training time and prediction error as the final number of IMF components.
Figure 5 shows the decay graph of the capacity of SC5 with the cycle times and the VMD decomposition graph of the capacity decline curve. It shows that the capacity exhibits a degradation trend as the number of cycles increases, and the attenuation of capacity is often accompanied by an increase in the internal resistance of the battery. During the use of supercapacitors, changes in internal resistance can often lead to performance degradation. An increase in the internal resistance will reduce the power output and energy efficiency of supercapacitors. There is a capacity regeneration phenomenon during the capacity drop process. In some cases, supercapacitors may experience partial capacity recovery after a period of rest or appropriate voltage/temperature treatment. IMF1 and IMF2 reflect the overall trend of the original data, IMF3 shows the fluctuation within a smaller time period, and IMF4–IMF5 represent the changes in higher frequency bands.
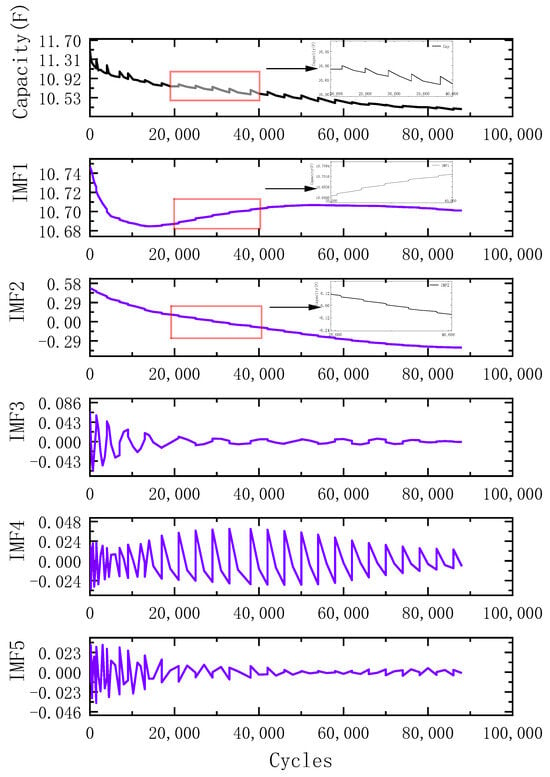
Figure 5.
The VMD decomposition results of SC5.
4.2. Data Processing and Evaluation Index
We found that the cycle number and capacity decay of supercapacitors have a close relationship with a Pearson correlation coefficient of −0.9 or higher, indicating a high degree of negative correlation. Therefore, we included both the cycle number and decomposed capacitance as inputs to our BiLSTM model. Normalization was performed first as follows.
Normalization is a prevalent technique in deep learning for preparing datasets before training models. Its main aim is to neutralize the influence of varying scales of numerical features within the data on the model’s predictive outcomes [62]. For example, the lifespan of supercapacitors is considerable, potentially extending to hundreds of thousands of charge–discharge cycles. In contrast, the capacity of supercapacitors measures around 10 F. The discrepancy in the magnitude between these two data is huge. In addition, normalization can accelerate the speed with which the model processes data [63].
To ensure an accurate evaluation of the model performance, this paper adopted three evaluation indicators, namely the root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) as the evaluation indicators. The calculation formulas for these indicators are as follows:
4.3. SSA Optimization Results
The quantity of hidden layer units is a critical parameter of BiLSTM. When there are too few units in the hidden layer, the neural network does not learn enough about the information in the training set, which will lead to underfitting. When a neural network has too many hidden layer units, the insufficient information within the training dataset leads to overfitting, as it cannot adequately train all the neurons in the hidden layer [64]. Furthermore, even when the training data is rich in information, the excessive number of units in the hidden layer can extend the training duration, which may hinder the achievement of the desired outcomes. The same is true for epochs, where if they are too small, it can lead to underfitting, and if they are too large, it will lead to overfitting. In addition, a suitable initial learning rate enables the objective function to converge to a local minimum at an appropriate time. Obviously, selecting appropriate hyperparameters is crucial [65,66].
The SSA optimization results in different temperature groups are shown in Table 2. The SSA optimization results in different voltage groups are shown in Table 3.

Table 2.
SSA optimization results under different temperatures.

Table 3.
SSA optimization results under different voltages.
4.4. Experimental Results and Comparative Analysis
In this experiment, the first 70% of the data was selected as the training set, and the remaining 30% was reserved for the test set. To verify the superiority and robustness of the proposed VMD-SSA-BiLSTM model, the BiLSTM and VMD-BiLSTM methods were used as comparisons. The training and prediction results of the proposed model were compared with the measured values, as well as the BiLSTM and VMD-BiLSTM models, as shown in Figure 6. Figure 6A–C shows the prediction results at different temperatures, and Figure 6D–F shows the prediction results at different voltages. As shown in Figure 6, compared with the BiLSTM and VMD-BiLSTM methods, the capacity prediction curve of the VMD-SSA-BiLSTM method was closest to the true degradation trend. In addition, it was observed that the VMD-BiLSTM method had inferior prediction results to the BiLSTM method for some supercapacitors. This may be due to the larger data size resulting from the decomposition of the capacity degradation data, which led to an underfitting caused by mismatched hyperparameters and input data, such as the number of hidden layer units.
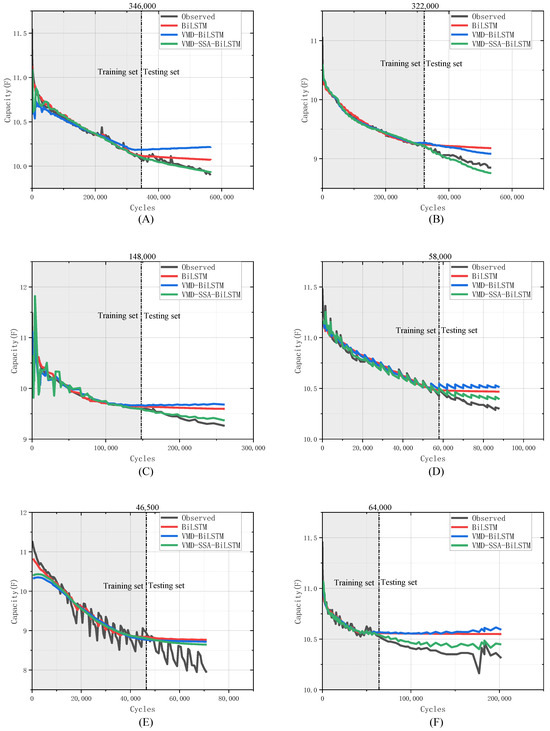
Figure 6.
Comparison of the prediction results under different aging conditions. (A) SC1: 2.9 V, 3 A, 25 °C; (B) SC2: 2.9 V, 3 A, 50 °C; (C) SC3: 2.9 V, 3 A, 65 °C; (D) SC4: 2.7 V, 3 A, 25 °C; (E) SC5: 3.2 V, 3 A, 25 °C; (F) SC6: 3.7 V, 3 A, 25 °C.
The estimation errors under different temperatures are shown in Table 4. The estimation errors under different voltages are shown in Table 5. Among them, the smaller the RMSE, MAE, and MAPE, the higher the prediction accuracy of the prediction model. Whether at different temperatures or voltages, the RUL calculation results of VMD-SSA-BiLSTM displayed the least amount of error. In the testing set, the minimum RMSE achievable was 0.031426, while the minimum MAE was 0.024544, and the minimum MAPE was 0.24534%.

Table 4.
Estimation errors of the supercapacitors under different temperatures.

Table 5.
Estimation errors of the supercapacitors under different voltages.
In different temperature groups, the capacity degradation curves of the supercapacitor were relatively smooth without significant fluctuations. Therefore, the predictive results of VMD-SSA-BiLSTM had a good fitting effect with the actual values.
In different voltage groups, the capacitance degradation curves of the supercapacitors exhibited significant fluctuations. This is due to complex physical and chemical reactions and environmental factors, resulting in capacity recovery phenomena and noise in the degradation curves of the supercapacitors. Figure 6D shows that the prediction results of the BiLSTM model did not reflect the trend of the capacity fluctuations, while the VMD-BiLSTM model and VMD-SSA-BiLSTM reflected the trend of the capacity degradation curve fluctuations. This is due to the use of a sequence of inherent mode functions that characterize local features obtained through VMD decomposition. Moreover, after the optimization of the SSA, the predicted results of VMD-SSA-BiLSTM were closer to the actual value than BiLSTM, which shows that the SSA method supports the optimization of the hyperparameter of BiLSTM to have good results.
Compared with different temperature groups, the degradation curves of the supercapacitors in the different voltage groups showed significant fluctuations, which affected the prediction accuracies to some extent. However, VMD-SSA-BiLSTM still reflected the degradation trend and capacity regeneration phenomenon, and compared with the control group, the accuracy was still the highest.
With respect to intuitively assessing the accuracies of the three approaches, Figure 7 and Figure 8 show the statistical errors of their predictions. Observing these figures reveals that the VMD-SSA-BiLSTM model consistently yielded the smallest error and highest precision across various temperatures and voltages. Other models exhibited limited generalization ability to data under diverse conditions and had large errors.
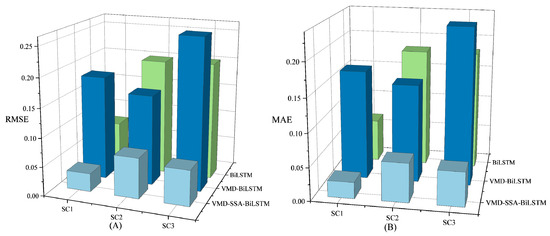
Figure 7.
Bar chart for the statistical errors of the predictions of the RULs of supercapacitors under different temperatures: (A) RMSE; (B) MAE.
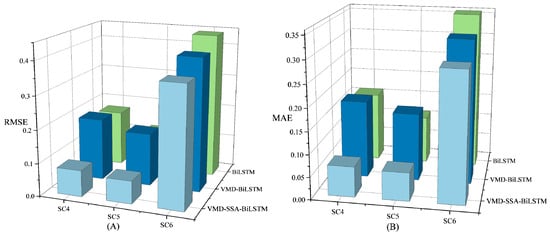
Figure 8.
Bar chart for the statistical errors of the predictions of the RULs of supercapacitors under different voltages: (A) RMSE; (B) MAE.
5. Conclusions
With the continuous improvements in the energy density and power performance requirements in energy storage systems, researchers have invested more and more attention in research into advanced electrochemical energy storage devices. As an important member of these energy storage devices, the condition of supercapacitors is closely related to the safe and stable operation of the entire energy storage system. This article proposed a method that combines VMD decomposition, SSA optimization, and the BiLSTM network to accurately predict the RULs of supercapacitors. VMD decomposition effectively reduced the noise interference in the data through modular processing, such as capacity recovery and testing errors; the BiLSTM network could capture complex features in time series data; the SSA, with its powerful optimization ability and fast convergence speed, was used to optimize the number of hidden layer units, epochs, and the initial learning rate of BiLSTM networks, thereby improving the matching degree between the data and network structure.
In this study, we selected temperature and voltage as the input variables, which had the most significant impacts on the degradation of supercapacitor capacity in the aging experiments of supercapacitors. We input the input variables into the VMD-SSA-BiLSTM model to predict the remaining service life. The results of the experiments showed that the model performed well in predicting the RULs of the supercapacitors and could maintain high prediction accuracy and strong robustness under different temperature and voltage conditions.
Author Contributions
Conceptualization, G.Q.; methodology, G.Q.; software, G.Q.; validation, K.W.; formal analysis, G.Q., K.W.; investigation, N.M.; resources, N.M.; data curation, N.M.; writing—original draft preparation, G.Q.; writing—review and editing, K.W.; supervision, K.W.; project administration, N.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Youth Fund of Shandong Province Natural Science Foundation (No. ZR2020QE212) and the Key Projects of Shandong Province Natural Science Foundation (No. ZR2020KF020).
Data Availability Statement
The data and materials used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
Ning Ma was employed by the company Shandong Suoxiang Intelligent Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Glossary
| The decomposed component IMF. | The maximum number of iterations. | ||
| The center frequency. | The warning value. | ||
| The convolution process. | The safe value. | ||
| The unit pulse function. | A random number that follows a normal distribution. | ||
| The penalty parameter. | The globally worst position. | ||
| The Lagrange multiplier. | The best position occupied by the producer. | ||
| The hidden state. | The global optimum position. | ||
| The forward-propagated hidden layer output state. | The step size control parameter that follows a normal distribution. | ||
| The backward-propagated hidden layer output state. | The step control parameter. | ||
| The current input. | The global best fitness values. | ||
| The forward hidden layer state. | The global worst fitness values. | ||
| The backward hidden layer state. | The fitness value of the i-th sparrow. | ||
| The output weight of the forward propagation unit hidden layer. | The dataset processed using standardization. | ||
| The output weight of the backward propagation unit hidden layer. | y | The dataset before standardization. | |
| The bias optimization parameter for the hidden layer at the present moment. | The minimum value in the data before standardization. | ||
| The number of sparrows. | The maximum value in the dataset. | ||
| The dimension of the variable to be optimized. | The actual value. | ||
| The number of current iterations. | The predicted value. |
References
- Zhang, L.; Hu, X.S.; Wang, Z.P.; Sun, F.C.; Dorrell, D.G. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Zhang, X.D.; Lin, Z.Y.; Chen, B.; Zhang, W.; Sharma, S.; Gu, W.T.; Deng, Y.L. Solid-state flexible polyaniline/silver cellulose nanofibrils aerogel supercapacitors. J. Power Sources 2014, 246, 283–289. [Google Scholar] [CrossRef]
- Pameté, E.; Köps, L.; Kreth, F.A.; Pohlmann, S.; Varzi, A.; Brousse, T.; Balducci, A.; Presser, V. The Many Deaths of Supercapacitors: Degradation, Aging, and Performance Fading. Adv. Energy Mater. 2023, 13, 2301008. [Google Scholar] [CrossRef]
- Berrueta, A.; Ursua, A.; San Martin, I.; Eftekhari, A.; Sanchis, P. Supercapacitors: Electrical Characteristics, Modeling, Applications, and Future Trends. IEEE Access 2019, 7, 50869–50896. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, J.; Sun, Y.; Fan, J. A Measurement-Based Dynamic Harmonic Model for Single-Phase Diode Bridge Rectifier-Type Devices. IEEE Trans. Instrum. Meas. 2024, 73, 1–13. [Google Scholar] [CrossRef]
- Wei, Y.W.; Sun, H.R.; Zhang, T.; Jiang, J.H.; Su, X.J.; Zeng, N.Y. Study of inductively coupled fuel cell DMPPT converters. Electr. Eng. 2024, 1–13. [Google Scholar] [CrossRef]
- Laadjal, K.; Cardoso, A.J.M. A review of supercapacitors modeling, SoH, and SoE estimation methods: Issues and challenges. Int. J. Energy Res. 2021, 45, 18424–18440. [Google Scholar] [CrossRef]
- León, L.M.; Romero-Quete, D.; Merchán, N.; Cortés, C.A. Optimal design of PV and hybrid storage based microgrids for healthcare and government facilities connected to highly intermittent utility grids. Appl. Energy 2023, 335, 120709. [Google Scholar] [CrossRef]
- Mwambeleko, J.J.; Kulworawanichpong, T. Supercapacitor and accelerating contact lines hybrid tram system. J. Energy Storage 2021, 44, 103277. [Google Scholar] [CrossRef]
- Guo, L.C.; Hu, P.; Wei, H. Development of supercapacitor hybrid electric vehicle. J. Energy Storage 2023, 65, 107269. [Google Scholar] [CrossRef]
- Deng, Y.B.; Li, C.S.; Deng, Y.; Chen, T.; Feng, S.Y.; Chu, Y.J.; Li, C.M. Energy Efficiency Optimization of Collaborative Power Supply System with Supercapacitor Storages. Energies 2023, 16, 1227. [Google Scholar] [CrossRef]
- Sawant, V.; Deshmukh, R.; Awati, C. Machine learning techniques for prediction of capacitance and remaining useful life of supercapacitors: A comprehensive review. J. Energy Chem. 2023, 77, 438–451. [Google Scholar] [CrossRef]
- Naseri, F.; Karimi, S.; Farjah, E.; Schaltz, E. Supercapacitor management system: A comprehensive review of modeling, estimation, balancing, and protection techniques. Renew. Sustain. Energy Rev. 2022, 155, 111913. [Google Scholar] [CrossRef]
- Liu, S.; Wei, L.; Wang, H. Review on reliability of supercapacitors in energy storage applications. Appl. Energy 2020, 278, 115436. [Google Scholar] [CrossRef]
- Haris, M.; Hasan, M.N.; Qin, S.Y. Early and robust remaining useful life prediction of supercapacitors using BOHB optimized Deep Belief Network. Appl. Energy 2021, 286, 116541. [Google Scholar] [CrossRef]
- Pan, S.; Cao, B.; Yuan, D.; Jiao, T.; Zhang, Q.; Tang, S. Complexes of cupric ion and tartaric acid enhanced calcium peroxide Fenton-like reaction for metronidazole degradation. Chin. Chem. Lett. 2023, 35, 109185. [Google Scholar] [CrossRef]
- Yi, Z.X.; Zhao, K.; Sun, J.R.; Wang, L.C.; Wang, K.; Ma, Y.Z. Prediction of the Remaining Useful Life of Supercapacitors. Math. Probl. Eng. 2022, 2022, 7620382. [Google Scholar] [CrossRef]
- Ayob, A.; Ansari, S.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.M. SOC, SOH and RUL Estimation for Supercapacitor Management System: Methods, Implementation Factors, Limitations and Future Research Improvements. Batteries 2022, 8, 189. [Google Scholar] [CrossRef]
- Park, J.E.; Chung, J.M. Capacitance Degradation Curve Prediction of Supercapacitors Based on Maximum Curvature Point Using Deep Neural Network. IEEE Electron Device Lett. 2023, 44, 1792–1795. [Google Scholar] [CrossRef]
- Ghosh, S.; Rao, G.R.; Thomas, T. Machine learning-based prediction of supercapacitor performance for a novel electrode material: Cerium oxynitride. Energy Storage Mater. 2021, 40, 426–438. [Google Scholar] [CrossRef]
- Yu, X.F.; Ai, T.T.; Wang, K. Application of nanogenerators in acoustics based on artificial intelligence and machine learning. APL Mater. 2024, 12, 020602. [Google Scholar] [CrossRef]
- Adekoya, G.J.; Adekoya, O.C.; Ugo, U.K.; Sadiku, E.R.; Hamam, Y.; Ray, S.S. A mini-review of artificial intelligence techniques for predicting the performance of supercapacitors. In Proceedings of the International Symposium on Nanostructured and Advanced Materials (ISNNAM), Electr Network, Online, 7–9 May 2021; pp. S184–S188. [Google Scholar]
- Ding, S.C.; Hang, J.; Wei, B.L.; Wang, Q.J. Modelling of supercapacitors based on SVM and PSO algorithms. IET Electr. Power Appl. 2018, 12, 502–507. [Google Scholar] [CrossRef]
- Nanda, S.; Ghosh, S.; Thomas, T. Machine learning aided cyclic stability prediction for supercapacitors. J. Power Sources 2022, 546, 231975. [Google Scholar] [CrossRef]
- Ma, X.; Fu, Y.; Gao, K.; Zhu, L.; Sadollah, A. A Multi-Objective Scheduling and Routing Problem for Home Health Care Services via Brain Storm Optimization. Complex Syst. Model. Simul. 2023, 3, 32–46. [Google Scholar] [CrossRef]
- Guo, F.; Lv, H.T.; Wu, X.W.; Yuan, X.H.; Liu, L.L.; Ye, J.L.; Wang, T.; Fu, L.J.; Wu, Y.P. A machine learning method for prediction of remaining useful life of supercapacitors with multi-stage modification. J. Energy Storage 2023, 73, 109160. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, D.Q. Adaptive Individual Q-Learning-A Multiagent Reinforcement Learning Method for Coordination Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–12. [Google Scholar] [CrossRef]
- Liao, D.Y.; Zhang, Z.; Song, T.T.; Liu, M.Y. An Efficient Centralized Multi-Agent Reinforcement Learner for Cooperative Tasks. IEEE Access 2023, 11, 139284–139294. [Google Scholar] [CrossRef]
- Jha, S.; Yen, M.T.; Salinas, Y.S.; Palmer, E.; Villafuerte, J.; Liang, H. Machine learning-assisted materials development and device management in batteries and supercapacitors: Performance comparison and challenges. J. Mater. Chem. A 2023, 11, 3904–3936. [Google Scholar] [CrossRef]
- Tawfik, W.Z.; Mohammad, S.N.; Rahouma, K.H.; Salama, G.M.; Tammam, E. Machine learning models for capacitance prediction of porous carbon-based supercapacitor electrodes. Phys. Scr. 2024, 99, 026001. [Google Scholar] [CrossRef]
- Wang, C.X.; Xiong, R.; Tian, J.P.; Lu, J.H.; Zhang, C.M. Rapid ultracapacitor life prediction with a convolutional neural network. Appl. Energy 2022, 305, 117819. [Google Scholar] [CrossRef]
- Saad, A.G.; Emad-Eldeen, A.; Tawfik, W.Z.; El-Deen, A.G. Data-driven machine learning approach for predicting the capacitance of graphene-based supercapacitor electrodes. J. Energy Storage 2022, 55, 105411. [Google Scholar] [CrossRef]
- Liu, Y.S.; Li, Q.; Wang, K. Revealing the degradation patterns of lithium-ion batteries from impedance spectroscopy using variational auto-encoders. Energy Storage Mater. 2024, 69, 103394. [Google Scholar] [CrossRef]
- Fu, Y.; Ma, X.; Gao, K.; Li, Z.; Dong, H. Multi-Objective Home Health Care Routing and Scheduling with Sharing Service via a Problem-Specific Knowledge-Based Artificial Bee Colony Algorithm. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1706–1719. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, Z.W.; Zheng, Y.S.; Liu, Y.J.; Li, H.; Che, Y.H.; Peng, J.; Teodorescu, R. Spatial-temporal data-driven full driving cycle prediction for optimal energy management of battery/supercapacitor electric vehicles. Energy Convers. Manag. 2023, 277, 116619. [Google Scholar] [CrossRef]
- Dubey, R.; Guruviah, V. A data-driven approach for evaluation of electrolyte informatics on electrochemical performance of carbon-based electrode materials. Ionics 2022, 28, 2169–2183. [Google Scholar] [CrossRef]
- Dong, X.J.; Liu, X.Z.; Shen, P.K.; Zhu, J.L. Phase Evolution of VC-VO Heterogeneous Particles to Facilitate Sulfur Species Conversion in Li-S Batteries. Adv. Funct. Mater. 2023, 33, 10987. [Google Scholar] [CrossRef]
- Huang, G.; Hu, M.; Xu, X.T.; Alothman, A.A.; Mushab, M.S.S.; Ma, S.J.; Shen, P.K.; Zhu, J.L.; Yamauchi, Y. Optimizing Heterointerface of Co2P-CoxOy Nanoparticles within a Porous Carbon Network for Deciphering Superior Water Splitting. Small Struct. 2023, 4, 00235. [Google Scholar] [CrossRef]
- Lang, X.M.; Li, P.; Cao, J.T.; Li, Y.; Ren, H. A Small Leak Localization Method for Oil Pipelines Based on Information Fusion. IEEE Sens. J. 2018, 18, 6115–6122. [Google Scholar] [CrossRef]
- Lang, X.M.; Li, P.; Guo, Y.; Cao, J.T.; Lu, S.Y. A Multiple Leaks’ Localization Method in a Pipeline Based on Change in the Sound Velocity. IEEE Trans. Instrum. Meas. 2020, 69, 5010–5017. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.S.; Hu, C.H.; Zhang, J.X. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Park, K.; Choi, Y.; Choi, W.J.; Ryu, H.Y.; Kim, H. LSTM-Based Battery Remaining Useful Life Prediction With Multi-Channel Charging Profiles. IEEE Access 2020, 8, 20786–20798. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, H.; Kang, L.; Zhang, Y.; Wang, L.; Wang, K. Prediction of Health Level of Multiform Lithium Sulfur Batteries Based on Incremental Capacity Analysis and an Improved LSTM. Prot. Control Mod. Power Syst. 2024, 9, 21–31. [Google Scholar] [CrossRef]
- Lyu, G.Z.; Zhang, H.; Miao, Q. Parallel State Fusion LSTM-based Early-cycle Stage Lithium-ion Battery RUL Prediction Under Lebesgue Sampling Framework. Reliab. Eng. Syst. Saf. 2023, 236, 109315. [Google Scholar] [CrossRef]
- Lou, G.M.; Lin, W.W.; Huang, G.X.; Xiang, W. A two-stage online remaining useful life prediction framework for supercapacitors based on the fusion of deep learning network and state estimation algorithm. Eng. Appl. Artif. Intell. 2023, 123, 106399. [Google Scholar] [CrossRef]
- Guo, X.F.; Wang, K.Z.; Yao, S.; Fu, G.J.; Ning, Y. RUL prediction of lithium ion battery based on CEEMDAN-CNN BiLSTM model. Energy Rep. 2023, 9, 1299–1306. [Google Scholar] [CrossRef]
- Ma, Y.; Li, J.Q.; Gao, J.W.; Chen, H. State of health prediction of lithium-ion batteries under early partial data based on IWOA-BiLSTM with single feature. Energy 2024, 295, 131085. [Google Scholar] [CrossRef]
- Lin, C.S.; Tuo, X.; Wu, L.X.; Zhang, G.Y.; Zeng, X.L. Accurate Capacity Prediction and Evaluation with Advanced SSA-CNN-BiLSTM Framework for Lithium-Ion Batteries. Batteries 2024, 10, 71. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.L.; Chen, L.; Qi, C.S.; Fernandez, C. Multiple layer kernel extreme learning machine modeling and eugenics genetic sparrow search algorithm for the state of health estimation of lithium-ion batteries. Energy 2023, 282, 128776. [Google Scholar] [CrossRef]
- Xue, J.K.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Sun, J.Q.; Sun, H.R.; Jiang, J.H. An improved modulation method for low common-mode current non-isolated series simultaneous power supply dual-input inverters for new energy generation applications. Electr. Eng. 2024, 1–11. [Google Scholar] [CrossRef]
- Ouyang, M.S.; Shen, P.C. Prediction of Remaining Useful Life of Lithium Batteries Based on WOA-VMD and LSTM. Energies 2022, 15, 8918. [Google Scholar] [CrossRef]
- Chaari, R.; Briat, O.; Vinassa, J.M. Capacitance recovery analysis and modelling of supercapacitors during cycling ageing tests. Energy Convers. Manag. 2014, 82, 37–45. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Yu, X.F.; Shang, Y.C.; Zheng, L.; Wang, K. Application of Nanogenerators in the Field of Acoustics. ACS Appl. Electron. Mater. 2023, 5, 5240–5248. [Google Scholar] [CrossRef]
- Wu, C.L.; Fu, J.C.; Huang, X.R.; Xu, X.F.; Meng, J.H. Lithium-Ion Battery Health State Prediction Based on VMD and DBO-SVR. Energies 2023, 16, 3993. [Google Scholar] [CrossRef]
- Tao, Q.; Lv, J.; Wu, J. Residual life prediction of lithium battery based on hybrid model of WOA-VMD and attention mechanism. Int. J. Low-Carbon Technol. 2024, 19, 798–806. [Google Scholar] [CrossRef]
- German, R.; Sari, A.; Briat, O.; Vinassa, J.M.; Venet, P. Impact of Voltage Resets on Supercapacitors Aging. IEEE Trans. Ind. Electron. 2016, 63, 7703–7711. [Google Scholar] [CrossRef]
- Kötz, R.; Ruch, P.W.; Cericola, D. Aging and failure mode of electrochemical double layer capacitors during accelerated constant load tests. J. Power Sources 2010, 195, 923–928. [Google Scholar] [CrossRef]
- Ding, G.R.; Wang, W.B.; Zhu, T. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on CS-VMD and GRU. IEEE Access 2022, 10, 89402–89413. [Google Scholar] [CrossRef]
- Xia, Q.T.; Li, X.K.; Wang, K.; Li, Z.H.; Liu, H.J.; Wang, X.; Ye, W.N.; Li, H.S.; Teng, X.L.; Pang, J.B.; et al. Unraveling the Evolution of Transition Metals during Li Alloying- Dealloying by In-Operando Magnetometry. Chem. Mater. 2022, 34, 5852–5859. [Google Scholar] [CrossRef]
- Meng, Q.; Lang, X.M.; Lin, M.Q.; Cai, Z.H.; Zheng, H.; Song, H.D.; Liu, W. Leak Localization of Gas Pipeline Based on the Combination of EEMD and Cross-Spectrum Analysis. IEEE Trans. Instrum. Meas. 2022, 71, 3130680. [Google Scholar] [CrossRef]
- Khalik, Z.; Donkers, M.C.F.; Sturm, J.; Bergveld, H.J. Parameter estimation of the Doyle-Fuller-Newman model for Lithium-ion batteries by parameter normalization, grouping, and sensitivity analysis. J. Power Sources 2021, 499, 229901. [Google Scholar] [CrossRef]
- Xi, Z.M.; Wang, R.; Fu, Y.H.; Mi, C. Accurate and reliable state of charge estimation of lithium ion batteries using time-delayed recurrent neural networks through the identification of overexcited neurons. Appl. Energy 2022, 305, 117962. [Google Scholar] [CrossRef]
- Weng, W.X.; Deng, Q.W.; Yang, P.Y.; Yin, K. Femtosecond laser-chemical hybrid processing for achieving substrate-independent superhydrophobic surfaces. J. Cent. South Univ. 2024, 31, 1–10. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Zhang, Y.; Wang, L.; Wang, K. Summary of Health-State Estimation of Lithium-Ion Batteries Based on Electrochemical Impedance Spectroscopy. Energies 2023, 16, 5682. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).