Abstract
In order to improve wind power utilization efficiency and reduce wind power prediction errors, a combined prediction model of EMD-KPCA-BilSTM-ATT is proposed, which includes a data processing method combining empirical mode decomposition (EMD) and kernel principal component analysis (KPCA), and a prediction model combining bidirectional long short-term memory (BiLSTM) and an attention mechanism (ATT). Firstly, the influencing factors of wind power are analyzed. The quartile method is used to identify and eliminate the original abnormal data of wind power, and the linear interpolation method is used to replace the abnormal data. Secondly, EMD is used to decompose the preprocessed wind power data into Intrinsic Mode Function (IMF) components and residual components, revealing the changes in data signals at different time scales. Subsequently, KPCA is employed to screen the key components as the input of the BiLSTM-ATT prediction model. Finally, a prediction is made taking an actual wind farm in Anhui Province as an example, and the results show that the EMD-KPCAM-BiLSTM-ATT combined model has higher prediction accuracy compared to the comparative model.
1. Introduction
Wind energy is a crucial clean and renewable energy source with approximately 1021 GW installed capacity throughout the whole world at the end of 2023 [1]. Its growth rate over the past decade has been about 8% annually [2]. Technological advancements have improved efficiency and reduced costs, making wind power an increasingly significant player in energy transition and sustainable development. However, its reliance on environmental factors leads to instability and intermittency in power output, necessitating accurate wind power prediction for reliable electricity supply and grid stability [3,4,5].
With rapid progress in computer science and artificial intelligence [6], data-driven neural network models have made significant strides in wind power prediction. Models such as Artificial Neural Network (ANN), Support Vector Machine (SVM), Random Forest (RF), and Extreme Learning Machine (ELM) have been used for wind power prediction [7,8,9]. However, due to volatility and unpredictability of wind power, the accuracy of simple models may no longer meet engineering requirements [10]. Consequently, combined prediction models have become a research focus. Reference [11] proposes the use of SVM and an improved dragonfly algorithm to predict short-term wind power generation through a hybrid prediction model. The performance of the prediction model is enhanced by optimizing the dragonfly algorithm and selecting the optimal parameters of the SVM. Reference [12] proposes a deep learning model that combines convolutional neural network (CNN) and long short-term memory (LSTM) networks. The model utilizes convolutional and pooling layers to extract feature information from wind power data, which is then fed into the LSTM network to capture the temporal relationships within the data and make predictions for wind power. Reference [13] proposes an ultra-short-term wind power prediction algorithm based on LSTM combined with an extreme gradient boosting algorithm; utilizing the error reciprocal method, the prediction results of the LSTM network and the temporal convolutional neural network are weighted and summed, which improves the prediction accuracy of wind power. Reference [14] proposes a wind power prediction algorithm based on a LSTM network model, which increases the weight of input features through an attention mechanism (ATT), thus improving the prediction accuracy of the model.
Considering the volatility and non-stationarity of actual wind power data, directly using a time series composite model to predict the original sequence may lead to inaccuracies. Therefore, processing the complex and variable wind power time series data is essential [15]. Reference [16] proposes using wavelet decomposition to decompose a wind speed sequence into a three-layer scale detail signal and approximate signal, and adopting the time-frequency analysis ability of wavelet decomposition to mine the original sequence information. Reference [17] proposes using the non-recursive advantage of variational mode decomposition (VMD) to decompose the original data. Through comparison with the BP and GRU models, VMD decomposition has been shown to effectively extract the detail information of wind power sequence. Reference [18] proposes a hybrid optimization algorithm combining VMD, maximum relevance and minimum redundancy algorithm (mRMR), LSTM, and firefly algorithm (FA). The algorithm first utilizes VMD to decompose wind power data into feature model functions, then selects the optimal feature set through mRMR, and finally optimizes LSTM parameters using FA. The prediction result is obtained by adding the prediction results of all the subsequences. Reference [19] proposes using empirical mode decomposition (EMD) to process the original data, which improves the prediction accuracy of wind power. The results of the example show that after the EMD algorithm is decomposed, each sequence signal is relatively stable. The more stable the time series is, the more accurate the prediction result is. The EMD ensemble method can obtain multi-layer modal components and better reflect the variation characteristics of wind speed series, and has higher decomposition accuracy and prediction accuracy. However, when the number of modal components after decomposition is large, it is necessary to build a prediction model for each modal component separately. The calculation amount increases, the difficulty of data integration increases, and the prediction accuracy is reduced.
According to the existing literature review, the current data decomposition algorithms may produce many components, and simple prediction models find it difficult to make full use of all the decomposed modal component information, thus affecting the experimental results. Therefore, many studies use ATT combined with the advantages of a neural network model to process multi-data for prediction to achieve better prediction results. Based on the above literature analysis, in order to solve the problem that more modal components after EMD decomposition result in poorer experimental results, the prediction effects of simple prediction models are not ideal. Kernel principal component analysis (KPCA) is proposed to screen the modal components after EMD decomposition, reduce the dimension of input parameters, and eliminate the redundancy of different time series decomposed by EMD, then the bidirectional long short-term memory (BiLSTM) model combined with ATT is used to predict wind power. Consequently, the EMD-KPCA-BiLSTM-ATT wind power prediction model is proposed. The results of the example analysis show that compared with the six models of LSTM, BiLSTM, BiLSTM-ATT, EMD-BiLSTM, EMD-BiLSTM-ATT, and EMD-KPCA-BiLSTM, the EMD-KPCA-BiLSTM-ATT combined prediction model has obvious advantages in prediction accuracy and stability.
The main research objectives of the paper are as follows:
(1) Introducing the quartile method for handling abnormal wind power data, reducing the impact of abnormal data on the experiments and improving the accuracy of subsequent predictions.
(2) Proposing the EMD-KPCA data processing method to ensure the reduction of feature dimensions without losing the original data information, thereby improving the computational efficiency and accuracy of feature extraction.
(3) Presenting the BiLSTM-ATT prediction model, and verifying the superiority of the proposed prediction model by the examples.
The rest of the paper is organized as follows: Section 2 introduces the methods used in wind power prediction models, including EMD, KPCA, BiLSTM, and ATT, and establishes an EMD-KPCA-BiLSTM-ATT combined model. Section 3 analyzes the correlation coefficients between environmental factors and wind power, and processes abnormal data using the quarterback method. Section 4 provides a detailed overview of the results obtained from each experiment and validates the effectiveness of the proposed model method. Section 5 summarizes the paper, discusses limitations, and outlines future research directions.
2. Prediction Model Proposal
2.1. Empirical Mode Decomposition (EMD)
EMD is a data-based adaptive signal decomposition method, which can decompose nonlinear and non-stationary signals into several IMFs. The basic principle of the EMD method is to decompose the signal into a series of IMFs with different frequencies and amplitudes, and each IMF is a function of the local characteristics of the signal [20]. The specific decomposition process is as follows:
(1) The extreme points of the original signal sequence are connected to form upper and lower envelopes, is the mean value of the upper and lower envelopes, and the first component is .
(2) In the second screening process, is regarded as a new sequence data, and step (1) is repeated to determine , which will be stopped when IMF conditions are met after k times. Note as the first IMF component, containing the highest frequency component in the original time series.
(3) Remove from the original sequence to yield a difference of .
(4) Take the difference as the initial time series, and repeat steps (1)~(3) to obtain n IMF components and the final residual , until is met, then terminate, where is the limiting value.
The original signal is decomposed into a series of IMFs and a residual term by the EMD method. Each IMF represents a local feature in the signal with different frequencies and amplitudes. It can adapt well to nonlinear and nonstationary signals, and has been widely used in signal processing and analysis.
2.2. Kernel Principal Component Analysis
The KPCA algorithm is an extended method of kernel function based on the PCA algorithm. Firstly, the data are mapped to the high-dimensional feature space, then the linear transformation is carried out in the high-dimensional space to achieve the effect of data discrimination and dimension reduction. Therefore, when the input data features are nonlinear, the KPCA algorithm solves the problem that the PCA algorithm can only process linear data. The specific steps are as follows:
(1) By selecting the appropriate kernel function, the original data set is mapped to the high-dimensional space to obtain the data matrix of the high-dimensional space. The multinomial kernel function is shown in Formula (1).
where and are original data samples; is a mapping function that maps data to a high-dimensional feature space; K is a high-dimensional data matrix; and d is the highest order term.
(2) The centralized kernel matrix Kc is calculated, which is used to modify the nuclear distance. The calculation formula is as follows:
where is an N by N matrix with each element being 1/N.
(3) The eigenvalue decomposition of the kernel matrix is carried out to obtain the eigenvalues and eigenvectors.
(4) The Schmidt orthogonalization method is used to orthogonalize and unit the eigenvectors, .
(5) The cumulative contribution rate of eigenvalue is calculated, and is selected according to the given cumulative contribution rate p. If > p, the first t principal components are used as the data after dimensionality reduction, and if < p, select again.
2.3. Attention Mechanism
ATT is a model that simulates the attention of the human brain through algorithms. The model takes advantage of the characteristics of the human brain to focus on certain important areas and pay less attention to other parts. It is widely used in natural language processing, statistical learning, and computer fields. In massive information sets, the key information is paid attention to according to the weight of attention allocation, and the influence rate of different features on the output is reasonably allocated so as to reduce the attention to non-key information and further improve the accuracy of the prediction model [21]. The ATT formula is as follows:
where is the attention distribution value of time t; u and w are the attention weight vectors; is a hyperbolic tangent function; is the hidden layer state vector at time t; e is the attention bias vector; is the scores for attention; is a natural exponential function; and is the attention distribution value of time j.
2.4. Bidirectional Long Short-Term Memory Neural Network
BiLSTM is composed of a layer of forward LSTM and a layer of reverse LSTM. The output of BiLSTM is determined by two layers of LSTM output, and its structure is shown in Figure 1. Through this structure, BiLSTM can well mine the forward and reverse dependency relationship in time series, and further improve the integrity and accuracy of the network’s extraction of time series features [22].
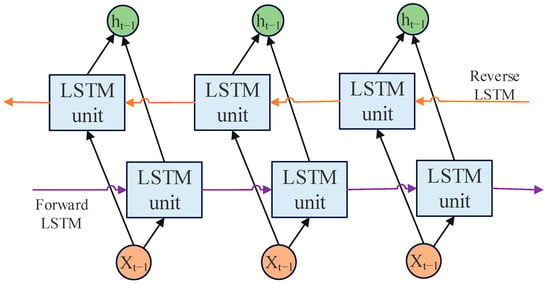
Figure 1.
BiLSTM schematic diagram.
The core of BiLSTM is the LSTM unit. The LSTM is a special Recurrent Neural Network (RNN) structure, which solves the problem of gradient disappearance and gradient explosion when dealing with long sequence data experienced by traditional RNN. It can effectively capture long-term dependencies in sequence data and has achieved remarkable results in tasks such as natural language processing, speech recognition, and machine translation. The unit structure diagram of the LSTM model is shown in Figure 2.
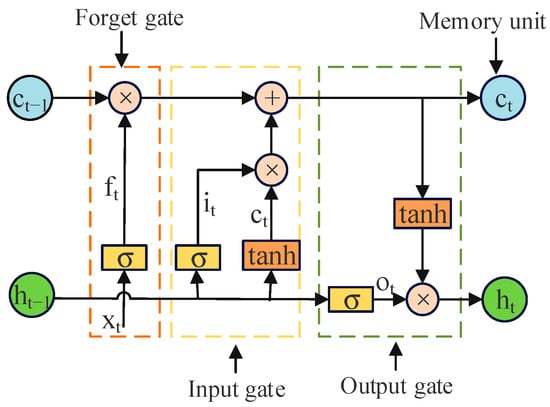
Figure 2.
The LSTM model unit structure.
As can be seen from Figure 2, the LSTM consists of the following four parts:
- (1)
- Forget gate (): Determines whether the memory of the previous moment is retained or not.
- (2)
- Input gate (): Determines whether the current input is added to the memory.
- (3)
- Output gate (): Determines the output for the current moment.
- (4)
- Memory unit (): The core component in the LSTM for storing and updating information.
The specific calculations of the forget gate, the input gate, and the output gate are shown in Formulas (5)~(10).
where σ is the activation function; , , , and are the weights corresponding to the forget gate, input gate, memory unit, and output gate, respectively; is the output of the unit at time t; , , , and are the corresponding gate offsets, respectively; is the state of the candidate cell; is the output sequence at time t; and is the memory unit at time t.
In the training process, LSTM updates the network parameters through back propagation algorithm and gradient descent, so that the value of the loss function is gradually reduced and the prediction performance of the network is improved. LSTM can learn parameters to better fit the training data and suit specific tasks.
2.5. Time Attention Module
The time attention module is composed of BiLSTM and ATT, which is used as a decoder to decode the output of the feature attention module. BiLSTM is used to perform bidirectional learning on the output of the feature attention module. The ATT adaptively assigns different weights to the hidden states of the output of BiLSTM. This is determined according to the degree of influence of the history nodes of t time steps on the current time step [23]. Its structure is shown in Formulas (11)~(15).
where and are the forward and reverse hiding states of BiLSTM network at time t, respectively; is the output of characteristic attention module; and are the forward and reverse weight matrices of BiLSTM network, respectively; is the bias vector; P is the preliminary prediction result; is the weight matrix of all connected layers; and is the fully connected layer bias vector.
2.6. Prediction Model of EMD-KPCA Combined with BiLSTM-ATT
Aiming at the problem of insufficient utilization of Numerical Weather Prediction (NWP) data and the unsatisfactory prediction effect of single prediction models, a wind power prediction method based on EMD-KPCA-BiLSTM-ATT model is proposed.
Firstly, the EMD-KPCA combination algorithm is used to ensure that the feature dimension is reduced without losing the original data information. This approach involves decomposing data using EMD to acquire IMFs. The IMF data are then mapped to the high-dimensional feature space using KPCA, where linear transformation is performed to achieve data identification and dimensional reduction, enabling a deeper understanding of the data structure and pattern.
Subsequently, to address the issue of the BiLSTM network’s inability to handle long-term time series dependencies, an attention module is introduced before the BiLSTM network. Using the weight that the attention module assigns to different features, the model highlights the impact of crucial components on the output while downplaying irrelevant parts. This enables the BiLSTM network to grasp the dynamic attributes of wind energy comprehensively, thereby enhancing the model’s accuracy and generalization capability.
Finally, the EMD-KPCA network integrated with the data processing module and the prediction model BiLSTM-ATT are combined for wind power prediction. The combined model is preconditioned to the data by the EMD-KPCA, which reduces the influence of external environmental factors on the prediction results. At the same time, the combination of BiLSTM and ATT can fully solve the long-term dependence problem of time series and improve the prediction accuracy.
3. Data Analysis and Prediction Process
3.1. Influencing Factor Analysis of Wind Power Generation
The experimental samples are the measured wind power data and the four environmental data factors, specifically wind speed, wind direction, air temperature, and air density, obtained by the environmental monitor corresponding to the wind farm. In order to analyze the influence of the above four factors on wind power [24], a Pearson correlation coefficient of Formula (16) is used for calculation.
where is the correlation coefficient; and are the two factor values of the i data, respectively; is the mean value of the environment data; and is the mean power data.
The correlation coefficient between the environmental factors and wind power is calculated by Formula (16), as shown in Table 1.

Table 1.
The correlation coefficient between environmental factors and wind power.
It can be seen from Table 1 that the wind speed has the greatest impact on power output, the correlation coefficient between the wind direction and the air density is negatively correlated, and the air temperature has a relatively small impact.
3.2. Processing of Abnormal Data
The collection of wind power data is affected by many factors such as wind speed, wind direction, air temperature, and air density. These factors may lead to abnormal data which generate a decrease in power prediction accuracy. Therefore, before training the wind power prediction model, it is necessary to process the abnormal data to improve the quality of the data [25].
Compared to traditional statistical methods and clustering algorithms, the quartile method is a commonly used data cleaning technique that is robust, intuitive, and easy to calculate. By identifying and processing outliers, this method can enhance data accuracy, maintain data distribution stability, and improve the reliability of data analysis. Choosing the quartile method for data cleaning can effectively enhance data quality and provide better support for subsequent data analysis and application.
The data processing method is to arrange the data set in order of size and divide it into four equal scores, namely, the first quantile , the median , the third quantile and the interquartile distance , with each equal fraction containing 25% of the data. Use the quartile method to clean abnormal data, the specific process is as follows:
(1) Arrange a set of data in ascending order to obtain the sorted data sample .
(2) Calculate the median .
(3) Calculate the first quantile and the third quantile . When , the original data X is divided into two parts by the median . The median of the two parts is calculated according to Formula (18), that is, and , and < .
When , then:
When ., then:
The interquartile distance is determined by:
According to the interquartile distance, the normal wind data range can be determined as:
where and are the upper and lower limits of normal data respectively.
Data outside the upper and lower limits of W1 and W2 are considered as abnormal data and need to be cleaned. At the same time, the cleaned data are filled using the linear interpolation method. The calculation formula is as follows:
where is the wind power data at time i.
Taking wind speed and power data as an example, the scatter diagram of wind power before and after cleaning is shown in Figure 3.
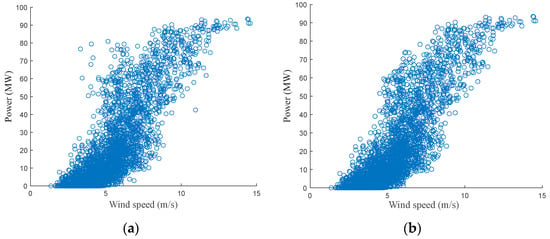
Figure 3.
Data cleaning process. (a) Original wind power scatter plot; (b) wind power scatter plot after cleaned.
It can be seen from Figure 3 that the use of the quartile algorithm effectively eliminates the scattered abnormal data in the original data, and the cleaned scatter plot is closer to the standard wind speed-power scatter.
3.3. Evaluation Indexes
In order to evaluate the prediction results of the model, Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE) and R-Squared (R2) were selected as evaluation indexes [26]. Each evaluation index is calculated as follows:
where m is the number of test sample; is the real output power of wind power; and and are the prediction and average values of wind power output, respectively.
3.4. Prediction Process
In order to improve the prediction accuracy, a combined prediction model was constructed using EMD-KPCA algorithm and BiLSTM-ATT network. The prediction process is shown in Figure 4, and the specific steps are as follows:
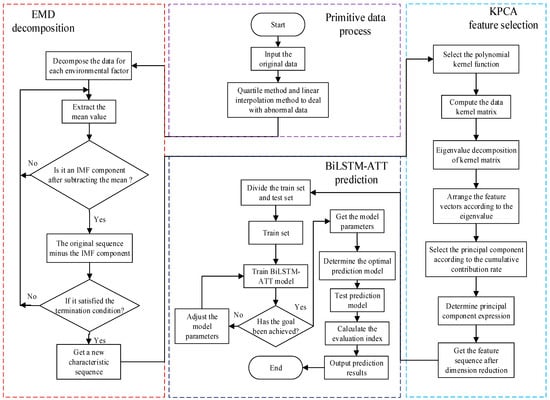
Figure 4.
EMD-KPCA-BiLSTM-ATT prediction flow chart.
(1) Abnormal data process: The original data are screened and filled by the quartile and linear interpolation methods.
(2) Empirical mode decomposition: EMD is used to decompose the data to obtain a series of IMF components and residual components.
(3) Kernel principal component analysis: The KPCA algorithm is used to calculate the contribution rate of each component for dimensionality reduction, and the feature data after dimensionality reduction will form a new data set.
(4) Data normalization process: The normalized data set is divided into a training set and a test set.
(5) Determination of optimal parameters of the proposed model: The training set data are used to train the BiLSTM-ATT combined prediction model, and the prediction results are compared to determine the hyperparameters to achieve the target accuracy.
(6) Wind power prediction: Using the test set data to test the prediction model, the wind power to be predicted is obtained, and the prediction effect is evaluated.
4. Example Analysis
In order to verify the effectiveness of the KPCA-EMD-BiLSTM-ATT combined prediction model in improving the accuracy of wind power prediction, the wind power of a wind farm in Anhui from 1 October 2022 to 30 April 2023 was taken as an example for analysis. The sampling interval was 15 min, and a total of 20,352 data samples were used. The first 70% of the sample data were used as the training set, and the last 30% of the sample data were used as the test set for prediction. The prediction model used the NWP data and power data of the first 6 days, and the NWP data of the next day to predict the 96 wind power values of the next day [27]. Simultaneously, utilizing the NWP data and the power data from the first 20 days of May 2023, 960 wind power values were predicted for the following 10 days [28]. The inputs of the model were wind power data and the four meteorological factors of wind speed, wind direction, air temperature, and air density. The output of the model was the wind power to be predicted. The seven models of LSTM, BiLSTM, BiLSTM-ATT, EMD-BiLSTM, EMD-BiLSTM-ATT, EMD-KPCA-BiLSTM, EMD-KPCA-BiLSTM-ATT were used for comparison predictions.
4.1. Analysis of the EMD Decomposition Results
The wind power data in the experimental sample are non-stationary signals, which are affected by environmental factors and have certain mutability and randomness. The EMD algorithm is used to decompose the input data to obtain the IMF component and residual component of each influencing factor. The EMD algorithm decomposes the original signal to obtain more effective feature information. The EMD decomposition process of wind speed feature sequence is shown in Figure 5, and the results of EMD decomposition of all feature sequences are shown in Table 2. There are 24 IMF components and four residual components, and a total of 28 feature sequences as a new feature sequence set.
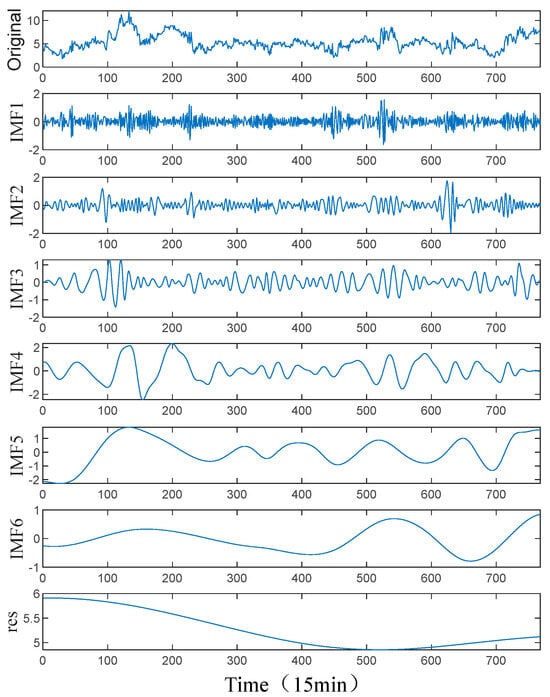
Figure 5.
The EMD decomposition process of the wind speed series.

Table 2.
The results of the EMD decomposition of all characteristic series.
It can be seen from Figure 5 and Table 2 that IMF1–IMF4 show unstable and oscillating characteristics, which belong to random terms. IMF5–IMF6 show a trend of smooth frequency reduction and periodicity, which is a trend item. Therefore, the EMD decomposition can highlight the local characteristics of the original wind speed series.
4.2. KPCA Reduction Dimension Result Analysis
The KPCA algorithm is used for component analysis of 28 feature series to reduce data dimension and remove data redundant information. Using polynomial kernel function for KPCA analysis, the contribution rate of each feature sequence is shown in Figure 6.
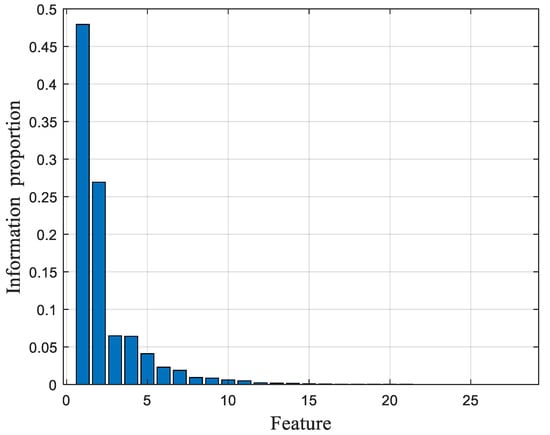
Figure 6.
The contribution rate of each characteristic sequence.
The contribution rate of each feature sequence is 95%, which has strong representativeness. The cumulative contribution rate of the top seven characteristic sequences calculated by Figure 6 reaches 95%. Therefore, the top seven characteristic sequences are used as the input data of the prediction model.
4.3. BiLSTM Model Parameter Setting
The parameters of the BiLSTM network prediction model are set as follows: the time step of the input layer is 1, the dimension of the input layer is 7, the number of the hidden layers is 2, and the number of the hidden layer units is 100. The specific parameters of the BiLSTM are shown in Table 3.

Table 3.
The BiLSTM parameter setting.
4.4. Comparative Analysis of the Prediction Results
In order to verify prediction validity and high accuracy of the EMD-KPCA-BiLSTM-ATT combined model, seven models (LSTM, BiLSTM, BiLSTM-ATT, EMD-BiLSTM, EMD-BiLSTM-ATT, EMD-KPCA-BiLSTM, and EMD-KPCA-BiLSTM-ATT) were used to predict the wind power on 1 March, 10 April, and 20–30 May 2023. The prediction results are shown in Figure 7, and the evaluation indexes of the prediction results are shown in Table 4.
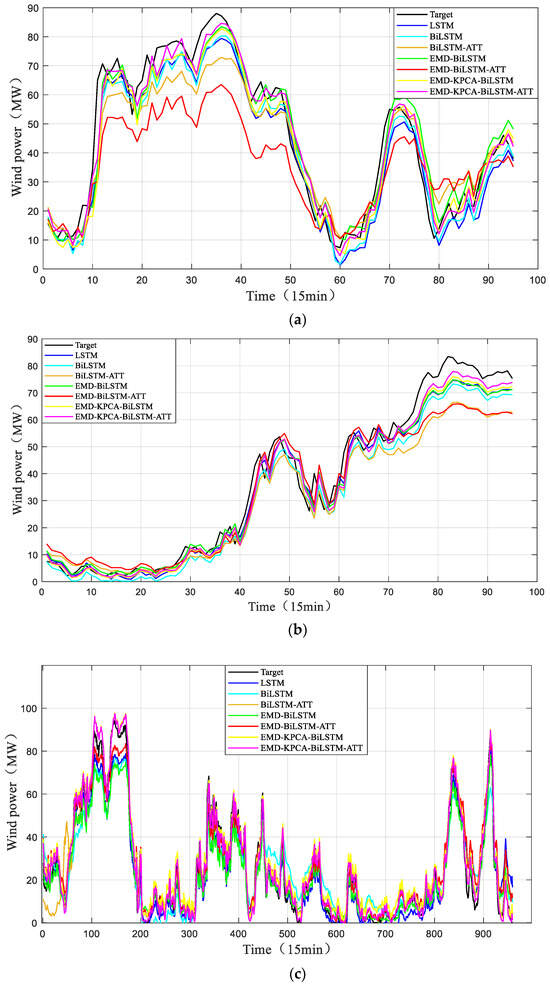
Figure 7.
The comparison of the model prediction results: (a) 1 March 2023; (b) 10 April 2023; (c) 20 to 30 May 2023.

Table 4.
Comparison of the evaluation indexes of different wind power prediction models.
(1) It can be observed from all the evaluation indexes of the prediction results of 1 March 2023 in Figure 7a and Table 4 that the BiLSTM and BiLSTM-ATT models outperform the LSTM model in terms of prediction accuracy, and the BiLSTM-ATT prediction effect is even better.
(2) It can be seen from the prediction data of 1 March 2023 in Table 4 that compared with the prediction results of the BiLSTM, EMD-BiLSTM, BiLSTM-ATT and EDM-BiLSTM-ATT, the data processed by EMD algorithm have a poorer prediction effect compared with the data without an EMD process as an input of the prediction model. MAE is increased by 63.59% and 63.65%, respectively, and RMSE is increased by 77.11% and 71.48%, respectively. Because the data are not filtered directly as a prediction model after the EMD algorithm decomposition, the input data dimension is too high, and the feature sequence is changed from 4 to 28. The input of all feature sequences reduces the learning ability of the model, and the prediction effect is poorer when only the EMD algorithm is used.
(3) From all the evaluation indexes in Table 4, it can be seen that the prediction accuracy is improved for the data processed by the EMD-KPCA combined algorithm as the input of the BiLSTM or BiLSTM-ATT prediction model, compared with the data without EMD-KPCA processed. The MAE is reduced by 19.45% and 17.42%, respectively, and the RMSE is reduced by 18.57% and 15.66%, respectively.
(4) The RMSE, MAPE, and MAE indexes of the EMD-KPCA-BiLSTM-ATT model are smaller than those of the other six methods, and the R2 is closer to 1. This shows that the EMD-KPCA-BiLSTM-ATT method performs better in prediction ability and prediction accuracy than the other six methods under the same input conditions.
(5) From the data of 10 April in Figure 7b and Table 4, it can be seen that the MAE, MAPE, and RMSE of the EMD-KPCA-BiLSTM-AT combined model are 4.3412, 7.4237%, and 5.547, respectively. Compared with the other model prediction results, the values of MAE, MAPE, and RMSE are the smallest, and the maximum R2 is closer to 1. The results show that the EMD-KPCA-BiLSTM-ATT combined model is superior to the other six models in predicting different data.
5. Conclusions
In order to make full use of historical data, improve the accuracy of wind power prediction, and meet the high-precision requirements of power system for wind power prediction, a short-term wind power prediction method based on the EMD-KPCA-BiLSTM-ATT model is proposed. First, the abnormal data were processed using the quartile method. Subsequently, the wind power data were analyzed and processed by EMD decomposition and KPCA selection of key components. Following this, the BiLSTM-ATT combined prediction model was utilized to predict the examples. Finally, seven methods were employed to predict the examples, and the results were compared. The effectiveness of the prediction method is verified by the example, and the following conclusions are obtained:
(1) When dealing with multivariate input data, the combination of EMD and KPCA is used to decompose input data and screen main feature sequences, which can fully exploit the information features and improve the prediction accuracy of the model.
(2) The prediction effect of the BiLSTM-ATT model is better than that of the LSTM model, and the LSTM model cannot process the hidden features in the data. The ATT can capture crucial information within the input sequence during prediction, and better focus on the output power related part of the input data, while BiLSTM is good at learning the long dependence characteristics in the data. Therefore, the combination of the two algorithms can improve the performance, interpretability and adaptability of the model, so that the model can better deal with complex input data.
(3) Compared with LSTM, BiLSTM, BiLSTM-ATT, EMD-BiLSTM, EMD-BiLSTM-ATT, and EMD-KPCA-BiLSTM models, the EMD-KPCA-BiLSTM-ATT model has smaller prediction error and higher accuracy, which verifies the effectiveness of the model in short-term wind power prediction for wind farms and provides a new idea for improving wind power prediction accuracy.
After analyzing the existing research, there are still some issues with power prediction. Firstly, existing wind power point prediction models are often influenced by changing weather conditions, leading to low prediction accuracy. Secondly, these models often only consider partial factors, lacking comprehensiveness and integration. Future research directions may include taking all aspects of power prediction into account, extending the prediction time span or adopting power range prediction, and exploring more complex machine learning algorithms or deep learning models to further improve prediction accuracy and stability.
Author Contributions
Conceptualization, Z.Z. and A.D.; methodology, Z.W.; formal analysis, J.L.; investigation, X.Y.; data curation, H.Z.; writing—original draft preparation, A.D.; writing—review and editing, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Henan Province Science and Technology Research Projects, grant number 242102241030.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from CGN New Energy Anhui Co. and are available from the authors with the permission of CGN New Energy Anhui Co.
Acknowledgments
The authors would like to thank Zhiwen Wang and Xiaoliang Yang for their valuable suggestions that have helped to improve the quality of the manuscript, as well as Jianyong Li and Hailiang Zhao for their support in providing data for this experiment.
Conflicts of Interest
Authors Jianyong Li, Hailiang Zhao were employed by the company CGN New Energy Anhui Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Di Piazza, A.; Di Piazza, M.C.; La Tona, G.; Luna, M. An artificial neural network-based forecasting model of energy-related time series for electrical grid management. Math. Comput. Simul. 2021, 184, 294–305. [Google Scholar] [CrossRef]
- Famoso, F.; Oliveri, L.M.; Brusca, S.; Chiacchio, F. A Dependability Neural Network Approach for Short-Term Production Estimation of a Wind Power Plant. Energies 2024, 17, 1627. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, S. Wind Power Interval Prediction via an Integrated Variational Empirical Decomposition Deep Learning Model. Sustainability 2023, 15, 6114. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Xue, X.; Saeed, A.; Hu, X. Short-term wind speed interval prediction based on ensemble GRU model. IEEE Trans. Sustain. Energy 2019, 11, 1370–1380. [Google Scholar] [CrossRef]
- Kawoosa, A.I.; Prashar, D.; Faheem, M.; Jha, N.; Khan, A.A. Using machine learning ensemble method for detection of energy theft in smart meters. IET Gener. Transm. Distrib. 2023, 17, 4794–4809. [Google Scholar] [CrossRef]
- Faheem, M.; Kuusniemi, H.; Eltahawy, B.; Bhutta, M.S.; Raza, B. A lightweight smart contracts framework for blockchain-based secure communication in smart grid applications. IET Gener. Transm. Distrib. 2024, 18, 625–638. [Google Scholar] [CrossRef]
- Wang, D.; Yang, M.; Zhang, W. Wind Power Group Prediction Model Based on Multi-Task Learning. Electronics 2023, 12, 3683. [Google Scholar] [CrossRef]
- He, Y.; Zhu, C.; An, X. A trend-based method for the prediction of offshore wind power ramp. Renew. Energy 2023, 209, 248–261. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, P.; Zhai, S.; Hou, D.; Wang, S.; Zhou, Y. Ultra short-term probability prediction of wind power based on LSTM network and condition normal distribution. Wind Energy 2020, 23, 63–76. [Google Scholar] [CrossRef]
- Zhang, P.; Li, C.; Peng, C.; Tian, J. Ultra-short-term prediction of wind power based on error following forget gate-based long short-term memory. Energies 2020, 13, 5400. [Google Scholar] [CrossRef]
- Li, L.-L.; Zhao, X.; Tseng, M.-L.; Tan, R.R. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J. Clean. Prod. 2020, 242, 118447. [Google Scholar] [CrossRef]
- Tang, Q.; Xiang, Y.; Dai, J.; Li, Z.; Sun, W. Power transfer prediction method for wind farms based on CNN-LSTM. Adv. Eng. Sci. 2024, 56, 91–99. [Google Scholar] [CrossRef]
- Fu, Y.; Ren, Z.; Wei, S.; Wang, Y.; Huang, L. Ultra short term power prediction of offshore wind power based on improved LSTM-TCN model. Proc. CSEE 2022, 42, 4292–4303. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Fu, Y.; Qiao, X.; Nazir, M.S.; Peng, T. A novel DWTimesNet-based short-term multi-step wind power forecasting model using feature selection and auto-tuning methods. Energy Convers. Manag. 2024, 301, 118045. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Villanueva, D.; Kulat, K. A review on hybrid empirical mode decomposition models for wind speed and wind power prediction. Energies 2019, 12, 254. [Google Scholar] [CrossRef]
- Qin, B.; Huang, X.; Wang, X.; Guo, L. Ultra-short-term wind power prediction based on double decomposition and LSSVM. Trans. Inst. Meas. Control 2023, 45, 2627–2636. [Google Scholar] [CrossRef]
- Sheng, S.; Jin, H.; Liu, C. Short and Medium term forecast of wind farm power generation based on VMD-WSGRU. Power Syst. Technol. 2022, 46, 897–904. [Google Scholar] [CrossRef]
- Qin, G.; Yan, Q.; Zhu, J.; Xu, C.; Kammen, D.M. Day-ahead wind power forecasting based on wind load data using hybrid optimization algorithm. Sustainability 2021, 13, 1164. [Google Scholar] [CrossRef]
- Wang, J.; Deng, B.; Wang, J. Short-term wind power prediction based on empirical mode decomposition and RBF neural network. Proc. CSU-EPSA 2020, 32, 109–115. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, H.; Wang, B. Short-term wind power prediction using differential EMD and relevance vector machine. Neural Comput. Appl. 2014, 25, 283–289. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Tang, Y. Clustered hybrid wind power prediction model based on ARMA, PSO-SVM, and clustering methods. IEEE Access 2020, 8, 17071–17079. [Google Scholar] [CrossRef]
- Yue, W.; Yonggang, L.; Binyuan, W. Improved regularized extreme learning machine short-term wind speed prediction based on gray correlation analysis. Wind Eng. 2021, 45, 667–679. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, H.; Xu, Y.; Jiang, W. A hybrid framework for short term multi-step wind speed forecasting based on variational model decomposition and convolutional neural network. Energies 2018, 11, 2292. [Google Scholar] [CrossRef]
- Yuan, K.; Zhang, K.; Zheng, Y.; Li, D.; Wang, Y.; Yang, Z. Irregular distribution of wind power prediction. J. Mod. Power Syst. Clean Energy 2018, 6, 1172–1180. [Google Scholar] [CrossRef]
- Wang, W.; Yang, S.; Yang, Y. An Improved Data-Efficiency Algorithm Based on Combining Isolation Forest and Mean Shift for Anomaly Data Filtering in Wind Power Curve. Energies 2022, 15, 4918. [Google Scholar] [CrossRef]
- Qi, M.; Gao, H.; Wang, L.; Xiang, Y.; Lv, L.; Liu, J. Wind power interval forecasting based on adaptive decomposition and probabilistic regularised extreme learning machine. IET Renew. Power Gener. 2020, 14, 3181–3191. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Yu, X.; Li, B.; Yang, M. Research on ultra-short-term wind power prediction considering source relevance. IEEE Access 2020, 8, 147703–147710. [Google Scholar] [CrossRef]
- Tan, L.; Han, J.; Zhang, H. Ultra-short-term wind power prediction by salp swarm algorithm-based optimizing extreme learning machine. IEEE Access 2020, 8, 44470–44484. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).