Leading Point Multi-Regression Model for Detection of Anomalous Days in German Energy System
Abstract
1. Introduction
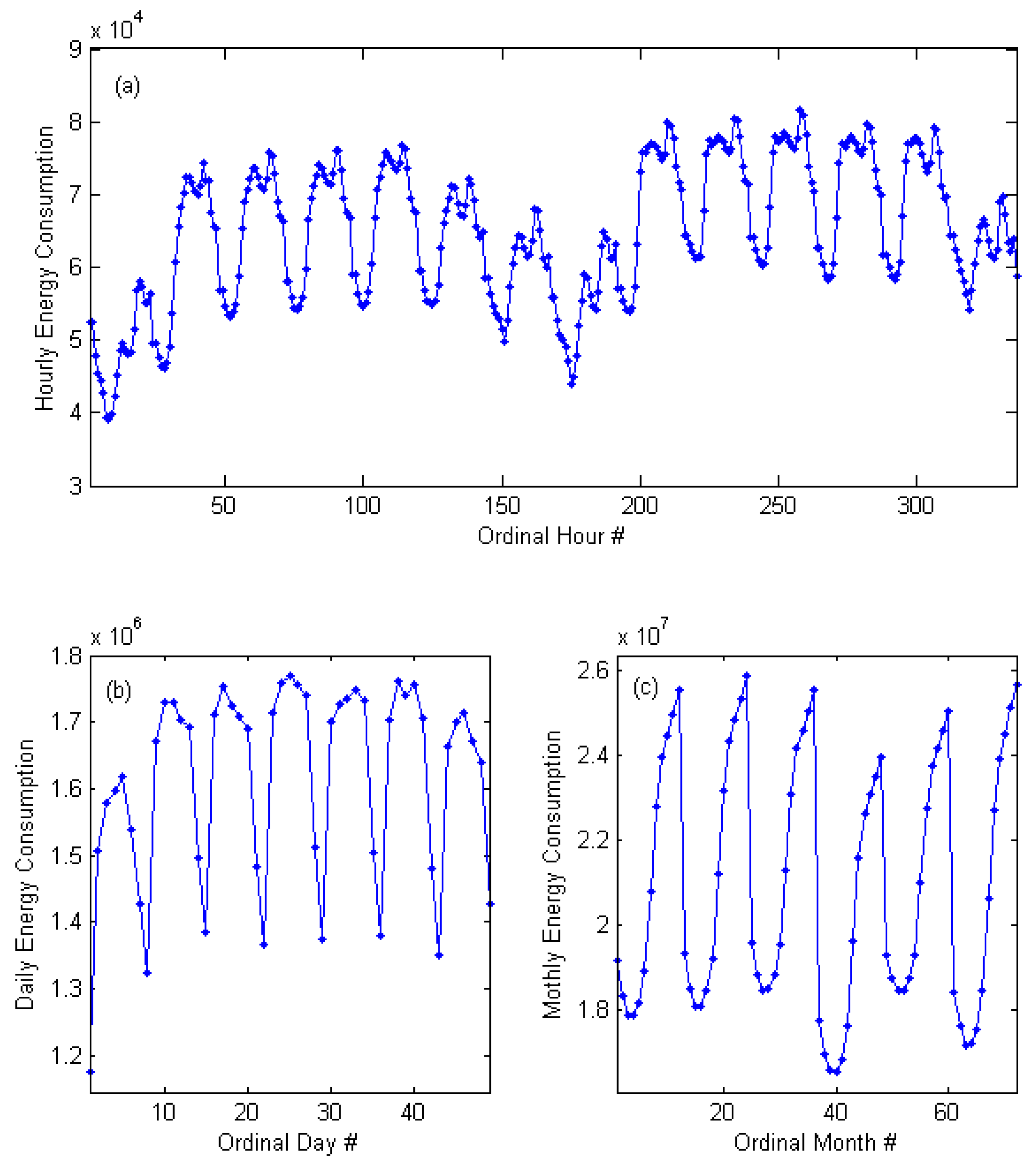
2. Data Characteristics
3. Leading Points Multi-Regression Model
3.1. The Model Formula
3.2. The Algorithm for Variables’ Selection
4. Model Estimation
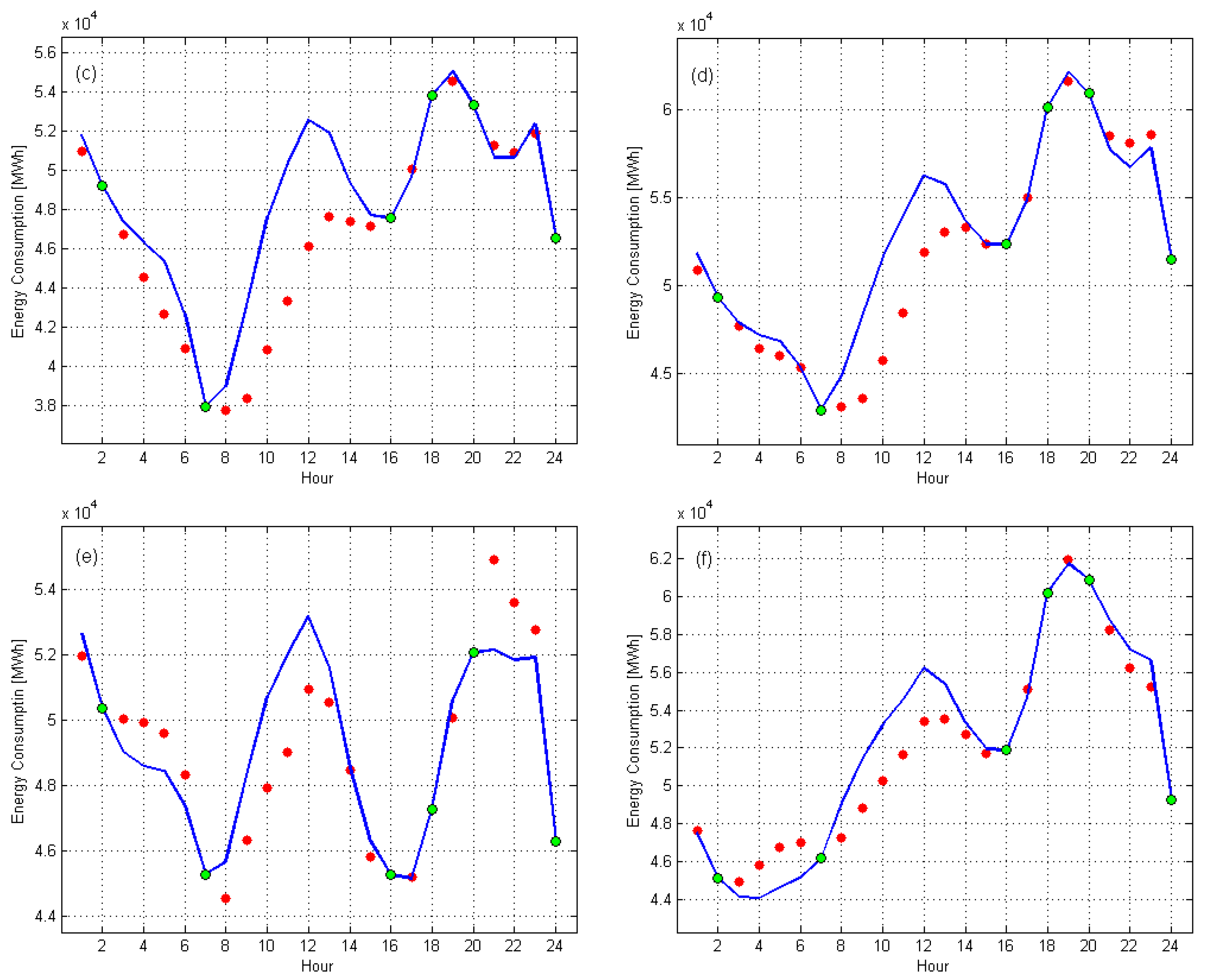
5. Detection of Anomalous Daily Profiles
5.1. Analysis of the Errors
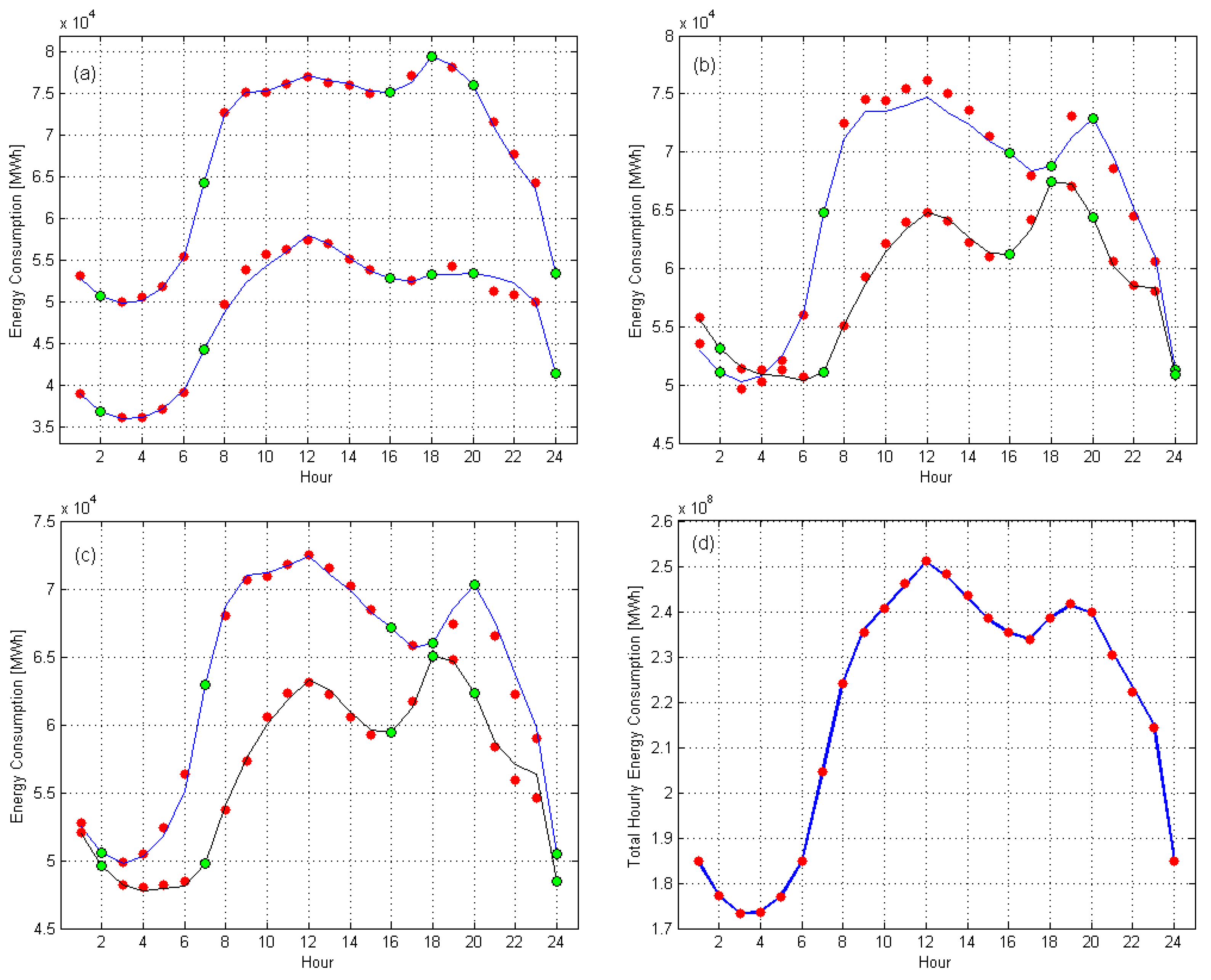
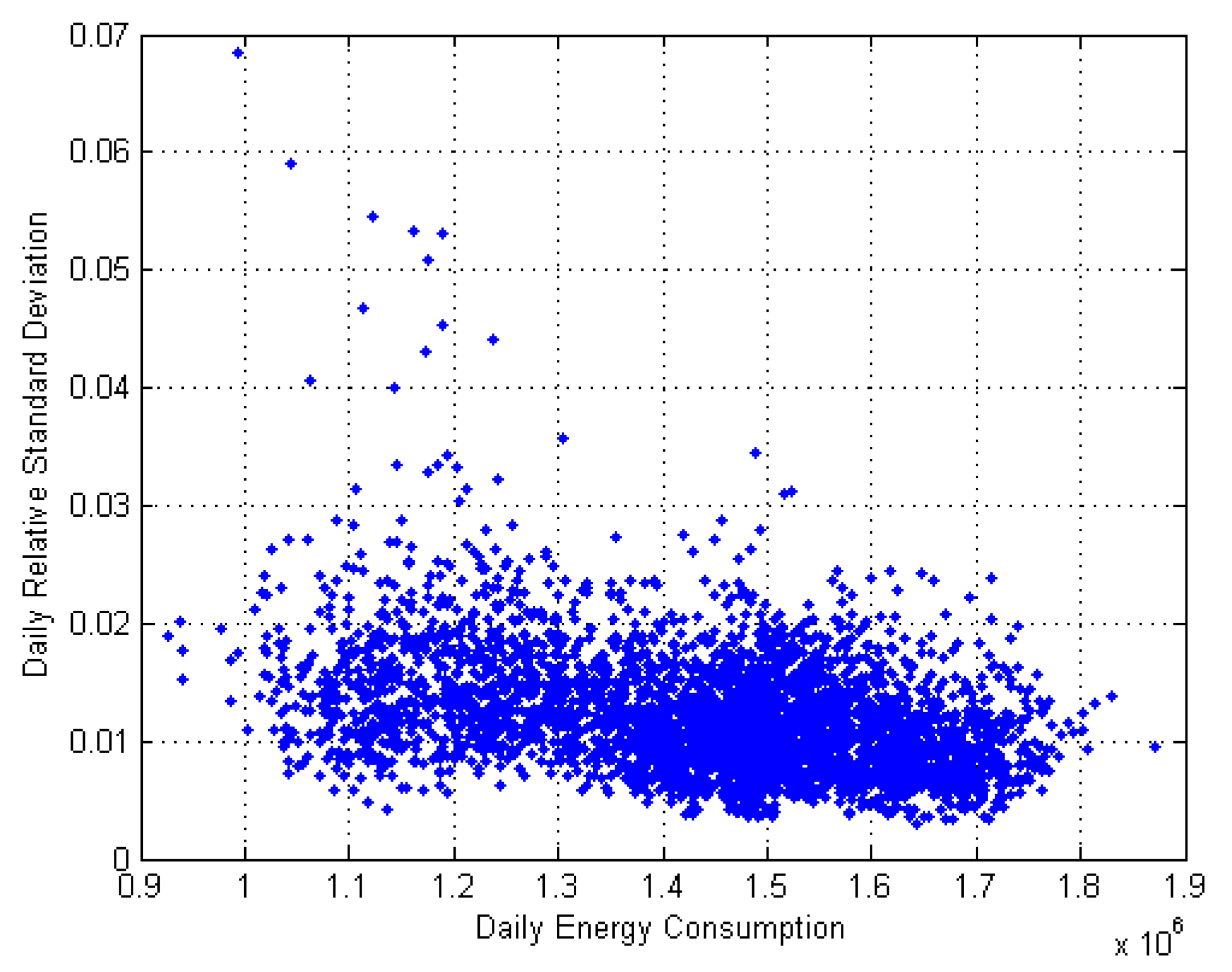
5.2. Identification of Anomalous Daily Energy Consumption Profiles
- (1)
- 0.04 ≤ RSD (−3.22 ≤ log(RSD));
- (2)
- 0.03 < RSD < 0.04 (−3.51 < log(RSD) < −3.22).
5.3. Discussion of the Results
6. Conclusions
- The novelty of LPMR is that it allows for modeling energy consumptions for the entire day using only a few selected hours.
- It has been shown that the energy consumption data can be modeled with high precision using six independent variables denoting energy consumption for the following hours: 16, 2, 24, 7, 18, and 20.
- The distribution of the model’s errors follows a Gaussian distribution with high accuracy.
- The anomalous days, with regard to energy consumption profiles, were accurately defined as these with high errors and falling into the range where the distribution deviates from Gaussian.
- Days with untypical profiles were mainly New Year and New Year’s Eve which was quite expected. However, there were a few other days that were considered atypical which were not so obvious. These were Holy Saturday and Good Friday which are connected to Catholic holidays. Also, other anomalous days were identified: National Day of Mourning, day when the Germany–Turkey match took place during the European Championship 2008, Daylight Saving Time end day in 2008, and six other days that are not connected to any type of holiday or special events.
- Anomalies in daily profiles were not observed in the case of other religious holidays as well as major public holidays, even when they fell on long weekends.
- It was observed that the majority of anomalous days were characterized by low energy consumption typical for holiday periods and non-working days.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sulich, A.; Sołoducho-Pelc, L. Changes in Energy Sector Strategies: A Literature Review. Energies 2022, 15, 7068. [Google Scholar] [CrossRef]
- Marinakis, V.; Koutsellis, T.; Nikas, A.; Doukas, H. AI and Data Democratisation for Intelligent Energy Management. Energies 2021, 14, 4341. [Google Scholar] [CrossRef]
- Chicco, G.; Mazza, A. Load profiling revisited: Prosumer profiling for local energy markets. In Local Electricity Markets; Pinto, T., Vale, Z., Winder-grean, S., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 215–242. [Google Scholar]
- Karpio, K.; Łukasiewicz, P.; Nafkha, R. Regression Technique for Electricity Load Modeling and Outlined Data Points Explanation. In Advances in Soft and Hard Computing; Peja’s, J., El Fray, I., Hyla, T., Kacprzyk, J., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2019; Volume 889, pp. 56–67. [Google Scholar]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Berrisch, J.; Narajewski, M.; Ziel, F. High-resolution peak demand estimation using generalized additive models and deep neural networks. Energy AI 2023, 13, 100236. [Google Scholar] [CrossRef]
- Parhizkar, T.; Rafieipour, E.; Parhizkar, A. Evaluation and improvement of energy consumption prediction models using principal component analysis based feature reduction. J. Clean. Prod. 2020, 279, 123866. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A novel stacked generalization ensemble-based hybrid LGBM-XGB-MLP model for Short-Term Load Forecasting. Energy 2020, 214, 118874. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.; Yang, L.; Li, Y. Event-Triggered Distributed Hybrid Control Scheme for the Integrated Energy System. IEEE Trans. Ind. Inform. 2021, 18, 835–846. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Sun, M.; Sun, C. Hybrid Policy-Based Reinforcement Learning of Adaptive Energy Management for the Energy Transmission-Constrained Island Group. IEEE Trans. Ind. Inform. 2023, 19, 10751–10762. [Google Scholar] [CrossRef]
- Khan, Z.A.; Khan, S.A.; Hussain, T.; Baik, S.W. DSPM: Dual sequence prediction model for efficient energy management in micro-grid. Appl. Energy 2024, 356, 122339. [Google Scholar] [CrossRef]
- Abu, F.; Yunus, A.R.; Majid, I.A.; Jabar, J.; Aris, A.; Sakidin, H.; Ahmad, A. Technology Acceptance Model (TAM): Empowering smart customer to participate in electricity supply system. J. Technol. Manag. Techno-Preneurship (JTMT) 2014, 2, 85–94. [Google Scholar]
- Gajowniczek, K.; Nafkha, R.; Ząbkowski, T. Electricity peak demand classification with artificial neural networks. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Prague, Czech Republic, 3–6 September 2017; pp. 307–315. [Google Scholar]
- Berthold, M.R.; Borgelt, C.; Höppner, F.; Klawonn, F.; Silipo, R. Guide to Intelligent Data Science: How to Intelligently Make Use of Real Data; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Madabhushi, S.; Dewri, R. A survey of anomaly detection methods for power grids. Int. J. Inf. Secur. 2023, 22, 1799–1832. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Ding, S.; Zhang, X. Power Consumption Predicting and Anomaly Detection Based on Transformer and K-Means. Front. Energy Res. 2021, 9, 779587. [Google Scholar] [CrossRef]
- Fu, T.; Zhou, H.; Ma, X.; Hou, Z.J.; Wu, D. Predicting peak day and peak hour of electricity demand with ensemble machine learning. Front. Energy Res. 2022, 10, 944804. [Google Scholar] [CrossRef]
- Zhang, W.; Dong, X.; Li, H.; Xu, J.; Wang, D. Unsupervised Detection of Abnormal Electricity Consumption Behavior Based on Feature Engineering. IEEE Access 2020, 8, 55483–55500. [Google Scholar] [CrossRef]
- Karpio, K.; Łukasiewicz, P.; Nafkha, R. New Method of Modeling Daily Energy Consumption. Energies 2023, 16, 2095. [Google Scholar] [CrossRef]
- Dai, S.; Meng, F.; Dai, H.; Wang, Q.; Chen, X. Electrical peak demand forecasting-A review. arXiv 2021, arXiv:2108.01393. [Google Scholar] [CrossRef]
- ENTSO-E. European Network of Transmission System Operators for Electricity. Brussels, Belgium. Available online: https://www.entsoe.eu/publications/data/power-stats//Monthly-hourly-load-values_2006-2015.xlsx (accessed on 2 February 2024).
- Clark, T.E.; West, K.D. Approximately normal tests for equal predictive accuracy in nested models. J. Econ. 2007, 138, 291–311. [Google Scholar] [CrossRef]
- Thomakos, D.D.; Guerard, J.B. Naïve, ARIMA, nonparametric, transfer function and VAR models: A comparison of forecasting performance. Int. J. Forecast. 2004, 20, 53–67. [Google Scholar] [CrossRef]
- Karpio, K.; Łukasiewicz, P. Detection of Anomalous Days in Energy Demand Using Leading Point Multi-regression Model. In Computational Science—ICCS 2023; Mikyška, J., de Mulatier, C., Paszynski, M., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M., Eds.; ICCS 2023, Lecture Notes in Computer Science; Springer: Cham, Swizterland, 2023; Volume 10475. [Google Scholar] [CrossRef]
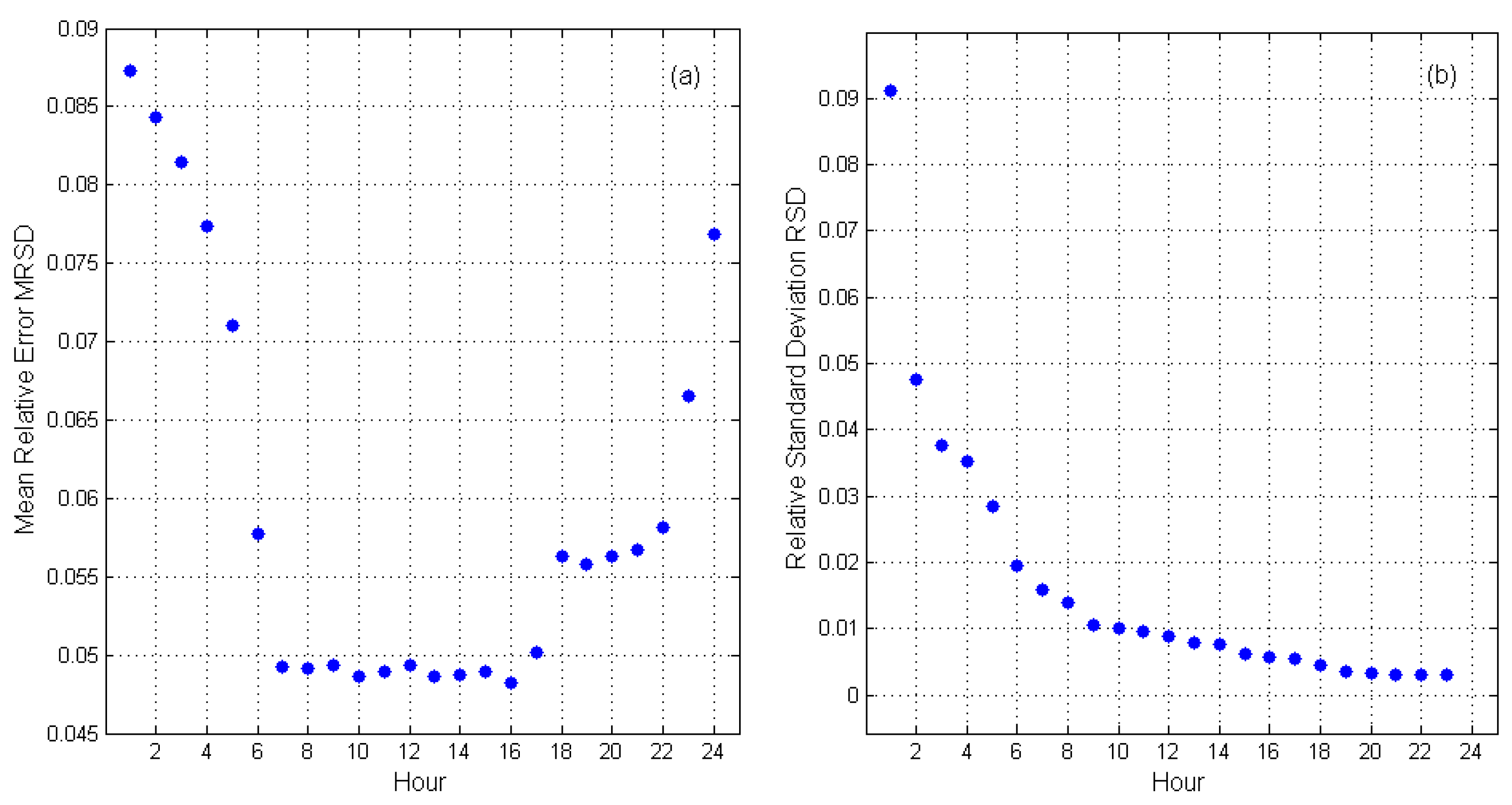




| Step | Hour | # Variables | # Equations | # Parameters | MRSD |
|---|---|---|---|---|---|
| 1 | 1 | 23 | 46 | 0.0914 | |
| 2 | 2 | 22 | 66 | 0.0463 | |
| 3 | 3 | 21 | 84 | 0.0378 | |
| 4 | 4 | 20 | 100 | 0.0341 | |
| 5 | 5 | 19 | 114 | 0.0292 | |
| 6 | 6 | 18 | 126 | 0.0198 |
| Sample | MSD (In MWh) | MRSD |
|---|---|---|
| Training | 799.06 | 0.0126 |
| Testing | 721.81 | 0.0117 |
| No | Date | Weekday | SD | RSD |
|---|---|---|---|---|
| 1 | 8 December 2009 | Monday | 378.8 | 0.0054 |
| 2 | 22 May 2009 | Thursday | 820.0 | 0.0171 |
| 3 | 28 October 2011 | Sunday | 1006.8 | 0.0143 |
| 4 | 17 December 2011 | Tuesday | 409.4 | 0.0066 |
| 5 | 28 March 2014 | Sunday | 677.5 | 0.0108 |
| 6 | 21 November 2015 | Thursday | 575.4 | 0.0102 |
| Variable | μ | σ | R2 |
|---|---|---|---|
| log(SD) | 6.582 ± 0.014 | 0.487 ± 0.007 | 0.991 |
| log(RSD) | −4.476 ± 0.005 | 0.541 ± 0.008 | 0.990 |
| No | Date | RSD | Weekday | Description |
|---|---|---|---|---|
| 1 | 1 January 2013 | 0.0685 | 2 | New Year |
| 2 | 1 January 2012 | 0.0591 | 7 | New Year |
| 3 | 1 January 2009 | 0.0547 | 4 | New Year |
| 4 | 1 January 2010 | 0.0532 | 5 | New Year |
| 5 | 1 January 2008 | 0.0531 | 2 | New Year |
| 6 | 1 January 2006 | 0.0508 | 7 | New Year |
| 7 | 1 January 2014 | 0.0469 | 3 | New Year |
| 8 | 1 January 2011 | 0.0453 | 6 | New Year |
| 9 | 1 January 2007 | 0.0442 | 1 | New Year |
| 10 | 31 December 2013 | 0.0431 | 2 | New Year’s Eve |
| 11 | 31 December 2012 | 0.0405 | 1 | New Year’s Eve |
| 12 | 1 January 2015 | 0.0400 | 4 | New Year |
| 13 | 19 March 2011 | 0.0357 | 6 | Other |
| 14 | 10 June 2011 | 0.0344 | 5 | Other |
| 15 | 31 December 2015 | 0.0343 | 4 | New Year’s Eve |
| 16 | 22 August 2010 | 0.0336 | 7 | Other |
| 17 | 16 May 2010 | 0.0335 | 7 | Other |
| 18 | 3 April 2010 | 0.0333 | 6 | Holy Saturday |
| 19 | 2 April 2010 | 0.0329 | 5 | Good Friday |
| 20 | 14 November 2010 | 0.0323 | 7 | National Day of Mourning |
| 21 | 31 December 2009 | 0.0315 | 4 | New Year’s Eve |
| 22 | 13 July 2014 | 0.0314 | 5 | Other |
| 23 | 22 March 2010 | 0.0313 | 1 | Other |
| 24 | 25 June 2008 | 0.0310 | 3 | Germany vs. Turkey match during European Championship |
| 25 | 28 October 2012 | 0.0303 | 7 | Daylight Saving Time ends |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karpio, K.; Łukasiewicz, P.; Ząbkowski, T. Leading Point Multi-Regression Model for Detection of Anomalous Days in German Energy System. Energies 2024, 17, 2531. https://doi.org/10.3390/en17112531
Karpio K, Łukasiewicz P, Ząbkowski T. Leading Point Multi-Regression Model for Detection of Anomalous Days in German Energy System. Energies. 2024; 17(11):2531. https://doi.org/10.3390/en17112531
Chicago/Turabian StyleKarpio, Krzysztof, Piotr Łukasiewicz, and Tomasz Ząbkowski. 2024. "Leading Point Multi-Regression Model for Detection of Anomalous Days in German Energy System" Energies 17, no. 11: 2531. https://doi.org/10.3390/en17112531
APA StyleKarpio, K., Łukasiewicz, P., & Ząbkowski, T. (2024). Leading Point Multi-Regression Model for Detection of Anomalous Days in German Energy System. Energies, 17(11), 2531. https://doi.org/10.3390/en17112531







