Numerical Analysis of Dual Droplet Simultaneous Oblique Impact on a Water Film
Abstract
1. Introduction
2. Physical Model and Numerical Method
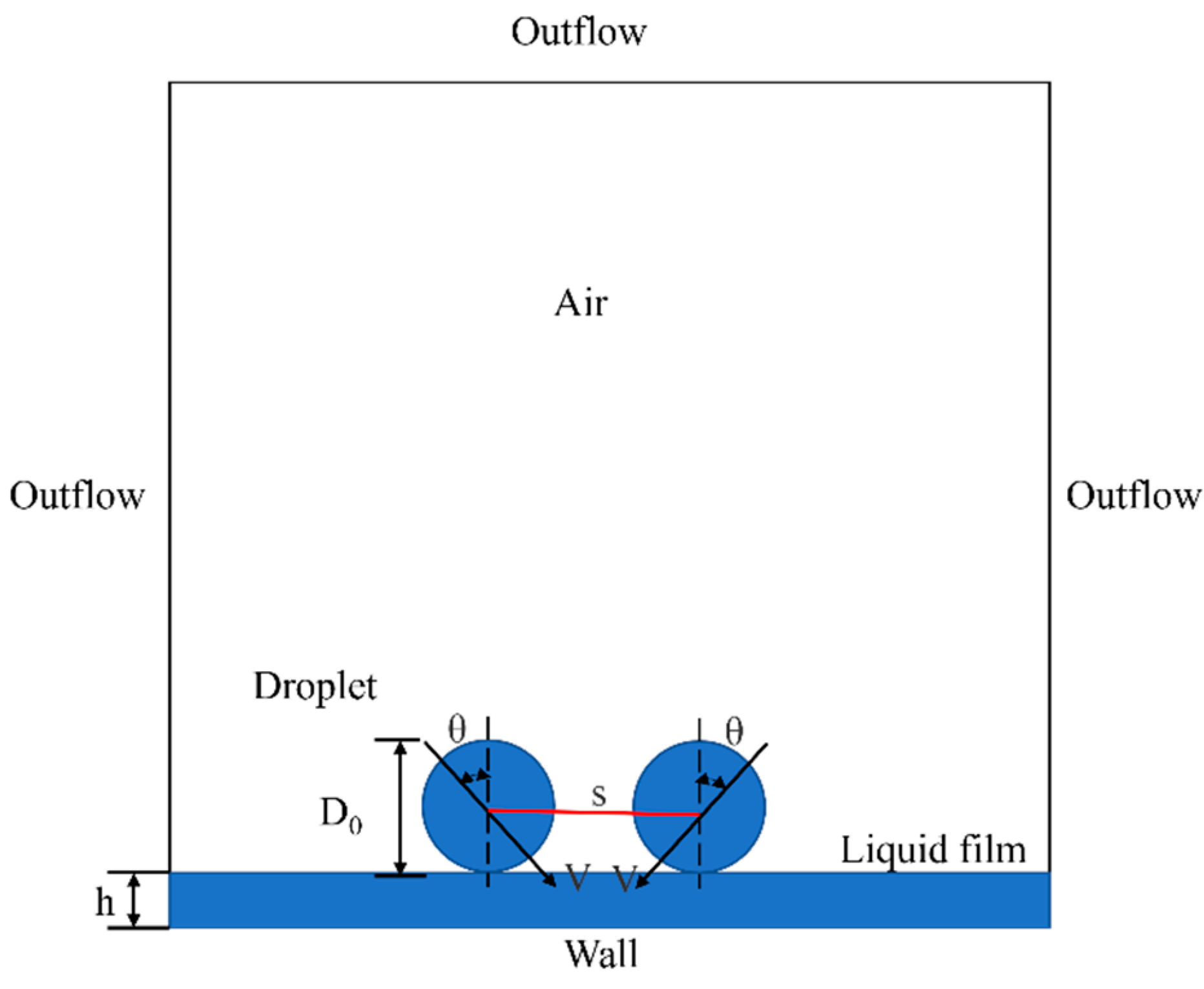
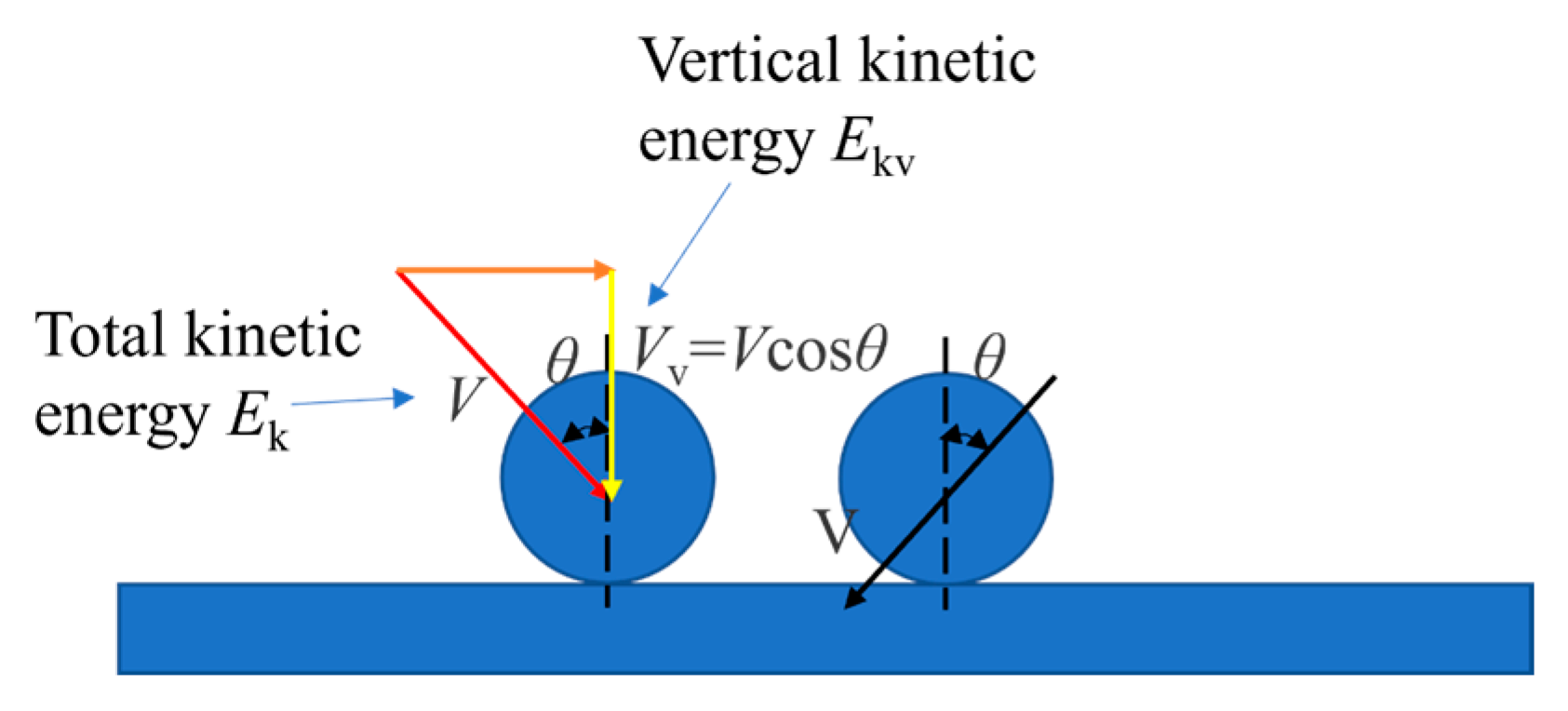
2.1. Physical Model
2.2. Numerical Method
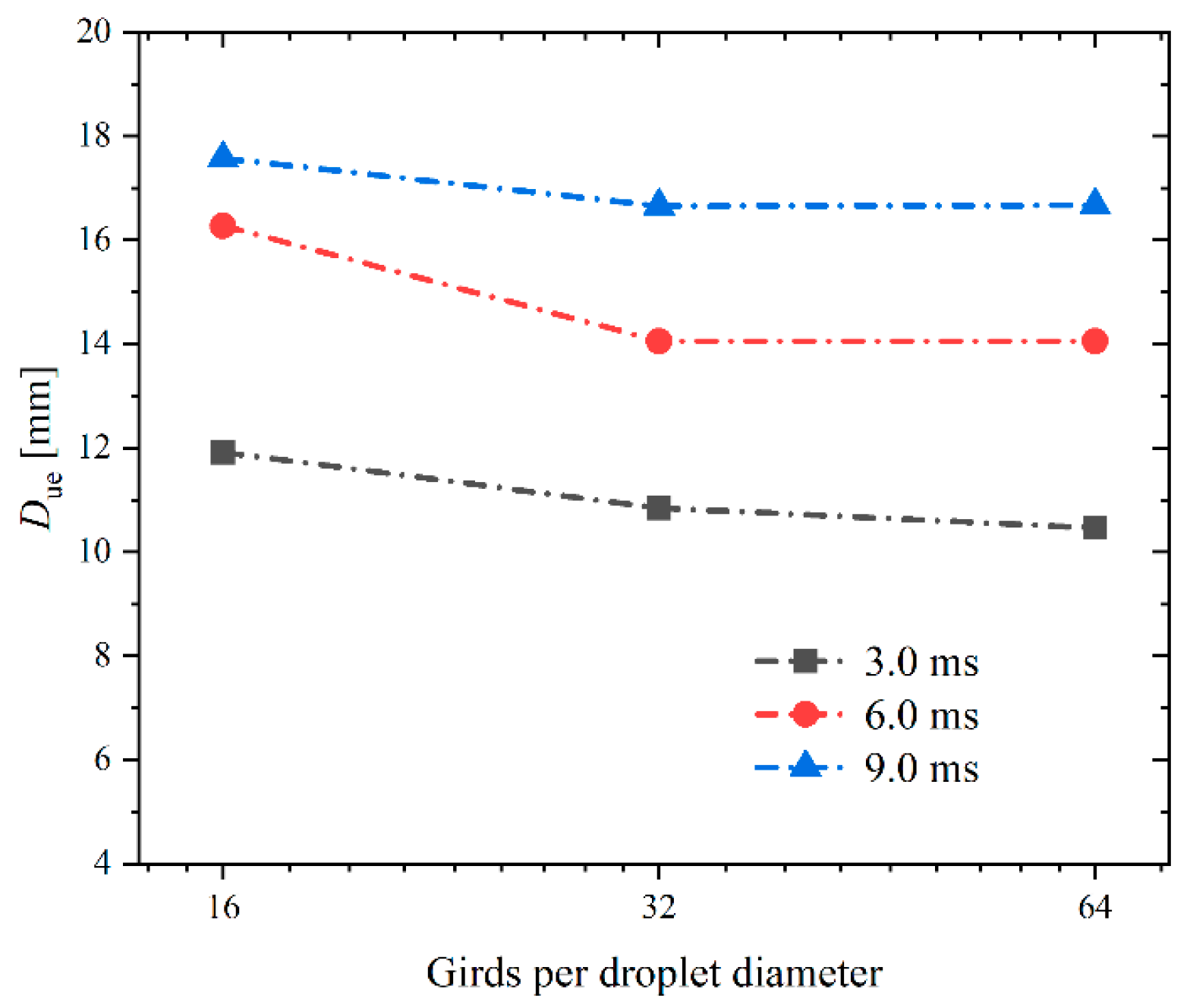
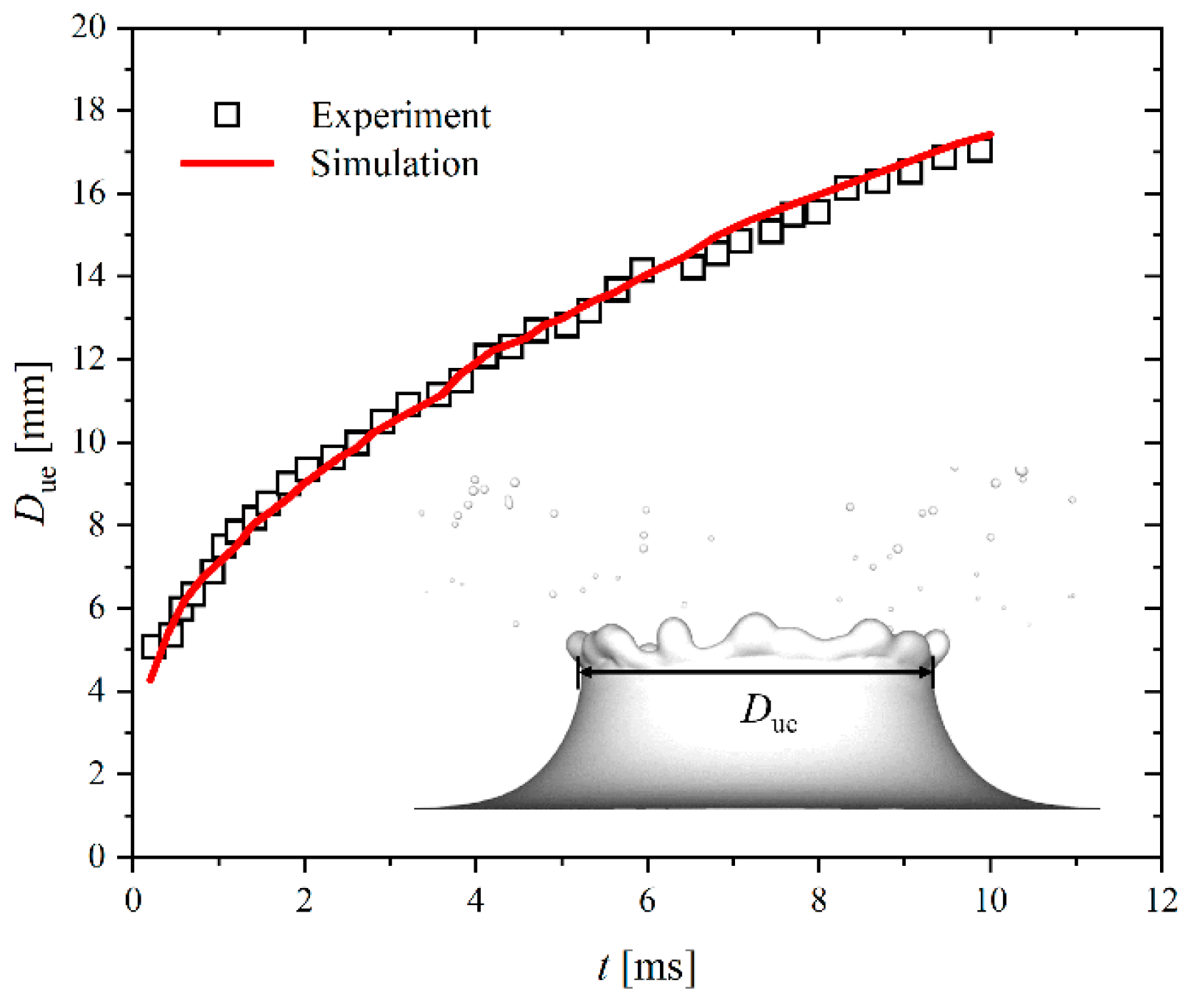
2.3. Grid Independency and Model Validation
3. Results and Discussion
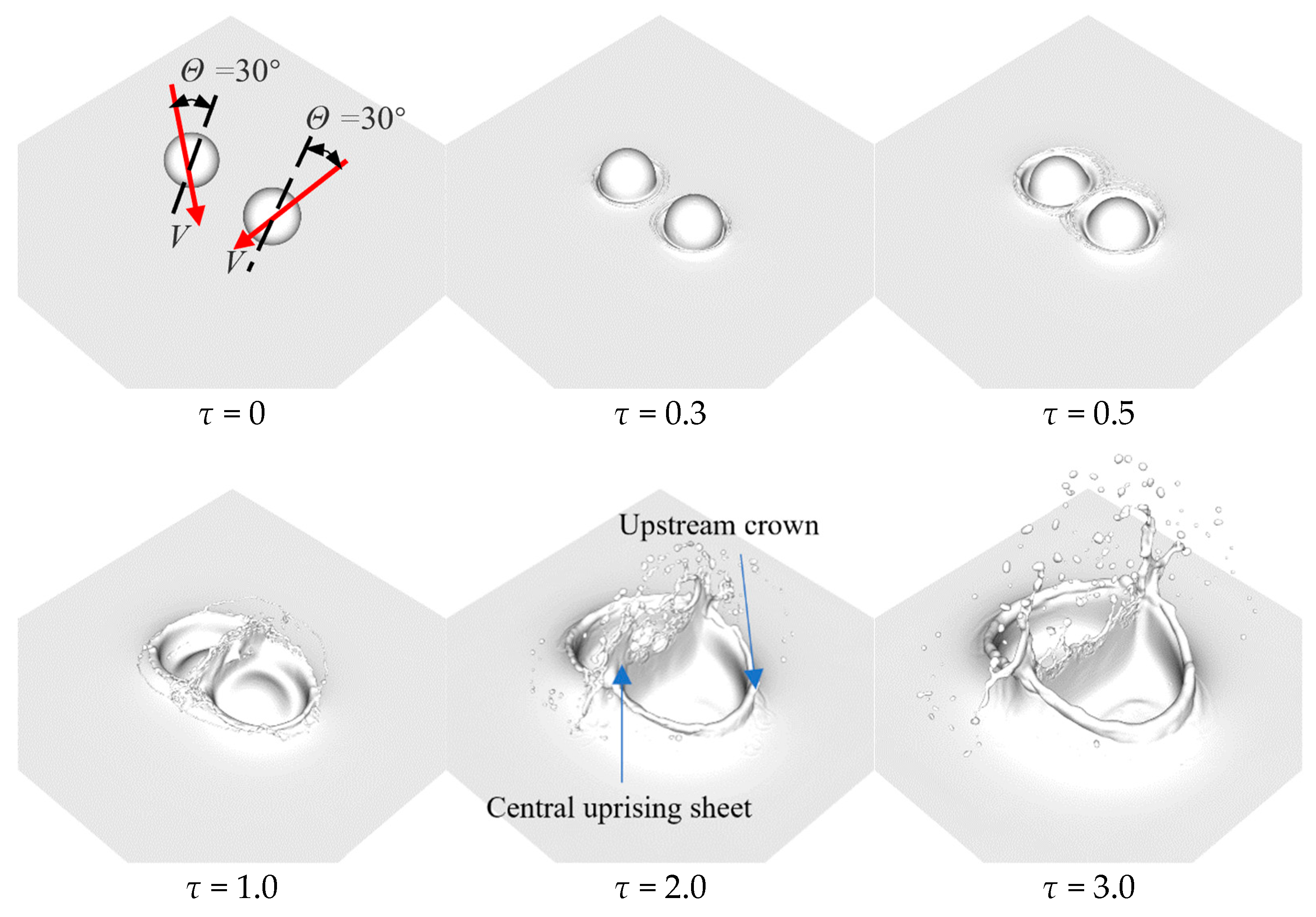
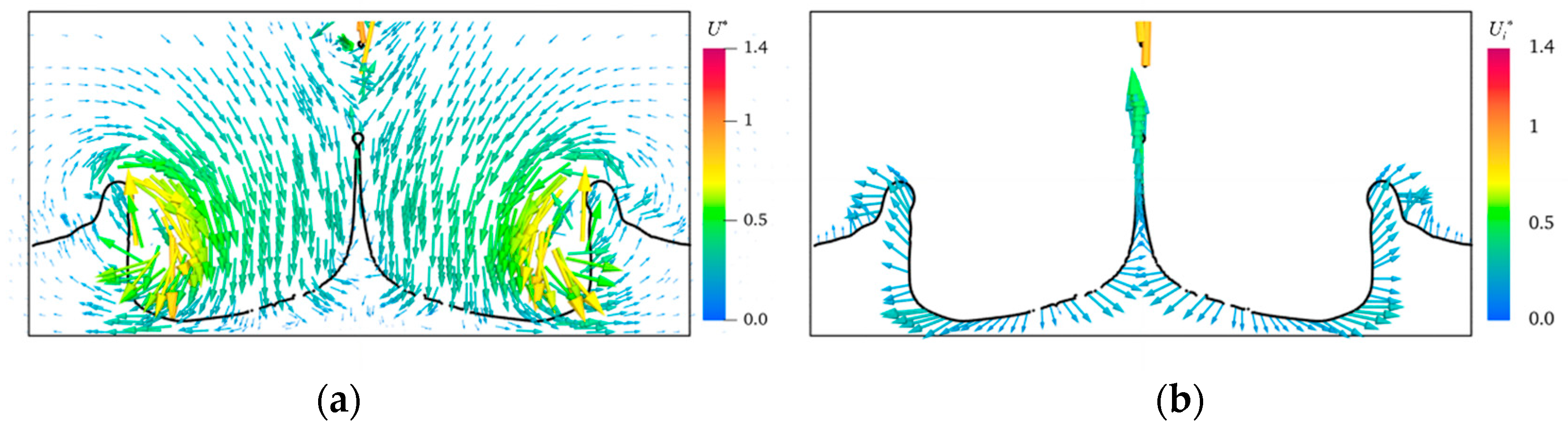
3.1. The Impact Process
3.2. Effects of Weber Number
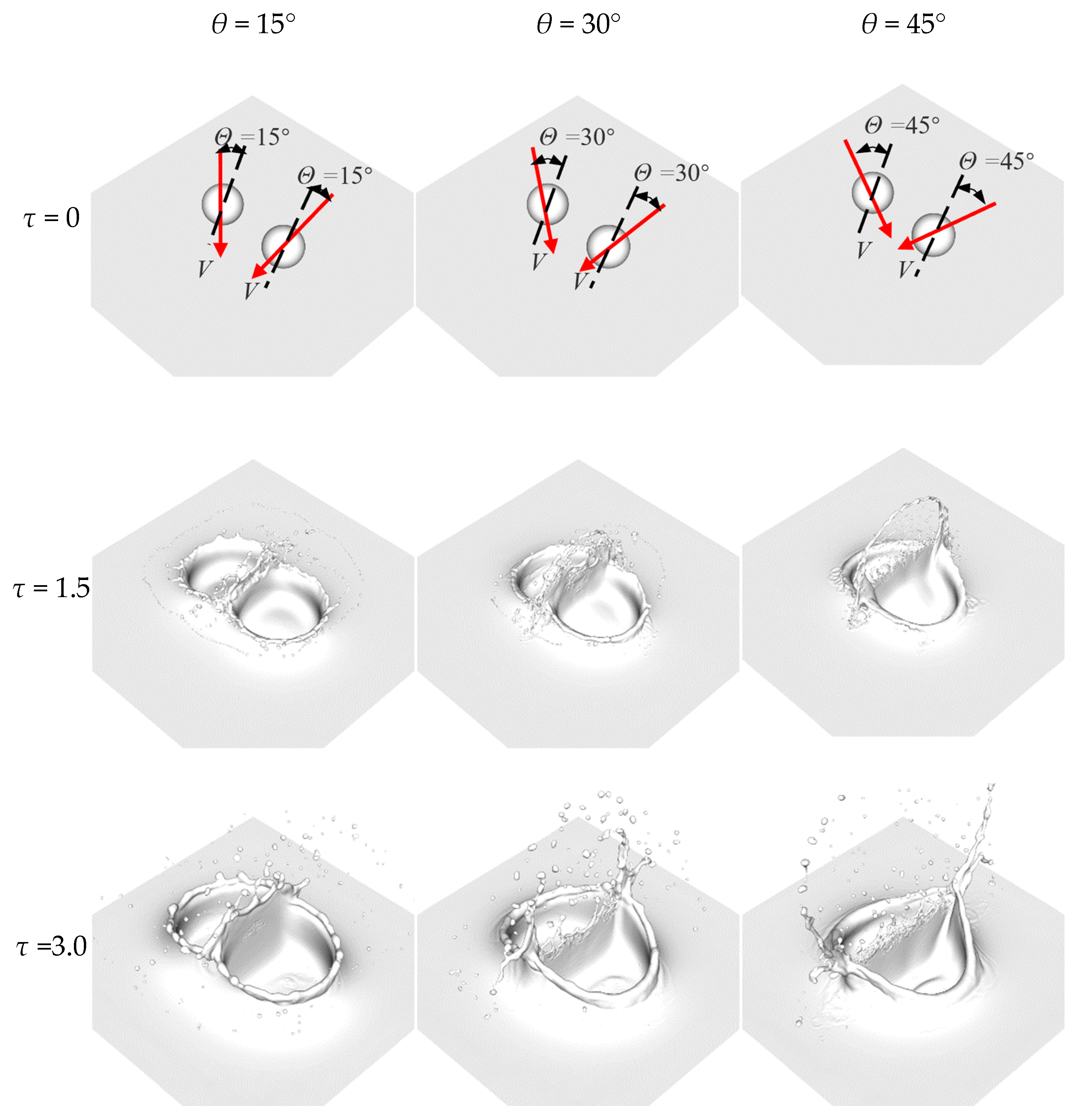
3.3. Effects of Impact Angle
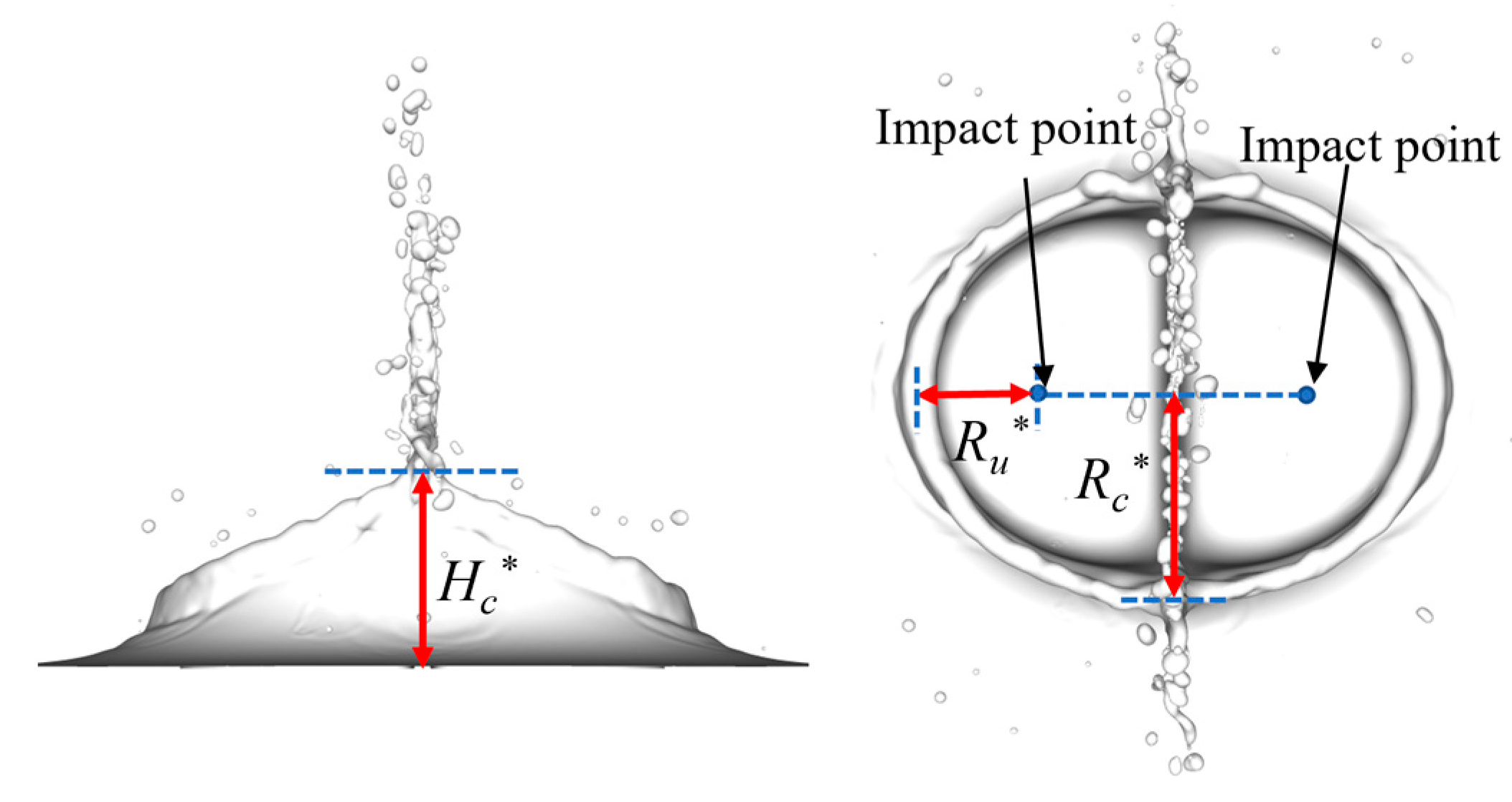
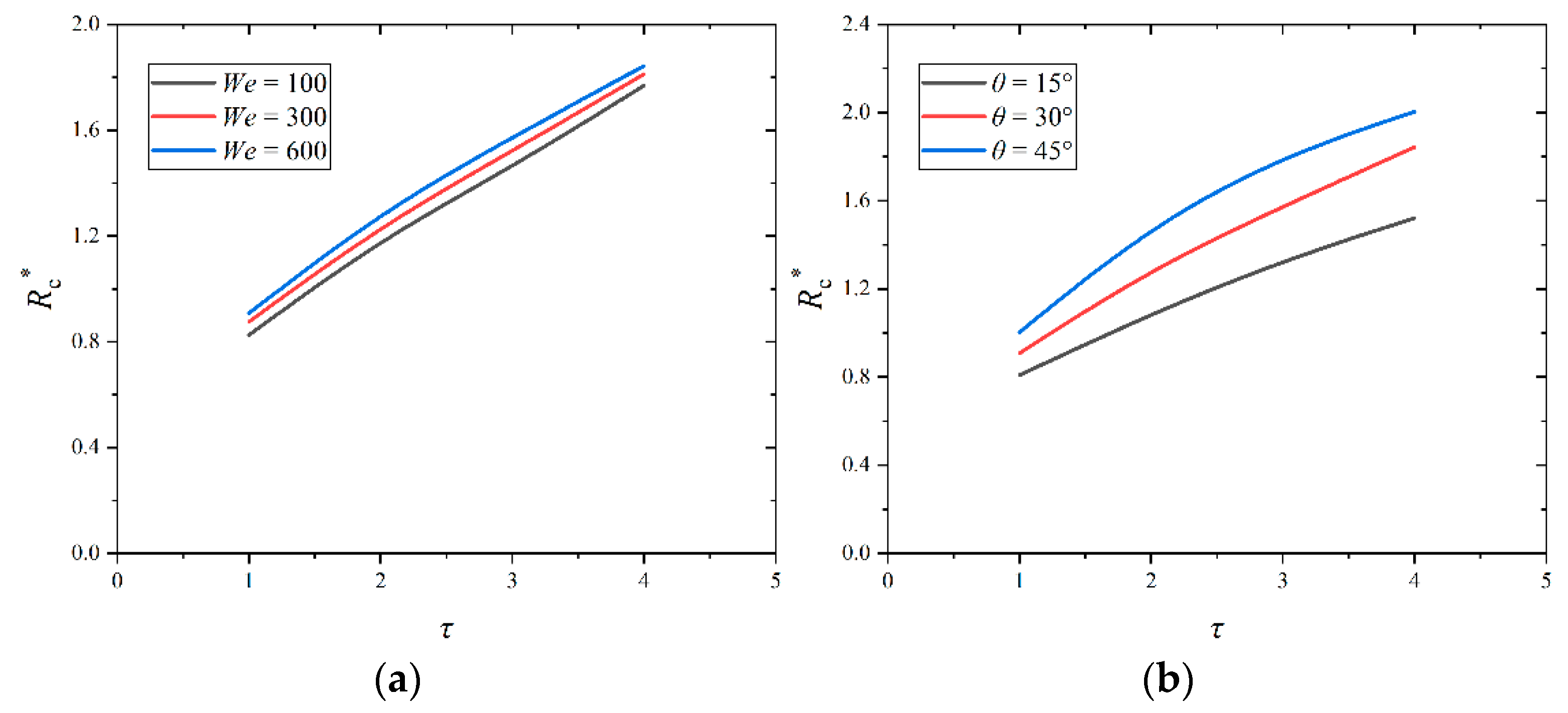
3.4. The Upstream Crown Radius
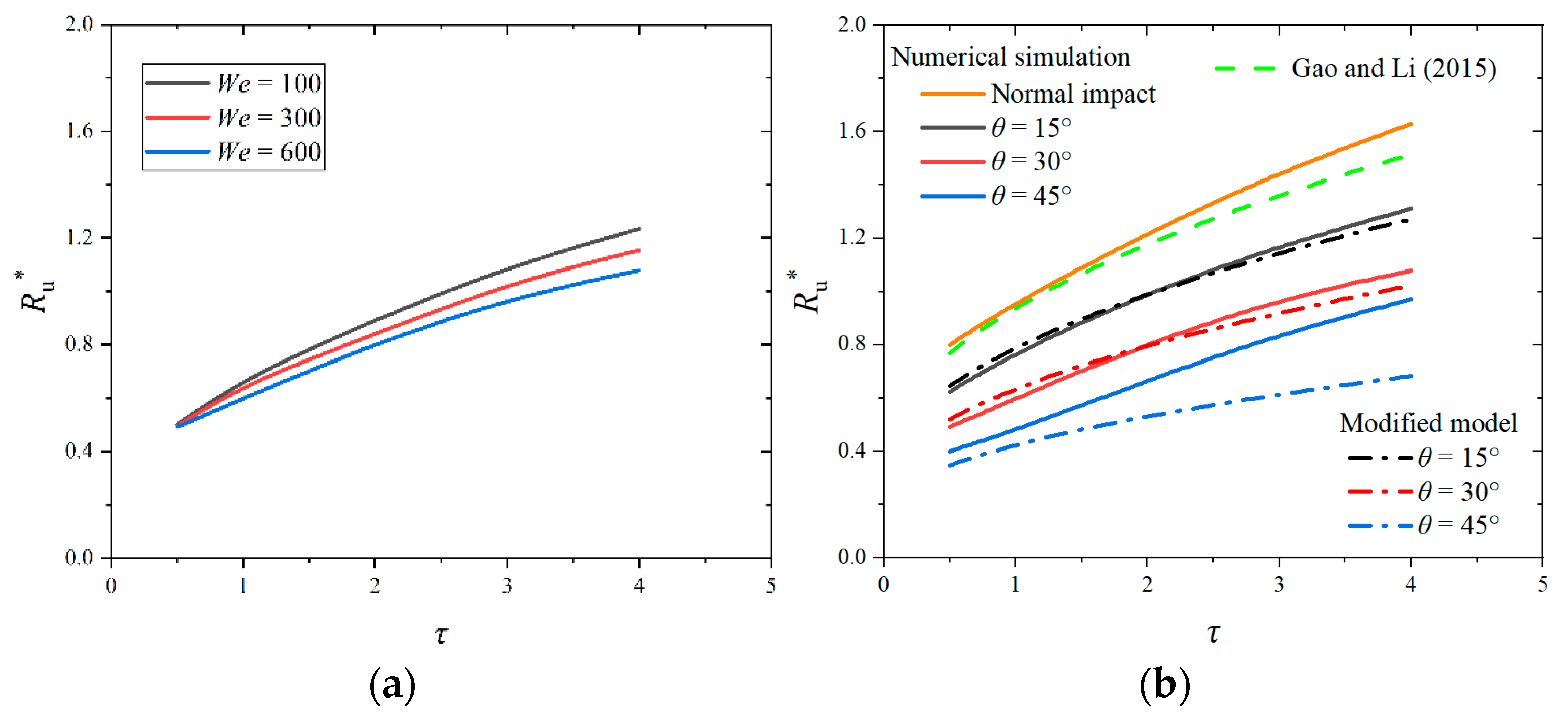
3.5. The Central Uprising Sheet Radius
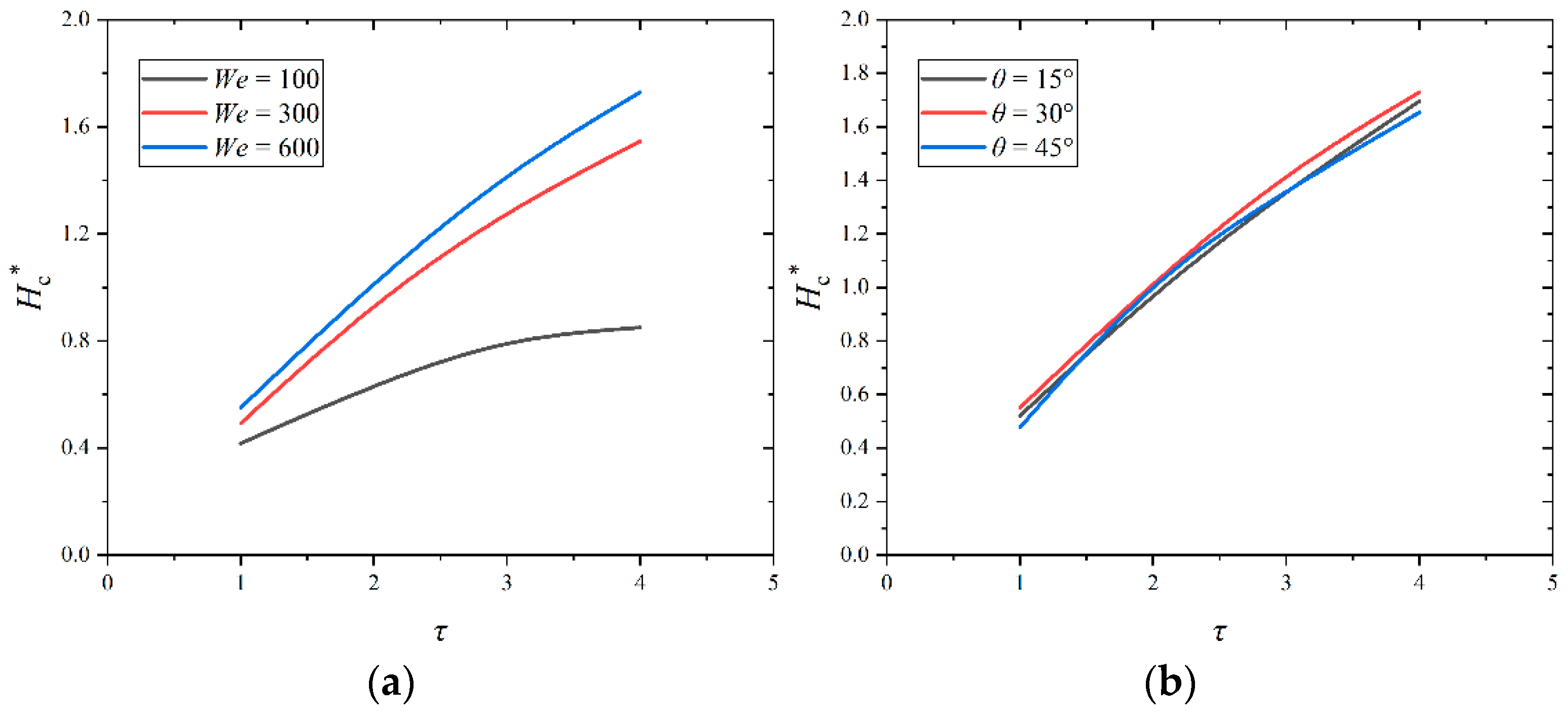
3.6. The Central Uprising Sheet Height
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Prosperetti, A.; Oguz, H.N. The impact of drops on liquid surfaces and the underwater noise of rain. Annu. Rev. Fluid Mech. 1993, 25, 577–602. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Aziz, S.D.; Chandra, S.; Mostaghimi, J. Cooling effectiveness of a water drop impinging on a hot surface. Int. J. Heat Fluid Flow 2001, 22, 201–210. [Google Scholar] [CrossRef]
- Panão, M.R.O.; Moreira, A.L.N. Flow characteristics of spray impingement in PFI injection systems. Exp. Fluids 2005, 39, 364–374. [Google Scholar] [CrossRef]
- Derby, B. Inkjet Printing of Functional and Structural Materials: Fluid Property Requirements, Feature Stability, and Resolution. Annu. Rev. Mater. Res. 2010, 40, 395–414. [Google Scholar] [CrossRef]
- Tyagi, P.K.; Kumar, R.; Mondal, P.K. A review of the state-of-the-art nanofluid spray and jet impingement cooling. Phys. Fluids 2020, 32, 121301. [Google Scholar] [CrossRef]
- Cossali, G.E.; Coghe, A.; Marengo, M. The impact of a single drop on a wetted solid surface. Exp. Fluids 1997, 22, 463–472. [Google Scholar] [CrossRef]
- Wang, A.; Chen, C. Splashing impact of a single drop onto very thin liquid films. Phys. Fluids 2000, 12, 2155–2158. [Google Scholar] [CrossRef]
- Thoroddsen, S.T. The ejecta sheet generated by the impact of a drop. J. Fluid Mech. 2002, 451, 373–381. [Google Scholar] [CrossRef]
- Rioboo, R.; Bauthier, C.; Conti, J.; Vou, M.; De Coninck, J. Experimental investigation of splash and crown formation during single drop impact on wetted surfaces. Exp. Fluids 2003, 35, 648–652. [Google Scholar] [CrossRef]
- Cossali, G.E.; Marengo, M.; Coghe, A.; Zhdanov, S. The role of time in single drop splash on thin film. Exp. Fluids 2004, 36, 888–900. [Google Scholar] [CrossRef]
- Vander Wal, R.L.; Berger, G.M.; Mozes, S.D. Droplets splashing upon films of the same fluid of various depths. Exp. Fluids 2006, 40, 33–52. [Google Scholar] [CrossRef]
- Okawa, T.; Shiraishi, T.; Mori, T. Production of secondary drops during the single water drop impact onto a plane water surface. Exp. Fluids 2006, 41, 965–974. [Google Scholar] [CrossRef]
- Motzkus, C.; Gensdarmes, F.; Géhin, E. Parameter study of microdroplet formation by impact of millimetre-size droplets onto a liquid film. J. Aerosol Sci. 2009, 40, 680–692. [Google Scholar] [CrossRef]
- Coppola, G.; Rocco, G.; de Luca, L. Insights on the impact of a plane drop on a thin liquid film. Phys. Fluids 2011, 23, 14. [Google Scholar] [CrossRef]
- Motzkus, C.; Gensdarmes, F.; Géhin, E. Study of the coalescence/splash threshold of droplet impact on liquid films and its relevance in assessing airborne particle release. J. Colloid Interface Sci. 2011, 362, 540–552. [Google Scholar] [CrossRef] [PubMed]
- Agbaglah, G.; Deegan, R.D. Growth and instability of the liquid rim in the crown splash regime. J. Fluid Mech. 2014, 752, 485–496. [Google Scholar] [CrossRef]
- Josserand, C.; Ray, P.; Zaleski, S. Droplet impact on a thin liquid film: Anatomy of the splash. J. Fluid Mech. 2016, 802, 775–805. [Google Scholar] [CrossRef]
- Fest-Santini, S.; Steigerwald, J.; Santini, M.; Cossali, G.E.; Weigand, B. Multiple drops impact onto a liquid film: Direct numerical simulation and experimental validation. Comput. Fluids 2021, 214, 104761. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of mass and momentum interactions during drop impact on a liquid film. Int. J. Heat Mass Transf. 2016, 101, 577–599. [Google Scholar] [CrossRef]
- Liang, G.; Zhang, T.; Yu, H.; Chen, H.; Shen, S. Simultaneous Impact of Multiple Droplets on Liquid Film. J. Ind. Eng. Chem. 2018, 65, 51–61. [Google Scholar] [CrossRef]
- Cossali, G.; Marengo, M.; Santini, M. Impact of single and multiple drop array on a liquid film. In Proceedings of the 19th Annual Meeting of ILASS, Nottingham, UK, 6–8 September 2004; pp. 1–8. [Google Scholar]
- Raman, K.A.; Jaiman, R.K.; Lee, T.S.; Low, H.T. On the dynamics of crown structure in simultaneous two droplets impact onto stationary and moving liquid film. Comput. Fluids 2015, 107, 285–300. [Google Scholar] [CrossRef]
- Li, L.; Jia, X.; Liu, Y.; Su, M. Simulation of double droplets impact on liquid film by a simplified lattice Boltzmann model. Appl. Therm. Eng. 2016, 98, 656–669. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Wang, T.; Yan, W. Asymmetric heat transfer characteristics of a double droplet impact on a moving liquid film. Int. J. Heat Mass Transf. 2018, 126, 649–659. [Google Scholar] [CrossRef]
- Liu, X.; Qu, Y.; Wang, Y.; Wang, M.; Wang, Z.; Sun, H. Numerical analysis of two hollow drops simultaneously impacting a wet surface. Phys. Fluids 2021, 33, 043312. [Google Scholar] [CrossRef]
- Liang, G.; Zhang, T.; Chen, Y.; Chen, L.; Shen, S. Non-simultaneous impact of multiple droplets on liquid film. Numer. Heat Transf. Part A Appl. 2019, 75, 137–147. [Google Scholar] [CrossRef]
- Liang, G.; Zhang, T.; Chen, H.; Yu, H.; Shen, S. Successive impact of multiple droplets on liquid film. Eur. J. Mech.—B/Fluids 2019, 74, 389–398. [Google Scholar] [CrossRef]
- Bao, M.; Guo, Y.; Gong, L.; Shen, S. Interface evolution characteristics of dual droplet successive oblique impact on liquid film. Phys. Fluids 2022, 34, 062115. [Google Scholar] [CrossRef]
- Thale, V.A.; Abouelsoud, M.; Chizari, H.; Thoraval, M. Impact force of an air-in-liquid compound drop. Phys. Fluids 2024, 36, 022110. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Bayeul-Lainé, A.; Murphy, D.; Katz, J.; Coutier-Delgosha, O. Analysis of high-speed drop impact onto deep liquid pool. J. Fluid Mech. 2023, 972, A31. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Khedher, N.B.; El-Zahar, E.R.; Seddek, L.F.; Ullah, Z.; Eldin, S.M. Amplitude and oscillating assessment of thermal and magnetic boundary layer flow across circular heated cylinder with heat source/sink. Case Stud. Therm. Eng. 2023, 49, 103216. [Google Scholar] [CrossRef]
- Ullah, Z.; Alkinidri, M. Oscillatory and transient role of heat transfer and magnetic flux around magnetic-driven stretching cylinder under convective boundary conditions. Case Stud. Therm. Eng. 2023, 50, 103514. [Google Scholar] [CrossRef]
- Al-Shammari, H.; Ullah, Z.; Mahrous, Y.M.; Aldhabani, M.S.; Said, M.A.; Al Arni, S.; Faqihi, A.A.; Khedher, N.B. Arrhenius activation energy and thermal radiation effects on oscillatory heat-mass transfer of Darcy Forchheimer nanofluid along heat generating cone. Case Stud. Therm. Eng. 2024, 57, 104294. [Google Scholar] [CrossRef]
- Boukholda, I.; Ullah, Z.; Mahrous, Y.M.; Alamer, A.; Amara, M.B.; Alsulami, M.D.; Faqihi, A.A.; Khedher, N.B. Analysis of thermal density and heat sink on dissipative nanofluid along magnetized sheet and applications in microelectronic cooling systems. Case Stud. Therm. Eng. 2024, 55, 104185. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop impact dynamics: Splashing, spreading, receding, bouncing…. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Yarin, A.L.; Weiss, D.A. Impact of drops on solid surfaces: Self-similar capillary waves, and splashing as a new type of kinematic discontinuity. J. Fluid Mech. 1995, 283, 141–173. [Google Scholar] [CrossRef]
- Liang, G.; Guo, Y.; Shen, S.; Yang, Y. Crown behavior and bubble entrainment during a drop impact on a liquid film. Theor. Comp. Fluid Dyn. 2014, 28, 159–170. [Google Scholar] [CrossRef]
- Gao, X.; Li, R. Impact of a single drop on a flowing liquid film. Phys. Rev. E 2015, 92, 053005. [Google Scholar] [CrossRef]
- Khan, T.; Jin, Z.; Yang, Z. Impact dynamics of non-spherical droplets on a thin water film. Phys. Fluids 2024, 36, 032130. [Google Scholar] [CrossRef]



| Fluid | Density | Dynamic Viscosity | Surface Tension |
|---|---|---|---|
| ρ [kg/m3] | μ [Pa·s] | σ [N/m] | |
| Air | 1.204 | 1.813 × 10−5 | - |
| Water | 998 | 1.002 × 10−3 | 0.073 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Jin, Z.; Yang, Z.; Yu, L. Numerical Analysis of Dual Droplet Simultaneous Oblique Impact on a Water Film. Energies 2024, 17, 2529. https://doi.org/10.3390/en17112529
Zhou B, Jin Z, Yang Z, Yu L. Numerical Analysis of Dual Droplet Simultaneous Oblique Impact on a Water Film. Energies. 2024; 17(11):2529. https://doi.org/10.3390/en17112529
Chicago/Turabian StyleZhou, Botong, Zheyan Jin, Zhigang Yang, and Lei Yu. 2024. "Numerical Analysis of Dual Droplet Simultaneous Oblique Impact on a Water Film" Energies 17, no. 11: 2529. https://doi.org/10.3390/en17112529
APA StyleZhou, B., Jin, Z., Yang, Z., & Yu, L. (2024). Numerical Analysis of Dual Droplet Simultaneous Oblique Impact on a Water Film. Energies, 17(11), 2529. https://doi.org/10.3390/en17112529





