Research on the EMA Control Method Based on Transmission Error Compensation
Abstract
1. Introduction
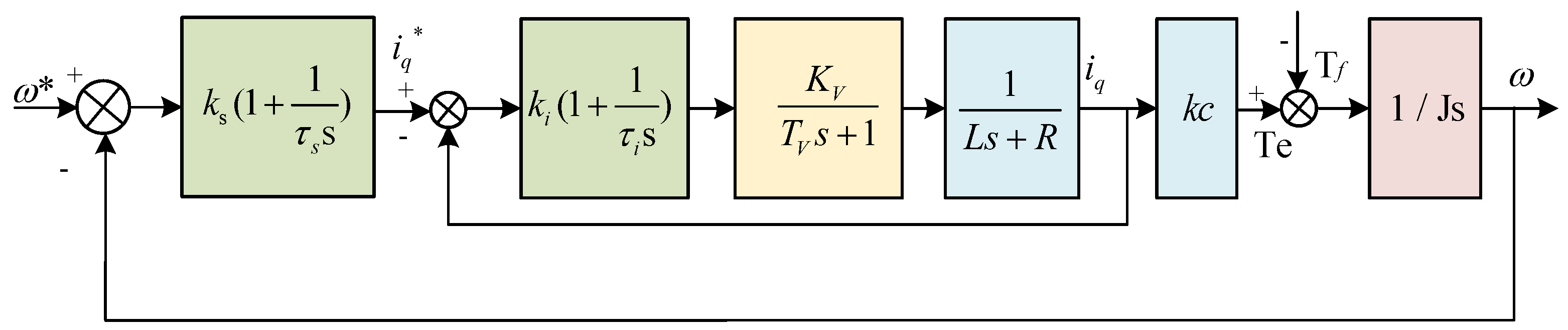
2. The PMSM Mathematical Model in the EMA
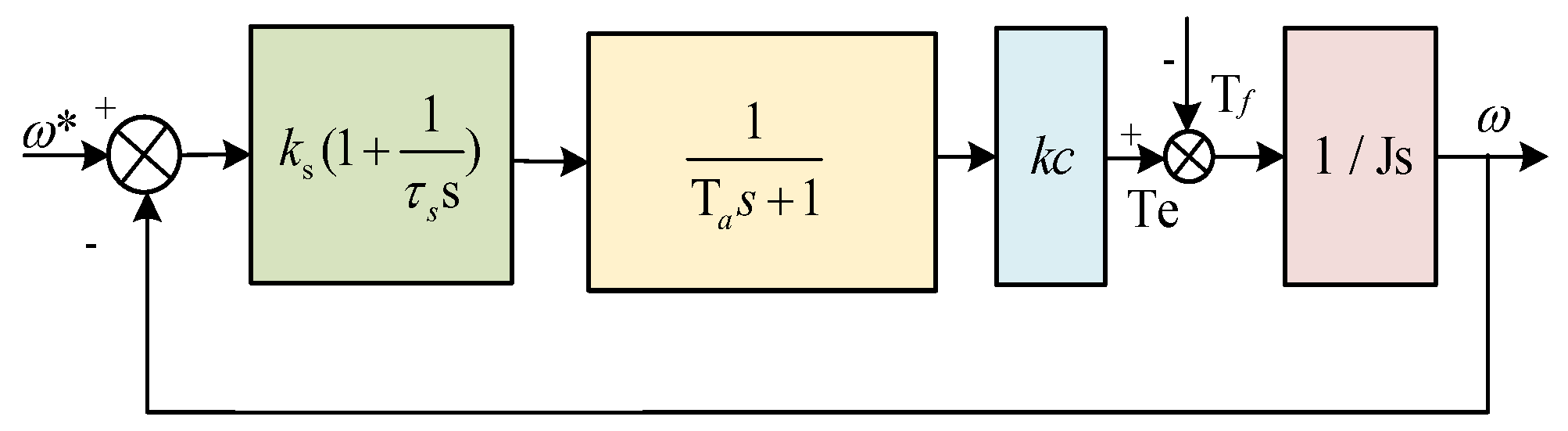
3. EMA Position Error Online Compensation
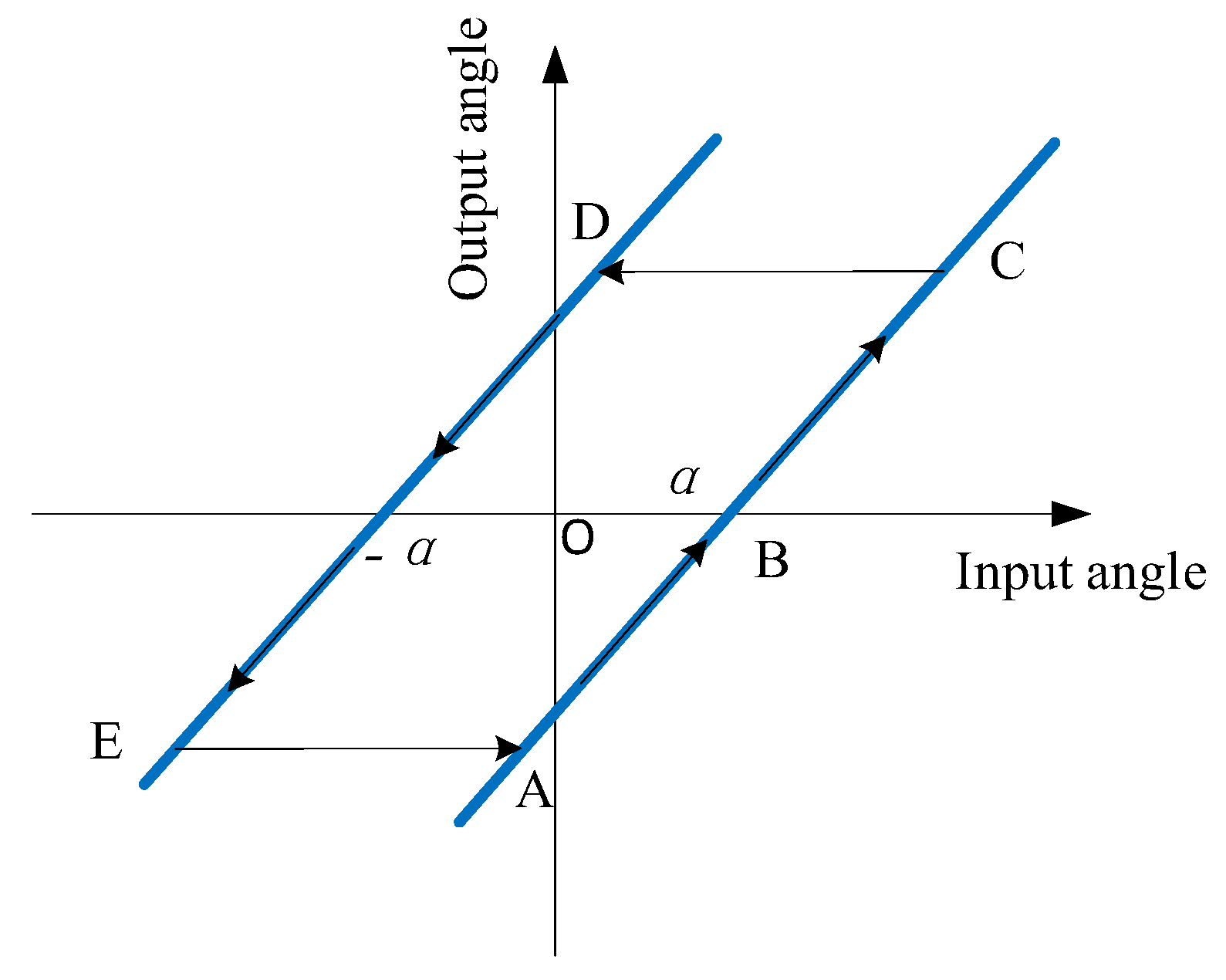
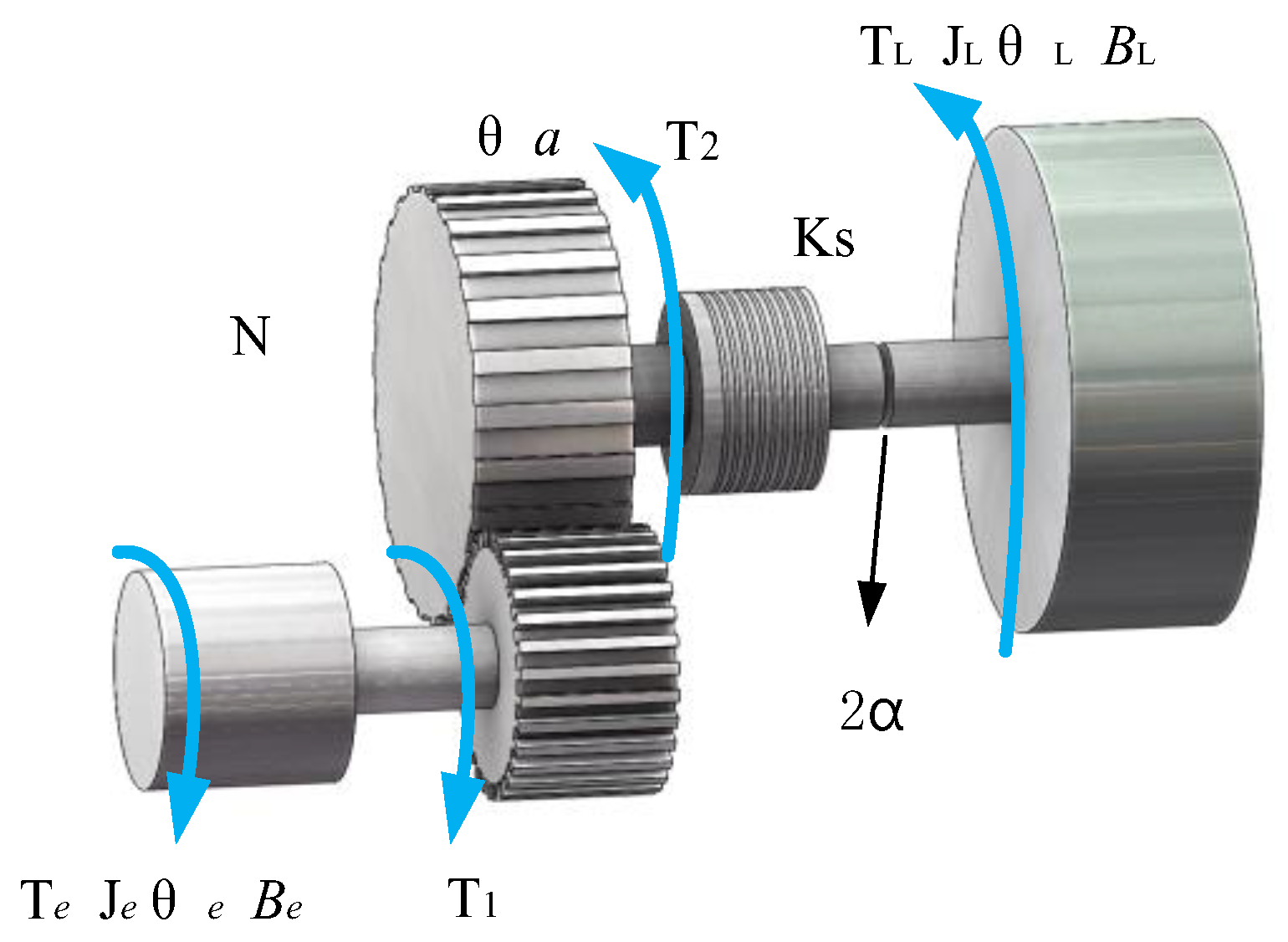
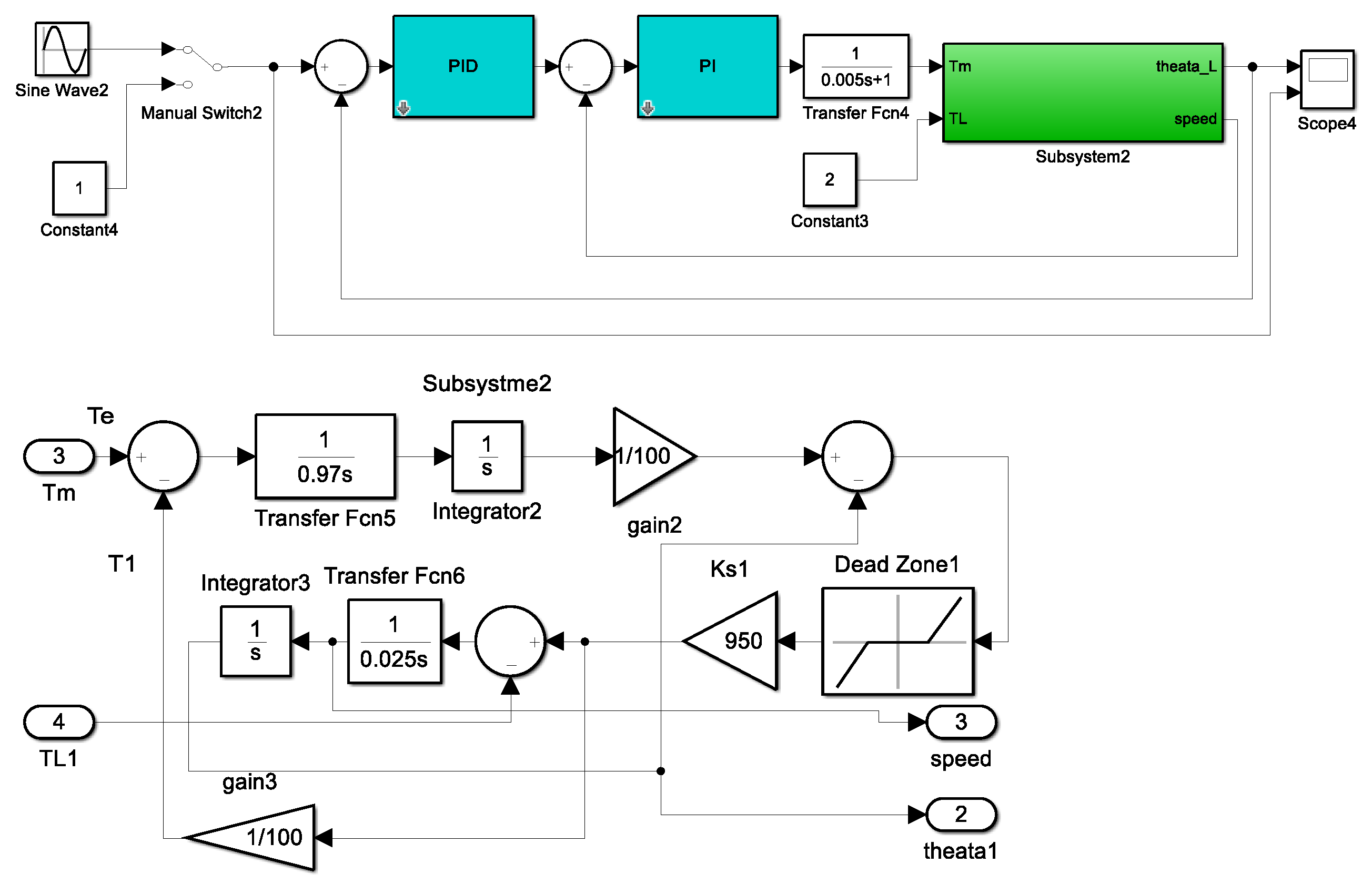
3.1. EMA Model with Gaps
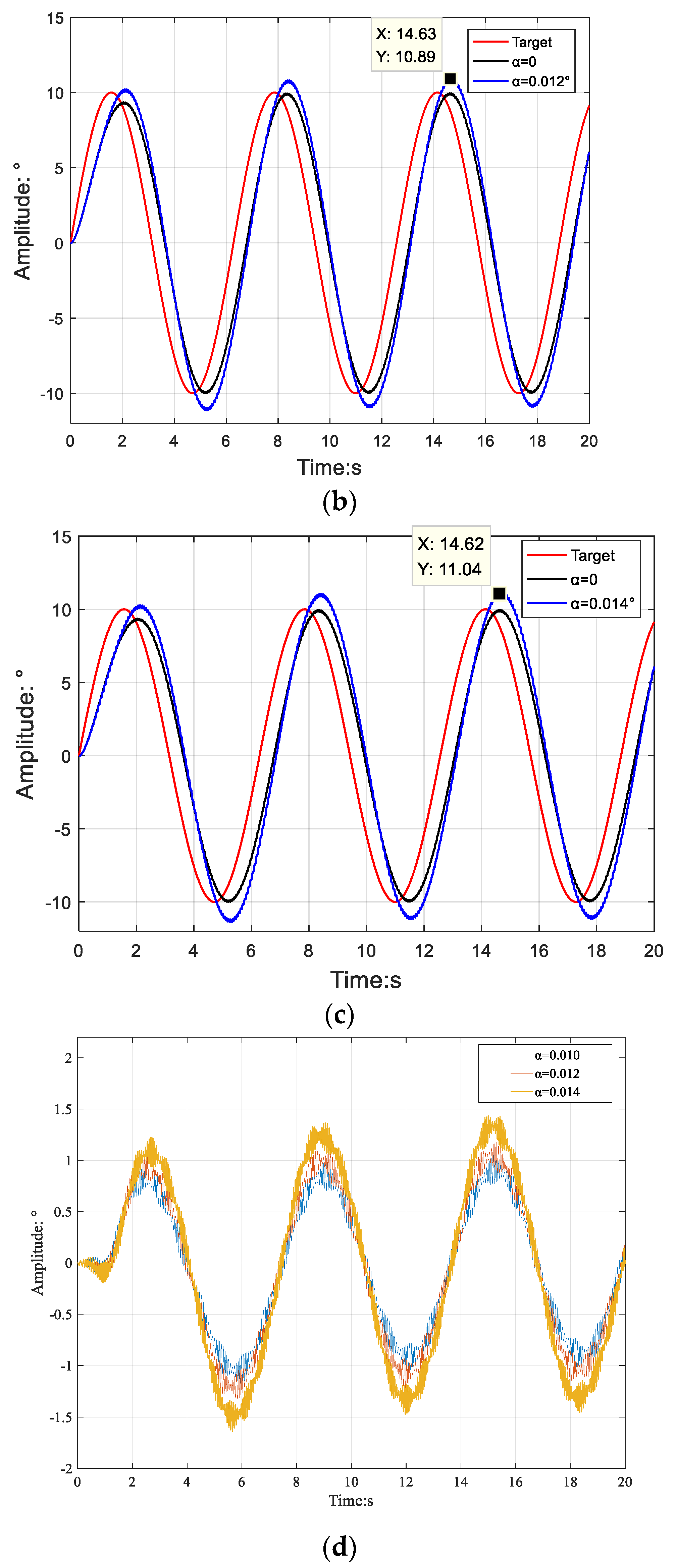
3.2. EMA Simulation Analysis with Gaps
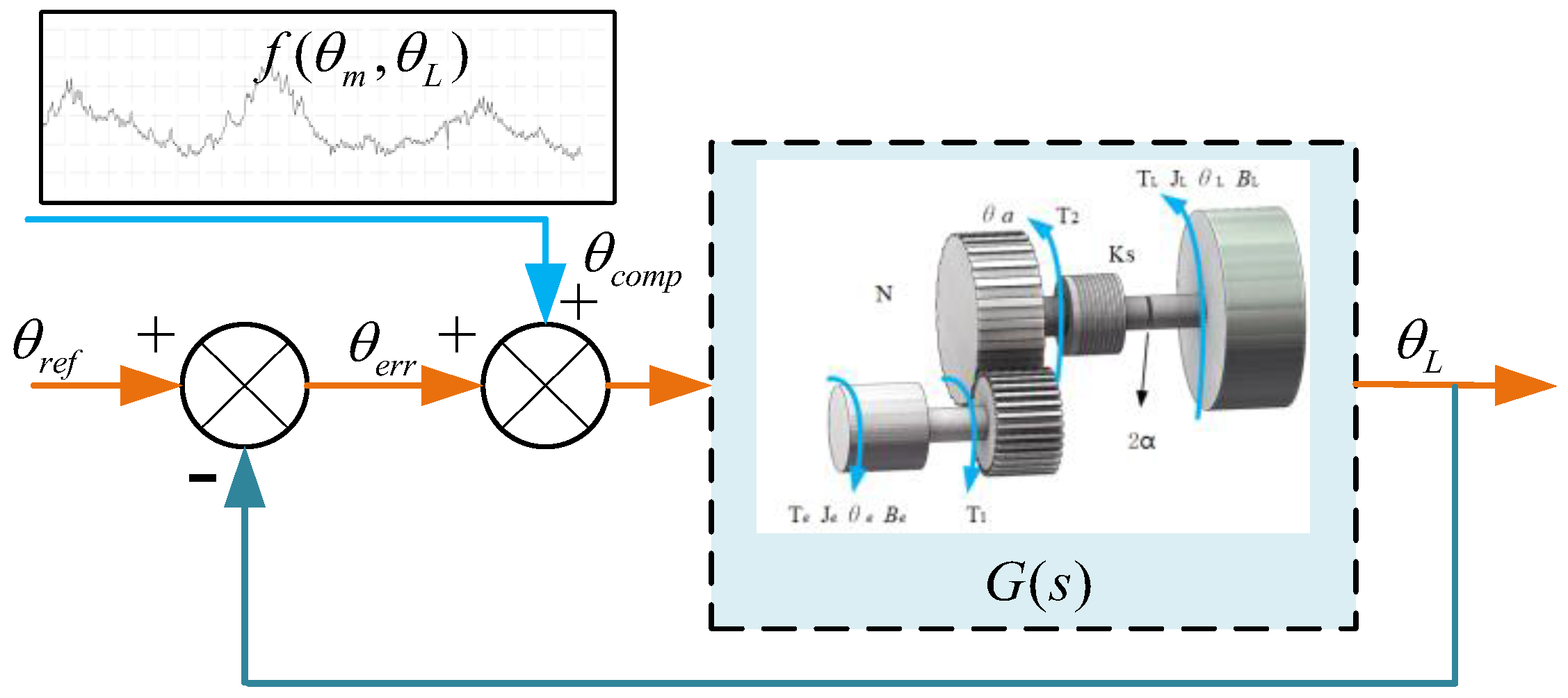
3.3. EMA Position Error Compensation
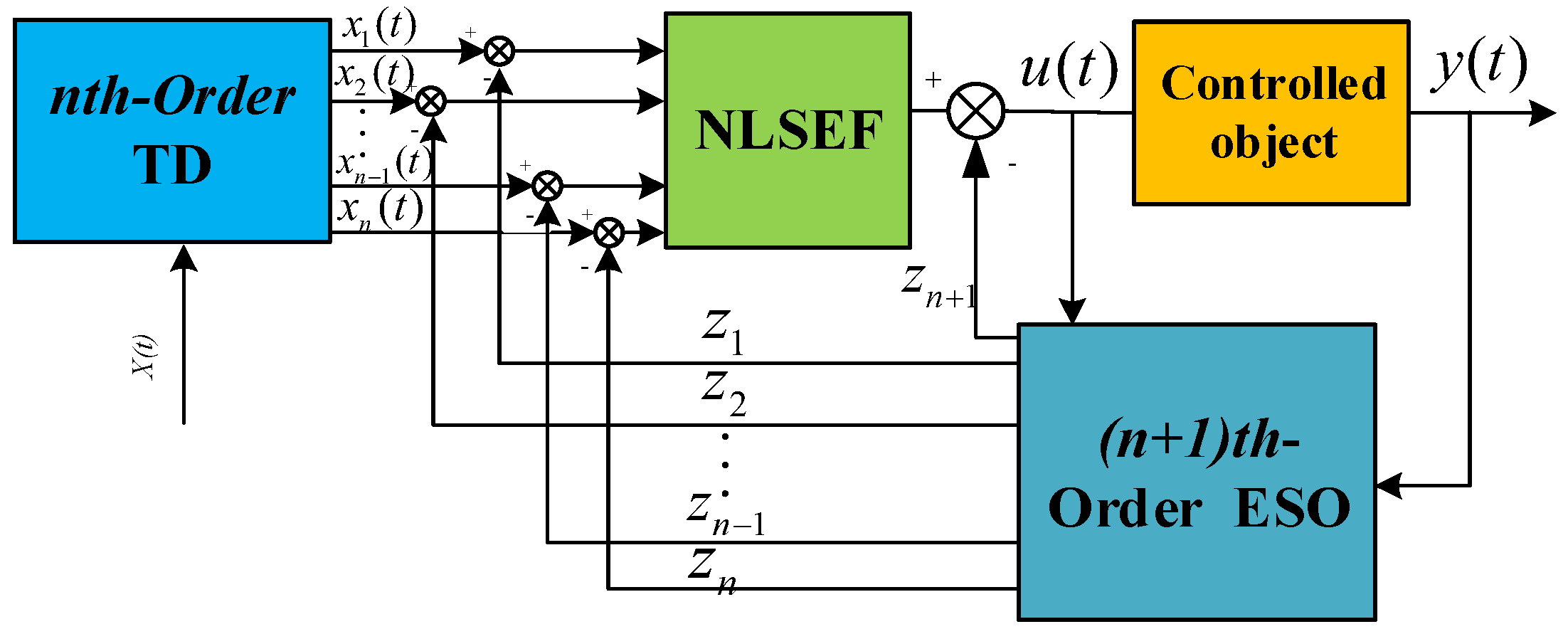
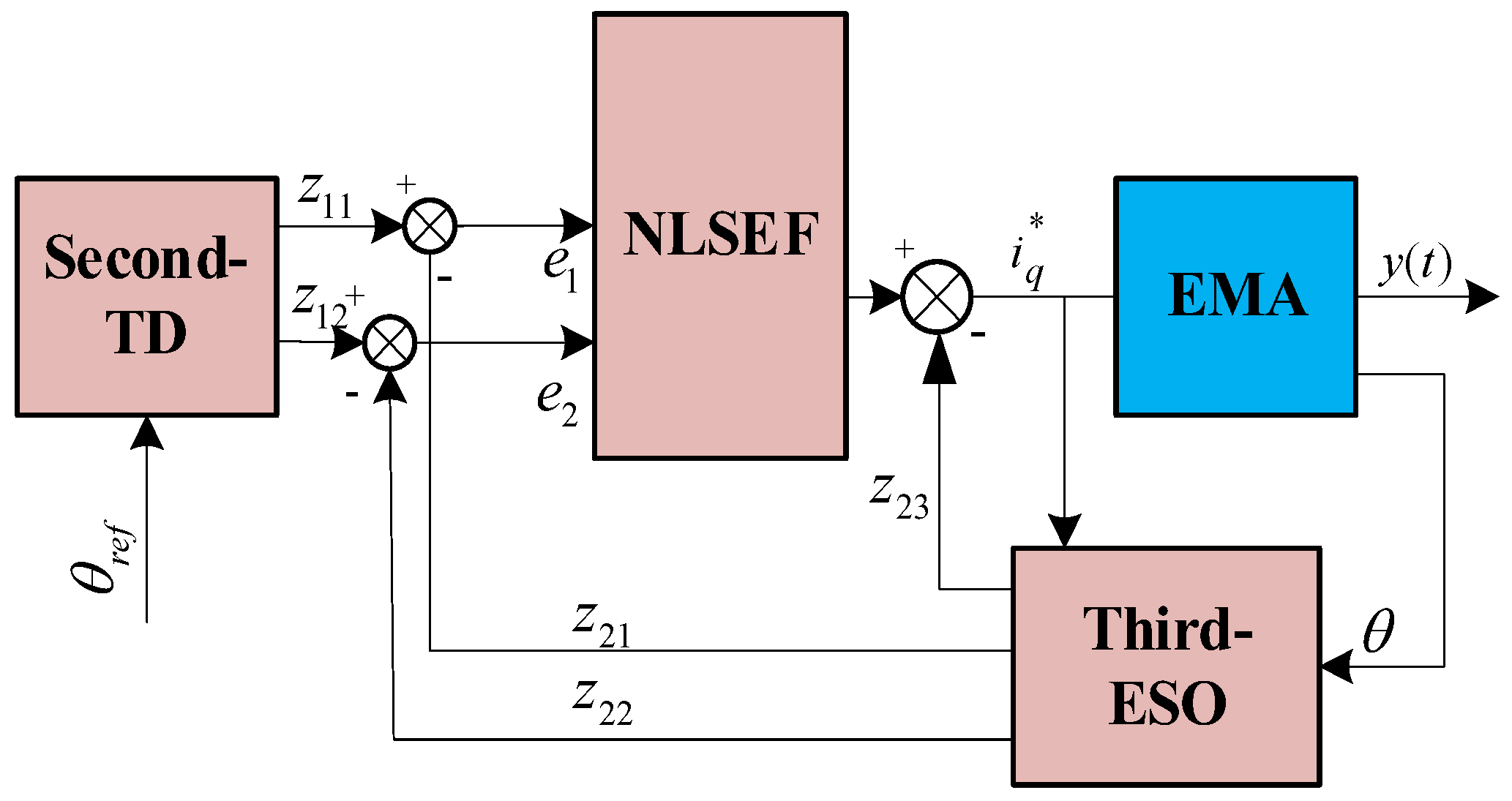
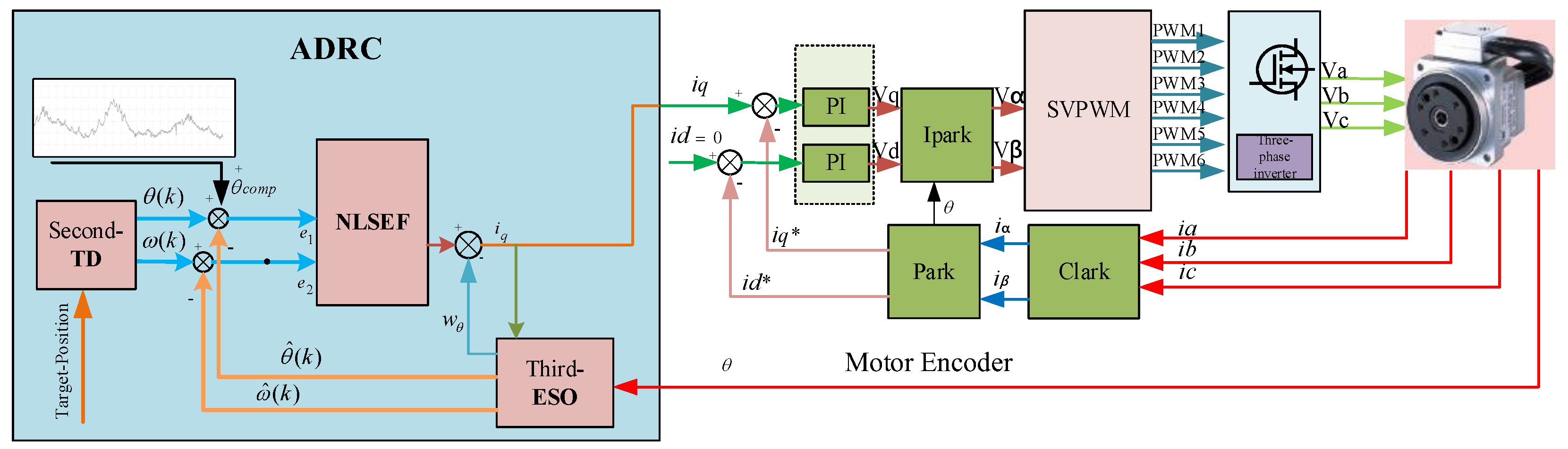
4. Position Loop Second-Order ADRC Design for Positional Errors
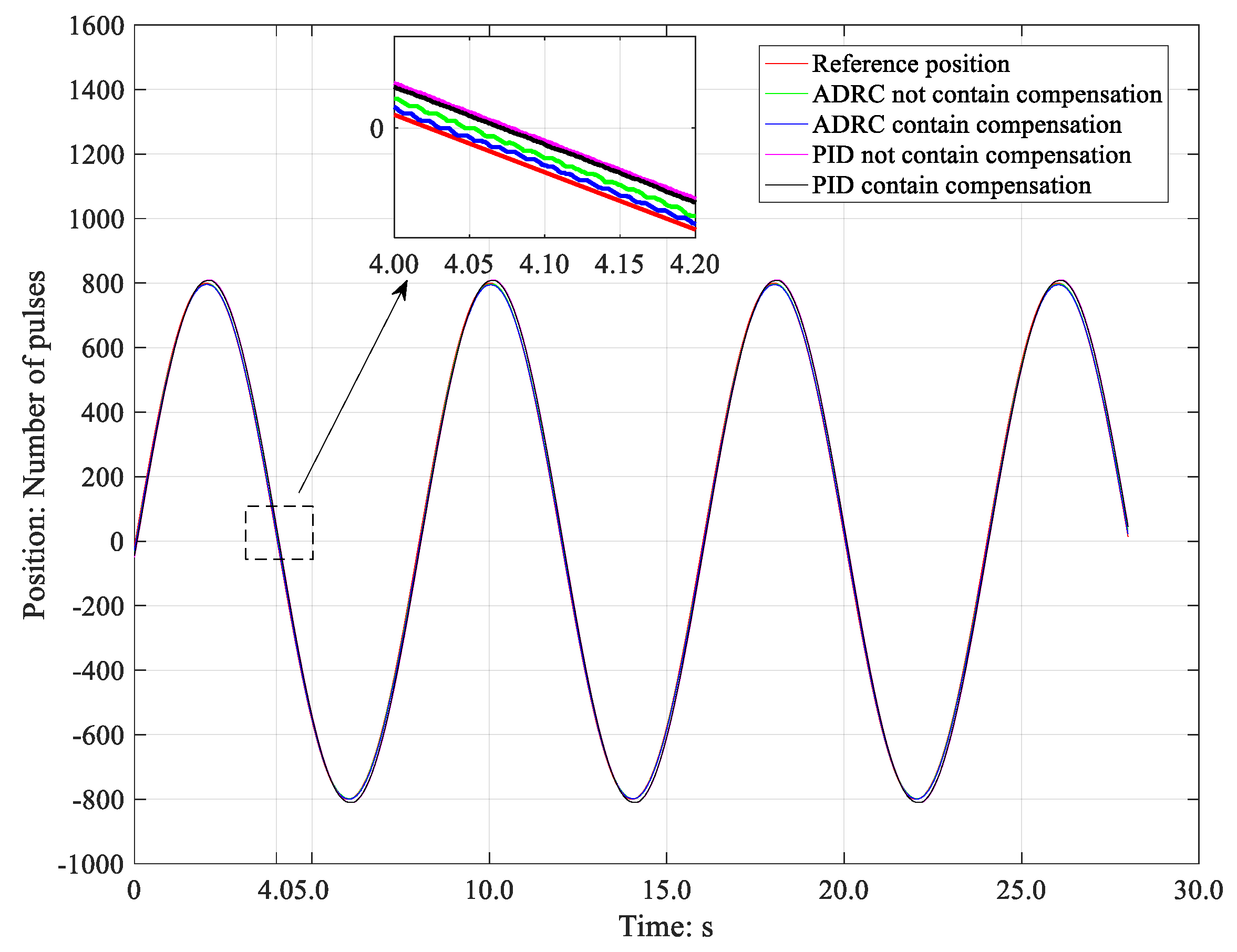
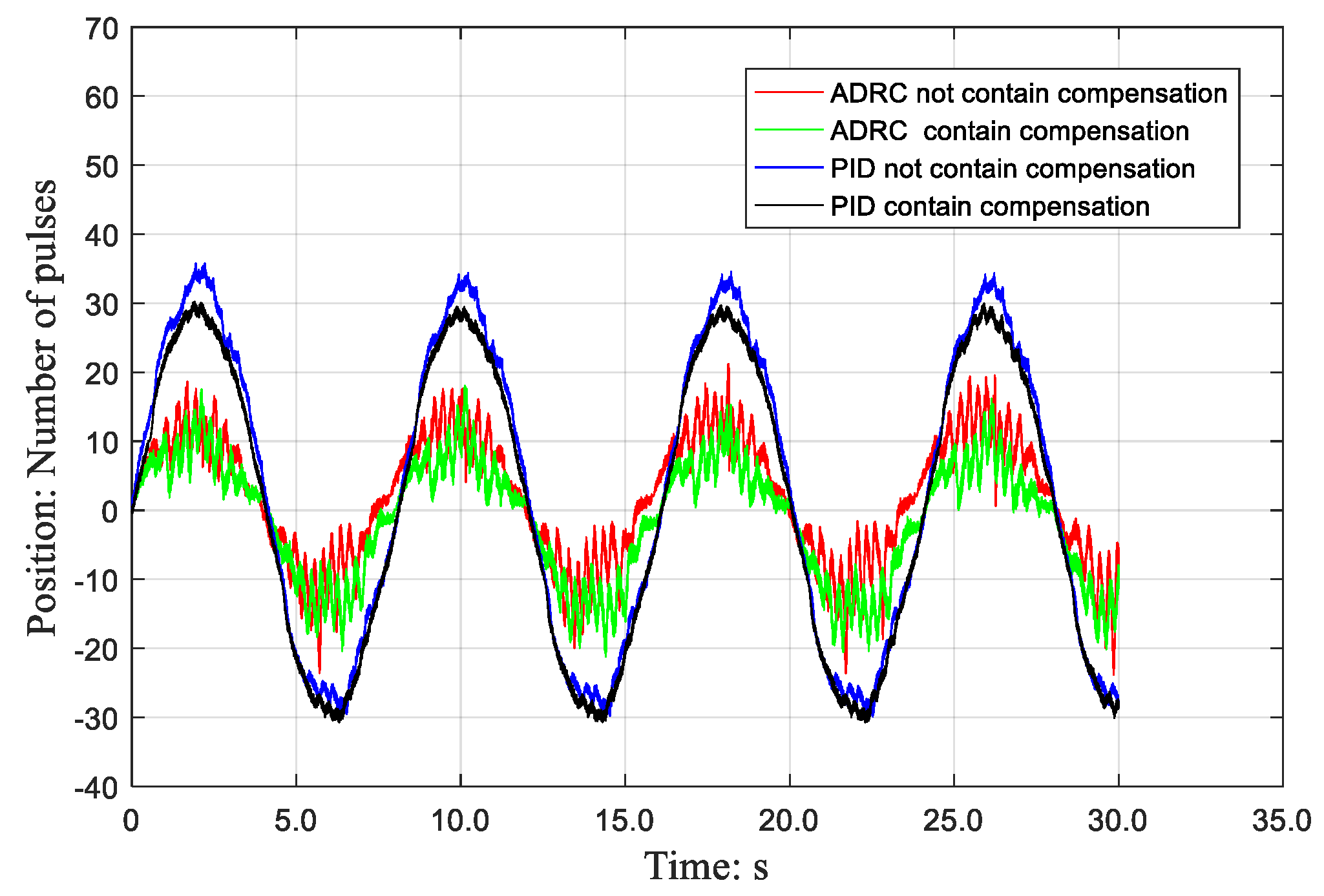
5. Experimental Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jung, B.J.; Kim, B.; Koo, J.C.; Choi, H.R.; Moon, H. Joint torque sensor embedded in harmonic drive using order tracking method for robotic application. IEEE/ASME Trans. Mechatron. 2017, 22, 1594–1599. [Google Scholar] [CrossRef]
- Ismail, M.A.A.; Windelberg, J.; Liu, G. Simplified sensorless torque estimation method for harmonic drive based electro-mechanical actuator. IEEE Robot. Autom. Lett. 2021, 6, 835–840. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Huang, P.Y.; Yen, J.Y. Frequency-domain identification algorithms for servo systems with friction. IEEE Trans. Control Syst. Technol. 2002, 10, 654–665. [Google Scholar] [CrossRef]
- Han, B.C.; Ma, J.J.; Li, H.T. Modeling and compensation of nonlinear friction in harmonic driver. Opt. Precis. Eng. 2011, 19, 1095–1103. [Google Scholar]
- Han, B.C.; Ma, J.J.; Li, H.T. Research on nonlinear friction compensation of harmonic drive in gimbal servo-system of DGCMG. Int. J. Control Autom. Syst. 2016, 14, 779–786. [Google Scholar] [CrossRef]
- Shi, Y.; Yu, Y.; Wang, Q.; Li, H.; Chen, X. Composite Control Based on Feed-Forward and FISMC Method for Accurate Speed of Gimbal System wth Harmonic Drive. IEEE Trans. Power Electron. 2023, 38, 6434–6443. [Google Scholar] [CrossRef]
- Ostapski, W. Analysis of the stress state in the harmonic drive generator-flexspline system in relation to selected structural parameters and manufacturing deviations. Bull. Pol. Acad. Sci.-Tech. Sciences. Sci. 2010, 58, 683–698. [Google Scholar] [CrossRef]
- Han, J. Active disturbance rejection controller and its applications. Control Decis. 1998, 13, 19–23. (In Chinese) [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and Parameterization Based Controller Tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Guo, B.Z.; Jin, F.F. The active disturbance rejection and sliding mode control approach to the stabilization of the Euler–Bernoulli beam equation with boundary input disturbance. Automatica 2013, 49, 2911–2918. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Discrete-time repetitive control-based ADRC for current loop disturbances suppression of PMSM drives. IEEE Trans. Ind. Inform. 2021, 18, 3138–3149. [Google Scholar] [CrossRef]
- Hezzi, A.; Ben Elghali, S.; Bensalem, Y.; Zhou, Z.; Benbouzid, M.; Abdelkrim, M.N. ADRC-based robust and resilient control of a 5-phase PMSM driven electric vehicle. Machines 2020, 8, 17. [Google Scholar] [CrossRef]
- Su, Y.X.; Zheng, C.H.; Duan, B.Y. Automatic disturbances rejection controller for precise motion control of permanent-magnet synchronous motors. IEEE Trans. Ind. Electron. 2005, 52, 814–823. [Google Scholar] [CrossRef]
- Li, S.; Xia, C.; Zhou, X. Disturbance rejection control method for permanent magnet synchronous motor speed regulation system. Mechatronics 2016, 22, 706–714. [Google Scholar] [CrossRef]
- Rong, Z.; Huang, Q. A new PMSM speed modulation system with sliding mode based on active-disturbance-rejection control. J. Cent. South Univ. 2016, 23, 1406–1415. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z. Adaptive speed control for permanent-magnet synchronous motor system with variations of load inertia. IEEE Trans. Ind. Electron. 2009, 56, 3050–3059. [Google Scholar]
- Zhu, H.; Weng, F.; Li, D.; Zhu, M. Active control of combustion oscillation with active disturbance rejection control (ADRC) method. J. Sound Vib. 2022, 540, 117245. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, J.; Xu, D.; Huang, Z.; Zhou, H. The decoupled vector-control of PMSM based on nonlinear multi-input multi-output decoupling ADRC. Adv. Mech. Eng. 2020, 12, 1687814020984255. [Google Scholar] [CrossRef]
- Kang, K.; Song, J.; Kang, C.; Sung, S.; Jang, G. Real-time detection of the dynamic eccentricity in permanent-magnet synchronous motors by monitoring speed and back EMF induced in an additional winding. IEEE Trans. Ind. Electron. 2017, 64, 7191–7200. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, W.; Chen, S.; Liu, Z. Complementary sliding mode control with adaptive switching gain for PMSM. Trans. Inst. Meas. Control 2019, 41, 3199–3205. [Google Scholar] [CrossRef]
- Lee, K.; Hong, S.; Oh, J.-H. Development of a Lightweight and High-efficiency Compact Cycloidal Reducer for Legged Robots. Int. J. Precis. Eng. Manuf. 2019, 21, 415–425. [Google Scholar] [CrossRef]
- Qi, L.; Bao, S.; Shi, H. Permanent-magnet synchronous motor velocity control based on second-order integral sliding mode control algorithm. Trans. Inst. Meas. Control 2013, 37, 875–882. [Google Scholar] [CrossRef]
- Jin, R.; Wang, J.; Ou, Y.; Li, J. Composite ADRC Speed Control Method Based on LTDRO Feedforward Compensation. Sensors 2024, 24, 2605. [Google Scholar] [CrossRef]
- Gao, S.; Wei, Y.; Zhang, D.; Qi, H.; Wei, Y. A Modified Model Predictive Torque Control with Parameters Robustness Improvement for PMSM of Electric Vehicles. Actuators 2021, 10, 132. [Google Scholar] [CrossRef]
- Yi, Y.; Sun, X.; Li, X.; Fan, X. Disturbance observer based composite speed controller design for PMSM system with mismatched disturbances. Trans. Inst. Meas. Control 2015, 38, 742–750. [Google Scholar] [CrossRef]
- Moon, H.T.; Kim, H.S.; Youn, M.J. A discrete-time predictive current control for PMSM. IEEE Trans. Power Electron. 2003, 18, 464–472. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model predictive current control for PMSM drives with parameter robustness improvement. IEEE Trans. Power Electron. 2018, 34, 1645–1657. [Google Scholar] [CrossRef]
- Ghorbel, F.H.; Gandhi, P.S.; Alpeter, F. On the kinematic error in harmonic drive gears. J. Mech. Des. 2001, 123, 90–97. [Google Scholar] [CrossRef]
- Roozing, W.; Malzahn, J.; Kashiri, N.; Caldwell, D.G.; Tsagarakis, N.G. On the stiffness selection for torque-controlled series-elastic actuators. IEEE Robot. Autom. Lett. 2017, 2, 2255–2262. [Google Scholar] [CrossRef]
- Ishida, T.; Takanishi, A. A robot actuator development with high back drivability. In Proceedings of the 2006 IEEE Conference on Robotics, Automation and Mechatronics, Bangkok, Thailand, 1–3 June 2006; pp. 1–6. [Google Scholar]
- Han, J.; Wang, H.; Jiao, G.; Cui, L.; Wang, Y. Research on active disturbance rejection control technology of electromechanical actuators. Electronics 2018, 7, 174. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, Y.; Zheng, H.; Wang, S.; Ma, J.; Liu, Y. A self-searching optimal ADRC for the pitch angle control of an underwater thermal glider in the vertical plane motion. Ocean Eng. 2018, 159, 98–111. [Google Scholar] [CrossRef]
- Gao, C.; Yuan, J.; Zhao, Y. ADRC for spacecraft attitude and position synchronization in libration point orbits. Acta Astronaut. 2018, 145, 238–249. [Google Scholar] [CrossRef]







| Control Mode | Peak to Peak | RMSE | MAE |
|---|---|---|---|
| PID | 65.671 | 21.558 | 19.425 |
| PID-compensation | 60.965 | 20.592 | 18.533 |
| ADRC | 45.000 | 9.121 | 7.898 |
| ADRC-compensation | 39.283 | 8.799 | 7.389 |
| Control Mode | Peak to Peak | RMSE | MAE |
|---|---|---|---|
| PID | 76.917 | 26.376 | 23.698 |
| PID-compensation | 68.419 | 23.468 | 21.139 |
| ADRC | 40.488 | 9.566 | 8.343 |
| ADRC-compensation | 33.867 | 9.046 | 7.631 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Shi, Z.; Yu, B.; Qi, H. Research on the EMA Control Method Based on Transmission Error Compensation. Energies 2024, 17, 2528. https://doi.org/10.3390/en17112528
Zhang P, Shi Z, Yu B, Qi H. Research on the EMA Control Method Based on Transmission Error Compensation. Energies. 2024; 17(11):2528. https://doi.org/10.3390/en17112528
Chicago/Turabian StyleZhang, Pan, Zhaoyao Shi, Bo Yu, and Haijiang Qi. 2024. "Research on the EMA Control Method Based on Transmission Error Compensation" Energies 17, no. 11: 2528. https://doi.org/10.3390/en17112528
APA StyleZhang, P., Shi, Z., Yu, B., & Qi, H. (2024). Research on the EMA Control Method Based on Transmission Error Compensation. Energies, 17(11), 2528. https://doi.org/10.3390/en17112528






