Nonlinear Impact of Topological Configuration of Coupled Inverter-Based Resources on Interaction Harmonics Levels of Power Flow
Abstract
1. Introduction
1.1. Current State-of-the-Art
1.2. Contribution of the Paper
1.3. Paper Organization
2. Analytical Explanation of the Relationship between Harmonics and Topological Configuration in Power Systems
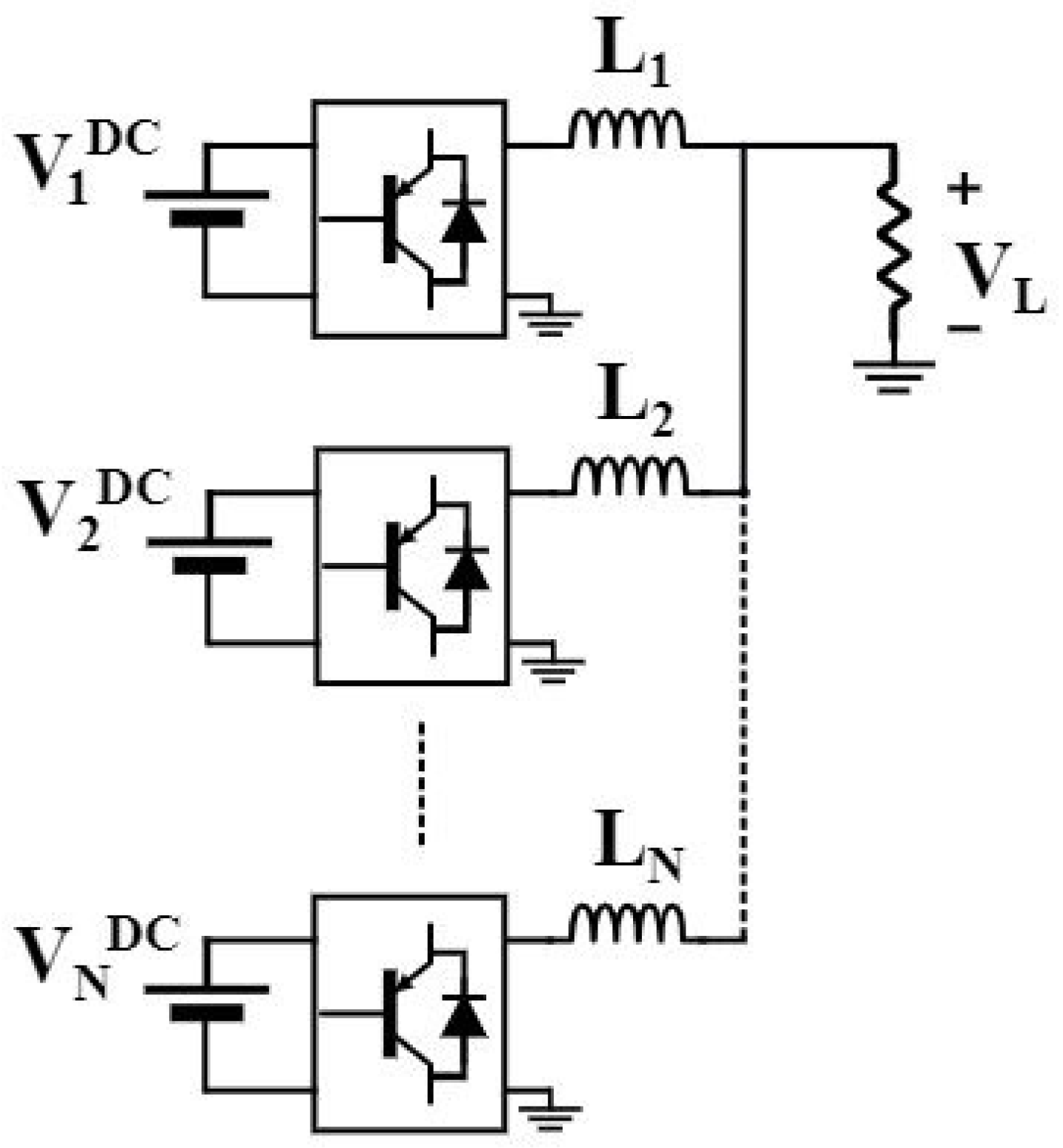
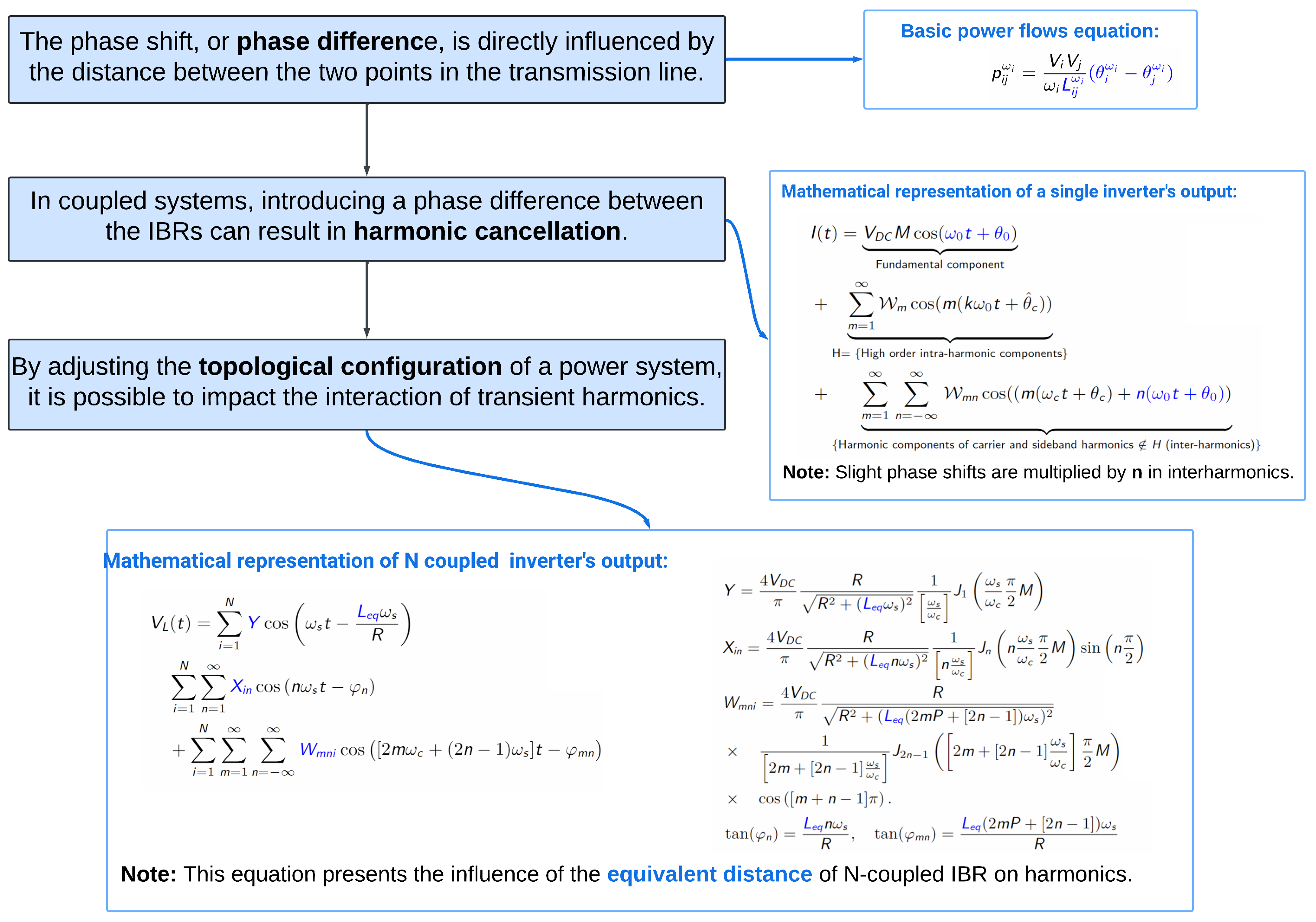
2.1. Explanation of the Relationship between Topological Configuration and Phase in Power Systems Using the Power Flow Equation
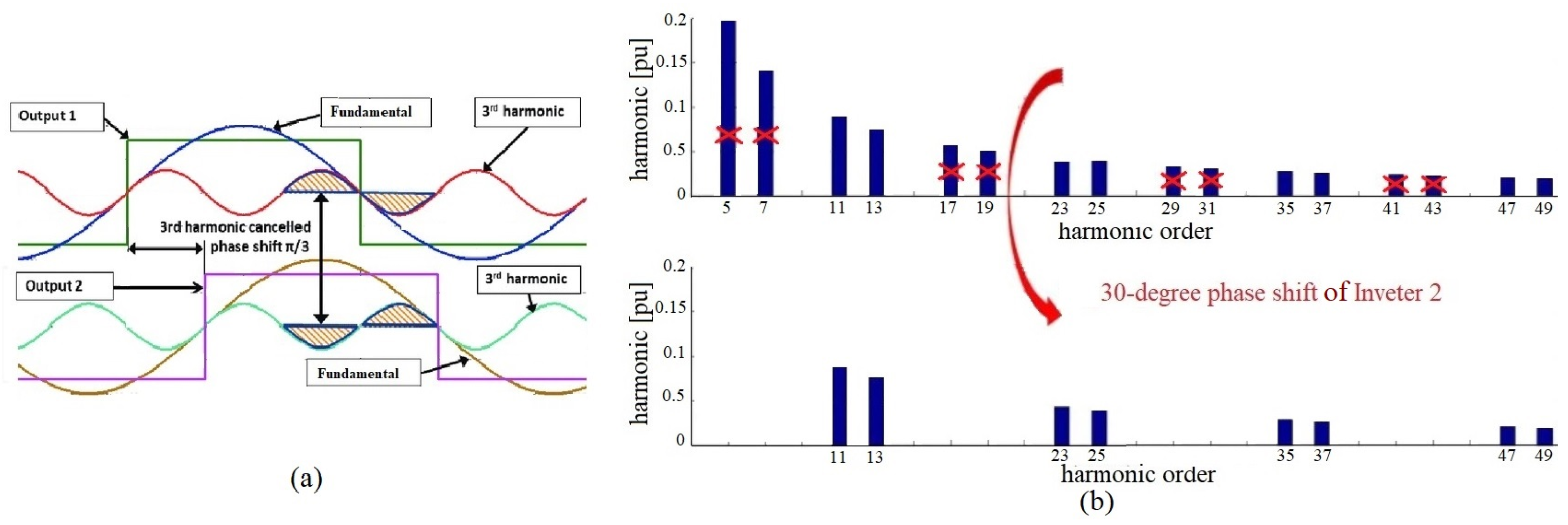
2.2. Exploring the Relationship between Harmonics and Phase
- It does not exert a substantial influence on the fundamental component; however, at higher frequencies, it notably affects the harmonic component.
- The process of harmonic alteration does not follow a linear relationship between harmonic levels and frequency because it may lead to a decrease or increase in harmonic level between two consecutive harmonics orders.
2.3. Terminology and Definitions Used in this Work
2.3.1. Definition of Electrical Distance
2.3.2. Relative Distance Ratio
2.3.3. Total Harmonic Distortion (THD)
3. Experiment Design and Primary Findings
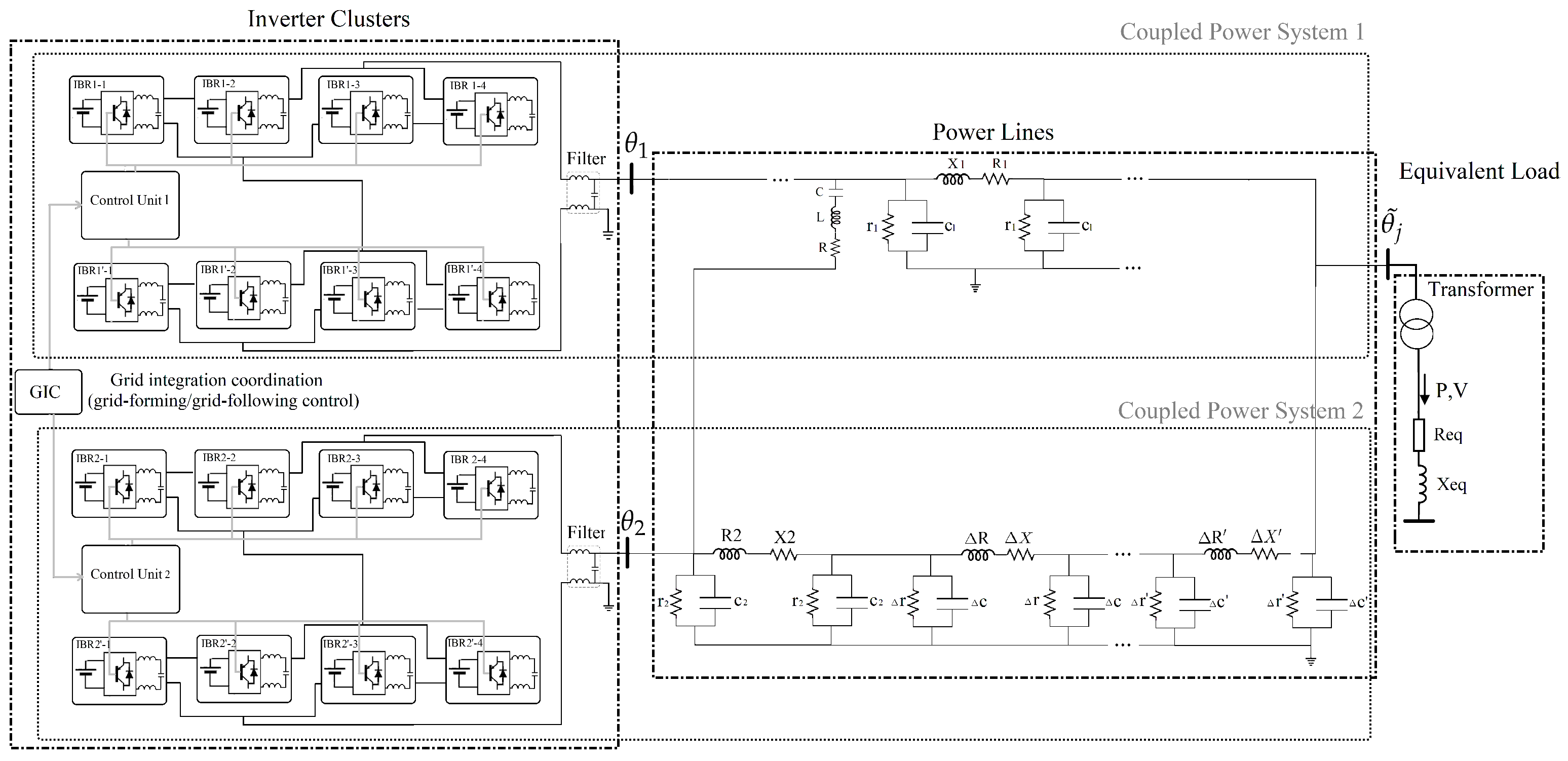
3.1. Test Scenarios and Experiment Setup
3.1.1. Design of Test Scenarios
3.1.2. Hardware Configuration of the Experimental Test Setup
- Using representative distribution line parameters and rodding geometries scaled down appropriately;
- Ensuring harmonic sources/loads had comparable behavior to full-scale inverter/rectifier harmonics operating at frequencies high enough that skin-effect scaling is maintained;
- Avoiding excessive thermal transients by using a short test duration.
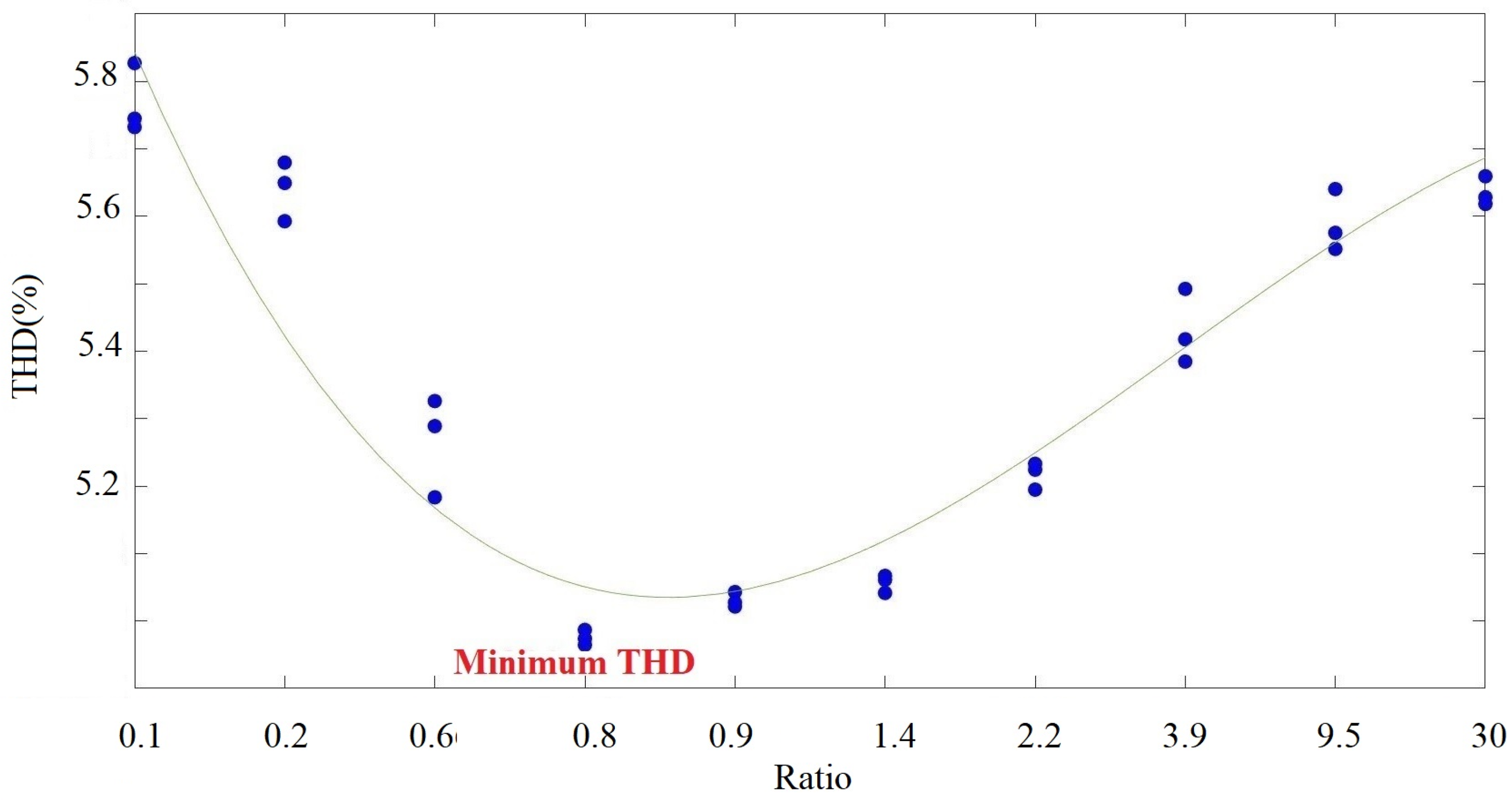
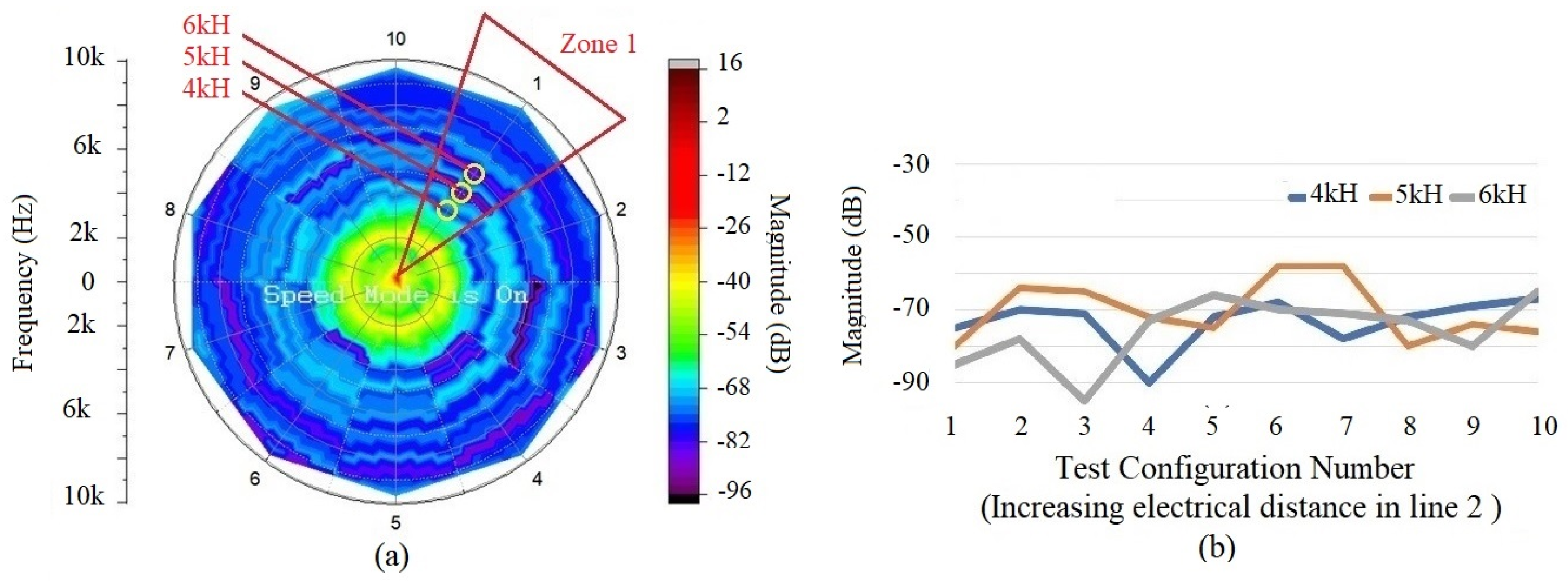
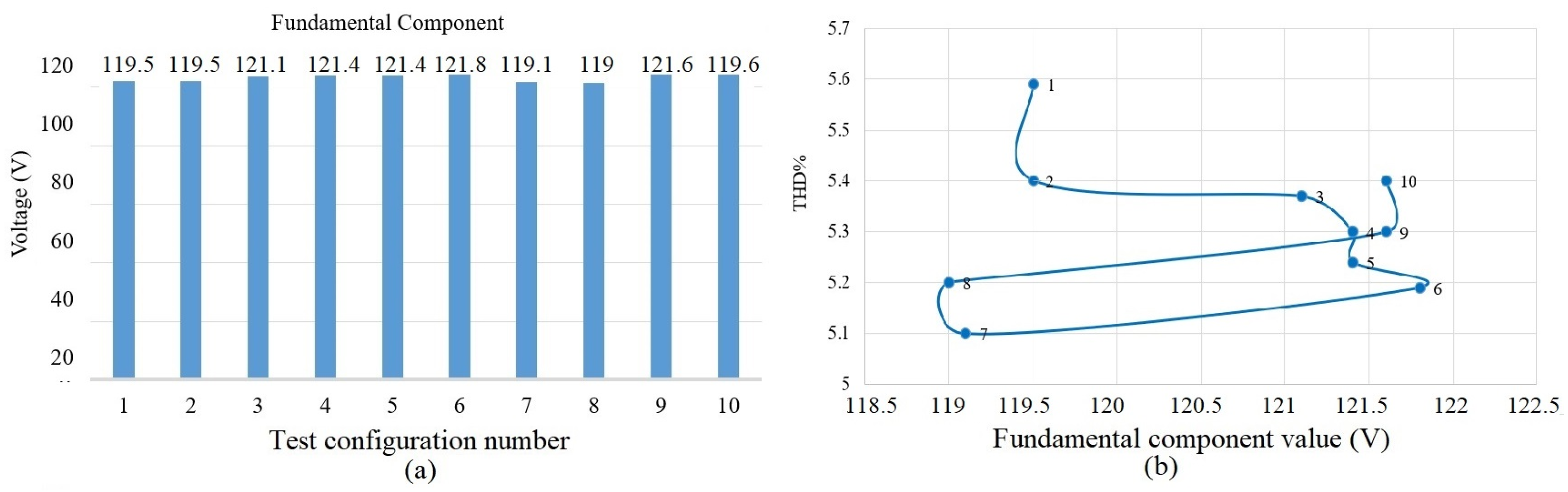
3.2. Demonstration of the Relationship between the Level of Total Harmonic Distortion and the Electrical Distance
4. Further Experimental Investigation Inspired by Analytical Studies
4.1. Design of Test Scenarios
4.2. Further Experimental Results and New Findings
4.2.1. Nonlinear Relationship between Topological Configuration and Harmonics
4.2.2. Harmonic Cancellation Effect through Self-Compensation
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, Y.; Green, T.C. Power System Stability with a High Penetration of Inverter-Based Resources. Proc. IEEE 2023, 111, 832–853. [Google Scholar] [CrossRef]
- Hoke, A.; Gevorgian, V.; Shah, S.; Koralewicz, P.; Kenyon, R.W.; Kroposki, B. Island power systems with high levels of inverter-based resources: Stability and reliability challenges. IEEE Electrific. Mag. 2021, 9, 74–91. [Google Scholar] [CrossRef]
- Matevosyan, J.; MacDowell, J.; Miller, N.; Badrzadeh, B.; Ramasubramanian, D.; Isaacs, A.; Quint, R.; Quitmann, E.; Pfeiffer, R.; Urdal, H.; et al. A future with inverter-based resources: Finding strength from traditional weakness. IEEE Power Energy Mag. 2021, 19, 18–28. [Google Scholar] [CrossRef]
- Leon, J.I.; Kouro, S.; Franquelo, L.G.; Rodriguez, J.; Wu, B. The essential role and the continuous evolution of modulation techniques for voltage-source inverters in the past, present, and future power electronics. IEEE Trans. Ind. Electron. 2016, 63, 2688–2701. [Google Scholar] [CrossRef]
- Impram, S.; Nese, S.V.; Oral, B. Challenges of Renewable Energy Penetration on Power System Flexibility: A Survey. Energy Strategy Rev. 2020, 31, 100539. [Google Scholar] [CrossRef]
- Zhang, Y.; Roes, M.; Hendrix, M.; Duarte, J. Symmetric-component decoupled control of grid-connected inverters for voltage unbalance correction and harmonic compensation. Int. J. Elect. Power Energy Syst. 2020, 115, 105490. [Google Scholar] [CrossRef]
- Tariq, M.; Upadhyay, D.; Khan, S.A.; Alhosaini, W.; Peltoniemi, P.; Sarwar, A. Novel Integrated NLC-SHE Control Applied in Cascaded Nine-Level H-Bridge Multilevel Inverter and Its Experimental Validation. IEEE Access 2023, 11, 22209–22220. [Google Scholar] [CrossRef]
- Muhammad, T.; Khan, A.U.; Abid, Y.; Khan, M.H.; Ullah, N.; Blazek, V.; Prokop, L.; Misák, S. An Adaptive Hybrid Control of Reduced Switch Multilevel Grid Connected Inverter for Weak Grid Applications. IEEE Access 2023, 11, 28103–28118. [Google Scholar] [CrossRef]
- Koiwa, K.; Takahashi, H.; Zanma, T.; Liu, K.-Z.; Natori, K.; Sato, Y. A Novel Filter With High Harmonics Attenuation and Small Dimension for Grid-Connected Inverter. IEEE Trans. Power Electron. 2023, 38, 2202–2214. [Google Scholar] [CrossRef]
- Hu, H.; Shi, Q.; He, Z.; He, J.; Gao, S. Potential harmonic resonance impacts of PV inverter filters on distribution systems. IEEE Trans. Sustain. Energy 2015, 6, 151–161. [Google Scholar] [CrossRef]
- Nduka, O.S.; Pal, B.C. Harmonic domain modeling of PV system for the assessment of grid integration impact. IEEE Trans. Sustain. Energy 2017, 8, 1154–1165. [Google Scholar] [CrossRef]
- Baburajan, S.; Wang, H.; Kumar, D.; Wang, Q.; Blaabjerg, F. DClink current harmonic mitigation via phase-shifting of carrier waves in paralleled inverter systems. Energies 2021, 14, 4229. [Google Scholar] [CrossRef]
- Moeini, A.; Wang, S.; Zhang, B.; Yang, L. A Hybrid Phase Shift-Pulsewidth Modulation and Asymmetric Selective Harmonic Current Mitigation-Pulsewidth Modulation Technique to Reduce Harmonics and Inductance of Single-Phase Grid-Tied Cascaded Multilevel Converters. IEEE Trans. Ind. Electron. 2020, 67, 10388–10398. [Google Scholar] [CrossRef]
- Du, L.; He, J. A Simple Autonomous Phase-Shifting PWM Approach for Series-Connected Multi-Converter Harmonic Mitigation. IEEE Trans. Power Electron. 2019, 34, 11516–11520. [Google Scholar] [CrossRef]
- Hemmati, R.; Kandezy, R.S.; Safarishaal, M.; Zoghi, M.; Jiang, J.N.; Wu, D. Impact of Phase Displacement among Coupled Inverters on Harmonic Distortion in MicroGrids. In Proceedings of the 2023 IEEE Transportation Electrification Conference Expo (ITEC), Detroit, MI, USA, 21 June 2023; pp. 1–6. [Google Scholar]
- Albadi, M. Power Flow Analysis. In Computational Models in Engineering; Intechopen: London, UK, 2020; pp. 11–13. [Google Scholar]
- Tyshko, A. Sequential Selective Harmonic Elimination and Outphasing Amplitude Control for the Modular Multilevel Converters Operating with the Fundamental Frequency. In Power System Harmonics—Analysis, Effects and Mitigation Solutions for Power Quality Improvement; Intechopen: London, UK, 2018; pp. 14–30. [Google Scholar]
- Mao, X.; Zhu, W.; Wu, L.; Zhou, B. Comparative study on methods for computing electrical distance. Int. J. Electr. Power Energy Syst. 2021, 130, 106923. [Google Scholar] [CrossRef]
- Poudel, S.; Ni, Z.; Sun, W. Electrical distance approach for searching vulnerable branches during contingencies. IEEE Trans Smart Grid. 2018, 9, 3373–3382. [Google Scholar] [CrossRef]
- Aghamohammadi, M.R.; Mahdavizadeh, S.F.; Rafiee, Z. Controlled Islanding Based on the Coherency of Generators and Minimum Electrical Distance. IEEE Access 2021, 9, 146830–146840. [Google Scholar] [CrossRef]
- Peng, P.; Chen, K.; Xu, T.; Li, C. A calculation method of electrical distance considering operation mode. J. Phys. Conf. Ser. 2019, 1176, 062018. [Google Scholar] [CrossRef]
- Fang, G.J.; Bao, H. A Calculation Method of Electric Distance and Subarea Division Application Based on Transmission Impedance. IOP Conf. Ser. Earth Environ. Sci. 2017, 104, 012006. [Google Scholar] [CrossRef]
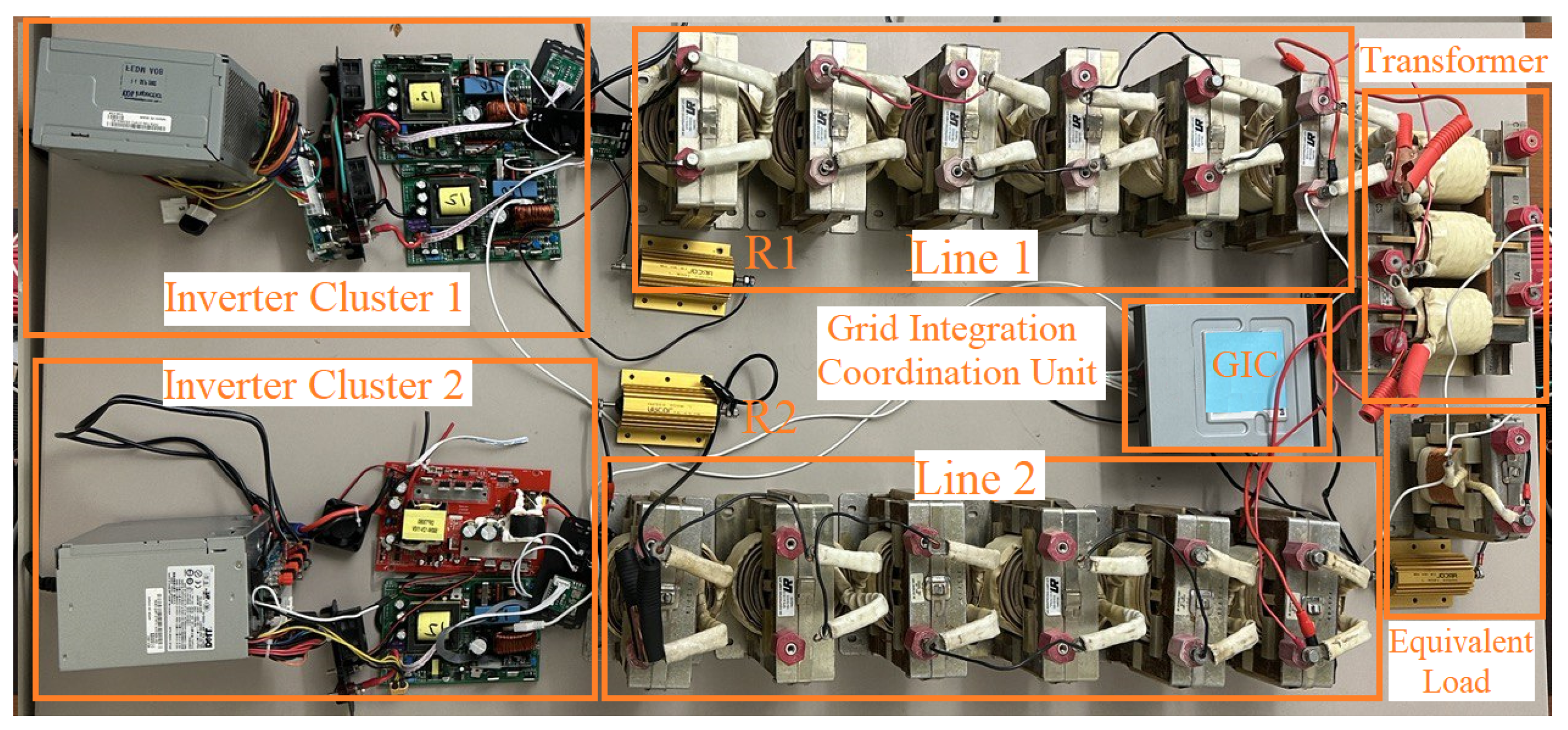
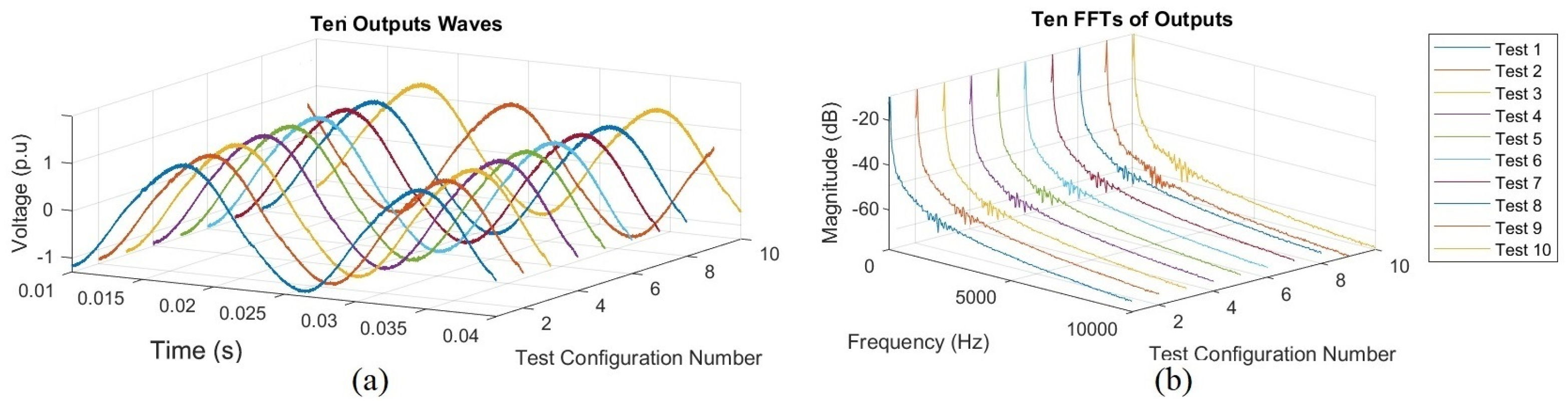
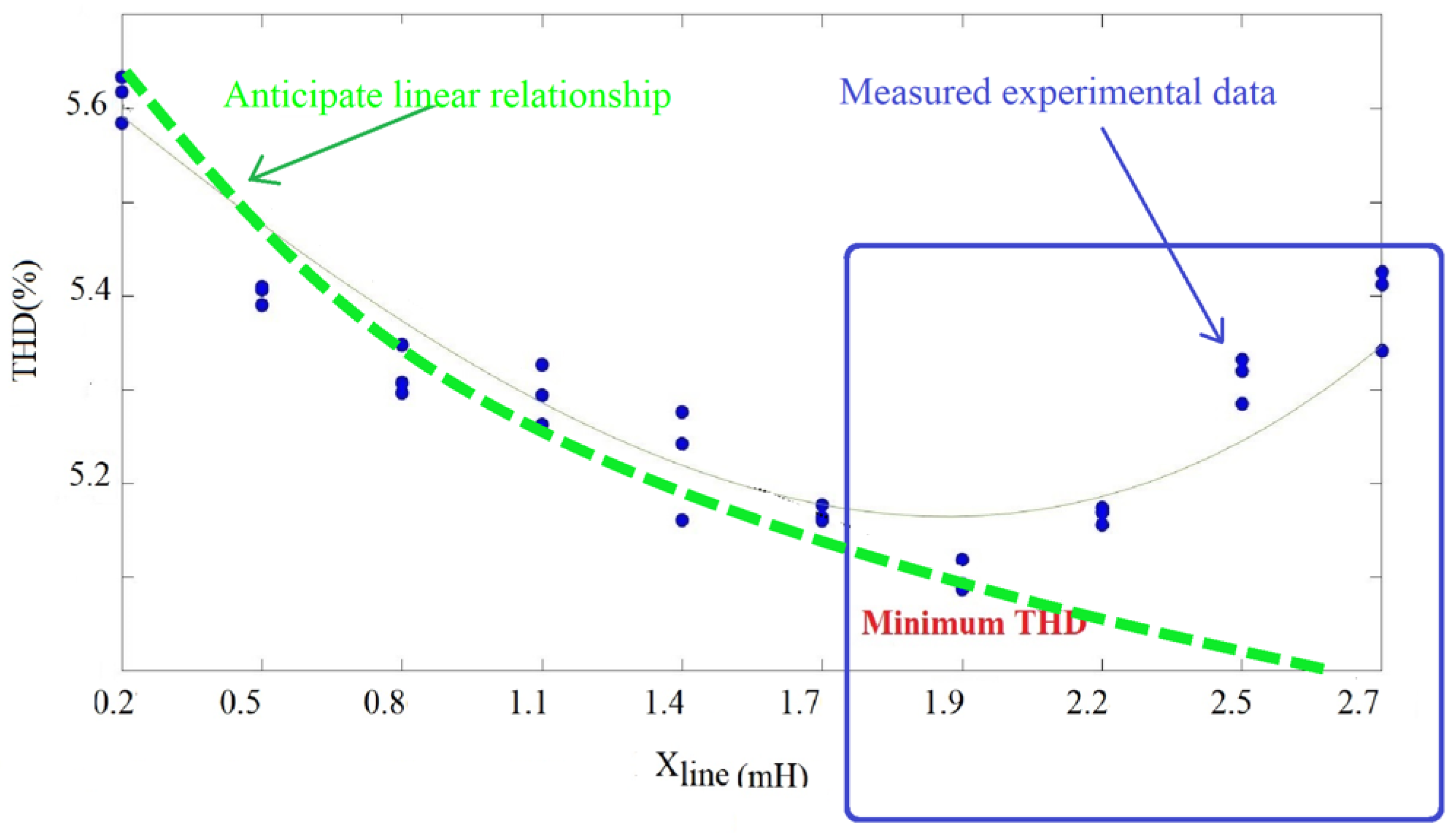
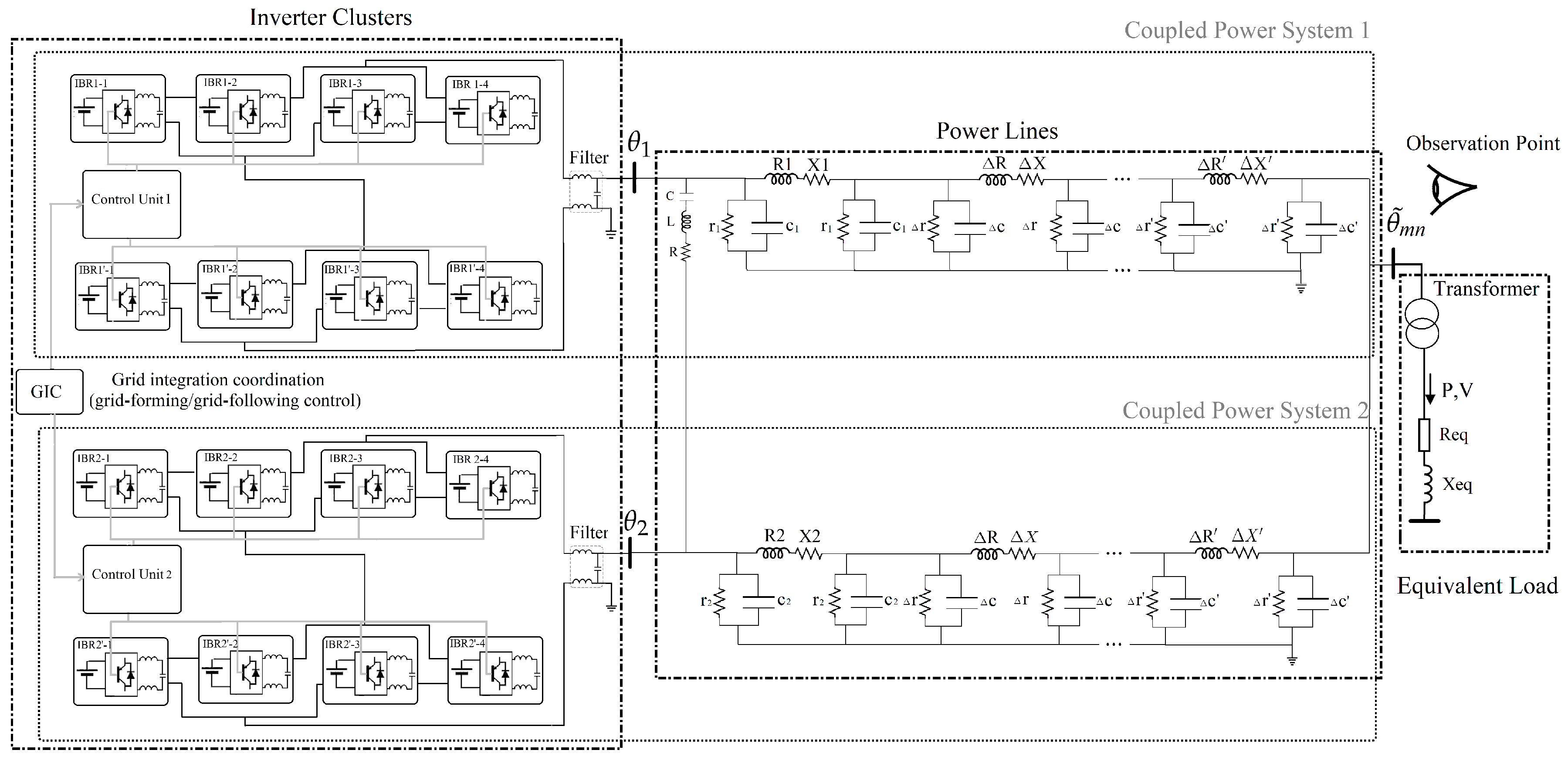
| Test Number | (mH) | (mH) | Ratio () |
|---|---|---|---|
| 1 | 0.280 | 0.279 | 0.99 |
| 2 | 0.280 | 0.570 | 2.03 |
| 3 | 0.280 | 0.864 | 3.08 |
| 4 | 0.280 | 1.136 | 4.05 |
| 5 | 0.280 | 1.429 | 5.10 |
| 6 | 0.280 | 1.708 | 6.10 |
| 7 | 0.280 | 1.989 | 7.10 |
| 8 | 0.280 | 2.245 | 8.01 |
| 9 | 0.280 | 2.528 | 9.02 |
| 10 | 0.280 | 2.797 | 9.98 |
| Parameter | Value | Explanation |
|---|---|---|
| DC source | 12 V | Dc voltage resource |
| IBR clusters | 120 V, 60 Hz, 0.5 kW | Pure sine wave inverters |
| R1 = R2 = R3 | 100 | Lines resistance |
| 100 | Equivalent load resistance | |
| 0.540 Hz | Equivalent load inductance | |
| Transformer | 120 V, 60 Hz | 1:1 |
| Test Number | (mH) | (mH) | Ratio () |
|---|---|---|---|
| 1 | 2.61 | 0.279 | 0.10 |
| 2 | 2.253 | 0.570 | 0.25 |
| 3 | 1.997 | 0.864 | 0.43 |
| 4 | 1.717 | 1.136 | 0.66 |
| 5 | 1.436 | 1.429 | 0.99 |
| 6 | 1.142 | 1.708 | 1.49 |
| 7 | 0.878 | 1.989 | 2.26 |
| 8 | 0.574 | 2.245 | 3.91 |
| 9 | 0.270 | 2.580 | 9.55 |
| 10 | 0.091 | 2.797 | 30 |
| Sc. No. | Definition of Scenarios | State of Change | Result |
|---|---|---|---|
| 1 | Increasing the reactance of line 1 while keeping line 2 fixed. | : Fix, : Increase | The nonlinear relationship between output THD and topological configuration changes. |
| 2 | Increasing the reactance of line 2 while keeping line 1 fixed. | : Increase, : Fix | Same as in scenario 1: The nonlinear relationship between output THD and topological configuration changes. |
| 3 | Simultaneous increase of the reactances of both lines with a constant rate. | : Increase, : Increase | The THD vs. distance curve varies more smoothly with electrical distance compared to the previous two scenarios. |
| 4 | Increase in the reactance of line 2, decrease in the reactance of line 1, and a sharp increase in the ratio. | : Increase, : Decrease | The THD vs. distance curve varies more sharply with electrical distance compared to the previous scenarios. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safarishaal, M.; Hemmati, R.; Saeed Kandezy, R.; Jiang, J.N.; Lin, C.; Wu, D. Nonlinear Impact of Topological Configuration of Coupled Inverter-Based Resources on Interaction Harmonics Levels of Power Flow. Energies 2024, 17, 2512. https://doi.org/10.3390/en17112512
Safarishaal M, Hemmati R, Saeed Kandezy R, Jiang JN, Lin C, Wu D. Nonlinear Impact of Topological Configuration of Coupled Inverter-Based Resources on Interaction Harmonics Levels of Power Flow. Energies. 2024; 17(11):2512. https://doi.org/10.3390/en17112512
Chicago/Turabian StyleSafarishaal, Masoud, Rasul Hemmati, Reza Saeed Kandezy, John N. Jiang, Chenxi Lin, and Di Wu. 2024. "Nonlinear Impact of Topological Configuration of Coupled Inverter-Based Resources on Interaction Harmonics Levels of Power Flow" Energies 17, no. 11: 2512. https://doi.org/10.3390/en17112512
APA StyleSafarishaal, M., Hemmati, R., Saeed Kandezy, R., Jiang, J. N., Lin, C., & Wu, D. (2024). Nonlinear Impact of Topological Configuration of Coupled Inverter-Based Resources on Interaction Harmonics Levels of Power Flow. Energies, 17(11), 2512. https://doi.org/10.3390/en17112512







