Enabling Passive Load-Holding Function and System Pressures Control in a One-Motor-One-Pump Motor-Controlled Hydraulic Cylinder: Simulation Study

Abstract

This paper is concerned with a hydraulic cylinder directly controlled by a variable speed motor-driven fixed-displacement pump. The considered configuration is referred to as a one-motor-one-pump (1M1P) motor-controlled hydraulic cylinder (MCC). A 1M1P MCC with a hydraulically driven passive load-holding function enabled by controlled system pressures is proposed. The proposed load-holding functionality works if there is a standstill command, a loss of power supply, or a hose rupture. Additionally, this paper conducts a comprehensive analysis of the proposed system’s operation and load-holding function across four quadrants. The simulation results demonstrate four-quadrant operation and good load-holding performance under the aforementioned scenarios. In conclusion, the proposed 1M1P MCC can be successfully used on practical applications characterized by overrunning loads and four quadrant operation.

1. Introduction

Valve-controlled hydraulic cylinders (VCCs) are used extensively in various industries, particularly in heavy load-carrying scenarios. VCCs offer numerous advantages, including a high power-to-weight ratio, flexible power transmission, inherent damping qualities, and a good liability. Despite decades of development, VCCs still face a major challenge: valve throttling losses. These losses are mainly from the system’s control and over-center valves [1]. For instance, control valves account for approximately 29% to 35% of the total energy losses in an excavator equipped with load-sensing functionality [2,3]. VCCs require brake throttling valves to operate in more than two quadrants and lack energy recuperation capability under overrunning loads, indirectly amplifying energy losses. The demand for efficient hydraulic systems has become increasingly critical with the growing global energy demand, environmental considerations, and sustainable industrial practices. Therefore, designing hydraulic cylinder systems that deliver comparable performance as VCCs while removing the throttling losses is important. In response to this trend, motor-controlled hydraulic cylinders (MCCs) have emerged as a promising technology, offering a more efficient alternative to VCCs.

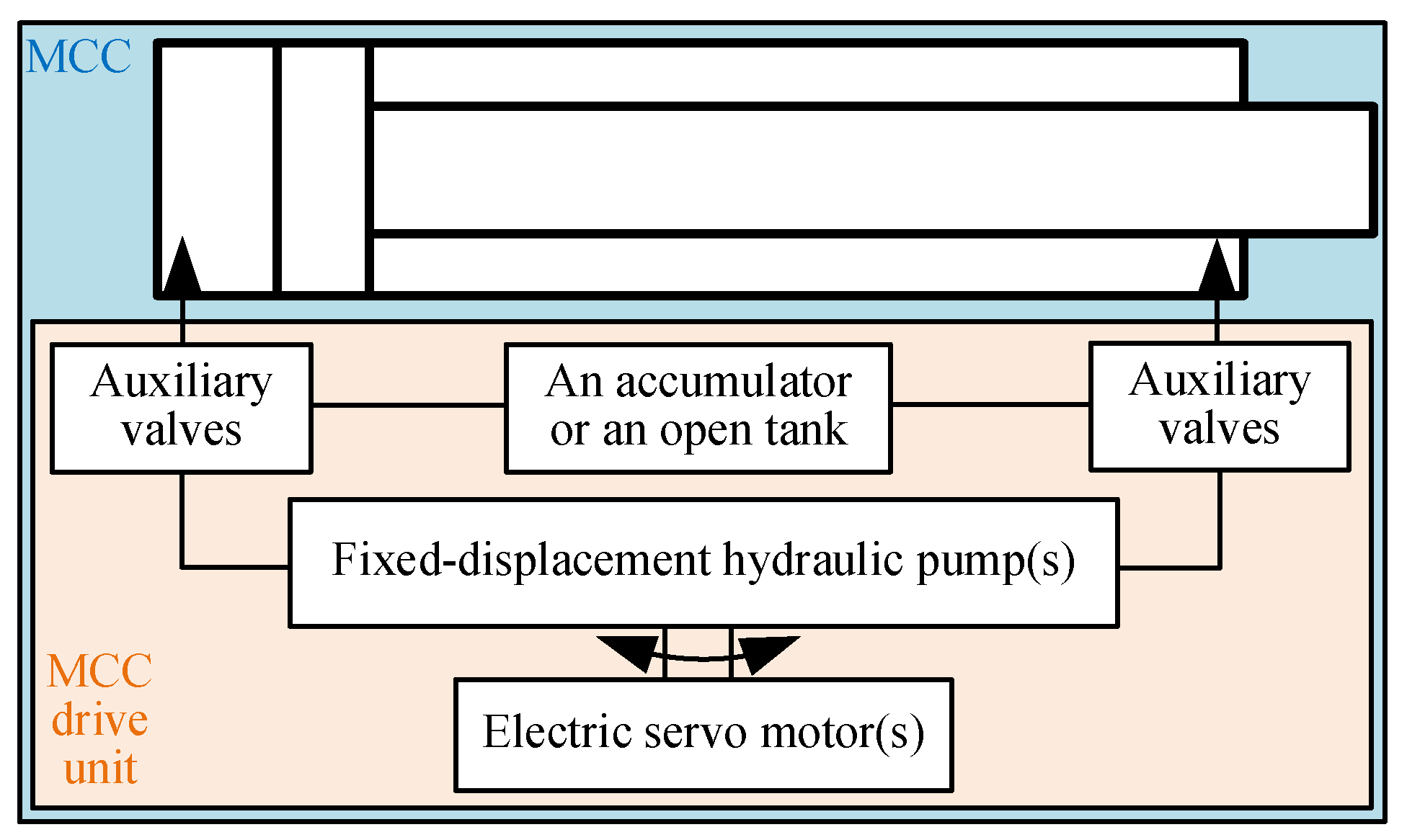
Figure 1 provides the general structure of an MCC. An MCC incorporates an electric motor(s) and hydraulic pump(s), an accumulator or an open tank, several auxiliary valves, and a differential hydraulic cylinder. The hydraulic cylinder is directly connected to one or two fixed-displacement hydraulic pumps driven by electric servo motors. Therefore, the cylinder motion is controlled by the electric servo motor’s angular velocity. The auxiliary valves compensate for the differential flow rate, enable load-holding functionality according to different MCC architectures, or avoid cavitation. MCCs can be classified into four groups based on the number of electric servo motors and fixed-displacement hydraulic pumps utilized: one-motor-one-pump (1M1P), one-motor-two-pumps (1M2P), one-motor-three-pumps (1M3P), and two-motors-two-pumps (2M2P) MCCs [4]. In contrast to VCCs, the absence of valve throttling in an MCC greatly improves the system’s energy efficiency. For example, a single-boom crane driven by a 1M1P MCC has been shown to consume 62% less energy than one driven by a VCC [5]. A study of implementing six 1M1P MCCs on an excavator was conducted, as described in [6]. Experimental results demonstrated that the MCCs consumed 47.8% less energy than the valve-controlled counterparts in a given working cycle. Furthermore, an excavator powered by three 1M2P MCCs was shown to achieve a system efficiency of 73.3% in a given working cycle in simulations [7]. This efficiency is significantly higher than that of the same excavator driven by three VCCs.

It was found that a single-boom crane driven by a 1M1P MCC achieved a 75% shorter settling time, 61% less overshoot, and 66% lower position tracking error compared to a single-boom crane driven by a VCC in a given working cycle [8]. The MCC’s advantages have led to increased interest in MCCs from the industry. Several commercial MCC products have become available in recent years, for example, from Parker Hannifin [9], Bosch Rexroth [10], and Thomson [11].

It is worth noting that most research and commercial products related to MCCs primarily focus on the compact installation approach [12]. In this approach, all components are mounted as an integrated unit, as depicted in Figure 2. This integrated design offers advantages in terms of saving total occupied space and simplified installation. However, it has been identified that MCCs in the compact installation approach may not be suitable for large-scale knuckle boom cranes for various reasons [12]. In such cases, MCCs utilizing a remote installation approach become necessary, such as the MCC drive unit shown in Figure 1 remotely installed in the crane hydraulic machine room and connected to the cylinder with pipelines [12].

Nevertheless, achieving a passive load-holding function in MCCs with the remote installation approach is challenging. The load-holding function in four-quadrant operation is enforced by legislation when a cylinder is used in lifting applications characterized by overrunning external loads, such as cranes, trailer lifts, and scissors tables. Additionally, activating the load-holding function during a standstill command is essential for energy savings and precise position control. Counterbalance valves, a well-established and proven technology commonly employed in VCCs, can provide load-holding functions in MCCs in general and, in particular, during a loss of power supply or hose rupture [13,14]. However, including counterbalance valves in an MCC can decrease the system’s efficiency because of the throttling losses of counterbalance valves, particularly when the load is very low. Moreover, an MCC incorporating counterbalance valves cannot realize four-quadrant operation and energy regeneration because the pilot pressures are too low to open the counterbalance valves in the second and fourth quadrants.

Besides counterbalance valves, two on/off electric valves can be used in MCCs for an active load-holding function without introducing any throttling losses [7,15]. While the normally closed on/off electric valves can offer a load-holding function during loss of power supply, implementing load-holding functions during hose ruptures can pose challenges in a remotely installed MCC. A novel load-holding strategy for a 1M1P MCC was presented in [16]. It incorporates two pilot-operated check valves (POCVs) as load-holding valves. An electric valve connects the pilot line to the cylinder load pressures. This configuration enables the load-holding valves to be opened by hydraulic pressures instead of electric signals. Nevertheless, similar to the concept of using two on/off electric valves, this strategy lacks the capability to provide load-holding functionality in the event of hose ruptures or sudden drops in line pressure.

A 2M2P MCC with a fully passive hydraulically driven load-holding device was introduced in [17]. In that study, a secondary electric servo motor and a secondary hydraulic pump were incorporated into a 1M1P MCC to manage the differential flow rate and control the minimum cylinder pressure. The load-holding valves were opened by controlling the minimum cylinder pressure over a certain level. This setup provided the desired fully hydraulically driven load-holding function, handling hose ruptures or sudden line pressure drops. However, it is important to note that the 2M2P MCC is less suitable for four-quadrant operation because the secondary servo motor and hydraulic pump cannot contribute to the cylinder’s output power in quadrants II and III [18]. Therefore, a 1M1P MCC with a fully hydraulically driven passive load-holding function best fits the four-quadrant operation. Nevertheless, further research in this area is currently lacking.

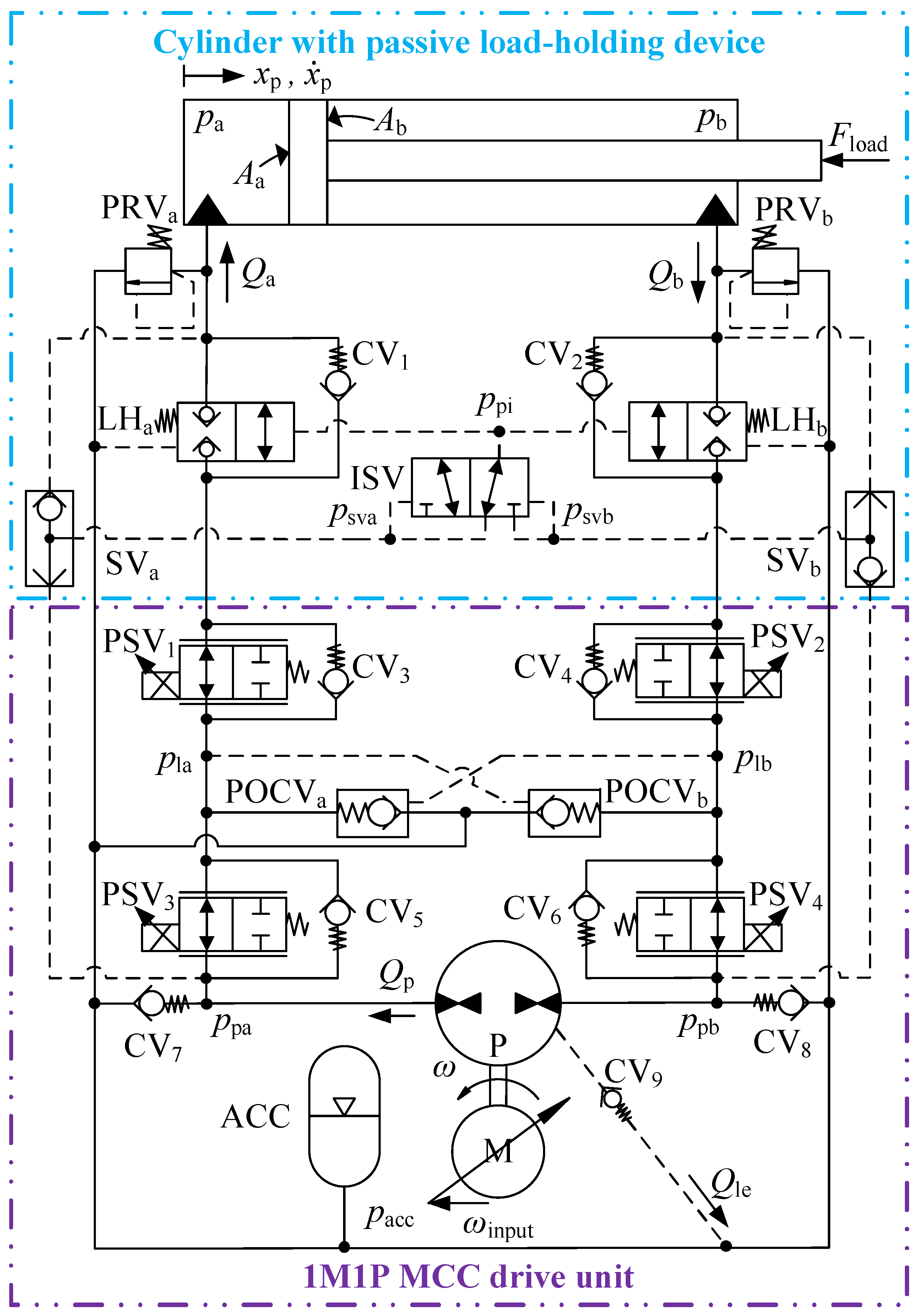
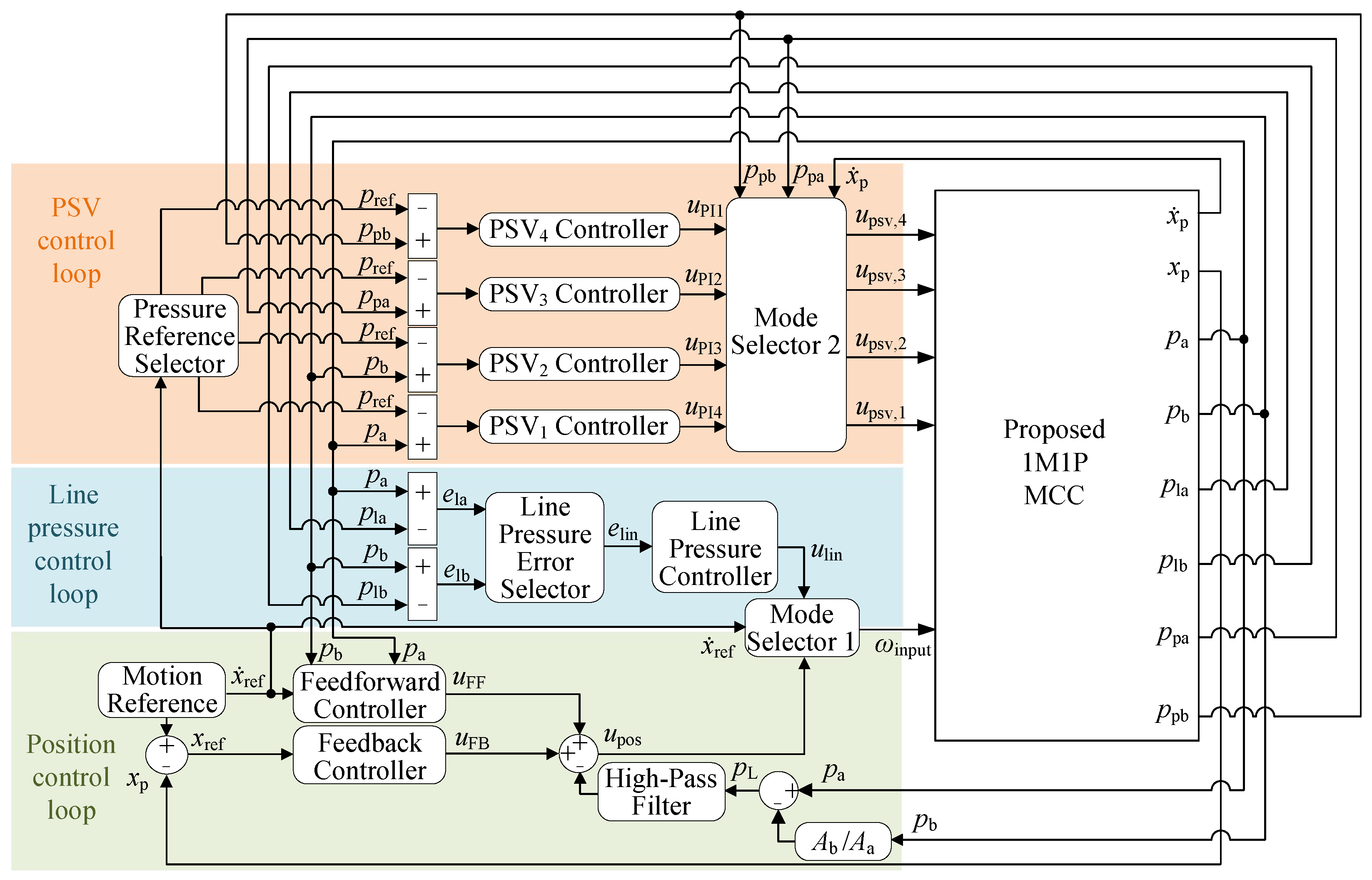
This paper proposes a new 1M1P MCC design that offers a hydraulically driven passive load-holding function to address the gap mentioned above. The proposed design’s functionalities are comprehensively analyzed and validated through simulations.

2. Proposed System

2.1. System Architecture

The proposed 1M1P MCC is shown in Figure 3. The system consists of two primary parts: the 1M1P MCC drive unit and the cylinder with passive load-holding devices. These two parts can be either physically integrated or positioned in separate locations connected by pipelines.

The 1M1P MCC drive unit, framed by purple dashed lines, comprises a fixed-displacement pump/motor unit (P) connected to an electric servo motor/generator unit (M). A low-pressure accumulator (ACC) is used as the pressurized reservoir to supply or store the differential volume between the cylinder rod and bore sides through two pilot-operated check valves ${\mathrm{POCV}}_{\mathrm{a}}$ and ${\mathrm{POCV}}_{\mathrm{b}}$. The pilot pressures for ${\mathrm{POCV}}_{\mathrm{a}}$ and ${\mathrm{POCV}}_{\mathrm{b}}$ are line pressures $p_{\mathrm{la}}$ and $p_{\mathrm{lb}}$, respectively. ACC maintains the minimum pump/motor unit pressure through check valves ${\mathrm{CV}}_7$ and ${\mathrm{CV}}_8$ to prevent cavitation. The leakage line of P is also connected to ACC via check valve ${\mathrm{CV}}_9$. The ACC pressure $p_{\mathrm{acc}}$ is less than 3 bar during operations. Four 2/2 proportional solenoid valves, ${\mathrm{PSV}}_1$ to ${\mathrm{PSV}}_4$, are installed symmetrically around ${\mathrm{POCV}}_{\mathrm{a}}$ and ${\mathrm{POCV}}_{\mathrm{b}}$ to control the cylinder bore-side pressure $p_{\mathrm{a}}$, cylinder rod-side pressure $p_{\mathrm{b}}$, pump/motor unit pressure on the cylinder bore side $p_{\mathrm{pa}}$, and pump/motor unit pressure on the cylinder rod side $p_{\mathrm{pb}}$ by throttling flows in one specific direction. Four check valves, ${\mathrm{CV}}_3$ to ${\mathrm{CV}}_6$, are installed in parallel to the PSVs to ensure free flow in the other direction. The pressure control principle is explained in detail in Section 2.2.

The cylinder with passive load-holding devices is framed by light blue dashed lines. Two pressure relief valves, ${\mathrm{PRV}}_{\mathrm{a}}$ and ${\mathrm{PRV}}_{\mathrm{b}}$, are installed to limit the maximum cylinder pressures. Two 2/2 normally closed load-holding valves, ${\mathrm{LH}}_{\mathrm{a}}$ and ${\mathrm{LH}}_{\mathrm{b}}$, are opened by the pilot pressure $p_{\mathrm{pi}}$ when it is higher than the cracking pressure $p_{\mathrm{lh}}=$ 10 bar. Two check valves, ${\mathrm{CV}}_1$ and ${\mathrm{CV}}_2$, are installed in parallel to ${\mathrm{LH}}_{\mathrm{a}}$ and ${\mathrm{LH}}_{\mathrm{b}}$ to ensure free flow to the cylinder. $p_{\mathrm{pi}}$ is chosen as the minimum pressure between $p_{\mathrm{sva}}$ and $p_{\mathrm{svb}}$ by the inverse shuttle valve (ISV). $p_{\mathrm{sva}}$ and $p_{\mathrm{svb}}$ are the output pressures of two shuttle valves ${\mathrm{SV}}_{\mathrm{a}}$ and ${\mathrm{SV}}_{\mathrm{b}}$, respectively. $p_{\mathrm{sva}}$ equals the maximum pressure between $p_{\mathrm{a}}$ and $p_{\mathrm{pa}}$. $p_{\mathrm{svb}}$ equals the maximum pressure between $p_{\mathrm{b}}$ and $p_{\mathrm{pb}}$.

2.2. System Analysis in Operation Mode

In operation mode, the system can be operated in four quadrants, ${\mathrm{Q}}_{\mathrm{I}}$ to ${\mathrm{Q}}_{\mathrm{IV}}$; see Figure 4. In ${\mathrm{Q}}_{\mathrm{I}}$, the bore side pressure $p_{\mathrm{a}}$ is the highest pressure (represented in red) in the system. M works as an electric servo motor. P works as a hydraulic pump, pumping the oil from the cylinder rod side and ACC to the cylinder bore side. ${\mathrm{LH}}_{\mathrm{a}}$, ${\mathrm{LH}}_{\mathrm{b}}$, ${\mathrm{PSV}}_1$, ${\mathrm{PSV}}_3$, and ${\mathrm{PSV}}_4$ are fully opened. Therefore, $p_{\mathrm{a}}$, $p_{\mathrm{la}}$, $p_{\mathrm{pa}}$, and $p_{\mathrm{sva}}$ are equal. $p_{\mathrm{la}}$ is higher than $p_{\mathrm{lb}}$, causing the opening of ${\mathrm{POCV}}_{\mathrm{b}}$. The accumulator flow rate $Q_{\mathrm{acc}}$ joins the flow from the cylinder rod side and, thereby, goes to the P inlet port to compensate for the differential flow rate, resulting in $p_{\mathrm{pb}}=p_{\mathrm{lb}}=p_{\mathrm{acc}}=$ 3 bar (represented in green). ${\mathrm{PSV}}_2$ is used as an active control element throttling the flow so that $p_{\mathrm{b}}$ remains above the load-holding valve crack pressure $p_{\mathrm{lh}}=10$ bar. Because of the selective functions of ISV and ${\mathrm{SV}}_{\mathrm{b}}$, $p_{\mathrm{pi}}$ is equal to $p_{\mathrm{b}}$. Thus, ${\mathrm{LH}}_{\mathrm{a}}$ and ${\mathrm{LH}}_{\mathrm{b}}$ are open. In ${\mathrm{Q}}_{\mathrm{II}}$, the external load is assistive and, potentially, overrunning. The rod side pressure $p_{\mathrm{b}}$ is the highest pressure (represented in red) in the system. M works as an electric generator. P works as a hydraulic motor, motoring the oil from the rod side to the bore side. ${\mathrm{LH}}_{\mathrm{a}}$, ${\mathrm{LH}}_{\mathrm{b}}$, ${\mathrm{PSV}}_1$, ${\mathrm{PSV}}_2$, and ${\mathrm{PSV}}_4$ are fully opened. Therefore, $p_{\mathrm{b}}$, $p_{\mathrm{lb}}$, $p_{\mathrm{pb}}$, and $p_{\mathrm{svb}}$ are equal. $p_{\mathrm{lb}}$ is higher than $p_{\mathrm{la}}$, causing the opening of ${\mathrm{POCV}}_{\mathrm{a}}$. The accumulator flow rate $Q_{\mathrm{acc}}$ joins the return flow from P and is, thereby, directed toward the piston side of the cylinder to compensate for the differential volume, resulting in $p_{\mathrm{a}}=p_{\mathrm{la}}=p_{\mathrm{acc}}$ (represented in green). ${\mathrm{PSV}}_3$ is used as an active control element, throttling the flow so that $p_{\mathrm{pa}}$ remains above the load-holding valve crack pressure $p_{\mathrm{lh}}$. Because of the selective functions of ISV and ${\mathrm{SV}}_{\mathrm{a}}$, $p_{\mathrm{pi}}$ is equal to $p_{\mathrm{pa}}$. Thus, ${\mathrm{LH}}_{\mathrm{a}}$ and ${\mathrm{LH}}_{\mathrm{b}}$ are open.

In ${\mathrm{Q}}_{\mathrm{III}}$, $p_{\mathrm{b}}$ is the highest pressure (represented in red) in the system. M works as an electric servo motor. P works as a hydraulic pump, pumping oil from the bore side to the rod side. ${\mathrm{LH}}_{\mathrm{a}}$, ${\mathrm{LH}}_{\mathrm{b}}$, ${\mathrm{PSV}}_2$, ${\mathrm{PSV}}_3$, and ${\mathrm{PSV}}_4$ are fully opened. Therefore, $p_{\mathrm{b}}$, $p_{\mathrm{lb}}$, $p_{\mathrm{pb}}$, and $p_{\mathrm{svb}}$ are equal. $p_{\mathrm{lb}}$ is higher than $p_{\mathrm{la}}$, causing the opening of ${\mathrm{POCV}}_{\mathrm{a}}$. The flow rate from the bore side is too high to be the P inlet flow rate. The differential flow goes back to the accumulator ($Q_{\mathrm{acc}}$), resulting in $p_{\mathrm{la}}=p_{\mathrm{pa}}=p_{\mathrm{acc}}$ (represented in green). ${\mathrm{PSV}}_1$ is used as an active control element, throttling the flow so that $p_{\mathrm{a}}$ remains above the load-holding valve crack pressure $p_{\mathrm{lh}}$. Because of the selective functions of ISV and ${\mathrm{SV}}_{\mathrm{a}}$, $p_{\mathrm{pi}}$ is equal to $p_{\mathrm{a}}$. Thus, ${\mathrm{LH}}_{\mathrm{a}}$ and ${\mathrm{LH}}_{\mathrm{b}}$ are open.

In ${\mathrm{Q}}_{\mathrm{IV}}$, the external load is assistive and, potentially, overrunning. The bore side pressure $p_{\mathrm{a}}$ is the highest pressure (represented in red) in the system. M works as an electric generator. P works as a hydraulic motor, motoring oil from the bore side to the rod side. ${\mathrm{LH}}_{\mathrm{a}}$, ${\mathrm{LH}}_{\mathrm{b}}$, ${\mathrm{PSV}}_1$, ${\mathrm{PSV}}_2$, and ${\mathrm{PSV}}_3$ are fully opened. Therefore, $p_{\mathrm{a}}$, $p_{\mathrm{la}}$, $p_{\mathrm{pa}}$, and $p_{\mathrm{sva}}$ are equal. $p_{\mathrm{la}}$ is higher than $p_{\mathrm{lb}}$, causing the opening of ${\mathrm{POCV}}_{\mathrm{b}}$. The flow rate from the bore side passing through the p is too high for the rod side. The differential flow goes back to the accumulator ($Q_{\mathrm{acc}}$), resulting in $p_{\mathrm{b}}=p_{\mathrm{la}}=p_{\mathrm{acc}}$ (represented in green). ${\mathrm{PSV}}_4$ is used as an active control element, throttling the flow so that $p_{\mathrm{pb}}$ remains above the load-holding valve crack pressure $p_{\mathrm{lh}}$. Because of the selective functions of ISV and ${\mathrm{SV}}_{\mathrm{b}}$, $p_{\mathrm{pi}}$ is equal to $p_{\mathrm{pb}}$. Thus, ${\mathrm{LH}}_{\mathrm{a}}$ and ${\mathrm{LH}}_{\mathrm{b}}$ are open.

2.3. System Analysis in Load-Holding Mode

For all four quadrants, the load holding can be introduced quite simple by opening the active control elements fully. In this case, $p_{\mathrm{pi}}$ always goes below the $p_{\mathrm{lh}}$ value, and the load-holding valves close. This is illustrated in Figure 5.

3. System Modeling

The dynamic system model of the proposed 1M1P MCC is derived based on the experimentally validated system model of a 2M2P MCC utilized in [18]. The selected off-the-shelf components of the proposed 1M1P MCC are listed in

Table 1. Off-the-shelf components of the proposed 1M1P MCC in Figure 3.

Components	Manufacturer	Product Number
M	Bosch Rexroth, Lohr am Main, Germany	MS2N07-D
P	Bosch Rexroth	A10FZG
ACC	Bosch Rexroth	HAD3,5-250-2X
ISV	Bucher, Zurich, Switzerland	HOSV-10
LH	Sun Hydraulics, Sarasota, FL, USA	DKHSXHN
CV	Bosch Rexroth	RE20380
PRV	Bosch Rexroth	RE 25402
PSV	Bosch Rexroth	KKDSR1PB
POCV	Sun Hydraulics	CKEBXCN
SV	Bosch Rexroth	MHSU2KA1X/420
Cylinder	LJM, Farmingdale, NY, USA	NH41-0-SD

. The modeling parameters are from the datasheet of these components.

M is modeled by a second-order transfer function; see Equation (1). In this equation, ${\omega }_{\mathrm{input}}$ denotes the input signal to the motor from the position controller, and $\omega$ represents the resulting motor shaft velocity. The motor dynamics are characterized by a natural frequency ${\omega }_{\mathrm{n}}$ of 23.8 Hz and a damping ratio $\zeta$ of 0.73. According to the datasheet, the energy efficiency (${\eta }_{\mathrm{M}}$) of M is 95%. For the purposes of this paper, saturation limits for M are not reached and are thus disregarded.

$$\frac{\omega }{{\omega }_{\mathrm{input}}}=\frac{{\omega }_{\mathrm{n}}^2}{s^2+2{\omega }_{\mathrm{n}}\zeta s+{\omega }_{\mathrm{n}}^2}$$

(1)

P is rigidly connected to M and rotates at the same angular velocity $\omega$. The pump flow rate $Q_{\mathrm{p}}$ is modeled using Equation (2), with a displacement of $D=6$ cc/rev. The modeling of leakages $Q_{\mathrm{le},\mathrm{l}}$ and $Q_{\mathrm{le},\mathrm{r}}$ in P uses Equations (3) and (4), respectively. $\mathsf{\Delta }{p}_{\mathrm{l}}$ represents the pressure difference between the left side of the pump and the accumulator. In contrast, $\mathsf{\Delta }{p}_{\mathrm{r}}$ represents the pressure difference between the right side of the pump and the accumulator. The pump leakage coefficient $k_{\mathrm{le}}$ is $2.5·{10}^{-3}$ L/min/bar. Therefore, the pump flow rates on the right side ($Q_{\mathrm{pa}}$) and left side ($Q_{\mathrm{pb}}$) are expressed in Equations (5) and (6), respectively. Experimental data in [18] indicate that the leakage between the two sides of the cylinder is insignificant, and therefore, it is neglected.

$$Q_{\mathrm{p}}=D\omega$$

(2)

$$Q_{\mathrm{le},\mathrm{l}}=\mathsf{\Delta }{p}_{\mathrm{l}}{k}_{\mathrm{le}}$$

(3)

$$Q_{\mathrm{le},\mathrm{r}}=\mathsf{\Delta }{p}_{\mathrm{r}}{k}_{\mathrm{le}}$$

(4)

$$Q_{\mathrm{pa}}=D\omega -Q_{\mathrm{le},\mathrm{l}}$$

(5)

$$Q_{\mathrm{pb}}=-D\omega -Q_{\mathrm{le},\mathrm{r}}$$

(6)

The theoretical torque $T_{\mathrm{th}}$ of P is derived via Equation (7). The torque loss $T_{\mathrm{s}}$ of P is derived by scaling a reference torque loss $T_{\mathrm{s},\mathrm{ref}}$ from steady-state experimental data of a reference axial-piston unit with displacement equal to $D_{\mathrm{ref}}$ = 75 cc/rev [19]. $T_{\mathrm{s},\mathrm{ref}}$ is a function of $\omega$ and $p_{\mathrm{pa}}-p_{\mathrm{pb}}$. The same method was also used in [16]. The scaling factor $\lambda$ and torque loss $T_{\mathrm{s}}$ are calculated via Equations (8) and (9), respectively.

$$T_{\mathrm{th}}=D(p_{\mathrm{pa}}-p_{\mathrm{pb}})$$

(7)

$$\lambda =\sqrt[3]{\frac{D}{D_{\mathrm{ref}}}}$$

(8)

$$T_{\mathrm{s}}={\lambda }^3{T}_{\mathrm{s},\mathrm{ref}}$$

(9)

The hydraulic system is simulated using an approach where the effective bulk modulus (${\beta }_{\mathrm{chb},i}$) of the fluid in the i-th hydraulic chamber is determined through a combination of Equations (10)–(12). ${\beta }_{\mathrm{oil}}=7000$ bar is the hydraulic oil’s bulk modulus. $p_{\mathrm{chb},i}$ is the pressure in the i-th hydraulic chamber. $p_{\mathrm{atm}}=$ 1 bar is the atmospheric pressure. $k_{\mathrm{air}}=$ 1.4 is the air adiabatic constant. ${\beta }_{\mathrm{chb},\mathrm{air},i}$ is the i-th chamber entrapped air bulk modulus. $V_{\mathrm{atm},\epsilon }=$ 0.01 is the entrapped air relative volume at atmospheric pressure. $V_{\mathrm{chb},\epsilon ,i}$ is the entrapped air relative volume in the i-th chamber. The Greek letter $\epsilon$ represents the volume ratio between undissolved gas and oil at atmospheric pressure.

$${\beta }_{\mathrm{chb},i}=p_{\mathrm{chb},i}{k}_{\mathrm{air}}$$

(10)

$$V_{\mathrm{chb},\epsilon ,i}=V_{\mathrm{atm},\epsilon }{\left(\frac{p_{\mathrm{atm}}}{p_{\mathrm{chb},i}}\right)}^{\frac{1}{k_{\mathrm{air}}}}$$

(11)

$${\beta }_{\mathrm{chb},i}=\frac{1}{\frac{1}{{\beta }_{\mathrm{oil}}}+\frac{V_{\mathrm{chb},\epsilon ,i}}{{\beta }_{\mathrm{chb},\mathrm{air},i}}}$$

(12)

The hydraulic cylinder model comprises three parts: pressure build-up, pressure-force conversion, and cylinder friction. The pressure build-up on the bore side (${\dot{p}}_{\mathrm{a}}$) and rod side (${\dot{p}}_{\mathrm{b}}$) of the cylinder are represented by Equations (13) and (14), respectively. The flow rates going in or out of the cylinder bore and rod sides are denoted by $Q_{\mathrm{a}}$ and $Q_{\mathrm{b}}$, respectively. The piston position and velocity are represented by $x_{\mathrm{p}}$ and ${\dot{x}}_{\mathrm{p}}$, respectively. The bore and rod side areas are denoted by $A_{\mathrm{a}}$ and $A_{\mathrm{b}}$, respectively. The maximum cylinder stroke is $x_{\mathrm{end}}=$ 400 mm, the bore side diameter is 63 mm, and the rod side diameter is 45 mm. The cylinder dead volume plus line volume is denoted by $V_0$. The pressure-force conversion $F_{\mathrm{cyl}}$ is modeled via Equation (15). The friction between the cylinder and piston is modeled as Stribeck friction; see Equation (16). The viscous friction coefficient is denoted as $f_{\mathrm{v}}$ and is equal to 4000 Ns/m. The Coulomb friction force is represented by $F_{\mathrm{C}}$ and is equal to 75 N. The hyperbolic tangent coefficient is $\gamma$, which is equal to 250 s/m. The static friction force is $F_{\mathrm{S}}$, with a value of 500 N. The static friction time constant is $\tau$, with a value of 0.02 m/s. It should be noted that the complexity of cylinder friction can vary, and incorporating factors like the pressure difference ($p_{\mathrm{a}}-p_{\mathrm{b}}$) may provide a more detailed representation. However, in this study, the pressure levels are similar across experiments. Therefore, the Stribeck friction model is considered adequate.

$${\dot{p}}_{\mathrm{a}}=\frac{{\beta }_{\mathrm{chb},\mathrm{a}}(Q_{\mathrm{a}}-{\dot{x}}_{\mathrm{p}}{A}_{\mathrm{a}})}{V_0+x_{\mathrm{p}}{A}_{\mathrm{a}}}$$

(13)

$${\dot{p}}_{\mathrm{b}}=\frac{{\beta }_{\mathrm{chb},\mathrm{b}}({\dot{x}}_{\mathrm{p}}{A}_{\mathrm{b}}-Q_{\mathrm{b}})}{V_0+(x_{\mathrm{end}}-x_{\mathrm{p}})A_{\mathrm{b}}}$$

(14)

$$F_{\mathrm{cyl}}=p_{\mathrm{a}}{A}_{\mathrm{a}}-p_{\mathrm{b}}{A}_{\mathrm{b}}$$

(15)

$$F_{\mathrm{f}}=f_{\mathrm{v}}{\dot{x}}_{\mathrm{p}}+tanh\left(\gamma {\dot{x}}_{\mathrm{p}}\right)\left(F_{\mathrm{C}}+F_{\mathrm{S}}{\mathrm{e}}^{\frac{-{\dot{x}}_{\mathrm{p}}tanh\left(\gamma {\dot{x}}_{\mathrm{p}}\right)}{\tau }}\right)$$

(16)

The modeling approach for the bladder accumulator follows the method proposed in [20]. According to Equation (17), the gas pressure $p_{\mathrm{g}}$ is equivalent to the fluid pressure $p_{\mathrm{f}}$ when the fluid pressure is greater than the pre-charged gas pressure ($p_{\mathrm{g}0}=$ 0.96 bar), which, in this paper, is considered to be always true. When the gas pressure changes, the gas volume $V_{\mathrm{g}}$ is modeled via Equation (18). The symbol n represents the adiabatic gas constant. The fluid volume $V_{\mathrm{f}}$ is calculated as the difference in total accumulator volume $V_{\mathrm{g}0}$ (2.8 L) and gas volume $V_{\mathrm{g}}$, as shown in Equation (19). The fluid pressure build-up ${\dot{p}}_{\mathrm{f}}$ is modeled via Equation (20). The fluid volume changing rate ${\dot{V}}_{\mathrm{f}}$ is calculated via Equation (21). The accumulator pressure $p_{\mathrm{acc}}$ is equal to the fluid pressure $p_{\mathrm{f}}$.

$$p_{\mathrm{g}}=\left\{\begin{array}{cc}{p}_{\mathrm{f}}\hfill & \mathrm{if}{p}_{\mathrm{g}}\ge p_{\mathrm{g}0}\hfill \\ p_{\mathrm{g}0}\hfill & \mathrm{if}{p}_{\mathrm{f}}<p_{\mathrm{g}0}\hfill \end{array}\right.$$

(17)

$$V_{\mathrm{g}}={\left(\frac{p_{\mathrm{g}0}{V}_{\mathrm{g}0}^n}{p_{\mathrm{g}}}\right)}^{\frac{1}{n}}$$

(18)

$$V_{\mathrm{f}}=V_{\mathrm{g}0}-V_{\mathrm{g}}$$

(19)

$${\dot{p}}_{\mathrm{f}}=\frac{{\beta }_{\mathrm{chb},\mathrm{acc}}}{V_{\mathrm{f}}}(Q_{\mathrm{acc}}-{\dot{V}}_{\mathrm{f}})$$

(20)

$${\dot{V}}_{\mathrm{f}}=-{\dot{V}}_{\mathrm{g}}=\left(\frac{1}{1+\frac{n{p}_{\mathrm{f}}{V}_{\mathrm{f}}}{{\beta }_{\mathrm{chb},\mathrm{acc}}{V}_{\mathrm{g}}}}\right)Q_{\mathrm{acc}}$$

(21)

Nine CVs are used in the proposed 1M1P MCC, as shown in Figure 3. Equation (22) is used to model the behavior of all these CVs. $\mathsf{\Delta }{p}_{\mathrm{cv},\mathrm{i}}$ represents the pressure drop across the i-th CV, and $Q_{\mathrm{cv},\mathrm{i}}$ denotes the corresponding flow rate. The same cracking pressure $p_{\mathrm{cv},\mathrm{cr}}=$ 0.2 bar is used for all CVs, and they all have the same CV flow rate constant of $k_{\mathrm{cv}}=$ 500 L/min/bar.

$$Q_{\mathrm{cv},\mathrm{i}}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}(\mathsf{\Delta }{p}_{\mathrm{cv},i}-p_{\mathrm{cv},\mathrm{cr}})\le 0\hfill \\ (\mathsf{\Delta }{p}_{\mathrm{cv},i}-p_{\mathrm{cv},\mathrm{cr}})k_{\mathrm{cv}}\hfill & \mathrm{if}(\mathsf{\Delta }{p}_{\mathrm{cv},i}-p_{\mathrm{cv},\mathrm{cr}})>0\hfill \end{array}\right.$$

(22)

Two SVs and an ISV are used in the pilot lines. They are modeled as logic elements. Equation (23) shows the logic of ISV. Equations (24) and (25) show the logic of ${\mathrm{SV}}_{\mathrm{a}}$ and ${\mathrm{SV}}_{\mathrm{b}}$, respectively.

$$p_{\mathrm{pi}}=\left\{\begin{array}{cc}{p}_{\mathrm{sva}}\hfill & \mathrm{if}{p}_{\mathrm{sva}}\le p_{\mathrm{svb}}\hfill \\ p_{\mathrm{svb}}\hfill & \mathrm{if}{p}_{\mathrm{sva}}>p_{\mathrm{svb}}\hfill \end{array}\right.$$

(23)

$$p_{\mathrm{sva}}=\left\{\begin{array}{cc}{p}_{\mathrm{pa}}\hfill & \mathrm{if}{p}_{\mathrm{a}}\le p_{\mathrm{pa}}\hfill \\ p_{\mathrm{a}}\hfill & \mathrm{if}{p}_{\mathrm{a}}>p_{\mathrm{pa}}\hfill \end{array}\right.$$

(24)

$$p_{\mathrm{svb}}=\left\{\begin{array}{cc}{p}_{\mathrm{pb}}\hfill & \mathrm{if}{p}_{\mathrm{b}}\le p_{\mathrm{pb}}\hfill \\ p_{\mathrm{b}}\hfill & \mathrm{if}{p}_{\mathrm{b}}>p_{\mathrm{pb}}\hfill \end{array}\right.$$

(25)

The modeling approach for the two non-vented, pressure-operated check valves (POCVs) aligns with the method presented in [16]. The calculation of the flow rates through POCVs, denoted as $Q_{\mathrm{POCV},i}$, is performed using the orifice equation, Equation (26).

$$Q_{\mathrm{POCV},i}=\left\{\begin{array}{cc}0\hfill & \mathrm{if}{p}_{\mathrm{out},i}>p_{\mathrm{in},i}+\psi p_{\mathrm{x},i}\hfill \\ K_{\mathrm{pocv},i}{u}_i\mathrm{SIGN}\left(\mathsf{\Delta }{p}_i\right)\sqrt{\frac{2}{\rho }\left|\mathsf{\Delta }{p}_i\right|}\hfill & \mathrm{if}{p}_{\mathrm{out},i}\le p_{\mathrm{in},i}+\psi p_{\mathrm{x},i}\hfill \end{array}\right.$$

(26)

This equation takes the following properties into account: a pressure differential across the valve $\mathsf{\Delta }{p}_i$, a valve opening constant $K_{\mathrm{pocv},i}$, a dimensionless poppet lift $u_i$, a pilot ratio ($\psi$), fluid density $\rho$, a valve inlet pressure $p_{\mathrm{in},i}$, and a valve outlet pressure $p_{\mathrm{out},i}$. The symbol i represents the i-th POCV. The dimensionless poppet lift $u_i$ is computed in two different ways depending on the mode of operation. If the POCV is acting as a regular check valve, it is computed via Equation (27), and if it is acting as a pilot-operated check valve, it is computed via Equation (28).

$$u_i=\frac{p_{\mathrm{in},i}-p_{\mathrm{out},i}-p_{\mathrm{pocv},\mathrm{cr}}}{\mathsf{\Delta }{p}_{\mathrm{open}}}$$

(27)

$$u_i=\frac{\psi (p_{\mathrm{x},i}-p_{\mathrm{in},i})+(p_{\mathrm{in},i}-p_{\mathrm{out},i})-p_{\mathrm{pocv},\mathrm{cr}}}{\mathsf{\Delta }{p}_{\mathrm{open}}}$$

(28)

In the equations, $p_{\mathrm{x},i}$ represents the pilot pressure, $p_{\mathrm{pocv},\mathrm{cr}}$ represents the valve cracking pressure, and $\mathsf{\Delta }{p}_{\mathrm{open}}$ represents the pressure difference required to fully open the check valve.

The modeling approach of four PSVs is similar to that of the POCVs, i.e., Equation (29). The symbol $K_{\mathrm{psv},i}$ is the opening area constant for the i-th PSV. The symbol $\mathsf{\Delta }{p}_{\mathrm{psv},i}$ is the pressure differential across the i-th PSV. The dimensionless opening for each PSV, $u_{\mathrm{psv},i}$, is given by the control signal to the solenoid. Finally, the modeling approach for the two load-holding valves follows a similar orifice equation with the dimensionless opening defined from the pilot pressure $p_{\mathrm{pi}}$ and the valve crack pressure.

$$Q_{\mathrm{psv},i}=K_{\mathrm{psv},i}{u}_{\mathrm{psv},i}\mathrm{SIGN}\left(\mathsf{\Delta }{p}_{\mathrm{psv},i}\right)\sqrt{\frac{2}{\rho }\left|\mathsf{\Delta }{p}_{\mathrm{psv},i}\right|}$$

(29)

 $p_{\mathrm{la}}$, $p_{\mathrm{lb}}$, $p_{\mathrm{pa}}$, and $p_{\mathrm{pb}}$ are calculated using the pressure build-up equations, as shown in Equations (30)–(33). $V_{\mathrm{la}}$, $V_{\mathrm{lb}}$, $V_{\mathrm{pa}}$, and $V_{\mathrm{pb}}$ are the volumes of the transmission lines. Because of ${\mathrm{CV}}_3$ (or ${\mathrm{CV}}_4$), when the hose between ${\mathrm{LH}}_{\mathrm{a}}$ (or ${\mathrm{LH}}_{\mathrm{b}}$) and ${\mathrm{PSV}}_1$ (or ${\mathrm{PSV}}_2$) ruptures, $p_{\mathrm{la}}$ (or $p_{\mathrm{lb}}$) becomes zero. 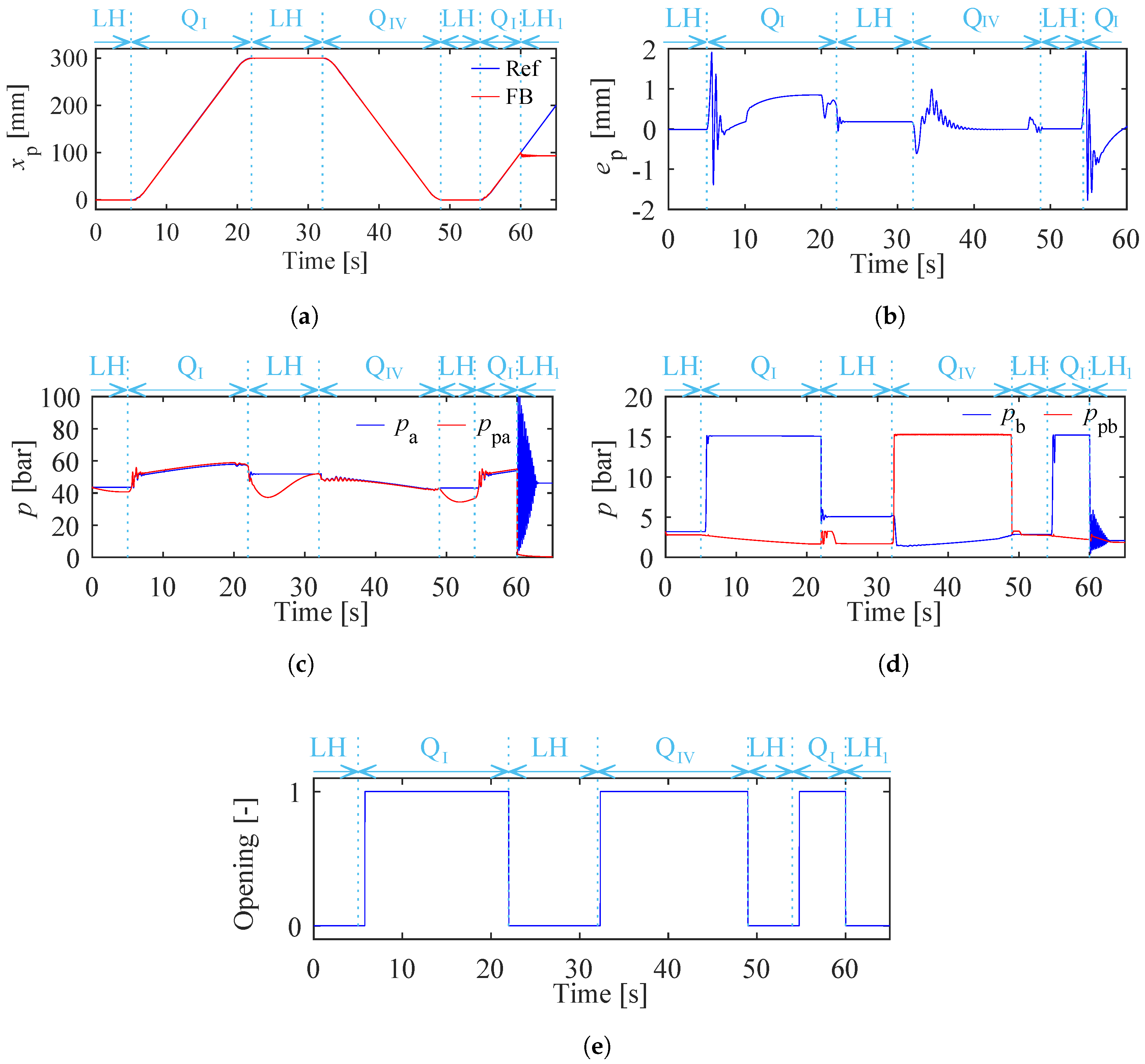Therefore, the hose rupture is realized by forcing $p_{\mathrm{la}}$ (or $p_{\mathrm{lb}}$) to zero at 60 s in simulations.

$${\dot{p}}_{\mathrm{la}}=\frac{{\beta }_{\mathrm{chb},\mathrm{la}}(Q_{\mathrm{pocv},a}+Q_{\mathrm{psv},3}-Q_{\mathrm{psv},1})}{V_{\mathrm{la}}}$$

(30)

$${\dot{p}}_{\mathrm{lb}}=\frac{{\beta }_{\mathrm{chb},\mathrm{lb}}(Q_{\mathrm{pocv},b}+Q_{\mathrm{psv},4}-Q_{\mathrm{psv},2})}{V_{\mathrm{lb}}}$$

(31)

$${\dot{p}}_{\mathrm{pa}}=\frac{{\beta }_{\mathrm{chb},\mathrm{pa}}(Q_{\mathrm{pa}}-Q_{\mathrm{psv},3})}{V_{\mathrm{pa}}}$$

(32)

$${\dot{p}}_{\mathrm{pb}}=\frac{{\beta }_{\mathrm{chb},\mathrm{pb}}(Q_{\mathrm{pb}}-Q_{\mathrm{psv},4})}{V_{\mathrm{pb}}}$$

(33)

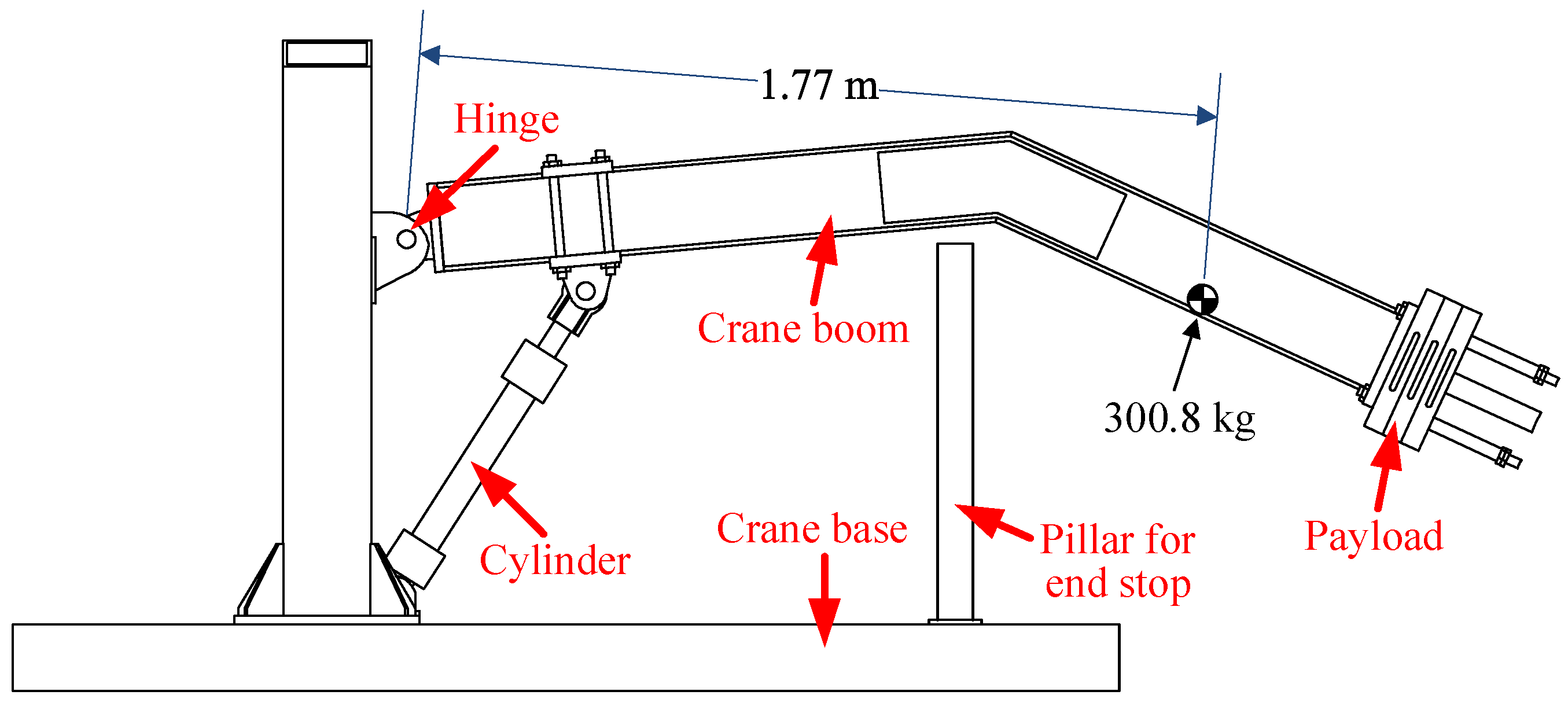
The laboratory single-boom crane investigated in a previous experimental study [18] is used in this paper as an application to verify the proposed 1M1P MCC’s functionalities. This crane is modeled in the Simulink-Simscape. The crane model receives the hydraulic cylinder force from the hydraulic system model and provides piston position and velocity back to the hydraulic system model. The crane is shown in Figure 6 with some of the main inertia data. The total mass of the crane boom and the payload is 300.8 kg, with the mass center located at a distance of 1.77 m from the hinge. It is important to emphasize that, within this crane system, our analysis solely incorporates the friction between the cylinder and the piston, as modeled by Equation (16). Any additional frictional effects at the hinges have been disregarded for simplicity.

4. Controls

The control algorithm for the proposed 1M1P MCC is presented in this section. Figure 7 illustrates the control algorithm, which incorporates three distinct control loops: the position control loop, the line pressure control loop, and the PSV control loop. These control loops enable the MCC to be in either the operation mode or the load-holding mode, depending on the specific working conditions.

4.1. Position Control Loop

The green area in Figure 7 shows the position control loop. It is activated via the Mode Selector 1 block in the operation mode. Mode Selector 1 works based on the speed reference ${\dot{x}}_{\mathrm{ref}}$, as illustrated in Equation (34). ${\omega }_{\mathrm{input}}$ is the input command to M. $u_{\mathrm{pos}}$ is the position control loop output. $u_{\mathrm{lin}}$ is the line pressure control loop output.

$${\omega }_{\mathrm{input}}=\left\{\begin{array}{cc}{u}_{\mathrm{pos}}\hfill & \mathrm{if}{\dot{x}}_{\mathrm{ref}}\ne 0\left(\mathrm{operation}\mathrm{mode}\right)\hfill \\ u_{\mathrm{lin}}\hfill & \mathrm{if}{\dot{x}}_{\mathrm{ref}}=0\left(\mathrm{load}-\mathrm{holding}\mathrm{mode}\right)\hfill \end{array}\right.$$

(34)

The position control loop comprises three terms: feedforward, feedback, and a high pass filtered pressure feedback. The feedforward controller estimates the required speed of M ($u_{\mathrm{FF}}$) via Equation (35). The cylinder bore-side area $A_{\mathrm{a}}$, the cylinder rod-side area $A_{\mathrm{b}}$, and the displacement D of P are recalled. A proportional-integral controller yields the necessary feedback controller command ($u_{\mathrm{FB}}$) to correct the feedforward prediction. The proportional gain is 5.85·10⁵ rev/min/m, and the integral gain is 1750 rev/m.

$$u_{\mathrm{FF}}=\left\{\begin{array}{cc}\frac{{\dot{x}}_{\mathrm{ref}}{A}_{\mathrm{a}}}{D}\hfill & \mathrm{if}{p}_{\mathrm{a}}\ge p_{\mathrm{b}}\left(Q_{\mathrm{I}}\mathrm{and}{Q}_{\mathrm{IV}}\right)\hfill \\ \frac{{\dot{x}}_{\mathrm{ref}}{A}_{\mathrm{b}}}{D}\hfill & \mathrm{if}{p}_{\mathrm{a}}<p_{\mathrm{b}}\left(Q_{\mathrm{II}}\mathrm{and}{Q}_{\mathrm{III}}\right)\hfill \end{array}\right.$$

(35)

A load-pressure feedback signal $p_{\mathrm{L}}$, calculated via the bore-side pressure $p_{\mathrm{a}}$, the rod-side pressure $p_{\mathrm{b}}$, and the area ratio $A_{\mathrm{b}}/A_{\mathrm{a}}$, is filtered by a high-pass filter $G_{\mathrm{HP}}$, as shown in Equation (36). The cut-off frequency ${\omega }_{\mathrm{HP}}$ is 3 rad/s. The filter gain $k_{\mathrm{HP}}$ is 5 rev/min/bar. The negative filtered load-pressure feedback signal is added to increase the system damping.

$$G_{\mathrm{HP}}=k_{\mathrm{HP}}\frac{s}{s+{\omega }_{\mathrm{HP}}}$$

(36)

4.2. Line Pressure Control Loop

The blue area in Figure 7 represents the line pressure control loop. The primary objective of this control loop is to minimize the pressure deviation between the cylinder pressure ($p_{\mathrm{a}}$ or $p_{\mathrm{b}}$) and the line pressure ($p_{\mathrm{la}}$ or $p_{\mathrm{lb}}$) in load-holding mode. By doing so, the piston oscillation that occurs during the transition between the operation and load-holding modes can be effectively mitigated.

Only the line pressure on the load-holding side, i.e., $p_{\mathrm{la}}$ in $Q_{\mathrm{I}}$ and $Q_{\mathrm{IV}}$ or $p_{\mathrm{lb}}$ in $Q_{\mathrm{II}}$ and $Q_{\mathrm{III}}$, is controlled in this loop. This is realized by the line pressure error selector block represented via Equation (37). $e_{\mathrm{lin}}$ is the line pressure error to the controller. $e_{\mathrm{la}}=p_{\mathrm{a}}-p_{\mathrm{la}}$ is the line pressure error on the cylinder bore side. $e_{\mathrm{lb}}=p_{\mathrm{b}}-p_{\mathrm{lb}}$ is the line pressure error on the cylinder rod side. $p_{\mathrm{o}}=$ 2 bar is a pressure offset to ensure the line pressure is lower than the cylinder pressure. This offset is essential to prevent the control loop from causing a control overshoot, which can raise the line pressures above the cylinder pressures before opening the load-holding valves. In this case, the cylinder begins moving before the load-holding valves are fully open.

$$e_{\mathrm{lin}}=\left\{\begin{array}{cc}{e}_{\mathrm{la}}-p_{\mathrm{o}}\hfill & \mathrm{if}{p}_{\mathrm{a}}\ge p_{\mathrm{b}}\left(Q_{\mathrm{I}}\mathrm{and}{Q}_{\mathrm{IV}}\right)\hfill \\ e_{\mathrm{lb}}-p_{\mathrm{o}}\hfill & \mathrm{if}{p}_{\mathrm{a}}<p_{\mathrm{b}}\left(Q_{\mathrm{II}}\mathrm{and}{Q}_{\mathrm{III}}\right)\hfill \end{array}\right.$$

(37)

The line pressure controller, a proportional-integral controller, generates the command $u_{\mathrm{lin}}$ to the mode selector 1. The proportional gain is 24 rev/bar, and the integral gain is 12 rev/bar/s.

4.3. PSV Control Loop

The orange area in Figure 7 shows the PSV control loop. As analyzed in Section 2, the system incorporates four normally open PSVs to regulate the pressures ($p_{\mathrm{a}}$, $p_{\mathrm{b}}$, $p_{\mathrm{pa}}$, and $p_{\mathrm{pb}}$), which operate the load-holding device and mitigate the pump mode oscillation. These PSVs are individually controlled by identical feedback proportional-integral controllers. The proportional gain is 1 ${\mathrm{bar}}^{-1}$, and the integral gain is 0.01 s/bar. It should be noted that the control errors are generated using the feedback pressures minus the reference pressures. In this way, PSVs are opened by the controllers if the reference pressure is higher than the feedback pressure and closed if the reference pressure is lower than the feedback pressure. The pressure reference $p_{\mathrm{ref}}$ is the same for all controllers. The pressure reference selector generates two different pressure references according to different modes, as expressed in Equation (38). Because the ACC pressure $p_{\mathrm{acc}}$ is 3 bar, PSVs are fully opened in the load-holding mode. Higher pressure reference in operation mode increases the PSV energy losses. Thus, a low pressure reference is preferred. However, it cannot be lower than 10 bar, which is the cracking pressure of the load-holding valves. Hence, 15 bar is chosen as the pressure reference in the operation mode, considering a safety factor.

$$p_{\mathrm{ref}}=\left\{\begin{array}{cc}15\mathrm{bar}\hfill & \mathrm{if}{\dot{x}}_{\mathrm{ref}}\ne 0\left(\mathrm{operation}\mathrm{mode}\right)\hfill \\ 3\mathrm{bar}\hfill & \mathrm{if}{\dot{x}}_{\mathrm{ref}}=0\left(\mathrm{load}-\mathrm{holding}\mathrm{mode}\right)\hfill \end{array}\right.$$

(38)

In ${\mathrm{Q}}_{\mathrm{III}}$, ${\mathrm{PSV}}_1$ is actively controlled, while the other PSVs are fully open. Similarly, in QI, ${\mathrm{PSV}}_2$ is actively controlled, while the other PSVs are fully open. This pattern continues in ${\mathrm{Q}}_{\mathrm{II}}$ and ${\mathrm{Q}}_{\mathrm{IV}}$, where ${\mathrm{PSV}}_3$ and ${\mathrm{PSV}}_4$ are actively controlled, respectively, with the remaining PSVs fully open. These control actions are implemented through the Mode Selector 2 block using Equations (39)–(42). Here, $u_{\mathrm{psv},1}$ to $u_{\mathrm{psv},4}$ represent PSV input commands, while $u_{\mathrm{PI}1}$ to $u_{\mathrm{PI}4}$ denote the outputs of the four PSV controllers.

$$u_{\mathrm{psv},1}=\left\{\begin{array}{cc}{u}_{\mathrm{PI}1}\hfill & \mathrm{if}{\dot{x}}_{\mathrm{P}}\le 0\mathrm{and}(p_{\mathrm{a}}-p_{\mathrm{b}})\le 0\hfill \\ 1\hfill & \mathrm{Other}\hfill \end{array}\right.$$

(39)

$$u_{\mathrm{psv},2}=\left\{\begin{array}{cc}{u}_{\mathrm{PI}2}\hfill & \mathrm{if}{\dot{x}}_{\mathrm{P}}\ge 0\mathrm{and}(p_{\mathrm{a}}-p_{\mathrm{b}})\ge 0\hfill \\ 1\hfill & \mathrm{Other}\hfill \end{array}\right.$$

(40)

$$u_{\mathrm{psv},3}=\left\{\begin{array}{cc}{u}_{\mathrm{PI}3}\hfill & \mathrm{if}{\dot{x}}_{\mathrm{P}}\ge 0\mathrm{and}(p_{\mathrm{a}}-p_{\mathrm{b}})\le 0\hfill \\ 1\hfill & \mathrm{Other}\hfill \end{array}\right.$$

(41)

$$u_{\mathrm{psv},4}=\left\{\begin{array}{cc}{u}_{\mathrm{PI}4}\hfill & \mathrm{if}{\dot{x}}_{\mathrm{P}}\le 0\mathrm{and}(p_{\mathrm{a}}-p_{\mathrm{b}})\ge 0\hfill \\ 1\hfill & \mathrm{Other}\hfill \end{array}\right.$$

(42)

5. Simulation Results

In order to evaluate the proposed 1M1P MCC in four-quadrant operation and its load-holding functions, a representative working trajectory is used for the 1M1P MCC driving the single-boom crane in simulations. This trajectory encompasses the extension and retraction of the hydraulic cylinder across three distinct load-holding periods. The given trajectory corresponds to a piston velocity of 20 mm/s, representing a common working speed of the single-boom crane. In the result plots, LH and ${\mathrm{LH}}_1$ indicate the load-holding modes under the standstill command and hose rupture situation, respectively, while ${\mathrm{Q}}_{\mathrm{I}}$, ${\mathrm{Q}}_{\mathrm{II}}$, ${\mathrm{Q}}_{\mathrm{III}}$, and ${\mathrm{Q}}_{\mathrm{IV}}$ denote the system’s operation in the first, second, third, and fourth quadrants, respectively.

The system achieves four-quadrant operation by manipulating the direction of gravity, generating two distinct scenarios: scenario A and scenario B. In scenario A, gravity is directed downward, allowing the system to operate in quadrants ${\mathrm{Q}}_{\mathrm{I}}$ and ${\mathrm{Q}}_{\mathrm{IV}}$, as depicted in Figure 8a. Conversely, in scenario B, gravity is directed upward, enabling the system to operate in quadrants ${\mathrm{Q}}_{\mathrm{II}}$ and ${\mathrm{Q}}_{\mathrm{III}}$, as illustrated in Figure 8b.

5.1. Results in Scenario A

The position tracking performance in scenario A is shown in Figure 9a,b. The hose connecting the drive unit and the cylinder on the high-pressure side ruptures at 60 s, which is realized via forcing $p_{\mathrm{la}}$ (or $p_{\mathrm{lb}}$) to zero. The position feedback signal (FB) tracks the position reference (Ref) well. The tracking error before hose rupture falls well within ±2 mm. The error peaks occur at transitions between load-holding and operation modes. It is important to note that the tracking error after 60 s is not shown in the figure, as the feedback signal cannot follow the reference because of the hose rupture situation. The stable error in LH demonstrates the load-holding function under the standstill command. It is important to emphasize that the standstill command scenario is analogous to a system power loss emergency. Therefore, the load-holding function during system power loss is also successfully verified. Furthermore, the maintained piston position in ${\mathrm{LH}}_1$ demonstrates the load-holding function after hose rupture at 60 s.

System pressures in scenario A are shown in Figure 9c,d. $p_{\mathrm{pa}}$ is controlled to be close to $p_{\mathrm{a}}$, demonstrating the functionality of the line pressure control loop. Furthermore, the stability observed in $p_{\mathrm{a}}$ and $p_{\mathrm{b}}$ during LH provides additional evidence of the effective load-holding function. However, at the beginning of ${\mathrm{LH}}_1$, significant pressure oscillations in $p_{\mathrm{a}}$ and $p_{\mathrm{b}}$ occur because of the sudden hose rupture. These oscillations gradually cease after a transitional period. Because of the hose rupture, $p_{\mathrm{pa}}$ drops to zero promptly. Before the hose ruptures, $p_{\mathrm{b}}$ is controlled at 15 bar by ${\mathrm{PSV}}_2$ in ${\mathrm{Q}}_{\mathrm{I}}$. $p_{\mathrm{pb}}$ is controlled at 15 bar by ${\mathrm{PSV}}_4$ in ${\mathrm{Q}}_{\mathrm{IV}}$. These two controlled pressures are used to open the load-holding valves. Figure 9e shows the load-holding valve opening state. The load-holding valve opening state is linked to the controlled pressures $p_{\mathrm{b}}$ and $p_{\mathrm{pb}}$. Notably, a delay in opening the load-holding valves is observed at the beginning of ${\mathrm{Q}}_{\mathrm{I}}$. This delay is because $p_{\mathrm{b}}$ is increased by the pump/motor unit via increasing $p_{\mathrm{a}}$, and the commanded pump/motor unit speed is slow at the beginning of ${\mathrm{Q}}_{\mathrm{I}}$. Consequently, this delay contributes to peak errors in position tracking, as illustrated in Figure 9b. As shown in Figure 9e, the load-holding valves are closed immediately in both LH and ${\mathrm{LH}}_1$.

5.2. Results in Scenario B

As shown in Figure 8b, the gravity in scenario B is directed to the opposite of scenario A to generate operations in ${\mathrm{Q}}_{\mathrm{II}}$ and ${\mathrm{Q}}_{\mathrm{III}}$. Figure 10a,b show the position tracking performance in scenario B. The tracking error before the hose rupture on the high-pressure side (Equation (31)) falls well within ±3 mm. Because of the delay in opening the load-holding valves, the error peaks occur at transitions between load-holding and operation modes. The position drop after the hose rupture in scenario B is greater than in scenario A. This is because gravity is an assisting load in ${\mathrm{Q}}_{\mathrm{II}}$. As shown in Figure 10c,d, $p_{\mathrm{pa}}$ is controlled at 15 bar by ${\mathrm{PSV}}_3$ in ${\mathrm{Q}}_{\mathrm{II}}$, and $p_{\mathrm{a}}$ is controlled at 15 bar by ${\mathrm{PSV}}_1$ in ${\mathrm{Q}}_{\mathrm{III}}$. The load-holding valves are opened by these pressures accordingly. After the hose ruptures on the high-pressure side, $p_{\mathrm{pb}}$ drops to zero immediately, and severe oscillations are triggered in $p_{\mathrm{a}}$ and $p_{\mathrm{b}}$. However, these oscillations gradually cease after a transition period. As shown in Figure 10e, the load-holding valves are closed immediately in both LH and ${\mathrm{LH}}_1$.

5.3. System Energy Efficiency and PSV Losses

The energy efficiency calculation is only conducted in scenario A. The total power input $P_{\mathrm{M}}$ is derived via Equation (43). $\omega$ is the shaft velocity of M. $T_{\mathrm{e}}$ is the effective shaft torque, including the servo motor energy efficiency ${\eta }_{\mathrm{M}}$. $T_{\mathrm{e}}$ is calculated via Equation (44). The total output power of the cylinder ($P_{\mathrm{C}}$) is calculated via Equation (45).

$$P_{\mathrm{M}}=\omega T_{\mathrm{e}}$$

(43)

$$T_{\mathrm{e}}=\left\{\begin{array}{cc}\frac{T_{\mathrm{th}}+T_{\mathrm{s}}}{{\eta }_{\mathrm{M}}}\hfill & \mathrm{in}{\mathrm{Q}}_{\mathrm{I}}\hfill \\ (T_{\mathrm{th}}-T_{\mathrm{s}}){\eta }_{\mathrm{M}}\hfill & \mathrm{in}{\mathrm{Q}}_{\mathrm{IV}}\hfill \end{array}\right.$$

(44)

$$P_{\mathrm{C}}=(F_{\mathrm{cyl}}-F_{\mathrm{f}}){\dot{x}}_{\mathrm{p}}$$

(45)

$${\eta }_{\mathrm{sys}}=\left\{\begin{array}{cc}\frac{P_{\mathrm{C}}}{P_{\mathrm{M}}}\hfill & \mathrm{in}{\mathrm{Q}}_{\mathrm{I}}\hfill \\ \frac{P_{\mathrm{M}}}{P_{\mathrm{C}}}\hfill & \mathrm{in}{\mathrm{Q}}_{\mathrm{IV}}\hfill \end{array}\right.$$

(46)

$P_{\mathrm{M}}$ and $P_{\mathrm{C}}$ in scenario A are illustrated in Figure 11a. In ${\mathrm{Q}}_{\mathrm{I}}$, $P_{\mathrm{M}}$ is greater than $P_{\mathrm{C}}$. P is in pumping mode. The energy is transferred from M to the cylinder. In ${\mathrm{Q}}_{\mathrm{IV}}$, $P_{\mathrm{C}}$ is greater than $P_{\mathrm{M}}$. P is in motoring mode. The energy is transferred from the cylinder to M. In load-holding mode, $P_{\mathrm{C}}$ is zero because the piston speed is zero. $P_{\mathrm{M}}$ is slightly over zero because the bore-side line pressure needs to be maintained at a certain level. The system energy efficiency ${\eta }_{\mathrm{sys}}$ is calculated via Equation (46). The resulting ${\eta }_{\mathrm{sys}}$, depicted in Figure 11b, is obtained after mitigating noise and transition oscillations. In quadrant ${\mathrm{Q}}_{\mathrm{I}}$, ${\eta }_{\mathrm{sys}}$ is approximately 66%, indicating a relatively efficient energy transfer from M to the cylinder. In contrast, in ${\mathrm{Q}}_{\mathrm{IV}}$, ${\eta }_{\mathrm{sys}}$ is approximately 41%, suggesting a lower efficiency when the energy is regenerated from the cylinder to M.

The hydraulic power losses in the PSVs can be calculated by multiplying the pressure drop across the PSVs by the flow rates through the PSVs. ${\mathrm{PSV}}_2$ and ${\mathrm{PSV}}_4$ operate in scenario A. Their power losses ($P_{\mathrm{PSV}2}$ and $P_{\mathrm{PSV}4}$) are illustrated in Figure 11c. The power loss caused by ${\mathrm{PSV}}_2$ in ${\mathrm{Q}}_{\mathrm{I}}$ is approximately 39 W. The power loss caused by ${\mathrm{PSV}}_4$ in ${\mathrm{Q}}_{\mathrm{IV}}$ is approximately 77 W. The disparity in power losses between the two PSVs can be attributed to the different flow rates resulting from the differential areas of the cylinder. Figure 11d provides the representation of PSV power losses as a percentage of the total system power. Notably, around 8% of the power transferred from M to the cylinder is dissipated in ${\mathrm{PSV}}_2$ in ${\mathrm{Q}}_{\mathrm{I}}$. Furthermore, approximately 26% of the power transferred from the cylinder to M is lost in ${\mathrm{PSV}}_4$ in ${\mathrm{Q}}_{\mathrm{IV}}$. It is important to note that the power losses in PSVs remain constant regardless of the load magnitude. Consequently, the percentages of power losses attributed to the PSVs decrease when the load is larger.

The total energy used $E_{\mathrm{u}}$, total energy losses $E_{\mathrm{l}}$, and total PSV losses ${\mathrm{PSV}}_{\mathrm{l}}$ are shown in Figure 11e. $E_{\mathrm{u}}$ is calculated by integrating $P_{\mathrm{M}}$. $E_{\mathrm{l}}$ is calculated by integrating the absolute difference between $P_{\mathrm{M}}$ and $P_{\mathrm{C}}$. ${\mathrm{PSV}}_{\mathrm{l}}$ is calculated by integrating $P_{\mathrm{PSV}2}$ and $P_{\mathrm{PSV}4}$. Because of energy regeneration, $E_{\mathrm{u}}$ decreases in ${\mathrm{Q}}_{\mathrm{IV}}$. In contrast, $E_{\mathrm{l}}$ increases in both ${\mathrm{Q}}_{\mathrm{I}}$ and ${\mathrm{Q}}_{\mathrm{IV}}$, eventually equaling $E_{\mathrm{u}}$. The total PSV losses, denoted by ${\mathrm{PSV}}_{\mathrm{l}}$, exhibit a similar trend to $E_{\mathrm{l}}$ and account for 35% of $E_{\mathrm{l}}$.

6. Discussion

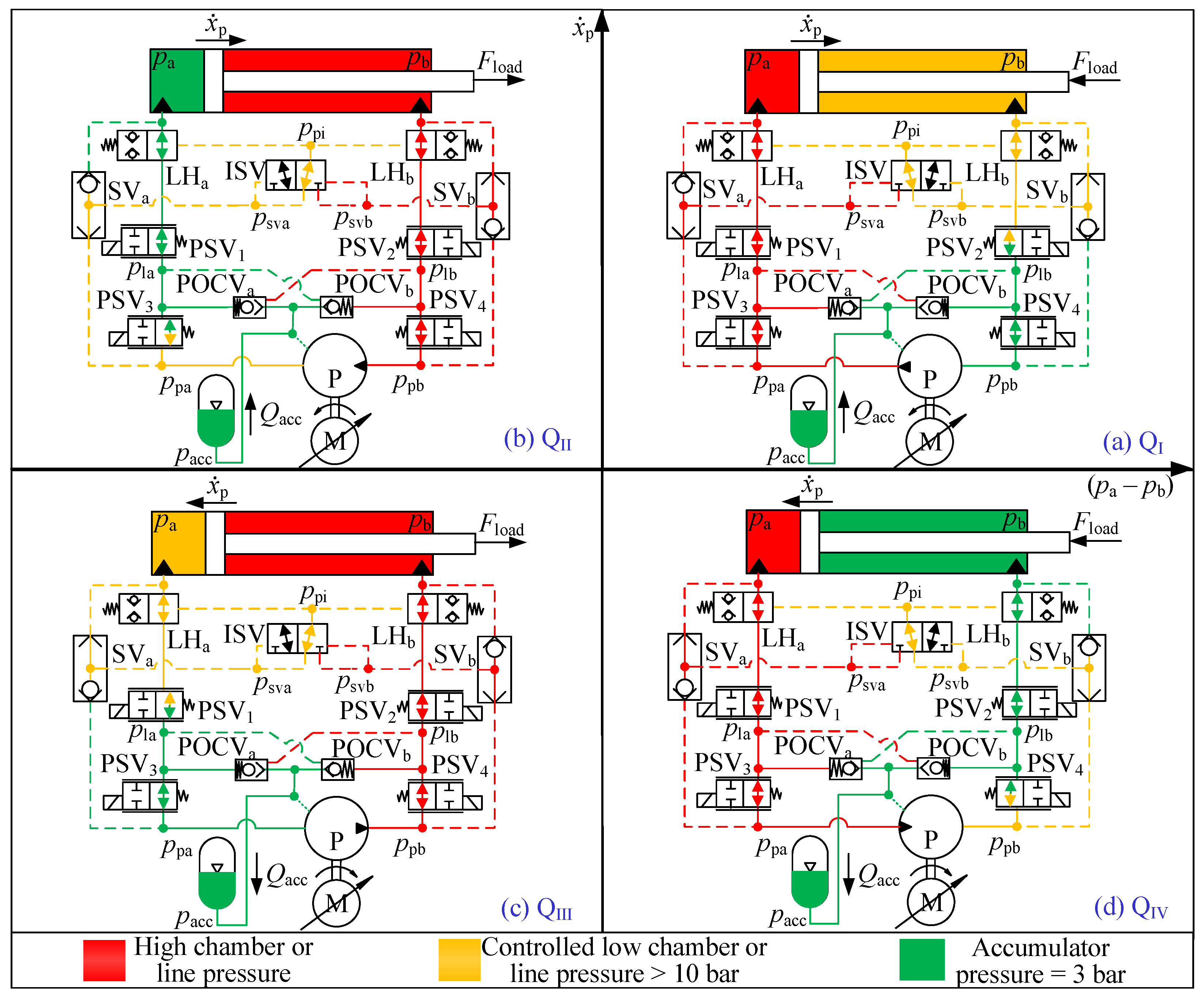
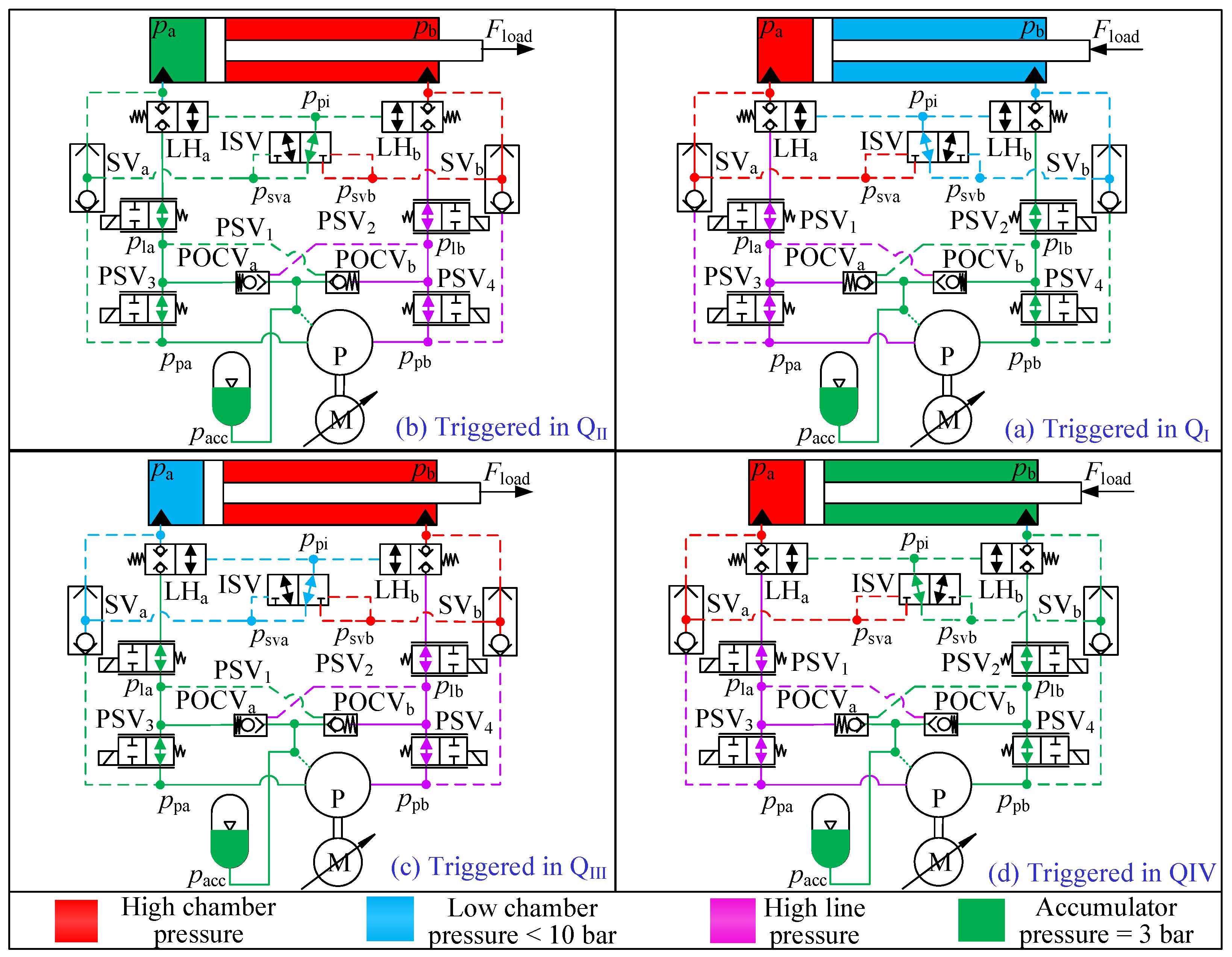
The proposed 1M1P MCC can realize the system pressure control, four-quadrant operation, and passive load-holding function triggered by emergencies, such as power loss and hose rupture. Furthermore, it can be deployed in remote installation [12], where the 1M1P MCC drive unit and the cylinder with a passive load-holding device are installed separately and connected via pipelines. Compared with the 2M2P MCC proposed in [18], which can offer the same functionalities, 1M1P MCC has disadvantages and advantages.

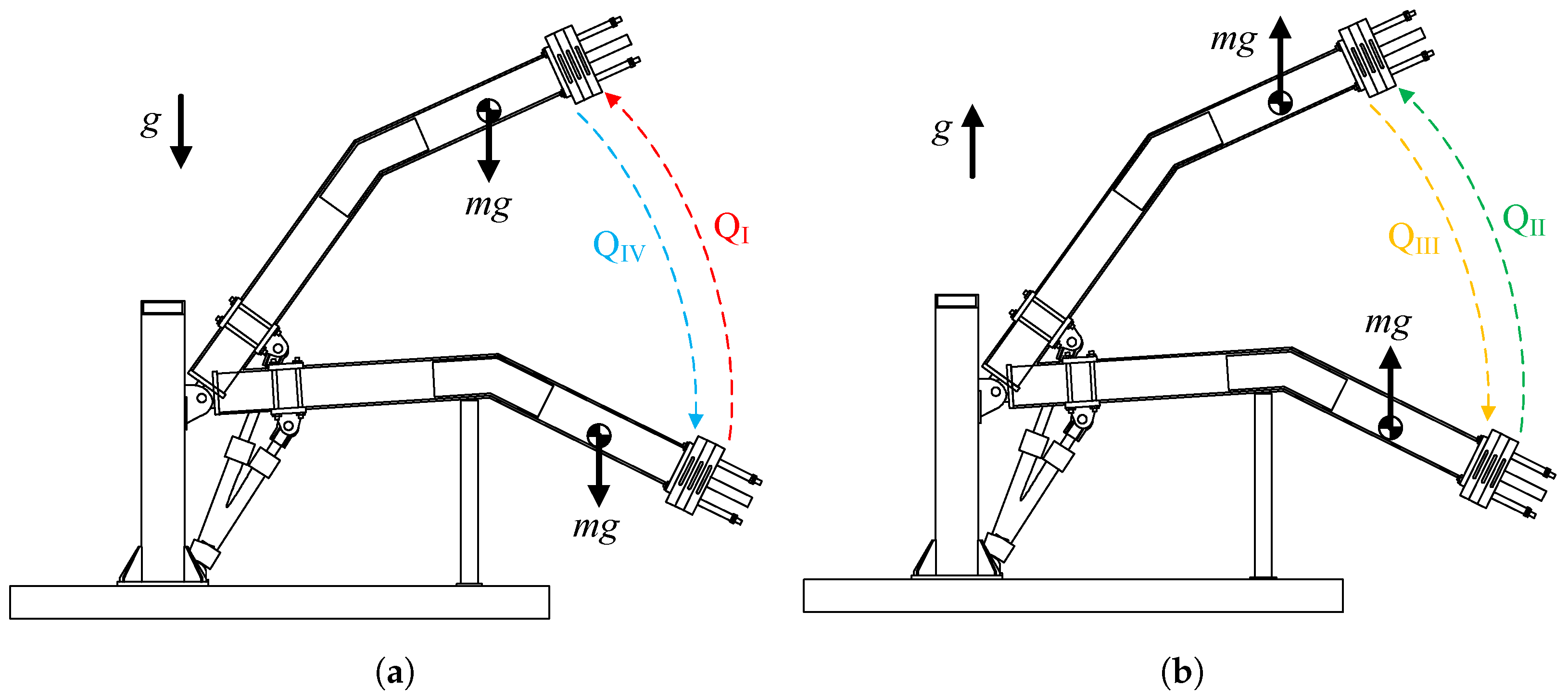
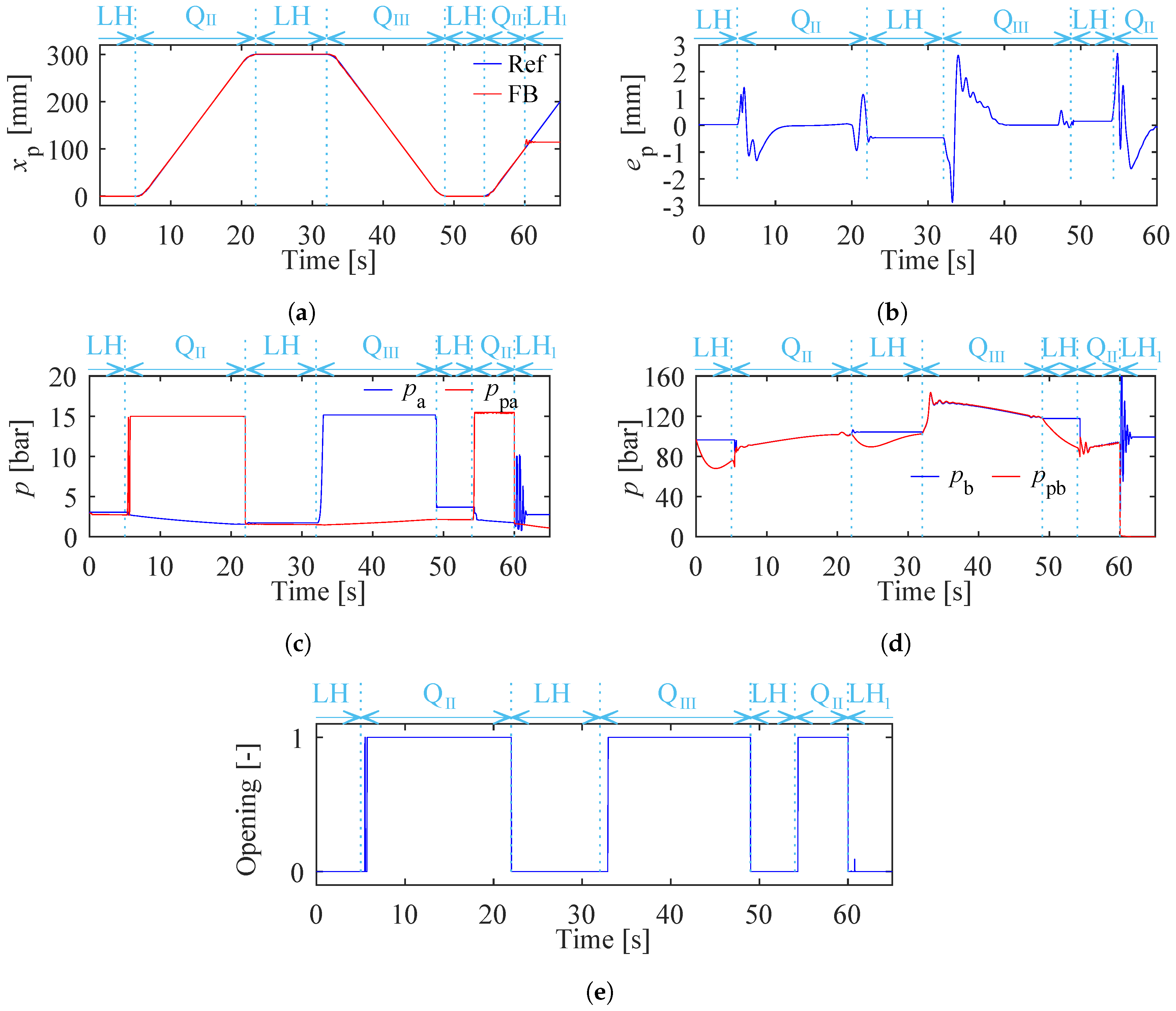
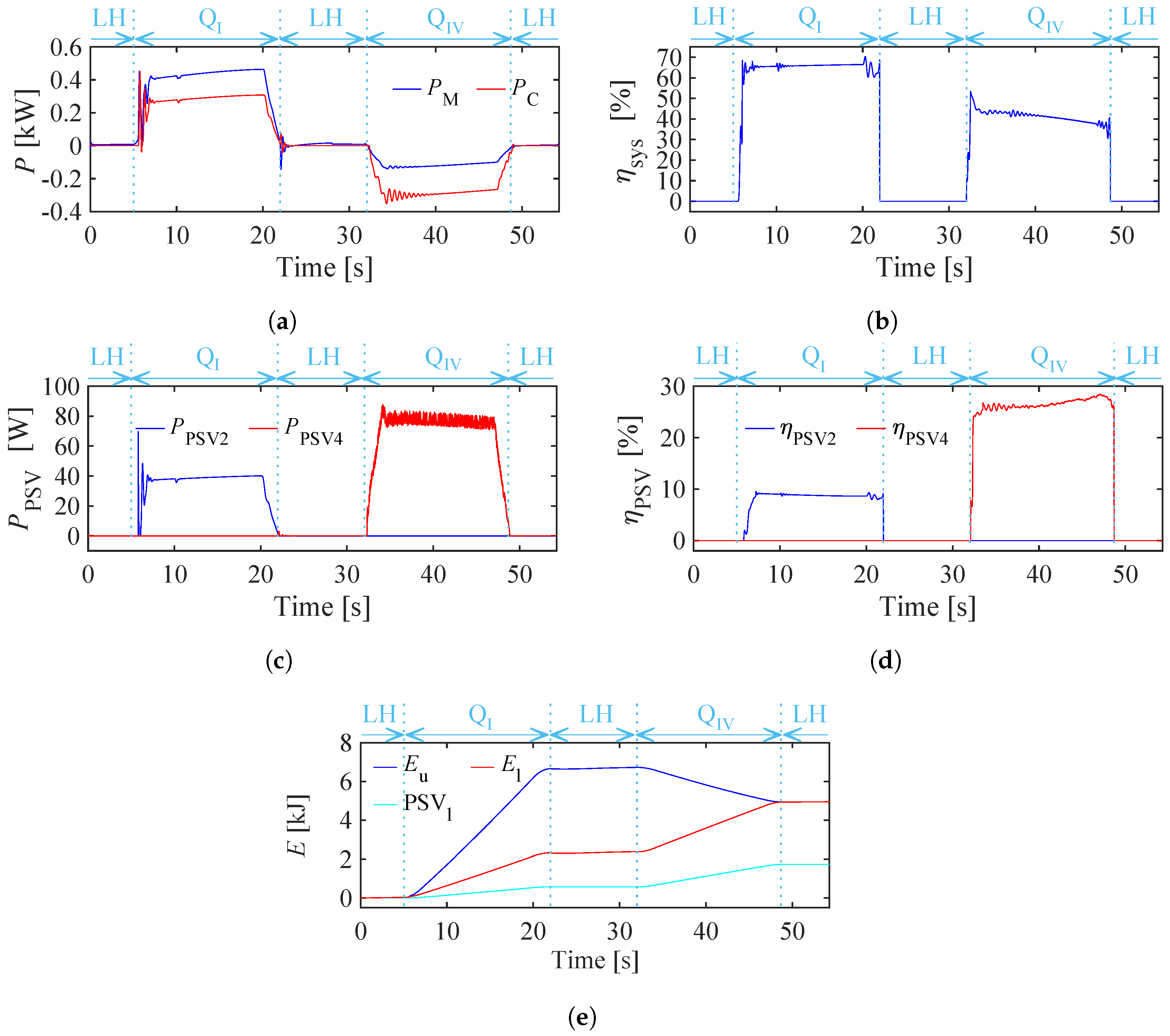
As described in Section 5.3, the PSVs in the 1M1P MCC cause energy losses ranging from 8% to 26%, depending on the specific operational conditions. These losses are due to the throttling losses in the PSVs. It is important to note that the energy losses in PSVs remain independent of the output powers. Additionally, in scenario A, the highest working pressure is below 60 bar, considerably lower than typical industrial applications. Consequently, with increased load and output power, the proportion of PSV losses is expected to diminish significantly. In contrast, there were no throttling losses in the 2M2P MCC investigated in [18]. This 2M2P MCC used the same load-holding circuit. Therefore, in theory, it has higher system energy efficiency than the proposed 1M1P MCC. Additionally, since no valves are required to compensate for the cylinder differential flow rate, the issue of pump mode oscillation does not arise in 2M2P MCCs.

The proposed 1M1P MCC surpasses the 2M2P MCC in [18] because of its superior suitability for four-quadrant operation. In the proposed 1M1P MCC, the electric servo motor and hydraulic pump/motor unit effectively contribute to the cylinder’s output power in ${\mathrm{Q}}_{\mathrm{I}}$ and ${\mathrm{Q}}_{\mathrm{III}}$ or engage in power regeneration in ${\mathrm{Q}}_{\mathrm{II}}$ and ${\mathrm{Q}}_{\mathrm{IV}}$. In contrast, the 2M2P MCC’s secondary electric servo motor and hydraulic pump/motor unit can only contribute to the cylinder’s output power in ${\mathrm{Q}}_{\mathrm{I}}$ or engage in power regeneration in ${\mathrm{Q}}_{\mathrm{IV}}$ [18]. Additionally, the secondary electric servo motor’s rated power in the 2M2P MCC must be greater than the main electric servo motor’s power because of the system pressure control [18]. Consequently, when significant cylinder output power in ${\mathrm{Q}}_{\mathrm{III}}$ is required, an applicable 2M2P MCC becomes more costly and significantly larger than a 1M1P MCC. Therefore, the 2M2P MCC is more suitable for operations only in ${\mathrm{Q}}_{\mathrm{I}}$ and ${\mathrm{Q}}_{\mathrm{IV}}$.

The proposed control algorithm holds promise for application to other motor-controlled cylinders featuring a similar load-holding mechanism. However, adjustments are necessary to tailor the algorithm to accommodate varying numbers of hydraulic pumps and electric motors utilized in different setups. Moreover, while this paper introduces a novel concept in motor-controlled cylinder structures, the robustness and limitations of the control algorithm remain to be extensively explored. Further research efforts are needed in this regard.

7. Conclusions

Realizing a fully hydraulically driven passive load-holding function coping with standstill command, power blackout, and hose rupture presents significant challenges in a regular 1M1P MCC. This paper proposes a novel 1M1P MCC to overcome these challenges through the following key aspects:

• A novel 1M1P MCC with a fully hydraulically driven passive load-holding function was implemented in simulations on a laboratory single-boom crane. The system’s operation and passive load-holding modes in all four quadrants and its capability to mitigate pump mode oscillation were extensively analyzed.
• A dynamic model of the proposed 1M1P MCC was developed, and a control algorithm was designed. This control algorithm consists of three control loops to achieve precise control over the piston position and system pressures and a smooth transition between different modes.
• The position tracking error is within ±2 mm in ${\mathrm{Q}}_{\mathrm{I}}$ and ${\mathrm{Q}}_{\mathrm{IV}}$ and within ±3 mm in ${\mathrm{Q}}_{\mathrm{II}}$ and ${\mathrm{Q}}_{\mathrm{III}}$. The error peaks occur during the transition between the operation and load-holding modes. The system pressure to open the load-holding valves is well controlled at around 15 bar. The load-holding function is performed under the standstill command, power blackout, and hose rupture situations.
• The overall system energy efficiency is about 66% when the hydraulic pump/motor unit is in pumping mode (${\mathrm{Q}}_{\mathrm{I}}$) and 41% when the hydraulic pump/motor unit is in energy regeneration mode (${\mathrm{Q}}_{\mathrm{IV}}$). PSVs cause around 8% energy loss in ${\mathrm{Q}}_{\mathrm{I}}$ and around 26% energy loss in ${\mathrm{Q}}_{\mathrm{IV}}$.
• The advantages and disadvantages of the proposed 1M1P MCC are discussed in comparison to a 2M2P MCC with equivalent functionality. It is found that the proposed 1M1P MCC is more suitable than the 2M2P MCC for four-quadrant operation. However, the inclusion of PSVs in the proposed 1M1P MCC leads to a minor level of energy losses.

In conclusion, the simulation results presented in this paper verify the effectiveness of the functionality of the 1M1P MCC and the proposed control algorithm. This technique holds promise for various industrial applications, particularly those necessitating four-quadrant operation and seamless transitions between motion and load-holding modes, such as industrial cranes and pitch angle control systems for wind turbines. Future work will cover a coupling analysis between the position control and the system pressure control, exploring the robustness and limitations of the control algorithm and conducting experimental tests to validate the simulation results.