FCS-MPC Based on Dimension Unification Cost Function
Abstract
1. Introduction
2. Predictive Mode of a NPC Three-Level Inverter with Induction Motor Load
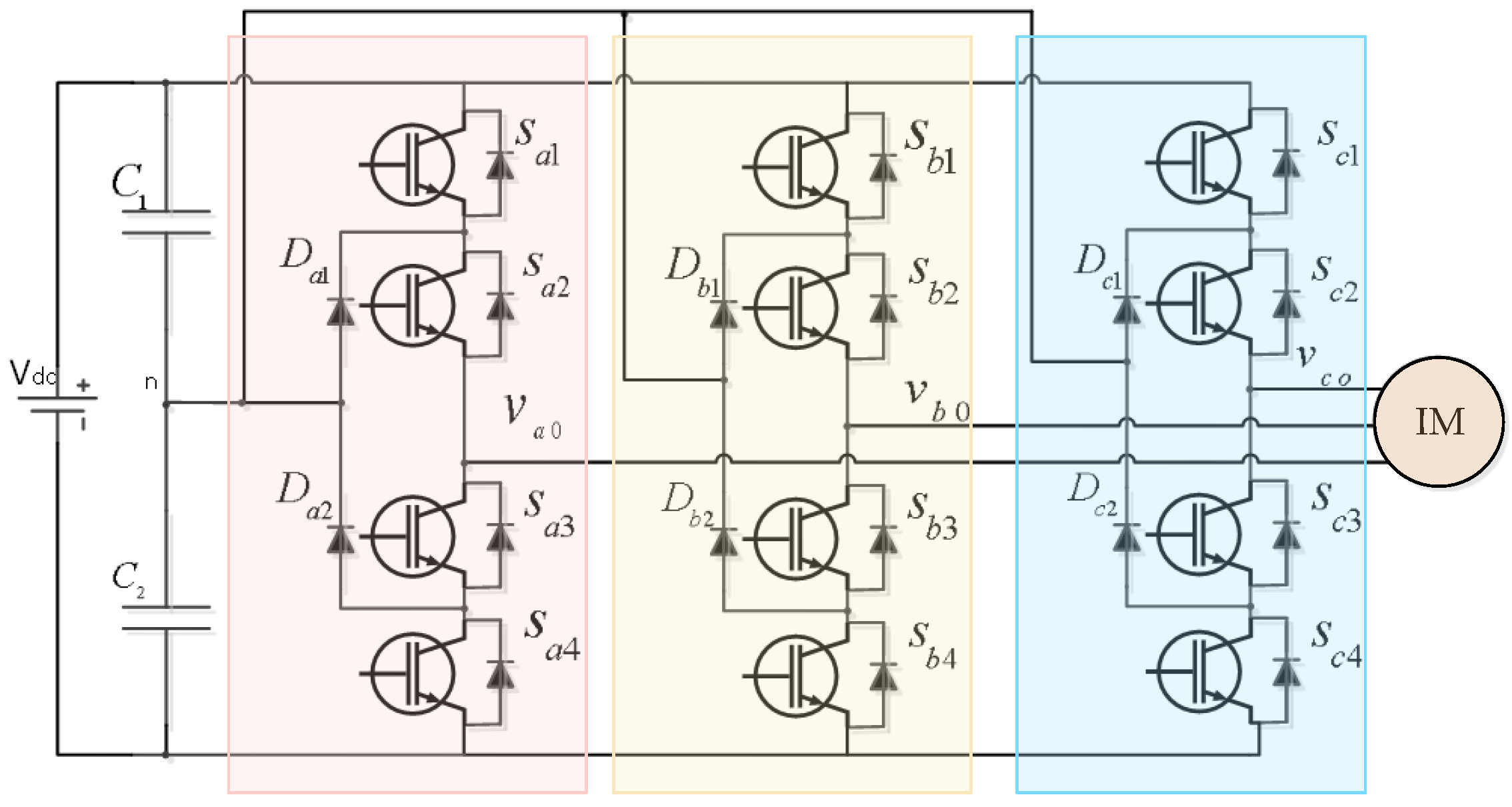
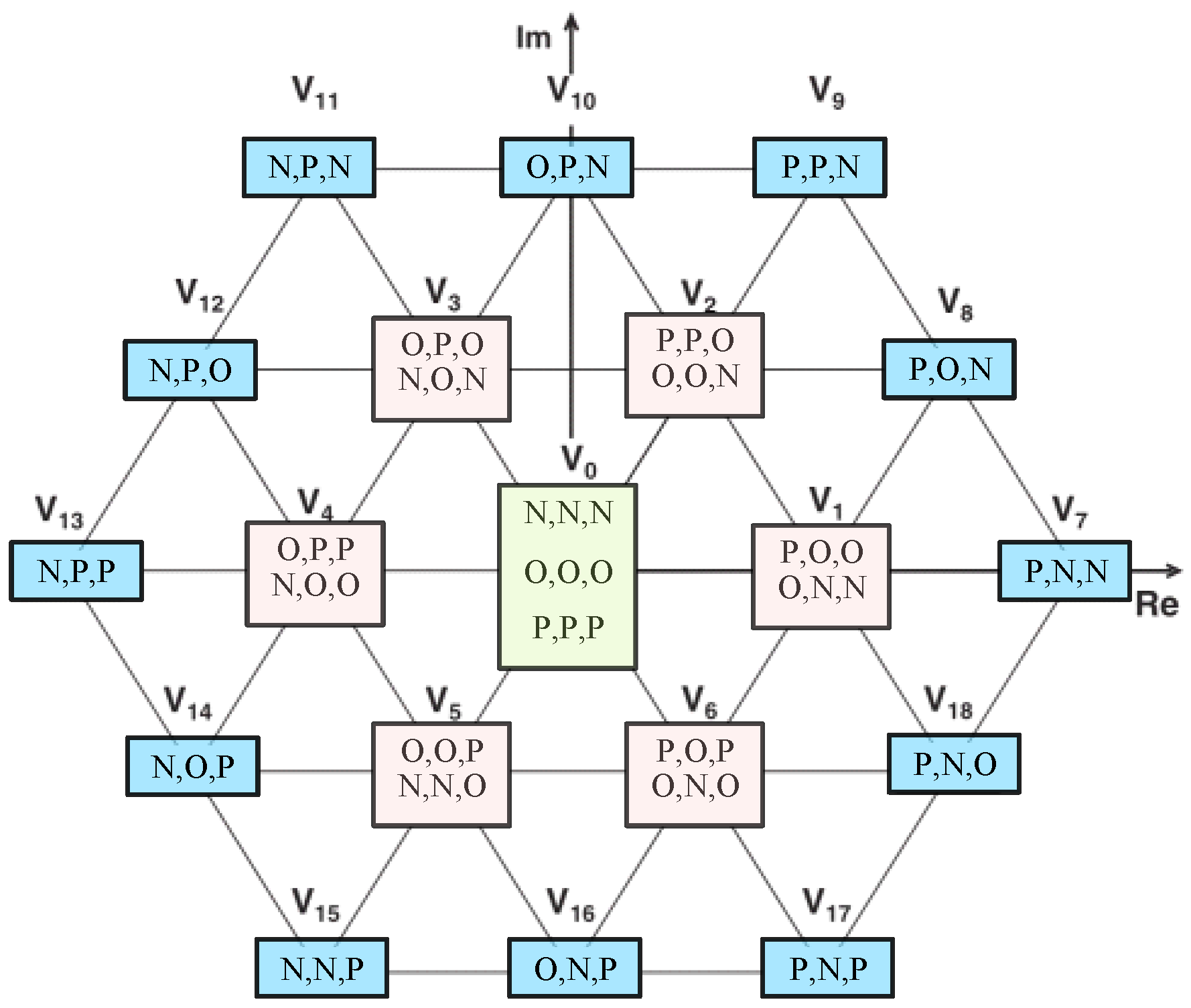
2.1. Mathematical Model of a NPC Three-Level Inverter
- (1)
- State P: Switches Sa1 and Sa2 conduct simultaneously, while switches Sa3 and Sa4 are both off. In this state, Vao = Vdc/2.
- (2)
- State O: Switches Sa2 and Sa3 conduct simultaneously, while switches Sa1 and Sa4 are both off. In this state, Vao = 0.
- (3)
- State N: Switches Sa3 and Sa4 conduct simultaneously, while switches Sa1 and Sa2 are both off. In this state, Vao = −Vdc/2.
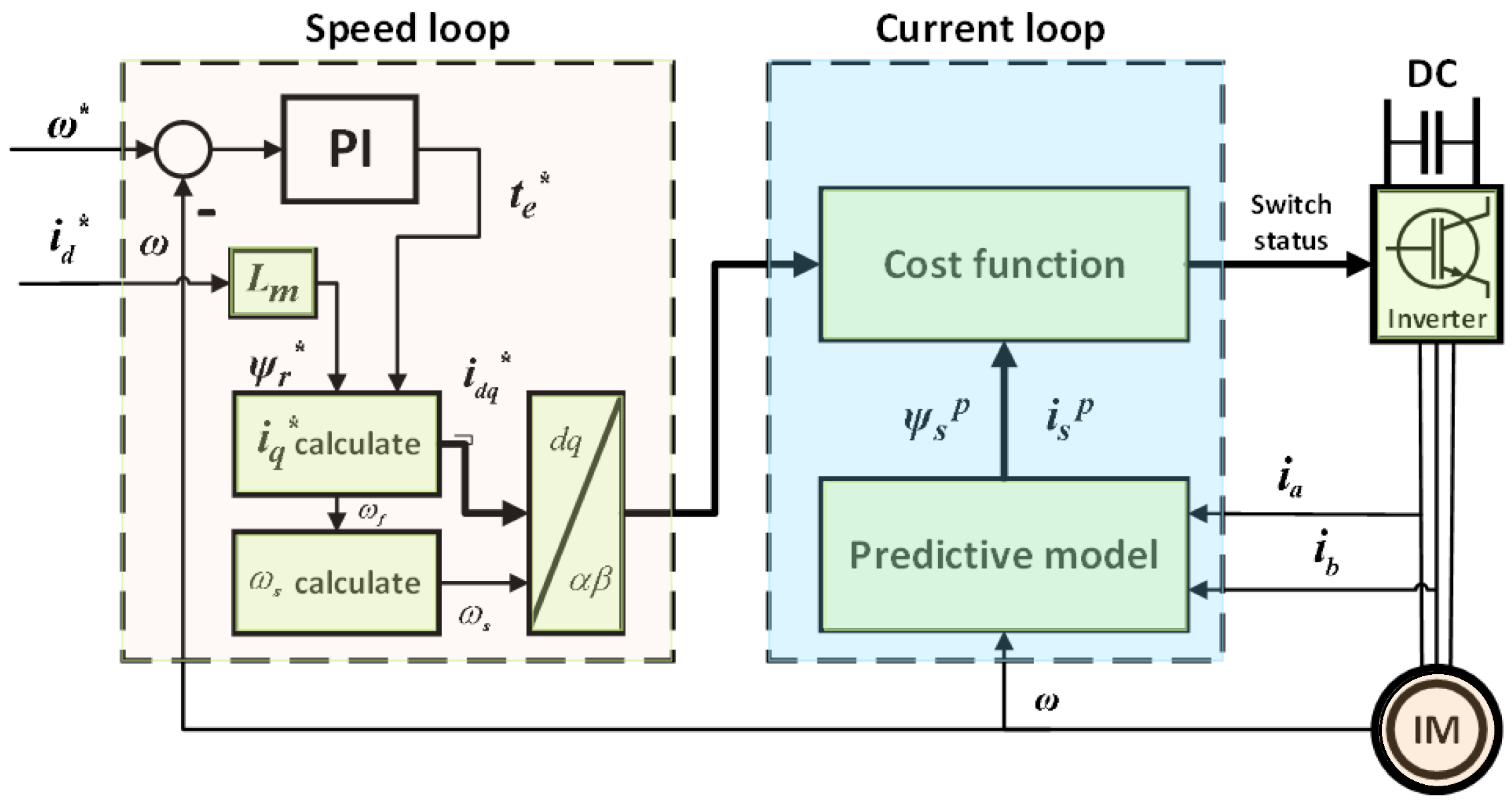
2.2. Traditional Model Predictive Current Control
2.3. Traditional Design Methods for Switching Frequency Weighting Coefficients
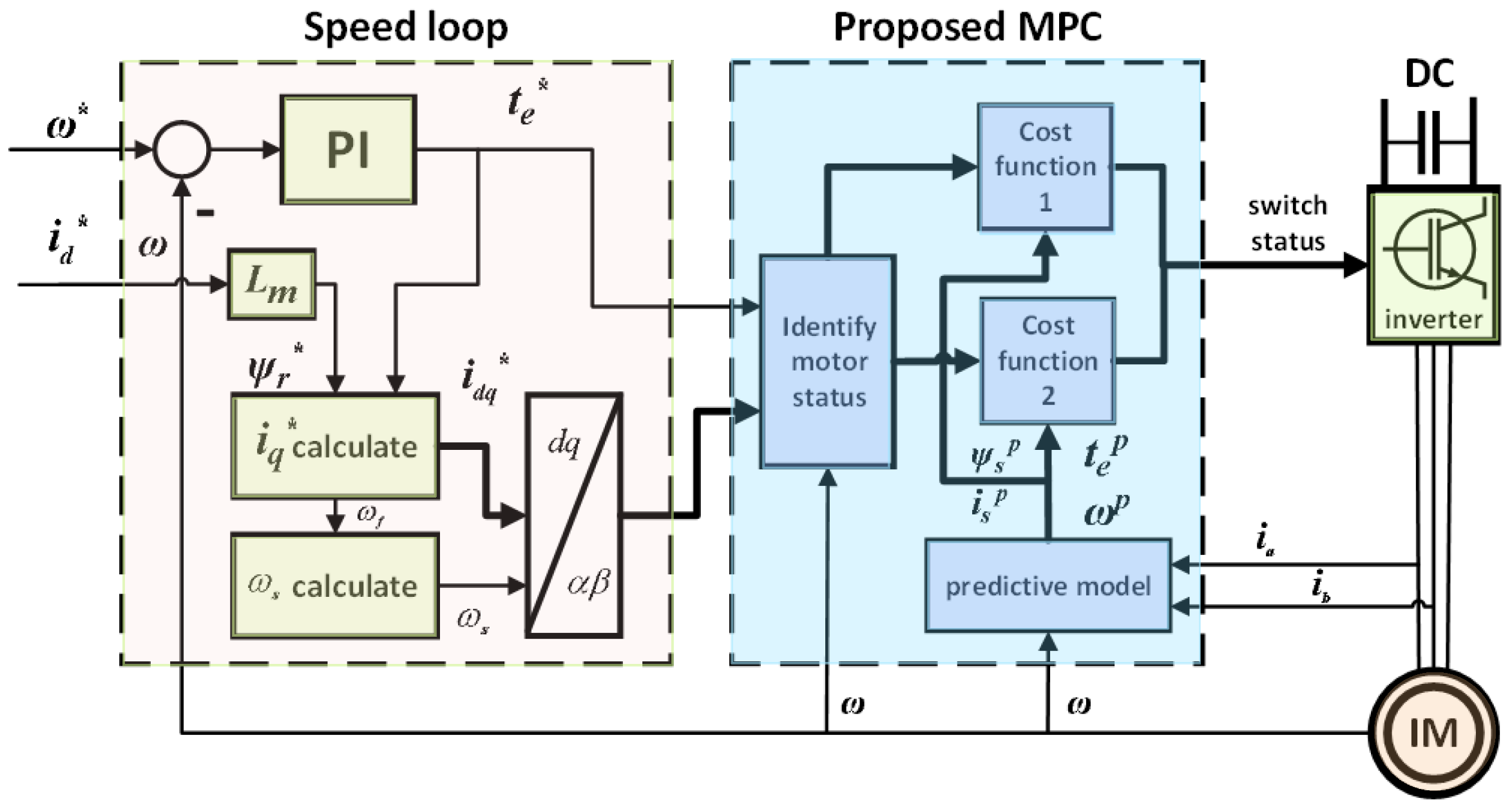
3. Proposed Improved Cost Function Design Method
3.1. Proposed Method for Weighting Coefficient Design with Unified Dimensions
3.2. Proposed Composite Cost Function for Model Predictive Control
4. Simulation and Experimental
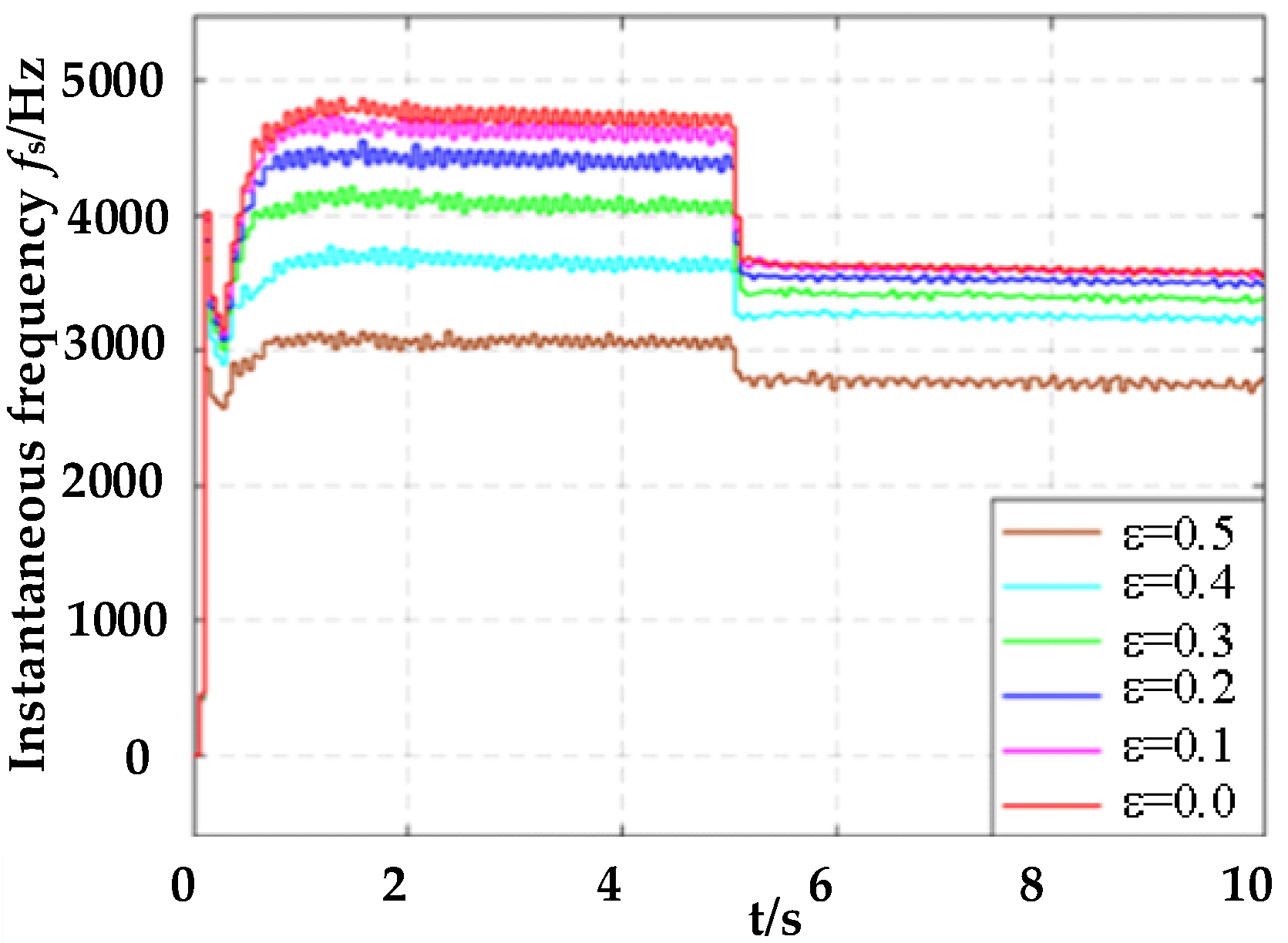
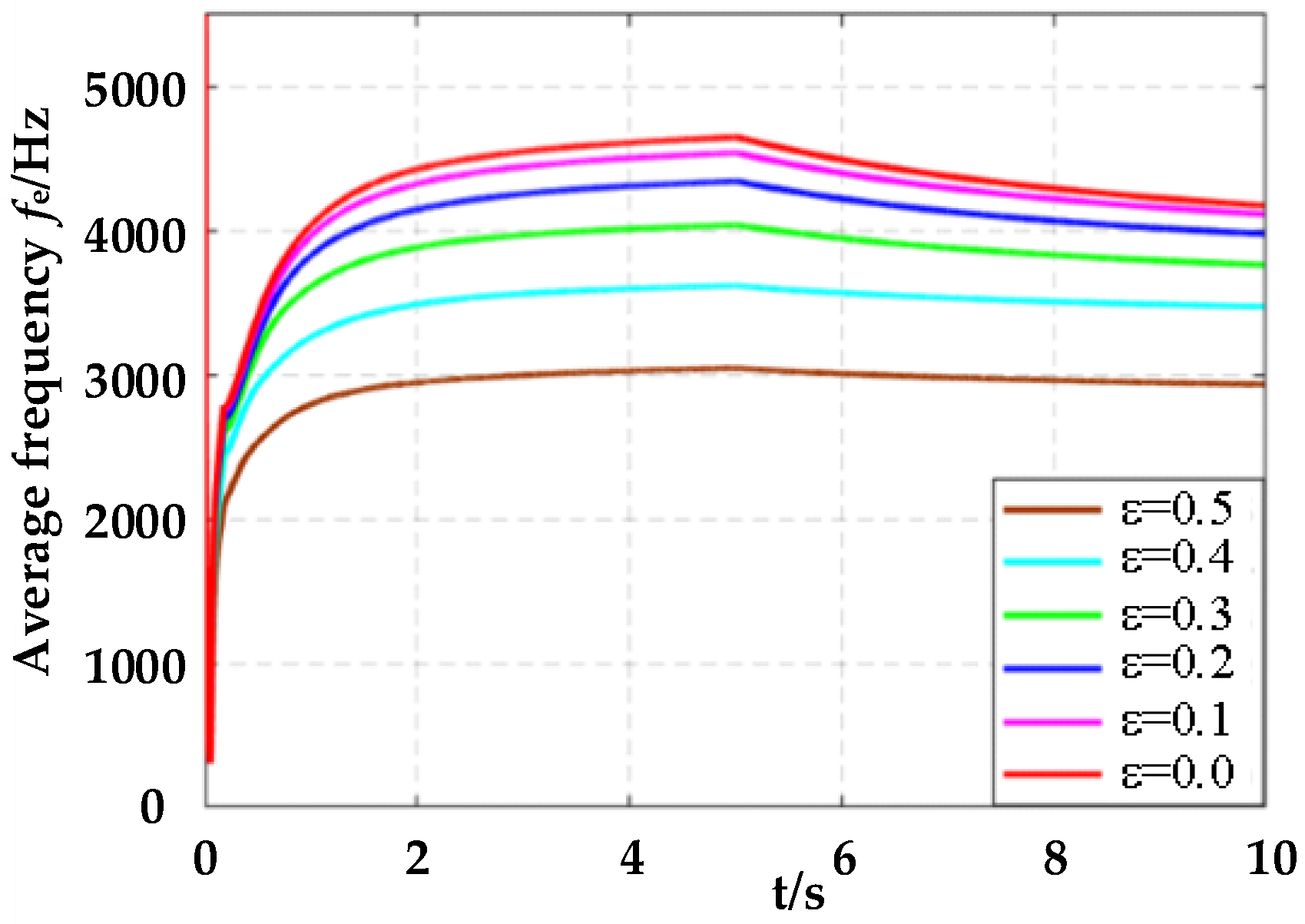
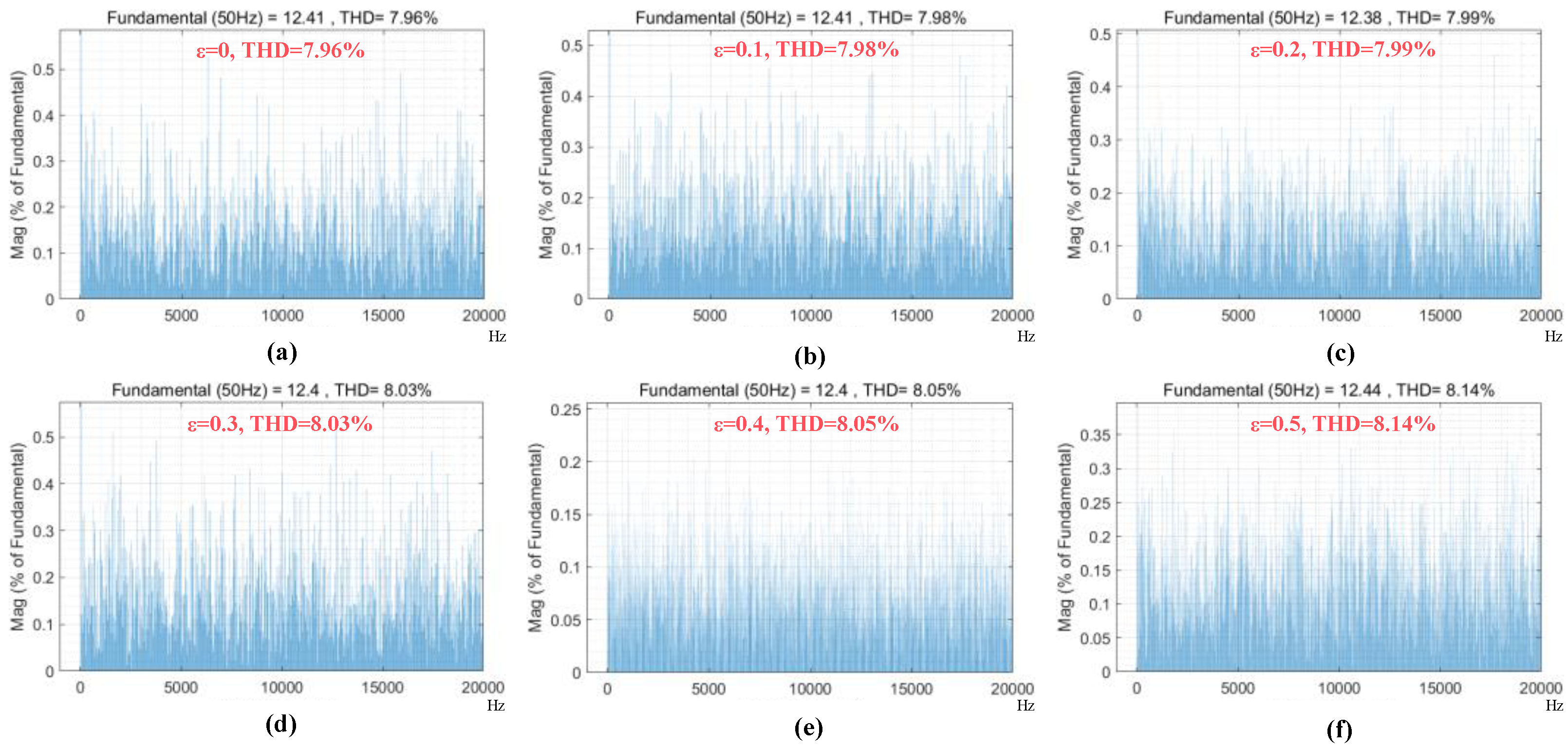
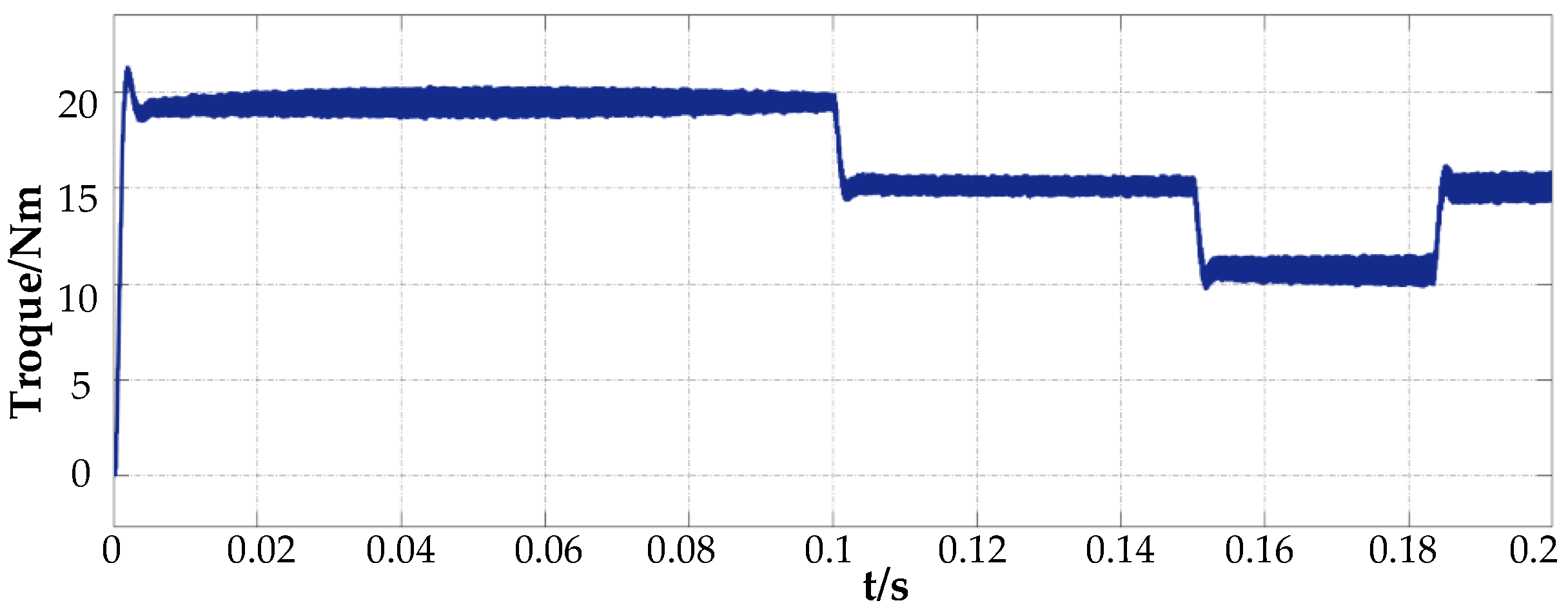
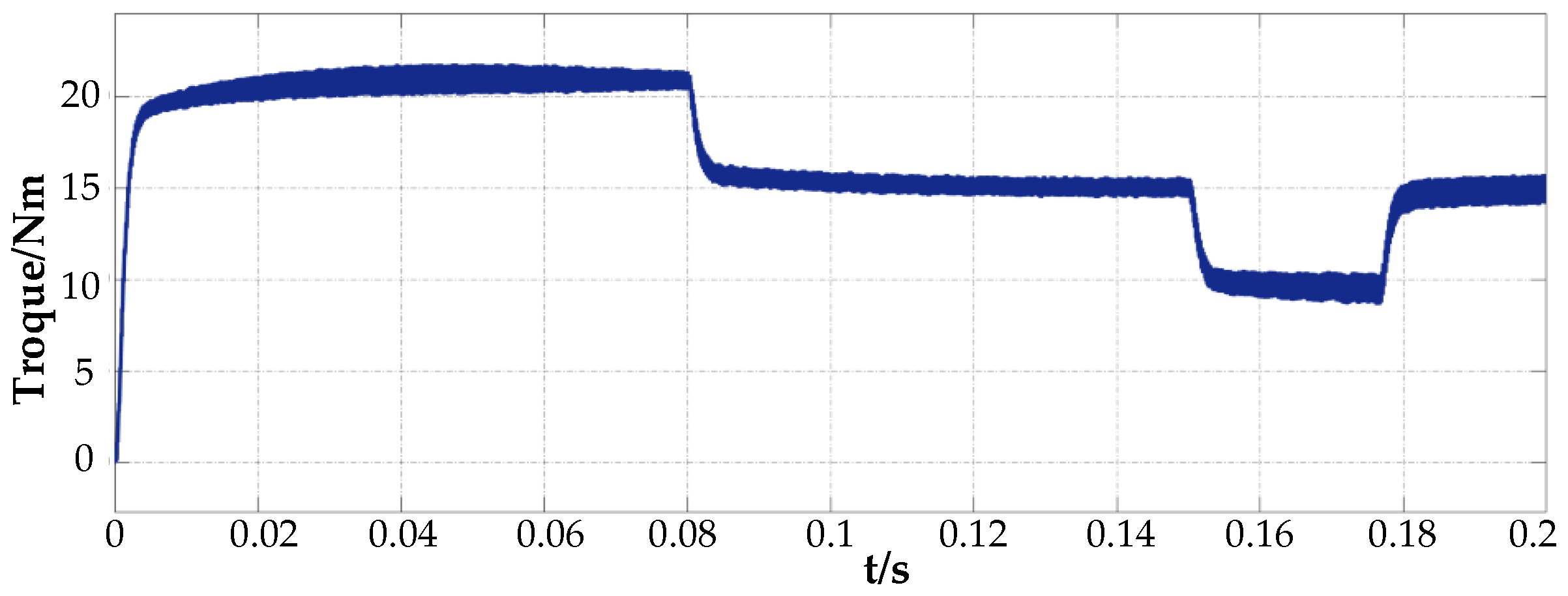
4.1. Simulation Verification of the Proposed Method
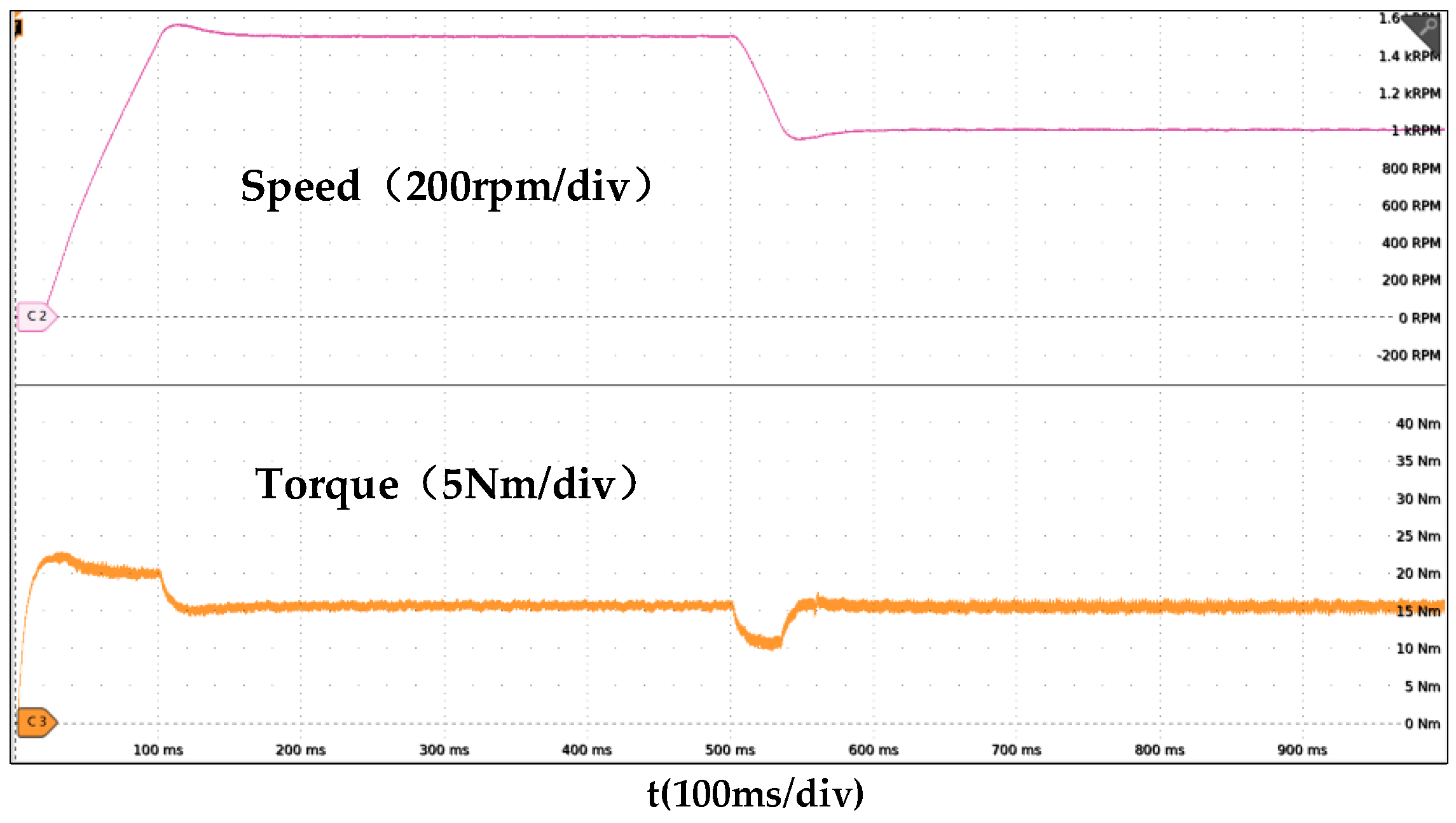
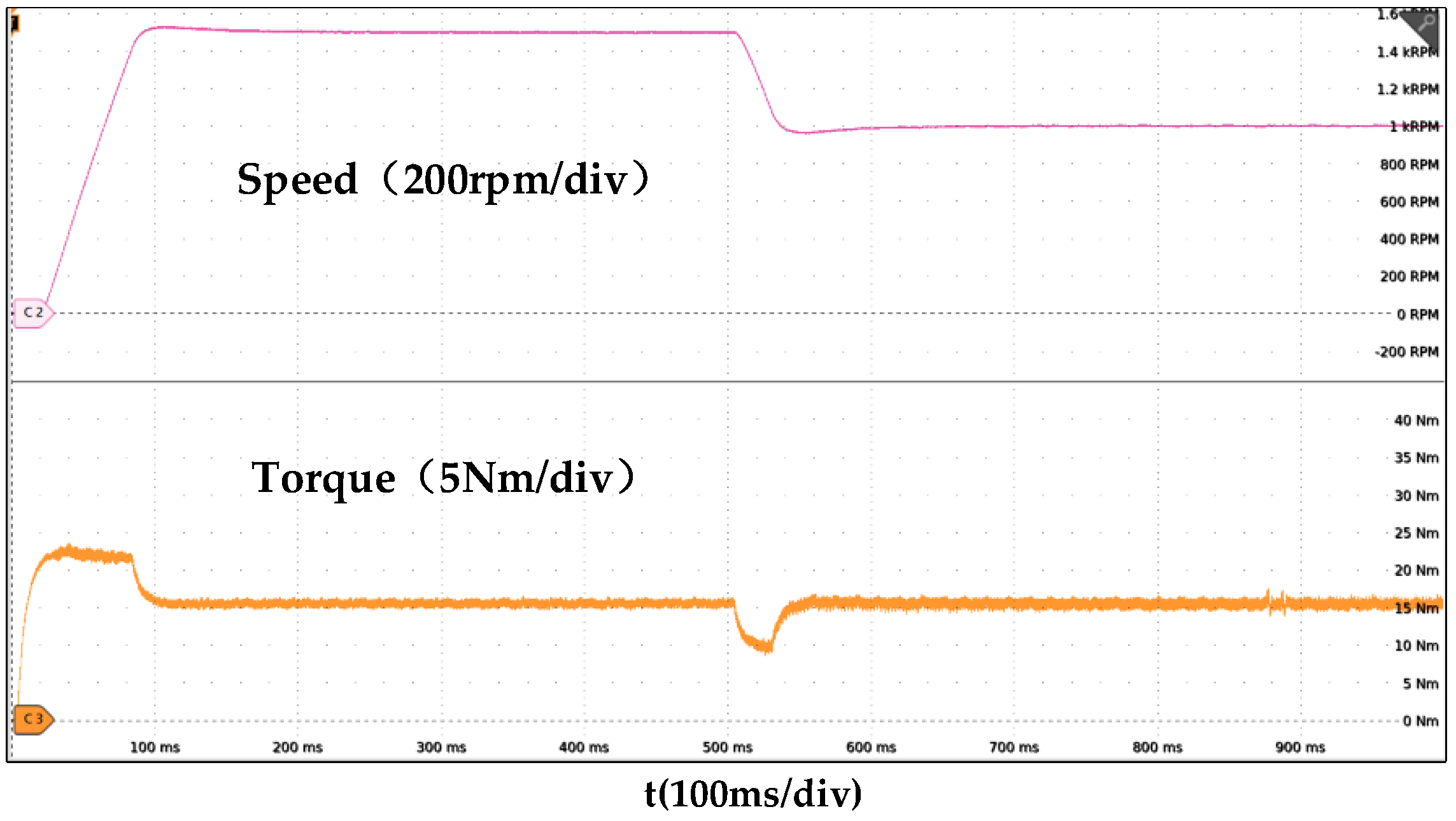
4.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Ma, Z.; Niu, H.; Huang, J.; Lin, G. Finite-Control-Set Model-Predictive Control with Data-Driven Switching Frequency Control for Single-Phase Three-Level NPC Rectifiers. IEEE Trans. Ind. Electron. 2024, 71, 7180–7189. [Google Scholar] [CrossRef]
- De Martin, I.D.; Brosch, A.; Tinazzi, F.; Zigliotto, M. Continuous Control Set Model Predictive Torque Control with Minimum Current Magnitude Criterion for Synchronous Motor Drives. IEEE Trans. Ind. Electron. 2023, 71, 6787–6796. [Google Scholar] [CrossRef]
- Zhao, B.; Li, H.; Mao, J. Double-Objective Finite Control Set Model-Free Predictive Control with DSVM for PMSM Drives. J. Power Electron. 2019, 19, 168–178. [Google Scholar]
- Yang, Q.; Karamanakos, P.; Liegmann, E.; Tian, W.; Geyer, T.; Kennel, R.; Heldwein, M.L. A Fixed Switching Frequency Direct Model Predictive Control for Neutral-Point-Clamped Three-Level Inverters with Induction Machines. IEEE Trans. Power Electron. 2023, 38, 13703–13716. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, S.; Ren, G.; Yao, C.; Ma, G.; Jatskevich, J. Weighting-Factor-Less Model Predictive Control with Multiobjectives for Three-Level Hybrid ANPC Inverter Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4726–4738. [Google Scholar] [CrossRef]
- Bao, G.; Qi, W.; He, T. Direct Torque Control of PMSM with Modified Finite Set Model Predictive Control. Energies 2020, 13, 234. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Mei, X.; Rodriguez, J.; Kennel, R. Advanced Control Strategies of Induction Machine: Field Oriented Control, Direct Torque Control and Model Predictive Control. Energies 2018, 11, 120. [Google Scholar] [CrossRef]
- Feng, S.; Wei, C.; Lei, J. Reduction of Prediction Errors for the Matrix Converter with an Improved Model Predictive Control. Energies 2019, 12, 3029. [Google Scholar] [CrossRef]
- Bakini, H.; Mesbahi, N.; Kermadi, M.; Mekhilef, S.; Zahraoui, Y.; Mubin, M.; Seyedmahmoudian, M.; Stojcevski, A. An Improved Mutated Predictive Control for Two-Level Voltage Source Inverter with Reduced Switching Losses. IEEE Access 2024, 12, 25797–25808. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.; Lei, G.; Guo, Y.; Yang, Z.; Zhu, J. Finite-Control-Set Model Predictive Control of Permanent Magnet Synchronous Motor Drive Systems—An Overview. IEEE/CAA J. Autom. Sin. 2022, 9, 2087–2105. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Z.; Hua, W.; Wang, Z.; Cheng, M. Simplified Model Predictive Current Control of Primary Permanent-Magnet Linear Motor Traction Systems for Subway Applications. Energies 2019, 12, 4144. [Google Scholar] [CrossRef]
- Arahal, M.R.; Barrero, F.; Satué, M.G.; Ramírez, D.R. Predictive Control of Multi-Phase Motor for Constant Torque Applications. Machines 2022, 10, 211. [Google Scholar] [CrossRef]
- Arahal, M.R.; Barrero, F.; Durán, M.J.; Ortega, M.G.; Martín, C. Trade-offs analysis in predictive current control of multi-phase induction machines. Control Eng. Pract. 2018, 81, 105–113. [Google Scholar] [CrossRef]
- Abbaszadeh, A.; Khaburi, D.A.; Mahmoudi, H.; Rodríguez, J. Simplified Model Predictive Control with Variable Weighting Factor for Current Ripple Reduction. IET Power Electron. 2017, 10, 1165–1174. [Google Scholar] [CrossRef]
- Kowal G., A.; Arahal, M.R.; Martin, C.; Barrero, F. Constraint Satisfaction in Current Control of a Five-Phase Drive with Locally Tuned Predictive Controllers. Energies 2019, 12, 2715. [Google Scholar] [CrossRef]
- Arahal, M.R.; Satué, M.G.; Barrero, F.; Ortega, M.G. Adaptive Cost Function FCSMPC for 6-Phase IMs. Energies 2021, 14, 5222. [Google Scholar] [CrossRef]
- Lin, S.; Fang, X.; Wang, X.; Yang, Z.; Lin, F. Multiobjective Model Predictive Current Control Method of Permanent Magnet Synchronous Traction Motors with Multiple Current Bounds in Railway Application. IEEE Trans. Ind. Electron. 2022, 69, 12348–12357. [Google Scholar] [CrossRef]
- Davari, S.A.; Nekoukar, V.; Azadi, S.; Flores-Bahamonde, F.; Garcia, C.; Rodriguez, J. Discrete Optimization of Weighting Factor in Model Predictive Control of Induction Motor. IEEE Open J. Ind. Electron. Soc. 2023, 4, 573–582. [Google Scholar] [CrossRef]
- Kaymanesh, A.; Chandra, A.; Al-Haddad, K. Model Predictive Control of MPUC7-based STATCOM using Autotuned Weighting Factors. IEEE Trans. Ind. Electron. 2022, 69, 2447–2458. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T. Guidelines for the design of finite control set model predictive controllers. IEEE Trans. Power Electron. 2020, 35, 7434–7450. [Google Scholar] [CrossRef]



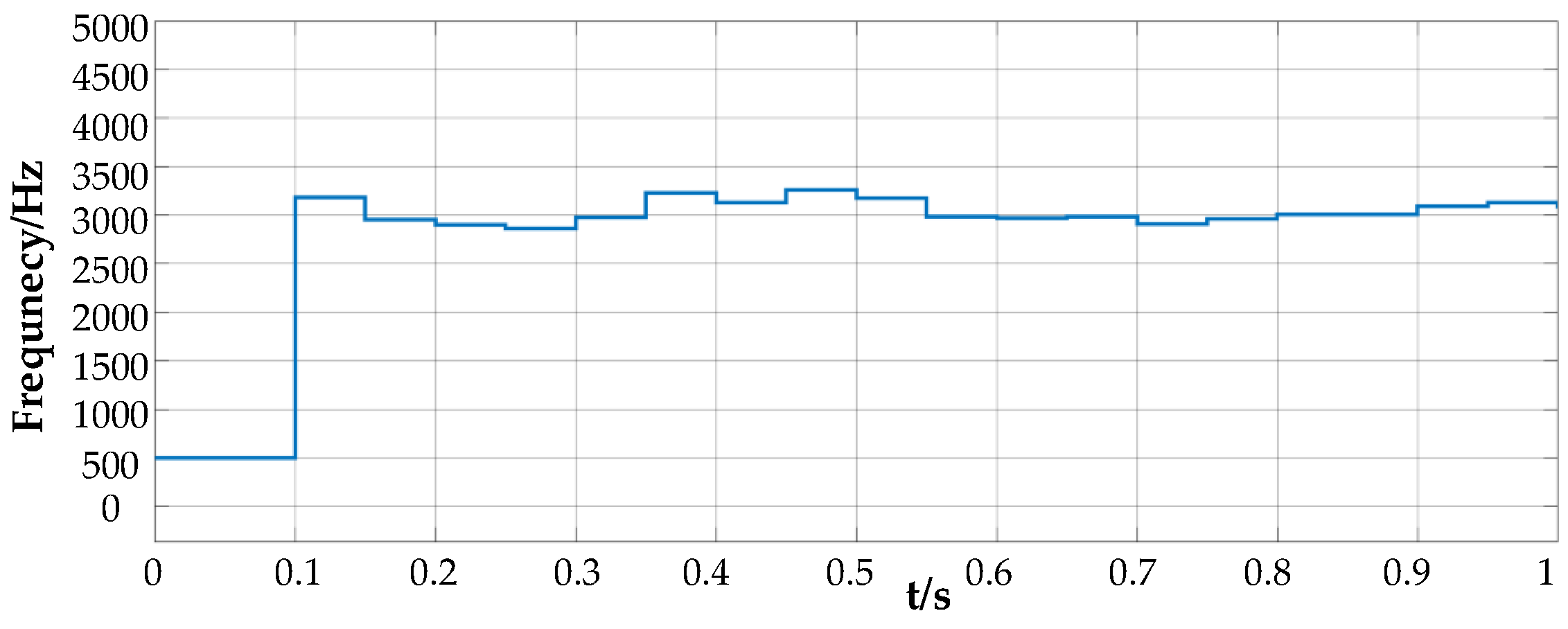
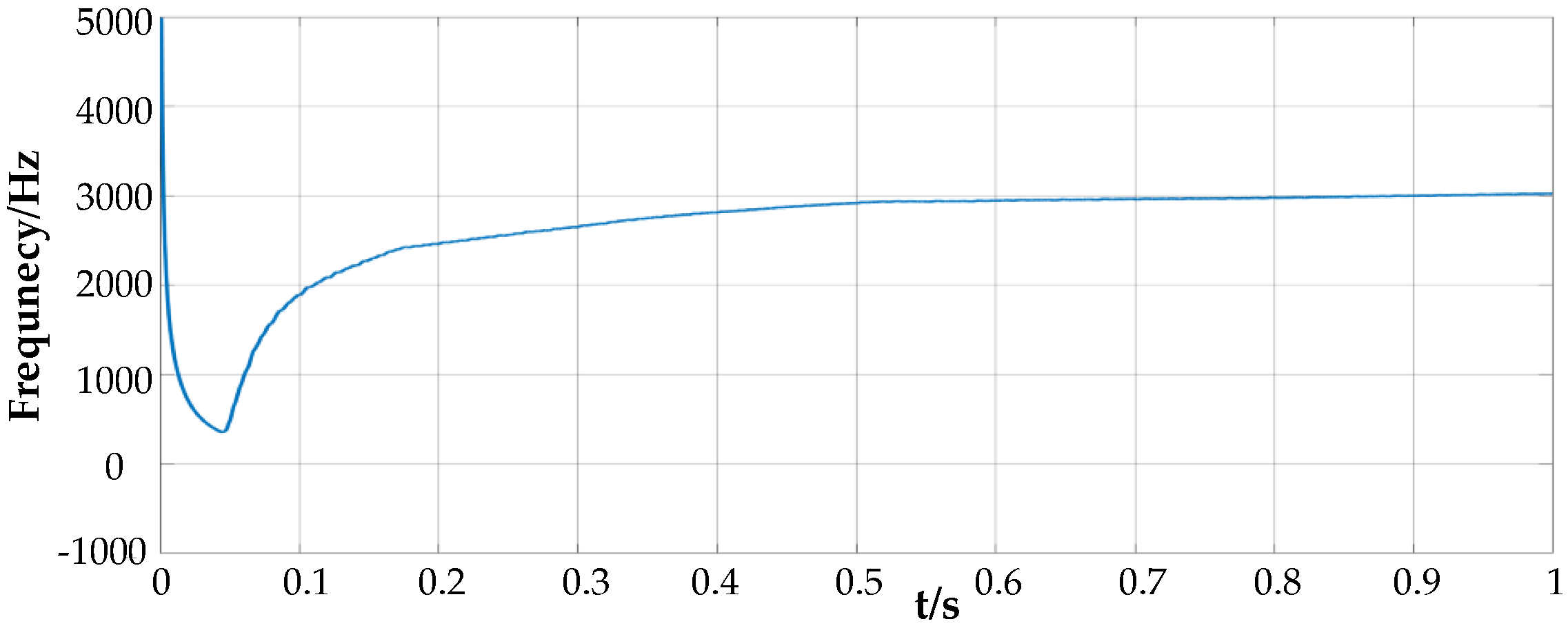
| Parameter | Value | Unit |
|---|---|---|
| Sampling period | 25 | μs |
| DC-Link voltage | 500 | Vdc/V |
| DC capacitor | 900 | μF |
| Rated Speed | 1500 | rpm |
| Stator resistance | 1 | Rs/Ω |
| Rotor resistance | 0.98 | Rr/Ω |
| Stator inductance | 0.00223 | Ls/H |
| Rotor inductance | 0.00224 | Lr/H |
| Mutual inductance | 0.002 | Lm/H |
| Pole pairs | 2 | - |
| Speed | ε = 0 | ε = 0.1 | ε = 0.2 | ε = 0.3 | ε = 0.4 | ε = 0.5 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| THD | fs | Loss | THD | fs | Loss | THD | fs | Loss | THD | fs | Loss | THD | fs | Loss | THD | fs | Loss | |
| Low Speed (300 rpm) | 7.93% | 1.4 | 9.298 | 7.94% | 1.35 | 9.199 | 7.97% | 1.31 | 9.105 | 8.00% | 1.24 | 9.113 | 8.05% | 1.19 | 8.909 | 8.07% | 1.15 | 8.589 |
| Medium Speed (900 rpm) | 7.94% | 3.8 | 10.311 | 7.94% | 3.75 | 10.254 | 7.98% | 3.7 | 10.102 | 7.97% | 3.5 | 10.032 | 8.01% | 3.4 | 9.899 | 8.10% | 2.8 | 9.582 |
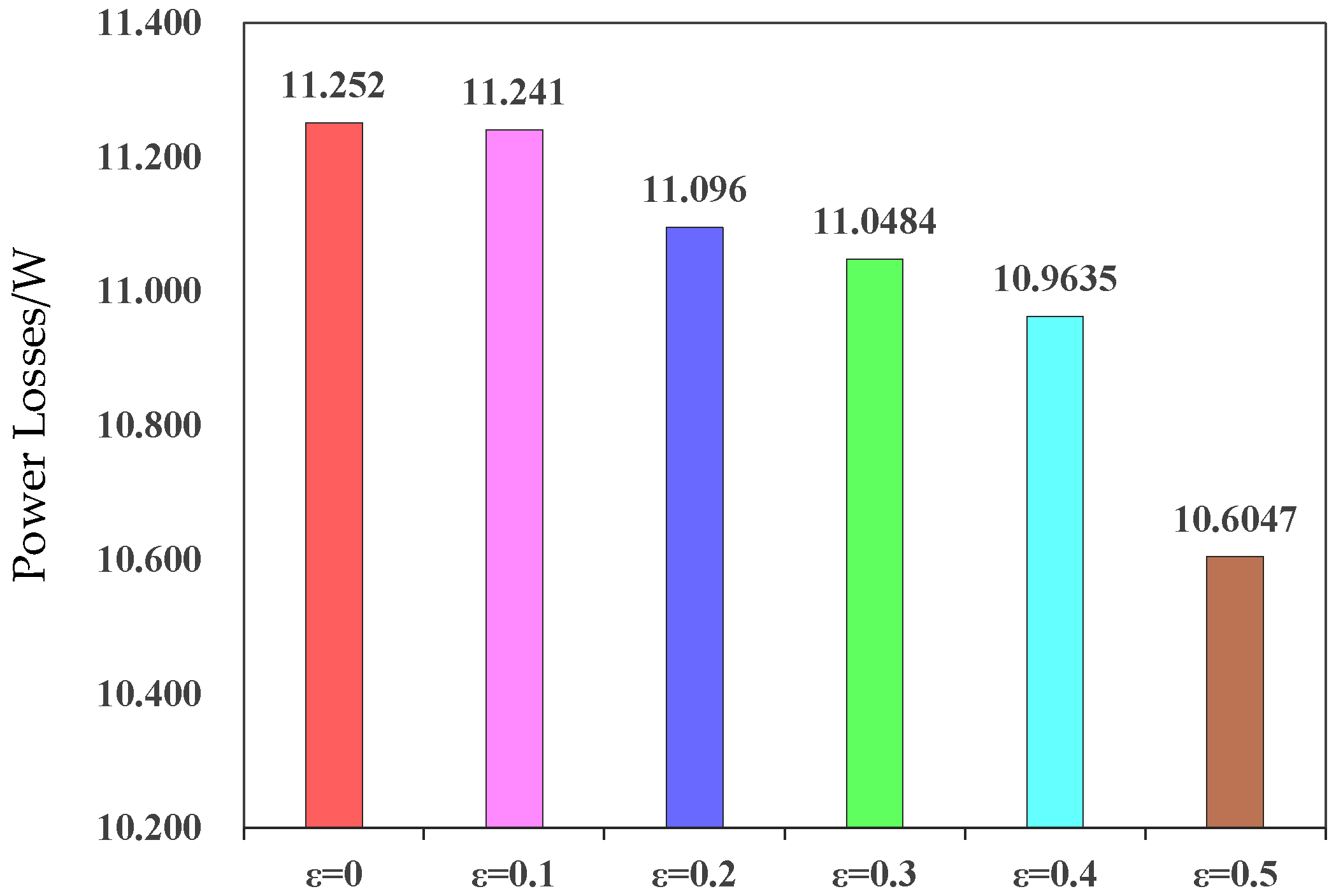
| High Speed (1500 rpm) | 7.96% | 4.8 | 11.252 | 7.98% | 4.7 | 11.241 | 7.99% | 4.5 | 11.096 | 8.03% | 4.1 | 11.048 | 8.05% | 3.7 | 10.964 | 8.14% | 3.0 | 10.605 |
 : fs ≤ 2 kHz;
: fs ≤ 2 kHz;  : 2 kHz < fs ≤ 4 kHz;
: 2 kHz < fs ≤ 4 kHz;  : fs > 4 kHz.
: fs > 4 kHz.Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Yuan, H.; Li, W.; Zhou, L.; Deng, C.; Yan, M. FCS-MPC Based on Dimension Unification Cost Function. Energies 2024, 17, 2479. https://doi.org/10.3390/en17112479
Han J, Yuan H, Li W, Zhou L, Deng C, Yan M. FCS-MPC Based on Dimension Unification Cost Function. Energies. 2024; 17(11):2479. https://doi.org/10.3390/en17112479
Chicago/Turabian StyleHan, Jinyang, Hao Yuan, Weichao Li, Liang Zhou, Chen Deng, and Ming Yan. 2024. "FCS-MPC Based on Dimension Unification Cost Function" Energies 17, no. 11: 2479. https://doi.org/10.3390/en17112479
APA StyleHan, J., Yuan, H., Li, W., Zhou, L., Deng, C., & Yan, M. (2024). FCS-MPC Based on Dimension Unification Cost Function. Energies, 17(11), 2479. https://doi.org/10.3390/en17112479






