Abstract
In recent years, various solutions have been developed to control power electronic converters using devices available on the market that are powerful and easy to use. These solutions, in most cases, offer high performance. However, these have high implementation costs because the required devices are expensive. For this reason, this document presents the implementation of two discrete-time controllers widely used in the literature for a boost converter implemented on a low-cost platform. The objective is to obtain a constant voltage at the converter’s output for photovoltaic system applications. The proportional-integral control is implemented as the first case, and the second case is a sliding mode control. In addition, a prior analysis is presented through simulation. Both control algorithms are implemented on the TMS320F28379D microcontroller from Texas Instruments through the same manufacturer’s integrated development software based on an optimized C/C++ language compiler. The results of the non-linear algorithm reveal better performance in reducing the time response, the overshoot of the transient state, and the steady-state error. Finally, the significant economic savings associated with the implementation costs of the controllers tested on a low-cost platform differentiate this work from other similar ones.
1. Introduction
For some practical applications, electricity, whether alternating current (AC) or direct current (DC), is intended to be converted from one form to another, such as AC-DC, DC-AC, AC-AC, or DC-DC. Therefore, techniques and devices must be required to facilitate this task. The emergence of semiconductor switches resulted in power electronics [].
Power electronics are critical tools for achieving efficient energy conversion; approximately 70% of electricity is converted by power electronic devices before reaching users []. Power electronic converters play a fundamental role in efficiently using renewable energy and its various applications [].
The boost-type power converter is a device that operates through the closing and opening of a switch. It is known as a booster because the output voltage is always higher than the input voltage. For this reason, the boost converter is usually used in low-voltage applications like photovoltaic systems [].
The design of control systems for power electronic converters is an exciting challenge because these are non-linear and time-variant systems. For this, small-signal linearized mathematical models have been developed, facilitating the application of classic controls such as PI control []. However, the main disadvantage of linear models and controllers is that this only guarantees that the system functions correctly at intervals of the operating point [].
There are other approaches, such as sliding mode control, where the non-linear characteristics of the plant are used for the design of the controller []. This control approach has been most applied to power electronic converters [].
With the invention of digital circuits, it is increasingly common to migrate from continuous to discrete-time design []. The main advantages of applying digital control instead of analog control are lower measurement error, reduced implementation errors due to variations in control system parameters, greater flexibility to make changes after implementing the controller, higher-speed hardware, and decreased device costs [].
Digital control-oriented hardware has recently been developed for closed and expensive platforms. However, open-source and hardware alternatives are currently in full swing, enabling the development of new low-cost platforms and products. These aspects greatly benefit the research community because users can add and modify hardware devices, thus making the system more flexible [].
In recent years, different devices have been developed to implement digital control. One of the most relevant is the dSPACE due to its versatility in controlling power electronic converters []. OPAL-RT is another alternative for both real-time simulation and testing for rapid prototyping control (RPC) []. Furthermore, devices with similar features like BoomBox, RT-BOX, PED-Board, or HIL404 are available on the market. Most of these are closed software and hardware solutions, which makes them expensive and less flexible for specific purposes []. Low-cost hardware alternatives are the Texas Instruments microcontrollers. One of the most used is the LAUNCHXL-F28379D, a low-cost evaluation and development tool that provides a standardized integrated development environment (IDE) and is easy to use [].
There is a variety of work related to controlling power electronic converters, such as in [], in which an analysis of a boost converter was performed to design a PI control that fulfills the function of reducing harmonics in the output voltage of a converter; the validation of this controller is conducted through simulation using the Matlab/Simulink software. As in [], the aim is to regulate the voltage at the output of a boost converter that employs a sliding mode control (SMC) where the inductor current and the desired current value determine the sliding surface. A second control loop (in this case, a PI controller), determines the desired current value. The results are validated by simulation and experimentation to evaluate the performance of a boost converter that increases a low DC voltage to a level of 400 volts DC. In [], a performance analysis is conducted on a high-power converter, and a control strategy is presented where an external PI control loop is used for voltage regulation and an internal loop for current control using a proportional-plus-integral compensator. The validation of the results is presented through simulation and experimentation. In [], two control systems are proposed to achieve a proportional distribution of the load power between modular distributed generators (DGs) connected to inverters with standard AC and DC buses in isolated AC microgrids. System validation was completed through simulation and implementation.
There are also works related to the design and implementation of digital controllers, such as [], in which a digital controller is obtained for a boost converter to store thermoelectric energy, with a higher efficiency of 15% compared to other articles in the literature. Alternatively, as in [], a digital controller is developed for a DC-DC boost converter in continuous conduction mode (CCM). That is implemented on an FPGA through output voltage sensing and inductor current estimation.
Works can be found in the literature in the field of control design and implementation in renewable energy applications. Like in [], a discrete adaptive proportional–Integral–Derivative (PID) controller applied to a boost power converter was proposed for regulating the output current of a 400-watt turbine, where the maximum power point is achieved without significant overshoots or oscillations. In [], a neural high-order sliding-mode (NHOSM) controller is developed for a wind turbine, and a comparison is made between its performance and that of a simple SMC.
In addition, the literature observes the implementation of digital controllers in various development platforms. For example, in [], a discrete-time current controller is implemented on a field-programmable gate array (FPGA) for the control of a boost converter. The environment used for programming is Quartus II Web Edition. In [], a discrete feedback control was implemented on the dSPACE 1104 control card for voltage regulation at a buck converter’s output using the ControlDesk 6.2 programming software. In [], a PID controller is designed to regulate the DC voltage output and avoid limit-cycle oscillation for a boost converter. It is implemented through the Xilinx (San Jose, CA, USA) FPGA VIRTEX-II PRO device (retired and no longer for sale by the manufacturer). In [], a water-pumping system powered by a photovoltaic system is shown. This system is chiefly composed of a boost converter, a solar panel, an inverter, and a dSPACE DS1104 control card, the latter overseeing the control and MPPT algorithm of the system; programming is conducted through a block diagram using the MATLAB tool “Simulink Coder”. In [], a performance comparison of the platforms TMS320F28379D microcontroller (included in LAUNCHXL-F28379D), dSPACE, and OPAL-RT is presented for the implementation of digital controllers in DC-AC converters; the programming of the algorithm is deployed using Simulink Coder. In [], a performance comparison is made between the LAUNCHXL-F28379D from Texas Instruments and the dSPACE 1006. In both, a model predictive control (MPC) is implemented to optimize the power of a photovoltaic system. The programming is conducted in the Simulink environment using a block diagram. In [], a digital controller is implemented in power electronic converters on the LAUNCHXL-F28379D MCU to show the use of rapid prototyping oriented to digital control for academic purposes; software PLECS is used to simulate and implement the control algorithm. In [], an experimental platform for microgrid analysis and control is presented. In this case, the physical system is implemented and validated using the OPAL-RT, which is used for rapid control prototyping. In [], an application example of digital control is shown, where a PED-Board is used to implement a field-oriented control (FOC) in a permanent magnet machine. The controller algorithm is performed using Lab-View software. In [], a novel graphical loop-shaping technique is presented. This technique controls an interleaved boost converter (IBC) and is implemented using the hardware Typhoon Hil 402.
Table 1 compares some of the most-used devices for digital control applications, and Table 2 compares the costs of some IDEs with tools to program digital control devices.

Table 1.
Comparison of devices available on the market used in digital control applications.

Table 2.
Price comparison between programming environments for digital control devices (individual license).
This document presents the cases of two discrete-time controllers implemented in a low-cost embedded card to regulate the voltage at the output of a DC-DC boost converter in continuous conduction mode. These control algorithms calculate a duty cycle value for the opening and closing of a switch using a pulse-width modulator (PWM). Simulations of these controllers in the event of possible disturbances are also presented. Finally, the results obtained through implementing the control algorithms in the plant are reported.
The controllers presented in this work are widely studied in the literature for a boost converter. However, the significant economic savings associated with the implementation costs of the controllers on a low-cost platform differentiate this paper from other similar ones reported in the literature.
The document’s content distribution is as follows: Section 2 presents the mathematical model of switched, large-signal averaged, small-signal averaged, and transfer functions of the DC-DC boost converter. Section 3 shows the case of a PI control discretized by the Forward Euler method. Section 4 explains the case of a discrete sliding-mode controller to achieve a sliding surface related to a desired current value and an external PI control loop that defines the desired current value based on a voltage reference value. Section 5 evaluates the controllers through simulation in the event of certain disturbances. Section 6 illustrates the devices involved, as well as the response of the controllers by implementing them in the TMS320F28379D MCU from Texas Instruments. Section 7 presents robustness tests for the controller that obtained the best simulation and implementation performance. Finally, Section 8 presents the conclusions regarding the design and implementation.
2. Mathematical Model
This section presents the mathematical models: switched, large-signal averaged, small-signal averaged, and transfer functions of the DC-DC-boost power converter. The topology of a DC-DC boost converter is presented in []. However, in the electrical circuit of the converter employed in this work, the parameters of the parasitic elements of the capacitor and inductor were added, as shown in Figure 1.
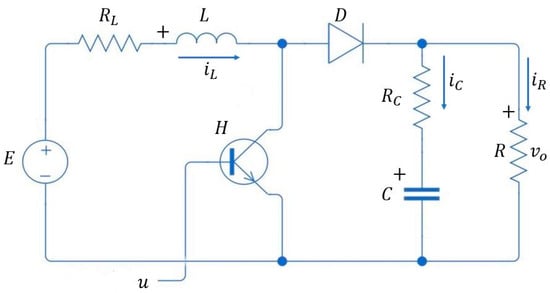
Figure 1.
Circuit of a DC-DC boost converter.
This circuit representation of the boost converter consists of a DC input source , a controlled metal oxide silicon field effect transistor (MOSFET) , a rectifier diode , a filtering inductor , a filtering capacitor , a load resistance , and the parameters of equivalent serial resistance (ESR) of the capacitor and the ESR of the inductor . Table 3 indicates the real values of the plant parameters.

Table 3.
System parameters.
2.1. Switched Model
Through the analysis presented in [], the switched model of the boost converter was obtained. In this document, the parameters of equivalent serial resistance of the capacitor and the ESR of the inductor are incorporated into the said analysis. This development is observed in (1)
where represents the inductor current, is the inductance value, is the capacitance value, is the supply voltage, is the resistive value of the load, is the capacitor voltage, and represents the control input (logic “1” when the switch is open and logic “0” when the switch is closed). The state space that represents this analysis is presented in (2)
where .
2.2. Large-Signal Averaged Model
From (2), an averaged model is proposed where the control input is changed by a duty cycle value . This representation is shown in (3).
2.3. Small-Signal Averaged Model
The small-signal averaged model shown in (4) is based on the analysis presented in []
where represents the averaged derivative of the inductor current at a steady state, is the inductor current at a steady state, is the capacitor voltage at a steady state, is the duty cycle in the steady state, is the average of the derivative of the capacitor voltage in the steady state, and , , and are the small variations of the duty cycle and the states and , respectively.
In order to obtain , , and , Equation (5) was used, which were obtained by solving the values of and from (1).
2.4. Transfer Functions
The plant transfer functions are found by replacing the parameters described in Table 3 in (4). In this case, the transfer functions were obtained for the voltage-duty cycle and current-duty cycle channels. The transfer functions (6) and (7) represent the linearized plant.
2.5. Mathematical Model in Discrete Time
A discretized boost-converter model is obtained from the continuous-time plant analysis presented in []. The discretization is conducted using the Forward Euler method, where it is considered that and . The discrete-time equations of the converter are shown in
where represents the switching period and , with being the sample number or index.
3. PI Controller
Proportional–Integral–Derivative (PID) control is the most used controller. It is estimated that around 90% of controllers use PID control, in many cases with derivative gain equal to zero (PI control) []. This section presents the case of a PI control system.
For the boost converter to have adequate performance in renewable energy applications, the following requirements for the PI controller were considered:
- Overshoot () no more than 5%.
- Transient state time () no longer than 100 milliseconds.
- Gain margin () greater than 10.
- Phase margin () between 45 and 60 degrees.
- Damping factor () between 0 and 1.
3.1. Continuous-Time PI Controller
For the continuous-time PI controller, the MATLAB 2016 “Control System Designer” software was used, where the plant model for the voltage-duty cycle channel shown in (7) was entered to obtain a controller that achieves the requirements. The transfer function that represents the obtained controller is described in (9)
3.2. PI Controller Discretization
Because the devices dedicated to digital control work in discrete time instants, it is necessary to discretize the transfer function of the controller presented in (9). For this, the Forward Euler method is used. In (10), an approximate equivalence of s in terms of the domain is presented, where is the sampling period.
The mathematical model of the controller is illustrated in (11) with a sampling frequency and a sampling period s.
4. Sliding-Mode Control
The main characteristic of sliding mode control consists of choosing a sliding surface within the state space that must be achieved to satisfy the desired dynamics of the closed-loop system. Its main advantages lie in the system’s robustness in handling modeling uncertainties or disturbances, the need for a smaller amount of information compared to other control techniques, and obtaining stability in specific non-linear systems where linear control laws are incapable [].
In this section, the case of a double-loop control is presented. The internal loop corresponds to a sliding-mode control in discrete time to regulate the inductor current. On the other hand, the external loop is a PI controller in discrete time, which provides the sliding surface for the sliding mode control based on a voltage reference . The developed control structure is illustrated in Figure 2.
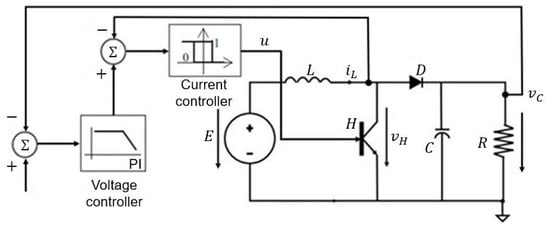
Figure 2.
Controller structure.
4.1. Internal-Loop Control
For this controller, it is necessary to comply with (12)
where represents the sliding surface over time and is the desired current.
Because the goal is implementing a discrete-time control system, it is necessary to represent (12) as a discrete signal; this representation is observed in (13)
where represents the sample number, , and is the vector of discrete states of the converter.
To ensure that the sliding surface is reached, conditions (14) must be fulfilled,
where is the increment of the switching sliding surface [], which can be represented by (15).
For this application, the equivalent control law is applied, where the aim is to find a duty cycle value for a square PWM function that is responsible for switching. Hence, in this application, it is considered that the sliding surface is reached, (that is, ), and from the analysis in (8), an equivalent control equation is obtained represented by (16), where .
The duty cycle value must satisfy the condition expressed in (17), so a saturation function is required, as was proposed in [], in this case, to limit the duty cycle value. This saturation function (18) considers a minimum converter efficiency of 80%.
To determine if the sliding surface is reached, the worst cases are considered; that is, when the value of is saturated. Therefore, to guarantee the reachability of the sliding surface, the value of is substituted in (8), where (19) is the expression when and (20) represents the case when .
The inequality expressed in (19) is satisfied because, in the boost converter, the output voltage must be greater than the input voltage with , and (20) holds if and only if . Therefore, it can be said that the sliding surface is reached in the interval , and a maximum voltage amplification at the output of approximately three times with respect to the input voltage.
4.2. External-Control Loop
The mathematical model of the external-control loop (PI) in continuous time is presented in (21).
Following this, the discretization of this controller is presented in (22).
5. Testing through Simulation
This section presents a comparison between the two control cases in the event of disturbances in the voltage reference and disturbances in the input voltage with a load of 120 , which is the maximum load supported by the converter. All simulations presented in this document are performed with the following configuration: solver type of fixed step (Forward Euler) and a fundamental sample time of s.
5.1. Tests against Disturbances in the Voltage Reference
Figure 3 shows the testing of the controllers with a voltage reference change from 15 volts to 20 volts and vice versa, both with a load of 120 .
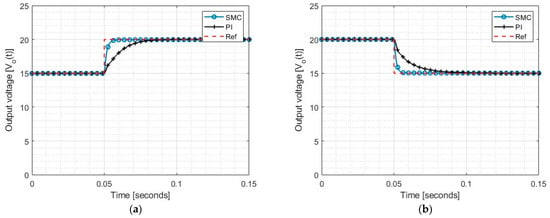
Figure 3.
Tests against disturbances in the voltage reference: (a) Change in voltage reference from 15 volts to 20 volts; (b) change in voltage reference from 20 volts to 15 volts.
Although both controllers reach the voltage reference in an acceptable time according to the requirements, the SMC achieves it more quickly.
5.2. Tests against Disturbances in the Input Voltage
Figure 4 shows the testing of the controllers with a change in the input voltage from 12 volts to 15.4 volts with a voltage reference of 17 volts and a load of 120 .
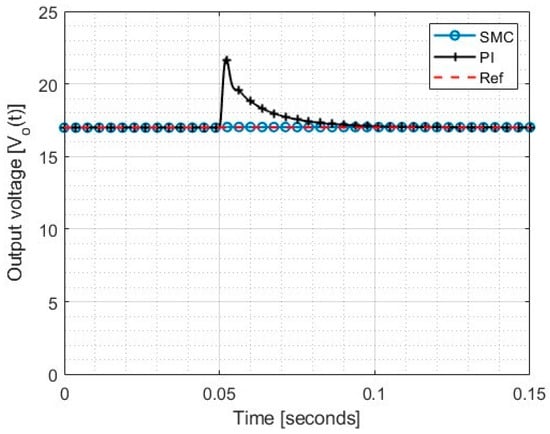
Figure 4.
Change in input voltage from 12 volts to 15.4 volts.
Although both controllers manage to return to the reference value, the SMC has a better response because it is less affected by the disturbance.
6. Experimental Results
The controllers are implemented for the DC-DC boost converter to validate the results. The plant parameters are displayed in Table 2. The controllers are implemented on the Texas Instruments TMS3020F28379D MCU (low-cost development and evaluation kit called LAUNCHXL-F28379D). Figure 5 shows a photograph of the boost converter, together with the devices involved in the control system.

Figure 5.
Implementation of the controllers to a DC-DC boost converter in the mechatronics and control laboratory.
This implementation mainly consists of three devices: the MCU, which controls the converter’s output voltage through the implementation via software (compiled versions of C/C++ language) of the digital control algorithms previously described (PI and SMC); a signal-conditioning board with an LV25-P voltage sensor and a CSNE151 current sensor; and the prototype of the boost converter.
In this work, two DC sources supplied power to the sensors and the converter’s MOSFET driver (MICREL INC acquired by Microchip Technology (San José, CA, USA)), while the oscilloscope was used as a data-acquisition system. Figure 6 illustrates the connection diagram for implementing both control systems.

Figure 6.
Connection diagram of the devices for the control system to regulate the output voltage of the boost converter.
6.1. Programming Controllers within the Code Composer Studio Development Environment
The two control cases are implemented using the Texas Instruments “Code Composer Studio” IDE through an optimized C/C++ language compiler. The main advantage of using Code Composer Studio directly without having to use other programming software is that CCS does not require a license fee.
The control algorithms employ a 12-bit ADC resolution and PWM with a fixed switching frequency of 40 KHz. Table 4 describes the most important features of the LAUNCHXL-F28379D MCU for these implementations [].

Table 4.
Features of the LAUNCHXL-F28379D.
Texas Instruments provides aid to facilitate the implementation of PID control. In [], examples of PID control applications and some results through simulations are presented. In [], the operation of the digital control library (DCL) is explained, and it contains examples of PID control classes and compensators. Although these examples are considered a starting point, for this implementation, a modified algorithm is developed due to the differences that the DCL architectures provide concerning the one presented in this document.
In the case of the SMC, Texas Instruments does not provide manuals or example codes that help implement the controller presented in this document. Therefore, this work develops and implements a version of the controller algorithm via software. The programming algorithms are expressed through flowcharts, which are illustrated in Figure 7. The box indicated in red represents the new blocks that are required for the implementation of the SMC.
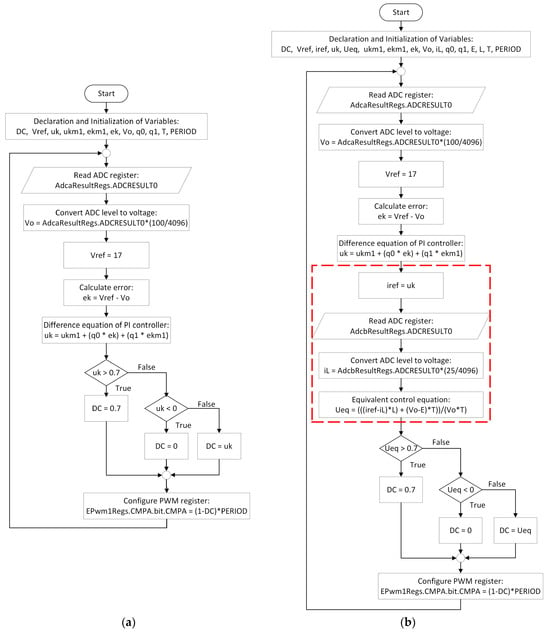
Figure 7.
Control algorithms expressed through flowcharts: (a) PI controller algorithm flowchart; (b) SMC algorithm flowchart.
Table 5 presents the meaning of each variable and the control algorithm to which it belongs.

Table 5.
Variables of digital control algorithms.
6.2. Current and Voltage Measurements
For the proper operation of the control algorithms, it is necessary to measure the current and voltage values in the boost converter. A maximum voltage at the output of the converter is considered to be 100 volts. However, the analog-digital converter (ADC) of the MCU has a measurement range of 0 to 3 volts. Therefore, in this case, it is necessary to transform the voltage signal of the boost converter to be sampled by the ADC. The LEM LV25-P Hall effect voltage sensor is used to accomplish this task.
Figure 8 shows the electrical circuit for the voltage sensor, where is the input voltage and is the supply voltage, according to the technical datasheet [].
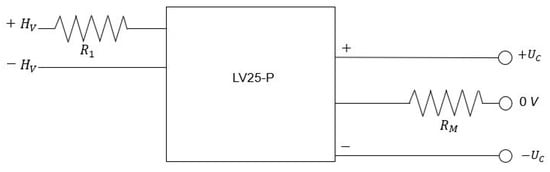
Figure 8.
Electrical circuit of the LV25-P voltage sensor.
Based on this circuit, it is necessary to choose the values of resistors and appropriately. It is known that the maximum current at the input is 10 mA, taking its technical datasheet as a reference. Therefore, by setting a maximum voltage range at the input of the sensor of 100 volts, Equation (23) is obtained by considering Ohm’s law.
The maximum current at the sensor output is 25 mA, and the maximum voltage that can be applied to an input port pin of the launchpad ADC is 3 volts. Therefore, in (24), the value of is calculated by Ohm’s law. The voltage at the sensor output is measured in .
The current must be transformed into an equivalent voltage value to be sensed by the ADC of the MCU. This is achieved by considering the scheme of the Honeywell CSNE151 current sensor illustrated in Figure 9.
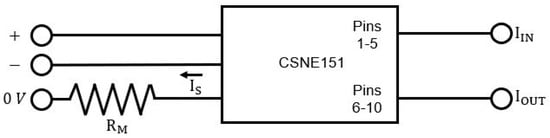
Figure 9.
Electrical circuit of the CSNE151 current sensor with and being the current sensor terminals and is the output current of the sensor.
Ohm’s law is applied as shown in (25) to calculate . For this reason, a maximum input current of 25 A and a maximum output current of 25 mA are considered, according to the technical datasheet [].
A printed circuit board (PCB) is designed to develop the signal conditioning board using KiCad 7.0 software. The KiCad PCB editor is an easy-to-use free software tool that generates complex designs []. Figure 10 illustrates the result of the PCB design.
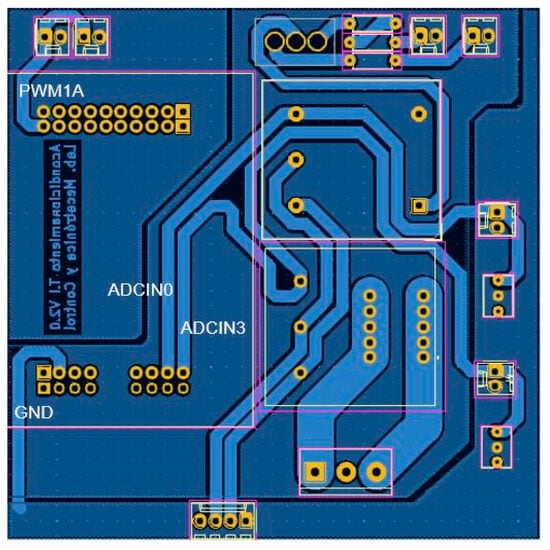
Figure 10.
PCB for signal conditioning board.
6.3. Costs of Implementation Elements
Table 6 reports the costs of implementation elements for both controllers. Note that laboratory equipment such as DC sources or oscilloscopes are not considered. Table 7 presents a comparison between the approximate economic costs of the most expensive and cheapest work referenced in Table 1 and Table 2 according to the software and hardware used.

Table 6.
Costs of implementation elements.

Table 7.
Comparison between the cheapest and most expensive cases.
6.4. PI Controller Response
Figure 11 illustrates the response of the PI controller to a reference voltage of 17 volts, an input voltage of 12 volts through a solar battery, and a load of 120 . The graph shows both the response in simulation and implementation as a comparison between them.
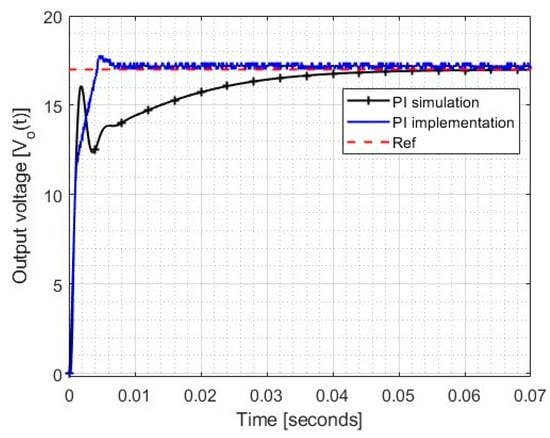
Figure 11.
Response of the PI controller to a voltage reference of 17 volts and an input voltage of 12 volts.
In Figure 11, it can be observed that the implementation result is different from the simulated one. This is mainly due to the linearization of the elements and the disturbances not considered in the simulation.
6.5. SMC Response
Figure 12 shows the response of the SMC under the same test parameters as the implementation of the PI controller. In the same way, as in Figure 11, a comparison is made between the system’s response through simulation and the response obtained when conducting the implementation.
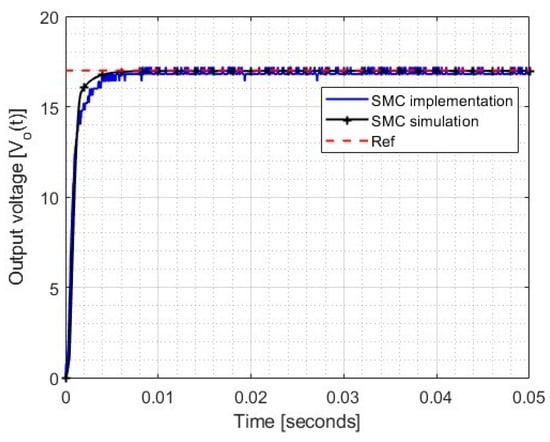
Figure 12.
Response of the SMC to a voltage reference of 17 volts and an input voltage of 12 volts.
Mathematical models that consider a greater number of non-ideal parameters and possible disturbances are necessary to obtain similar results between simulation and implementation. However, these considerations would have a higher computational cost. The mathematical modeling presented in this document allows for the simulation of the plant in an approximate manner and the obtaining of controllers that satisfy the requirements.
6.6. Comparison between Controllers
A comparison is presented through the graphs obtained in the implementation of the controllers to determine the controller with the best performance. Figure 13 shows the response of the SMC, PI, and the voltage reference. Table 8 illustrates the comparison of the controllers by considering the transient-state approximation time , maximum overshoot percentage , and the steady-state error percentage .
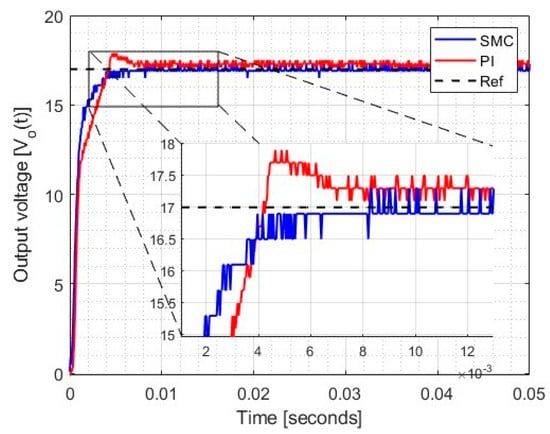
Figure 13.
Comparison of controller-response graphs.

Table 8.
Comparison between controllers.
According to the data obtained from both simulation and implementation, the SMC performs better in the sense of reducing the time response, the overshooting, and the steady-state error with respect to the PI control. Therefore, the risk of damage to the load or connected devices is reduced. For this reason, the SMC is the most adequate for photovoltaic system applications where the system is affected by different disturbances.
7. Robustness Tests to the SMC
Finally, robustness tests are conducted on the controller that obtained the best performance (in this case, the SMC) to validate it against disturbances in the input voltage and voltage reference.
7.1. Disturbances in the Voltage Reference
Figure 14 shows the controller tests with a voltage reference change from 15 to 20 volts and vice versa, both with a load of 120 and an input voltage of 12 volts.
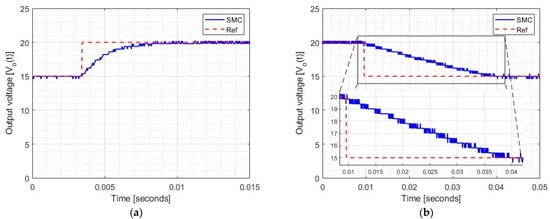
Figure 14.
Disturbances in the voltage reference: (a) Change in voltage reference from 15 volts to 20 volts in implementation; (b) change in voltage reference from 20 volts to 15 volts in implementation.
7.2. Disturbances in the Input Voltage
Figure 15 illustrates the test of the controller with a change in the input voltage from 12 volts to 15.4 volts with a load of 120 and a voltage reference of 17 volts.
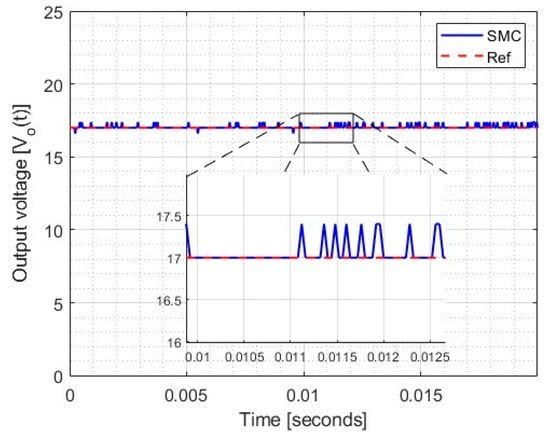
Figure 15.
Change in input voltage from 12 volts to 15.4 volts in implementation.
8. Conclusions
This document demonstrates that linear and non-linear controllers can be implemented using low-cost platforms. This objective is achieved by implementing two control systems as test cases for the voltage regulation of a DC-DC boost converter for photovoltaic system applications. Frequently, in the literature, high-performance software/hardware is used. Although that allows for the implementation of increasingly sophisticated and more straightforward controllers, the implementation costs of the system are high. Therefore, an important task is selecting the device for control implementation based on the requirements of the application to which it is directed. This work reduces the economic implementation costs between 11 and 187 times compared to other works in the literature.
The PI controller was initially presented continuously to satisfy the requirements, and the discretization of the controller was subsequently performed using the Forward Euler method; on the other hand, the SMC was obtained directly in discrete time.
It was possible to corroborate that both controllers satisfy the requirements for which these were developed. However, their performance in practice, especially in the case of the PI controller, was different from those obtained in simulation. These variations are mainly due to the idealized nonlinearities of the models, high switching frequency, and charging and discharging time of the capacitor, among others. Both in implementation and simulation, the SMC performed better than the PI. This difference is because, while the PI was chosen for a specific operating point, the SMC aimed to cover a more extensive operating range.
Simultaneously, despite the uncertainties that mathematical models of the plant may have, the SMC proved to be robust to disturbances such as changes in the voltage reference and changes in input voltage. Therefore, for applications of renewable energies, the SMC is the most viable between the two cases of controllers implemented.
The work presented in this scientific article has many potential practical applications where robust and low-cost control systems are required. For this reason, the implementation of these algorithms in greenhouse energy supply or electromobility applications is envisioned as future work.
Author Contributions
Conceptualization, J.A.G.-C., M.A.A.-C., G.J.R.-A. and D.E.C.-P.; methodology, G.J.R.-A. and D.E.C.-P.; software, J.A.G.-C. and D.E.C.-P.; validation, G.J.R.-A., J.D.S.-T. and D.E.C.-P.; formal analysis, J.A.G.-C., G.J.R.-A., J.D.S.-T. and D.E.C.-P.; investigation, J.A.G.-C., G.J.R.-A. and D.E.C.-P.; resources, G.J.R.-A. and M.M.-M.; data curation, J.A.G.-C., M.M.-M. and J.C.C.-N.; writing—original draft preparation, J.A.G.-C., D.E.C.-P. and G.J.R.-A.; writing—review and editing, J.D.S.-T., J.C.C.-N., M.M.-M. and M.A.A.-C.; visualization, G.J.R.-A. and D.E.C.-P.; supervision, G.J.R.-A. and D.E.C.-P.; project administration, D.E.C.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article.
Acknowledgments
The authors appreciate the support of Consejo Nacional de Humanidades, Ciencias y Tecnologías (CONACYT) and Tecnológico Nacional de México (TecNM).
Conflicts of Interest
The authors declare no potential conflict of interest.
References
- Kouhnavard, M.; Ikeda, S.; Ludin, N.A.; Ahmad-Khairudin, N.B.; Ghaffari, B.V.; Ibrahim, M.A.; Sepai, S.; Sopian, K. A review of semiconductor materials as densitizers for quantum dot-sensitized sollar cells. Renew. Sustain. Energy Rev. 2014, 37, 397–407. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Z.; Zhang, B.; Halang, W. Power electronics converters: Past, present and future. Renew. Sustain. Energy Rev. 2018, 81, 2028–2044. [Google Scholar] [CrossRef]
- Justo, J.J.; Mwasilu, F.; Lee, J.; Jung, J. AC-microgrids versus DC-microgrids with distributed energy resources: A review. Renew. Sustain. Energy Rev. 2013, 24, 387–405. [Google Scholar] [CrossRef]
- Baek, J.W.; Ryo, M.H.; Jim, T.J.; Yoo, D.W.; Kim, J.S. High Boost Converter Using Voltage multiplier. In Proceedings of the 31st Annual Conference of IEEE Industrial Electronics Society, Raleigh, NC, USA, 6–10 November 2005. [Google Scholar] [CrossRef]
- Santi, E.; Monti, A.; Li, D.; Proddutur, K.; Dougal, R.A. Synergetic Control for DC-DC Boost Converter: Implementation Options. IEEE Trans. Ind. Appl. 2003, 39, 1803–1813. [Google Scholar] [CrossRef]
- Maranesi, P.G.; Monti, A.; Rampoldi, A.; Riva, M. Automatic synthesis of large signal models for power electronic circuits. In Proceedings of the 30th Annual IEEE Power Electronics Specialists Conference, Charleston, SC, USA, 1 July 1999; Volume 2, pp. 1019–1023. [Google Scholar] [CrossRef]
- Utkin, V. Variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Volosencu, C.; Saghafinia, A.; Du, X.; Chakrabarty, S. Control Theory in Engineering; IntechOpen: Bucharest, Romania, 2020. [Google Scholar] [CrossRef]
- Fadali, M.S. Digital Control Engineering: Analysis and Design; Academic Press: Burlington, ON, Canada, 2009. [Google Scholar]
- Soriano, A.; Marin, L.; Valles, M.; Valera, A.; Albertos, P. Low Cost Platform for Automatic Control Education Based on Open Hardware. IFAC Proc. 2014, 47, 9044–9050. [Google Scholar] [CrossRef]
- dSPACE Your Partner in Simulation and Validation. Available online: https://www.dspace.com/en/pub/home/applicationfields/ind-appl/automotive-industry/emobility/electricaldrive.cfm (accessed on 16 April 2024).
- Real-Time Simulation | OPAL-RT. Available online: https://www.opal-rt.com/ (accessed on 16 April 2024).
- Aravena, J.; Carrasco, D.; Diaz, M.; Uriarte, M.; Rojas, F.; Cardenas, R.; Travieso, J.C. Design and Implementation of a Low-Cost Real-Time Control Platform for Power Electronics Applications. Energies 2020, 13, 1527. [Google Scholar] [CrossRef]
- Texas Instruments | LAUNCHXL-F28379D. Available online: https://www.ti.com/tool/LAUNCHXL-F28379D?utm_source=google&utm_medium=cpc&utm_campaign=epd-null-null-GPN_EN_EVM-cpc-evm-google-wwe&utm_content=Tool&ds_k=LAUNCHXL-F28379D&DCM=yes&gad_source=1&gclid=EAIaIQobChMIgubU76jHhQMVEzfUAR1RqAyaEAAYASAAEgKri_D_BwE&gclsrc=aw.ds (accessed on 16 April 2024).
- Dave, M.R.; Dave, K.C. Analysis of Boost Converter Using PI Control Algorithms. Int. J. Eng. Trends Technol. 2012, 3, 71–73. [Google Scholar]
- Lopez-Santos, O.; Martinez-Salamero, L.; Garcia, G.; Valderrama-Blavi, H.; Sierra-Polanco, T. Robust Sliding-Mode Control Design for a Voltage Regulated Quadratic Boost Converter. IEEE Trans. Power Electron. 2015, 30, 2313–2327. [Google Scholar] [CrossRef]
- Kheraluwala, M.N.; Gascoigne, R.W.; Divan, D.M.; Baumann, E.D. Performance characterization of a high-power dual active bridge DC-to-DC converter. IEEE Trans. Ind. Appl. 1992, 28, 1294–1301. [Google Scholar] [CrossRef]
- Aquib, M.; Vijay, A.S.; Doolla, S.; Chandorkar, M.C. Power Sharing Enhancement Strategies for Parallel-Connected Voltage Source Inverters with Common dc and ac Buses in Islanded Microgrids: Two New Control Schemes. IEEE Ind. Appl. Mag. 2024, 30, 12–26. [Google Scholar] [CrossRef]
- Carlson, E.J.; Strunz, K.; Otis, B.P. A 20 mV Input Boost Converter with Efficient Digital Control for Thermoelectric Energy Harvesting. IEEE J. Solid-State Circuits 2010, 45, 741–750. [Google Scholar] [CrossRef]
- Mattavelli, P. Digital control of DC-DC boost converters with inductor current estimation. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 22–26 February 2004; Volume 1, pp. 74–80. [Google Scholar] [CrossRef]
- Lopez-Flores, D.R.; Duran-Gomez, J.L.; Vega-Pineda, J. Discrete-Time Adaptive PID Current Controller for Wind Boost Converter. IEEE Lat. Am. Trans. 2023, 21, 98–107. [Google Scholar] [CrossRef]
- Djilali, L.; Badillo-Olvera, A.; Rios, Y.; López-Beltrán, H.; Saihi, L. Neural High Order Sliding Mode Control for Doubly Fed Induction Generator based Wind Turbine. IEEE Lat. Am. Trans. 2022, 20, 223–232. [Google Scholar] [CrossRef]
- Jappe, T.K.; Musa, S.A. Discrete-time current control techniques applied in PFC boost converter at instantaneous power interruption. In Proceedings of the Brazilian Power Electronics Conference, Bonito-Mato Grosso do Sul, Brazil, 27 September–1 October 2009; pp. 1118–1123. [Google Scholar] [CrossRef]
- Alarcón-Carbajal, M.A.; Carvajal Rubio, J.E.; Sánchez Torres, J.D.; Castro-Palazuelos, D.E.; Rubio-Astorga, G.J. An Output Feedback Discrete-Time Controller for the DC-DC Buck Converter. Energies 2022, 15, 5288. [Google Scholar] [CrossRef]
- Shen, S.; Yan, N.; Min, H. A Multimode Digitally Controlled Boost Converter with PID Autotuning and Constant Frequency/Constant Off-Time Hybrid PWM Control. IEEE Trans. Power Electron. 2011, 26, 2588–2598. [Google Scholar] [CrossRef]
- Hmidet, A.; Subramaniam, U.; Elavarasan, R.M.; Raju, K.; Diaz, M.; Das, N.; Mehmood, K.; Karthick, A.; Muhibbullah, M.; Boubaker, O. Design of Efficient Off-Grid Solar Photovoltaic Water Pumping System Based on Improved Fractional Open Circuit Voltage MPPT Technique. Int. J. Photoenergy 2021, 2021, 4925433. [Google Scholar] [CrossRef]
- Vazquez-Plata, J.D.; Lopez-Chavarro, A.F.; Sanabria-Torres, E.A.; Patarroyo-Montenegro, J.F.; Andrade, F. Benchmarking Real-Time Control Platforms Using a Matlab/Simulink Coder with Applications in the Control of DC/AC Switched Power Converters. Energies 2022, 15, 6940. [Google Scholar] [CrossRef]
- Metry, M.; Guler, N.; Rohouma, W.; Balog, R.S. Performance Comparison of dSPACE and MCU MPC Implementation in PV Power Optimizer. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 6266–6272. [Google Scholar] [CrossRef]
- Lamo, P.; Azcondo, F.J.; Pigazo, A. Academic Use of Rapid Prototyping in Digitally Controlled Power Factor Correctors. Electronics 2022, 11, 3600. [Google Scholar] [CrossRef]
- Wang, Y.; Nguyen, T.L.; Xu, Y.; Li, Z.; Tran, Q.; Caire, R. Cyber-Physical Design and Implementation of Distributed Event-Triggered Secondary Control in Islanded Microgrids. IEEE Trans. Ind. Appl. 2019, 55, 5631–5642. [Google Scholar] [CrossRef]
- Lidozzi, A.; Di-Benedetto, M.; Sabatini, V.; Solero, M.; Crescimbini, F. Towards LabVIEW and System on Module for Power Electronics and Drives Control Applications. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 4995–5000. [Google Scholar] [CrossRef]
- Chapparya, V.; Krishna, G.M.; Dwivedi, P.; Bose, S. Loop shaping controller design for constant output interleaved boost converter using real-time hardware in-the-loop (HIL). In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 14–16 March 2018; pp. 1–6. [Google Scholar]
- Hart, D. Power Electronics; Tata McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power Electronic Converters Modeling and Control; Springer: London, UK, 2014. [Google Scholar]
- Knospe, C. PID control. IEEE Control Syst. Mag. 2006, 26, 30–31. [Google Scholar] [CrossRef]
- Perruqueti, W.; Barbot, J.P. Sliding Mode Control in Engineering; Marcel Denker Inc.: New York, NY, USA, 2002. [Google Scholar]
- El-Aroudi, A.; Martinez-Treviño, B.A.; Vidal-Idiarte, E.; Martinez-Salamero, L. Discrete-Time Sliding Mode Control of a Boost Converter Loaded by a CPL. In Proceedings of the 2018 International Symposium on Nonlinear Theory and Its Applications, Tarragona, Spain, 2–6 September 2018. [Google Scholar]
- Vidal-Idiarte, E.; Marcos-Pastor, A.; Gracia, G.; Cid-Pastor, A.; Martinez-Salamero, L. Discrete-time sliding-mode-based digital pulse width modulation control of a boost converter. IET Power Electron. 2015, 8, 708–714. [Google Scholar] [CrossRef]
- Texas Instruments TMS320F2837xD Dual-Core Microcontrollers. Available online: https://www.ti.com/lit/ds/sprs880p/sprs880p.pdf?ts=1713545949819&ref_url=https%253A%252F%252Fwww.ti.com%252Ftool%252FLAUNCHXL-F28379D%253Futm_source%253Dgoogle%2526utm_medium%253Dcpc%2526utm_campaign%253Depd-null-null-GPN_EN_EVM-cpc-evm-google-wwe%2526utm_content%253DTool%2526ds_k%253DLAUNCHXL-F28379D%2526DCM%253Dyes%2526gad_source%253D1%2526gclid%253DEAIaIQobChMI9fGOgeDOhQMV8kd_AB33zAm3EAAYASAAEgIffvD_BwE%2526gclsrc%253Daw.ds (accessed on 5 May 2024).
- Texas Instruments. Implementation of PID and Deadbeat Controller with the TMS320 Family. Available online: https://www.ti.com/lit/an/spra083/spra083.pdf (accessed on 5 May 2024).
- C2000™ Digital Control Library User’s Guide. Available online: https://www.ti.com/lit/ug/spruid3/spruid3.pdf?ts=1713373358834&ref_url=https%253A%252F%252Fwww.google.com%252F (accessed on 5 May 2024).
- Voltage Transducer LV25-P. Available online: https://www.farnell.com/datasheets/1866272.pdf (accessed on 5 May 2024).
- Honeywell Sensing and Control. Solid State Sensors Closed Loop Current Sensors. Available online: https://www.farnell.com/datasheets/2602959.pdf (accessed on 29 July 2024).
- KiCad EDA A Cross Platform and Open Source Electronics Design Automation Suite. Available online: https://www.kicad.org/ (accessed on 1 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).