Design, Simulation and Optimization of a Novel Transpired Tubular Solar Air Heater
Abstract
1. Introduction
1.1. Introduction
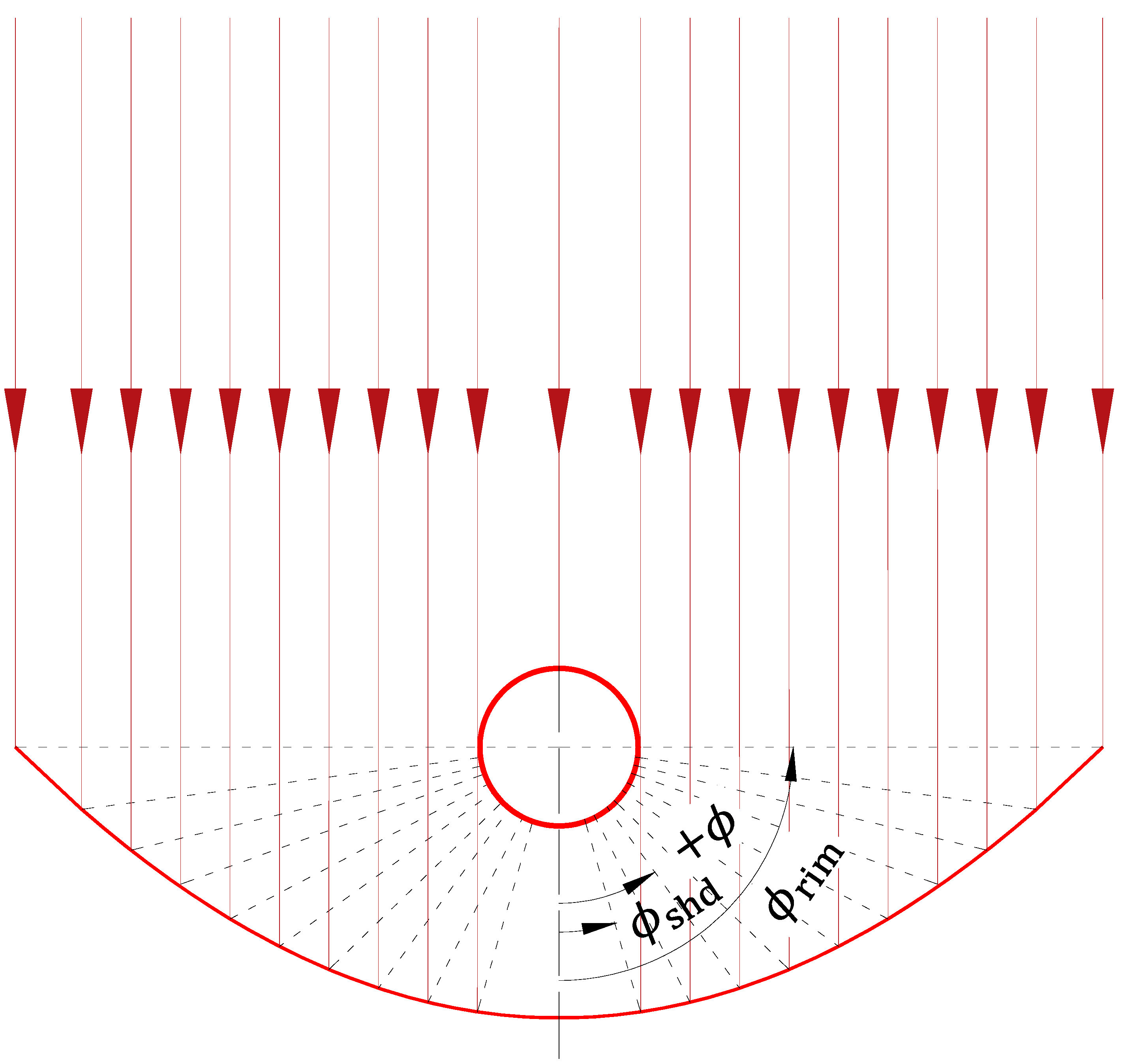
1.2. Problem Description
2. Numerical Simulation
2.1. Governing Equations
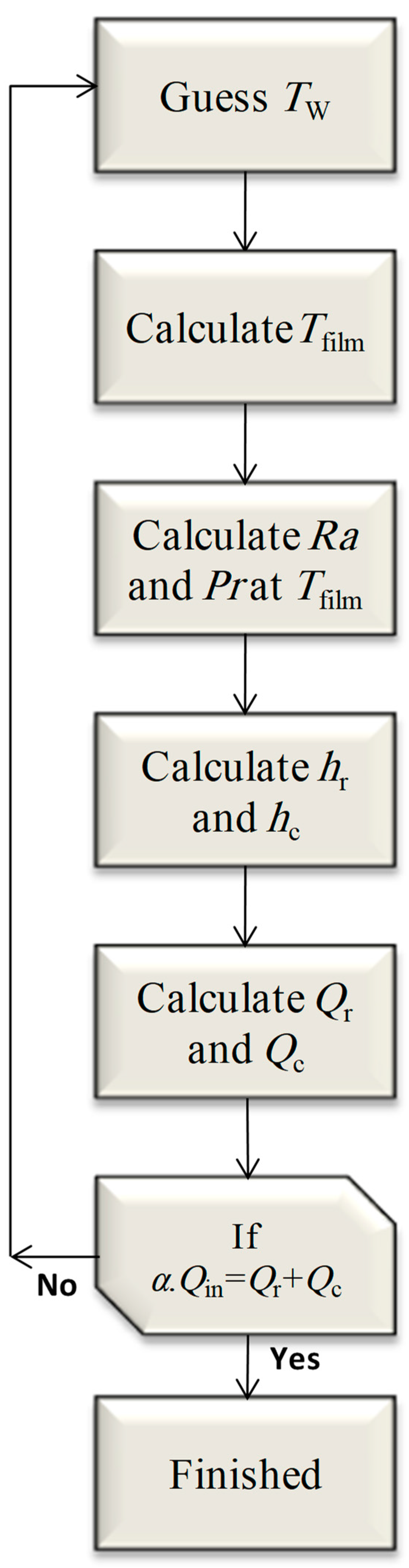
2.2. Solution Methodology
3. Data Processing and Discussion
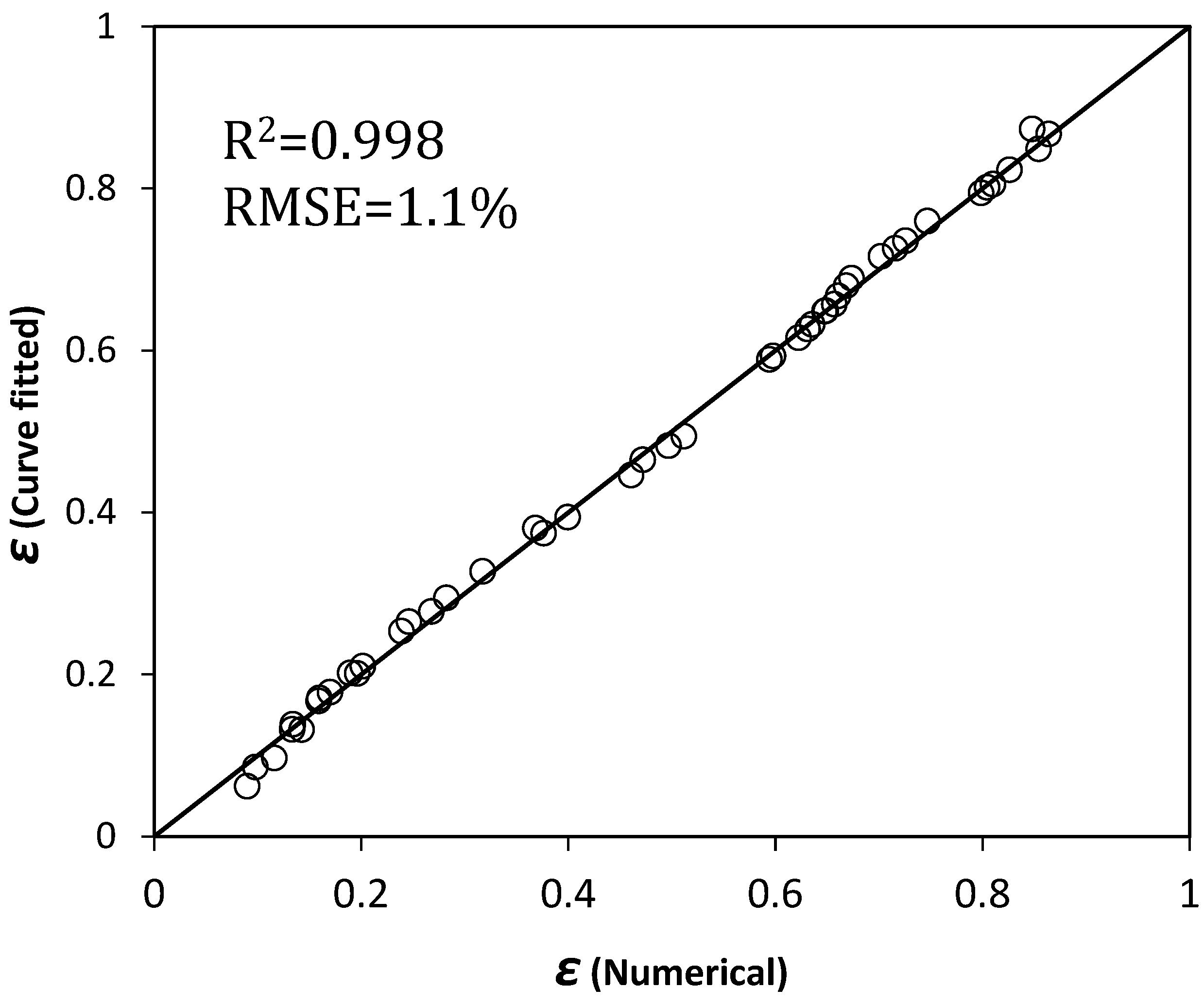
3.1. Data Analysis
3.2. Energy Analysis of a UTTA
3.3. Exergy Analysis of a UTTA
3.4. Analysis of a Real Case
4. UTTA Optimization
5. Summary
- -
- The glass tube is eliminated, which results in a considerable reduction in construction and maintenance costs;
- -
- Hot air can be mixed with fresh air to derive an adequate amount of warm air at the desired temperature. So, the air outlet temperature is under the control;
- -
- The mixing can be done at the destination, and therefore, smaller ducts are required to transfer hot air;
- -
- The temperature rise in this collector is relatively high. A higher temperature for thermal energy means a higher level of availability and exergy.
- -
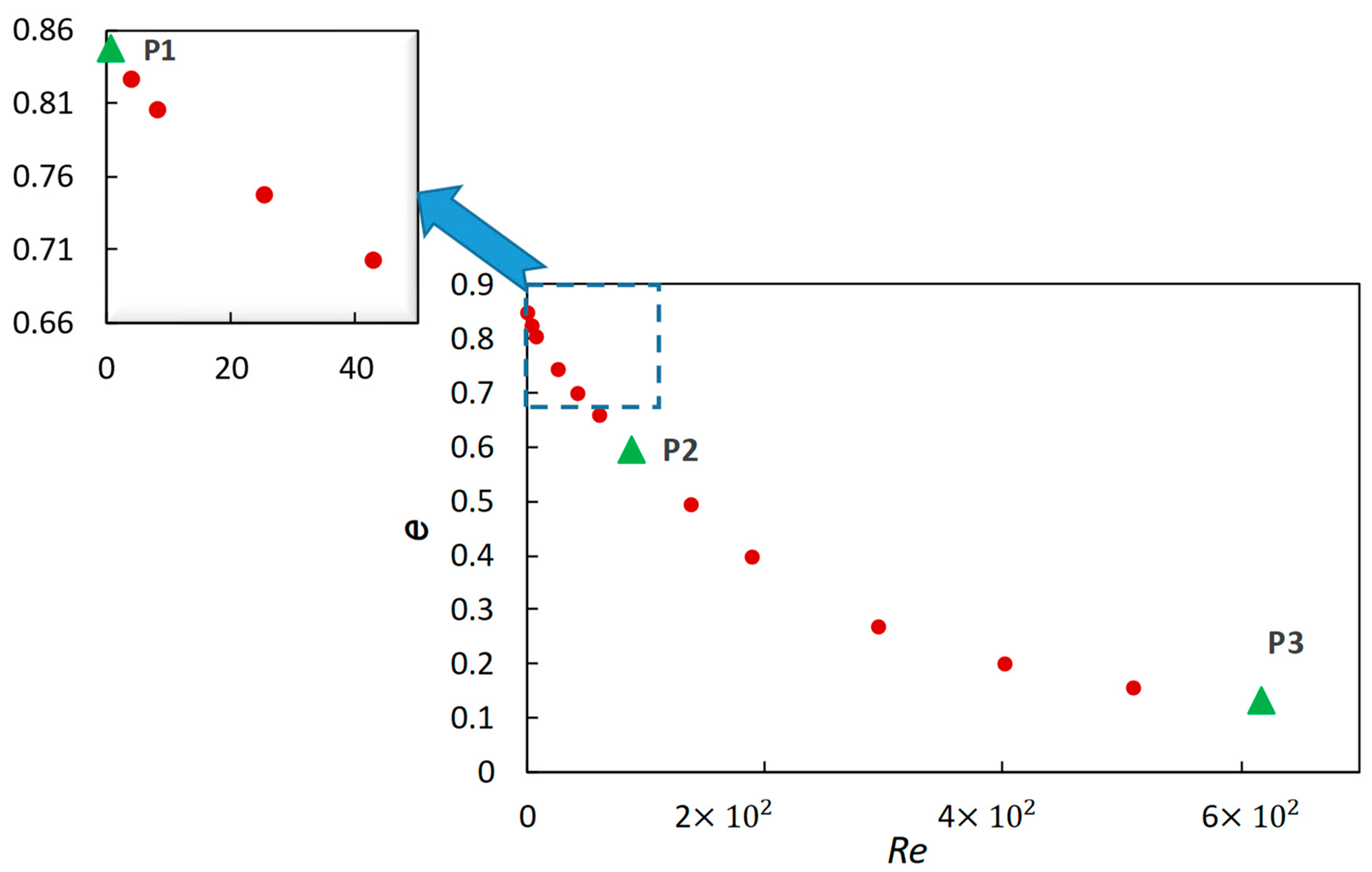
- Low suction—Only a narrow layer of gas adjacent to the wall is drawn in and the effectiveness has a weak dependency on . The effectiveness approaches very slowly to a value less than unity when the suction value reduces toward zero. Consequently, most of the thermal energy is wasted and nothing is recovered;
- -
- Moderate suction—A part of the thermal boundary layer is sucked. So, only a part of thermal energy is recovered and the rest is wasted. The effectiveness depends on the ratio of and ;
- -
- High suction—Fresh air in addition to the boundary layer is sucked. So, almost nothing is wasted. From this point on, the amount of total energy is fixed, and by increasing the air flow rate, temperature rise proportionally decreases.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Absorber tube heat transfer area per unit length of the tube (m2/m) |
| B | Dimensionless exergy destruction or loss |
| Air specific heat capacity (J/kgK) | |
| D | Tube outer diameter (m) |
| Ex | Exergy (W) |
| f | Focal length (m) |
| Gravitational acceleration vector in the y direction (m/s2) | |
| h | Heat transfer coefficient (W/m2 K) |
| I | Solar intensity (W/m2) |
| k | Thermal conductivity (W/m·K) |
| Air mass flow rate per meter (kg/m.s) | |
| Nu | Air Nusselt number |
| P | Pressure (Pa) |
| Pr | Air Prandtl number |
| q | Absorbed solar heat flux over the tube (W/m2) |
| Q | Heat transfer per unit length of the tube (W/m) |
| Ra | Air Rayleigh number for a tube |
| Re | Air Reynolds number |
| T | Temperature (K) |
| Velocity in the x direction (m/s) | |
| v | Velocity in the y direction (m/s) |
| Slit width (m) | |
| Greek characters | |
| Tube absorptivity | |
| Air thermal expansion coefficient (1/K) | |
| Effectiveness | |
| Emissivity | |
| First-law efficiency | |
| Second-law efficiency | |
| Dimensionless temperature, | |
| Air viscosity (Pa.s) | |
| Air kinematic viscosity (m2/s) | |
| ρ | Air density (kg/m3) |
| ρ | Reflectivity |
| Stefan–Boltzmann constant, 5.67 × 10−8 kg/s3·K4 | |
| Angle (rad) | |
| Subscripts | |
| abs | Absorption |
| Atmosphere | |
| c | Convection |
| dest | Destruction |
| film | Film temperature (average of ambient and wall) |
| gain | Gained |
| in | Inlet |
| loss | Loss |
| r | Radiation |
| refl | Reflection |
| rim | Rim angle |
| s | Solid |
| shd | Shade angle |
| sl | Slit |
| sun | Sun |
| w | Wall |
| Ambient | |
| Abbreviation | |
| CPC | Compound parabolic collector |
| MOGA | Multi-objective genetic algorithm |
| UTTA | Unglazed transpired tubular absorber |
Appendix A
- -
- Density (kg/m3):
- -
- Specific heat capacity (J/kgK):
- -
- Viscosity (Pa.s):
- -
- Thermal conductivity (W/m·K):
References
- Nemati, H.; Javanmardi, M. Exergy optimization of domestic solar cylindrical-parabolic cooker. J. Renew. Sustain. Energy 2012, 4, 063134. [Google Scholar] [CrossRef]
- Víg, P.; Seres, I.; Vladár, P. Improving efficiency of domestic solar thermal systems by a flow control. Sol. Energy 2021, 230, 779–790. [Google Scholar] [CrossRef]
- Li, T.; Qin, H.; Wang, J.; Gao, X.; Meng, N.; Jia, Y.; Liu, Q. Energetic and exergetic performance of a novel polygeneration energy system driven by geothermal energy and solar energy for power, hydrogen and domestic hot water. Renew. Energy 2021, 175, 318–336. [Google Scholar] [CrossRef]
- Chopra, K.; Tyagi, V.; Pandey, A.; Popli, S.; Singh, G.; Sharma, R.; Sari, A. Effect of simultaneous & consecutive melting/solidification of phase change material on domestic solar water heating system. Renew. Energy 2022, 188, 329–348. [Google Scholar]
- Moghimi, M.; Craig, K.; Meyer, J.P. Optimization of a trapezoidal cavity absorber for the Linear Fresnel Reflector. Sol. Energy 2015, 119, 343–361. [Google Scholar] [CrossRef]
- Moghimi, M.; Craig, K.; Meyer, J. Simulation-based optimisation of a linear Fresnel collector mirror field and receiver for optical, thermal and economic performance. Sol. Energy 2017, 153, 655–678. [Google Scholar] [CrossRef]
- Lingayat, A.; Chandramohan, V. Numerical investigation on solar air collector and its practical application in the indirect solar dryer for banana chips drying with energy and exergy analysis. Therm. Sci. Eng. Prog. 2021, 26, 101077. [Google Scholar] [CrossRef]
- El-Sebaey, M.S.; Mousavi, S.M.; El-Din, S.S.; Essa, F.A. An experimental case study on development the design and the performance of indirect solar dryer type for drying bananas. Sol. Energy 2023, 255, 50–59. [Google Scholar] [CrossRef]
- Fang, X.-M.; Liu, Z.-L.; Xiao, H.-M.; Torki, M.; Orsat, V.; Raghavan, G.; Xiao, H.-W.; Wang, H. Performance assessment of an evacuated tube solar-electric hybrid dryer for lotus seeds drying: Moisture removal behavior, GHG emission and thermodynamic analysis. J. Clean. Prod. 2023, 406, 136972. [Google Scholar] [CrossRef]
- Nasri, M.Y.; Belhamri, A. Effects of the climatic conditions and the shape on the drying kinetics, Application to solar drying of potato-case of Maghreb’s region. J. Clean. Prod. 2018, 183, 1241–1251. [Google Scholar] [CrossRef]
- El-Sebaey, M.S.; Ellman, A.; El-Din, S.S.; Essa, F.A. Thermal performance evaluation for two designs of flat-plate solar air heater: An experimental and CFD investigations. Processes 2023, 11, 1227. [Google Scholar] [CrossRef]
- Dake, R.A.; N’Tsoukpoe, K.E.; Kuznik, F.; Lèye, B.; Ouédraogo, I.W. A review on the use of sorption materials in solar dryers. Renew. Energy 2021, 175, 965–979. [Google Scholar] [CrossRef]
- Golneshan, A.; Nemati, H. Exergy analysis of unglazed transpired solar collectors (UTCs). Sol. Energy 2014, 107, 272–277. [Google Scholar] [CrossRef]
- Gao, M.; Wang, D.; Liu, Y.; Wang, Y.; Zhou, Y. A study on thermal performance of a novel glazed transpired solar collector with perforating corrugated plate. J. Clean. Prod. 2020, 257, 120443. [Google Scholar] [CrossRef]
- Ahmadi, A.; Ehyaei, M.; Doustgani, A.; Assad, M.E.H.; Hmida, A.; Jamali, D.; Kumar, R.; Li, Z.; Razmjoo, A. Recent residential applications of low-temperature solar collector. J. Clean. Prod. 2021, 279, 123549. [Google Scholar] [CrossRef]
- Khanlari, A.; Sözen, A.; Şirin, C.; Tuncer, A.D.; Gungor, A. Performance enhancement of a greenhouse dryer: Analysis of a cost-effective alternative solar air heater. J. Clean. Prod. 2020, 251, 119672. [Google Scholar] [CrossRef]
- Venkatramanan, R.; Arjunan, T.; Seenivasan, D.; Kumar, A.V. Parametric study of evacuated tube collector solar air heater with inserted baffles on thermal network for low-temperature applications. J. Clean. Prod. 2022, 367, 132941. [Google Scholar] [CrossRef]
- Aslfattahi, N.; Loni, R.; Bellos, E.; Najafi, G.; Kadirgama, K.; Harun, W.; Saidur, R. Efficiency enhancement of a solar dish collector operating with a novel soybean oil-based-MXene nanofluid and different cavity receivers. J. Clean. Prod. 2021, 317, 128430. [Google Scholar] [CrossRef]
- Nixon, J.D.; Dey, P.; Davies, P. Design of a novel solar thermal collector using a multi-criteria decision-making methodology. J. Clean. Prod. 2013, 59, 150–159. [Google Scholar] [CrossRef]
- Lei, D.; Wang, Z.; Li, J. The calculation and analysis of glass-to-metal sealing stress in solar absorber tube. Renew. Energy 2010, 35, 405–411. [Google Scholar] [CrossRef]
- Lei, D.; Fu, X.; Ren, Y.; Yao, F.; Wang, Z. Temperature and thermal stress analysis of parabolic trough receivers. Renew. Energy 2019, 136, 403–413. [Google Scholar] [CrossRef]
- Montoya Sancha, A.; Rodríguez Sánchez, M.d.l.R.; López Puente, J.; Santana Santana, D.J. Influence of longitudinal clips in thermal stresses and deflection in solar tubular receivers. Sol. Energy 2020, 198, 224–238. [Google Scholar] [CrossRef]
- Nemati, H.; Moradaghay, M. Parametric study of natural convection over horizontal annular finned tube. J. Cent. South Univ. 2019, 26, 2077–2087. [Google Scholar] [CrossRef]
- Nemati, H.; Moradaghay, M.; Moghimi, M.; Meyer, J. Natural convection heat transfer over horizontal annular elliptical finned tubes. Int. Commun. Heat Mass Transf. 2020, 118, 104823. [Google Scholar] [CrossRef]
- Nemati, H.; Ardekani, M.M.; Cemal Benim, A.; Meyer, J. Optimization of horizontal annular finned tube under natural convection heat transfer. Heat Transf. Eng. 2022, 43, 1451–1463. [Google Scholar] [CrossRef]
- Churchill, S.W. Free convection around immersed bodies. Heat Exch. Des. Handb. 2002, 2, 063134. [Google Scholar]
- Morgan, V.T. The overall convective heat transfer from smooth circular cylinders. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1975; Volume 11, pp. 199–264. [Google Scholar]
- Bejan, A. Convection Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bergman, T.L.; Incropera, F.P.; Dewitt, D.P.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Petela, R. Exergy of undiluted thermal radiation. Sol. Energy 2003, 74, 469–488. [Google Scholar] [CrossRef]
- Bejan, A.; Kearney, D.; Kreith, F. Second law analysis and synthesis of solar collector systems. J. Sol. Energy Eng. 1981, 103, 23–28. [Google Scholar] [CrossRef]
- Khanna, S.; Sharma, V. Explicit analytical expression for solar flux distribution on an undeflected absorber tube of parabolic trough concentrator considering sun-shape and optical errors. J. Sol. Energy Eng. 2016, 138, 011010. [Google Scholar] [CrossRef]
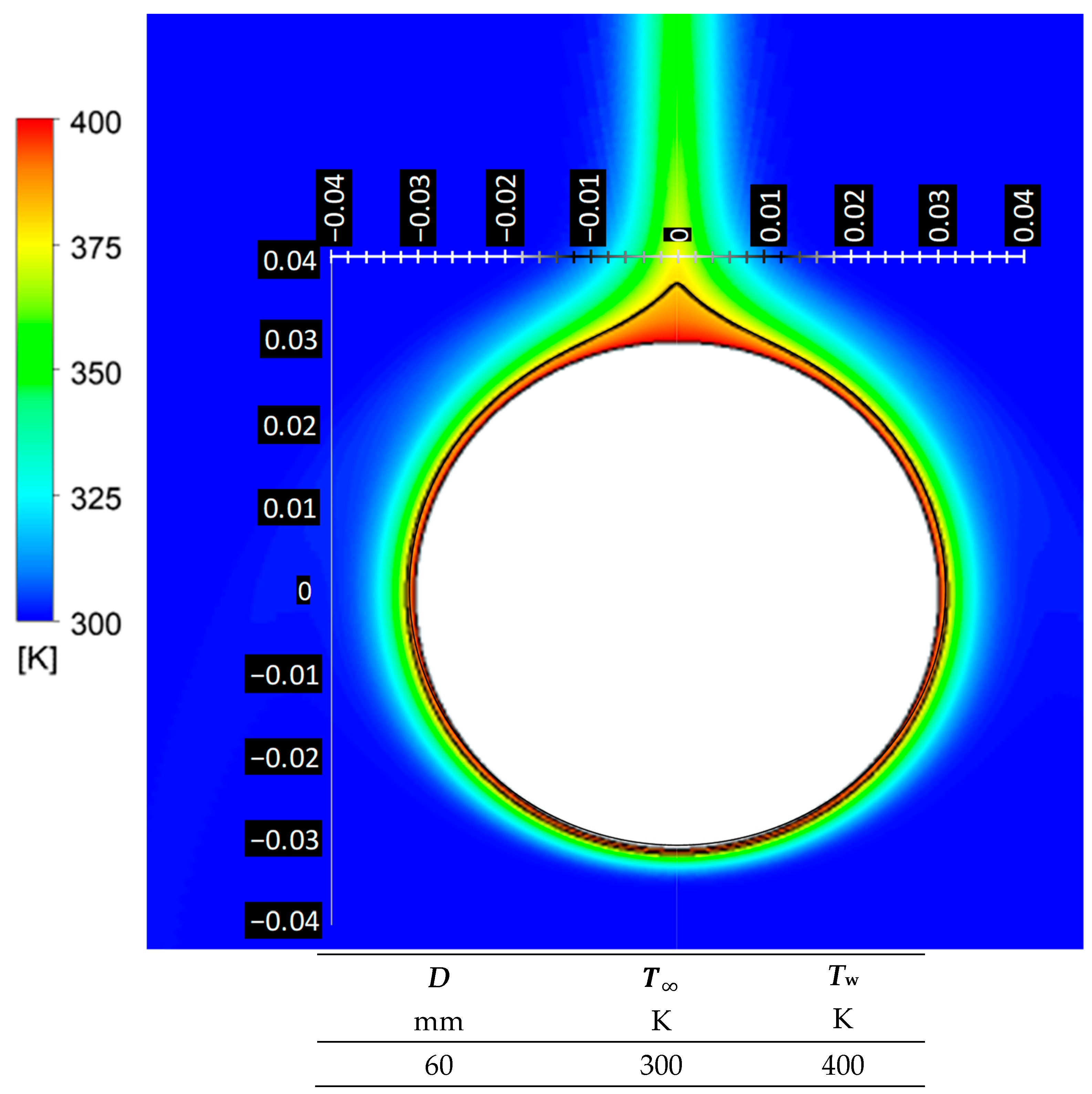
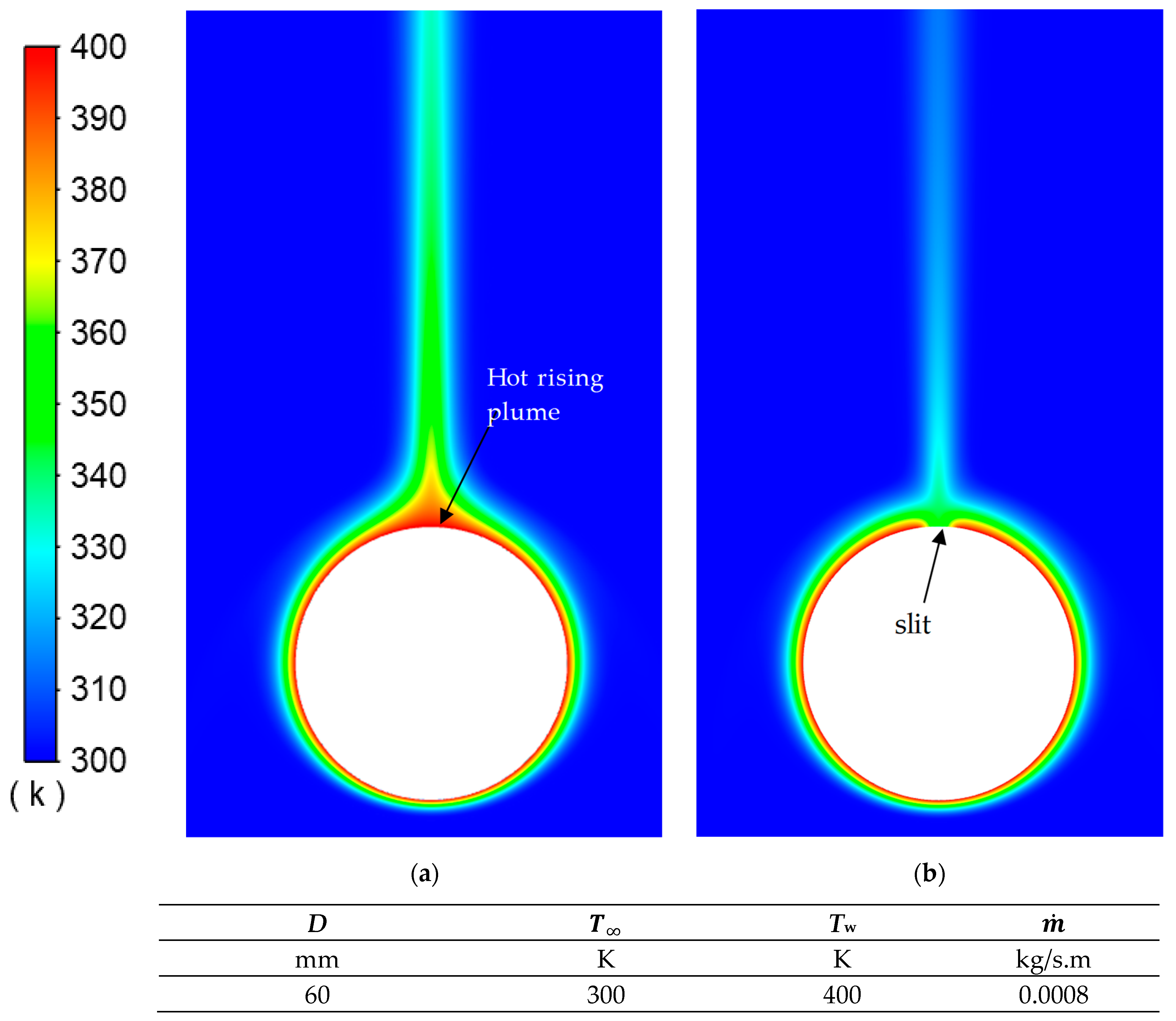
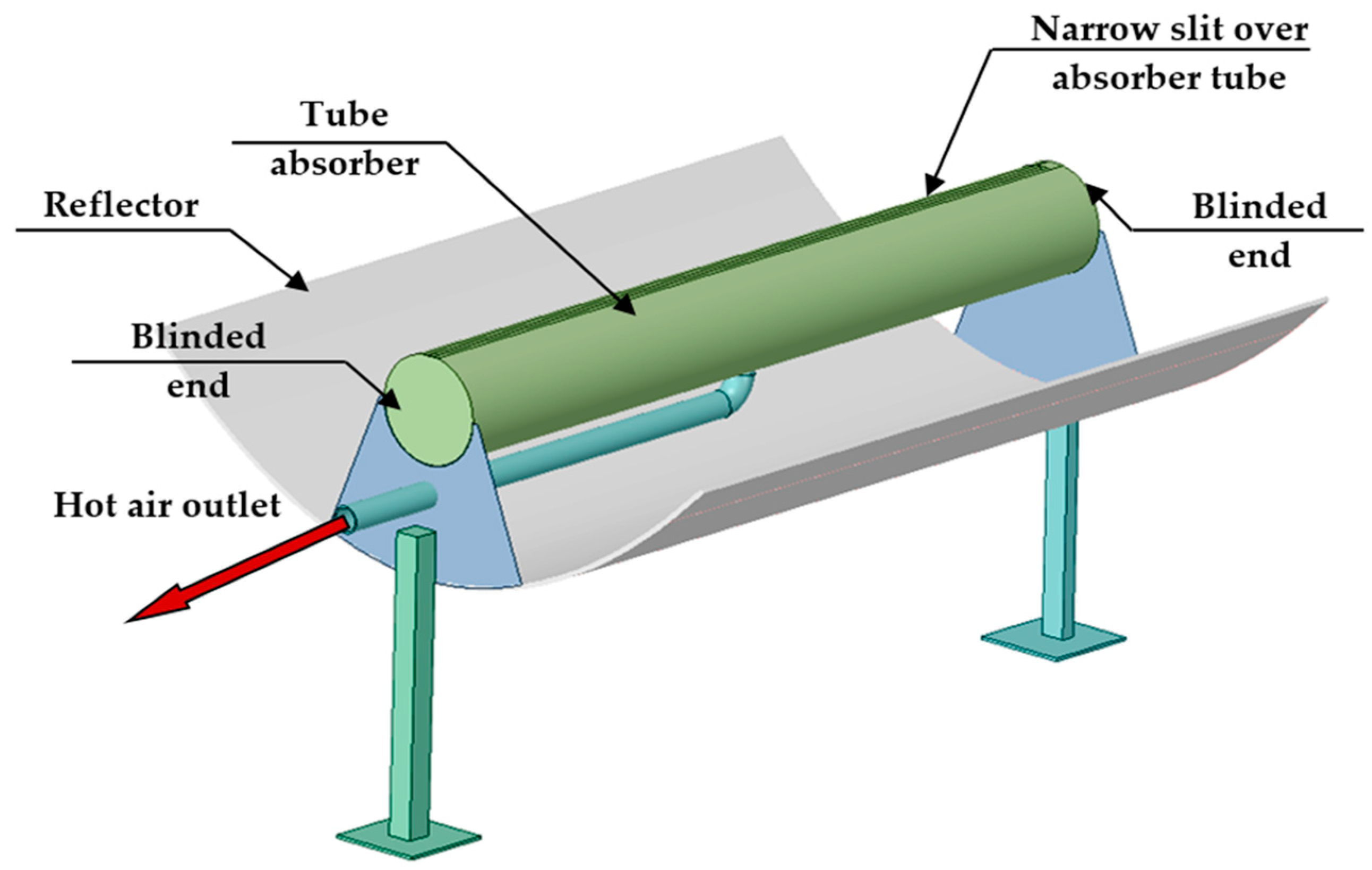


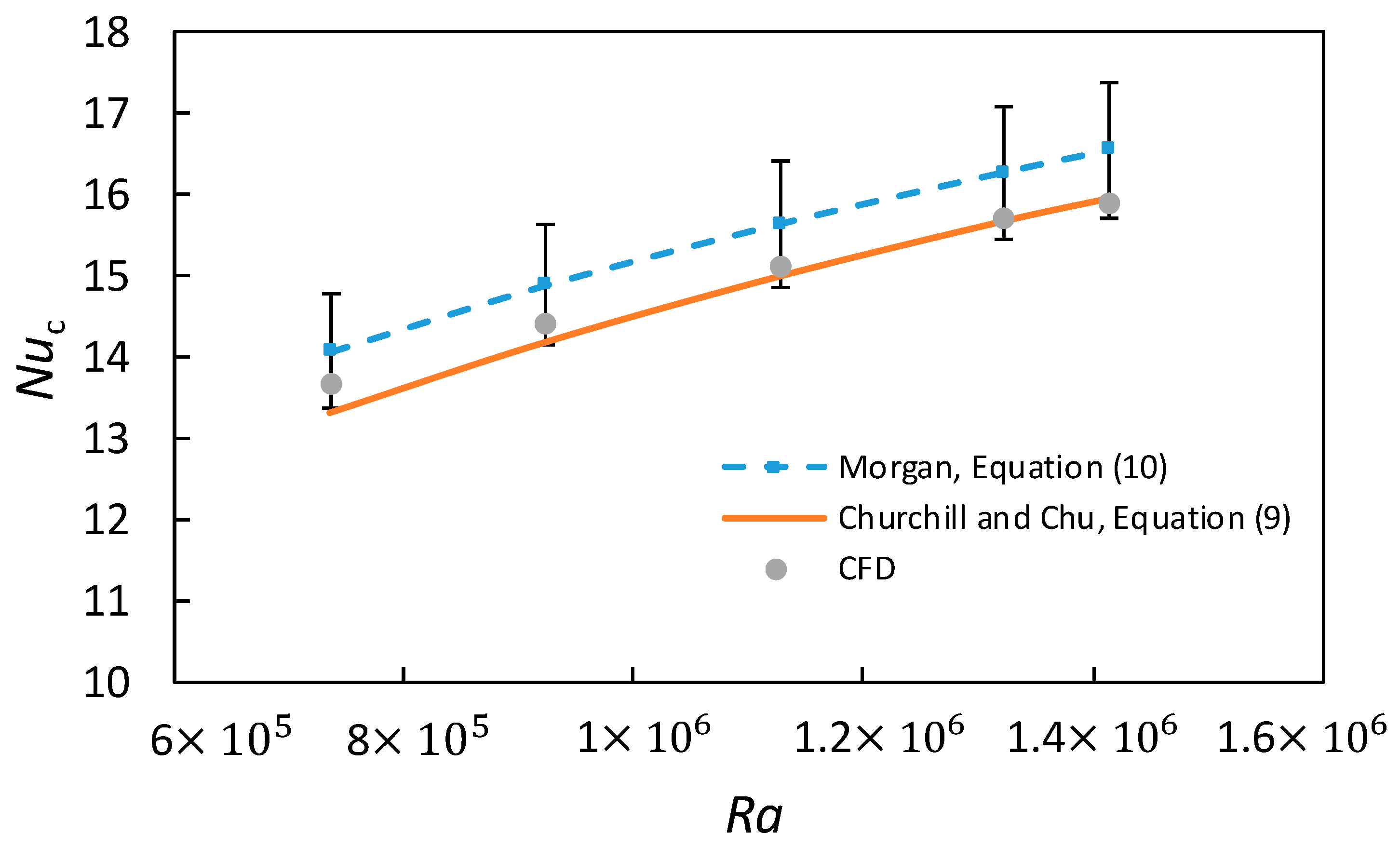




| D | ||
|---|---|---|
| (mm) | (k) | (kg/s·m) |
| [21, 140] | [50, 250] | [ |
| Parameter | Value | |
|---|---|---|
| Reflector width | 0.4 | M |
| Reflector focal length | 0.1 | m |
| Tube outer diameter | 0.06 | m |
| Tube thickness | 4 | mm |
| Slit width | 8 | mm |
| rad | ||
| 0.298 | rad | |
| A | 0.18 * | m2/m |
| (Analytical) | (Numerical) | |||
|---|---|---|---|---|
| (kg/s·m) | (---) | (---) | (K) | (K) |
| 0.0001 | 8.95 | 0.801 | 385.9 | 385.8 |
| 0.0005 | 45.64 | 0.706 | 375.8 | 374.0 |
| 0.001 | 93.93 | 0.573 | 361.4 | 361.7 |
| 0.002 | 196.47 | 0.374 | 340.1 | 339.0 |
| 0.003 | 302.47 | 0.264 | 328.3 | 326.1 |
| 0.004 | 409.62 | 0.200 | 321.5 | 319.4 |
| (1/K) | (W/m2 K) |
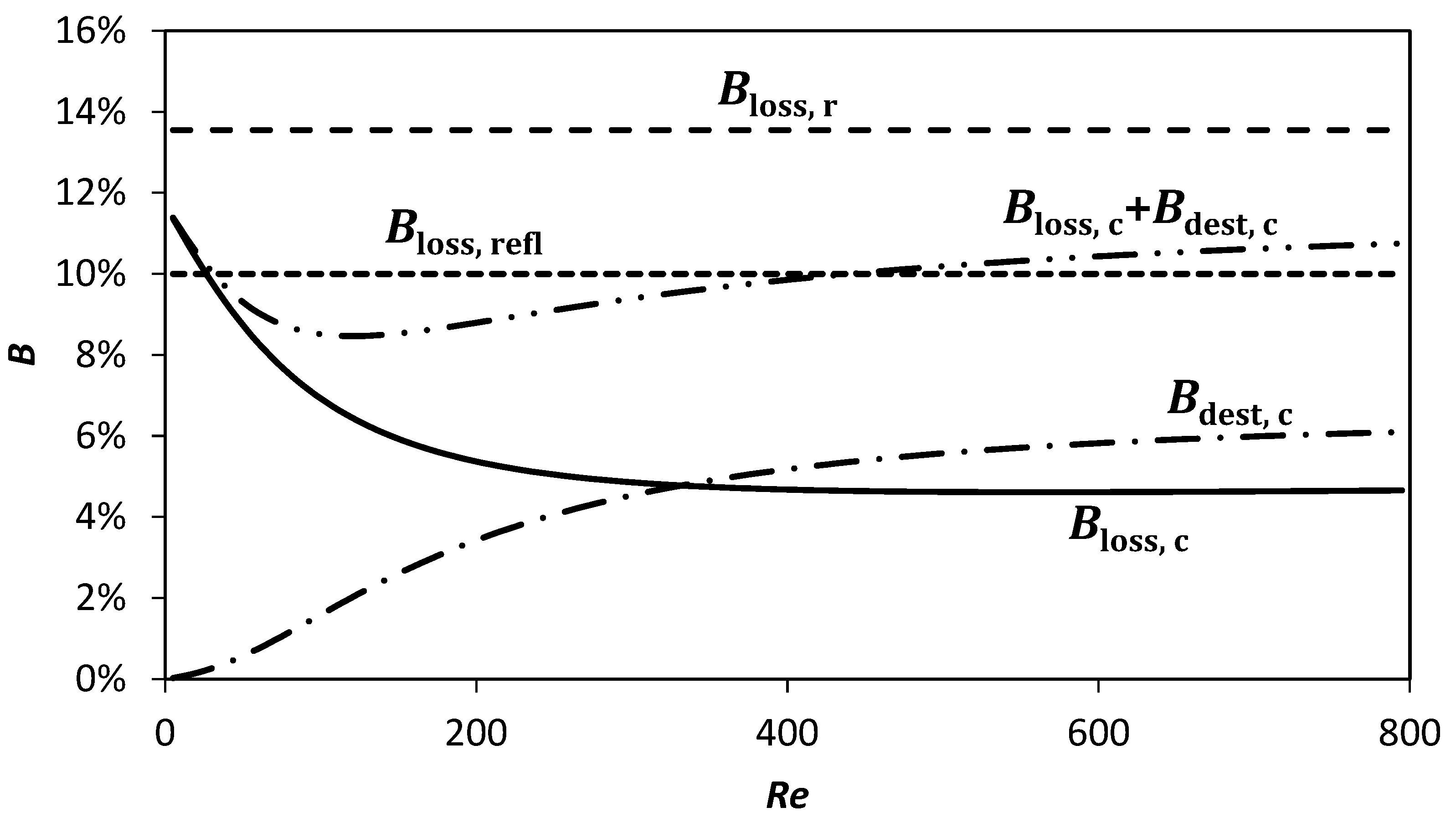
| (W/m) | |
| (W/m) | |
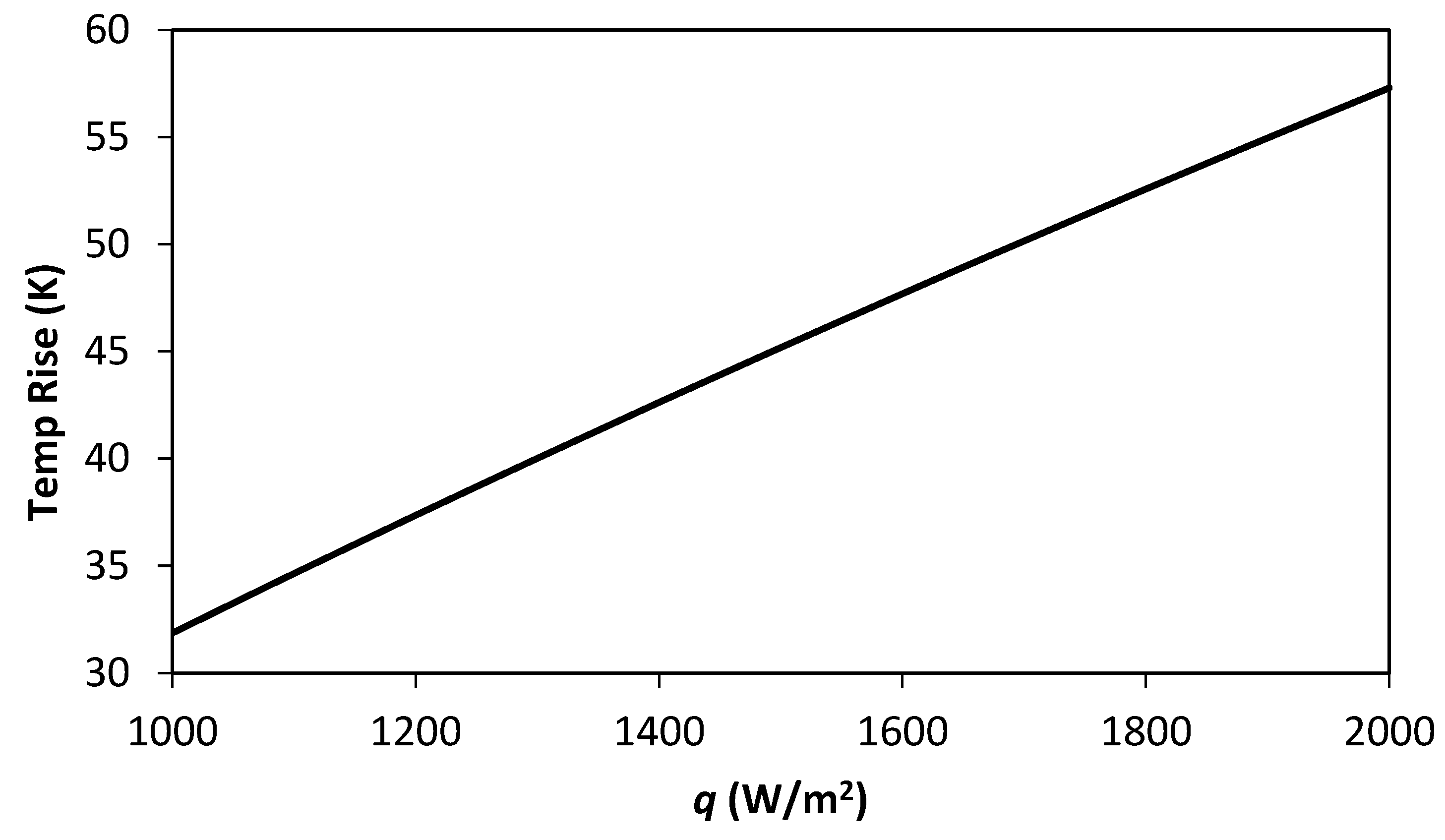
| (W/m2 K) | (K) |
| (K) | ||||
|---|---|---|---|---|
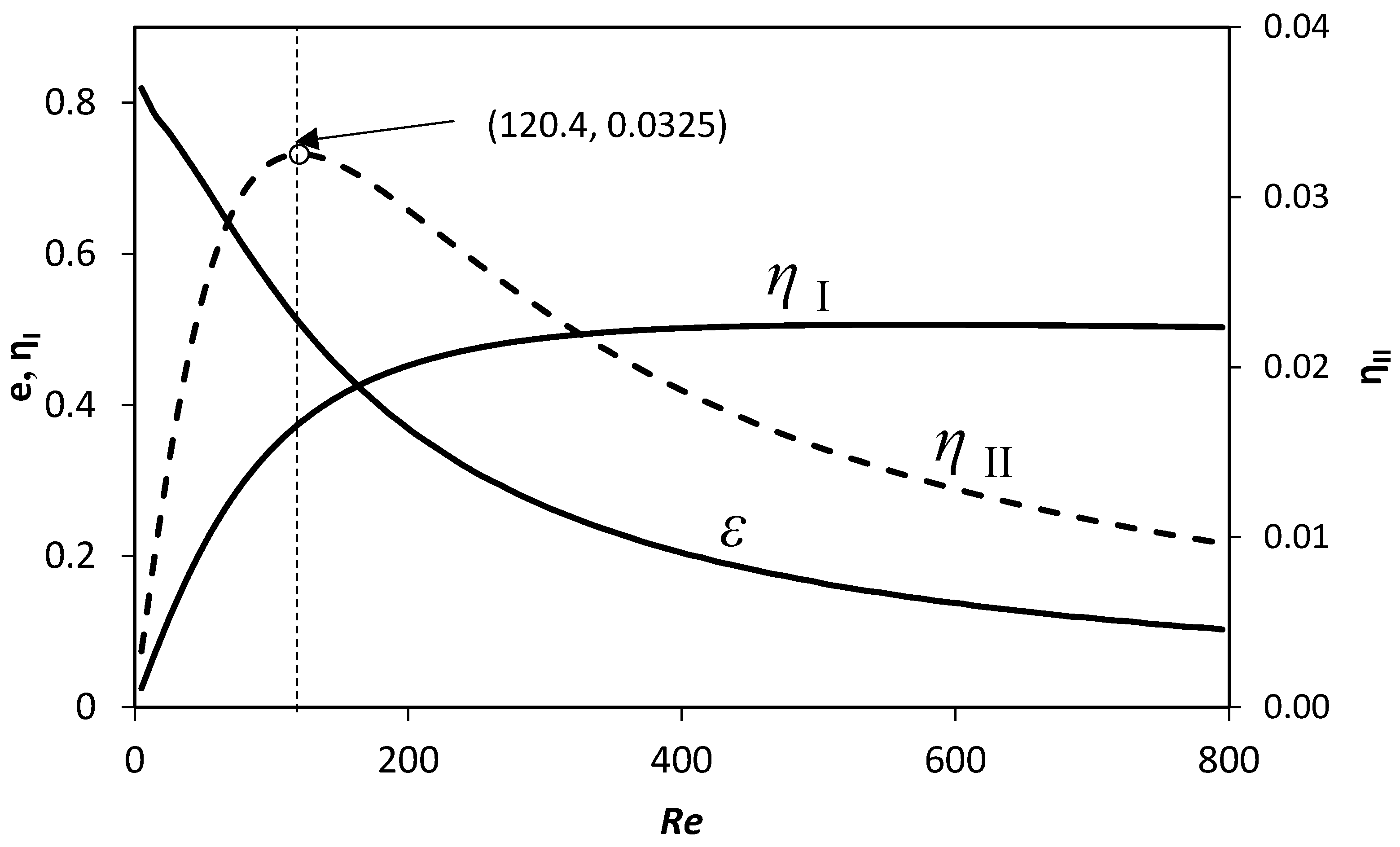
| 120.4 | 0.51 | 0.376 | 0.0325 | 354.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nemati, H. Design, Simulation and Optimization of a Novel Transpired Tubular Solar Air Heater. Energies 2024, 17, 2323. https://doi.org/10.3390/en17102323
Nemati H. Design, Simulation and Optimization of a Novel Transpired Tubular Solar Air Heater. Energies. 2024; 17(10):2323. https://doi.org/10.3390/en17102323
Chicago/Turabian StyleNemati, Hossain. 2024. "Design, Simulation and Optimization of a Novel Transpired Tubular Solar Air Heater" Energies 17, no. 10: 2323. https://doi.org/10.3390/en17102323
APA StyleNemati, H. (2024). Design, Simulation and Optimization of a Novel Transpired Tubular Solar Air Heater. Energies, 17(10), 2323. https://doi.org/10.3390/en17102323






