Optimizing High-Voltage Direct Current Transmission Corridors: Dynamic Thermal Line Rating for Enhanced Renewable Generation and Greenhouse Gas Emission Reductions
Abstract
1. Introduction
2. Principles of the Dynamic Thermal Line Rating (DTLR)
2.1. Overview of Technical Standards
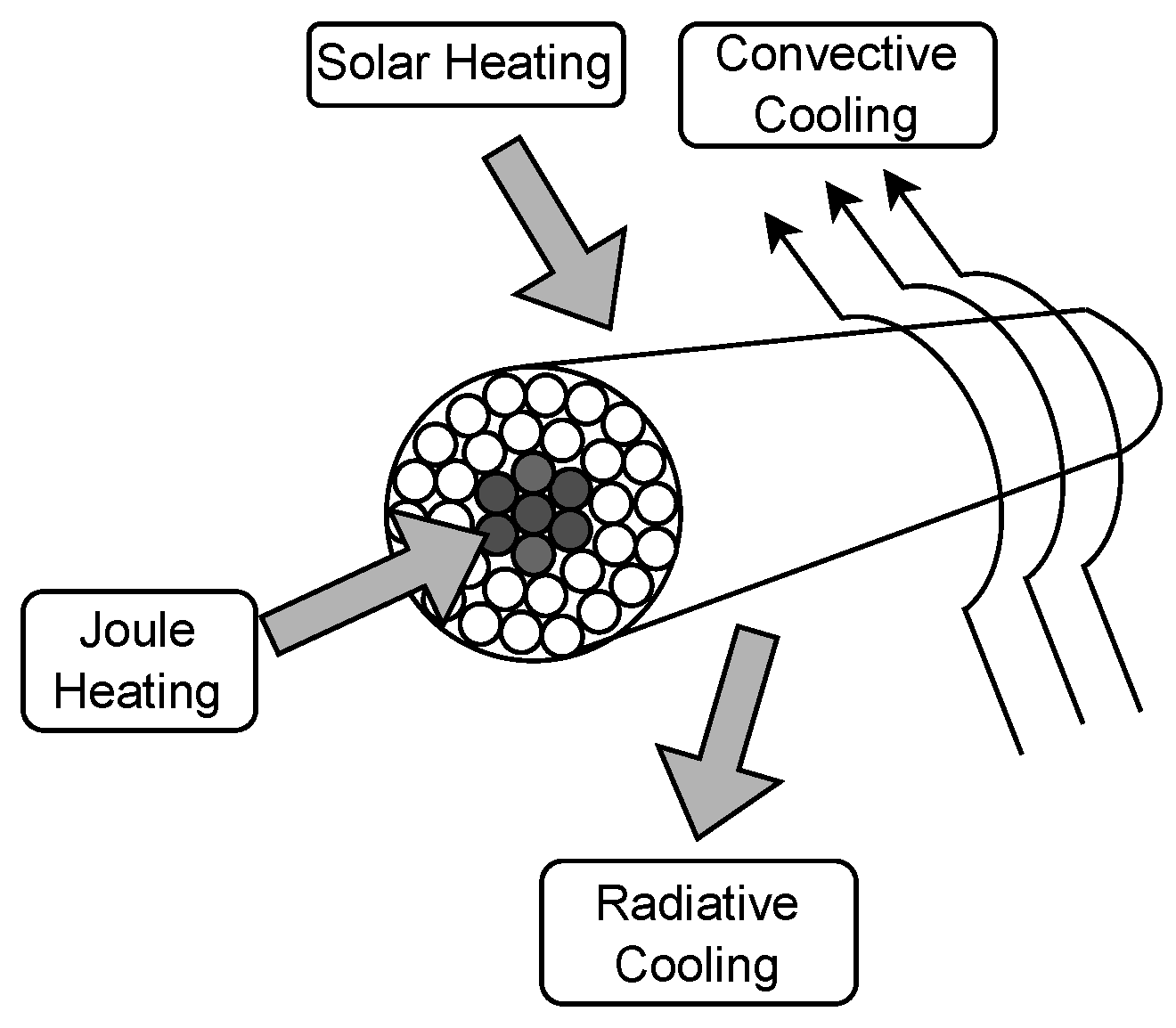
2.2. Mathematical Formulation
- convective cooling [W/m].
- radiative cooling [W/m].
- joule heating [W/m].
- solar heating [W/m].
2.3. Methods for Determining Dynamic Thermal Line Ratings
- 1.
- Thermal state monitoring:The thermal-monitoring-based approach relies on measuring the conductor temperature in real time to understand the line loading [39,40]. These devices are usually driven by the magnetic field generated by the conductor current. The Power Donut Line Monitor [41,42], smART SMT Sensor [40], FMC-T6, OTLM Device, Lindsey TLM system, and EMO are some examples. These devices are capable of measuring either all or a few of the following: the root mean square (RMS) current, voltage, power, conductor temperature, surface temperature, vibration, and sag [43].
- 2.
- Mechanical state monitoring:Mechanical-based approaches are based on measuring the line tension, sag, or clearance to the ground. The measured quantities can then be used to calculate the line temperature which is directly proportional to sag and inversely proportional to tension and clearance [39]. CAT-1 is a commercially available tension monitoring device that also has a separate system to measure the weather parameters indirectly [44].The Sagometer, which is based on image processing, is the only commercially available technology for real-time sag monitoring. There are some other proposed systems such as Ampacimon which measures sag via vibrations [40].
- 3.
- Weather parameter monitoring:Monitoring weather parameters such as the ambient temperature, wind speed, wind direction, and solar radiation is an indirect method of calculating the DTLR. This is the simplest yet the least disturbing system, as it is not necessary to install sensors on the line nor does it require any sort of communication methods such as fiber optic or satellite. Instead, the weather stations installed at the substations can be used [39].
3. GHG Emissions from the Electric Sector
4. HVDC System Case Study for DTLR Analysis
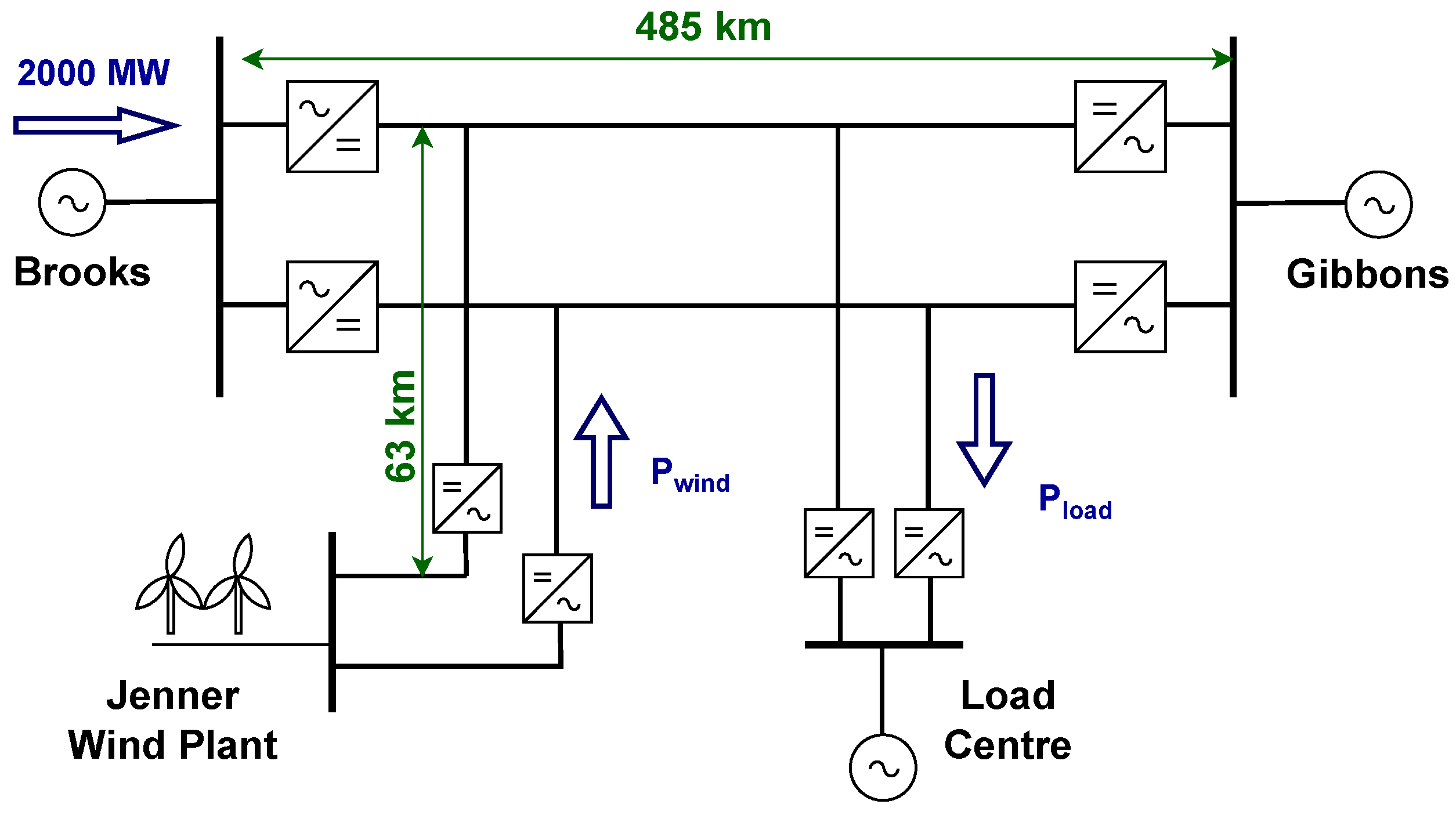
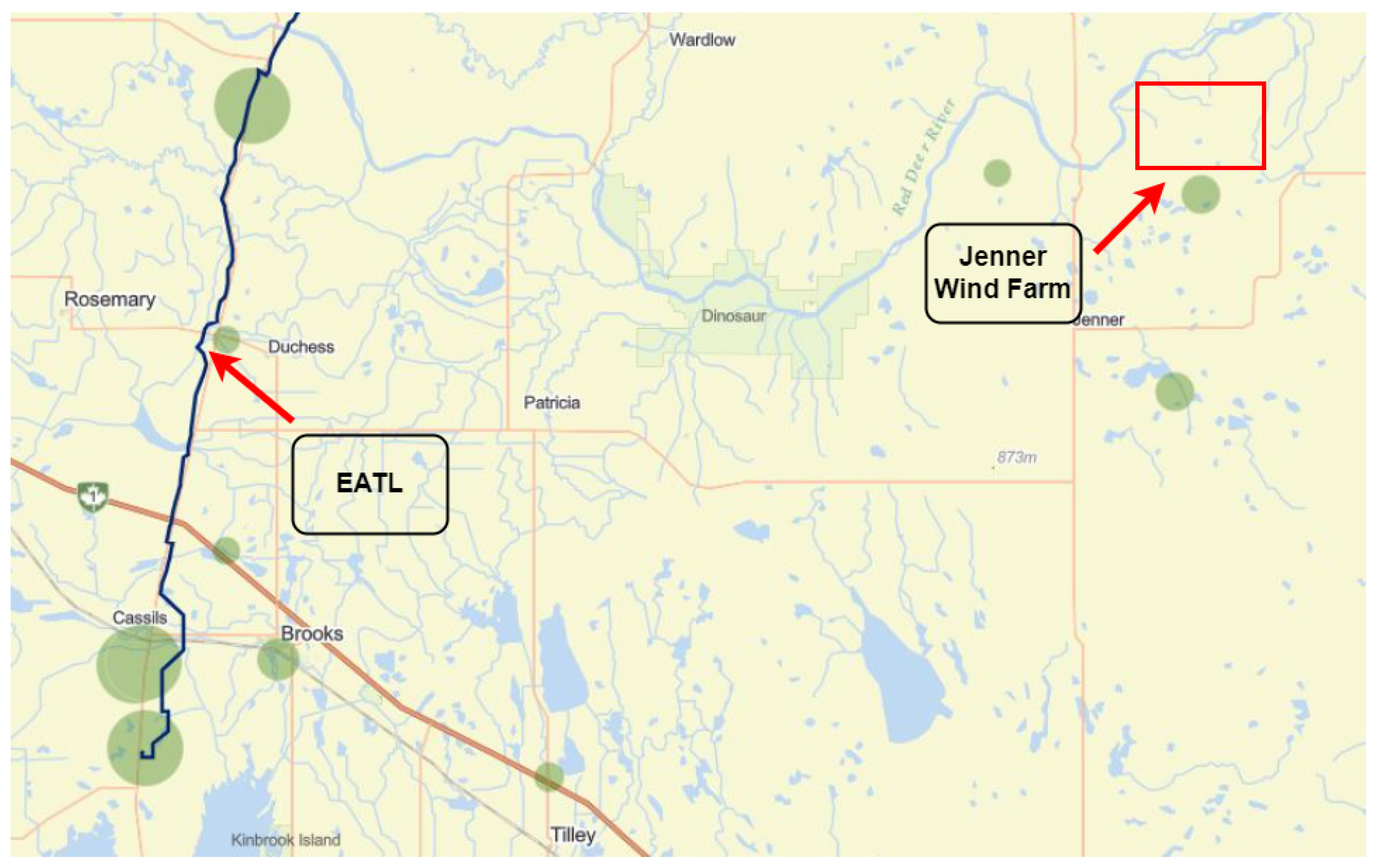
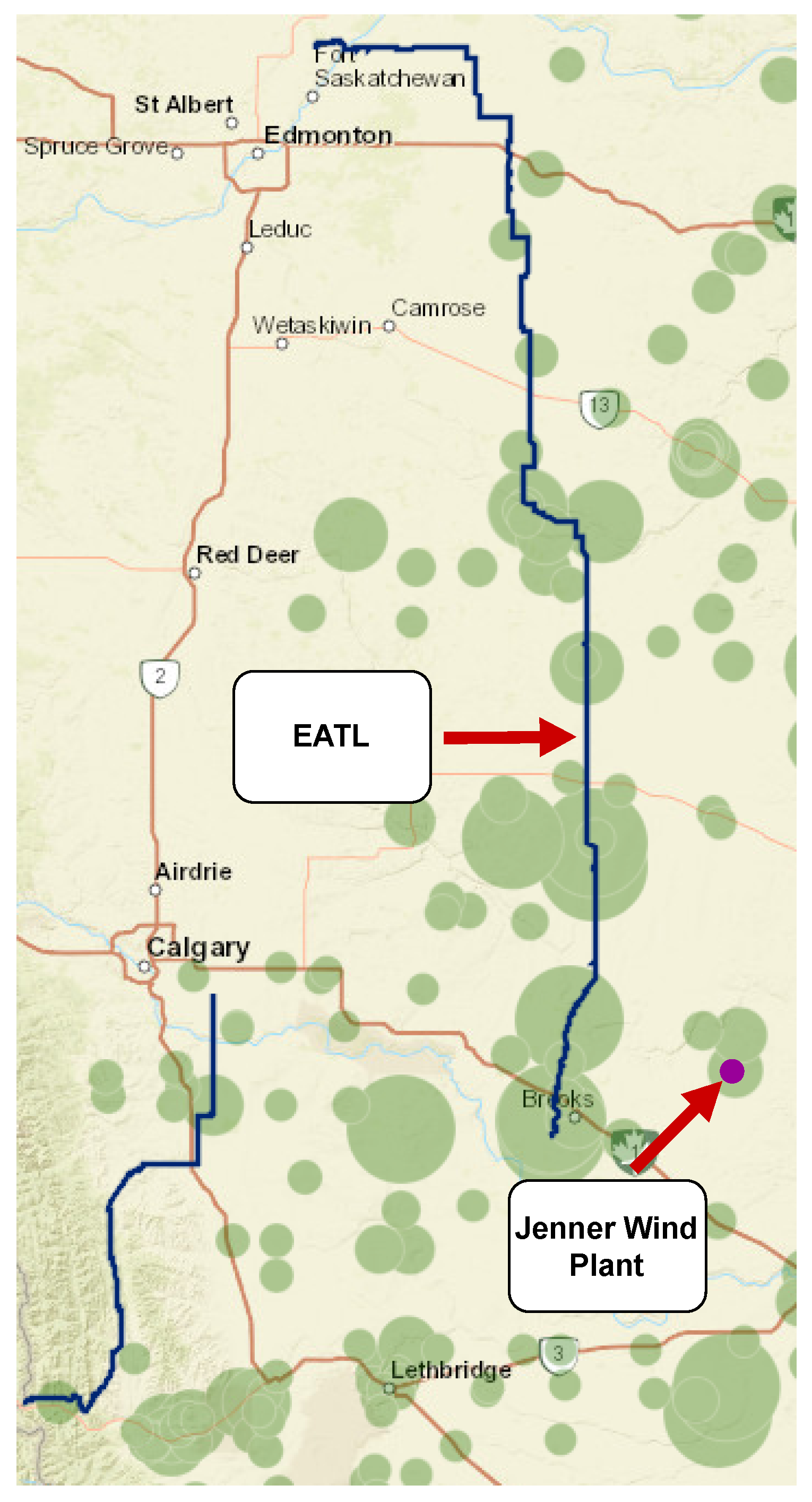
4.1. Study System
4.2. Meteorological Data Collection
4.3. Calculation Methodology
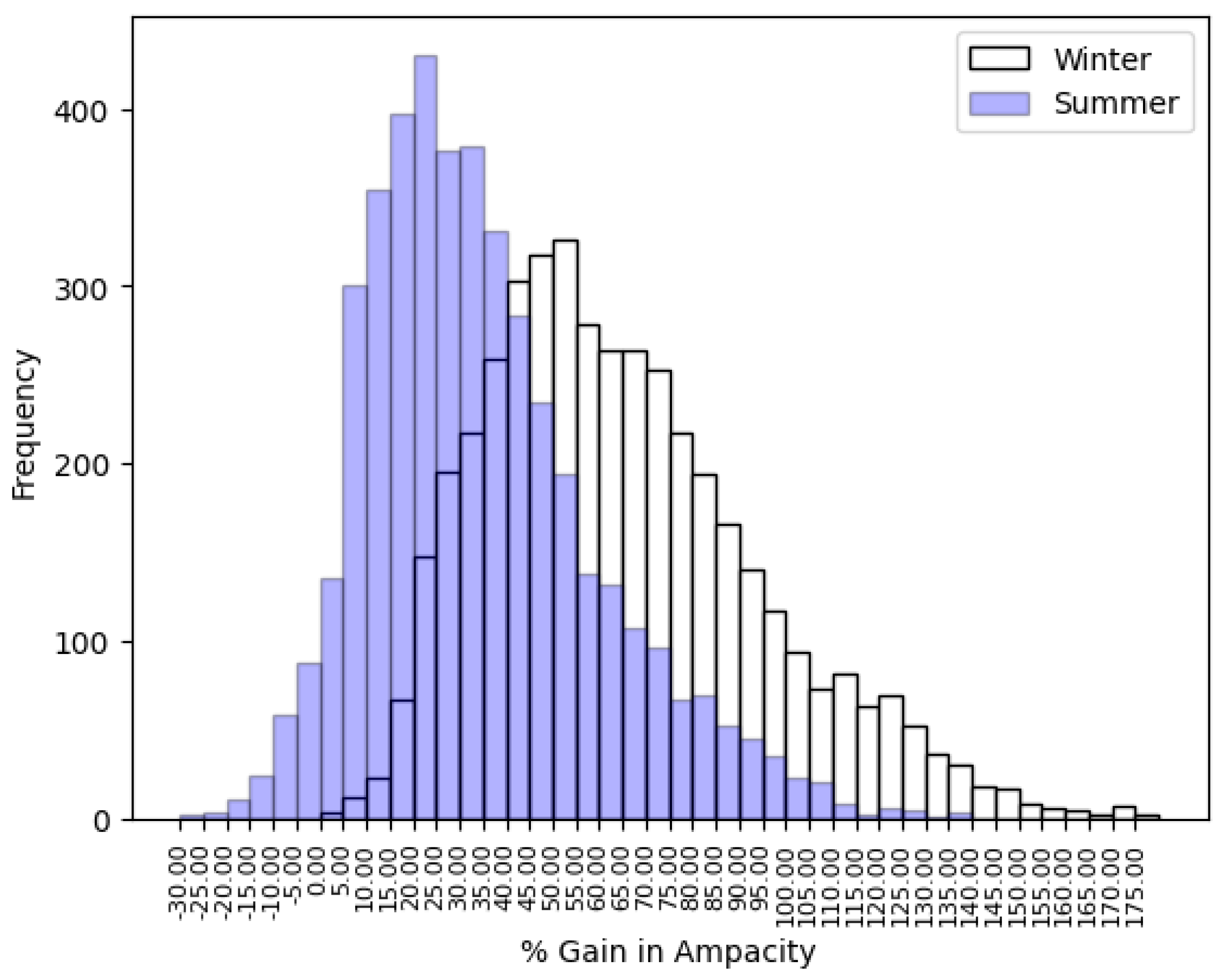
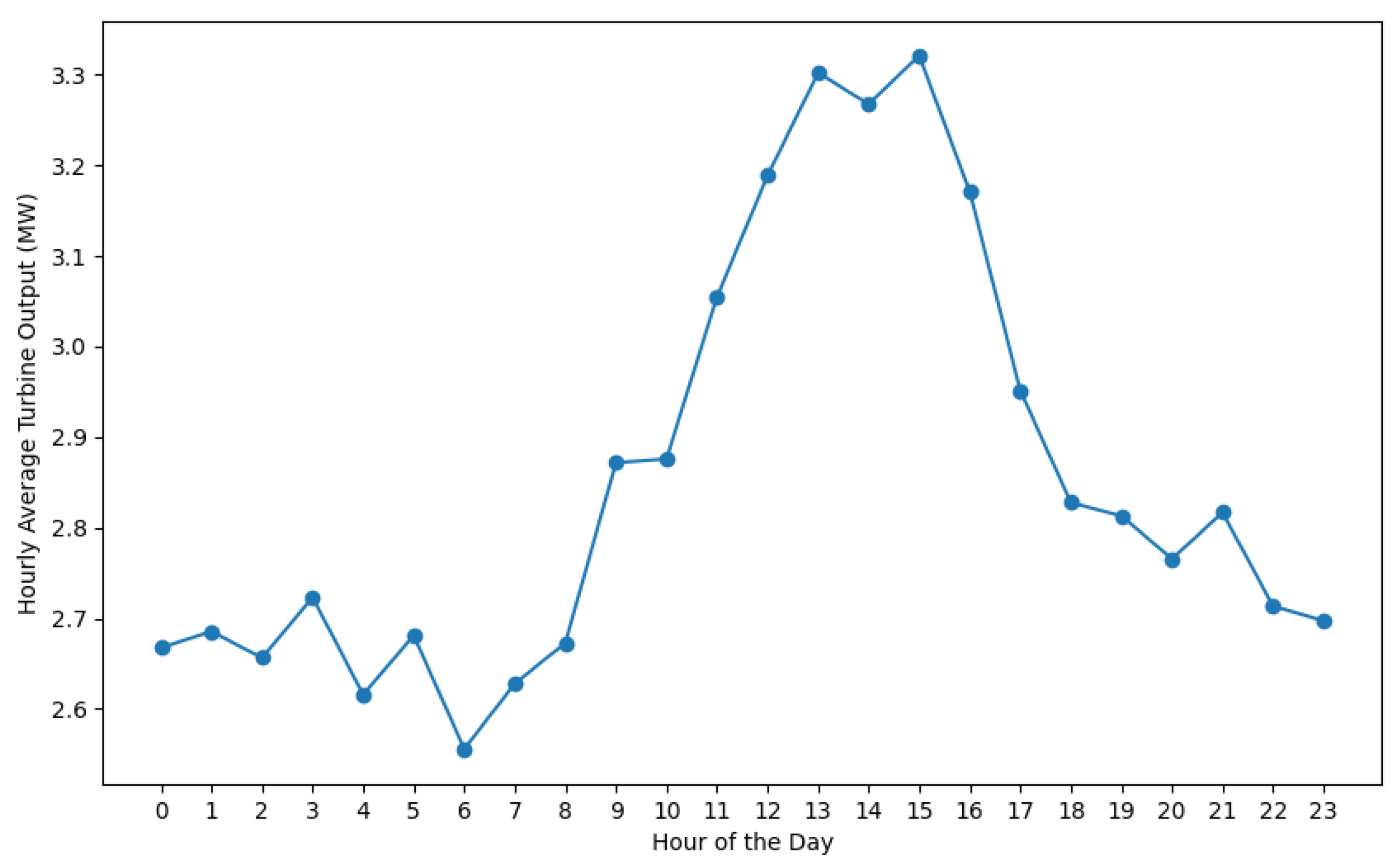
5. Results
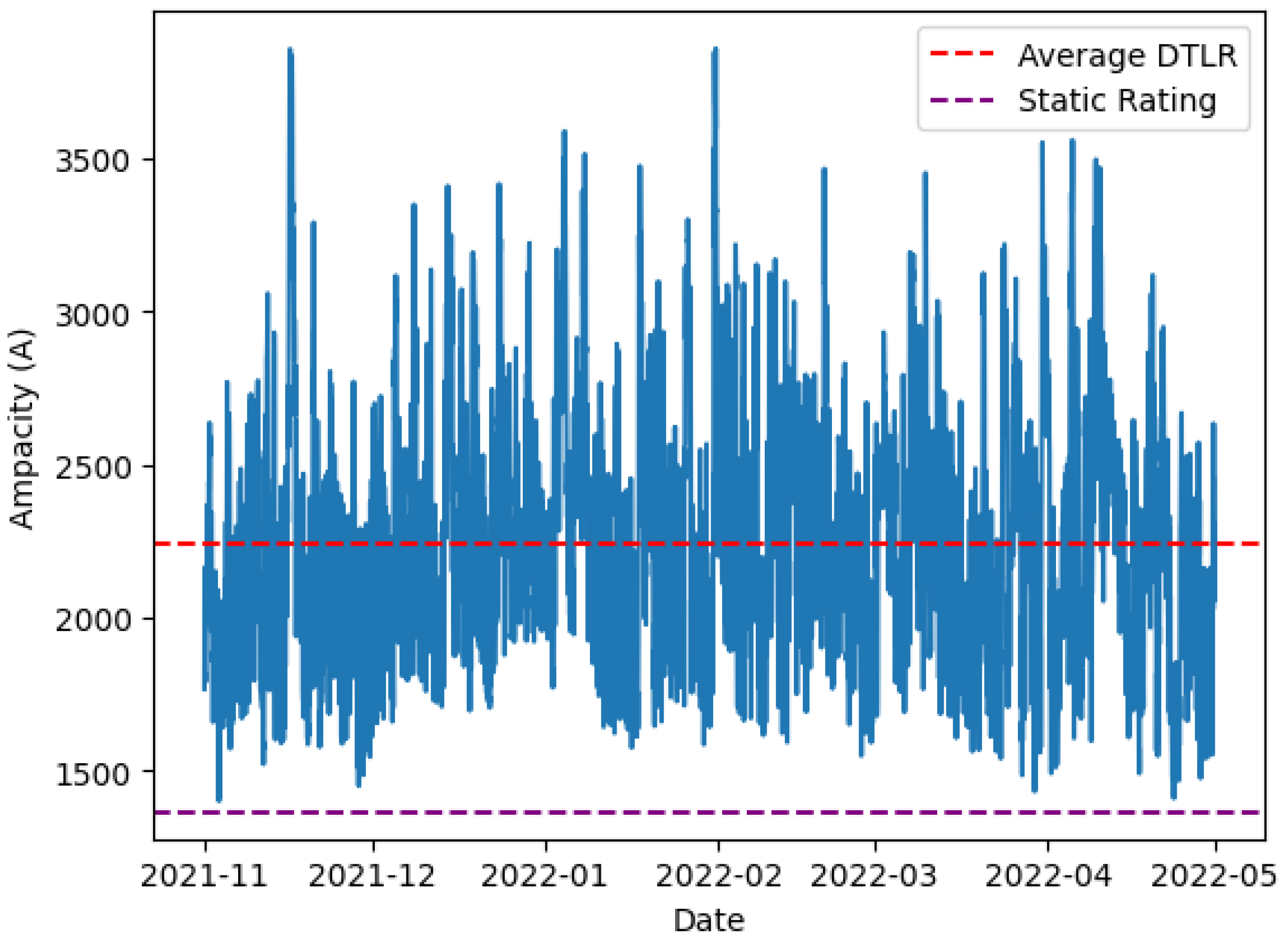
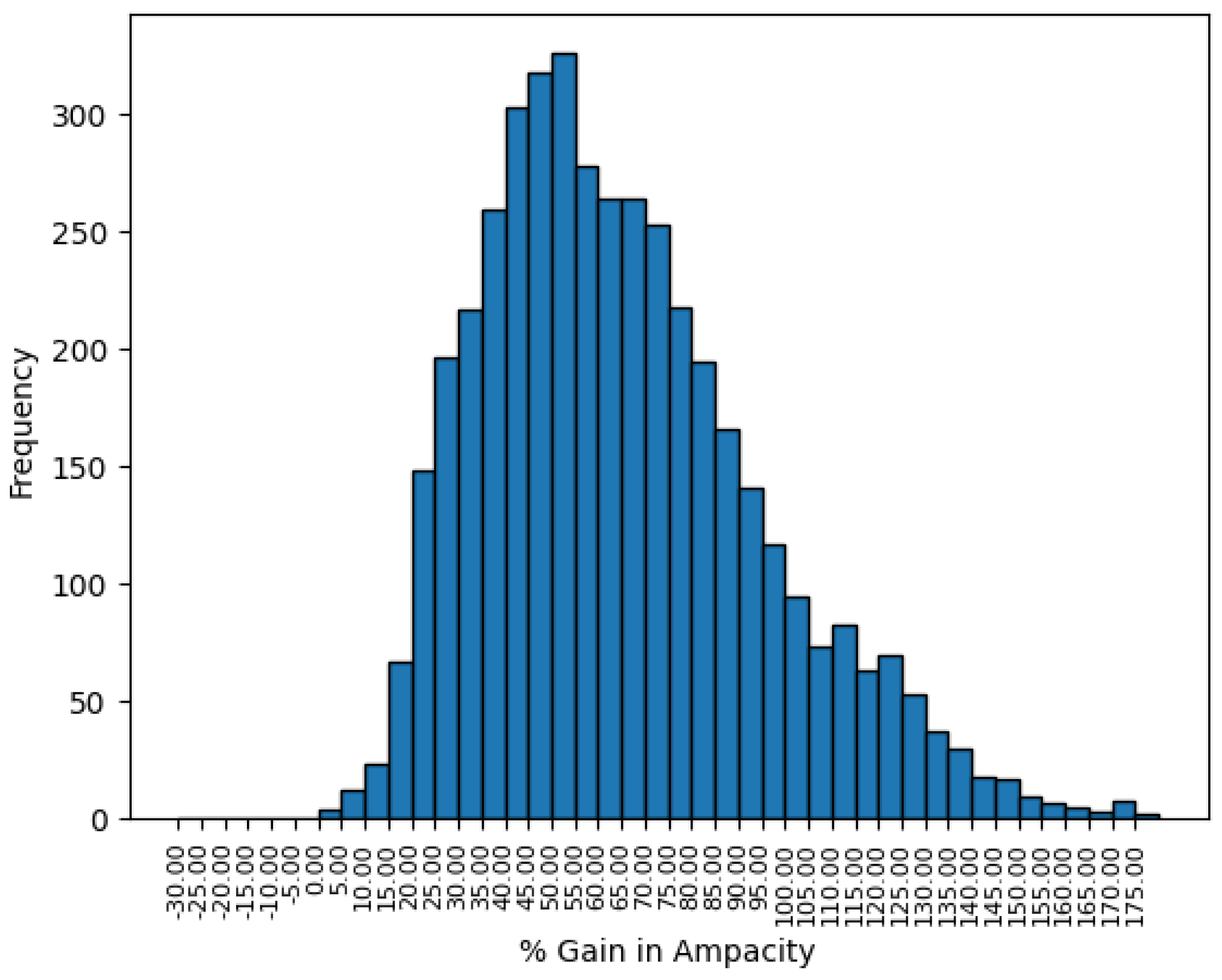
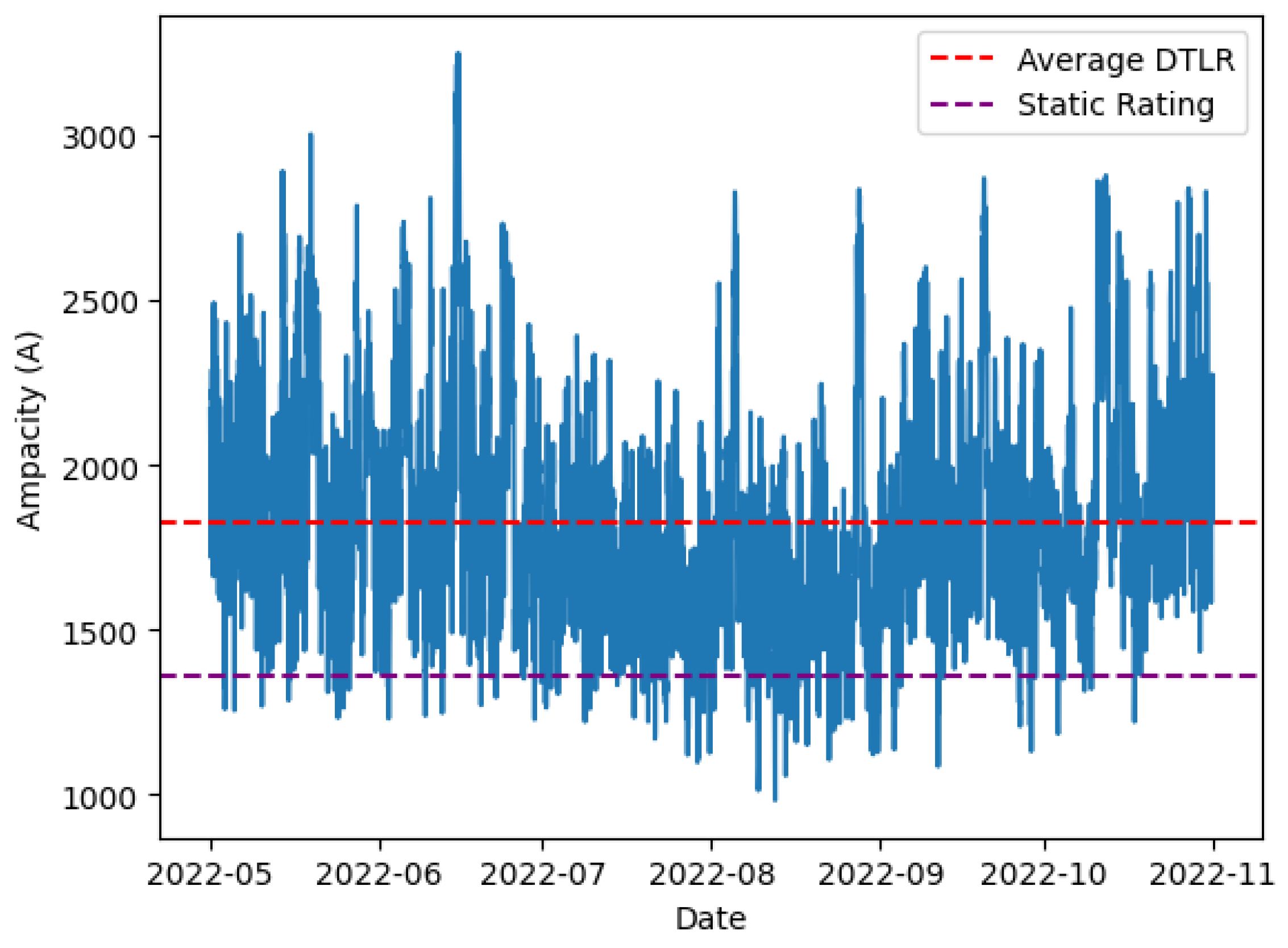
5.1. Dynamic Thermal Line Rating Calculation
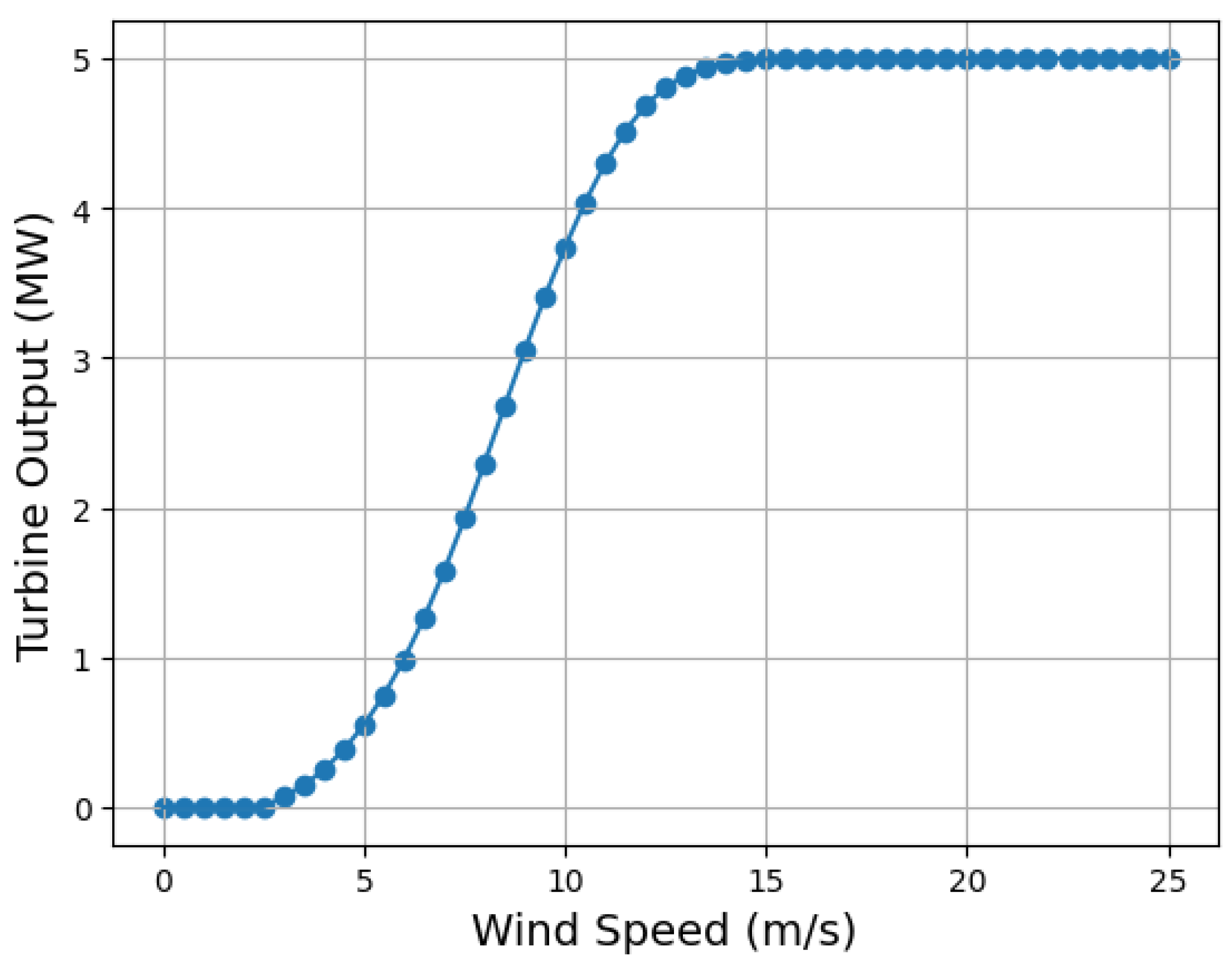
5.2. Wind Power Generation
5.3. GHG Reduction
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | alternating current |
| ACIS | Alberta Climate Information Service |
| ACSR | aluminium conductor steel-reinforced |
| AESO | Alberta Electric System Operator |
| DTLR | dynamic thermal line rating |
| EATL | Eastern Alberta transmission line |
| GHG | greenhouse gas |
| JWPP | Jenner wind power project |
| HVDC | high-voltage direct current |
| LCC | line-commutated converter |
| SR | static rating |
| VSC | voltage source converter |
| WATL | Western Alberta transmission line |
References
- Kacejko, P.; Wydra, M.; Nowak, W.; Szpyra, W.; Tarko, R. Advantages, Benefits, and Effectiveness Resulting from the Application of the Dynamic Management of Transmission Line Capacities. In Proceedings of the 2018 15th International Conference on the European Energy Market (EEM), Lodz, Poland, 27–29 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Bao, W.; Yan, Y.; Zhang, W.; Xin, J.; Li, Z.; Tang, R. Field study of a novel dynamic rating system for power transmission lines. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; pp. 1726–1731. [Google Scholar] [CrossRef]
- Foss, S.D.; Lin, S.H.; Fernandes, R.A. Dynamic Thermal Line Ratings Part I Dynamic Ampacity Rating Algorithm. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 1858–1864. [Google Scholar] [CrossRef]
- Bhattarai, B.P.; Gentle, J.P.; McJunkin, T.; Hill, P.J.; Myers, K.S.; Abboud, A.W.; Renwick, R.; Hengst, D. Improvement of Transmission Line Ampacity Utilization by Weather-Based Dynamic Line Rating. IEEE Trans. Power Deliv. 2018, 33, 1853–1863. [Google Scholar] [CrossRef]
- Fernandez, E.; Albizu, I.; Bedialauneta, M.; Mazon, A.; Leite, P. Review of dynamic line rating systems for wind power integration. Renew. Sustain. Energy Rev. 2016, 53, 80–92. [Google Scholar] [CrossRef]
- Michiorri, A.; Nguyen, H.M.; Alessandrini, S.; Bremnes, J.B.; Dierer, S.; Ferrero, E.; Nygaard, B.E.; Pinson, P.; Thomaidis, N.; Uski, S. Forecasting for dynamic line rating. Renew. Sustain. Energy Rev. 2015, 52, 1713–1730. [Google Scholar] [CrossRef]
- Morgan, V. Rating of bare overhead conductors for continuous currents. Proc. Inst. Electr. Eng. 1967, 114, 1473–1482. [Google Scholar] [CrossRef]
- House, H.E.; Tuttle, P.D. Current-Carrying Capacity of ACSR. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1958, 77, 1169–1173. [Google Scholar] [CrossRef]
- Davis, M. A new thermal rating approach: The real time thermal rating system for strategic overhead conductor transmission lines – Part I: General description and justification of the real time thermal rating system. IEEE Trans. Power Appar. Syst. 1977, 96, 803–809. [Google Scholar] [CrossRef]
- Raniga, J.; Rayudu, R. Dynamic rating of transmission lines-a New Zealand experience. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.00CH37077), Singapore, 23–27 January 2000; Volume 4, pp. 2403–2409. [Google Scholar] [CrossRef]
- Yip, T.; An, C.; Lloyd, G.; Aten, M.; Ferri, B. Dynamic line rating protection for wind farm connections. In Proceedings of the 2009 CIGRE/IEEE PES Joint Symposium Integration of Wide-Scale Renewable Resources Into the Power Delivery System, Glasgow, UK, 17–20 March 2008; pp. 1–5. [Google Scholar]
- Cloet, E.; Lilien, J.L. Uprating Transmission Lines through the use of an innovative real-time monitoring system. In Proceedings of the 2011 IEEE PES 12th International Conference on Transmission and Distribution Construction, Operation and Live-Line Maintenance (ESMO), Providence, RI, USA, 16–19 May 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Kim, S.D.; Morcos, M.M. An Application of Dynamic Thermal Line Rating Control System to Up-Rate the Ampacity of Overhead Transmission Lines. IEEE Trans. Power Deliv. 2013, 28, 1231–1232. [Google Scholar] [CrossRef]
- Glaum, P.; Hofmann, F. Leveraging the existing German transmission grid with dynamic line rating. Appl. Energy 2023, 343, 121199. [Google Scholar] [CrossRef]
- Wijethunga, A.; Wijayakulasooriya, J.; Ekanayake, J.; De Silva, N. Conductor temperature based low cost solution for dynamic line rating calculation of power distribution lines. In Proceedings of the 2015 IEEE 10th International Conference on Industrial and Information Systems (ICIIS), Peradeniya, Sri Lanka, 18–20 December 2015; pp. 128–133. [Google Scholar] [CrossRef]
- Negari, S.; Raahemifar, K.; Xu, D. Predictive line rating in underground transmission lines going beyond dynamic line rating. In Proceedings of the 2016 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Vancouver, BC, Canada, 15–18 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Hertem, D.V.; Gomis-Bellmunt, O.; Liang, J. LCC-HVDC Systems. In HVDC Grids—For Offshore and Supergrid of the Future; John Wiley & Sons: Hoboken, NJ, USA, 2016; Chapter 3.2. [Google Scholar]
- Pytlak, P.; Musilek, P.; Doucet, J. Using Dynamic Thermal Rating systems to reduce power generation emissions. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Alberta Electric System Operator. AESO 2022 Long-term Transmission Plan. In Technical Report; Alberta Electric System Operator: Calgary, AB, Canada, 2022. [Google Scholar]
- Rajaram, H.R.; Balamurugan, G. A Study on Green House Gas Mitigation from Solar Parks in India. In Proceedings of the 2020 International Conference and Utility Exhibition on Energy, Environment and Climate Change (ICUE), Pattaya, Thailand, 20–22 October 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Paraschiv, L.S.; Paraschiv, S. Contribution of renewable energy (hydro, wind, solar and biomass) to decarbonization and transformation of the electricity generation sector for sustainable development. Energy Rep. 2023, 9, 535–544. [Google Scholar] [CrossRef]
- Fernandez, E.; Albizu, I.; Buigues, G.; Valverde, V.; Etxegarai, A.; Olazarri, J.G. Dynamic line rating forecasting based on numerical weather prediction. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Abdelkader, S.; Morrow, D.; Fu, J.; Abbot, S. Field Measurement Based PLS Model for Dynamic Rating of Overhead Lines in Wind Intensive Areas. Renew. Energy Power Qual. J. 2013, 1, 808–813. [Google Scholar] [CrossRef]
- Schell, P.; Lambin, J.; Godard, B.; Nguyen, H.M.; Lilien, J.L. Using Dynamic Line Rating to Minimize Curtailment of Wind Power Connected to Rural Power Networks. In Proceedings of the 10th International Workshop on Large-Scale Integration of Wind Power into Power Systems, Aarhus, Denmark, 25–26 October 2011. [Google Scholar]
- Talpur, S.; Wallnerstrom, C.J.; Flood, C.; Hilber, P. Implementation of Dynamic Line Rating in a Sub-Transmission System for Wind Power Integration. Smart Grid Renew. Energy 2015, 6, 233–249. [Google Scholar] [CrossRef][Green Version]
- Sun, J.; Li, M.; Zhang, Z.; Xu, T.; He, J.; Wang, H.; Li, G.J. Renewable energy transmission by HVDC across the continent: System challenges and opportunities. CSEE J. Power Energy Syst. 2017, 3, 353–364. [Google Scholar] [CrossRef]
- Borbáth, T.; Chaffey, G.; Kaushal, A.; Van Hertem, D. Dynamic rating of HVDC interconnectors. In Proceedings of the 19th International Conference on AC and DC Power Transmission (ACDC 2023), Glasgow, UK, 1 March 2023; Volume 2023, pp. 254–259. [Google Scholar] [CrossRef]
- Britned. Dynamic Rating Trial. Available online: https://www.britned.com/knowledge-base/britned-basics/dynamic-rating-trial/ (accessed on 25 September 2023).
- Nemo Link. Nemo Link Announces Transient Overflow Facility. Available online: https://www.nemolink.co.uk/news-news/nemo-link-announces-transient-overflow-facility-2/ (accessed on 25 September 2023).
- Nord Pool Group. Principles for Determining the Transfer Capacities. Available online: https://www.nordpoolgroup.com/493abd/globalassets/download-center/tso/principles-for-determining-the-transfer-capacities-2023-03-23.pdf (accessed on 25 September 2023).
- Aidong, X.; Xiaochen, W.; Chao, H.; Xiaoming, J.; Peng, L. Study on Overload Capability and Its Application of HVDC Transmission System in China Southern Power Grid. In Proceedings of the 2007 IEEE Power Engineering Society Conference and Exposition in Africa—PowerAfrica, Johannesburg, South Africa, 16–20 July 2007; pp. 1–4. [Google Scholar] [CrossRef]
- Alberta Electric System Operator. AESO 2020 Long-Term Transmission Plan; Technical Report; Alberta Electric System Operator: Calgary, AB, Canada, 2020. [Google Scholar]
- Alberta Electric System Operator. Current Supply Demand Report; Technical Report; Alberta Electric System Operator: Calgary, AB, Canada, 2023. [Google Scholar]
- CIGRE WG B2. 42. Guide for Thermal Rating Calculations of Overhead Lines. In Technical Report Technical Brochure 601; CIGRE: Paris, France, 2014. [Google Scholar]
- IEEE Std 738-2012 (Revision of IEEE Std 738-2006–Incorporates IEEE Std 738-2012 Cor 1-2013); IEEE Standard for Calculating the Current-Temperature Relationship of Bare Overhead Conductors. IEEE: Piscataway, NJ, USA, 2013; pp. 1–72. [CrossRef]
- Staszewski, L.; Rebizant, W. The differences between IEEE and CIGRE heat balance concepts for line ampacity considerations. In Proceedings of the 2010 Modern Electric Power Systems, Wroclaw, Poland, 20–22 September 2010; pp. 1–4. [Google Scholar]
- Morgan, V. The thermal rating of overhead-line conductors Part I. The steady-state thermal model. Electr. Power Syst. Res. 1982, 5, 119–139. [Google Scholar] [CrossRef]
- Schmidt, N. Comparison between IEEE and CIGRE ampacity standards. IEEE Trans. Power Deliv. 1999, 14, 1555–1559. [Google Scholar] [CrossRef]
- Erdinç, F.G.; Erdinç, O.; Yumurtacı, R.; Catalão, J.P.S. A Comprehensive Overview of Dynamic Line Rating Combined with Other Flexibility Options from an Operational Point of View. Energies 2020, 13, 6563. [Google Scholar] [CrossRef]
- Fernandez, E.; Albizu, I.; Bedialauneta, M.; Mazon, A.; Leite, P. Dynamic line rating systems for wind power integration. In Proceedings of the IEEE Power and Energy Society Conference and Exposition in Africa: Intelligent Grid Integration of Renewable Energy Resources (PowerAfrica), Johannesburg, South Africa, 9–13 July 2012; pp. 1–7. [Google Scholar] [CrossRef]
- Foss, S.D.; Lin, S.H.; Stillwell, H.R.; Fernandes, R.A. Dynamic Thermal Line Ratings Part II Conductor Temperature Sensor and Laboratory Field test Evaluation. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 1865–1876. [Google Scholar] [CrossRef]
- Engelhardt, J.; Basu, S. Design, installation, and field experience with an overhead transmission dynamic line rating system. In Proceedings of the 1996 Transmission and Distribution Conference and Exposition, Los Angeles, CA, USA, 15–20 September 1996; pp. 366–370. [Google Scholar] [CrossRef]
- Akpolat, A.N.; Nese, S.V.; Dursun, E. Towards to smart grid: Dynamic line rating. In Proceedings of the 2018 6th International Istanbul Smart Grids and Cities Congress and Fair (ICSG), Istanbul, Turkey, 25–26 April 2018; pp. 96–100. [Google Scholar] [CrossRef]
- Black, C.R.; Chisholm, W.A. Key Considerations for the Selection of Dynamic Thermal Line Rating Systems. IEEE Trans. Power Deliv. 2015, 30, 2154–2162. [Google Scholar] [CrossRef]
- Ahmed, I.; Rehan, M.; Basit, A.; Hong, K.S. Greenhouse gases emission reduction for electric power generation sector by efficient dispatching of thermal plants integrated with renewable systems. Sci. Rep. 2022, 12, 12380. [Google Scholar] [CrossRef] [PubMed]
- Alberta Public Affairs Bureaur. Jenner Wind Project (Phase 1, 2, and 3). Available online: https://majorprojects.alberta.ca/details/Jenner-Wind-Project-Phase-1-2-and-3/4443 (accessed on 4 October 2023).
- For International Development Cooperation RoAid, R.A. The Expansion of the Qartli Wind Farm—A Study of Opportunity, 2019.Technical Report; Ridgeline Industrial, Bucuresti, Romania. 2020. Available online: https://ridgeline-industrial.ro/Georgia_III_Report-50MW_and_Hydrogen_V1_10-Nov-2020.pdf (accessed on 20 August 2023).
- Alberta Climate Information Service. Available online: https://acis.alberta.ca (accessed on 20 August 2023).





| Technology | Avg. CO2 per kWh |
|---|---|
| Wood | 1500 g |
| Coal | 800–1050 g |
| Natural gas | 430 g |
| Photovoltaic solar | 60–150 g |
| Nuclear | 6 g |
| Hydro | 4 g |
| Wind | 3–22 g |
| Compound | Avg. CO2 per kWh |
|---|---|
| Carbon Dioxide () | 371.95 g |
| Sulphur Dioxide () | 2.72 g |
| Nitrogen Oxides () | 1.81 g |
| Methane () | 476.27 g |
| Mercury () | 4.08 × g |
| Parameter | Value |
|---|---|
| Conductor type | 1590 Falcon |
| Nominal rating | 1359 A |
| Inside diameter | 13.08 mm |
| Outside diameter | 39.22 mm |
| DC resistance at 20 °C | |
| DC resistance at 50 °C | |
| Absorptivity | 0.8 |
| Emissivity | 0.8 |
| Parameter | Value |
|---|---|
| Turbine model | Enercon E-147 |
| Number of turbines | 13 |
| Rated Power | 5000 kW |
| Cut-in speed | 2.5 m/s |
| Cut-out speed | 25 m/s |
| Hub height | 126 m |
| Compound | Avg. (t/h) from JWPP2 |
|---|---|
| Carbon Dioxide | 13.78 |
| Sulphur Dioxide | 0.10 |
| Nitrogen Oxides | 0.067 |
| Methane | 15.79 |
| Mercury | 1.51 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pemachandra, V.; Musilek, P.; Kish, G. Optimizing High-Voltage Direct Current Transmission Corridors: Dynamic Thermal Line Rating for Enhanced Renewable Generation and Greenhouse Gas Emission Reductions. Energies 2024, 17, 2318. https://doi.org/10.3390/en17102318
Pemachandra V, Musilek P, Kish G. Optimizing High-Voltage Direct Current Transmission Corridors: Dynamic Thermal Line Rating for Enhanced Renewable Generation and Greenhouse Gas Emission Reductions. Energies. 2024; 17(10):2318. https://doi.org/10.3390/en17102318
Chicago/Turabian StylePemachandra, Veenavi, Petr Musilek, and Gregory Kish. 2024. "Optimizing High-Voltage Direct Current Transmission Corridors: Dynamic Thermal Line Rating for Enhanced Renewable Generation and Greenhouse Gas Emission Reductions" Energies 17, no. 10: 2318. https://doi.org/10.3390/en17102318
APA StylePemachandra, V., Musilek, P., & Kish, G. (2024). Optimizing High-Voltage Direct Current Transmission Corridors: Dynamic Thermal Line Rating for Enhanced Renewable Generation and Greenhouse Gas Emission Reductions. Energies, 17(10), 2318. https://doi.org/10.3390/en17102318







