A Study of the Thermal Management and Discharge Strategies of Lithium-Ion Batteries in a Wide Temperature Range
Abstract
1. Introduction
2. Methods and Validation
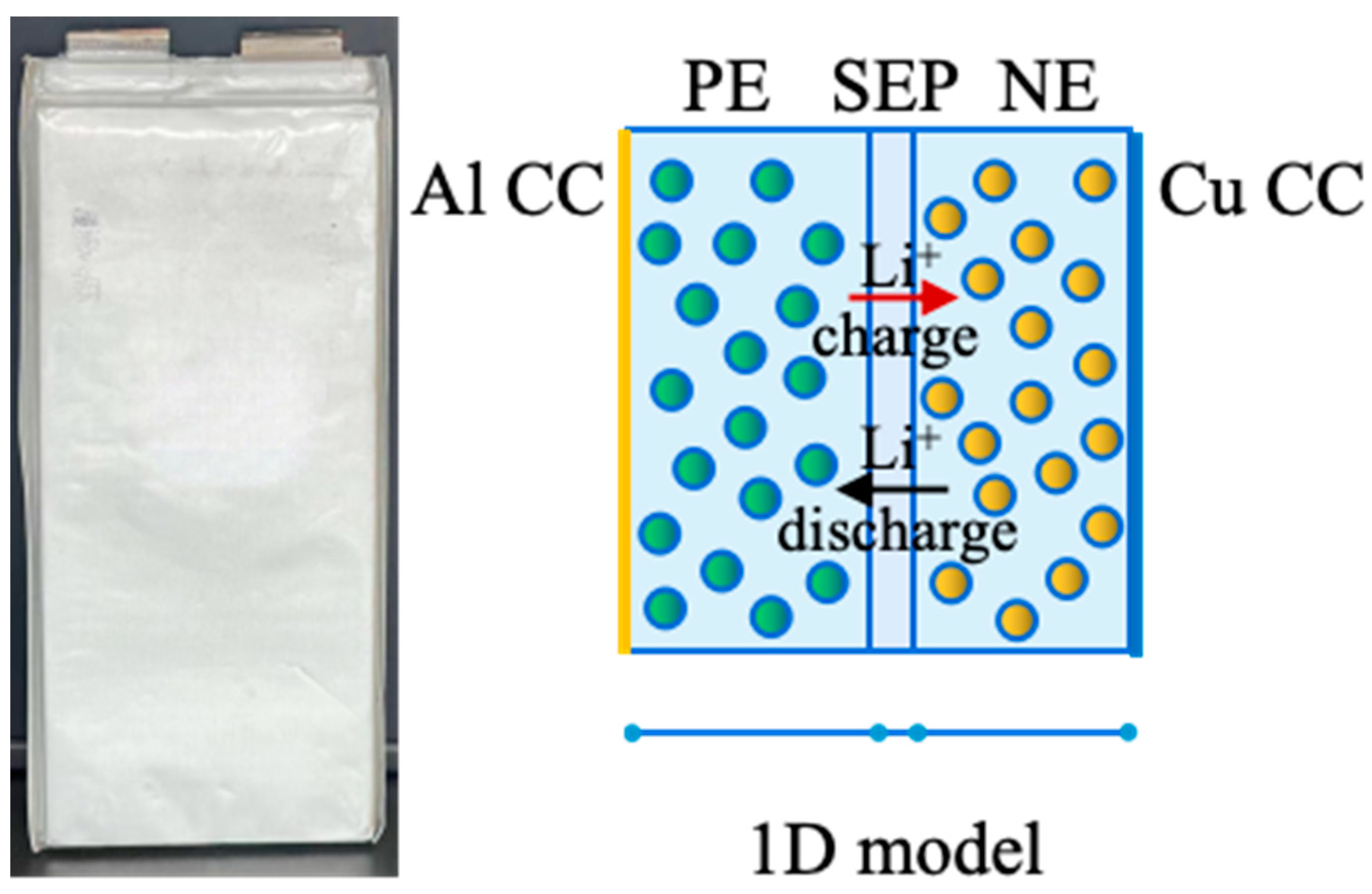
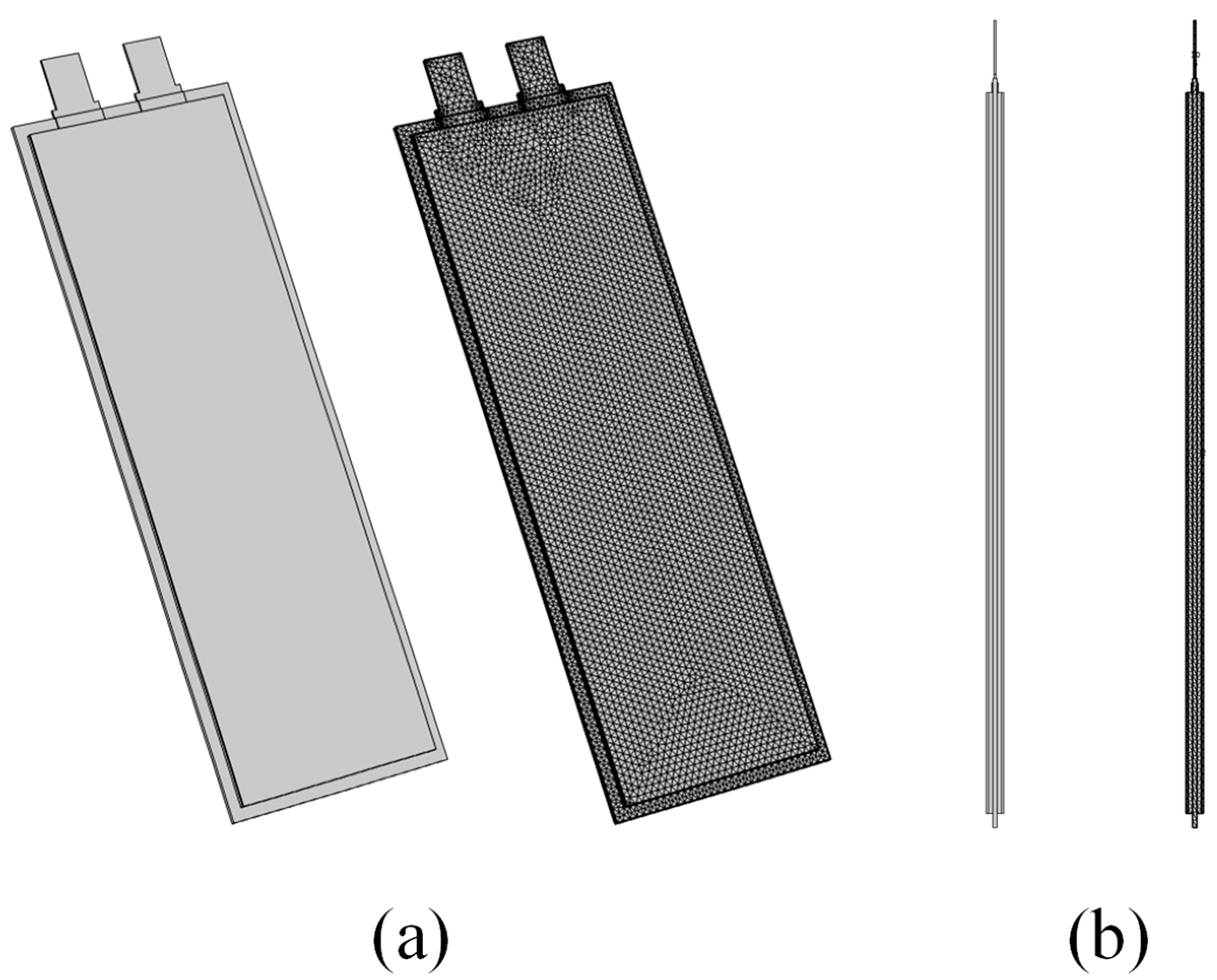
2.1. Model Description
2.1.1. Electrochemical Model
2.1.2. Thermal Model
2.2. Model Parameters
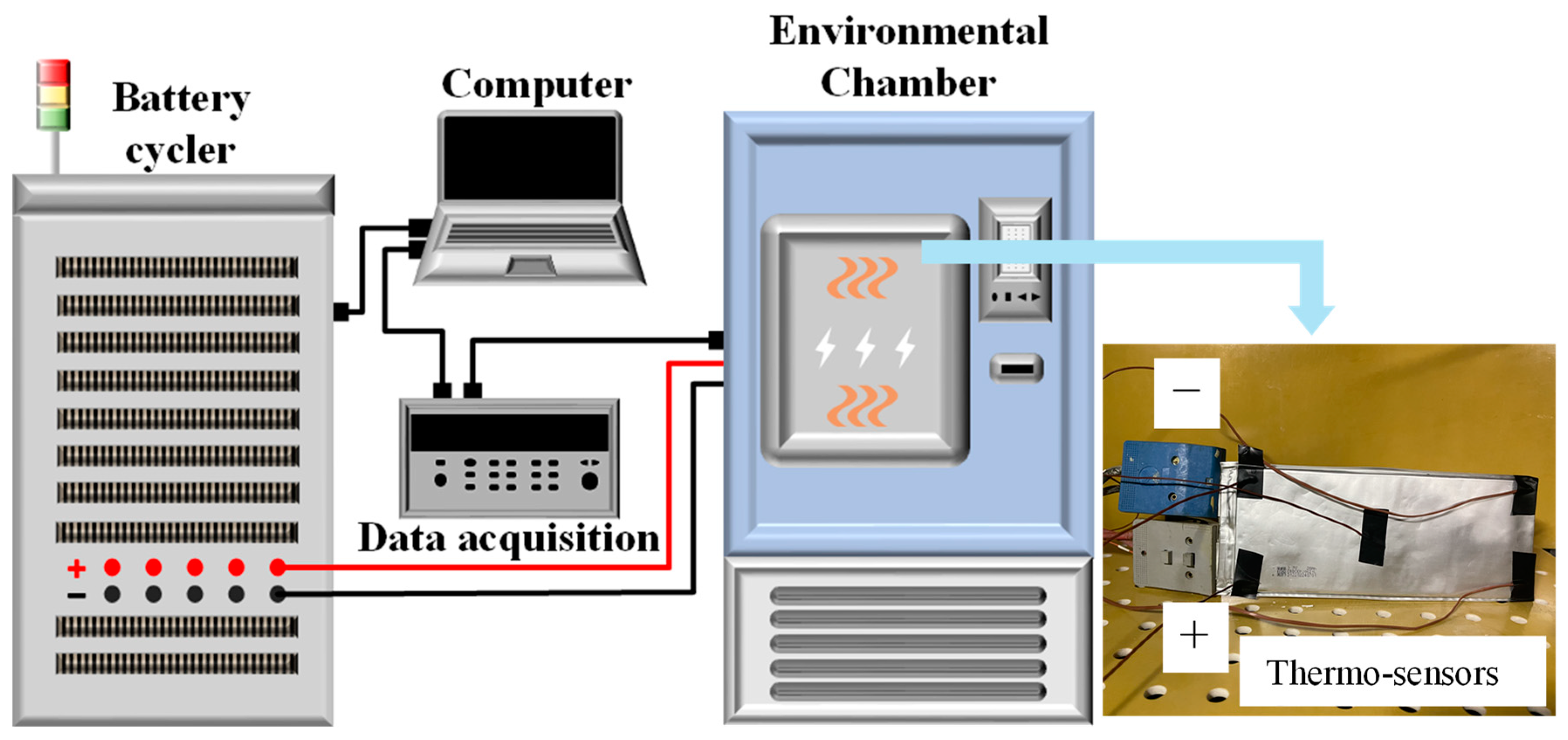
2.3. Model Validation
3. Results and Discussion
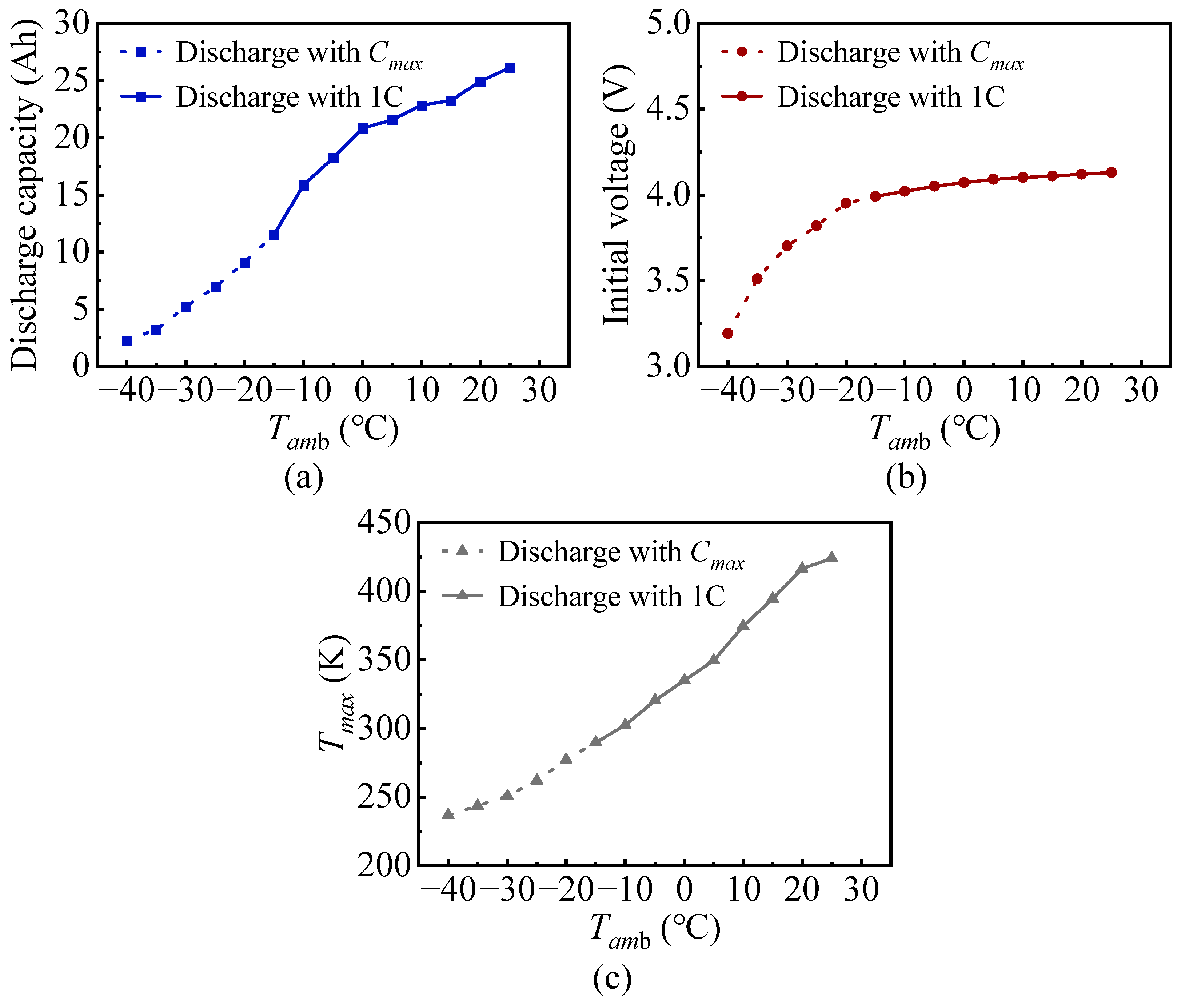
3.1. The Impact of the Tamb on Battery Discharge Rate
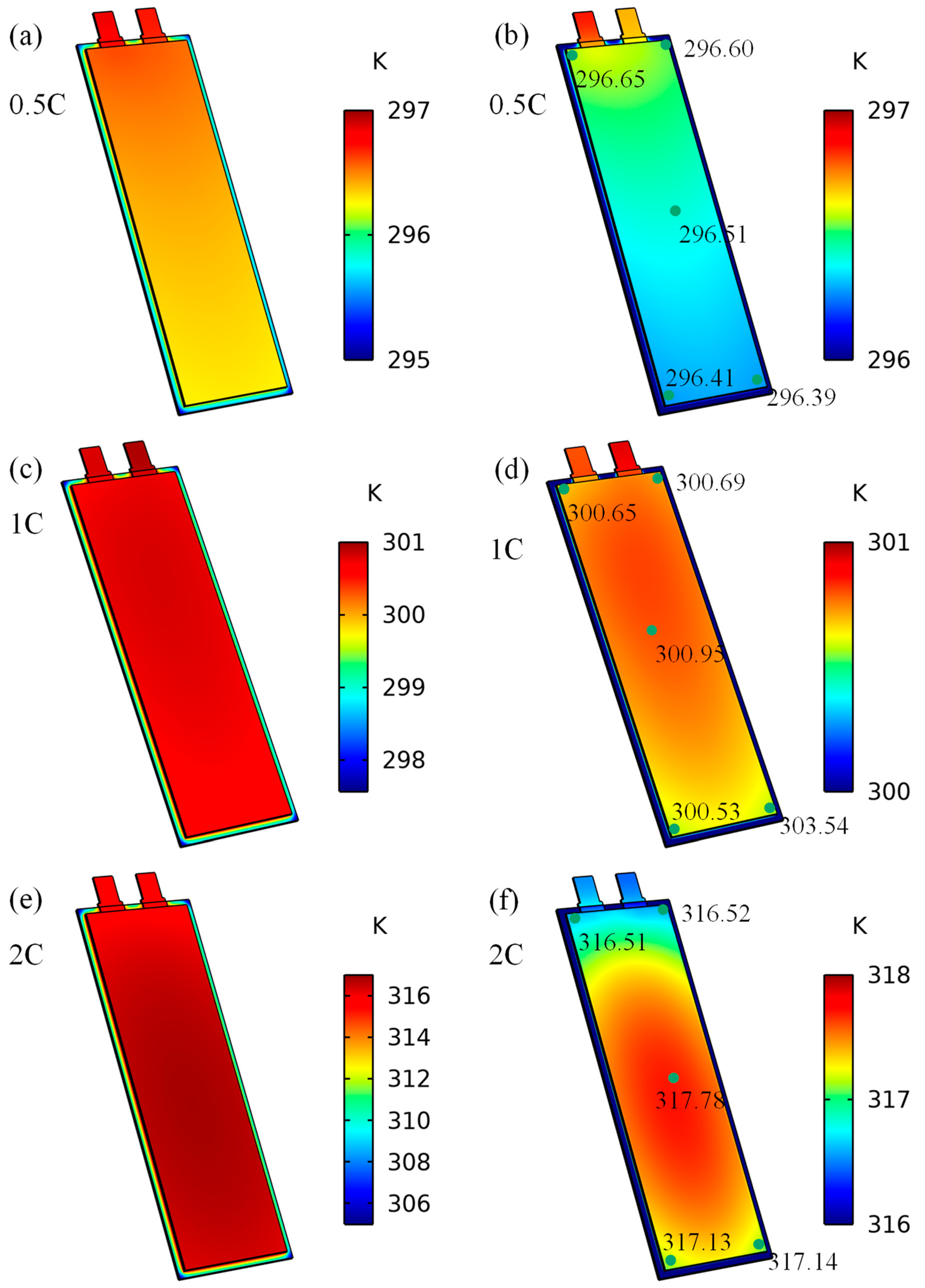
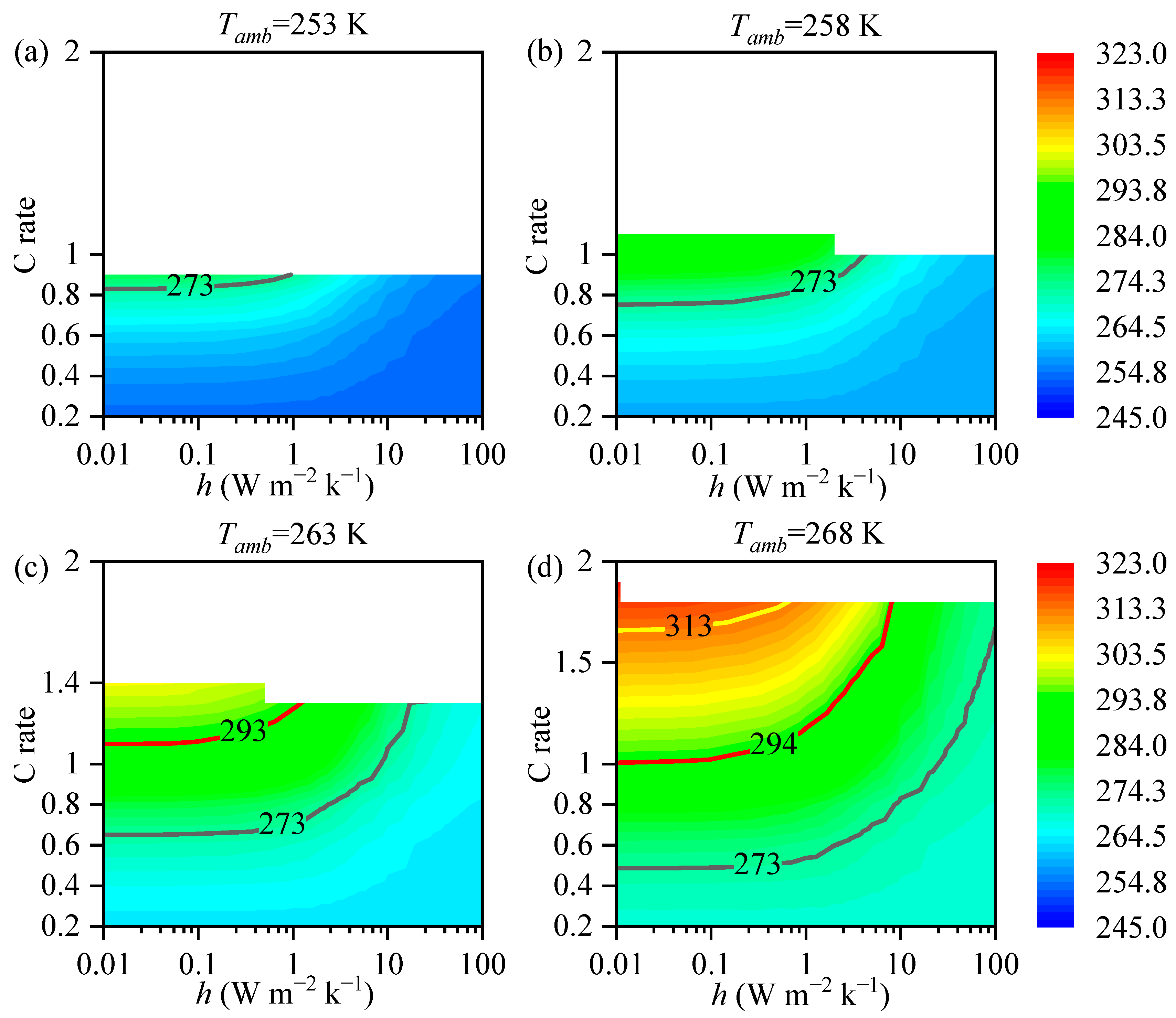
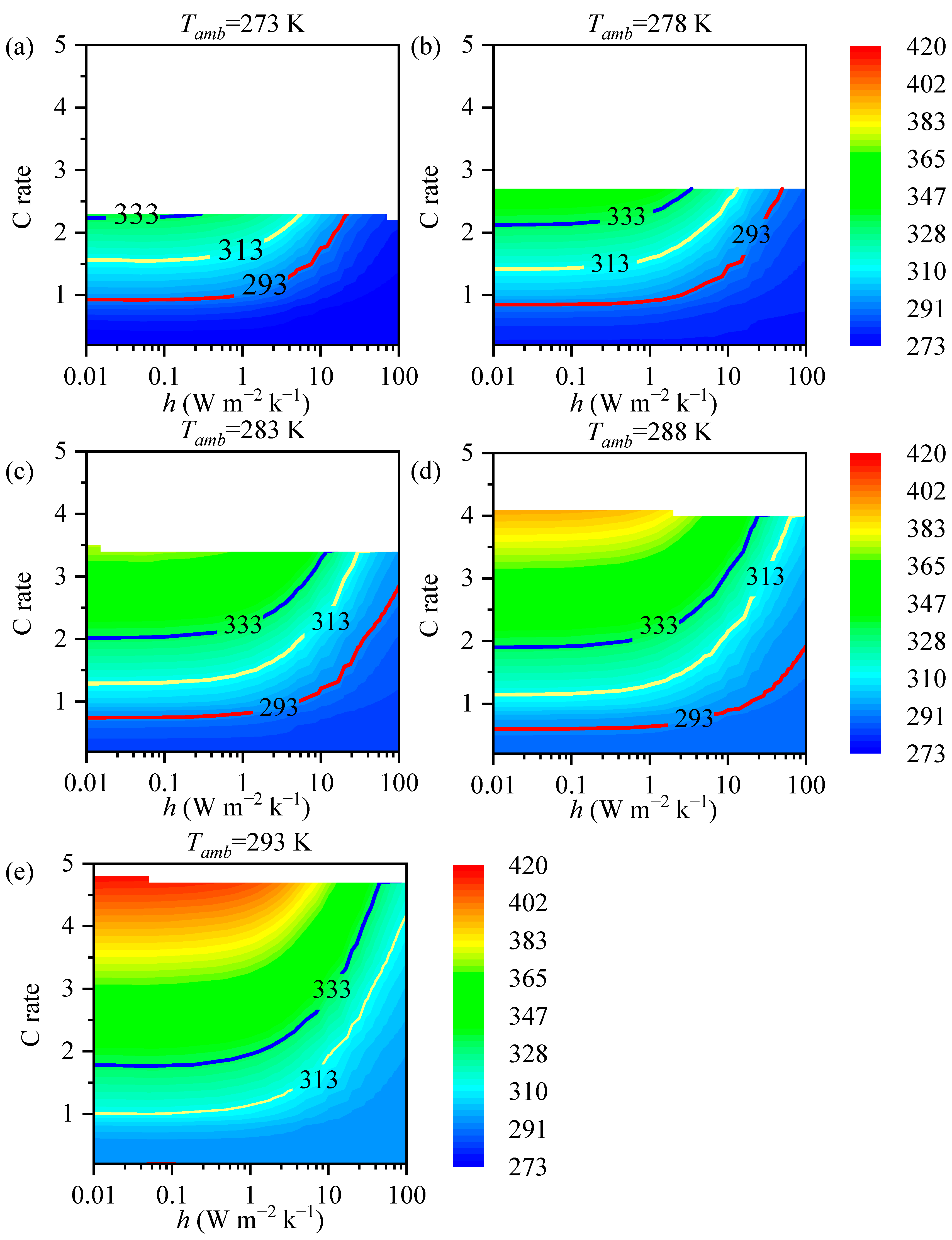
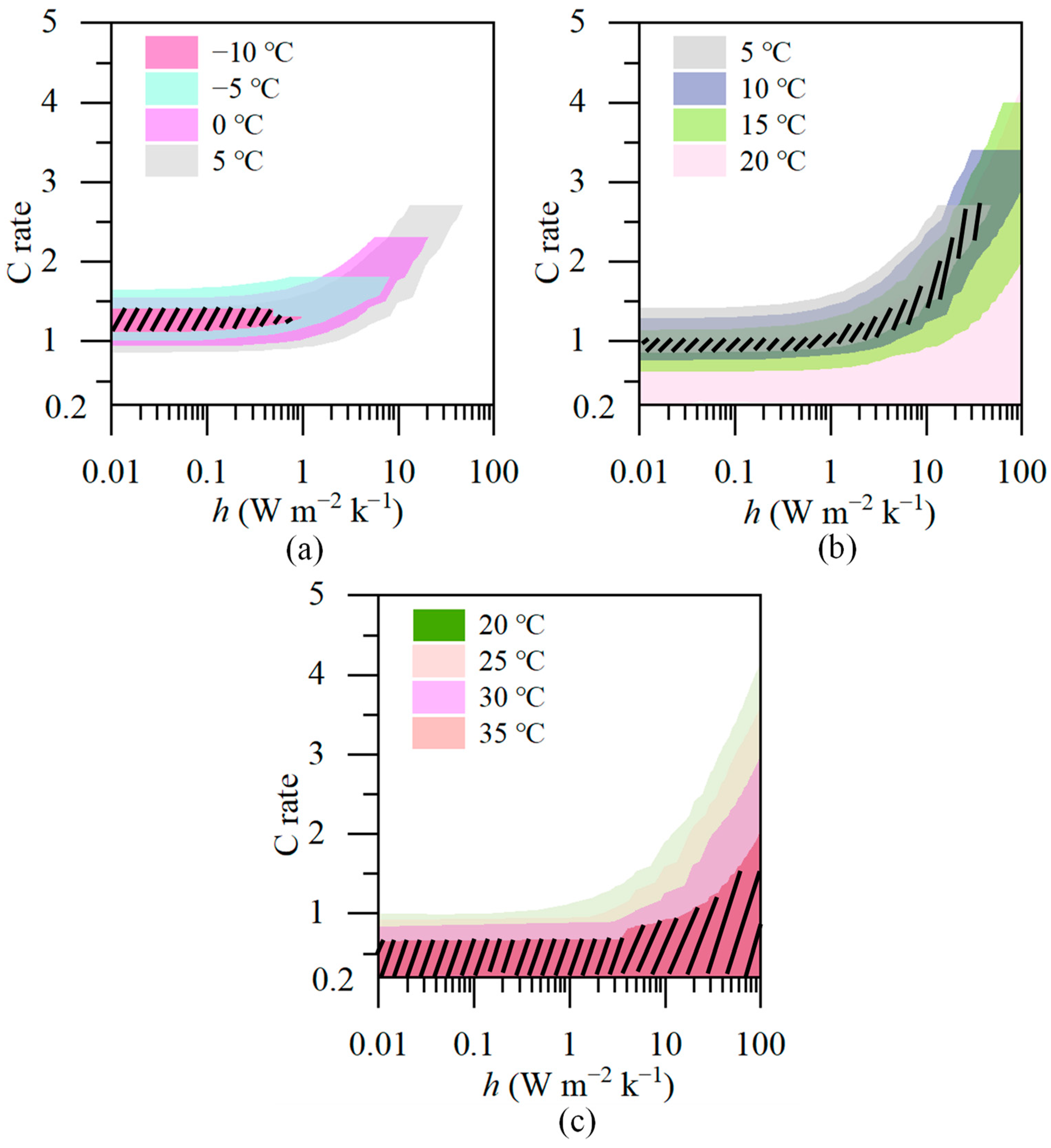
3.2. The impact of the Heat Transfer Coefficient on Battery Temperature
3.3. Analysis
4. Conclusions
- (1)
- Ambient temperature significantly impacts the electrochemical and thermal performance of lithium-ion batteries. Higher discharge rates lead to increased polarization and ion transport resistance, demanding higher reaction temperatures. Consequently, the maximum discharge rate of the cell decreases at low temperatures.
- (2)
- The maximum temperature of the battery is correlated with the heat transfer coefficient. The required magnitude of the heat transfer coefficient varies with different ambient temperatures. At low temperatures, adiabatic conditions are required to provide thermal insulation for the battery, while at high temperatures, increasing the heat transfer coefficient is necessary for effective heat dissipation from the battery.
- (3)
- Different heat transfer coefficients correspond to various thermal management strategies. Designing a BTMS with tailored heat transfer coefficients for typical environmental conditions and discharge rates can enhance battery performance accurately and efficiently. Additionally, taking into account the time or power dependence of heat generation based on battery geometry is crucial. These research findings offer a reference for designing future lithium-ion BTMS.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | specific surface area (m−1) |
| c | Li+ concentration (mol m−3) |
| Cp,bat | volumetric heat capacity (J m−3 K−1) |
| CCCV | constant current constant voltage |
| Cmax | maximum discharge rate |
| d | battery thickness (m) |
| D | diffusion coefficient (m2 s−1) |
| f | thermodynamic factor |
| F | faraday constant (C mol−1) |
| G | relevant parameters of porous properties |
| h | heat convection coefficient (W m−2 K−1) |
| iapp | external current (A) |
| j0 | exchange current density (A m−2) |
| jloc | local current density (A m−2) |
| jLi | transfer current density (A m−3) |
| k | reaction rate coefficient (m−1 s−1) |
| L | length of each layer (μm) |
| q | heat generation of each part (W m−3) |
| Qgen | rate of total heat generation (W m−3) |
| r | distance to the center of the particle (μm) |
| R | active particle radius (μm) |
| Rg | ideal gas constant (J mol−1 K−1) |
| SOC | state of charge |
| t+ | transference number of lithium ion |
| T | temperature (K) |
| U | electrode potential (V) |
| V | terminal voltage (V) |
| α | transfer coefficient |
| γ | correction coefficient |
| ε | volume fraction |
| η | overpotential (V) |
| λ | thermal conductivity (W m−1 K−1) |
| ρ | density (kg m−3) |
| σ | conductivity (S m−1) |
| φ | electric potential (V) |
| a | anode |
| ave | average |
| pol | polarized |
| amb | ambient |
| bat | battery |
| ca | cathode |
| conv | convective heat |
| e | electrolyte phase |
| eff | effective parameter |
| eq | equilibrium |
| irrev | irreversible |
| max | maximum |
| n | negative electrode |
| ohm | ohmic |
| p | positive electrode |
| ref | reference value |
| rev | reversible |
| s | solid phase |
| se | separator |
| surf | surface |
References
- Tran, M.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Suresh Patil, M.; Seo, J.; Lee, M. A novel dielectric fluid immersion cooling technology for Li-ion battery thermal management. Energy Convers. Manag. 2021, 229, 113715. [Google Scholar] [CrossRef]
- Zhou, G.; Li, Y.; Liu, Y.; Zhang, Q.; Wei, Z.; Li, S.; Yang, S.; Yuan, S.; Fan, T.; Huang, Q. Preparation of a novel environmental-friendly lithium-ion battery fire suppression microcapsule and its fire extinguishing mechanism in coordination with ABC dry powder. J. Clean. Prod. 2024, 448, 141438. [Google Scholar] [CrossRef]
- Hassan, M.K.; Hameed, N.; Hossain, M.D.; Hasnat, M.R.; Douglas, G.; Pathirana, S.; Rahnamayiezekavat, P.; Saha, S. Fire Incidents, Trends, and Risk Mitigation Framework of Electrical Vehicle Cars in Australia. Fire 2023, 6, 325. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Duan, J.; Panchal, S.; Yuan, J.; Fraser, R.; Fowler, M.; Chen, M. Simulation of cooling plate effect on a battery module with different channel arrangement. J. Energy Storage 2022, 49, 104113. [Google Scholar] [CrossRef]
- Vashisht, S.; Rakshit, D.; Panchal, S.; Fowler, M.; Fraser, R. Thermal behaviour of Li-ion battery: An improved electrothermal model considering the effects of depth of discharge and temperature. J. Energy Storage 2023, 70, 107797. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, Y.; Dong, Z.; Zheng, J.; Liu, Y. Numerical study on the heat generation and thermal control of lithium-ion battery. Appl. Therm. Eng. 2023, 221, 119852. [Google Scholar] [CrossRef]
- He, T.; Zhang, T.; Wang, Z.; Cai, Q. A comprehensive numerical study on electrochemical-thermal models of a cylindrical lithium-ion battery during discharge process. Appl. Energy 2022, 313, 118797. [Google Scholar] [CrossRef]
- Sun, Z.; Fan, R.; Zheng, N. Thermal management of a simulated battery with the compound use of phase change material and fins: Experimental and numerical investigations. Int. J. Therm. Sci. 2021, 165, 106945. [Google Scholar] [CrossRef]
- Rodrigues, M.T.F.; Son, S.; Colclasure, A.M.; Shkrob, I.A.; Trask, S.E.; Bloom, I.D.; Abraham, D.P. How Fast Can a Li-Ion Battery Be Charged? Determination of Limiting Fast Charging Conditions. ACS Appl. Energy Mater. 2021, 4, 1063–1068. [Google Scholar] [CrossRef]
- Ruan, H.; Sun, B.; Zhang, W.; Su, X.; He, X. Quantitative Analysis of Performance Decrease and Fast-Charging Limitation for Lithium-Ion Batteries at Low Temperature Based on the Electrochemical Model. IEEE Trans. Intell. Transp. Syst. 2021, 22, 640–650. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, T.S.; Xu, Q.; An, L.; Zhao, G. Effects of operating temperature on the performance of vanadium redox flow batteries. Appl. Energy 2015, 155, 349–353. [Google Scholar] [CrossRef]
- Fraser, R. Mathematical Heat Transfer Modeling and Experimental Validation of Lithium-Ion Battery Considering: Tab and Surface Temperature, Separator, Electrolyte Resistance, Anode-Cathode Irreversible and Reversible Heat. Batteries 2020, 6, 61. [Google Scholar] [CrossRef]
- Yue, Q.L.; He, C.X.; Wu, M.C.; Zhao, T.S. Advances in thermal management systems for next-generation power batteries. Int. J. Heat. Mass. Transf. 2021, 181, 121853. [Google Scholar] [CrossRef]
- Thakur, A.K.; Prabakaran, R.; Elkadeem, M.R.; Sharshir, S.W.; Arıcı, M.; Wang, C.; Zhao, W.; Hwang, J.-Y.; Saidur, R. A state of art review and future viewpoint on advance cooling techniques for Lithium–ion battery system of electric vehicles. J. Energy Storage 2020, 32, 101771. [Google Scholar] [CrossRef]
- Tete, P.R.; Gupta, M.M.; Joshi, S.S. Developments in battery thermal management systems for electric vehicles: A technical review. J. Energy Storage 2021, 35, 102255. [Google Scholar] [CrossRef]
- Zhu, X.; Sun, Z.; Wang, Z.; Wang, H.; Lin, N.; Shan, C. Thermal runaway in commercial lithium-ion cells underover heating condition and the safety assessment method Effects of SoCs, cathode materials and packaging forms. J. Energy Storage 2023, 68, 107768. [Google Scholar] [CrossRef]
- Sharma, D.K.; Prabhakar, A. A review on air cooled and air centric hybrid thermal management techniques for Li-ion battery packs in electric vehicles. J. Energy Storage 2021, 41, 102885. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, J.; Pan, W. A review of battery thermal management systems about heat pipe and phase change materials. J. Energy Storage 2023, 62, 106827. [Google Scholar] [CrossRef]
- Lee, S.; Han, U.; Lee, H. Development of a hybrid battery thermal management system coupled with phase change material under fast charging conditions. Energy Convers. Manag. 2022, 268, 116015. [Google Scholar] [CrossRef]
- Roe, C.; Feng, X.; White, G.; Li, R.; Wang, H.; Rui, X.; Li, C.; Zhang, F.; Null, V.; Parkes, M.; et al. Immersion cooling for lithium-ion batteries—A review. J. Power Sources 2022, 525, 231094. [Google Scholar] [CrossRef]
- Xiao, M.; Choe, S.Y. Dynamic modeling and analysis of a pouch type LiMn2O4/Carbon high power Li-polymer battery based on electrochemical-thermal principles. J. Power Sources 2012, 218, 357–367. [Google Scholar] [CrossRef]
- Baveja, R.; Bhattacharya, J.; Panchal, S.; Fraser, R.; Fowler, M. Predicting temperature distribution of passively balanced battery module under realistic driving conditions through coupled equivalent circuit method and lumped heat dissipation method. J. Energy Storage 2023, 70, 107967. [Google Scholar] [CrossRef]
- Li, H.; Saini, A.; Liu, C.; Yang, J.; Wang, Y.; Yang, T.; Pand, C.; Chen, L.; Jiang, H. Electrochemical and thermal characteristics of prismatic lithium-ion battery based on a three-dimensional electrochemical-thermal coupled model. J. Energy Storage 2021, 42, 102976. [Google Scholar] [CrossRef]
- Guo, M.; White, R.E. Thermal Model for Lithium Ion Battery Pack with Mixed Parallel and Series Configuration. J. Electrochem. Soc. 2011, 158, A1166–A1176. [Google Scholar] [CrossRef]
- Celik, A.; Coban, H.; Göcmen, S.; Ezan, M.A.; Gören, A.; Erek, A. Passive thermal management of the lithium-ion battery unit for a solar racing car. Int. J. Energy Res. 2019, 43, 3681–3691. [Google Scholar] [CrossRef]
- He, C.X.; Yue, Q.L.; Wu, M.C.; Chen, Q.; Zhao, T.S. A 3D electrochemical-thermal coupled model for electrochemical and thermal analysis of pouch-type lithium-ion batteries. Int. J. Heat Mass Transf. 2021, 181, 121855. [Google Scholar] [CrossRef]
- Lyu, P.; Huo, Y.; Qu, Z.; Rao, Z. Investigation on the thermal behavior of Ni-rich NMC lithium ion battery for energy storage. Appl. Therm. Eng. 2020, 166, 114749. [Google Scholar] [CrossRef]
- Liang, J.; Gan, Y.; Song, W.; Tan, M.; Li, Y. Thermal–Electrochemical simulation of electrochemical characteristics and temperature difference for a battery module under two-stage fast charging. J. Energy Storage 2020, 29, 101307. [Google Scholar] [CrossRef]
- Perez Estevez, M.A.; Calligaro, S.; Bottesi, O.; Caligiuri, C.; Renzi, M. An electro-thermal model and its electrical parameters estimation procedure in a lithium-ion battery cell. Energy 2021, 234, 121296. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Xu, J.; Gao, P.; Qiu, X.; Li, H.; Zhuang, Q.; Wu, K.; Zheng, H. Kinetic and transport characteristics of LiNi0.8Co0.1Mn0.1O2 lithium-ion batteries. Solid State Ion 2023, 395, 116216. [Google Scholar]
- Newman, J.; Thielemann, W. Porous-Electrode Theory with Battery Applications. AlChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef]
- Schweiss, R. Validation of 1D porous electrode theory using steady-State measurements of flooded electrodes at variable electrolyte compositions. Chem. Eng. Sci. 2020, 226, 115841. [Google Scholar] [CrossRef]
- Liu, K.; Gao, Y.; Zhu, C.; Li, K.; Fei, M.; Peng, C.; Zhang, X.; Han, Q.-L. Electrochemical modeling and parameterization towards control-oriented management of lithium-ion batteries. Control Eng. Pract. 2022, 124, 105176. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Wang, K.; Zhang, H.; Huang, H. Numerical investigation on the elastoplastic behavior and fatigue life of the current collector of lithium-ion batteries based on the electrochemical-thermal-mechanical coupling model. J. Energy Storage 2023, 68, 107792. [Google Scholar] [CrossRef]
- Alkhedher, M.; Al Tahhan, A.B.; Yousaf, J.; Ghazal, M.; Shahbazian-Yassar, R.; Ramadan, M. Electrochemical and thermal modeling of lithium-ion batteries: A review of coupled approaches for improved thermal performance and safety lithium-ion batteries. J. Energy Storage 2024, 86, 111172. [Google Scholar] [CrossRef]
- Dao, T.; Vyasarayani, C.P.; McPhee, J. Simplification and order reduction of lithium-ion battery model based on porous-electrode theory. J. Power Sources 2012, 198, 329–337. [Google Scholar] [CrossRef]
- Ren, D.; Smith, K.; Guo, D.; Han, X.; Feng, X.; Lu, L.; Ouyang, M.; Li, J. Investigation of Lithium Plating-Stripping Process in Li-Ion Batteries at Low Temperature Using an Electrochemical Model. J. Electrochem. Soc. 2018, 165, A2167–A2178. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part I: Diffusion simplification and single particle model. J. Power Sources 2015, 278, 802–813. [Google Scholar]
- Li, J.; Cheng, Y.; Ai, L.; Jia, M.; Du, S.; Yin, B.; Woo, S.; Zhang, H. 3D simulation on the internal distributed properties of lithium-ion battery with planar tabbed configuration. J. Power Sources 2015, 293, 993–1005. [Google Scholar] [CrossRef]
- Xu, W.; Hu, P. Numerical study on thermal behavior and a liquid cooling strategy for lithium-ion battery. Int. J. Energy Res. 2020, 44, 7645–7659. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, G.; Xia, Y.; Tian, S. Numerical study of thermal management of pouch lithium-ion battery based on composite liquid-cooled phase change materials with honeycomb structure. J. Energy Storage 2023, 70, 108001. [Google Scholar] [CrossRef]
- Ouyang, T.; Ye, J.; Xu, P.; Wang, C.; Xu, E. Estimation of state-of-charge and state-of-health for lithium-ion battery based on improved firefly optimized particle filter. J. Energy Storage 2023, 68, 107733. [Google Scholar] [CrossRef]
- Wu, S.; Xiong, R.; Li, H.; Nian, V.; Ma, S. The state of the art on preheating lithium-ion batteries in cold weather. J. Energy Storage 2020, 27, 101059. [Google Scholar] [CrossRef]
- He, F.; Li, X.; Zhang, G.; Zhong, G.; He, J. Experimental investigation of thermal management system for lithium ion batteries module with coupling effect by heat sheets and phase change materials. Int. J. Energy Res. 2018, 42, 3279–3288. [Google Scholar] [CrossRef]
- Hunt, I.A.; Zhao, Y.; Patel, Y.; Offer, G.J. Surface Cooling Causes Accelerated Degradation Compared to Tab Cooling for Lithium-Ion Pouch Cells. J. Electrochem. Soc. 2016, 163, A1846–A1852. [Google Scholar] [CrossRef]

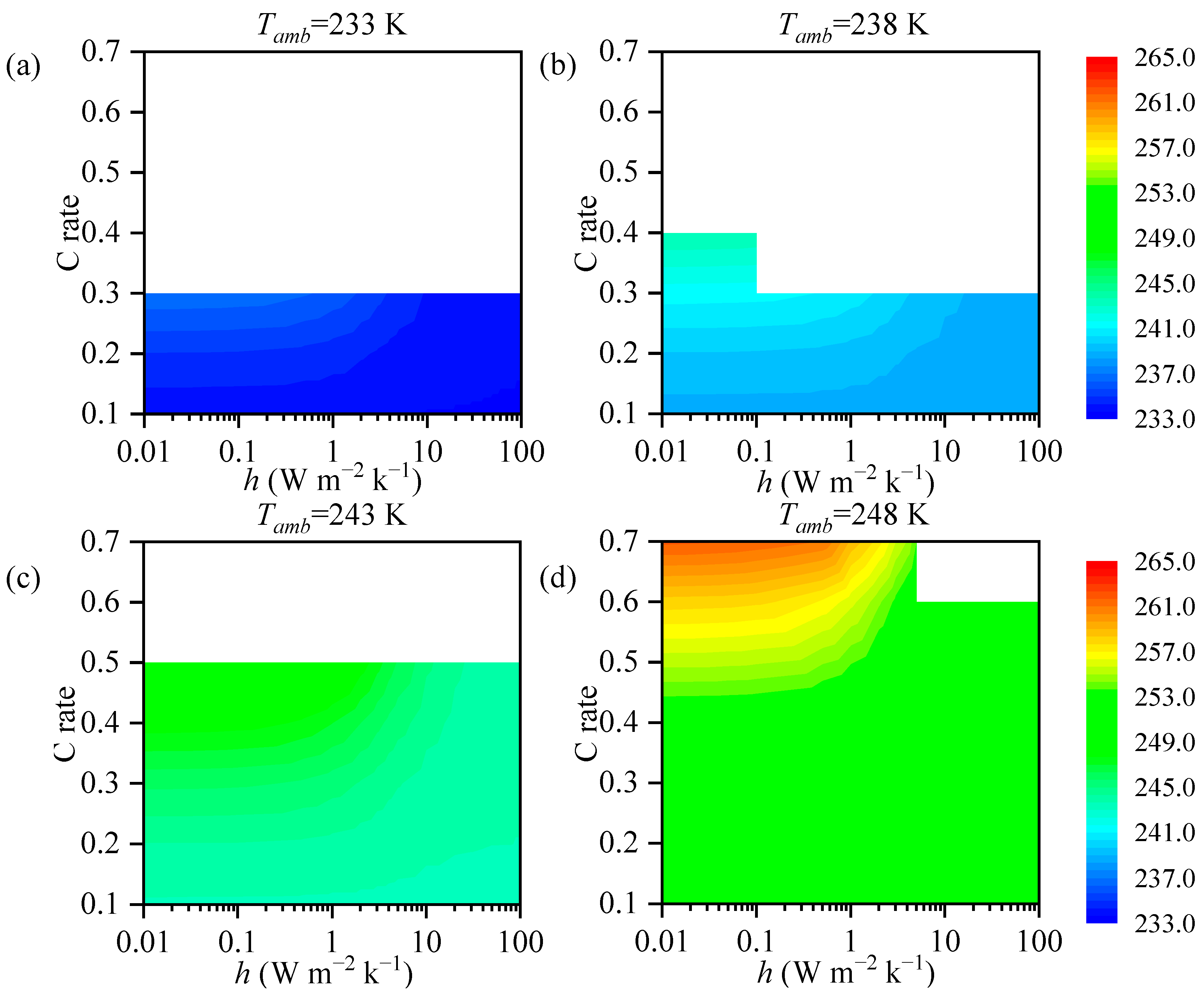



| Property | Specification |
|---|---|
| Nominal voltage | 3.6 V |
| Maximum charge voltage | 4.2 V |
| Maximum discharge rate | 5C |
| Charge cut-off current | 500 mA |
| Discharge cut-off voltage | 2.7 V |
| Electrode chemistry | NMC/graphite |
| Electrolyte chemistry | LiPF6 and 3:7 EC:EMC |
| Size | 342 × 118 × 8 mm3 |
| Electrochemical Model | Governing Equation | Boundary and Continuity Conditions |
|---|---|---|
| Mass conservation in solid phase | ||
| Mass conservation in liquid phase | ||
| Charge conservation in solid phase | ||
| Charge conservation in liquid phase | ||
| Electrochemical dynamics |
| Parameters | Values | Ref. |
|---|---|---|
| Length, Li (μm) | 55/10/65 for PE/SEP/NE | [41] |
| Liquid phase volume fraction, εe,i | 0.30/0.37/0.30 for PE/SEP/NE | [36] |
| Solid phase volume fraction, εs,i | 0.48/0.6/0.528 for PE/SEP/NE | [36] |
| Additive volume fraction, εelse,i (μm) | 0.19/0.068 for PE/NE | [36] |
| Solid active particles radius, Rs,I (μm) | 2.7/1.5 for PE/NE | [34] |
| Maximum concentration of Li+ in active material, Cs,max.i (mol m−3) | 31,507/38,021 for PE/NE | [34] |
| Reaction rate coefficient, ks,0 | 7 × 10−12 | [41] |
| Initial electrolyte concentration, ce,0 (mol m−3) | 1200 | [34] |
| Specific surface area, As,I. (m−1) | 3εs,i/Rs,i | |
| Transference number of Li+, t+ | 0.363 | [41] |
| Transfer coefficient, ai | 0.5 | [42] |
| Ideal gas constant, Rg (J mol−1 K−1) | 8.314 | [42] |
| Reference temperature, Tref (K) | 293.15 | |
| Volumetric heat capacity, Cpbat (J m−3 K−1) | 960.65 | [43] |
| Faraday constant, F (C mol−1) | 96,487 | |
| Battery density, rbat (kg m−3) | 2571.6 | [43] |
| Thermal conductivity, λx,y,z (W m−2 K−1) | 36.2/36.2/1.204 for x/y/z direction | [43] |
| Parameters | Equations |
|---|---|
| Solid diffusion coefficient of electrode kinetics | |
| Reaction rate | |
| Electrode thermodynamic properties of equilibrium potential | |
| Entropy changes of electrodes | |
| Electrolyte diffusion coefficients | |
| Dynamic variables in electrolyte related to the Li+ transport | |
| Thermodynamic factor | |
| Electrolyte conductivity |
| Tamb (°C) | Cmax | Discharge Capacity (Ah) | Initial Voltage (V) | Tmax (K) |
|---|---|---|---|---|
| −40 | 0.3 | 2.24 (0.3C) | 3.19 (0.3C) | 236.82 (0.3C) |
| −35 | 0.4 | 3.18 (0.4C) | 3.51 (0.4C) | 243.68 (0.4C) |
| −30 | 0.5 | 5.24 (0.5C) | 3.70 (0.5C) | 250.77 (0.5C) |
| −25 | 0.7 | 6.93 (0.7C) | 3.82 (0.7C) | 261.85 (0.7C) |
| −20 | 0.9 | 9.12 (0.9C) | 3.95 (0.9C) | 277.07 (0.9C) |
| −15 | 1.2 | 11.56 (1C) | 3.99 (1C) | 289.58 (1C) |
| −10 | 1.4 | 15.83 (1C) | 4.02 (1C) | 302.27 (1C) |
| −5 | 1.9 | 18.24 (1C) | 4.05 (1C) | 320.39 (1C) |
| 0 | 2.2 | 20.82 (1C) | 4.07 (1C) | 334.8 (1C) |
| 5 | 2.7 | 21.55 (1C) | 4.09 (1C) | 349.51 (1C) |
| 10 | 3.5 | 22.81 (1C) | 4.10 (1C) | 374.7 (1C) |
| 15 | 4.1 | 23.25 (1C) | 4.11 (1C) | 394.54 (1C) |
| 20 | 4.8 | 24.93 (1C) | 4.12 (1C) | 416.38 (1C) |
| 25 | 5 (rated) | 26.12 (1C) | 4.13 (1C) | 424.08 (1C) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Sun, C.; Zhang, M.; Wang, S.; Wei, B.; Cheng, Y.; Ju, X.; Xu, C. A Study of the Thermal Management and Discharge Strategies of Lithium-Ion Batteries in a Wide Temperature Range. Energies 2024, 17, 2319. https://doi.org/10.3390/en17102319
Li K, Sun C, Zhang M, Wang S, Wei B, Cheng Y, Ju X, Xu C. A Study of the Thermal Management and Discharge Strategies of Lithium-Ion Batteries in a Wide Temperature Range. Energies. 2024; 17(10):2319. https://doi.org/10.3390/en17102319
Chicago/Turabian StyleLi, Kaixuan, Chen Sun, Mingjie Zhang, Shuping Wang, Bin Wei, Yifeng Cheng, Xing Ju, and Chao Xu. 2024. "A Study of the Thermal Management and Discharge Strategies of Lithium-Ion Batteries in a Wide Temperature Range" Energies 17, no. 10: 2319. https://doi.org/10.3390/en17102319
APA StyleLi, K., Sun, C., Zhang, M., Wang, S., Wei, B., Cheng, Y., Ju, X., & Xu, C. (2024). A Study of the Thermal Management and Discharge Strategies of Lithium-Ion Batteries in a Wide Temperature Range. Energies, 17(10), 2319. https://doi.org/10.3390/en17102319






