Abstract
Energy management systems allow the Smart Grids industry to track, improve, and regulate energy use. Particularly, demand-side management is regarded as a crucial component of the entire Smart Grids system. Therefore, by aligning utility offers with customer demand, anticipating future energy demands is essential for regulating consumption. An updated examination of several forecasting techniques for projecting energy short-term load forecasts is provided in this article. Each class of algorithms, including statistical techniques, Machine Learning, Deep Learning, and hybrid combinations, are comparatively evaluated and critically analyzed, based on three real consumption datasets from Spain, Germany, and the United States of America. To increase the size of tiny training datasets, this paper also proposes a data augmentation technique based on Generative Adversarial Networks. The results show that the Deep Learning-hybrid model is more accurate than traditional statistical methods and basic Machine Learning procedures. In the same direction, it is demonstrated that more comprehensive datasets assisted by complementary data, such as energy generation and weather, may significantly boost the accuracy of the models. Additionally, it is also demonstrated that Generative Adversarial Networks-based data augmentation may greatly improve algorithm accuracy.
1. Introduction
Nowadays, global power consumption is increasing at an exponential rate. Electricity is widely employed in a variety of industries, including industrial processes, transportation, public illumination, residential appliances, and product manufacturing. This unprecedented energy demand has resulted in increased use of fossil fuels, causing a variety of environmental and public health issues around the world, including global warming gas emissions (e.g., approximately 78% of US global warming emissions were energy-related) and air and water pollution. As a result, relying on renewable energy sources (RESs) and ICT-driven architectures will be critical to increasing energy efficiency. The smart grid (SG) concept emerged as a result of the integration of these elements into the power infrastructure.
SG systems are used to match electric energy use with the appropriate amount of supply, as excess electricity output necessitates the development of additional storage technologies, increasing costs and resources. To achieve supply-demand balance, energy demand forecasting must be performed on a continuous basis, allowing energy suppliers to reduce peak load demand and alter the energy consumption profile at particular time intervals. Furthermore, consumers can actively engage in this process by adjusting their energy usage schedules to variable-rate energy pricing.
Demand-side management requires precise historical information about energy load patterns, which is becoming more feasible with the advancement of the smart metering sector. Furthermore, load forecasting is a crucial component of smart grid demand management, helping demand response programs, renewable energy integration, resource optimization, grid stability, and overall cost reduction in the electrical supply chain.
Smart meters are capable of transmitting energy consumption and environmental data to a central server, allowing utilities to process it to forecast how the data features will evolve over time and trigger suitable control actions. Energy demand is a complex stochastic process, potentially influenced by several factors, such as weather, day periods, holidays or working days, and living habits, to name a few. This paper considers some of the most influential parameters, namely energy consumption data, time of day, and weather conditions. These data will be jointly processed to build a robust prediction model that can be used to forecast the amount of energy that will be consumed in a future period. Energy demand forecasting is among the most challenging topics in the smart energy management area. For this purpose, several techniques can be used.
Although the previous electrical load forecasting models were largely restricted to traditional statistical techniques, load forecasting technologies have advanced significantly with the advancement of modern science. Recently, machine learning-based forecasting models have gained increasing popularity in the power load forecasting industry. When choosing the models, a number of criteria were looked at, including the prediction horizon time frame, temporal resolution, inputs, outputs, data pre-processing, etc.
Some selected models are particularly suitable and commonly preferred for electricity load forecasting, including models based on regression analysis and artificial neural networks. Among the latter, artificial neural networks stand out as the most widely used models for electricity load forecasting. More specifically, they are mainly used for short-term forecasts, taking into account the complex patterns inherent in electricity and energy consumption. Regression models, on the other hand, are still popular and useful for long-term forecasting jobs, particularly when periodicity and variability are significant. Moreover, the support vector machine model appears in significant research, which suggests the growing interest it is generating. On the other hand, although statistical models are not as common as they formerly were, their significance and importance are still present.
These techniques are herein classified into four main categories: statistical, machine learning (ML), deep learning (DL), and hybrid techniques. Each category has its advantages and limitations, depending on the use case and the characteristics of the considered dataset. In the last few years, there has been considerable interest in surveying different load forecasting techniques in the energy sector, providing a comparative analysis, and proposing new architectures based on the most accurate models. The most relevant to the present paper are [1,2,3]. However, some of these works lack numerical results that sustain the provided comparison insights [2,3,4,5,6], whereas other papers borrow and build upon the results of other works [1,3,7].
2. Related Research
Table 1 summarizes some recent papers proposing load forecasting techniques, which also provide performance results, highlighting the differences in the present paper.

Table 1.
Comparative analysis of our work and existing studies.
In [8], the authors compare the performance of different ML (SVM, quadratic SVM, and cubic SVM) and DL-based residential load forecasting models. They analyzed historical data from a single profile at a frequency of one minute. However, in [9], they used historical load and temperature data from the university profile on a daily basis to estimate short-term load demand. Expert knowledge is the technique employed with the new convolutional LSTM for holiday load forecasts based on historical data, temperature data, and date information at a 15-min interval [10]. Furthermore, [11] used DL-hybrid models using historical and weather data with hourly frequencies. A CNN-BiGRU hybrid model with a random forest-like feature selection strategy was used on two datasets [12].
Based on Table 1 and the above considerations, the main contributions of this paper are stated as follows:
- To present a work that provides an extensive comparison between all load forecasting techniques based on artificial intelligence, and highlights the models used in the load forecasting field, in order to guide the readers and facilitate the process of selecting the most appropriate models concerning load forecasting. All the algorithms were implemented by the authors in order to ensure a fair comparison. As far as the authors know, this has not been offered by previous works.
- Evaluation of various AI techniques for load forecasting including Statistical models, Machine learning, Deep Learning, and hybrid models on three cases of data from three countries: USA, Spain, and Germany. In order to identify the best-performing and most appropriate models for various data structures, this was done taking into account the same parameters as the pre-processing techniques, such as sampling.
- Analysis of the effect of some parameters, such as weather variables, temperature, and energy generation characteristics, on the performance of the models to forecast the output.
- Evaluation of the impact of applying data augmentation based on Generative Adversarial Networks (GANs) on the performance of load forecasting models.
The obtained results have shown good performance of the applied hybrid LSTM-CNN model, both with only original data and with the augmented data generated by the GAN model, which was consistent across the three data sets. The remainder of this paper is structured as follows. Section 3 presents the background and state-of-the-art load forecasting techniques. Section 4 presents the load forecasting process. Section 5 presents the data augmentation with the TimeGAN integration model. Section 6 performs a comparative evaluation of different models using different real-world datasets. Section 7 presents challenges and future trends in load forecasting. Finally, conclusion and future work.
3. Load Forecasting Techniques: Background and State of the Art
This section presents the state of the art of the most used energy load forecasting techniques. These techniques are divided into four main classes: statistical, ML, DL, and hybrid techniques. Statistical models leverage mathematical tools for problem modeling and finding relationships between various variables. ML models are more sophisticated and could learn insights from data to provide more accurate results. On the other hand, DL techniques exploit a specific architecture to mimic the behavior of the human brain by using an Artificial Neural Network (ANN) comprising several layers of neurons to progressively extract higher-level features from the input data. Finally, hybrid techniques combine two or more algorithms belonging to the previous three classes to increase global performance.
3.1. Statistical Methods
Predictive statistical models are a mathematical representation in which probability distribution and data mining are applied to predict the future evolution of the observed event. The objective is to develop predictive models that process historical data to extract the relevant patterns and be able to compute the probability of occurrence of a given event. Meanwhile, due to the recent advances in computational capabilities and sophisticated algorithms, these techniques are less accurate than classical predictive techniques. Recent advances in computing capabilities have led to the emergence of a special sub-category known as classical time-series forecasting methods. These emphasize the linear relationships linking the input data. On the other hand, these models are less accurate than other techniques (i.e. ML and DL techniques). Nevertheless, some models such as ARIMA and ARIMAX [13] are still widely used in a wide range of problems, including load forecasting, and often serve as a benchmark for the evaluation of other techniques. In [14] the authors used SARIMA algorithms to forecast Turkey’s main energy demand from 2005 to 2020. Also, in [15], it was found that using ARIMA for demand forecasting required a high volume of data and estimations using Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) models. This is due to their good interaction between performance and complexity.
3.2. Machine Learning Techniques
Machine learning techniques consist of using mathematical models to find a general understanding of the data and feature dependencies, enabling prediction. Although this class is very broad, this section will address only the main techniques that have been applied so far to the problem of energy load forecasting. The Support Vector Machine (SVM) is a supervised ML algorithm, largely adopted in previous literature because it produces good accuracy with less computing power. Support Vector Regressor (SVR) is a regression version of the SVM algorithm, widely used for classification problems too. The objective of the SVR algorithm is to find a hyperplane with maximum margin distance in N-dimensional space (N is the number of features), which distinctly classifies the data points. SVR was successfully used to predict the electrical load of building service systems [16] and is often used as a reference scenario [16]. Another supervised machine learning approach that may be used to address classification and regression issues is k-Nearest Neighbors (KNN).
A supervised ML method uses labeled input data to train a function that, when applied to additional unlabeled data, generates the desired output. The KNN algorithm assumes that similar features characterize the points that are near each other. An example of using KNN in short-term load forecasting can be found in [17,18]. Decision Tree (DT) and its derivatives form an important class of ML algorithms. The DT algorithm determines observations, which are represented in the branches of the tree, to the predicted value represented in the leaves. This is used for both classification and regression. One of its derivatives is Random Forest (RF), which is based on voting or averaging different DTs trained from different random subsets of the dataset features. Boosting algorithms build DTs in a sequence, where each DT will improve decisions based on the previous one. In particular, gradient boosting allows the decision errors to be minimized by applying the gradient descent algorithm. XGBoost belongs to the latter class of algorithms and introduces additional optimization features, such as parallelization, tree pruning, and caching of gradient statistics. In [19], the authors propose an online scheme for heat load forecasting based on a DT algorithm. XGBoost is used in [20] to predict short-term load forecasting of industrial customers.
ANN is an umbrella term that encompasses both single-layer perceptrons and multiple-layer (deep) neural networks. However, due to the current importance of DL models, they will be treated in a separate section. The input layer, hidden layer, and output layer are the three layers that make up a standard feed-forward basic ANN. Each artificial neuron has inputs and a single output. The output consists of a non-linear function (activation function) of the weighted sum of the inputs. The learning procedure consists of finding the values of the weights that better approximate the target function at the output of the output layer. ANNs use supervised learning, based on a set of learning rules called backpropagation of error, to refine their output results. ANN models have been extensively implemented to produce accurate results for power generation and load forecasting and are often used as a baseline in comparison with DL techniques [21].
3.3. Deep Learning Techniques
DL techniques are based on the stacking of multiple layers, with each layer applying a nonlinear transformation to its output. In general, deeper neural networks increase their performance when trained with more data. Each layer usually consists of an ANN. The most common types of DL algorithms are Convolutional Neural Networks (CNN), Recurrent Neural Networks (RNN), and Long Short-Term Memory (LSTM). DL techniques constitute the current trend in load forecasting. CNN uses convolution and filters to extract features from data. It is mainly used in the image processing field, as it can analyze multidimensional data. However, its application is expanding to other domains such as text and audio processing, and time series forecasting. The authors of [22] used CNN for individual energy load forecasting. The RNN consists of using sequential information. They are called recurrent because they perform the same process for each element of a sequence, the output depending on the previous calculations, as they have a ”memory” which captures the information that has been calculated so far. However, RNNs have some trouble when working with long sequences [3].
The LSTM was developed to solve this issue based on its capability of learning long-term dependencies. In fact, LSTMs are a type of RNN capable of learning order dependencies in sequence prediction problems. LSTM also makes it easy to manage the provided information, instead of developing and working on complex equations, as is the case of Autoregressive Integrated Moving Average with Explanatory Variable (ARIMAX). A higher number of variables can be transmitted to the LSTM to improve the accuracy of the forecasts. This is required behavior in complex problem areas, such as machine translation, speech recognition, and time series problems. In [23], an LSTM model is used for short-term residential load forecasting. In [24], it is used for long-term load forecasting. In [25], LSTM is compared with feedforward Deep Neural Network (DNN), and AutoRegressive Integrated Moving Average (ARIMA) and Linear Regression (LR), integrated with data clustering, for short-term load forecasting. Here, the feedforward network DNN was able to follow the load peaks closer than the LSTM, though both were better than the other two techniques. The Gated Recurrent Unit (GRU) is another gated RNN variant. The main difference between LSTM and GRU is that GRU has only two gates, which is simpler and more efficient, whereas LSTM has a more complex structure with three gates, being more complex but also more powerful to capture long-term dependencies. In [26], GRU and LSTM are compared in short-term load forecasting. In this study, GRU shows better performance.
3.4. Hybrid Techniques
To improve the accuracy of previous models, researchers are trying to combine two or more models of the same or different families, to extract more insights from data and get better results. This type of model can be classified into two categories. The first one consists of running several algorithms in parallel, with each independently forecasting electricity load, then combining and mixing the obtained results. In the second category, models and algorithms are concatenated sequentially and integrated into one single model wherein the final block processes and relies on the results of the former block. In [27], the author has proposed a new hybrid model composed of an ARIMA model, improved empirical mode decomposition (IEMD), and wavelet neural network (WNN) for load forecasting. In [28], the authors have adopted a hybrid model that combines four algorithms for short-term gas load forecasting: the Fruit Fly Optimization Algorithm (FFOA), Simulated Annealing algorithm (SA), Cross Factor (CF) and SVR. In [29], an electricity load forecasting hybrid model is proposed. It consists of load demand time series decomposition and processing of external input variables, with the help of correlation analysis. The load demand time series and the corresponding external variables are processed in parallel. In [30], a Deep Belief Network and two restricted Boltzmann machines were used to model each of the extracted intrinsic mode functions so that the trends of these intrinsic mode functions can be accurately predicted.
A currently popular configuration of DL models in load forecasting is to combine CNN with a RNN or one of its gated variations. This takes advantage of the best features of the two models: the time dependency of the RNN and the features extraction of the CNN. The architecture of a CNN-LSTM is presented in [31]. In this model, CNN and LSTM are used in parallel, to avoid the correlation between the two models to make sure that all models benefit from all insights of the input data. In [32], the CNN and LSTM are again integrated. In [11], the authors compare the performance of the following combinations: CNN-RNN, CNN-LSTM, and CNN-GRU. They have concluded that the best performance during the test phase was by CNN-LSTM, followed by CNN-GRU. In [33], the authors propose a short-term load forecasting framework, having at its core a bi-directional based Encoder-Decoder model, complemented with feature weighting attention, temporal attention, and similar day information. The proposed model compares positively with other ML models, including DL models such as CNN-LSTM.
3.5. Analysis and Synthesis
Based on previous studies, Table 2 describes the main advantages and shortcomings of each model. Statistical models are less complex and easier to use, providing accurate results when dealing with small and linear datasets. ANNs and Multi-Layer Perceptrons (MLPs) are more accurate in short periods and can also be used for long periods when operating on large amounts of data at the cost of more computational power. On the other hand, SVR is more suitable for classification problems with low power resources. It has also proven to be very suitable for energy forecasting problems. KNN is mostly used for classification problems, such as classifying regions, consumers, or utilities based on their consumption or generation. DL techniques are usually able to cope with big datasets and complex, nonlinear variable relationships. LSTM, an enhanced version of the RNN model, is known to be more accurate for forecasting energy consumption and load for long periods, and it is capable of extracting features from complex and nonlinear data.

Table 2.
Comparison of different forecasting techniques.
Some studies have taken advantage of the best features from several models to build an optimized and customized model, which is called the hybrid model. This kind of model has shown better performance in several studies compared to other conventional models.
4. Load Forecasting Process
According to the literature, the most widely-employed load forecasting approaches use a common methodology during the process of predicting energy demand. Figure 1 illustrates the flow chart of the main steps of this process.
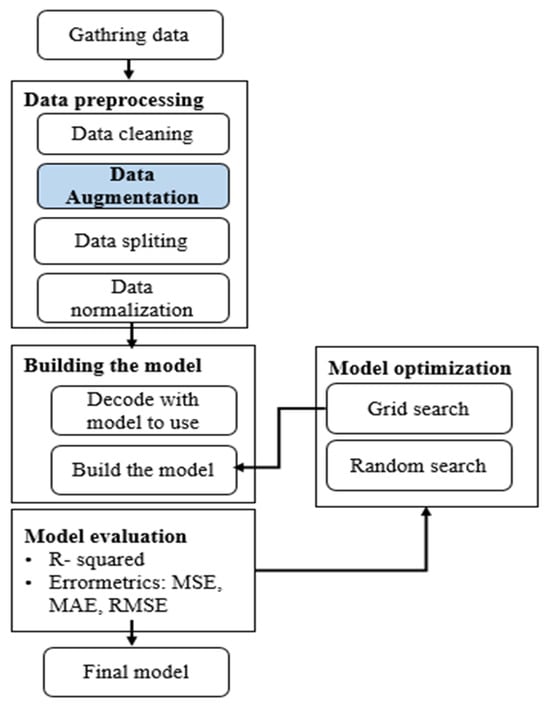
Figure 1.
A flow chart highlighting the commonly used steps in the energy load forecasting process.
4.1. Data Gathering
In general, the first step in the above methodology is gathering data. The advancement of smart metering and IoT technologies helps gather accurate energy consumption and weather data in real-time and store it in server machines for further processing. For each forecasting problem, the quality of data is the most important parameter that directly affects the accuracy of the model prediction and the quality of results. To build a more effective model, this work makes use of three different datasets, corresponding to energy consumption data from Germany, the USA, and Spain.
4.2. Data Pre-Processing
The data pre-processing stage is crucial in data analysis and ML problems, as it helps to enhance the quality of data in order to extract meaningful insights from the data [34,35]. Data pre-processing refers to the technique of preparing, cleaning, organizing, augmenting, and transforming the raw data to make it suitable for training ML and DL models. In this paper, we propose data augmentation using the GAN technique, which will be explained in detail in Section 5.
4.3. Model Building
Before building the model, one needs to consider which ML model to choose. This action is taken based on the kind of problem to solve, i.e., whether it is a regression or classification problem, or whether it belongs to supervised or unsupervised learning. The choice is affected by data and several other parameters. For instance, we used predictive algorithms for the challenge of load forecasting in smart grids.
4.4. Model Optimization
To develop an optimal ML model, one needs to choose a good model architecture; there is a range of possibilities. There are many possible model architectures, and it is difficult to test each architecture manually. Hence, the machine will be configured to perform this exploration and select the optimal model architecture automatically. Parameters that define the model architecture are referred to as hyperparameters. This process of searching for the ideal model architecture is called hyperparameter tuning. An optimization procedure involves defining a search space, where each dimension represents a hyperparameter and each point represents a single model configuration. A range of different optimization algorithms may be used, although two of the simplest and most common methods are random search and grid search:
- Random Search: Define a search space as a bounded domain of hyperparameter values and randomly sample points in that domain [36,37,38,39,40].
- Grid Search: Define a search space as a grid of hyperparameter values and evaluate every position in the grid [41,42].
4.5. Model Evaluation
To make sure that the model predicts the right values, it needs to be evaluated. For this purpose, multiple evaluation metrics are used for building an effective ML model. These include classification accuracy, logarithmic loss, confusion matrix, F1 score, etc., used for classification, and Mean Absolute Error (MAE) in Equation (1), Mean Square Error (MSE) in Equation (2), Root Mean Square Error (RMSE) in Equation (3), and R2 for regression problems in Equation (4). These last metrics are more interesting for the present work, as its focus is to solve a forecasting problem. The expressions are as follows:
5. Data Augmentation with Generative Adversarial Networks
To improve energy efficiency, be it by using better management, or by accurate energy load forecasting, the energy consumption data is the only manner to do so. However, collecting energy data can be a very challenging task as the process is very expensive and time-consuming, in addition to the privacy concerns around user data. Even when setting up the process of collecting the data, long periods (e.g., measured in years) would be needed to collect a good amount of data that would make accurate forecasting results possible.
This section addresses those challenges by using GAN to artificially generate additional energy consumption data from a reduced amount of original data. GAN is an approach for generative modeling using DL algorithms [43], such as LSTM [23,24,25], CNN [44], RNN [3], etc. The GAN model is considered an unsupervised learning task in the Artificial Intelligence field. The model automatically engages to discover and learn the hidden patterns in the input data in such a way that the model can be used to generate new data samples that could presumably have been taken from the original dataset. The GAN model consists of training a generative model by framing the problem as a supervised learning problem with two components: the generator model that we train to generate new samples, and the discriminator model that tries to classify those samples as either real or fake (generated).
The two models are trained together on the same dataset in a continuous way, until the discriminator model is unable to differentiate between real and fake samples, meaning that the generator model is generating realistic examples. By using the original data for supervision, the model is encouraged to capture time-conditional distribution within the data. A model called Time-series Generative Adversarial Network (TimeGAN) [45] was used to implement the GAN model based on our time-series data. The TimeGAN is a good generative model for time-series data that preserves temporal dynamics in the newly generated sequences which respect the original relationships between variables across time.
TimeGAN is a framework used to synthesize sequential data composed of four networks, which play distinct roles in the process of modeling the data: the expected generator and discriminator, but also the recovery and embedder models as shown in Figure 2. The latter pair maps between feature and latent space, allowing the adversarial network to learn the underlying temporal insights from the data. The energy dataset appears as a simple tabular dataset with each row representing a different time step and its related data points in the form of features.
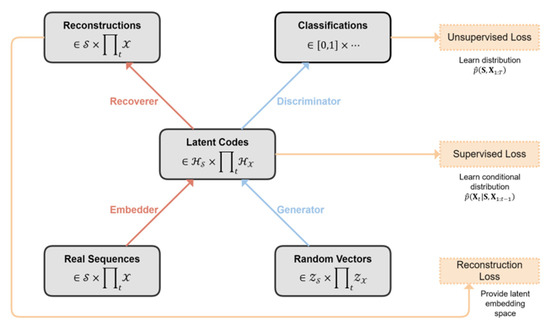
Figure 2.
TimeGAN architecture that presents a clearer training method of TimeGAN model [46].
After reading the energy dataset, pre-processing in the form of data transformation is carried out. In essence, this pre-processing phase scales the data in the [0, 1] range and executes the data transformation. After that, the pre-processed data is utilized to train the TimeGAN model, and the trained model is then used to produce new records.
6. A Comparative Assessment of Various Load Forecasting Techniques: Results and Discussion
This section presents an overview of the data, the hyperparameters used, and a comparative evaluation of different load forecasting techniques. Popular models for energy load forecasting were selected, which belong to different categories: statistical techniques (ARIMA and SARIMA), ML techniques (LR, KNN, SVR, RF, XGBoost, and DT), DL techniques (LSTM, RNN and MLP), and hybrid (LSTM-CNN and CNN-GRU). We have implemented and tested Hybrid-GRU-CNN, but the results were worse than for Hybrid-LSTM-CNN, which prompted us to keep the LSTM-CNN model. The selected ML algorithms were applied to the datasets and compared using the most-used evaluation metrics in a regression problem, such as MSE, RMSE, MAE, and R2. All results are presented in Table 4, which includes the accuracy and error metric values, to better illustrate the differences between the compared algorithms and their use cases.
In this study, we used three datasets collected in Spain, Germany, and the United States. These three datasets are shown in this section according to size, data frequency, and attributes.
The USA dataset [46] is hourly energy consumption data expressed in megawatts (MW) in the USA from 2004–2018; the dataset size is 121,273 samples, and training was performed on historical data of energy consumption per hour. Figure 3 presents the distribution of energy consumption in the USA each year.
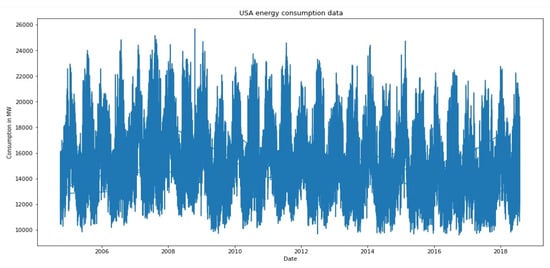
Figure 3.
USA data distribution.
The Germany dataset [47] is the total of electricity consumption, wind power generation, and solar power generation nationwide for Germany from 2006 to 2017; the dataset size is 4383 samples, and training was performed on historical data on electricity consumption per day. Figure 4 shows the German energy consumption distribution.
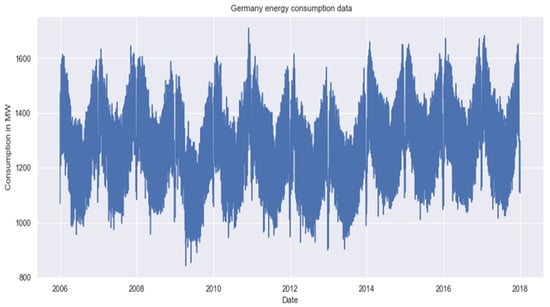
Figure 4.
Germany Data distribution.
The Spain data set [48] is composed of hourly electricity consumption in Spain from 2015 to 2019; the dataset size is 35,064 samples, comprising meteorological data (temperature, wind speed, humidity, precipitation). Figure 5 presents the distribution of energy consumption in Spain.
Figure 5.
Spain data distribution.
Random search is great for discovering hyperparameter combinations that one would not have guessed intuitively, although it often requires more time to execute. For this reason, in this work, the GridSearchCV algorithm is used, which corresponds to Grid Search with Cross-Validation (CV). CV is a statistical method used to estimate the performance of ML models. It is commonly used to select the most suitable model for a given predictive modeling problem. The main inputs of the GridSearchCV are the model to optimize, its hyperparameters, and the scoring parameter, generally R2 for regression problems. Its output corresponds to the best model architecture. We meticulously checked each model separately, fine-tuning specific hyperparameters for each. Table 3 illustrates an example for the LSTM model, including its specific hyperparameters. This table outlines the most significant hyperparameters utilized, along with their tested and optimal values.

Table 3.
Hyperparameters used in the LSTM model.
6.1. Results
6.1.1. Use Case 1 (Germany Dataset)
In this first case study, we have applied several algorithms to the first dataset, which is the German global consumption data. In the results table, each row represents the tested algorithm using different evaluation metrics (MSE, MAE, RMSE, and R2). Table 4 shows that the Hybrid LSTM-CNN model is more suitable in this case, providing the best results in terms of errors (the lowest error metrics). Its accuracy attains a score of more than 92%, which is considered a high value for a regression problem, especially for a time-series forecasting problem. Adding TimeGAN model to increase the volume of the data increases the accuracy of the model to 95%.

Table 4.
Evaluation metrics results.
In general, DL models have good results. Next to DL, the best ML algorithm is RF, featuring an accuracy of more than 85%, and low error metrics, in fact surpassing LSTM. Some other ML models like XGBoost and KNN also give good results, since their R2 exceeds 80%. On the other hand, the SVR model gives the worst results, so it is not considered a good solution in this case. SVR resulted in a very low R2, which means that it is not learning properly from the dataset, and it predicts the future consumption with a high error margin, thus presenting the highest error metric values. It should be noted that the best results are attained by DL models, which is because this kind of model is especially effective when the data volume exceeds thousands of rows.
6.1.2. Use Case 2 (USA Dataset)
The second use case is the USA dataset. Again, the best algorithm is the hybrid model which gives the best results with an R2 of 96% and 97%, respectively without and with the TimeGAN layer. We remark that, in this case, DL model results are far better than the other standard ML or statistical models, as the volume of data is larger than in the Germany dataset. Again, DL models show the ability to learn better from large volumes of data. As such, RNN, LSTM, and CNN-based models provide the best accuracy. The reason why recurrent models give better results is that the recurrency feature allows them to remember the previous data. This feature gives the model the capability of predicting accurate results in the future. The SVR model has again the worst results for this dataset, with a negative R2, which means that the model is not predicting the values correctly.
6.1.3. Use Case 3 (Spain Dataset)
In this case study, we obtained very good results even with fewer data compared to the previous case studies. This is because of the integration of multiple features in the data analytics. This variety of features, such as weather, consumption, and energy production variables, help the predictive models to learn better, based on extra, more hidden insights, by exploring the correlation between features. This leads to an increase in the accuracy and therefore a decrease in the error metrics. DL models are again the best in this case. The hybrid LSTM-CNN provides an R2 of 98% and 96%, respectively with and without the TimeGAN layer. Some other ML models, such as XGBoost, KNN, RF, and DT also perform well, showing their ability to extract data patterns from multiple cross-correlated features. As usual, SVR was not very effective, presenting the lowest R2 and the highest error metrics.
6.2. Discussion
After building, training, and testing all the above models, we can conclude that the data structure is playing a vital role in the model structure and model accuracy. In other words, the quality of data (real data, no missing values, correct values, etc.) affects the accuracy of a predictive model. The shape and the volume of data also affect the quality of results. We did not compare these findings with existing literature since our analysis was conducted on distinct datasets and utilized different preprocessing methods. Furthermore, there is no prior research that has undertaken a complete analysis like our study.
In this study, we have applied several ML and DL extensive analyses on different energy load datasets from different regions: Germany, the USA, and Spain. In all three use cases, we have found that the SVR algorithm gives the worst results. Indeed, this is the regression version of the SVM algorithm, which is a classification model that performs better for classification problems. However, SVR is still being used in some cases by researchers, particularly in energy demand forecasting and, in general, in some regression problems.
On the other hand, DL algorithms and especially recurrent algorithms (RNN, LSTM) have shown better results. This kind of model could extract more features from the data, and hence achieve more accurate results. However, they need more data as input, which conducts us to introduce the generative modeling aspect in our study. We have chosen TimeGAN, a derivative of the GAN models collection that is more suitable for tabular and time-series data. It preserves temporal dynamics and respects the original relationship between variables. This model allowed us to increase the size of the datasets while keeping the statistical characteristics of the data, which allows the training to be improved. In particular, when combining the best DL models in the Hybrid LSTM-CNN, coupling it with TimeGAN, we get the most accurate prediction among all algorithms.
As CNN is more suitable for feature extraction, it can extract more insights from data, which helps in the training process. On the other hand, the LSTM model is good for learning time dependencies in sequential data. The TimeGAN model has shown its ability to increase the volume of the dataset, respecting the original relationships between all data variables. Therefore, the combination of those three models has brought a new added value for time-series forecasting problems, namely for energy load forecasting.
Figure 6 illustrates the R2 values for each model in all the datasets used. We only have four years of historical and meteorological data for Spain, but even with this limited data, we achieved the best performance of almost all models. In addition, we achieved good results in the case of Germany, where we have 10 years of historical data with energy production characteristics. In contrast, we only have historical data for the USA, which spans 14 years, which is also the longest duration, yet we also found good results. We can therefore conclude that our chances of making accurate forecasts increase with the number of different feature types we have, despite a shorter data period.
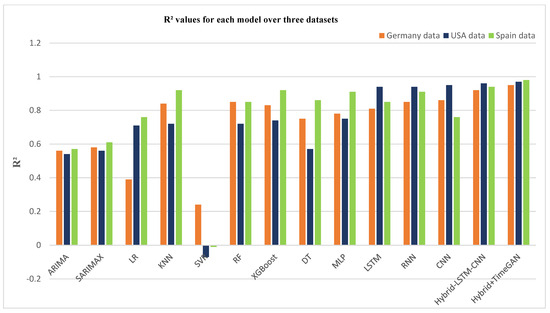
Figure 6.
R2 performance for each model across all scenarios.
6.2.1. Challenges and Future Trends
Trends: Load forecasting data is used to feed Smart Grid control systems. The complexity of the Smart Grid makes it very difficult to optimize in a purely centralized way. As such, optimization is inherently distributed, with control components being distributed across the grid, exchanging information to coordinate their decisions. These algorithms are also increasingly based on AI techniques, sometimes integrated into Digital Twins of the physical components. This section presents some of the current trends regarding these mechanisms.
- Deep Reinforcement learning
Agent-based optimization with Deep Reinforcement Learning (DRL) [49] is a new trend in the Smart Grid area [50]. Reinforcement Learning (RL) is a ML process, where an agent is trained to optimize the selection of actions based on the current state of the system. For each action taken, the agent receives a reward. The objective is to maximize the overall long-term reward. DRL integrates RL and DL. In DRL, a Deep Neural Network is trained and used to output the action that the agent should follow given the values of variables that represent the state of the environment. Utilizing distributed RL techniques, such as Advantage Actor-Critic (A2C), a set of agents (actors) can be trained in parallel, and given rewards by a common critic, allowing joint training of multi-agent systems, leading to emergent coordinated behavior. More scalable schemes are based on local interactions, where each agent only uses data from its vicinity, which is shared with the neighbor agents.
- Split Learning and Federated Learning
Split learning is very suitable for sensitive data and ensures data privacy. The data consumption is stored in different parties. Sharing individual data directly might cause security problems not only for individuals but also for national security [51,52]. A federated learning [53] infrastructure for SGs could help establish collaborative energy consumption pattern learning without sharing individual data [54]. In most cases, to protect user privacy and secure power traces, the collected raw data are stored locally in the user system, and the model also should be trained locally to prevent data leakage, while the model’s results are encrypted before the exchange. While some recent works focus on forecasting, they also address federated learning methodologies and other forms of energy. The work in [55] presents a novel approach to solar output forecasting, called “Federated transfer learning with orchard-optimized Conv-SGRU”. Focusing on safety and accuracy in solar power forecasting, the work discusses advances in federated transfer learning and uses an orchard-optimized Conv-SGRU model to improve forecasting capabilities. The goal of the study in [56] is to enhance smart grid security and dependability within the framework of Industry 5.0. The suggested method uses a hybrid deep learning model with federated learning support that is especially made to identify power theft using smart meters. With regard to ensuring the integrity of smart grids and addressing the issues around unlawful electricity consumption, this work is a major advancement.
- Transfer Learning
The principle is to reuse and capitalize on the knowledge and experience gained from resolving a given problem and apply it to another new but similar target problem. In the context of SGs, the basic idea is to benefit from the previously acquired learning in other related sectors, or among different SG functions [57,58]. For example, the work in [59] aims to create an inventive hybrid deep learning model (DLM) for resource-efficient photovoltaic (PV) energy production forecasting by combining CNN, LSTM, and Bi-LSTM. This model employs a hybrid deep learning strategy based on transductive transfer learning and is intended to be used in Industry 5.0. Enhancing PV power generation forecasting accuracy and efficiency is the main goal, with implications for optimizing energy management in industrial settings and smart grid operations.
- Collective intelligence
Conventional AI techniques are used by having each node selfishly benefit from its activities while cooperating with the other nodes to improve the SG’s global performance. As a result, the nodes are responsible for managing the inherent communication overhead. In the next decade, it is anticipated that the SG will make use of collective intelligence, where local data (such as historical and current parameters and observations) will serve as the foundation for each node’s decision-making about the best course of action (such as choosing a technology) that will positively affect the overall functioning of the SG without requiring direct communication between the participating nodes. For example, the SG can be represented using a game theory method, and DRL techniques can be used to converge on the best course of action for every node. The case of intercarrier interference avoidance in mMIMO-enabled networks has effectively studied this combination. To limit the amount of data required locally to gain a global advantage, research still has to overcome some technological challenges linked to the late convergence time of neural networks and scalable approaches (e.g. via offline training).
6.2.2. Open Research Questions
As a result of our study, we can see that the majority of publications focused on short- or medium-term forecasting, but we were unable to locate any studies that applied and worked on long-term forecasting. In our future work, we plan to explore further in this direction. We also plan to apply these models to other datasets from various countries to establish which load forecasting models perform well and are most accurate for any particular data format. We also intend to collect weather data and add it to the historical data, essentially providing various insights to help the models train, and to capture different features to improve model performance. In addition, we plan to expand our research focus to include various forms of renewable energy, such as solar and wind power. This expansion will cover not only consumption, but also energy production, management, optimization, and control.
7. Conclusions
Demand-side management is one of the biggest topics in SG systems, and energy forecasting is essential to its operation. Managing efficient forecasting while ensuring the least possible prediction error is the objective in the grid today. Hence, several research works have developed and implemented different predictive models to improve the accuracy level of the forecasting results. This paper has provided an overview and comparison of state-of-the-art ML, DL, statistical methods, and hybrid techniques applied in energy load forecasting. Simulation results were used to support comparative analysis of the different methods.
The simulations were carried out with three different datasets belonging to three different countries: Germany, USA, and Spain. However, uncertainty in the SG data from exogenous factors, such as weather and social behavior, is a major challenge, requiring special hybrid models combining the best approaches to increase accuracy. Several combinations between models were tested, leading to a parallel LSTM-CNN model, which provides the best results for all datasets. In this hybrid model, the CNN is used to extract the maximum features from the input data, while the LSTM is used to capture the time dependencies in the time-series data. To improve the accuracy of the model even further, a data augmentation technique was applied, which is based on TimeGAN.
Therefore, based on this research, we can say that, among the analyzed models, LSTM-CNN with TimeGAN gave better results. We also found that varying the types of data (historical, meteorological, behavioral, etc.) and the duration of data collection are beneficial for improving the accuracy of forecast results.
Finally, it is noteworthy to mention that the current paper is part of an internationally funded project wherein we are looking at a particular well-defined forecasting scenario characterized by short-term load forecasting objectives, a limited-size consumption dataset, and a decision support tool without time computation constraints. Considering all the aforementioned factors, and bearing in mind that the choice of which AI model to use depends on the specific requirements, resources, and constraints of the project at hand, it is therefore important to evaluate the strengths and weaknesses of each model and choose the one that is best suited for the task at hand. Therefore, the comparative analysis in this paper has considered, on the one hand, the most popular techniques used in prior art and, on the other hand, the recent trend from the literature research such as data augmentation (e.g., TimeGAN) and hybrid models (e.g., LSTM-CNN) that provide a good trade-off between performance and training complexity compared to other simpler standalone models.
Author Contributions
Methodology, Writing—original draft, R.H. and M.L.; Writing—review & editing, R.H.; Supervision, A.G., A.C. and R.B.; Project administration, R.B; Resources, A.T. and B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by the Institut de Recherche en Energie Solaire et ’Energies Nouvelles (IRESEN) in the context of the project´ “Inno ESPAMAROC ENERGY 2018/EnROptimizer”, and has also been supported by the Portuguese national funds through FCT, Fundacçao para a Ciencia e a Tecnologia, under project UIDB/50021/2020.
Data Availability Statement
The datasets used during the current study are public data and referenced in the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| SG | Smart Grid |
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| ARIMA | AutoRegressive Integrated Moving Average |
| ARIMAX | Autoregressive Integrated Moving Average with Explanatory Variable |
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| DRL | Deep Reinforcement Learning |
| DT | Decision Tree |
| DNN | Deep Neural Network |
| GAN | Generative Adversarial Network |
| GRU | Gated Recurrent Unit |
| KNN | K-Nearest Neighbors |
| LR | Linear Regression |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| MLSE | Maximum Likelihood Sequence Estimation |
| MSE | Mean Square Error |
| RF | Random Forest |
| RL | Reinforcement Learning |
| RNN | Recurrent Neural Network |
| SVM | Support Vector Machine |
| SVR | Support Vector Regressor |
| RMSE | Root Mean Square Error |
| TimeGAN | Time-series Generative Adversarial Network |
References
- Al Mamun, A.; Sohel, M.; Mohammad, N.; Sunny, S.H.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Pham, Q.V.; Liyanage, M.; Deepa, N.; VVSS, M.; Reddy, S.; Maddikunta, P.K.R.; Khare, N.; Gadekallu, T.R.; Hwang, W.J. Deep Learning for Intelligent Demand Response and Smart Grids: A Comprehensive Survey. arXiv 2021, arXiv:2101.08013. [Google Scholar]
- Aslam, S.; Herodotou, H.; Mohsin, S.M.; Javaid, N.; Ashraf, N.; Aslam, S. A survey on deep learning methods for power load and renewable energy forecasting in smart microgrids. Renew. Sustain. Energy Rev. 2021, 144, 110992. Available online: https://www.sciencedirect.com/science/article/pii/S1364032121002847 (accessed on 5 August 2023). [CrossRef]
- Omitaomu, O.A.; Niu, H. Artificial Intelligence Techniques in Smart Grid: A Survey. Smart Cities 2021, 4, 548–568. [Google Scholar] [CrossRef]
- Mhlanga, D. Artificial Intelligence and Machine Learning for Energy Consumption and Production in Emerging Markets: A Review. Energies 2023, 16, 745. Available online: https://www.mdpi.com/1996-1073/16/2/745 (accessed on 8 August 2023). [CrossRef]
- Pérez-Gomariz, M.; López-Gómez, A.; Cerdán-Cartagena, F. Artificial Neural Networks as Artificial Intelligence Technique for Energy Saving in Refrigeration Systems—A Review. Clean Technol. 2023, 5, 116–136. [Google Scholar] [CrossRef]
- Olabi, A.; Abdelghafar, A.A.; Maghrabie, H.M.; Sayed, E.T.; Rezk, H.; Al Radi, M.; Obaideen, K.; Abdelkareem, M.A. Application of artificial intelligence for prediction, optimization, and control of thermal energy storage systems. Therm. Sci. Eng. Prog. 2023, 39, 101730. [Google Scholar] [CrossRef]
- Shabbir, N.; Kütt, L.; Raja, H.A.; Ahmadiahangar, R.; Rosin, A.; Husev, O. Machine Learning and Deep Learning Techniques for Residential Load Forecasting: A Comparative Analysis. In Proceedings of the 2021 IEEE 62nd International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), Riga, Latvia, 15–17 November 2021; Available online: https://ieeexplore.ieee.org/abstract/document/9711741 (accessed on 10 August 2023).
- Khotsriwong, N.; Boonraksa, P.; Sarapan, W.; Boonraksa, T.; Boonrakchat, N.; Marungsri, B. Short-term Load Demand Forecasting using Supervised Deep Learning Techniques: A Case Study of Suranaree University of Technology. In Proceedings of the 2023 International Electrical Engineering Congress (iEECON); 2023; pp. 417–420. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, S.; Sun, S. A Deep Learning model for day-ahead load forecasting taking advantage of expert knowledge. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–5. [Google Scholar]
- Unlu, A.; Peña, P.; Wang, Z. Comparison of the Combined Deep Learning Methods for Load Forecasting. In Proceedings of the 2023 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–19 January 2023; Available online: https://ieeexplore.ieee.org/abstract/document/10066449 (accessed on 16 August 2023).
- Xuan, Y.; Si, W.; Zhu, J.; Sun, Z.; Zhao, J.; Xu, M.; Xu, S. Multi-Model Fusion Short-Term Load Forecasting Based on Random Forest Feature Selection and Hybrid Neural Network. IEEE Access 2021, 9, 69002–69009. Available online: https://ieeexplore.ieee.org/abstract/document/9321361 (accessed on 20 August 2023). [CrossRef]
- Wangdi, K.; Singhasivanon, P.; Silawan, T.; Lawpoolsri, S.; White, N.J.; Kaewkungwal, J. Development of temporal modelling for forecasting and prediction of malaria infections using time-series and ARIMAX analyses: A case study in endemic districts of Bhutan. Malar. J. 2010, 9, 251. Available online: https://malariajournal.biomedcentral.com/articles/10.1186/1475-2875-9-251 (accessed on 22 August 2023). [CrossRef]
- Ediger, V.Ş.; Akar, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy 2007, 35, 1701–1708. [Google Scholar] [CrossRef]
- Fattah, J.; Ezzine, L.; Aman, Z.; Moussami, H.E.; Lachhab, A. Forecasting of demand using ARIMA model. Int. J. Eng. Bus. Manag. 2018, 10, 184797901880867. [Google Scholar] [CrossRef]
- Ma, Z.; Ye, C.; Li, H.; Ma, W. Applying support vector machines to predict building energy consumption in China. Energy Procedia 2018, 152, 780–786. Available online: https://www.sciencedirect.com/science/article/pii/S1876610218307902 (accessed on 24 August 2023). [CrossRef]
- Fan, G.-F.; Guo, Y.-H.; Zheng, J.-M.; Hong, W.-C. Application of the Weighted K-Nearest Neighbor Algorithm for Short-Term Load Forecasting. Energies 2019, 12, 916. [Google Scholar] [CrossRef]
- Atanasovski, M.; Kostov, M.; Arapinoski, B.; Spirovski, M. K-Nearest Neighbor Regression for Forecasting Electricity Demand. In Proceedings of the 2020 55th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Nis, Serbia, 10–12 September 2020; Available online: https://ieeexplore.ieee.org/abstract/document/9232768 (accessed on 27 August 2023).
- Hubana, T.; Šemić, E.; Laković, N. Machine Learning Based Electrical Load Forecasting Using Decision Tree Algorithms. In Advanced Technologies, Systems, and Applications V; IAT 2020. Lecture Notes in Networks and Systems; Avdaković, S., Volić, I., Mujčić, A., Uzunović, T., Mujezinović, A., Eds.; Springer: Cham, Switzerland, 2020; Volume 142. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, S.; Chen, X.; Zeng, X.; Kong, Y.; Chen, J.; Guo, Y.; Wang, T. Short-term load forecasting of industrial customers based on SVMD and XGBoost. Int. J. Electr. Power Energy Syst. 2021, 129, 106830. [Google Scholar] [CrossRef]
- Lu, Y.-S.; Lai, K.-Y. Deep-Learning-Based Power Generation Forecasting of Thermal Energy Conversion. Entropy 2020, 22, 1161. [Google Scholar] [CrossRef]
- Amarasinghe, K.; Marino, D.L.; Manic, M. Deep neural networks for energy load forecasting. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1483–1488. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Dong, M.; Grumbach, L. A Hybrid Distribution Feeder Long-Term Load Forecasting Method Based on Sequence Prediction. IEEE Trans. Smart Grid 2020, 11, 470–482. [Google Scholar] [CrossRef]
- Syed, D.; Abu-Rub, H.; Ghrayeb, A.; Refaat, S.S.; Houchati, M.; Bouhali, O.; Banales, S. Deep Learning-Based Short-Term Load Forecasting Approach in Smart Grid with Clustering and Consumption Pattern Recognition. IEEE Access 2021, 9, 54992–55008. [Google Scholar] [CrossRef]
- Zor, K.; Buluş, K. A benchmark of GRU and LSTM networks for short-term electric load forecasting. In Proceedings of the 2021 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT), Zallaq, Bahrain, 29–30 September 2021; pp. 598–602. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, Y.-M.; Li, D.; Tan, Z.; Zhou, J. Short term electricity load forecasting using a hybrid model. Energy 2018, 158, 774–781. [Google Scholar] [CrossRef]
- Lu, H.; Azimi, M.; Iseley, T. Short-term load forecasting of urban gas using a hybrid model based on improved fruit fly optimization algorithm and support vector machine. Energy Rep. 2019, 5, 666–677. [Google Scholar] [CrossRef]
- Haq, R.; Ni, Z. A New Hybrid Model for Short-Term Electricity Load Forecasting. IEEE Access 2019, 7, 125413–125423. [Google Scholar] [CrossRef]
- Qiu, X.; Ren, Y.; Suganthan, P.N.; Amaratunga, G.A. Empirical Mode Decomposition based ensemble deep learning for load demand time series forecasting. Appl. Soft Comput. 2017, 54, 246–255. Available online: https://www.sciencedirect.com/science/article/pii/S1568494617300273 (accessed on 4 September 2023). [CrossRef]
- Farsi, B.; Amayri, M.; Bouguila, N.; Eicker, U. On Short-Term Load Forecasting Using Machine Learning Techniques and a Novel Parallel Deep LSTM-CNN Approach. IEEE Access 2021, 9, 31191–31212. Available online: https://ieeexplore.ieee.org/abstract/document/9356582 (accessed on 12 September 2023). [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y.; Ali, I.H.O. CNN-LSTM: An efficient hybrid deep learning architecture for predicting short-term photovoltaic power production. Electr. Power Syst. Res. 2022, 208, 107908. Available online: https://www.sciencedirect.com/science/article/pii/S0378779622001389 (accessed on 3 October 2023). [CrossRef]
- Xiong, J.; Zhang, Y. A Unifying Framework of Attention-Based Neural Load Forecasting. IEEE Access 2023, 11, 51606–51616. Available online: https://ieeexplore.ieee.org/abstract/document/10122506 (accessed on 11 October 2023). [CrossRef]
- Alasadi, S.A.; Bhaya, W.S. Review of Data Preprocessing Techniques in data mining. J. Eng. Appl. Sci. 2017, 12, 4102–4107. [Google Scholar]
- Mishra, P.; Biancolillo, A.; Roger, J.M.; Marini, F.; Rutledge, D.N. New data preprocessing trends based on ensemble of multiple preprocessing techniques. TrAC Trends Anal. Chem. 2020, 132, 116045. [Google Scholar] [CrossRef]
- Andradóttir, A.S. Chapter 20 An overview of simulation optimization via random search. In Handbooks in Operations Research and Management Science; Henderson, S.G., Nelson, B.L., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 13, pp. 617–631. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Li, L.; Talwalkar, A. Random search and reproducibility for neural architecture search. Uncertain. Artif. Intell. PMLR 2020, 115, 367–377. [Google Scholar]
- Rufino, A.B.S.; Saraiva, F. Use of Augmented Random Search Algorithm for Transmission Line Control in Smart Grids—A Comparative Study with RNA-Based Algorithms; Anais do XX Encontro Nacional de Inteligência Artificial e Computacional. SBC: Belo Horizonte, Brazil, 2023. [Google Scholar]
- Yennimar, Y.; Rasid, A.; Kenedy, S. Implementation of support vector machine algorithm with hyper-tuning randomized search in stroke prediction. J. Sist. Inf. Dan Ilmu Komput. Prima (JUSIKOM PRIMA) 2023, 6, 61–65. [Google Scholar] [CrossRef]
- Fayed, H.A.; Atiya, A.F. Speed up grid-search for parameter selection of support vector machines. Appl. Soft Comput. 2019, 80, 202–210. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, S.; Zhang, Z.; Jia, W. An improved grid search algorithm to optimize SVR for prediction. Soft Comput. 2021, 25, 5633–5644. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 588–598. [Google Scholar]
- Le, T.; Vo, M.T.; Vo, B.; Hwang, E.; Rho, S.; Baik, S.W. Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM. Appl. Sci. 2019, 9, 4237. [Google Scholar] [CrossRef]
- Yoon, J.; Jarrett, D.; Van der Schaar, M. Time-series generative adversarial networks. Adv. Neural Inf. Process. Syst. 2019, 32. Available online: https://proceedings.neurips.cc/paper/2019/file/c9efe5f26cd17ba6216bbe2a7d26d490-Paper.pdf (accessed on 24 August 2023).
- USA Electricity Hourly Power Consumption. Available online: https://www.kaggle.com/datasets/robikscube/hourly-energy-consumption (accessed on 20 August 2023).
- Open Power System Data. Germany Electricity Power for 2006–2017. Available online: https://www.kaggle.com/datasets/mvianna10/germany-electricity-power-for-20062017 (accessed on 18 August 2023).
- Hour Energy Demand Generation and Weather. Available online: https://www.kaggle.com/datasets/nicholasjhana/energy-consumption-generation-prices-and-weather (accessed on 24 August 2023).
- Connell, J.H.; Mahadevan, S. ROBOT LEARNING, edited by Jonathan H. Connell and Sridhar Mahadevan, Kluwer, Boston, 1993/1997, xii+240 pp., ISBN 0-7923-9365-1 (Hardback, 218.00 Guilders, $120.00, £89.95). Robotica 1999, 17, 229235. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, K.; Li, J.; Wang, S. Modified deep learning and reinforcement learning for an incentive-based demand response model. Energy 2020, 205, 118019. [Google Scholar] [CrossRef]
- Gupta, O.; Raskar, R. Distributed learning of deep neural network over multiple agents. J. Netw. Comput. Appl. 2018, 116, 1–8. [Google Scholar] [CrossRef]
- Alromih, A.; Clark, J.A.; Gope, P. Privacy-Aware Split Learning Based Energy Theft Detection for Smart Grids. In Information and Communications Security; Alcaraz, C., Chen, L., Li, S., Samarati, P., Eds.; ICICS 2022. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2022; Volume 13407. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated Learning: Challenges, Methods, and Future Directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, Z.; Liu, B.; Xu, Y.; Ding, Z. FedForecast: A federated learning framework for short-term probabilistic individual load forecasting in smart grid. Int. J. Electr. Power Energy Syst. 2023, 152, 109172. [Google Scholar] [CrossRef]
- Bukhari, S.M.S.; Moosavi, S.K.R.; Zafar, M.H.; Mansoor, M.; Mohyuddin, H.; Ullah, S.S.; Alroobaea, R.; Sanfilippo, F. Federated transfer learning with orchard-optimized Conv-SGRU: A novel approach to secure and accurate photovoltaic power forecasting. Renew. Energy Focus 2024, 48, 100520. [Google Scholar] [CrossRef]
- Zafar, M.H.; Bukhari, S.M.S.; Houran, M.A.; Moosavi, S.K.R.; Mansoor, M.; Al-Tawalbeh, N.; Sanfilippo, F. Step towards secure and reliable smart grids in Industry 5.0: A federated learning assisted hybrid deep learning model for electricity theft detection using smart meters. Energy Rep. 2023, 10, 3001–3019. [Google Scholar] [CrossRef]
- Himeur, Y.; Elnour, M.; Fadli, F.; Meskin, N.; Petri, I.; Rezgui, Y.; Bensaali, F.; Amira, A. Next-generation energy systems for sustainable smart cities: Roles of transfer learning. Sustain. Cities Soc. 2022, 85, 104059. [Google Scholar] [CrossRef]
- Grubinger, T.; Chasparis, G.C.; Natschläger, T. Generalized online transfer learning for climate control in residential buildings. Energy Build. 2017, 139, 63–71. [Google Scholar] [CrossRef]
- Khan, U.A.; Khan, N.M.; Zafar, M.H. Resource efficient PV power forecasting: Transductive transfer learning based hybrid deep learning model for smart grid in Industry 5.0. Energy Convers. Manag. X 2023, 20, 100486. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).