Power Transformer Fault Detection: A Comparison of Standard Machine Learning and autoML Approaches
Abstract
:1. Introduction
- ML algorithms: Several single classifiers have been used such as the artificial neural network (ANN) [1,12,13,15,19]; expert-guided ANN [15,20]; Bayes network [1]; decision tree (DT) [1,13]; extreme learning machine (ELM) [15]; K-nearest neighbors (KNN) [1,12,13,19]; logical analysis of data (LDA) [21]; logistic (LR) and regularized (LASSO) regression [13]; probabilistic neural network (PNN) [12,22]; softmax regression (SR) [15]; and support vector machine (SVM) [13,19]. Ensembles include boosting and bagging [1,23]; eXtreme gradient boosting (XGBoost) [24]; stacked ANN [2]; and even state-of-the-art algorithms such as few-shot learning with belief functions [5].
- Data pre-processing methods: Several data transformations have been used such as data binarization [21]; key [1,2,5,13,15,22,24] and custom gas ratios [2]; logarithmic transformation [1,2,13]; mean subtraction and normalization [2]; standardization [1,2,13]; imputation of missing values using simple approaches [25]; dimensionality reduction such as linear discriminant and principal components analyses [12], and belief functions [5]; feature extraction such as genetic programming [19]; knowledge- based transformations such as expert knowledge rules [15]; and oil–gas thermodynamics [2].
- Parameters optimization: Algorithm parameters have been optimized by hand [2] and through trial and error [12]; exact methods such as grid search (GS) [13,20] and mixed integer linear programming [21]; Bayesian methods [24]; and metaheuristics such as the bat algorithm [22] and genetic and mind evolutionary algorithms [15].
2. Materials and Methods
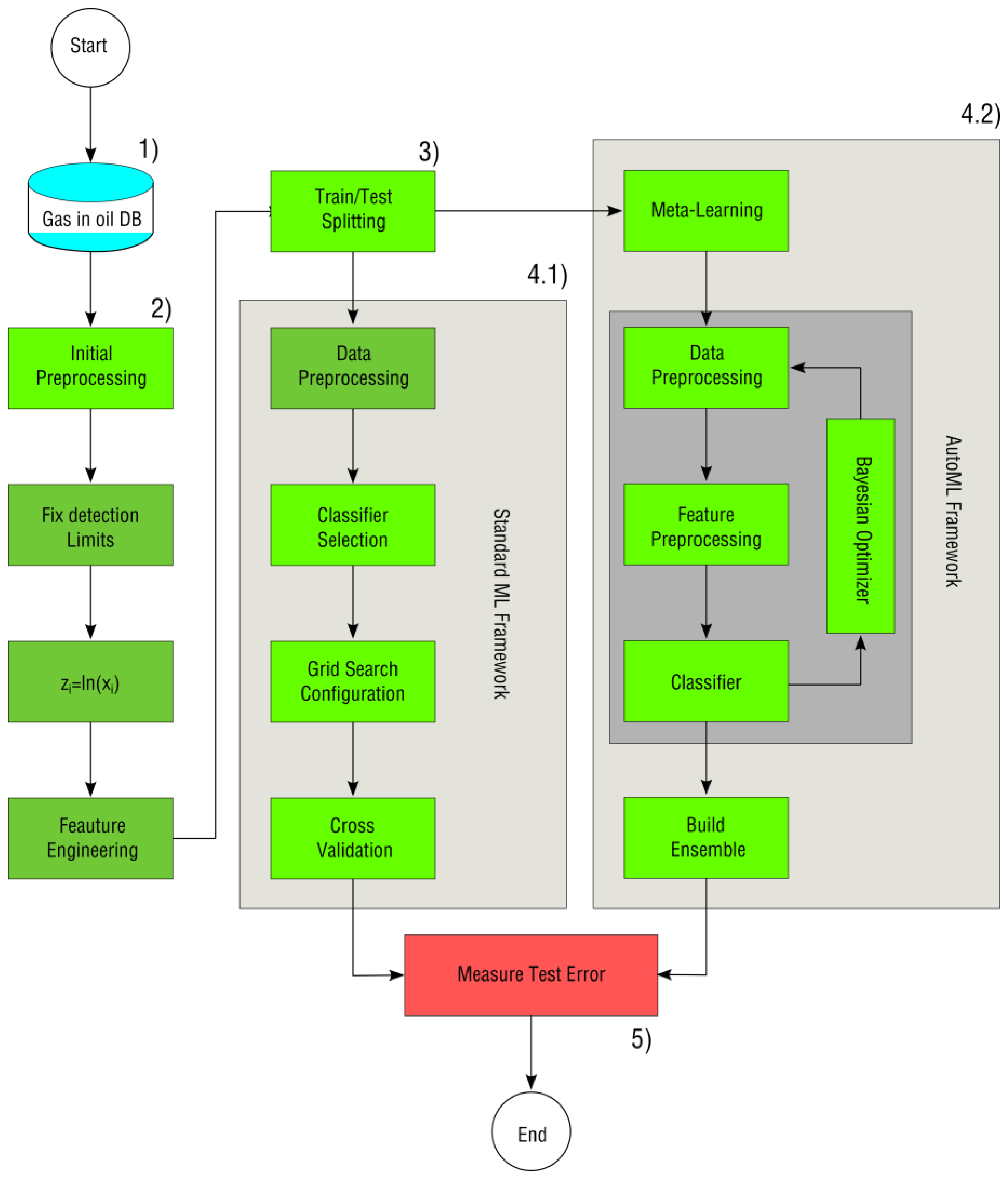
- Data recollection and labeling. In this step, we transformed dissolved gas-in-oil and conducted corresponding diagnostics. We double-checked transformers’ diagnostics: first using the Duval pentagons method to obtain the fault severity (if not available), and then using the IEEE C57.104-2019 standard and expert validation to identify normal operating transformers.
- Initial pre-processing. In this step, we pre-processed gas-in-oil information using several methods found in the literature, namely, the replacement of zero measurements, natural logarithm escalation, and derivation of key gas ratios.
- Data separation into training (i.e., Xtrain and Ytrain) and testing (i.e., Xtest and Ytest) datasets. For this splitting, we considered the number of samples in each class, to avoid leaving classes unrepresented in any of the datasets.
- Training the ML system:
- Standard ML framework. In this step, we carried out a second data pre-processing stage, training, and parameter optimization. We optimized the parameters from single and ensemble classifiers using a grid search (GS) and cross-validation (CV) procedures.
- AutoML framework. In this step, the code automatically carried out a warm-start procedure, additional data and feature pre-processing methods, classifier optimization, and ensemble construction.
- Measuring the test error using several multi-class performance measures. In this step, we evaluated the algorithms comprehensively using several multi-class performance measures such as the κ score, balanced accuracy, and the micro and macro F1-measure.
2.1. DGA Data
2.2. Initial Pre-Processing of DGA Data
2.3. Splitting Data and Training the ML System
2.3.1. Standard ML Framework
2.3.2. AutoML Framework
2.4. Classification Performance Metrics
2.5. Software
3. Results
3.1. Overall Classifier Performance for the TFD Problem
3.2. Analysis of the Frameworks’ Performance
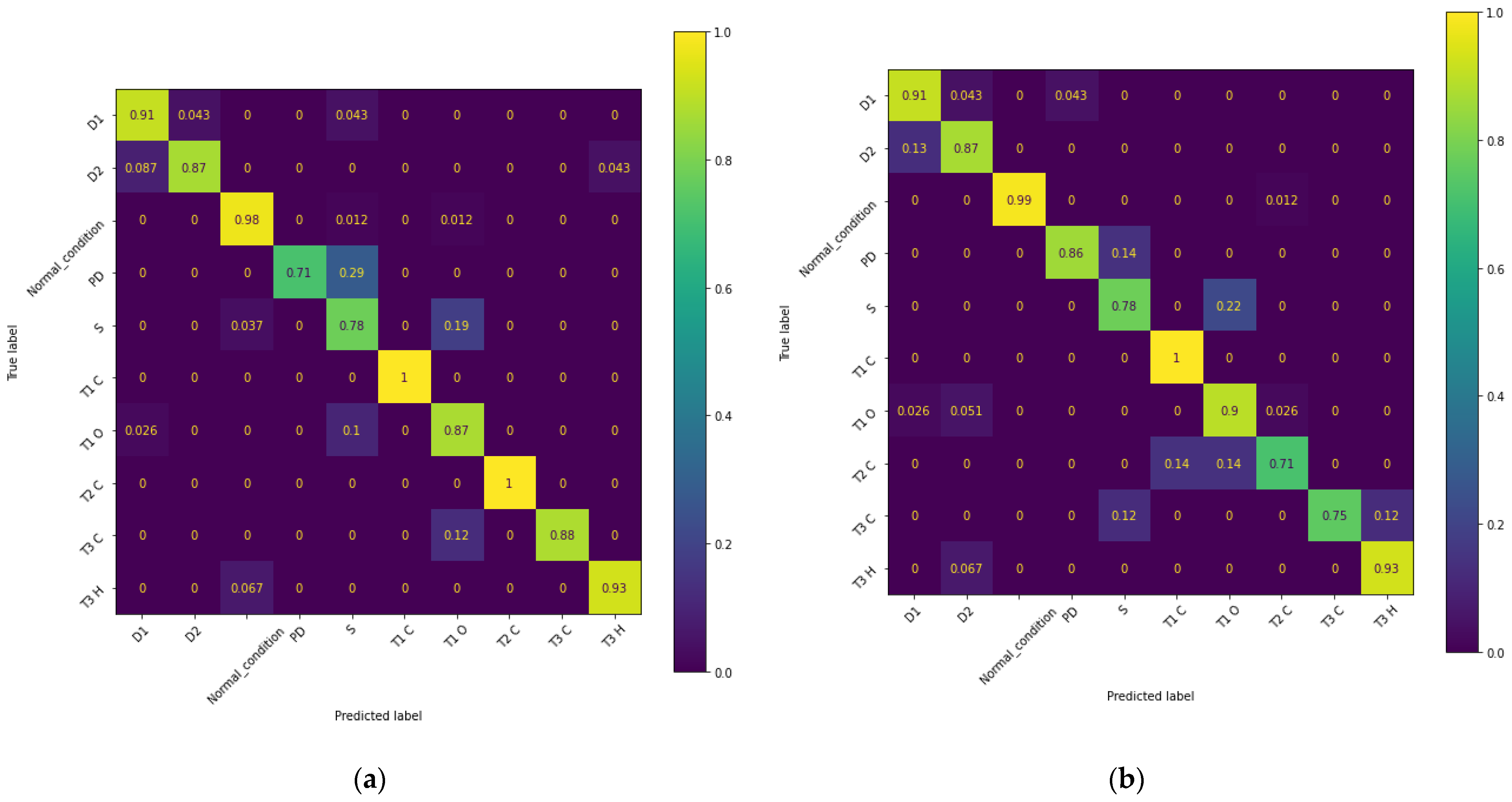
3.3. Transformers’ Fault Diagnosis in Detail
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Machine Learning Algorithms
Appendix A.1. Single Classifiers
Appendix A.1.1. Artificial Neural Networks
Appendix A.1.2. Decision Trees
Appendix A.1.3. Gaussian Processes
Appendix A.1.4. K-Nearest Neighbors
Appendix A.1.5. Naive Bayes
Appendix A.1.6. Logistic Regression
Appendix A.1.7. Support Vector Machines
Appendix A.2. Ensembles
Appendix A.2.1. Random Forest
Appendix A.2.2. Bagging Classifier
Appendix A.2.3. Gradient Boosting
Appendix A.2.4. Stacking Ensemble
Appendix B. AutoML Algorithms
Appendix C. Performance Measures
Appendix C.1. Confusion Matrix

Appendix C.2. Precision and Recall
Micro and Macro Averages for Multi-Class
Appendix C.3. Balanced Accuracy
Appendix C.4. F1-Measure
Appendix C.5. Matthews’ Correlation Coefficient
Appendix C.6. Cohen’s Kappa
References
- Senoussaoui, M.E.A.; Brahami, M.I.; Fofana, I. Combining and comparing various machine learning algorithms to improve dissolved gas analysis interpretation. IET Gener. Transm. Distrib. 2018, 12, 3673–3679. [Google Scholar] [CrossRef]
- Taha, I.B.; Dessouky, S.S.; Ghoneim, S.S. Transformer fault types and severity class prediction based on neural pattern-recognition techniques. Electr. Power Syst. Res. 2020, 191, 106899. [Google Scholar] [CrossRef]
- Baker, E.; Nese, S.V.; Dursun, E. Hybrid Condition Monitoring System for Power Transformer Fault Diagnosis. Energies 2023, 16, 1151. [Google Scholar] [CrossRef]
- Velasquez, R.M.A.; Lara, J.V.M. Root cause analysis improved with machine learning for failure analysis in power transformers. Eng. Fail. Anal. 2020, 115, 104684. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Wang, Y.; Zhong, D.; Zhang, G. Improved few-shot learning method for transformer fault diagnosis based on approximation space and belief functions. Expert Syst. Appl. 2021, 167, 114105. [Google Scholar] [CrossRef]
- Duque, J.F.P.; Martinez, M.T.V.; Hurtado, A.P.; Carrasco, E.M.; Sancho, B.L.; Krommydas, K.F.; Plakas, K.A.; Karavas, C.G.; Kurashvili, A.S.; Dikaiakos, C.N.; et al. Inter-Area Oscillation Study of the Greek Power System Using an Automatic Toolbox. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18–21 October 2021; pp. 1–6. [Google Scholar]
- Arias, R.; Mejia, J. Health index for transformer condition assessment. IEEE Lat. Am. Trans. 2018, 16, 2843–2849. [Google Scholar] [CrossRef]
- Ghoneim, S.S.M.; Taha, I.B.M. Comparative study of full and reduced feature scenarios for health index computation of power transformers. IEEE Access 2020, 8, 181326–181339. [Google Scholar] [CrossRef]
- Rogers, R. IEEE and IEC Codes to Interpret Incipient Faults in Transformers, Using Gas in Oil Analysis. IEEE Trans. Electr. Insul. 1978, 13, 349–354. [Google Scholar] [CrossRef]
- CIGRE. Transformer Reliability Surveys; CIGRE Technical Brochure 642; WW.G. A2.; CIGRE: Paris, France, 2015. [Google Scholar]
- Bartley, W. Analysis of transformer failures. In Proceedings of the International Association OF Engineering Insurers 36th Annual Conference, Stockholm, Sweden, 15–17 September 2003; pp. 1–12. [Google Scholar]
- Nagpal, T.; Brar, Y.S. Artificial neural network approaches for fault classification: Comparison and performance. Neural Comput. Appl. 2014, 25, 1863–1870. [Google Scholar] [CrossRef]
- Mirowski, P.; Lecun, Y. Statistical machine learning and dissolved gas analysis: A review. IEEE Trans. Power Deliv. 2012, 27, 1791–1799. [Google Scholar] [CrossRef]
- Golarz, J. Understanding Dissolved Gas Analysis (DGA) techniques and interpretations. In Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference, Dallas, TX, USA, 3–5 May 2016. [Google Scholar]
- Wu, Q.; Zhang, H. A novel expertise-guided machine learning model for internal fault state diagnosis of power transformers. Sustainability 2019, 11, 1562. [Google Scholar] [CrossRef]
- Li, E.; Wang, L.; Song, B. Fault diagnosis of power transformers with membership degree. IEEE Access 2019, 7, 28791–28798. [Google Scholar] [CrossRef]
- Cheim, L.; Duval, M.; Haider, S. Combined duval pentagons: A simplified approach. Energies 2020, 13, 2859. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Zhang, F.; Wan, J.; Kou, L.; Ke, W. Review on evolution of intelligent algorithms for transformer condition assessment. Front. Energy Res. 2022, 10, 904109. [Google Scholar] [CrossRef]
- Shintemirov, A.; Tang, W.; Wu, Q.H. Power transformer fault classification based on dissolved gas analysis by implementing bootstrap and genetic programming. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 69–79. [Google Scholar] [CrossRef]
- Wu, X.; Wang, P.; Wang, L.; Xu, Y.; Zhao, Z. Transformer combination weighting evaluation model based on bp neural network. In Proceedings of the Genetic and Evolutionary Computing. ICGEC 2021. Lecture Notes in Electrical Engineering, Jilin, China, 21–23 October 2022. [Google Scholar]
- Mortada, M.A.; Yacout, S.; Lakis, A. Fault diagnosis in power transformers using multi-class logical analysis of data. J. Intell. Manuf. 2014, 25, 1429–1439. [Google Scholar] [CrossRef]
- Yang, X.; Chen, W.; Li, A.; Yang, C.; Xie, Z.; Dong, H. BA-PNN-based methods for power transformer fault diagnosis. Av. Eng. Inform. 2019, 39, 178–185. [Google Scholar] [CrossRef]
- AI, K.; PV, M.; SA, E.; VZ, M.; AM, B. Romanov AM. Data Mining Applied to Decision Support Systems for Power Transformers’ Health Diagnostics. Mathematics 2022, 10, 2486. [Google Scholar]
- Zhang, D.; Li, C.; Shahidehpour, M.; Wu, Q.; Zhou, B.; Zhang, C. A bi-level machine learning method for fault diagnosis of oil-immersed transformers with feature explainability. Int. J. Electr. Power Energy Syst. 2022, 134, 107356. [Google Scholar] [CrossRef]
- Cheim, L. Machine Learning Tools in Support of Transformer Diagnostics; CIGRE: Paris, France, 2018; pp. A2–A206. [Google Scholar]
- Zöller, M.-A.; Huber, M.F. Benchmark and Survey of Automated Machine Learning Frameworks. J. Artif. Intell. Res. 2021, 70, 409–472. [Google Scholar] [CrossRef]
- Thornton, C.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; Part F128815. pp. 847–855. [Google Scholar]
- Feurer, M.; Klein, A.; Eggensperger, K.; Springenberg, J.T.; Blum, M.; Hutter, F. Efficient and Robust Automated Machine Learning. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2962–2970. [Google Scholar]
- Duval, M.; Lamarre, L. The Duval pentagon-a new complementary tool for the interpretation of dissolved gas analysis in transformers. IEEE Electr. Insul. Mag. 2014, 30, 9–12. [Google Scholar]
- Jakob, F.; Dukarm, J.J. Thermodynamic estimation of transformer fault severity. IEEE Trans. Power Deliv. 2015, 30, 1941–1948. [Google Scholar] [CrossRef]
- Dukarm, J.; Jakob, F. Thermodynamic estimation of transformer fault severity. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016. [Google Scholar] [CrossRef]
- Londono, S.M.P.; Cadena, J.A.; Cadena, J.M. Aplicacion de redes neuronales probabilısticas en la deteccion de fallas incipientes en transformadores. Sci. Et Tech. 2008, 2, 48–53. [Google Scholar]
- Ranga, C.; Chandel, A.K.; Chandel, R. Condition assessment of power transformers based on multi-attributes using fuzzy logic. IET Sci. Meas. Technol. 2017, 11, 983–990. [Google Scholar] [CrossRef]
- Mharakurwa, E.T.; Goboza, R. Multiparameter-based fuzzy logic health index assessment for oil-immersed power transformers. Adv. Fuzzy Syst. 2019, 2019, 2647157. [Google Scholar] [CrossRef]
- CIGRE TB 761 Condition Assessment of Power Transformers; CIGRE: Paris, France, 2019.
- IEEE Guide for the Interpretation of Gases Generated in Mineral Oil-Immersed Transformers; IEEE: New York, NY, USA, 2019.
- Truong, A.; Walters, A.; Goodsitt, J.; Hines, K.; Bruss, C.B.; Farivar, R. Towards automated machine learning: Evaluation and comparison of AutoML approaches and tools. In Proceedings of the IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 1471–1479. [Google Scholar]
- Osborne, J. Notes on the use of data transformations, Practical assessment. Res. Eval. 2002, 8, 6. [Google Scholar]
- Feurer, M.; Eggensperger, K.; Falkner, S.; Lindauer, M.; Hutter, F. Auto-Sklearn 2.0: Hands-free AutoML via Meta-Learning. J. Mach. Learn. Res. 2020, 23, 11936–11996. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Oliphant, T.E. A Guide to NumPy; Trelgol Publishing: New York, NY, USA, 2006; Volume 1. [Google Scholar]
- McKinney, W. pandas: A foundational python library for data analysis and statistics. In Proceedings of the Workshop Python for High Performance and Scientific Computing, Tsukuba, Japan, 1–3 June 2011; pp. 1–9. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, ACM, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Freitas, A.A. A critical review of multi-objective optimization in data mining. ACM SIGKDD Explor. Newsl. 2004, 6, 77–86. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, Springer Series in Statistics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Rokach, L.; Maimon, O.Z. Data Mining with Decision Trees: Theory and Applications; World Scientific: Singapore, 2007; Volume 69. [Google Scholar]
- Matthews, A.G.D.G.; Rowland, M.; Hron, J.; Turner, R.E. Gaussian process behaviour in wide deep neural networks. Int. Conf. Learn. Represent 2018, 4, 77–86. [Google Scholar]
- Mitchell, T.M.; Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Shobha, G.; Rangaswamy, S.; Chapter; Gudivada, V.N.; Rao, C. Computational Analysis and Understanding of Natural Languages: Principles, Methods and Applications, Vol. 38 of Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2018; pp. 197–228. [Google Scholar]
- Benjamini, Y.; Leshno, M. Statistical methods for data mining. In Data Mining and Knowledge Discovery Handbook; Springer: Berlin/Heidelberg, Germany, 2005; pp. 565–587. [Google Scholar]
- Scholkopf, B.; Smola, A.J.; Bach, F. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Gunn, S.R. Support vector machines for classification and regression. Analyst 1998, 135, 230–267. [Google Scholar]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Sutton, C.D. Classification and regression trees, bagging, and boosting. Handb. Stat. 2005, 24, 303–329. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting; Computational statistics & data analysis. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar]
- Moon, J.; Jung, S.; Rew, J.; Rho, S.; Hwang, E. Combination of short-term load forecasting models based on a stacking ensemble approach. Energy Build. 2020, 216, 109921. [Google Scholar] [CrossRef]
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art, Knowledge-Based Systems 212 (Dl). arXiv 2021, arXiv:1908.00709. [Google Scholar]
- Kautz, T.; Eskofier, B.M.; Pasluosta, C.F. Generic performance measure for multiclass-classifiers. Pattern Recognit. 2017, 68, 111–125. [Google Scholar] [CrossRef]
- Grandini, M.; Bagli, E.; Visani, G. Metrics for multi-class classification: An overview. arXiv 2020, arXiv:2008.05756. [Google Scholar]
- Markoulidakis, I.; Rallis, I.; Georgoulas, I.; Kopsiaftis, G.; Doulamis, A.; Doulamis, N. Multiclass confusion matrix reduction method and its application on net promoter score classification problem. Technologies 2021, 9, 81. [Google Scholar] [CrossRef]
- Warrens, M.J. Five ways to look at cohen’s kappa. J. Psychol. Psychother. 2015, 5, 1. [Google Scholar] [CrossRef]

| Fault Type | Freq. | % |
|---|---|---|
| Normal condition | 270 | 33 |
| D1 | 78 | 10 |
| D2 | 77 | 9 |
| PD | 23 | 3 |
| S | 83 | 11 |
| T1-C | 4 | >1 |
| T1-O | 97 | 16 |
| T2-C | 23 | 3 |
| T3-C | 25 | 3 |
| T3-H | 97 | 12 |
| Feature Name | Definition | Feature Name | Definition |
|---|---|---|---|
| F1 | H2 | F13 | CH4/THC |
| F2 | CH4 | F14 | C2H2/THC |
| F3 | C2H2 | F15 | C2H4/THC |
| F4 | C2H4 | F16 | C2H6/THC |
| F5 | C2H6 | F17 | CH4/H2 |
| F6 | THC = CH4 + C2H2 + C2H4 + C2H6 | F18 | C2H6/CH4 |
| F7 | TGC = H2 + THC | F19 | C2H4/CH4 |
| F8 | H2/TGC | F20 | C2H2/CH4 |
| F9 | CH4/TGC | F21 | C2H4/C2H6 |
| F10 | C2H2/TGC | F22 | C2H2/C2H6 |
| F11 | C2H4/TGC | F23 | C2H2/C2H4 |
| F12 | C2H6/TGC | - | - |
| Model | Parameter | Value Range |
|---|---|---|
| Activation function | SVM | |
| ANN | Hidden layer sizes | 10–30 |
| L2 regularization | Linear, Radial | |
| Learning rate (initial) | 0.001–0.4 | |
| Base model | SVM | |
| C | 10–30 | |
| BC | Kernel | Linear, Radial |
| γ | 0.001–0.4 | |
| No. of models | 10–100 | |
| Max. depth | 2–20 | |
| DT | Min. samples per leaf Obj. function | 2–5 Gini, Entropy |
| Split strategy | Best | |
| L2 regularization | 1–1.5 | |
| Learning rate | 0.1–0.15 | |
| GB | Max. iterations | 100–200 |
| Max. depth | 2–5 | |
| GP | Kernel | RBF, Matern |
| K-neighbors | 2–10 | |
| KNN | Weight | 2–10 |
| p | 1–3, 10 | |
| LR | Penalty | L2 |
| NB | Variance smoothing | log10 (0 to −9) |
| Class weights | Balanced, Balanced Sub-samples | |
| No. of trees | 200, 500 | |
| RF | Max. depth | 2, 3, 10 |
| Max. features | ||
| Obj. function | Gini, Entropy | |
| First model | SVM | |
| C | 0.1–8 | |
| SE | Kernel | Linear |
| Second model | NB | |
| Variance smoothing | 1 × 10−9 | |
| Kernel | Linear, Radial | |
| SVM | C | 0.1, 0.5, 1 |
| γ | ||
| ε | 0.25–0.4 |
| Model | BA | F1-Micro | F1-Macro | κ | MCC |
|---|---|---|---|---|---|
| vanilla auto-Sklearn | 0.812 | 0.866 | 0.769 | 0.837 | 0.837 |
| robust auto-Sklearn | 0.893 | 0.906 | 0.909 | 0.885 | 0.885 |
| ANN | 0.840 | 0.882 | 0.785 | 0.856 | 0.857 |
| BC | 0.745 | 0.858 | 0.742 | 0.825 | 0.826 |
| DT | 0.744 | 0.837 | 0.695 | 0.802 | 0.802 |
| GP | 0.728 | 0.900 | 0.746 | 0.875 | 0.876 |
| HGB | 0.723 | 0.886 | 0.706 | 0.860 | 0.862 |
| KNN | 0.765 | 0.858 | 0.756 | 0.823 | 0.823 |
| LR | 0.666 | 0.823 | 0.673 | 0.791 | 0.792 |
| NB | 0.700 | 0.764 | 0.650 | 0.714 | 0.715 |
| RF | 0.717 | 0.870 | 0.721 | 0.840 | 0.841 |
| SE | 0.838 | 0.886 | 0.809 | 0.860 | 0.861 |
| SVM | 0.766 | 0.882 | 0.767 | 0.856 | 0.857 |
| XGB | 0.702 | 0.861 | 0.683 | 0.831 | 0.833 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santamaria-Bonfil, G.; Arroyo-Figueroa, G.; Zuniga-Garcia, M.A.; Azcarraga Ramos, C.G.; Bassam, A. Power Transformer Fault Detection: A Comparison of Standard Machine Learning and autoML Approaches. Energies 2024, 17, 77. https://doi.org/10.3390/en17010077
Santamaria-Bonfil G, Arroyo-Figueroa G, Zuniga-Garcia MA, Azcarraga Ramos CG, Bassam A. Power Transformer Fault Detection: A Comparison of Standard Machine Learning and autoML Approaches. Energies. 2024; 17(1):77. https://doi.org/10.3390/en17010077
Chicago/Turabian StyleSantamaria-Bonfil, Guillermo, Gustavo Arroyo-Figueroa, Miguel A. Zuniga-Garcia, Carlos Gustavo Azcarraga Ramos, and Ali Bassam. 2024. "Power Transformer Fault Detection: A Comparison of Standard Machine Learning and autoML Approaches" Energies 17, no. 1: 77. https://doi.org/10.3390/en17010077
APA StyleSantamaria-Bonfil, G., Arroyo-Figueroa, G., Zuniga-Garcia, M. A., Azcarraga Ramos, C. G., & Bassam, A. (2024). Power Transformer Fault Detection: A Comparison of Standard Machine Learning and autoML Approaches. Energies, 17(1), 77. https://doi.org/10.3390/en17010077










