Abstract
In this paper, we propose a battery management algorithm to optimize the lifetimes of retired lithium batteries with heterogeneous states of health in a battery energy storage system under dynamic power demand. A battery energy storage system allows for the use of retired lithium batteries for applications such as backup power in homes, data centers, etc. In a battery energy storage system, a battery pack consists of several retired batteries connected in parallel or in series to fulfill the required power demand. Owing to the retired batteries’ different capacity levels, i.e., states of health, a scheduling strategy is required to turn battery cells inside the battery pack on and off such that the secondary lifetimes of the retired batteries are extended. To establish the optimal scheduling policy, it is necessary to determine the correct states of each battery cell, including the state of charge and the state of health. To that end, the proposed algorithm first estimates the state of charge and state of health for all cells based on data measured using an extended Kalman filter. Then, a deep reinforcement learning scheduling algorithm is implemented to connect/disconnect the battery cells to/from the battery pack based on their states. Via simulation, we show that the proposed algorithm estimates the state of charge and state of health of each battery cell with low error and extends the lifetime of battery packs by 20.6%, compared to methods proposed in previous works.
1. Introduction
Lithium-ion batteries have become an essential component of modern life, powering everything from smartphones to electric vehicles (EVs) [1]. Their advantages include high energy efficiency, minimal memory effects, extended lifespans, and low self-discharge rates compared to other battery types, and they are now widely used [2]. However, lithium-ion batteries for EVs have a limited lifespan and (eventually, for safety) require replacement when their capacity drops to 80% or lower [3]. The total amount of retired battery-pack power is forecast to reach 120 GWh globally by 2030 [4]. This will create a significant amount of waste and financial burden, particularly as the demand for lithium-ion batteries continues to grow. As a result, it is becoming increasingly urgent and necessary to identify solutions to reuse retired lithium-ion batteries.
One promising application for retired lithium-ion batteries is in battery energy storage systems (BESSs) that can then be used for backup power in homes, EV charging stations, or telecommunication and data center systems [5]. BESSs have the potential to significantly reduce the demand for new batteries and can help reduce the environmental impact of battery production. A battery energy storage system (BESS) has a battery pack in which multiple batteries are connected in parallel or in series to increase the capacity or voltage of the battery pack. A switch is added to each battery cell to connect it to or disconnect it from the battery pack [6]. Cells in a battery pack have different capacity levels (i.e., heterogeneous states of health), which hinders the effective utilization of the batteries and, consequently, affects the performance of the battery pack. A scheduling policy is required to control the switches in battery cells to prolong the lifetime of the battery pack in the BESS and reduce the imbalanced capacities of battery cells.
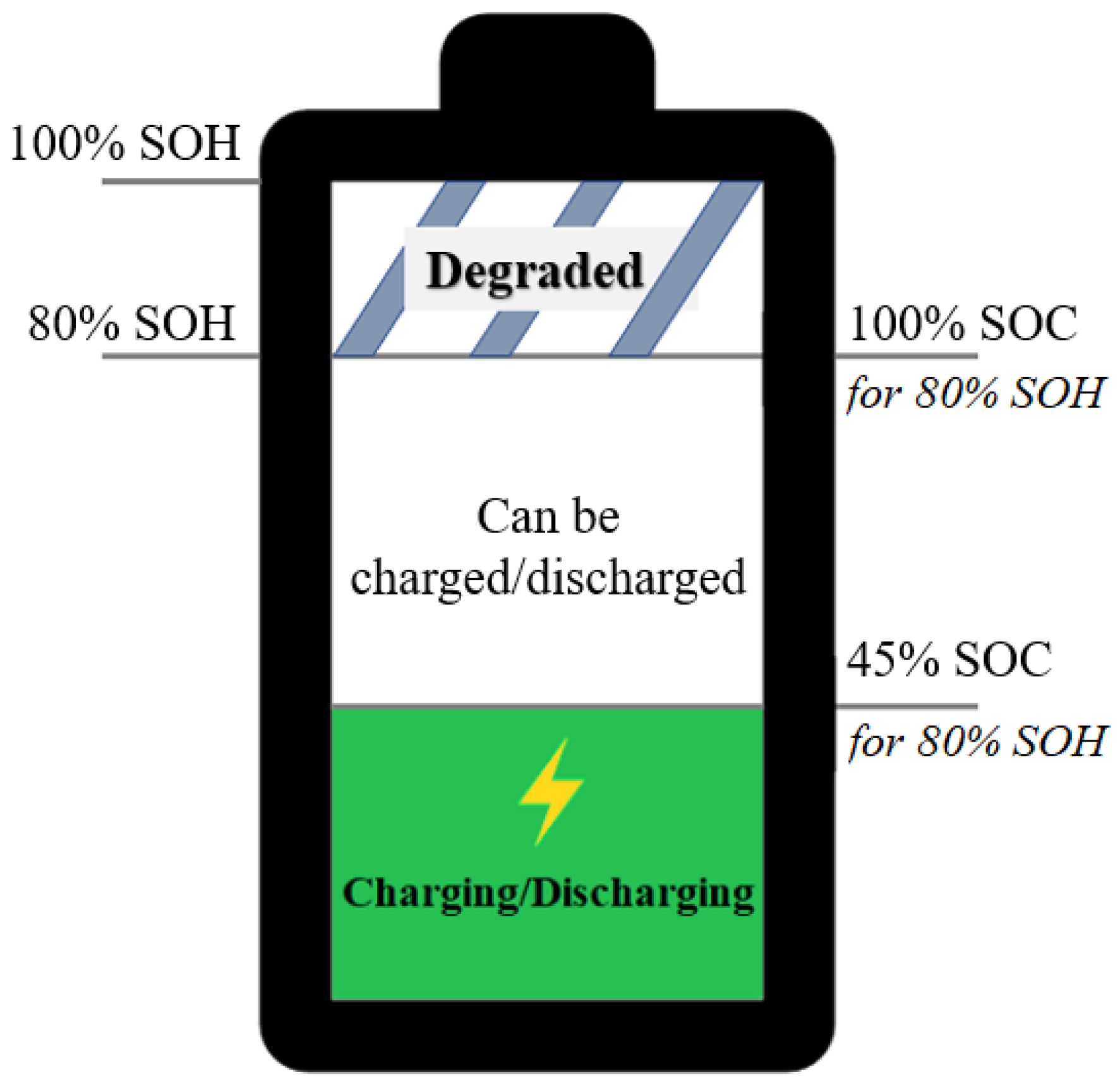
For an optimal scheduling policy in a BESS, correct identification of battery characteristics, including the state of charge (SOC) and state of health (SOH), is important. The SOC of a battery is the level of charge relative to the battery’s capacity, whereas the SOH is the ratio of the maximum battery charge to its rated capacity. The relationships between SOC and SOH are illustrated in Figure 1. Information on SOC and SOH in a scheduling policy protects the battery cells by preventing them from overcharging or discharging excessively and increases the capacity of the BESS. SOC and SOH parameters cannot be measured directly from a battery cell. Instead, they are estimated through measurable parameters such as voltage, current, and cell temperature. Based on the states of the battery cells in a pack (including the SOC and SOH), the ON/OFF switches for the batteries in the pack are scheduled so that the states of health of all batteries are balanced. As a result, the lifetime of the battery pack is extended. Therefore, the correct estimation of SOC and SOH, along with the scheduling of battery cell switches, is necessary to optimize the performance of a BESS.
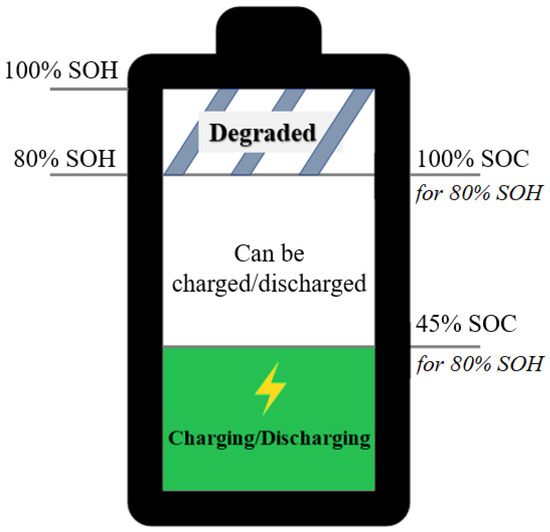
Figure 1.
The relationships between state of charge and state of health.
Battery state estimation approaches have been explored in the literature. The Coulomb counting method [7,8] calculates the SOC of cells by counting the amount of charge that enters or exits a cell. However, the Coulomb counting method was unable to measure the SOC of cells in an online parallel-connected battery pack following a sharp drop in SOH. An algorithm was proposed for the online estimation of SOC using deep learning [9], but this algorithm ignores the estimation of SOH. A neural network was used to estimate SOH using experimental datasets [10]. However, the authors did not consider SOC estimation. Information on both SOCs and SOHs of battery cells is required for efficient scheduling of a battery pack to optimize BESS performance. The authors of [11] proposed joint lithium battery SOC and SOH estimation using a data-driven method. This approach required a large dataset to train the model before operation on site. Kalman filter-based approaches can estimate SOC and SOH levels [12] but depend on the correctness of electrochemical impedance spectroscopy (EIS) parameters, including a resistor and one or more resistor–capacitor (RC) pairs. However, the effect of SOH reduction on EIS parameters is ignored in Kalman filter approaches [13]. In [14], SOH reduction was considered to reidentify EIS parameters, but the SOH was updated only offline. Several researchers have studied the problem of cell scheduling in a parallel-connected battery pack. The authors of [15] utilized a fuzzy logic control strategy to adjust the number of cells in a circuit in accordance with the load demand for the purpose of reducing loop current, which leads to battery inconsistency. In [16], battery resistance degradation was monitored to detect weak cells and disconnect them from the battery pack. This approach solved the issue of mismatched characteristics but requires a complex measuring system or incurs a high computational burden. In [17], the weighted-k round-robin (kRR) scheduling framework was proposed to extend the lifetime of a battery pack by considering load demand and SOH reduction. However, kRR-based scheduling can be implemented only for a fixed model, i.e., the number of cells in the battery pack or the battery models inside the pack cannot change. In [6], a multiactor–critic method was proposed to solve battery scheduling problems. This approach prolonged the lifetime of the battery pack and reduced the imbalance between the batteries but ignored dynamic power demand. In [18], a strategy for a battery management system was proposed, including SOC estimation using an extended Kalman filter algorithm and a scheduler to reduce the difference between the SOCs of battery cells. However, SOH and power demand were not considered in that approach. The main challenge is to determine the accurate state (i.e., SOC and SOH) of a battery cell in a battery pack, then schedule the turning ON/OFF of battery cells based on their current states such that the imbalance in SOHs of cells is reduced.
The main contributions of our work are as follows:
- A scheduling algorithm is proposed to maximize the lifetime of a battery pack consisting of parallel-connected battery cells with heterogeneous states of health in a BESS.
- We define the battery lifetime maximization problem as the reduction in the SOH of a battery pack that can be achieved by reducing the imbalance in the SOHs of battery cells in a battery pack.
- A deep reinforcement learning (DRL) framework is implemented in the scheduling algorithm that uses battery cells’ states to set their ON/OFF status and balance the SOHs.
- To measure the battery cells’ states to schedule their ON/OFF status, an extended Kalman filter (EKF)-based algorithm is proposed to estimate SOC and SOH.
- A dataset of real measurements is used to determine the accuracy of the proposed estimation algorithm. The proposed algorithm achieves minimal error compared to methods proposed in other works. Simulation results show that the proposed algorithm outperforms previous studies by extending the lifetime of a battery pack under constant and dynamic power demands.
The remainder of this paper is organized as follows. Section 2 discusses the proposed parallel-connected battery model and the scheduling issues. Section 3 presents the framework of the proposed combined algorithm, which includes EKF-based and DRL-based algorithms. Section 4 describes the simulation and presents the results and impacts of the algorithm. Finally, we conclude this work in Section 5.
For ease of presentation, the key notations listed in Table 1 are used throughout this paper.

Table 1.
Summary of notations.
2. System Model
2.1. Overall System
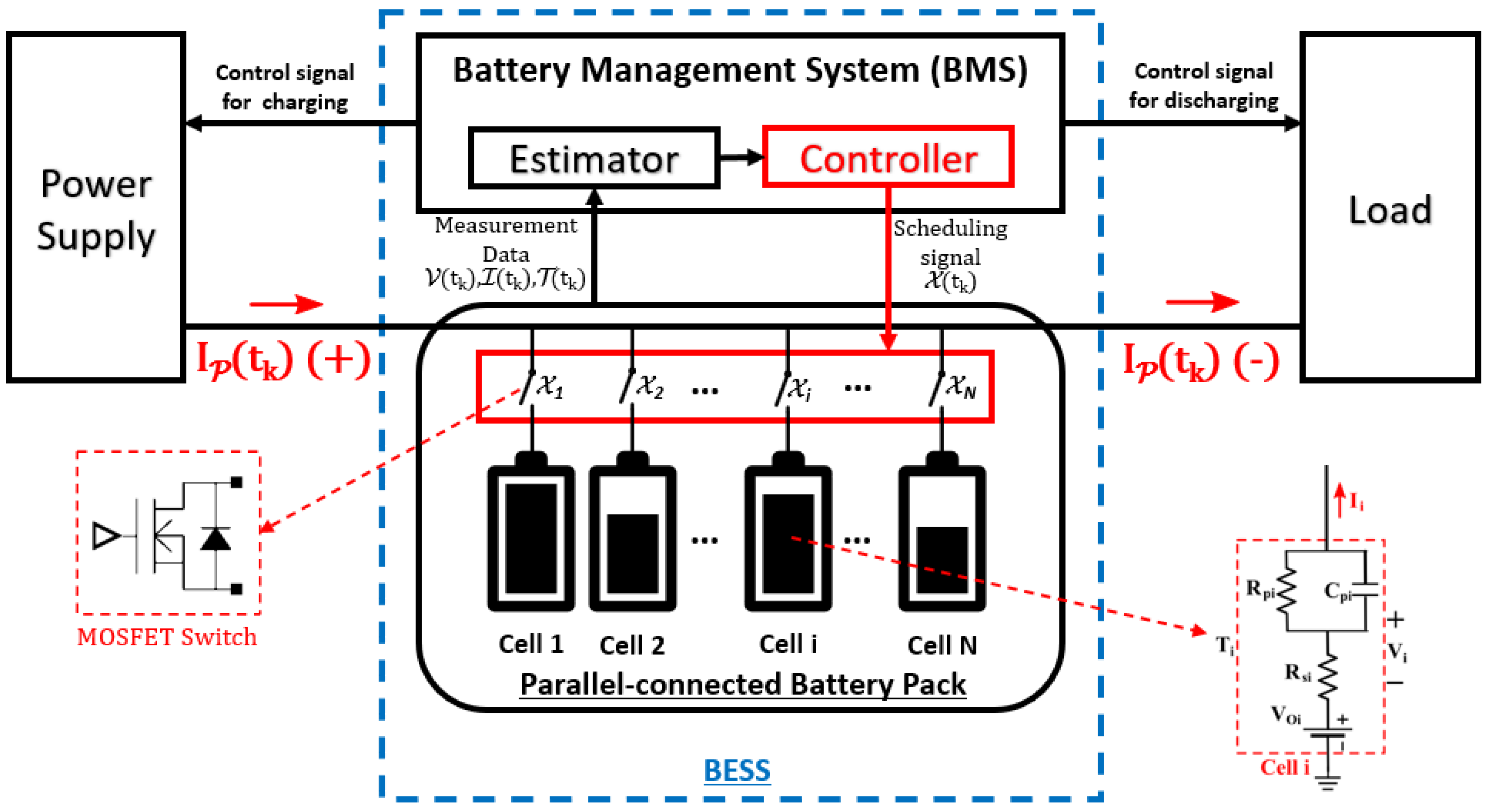
In this paper, we consider a parallel-connected BESS [19,20] with a power supply and a load, as shown in Figure 2. The BESS comprises a battery pack and a battery management system (BMS) connected to a power supply and a load. We consider a discrete-time model, where the working time () is divided into w time slots such that with durations of .
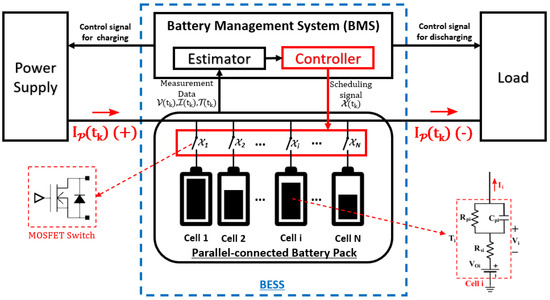
Figure 2.
Implementation of a parallel-connected BESS.
The battery pack consists of N lithium battery cells connected in parallel. A first-order Thévenin equivalent model is considered for the cells [21]. Cell has EIS parameters including an open-circuit voltage (); internal resistance (); and an RC pair, which includes a resistor () and capacitor () connected in parallel. The terminal voltage of cell i at time t () is computed as
where is the polarization voltage applied to the parallel RC network, calculated as [14]
There are N switches corresponding to N cells linking them to the battery circuit. shows whether a switch of cell i is connected to a battery circuit or not, such that
Similarly, sets , , and consist of terminal voltages, currents, and temperatures of all cells at time , respectively.
A BMS monitors the states of the battery pack and estimates both the SOC and the SOH of cells in order to schedule the switches in the battery pack. We mathematically define the SOC of cell i at time as
where is the capacity level of cell i at time , and is the Coulombic efficiencies of the discharging or charging process. Similarly, the SOH of cell i at time is defined as
where is the initial capacity of new cell i. Sets and consist of the SOCs and SOHs of all the cells at time , respectively. We define the SOH of the battery pack () as
Power supply and load are used for charging and discharging of the battery pack. The battery pack current at time () has a positive value when discharging and a negative value when charging. The battery pack fulfills the load demand when discharging, then recharges to recover the corresponding amount of power. The process of complete charging and discharging of a battery pack is referred to as a cycle. During the working time (), an arbitrary cycle (j) has multiple time slots based on the power demand. If time slot belongs to cycle j, we consider and to be the amount of power load when discharging and charging in cycle j, respectively, up to time slot , which are calculated as
and
where represents the slot number when cycle j starts, i.e., cycle j starts at time .
2.2. Problem Formulation
The objective of this paper is to prolong the lifetime of a battery pack by reducing the rate of aging in cells. To that end, the problem is formulated to minimize the SOH reduction of the battery pack during working time (), which is mathematically expressed as
3. The Proposed Algorithm
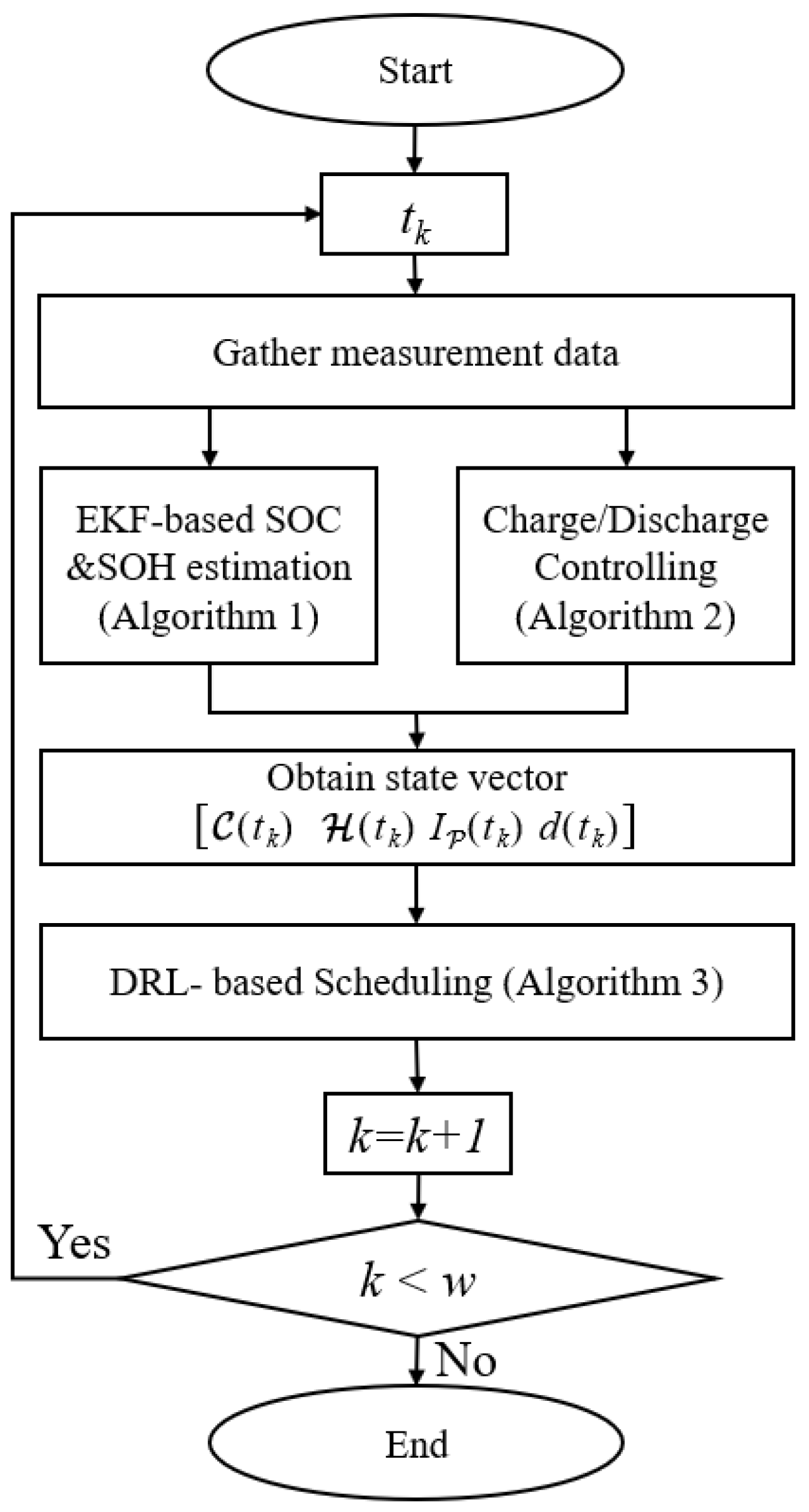
To tackle the optimization problem (9), we propose a battery-scheduling algorithm that is run by the BMS. In each time slot, the algorithm first collects measurement data that include the terminal voltage, current, and temperature of each cell, then estimates the SOC and the SOH (Algorithm 1) and controls the charging or discharging process of the BESS based on the load demand (Algorithm 2). Algorithms 1 and 2 return a state vector consisting of a set of SOC values of cells () a set of SOH values of cells (), as well as the battery pack current () and power demand (), triggering the DRL-based battery-scheduling algorithm (Algorithm 3). The overall flow of the proposed algorithm is shown in Figure 3. Each part of the proposed algorithm is discussed in detail in the subsections below.
| Algorithm 1 EKF-based SOC and SOH estimation |
|
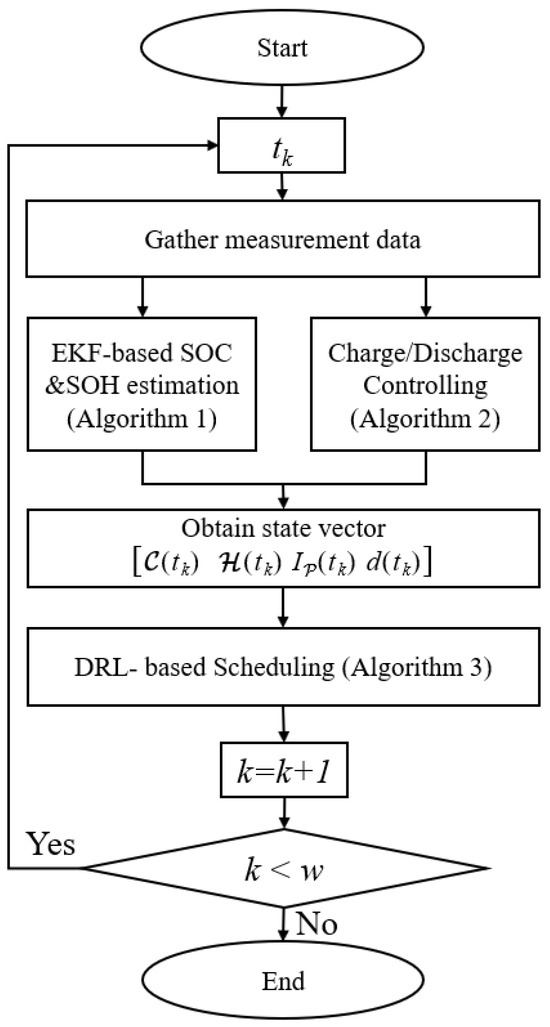
Figure 3.
Overall flow chart of the proposed algorithm.
| Algorithm 2 The Charge/Discharge Control Algorithm |
|
| Algorithm 3 The Deep Q Network Switches Scheduling Algorithm |
|
3.1. EKF-Based SOC and SOH Estimation
The algorithm estimates the SOC and SOH of each cell in the battery pack to observe the states of the battery cells using a third-order EKF. To obtain the SOC and SOH of battery cell i at , the algorithm first estimates state vector and error covariance as
and
where is the state vector of cell i at time , which is defined as
and and denote the transition matrix and the input matrix, respectively, which are defined as follows
where is the measured current of cell i at . , , and are functions of , , and , respectively, which are obtained from two-dimensional look-up tables (A dataset [22] is used to construct look-up tables where , , and are exponential functions of , such as , and , , and are real numbers. These real numbers change when decreases). Then, the algorithm estimates the terminal voltage (), using and Jacobian matrices and as
where the open-circuit voltage () is identified by exploiting the look-up tables ( is the ath-order polynomial function of , which is defined as , where is a real number that changes when decreases). The algorithm calculates the Kalman gain () to determine the error between the real, measured value and the estimated value using (13) as
Based on the estimated terminal voltage (), estimated state vector (), Kalman gain (), and measured terminal voltage (), the algorithm obtains the correct state vector () as
Similarly, the algorithm corrects error covariance () as
From corrected state vector (), the proposed algorithm obtains and . The algorithm updates the SOH of cell i after one cycle (complete charging and discharging of the battery pack), since the SOH does not decrease after one or several time slots [23]. The algorithm updates the SOH of cell i at time slot as
where is the effective current capacity (on average) of cell i in cycle j, which has time slots if cycle j is completed at time slot . The effective current capacity (on average) of cell i is calculated as
where cycle j starts at and ends at . Algorithm 1 summarizes the EKF-based estimation for the SOH and SOC of cells.
3.2. The Charge/Discharge Control Algorithm
To control the process of charging and discharging the battery pack in the BESS, the algorithm first identifies the process that is underway. If the current of the battery pack is positive, i.e., , we calculate the amount of electric power discharged in cycle j using (7). If reaches electrical demand (), the BMS converts the BESS process from discharging to charging. Otherwise, the discharge process continues.
If is negative, the algorithm determines (the amount of electrical power charged in cycle j) using (8) and compares it with electrical demand (). If reaches , the algorithm converts the BESS process from charging to discharging for a new cycle ; otherwise, it continues charging. The process of charging and discharging the battery pack is summarized in Algorithm 2.
3.3. Deep Reinforcement Learning-Based Scheduling Algorithm
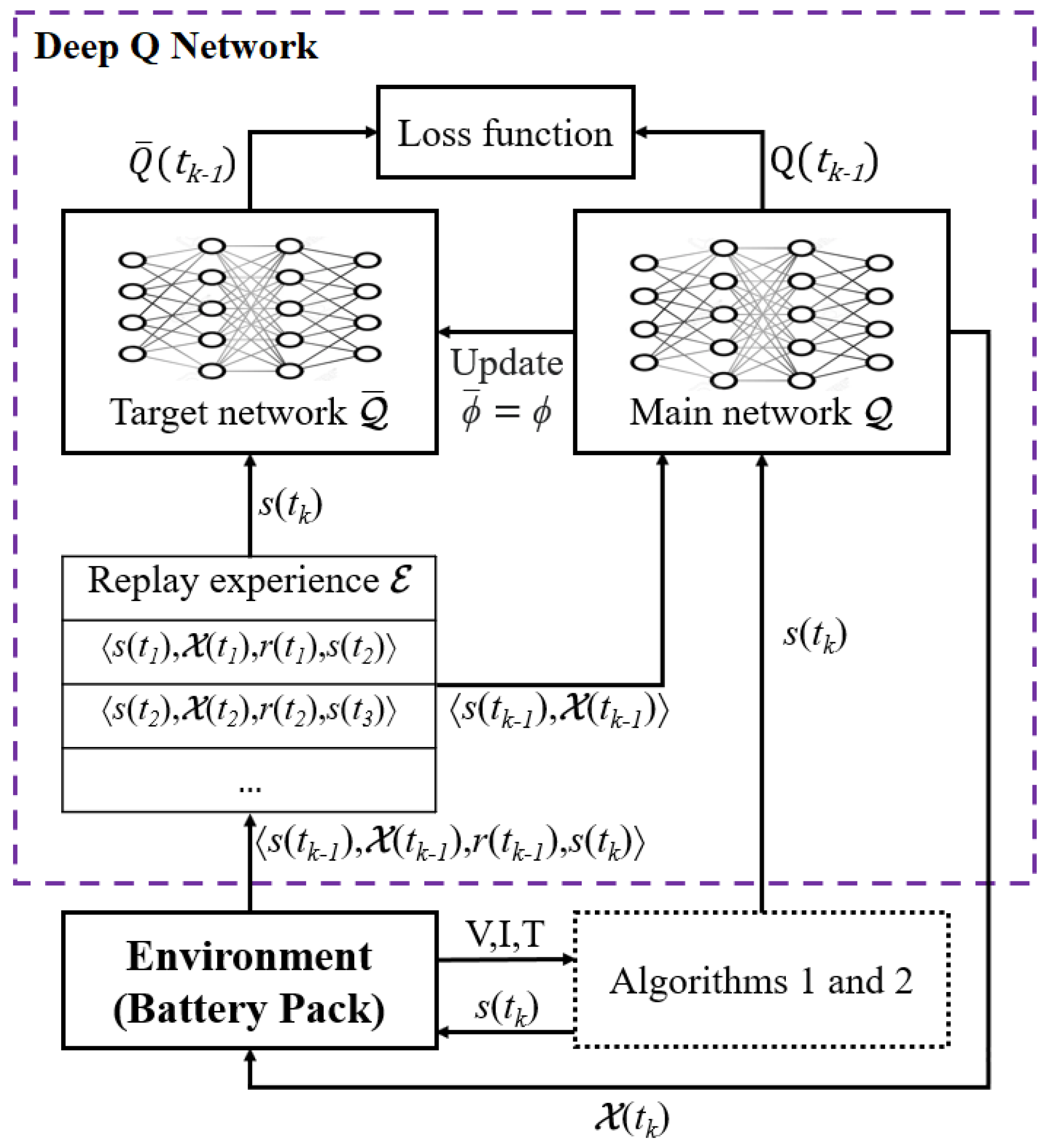
A deep Q network (DQN) scheduling algorithm is proposed for the ON/OFF cell switches in the battery pack. The scheduling algorithm has three elements: state , which represents the current state of the BESS; action , which indicates cell switches that are ON or OFF; and reward function based on action . The algorithm selects action by interacting with the environment, i.e., the BESS, to perceive the state of the battery pack () to maximize the cumulative reward (), i.e., to minimize SOH reduction of the battery pack. To choose an optimal schedule as for state , the algorithm utilizes and updates acquired knowledge () using deep reinforcement learning. That knowledge includes a switch-scheduling policy for the given battery states and the corresponding scheduling of rewards. The DQN-based scheduling algorithm is summarized in Algorithm 3.
The algorithm first observes the current environmental state of the battery pack and obtains state vector , which is defined as
where and are sets of the SOCs and SOHs of N cells, respectively; is the load current of the battery pack; and is the load demand. Then, the algorithm initializes knowledge () that includes replay experience () with samples , a main network (), and a target network () with random weights. Neural networks and have the same structure. The algorithm explores actions based on past experiences to update the acquired knowledge that leads to a long-term benefit. The DQN updates acquired knowledge () by minimizing loss function using gradient descent. The loss function is defined as
which is the DQN network parameter (weight of the main network) and is calculated as
where is the learning factor. shows the expected discounted cumulative reward after time slot in main network , and is the target action value of the target network (), which represents the maximum cumulative reward, i.e., the minimum SOH reduction for the battery pack. and are calculated as
and
where is the discount cumulative factor indicating the degree of emphasis of future rewards, and and represent the weights of networks and , respectively. After determining the loss based on an action, the target network () copies the weight of the main network (), i.e., .
To utilize the past experience in a DQN-based scheduling algorithm, the proposed algorithm looks at the acquired knowledge ( to determine whether state is in or not. If state is in , the algorithm chooses action based on an -greedy policy, i.e., it chooses a random action with probability or the action with probability that has the largest value for . Based on the -greedy policy [24], action is defined as
In the case in which state is not in , scheduling action is performed at random. After taking action based on observed state , the algorithm evaluates the immediate reward as
Then, the algorithm determines the cumulative reward () by interacting with the environment and looks for an optimal policy to maximize . The cumulative reward () is calculated as
The algorithm minimizes loss function so that action value has the same value as target action value , which also means that the SOH of the battery pack is optimized. The DQN-based scheduling algorithm is summarized in Algorithm 3, and the DQN training process is shown in Figure 4.
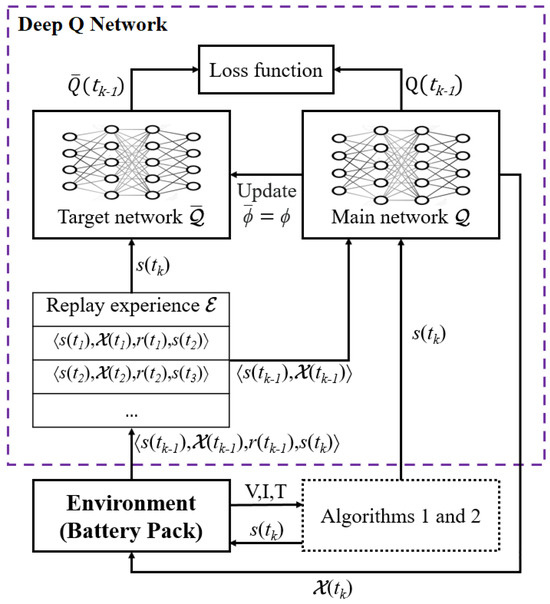
Figure 4.
The training process in the DQN.
4. Performance Evaluation
4.1. Simulation Environment
The simulation was conducted using a lithium-ion battery model and was implemented in MATLAB and Simulink R2022a. To evaluate the performance of the proposed algorithm, we consider a parallel-connected battery pack including four lithium 3.7 V/2.2 Ah batteries with heterogeneous states of health (90.01%, 86.77%, 84.13%, and 78.15% corresponding to cells 1 to 4, respectively). MOSFETs with low ON resistance and low power are installed to connect and disconnect the battery cells from the battery pack. We consider different power demand conditions to evaluate the effectiveness of the algorithm. Based on the maximum capacity of a battery pack with new battery cells, we obtain a dynamic power demand profile by generating values from a uniform distribution across 20% to 60% of the maximum energy of a battery pack (i.e., between 6.51 Wh and 19.54 Wh). For the constant power demand, we calculate the mean value of the dynamic power demand profile as
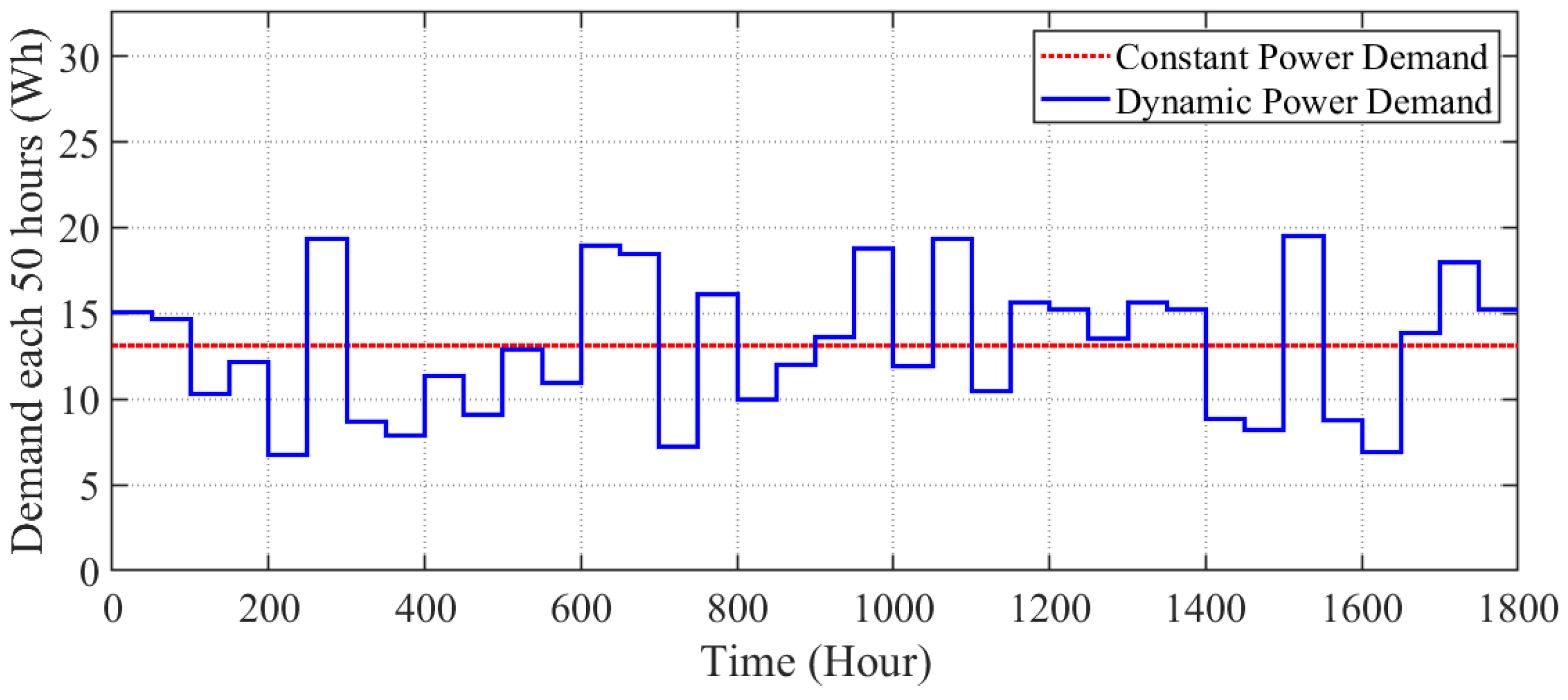
where is the power demand at time slot , and W is the number of time slots during working time (). Figure 5 shows dynamic and constant power demand profiles. Constant power demand is equal to 13.13 Wh (i.e., of the maximum energy of a new battery pack). We set the load current of the battery pack when discharging and charging to 8 A.
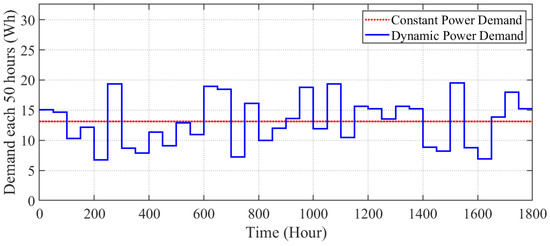
Figure 5.
Load demand profile.
A dataset compiled by NASA [22] was used to model a first-order Thévenin equivalent battery model with a reduction in SOH. We also use the dataset to obtain actual SOC and SOH values, which are compared with the estimated values. The dataset includes 28 lithium cobalt oxide 18,650 cells with a nominal capacity of 2.2 Ah, including in-cycle measurements of terminal voltage, current, and cell temperature. The dataset also includes measurements for discharging capacity and EIS impedance readings. We identify the EIS parameters, which include , , , and , in the 90% to 60% SOH range using the dataset.
The structure of neural networks includes one 10-dimension input layer, two 256-dimension hidden layers, one 256-dimension LSTM layer, and one 16-dimension output layer. The input layer consists of 10 elements of the battery state (), since there are four battery cells in a battery pack. The output layer consists of 11 cases (There must be at least two batteries ON at the same time, since we consider current during discharging and the maximum output current of one battery is 4 A) of schedule action . We set the learning rate () to , the -greedy value to , and the discount factor () to . The period of the target network update is 10 time steps. Other simulation parameters are summarized in Table 2.

Table 2.
Simulation parameters.
For the performance evaluation, we first verify the accuracy of the estimation algorithm by determining the error between estimated and actual values. Then, we investigate the effect of the proposed algorithm on the lifetime of a battery pack and the SOHs of the cells under dynamic and constant loads. To validate the performance of the proposed algorithm, we compare it with methods proposed in previous works, including an enhanced Coulomb counting method [7], a hybrid statistical data-driven estimation method [11], and a multi-actor–critic scheduling algorithm [6]. For comparison, we combine the scheduling and estimation algorithms and obtain the BESS performance. We also compare the proposed estimation algorithm with the enhanced Coulomb counting method and the hybrid statistical data-driven estimation method. For the sake of simplicity, we denote the proposed third-order extended Kalman filter (EKF) estimation algorithm as EKFest, the proposed deep Q network scheduling algorithm as DQNsch, the multi-actor–critic scheduling algorithm as MACsch, the hybrid statistical data-driven estimation method as DDest, the enhanced Coulomb counting method as ECest, and simulations without any scheduling algorithm as Non Schedule.
4.2. State Estimation Verification
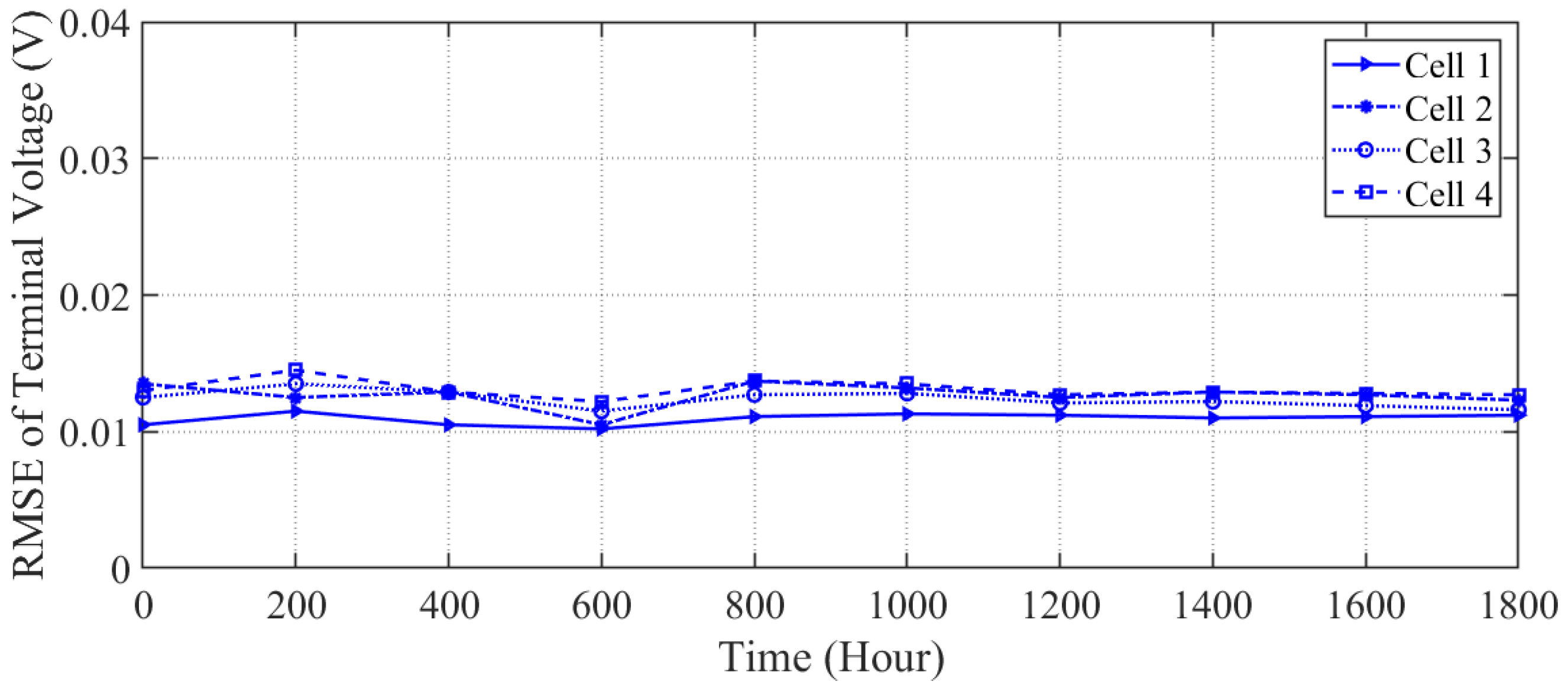
To evaluate the performance results of the proposed algorithm in estimating the SOC and SOH for each cell, we first show the estimated terminal voltage of each cell in a battery pack. Figure 6 shows the root mean square error (RMSE) between the measured terminal voltage and the estimated terminal voltage. The RMSE between the measured and estimated values of the terminal voltage for each cell is close to 0.01 V and remains small over time. The small difference between measured and estimated terminal voltages shows that the proposed algorithm accurately models terminal voltage, which leads to a more accurate estimation of the SOC and SOH of a cell.
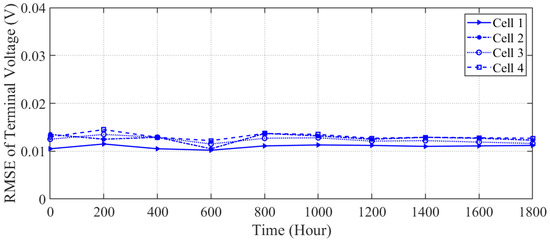
Figure 6.
Root mean square error between actual and estimated terminal voltage using the proposed algorithm.
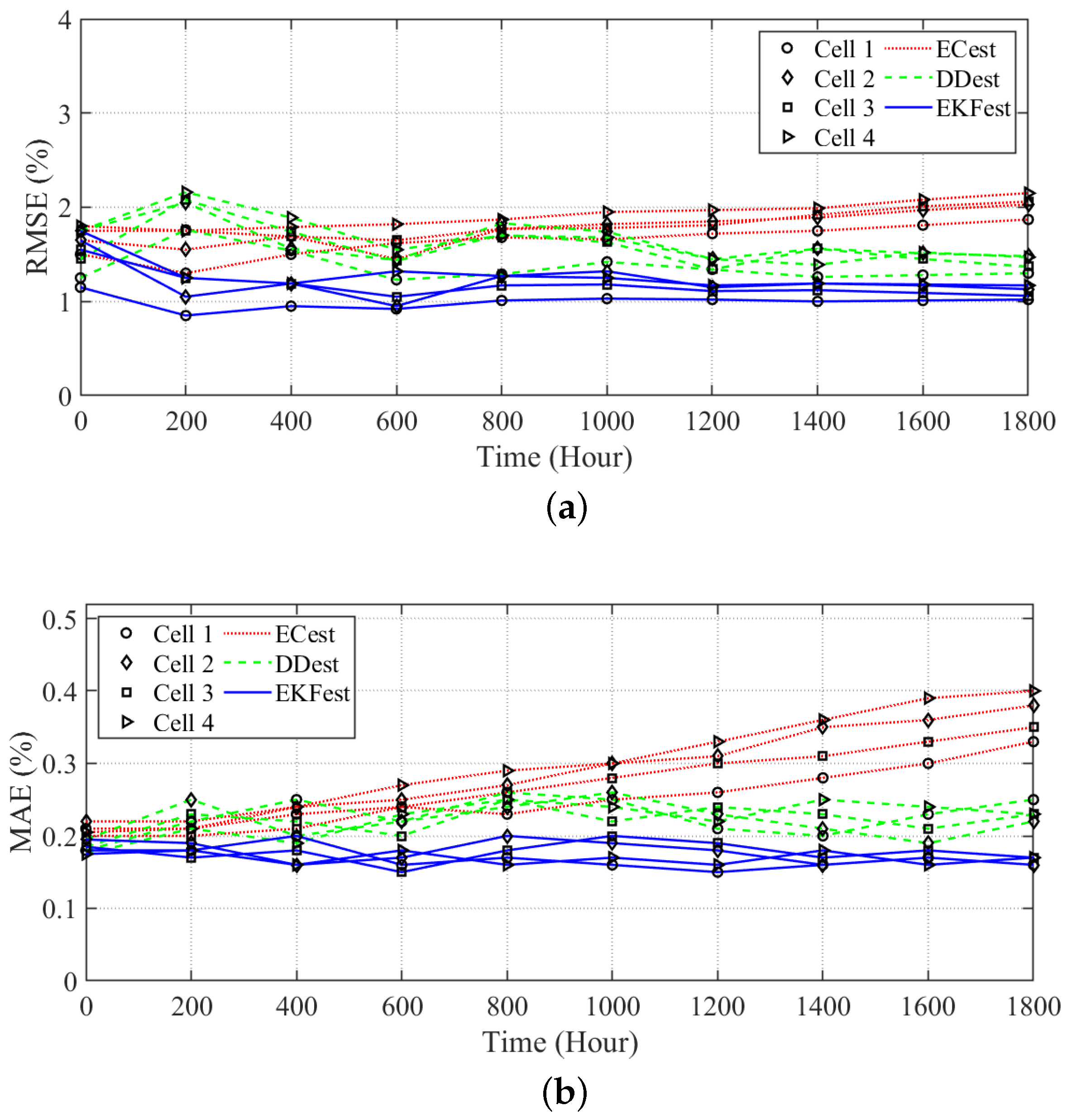
The performance results of the proposed algorithm in estimating the SOC and SOH for each cell in terms of RMSE and mean absolute error (MAE), respectively, are shown in Figure 7. The proposed estimation algorithm has the lowest RMSE compared to other works in estimating the SOCs of cells, as shown in Figure 7a. The RMSE between the actual and estimated values of the SOC for each cell is close to 1% under the proposed algorithm. The error of the proposed algorithm in estimating the SOHs of the cells is shown in Figure 7b. The proposed algorithm has an error of less than 0.2% for SOH, which is 50% less than the other estimation algorithms. ECest shows the worst performance, degrading over time. Note that the performance of the proposed estimation algorithm becomes more stable over time. Estimating the SOC and SOH of the cells with low error is of great significance in order to obtain optimal ON/OFF cell scheduling that extends the lifetime of a battery pack.
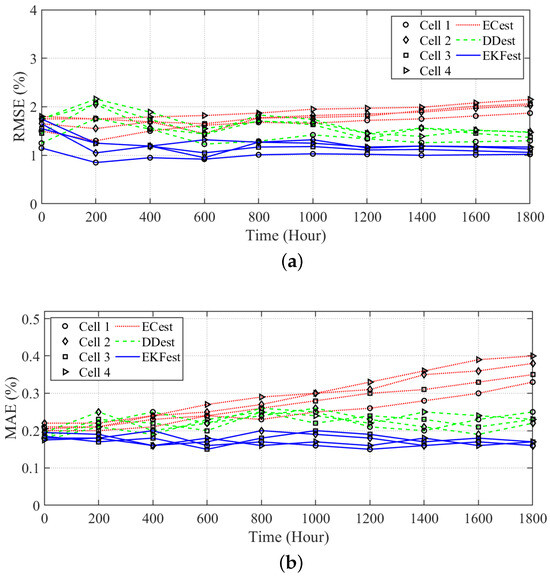
Figure 7.
State estimation evaluation: (a) root mean square error of SOC estimation and (b) mean absolute error of SOH estimation.
4.3. Impact of the Proposed Algorithms on Battery Pack Lifetime
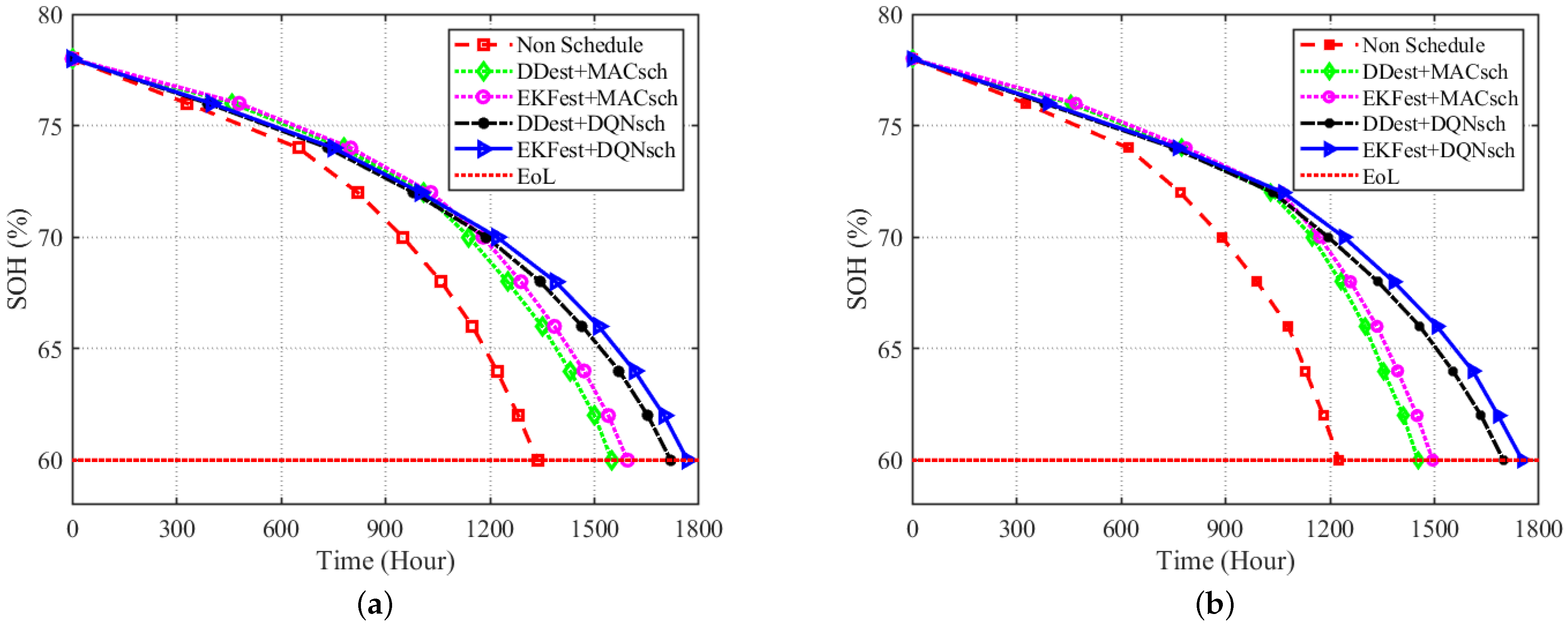
The impact of the proposed algorithm on battery pack lifetime in terms of SOH reduction under constant and dynamic power demands is evaluated and shown in Figure 8. The proposed algorithm achieves better performance under both constant and dynamic power demands compared to other algorithms. The proposed algorithm reduces the SOH decay in the battery pack by efficiently scheduling the ON/OFF switching of the cells based on accurate estimation of SOHs and SOCs, resulting in an increase in battery pack lifetime.
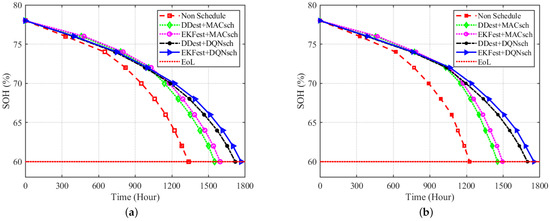
Figure 8.
SOH reduction of the battery pack under (a) constant power demand and (b) dynamic power demand.
The SOH of the battery pack reaches 60% (the end of its second life (EoL)) after a working time of 1767 h under constant power demand, which represents a 13.9% increase in battery pack lifetime compared to previous work (DDest + MACsch). Under dynamic power demand, battery pack lifetime also increases by 20.6% under the proposed algorithm compared to previous work. In addition, the difference in the performance of the proposed algorithm under constant and dynamic power demand is quite small, but the performance of methods proposed in previous work degrades under dynamic power demand. Hence, the proposed algorithm can hence efficiently schedule ON/OFF switching of battery cells to adapt to dynamic power demand.
Compared to DDest + MACsh, the lifetime of the battery pack is higher under EKFest + MACsch and DDest + DQNsch. This shows that the proposed estimation algorithm, as well as the scheduling algorithm, can an impact in extending the lifetime of a battery pack. DDest + DQNsch achieves better performance than EKFest + MACsch, which means optimal scheduling is a more dominant factor in prolonging battery pack lifetime. MACsch achieves worse performance, since it does not consider SOC while scheduling the ON/OFF cell switches to meet power demand. Without scheduling (Non-Schedule), the lifetime of the battery pack reduces rapidly because the weakest cell, i.e., the cell with the lowest SOH, operates continuously.
4.4. Impact of the Proposed Algorithm on Capacity Balancing
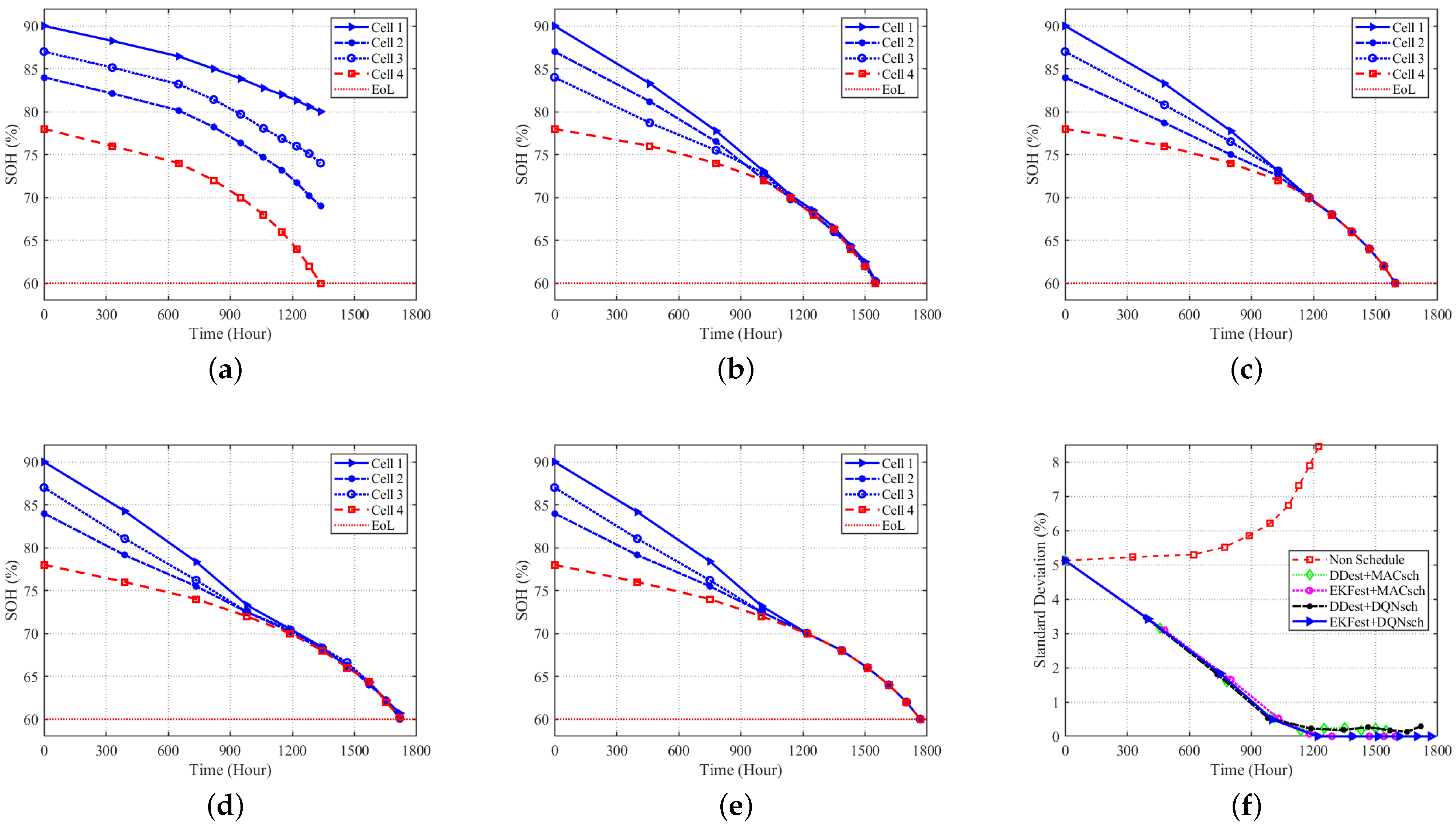
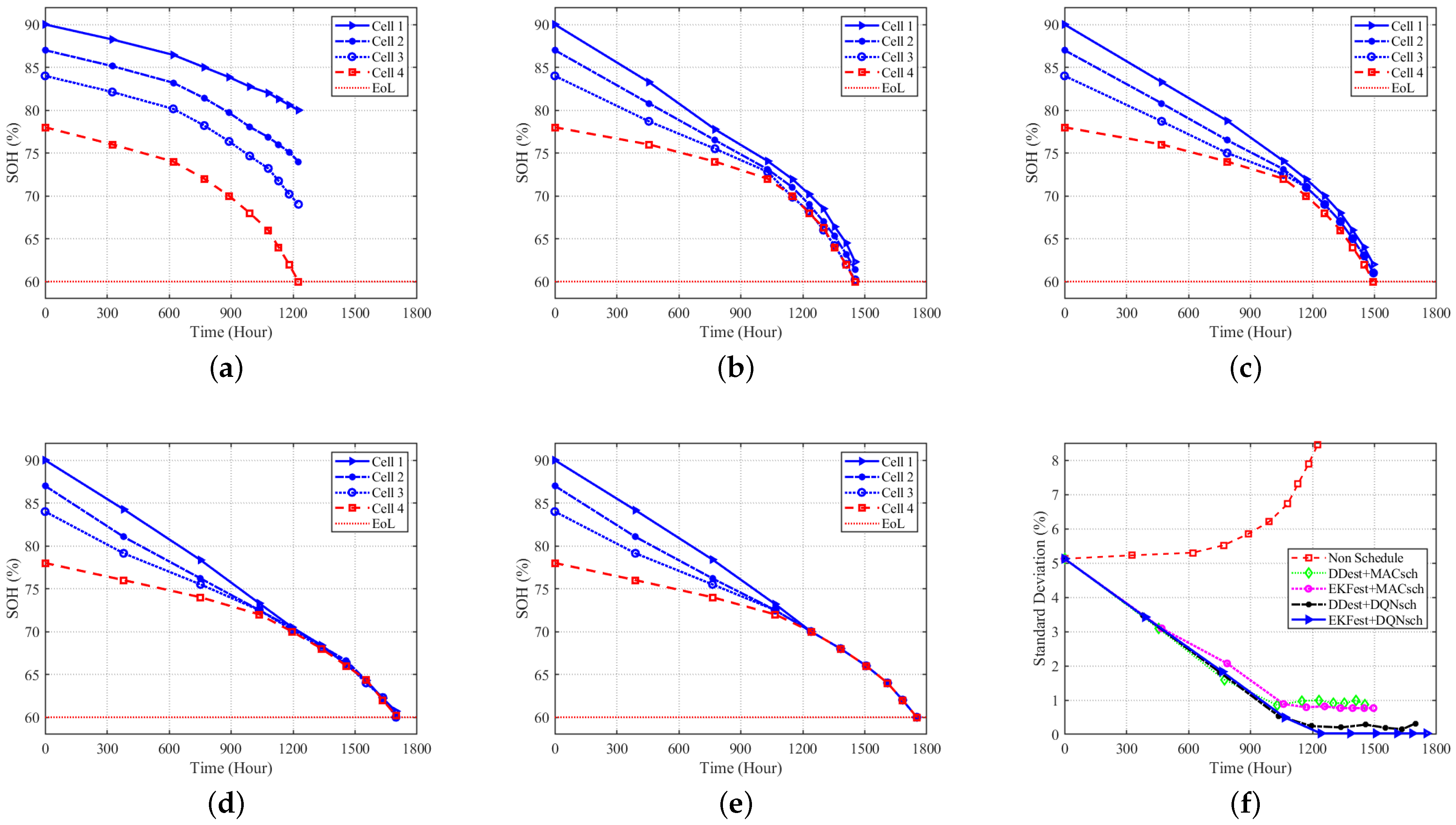
The effectiveness of the proposed algorithm in balancing the SOH of cells under constant and dynamic load demands is shown in Figure 9 and Figure 10, respectively. Without a scheduling algorithm (Non-Schedule), all the cells in the battery pack are utilized all the time, irrespective of their SOC and SOH, resulting in imbalanced states of health and increasing SOH reduction in the battery pack, irrespective of load demand conditions, as shown in Figure 9a and Figure 10a.
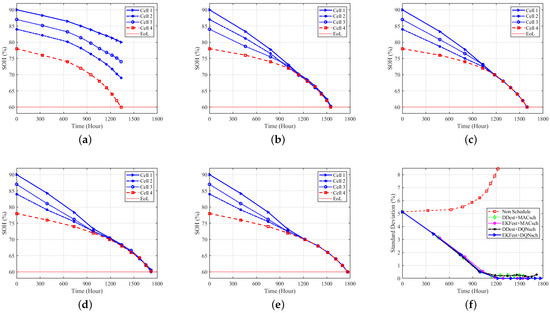
Figure 9.
SOH balancing under constant power demand with (a) Non-Schedule, (b) DDest + MACsch, (c) EKFest + MACsch, (d) DDest + DQNsch, (e) EKFest + DQNsch, and (f) the standard deviation of SOHs among the cells.
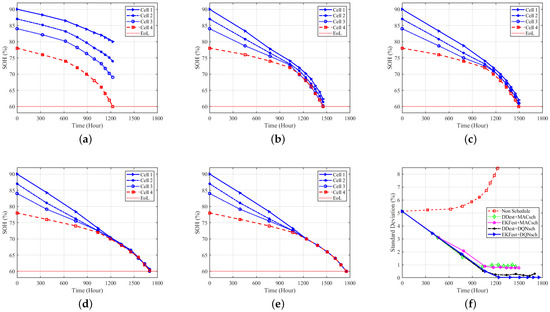
Figure 10.
SOH balancing under dynamic power demand with (a) Non-Schedule, (b) DDest + MACsch, (c) EKFest + MACsch, (d) DDest + DQNsch, (e) EKFest + DQNsch, and (f) the standard deviation of SOHs among the cells.
All the algorithms balance the SOH of cells in the battery pack under constant and dynamic load demands, as shown in Figure 9b–e and Figure 10b–e, respectively. Even though the methods proposed in other works achieve SOH balancing among battery pack cells, battery lifetime (the SOH of each cell) decreases rapidly under the other algorithms compared to the proposed algorithm. This means that with heterogeneous states of health for cells in a battery pack, the proposed algorithm offers better performance than other algorithms by extending the second life of battery cells. All the algorithms achieve SOH standard deviations close to zero by balancing the capacity of each cell over time under constant power demand, which can be seen in Figure 9f.
Under dynamic load demand, EKFest + DQNsch achieves more even SOH balancing and reduces the standard deviation of the cells’ SOHs to zero, while other algorithms fail to balance the SOHs of cells, except for the DDest + DQNsch, which achieves the second-best performance, as shown in Figure 10b–f. The SOH of the weakest cell (cell 4, which has the lowest initial SOH) reaches 60%, while other cells have SOHs of more than 60% under algorithms proposed in other works, resulting in higher standard deviations and earlier end of second life of the battery pack. DDest + DQNsch reduces the standard deviation of SOHs and extends battery life compared to other scheduling algorithms. This shows the effectiveness of the proposed scheduling algorithm in managing a parallel-connected BESS, even with a less accurate estimation algorithm. The superior performance of the proposed algorithm under the different load demand conditions shows the robustness of the algorithm to load demands.
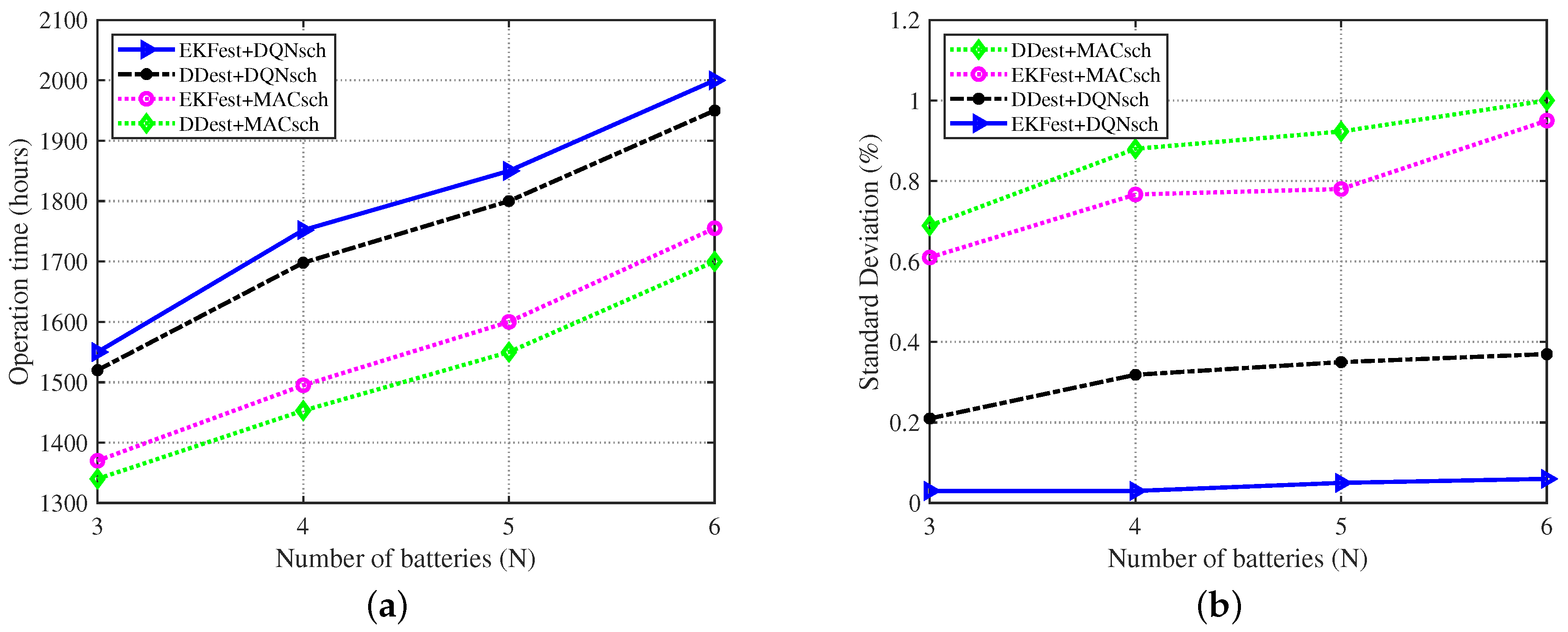
4.5. Impact of Numbers of Batteries on the Proposed Algorithm
We study the impact of the number of parallel-connected batteries for the BESS on the proposed algorithm under dynamic load demand according to the SOH profiles shown in Table 3. The SOH profiles of batteries have the same SOH average () and standard deviation ().

Table 3.
SOHs of batteries.
The performance of the proposed algorithm under different battery conditions in terms of the operational working time and standard deviation in SOHs is shown in Figure 11. The proposed algorithm (EKFest + DQNsch) achieves higher operational time (i.e., extends the second life of a battery pack) compared to other algorithms, as can be seen in Figure 11a. The proposed algorithm minimizes the SOH reduction of the battery pack in each time slot by balancing the SOHs of battery cells, thereby extending the battery pack’s lifetime.
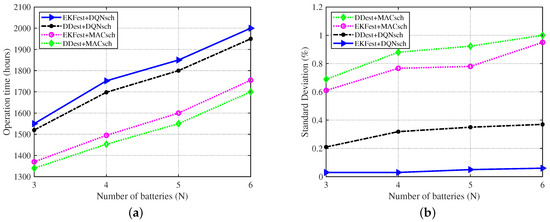
Figure 11.
Performance of the scheduling algorithms with different numbers of batteries under dynamic power demand: (a) operation time of the battery pack until the SOH reaches 60% and (b) standard deviation of SOHs among the batteries.
The proposed algorithm achieves the lowest standard deviation with different numbers of batteries in a battery pack, as shown in Figure 11b. The standard deviation in SOHs increases by a minimal amount under the proposed algorithm with an increase in the number of batteries compared to other algorithms. The combinations of the proposed estimation and the proposed scheduling algorithms with the algorithms proposed in previous works (EKFest + MACsch and DDest + DQNsch) increase the lifetime of a battery pack and achieve a more uniform SOH balance compared to the combination of previously proposed algorithms (i.e., DDest + MACsch). This shows the effectiveness of both parts of the proposed algorithm in the optimization of BESSs. Figure 11 shows that the proposed algorithm is robust to the number of battery cells in a battery pack in a BESS.
5. Conclusions and Future Work
In this paper, we proposed a DRL-based battery management algorithm to optimize battery lifetime for retired batteries with heterogeneous SOHs in a parallel-connected BESS. The proposed algorithm
- (i)
- estimated the SOCs and SOHs of all battery cells using EKF;
- (ii)
- used estimated SOCs and SOHs to represent the state of a BESS for DRL-based scheduling; and
- (iii)
- controlled the ON/OFF switches of battery cells inside the battery pack utilizing deep Q network knowledge.
Via simulation, we showed that the proposed algorithm outperformed other proposed algorithms by showing lower estimation errors for battery cell states and extending the battery pack’s second life. The proposed algorithm extended the operation time of the battery pack by 13.9% and 20.6% compared to other algorithms under constant and dynamic power demand, respectively.
Regarding future work, we will consider a BESS in which multiple battery packs are connected in series and each battery pack has parallel-connected battery cells. Such a configuration leads to high dimensions of state space. Furthermore, the deployment of smart-grid technologies that include energy storage systems [25] requires hundreds of battery cells connected in parallel or in series in a BESS. In such systems, DRL-based battery management algorithms can achieve limited performance due to high-dimensional state space. We will investigate a distributed reinforcement learning approach to counter the limitations of centralized approaches for large-scale energy storage systems. Additionally, an experimental setup will be considered to observe the impact of the battery management algorithm on real systems.
Author Contributions
Conceptualization, N.Q.D., S.M.S. and S.K.; methodology, N.Q.D., S.M.S., S.-J.C. and S.K.; software, N.Q.D.; validation, N.Q.D., S.M.S., S.-J.C. and S.K.; formal analysis, N.Q.D., S.M.S. and S.K.; investigation, N.Q.D., S.M.S. and S.K.; writing—original draft preparation, N.Q.D. and S.M.S.; supervision, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (NRF-2021R1I1A3A0 4037415) and the Korea Hydro and Nuclear Power Co. (2023).
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.nasa.gov/intelligent-systems-division/discovery-and-systems-health/pcoe/pcoe-data-set-repository/.
Acknowledgments
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (NRF-2021R1I1A3A0 4037415) and the Korea Hydro and Nuclear Power Co. (2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marinaro, M.; Bresser, D.; Beyer, E.; Faguy, P.; Hosoi, K.; Li, H.; Sakovica, J.; Amine, K.; Wohlfahrt-Mehrens, M.; Passerini, S. Bringing forward the development of battery cells for automotive applications: Perspective of R&D activities in China, Japan, the EU and the USA. J. Power Sources 2020, 459, 228073. [Google Scholar]
- Ding, Y.L.; Cano, Z.; Yu, A.; Lu, J.; Chen, Z. Automotive Li-Ion Batteries: Current Status and Future Perspectives. Electrochem. Energy Rev. 2019, 2, 1–28. [Google Scholar] [CrossRef]
- Hunt, G. USABC Electric Vehicle Battery Test Procedures Manual. Revision 2; USDOE: Washington, DC, USA, 1996.
- I.E.A. Global EV Outlook 2019; International Energy Agency: Paris, France, 2019.
- Martinez-Laserna, E.; Gandiaga, I.; Sarasketa-Zabala, E.; Badeda, J.; Stroe, D.I.; Swierczynski, M.; Goikoetxea, A. Battery second life: Hype, hope or reality? A critical review of the state of the art. Renew. Sustain. Energy Rev. 2018, 93, 701–718. [Google Scholar] [CrossRef]
- Sui, Y.; Song, S. A Multi-Agent Reinforcement Learning Framework for Lithium-ion Battery Scheduling Problems. Energies 2020, 13, 1982. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Zhao, L.; Lin, M.; Chen, Y. Least-squares based coulomb counting method and its application for state-of-charge (SOC) estimation in electric vehicles. Int. J. Energy Res. 2016, 40, 1389–1399. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, L.; Yu, Q.; Liu, S.; Zhou, G.; Shen, W. State of charge estimation for lithium-ion batteries based on cross-domain transfer learning with feedback mechanism. J. Energy Storage 2023, 70, 108037. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, Y.; Li, K.; Chen, Z. State of health estimation for lithium-ion batteries using Gaussian process regression-based data reconstruction method during random charging process. J. Energy Storage 2023, 72, 108390. [Google Scholar] [CrossRef]
- Song, Y.; Liu, D.; Liao, H.; Peng, Y. A hybrid statistical data-driven method for on-line joint state estimation of lithium-ion batteries. Appl. Energy 2020, 261, 114408. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined State of Charge and State of Health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Song, C.; Shao, Y.; Song, S.; Chang, C.; Zhou, F.; Peng, S.; Xiao, F. Energy Management of Parallel-Connected Cells in Electric Vehicles Based on Fuzzy Logic Control. Energies 2017, 10, 404. [Google Scholar] [CrossRef]
- Zhang, H.; Pei, L.; Sun, J.; Song, K.; Lu, R.; Zhao, Y.; Zhu, C.; Wang, T. Online Diagnosis for the Capacity Fade Fault of a Parallel-Connected Lithium Ion Battery Group. Energies 2016, 9, 387. [Google Scholar] [CrossRef]
- Kim, H.; Shin, K.G. Scheduling of Battery Charge, Discharge, and Rest. In Proceedings of the 2009 30th IEEE Real-Time Systems Symposium, Washington, DC, USA, 1–4 December 2009; pp. 13–22. [Google Scholar]
- Sun, B.; Xiong, L.; Liu, X.; Zhu, H. Research on Electromagnetic Compatibility in the Design of Battery Management System. In Proceedings of the 2023 IEEE International Conference on Mechatronics and Automation (ICMA), Harbin, China, 6–9 August 2023; pp. 363–368. [Google Scholar]
- Bruen, T.; Marco, J.; Gama, M. Current Variation in Parallelized Energy Storage Systems. In Proceedings of the 2014 IEEE Vehicle Power and Propulsion Conference (VPPC), Coimbra, Portugal, 27–30 October 2014; pp. 1–6. [Google Scholar]
- Kim, J.; Cho, B. Screening process-based modeling of the multi-cell battery string in series and parallel connections for high accuracy state-of-charge estimation. Energy 2013, 57, 581–599. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Bole, B.; Kulkarni, C.; Daigle, M. Randomized Battery Usage Data Set. In NASA Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2009. [Google Scholar]
- Liu, X.; Li, J.; Yao, Z.; Wang, Z.; Si, R.; Diao, Y. Research on battery SOH estimation algorithm of energy storage frequency modulation system. Energy Rep. 2022, 8, 217–223. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; A Bradford Book: Cambridge, MA, USA, 2018. [Google Scholar]
- Giannelos, S.; Borozan, S.; Aunedi, M.; Zhang, X.; Ameli, H.; Pudjianto, D.; Konstantelos, I.; Strbac, G. Modelling Smart Grid Technologies in Optimisation Problems for Electricity Grids. Energies 2023, 16, 5088. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).