Development Review of Broadband and Multi-Band Outphasing Power Amplifiers for High-Efficiency Amplification
Abstract
:1. Introduction
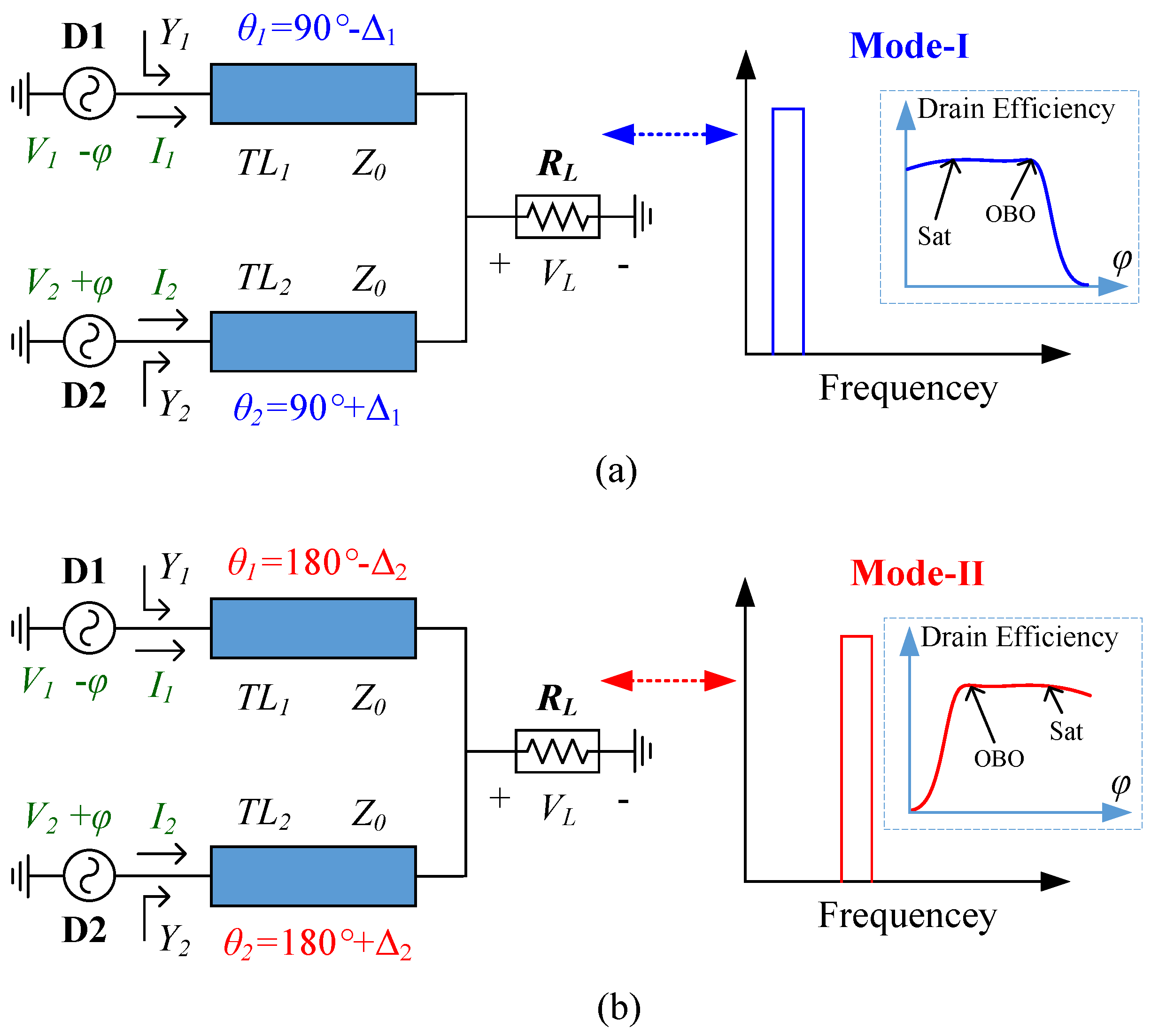
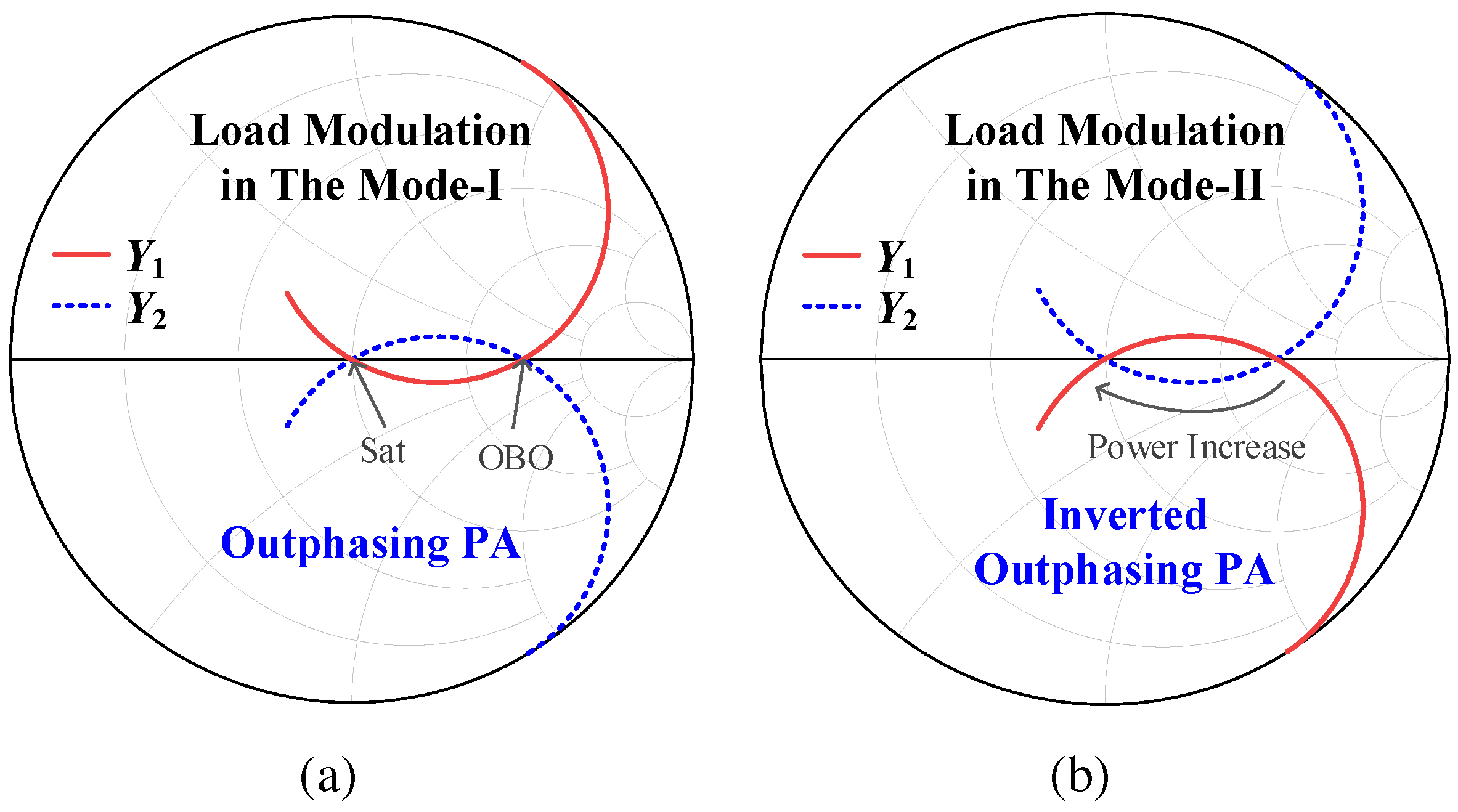
2. Load Modulation of OPAs
3. Review of Broadband OPAs
3.1. Broadband Class-E OPAs
3.2. Broadband Reconfigurable OPAs
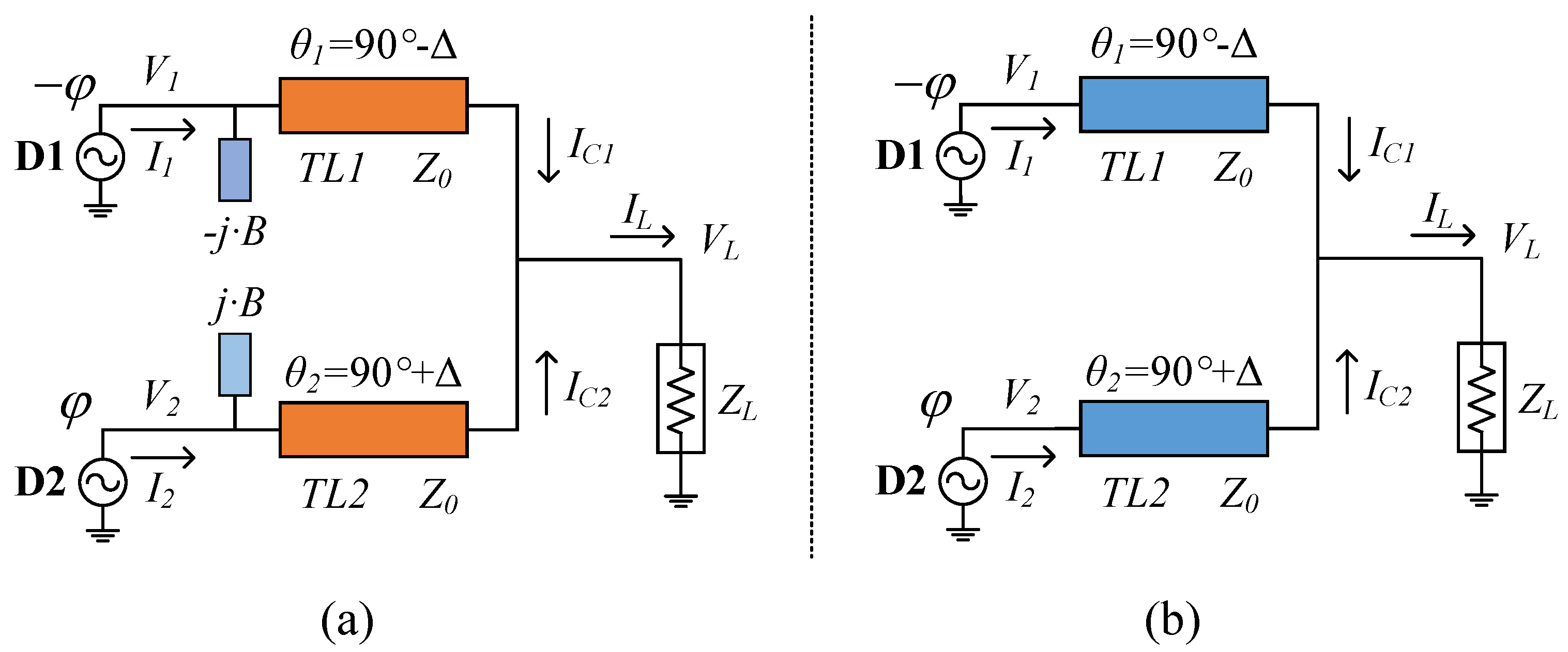
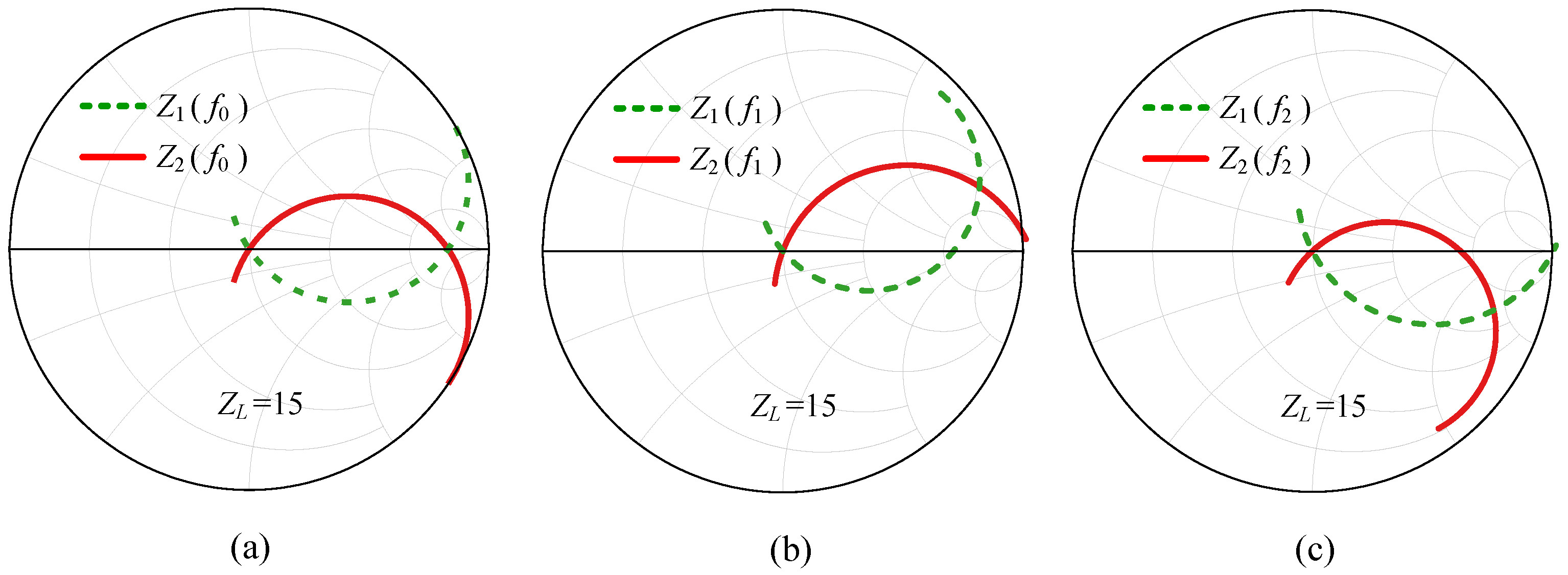
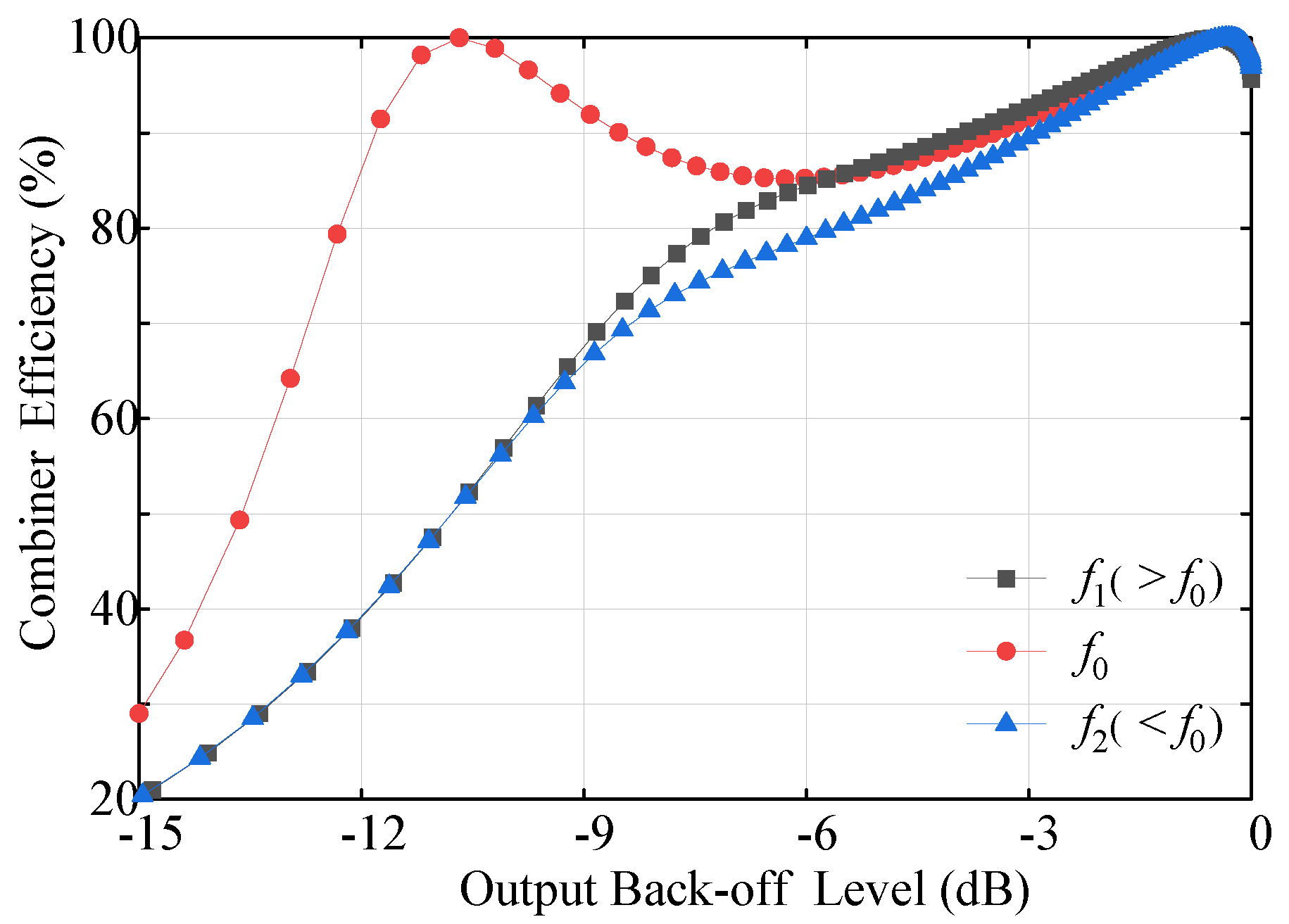
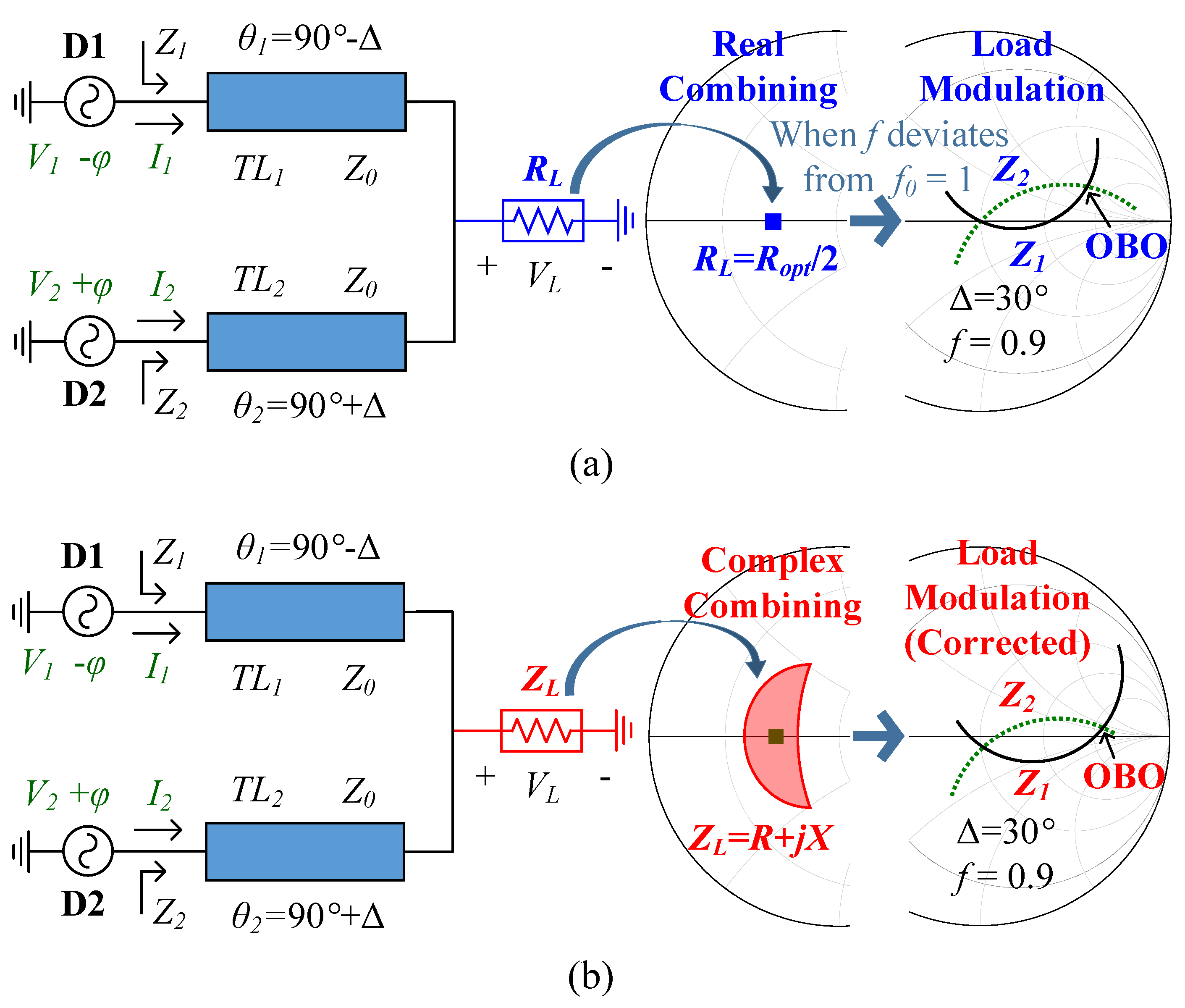
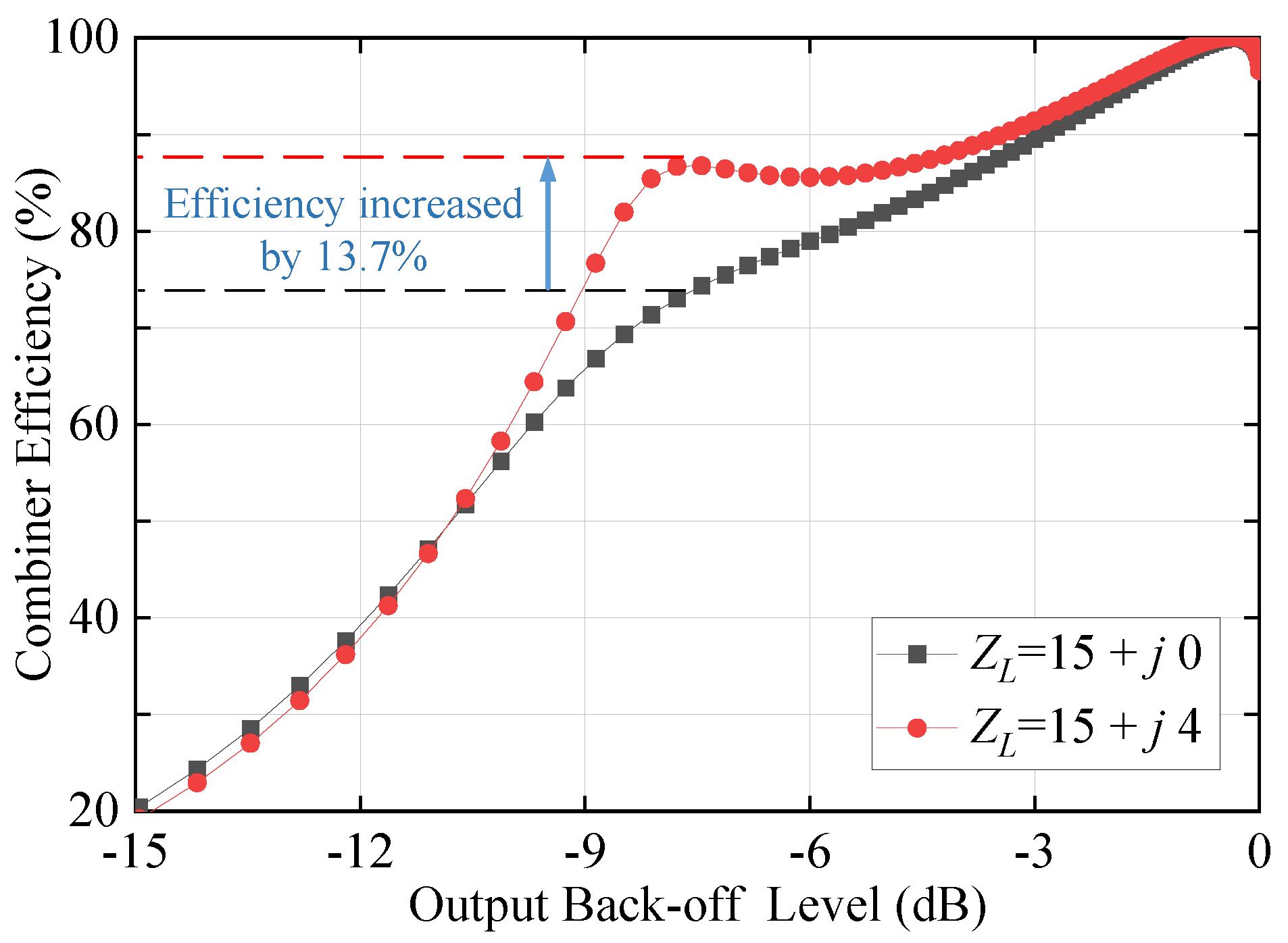
3.3. Complex Combining Impedance for Broadband Applications
4. Review of Multi-Band OPAs
4.1. Reconfigurable OPAs for Multi-Band Applications
4.2. Multi-Band Matching Topology for Multi-Band OPAs
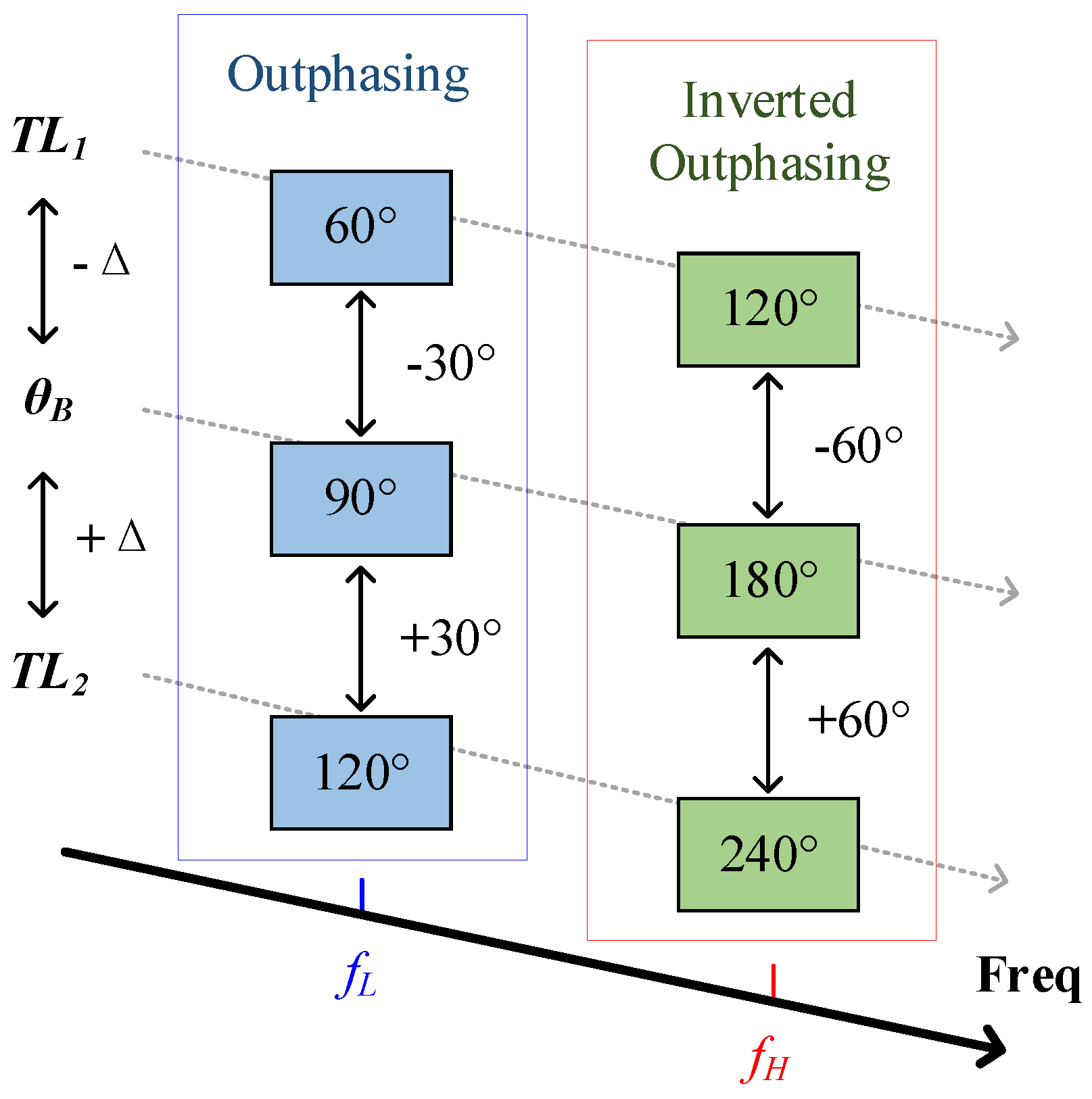
4.3. Multi-Mode Multi-Band OPAs Based on Frequency Periodicity
5. Potential Solutions for Broadband and Multi-Band OPAs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chireix, H. High power outphasing modulation. Proc. Inst. Radio Eng. 1935, 11, 1370–1392. [Google Scholar] [CrossRef]
- Barton, T. Not just a phase: Outphasing power amplifiers. IEEE Microw. Mag. 2016, 2, 18–31. [Google Scholar] [CrossRef]
- Ghahremani, A.; Annema, A.; Nauta, B. Outphasing class-E power amplifiers: From theory to back-off efficiency improvement. IEEE J. Solid-State Circuits 2018, 5, 1374–1386. [Google Scholar] [CrossRef]
- Afanasyev, P.; Grebennikov, A.; Farrell, R.; Dooley, J. Analysis and design of Outphasing transmitter using class-E power amplifiers with shunt capacitances and shunt filters. IEEE Access 2020, 8, 208879–208891. [Google Scholar] [CrossRef]
- Hwang, T.; Azadet, K.; Wilson, R.S.; Lin, J. Characterization of class-F power amplifier with wide amplitude and phase bandwidth for Outphasing architecture. IEEE Microw. Wireless Compon. Lett. 2014, 3, 188–190. [Google Scholar] [CrossRef]
- de Falco, P.E.; Pednekar, P.; Mimis, K.; Smida, S.B.; Watkins, G.; Morris, K.; Barton, T.W. Load modulation of harmonically tuned amplifiers and application to Outphasing systems. IEEE Trans. Microw. Theory Tech. 2017, 10, 3596–3612. [Google Scholar] [CrossRef]
- Raab, F.H. Efficiency of outphasing RF power-amplifier systems. IEEE Trans. Commun. 1985, 10, 1094–1099. [Google Scholar] [CrossRef]
- Litchfield, M.; Cappello, T. The various angles of Outphasing PAs: Competitiveness of Outphasing in efficient linear PA applications. IEEE Microw. Mag. 2019, 4, 135–145. [Google Scholar] [CrossRef]
- Birafane, A.; Kouki, A.B. On the linearity and efficiency of outphasing microwave amplifiers. IEEE Trans. Microw. Theory Tech. 2004, 7, 1702–1708. [Google Scholar] [CrossRef]
- Hakala, I.; Choi, D.K.; Gharavi, L.; Kajakine, N.; Koskela, J.; Kaunisto, R. A 2.14-GHz Chireix outphasing transmitter. IEEE Trans. Microw. Theory Tech. 2005, 6, 2129–2138. [Google Scholar] [CrossRef]
- Eun, S.-K.; Ji, S.H.; Cho, C.S.; Lee, J.W.; Kim, J. A high linearity Chireix outphasing power amplifier using composite right/left-handed transmission lines. In Proceedings of the 2007 European Microwave Conference, Munich, Germany, 10–12 October 2007; pp. 1622–1625. [Google Scholar]
- El-Asmar, M.; Birafane, A.; Helaoui, M.; Kouki, A.B.; Ghannouchi, F.M. Analytical design methodology of Outphasing amplification systems using a new simplified Chireix combiner model. IEEE Trans. Microw. Theory Tech. 2012, 6, 1886–1895. [Google Scholar] [CrossRef]
- Faraji, N.; Barton, T.W. An RF-input chireix outphasing power amplifier. In Proceedings of the 2016 IEEE Topical Conference on Power Amplifiers for Wireless and Radio Applications (PAWR), Austin, TX, USA, 24–27 January 2016; pp. 11–14. [Google Scholar]
- Gerhard, W.; Knoechel, R. Novel transmission line combiner for highly efficient Outphasing RF power amplifiers. In Proceedings of the 37th European Microwave Conference, Munich, Germany, 9–12 October 2007; pp. 1433–1436. [Google Scholar]
- Gerhard, W.; Knoechel, R. Improved design of outphasing power amplifier combiners. In Proceedings of the 2009 German Microwave Conference, Munich, Germany, 16–18 March 2009; pp. 1–4. [Google Scholar]
- Jang, H.; Wilson, R.; Canning, T.; Seebacher, D.; Schuberth, C.; Arigong, B.; Trang, F.; Ward, S. RF-input self-outphasing Doherty–Chireix combined amplifier. IEEE Trans. Microw. Theory Tech. 2016, 12, 4518–4534. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Barton, T.W. Linearity Characterization of RF-input Chireix Outphasing Power Amplifier. In Proceedings of the IInd General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Montreal, QC, Canada, 19–26 August 2017; pp. 1–4. [Google Scholar]
- Perreault, D.J. A new power combining and outphasing modulation system for high-efficiency power amplification. IEEE Trans. Circuits Syst. I Reg. Pap. 2011, 8, 1713–1726. [Google Scholar] [CrossRef]
- Barton, T.W.; Dawson, J.L.; Perreault, D.J. Four-way lossless outphasing and power combining with hybrid microstrip/discrete combiner for microwave power amplification. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013; pp. 1–4. [Google Scholar]
- Barton, T.W.; Perreault, D.J. Four-way microstrip-based power combining for microwave Outphasing power amplifiers. IEEE Trans. Circuits Syst. Regul. Pap. 2014, 10, 2987–2998. [Google Scholar] [CrossRef]
- Barton, T.W.; Jurkov, A.S.; Perreault, D.J. Transmission-line based multi-way lossless power combining and outphasing system. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar]
- Barton, T.W.; Perreault, D.J. Theory and implementation of RF-input outphasing power amplification. IEEE Trans. Microw. Theory Tech. 2015, 12, 4273–4283. [Google Scholar] [CrossRef]
- Barton, T.W.; Jurkov, A.S.; Pednekar, P.H.; Perreault, D.J. Multi-Way Lossless Outphasing System Based on an All-Transmission-Line Combiner. IEEE Trans. Microw. Theory Tech. 2016, 4, 1313–1326. [Google Scholar] [CrossRef]
- Komatsuzaki, Y.; Ma, R.; Benosman, M.; Nagai, Y.; Sakata, S.; Nakatani, K.; Shinjo, S. A Novel 1.4–4.8 GHz ultra-wideband, over 45% high efficiency digitally assisted frequency-periodic load modulated amplifier. In Proceedings of the 2019 IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2019; pp. 706–709. [Google Scholar]
- Ozen, M.; Heijden, M.; Acar, M.; Jos, R.; Fager, C. A generalized combiner synthesis technique for class-E outphasing transmitters. IEEE Trans. Circuits Syst. Reg. Pap. 2017, 5, 1126–1139. [Google Scholar] [CrossRef]
- Holzer, K.D.; Yuan, W.; Walling, J.S. Wideband techniques for Outphasing power amplifiers. IEEE Trans. Circuits Syst. Reg. Pap. 2018, 9, 2715–2725. [Google Scholar] [CrossRef]
- Heijden, M.; Acar, M. A radio-frequency reconfigurable CMOS-GaN class-E Chireix power amplifier. In Proceedings of the IEEE MTT-S International Microwave Symposium, Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar]
- Hu, C.; Yang, R.; Shi, W.; Li, L.; Gao, R.; Dai, Z.; Pang, J.; Li, M. Analysis and design of broadband Outphasing power amplifier based on complex combining impedance. IEEE Trans. Circuits Syst. Reg. Pap. 2023, 4, 1542–1554. [Google Scholar] [CrossRef]
- Ruiz, M.N.; Morante, R.; Rizo, L.; García, J.A.; Gilabert, P.L.; Montoro, G. A dual-band outphasing transmitter using broadband class-E power amplifiers. In Proceedings of the 2014 International Workshop on Integrated Nonlinear Microwave and Millimetre-Wave Circuits (INMMiC), Leuven, Belgium, 2–4 April 2014; pp. 1–3. [Google Scholar]
- Aggrawal, E.; Rawat, K. Reconfigurable Chireix Outphasing power amplifier over multiple frequency bands. IEEE Trans. Circuits Syst. II Express Briefs 2020, 6, 1019–1023. [Google Scholar] [CrossRef]
- Wang, W.; Chen, S.; Cai, J.; Zhou, X.; Chan, W.S.; Wang, G. A high efficiency dual-band outphasing power amplifier design. Int. J. Microw. Comput. Eng. 2021, 31, e22515. [Google Scholar]
- Wang, W.; Chen, S.; Cai, J.; Zhou, X.; Chan, W.S.; Wang, G.; Xue, Q. A dual-band Outphasing power amplifier based on noncommensurate transmission line concept. IEEE Trans. Microw. Theory Tech. 2020, 7, 3079–3089. [Google Scholar] [CrossRef]
- Huang, J.; Chen, S.; Cai, J.; Xu, K.; Wang, G.; Zhou, X. A dual-band Outphaisng power amplifier based on multi-topology fitting. In Proceedings of the 2023 IEEE MTT-S International Wireless Symposium (IWS), Qingdao, China, 14–17 May 2023; pp. 1–3. [Google Scholar]
- Hu, C.; Shi, W.; Yang, R.; Lin, S.; Dai, Z.; Pang, J.; Li, M. Design of dual-mode dual-band Outphasing power amplifier leveraging on periodicity of non-commensurate transmission line combiner. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 4384–4388. [Google Scholar] [CrossRef]
- Andersson, C.; Gustafsson, D.; Cahuana, J.C.; Hellberg, R.; Fager, C. A 1–3-GHz digitally controlled dual-RF input power-amplifier design based on a Doherty-outphasing continuum analysis. IEEE Trans. Microw. Theory Tech. 2013, 10, 3743–3752. [Google Scholar] [CrossRef]
- Kantana, C.; Benosman, M.; Ma, R.; Komatsuzaki, Y. A System Approach for Efficiency Enhancement and Linearization Technique of Dual-Input Doherty Power Amplifier. IEEE J. Microw. 2023, 3, 115–133. [Google Scholar] [CrossRef]
- Mengozzi, M.; Gibiino, G.P.; Angelotti, A.M.; Santarelli, A.; Florian, C.; Colantonio, P. Automatic Optimization of Input Split and Bias Voltage in Digitally Controlled Dual-Input Doherty RF PAs. Energies 2022, 15, 4892. [Google Scholar] [CrossRef]
- Barthwal, A.; Rawat, K.; Koul, S.K. Dual Input Digitally Controlled Broadband Three-Stage Doherty Power Amplifier with Back-off Reconfigurability. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 1421–1431. [Google Scholar] [CrossRef]
- Shi, W.; He, S.; Peng, J.; Wang, J. Digital Dual-Input Doherty Configuration for Ultrawideband Application. IEEE Trans. Ind. Electron. 2020, 67, 7509–7518. [Google Scholar] [CrossRef]
- Kalyan, R.; Rawat, K.; Koul, S.K. A Digitally Assisted Dual-Input Dual-Band Doherty Power Amplifier With Enhanced Efficiency and Linearity. IEEE Trans. Circuits Syst. Express Briefs 2019, 66, 297–301. [Google Scholar] [CrossRef]

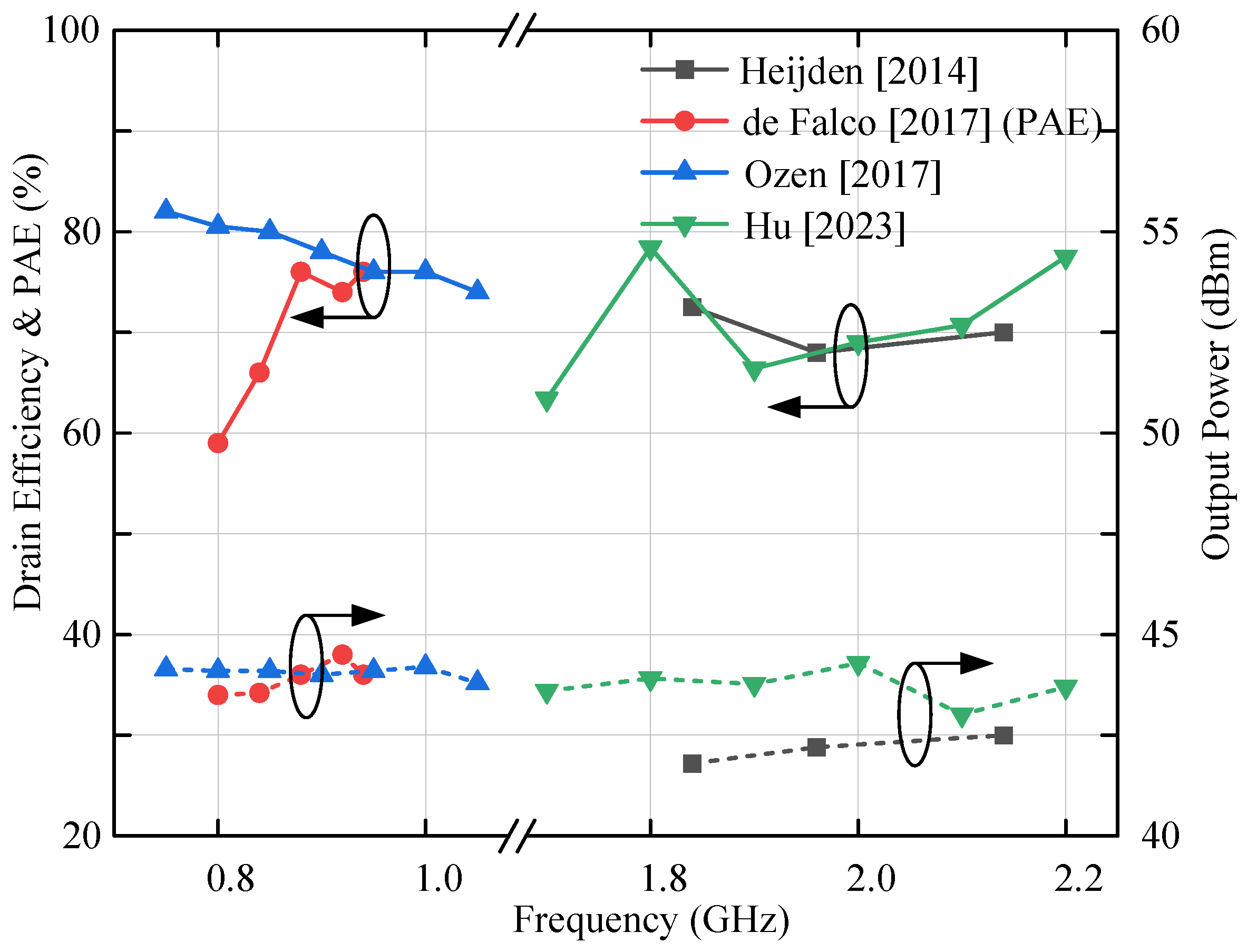
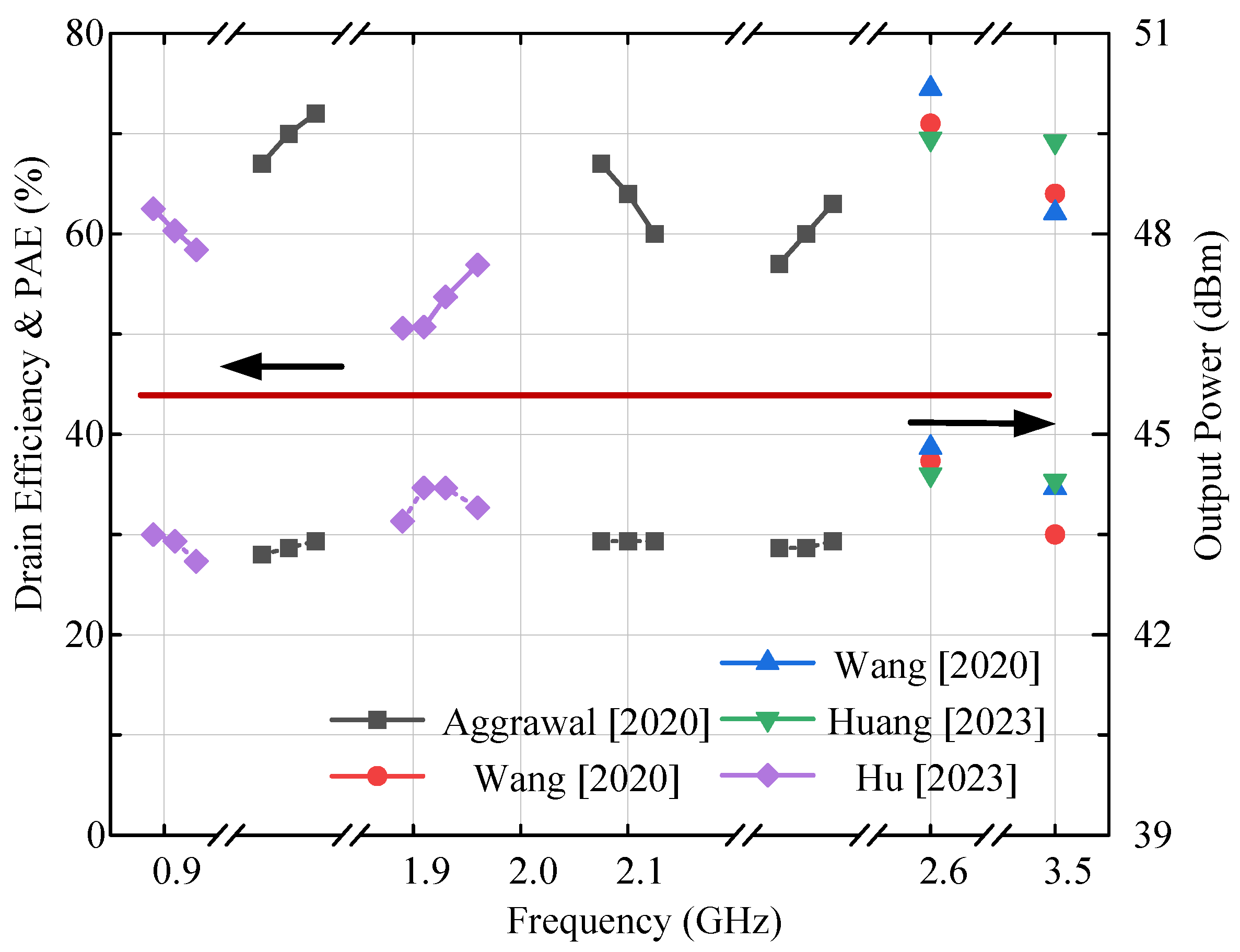
| Ref., Year | Freq. (GHz) | BW. (GHz/%) | Pmax (dBm) | DE@Sat (%) | OBO (dB) | DE@OBO (%) |
|---|---|---|---|---|---|---|
| [27] 2014 | 1.8–2.2 * | 0.4/20 | 41.8–42.5 | 68–72.5 | 6/8 | >60/>55 |
| [6] 2017 | 0.8–0.94 | 0.14/16 | 43.5–44.6 | 64–83 | 7 | >60 |
| [25] 2017 | 0.75–1.05 | 0.3/33.3 | 43.8–44.2 | 68–85 | 6 | >60 |
| [28] 2023 | 1.7–2.0 | 0.3/16.2 | 43.4–44.3 | 63.4–78.4 | 8 | 44–61.9 |
| Ref., Year | Freq. (GHz) | Pmax (dBm) | DE@Sat (%) | DE@OBO (%) |
|---|---|---|---|---|
| [30] 2020 | 1.65 ± 0.025 | 43.2–43.4 | >67 | >60 |
| 2.1 ± 0.025 | 43.4 | >60 | >45 | |
| 2.35 ± 0.025 | 43.4 * | >57 | 35 * | |
| [31] 2020 | 2.6/3.5 | 44.6/43.5 | 71/64 | 58.4/50.1 |
| [32] 2020 | 2.6/3.5 | 44.8/44.2 | 74.5/62.1 | 63.8/54.9 |
| [33] 2023 | 2.6/3.5 | 44.4/44.3 | 69.5/69.2 | 62.4/63.5 |
| [34] 2023 | 0.89–0.93 | 43.1–43.5 | 58.4–62.5 | 41.3–46.2 |
| 1.89–1.96 | 43.7–44.3 | 50.6–57.7 | 50.1–62.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hu, C.; Liu, X.; Wang, J.; Zhong, W.; Tian, P.; Lin, S.; Shi, W. Development Review of Broadband and Multi-Band Outphasing Power Amplifiers for High-Efficiency Amplification. Energies 2024, 17, 39. https://doi.org/10.3390/en17010039
Zhang Y, Hu C, Liu X, Wang J, Zhong W, Tian P, Lin S, Shi W. Development Review of Broadband and Multi-Band Outphasing Power Amplifiers for High-Efficiency Amplification. Energies. 2024; 17(1):39. https://doi.org/10.3390/en17010039
Chicago/Turabian StyleZhang, Yu, Chunyu Hu, Xia Liu, Jun Wang, Wenxu Zhong, Ping Tian, Shuai Lin, and Weimin Shi. 2024. "Development Review of Broadband and Multi-Band Outphasing Power Amplifiers for High-Efficiency Amplification" Energies 17, no. 1: 39. https://doi.org/10.3390/en17010039
APA StyleZhang, Y., Hu, C., Liu, X., Wang, J., Zhong, W., Tian, P., Lin, S., & Shi, W. (2024). Development Review of Broadband and Multi-Band Outphasing Power Amplifiers for High-Efficiency Amplification. Energies, 17(1), 39. https://doi.org/10.3390/en17010039







