Application of the Semi-Markov Processes to Model the Enercon E82-2 Preventive Wind Turbine Maintenance System
Abstract
:1. Introduction
2. Materials and Methods
3. Model of Preventive Maintenance System Based on Wind Turbine Age
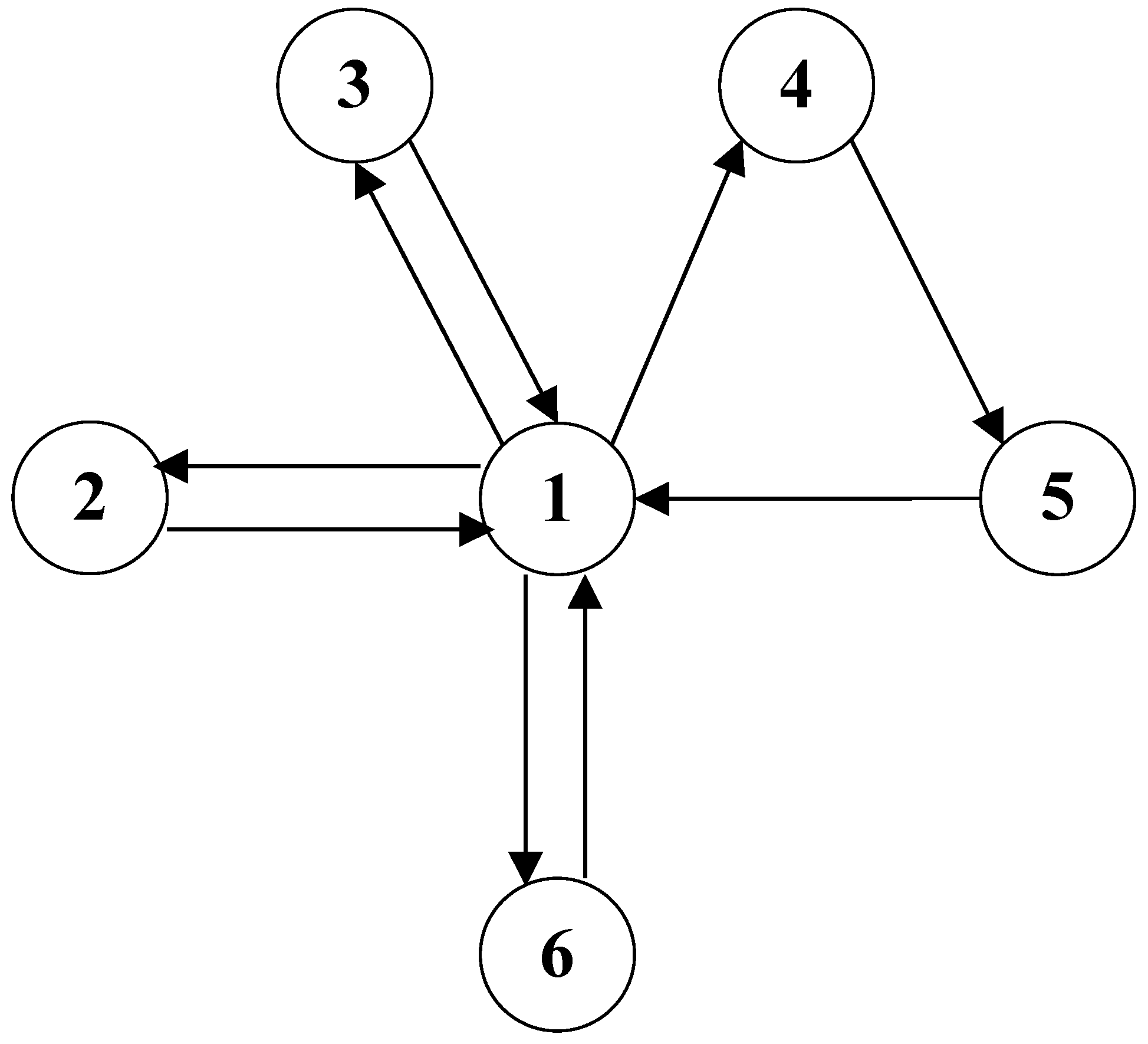
3.1. States of the Preventive Maintenance System Model
- State 1: Task execution state—electricity production state;
- State 2: Downtime state caused by lack of access to the power grid;
- State 3: Downtime state caused by weather conditions;
- State 4: Waiting state for corrective maintenance after a failure or damage;
- State 5: Corrective maintenance state after a failure or damage;
- State 6: Preventive maintenance state—a state in which the operational technical object undergoes preventive maintenance after operating hours and in accordance with the strategy.
3.2. Mathematical Model of the Preventive Maintenance System
- πi, i = 1 to 6—the steady-state probability of the embedded Markov chain.
3.3. Steady-State Distribution of the Markov Chain Embedded within Semi-Markov Process X(t)
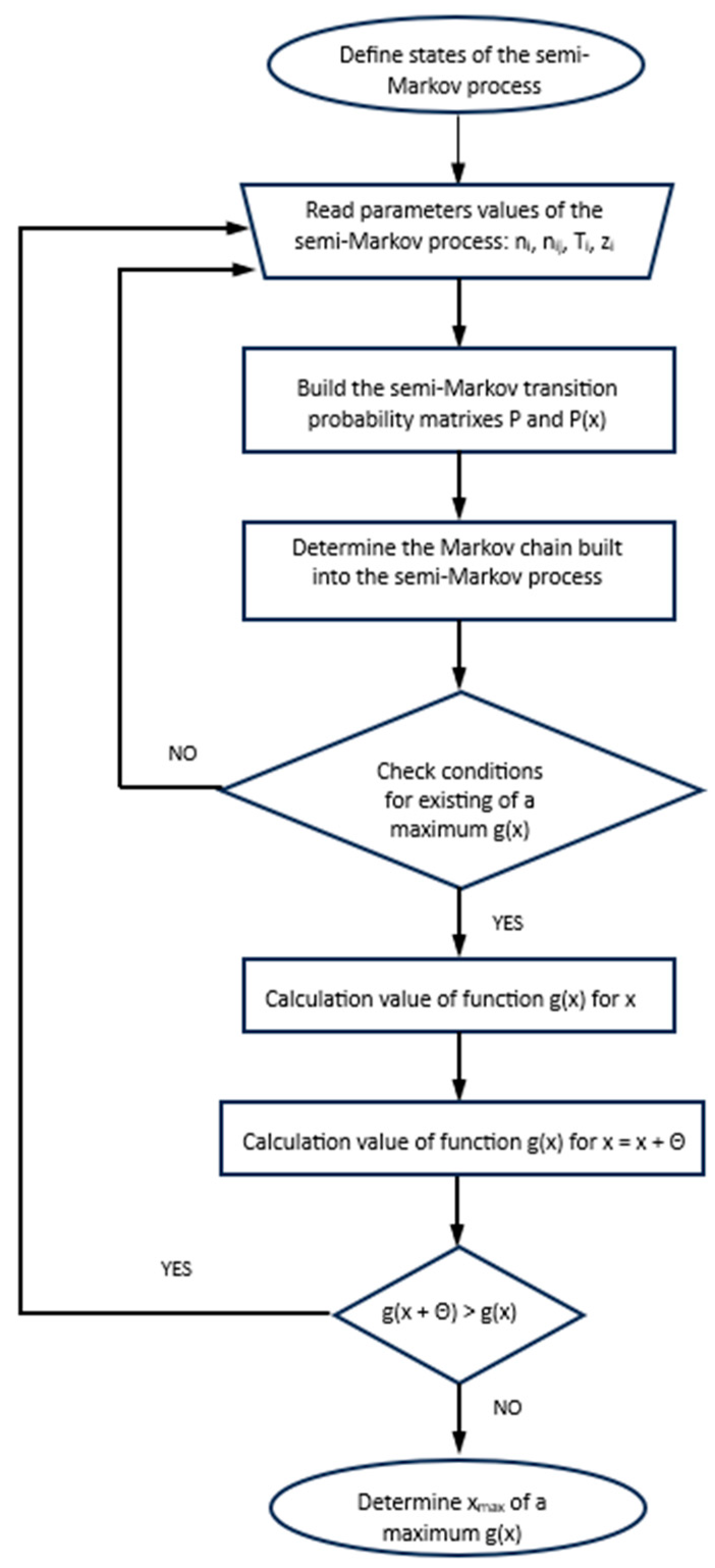
4. Defining the Objective Function
p13(x) = p13 · F13(x)
p14(x) = p14 · F14(x)
p16(x) = p16 · F16(x) + R1(x)
4.1. Conditions for the Existence of a Function Maximum: Profit over Time
- Z1: z1 > 0, zi < 0, for i = 2 to 6; meaning that a technical object generates profit while in state 1 (+) and generates expenses while in states 2–6 (−);
- Z2: z6 < z5; meaning the cost per unit in state 6 (preventive service) is smaller than the cost per unit in state 5 (correction repair);
- Z3: z2 < z6 < z5; meaning the cost per unit in state 2 (downtime caused by energy shortage) is smaller than the cost per unit in states 6 (preventive service) and 5 (correction repair);
- Z4: z3 < z6 < z5; meaning the cost per unit in state 3 (caused by weather conditions) is smaller than the unit cost in states 6 (preventive service) and 5 (correction repair);
- Z5: z4 < z6 < z5; meaning the cost per unit in state 4 (awaiting correction repair) is smaller than the cost per unit in states 6 (preventive service) and 5 (correction repair);
- Z6: ET4 + ET5 > ET6; meaning that the average downtime caused by damage to the technical object (total of average time of awaiting correction repair and average correction repair time) is longer than the average preventive service time;
- Z7: ET4 + ET5 > ET2; meaning that the average downtime caused by damage to the technical object (total of average time of awaiting correction repair and average correction repair time) is longer than the average downtime caused by energy shortage;
- Z8: ET4 + ET5 > ET3; meaning that the average downtime caused by damage to the technical object (total of average time of awaiting correction repair and average correction repair time) is longer than the average downtime caused by weather conditions.
β = A1 · C − A · C1 = z1 · C − C1
γ = B1 · C − B · C1
- coefficient α is defined as:
- Inequality α < 0 is equal to inequality:
- coefficient β is defined as:
- coefficient γ is defined using the formula:
4.2. Conditions for the Existence of Criterion Function Maximum: Availability
β = C = ET6; β > 0,
γ = 0,
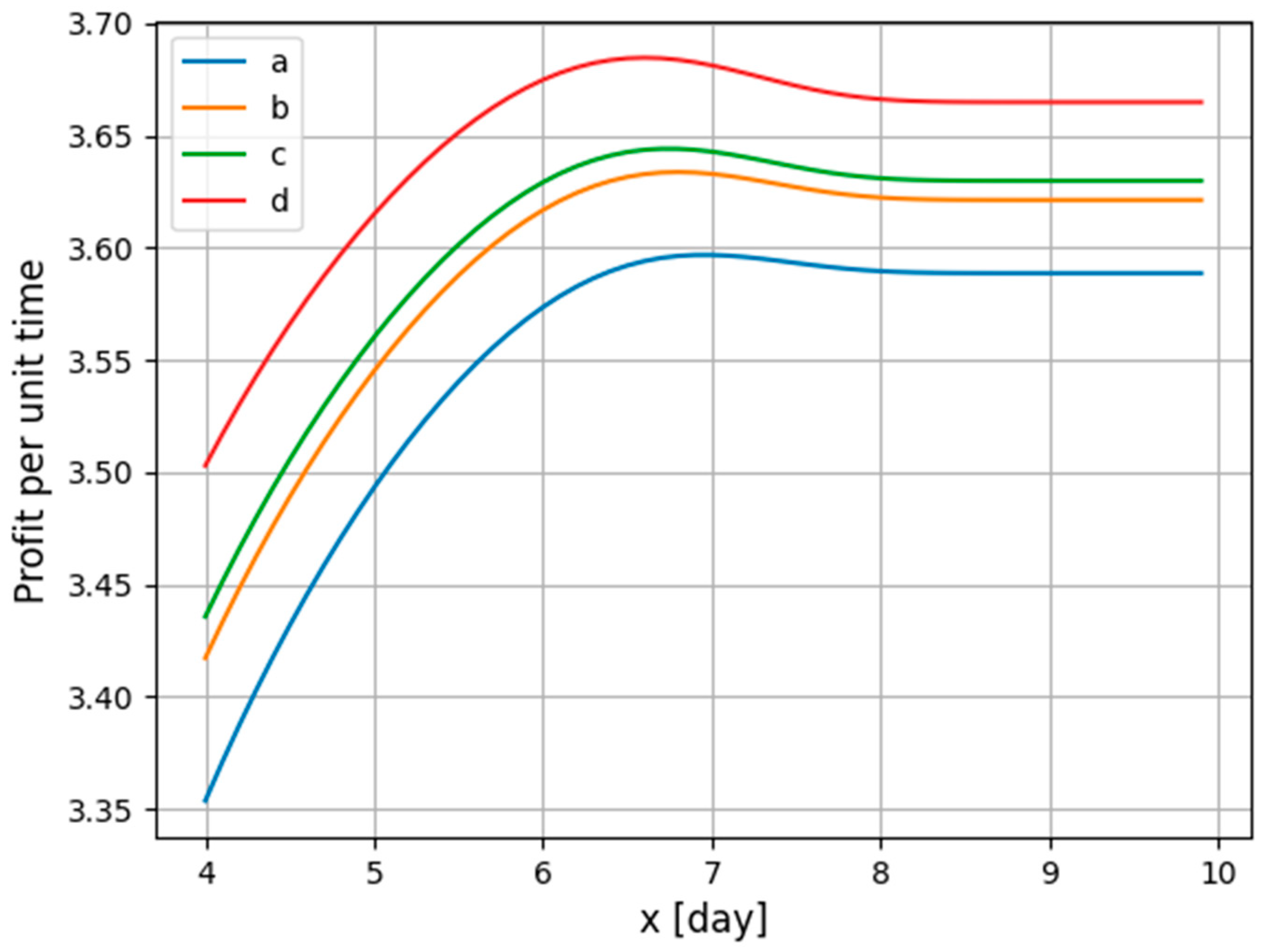
5. Calculations Confirming the Model
- probability matrix values of model P state changes:
- average time of the technical object in a model state in (day): ET2 = 0.11, ET3 = 0.17, ET4 = 0.48, ET5 = 0.44, ET6 = 0.21; for task completion time (useful life) for T1, the Weibull distribution has been adopted, for which the parameter scale value = 8. Four scenarios were studied, where the shape parameter value of the Weibull distribution is ∈{6.5, 8, 9.5, 11};
- average profit (cost) values per time unit in particular model states in (1k PLN/day): z1 = 4.1, z2 = −2.6, z3 = −2.6, z4 = −2.6, z5 = −17.3, z6 = −7.1.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CM | corrective maintenance |
| ET(x) | the time spent in state |
| Fj(x) | conditional distribution functions of the time in state |
| IFR | Increasing failure rate |
| λ(t) | damage failure rate |
| M(x) | being a denominator of criterion function g(x) |
| MR | minimal repair |
| MTFR | Mean time to failure or repair |
| P | transition matrix of probabilities with which the process moves from state to state |
| PM | preventive maintenance |
| R(x) | the reliability function of the random variable T |
| SCADA | Supervisory Control and data acquisition; |
| T | time to preventive maintenance or repair when it is damaged, whichever occurs first |
| x | time |
| Z = g(x) | objective function describing the cumulative profit or loss over time. |
References
- Shi, H.; Dong, Z.; Xiao, N.; Huang, Q. Wind speed distributions used in wind energy assessment: A review. Front. Energy Res. 2021, 9, 769920. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Chichester, UK, 2010. [Google Scholar]
- Jain, P. Wind Energy Engineering; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Chiodo, E.; Mazzanti, G.; Karimian, M. Bayes estimation of Inverse Weibull distribution for extreme wind speed prediction. In Proceedings of the International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015. [Google Scholar]
- Pryor, S.C.; Barthelmie, R.J.; Bukovsky, M.S.; Leung, L.R.; Sakaguchi, K. Climate change impacts on wind power generation. Nat. Rev. Earth Environ. 2020, 1, 627–643. [Google Scholar] [CrossRef]
- Carroll, J.; McDonald, A.; Dinwoodie, I.; McMillan, D.; Revie, M.; Lazakis, I. Availability, operation and maintenance costs of offshore wind turbines with different drive train configurations. Wind Energy 2017, 20, 361–378. [Google Scholar] [CrossRef]
- Cheng, E.; Yeung, C. Generalized extreme gust wind speeds distributions. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1657–1669. [Google Scholar] [CrossRef]
- Letcher, T. Wind Energy Engineering: A Handbook for Onshore and Offshore Wind Turbines, 1st ed.; Academic Press; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Taboada, J.; Diaz-Casas, V.; Yu, X. Reliability and Maintenance Management Analysis on OffShore Wind Turbines (OWTs). Energies 2021, 14, 7662. [Google Scholar] [CrossRef]
- McMillan, D.; Ault, G.W. Specification of reliability benchmarks for offshore wind farms. In Proceedings of the European Safety and Reliability, Valencia, Spain, 22–25 September 2008; pp. 22–25. [Google Scholar]
- Tchakoua, P.; Wamkeue, R.; Ouhrouche, M.; Slaoui-Hasnaoui, F.; Tameghe, T.A.; Ekemb, G. Wind turbine condition monitoring: State-of-the-art review, new trends, and future challenges. Energies 2014, 7, 2595–2630. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Chan, P.W.; Chen, D. On the failure probability of offshore wind turbines in the China coastal waters due to typhoons: A case study using the OC4-DeepCwind semisubmersible. IEEE Trans. Sustain. Energy 2018, 10, 522–532. [Google Scholar] [CrossRef]
- Lau, B.C.P.; Ma, E.W.M.; Pecht, M. Review of offshore wind turbine failures and fault prognostic methods. In Proceedings of the IEEE 2012 Prognostics and System Health Management Conference (PHM-2012 Beijing), Beijing, China, 23–25 May 2012; pp. 1–5. [Google Scholar]
- Odgaard, P.F.; Johnson, K.E. Wind turbine fault detection and fault tolerant control-an enhanced benchmark challenge. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 4447–4452. [Google Scholar]
- Habibi, H.; Howard, I.; Simani, S. Reliability improvement of wind turbine power generation using model-based fault detection and fault tolerant control: A review. Renew. Energy 2019, 135, 877–896. [Google Scholar] [CrossRef]
- Abid, K.; Sayed Mouchaweh, M.; Cornez, L. Fault prognostics for the predictive maintenance of wind turbines: State of the art. In Proceedings of the ECML PKDD 2018 Workshops: DMLE 2018 and IoTStream 2018, Dublin, Ireland, 10–14 September 2018; Springer International Publishing: Cham, Switzerland, 2019; pp. 113–125. [Google Scholar]
- Knopik, L.; Migawa, K. Optimal age-replacement policy for non-repairable technical objects with warranty. Maint. Reliab. 2017, 19, 172–178. [Google Scholar] [CrossRef]
- Pham, H.; Wang, H. Imperfect maintenance. Eur. J. Oper. Res. 1996, 94, 425–438. [Google Scholar] [CrossRef]
- Knopik, L.; Migawa, K. Multi-state model of maintenance policy. Maint. Reliab. 2018, 20, 125–130. [Google Scholar]
- Borowski, S.; Migawa, K.; Sołtysiak, A.; Neubauer, A.; Mazurkiewicz, A. Regression model in the operation of wind turbines. In Proceedings of the MATEC Web of Conferences, Kalavakkam, India, 14–15 February 2021; Volume 351, pp. 1–7. [Google Scholar] [CrossRef]
- Borowski, S.; Sołtysiak, A.; Migawa, K.; Neubauer, A. Simple mathematical model to predict the amount of energy produced in wind turbine—Preliminary study. In Proceedings of the MATEC Web of Conference, Virtual, 23–25 June 2021; Volume 332, pp. 1–7. [Google Scholar]
- Grabski, F. Semi-Markowskie Modele Niezawodności i Eksploatacji (Semi-Markov Models of Reliability and Maintenance); IBS PAN: Warszawa, Poland, 2002. [Google Scholar]
- Grabski, F. Semi-Markov Processes: Applications in System Reliability and Maintenance; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Oszczypała, M.; Ziółkowski, J.; Małachowski, J. Semi-Markov approach for reliability modelling of light utility vehicles. Eksploat. Niezawodn.—Maint. Reliab. 2023, 25, 161859. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szubartowski, M.; Migawa, K.; Borowski, S.; Neubauer, A.; Hujo, Ľ.; Kopiláková, B. Application of the Semi-Markov Processes to Model the Enercon E82-2 Preventive Wind Turbine Maintenance System. Energies 2024, 17, 199. https://doi.org/10.3390/en17010199
Szubartowski M, Migawa K, Borowski S, Neubauer A, Hujo Ľ, Kopiláková B. Application of the Semi-Markov Processes to Model the Enercon E82-2 Preventive Wind Turbine Maintenance System. Energies. 2024; 17(1):199. https://doi.org/10.3390/en17010199
Chicago/Turabian StyleSzubartowski, Mirosław, Klaudiusz Migawa, Sylwester Borowski, Andrzej Neubauer, Ľubomír Hujo, and Beáta Kopiláková. 2024. "Application of the Semi-Markov Processes to Model the Enercon E82-2 Preventive Wind Turbine Maintenance System" Energies 17, no. 1: 199. https://doi.org/10.3390/en17010199
APA StyleSzubartowski, M., Migawa, K., Borowski, S., Neubauer, A., Hujo, Ľ., & Kopiláková, B. (2024). Application of the Semi-Markov Processes to Model the Enercon E82-2 Preventive Wind Turbine Maintenance System. Energies, 17(1), 199. https://doi.org/10.3390/en17010199





