Optimal Preventive Maintenance Scheduling for Wind Turbines under Condition Monitoring

Abstract

Renewable energy sources, such as wind and solar, are positioned to play a pivotal role in future energy systems. In this paper, we propose a mathematical model for calculating and regularly updating the next preventive maintenance plan for a wind farm. Our optimization criterion considers various factors, including the current ages of key components, major maintenance costs, eventual energy production losses, and available data monitoring the condition of the wind turbines. Employing Cox proportional hazards analysis, we develop a comprehensive approach that accounts for the current ages of critical components, significant maintenance costs, potential energy production losses, and data collected from monitoring the condition of wind turbines. We illustrate the effectiveness of our approach through a case study based on data collected from multiple wind farms in Sweden. Our results demonstrate that preventive maintenance planning yields positive effects, particularly when the wind turbine components in question have significantly shorter lifespans than the turbine itself.

1. Introduction

Renewable energy sources like wind and solar are set to play a major role in the energy systems of the future. According to some projections, like the one presented by DNV GLAS [1], more than 50% of total electricity might come from renewable energy sources by 2050. These projections mean that wind turbines will grow to a much larger number in the near future, both on- and offshore. To cope with such a large number of assets, it will become crucial to automate processes around the operation and maintenance of these systems. In addition to simplifying and streamlining decision making, such automated processes might also allow for optimization around maintenance costs, which even today account for quite a considerable portion of the operational life cycle cost for wind turbine assets, especially for offshore installations.

Maintenance optimization can be viewed as the process of deciding the best moment in time, both from economic and technical perspectives, to replace one or more components considering the impact of each maintenance activity on the life cycle cost of an asset or assets. The recent literature on wind turbine preventive maintenance planning extends the modeling scope by paying special attention to particular performance factors for the wind power systems. Zheng et al. [2] looks into the effects of varying wind speeds on wind turbine maintenance planning. Davoodi et al. [3] singles out the converter as a crucial component of the wind turbine and builds an optimization model to find the optimal replacement times for the converters. Wang et al. [4] and Zhang et al. [5] deal with imperfect preventive maintenance.

Structural health monitoring (SHM) and condition monitoring techniques play a crucial role in the maintenance and reliability of wind turbines. SHM involves continuous monitoring of the structural integrity of wind turbine components, detecting any signs of damage or deterioration. These techniques employ various sensors, such as accelerometers, strain gauges, and acoustic emission sensors, to collect data on the structural behavior and performance of the turbine. In addition, condition monitoring techniques focus on monitoring the operational parameters and health status of wind turbine components. This includes regular inspections, vibration analysis, oil analysis, and thermal imaging to identify early signs of faults or deviations from normal operating conditions. These techniques facilitate the proactive identification of potential issues and allow for timely maintenance interventions. A recent review by Civera and Surace [6] provides a comprehensive overview of the latest advancements and applications of SHM and condition monitoring techniques in the wind turbine industry, emphasizing their significance in ensuring the reliability and optimal performance of wind turbines.

Sheng [7] presents a comprehensive overview of the current status and potential future developments in the field of Prognostics and Health Management for wind turbines. Prognostics and Health Management plays a crucial role in maintaining and ensuring the reliability of wind turbines by continuously monitoring key parameters and analyzing data to detect potential faults and predict future failures. The article explores a range of techniques and technologies employed in Prognostics and Health Management, including advanced sensor systems, data analytics, and machine learning algorithms. Furthermore, it discusses the benefits of implementing Prognostics and Health Management, such as the enhanced maintenance planning, minimized downtime, and increased overall efficiency of wind farms.

By utilizing the information about the state of various critical components, the maintenance routines can be further improved. Cox’s Proportional Hazards Model (PHM), proposed in Cox and Oakes [8], utilizes measurable entities as covariates to update the hazard function for a component, making the PHM quite handy for application with data from a condition monitoring system (CMS). Several research teams have suggested various optimization models in an attempt to make use of condition monitoring data by applying some version of the PHM (see, for example, Wu and Ryan [9], You and Meng [10], Li et al. [11], and Pham et al. [12]). Furthermore, [13] developed a probabilistic model to estimate the remaining lifetime of machinery using data from a CMS. Their probabilistic approach involves a PHM with Weibull baseline hazard and a Markov process model. Vibration data are used as an input from the CMS to illustrate a practical application of this probabilistic model. Similarly, Banjevic and Jardine [14] represent the failure process along with the covariate process with a discrete Markov process. A PHM algorithm is proposed for predicting the remaining lifetime of the machinery based on a condition monitoring process.

In Wang et al. [15], the authors feed the online vibration and temperature signals of bearings from the CMS into a neural network and predict the features of bearing vibration signals at any time horizon. Furthermore, according to the features, the degradation factor is defined. A PHM is generated to estimate the survival function and forecast the remaining lifetime of the bearing.

Ghasemi et al. [16] is built upon a hidden Markov model, assuming that the equipment’s unobservable degradation state evolves as a Markov chain. The Bayes rule is used to determine the probability of being in a certain degradation state at each observation moment. Cox’s time-dependent PHM is applied to deal with the equipment’s failure rate. Two main problems are addressed: the problem of imperfect observations and the problem of taking into account the whole history of observations.

The recent papers by Bangalore and Patriksson [17] and Bangalore et al. [18] develop a machine learning approach to maintenance scheduling for a wind turbine whose condition is monitored by a time series $\left\{x\right(1),x(2),\dots ,x(t\left)\right\}$ summarizing some key characteristics of the turbine, which can be used for predicting the failure times after time t. A deep learning algorithm was trained for a prediction $\widehat{x}(t+1)$ of the next value $x(t+1)$ based on a time series observed up to the current time t. Then, at time $t+1$, depending on a certain measure of discrepancy between the observed $x(t+1)$ and predicted $\widehat{x}(t+1)$ values, a decision is made regarding whether preventive maintenance (PM) should be performed in the near future or not. One of the key simplifying assumptions requires that the turbine’s component in question has an exponential life length distribution.

Most of the research towards condition-based maintenance utilizes the data from vibration-based CMSs. The vibration data are measured at a high frequency, in the kHz range, and the data are processed using various algorithms before they are stored. It might, in some cases, also be difficult to obtain access to data from the vibration-based systems. Hence, in this paper we focus on creating a decision-making model that utilizes easily available signals such as component temperatures.

Modern wind turbines are equipped with a Supervisory Control and Data Acquisition (SCADA) system, which measures and stores the data for various component temperatures. These data have been utilized along with information about historical failures to create a model to estimate the condition-based failure rate of gearboxes. Furthermore, in this paper, the common assumption of exponential life length distribution (constant failure rate) is relaxed using the Weibull statistical model.

The optimization model presented in this paper is a slight variation of the one proposed in Yu et al. [19], where a multiple-component setting for a single wind turbine (without condition monitoring data) was addressed.

The rest of this paper is organized as follows. Section 2 describes how one can utilize condition monitoring data to estimate the Weibull parameters of aging gearboxes. Section 3 gives a detailed description of the optimization model for n wind turbines, each represented by their gearboxes. Section 4 presents a simulated case study demonstrating the effectiveness of the method. Section 5 presents a detailed case study based on data collected from several onshore wind farms in Sweden. Section 6 has a closer look at a particular wind farm. Section 7 offers a comprehensive analysis of the suitability and effectiveness of the research methodologies employed in this study. Finally, Section 8 presents the conclusions drawn from our findings.

2. Weibull Parameters under Condition Monitoring

The key ingredient of the optimization model of this paper is the Weibull distribution for the life length L of a generic gearbox:

$$\mathrm{P}(L>t)=e^{-\theta t^{\kappa }},t>0.$$

(1)

It is assumed that under the normal conditions the Weibull parameters $(\theta ,\kappa )$ of a gearbox take certain baseline values $({\theta }_0,{\kappa }_0)$, so that the baseline hazard function (failure rate at age t) takes the form

$$r_0\left(t\right)={\theta }_0{\kappa }_0{t}^{{\kappa }_0-1}.$$

(2)

Suppose that time series data

$$\mathit{x}=\left(x\right(1),x(2),\dots )$$

measuring an appropriate covariate $x\left(t\right)$ at different times t can be utilized to monitor the condition of a given gearbox. It is worth noting that we treat $\mathit{x}$ and x as two distinct variables. Specifically, $\mathit{x}$ represents the time series data, while $x\left(t\right)$ represents the corresponding scalar covariate. Assuming that the shape parameter ${\kappa }_0$ of the Weibull distribution of the gearbox’s life length is constant over time, the task addressed in this section is to find an appropriate value of the scale parameter $\theta =\theta (\mathit{x},t)$, which would update the failure rate of the gearbox

$$r(\mathit{x},t)=\theta (\mathit{x},t){\kappa }_0{t}^{{\kappa }_0-1}$$

(3)

by incorporating the available condition monitoring data $x\left(1\right),\dots ,x\left(t\right)$.

2.1. Finding $({\theta }_0,{\kappa }_0)$ Using Training Data

Consider a set of historical data containing the observed ages of still operational gearboxes $u_1,\dots ,u_K$, and yet another historical data set for gearboxes that have failed

$$\begin{array}{c}\hfill (v_1,{\mathit{x}}^{\left(1\right)}),\dots ,(v_N,{\mathit{x}}^{\left(N\right)}),\end{array}$$

(4)

where $v_k$ is the failure age of a gearbox k and ${\mathit{x}}^{\left(k\right)}=(x_1^{\left(k\right)},\dots ,x_{v_k}^{\left(k\right)})$ is the corresponding recorded history of the monitoring data. The baseline Weibull parameter values $({\theta }_0,{\kappa }_0)$ are estimated from the two sets of observed lifetimes

$$U=\{u_1,\dots ,u_K\},V=\{v_1,\dots ,v_N\},$$

by maximising the likelihood function

$$\mathcal{L}(\theta ,\kappa )=\prod _{t\in V}\mathrm{P}(L=t)\prod _{t\in U}\mathrm{P}(L>t)=\prod _{t\in V}(e^{-\theta {(t-1)}^{\kappa }}-e^{-\theta t^{\kappa }})\prod _{t\in U}{e}^{-\theta t^{\kappa }}.$$

(5)

2.2. The Use of Proportional Hazard Method

To be able to update the hazard rate by means of (3), the following version of PHM is suggested:

$$\begin{array}{c}\hfill \theta (\mathit{x},t)={\theta }_0{e}^{\beta (\overline{x}\left(t\right)-\overline{x})},j=1,\dots ,n,\end{array}$$

(6)

where

$$\overline{x}=\frac{x\left(1\right)+\dots +x\left(12\right)}{12}$$

(7)

is the first-year average of the covariate x and

$$\overline{x}\left(t\right)=\frac{x(t-2)+x(t-1)+x\left(t\right)}{3}$$

(8)

is the latest three-month moving average. Obviously, this approach requires that the farm has been in operation for at least 15 months.

The Cox regression parameter $\beta$ mentioned in (6) is estimated from the training data set (4), assuming that the data are labeled in such a way that the failure times are sorted in the ascending order

$$v_1<v_2<\dots <v_N.$$

(9)

The key argument of the Cox method [8] is that expressions (3) and (6) imply the following expression for the partial likelihood function of the regression parameter $\beta$:

$${\mathcal{L}}^{*}\left(\beta \right)=\prod _{j=1}^N\frac{r(v_j,{\mathit{x}}^{\left(j\right)})}{{\sum }_{i=j}^{N}r(v_j,{\mathit{x}}^{\left(i\right)})}=\prod _{j=1}^N\frac{exp\left\{\beta {\overline{x}}^{\left(j\right)}\left(v_j\right)\right\}}{{\sum }_{i=j}^{N}exp\left\{\beta {\overline{x}}^{\left(i\right)}\left(v_j\right)\right\}}.$$

(10)

Maximisation of the partial likelihood ${\mathcal{L}}^{*}\left(\beta \right)$ leads to the desired maximum likelihood estimate ${\beta }_0$.

As a result for the current n component setting, we obtain the updating formulas for the n pairs of the Weibull parameters

$$\begin{array}{c}\hfill {\theta }_j={\theta }_0{\varphi }_j\left(t\right),{\kappa }_j={\kappa }_0,j=1,\dots ,n,\end{array}$$

(11)

involving Cox factors

$$\begin{array}{c}\hfill {\varphi }_j\left(t\right)=e^{{\beta }_0({\overline{x}}_j\left(t\right)-{\overline{x}}_j)},j=1,\dots ,n,\end{array}$$

(12)

based on n times series

$${\mathit{x}}_j=(x_j\left(1\right),x_j\left(2\right),\dots ),j=1,\dots ,n.$$

The Cox factor (12) has the following effect on the failure rate of the gearbox j, provided ${\beta }_0$ is positive (in other words, assuming that the chosen covariate is such that higher values of $x\left(t\right)$ indicate higher stress on the gearbox at time t). At the time of observation t, the first-year average ${\overline{x}}_j$ is compared with the last three-month average ${\overline{x}}_j\left(t\right)$. If the difference ${\overline{x}}_j\left(t\right)-{\overline{x}}_j$ is close to zero, then the current condition of the turbine j is deemed to be normal, and formula (11) suggests using the baseline parameters ${\theta }_j={\theta }_0$ and ${\kappa }_j={\kappa }_0$ for describing the failure rate of the gearbox j. However, if it turns out that ${\overline{x}}_j\left(t\right)>{\overline{x}}_j$, so that ${\theta }_j>{\theta }_0$, then the corresponding hazard rate

$$r_j\left(t\right)={\theta }_j{\kappa }_0{t}^{{\kappa }_0-1}$$

(13)

becomes larger that the base line value $r_0\left(t\right)$. Alternatively, if ${\overline{x}}_j\left(t\right)<{\overline{x}}_j$, then, of course, the failure rate of the gearbox at time t is below the normal: $r_j\left(t\right)<r_0\left(t\right)$.

3. Optimal Preventive Maintenance Schedule for $\mathit{n}$ Gearboxes

An efficient optimization model for a single wind turbine with several components was presented in Yu et al. [19]. In this section, the optimization model from Yu et al. [19] is adapted to a setting with n wind turbines, where each wind turbine is represented by its gearbox as the key component. Section 3.1 introduces the main cost parameters including so-called virtual maintenance costs. Section 3.3 presents the main step of our optimal scheduling algorithm summarized in Section 3.4.

3.1. Maintenance Costs

The maintenance costs of gearboxes are modeled in terms of the following parameters:

• g is the total cost of a corrective maintenance (CM), including the logistic cost, down-time cost, and the cost of a new gearbox;
• $h_0$ is the fixed cost of a preventive maintenance (PM) activity. This cost is the same regardless of how many gearboxes are planned to be replaced during this activity;
• h is the variable cost related to the PM replacement, which takes into account the replacement cost of a gearbox, the downtime cost, and the initial value loss of the gearbox in use;
• m is the monthly loss of the value for a gearbox in use.

To illustrate the use of the parameters $(h_0,h,m)$, consider a PM plan suggesting to simultaneously replace three components having ages $(a_1,a_2,a_3)$ in months. Then, the total cost associated with this PM activity, f, is calculated as

$$f=h_0+(h+a_{1}m)+(h+a_{2}m)+(h+a_{3}m)=h_0+3h+(a_1+a_2+a_3)m.$$

Given the Weibull parameter values $({\theta }_j,{\kappa }_0)$, using the approach of [19], the virtual replacement cost $b_j\left(a\right)$ for the gearbox of age a can be computed. (For further details on the exact calculation of $b_j\left(a\right)$ and the interpretation of the virtual replacement cost based on the renewal–reward argument, the reader is referred to [19].) In what follows,

$$B_j\left(a\right)=(h+am)\wedge b_j\left(a\right)$$

(14)

stands for the minimum between two age-specific costs: the age-specific PM cost and the virtual replacement cost.

3.2. Monthly Maintenance Replacement Cost c

Consider a wind farm with n new gearboxes at time $t=0$, where the time to the failure of the first gearbox is denoted by

$$L_0=min(L_1,\dots ,L_n)$$

(15)

Using the independence of random variables $L_1,\dots ,L_n$ and the Equation (1), we obtain

$$\mathrm{P}(L_0>t)=\prod _{i=1}^n\mathrm{P}(L_i>t)=e^{-n\theta t^{\kappa }}.$$

(16)

If the next PM is planned at time t, then the first renewal time of the system $X=X\left(t\right)$ can be calculated as presented in Equation (17).

$$X=L_0\wedge t=L_0·1_{\{L_0\le t\}}+t·1_{\{L_0>t\}}$$

(17)

For a condition C, the indicator function $1_{\left\{C\right\}}$ takes the value 1 when C holds and the value 0 otherwise.

Based on Yu et al. [19], the corresponding reward value $R=R\left(t\right)$ can be computed as

$$R=(g+(n-1)B_0\left(L_0\right))1_{\{L_0\le t\}}+(h_0+n{B}_0\left(t\right))1_{\{L_0>t\}},$$

(18)

where

$$B_0\left(a\right)=(h+am)\wedge b_0\left(a\right)$$

(19)

is the age-specific replacement cost, provided the gearbox’s Weibull parameters take the baseline values. Applying the renewal–reward theorem we find that the time-average maintenance cost $\frac{\mathrm{E}\left(R\right)}{\mathrm{E}\left(X\right)}$ is the following function of the planning time t:

$$q_t=\frac{g\mathrm{P}(L_0\le t)+(n-1)\mathrm{E}(B_0\left(L_0\right)·1_{\{L_0\le t\}})+(h_0+n{B}_0\left(t\right))\mathrm{P}(L_0>t)}{\mathrm{E}(L_0·1_{\{L_0\le t\}})+t\mathrm{P}(L_0>t)},$$

(20)

where $\mathrm{E}\left(L\right)$ is the expected value of the random variable L.

After minimizing $q_t$ over t, we can define the monthly maintenance replacement cost of the wind farm as a constant

$$c=\underset{t\ge 1}{min}{q}_t.$$

(21)

3.3. The Key Optimization Step

For the planning period $[s,T]$, where T is the end of life for the whole wind farm, a PM plan for any array can be defined as

$$({\mathit{w}}_s,{\mathit{y}}_s,z)=\{w_t^j,y_t,z:1\le j\le n,s+1\le t\le T\}$$

with binary components $w_t^j,y_t,z\in \{0,1\}$ satisfying the following linear constraints:

$$\begin{array}{cc}\hfill y_t& \ge w_t^j,t=s+1,\dots ,T,j=1,\dots ,n,\hfill \end{array}$$

(22a)

$$\begin{array}{cc}\hfill \sum _{j=1}^n{w}_t^j& \ge y_t,t=s+1,\dots ,T,\hfill \end{array}$$

(22b)

$$\begin{array}{cc}\hfill \sum _{t=s+1}^T{y}_t& =1-z.\hfill \end{array}$$

(22c)

Here, $w_t^j=1$ means that at time t a PM activity is planned for turbine j; otherwise, $w_t^j=0$. Similarly, $y_t=1$ means that at time t a PM activity is planned for at least one of the turbines in the wind farm, constraints (22a) and (22b). The equality $z=1$ means that no PM activity is planned during the whole time period $[s+1,T]$, constraint (22c).

Given the ages of n gearboxes at time s

$$\mathit{a}=(a_1,\dots ,a_n),$$

(23)

the first failure time is $s+L_{\mathit{a}}$, where (lifting the turbine index upstairs)

$$L_{\mathit{a}}=min(L_{a_1}^1,\dots ,L_{a_n}^n).$$

and

$$\mathrm{P}(L_a^j>t)=exp\left\{{\theta }_j\left(a^{{\kappa }_0}-{(a+t)}^{{\kappa }_0}\right)\right\},t\ge 0,$$

(24)

is the survival function conditional on the age a.

The cost assigned to a PM plan can be denoted as

$$\begin{array}{cc}\hfill F_{(s,\mathit{a})}({\mathit{y}}_s,z)& =\sum _{t=s+1}^T\left(g+(T-s-L_{\mathit{a}})c+\sum _{j\ne \gamma }{B}_j(a_j+L_{\mathit{a}})\right)1_{\{s+L_{\mathit{a}}\le t\}}{y}_t\hfill \\ \hfill & +\sum _{t=s+1}^T\left(h_0+(T-t)c+\sum _{j=1}^n{B}_j(a_j+t-s)\right)1_{\{s+L_{\mathit{a}}>t\}}{y}_t\hfill \\ \hfill & +\left(g+(T-s-L_{\mathit{a}})c+\sum _{j\ne \gamma }{B}_j(a_j+L_{\mathit{a}})\right)1_{\{s+L_{\mathit{a}}\le T\}}z,\hfill \end{array}$$

(25)

where $\gamma$ is the label of the gearbox that failed at time $s+L_{\mathit{a}}$. Notice that the total cost function $F_{(s,\mathit{a})}({\mathit{y}}_s,z)$ does not explicitly depend on ${\mathit{w}}_s$. The role of ${\mathit{w}}_s$ becomes explicit through the following additional constraint

$$\begin{array}{cc}\hfill & (h+(a_j+t-s)m)·w_t^j+b_j(a_j+t-s)·(y_t-w_t^j)=B_j(a_j+t-s)·y_t,\hfill \\ \hfill & t=s+1,\dots ,T,j=1,\dots ,n.\hfill \end{array}$$

(26)

If $y_t=1$, that is if a PM activity for at least one component is scheduled at time t, then for each component j there is a choice between two actions at time t: either perform a PM, so that $w_t^j=1$ and $y_t-w_t^j=0$, or do not perform a PM and compensate for the future extra costs caused by the current gearbox age using the virtual replacement cost value (corresponds to $w_t^j=0$ and $y_t-w_t^j=1$).

The optimal maintenance plan according to the presented approach is the solution of the linear optimization problem

$$\begin{array}{cc}\hfill \mathrm{minimise}& f_{(s,\mathit{a})}({\mathit{y}}_s,z)=\mathrm{E}\left(F_{(s,\mathit{a})}({\mathit{y}}_s,z)\right)\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{linear}\mathrm{constraints}\left(\text{22a}\right),\left(\text{22b}\right),\left(\text{22c}\right),\mathrm{and}\left(\text{26}\right),\hfill \\ \hfill & w_t^j\in \{0,1\},t=s+1,\dots T,j=1,\dots ,n,\hfill \\ \hfill & y_t\in \{0,1\},t=s+1,\dots T,\hfill \\ \hfill & z\in \{0,1\}.\hfill \end{array}$$

3.4. Optimal Scheduling Algorithm for n Gearboxes

In this section, the main result of this paper is summarized in the form of Algorithm 1 producing a PM plan for a given planning period $[s,T]$, focusing on the gearbox components of n wind turbines constituting a wind farm. It is assumed that the starting planning time s is such that $s\ge 15$ and that the length of the updating period is 3 months. The following data and parameters are assumed to be available:

–

Condition monitoring time series ${\mathit{x}}_j=(x_j\left(1\right),x_j\left(2\right))\dots$ for $j=1,\dots ,n$,;

–

Baseline Weibull parameters $({\theta }_0,{\kappa }_0)$ and Cox regression parameter ${\beta }_0$ obtained from the training data;

–

Maintenance cost parameters $(g,h_0,h,m)$;

–

Gearbox ages $\mathit{a}=(a_1,\dots ,a_n)$ at time s.

The key step of Algorithm 1, Step 2, is described in Section 3.3.

Step 4 requires clarification. If any of the gearboxes breaks down before the next planned PM, a CM replacement is performed alongside opportunistic replacements. The opportunistic replacement work is as follows: since the maintenance personal need to go there and perform CM on the broken component, they may as well maintain other gearboxes if they are close to breaking down to save the logistic cost. So, for each other component, we compare the virtual maintenance cost and the PM cost: if the virtual maintenance cost is higher, it means that the gearbox is too old and it is beneficial to perform PM on the corresponding gearbox (for more details, see Section 7 in Yu et al. [19]). After each replacement (either PM or CM), one has to update the vector of ages and the starting time s accordingly and then repeat the key step of the algorithm.    

Algorithm 1: Optimal scheduling algorithm

Input: $s,T,g,h_0,h,m,{\kappa }_0,{\beta }_0,{\theta }_0,a_1,\dots ,a_n$ Step 1: for $j=1:n$               if $a_j\le 2$ then                 Set ${\theta }_j:={\theta }_0$               else                 Collect the last three months of condition monitoring data                 and compute ${\theta }_j$ based on $(x_j(s-2),x_j(s-1),x_j\left(s\right))$               end if           end for Step 2: Apply the key optimization step, see Section 3.3, with            Output $t^{*},\mathcal{P}\subset \{1,\dots ,n\}$ Step 3: Suppose after time s, the first failure would be at time $t^{\prime }$           if $t^{\prime }\le min\{t^{*},s+3\}$ then              Put $t^{*}:=t^{\prime }$              Go to Step 4           else              Go to Step 5           end if Step 4: Apply opportunistic maintenance step at time $t^{*}$ with          Output $\mathcal{P}\subset \{1,\dots ,n\}$          Go to Step 6 Step 5: if $t^{*}\le s+3$             Go to Step 6          else             Update $a_j:=a_j+3,j\in \{1,\dots ,n\}$; $s:=s+3$             Go back to Step 1          end if Step 6: The gearboxes with labels in $\mathcal{P}$ are replaced by new ones          Update $a_j:=0,j\in \mathcal{P}$; $a_j:=a_j+t^{*}-s,j\notin \mathcal{P}$; $s:=t^{*}$          Go back to Step 1

4. Simulated Case Study

This section presents a simulation study in which our model is applied to a wind farm consisting of 50 wind turbines. The basic values of the model parameters are listed in

Table 1. Base values for the gearbox.

Component	${\mathit{g}}_0$, CM Replacement Cost (USD $1000)$	h, PM Replacement Cost (USD $1000)$	m, Value Loss per Month (USD $1000)$	Weibull Shape ${\mathit{\kappa }}_0$	Weibull Scale ${\mathit{\theta }}_0$
Gearbox	202	46.75	0.4	3	1.95 × 10${}^{-6}$

, and the suggested values of $(g_0,h,{\kappa }_0,{\theta }_0)$ are taken from the paper by Tian et al. [20].

The cost unit is USD 1000, and the time unit is one month. Following the approach in Lisa et al. [21], we assume a wind turbine lifetime of 20 years, corresponding to $T=240$. Other basic values of the model are

$$g=g_0+20,h_0=10,{\beta }_0=0.2.$$

(27)

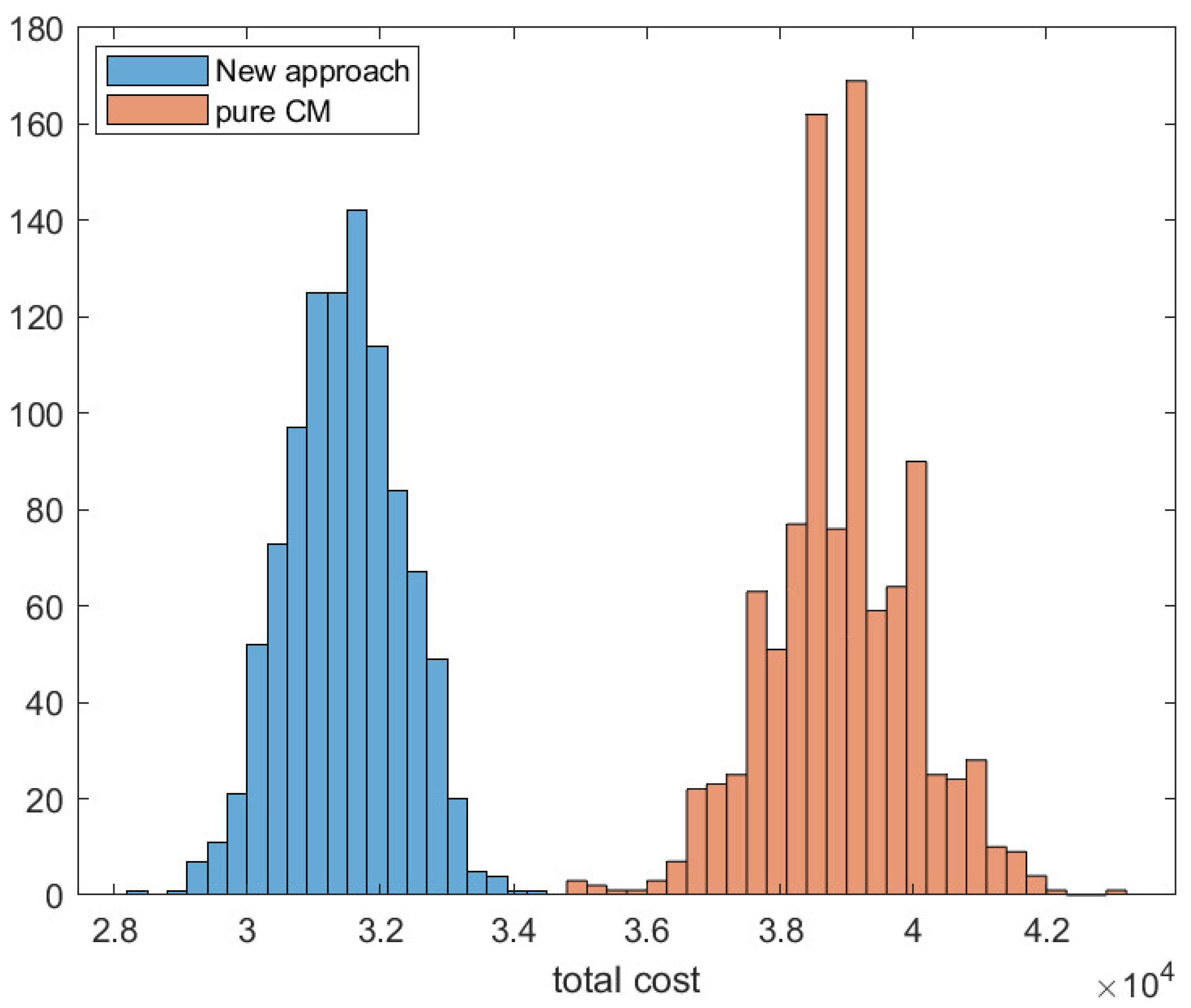
The simulation of $x\left(t\right)$ and the failure time is performed using Matlab R2022b. The simulated data can be accessed at https://github.com/QuanjiangYu/Optimal-preventive-maintenance-scheduling-for-wind-turbines-under-condition-monitoring (accessed on 20 November 2023). Based on 1000 simulations, the results shown in Figure 1 indicate that the average maintenance cost for 50 wind turbines during their lifetime is USD 38,921 when using the pure CM strategy. However, when our algorithm, the average maintenance cost is USD 31,460, representing a $23.71\%$ reduction compared to the pure CM strategy. Below is a histogram that illustrates the difference between the costs of the pure CM strategy and the costs of our approach.

This simulated case study effectively demonstrates the effectiveness of the method. Subsequently, we proceed to apply our approach to an actual wind farm.

5. Swedish Data Set on 20 Farms

The case study is based on data collected in November 2020 on 20 wind power farms located in Sweden (see

Table 2. Summary of the data on 20 farms: the 2nd column gives the number of wind turbines constituting each farm, and the 3rd column gives the number of gearbox failures during the number of months mentioned in the 4th column. The 5th column says whether a farm has temperature sensor data in SCADA or not.

Farm ID	# Turbines	# Failures	Time in Use (Month)	SCADA
1	5	0	126	yes
2	5	2	143	yes
3	6	1	124	yes
4	8	8	146	yes
5	8	10	140	yes
6	9	0	72	yes
7	11	0	72	yes
8	13	0	72	yes
9	16	8	137	yes
10	1	0	101	no
11	3	0	113	no
12	5	0	114	no
13	5	5	168	no
14	6	0	150	no
15	9	0	94	no
16	10	1	79	no
17	10	0	115	no
18	12	7	144	no
19	12	0	91	no
20	32	4	95	no

). The wind farms are located in the southern and middle parts of Sweden and were erected from 2006 to 2014 (one from 2006, three from 2008, three from 2009, two from 2010, three from 2011, one from 2012, three from 2013, and four from 2014). Column 1 sets labels to the farms, column 2 gives the number of turbines in each farm, column 3 gives the observed number of gearbox failures for the respective farm, column 4 says during how many months the farm was observed, and, finally, column 5 specifies whether the farm has temperature sensor data in SCADA or not. For example, the data for wind farm 9 that has 16 turbines are available for 137 months, and during this period of time, the wind farm experienced eight gearbox failures. A detailed case study on the data from wind farm 9 is presented in Section 6.

The total number of turbines is 186. The total number of gearboxes in this data set is 232, with 46 gearboxes that have failed and 186 gearboxes that still are in use. There are five wind turbines that have experienced gearbox break down twice. Using the method described in Section 2.1, one arrives to the following baseline parameter values:

$${\theta }_0=8.386\times {10}^{-4},{\kappa }_0=1.217,$$

(28)

corresponding to the mean life length for a gearbox of 316 months or 26 years. This estimate is in contrast to the reliability analysis results presented in the literature reporting much shorter life lengths for the gearboxes. However, the result is not surprising given that the data set consists only of onshore and relatively new wind turbines. Over the years, lot of progress has been made in the design of wind turbine gearboxes which has lead to fewer failures in more stable conditions. Furthermore, it must be noted that certain wind farms in the study have had an unusually high number of gearbox failures, such as wind farms 5 and 9. The estimated life expectancy for gearboxes in these wind farms is much shorter than 316 months. The maintenance optimization method presented here is beneficial when the life expectancy of the gearboxes is much shorter than the planned life of the wind turbines. Hence, in order to demonstrate the applicability of the method, the case studies are based on the following Weibull parameter values, presented in Tian et al. [20]:

$${\theta }_0=1.95\times {10}^{-6},{\kappa }_0=3.$$

(29)

With these baseline Weibull parameters, the mean life length for a gearbox becomes 71 months.

According to Table 2, among the gearboxes for which the SCADA condition monitoring data are available, 29 have experienced a failure. Out of these 29 gearboxes, 4 belonged to wind farm 4, which has been connected to SCADA since month 52 of its exploitation time. Furthermore, two of the failure times did not satisfy the requirement of 15 months monitoring data available. This leaves us with 23 gearboxes to which our approach can be applied.

Table 3. The data on 23 SCADA-connected gearboxes that went down during the time of observation. Column 2 specifies at which farm the failure was observed. Column 3 gives the life length of the gearbox. Column 4 gives the gearbox-specific Cox factor at the time of failure. Column 5 gives the Cox factors averaged across 55 non-failed gearboxes at the matching ages.

k	Farm ID	Failure Time ${\mathit{a}}_{\mathit{k}}$	Cox Factor ${\mathit{\varphi }}_{\mathit{k}}$	$\mathit{\varphi }\left({\mathit{a}}_{\mathit{k}}\right)$
1	4	21	2.60	$0.97\pm 0.12$
2	4	25	2.72	$1.16\pm 0.11$
3	4	25	3.47	$1.16\pm 0.11$
4	9	25	3.61	$1.16\pm 0.11$
5	4	37	3.85	$0.96\pm 0.14$
6	5	37	1.40	$0.96\pm 0.14$
7	9	43	1.67	$0.98\pm 0.10$
8	2	52	1.20	$1.15\pm 0.08$
9	5	61	2.12	$0.91\pm 0.11$
10	5	61	2.06	$0.91\pm 0.11$
11	5	66	1.26	$1.25\pm 0.16$
12	4	73	0.91	$1.07\pm 0.25$
13	9	73	1.42	$1.07\pm 0.25$
14	9	73	1.33	$1.07\pm 0.25$
15	5	80	1.80	$0.99\pm 0.19$
16	2	97	2.04	$1.01\pm 0.29$
17	4	97	0.97	$1.01\pm 0.29$
18	9	97	1.04	$1.01\pm 0.29$
19	9	109	1.28	$1.09\pm 0.30$
20	3	116	1.56	$1.03\pm 0.32$
21	9	121	1.71	$1.06\pm 0.31$
22	9	121	1.23	$1.06\pm 0.31$
23	5	133	0.93	$1.10\pm 0.39$

focuses on 23 gearboxes whose failure times are given in column 3 and for which the SCADA monitoring data are available. Implementing the approach of Section 2.1 based on (29), we applied the steepest descent algorithm and obtained

$${\beta }_0=0.203.$$

(30)

Column 4 of Table 3 gives the Cox factors ${\varphi }_k={\varphi }_k\left(a_k\right)$ obtained using (12) with $j=k$ and $t=a_k$, at the time prior to the failure of the gearbox in question. An immediate observation is that 19 out of 22 values for ${\varphi }_k$ are higher than the critical value 1, an indication of the increased risk of failure (conditioned on the current age). However, these results are very sensitive to the estimate ${\beta }_0$. It is more relevant to compare the Cox factor of the failed gearbox to the gearboxes that were still functioning at the age given in column 3 (see column 5, containing 95% confidence intervals) For the majority of gearboxes in use, the Cox factor $\varphi \left(a_k\right)<{\varphi }_k$ is estimated to be smaller.

6. Wind Farm 9: Test Study Using Historical Data

Here, we use the historical data available for wind farm 9 to see if our approach, based on estimates (29) and (30), is able to avoid the failure events by placing PM activities at the right times and for the right gearboxes. Recall that wind farm 9 consists of 16 wind turbines, with 8 of them having experienced failures at ages given in

Table 4. Gearbox failure times in wind farm 9.

Gearbox ID index k	4	7	13	14	18	19	21	22
Failure time (months)	25	43	73	73	97	109	121	121

below.

Observe that two pairs of equal failure times indicate violations of the model assumption of independence between the gearbox lifetimes. Our guess is that for each of the paired events, one of the gearboxes might have broken down earlier and the turbine stayed idle until the second gearbox went down, so that both gearboxes were replaced simultaneously.

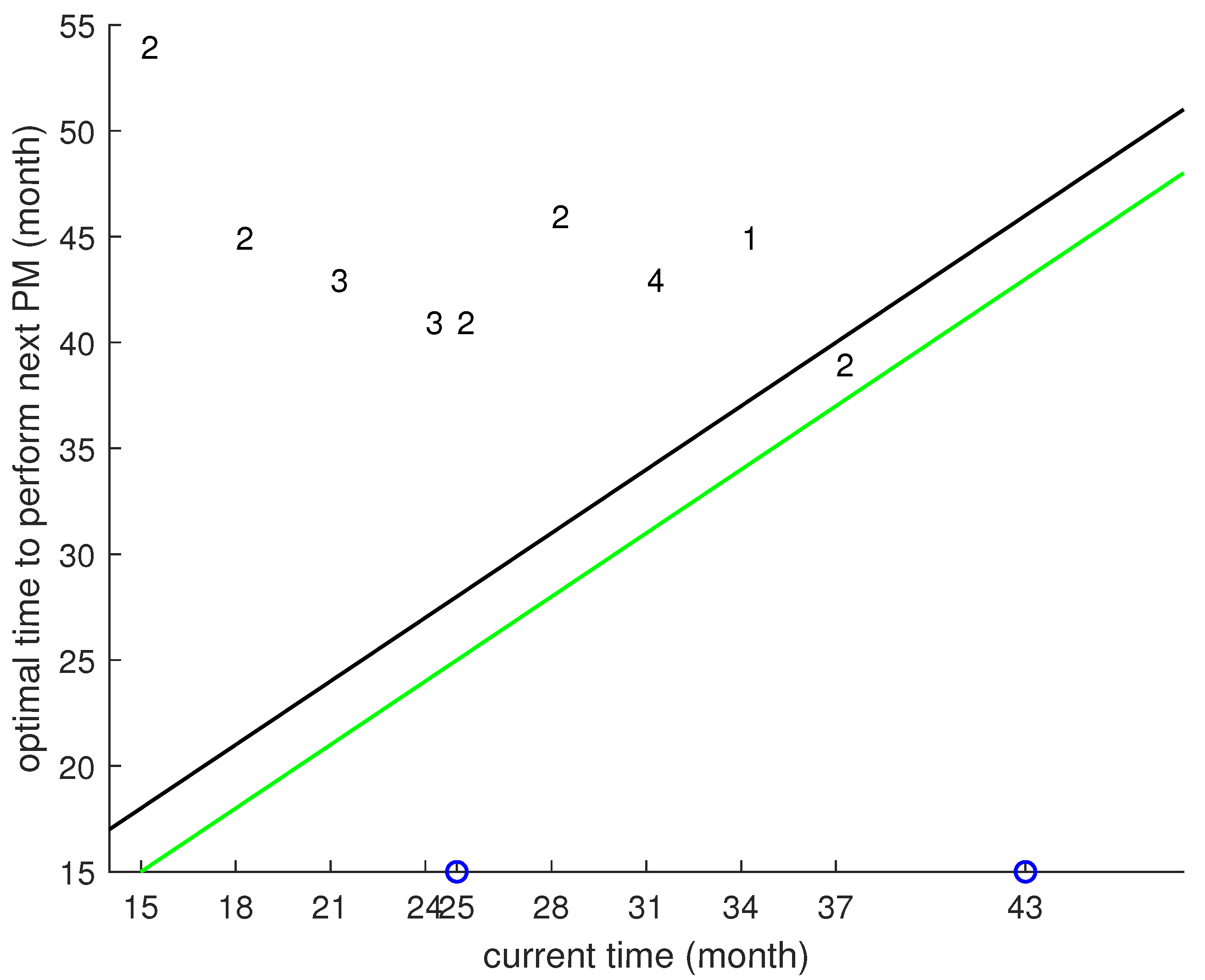
The results of our study based on the historical data for wind farm 9 are summarized in Figure 2. It shows the recurrent 3-month updates of the PM planning, so that if the next PM activity is planned later than in the next 3 month time period, it will not be performed. After 3 months, we update the data from the CMS and resolve the optimal problem again to obtain a new maintenance plan. The green line represents the observation time and the black line represents the planning horizon three months ahead. Each planning round giving the next time for PM as a point lying above the black diagonal will be followed by a new planning round with an updated time for the next PM. The next PM plan will be implemented only if the next PM point lies between the two diagonals on the graph.

As shown on the x-coordinate, the first PM schedule was produced at time step 15. The resulting optimal planning time at month 54 is shown on the y-coordinate. The corresponding point $(15,54)$ is marked on the graph by label 2, showing that 2 gearboxes out of 16 should be replaced at time 54. Since point $(15,54)$ lies above the black diagonal, we apply our algorithm once again at time step $15+3=18$ and find the new PM time to be at month 45 when gearboxes should be replaced. At time step 21, an updated PM plan says that three gearboxes should be replaced at month 43 and so on.

The most interesting points on the graph are time steps 25 and 37. At time step 24, the optimal PM plan was to replace gearbox 4 at month 41 together with two other gearboxes. What happened next, according to the historical data, is that gearbox 4 broke down at time step 25. Since we need to perform CM on gearbox 4, we apply opportunistic maintenance. We found out that for all other gearboxes the virtual maintenance cost for each gearbox is lower than the corresponding PM cost. Thus, the optimal plan at month 25 before the replacement is to only perform CM at gearbox 4. After the CM, we resolve the optimal model with update data of gearbox 4, i.e., age 0 and baseline Weibull parameters. The optimal plan is to replace two gearboxes at month 41.

At time step 37, the next PM time falls within the three-month window. It means that two gearboxes should be replaced in a planned manner at month 39. From the historical data, we see that gearbox 7, which has failure time 43 in the data, is closest to this PM time and is among the PM-replaced gearboxes.

In this case study, we used the following parameter values for the various maintenance costs. We normalized the data and used a virtual monetary unit:

$$g=1+d_t,m=0.008,h_0=0.13,h=0.294+d_t/6,$$

(31)

where the downtime cost $d_t$ depends on the month of the replacement:

The monthly downtime cost in

Table 5. Monthly downtime cost.

Month	Jan	Feb	Mar	Apr	May	Jun
$d_t$	0.075	0.044	0.067	0.053	0.059	0.069
Month	Jul	Aug	Sep	Oct	Nov	Dec
$d_t$	0.046	0.070	0.085	0.066	0.066	0.057

is calculated from monthly productions multiplied with the monthly selling price and averaged over three years. The production for each month comes from data from the eight turbines in wind farm 9 that have not replaced gearboxes yet and is from 2017 to 2019. The monthly selling price is a combination of monthly electricity spot prices from Nord Pool and monthly prices for the green certificates from Svensk Kraftmäkling for the same three years.

In February (September), the monthly downtime cost is the lowest (highest); this is due to the fact that the wind farm had a lot of problems with icing, which in turn means that the production during the winter season was not as high as predicted from the average wind speeds.

The CM cost is

$$g=c_g+c_m+d_t$$

(32)

where $c_g$ is the cost for a new gearbox (0.64) and $c_m$ is the maintenance cost. The maintenance cost is divided into four parts: the transport cost for the crane (0.04), the set-up cost for the crane (0.09), the working cost for the crane (0.16) and the manpower cost for replacing a gearbox (0.07). The sum of $c_g$ and $c_m$ is 1 virtual monetary unit. The different costs come from three different wind power operators, and the presented costs are averaged and normalized values from their data.

The shared maintenance cost for PM, $h_0$, consists of two parts of the maintenance cost, the transport cost for the crane (0.04) and the set-up cost for the crane (0.09), bringing it to a total of 0.13 virtual monetary units.

According to specification (31), h consists of the other two parts of the maintenance cost, the working cost for the crane (0.16) and the manpower cost for replacing a gearbox (0.07), as well as the initial loss of value of the gearbox (0.064) and the downtime cost for PM. The total is 0.294 plus the downtime cost. The initial loss of value of the gearbox is set to 10% of the value of a new gearbox.

The monthly value loss m is set to approximately 0.008 and is defined as the gearbox cost (0.64) minus the initial value loss (0.064) divided by the expected lifetime of the gearbox (71 months [20]) in virtual monetary units:

$$m=\frac{0.64-0.064}{71}\approx 0.008.$$

(33)

We assume an equal depreciation of the value of the gearbox per year during its lifetime.

Notice that the PM downtime cost is 6 times smaller than that of the CM counterpart, since a PM activity goes 6 times faster.

7. Discussion

Our study provides valuable insights into the optimization of preventive maintenance scheduling for wind turbines under condition monitoring. By utilizing Cox proportional hazards analysis, we have developed an optimal maintenance strategy that takes into consideration the critical component ages, maintenance costs, energy production losses, and condition monitoring data. The following points summarize the key findings of this research.

Our study demonstrates the effectiveness of Cox proportional hazards analysis in developing an optimal preventive maintenance plan for wind turbines. By considering the hazard rates of different components, we were able to identify the optimal timing of maintenance actions, minimizing the downtime and maximizing the operational efficiency of wind farms.

The integration of condition monitoring data into the maintenance scheduling process proved to be crucial. The continuous access to the status of wind turbine components enabled us to proactively identify potential issues and to plan maintenance actions accordingly, reducing the risk of unexpected failures and optimizing maintenance resources allocation.

Our findings emphasize the significance of preventive maintenance in wind turbine operations. By implementing a proactive maintenance strategy, wind farm operators can avoid costly unplanned downtime and minimize energy production losses. The optimized maintenance scheduling approach presented in this study provides a systematic framework for achieving these benefits while considering the specific characteristics and conditions of wind turbines.

Although our study focused on a specific case study involving wind farms in Sweden, the developed preventive maintenance scheduling strategy can be adapted and applied to other wind turbine installations worldwide. The proposed approach considers key factors that are commonly encountered in wind turbine maintenance, making it a valuable tool for wind farm operators seeking to optimize their maintenance plans.

It is important to acknowledge the limitations of our study. The case study used in this research was based on data collected from multiple wind farms in Sweden, and, therefore, the results may be influenced by specific operational and environmental conditions. Future research should aim to validate the proposed approach using additional data sets and diverse geographical locations to enhance the generalizability of the findings. Furthermore, the integration of advanced machine learning techniques and predictive analytics into the maintenance optimization process represents a promising avenue for future research.

8. Conclusions

In this paper, we adapted the optimization model of Yu et al. [19] developed for a single wind turbine with n components to a setting with n wind turbines constituting a wind farm. Then, the model was enhanced by adding a parameter updating step, allowing our maintenance scheduling optimization algorithm to take into account the real-time data from the CMS. This parameter updating step is based on the Cox proportional hazards method.

The integration of real-time data from the SCADA system enables a condition-based maintenance approach, which capitalizes on the continuous monitoring of key indicators to inform maintenance actions based on specific condition thresholds. This approach maximizes asset utilization and minimizes downtime by addressing maintenance needs as they arise. However, we must recognize the ongoing value of preventive maintenance in ensuring the long-term reliability and performance of wind turbines. Time-scheduled interventions, accounting for component aging characteristics and the advantages of proactive maintenance, offer additional safeguards against unforeseen failures.

Our study underscores the importance of both preventive and condition-based maintenance strategies in wind turbine operations. While the availability of SCADA data may favor a condition-based approach, the integration of preventive maintenance enhances the overall maintenance optimization process. Thus, the approach of this paper combines the benefits of these two methods, ensuring a comprehensive and effective maintenance strategy.

Using the suggested approach, we studied the recent historical data from several wind farms located in Sweden. A more careful analysis was performed using the data from one of these farms. Our analysis showed that the success of the scheduling using our model depends to a high extent on the baseline values of the Weibull parameters. One of the clear conclusions of our analysis is that PM planning gives some effect only if the wind turbine components in question live significantly shorter than the turbine itself. Provided the component’s lifetime is notably shorter than the turbine’s lifetime, our approach may result in appreciable savings due to the smart scheduling of PM activities by monitoring the ages of the components in use as well as using available real-time data supervising the condition of the wind turbines in a wind farm.